Short abstract
Rupture risk assessment of abdominal aortic aneurysms (AAA) by means of biomechanical analysis is a viable alternative to the traditional clinical practice of using a critical diameter for recommending elective repair. However, an accurate prediction of biomechanical parameters, such as mechanical stress, strain, and shear stress, is possible if the AAA models and boundary conditions are truly patient specific. In this work, we present a complete fluid-structure interaction (FSI) framework for patient-specific AAA passive mechanics assessment that utilizes individualized inflow and outflow boundary conditions. The purpose of the study is two-fold: (1) to develop a novel semiautomated methodology that derives velocity components from phase-contrast magnetic resonance images (PC-MRI) in the infrarenal aorta and successfully apply it as an inflow boundary condition for a patient-specific fully coupled FSI analysis and (2) to apply a one-way–coupled FSI analysis and test its efficiency compared to transient computational solid stress and fully coupled FSI analyses for the estimation of AAA biomechanical parameters. For a fully coupled FSI simulation, our results indicate that an inlet velocity profile modeled with three patient-specific velocity components and a velocity profile modeled with only the axial velocity component yield nearly identical maximum principal stress (σ1), maximum principal strain (ε1), and wall shear stress (WSS) distributions. An inlet Womersley velocity profile leads to a 5% difference in peak σ1, 3% in peak ε1, and 14% in peak WSS compared to the three-component inlet velocity profile in the fully coupled FSI analysis. The peak wall stress and strain were found to be in phase with the systolic inlet flow rate, therefore indicating the necessity to capture the patient-specific hemodynamics by means of FSI modeling. The proposed one-way–coupled FSI approach showed potential for reasonably accurate biomechanical assessment with less computational effort, leading to differences in peak σ1, ε1, and WSS of 14%, 4%, and 18%, respectively, compared to the axial component inlet velocity profile in the fully coupled FSI analysis. The transient computational solid stress approach yielded significantly higher differences in these parameters and is not recommended for accurate assessment of AAA wall passive mechanics. This work demonstrates the influence of the flow dynamics resulting from patient-specific inflow boundary conditions on AAA biomechanical assessment and describes methods to evaluate it through fully coupled and one-way–coupled fluid-structure interaction analysis.
Keywords: aneurysm, fluid flow, wall mechanics, magnetic resonance imaging, finite element modeling, rupture risk
1. Introduction
1.1. Background and Significance
1.1.1. AAA Disease and Current Patient Management Protocols.
Abdominal aortic aneurysm (AAA) is a focal dilation of the abdominal aorta by 50% or more, preferentially developed between the renal arteries and the iliac bifurcation. It is a common vascular disease affecting 8.9% of the population above the age of 65 [1]. In the US alone, AAA rupture is the cause of more than 15,000 deaths annually [2] and is the tenth leading cause of death in men over the age of 50 [3]. It is most prevalent among Caucasian men [4]. As this disease is asymptomatic, the patient does not exhibit symptoms unless the aneurysm ruptures or there is an impending rupture. AAAs are typically diagnosed by opportunistic detection through routine medical imaging done for an alternate purpose. Once the AAA is detected, the surgeon will decide to manage it either by watchful surveillance or by surgical intervention in the form of open surgery or endovascular repair, based upon estimates of the rupture risk compared to the risk of mortality or morbidity due to surgery and the patient's life expectancy. According to current practice, if the maximum diameter of the AAA exceeds 5–6 cm [5] or its growth rate is more than 1 cm/year, the rupture risk is considered high and the patient is usually recommended for repair. However, this protocol may lead to unnecessary surgical intervention of large but stable AAAs. On the other hand, smaller AAAs with a high risk of rupture may be left untreated, the overall mortality of these being as high as 50% [6,7].
1.1.2. Alternative Protocols for Estimation of AAA Rupture Risk Using Patient-Specific Geometries.
As it is evident that the arterial wall will rupture when its stress exceeds the failure strength of the tissue, a criterion for assessing rupture risk that includes biomechanical factors, such as wall stress and strength, may be a more reliable alternative to predict rupture on a patient-specific basis. Mathematical and computational models are used to predict these biomechanical factors in aneurismal aortas [8]. As techniques for creating computational 3D AAA models from clinical imaging modalities, such as computed tomography (CT) and magnetic resonance imaging (MRI), have emerged [9], computational prediction of wall stress in patient-specific AAA models has become possible. Fillinger et al. [10,11] pioneered such studies and successfully demonstrated that the maximum wall stress was 12% more accurate and 13% more sensitive in predicting AAA rupture than the maximum diameter alone. In these studies, the AAA models were subject to uniform peak systole blood pressure on the intraluminal surface. Other early computational studies identified several morphological features that affect the wall stress, such as asymmetry [12], tortuosity [13], wall thickness [14,15], and the presence of thrombus [16]. However, for the biomechanical prediction of AAA rupture to have translational potential in a clinical setting, an assessment of the accuracy of wall mechanics calculations is warranted. The accuracy of the computed AAA wall stress depends on several factors, such as the modeling protocol to obtain the AAA geometry from clinical images, the characterization of nonuniform wall thickness [14,15,17], the geometry of the thrombus [18], the constitutive material model for the AAA wall and intraluminal thrombus (ILT) [19], the boundary conditions used, and the inclusion of blood flow, among others.
1.1.3. Choice of Computational Approach.
The most popular computational approach used to estimate AAA peak wall stress (PWS) is the “computational solid stress – static analysis” (CSSs) technique, where a spatially uniform and temporally constant peak systolic pressure is applied to the inner surface of the solid domain (either wall only or wall and thrombus [9,11]). An augmentation of this approach is the “computational solid stress – transient analysis” (CSSt), where a time-varying but spatially uniform pressure load is used instead of a steady state load [17,20]. However, the physiologic intraluminal pressure is spatially nonuniform, due to the asymmetry and tortuosity of patient-specific AAAs, which can significantly affect the wall stress distribution. Furthermore, these techniques disregard the effect of hemodynamics and interaction between the pulsatile blood flow and the compliant arterial wall. To this end, fluid-structure interaction (FSI) modeling is essential to accurately estimating the wall mechanics, including wave propagation and reflections. Therefore, we believe that accurate prediction of PWS is possible only if the individual flow dynamics are also modeled through an FSI analysis. Di Martino et al. [18] presented the first fully coupled FSI framework for realistic modeling of patient-specific AAAs. Thereafter, continual investigation with CSSs, CSSt, and fully coupled FSI (FSIf) techniques with idealized AAA geometry and linear and nonlinear material models revealed that, compared to FSIf, CSSs and CSSt techniques underestimate the PWS on average by 20%–30% for variable wall thickness and 10% for uniform wall thickness [17,20,21]. As FSIf carries a high computational cost, new methods for partially coupled FSI (FSI1) analysis were tested for accuracy and efficiency. In a study with three patient-specific AAA geometries, Scotti and Finol [20] used a FSI1 analysis to find differences up to 6.5% in wall stress compared to FSIf. In the same study, CSSs was found to underestimate the PWS by 3%–25% compared to FSIf. Further studies by Papaharilaou et al. [22] and Wolters et al. [23] justified the use of FSI1 on patient-specific AAA models.
1.1.4. Effect of Boundary Conditions.
The computational modeling techniques depend strongly on the boundary conditions applied to the solid and fluid domains of the model. Scotti et al. [21] studied the effects of fixed inlet and outlet, axial stretch, external pressure, and spinal contact on the wall mechanics. Di Martino et al. [18] applied a time-dependent inlet plug velocity profile based on color Doppler measurements of average aortic blood flow velocity and a time-dependent, spatially uniform pressure relative to a diastolic pressure of 80 mmHg at the outlet boundary. Papaharilaou et al. [22] derived flow rates from Doppler ultrasound imaging of AAA patients, from which they applied an inlet Womersley velocity profile and a flow split ratio at the bifurcated outlets. Bluestein et al. [24] applied a uniform inlet steady plug velocity of 0.4 m/s, representing typical physiologic peak flow conditions, and a flow-induced pressure distribution superimposed on a uniform systolic pressure of 120 mmHg at the outlet. Wolters et al. [23], Leung et al. [25], Rissland et al. [26] and Xenos et al. [27] applied a generalized inlet plug velocity profile and outlet pressure, following data reported by Olufsen et al. [28,29]. This inlet plug velocity profile was obtained from MRI flow measurements in the ascending aorta of an AAA patient. The outflow pressures in the common iliac arteries were calculated using impedance-based, structured tree model for the smaller arteries to effectively capture the wave propagation effect of the downstream vasculature. While there is extensive research on coupled multidomain outflow boundary conditions that elucidate the explicit relationship between pressure and flow rate and its effect on the hemodynamics [30], literature on patient-specific inflow boundary conditions is scarce. To this end, studies by Kose et al. [31], Kim et al. [32], and Tan et al. [33] demonstrated the use of PC-MRI–derived inlet velocity, corresponding to the patient-specific arterial geometry in rigid-wall fluid flow analyses.
1.2. Hypothesis and Objectives.
We hypothesize that an FSI framework with patient-specific inflow velocity components derived from PC-MRI data will provide improved accuracy of the AAA wall mechanics calculations. In addition, we hypothesize that a one-way–coupled FSI approach with MRI-derived inflow velocity boundary condition will yield a reasonably accurate wall mechanics estimation with a lower computational cost than the fully coupled FSI approach. Therefore, the main objectives of this work are (1) to analyze the effect of four different inlet velocity boundary conditions (all derived from patient-specific PC-MR images) on the ensuing AAA biomechanical environment and (2) to study the efficiency and accuracy of a one-way–coupled FSI approach (FSI1) relative to a fully coupled FSI (FSIf) analysis and a transient computational solid stress analysis (CSSt).
2. Methods
2.1. AAA Geometry.
A patient-specific AAA model was developed for this study based on the CT images of an unruptured AAA from a 73-year-old male patient treated at Allegheny General Hospital (Pittsburgh, PA). The images were in Digital Imaging and Communications in Medicine (DICOM) format with the following imaging acquisition parameters: (i) image size 512 × 512 pixels, (ii) pixel size 0.8789 mm, (iii) pixel intensity 0–2000, and (iv) slice spacing 3.0 mm. This study was approved by the internal review boards of both Carnegie Mellon University and Allegheny General Hospital.
2.2. Segmentation, Reconstruction, and Meshing.
From the CT image dataset, a section of the aorta (14 cm long) that includes the aneurysm and the iliac bifurcation was segmented with the in-house semiautomatic vessel segmentation code VESSEG (Carnegie Mellon University, Pittsburgh, PA). VESSEG allows the user to reconstruct the multidomain AAA geometry with lumen, intraluminal thrombus, and AAA wall with variable wall thickness. With VESSEG, the lumen is detected automatically through an intensity threshold technique. The outer wall boundary can be detected either automatically or manually, and the inner wall boundary can be detected through training a neural network or by manual segmentation. Details of VESSEG's segmentation protocol are described by Martufi et al. [34] and Shum et al. [35]. An automatic meshing protocol developed in-house (Shum et al. [36] and Liu [37]) was used to mesh the lumen, thrombus, and wall domains with unstructured linear tetrahedral elements. For the AAA model used in this study, the lumen was meshed with 142,547 fluid elements, while the wall and ILT were meshed with 164,702 and 189,076 solid elements (353,778 total solid elements), respectively. A mesh sensitivity study was performed with fluid meshes ranging from 90,916 to 393,466 elements; the maximum velocity and maximum shear stress in the chosen mesh size yielded 1.8% and 4.4% relative errors, respectively, compared to the most refined fluid mesh. Likewise, a mesh sensitivity study was performed with structural meshes in the 177,071–539,639 element range. The effective stress, maximum principal stress, and maximum principal strain resulted in 6.5%, 17.1%, and 7.9% relative errors, respectively, compared to the most refined solid mesh. For flow stabilization at the outlet and numerical convergence benefits, both common iliac arteries were artificially extended by 3 cm in the longitudinal direction along the lumen centerline. The steps in the modeling process are illustrated in Fig. 1.
Fig. 1.
Steps in patient-specific AAA computational modeling: (a) CT images from AAA patient; (b) cross section processed with VESSEG showing segmentation of a CT image to identify lumen, ILT, and wall; (c) ADINA finite element models of lumen (fluid domain) and wall and thrombus (solid domain) and the surfaces and interfaces defined in each mesh. Iliac extensions shown are subject to a fully constrained boundary condition.
2.3. Finite Element Analysis.
We used the commercial multiphysics solver ADINA 8.6 (ADINA R&D Inc., Watertown, MA) for performing computational fluid dynamics (CFD), CSS, and FSI simulations with the AAA model. ADINA solves the mass and momentum conservation (Navier–Stokes) equations for the fluid domain and the equilibrium equations of elasticity for the solid domain using a finite element discretization method. It implements an arbitrary Lagrangian Eulerian (ALE) approach for updating the fluid mesh, necessary for FSI simulations where the fluid mesh conforms to the motion of the structure [38]. The fluid and solid domain meshes were independently converted into Nastran format files using an in-house code written in C language and then imported into ADINA for further analysis.
2.4. Constitutive Material Models.
Blood was modeled as a Newtonian fluid (a reasonable approximation given the rates of shear typically found in the human aorta [39]), with density ρf = 1.05 g/cm3 and dynamic viscosity μ = 0.035 Poise. Blood flow was assumed to be laminar and incompressible.
We have adopted the constitutive models for the AAA wall and ILT to be an isotropic, second order Mooney–Rivlin material model, for which strain energy function (SEF) is defined by Eqs. (1) and (2),
| (1) |
| (2) |
where C 1, C 3, C 2, and C 5 are constants and I 1 and I 2 are the first and second invariant of the left Cauchy–Green tensor. For the AAA wall constants, we used C 1 = 17.4 N/cm2 and C 3 = 188.1 N/cm2, which are the population averages obtained by Raghavan and Vorp [19]. For the ILT constants, we used population averages obtained by Vande Geest et al. [40], C 2 = 7.98 N/cm2, and C 5 = 8.71 N/cm2. For the FSI simulations, we assumed densities of the AAA wall and ILT to be 1.2 g/cm3 and 1.1 g/cm3, respectively.
2.5. Fluid Inflow Boundary Condition.
As discussed by Xenos et al. [27], the most consistent approach for studying patient-specific AAA disease progression should include inlet and outlet boundary conditions that are truly patient-specific. In this work, we present a novel semiautomated protocol that imposes patient-specific inlet velocity and outlet pressure boundary conditions. The time-dependent inlet velocity components were calculated by postprocessing the PC-MR images acquired from the AAA patient at 40 phases of the cardiac cycle. As one of the objectives of this work was to study the effect of different inlet boundary conditions on the AAA FSI analysis, we compared three different inlet velocity profiles in our FSI simulations: (1) Vxyz: velocity profile with all the three-velocity components measured by unenhanced PC-MRI immediately below the renal arteries; (2) Vz: velocity profile with only the longitudinal velocity component measured in (1); (3) Vwom: Womersley profile; and (4) Vplug: plug velocity profile calculated from the flow rate waveform derived from the PC-MRI segmentation in (1). Note that Vwom and Vplug have been used in previous studies by others, and we include them herein only for comparing them to Vxyz and Vz. Details on the derivation of the Womersley profile derivation are included in the Appendix. The protocol followed for velocity extraction and application as an inflow boundary condition is described as follows.
PC-MR images of the blood flow velocity field for the same 73-year-old male patient were acquired at Allegheny General Hospital (Pittsburgh, PA). The velocity field was recorded at three planes, where plane 1 corresponds to the inlet section below the renal arteries, plane 2 corresponds to the midsection of the AAA sac, and plane 3 corresponds to the outlets (2 cm below the iliac bifurcation), as shown in Fig. 2. The MR scan parameters are (i) image size 256 × 256 pixels, (ii) pixel size 1.4844 mm, (iii) 40 cardiac phases, (iv) heart rate 85 bpm, and (v) slice spacing 6 mm. A graphical user interface–based in-house code was written in matlab to extract the velocity profile and compute the flow rate waveform at any cross section from these MR images. The steps of this process are:
Fig. 2.
Derivation of patient-specific inlet velocity boundary conditions: (a) MR imaging at specified planes; (b) segmenting the lumen boundary and extracting velocity components from the lumen region of the MR image at the inlet plane; (c) extracting inlet nodal coordinates from the CFD model; (d) and (e) performing Schwarz–Christoffel (SC) mapping and interpolation to apply the MR-derived velocity as a boundary condition to the CFD inlet nodes
-
(1)
MRI dataset management: The raw MR image dataset is a stack of images (each 256 × 256 pixels) consisting of four intensity fields (Vx, Vy, Vz, and V mag) at each of 40 phases over one cardiac cycle. Our matlab code reads and extracts these image intensity data as matlab database files. During this process, the intensity at each pixel is multiplied by the encoding velocity constant (V enc) to convert to actual velocities in cm/s. The V enc value is part of the image-specific information set up before each imaging sequence.
-
(2)
Lumen segmentation: Manual segmentation was performed on the V mag image sets to extract the lumen boundary at each phase
-
(3)
Velocity extraction: The lumen boundary at each phase was applied to all other image sets to extract the three velocity components within the lumen
-
(4)
Mapping of the velocity onto the inlet mesh: As the aorta expands during systole and contracts during diastole, the segmented lumen boundary at the inlet changes from one phase to the next over the cardiac cycle. Conversely, the inlet cross section of the CT image-based CFD model of the AAA geometry is fixed during this period. Hence, the MRI-derived, time-varying inlet boundaries do not match the inlet boundary of the CFD model. Moreover, the raw velocity data of the MR images are recorded on a uniform Cartesian grid, while the nodes of the inlet mesh are not arranged on such a grid. Therefore, each of the velocity components extracted from the MR images needed to be mapped onto the fixed inlet mesh of the CFD model. We achieved this using the Schwarz–Christoffel (SC) mapping method, which is a conformal transformation that maps the upper half of a plane to the inside of a polygon. Using the SC mapping function in matlab [41], we developed a code to map the MR-derived lumen boundary onto a unit circle (mapping function f1 in Fig. 2) and the inlet boundary of the CFD mesh onto another unit circle (mapping function f2 in Fig. 2) at each of the 40 phases. Using a composite mapping function (mapping function f3 = f2 * inverse (f1) in Fig. 2), the grid points inside the lumen boundary of the MR image were then mapped onto the corresponding points inside the CFD lumen inlet. The velocities at these mapped MRI grid points were then interpolated onto the inlet mesh nodes. Finally, the interpolated velocity distribution was scaled such that the flow rate at the inlet of the CFD model matched the flow rate derived from the MR images at each phase. The steps in the inlet flow extraction process are illustrated in Fig. 2. The flow rate calculated for the 40 phases is shown in Fig. 4(b).
-
(5)
Comparison of inlet PC-MRI and boundary conditions: Figure 3(a) illustrates the MRI flow patterns at the AAA inlet at selected phases (i.e., phase 4 (early systole), phase 8 (peak systole), phase 10 (late systole), and phase 20 (early diastole)). The lumen and wall are identified manually in the MR images with a boundary contour. The anterior and posterior sides of the wall are indicated by A and P, respectively. The axial velocity profiles are presented in 2D and 3D to demonstrate the axial skewness of the patient-specific velocity profiles (FSIf-Vxyz) compared to the Womersley profile (FSIf-Vwom). Figure 3(b) shows the temporal distribution of the average velocity components (Vx, Vy, and Vz) calculated for each of the 40 phases in the cardiac cycle. These indicate that the peak axial velocity at phase 8 is approximately 28 cm/s, while the average in-plane velocities are in the range of ±10 cm/s.
Fig. 4.
Boundary conditions for computational modeling: (a) patient-specific AAA sac pressure obtained by scaling a human AAA sac pressure waveform (“typical”, from Ref. [42]) with this patient's systole/diastole cuff pressure (144/90 mmHg); (b) patient-specific flow rate derived from MR images at the inlet of the AAA model and patient-specific AAA pressure waveform (“smoothed” curve in (a)), both applied as boundary conditions for the FSI analysis
Fig. 3.
(a) MRI flow patterns at the AAA inlet at selected phases (i.e., phase 4 (early systole), phase 8 (peak systole), phase 10 (late systole), and phase 20 (early diastole)). 2D and 3D axial velocity profiles at the inlet of the FSI models representing the patient-specific inlet velocity profile (FSIf-Vxyz) and the Womersley velocity profile (FSIf-Vwom). The labels A and P denote anterior and posterior wall orientation of the artery. (b) Temporal distribution of average velocity components at inlet for the 40 phases.
2.6. Fluid Outflow Boundary Condition.
Van't Veer et al. [42] studied the correlation between noninvasive brachial cuff blood pressure measurements and invasive pressure measurements inside the aneurysm sac using a pigtail catheter on ten AAA patients. The brachial cuff measurements demonstrated an underestimation of 5% for peak systolic and an overestimation of 12% for diastolic pressure compared to the intraluminal pressure in the aneurysm. Using this information and the typical pressure waveform P ref (t) [42] within the aneurysm, we developed a protocol for obtaining patient-specific pressure outlet boundary conditions. The brachial cuff pressure measurements of our AAA subject were 144 mmHg for systole and 90 mmHg for diastole. Following the observations by Van't Veer et al. [42], the AAA intraluminal pressures were calculated as 152.58 mmHg for peak systole and 80.35 mmHg for late diastole. P ref (t) was subsequently scaled to match these systolic and diastolic pressures. To facilitate numerical convergence, we low-pass–filtered the pressure waveform to generate a smooth, patient-specific waveform prior to scaling, as shown in Fig. 4(a). This time-varying pressure was used as the outlet boundary condition at both common iliac outlets: and . The advantage of this protocol is that it incorporates patient specificity in the prescribed outlet pressures using the noninvasive, easily measured cuff pressure. Although more accurate patient-specific intraluminal pressure may be obtained by direct measurement (i.e., by introducing a catheter inside the AAA), in practice, vascular surgeons prefer not to perform this invasive procedure during AAA repair.
2.7. Solid Boundary Conditions.
At the inlet and outlet cross sections ( and ), as shown in Fig. 1, all the degrees of freedom for each solid domain node were set to zero. The nodes on the outer wall surface were prescribed to be traction-free. The combined wall-lumen and ILT-lumen interfaces were designated as the FSI interfaces. A rigid constraint was assumed at the ILT-wall interface (all relative degrees of freedom set to zero). The nodes on the outer surface of the outlet iliac extensions were also kept fixed.
2.8. FSI Methodology.
A fully coupled FSI (FSIf) analysis was carried out with the ADINA-FSI solver. Flow condition-based interpolation (FCBI) elements were used with the sparse solver to solve for the solid- and fluid-coupled governing equations. An initial stress loading was achieved by applying a constant 80 mmHg pressure at the inlet nodes and zero traction at the outlets for one cardiac cycle (0.70588 s). Two consecutive load cycles with time-varying inlet flow and outlet pressure waveform were applied subsequently until achieving a cycle-independent solution. Results from the last load cycle were considered for final postprocessing.
A loosely coupled FSI analysis (i.e., a one-way–coupled FSI (FSI1)) was conducted based on the benefits of decreased computational time and potentially reasonable accuracy when compared to FSIf. The method was originally proposed and tested by Scotti and Finol [20], but in this work, we implement it to model the FSI1 with patient-specific inlet and outlet boundary conditions. A comparison with a computational solid stress analysis with transient uniform pressure (CSSt) on the lumen surface is also presented. The FSI1 approach is a two-step process: (i) a transient computational fluid dynamics (CFDt) analysis is performed with patient-specific boundary conditions for four load cycles to achieve cycle-independent results and (ii) nodal reaction forces at the lumen surface from the last load cycle of CFDt are extracted and applied onto the nodes of the lumen surfaces, and , in the solid domain as force loads. CSSt with a nonuniform load on the lumen surface is then performed for three load cycles to obtain the final results.
Spatial maxima and averages of maximum principal stress (σ 1) and strain (ε 1) obtained from the aforementioned numerical approaches were compared for evaluating their performances. All simulations were performed on a Dell T7500 workstation; we used 12 processor cores and 24 GB of RAM for each of the FSI simulations.
3. Results
3.1. Baseline Simulation FSIf-Vxyz.
We have chosen our baseline to be the fully coupled FSI simulation with the three PC-MRI–derived fluid velocity components (FSIf-Vxyz) prescribed at the inlet. Evidently, FSIf-Vxyz is the most physiologically realistic of our computational models, albeit the most complex and computationally expensive.
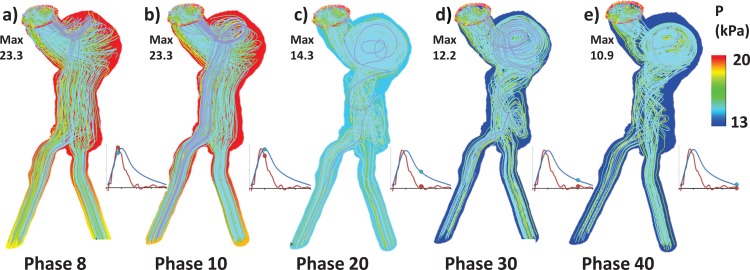
Figures 5(a)–5(e) depicts the flow field within the lumen at phases 8, 10, 20, 30, and 40. The direction of the flow is represented by streamlines, while colored lumen illustrates the pressure (P) distribution on the lumen surface. As expected, during peak systole (phases 8 and 10), the flow through the lumen is jet-like (with high-velocity magnitude), which follows the curvature of the geometry, whereas the flow velocity reduces and several vortices form inside the AAA sac during the transitional and diastole phases (20, 30, and 40). The flow through the sac is helical in nature, due to asymmetry and tortuosity of the geometry. Figures 6(a)–6(e) represent the flow-induced maximum wall shear stress (WSS) distributions on the lumen surface. Due to the asymmetry and tortuosity of the AAA model, the shear stress distribution is spatially nonuniform throughout, although this nonuniformity is most notorious during systole where large velocity gradients exist. High shear stresses are observed near the inlet and in the common iliac arteries during systole, since the smaller cross sections combined with the high flow rates lead to large viscous forces at the wall. The spatial maximum of WSS is found at the iliac bifurcation. However, shear stress contributes to only a small portion of the total stress, and hence, this finding is not deemed important for rupture risk prediction. Figures 7(a)–7(e) and 8(a)–8(e) represent, respectively, the maximum principal stress (σ1) and maximum principal strain (ε1). The location of the peak σ1 for each phase was consistently found to be at the neck-to-sac transition of the AAA wall, where intraluminal thrombus (ILT) is absent. The location of the peak ε1 was consistently found on the posterior AAA wall near the ILT AAA interface.
Fig. 5.
Fluid domain results from the fully coupled FSI simulation with three inlet velocity components prescribed from MRI (FSIf-Vxyz). Velocity streamlines depicting the flow at (a) phase 8 (systole, peak flow rate at inlet), (b) phase 10 (systole, peak pressure), (c) phase 20 (transition), (d) phase 30 (early diastole), and (e) phase 40 (late diastole). The colored background illustrates the pressure distribution on the lumen surface; max is the maximum pressure at each phase.
Fig. 6.
Fluid domain results from fully coupled FSI simulation with three inlet velocity components prescribed from MRI (FSIf-Vxyz). Wall shear stress (WSS) at (a) phase 8 (systole, peak flow rate at inlet), (b) phase 10 (systole, peak pressure), (c) phase 20 (transition), (d) phase 30 (early diastole), and (e) phase 40 (late diastole). Max is the maximum WSS at each phase.
Fig. 7.
Structure domain results from fully coupled FSI simulation with three inlet velocity components (FSIf-Vxyz). Maximum principal stress σ1 at (a) phase 8 (systole, peak flow rate at inlet), (b) phase 10 (systole, peak pressure), (c) phase 20 (transition), (d) phase 30 (early diastole), and (e) phase 40 (late diastole). Max is the maximum stress at each phase.
Fig. 8.
Structure domain results (cutaway plane revealing the interior of the AAA sac) from fully coupled FSI simulation with three inlet velocity components (FSIf-Vxyz). Maximum principal strain ε1 at (a) phase 8 (systole, peak flow rate at inlet), (b) phase 10 (systole, peak pressure), (c) phase 20 (transition), (d) phase 30 (early diastole), and (e) phase 40 (late diastole). Max is the maximum strain at each phase.
3.2. Comparison Among Inflow Boundary Conditions.
In this section, we demonstrate the impact of different patient-specific inlet velocity boundary conditions on the wall mechanics assessment of the AAA models, which is one of the main objectives of this work. For this purpose, we compare fully coupled FSI simulation results corresponding to the four inlet velocity profiles (FSIf-Vxyz, FSIf-Vz, FSIf-Vwom, and FSIf-Vplug). Recall that FSIf-Vxyz and FSIf-Vz employ inlet velocity distributions that are MRI-derived and hence entirely patient-specific, whereas FSIf-Vwom and FSIf-Vplug only match the patient-specific flow rate at the inlet and not the velocity profile over the inlet cross section. For each of these three simulations, spatial maxima and averages of the wall stress (σ1), strain (ε1), and wall shear stress (WSS) were calculated at each phase over a full cardiac cycle, as illustrated in Figs. 9(a)–9(c). For FSIf-Vxyz, FSIf-Vz, and FSIf-Vplug, the peaks of the spatial maxima and averages of all biomechanical parameters (σ1, ε1, and WSS) consistently occur at phase 8, which corresponds to the inlet maximum flow rate; however, for FSIf-Vwom, the peaks occur at phase 7. The spatial maxima/averages obtained from FSIf-Vz and FSIf-Vwom matched well with the FSIf-Vxyz maxima/average during diastole, while underestimation occurred during systole. The peaks of spatial maxima/averages of the biomechanical parameters are presented in Table 1. To quantify the relative difference in the assessment of the biomechanical parameters (X, which represents the peak wall stress (σ1), strain (ε1), or wall shear stress (WSS)), we calculated an error matrix using Eq. (3), which measures the underestimation of the peak stresses and strain by FSIf-Vz and FSIf-Vwom with respect to FSIf-Vxyz.
Fig. 9.
Spatial maximum and averages of (a) σ1, (b) ε1, and (c) WSS are compared among the fully coupled FSI simulation results with three different fluid inlet boundary conditions (FSIf-Vxyz, FSIf-Vz, and FSIf-Vwom). Results are shown for 40 phases in the cardiac cycle.
Table 1.
Spatial maximum and average of mechanical stress (σ1), strain (ε1), and wall shear stress (τmax) obtained from fully coupled FSI simulations with three different inlet velocity conditions (FSIf-Vxyz, FSIf-Vz, and FSIf-Vwom). Data in parentheses represent the relative percentage differences (%) calculated with respect to the fully coupled FSIf-Vxyz results.
|
Spatial maximum |
Spatial average |
|||||
|---|---|---|---|---|---|---|
| σ1, kPa | ε1 | WSS, Pa | σ1, kPa | ε1 | WSS, Pa | |
| FSIf-Vxyz | 870.5 | 0.2198 | 3.532 | 54.28 | 0.0444 | 0.439 |
| FSIf-Vz | 870.3 | 0.2198 | 3.509 | 54.26 | 0.0444 | 0.437 |
| (–0.02%) | (0.00%) | (–0.65%) | (–0.04%) | (0.00%) | (–0.46%) | |
| FSIf-Vwom | 826.6 | 0.2131 | 3.035 | 51.33 | 0.0426 | 0.366 |
| (–5.04%) | (–3.05%) | (–14.07%) | (–5.43%) | (–4.05%) | (–16.63%) | |
| FSIf-plug | 848.7 | 0.2161 | 3.199 | 52.81 | 0.0435 | 0.389 |
| (–2.50%) | (–1.68%) | (–9.43%) | (–2.71%) | (–2.03%) | (–11.39%) | |
| (3a) |
| (3b) |
Table 1 indicates that FSIf-Vz yields accurate results compared to FSIf-Vxyz, whereas FSIf-Vwom underestimates the peak σ 1 by approximately 5.0%, the peak ε1 by 3.1%, and the peak WSS by 14.1%. FSIf-Vwom underestimates the average σ1, ε1, and WSS by 5.4%, 4.1%, and 16.6%, respectively, compared to FSIf-Vxyz. FSIf-Vplug underestimates the peak σ 1 by approximately 2.5%, the peak ε1 by 1.7%, and the peak WSS by 9.4%. These results indicate that the in-plane fluid velocity components measured by PC-MRI immediately below the renal arteries play a trivial role in the prediction of the global hemodynamic and biomechanical AAA environment, subject to pressure outflow boundary conditions.
3.3. Comparison Among Computational Approaches.
The three different computational approaches (FSIf, FSI1, and CSSt) were compared with respect to computational cost and accuracy of predicted biomechanical parameters. As expected, we found that the FSIf simulations are the most demanding computationally. All the simulations took an average of 34 h for one cardiac cycle, with a maximum of 103 h (FSI-Vxyz) and a minimum of 95 h (FSI-Vwom) for the three consecutive cardiac cycles. In contrast, the FSI1 computations consistently took approximately 9.5 h to complete four fluid cycles and 3 h for three structure simulation cycles, using the same computational resources (memory and number of cores). Thus, the FSI1 simulations are approximately three to four times faster than their FSIf counterparts.
The FSI1 stress and strain fields were found to be close to the FSIf stresses and strains, and for clarity, we have chosen to present the comparison of FSIf-Vz and FSI1-Vz results only. The graphical representation of the maximum and averages of σ1, ε1, and WSS obtained from the FSI1-Vz and FSIf-Vz methods are presented in Figs. 10(a)–10(c). The principal stresses (σ1) obtained with the FSI1-Vz approach uniformly underestimated the FSIf-Vz results over the whole cardiac cycle. Conversely, the strains (ε1) obtained with FSI1-Vz approach slightly underestimated the FSIf-Vz results during systole but were a close match during diastole. In the fluid domain, the FSI1-Vz approach underestimated the spatial maximum WSS during systole but closely approximated it during diastole when compared to FSIf-Vz (Fig. 9(c)). However, the decoupled approach overestimated the spatial average WSS. Similar discrepancies were obtained when comparing the FSI1-Vxyz– and FSIf-Vxyz–derived parameters and the FSI1-Vwom and FSIf-Vwom results.
Fig. 10.
Spatial maxima and averages of (a) σ1, (b) ε1, and (c) WSS are compared between one-way–coupled FSI results with longitudinal velocity component (FSI1-Vz), fully coupled FSI results with same inlet condition (FSIf-Vz), and computational solid stress (CSSt) results. Notice that no fluid shear is obtained from the CSSt simulations. Results are shown for 40 phases in the cardiac cycle.
The CSSt approach yielded significant underestimation of the maximum and average parameters during systole but matched fairly well during diastole, as shown in Figs. 10(a) and 10(b). In addition, the peaks of the maximum and average σ1 and ε1 occurred at phase 10, which coincides with the maximum intraluminal pressure boundary condition.
A quantitative comparison of the computational approaches was performed by calculating the percent difference of the peak biomechanical parameters (maxima and averages of σ1, ε1, and WSS) obtained from the FSI1-Vz and CSSt approaches with respect to the corresponding FSIf-Vz counterparts, as shown in Table 2. Equations similar to Eq. (3) were used to calculate the percent difference; we found that CSSt underestimated the peak σ 1 by approximately 12.7% and the peak ε1 by 8.0%. The performance of the one-way–coupled FSI simulations was better than the CSSt simulations, as it was able to capture the hemodynamic characteristics (peak at phase 8) of the fully coupled FSI simulation. However, the FSI1-Vz underestimated the peak σ 1 by approximately 13.5%, peak ε1 by 4.4%, and peak WSS by 18.5%.
Table 2.
Spatial maximum and average of mechanical stress (σ1), strain (ε1), and wall shear stress (τmax) obtained from the fully coupled FSI simulation with the longitudinal inlet velocity condition (FSIf-Vz) are compared to the one-way–coupled FSI simulation (FSI1-Vz) and CSSt. Data in parentheses represent the percentage differences (%) calculated with respect to the fully coupled FSIf-Vz results.
|
Spatial maximum |
Spatial average |
|||||
|---|---|---|---|---|---|---|
| σ1, kPa | ε1 | WSS, Pa | σ1, kPa | ε1 | WSS, Pa | |
| FSIf-Vz | 870.3 | 0.2198 | 3.509 | 54.26 | 0.0444 | 0.437 |
| FSI1-Vz | 753.1 | 0.2102 | 4.158 | 49.17 | 0.0409 | 0.549 |
| (–13.47%) | (–4.37%) | (–18.50%) | (–9.38%) | (–7.88%) | (25.63%) | |
| CSSt | 759.6 | 0.2022 | N/A | 46.97 | 0.0398 | N/A |
| (–12.72%) | (–8.01%) | (–13.44%) | (–10.36%) | |||
We utilized a second method of performance assessment of the one-way–coupled approach (FSI1) by calculating the average deviation of the node-based parameters with respect to the FSIf-Vxyz approach. Equations (4) and (5) were used to calculate the average errors (err1t(X) and err2t(X)) at each phase (t):
| (4) |
| (5) |
Here, err1t(X) measures the average of the relative percent difference in the node-based parameters, whereas err2t(X) measures the average of the absolute percent difference. The temporal means of err1t(X) and err2t(X) (i.e., Merr1 and Merr2) computed over all the 40 phases are presented in Table 3.
Table 3.
Relative differences (%) in nodal values of mechanical properties (i.e., stress (σ1), strain (ε1), and wall shear stress (τmax)) calculated for each of the one-way–coupled FSI approaches (FSI1-Vxyz, FSI1-Vz, FSI1-Vwom) with respect to the fully coupled FSIf-Vxyz approach. The nodal average of the relative difference of the mechanical properties (X) at each phase (err1t(X)) and err2t(X)) are calculated following Eqs. (3) and (4). Subsequently, the temporal averages of the errors over 40 phases (Merr1 and Merr2) are computed.
|
Stress, σ1 |
Strain, ε1 |
WSS |
||||
|---|---|---|---|---|---|---|
| Merr1 | Merr2 | Merr1 | Merr2 | Merr1 | Merr2 | |
| FSI1-Vxyz | 6.23 | 6.62 | 4.67 | 4.86 | –17.84 | 21.51 |
| FSI1-Vz | 6.58 | 6.84 | 4.77 | 5.06 | 25.05 | 65.41 |
| FSI1-Vwom | 6.69 | 6.75 | 4.63 | 4.81 | –10.92 | 25.14 |
Following this assessment method, the discrepancies in the nodal results of σ 1 and ε 1 were found to be between 4% and 7% for all three one-way–coupled approaches (FSI1-Vxyz, FSI1-Vz, and FSI1-Vwom) when compared to the baseline FSIf-Vxyz approach. However, for WSS, the one-way–coupled FSI approaches consistently deviated from the baseline, either largely underestimating (Merr1 in FSI1-Vxyz and FSI1-Vwom) or overestimating (Merr2 in FSI1-Vz) the shear stress. It should be noted that, due to the pulsatile flow and pressure waveforms in the AAA sac, the WSS can be positive or negative at any node, thereby resulting in a larger absolute percent difference compared to the relative percent difference. These results indicate that any of the one-way FSI approaches provide a reasonably good approximation for wall stress and strain estimations, with a reasonable computational effort compared to the baseline FSIf-Vxyz approach.
To further characterize the difference between the hemodynamics in a fully coupled FSI simulation and a one-way–coupled FSI simulation, we present the volumetric flow rates calculated at different planes of the fluid domain in Fig. 12. As the pulsatile flow travels through the compliant arterial model, the flow waveforms exhibit a phase shift, backflow is introduced at the onset of the systole, and thereby the peak flow rate reduces progressively. This phenomenon is not observed in the FSI1 simulations, as the wall does not induce deformation of the aneurysm lumen.
Fig. 12.
(a) Volumetric flow rates at inlet (plane 1), aneurysm sac region (planes 2 and 3), and near the aortoiliac bifurcation (plane 4). Results are presented from a fully coupled FSI simulation with patient-specific inlet velocity components (FSIf-Vxyz) and one-way–coupled FSI simulation (FSI1-Vxyz).
4. Discussion
In this work, we analyze the effect of four different inlet velocity boundary conditions derived from patient-specific PC-MR images on the ensuing AAA wall mechanics and study the accuracy of a one-way–coupled FSI approach in comparison to a fully coupled FSI analysis and a transient computational solid stress analysis. The standard methods for assigning inflow boundary conditions are to apply mass or volume flow rates or, alternatively, plug, parabolic, or Womersley velocity profiles. However, these methods fail to incorporate the skewness in the inlet velocity, characteristic of the infrarenal aorta under resting conditions. As shown in Fig. 3(a), the method proposed in this work was successful in identifying and applying the velocity skewness towards the posterior wall of the artery in our patient-specific computational analyses. By comparison, the peak velocity was centrally located in the computational model with the Womersley inlet profile. Interestingly, the peak biomechanical stress was lower in the FSIf-Vwom model when compared to the FSIf-Vxyz model. The analysis with FSIf-Vplug resulted in lower peak biomechanical stresses compared to FSIf-Vxyz but higher than FSIf-Vwom. There might be an underlying correlation of the velocity profile skewness at the inlet with the wall mechanical stresses proximal to the jet flow; however, our study based on a single AAA geometry does not offer a conclusive understanding of this phenomenon. A similar observation was reported in a previous work in our laboratory by Scotti and Finol [20], where the flow dynamics appeared to influence the wall stress distribution when the FSI model was compared to the CSS model in three patient-specific geometries. Future studies with multiple patient-specific anatomies might reveal the relationship between velocity profile skewness and spatial and temporal distributions of wall stresses. Nevertheless, comparing the FSIf-Vxyz and FSIf-Vz model results, we observe that in-plane velocities at the AAA inlet do not have any significant effect on the hemodynamic and mechanical stresses.
4.1. Validation of Computational Results.
Validation of the computationally measured tensile stress is a challenging task, as an in vivo measurement of arterial wall stress is not yet feasible. Ex vivo studies, like tensile testing, are capable of measuring the strength of the aortic wall, as in the work of Di Martino et al. [16] and Vande Geest et al. [40]; however, for stress analysis, others in the field have had to resort to computational modeling and analysis. Initial CSS studies by Raghavan et al. [9] reported that peak wall stress among AAA patients varied from 290 kPa to 450 kPa and was found on the posterior wall in all six patient-specific models. Early FSI analyses with compliant arteries performed in our laboratory by Scotti et al. [21] found arterial wall stress to increase by as much as 25% when compared to CSS-predicted wall stress, with the peak wall stresses ranging from 275 kPa to 398 kPa. In contrast, our present work resulted in higher peak wall stresses, with the maximum principal stress in the 750–870-kPa range for all computational approaches. Noteworthy is that the aforementioned previous studies used an idealized uniform wall thickness, whereas in our studies, a patient-specific nonuniform wall thickness was modeled, which may contribute to the higher stresses.
To demonstrate reliability of the computational models, we present a comparison of results from fully coupled, FSI-predicted flow patterns (FSIf-Vxyz, FSIf-Vz, FSIf-Vwom, and FSIf-Vplug) with the PC-MRI flow patterns at the AAA midsection PC-MR images at selected phases representing important stages of the cardiac cycle (i.e., phase 4 – early systole, phase 8 – peak systole, phases 10 and 12 – late systole, phase 20 – early diastole, and phase 40 – late diastole) in Fig. 11(a). The velocity profiles in the fluid domain and the structural geometry (wall and ILT) in the solid domain are derived from the midsection of all four FSI simulations and presented alongside the PC-MR images. Noteworthy is that the computational geometry is derived from the CT images; therefore, the arterial lumen does not match precisely with the lumen segmented in the PC-MR images. The characteristic skewness of the axial velocity was captured by the FSI simulations as the location of the peak velocity was found to be on the posterior region of the lumen, an observation supported by the PC-MR images at phases 8, 10, and 12. Though the location of the peak velocity is not an exact match with the PC-MR images, the FSIf-Vxyz and FSIf-Vz models fared better (phases 8–12) in reproducing the skewness when compared to FSIf-Vwom and FSIf-Vplug. The discrepancy may be attributed to multiple reasons, mainly due to the presence of a helical flow pattern in the abdominal aorta, which is not predicted adequately with the current FSI setup; the lack of physiologic wall motion in the FSI simulations, as contact with the spinal column was neglected and the material models are hyperelastic isotropic; and the inaccurate assessment of wave propagation in the aorta, due to nonpatient-specific arterial wall mechanical properties. We further calculated the velocities from the PC-MR images at the AAA midsection, computed the volume flow rate, and compared it with the flow rates from the FSI simulations. It was found that PC-MR velocities at the midsection were one order of magnitude larger than the velocities at the inlet. This indicates that there might be discrepancies in the image acquisition at the midsection or lack of alignment of the MR acquisition plane at a cross section that is not normal to the centerline of the artery, or it might require a different Venc value for conversion of the pixel intensity to velocities. Therefore, for qualitative comparison purposes, we scaled the velocities such that the average flow rate at each phase is conserved. The resultant volume flow rate waveforms are compared in Fig. 11(b). The overall qualitative comparison was acceptable, as the FSI-predicted axial flow rate was found to increase from early systole (phase 4) and reach peak systole at phase 10, whereas the PC-MRI flow rate reached the peak at phase 13. The flow rates from the FSI simulations were observed to decrease postsystole, and the onset of diastole (phase 20) was found to be in phase with the PC-MR–derived flow rate, as shown in Fig. 11(b). Qualitatively, the FSI simulations were found to replicate some of the characteristics of the flow transients, mainly the phase delay of peak systole with respect to the inlet flow waveform, the backflow at the onset of systole, and the same time-averaged diastolic flow rate. Further studies on advanced MR imaging and segmentation techniques will be needed to reduce the error between the velocity measurements at the AAA midsection and inlet and therefore reduce the discrepancy between the flow rates obtained from this comparison. Nevertheless, we were able to show the effect of aortic wave reflections on the flow profiles obtained at multiple planes in the FSIf-Vxyz model (Fig. 12). The delay in peak systolic flow and its reduction as the wave travels through the abdominal aorta is found to be characteristic of flow through compliant arteries and may explain the differences observed in the PC-MRI flow waveforms at the inlet and midsection.
Fig. 11.
(a) PC-MR images of the lumen and ILT/wall at the AAA midsection compared with velocity profiles obtained from three FSI simulation models (FSIf-Vxyz, FSIf-Vz, and FSIf-Vwom) at phase 4 (early systole), phase 8 (peak systole), phases 10 and 12 (late systole), phase 20 (early diastole), and phase 40 (late diastole); (b) comparison of volume flow rates obtained at the midsection from the PC-MRI (scaled) and FSI simulation results
4.2. Limitations.
The AAA geometry used in this work was reconstructed from CT images obtained through electrocardiogram-gated acquisition. Therefore, the reconstructed AAA corresponds to an already pressurized state of the abdominal aorta. The application of physiologic boundary conditions in this aneurysm would then underestimate the ensuing wall stress. To predict the wall mechanics accurately, we should either assume initial nonzero stresses or reconstruct the geometry corresponding to a zero-pressure configuration, which was not done in this work. The error associated with AAA flow measurements from PC-MRI is also worth discussing. The present framework for extracting velocity distributions from PC-MR images requires manual intervention in the segmentation of the images. Users need to develop significant expertise to recognize correctly the lumen boundary, especially during late diastole. Lack of sufficient resolution (i.e., pixel size and axial slice spacing) and the lack of contrast enhancement of the MR images create further challenges for the segmentation. The noise associated with the image acquisitions introduces additional errors in the flow rate calculations. Further refinements of the velocity extraction method from PC-MR images are required to overcome these shortcomings, although these are estimated to have a lesser effect on the generation of the inflow boundary condition compared to the inherent limitations of the PC-MRI acquisition sequences.
4.3. Significance.
Computational assessment of AAA rupture risk can be clinically relevant only if the biomechanical analysis is exceptionally accurate. Our study demonstrates that the numerical approach and the choice of inflow boundary condition have a profound effect in the ensuing hemodynamics and peak wall stress. Following a rigorous simulation framework, we have demonstrated that a fully coupled fluid-structure interaction analysis of patient-specific AAA with a PC-MRI–derived axial velocity inflow boundary condition and a quasipatient-specific outflow pressure is adequate in capturing the intra-aneurysmal hemodynamics and thus appropriate for evaluating wall mechanics for rupture risk assessment. Furthermore, this method can be used alternatively to estimate changes in aneurysmal flow as it relates to thrombus initiation, progression, and AAA evolution.
5. Conclusion
We have presented a fluid-structure interaction study of wall mechanics and flow-induced stresses in a patient-specific abdominal aortic aneurysm model. The novelty of this work is based on our ability to (1) perform a comparative fully coupled FSI analysis based on four different inflow boundary conditions obtained from the application of an algorithm that derives blood flow velocity components from subject-specific PC-MRI and applies them (through Schwarz–Christoffel mapping and extrapolation) as velocity profiles and (2) compare a one-way–coupled FSI analysis technique with equivalent transient computational solid stress and fully coupled FSI approaches to test the predictive capability of the former to estimate the AAA wall mechanics. The analysis with the four inlet boundary conditions revealed that utilizing a velocity profile based only on the PC-MRI–derived axial velocity component results in almost identical wall stresses, strains, and shear stresses compared to those obtained with a three-velocity component inlet velocity profile. Conversely, the Womersley and plug velocity profiles yielded an underestimation of the same flow-induced parameters. However, the plug velocity profile proved to better approximate the peak wall stress and strain in contrast to the Womersley profile. A one-way–coupled FSI approach resulted in a reasonably accurate estimation of the wall mechanics with significantly less computational effort compared to a fully coupled FSI approach. Our study also indicates that peak wall stress, strain, and shear stress are influenced by the flow dynamics resulting from the inflow boundary condition application as they occur at peak systolic flow. Therefore, a biomechanical approach for AAA rupture risk assessment should account for the dynamic interaction of the intraluminal flow dynamics and the aortic wall governed by patient-specific inflow boundary conditions.
Acknowledgment
The authors would like to acknowledge research funding from NIH grants R21EB007651, R21EB008804, and R15HL087268. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This research was also supported by an allocation of advanced computing resources supported by the National Science Foundation (Teragrid grant TG-CTS050051N). The computations were performed on the Pople system at the Pittsburgh Supercomputing Center.
Glossary
Nomenclature
- r =
radial distance of the node from the center of hydraulic circle
- R =
radius of the hydraulic circle
- t =
time
- Φk =
phase lag corresponding to the kth Fourier component
- ωk =
frequency corresponding to the kth Fourier component
Appendix: Womersley Velocity Profile Calculation
According to the Womersley solution to fully developed oscillatory flow conditions [43], the total velocity at any point in the cardiac cycle is obtained by superimposition using Eq. (A1),
| (A1) |
where
| (A2) |
| (A3) |
Vk(r, t) is the velocity profile corresponding to the kth Fourier component of the pulsatile waveform.
By rearranging the oscillatory flow equation given in Ref. [43], one can derive
| (A4) |
Jn (*) denotes Bessel function of nth order and of first kind.
, where is the Womersley number, ν is the kinematic viscosity, and .
The individual Womersley profiles corresponding to each frequency were generated using Eq. (A3) and superimposed to arrive at the flow profile referred to as patient-specific Womersley profile (Vwom). These data were exported as nodal time functions and applied as an inlet fluid boundary condition in the ADINA-FSI solver.
Contributor Information
Santanu Chandra, Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN 46556, e-mail: santanu.chandra@gmail.com.
Samarth S. Raut, Department of Mechanical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, e-mail: sraut@andrew.cmu.edu
Anirban Jana, Pittsburgh Supercomputing Center, Pittsburgh, PA 15213, e-mail: anirban@psc.edu.
Robert W. Biederman, e-mail: rbiederm@wpahs.org
Mark Doyle, e-mail: mdoyle@wpahs.org, Cardiovascular Magnetic Resonance Imaging, Allegheny General Hospital, Pittsburgh, PA 15212.
Satish C. Muluk, Division of Vascular Surgery, Western Pennsylvania Allegheny Health Systems, Pittsburgh, PA 15212, e-mail: muluk@usa.net
Ender A. Finol, Department of Biomedical Engineering, AET 1.360, The University of Texas at San Antonio, One UTSA Circle, San Antonio, TX 78249, e-mail: ender.finol@utsa.edu.
References
- [1]. Newman, A. B. , Arnold, A. M. , Burke, G. L. , O'Leary, D. H. , and Manolio, T. A. , 2001, “Cardiovascular Disease and Mortality in Older Adults With Small Abdominal Aortic Aneurysms Detected by Ultrasonography: The Cardiovascular Health Study,” Ann. Intern. Med., 134, pp. 182–190. 10.7326/0003-4819-134-3-200102060-00008 [DOI] [PubMed] [Google Scholar]
- [2]. Upchurch, Jr., G. R. , and Schaub, T. A. , 2006, “Abdominal Aortic Aneurysm,” Am. Fam. Physician, 73, pp. 1198–1204. [PubMed] [Google Scholar]
- [3]. Lederle, F. A. , Johnson, G. R. , Wilson, S. E. , Chute, E. P. , Littooy, F. N. , Bandyk, D. , Krupski, W. C. , Barone, G. W. , Acher, C. W. , and Ballard, D. J. , 1997, “Prevalence and Associations of Abdominal Aortic Aneurysm Detected Through Screening. Aneurysm Detection and Management (ADAM) Veterans Affairs Cooperative Study Group,” Ann. Intern. Med., 126, pp. 441–449. 10.7326/0003-4819-126-6-199703150-00004 [DOI] [PubMed] [Google Scholar]
- [4]. Cornuz, J. , Sidoti Pinto, C., Tevaearai , H., and Egger , M., 2004, “Risk Factors for Asymptomatic Abdominal Aortic Aneurysm: Systematic Review and Meta-analysis of Population-Based Screening Studies,” Eur. J. Public Health, 14, pp. 343–349. 10.1093/eurpub/14.4.343 [DOI] [PubMed] [Google Scholar]
- [5]. Scott, R. A. , Ashton, H. A. , Lamparelli, M. J. , Harris, G. J. , and Stevens, J. W. , 1999, “A 14-Year Experience With 6 cm as a Criterion for Surgical Treatment of Abdominal Aortic Aneurysm,” Br. J. Surg., 86, pp. 1317–1321. 10.1046/j.1365-2168.1999.01227.x [DOI] [PubMed] [Google Scholar]
- [6]. Valentine, R. J. , Decaprio, J. D. , Castillo, J. M. , Modrall, J. G. , Jackson, M. R. , and Clagett, G. P. , 2000, “Watchful Waiting in Cases of Small Abdominal Aortic Aneurysms- Appropriate for All Patients?” J. Vasc. Surg., 32, pp. 441–450. 10.1067/mva.2000.108635 [DOI] [PubMed] [Google Scholar]
- [7]. The UK Small Aneurysm Trial Participants, 1998, “Mortality Results for Randomised Controlled Trial of Early Elective Surgery or Ultrasonographic Surveillance for Small Abdominal Aortic Aneurysms,” Lancet, 352(9141), pp. 1649–1655. 10.1016/S0140-6736(98)10137-X [DOI] [PubMed] [Google Scholar]
- [8]. Raghavan, M. L. , Webster, M. W. , and Vorp, D. A. , 1996, “Ex Vivo Biomechanical Behavior of Abdominal Aortic Aneurysm: Assessment Using a New Mathematical Model,” Ann. Biomed. Eng., 24, pp. 573–582. 10.1007/BF02684226 [DOI] [PubMed] [Google Scholar]
- [9]. Raghavan, M. L. , Vorp, D. A. , Federle, M. P. , Makaroun, M. S. , and Webster, M. W. , 2000, “Wall Stress Distribution on Three-Dimensionally Reconstructed Models of Human Abdominal Aortic Aneurysm,” J. Vasc. Surg., 31, pp. 760–769. 10.1067/mva.2000.103971 [DOI] [PubMed] [Google Scholar]
- [10]. Fillinger, M. F. , Raghavan, M. L. , Marra, S. P. , Cronenwett, J. L. , and Kennedy, F. E. , 2002, “ In Vivo Analysis of Mechanical Wall Stress and Abdominal Aortic Aneurysm Rupture Risk,” J. Vasc. Surg., 36, pp. 589–597. 10.1067/mva.2002.125478 [DOI] [PubMed] [Google Scholar]
- [11]. Fillinger, M. F. , Marra, S. P. , Raghavan, M. L. , and Kennedy, F. E. , 2003, “Prediction of Rupture Risk in Abdominal Aortic Aneurysm During Observation: Wall Stress Versus Diameter,” J. Vasc. Surg., 37, pp. 724–732. 10.1067/mva.2003.213 [DOI] [PubMed] [Google Scholar]
- [12]. Vorp, D. A. , Raghavan, M. L. , and Webster, M. W. , 1998, “Mechanical Wall Stress in Abdominal Aortic Aneurysm: Influence of Diameter and Asymmetry,” J. Vasc. Surg., 27, pp. 632–639. 10.1016/S0741-5214(98)70227-7 [DOI] [PubMed] [Google Scholar]
- [13]. Sacks, M. S. , Vorp, D. A. , Raghavan, M. L. , Federle, M. P. , and Webster, M. W. , 1999, “ In Vivo Three-Dimensional Surface Geometry of Abdominal Aortic Aneurysms,” Ann. Biomed. Eng., 27, pp. 469–479. 10.1114/1.202 [DOI] [PubMed] [Google Scholar]
- [14]. Raghavan, M. , Kratzberg, J. , and da Silva, E. S. , 2004, “Heterogeneous, Variable Wall-Thickness Modeling of a Ruptured Abdominal Aortic Aneurysm,” ASME Conf. Proc., 2004(47039), pp. 271–272. [Google Scholar]
- [15]. Scotti, C. M. , Shkolnik, A. D. , Muluk, S. , and Finol, E. A. , 2005, “Biomechanics of Compliant Abdominal Aortic Aneurysms: The Effect of Asymmetry and Wall Thickness,” Proceedings of the 2005 Summer Bioengineering Conference. [Google Scholar]
- [16]. Di Martino, E. S. , and Vorp, D. A. , 2003, “Effect of Variation in Intraluminal Thrombus Constitutive Properties on Abdominal Aortic Aneurysm Wall Stress,” Ann. Biomed. Eng., 31, pp. 804–809. 10.1114/1.1581880 [DOI] [PubMed] [Google Scholar]
- [17]. Scotti, C. M. , Shkolnik, A. D. , Muluk, S. C. , and Finol, E. A. , 2005, “Fluid-Structure Interaction in Abdominal Aortic Aneurysms: Effects of Asymmetry and Wall Thickness,” Biomed. Eng. Online, 4, p. 64. 10.1186/1475-925X-4-64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Di Martino, E. S., Guadagni , G., Fumero , A., Ballerini , G., Spirito , R., Biglioli , P., and Redaelli , A., 2001, “Fluid-Structure Interaction Within Realistic Three-Dimensional Models of the Aneurysmatic Aorta as a Guidance to Assess the Risk of Rupture of the Aneurysm,” Med. Eng. Phys., 23, pp. 647–655. 10.1016/S1350-4533(01)00035-2 [DOI] [PubMed] [Google Scholar]
- [19]. Raghavan, M. L. , and Vorp, D. A. , 2000, “Toward a Biomechanical Tool to Evaluate Rupture Potential of Abdominal Aortic Aneurysm: Identification of a Finite Strain Constitutive Model and Evaluation of Its Applicability,” J. Biomech., 33, pp. 475–482. 10.1016/S0021-9290(99)00201-8 [DOI] [PubMed] [Google Scholar]
- [20]. Scotti, C. M. , and Finol, E. A. , 2007, “Compliant Biomechanics of Abdominal Aortic Aneurysms: A Fluid Structure Interaction Study,” Comput. Struct., 85, pp. 1097–1113. 10.1016/j.compstruc.2006.08.041 [DOI] [Google Scholar]
- [21]. Scotti, C. M. , Jimenez, J. , Muluk, S. C. , and Finol, E. A. , 2008, “Wall Stress and Flow Dynamics in Abdominal Aortic Aneurysms: Finite Element Analysis vs. Fluid-Structure Interaction,” Comput. Methods Biomech. Biomed. Eng., 11, pp. 301–322. 10.1080/10255840701827412 [DOI] [PubMed] [Google Scholar]
- [22]. Papaharilaou, Y. , Ekaterinaris, J. A. , Manousaki, E. , and Katsamouris, A. N. , 2007, “A Decoupled Fluid Structure Approach for Estimating Wall Stress in Abdominal Aortic Aneurysms,” J. Biomech., 40, pp. 367–377. 10.1016/j.jbiomech.2005.12.013 [DOI] [PubMed] [Google Scholar]
- [23]. Wolters, B. J. , Rutten, M. C. , Schurink, G. W. , Kose, U. , de Hart, J. , and van de Vosse, F. N. , 2005, “A Patient-Specific Computational Model of Fluid-Structure Interaction in Abdominal Aortic Aneurysms,” Med. Eng. Phys., 27, pp. 871–883. 10.1016/j.medengphy.2005.06.008 [DOI] [PubMed] [Google Scholar]
- [24]. Bluestein, D. , Dumont, K. , De Beule, M. , Ricotta, J. , Impellizzeri, P. , Verhegghe, B. , and Verdonck, P. , 2009, “Intraluminal Thrombus and Risk of Rupture in Patient Specific Abdominal Aortic Aneurysm-FSI Modeling,” Comput. Methods Biomech. Biomed. Eng., 12, pp. 73–81. 10.1080/10255840802176396 [DOI] [PubMed] [Google Scholar]
- [25]. Leung, J. H. , Wright, A. R. , Cheshire, N. , Crane, J. , Thom, S. A. , Hughes, A. D. , and Xu, Y. , 2006, “Fluid Structure Interaction of Patient Specific Abdominal Aortic Aneurysms: A Comparison With Solid Stress Models,” Biomed. Eng. Online, 5, p. 33. 10.1186/1475-925X-5-33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Rissland, P. , Alemu, Y. , Einav, S. , Ricotta, J. , and Bluestein, D. , 2009, “Abdominal Aortic Aneurysm Risk of Rupture: Patient-Specific FSI Simulations Using Anisotropic Model,” ASME, J. Biomech. Eng., 131, p. 031001. 10.1115/1.3005200 [DOI] [PubMed] [Google Scholar]
- [27]. Xenos, M. , Rambhia, S. H. , Alemu, Y. , Einav, S. , Labropoulos, N. , Tassiopoulos, A. , Ricotta, J. J. , and Bluestein, D. , 2010, “Patient-Based Abdominal Aortic Aneurysm Rupture Risk Prediction With Fluid Structure Interaction Modeling,” Ann. Biomed. Eng., 38, pp. 3323–3337. 10.1007/s10439-010-0094-3 [DOI] [PubMed] [Google Scholar]
- [28]. Olufsen, M. S. , 1999, “Structured Tree Outflow Condition for Blood Flow in Larger Systemic Arteries,” Am. J. Physiol. Heart Circ. Physiol., 276, pp. H257–H268. [DOI] [PubMed] [Google Scholar]
- [29]. Olufsen, M. S. , Peskin, C. S. , Kim, W. Y. , Pedersen, E. M. , Nadim, A. , and Larsen, J. , 2000, “Numerical Simulation and Experimental Validation of Blood Flow in Arteries With Structured-Tree Outflow Conditions,” Ann. Biomed. Eng., 28, pp. 1281–1299. 10.1114/1.1326031 [DOI] [PubMed] [Google Scholar]
- [30]. Steele, B. N. , and Taylor, C. A. , 2003, “Simulation of Blood Flow in Abdominal Aorta at Rest and During Exercise Using 1D Finite Element Method With Impedance Boundary Conditions Derived From a Fractal Tree,” Proceedings of the 2003 ASME Summer Bioengineering Conference. [Google Scholar]
- [31]. Kose, U. , Hoogeveen, R. , Breeuwer, M. , and dePutter, S. , 2006, “Computational Fluid Dynamics of Abdominal Aortic Aneurysms With Patient Specific Inflow Boundary Conditions,” Proc. SPIE, 6143, p. 61432D. 10.1117/12.649755 [DOI] [Google Scholar]
- [32]. Kim, Y. H. , Kim, J. E. , Ito, Y. , Shih, A. M. , Brott, B. , and Anayiotos, A. , 2008, “Hemodynamic Analysis of a Compliant Femoral Artery Bifurcation Model Using a Fluid Structure Interaction Framework,” Ann. Biomed. Eng., 36, pp. 1753–1763. 10.1007/s10439-008-9558-0 [DOI] [PubMed] [Google Scholar]
- [33]. Tan, F. P. P. , Xu, X. Y. , Torii, R. , Wood, N. B. , Delahunty, N. , Mullen, M. , Moat, N. , and Mohiaddin, R. , 2012, “Comparison of Aortic Flow Patterns Before and After Transcatheter Aortic Valve Implantation,” Cardiovasc. Eng. Tech., 3, pp. 123–135. 10.1007/s13239-011-0073-3 [DOI] [Google Scholar]
- [34]. Martufi, G. , Di Martino, E. S. , Amon, C. H. , Muluk, S. C. , and Finol, E. A. , 2009, “Three-Dimensional Geometrical Characterization of Abdominal Aortic Aneurysms: Image-Based Wall Thickness Distribution,” ASME, J. Biomech. Eng., 131, p. 061015. 10.1115/1.3127256 [DOI] [PubMed] [Google Scholar]
- [35]. Shum, J. , Di Martino, E. S. , Goldhammer, A. , Goldman, D. H. , Acker, L. C. , Patel, G. , Ng, J. H. , Martufi, G. , and Finol, E. A. , 2010, “Semi-automatic Vessel Wall Detection and Quantification of Wall Thickness in CT Images of Human Abdominal Aortic Aneurysms,” Med. Eng. Phys., 37, pp. 638–648. 10.1118/1.3284976 [DOI] [PubMed] [Google Scholar]
- [36]. Shum, J. , Xu, A. , Chatnuntawech, I. , and Finol, E. A. , 2011, “A Framework for the Automatic Generation of Surface Topologies for Abdominal Aortic Aneurysm Models,” Ann. Biomed. Eng., 39, pp. 249–259. 10.1007/s10439-010-0165-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Liu, P. , 2010, “A Volume Meshing Strategy for Patient Specific Abdominal Aortic Aneurysms,” M.S. thesis, Carnegie Mellon University, Pittsburgh.
- [38]. Bathe, K. J. , 2009, ADINA 8.6 User Interface Command Reference Manual, Adina R&D Inc., Watertown, MA. [Google Scholar]
- [39]. Fournier, R. L. , 1998, Basic Transport Phenomena in Biomedical Engineering, Taylor & Francis, Philadelphia. [Google Scholar]
- [40]. Vande Geest, J. P. , Sacks, M. S. , and Vorp, D. A. , 2006, “A Planar Biaxial Constitutive Relation for the Luminal Layer of Intra-luminal Thrombus in Abdominal Aortic Aneurysms,” J. Biomech., 39, pp. 2347–2354. 10.1016/j.jbiomech.2006.05.011 [DOI] [PubMed] [Google Scholar]
- [41]. Driscoll, T. , 1996, “Algorithm 756: A MATLAB Toolbox for Schwarz-Christoffel Mapping,” ACM Trans. Math. Softw., 22, pp. 168–186. 10.1145/229473.229475 [DOI] [Google Scholar]
- [42]. Van't Veer, M. , Buth, J. , Merkx, M. , Tonino, P. , Bosch, H. V. , Pijlis, N. , and Vosse, F. , 2008, “Biomechanical Properties of Abdominal Aortic Aneurysms Assessed by Simultaneously Measured Pressure and Volume Changes in Humans,” J. Vasc. Surg., 48, pp. 1401–1407. 10.1016/j.jvs.2008.06.060 [DOI] [PubMed] [Google Scholar]
- [43]. Womersley, J. R. , 1955, “Method for the Calculation of the Velocity, Rate of Flow and Viscous Drag in Arteries When Pressure Gradient Is Known,” J. Physiol, 127, pp. 533–563. [DOI] [PMC free article] [PubMed] [Google Scholar]