Short abstract
Arteriovenous fistulae are surgically created to provide adequate access for dialysis patients suffering from end-stage renal disease. It has long been hypothesized that the rapid blood vessel remodeling occurring after fistula creation is, in part, a process to restore the mechanical stresses to some preferred level, i.e., mechanical homeostasis. We present computational hemodynamic simulations in four patient-specific models of mature arteriovenous fistulae reconstructed from 3D ultrasound scans. Our results suggest that these mature fistulae have remodeled to return to ‘‘normal’’ shear stresses away from the anastomoses: about 1.0 Pa in the outflow veins and about 2.5 Pa in the inflow arteries. Large parts of the anastomoses were found to be under very high shear stresses Pa, over most of the cardiac cycle. These results suggest that the remodeling process works toward restoring mechanical homeostasis in the fistulae, but that the process is limited or incomplete, even in mature fistulae, as evidenced by the elevated shear at or near the anastomoses. Based on the long term clinical viability of these dialysis accesses, we hypothesize that the elevated nonhomeostatic shear stresses in some portions of the vessels were not detrimental to fistula patency.
Introduction
Hemodialysis is a common treatment for approximately 370,000 patients in the United States with end-stage renal disease [1]. To optimize the procedure, the dialysis access site must be easily accessible but must also be able to continuously provide high blood flow rates: mL/min [2]. If there is insufficient blood flow through the access, then the dialysis procedure becomes impractical or ineffective. To provide these features, an arteriovenous (AV) fistula is typically surgically created in the arm: an artery and a vein are anastomosed together, bypassing the high flow resistance of the capillary bed and providing enhanced flow through the artery and into the access vein.
Unfortunately, as many as 60% of AV fistulae require an intervention within one year to maintain clinical patency [3,4]. There are two major causes of patency loss: thrombotic occlusion, brought on by aggressive intimal hyperplasia and stenotic lesions, or impaired dilation, whereby impaired venous remodeling does not provide a sufficient flow rate at the access site [2]. In the United States alone, it is estimated that the total expenditures related to access site complications and revisions exceed $2 billion per year [1].
After the creation of the fistula, the vein undergoes a rapid remodeling process, leading to an increase in the diameter of the lumen and increased muscular thickness in the wall, which is a process referred to as vein arterialization [5]. It has long been hypothesized that hemodynamic forces constitute the primary external influence on the remodeling process [6,7]. Since an AV fistula causes a dramatic rise in the flow rate and wall shear stress outside of normal physiological values, it is hypothesized that the vein and artery lumens chronically increase as a way to renormalize the value of the wall shear stress. The remodeling of the vessels has been shown to correlate with the initial time-averaged wall shear stress as evidenced by animal models of AV fistulae [6,7] and ultrasound surveillance in dialysis patients [5,8]. These studies hypothesized that the remodeling stops once the mean wall shear stress in the fistulae reach about 1.5 Pa in the radial artery and about 1.0 Pa in the cephalic vein. The renormalization of shear stress in the fistula vessels has been interpreted as evidence of a “mechanical homeostasis” [9]: the vessels seek to maintain a preferred mechanical state through a process of growth and remodeling. The shear-induced remodeling is widely hypothesized to be regulated in part by the vascular endothelium [10].
Despite the pervasive use of the AV fistula for dialysis access, the mechanisms which drive a fistula to either successful remodeling and patency versus occlusion and failure remain unclear [11]. Even though blood flow is thought to play an important role in fistula remodeling, the characterization of the hemodynamic stresses occurring within fistulae remain ambiguous [12], even within functioning accesses [13]. Characterizing the fistula hemodynamics has been hindered, in part, due to the relative complexity of the flow, including separation, vortex shedding, and swirling flows [14].
In this study, we use 3D ultrasound imaging and computational fluid dynamics to determine the hemodynamics in four mature AV fistulae of hemodialysis patients. The hemodynamic analysis aims to quantify the mechanical stresses occurring due to complex secondary flows. It is important to first characterize the hemodynamics in patent accesses in order to eventually understand the negative influence of hemodynamics in failing accesses [11]. It is furthermore unlikely that effective clinical treatments for fistula maturation will be successful until a more precise characterization of fistula hemodynamics is articulated [10].
Methods
Ultrasound Imaging.
Four female patients with AV fistulae in the arm used for dialysis access are examined in this study with a protocol approved by the University of Washington's Institutional Review Board. The mean age of the patients is 70 years (78, 91, 68, and 42 years for patients 1 through 4, respectively). The mean age of the fistula from the time of surgical creation to our examination is 3.8 years (7.6, 2.0, 3.3, and 2.2 years, respectively). Each fistula was functioning for dialysis access at the time of our examination. We study two fistulae (patients 1 and 3) with an end-to-side anastomosis configuration where the cephalic vein is excised and its proximal end is connected to the side of either the radial or the brachial artery. We also study two fistulae (patients 2 and 4) with a side-to-side anastomosis configuration where incisions are made on adjacent sides of both the cephalic vein and the radial or the brachial artery artery. The vessels are sutured together leaving a large anastomosis between them and preserving their anatomical proximal-distal configuration.
Vessel imaging was performed with a custom three-dimensional imaging system that has been described in detail elsewhere [15,16]. Briefly, a magnetic tracking system (Flock of Birds, Ascension Technology, Burlington, VT) provides measurements of the location and orientation of the ultrasound scanhead during the examination. The ultrasound imager (SonixTouch, Ultrasonix Medical Corporation, Richmond, BC, Canada) and magnetic tracking system are interfaced with a personal computer equipped with custom software for simultaneous acquisition of the ultrasound images and the associated location data. The blood vessels are imaged in cross-section and 2D gray-scale images are continuously captured at a rate of 30 frames/s as the scanhead is manually swept along the vessels of interest. Spectral Doppler waveforms are also recorded at several locations in the proximal vessels and in the anastomoses. The spectral Doppler system records the distribution of blood velocities over time at a selected region within a vessel.
The lumen of the blood vessels was manually outlined on a subset of the captured images using custom software [17]. Additional custom software within matlab (The MathWorks, Natick, MA, USA) was used to reconstruct 3D surfaces from cross-sectional outlines [15]. The software connects the contour points to neighboring outlines using B-splines to generate a 3D surface model. The error in the cross-sectional areas of the vessels and anastomoses has been determined to be within [16].
Computational Fluid Dynamics.
The 3D Navier-Stokes equations are solved using ® FLUENT ® (Release 12.1, ANSYS, Inc. Cannonsburg, PA). A second-order upwind scheme is used for the spatial discretization of the advective term in the momentum equation. Time integration is done by a second-order pressure-implicit-splitting of operators scheme [18]. The geometries are discretized with a semistructured mesh with the package ® Gambit ® (Release 2.4, ANSYS, Inc., Cannonsburg, PA). Prismatic triangle boundary layer elements are used near walls and tetrahedral elements are used away from walls. The boundary layer cells near the walls have characteristic thicknesses of 80–120 . The tetrahedral cells have characteristic widths of 150 . The number of computational cells for each model is 5.92, 2.87, 4.65, and 5.76 × 106, respectively. Details of a computational mesh resolution study are provided in the Appendix. Blood is modeled as an incompressible and Newtonian fluid with a dynamic viscosity of and a density, of 1050.0 kg/ [19].
For each inflow artery, an unsteady Womersley velocity profile [20] is matched to the in vivo centerline velocity measured by Doppler ultrasound. For each patient, the mean and eight harmonic components are used in the specification of the inflow velocity. At the proximal veins and distal vessels, a stress-free condition is enforced; the pressure stress and normal viscous stress on the outflow boundary are balanced, and the tangential viscous stresses are zero. The pressure on all proximal veins and all distal vessels are prescribed by using two-element Windkessel, i.e., resistance-capacitance models [21] (one exception is the distal artery in patient 4 where an inflow is prescribed using a Womersley velocity profile). In vivo measurements of fistula outflow vein impedance show that it is well approximated by a single resistive element up to Hz [22]. However, we use two-element models as they are more numerically stable. The Windkessel models are integrated in time by a fully-implicit second-order backward difference formula (see the supplementary material [23]). Two test cycles are performed in order to manually tune the Windkessel parameters so that the simulated proximal venous flows rates match that of the in vivo measurements to within a 10% difference which is less than the uncertainty of the ultrasound derived flow rates. Numerical values of the Windkessel parameters are given in the supplementary material [23]. The in vivo venous flow rates are calculated by multiplying the cross-sectionally averaged Doppler ultrasound velocities by the cross-sectional area of the vessel. This technique gives an uncertainty in the in vivo flow rates of [24]. Flow rates in the distal vessels are calculated by applying a mass balance through the fistulae and asserting that the time-averaged flow rates must sum to zero.
The blood flow is simulated for a total of seven cardiac cycles in each patient. In each case, however, the first two cycles are discarded in order to eliminate simulation start-up transients. Thus, five cardiac cycles are used to compute the phase averages and variability of the flow and mechanical stress.
Mechanical Stress Parameters.
We define the Reynolds number for a given vessel with a diameter as
| (1) |
where is the time-averaged flow rate through the vessel. We compute the instantaneous wall shear stress as the absolute value of the wall shear stress vector at position and time such that
| (2) |
where and are the streamwise and spanwise components, respectively, of the wall shear stress vector. We compute the time-averaged wall shear stress (TAWSS) over number of cardiac cycles using a commonly accepted averaging procedure [25] as
| (3) |
where is the period of the cardiac cycle. We also use an alternate definition of the time-averaged wall shear stress to quantify the sensitivity of our results to the choice of average shear stress. The alternative time-averaged shear stress, denoted as , is defined as
| (4) |
Unless otherwise stated, descriptions of the time-averaged wall shear stress in the text will refer to Eq. (3) and not Eq. (4). Furthermore, we calculate a “wall shear stress duty factor,” , which quantifies the fraction of the cardiac cycle for which the wall shear stress is above a certain stress threshold as
| (5) |
where
| (6) |
and where is some shear stress threshold. We also calculate the “highly stressed lumen area,” as
| (7) |
where is the luminal surface area. This is an arbitrary yet simple measure of high shear acting on the vessels. Since the duty factor can only range from 0 to 1, the stressed area is weighted by the length of time the shear is above the given threshold.
Results
In Vivo Flow Rates.
Time-averaged proximal artery flow rate averaged between the four patients is 846 mL/min, corresponding to an intersubject mean Reynolds number of 894. The intersubject mean proximal vein flow rate is 844 mL/min, while the simulated intersubject mean proximal vein flow rate is 840 mL/min, corresponding to a mean venous Reynolds number of 613. These flow rates are consistent with previously published values in human AV fistulae [26,27]. The venous outflows are greater than what is necessary for adequate dialysis, mL/min [27], which confirms that these fistulae are functional accesses. The flow parameters are summarized in Table 1.
Table 1.
In vivo and simulated flow parameters
| Patient | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Anastomosis type | ETS | STS | ETS | STS |
| Mean proximal artery flow rate (mL/min) | 652 | 368 | 1130 | 1233 |
| Artery Re number | 887 | 465 | 892 | 1331 |
| simulated mean proximal vein | ||||
| Flow rate (mL/min) | −632 | −330 | −1092 | −1307 |
| In vivo proximal vein flow rate (mL/min) | −628 | −310 | −1140 | −1297 |
| Difference in vivo versus | ||||
| simulated venous flow rate (%) | 0.63 | 6.1 | 4.3 | 0.77 |
| Simulated vein Re number | 575 | 392 | 669 | 817 |
| Mean distal artery flow rate (mL/min) | 21 | 33 | 39 | −100 |
| Mean distal vein flow rate (mL/min) | N/A | 5 | N/A | 34 |
| Cardiac cycle period (s) | 0.84 | 1.08 | 0.75 | 0.64 |
Note: ETS and STS stand for “end-to-side” and “side-to-side,” respectively. Positive flow rates are antegrade (toward the hand) and negative flow rates are retrograde (toward the heart).
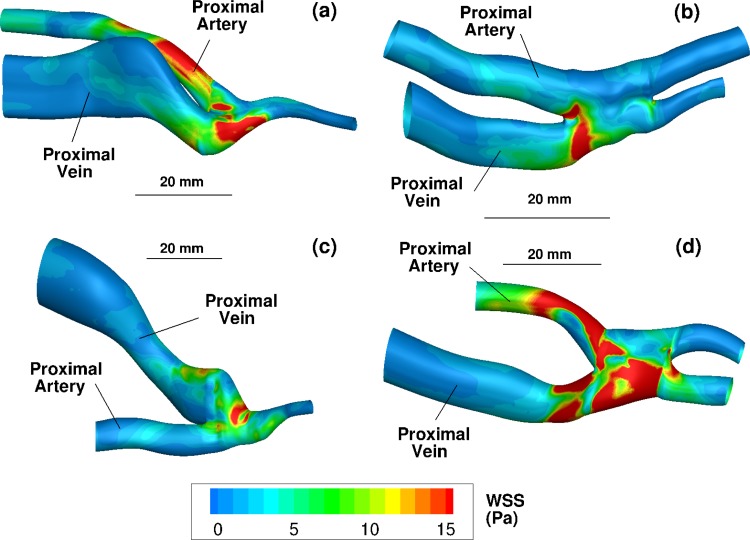
The anatomies of the four fistulae are shown in Fig. 1. Although the two anastomotic configurations are unique surgical techniques, the flow rates through the distal veins in patients 2 and 4 are very small, 1.5% and 2.6%, respectively, compared to the proximal vein flow rates. We therefore consider, as a first approximation, that the fistulae hemodynamics are independent of anastomotic configuration. We hypothesize that the flow inertia and Reynolds number are the dominant parameters which determine the hemodynamics.
Fig. 1.
Three-dimensional ultrasound reconstructions of the four fistulae with the lumen colored by time-averaged wall shear stress (Eq. (3)) in Pa. (a), (b), (c), and (d) Reconstructions from patients 1, 2, 3, and 4, respectively. The view in each subfigure is shown from the skin toward the fistula. The bar labeled 20 mm shows the relative size of each figure.
Simulated Velocities and Stresses.
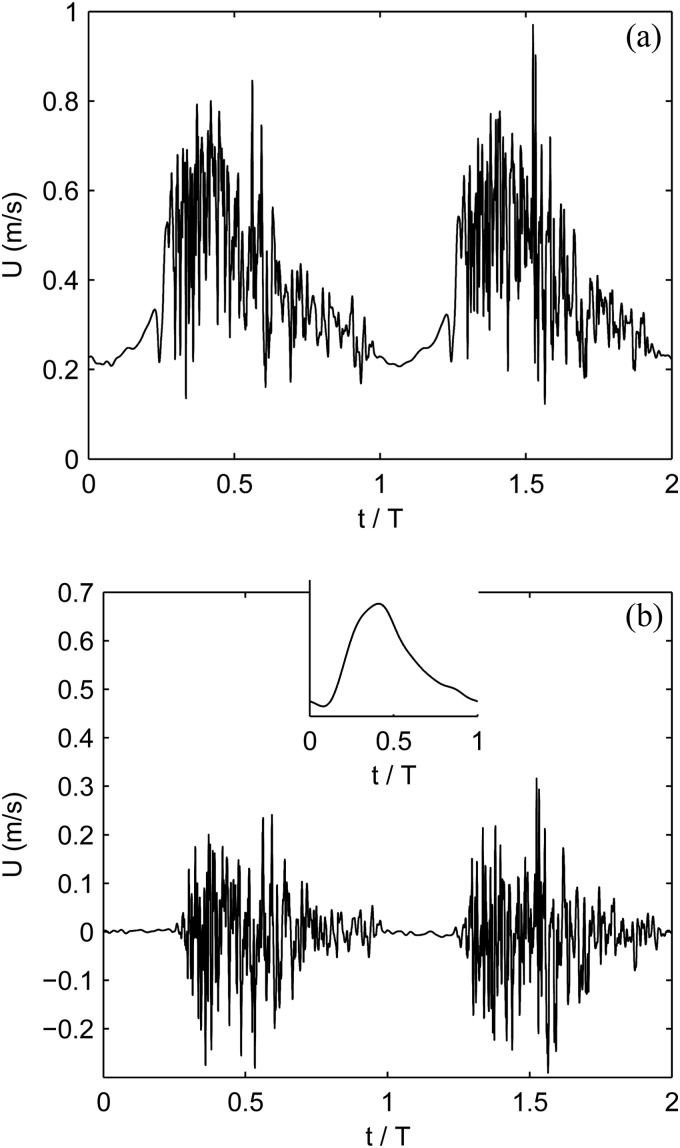
In each of the four fistulae, chaotic flow is observed; it is determined by nonzero deviations from the phase-averaged velocity and is associated with significant vortex shedding. The root-mean-square of the cycle-to-cycle velocity fluctuations are of the mean velocities in all four patients. Figure 2 shows a typical chaotic velocity pattern at a spatial point in the outflow vein of patient 1. The flow instabilities are most pronounced during systole but oftentimes persist through much of or even all of diastole. The flow instability is, in part, due to the relatively high Reynolds numbers and the pulsatility of the flow, but also due to the complex geometry. The majority of the flow entering the fistula through the proximal artery must make a ° turn as it leaves through the proximal vein. Secondary flows created at the anastomoses are advected into the outflow vein. The venous flows re-laminarize a few centimeters downstream of the anastomoses.
Fig. 2.
Streamwise blood velocity versus time for two cardiac cycles. The time history is taken from a point in the venous outflow of patient 1 about 5 mm downstream of the anastomosis in the center of the vessel. (a) The raw time-signal. (b) The time signal with the 5 cycle phase-averaged velocity removed. The inset shows the phase of the arterial inflow.
In all cases, the blood flow entering through the proximal artery impinges onto the opposite side of the anastomotic wall (see Figs. 1 and 4). This produces a stagnation point-like flow and results in very high shear stresses on a ring around the stagnation point at the anastomoses. Instantaneous systolic shear stresses exceed 25 Pa at the anastomoses of all patients. Figure 1 shows the time-averaged wall shear stress, using Eq. (3), on the vessel wall of each patient.
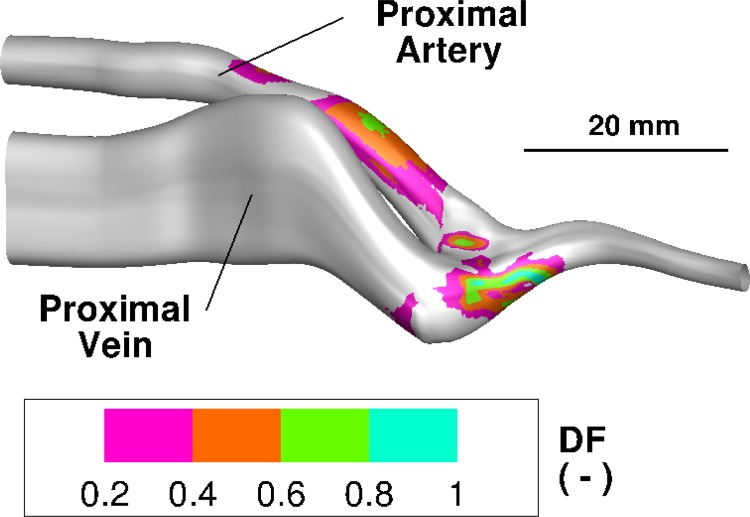
Fig. 4.
Shear stress duty factor distribution on the lumen for patient no. 1 using a threshold shear of 15 Pa. The bar labeled 20 mm shows the relative size. The large values of the duty factor in the proximal artery are due to the vessel curvature which produces a strong secondary helical flow. The large value of the duty factor on the anastomosis is due to the impingement and stagnation point flow.
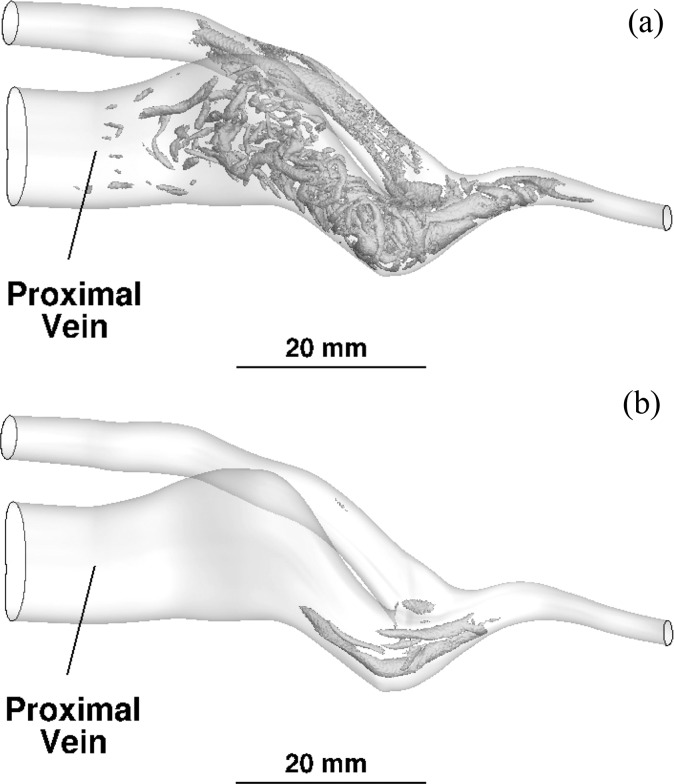
To visualize the nature of the flow transition, vortices within patient 1 are shown in Fig. 3 using the Q-criterion. Figure 3(a) shows an instantaneous view at peak systole and Figure 3(b) is an instantaneous view at end diastole. The plotted value of Q is 0.5 when normalized by the mean centerline velocity and radius of the proximal artery. As the proximal artery sweeps downward toward the anastomosis, a helical flow is created; the longer vortices in the artery in Fig. 3(a) are due to the helical motion. The wormlike structures in the vein are vortices which are created at the anastomosis and are advected into the vein. Even during diastole, some vortex motion is created on the anastomosis at the flow impingement point; the long vortex tubes at the anastomosis in Fig. 3(b) are two counter-rotating vortices which have “escaped” the stagnation point. The vortex structures are produced at the impingement point in all patients.
Fig. 3.
Visualization of transitional flow vortices using the Q-criterion for patient no. 1 at (a) peak systole, and (b) end diastole. The value of Q is 0.5 when normalized by the mean centerline velocity and radius of the proximal artery.
Figure 4 shows the shear duty factor (using a threshold of 15 Pa) for patient 1. The anastomosis shows a shear duty factor greater than 0.2, meaning that it is exposed to more than 15 Pa for at least 20% of the cardiac cycle. The highly stressed area has values of 147, 31.7, 80.9, and 459 respectively. These values represent a substantial portion of the anastomotic and venous surface areas. To highlight the large proportion of the highly stressed area, we normalize each value with the square of the proximal artery diameter and obtain normalized areas of 6.73, 1.25, 1.24, and 13.19 for each respective patient.
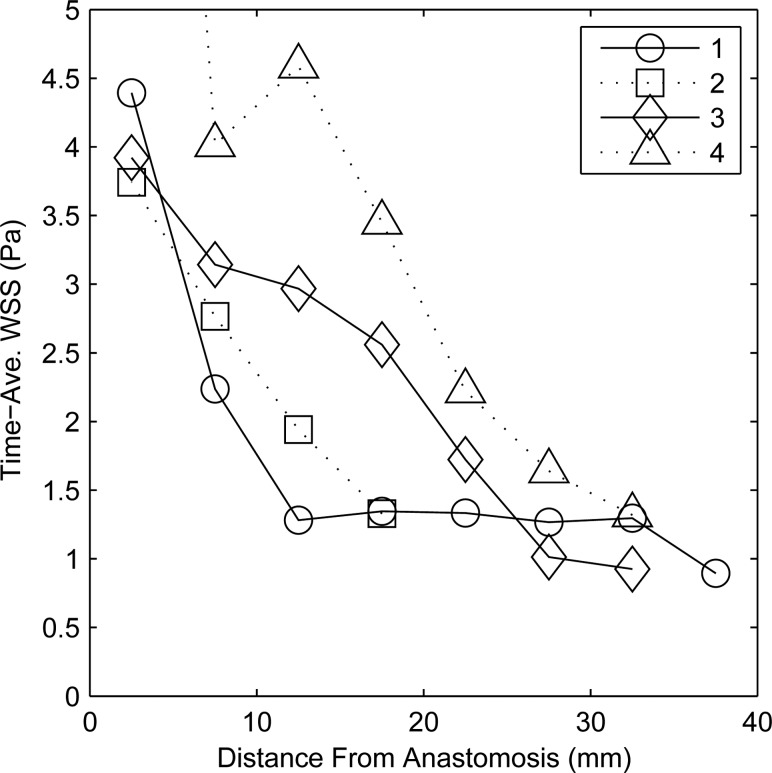
Shear in the outflow veins remains elevated above what might be considered normal: 1 Pa [5]. This is due to the advection into the vein of the secondary flows created at the anastomosis. The time-averaged shear decreases along the pathlines down the vein and becomes approximately constant about 20–30 mm downstream of the anastomoses. The time-averaged shear using Eq. (3) was also spatially averaged on the vein wall along 5 mm “bands” perpendicular to the axis of the vessel. Figure 5 displays this spatially-averaged shear along the vein pathline. The “origin” of the anastomosis on the abscissa of Fig. 5 is taken to be the location where the vein axis centerline crosses perpendicular to the apex of the anastomosis. Near the anastomoses ( mm), the space- and- time-averaged shear stresses are high: 4.32, 3.74, 3.90, and 12.9 Pa. The flow instabilities decay as they are advected downstream in the vein; see, in Fig. 3(a), the absence of vortices toward the end segment of the vein. Thus, the shear stresses return to physiologically normal values farther away from the anastomoses. Between 25–30 mm downstream from the anastomoses, the spatial- and- time-averaged shear stresses in the vein are 1.27, 1.33, 1.01, and 1.64 Pa. In comparison, the time-averaged shear stresses in the proximal artery at the domain inflow are 3.78, 1.74, 1.64, and 3.57 Pa, while the temporal maxima in the artery are 7.17, 4.29, 4.46, and 6.18 Pa. The values of the band-averaged shear stress, both time-averaged and maximum, in the proximal veins are summarized in Table 2.
Fig. 5.
Space- and time-averaged shear (Eq. (3)) in Pa at 5 mm increments along the length of the proximal vein of all four patients. The data point of shear for patient no. 4 located at a distance of 2.5 mm is not shown on the scale but is equal to 12.9 Pa.
Table 2.
Summary of wall shear stress in proximal veins (in Pa)
| Patient | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Near anastomosis | TAWSS | 4.32 | 3.74 | 3.90 | 12.9 |
| ( mm) | 3.75 | 3.24 | 3.61 | 12.3 | |
| Max WSS | 9.08 | 9.02 | 7.50 | 26.8 | |
| Far from anastomosis | TAWSS | 1.27 | 1.33 a | 1.01 | 1.64 |
| (25–30 mm) | 1.12 | 1.20 a | 0.60 | 1.40 | |
| Max WSS | 2.42 | 3.10 a | 2.94 | 3.58 | |
| WSS-Poiseuille's law | 0.74 | 1.19 | 0.58 | 0.73 |
Note: Shear by Poiseuille's law calculated by using the time-averaged flow rate and the diameter averaged along the vein axis.
For patient 2, shear is averaged between 15–20 mm from anastomosis since the model vein is less than 25 mm long.
Time-averaged shear stresses were recomputed using Eq. (4) for for each patient model. The differences between the two quantities at each surface mesh point were integrated and averaged over the lumen of each model, resulting in average percent differences of 6.4, 7.7, 10.9, and 6.5%, respectively, for each model. The surface-averaged norm of the TAWSS is used as the scale to calculate percentage. The values of the average shear using Eq. (4) were always lower than those computed with Eq. (3), i.e., . Although the two averaging procedures do give different values, we would consider these differences to be minor, given that the random uncertainties in shear stress are at least 25–30% [19] due to errors in model input parameters, e.g., the flow rate or geometry. The time-averaged wall shear stress, using Eq. (4), in the proximal veins also shows similar trends to those previously described: high shear near the anastomosis (intersubject mean of 5.72 Pa) but normal shear away from the anastomosis (intersubject mean of 1.08 Pa). The values of the space- and- time-averaged shear stress using on segments of the proximal veins are summarized in Table 2 in order to facilitate comparison.
We also examine the extent of low time-averaged wall shear stress in relation to its hypothesized link to intimal hyperplasia and stenosis formation [12,28]. The regions of low shear are due to flow separation at the anastomosis wall and the subsequent slow moving separation bubble along the vein wall. We compute the surface area in the vein exposed to time-averaged shear (Eq. 3), to be less than 0.5 Pa and 0.25 Pa. The area exposed to Pa time-averaged shear is 56.3, 91.2, 59.4, and 5.33 . The values normalized by the square of the patient's vein diameter are 0.88, 2.99, 0.54, and 0.051. No segment of the lumen was exposed to time-average shear Pa with the exception of patient 2 with an area of 13.6 (normalized area 0.45).
Finally, we seek to quantify the dependence of the highly stressed area on the inflow conditions. We correlate the normalized highly stressed area versus both the square of the mean proximal arterial centerline velocity and the proximal artery Reynolds number. The square of the centerline velocity represents the momentum flux of the incoming flow, which we expect to correlate with the magnitude of the anastomotic shear stress. The arterial Reynolds number represents the relative strength of the inflow inertia. We would, therefore, expect a flow with a high inertia to have a more powerful impingement on the anastomotic wall [29] and, thus, to correlate with the highly stressed area. A least squares linear regression and Pearson's coefficient of determination are used to assess the strength of the correlations. We compute regressions based on three values of the threshold shear stress, 7.5 Pa, 10 Pa, and 15 Pa, in order to assess the sensitivity of our results to the threshold.
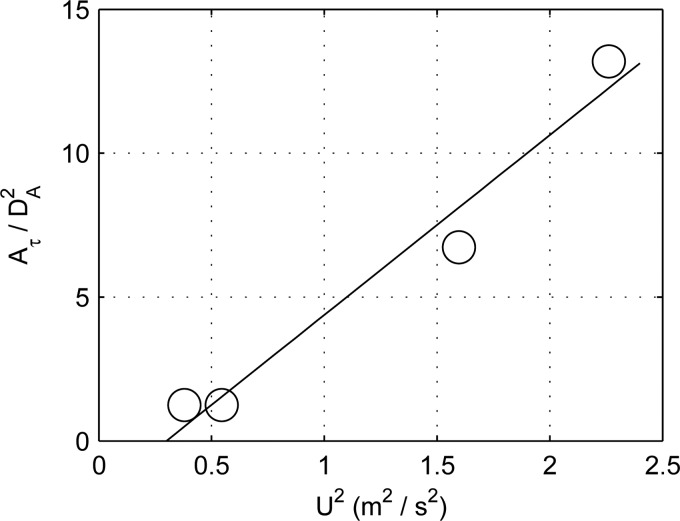
The correlations of the highly stressed area versus the inflow velocity squared are very strong, (, two-tailed t-test), and are insensitive to the choice of a shear threshold. Figure 6 shows the regression analysis using the inflow velocity squared for the case of a threshold shear of 15 Pa. Using the Reynolds number as the regressor, correlations are moderate to strong with ranging from 0.70 to 0.74 and are also insensitive to the choice of threshold. However, the Reynolds number correlations are not statistically significant (, two-tailed t-test) due to the small sample size. Coefficients of determination and significance levels are presented in Table 3. These results further support the notion that the high shear at the anastomoses are caused by the impingement of the high inertia arterial flow as it passes through the fistula.
Fig. 6.
Normalized highly stressed area when Pa in all four patients versus the mean centerline arterial inflow velocity squared . The solid line is a least squares regression. The coefficient of determination is 0.96 and .
Table 3.
Coefficients of determination for versus mean centerline inflow velocity squared or artery Re for different threshold values of the wall shear stress duty factor
| Re | ||||
|---|---|---|---|---|
| (Pa) | ||||
| 7.5 | 0.70 | 0.16 | 0.99 | <0.01 |
| 10 | 0.72 | 0.15 | 0.99 | <0.01 |
| 15 | 0.74 | 0.14 | 0.96 | <0.05 |
Note: Significance determined by two-tailed t-test. Here, is the threshold value of the wall shear stress for the duty factor.
Discussion
Although it is generally accepted that the vessel remodeling after fistula creation is a process of mechanical homeostasis [9], increasing evidence is questioning the traditional view that there is a complete restoration of a normal homeostatic shear stress at the end of the normal maturation process [13,30]. Instead, it has been suggested that there is only a partial restoration of homeostatic shear stress [31]. We provide further evidence that there is only a partial restoration of homeostatic shear stress in mature AV fistulae. We found “normal” shear stresses in both the arteries and veins 20–30 mm away from the anastomoses: time-averaged Eq. (3) intersubject mean in the arteries and veins are 2.68 Pa and 1.31 Pa, respectively. The diameters and flow rates of both the veins and arteries examined in this study are much larger than the physiological values for these vessels, which suggests that remodeling has followed its due course. The normal radial artery diameter is about 2.5 mm [26], compared to an intersubject mean of 5.9 mm here; the normal cephalic vein diameter is about 2.3 mm [5], compared to a mean of 8.2 mm here. Normal radial artery flow is 20–30 mL/min [26] compared to a mean of 846 mL/min here.
Thus, on the one hand, the shear stresses away from the anastomoses reported here are consistent with previously published results of homeostatic shear stresses in human AV fistulae. Dammers et al. [31] and Ene-Iordache et al. [26] reported a time-averaged wall shear stress of 2.5 Pa and 3.9 Pa, respectively, in the radial arteries of mature AV fistula using Doppler ultrasound derived shears. Similarly, a value of 1.04 Pa for the homeostatic wall shear stress in the outflow cephalic veins of mature AV fistula was reported by Corpataux et al. [5], also using Doppler ultrasound, which is consistent with the values we computed in the outflow portion of the proximal veins.
Yet, on the other hand, we observed shear stresses at the anastomoses or in the juxta-anastomotic vessels to be much higher than what is typically considered normal. The threshold of 15 Pa that we chose in order to compute the highly stressed area, is about two times higher than previously reported peak systolic radial arterial shear stresses inside mature fistulae ( Pa [26]) and is about eight times higher than the typical maximum shear stress in peripheral arteries ( Pa [31]). Even the juxta-anastomotic proximal vein segments ( mm from anastomosis) are subjected to mean shear stresses more than 3 times larger than the normal homeostatic value for the cephalic vein. In one patient (no. 4), the wall shear stress in the juxta-anastomotic vein segment is an order of magnitude larger than the “normal” homeostatic venous shear stress (see Table 2 and Fig. 5). The veins could, hypothetically, continue to remodel outward near the anastomoses in order to further reduce the shear stress; this does not appear to be the case here. Therefore, the elevated shear stresses in the venous segment contradict a scenario of a complete homeostatic shear stress restoration.
Furthermore, there was a trend of increasing high shear exposure with the increasing centerline velocity and Reynolds number (see Table 3 and Fig. 6). If there was a complete restoration of homeostatic shear stress, then the vessel wall shear stress would be independent of the inflow velocity or Reynolds number [6]. The high shear stresses at the anastomotic stagnation point could possibly be abated by outward remodeling of the proximal artery, reducing the inflow velocity and Reynolds number. However, this would require a nonlocal communication of mechanosensitive processes. Nevertheless, our result of increasingly high shear with velocity and Reynolds number also contradicts the scenario of complete homeostatic shear stress restoration. We conclude that homeostatic wall shear stresses are not completely restored at or near the anastomoses of the vessels, even in mature and functioning dialysis access fistulae.
The presence of nonhomeostatic shear stress immediately suggests the following question: does nonhomeostatic shear increase the risk of fistula failure? It is generally accepted that a large proportion of fistulae fail due to thrombotic occlusions associated with stenotic lesions brought on by aggressive intimal hyperplasia [11]. The role of high wall shear stress versus low wall shear stress in the development of venous intimal hyperplasia and stenoses remains controversial.
It has been suggested by Carroll et al. [13] that high shear (exceeding 15–20 Pa) can initiate aggressive intimal hyperplasia and patency threatening stenoses, based on computational observations that high shear in stenosis-free vessels is localized at sites which are generally prone to lesion formation. It was hypothesized in Ref. [13] that high shear stress either mechanically damages the endothelium and/or alters the endothelial phenotype, which might transform endothelial cells into a proliferative state leading to intimal hyperplasia. Additionally, in vitro experiments by Huynh et al. [32] reported that endothelial cells show increased apoptosis and increased denudation under turbulent flow conditions similar to those of the venous outflow in a fistula. They suggested that the loss of endothelial cell coverage due to increased shear stress under transitional flow makes the vessel prone to a cascade of events such as platelet adhesion, inflammation, and cytokine secretion, which could lead to cellular proliferation, intimal hyperplasia, and ultimately stenosis.
We hypothesize that the high ( Pa) shear stresses found in the anastomotic and juxta-anastomotic regions of these mature AV fistulae do not represent an immediate detriment to clinical patency for dialysis. These fistulae are all over two years old and were functioning accesses at the time of our ultrasound examinations. Since we cannot measure the venous intimal thickness in the current study, we cannot exclude the possibility of some venous intimal thickening. Nevertheless, there are also no significant stenoses ( venous diameter reduction) in any of the patients. Therefore, we hypothesize that the high wall shear stresses do not lead to patency threatening stenoses. This study provides evidence against the hypotheses of previous studies [13,32], which suggested that high venous shear stresses in AV fistulae can initiate or intensify stenoses and ultimately cause access failure.
Our hypothesis that high shear stress has no immediate detrimental effects to AV fistula patency is consistent with clinical observations. Low flow rates, not high flow rates, are usually associated with an increased risk of thrombotic occlusions [27,33]. Fistulae with venous flow rates mL/min are most at risk for thrombosis, while fistulae with flow rates mL/min have a low relative risk for such events.
Experimental animal models of venous intimal hyperplasia have shown that the extent of intimal thickening is inversely related to shear stress [34,35], suggesting that low shear stress is a factor in promoting aggressive intimal hyperplasia. As such, this “low wall shear stress” hypothesis stands as a converse to the “high wall shear stress” theory as a cause of dialysis access stenosis formation and occlusion. Ene-Iordache and Remuzzi [12] have recently suggested that low shear stress Pa, caused by flow separation, contributes to the development of stenotic lesions in the outflow veins. From computational hemodynamic simulations in idealized fistulae, they concluded that the most common sites of lesion formation were best correlated with sites of low wall shear stress and not with high shear stress. Furthermore, a study by Krishnamoorthy et al. [28] reported a correlation between the low wall shear stress and percent stenosis from an image-based computational hemodynamic study of a porcine AV fistula model.
In our results, the extent of the venous lumen exposed to low time-averaged shear stress is relatively small. This might suggest that the shear stress was either not low enough and/or the surface area coverage was too small to initiate aggressive stenotic lesion formation. Therefore, we concur with Ene-Iordache and Remuzzi [12] and suggest that localized pockets of low wall shear stress be further investigated as a cause of dialysis access venous stenosis.
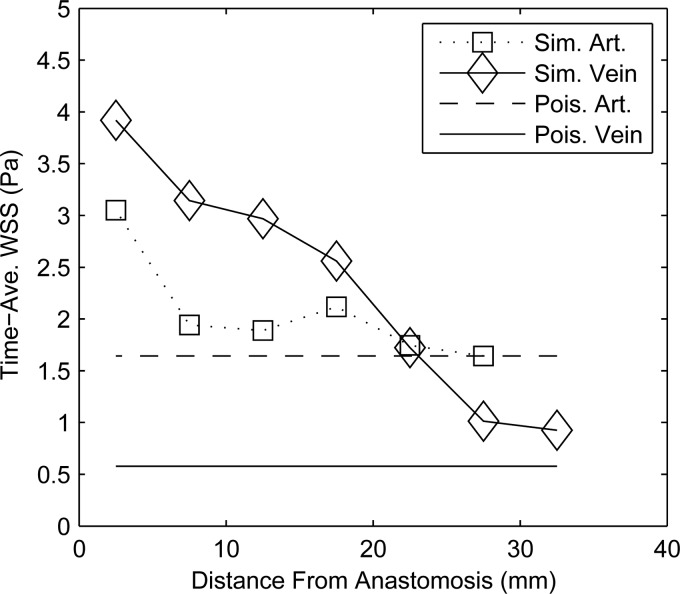
In previous studies of AV fistulae [6,8], Doppler ultrasound velocimetry, in conjunction with Poiseuille's law, has been used to estimate the wall shear stress. Transitional and nonlaminar flows have been reported near the anastomoses in vivo [7], which would render the application of Poiseuille's law inappropriate (i.e., ). Even though the flow is slightly lower and the diameter much greater in the proximal vein than that in the corresponding artery, shear stress near the anastomoses were significantly higher in the veins than in the arteries, as can be seen in Table 2 and Fig. 7. The discrepancy between the simulation and Poiseuille's law is a direct consequence of the transitional fully three dimensional character of the flow. It also highlights the limitation of Poiseuille flow arguments to estimate the shear stress from Doppler ultrasound or phase-contrast magnetic resonance imaging in AV fistulae. In the future, empirical correlations could be developed between the wall shear stress in AV fistulae and the square of the velocity as an alternative to Poiseuille's law.
Fig. 7.
Space- and- time-averaged shear (Eq. (3)) in Pa at 5 mm increments along the proximal artery and proximal vein of patient 3. The symbols represent the simulated values in the artery (Sim. Art.) and vein (Sim. Vein), while the solid lines are the shear predicted by Poiseuille's law for the artery (Pois. Art.) and vein (Pois. Vein) with the same flow rate and average diameter.
We conjecture that there are two main mechanisms which impair the restoration of normal shear stress. First, mechanical homeostasis is typically assumed to have some single “set point”’ target value within a given blood vessel [9]. It is possible, as suggested by Dammers et al. [31] that the target value for the shear during remodeling is rather a “set bandwidth,”’ i.e., there is a finite range of shear values under which normal tissue maintenance occurs. This possibility, however, would seem unlikely here, given that the shear near the anastomoses in our simulations is many times higher than “normal” shear. Typically, much smaller sustained increases in shear () can initiate vessel remodeling and diameter enlargement [6].
Second, the fistula remodeling is driven by competing biological processes which are stimulated by different mechanical stresses, e.g., increased fluid pressure and circumferential stress in the vein wall versus increased shear acting along the endothelial layer. For example, during the initial remodeling phase, the vessel must increase its size and mass through cellular proliferation and increased extracellular matrix synthesis [7]. Increased wall stress due to the increased transmural venous pressure is known to stimulate matrix synthesis and smooth muscle cell proliferation [36], which favor increases in wall mass. On the contrary, the increased shear on the endothelium upregulates nitric-oxide (which inhibits smooth muscle cell proliferation) and increases the production of matrix metalloproteinases [37] (which degrade the extracellular matrix) which, in combination, possibly disfavors increases in wall mass. When remodeling ceases, it could be because such competing mechanobological processes are in balance with one another [38]. It is, therefore, possible that the kinetics of the fistulae growth and remodeling in this study have reached a “stable equilibrium point” and thus do not continue remodeling. The margin of stability of these equilibria and, therefore, the clinical function of the fistulae, is an important topic for further study.
Study Limitations.
We acknowledge the small sample size of this study as a limitation. As such, only some of the correlations presented in Table 3 are statistically significant at the 95% level. Larger sample sizes are thus needed to ensure a robust validation of these correlations. Nevertheless, this study represents one of the largest cohorts to date for patient specific computational hemodynamic studies of AV fistulae. Second, we do not have longitudinal data of the fistulae anatomies. We do not know if significant remodeling was occurring either immediately before or after the time of our examination. Nonetheless, we would consider such an occurrence unlikely given that the fistulae were at least two years old and were fully functioning at the time of the examination. Most of the remodeling occurs in a 12 week period immediately after fistula creation. Remodeling after the initial 12 week period is rare [27,31].
Conclusions
We present evidence of high nonhomeostatic shear stresses and their lack of a negative effect on the clinical functionality of these fistulae. Instead, we suggest that there is a partial but incomplete restoration of a homeostatic shear stress. Our study further provides evidence against the “high wall shear stress” theory of dialysis access site failure due to occlusive stenoses [32]. Therefore, we suggest that the alternative “low wall shear stress” theory [12] needs to be further investigated as a factor in fistula stenosis formation and failure. Furthermore, due to the transitional flows generated at the anastomoses, measurements of shear stress based on velocity measurements and simplifying assumptions such as Poiseuille's law are highly compromised in AV fistulae. Finally, our results here confirm previous computational hemodynamic studies [13,30] of AV fistulae, which reported concentrations of very high wall shear stress in the proximal vein and at the anastomoses. Our study strengthens this evidence by collecting data from multiple patients rather than a single patient. In future studies, it is important to study the fistulae longitudinally, particularly in the first three months after surgery, when remodeling and patency loss are at their most rapid rates [5,27]. Last, we hope to quantify the hemodynamics in failing fistula in future studies in order to understand the specific mechanism whereby mechanical stresses initiate pathological remodeling.
Acknowledgment
This work has been financially supported by an R21 grant from NIDDK (Grant No. DK08-1823), by a fellowship from the Washington NASA Space Grant Consortium (NASA Grant No. NNX10AK64H), and by NSF CAREER Award (Grant No. CBET-0748133), a Washington Royalty Research Fund grant. We would like to thank Dr. Suhail Ahmad and Lori Linke at the Scribner Kidney Center (Northwest Kidney Centers, Seattle, WA) for their assistance with the imaging studies of the dialysis patients and Edward Stutzman of UW Vascular Surgery for help in performing the ultrasound examinations. We would also like to thank Ultrasonix Medical Corporation for the use of their SonixTouch ultrasound scanner for the patient imaging studies.
Appendix: Computational Mesh Resolution Study
A test of computational mesh resolution was performed to determine that the spatial and temporal resolution were adequate in the simulation. We studied patient 1 in more detail as a representative case. Successive meshes were implemented with a prismatic boundary layer and tetrahedral cells. Characteristic tetrahedra widths are 0.40, 0.25, and 0.15 mm, corresponding to cell counts of 0.338 × 106, 1.35 × 106, and 5.92 × 106, respectively. The time step size was 0.4 μs to 0.25 μs to 0.2 μs in each refinement. The flow was computed over five cardiac cycles. We compared the TAWSS between successive refinements. The surface-area-weighted root-mean-square difference of the TAWSS was between the 0.338 × 106 and 1.35 × 106 mesh and was between the 1.35 and 5.92 × 106 mesh. Similarly, the weighted RMS difference of the duty factor was and , using a threshold value of 10 Pa and 17% and 4.2%, using a threshold value of 15 Pa. The largest differences were computed at the anastomosis near the impingement region.
The large differences are due to the fact that the flow is chaotic and each simulated cycle represents a different realization of a stochastic process. For example, the time averaged shear stress between individual cardiac cycles varied by as much 10–20% at the anastomosis impingement point. With a finite number of cycles computed, the error between the computed averaged shear stress and true averaged shear stress is approximately , where is the number of cycles and is the standard deviation of the process. With five cycles computed and a standard deviation of 15%, the error of the average due to the finite number of cycles is . Recomputing the averaged root-mean-square difference of the TAWSS, but excluding the anastomosis from the calculation (where the flow is most chaotic), we calculate a difference in the wall shear stress as between the coarsest and medium mesh and between the medium and the finest mesh. We therefore consider the contribution of the mesh discretization to the error to be about 5%.
We also estimate the thickness of the boundary layer at the impingement region using the theory of Phares et al. [29]. Their theory was derived from solutions of the boundary layer equations for circular jets impinging onto flat walls. The boundary layer is estimated as
| (A1) |
where is the kinematic viscosity, is the diameter of the jet, is the peak velocity of the jet, and is a constant approximately equal to 3. Using the diameter of the artery, 4.6 mm, and the peak inflow velocity, 1.26 m/s, we obtain a boundary layer thickness of 0.3 mm. The prismatic near-wall computational cells are 0.08–0.12 mm in thickness and are four layers thick. The total prism layer thickness is about 0.4 mm.
The relatively large differences calculated here are, therefore, attributable to the chaotic flow field, rather than the discretization error. The variability in the shear stress between the two finest meshes contributes a small portion to the error. This error is comparable to, but not larger than, the uncertainty in the geometric () and physiological parameters (e.g., flow rate: ) from the patient specific models extracted from medical images, which can compound uncertainties in wall shear stress to [19].
Contributor Information
Patrick M. McGah, Research Assistant, Department of Mechanical Engineering, University of Washington, Stevens Way, Box 352600, Seattle, WA 98195, e-mail: pmcgah@uw.edu.
Daniel F. Leotta, Research Engineer, Applied Physics Laboratory, Center for Industrial and Medical Ultrasound, University of Washington, Box 355640, Seattle, WA 98195
Kirk W. Beach, Professor Emeritus
R. Eugene Zierler, Professor, Department of Surgery, Division of Vascular Surgery, University of Washington, Box 356410, Seattle, WA 98195
Alberto Aliseda, Associate Professor, University of Washington, Department of Mechanical Engineering, Stevens Way, Box 352600, Seattle, WA 98195.
References
- [1]. U.S. Renal Data System, 2011, “USRDS 2011 Annual Data Report: Atlas of End-Stage-Renal-Disease in the United States,” Technical Report, National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases, Bethesda, MD. [Google Scholar]
- [2]. Tordoir, J. H. M. , Rooyens, P. , Dammers, R. , van der Sande, F. M. , de Haan, M. , and Yo, T. I. , 2003, “Prospective Evaluation of Failure Modes in Autogenous Radiocephalic Wrist Access for Hemodialysis,” Nephrol. Dial. Transplant., 18, pp. 378–383. 10.1093/ndt/18.2.378 [DOI] [PubMed] [Google Scholar]
- [3]. Gibson, K. D. , Gilen, D. L. , Caps, M. T. , Kohler, T. R. , Sherrard, D. J. , and Stehman-Breen, C. O. , 2001, “Vascular Access Survival and Incidence of Revisions: A Comparison of Prosthetic Grafts, Simple Autogenous Fisulas, and Venous Transposition Fistulas From the United States Renal Data System Dialysis Morbidity and Mortality Study,” J. Vasc. Surg., 34(4), pp. 694–700. 10.1067/mva.2001.117890 [DOI] [PubMed] [Google Scholar]
- [4]. Lauvao, L. S. , Ihnat, D. M. , Goshima, K. R. , Chavez, L. , Gruessner, A. C. , and Mills, J. L., Sr. , 2009, “Vein Diameter is the Major Predictor of Fistula Maturation,” J. Vasc. Surg., 49, pp. 1499–14504. 10.1016/j.jvs.2009.02.018 [DOI] [PubMed] [Google Scholar]
- [5]. Corpataux, J. M. , Haesler, E. , Silacci, P. , Res, H. B. , and Hayoz, D. , 2002, “Low-Pressure Environment and Remodelling of the Forearm Vein in Brescia-Cimino Haemodialysis Access,” Nephrol. Dial. Transplant., 17, pp. 1057–1062. 10.1093/ndt/17.6.1057 [DOI] [PubMed] [Google Scholar]
- [6]. Kamiya, A. and Togawa, T. , 1980, “Adaptive Regulation of Wall Shear Stress to Flow Change in the Canine Carotid Artery,” Am. J. Physiol., 239(1), pp. H14–H21. [DOI] [PubMed] [Google Scholar]
- [7]. Zarins, C. K. , Zatina, M. A. , Giddens, D. P. , Ku, D. N. , and Glagov, S. , 1987, “Shear Stress Regulation of Artery Lumen Diameter in Experimental Atherogenesis,” J. Vasc. Surg., 5, pp. 413–420. [PubMed] [Google Scholar]
- [8]. Girerd, X. , London, G. , Boutouyrie, P. , Jaques Mourad, J. , Safar, M. , and Laurent, S. , 1996, “Remodeling of the Radial Artery in Response to a Chronic Increase in Shear Stress,” Hypertension, 27, pp. 799–803. 10.1161/01.HYP.27.3.799 [DOI] [PubMed] [Google Scholar]
- [9]. Humphrey, J. D. , 2008, “Vascular Adaptation and Mechanical Homeostasis at Tissue, Cellular, and Sub-Cellular Levels,” Cell Biochem. Biophys., 50, pp. 73–78. 10.1007/s12013-007-9002-3 [DOI] [PubMed] [Google Scholar]
- [10]. Owens, C. D. , Wake, N. , Kim, J. M. , Hentschel, D. , Conte, M. S. , and Schanzer, A. , 2010, “Endothelial Function Predicts Positive Arterial-Venous Fistula Remodeling in Subjects With Stage IV And V Chronic Kidney Disease,” J. Vasc. Access., 11(4), pp. 329–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Dixon, B. S. , 2006, “Why Don't Fistulas Mature?,” Kidney Int., 70, pp. 1413–1422. 10.1038/sj.ki.5001747 [DOI] [PubMed] [Google Scholar]
- [12]. Ene-Iordache, B. and Remuzzi, A. , 2012, “Disturbed Flow in Radial-Cephalic Arteriovenous Fistulae for Haemodialysis: Low and Oscillating Shear Stress Locates the Sites of Stenosis,” Nephrol. Dial. Transplant., 27(1), pp. 358–368. 10.1093/ndt/gfr342 [DOI] [PubMed] [Google Scholar]
- [13]. Carroll, G. T. , McGloughlin, T. M. , Burke, P. E. , Egan, M. , Wallis, F. , and Walsh, M. T. , 2011, “Wall Shear Stresses Remain Elevated in Mature Arteriovenous Fistulas: A Case Study,” ASME J. Biomech. Eng., 133(2), p. 021003. 10.1115/1.4003310 [DOI] [PubMed] [Google Scholar]
- [14]. Kharboutly, Z. , Deplano, V. , Bertrand, E. , and Legallais, C. , 2010, “Numerical and Experimental Study of Blood Flow Through a Patient-Specific Arteriovenous Fistula Used for Hemodialysis,” Med. Eng. Phys., 32, pp. 111–118. 10.1016/j.medengphy.2009.10.013 [DOI] [PubMed] [Google Scholar]
- [15]. Leotta, D. F. , Primozich, J. F. , Beach, K. W. , Bergelin, R. O. , and Strandness, D. E., Jr. , 2001, “Serial Measurement of Cross-Sectional Area in Peripheral Vein Grafts Using Three-Dimensional Ultrasound,” Ultrasound Med. Biol., 27(1), pp. 61–68. 10.1016/S0301-5629(00)00296-9 [DOI] [PubMed] [Google Scholar]
- [16]. Leotta, D. F. , Primozich, J. F. , Beach, K. W. , Bergelin, R. O. , Zierler, R. E. , and Strandness, D. E., Jr. , 2003, “Remodeling in Peripheral Vein Graft Revisions: Serial Study With Three-Dimensional Ultrasound Imaging,” J. Vasc. Surg., 37(4), pp. 798–807. 10.1067/mva.2003.137 [DOI] [PubMed] [Google Scholar]
- [17]. Legget, M. E. , Leotta, D. F. , Bolson, E. L. , McDonald, J. A. , Martin, R. W. , Li, X. N. , Otta, C. M. , and Sheehan, F. H. , 1998, “System for Quantitative Three-Dimensional Echocardiography of the Left Ventricle Based on a Magnetic-Field Position and Orientation Sensing System,” IEEE Trans. Biomed. Eng., 45(4), pp. 494–504. 10.1109/10.664205 [DOI] [PubMed] [Google Scholar]
- [18]. ANSYS, Inc., 2009, “ANSYS® FLUENT ® Theory Guide,” Release 12.1 ed., Cannonsburg, PA. [Google Scholar]
- [19]. Lee, S.-W. , and Steinman, D. A. , 2007, “On the Relative Importance of Rheology for Image-Based CFD Models of the Carotid Bifurcation,” ASME J. Biomech. Eng., 129(2), pp. 273–279. 10.1115/1.2540836 [DOI] [PubMed] [Google Scholar]
- [20]. Womersley, J. R. , 1955, “Method for the Calculation of Velocity, Rate of Flow and Viscous Drag in Arteries When the Pressure Gradient is Known,” J Physiol., 127, pp. 553–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Vignon-Clemente, I. , Figueroa, C. A. , Jansen, K. E. , and Taylor, C. A. , 2010, “Outflow Boundary Conditions for Three-Dimensional Simulations of Non-Periodic Blood Flow and Pressure Fields in Deformable Arteries,” Comput. Methods Biomech. Biomed. Eng., 13(5), pp. 525–640. [DOI] [PubMed] [Google Scholar]
- [22]. Schwartz, L. B. , Purut, C. M. , O'Donohoe, M. K. , Smith, P. K. , Otto Hagan, P. , and McCann, R. L. , 1991. “Quantitation of Vascular Outflow by Measurement of Impedance,” J. Vasc. Surg., 14(3), pp. 353–363. 10.1016/0741-5214(91)90088-C [DOI] [PubMed] [Google Scholar]
- [23].Supplementary material provides a description of the numerical scheme as well as numeric values used for the resistance-capacitance boundary conditions.
- [24]. Zierler, B. K. , Kirkman, T. R. , Kraiss, L. W. , Reiss, W. G. , Horn, J. R. , Bauer, L. A. , Clowes, A. W. , and Kohler, T. R. , 1992, “Accuracy of Duplex Scanning for Measurement of Arterial Volume Flow,” J. Vasc. Surg., 16(4), pp. 520–526. 10.1016/0741-5214(92)90159-6 [DOI] [PubMed] [Google Scholar]
- [25]. Lee, S.-W. , Antiga, L. , and Steinman, D. A. , 2009, “Correlations Among Indicators of Disturbed Flow at the Normal Carotid Bifurcation,” ASME J. Biomech. Eng., 131(6), p. 061013. 10.1115/1.3127252 [DOI] [PubMed] [Google Scholar]
- [26]. Ene-Iordache, B. , Mosconi, L. , Antiga, L. , Bruno, S. , and Anghileri, A. , 2003, “Radial Artery Remodeling in Response to Shear Stress Increase Within Arteriovenous Fistula for Hemodialysis Access,” Endothelium, 10, pp. 95–102. 10.1080/10623320303365 [DOI] [PubMed] [Google Scholar]
- [27]. Wong, V. , Ward, R. , Taylor, J. , Selvakumar, S. , How, T. V. , and Bakran, A. , 1996, “Factors Associated With Early Failure of Arteriovenous Fistulae for Haemodyialysis Access,” Eur. J. Vasc. Endovasc. Surg., 12, pp. 207–213. 10.1016/S1078-5884(96)80108-0 [DOI] [PubMed] [Google Scholar]
- [28]. Krishnamoorthy, M. K. , Banerjee, R. K. , Wang, Y. , Zhang, J. , Roy, A. S. , Khoury, S. F. , Arend, L. J. , Rudich, S. , and Roy-Chaudhury, P. , 2008, “Hemodynamic Wall Shear Stress Profiles Influence the Magnitude and Pattern of Stenosis in a Pig AV Fistula,” Kidney Int., 74, pp. 1410–1419. 10.1038/ki.2008.379 [DOI] [PubMed] [Google Scholar]
- [29]. Phares, D. J. , Smedley, G. T. , and Flagan, R. D. , 2000, “The Wall Shear Stress Produced by the Normal Impingement of a Jet on a Flat Surface,” J. Fluid Mech., 418, pp. 351–375. 10.1017/S002211200000121X [DOI] [Google Scholar]
- [30]. Ene-Iordache, B. , Mosconi, L. , Remuzzi, G. , and Remuzzi, A. , 2001, “Computational Fluid Dynamics of a Vascular Access Case for Hemodialysis,” ASME J. Biomech. Eng., 123(3), pp. 284–293. 10.1115/1.1372702 [DOI] [PubMed] [Google Scholar]
- [31]. Dammers, R. , Tordoir, J. H. M. , Kooman, J. P. , Welten, R. , Hameleers, J. M. M. , Kitslaar, P. , and Hoeks, A. P. G. , 2005, “The Effect of Flow Changes on the Arterial System Proximal to an Arteriovenous Fistula for Hemodialysis,” Ultrasound Med Biol, 31(10), pp. 1327–1333. 10.1016/j.ultrasmedbio.2005.03.017 [DOI] [PubMed] [Google Scholar]
- [32]. Huynh, T. N. , Chacko, B. K. , Teng, X. , Brott, B. C. , Allon, M. , Kelpke, S. S. , Thompson, J. A. , Patel, R. P. , and Anayiotos, A. S. , 2007, “Effects of Venous Needle Turbulence During Ex Vivo Hemodialysis on Endothelial Morphology and Nitric Oxide Formation,” J. Biomech., 40, pp. 2158–2166. 10.1016/j.jbiomech.2006.10.028 [DOI] [PubMed] [Google Scholar]
- [33]. Basile, C. , Ruggieri, G. , Vernaglione, L. , Montanaro, A. , and Giordano, R. , 2004, “The Natural History of Autogenous Radio-Cephalic Wrist Arteriovenous Fistulas of Haemodialysis Patients: A Prospective Obervational Study,” Nephrol. Dial. Transplant., 19, pp. 1231–1236. 10.1093/ndt/gfh073 [DOI] [PubMed] [Google Scholar]
- [34]. Jiang, Z. , Wu, L. , Miller, B. L. , Goldman, D. R. , Fernandez, C. M. , Abouhamze, Z. S. , Ozaki, C. K. , and Berceli, S. A. , 2003, “A Novel Vein Graft Model: Adaption to Differential Flow Environments,” Am. J. Physiol: Heart Circ. Physiol., 286, pp. 240–245. 10.1152/ajpheart.00760.2003 [DOI] [PubMed] [Google Scholar]
- [35]. Meyerson, S. L. , Skelly, C. L. , Curi, M. A. , Shakur, U. M. , Vosicky, J. E. , Glagov, S. , Christen, T. , Gabbiani, G. , and Schwartz, L. B. , 2001, “The Effects of Extremely Low Shear Stress on Cellular Proliferation and Neointimal Thickening in the Failing Bypass Graft,” J. Vasc. Surg., 34(1), pp. 90–97. 10.1067/mva.2001.114819 [DOI] [PubMed] [Google Scholar]
- [36]. Ben Driss, A. , Bennessiano, J. , Poitevin, P. , Levy, B. I. , and Baptiste Michel, J. , 1997, “Arterial Expansive Remodeling Induced by High Flow Rates,” Am. J. Physiol., 272(2), pp. H851–H858. [DOI] [PubMed] [Google Scholar]
- [37]. Tronc, F. , Mallat, Z. , Lehoux, S. , Wassef, M. , Esposito, B. , and Tedugui, A. , 2000, “Role of Matrix Matalloproteinases in Blood Flow-Induced Arterial Enlargement,” Arterioscler., Thromb., Vasc. Biol., 20, pp. e120–e126. 10.1161/01.ATV.20.12.e120 [DOI] [PubMed] [Google Scholar]
- [38]. Valentín, A. , Cardamone, L. , Baek, S. , and Humphrey, J. D. , 2009, “Complementary Vasoactivity and Matrix Remodelling in Arterial Adaptations to Altered Flow and Pressure,” J. R. Soc., Interface, 6, pp. 293–306. 10.1098/rsif.2008.0254 [DOI] [PMC free article] [PubMed] [Google Scholar]