Comparison of Approaches to Quantify Arterial Damping Capacity From Pressurization Tests on Mouse Conduit Arteries

Lian Tian; Zhijie Wang; Roderic S Lakes; Naomi C Chesler

doi:10.1115/1.4024135

. 2013 Apr 24;135(5):0545041–0545046. doi: 10.1115/1.4024135

Comparison of Approaches to Quantify Arterial Damping Capacity From Pressurization Tests on Mouse Conduit Arteries

Lian Tian ¹, Zhijie Wang ², Roderic S Lakes ³, Naomi C Chesler ^4,¹

PMCID: PMC3705827 PMID: 24231965

Short abstract

Large conduit arteries are not purely elastic, but viscoelastic, which affects not only the mechanical behavior but also the ventricular afterload. Different hysteresis loops such as pressure-diameter, pressure-luminal cross-sectional area (LCSA), and stress–strain have been used to estimate damping capacity, which is associated with the ratio of the dissipated energy to the stored energy. Typically, linearized methods are used to calculate the damping capacity of arteries despite the fact that arteries are nonlinearly viscoelastic. The differences in the calculated damping capacity between these hysteresis loops and the most common linear and correct nonlinear methods have not been fully examined. The purpose of this study was thus to examine these differences and to determine a preferred approach for arterial damping capacity estimation. Pressurization tests were performed on mouse extralobar pulmonary and carotid arteries in their physiological pressure ranges with pressure (P) and outer diameter (OD) measured. The P-inner diameter (ID), P-stretch, P-Almansi strain, P-Green strain, P-LCSA, and stress–strain loops (including the Cauchy and Piola-Kirchhoff stresses and Almansi and Green strains) were calculated using the P-OD data and arterial geometry. Then, the damping capacity was calculated from these loops with both linear and nonlinear methods. Our results demonstrate that the linear approach provides a reasonable approximation of damping capacity for all of the loops except the Cauchy stress-Almansi strain, for which the estimate of damping capacity was significantly smaller (22 ± 8% with the nonlinear method and 31 ± 10% with the linear method). Between healthy and diseased extralobar pulmonary arteries, both methods detected significant differences. However, the estimate of damping capacity provided by the linear method was significantly smaller (27 ± 11%) than that of the nonlinear method. We conclude that all loops except the Cauchy stress-Almansi strain loop can be used to estimate artery wall damping capacity in the physiological pressure range and the nonlinear method is recommended over the linear method.

Introduction

Large conduit arteries generally are not elastic, but viscoelastic, which is evidenced via the force-deformation or stress–strain hysteresis loop. The viscoelastic behavior is derived from both smooth muscle cells (SMCs) and components of the extracellular matrix [1–9]. Increased intima-medial thickening, such as that which occurs with both systemic and pulmonary hypertension [10,11], is known to increase arterial viscoelasticity [12]. The viscoelastic behavior of large conduit arteries can protect the artery wall from being overstretched by reducing the dynamic stresses and strains [1], but the overall impact on ventricular function remains unclear. In vitro experiments have suggested that increased conduit artery viscoelasticity increases stiffness, which increases the load on the heart [1], whereas in vivo data have suggested that increased viscoelasticity via SMC activation improves right ventricular-vascular coupling, which suggests a decreased load on the heart [13]. In order to better understand the effect of arterial viscoelasticity on health and disease, a better understanding of arterial viscoelasticity measurement methods is required.

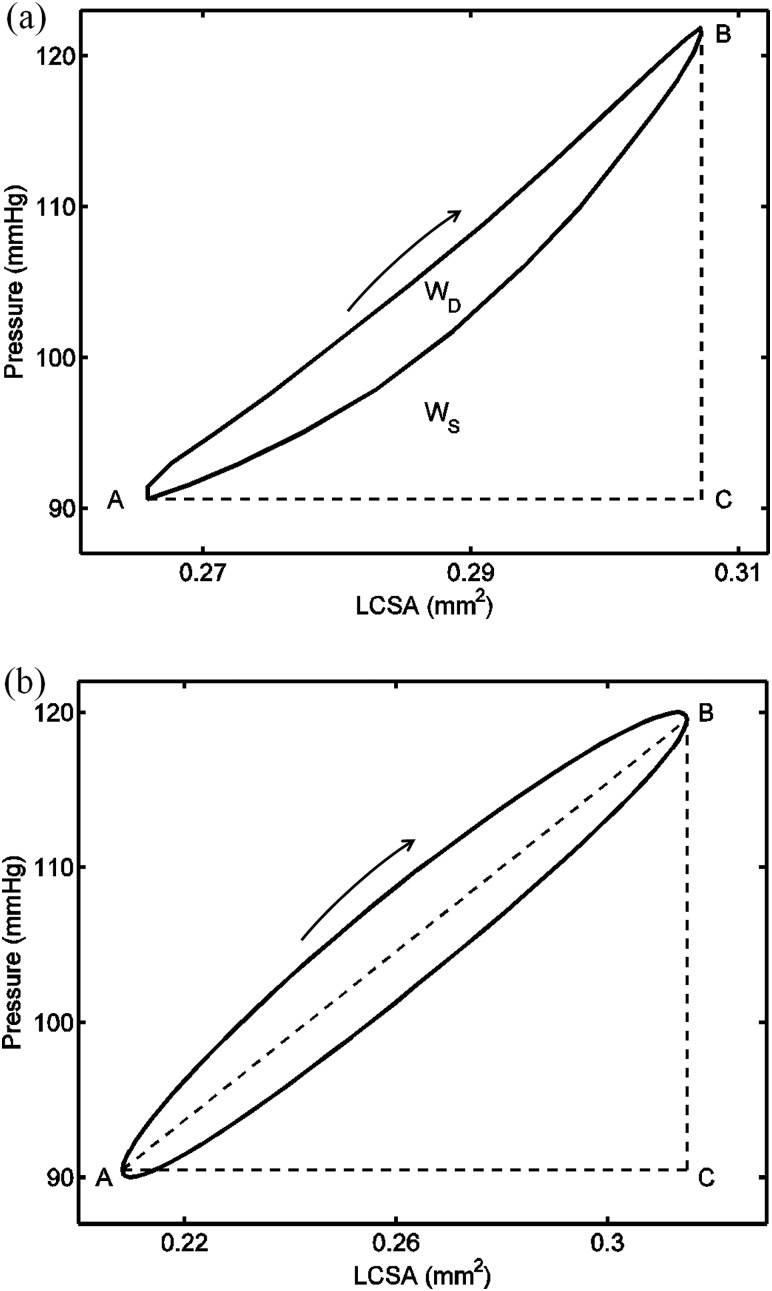
Arterial viscoelastic losses are most often characterized by the damping capacity, which is associated with the ratio of the dissipated energy to the stored energy during one dynamic cycle and can be calculated from a hysteresis loop [14–17]. From the stress–strain or pressure-LCSA loop, the dissipated energy is calculated as the hysteresis loop area and the stored energy is obtained by integrating the area under the loading curve (see Fig. 1(a)) [3,16,18]. This approach accurately accounts for the nonlinear behavior. Frequently, however, a linear approach is used in which the hysteresis loop is assumed to be elliptical and the stored energy is calculated as the sum of the elastic energy and half of the dissipated energy. The elastic energy is calculated as the area of the triangle defined by (A) the point on the hysteresis loop with the minimum abscissa value (typically deformation, stretch or strain), (B) the point on the loop with maximum abscissa value, and (C) a point not on the hysteresis loop with the maximum abscissa value and ordinate value at the minimum abscissa point (see Fig. 1(b)) [14,17]. With elastic energy separated from the total energy, the damping capacity can then be calculated. However, the accuracy of this method for nonlinearly elastic materials such as arteries, even in the physiological pressure range, remains unclear.

Fig. 1 — Illustration of the estimation of the damping capacity (a) with the nonlinear method on a clockwise pressure-luminal cross-sectional area (P-LCSA) loop obtained from a carotid artery at 10 Hz, and (b) with the linear method on an elliptical P-LCSA loop. Points A and B are the points corresponding to the maximum and minimum LCSA in the hysteresis loop, respectively. Point C is the point with the maximum LCSA value and the pressure value at point A. Here, *W_D* is the loop area and *W_S* is the area under the loading (upper) curve $\vec{A B}$ and above the straight line AC. Loading curves are indicated by the arrow. Note that the hysteresis loop in (a) shows a weak nonlinearity in that the loop deviates slightly from an elliptical shape.

Depending on whether measurements are obtained in vivo or in vitro and the available geometry data, different hysteresis loops are typically obtained and from which the damping capacity can be calculated: pressure (P)-OD, P-ID, P-LCSA, P-stretch, P-Green strain, P-Almansi strain, Cauchy stress-Almansi strain, the second Piola-Kirchhoff stress-Green strain, etc. Physically, only areas calculated from the P-LCSA and the conjugate stress–strain loops correspond to the energy and provide an accurate calculation of the stored, dissipated, and elastic energy. Nevertheless, loops created from other variables, sometimes easily measured or experimentally estimated, may also provide a good estimate of damping capacity. For example, pressure-inner diameter, pressure-stretch, and Cauchy stress-Almansi strain loops have been used to estimate damping capacity in the existing literature [18–20]. However, the differences in damping capacity estimated from these loops have not been examined. Therefore, this study sought to examine the differences between estimates of damping capacity from loops constructed from different variables with either a linear or nonlinear method.

Materials and Methods

Materials.

All procedures were approved by the Institutional Animal Care and Use Committee at the University of Wisconsin-Madison. Data from two strains of mice were used. The first is a transgenic strain (Col1a1) in which type I collagen is resistant to degradation in homozygous mutant mice (see Refs. [20,21] for more details on the mouse strain); there are no known defects in homozygous wild type mice. Left common carotid arteries were harvested from thirteen one-year old and five two-year old wildtype (Col1a1^+/+) and transgenic (Col1a1^R/R) mice after euthanasia. The second is an inbred strain of mouse (C57BL/6J), which is often used as a background strain for transgenic mice and is also commonly used to investigate the effects of hypoxia-induced pulmonary hypertension on pulmonary vascular remodeling [19,22–25]. Extralobar left main pulmonary arteries were harvested from five male mice exposed only to control (normoxic) conditions and another five male mice exposed to normobaric hypoxia (10% O₂) for 21 days and also injected once weekly with vascular endothelial growth factor inhibitor (SU5416, 20 mg/kg, intraperitoneal injection) to worsen the degree of pulmonary hypertension in these mice [26,27]. More details are provided in Table 1.

Table 1.

Summary of mouse strain, number, sex, age, and the treatment

Artery	Mouse strain	n	Sex	Age	Exposure/treatment
LCCA	Col1a1^+/+	3	1F, 2M	24 ± 0.1 months	None
	Col1a1^R/R	3	2F, 1M	23 ± 0.1 months	None
	Col1a1^+/+	5	2F, 3M	12 ± 0.1 months	None
Col1a1^R/R	8	4F, 4M	12 ± 0.1 months	None
LPA	C57BL/6J	5	5M	13 ± 1 weeks	None
5	5M	13 ± 1 weeks	21 days of hypoxia+ SU5416

Open in a new tab

Note: LCCA denotes the left common carotid artery; LPA denotes the left pulmonary artery; n is the number of mice; F denotes female; M denotes male; and SU5416, is a vascular endothelial growth factor inhibitor.

We chose these data because they represent healthy and diseased states for both systemic and pulmonary conduit arteries. This diversity allows us to check the robustness of the approaches for calculating the damping capacity for large arteries of different stiffness, thickness, and composition.

Isolated Vessel Pressurization Test.

The arteries were mounted to glass microcannulas (outer diameter of tip = 410 μm) in an arteriograph chamber (Living Systems Instrumentation, Burlington, VT) and longitudinally stretched (140% for left pulmonary arteries, an estimate of in vivo stretch, and 150% for left common carotid arteries, average measured in vivo stretch). Neither buckling nor collapse was observed during the test in the pressure range applied. The arteries were perfused and superfused with calcium- and magnesium-free phosphate-buffered saline (PBS). An oscillatory flow pump (EnduraTec TestBench, Bose Corporation, Eden Prairie, MN) was used to achieve sinusoidal pressurization at 10–50 mm Hg for the left pulmonary artery and 90–120 mm Hg for the carotid at the frequencies of 1, 5, and 10 Hz. During the dynamic tests, the pressure and outer diameter were simultaneously recorded by IonWizard software (Version 6.0, IonOptix, Milton, MA) using in-line pressure transducers (with an error of 1%; APT300, Harvard Apparatus, March-Hugstetten, Germany) with high-frequency amplifiers (Module TAM-A, Harvard Apparatus, March-Hugstetten, Germany) to measure pressure at an acquisition frequency of 250 Hz and a CCD camera (IonOptix, Milton, MA) connected to an inverted microscope (Olympus, Center Valley, PA) to measure the outer diameter (OD) at 4× magnification with an acquisition frequency of 240 Hz. The pressure-OD data during the dynamically steady state (usually after four sinusoidal cycles) were used for analysis. More details about the test system and protocols can be found elsewhere [19–21,25].

Calculations: Geometry, Stretch, and Stress.

To estimate the inner diameter (ID) and the circumferential stretch and strain of carotids at different pressures a short ring, approximately 0.5 mm long in the longitudinal direction, was cut from the proximal end before the dynamic test and cut open to obtain the strain- or stress-free state. A scaled digital image of the cross-sectional area of the opened artery ring was then obtained with an inverted microscope (TE-2000, Nikon, Melville, NY). Combining the geometry of carotids at the strain-free state (with a random error of less than 4%) and the longitudinal stretch and OD during the dynamic test, the ID during the dynamic test was estimated by assuming incompressibility. The circumferential stretch ( $λ$ ) at the mid-wall of the strain-free state was calculated as the ratio of the circumferences of the mid-wall at the strain-free state (C ₀) and at different pressures (C_P), i.e., $λ = C_{P} / C_{0}$ . Detailed calculations can be found elsewhere [28].

For the left pulmonary arteries, a slightly different procedure to estimate the ID and stretch was used due to its thin wall. The OD at zero pressure during the pressurization test was taken as the reference length (OD₀). The wall thickness was also obtained optically at a pressure of 40 mm Hg. Assuming incompressibility, the ID at different pressures was then calculated [20,21]. From the optically measured OD during the dynamic test, the circumferential stretch was calculated as $λ = {OD / OD}_{0}$ .

With the OD, ID, and stretch known, the stress and strain were calculated as follows. The mid-wall circumferential Green strain (E) and Almansi strain ( $e$ ) are $E = (1 / 2) (λ^{2} - 1)$ and $e = (1 / 2) (1 - (1 / λ^{2}))$ , respectively, where $λ$ is the mid-wall circumferential stretch. The luminal cross-sectional area (LCSA) is calculated as $LCSA = π {ID}^{2} / 4$ . Because the thickness-to-ID ratios were 0.025 ± 0.003 and 0.052 ± 0.012 for left pulmonary arteries at 10 mm Hg and carotids at 90 mm Hg, respectively, a thin-walled assumption was adopted for simplicity. With this assumption, the average circumferential Cauchy stress can be estimated as $σ = P \cdot ID / 2 h$ [7], where h is the arterial wall thickness of the artery at an internal pressure P. The second Piola-Kirchhoff stress can be expressed as $S = σ / λ^{2}$ .

Calculation: Damping Capacity.

Nonlinear and linear methods were used to calculate the damping capacity from a dynamic hysteresis loop, as shown in Fig. 1. For the nonlinear method, the total stored energy (W_S) due to loading was calculated as the area enclosed by the loading (upper) curve $\vec{A B}$ and the two straight lines BC and CA (see Fig. 1(a)). The dissipated energy (W_D) is defined as the area of the hysteresis loop for any x-y pair of deformation/strain and pressure/stress [3,14,15,17], i.e., $W_{D} = \int_{A}^{B} y \cdot d x$ + $\int_{B}^{A} y \cdot d x$ , with the first and second integrals using the loading (upper) and unloading (lower) curves, respectively. The damping capacity (d) is then defined as

d = \frac{W_{D}}{W_{S}}

(1)

Since the product of the pressure and LCSA is the total external mechanical work done by the blood in vivo or PBS in the pressurization test in vitro, we chose the damping capacity calculated from the P-LCSA loop as a reference for comparison with that from other hysteresis loops.

For the linear method, it is assumed that the hysteresis loop has a slanted elliptical shape. In this case, the stored energy is calculated as the area enclosed by the straight lines AB, BC, and CA plus half the dissipated energy (see Fig. 1(b)) and the area of the triangle ABC is the stored elastic energy during the loading phase W_E (see Fig. 1(b)) [14,15]. The damping capacity, using this linear assumption ( $d'$ ), was calculated as

d' = \frac{W_{D}}{W_{S}'} = \frac{W_{D}}{W_{E} + \frac{1}{2} W_{D}}

(2)

Note that the linear method is only strictly valid for an elliptical loop generated by a linear material. This method was applied in order to examine its appropriateness for the approximation for nonlinear materials (i.e., arteries) loaded in their physiological pressure ranges.

Statistics.

All of the data are presented as mean ± SD unless specified otherwise. Simple linear correlations were determined between the damping capacity calculated from different load-deformation loops and between the nonlinear and linear methods. The Anderson-Darling test was used to test the normal distribution of the damping capacity in each group and Student's t-test was used to compare the average damping capacity between groups. The paired t-test was used to compare the damping capacity calculated from the pressure-LCSA, Cauchy stress-Almansi strain, and the second Piola-Kirchhoff stress-Green strain loops and between the nonlinear and linear methods. A P-value of less than 0.05 was considered significant.

Results

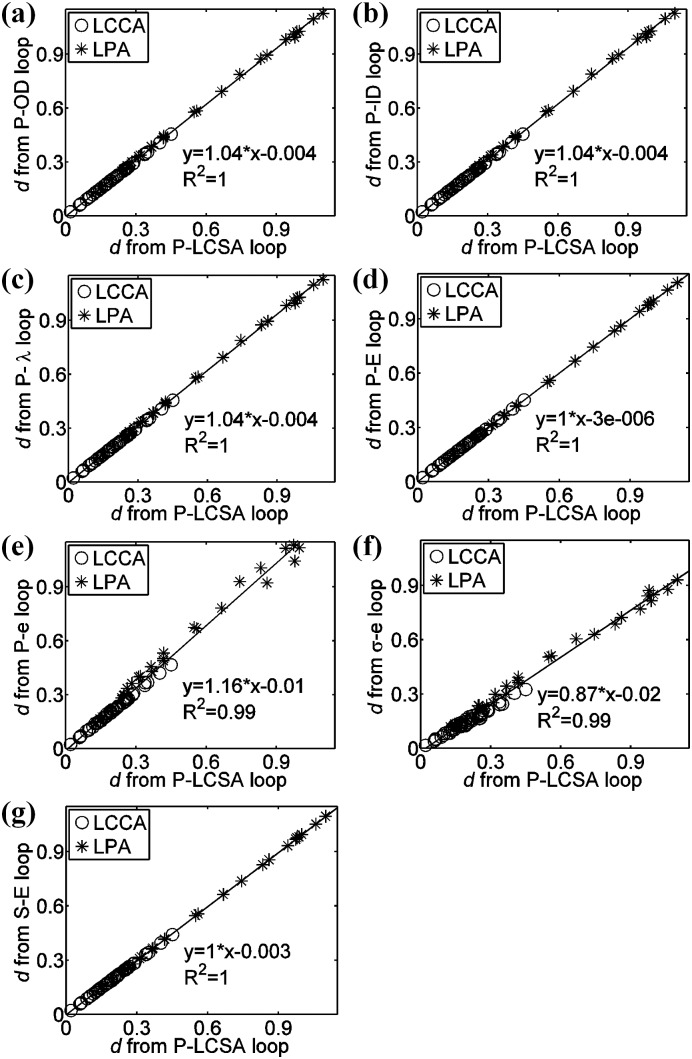
We observed linear correlations between the damping capacity calculated from the pressure (P)-LCSA loop and those from other hysteresis loops via the nonlinear method, as shown in Fig. 2. Because the damping capacity varies with frequency, we considered the damping capacity at all three tested frequencies (1, 5, and 10 Hz) with each point indicating one artery at one frequency. Strong linear correlations were evident, with the goodness of fit represented by the coefficient of determination (R ² > 0.99 for all of the correlations). The damping capacity calculated from the Cauchy stress-Almansi strain and the second Piola-Kirchhoff stress-Green strain loops were consistently less than that calculated from the P-LCSA loop, with average differences of −22 ± 8% and −1.6 ± 0.9%, respectively. These differences were statistically significant (P < 0.00001). With the linear method, strong linear correlations between the damping capacity calculated from these loops were also observed (data not shown; R ² = 0.96 for the Cauchy stress-Almansi strain versus the P-LCSA and R ² > 0.99 for all of the other correlations). As with the nonlinear method, the damping capacity calculated using the linear method from the Cauchy stress-Almansi strain and the second Piola-Kirchhoff stress-Green strain loops were consistently smaller than that calculated from the P-LCSA loop with average differences of −31 ± 10% and −1.2 ± 0.6%, respectively (P < 0.00001).

Fig. 2 — Linear correlation between the damping capacity (d via the nonlinear method) calculated from the (a) pressure (P)-OD, (b) P-ID, (c) P-stretch ( $λ$ ), (d) P-Green strain (E), (e) P-Almansi strain (e), (f) Cauchy stress-Almansi strain (*σ-e*), and (g) the second Piola-Kirchhoff stress-Green strain (*S-E*) loops and that calculated from the P-LCSA loop at the frequencies of 1, 5, and 10 Hz. (LCCA denotes the left common carotid artery and LPA denotes the left pulmonary artery.)

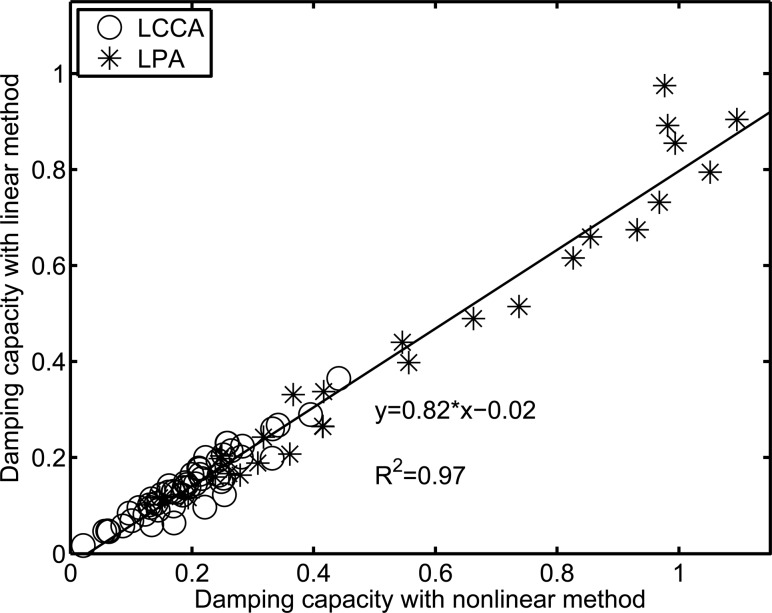
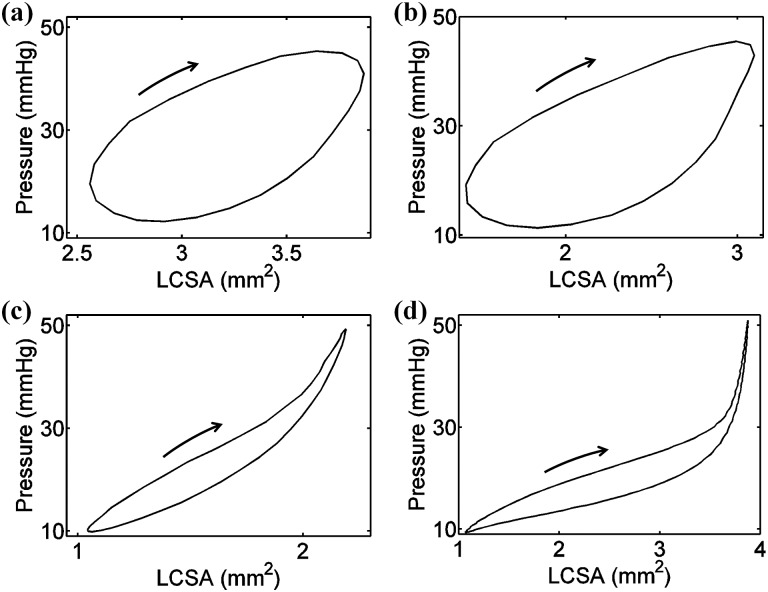
To compare the difference in the damping capacity calculated from the nonlinear method and the linear method based on the P-LCSA, the damping capacity calculated via the linear method is plotted versus that from the nonlinear method (see Fig. 3). A strong linear correlation was observed (R ² = 0.97), but the slope (0.82) was less than 1. The linear method provided a consistently smaller estimate of damping capacity compared to the nonlinear method, with an average difference of −27 ± 11% (P < 0.00001). Only about 27% of cases had an absolute difference of less than 20% and the differences reached 30% and even 40% for some cases in which the hysteresis loops were far from an elliptical shape (see Fig. 4 for an example with varied differences).

Fig. 3 — Linear correlation between the damping capacity calculated from the P-LCSA loops at all three frequencies (1, 5, and 10 Hz) with the linear and nonlinear methods. (LCCA denotes the left common carotid artery and LPA denotes the left pulmonary artery.)

Fig. 4 — Representative experimental pressure-LCSA loops that have different damping capacities calculated from the linear method versus the nonlinear method with differences of (a) −0.4% from a left pulmonary artery (LPA) at 10 Hz, (b) −9.7% from a LPA at 10 Hz, (c) −24% from a LPA at 5 Hz, and (d) −43% from a LPA at 1 Hz. Loading curves are indicated by the arrow. Note that the loops in (c) and (d) show a strong nonlinearity.

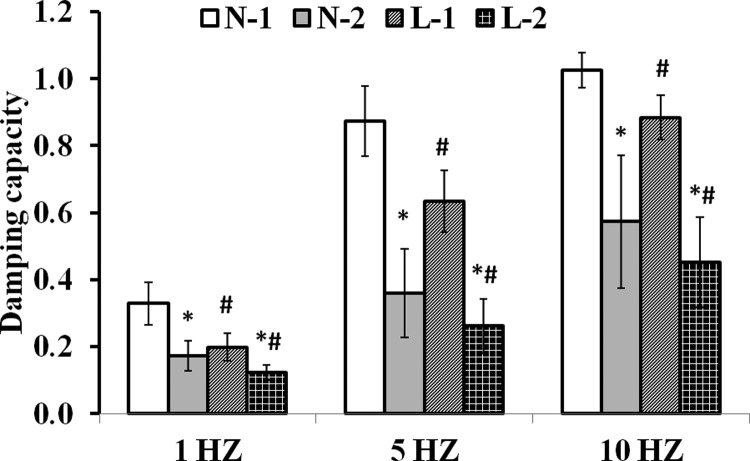
To investigate the ability of the linear method to detect the differences between healthy and diseased conditions and at different frequencies, we chose the C57BL/6J mice under normoxia condition as group 1 and the pulmonary hypertensive (hypoxia- and SU5416-treated) C57Bl/6J mice as group 2. We then compared the damping capacity calculated from the nonlinear and linear methods (see Fig. 5). Both methods detected a significantly smaller damping capacity in group 2 as compared to group 1 at all three frequencies (P < 0.007). In addition, both methods detected significant increases in the damping capacity as the frequency increased (P < 0.01) for both groups, except for group 1 between 5 and 10 Hz via the nonlinear method (P = 0.06). The linear method provided a significantly smaller estimate of the damping capacity compared to the nonlinear method for the two groups at all frequencies (P < 0.04).

Fig. 5 — Damping capacity calculated from the nonlinear and linear methods with the P-LCSA at different frequencies (1, 5, and 10 Hz). In the legend, N denotes the nonlinear method; L denotes the linear method; 1 denotes group 1; 2 denotes group 2. The symbol ‘*’ denotes P < 0.05 for group 1 versus group 2 for the same method (nonlinear or linear); the ‘#’ symbol denotes P < 0.05 for the linear versus nonlinear method for the same group.

Discussion

In this study we compared the damping capacity calculated from several different types of loading-deformation loops of extralobar pulmonary arteries and common carotid arteries at physiological pressures and from nonlinear and linear methods. Our major finding is that all of the types of loading-deformation hysteresis loops provide almost the same value of damping capacity with either the linear or nonlinear method except for the Cauchy stress-Almansi strain loop, which generates significantly smaller values. Both the linear and nonlinear methods can detect significant differences in damping capacity between groups, although the damping capacity calculated from the linear method was consistently smaller than that from the nonlinear method.

The damping capacity calculated from the pressure (P)-OD, P-ID, P-stretch, P-Almansi strain, and P-Green strain loops were almost the same as that calculated from the P-luminal cross-sectional area (LCSA) loop. The reason for such good agreement between different loops is that the OD, ID, stretch, Almansi strain, and Green strain are approximately linearly related to the LCSA in a physiological pressure range. For an arbitrary pressure range, these parameters (ID, OD, etc.) are nonlinearly related to each other. However, for the left pulmonary artery and carotid artery in the physiological pressure ranges, artery deformation is small and, consequently, a linear approximation is reasonable. As a result, the linear relationship between the LCSA and the other parameters (OD, ID, stretch, and strains) leads to linear increases or decreases in both the increased stored energy (W_S) and the dissipated energy (W_D). The damping capacity, which is associated with the ratio of the two energies, as defined in Eq. (1), remains the same. It is worth noting that these P-OD, P-ID, P-stretch, P-Almansi strain, and P-Green strain loops do not reveal energy. However, due to the aforementioned nearly linear relationship, these loops provide a good estimate of the damping capacity.

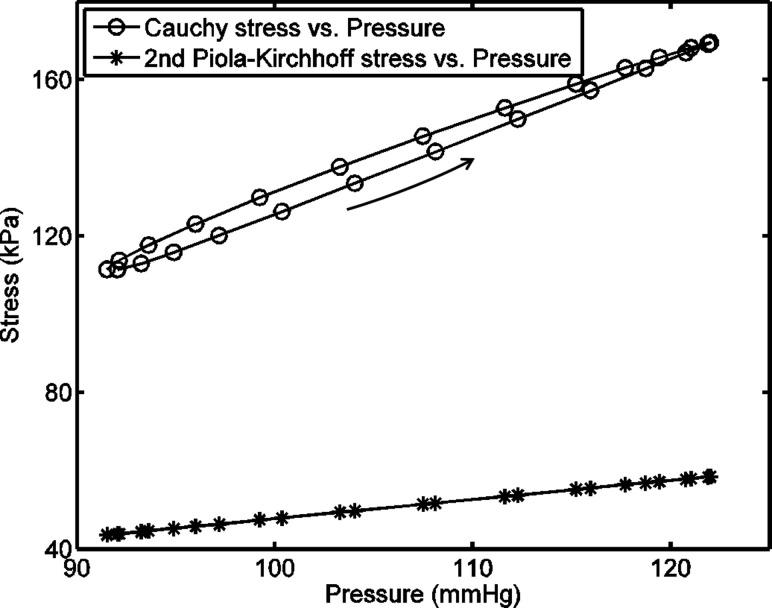
The damping capacity calculated from the Cauchy stress-Almansi strain and the second Piola-Kirchhoff stress-Green strain loops show a different correlation than that from the P-LCSA loop (see Fig. 2). The reason for this difference is that the Cauchy stress and the second Piola-Kirchhoff stress have different relationships with pressure, as shown in Fig. 6. An approximately linear relationship exists between the second Piola-Kirchhoff stress and pressure, which, when combined with the approximately linear relationship between Green strain and LCSA, leads to almost the same result of the damping capacity calculated from the second Piola-Kirchhoff stress-Green strain and P-LCSA loops. However, the Cauchy stress is nonlinearly related to pressure and the difference of the dependence of the Cauchy stress on loading and unloading results in an anticlockwise Cauchy stress-pressure loop. Such an anticlockwise loop then leads to a thinner Cauchy stress-Almansi strain loop than the P-LCSA loop, which decreases the calculated dissipated energy (i.e., the loop area) and, thus, the damping capacity.

Fig. 6 — Representative relations between the pressure and two stresses (the Cauchy and the second Piola-Kirchhoff stresses) in one observed dynamic cycle for a carotid artery at 10 Hz. The loading curve is indicated by the arrow. Note that the Cauchy stress-pressure loop is anticlockwise.

The difference between the Cauchy stress-Almansi strain and the second Piola-Kirchhoff stress-Green loops can be explained from the energy point of view. In solid mechanics, a conjugate pair of stress and strain should be used to calculate the strain energy. The second Piola-Kirchhoff stress is conjugate to the Green strain [29]; however, the Cauchy stress is not conjugate to the Almansi strain [30]. Therefore, while the product of the second Piola-Kirchhoff stress and Green strain results in the strain energy, the product of the Cauchy stress and Almansi strain does not. The use of the Cauchy stress-Almansi strain loop for the estimation of damping capacity is suitable only when both the Cauchy stress and Almansi strain are (approximately) linearly related to the second Piola-Kirchhoff stress and Green strain, respectively.

It is important to note that in the isolated vessel test, the artery deforms in both the circumferential and radial directions. The energy calculated from the P-LCSA loops represents the total external work and the damping capacity calculated from this loop provides the overall damping behavior of the artery in both the circumferential and radial directions. In contrast, the second Piola-Kirchhoff stress-Green strain loop in this study only represents the deformation and energy in the circumferential direction and the damping capacity calculated from this loop only provides the damping property in the circumferential direction. Nevertheless, the damping capacity in the circumferential direction calculated from the second Piola-Kirchhoff stress-Green strain loop is well correlated to the overall damping capacity calculated from the P-LCSA loop (slope = 0.996, R ² = 1.0, see Fig. 2(g)) with a very small difference of −1.6% ± 0.9%, indicating that either the damping capacity in the radial direction is close to that in the circumferential direction or the dissipated and stored elastic energies in the radial direction are much less than those in the circumferential direction and can be neglected. For either case, the damping capacity in the circumferential direction is a good estimation of the overall damping capacity.

For the same loops, the nonlinear and linear methods provide similar damping capacity values in some cases but large differences (greater than 20%) in other cases. Theoretically, the linear method is suitable for linear materials with an elliptical stress–strain loop under sinusoidal loading and the nonlinear method can be applied to both linear and nonlinear materials. The mechanical behavior of arteries is generally nonlinear and thus, the elastic energy ( $W_{S}^{'}$ ) calculated as the triangle area (see Fig. 1(b)), overestimates the true elastic energy. This leads to an overestimate of the total increased energy and an underestimate of the damping capacity (see Eq. (2)). However, the arteries may behave linearly in a limited pressure range. In this case, the damping capacity calculated from the linear and nonlinear methods should agree. Such behavior is seen in our data for some arteries at certain frequencies (see Figs. 4(a) and 4(b)). For other cases, however, the loops are no longer elliptical but banana-shaped, squash-shaped, etc. (see Figs. 4(c) and 4(d)). As a result, the linear method provides different damping capacity estimates and significantly different average values for the same group (see Fig. 5). Therefore, the linear method should not be used if the shape of the loop deviates noticeably from elliptical even though this approach is computationally simpler.

Several limitations in our study should be noted. First, we did not perform dynamic mechanical tests in a larger-than-physiological pressure range in which the stress–strain relationships would have become more nonlinear. More nonlinear stress–strain relationships would likely result in more different damping capacity estimates from the P-OD, P-ID, P-stretch, and P-strain loops versus the P-LCSA loops such that the damping capacity estimates from the P-OD, P-ID, P-stretch, and P-strain loops would not be valid. Second, the arteries were only tested in a passive state with smooth muscle cells inactivated by a lack of calcium in the perfusate and superfusate. Because smooth muscle cells also contribute to arterial viscoelastic losses, our calculated damping capacities may differ from those found in vivo. These limitations remain to be considered in future studies but are unlikely to affect our conclusions that the nonlinear method is preferred and energy conjugate pairs of pressure/stress-deformation/strain should be used to calculate damping capacity.

In summary, we have compared the damping capacity calculated from dynamic pressurization tests of large conduit arteries of mice in physiological pressure ranges from several different types of hysteresis loops and from linear and nonlinear methods. We found that the damping capacity calculated from the P-OD, P-ID, P-stretch, P-strain, the second Piola-Kirchhoff stress-Green strain, and the P-LCSA loops are interchangeable and greater than that calculated from the Cauchy stress-Almansi strain loop for both methods and that both methods can detect significant differences in the damping capacity between healthy and diseased states. The linear method consistently underestimated the damping capacity obtained with the nonlinear method and the differences are likely greater with larger pressure ranges for testing. We conclude that the nonlinear method applied to all loop types, except the Cauchy stress-Almansi strain loop, is recommended for the estimation of damping capacity in arteries in physiological pressure ranges.

Acknowledgment

This study is supported in part by the National Institutes of Health (NIH) Grant Nos. R01-HL086939 (N.C.C.) and R01-HL105598 (N.C.C.), and the AHA Midwest Affiliate Postdoc Fellowship Grant No. 10POST2640148 (Z.W.). We thank undergraduate student, Mr. Kevin McConnell, for measuring the geometry of carotid arteries at the strain-free state. We gratefully thank Dr. Gerhard A. Holzapfel for helpful discussions.

Contributor Information

Lian Tian, e-mail: ltian22@wisc.edu.

Zhijie Wang, e-mail: zwang48@wisc.edu, Department of Biomedical Engineering, University of Wisconsin-Madison, Madison, WI 53706-1609.

Roderic S. Lakes, Department of Biomedical Engineering, Department of Engineering Physics, and Department of Materials Science and Engineering, University of Wisconsin-Madison, Madison, WI 53706-1609, e-mail: lakes@engr.wisc.edu

Naomi C. Chesler, Department of Biomedical Engineering, University of Wisconsin-Madison, Madison, WI 53706-1609, e-mail: chesler@engr.wisc.edu.

References

[1]. Armentano, R. L. , Barra, J. G. , Pessana, F. M. , Craiem, D. O. , Graf, S. , Santana, D. B. , and Sanchez, R. A. , 2007, “Smart Smooth Muscle Spring-Dampers. Smooth Muscle Smart Filtering Helps to More Efficiently Protect the Arterial Wall,” IEEE Eng. Med. Biol. Mag., 26(1), pp. 62–70. 10.1109/MEMB.2007.289123 [DOI] [PubMed] [Google Scholar]
[2]. Bia, D. , Grignola, J. C. , Armentano, R. L. , and Ginés, F. F. , 2003, “Improved Pulmonary Artery Buffering Function During Phenylephrine-Induced Pulmonary Hypertension,” Mol. Cell Biochem., 246(1–2), pp. 19–24. 10.1023/A:1023491525659 [DOI] [PubMed] [Google Scholar]
[3]. Boutouyrie, P. , Bézie, Y. , Lacolley, P. , Challande, P. , Chamiot-Clerc, P. , Benetos, A. , De la Faverie, J. F. , Safar, M. , and Laurent, S. , 1997, “In Vivo/In Vitro Comparison of Rat Abdominal Aorta Wall Viscosity. Influence of Endothelial Function,” Arterioscler., Thromb., Vasc. Biol., 17(7), pp. 1346–1355. 10.1161/01.ATV.17.7.1346 [DOI] [PubMed] [Google Scholar]
[4]. Cox, R. H. , 1982, “Comparison of Mechanical and Chemical Properties of Extra- and Intralobar Canine Pulmonary Arteries,” Am. J. Physiol., 242(2), pp. H245–H253. [DOI] [PubMed] [Google Scholar]
[5]. Cox, R. H. , 1984, “Viscoelastic Properties of Canine Pulmonary Arteries,” Am. J. Physiol., 246(1–2), pp. H90–H96. [DOI] [PubMed] [Google Scholar]
[6]. Fratzl, P. , 2008, Collagen: Structure and Mechanics, Springer, New York. [Google Scholar]
[7]. Fung Y. C., 1993, Biomechanics: Mechanical Properties of Living Tissues, Springer-Verlag, New York. [Google Scholar]
[8]. Santana, D. B. , Barra, J. G. , Grignola, J. C. , Ginés, F. F. , and Armentano, R. L. , 2005, “Pulmonary Artery Smooth Muscle Activation Attenuates Arterial Dysfunction During Acute Pulmonary Hypertension,” J. Appl. Physiol., 98(2), pp. 605–613. 10.1152/japplphysiol.00361.2004 [DOI] [PubMed] [Google Scholar]
[9]. Silver, F. H. , Horvath, I. , and Foran, D. J. , 2001, “Viscoelasticity of the Vessel Wall: The Role of Collagen and Elastic Fibers,” Crit. Rev. Biomed. Eng., 29(3), pp. 279–301. 10.1615/CritRevBiomedEng.v29.i3.10 [DOI] [PubMed] [Google Scholar]
[10]. Gariepy, J. , Massonneau, M. , Levenson, J. , Heudes, D. , and Simon, A. , 1993, “Evidence for In Vivo Carotid and Femoral Wall Thickening in Human Hypertension,” Hypertension, 22(1), pp. 111–118. 10.1161/01.HYP.22.1.111 [DOI] [PubMed] [Google Scholar]
[11]. Ivy, D. D. , Neish, S. R. , Knudson, O. A. , Nihill, M. R. , Schaffer, M. S. , Tyson, R. W. , Abman, S. H. , Shaffer, E. M. , and Valdes-Cruz, L. , 1998, “Intravascular Ultrasonic Characteristics and Vasoreactivity of the Pulmonary Vasculature in Children With Pulmonary Hypertension,” Am. J. Cardiol., 81(6), pp. 740–748. 10.1016/S0002-9149(97)01031-X [DOI] [PubMed] [Google Scholar]
[12]. Armentano, R. L. , Graf, S. , Barra, J. G. , Velikovsky, G. , Baglivo, H. , Sánchez, R. , Simon, A. , Pichel, R. H. , and Levenson, J. , 1998, “Carotid Wall Viscosity Increase is Related to Intima-Media Thickening in Hypertensive Patients,” Hypertension, 31(1–2), pp. 534–539. 10.1161/01.HYP.31.1.534 [DOI] [PubMed] [Google Scholar]
[13]. Grignola, J. C. , Ginés, F. , Bia, D. , and Armentano, R. , 2007, “Improved Right Ventricular-Vascular Coupling During Active Pulmonary Hypertension,” Int. J. Cardiol., 115(2), pp. 171–182. 10.1016/j.ijcard.2006.03.007 [DOI] [PubMed] [Google Scholar]
[14]. Lakes, R. S. , 2009, Viscoelastic Materials, Cambridge University Press, Cambridge/New York. [Google Scholar]
[15]. Graesser, E. J. , and Wong, C. R. , 1991, “Analysis of Strain Dependent Damping in Materials via Modeling of Material Point Hysteresis,” David Taylor Research Center, U.S. Navy, Report No. DTRC-SME-91-34. [Google Scholar]
[16]. Boutouyrie, P. , Boumaza, S. , Challande, P. , Lacolley, P. , and Laurent, S. , 1998, “Smooth Muscle Tone and Arterial Wall Viscosity: An In Vivo/In Vitro Study,” Hypertension, 32(2), pp. 360–364. 10.1161/01.HYP.32.2.360 [DOI] [PubMed] [Google Scholar]
[17]. Graesser, E. J. , and Wong, C. R. , 1992, “Relationship of Traditional Damping Measures for Materials With High Damping Capacity: A Review,” Symposium on M3D: Mechanics and Mechanisms of Material Damping, Kinra V. K., and Wolfenden A., eds., American Society for Testing Materials, Philadelphia, pp. 316–343. [Google Scholar]
[18]. Shau, Y. W. , Wang, C. L. , Shieh, J. Y. , and Hsu, T. C. , 1999, “Noninvasive Assessment of the Viscoelasticity of Peripheral Arteries,” Ultrasound Med. Biol., 25(9), pp. 1377–1388. 10.1016/S0301-5629(99)00097-6 [DOI] [PubMed] [Google Scholar]
[19]. Kobs, R. W. , Muvarak, N. E. , Eickhoff, J. C. , and Chesler, N. C. , 2005, “Linked Mechanical and Biological Aspects of Remodeling in Mouse Pulmonary Arteries With Hypoxia-Induced Hypertension,” Am. J. Physiol. Heart Circ. Physiol., 288(3), pp. H1209–H1217. 10.1152/ajpheart.01129.2003 [DOI] [PubMed] [Google Scholar]
[20]. Wang, Z. , and Chesler, N. C. , 2012, “Role of Collagen Content and Cross-Linking in Large Pulmonary Arterial Stiffening After Chronic Hypoxia,” Biomech. Model. Mechanobiol., 11(1–2), pp. 279–289 10.1007/s10237-011-0309-z [DOI] [PMC free article] [PubMed] [Google Scholar]
[21]. Ooi, C. Y. , Wang, Z. , Tabima, D. M. , Eickhoff, J. C. , and Chesler, N. C. , 2010, “The Role of Collagen in Extralobar Pulmonary Artery Stiffening in Response to Hypoxia-Induced Pulmonary Hypertension,” Am. J. Physiol. Heart Circ. Physiol., 299(6), pp. H1823–H1831. 10.1152/ajpheart.00493.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
[22]. Fagan, K. A. , Fouty, B. W. , Tyler, R. C. , Morris, K. G. , Hepler, L. K. , Sato, K. , LeCras, T. D. , Abman, S. H. , Weinberger, H. D. , Huang, P. L. , McMurtry, I. F. , and Rodman, D. M. , 1999, “The Pulmonary Circulation of Homozygous or Heterozygous eNOS-Null Mice is Hyperresponsive to Mild Hypoxia,” J. Clin. Invest., 103(2), pp. 291–299. 10.1172/JCI3862 [DOI] [PMC free article] [PubMed] [Google Scholar]
[23]. Quinlan, T. R. , Li, D. , Laubach, V. E. , Shesely, E. G. , Zhou, N. , and Johns, R. A. , 2000, “eNOS-Deficient Mice Show Reduced Pulmonary Vascular Proliferation and Remodeling to Chronic Hypoxia,” Am. J. Physiol. Lung Cell Mol. Physiol., 279(4), pp. L641–L650. [DOI] [PubMed] [Google Scholar]
[24]. Ozaki, M. , Kawashima, S. , Yamashita, T. , Ohashi, Y. , Rikitake, Y. , Inoue, N. , Hirata, K. I. , Hayashi, Y. , Itoh, H. , and Yokoyama, M. , 2001, “Reduced Hypoxic Pulmonary Vascular Remodeling by Nitric Oxide From the Endothelium,” Hypertension, 37(2), pp. 322–327. 10.1161/01.HYP.37.2.322 [DOI] [PubMed] [Google Scholar]
[25]. Tabima, D. M. , and Chesler, N. C. , 2010, “The Effects of Vasoactivity and Hypoxic Pulmonary Hypertension on Extralobar Pulmonary Artery Biomechanics,” J. Biomech., 43(10), pp. 1864–1869. 10.1016/j.jbiomech.2010.03.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
[26]. Ciuclan, L. , Bonneau, O. , Hussey, M. , Duggan, N. , Holmes, A. M. , Good, R. , Stringer, R. , Jones, P. , Morrell, N. W. , Jarai, G. , Walker, C. , Westwick, J. , and Thomas, M. , 2011, “A Novel Murine Model of Severe Pulmonary Arterial Hypertension,” Am. J. Respir. Crit. Care Med., 184(10), pp. 1171–1182. 10.1164/rccm.201103-0412OC [DOI] [PubMed] [Google Scholar]
[27]. Wang, Z. , Lakes, R. S. , and Chesler, N. C. , 2012, “Changes in Conduit Pulmonary Arterial Static and Dynamic Mechanical Properties During Severe Hypoxic Pulmonary Hypertension,” 2012 ASME Summer Bioengineering Conference, Fajardo, Puerto Rico. [Google Scholar]
[28]. Tian, L. , Lammers, S. R. , Kao, P. H. , Albietz, J. A. , Stenmark, K. R. , Qi, H. J. , Shandas, R. , and Hunter, K. S. , 2012, “Impact of Residual Stretch and Remodeling on Collagen Engagement in Healthy and Pulmonary Hypertensive Calf Pulmonary Arteries at Physiological Pressures,” Ann. Biomed. Eng., 40(7), pp. 1419–1433. 10.1007/s10439-012-0509-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
[29]. Humphrey, J. D. , 1995, “Mechanics of the Arterial Wall: Review and Directions,” Crit. Rev. Biomed. Eng., 23(1–2), pp. 1–162. [PubMed] [Google Scholar]
[30]. Holzapfel, G. A. , 2000, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, Wiley, Chichester/New York. [Google Scholar]

[B1] [1]. Armentano, R. L. , Barra, J. G. , Pessana, F. M. , Craiem, D. O. , Graf, S. , Santana, D. B. , and Sanchez, R. A. , 2007, “Smart Smooth Muscle Spring-Dampers. Smooth Muscle Smart Filtering Helps to More Efficiently Protect the Arterial Wall,” IEEE Eng. Med. Biol. Mag., 26(1), pp. 62–70. 10.1109/MEMB.2007.289123 [DOI] [PubMed] [Google Scholar]

[B2] [2]. Bia, D. , Grignola, J. C. , Armentano, R. L. , and Ginés, F. F. , 2003, “Improved Pulmonary Artery Buffering Function During Phenylephrine-Induced Pulmonary Hypertension,” Mol. Cell Biochem., 246(1–2), pp. 19–24. 10.1023/A:1023491525659 [DOI] [PubMed] [Google Scholar]

[B3] [3]. Boutouyrie, P. , Bézie, Y. , Lacolley, P. , Challande, P. , Chamiot-Clerc, P. , Benetos, A. , De la Faverie, J. F. , Safar, M. , and Laurent, S. , 1997, “In Vivo/In Vitro Comparison of Rat Abdominal Aorta Wall Viscosity. Influence of Endothelial Function,” Arterioscler., Thromb., Vasc. Biol., 17(7), pp. 1346–1355. 10.1161/01.ATV.17.7.1346 [DOI] [PubMed] [Google Scholar]

[B4] [4]. Cox, R. H. , 1982, “Comparison of Mechanical and Chemical Properties of Extra- and Intralobar Canine Pulmonary Arteries,” Am. J. Physiol., 242(2), pp. H245–H253. [DOI] [PubMed] [Google Scholar]

[B5] [5]. Cox, R. H. , 1984, “Viscoelastic Properties of Canine Pulmonary Arteries,” Am. J. Physiol., 246(1–2), pp. H90–H96. [DOI] [PubMed] [Google Scholar]

[B6] [6]. Fratzl, P. , 2008, Collagen: Structure and Mechanics, Springer, New York. [Google Scholar]

[B7] [7]. Fung Y. C., 1993, Biomechanics: Mechanical Properties of Living Tissues, Springer-Verlag, New York. [Google Scholar]

[B8] [8]. Santana, D. B. , Barra, J. G. , Grignola, J. C. , Ginés, F. F. , and Armentano, R. L. , 2005, “Pulmonary Artery Smooth Muscle Activation Attenuates Arterial Dysfunction During Acute Pulmonary Hypertension,” J. Appl. Physiol., 98(2), pp. 605–613. 10.1152/japplphysiol.00361.2004 [DOI] [PubMed] [Google Scholar]

[B9] [9]. Silver, F. H. , Horvath, I. , and Foran, D. J. , 2001, “Viscoelasticity of the Vessel Wall: The Role of Collagen and Elastic Fibers,” Crit. Rev. Biomed. Eng., 29(3), pp. 279–301. 10.1615/CritRevBiomedEng.v29.i3.10 [DOI] [PubMed] [Google Scholar]

[B10] [10]. Gariepy, J. , Massonneau, M. , Levenson, J. , Heudes, D. , and Simon, A. , 1993, “Evidence for In Vivo Carotid and Femoral Wall Thickening in Human Hypertension,” Hypertension, 22(1), pp. 111–118. 10.1161/01.HYP.22.1.111 [DOI] [PubMed] [Google Scholar]

[B11] [11]. Ivy, D. D. , Neish, S. R. , Knudson, O. A. , Nihill, M. R. , Schaffer, M. S. , Tyson, R. W. , Abman, S. H. , Shaffer, E. M. , and Valdes-Cruz, L. , 1998, “Intravascular Ultrasonic Characteristics and Vasoreactivity of the Pulmonary Vasculature in Children With Pulmonary Hypertension,” Am. J. Cardiol., 81(6), pp. 740–748. 10.1016/S0002-9149(97)01031-X [DOI] [PubMed] [Google Scholar]

[B12] [12]. Armentano, R. L. , Graf, S. , Barra, J. G. , Velikovsky, G. , Baglivo, H. , Sánchez, R. , Simon, A. , Pichel, R. H. , and Levenson, J. , 1998, “Carotid Wall Viscosity Increase is Related to Intima-Media Thickening in Hypertensive Patients,” Hypertension, 31(1–2), pp. 534–539. 10.1161/01.HYP.31.1.534 [DOI] [PubMed] [Google Scholar]

[B13] [13]. Grignola, J. C. , Ginés, F. , Bia, D. , and Armentano, R. , 2007, “Improved Right Ventricular-Vascular Coupling During Active Pulmonary Hypertension,” Int. J. Cardiol., 115(2), pp. 171–182. 10.1016/j.ijcard.2006.03.007 [DOI] [PubMed] [Google Scholar]

[B14] [14]. Lakes, R. S. , 2009, Viscoelastic Materials, Cambridge University Press, Cambridge/New York. [Google Scholar]

[B15] [15]. Graesser, E. J. , and Wong, C. R. , 1991, “Analysis of Strain Dependent Damping in Materials via Modeling of Material Point Hysteresis,” David Taylor Research Center, U.S. Navy, Report No. DTRC-SME-91-34. [Google Scholar]

[B16] [16]. Boutouyrie, P. , Boumaza, S. , Challande, P. , Lacolley, P. , and Laurent, S. , 1998, “Smooth Muscle Tone and Arterial Wall Viscosity: An In Vivo/In Vitro Study,” Hypertension, 32(2), pp. 360–364. 10.1161/01.HYP.32.2.360 [DOI] [PubMed] [Google Scholar]

[B17] [17]. Graesser, E. J. , and Wong, C. R. , 1992, “Relationship of Traditional Damping Measures for Materials With High Damping Capacity: A Review,” Symposium on M3D: Mechanics and Mechanisms of Material Damping, Kinra V. K., and Wolfenden A., eds., American Society for Testing Materials, Philadelphia, pp. 316–343. [Google Scholar]

[B18] [18]. Shau, Y. W. , Wang, C. L. , Shieh, J. Y. , and Hsu, T. C. , 1999, “Noninvasive Assessment of the Viscoelasticity of Peripheral Arteries,” Ultrasound Med. Biol., 25(9), pp. 1377–1388. 10.1016/S0301-5629(99)00097-6 [DOI] [PubMed] [Google Scholar]

[B19] [19]. Kobs, R. W. , Muvarak, N. E. , Eickhoff, J. C. , and Chesler, N. C. , 2005, “Linked Mechanical and Biological Aspects of Remodeling in Mouse Pulmonary Arteries With Hypoxia-Induced Hypertension,” Am. J. Physiol. Heart Circ. Physiol., 288(3), pp. H1209–H1217. 10.1152/ajpheart.01129.2003 [DOI] [PubMed] [Google Scholar]

[B20] [20]. Wang, Z. , and Chesler, N. C. , 2012, “Role of Collagen Content and Cross-Linking in Large Pulmonary Arterial Stiffening After Chronic Hypoxia,” Biomech. Model. Mechanobiol., 11(1–2), pp. 279–289 10.1007/s10237-011-0309-z [DOI] [PMC free article] [PubMed] [Google Scholar]

[B21] [21]. Ooi, C. Y. , Wang, Z. , Tabima, D. M. , Eickhoff, J. C. , and Chesler, N. C. , 2010, “The Role of Collagen in Extralobar Pulmonary Artery Stiffening in Response to Hypoxia-Induced Pulmonary Hypertension,” Am. J. Physiol. Heart Circ. Physiol., 299(6), pp. H1823–H1831. 10.1152/ajpheart.00493.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B22] [22]. Fagan, K. A. , Fouty, B. W. , Tyler, R. C. , Morris, K. G. , Hepler, L. K. , Sato, K. , LeCras, T. D. , Abman, S. H. , Weinberger, H. D. , Huang, P. L. , McMurtry, I. F. , and Rodman, D. M. , 1999, “The Pulmonary Circulation of Homozygous or Heterozygous eNOS-Null Mice is Hyperresponsive to Mild Hypoxia,” J. Clin. Invest., 103(2), pp. 291–299. 10.1172/JCI3862 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B23] [23]. Quinlan, T. R. , Li, D. , Laubach, V. E. , Shesely, E. G. , Zhou, N. , and Johns, R. A. , 2000, “eNOS-Deficient Mice Show Reduced Pulmonary Vascular Proliferation and Remodeling to Chronic Hypoxia,” Am. J. Physiol. Lung Cell Mol. Physiol., 279(4), pp. L641–L650. [DOI] [PubMed] [Google Scholar]

[B24] [24]. Ozaki, M. , Kawashima, S. , Yamashita, T. , Ohashi, Y. , Rikitake, Y. , Inoue, N. , Hirata, K. I. , Hayashi, Y. , Itoh, H. , and Yokoyama, M. , 2001, “Reduced Hypoxic Pulmonary Vascular Remodeling by Nitric Oxide From the Endothelium,” Hypertension, 37(2), pp. 322–327. 10.1161/01.HYP.37.2.322 [DOI] [PubMed] [Google Scholar]

[B25] [25]. Tabima, D. M. , and Chesler, N. C. , 2010, “The Effects of Vasoactivity and Hypoxic Pulmonary Hypertension on Extralobar Pulmonary Artery Biomechanics,” J. Biomech., 43(10), pp. 1864–1869. 10.1016/j.jbiomech.2010.03.033 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B26] [26]. Ciuclan, L. , Bonneau, O. , Hussey, M. , Duggan, N. , Holmes, A. M. , Good, R. , Stringer, R. , Jones, P. , Morrell, N. W. , Jarai, G. , Walker, C. , Westwick, J. , and Thomas, M. , 2011, “A Novel Murine Model of Severe Pulmonary Arterial Hypertension,” Am. J. Respir. Crit. Care Med., 184(10), pp. 1171–1182. 10.1164/rccm.201103-0412OC [DOI] [PubMed] [Google Scholar]

[B27] [27]. Wang, Z. , Lakes, R. S. , and Chesler, N. C. , 2012, “Changes in Conduit Pulmonary Arterial Static and Dynamic Mechanical Properties During Severe Hypoxic Pulmonary Hypertension,” 2012 ASME Summer Bioengineering Conference, Fajardo, Puerto Rico. [Google Scholar]

[B28] [28]. Tian, L. , Lammers, S. R. , Kao, P. H. , Albietz, J. A. , Stenmark, K. R. , Qi, H. J. , Shandas, R. , and Hunter, K. S. , 2012, “Impact of Residual Stretch and Remodeling on Collagen Engagement in Healthy and Pulmonary Hypertensive Calf Pulmonary Arteries at Physiological Pressures,” Ann. Biomed. Eng., 40(7), pp. 1419–1433. 10.1007/s10439-012-0509-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B29] [29]. Humphrey, J. D. , 1995, “Mechanics of the Arterial Wall: Review and Directions,” Crit. Rev. Biomed. Eng., 23(1–2), pp. 1–162. [PubMed] [Google Scholar]

[B30] [30]. Holzapfel, G. A. , 2000, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, Wiley, Chichester/New York. [Google Scholar]

PERMALINK

Comparison of Approaches to Quantify Arterial Damping Capacity From Pressurization Tests on Mouse Conduit Arteries

Lian Tian

Zhijie Wang

Roderic S Lakes

Naomi C Chesler

Short abstract

Introduction

Fig. 1.