Flexing Computational Muscle: Modeling and Simulation of Musculotendon Dynamics

Short abstract

Muscle-driven simulations of human and animal motion are widely used to complement physical experiments for studying movement dynamics. Musculotendon models are an essential component of muscle-driven simulations, yet neither the computational speed nor the biological accuracy of the simulated forces has been adequately evaluated. Here we compare the speed and accuracy of three musculotendon models: two with an elastic tendon (an equilibrium model and a damped equilibrium model) and one with a rigid tendon. Our simulation benchmarks demonstrate that the equilibrium and damped equilibrium models produce similar force profiles but have different computational speeds. At low activation, the damped equilibrium model is 29 times faster than the equilibrium model when using an explicit integrator and 3 times faster when using an implicit integrator; at high activation, the two models have similar simulation speeds. In the special case of simulating a muscle with a short tendon, the rigid-tendon model produces forces that match those generated by the elastic-tendon models, but simulates 2–54 times faster when an explicit integrator is used and 6–31 times faster when an implicit integrator is used. The equilibrium, damped equilibrium, and rigid-tendon models reproduce forces generated by maximally-activated biological muscle with mean absolute errors less than 8.9%, 8.9%, and 20.9% of the maximum isometric muscle force, respectively. When compared to forces generated by submaximally-activated biological muscle, the forces produced by the equilibrium, damped equilibrium, and rigid-tendon models have mean absolute errors less than 16.2%, 16.4%, and 18.5%, respectively. To encourage further development of musculotendon models, we provide implementations of each of these models in OpenSim version 3.1 and benchmark data online, enabling others to reproduce our results and test their models of musculotendon dynamics.

1. Introduction

Researchers interested in understanding the physiological basis of human and animal movement have performed an extensive range of experiments at many different scales. Physiologists have studied isolated muscle to characterize activation dynamics, force development, and muscle–tendon contraction dynamics. At the other end of the spectrum, biomechanists have studied whole-body movement by measuring and analyzing joint motions, ground reaction forces, and electromyographic signals from thousands of subjects. Our understanding of human and animal movement would advance appreciably if it were not so challenging to reconcile experimental measurements of isolated muscle with biomechanical measurements of whole-body motion. This challenge exists, in part, because it is extremely difficult to measure important neuromuscular quantities (including muscle forces, muscle fiber lengths, and tendon strains) for the many muscles involved in the production of movement.

Muscle-driven dynamic simulations of movement augment experimental approaches to study movement. Muscle-driven simulations include mathematical models of muscle activation and contraction dynamics and allow calculation of muscle forces, fiber lengths, and other parameters that are not easily measured. Over the past two decades, muscle-driven simulations have been used in a wide variety of applications, including the analysis of human walking [1–6], running [7,8], jumping [9], cycling [10,11], pathological gait [12–16], functional electrical stimulation [17], orthopedic surgeries [18], and workplace ergonomics [19].

Muscle-driven simulations rely on computational models of musculotendon dynamics. There are two broad classes of musculotendon models: cross-bridge models [20–22] and Hill-type models [23–25]. Although cross-bridge models have the advantage of being derived from the fundamental structure of muscle [22], these models include many parameters that are difficult to measure and are rarely used in muscle-driven simulations that include many muscles. We focus here on Hill-type models because they are widely used in muscle-driven simulations [1–19].

Musculotendon models that are computationally fast and biologically accurate are required to simulate human movement. While other branches of computational mechanics have established benchmark problems to compare the speed and accuracy of various models (e.g., in multibody dynamics [26] and contact mechanics [27,28]), there are no analogous benchmark simulations for testing the speed and accuracy of musculotendon models. The lack of benchmark problems and comparative data from experiments has hindered the advancement of computational biomechanics.

The purpose of this paper is to compare the computational speed and biological accuracy of three musculotendon models. We first describe the equilibrium musculotendon model that is commonly used in muscle-driven simulations of movement. We then derive two alternative models: a damped equilibrium model and a rigid-tendon model. We compare the computational speed of each musculotendon model by simulating musculotendon dynamics over the operational range of the muscle using constant-activation, sinusoidal-displacement tests. We evaluate the biological accuracy of the equilibrium, damped equilibrium, and rigid-tendon models by comparing the simulated musculotendon forces to those measured experimentally from isolated rat soleus [29] and cat soleus [30] muscles. Analysis of these results allows us to make usage recommendations. To enable others to reproduce and extend our work, we have implemented these models in OpenSim version 3.1, an open-source software system for analyzing musculoskeletal dynamics [31–33]. We also provide benchmark data online2 so that the computational speed and biological accuracy of other musculotendon models can be evaluated.

2. Musculotendon Models

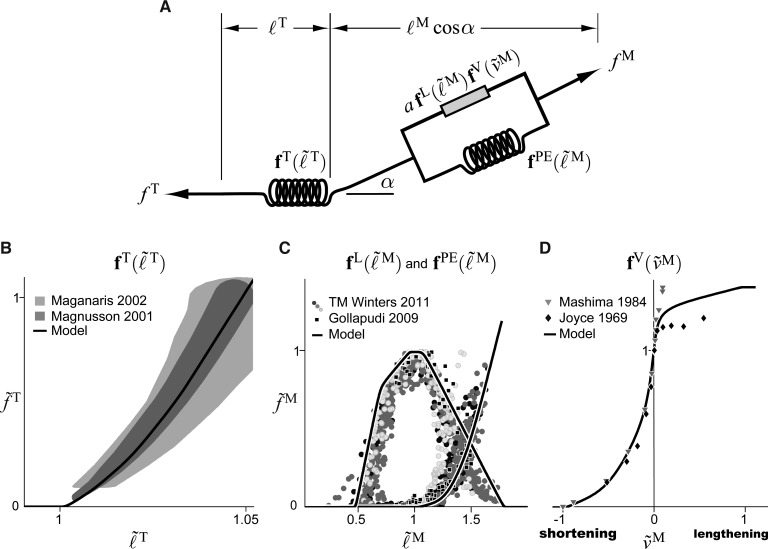
Since biological muscle is complex, many simplifications are made when developing musculotendon models. Musculotendon actuators are assumed to be massless, frictionless, extensible strings that attach to, and wrap around, bones and other structures. The fiber geometry is simplified [23] by assuming that all muscle fibers are straight, parallel, of equal length, and coplanar (Fig. 1). Biological muscle maintains a constant volume [34]; to mimic this property, the area and height of the fiber geometry (shaded gray in Fig. 1) are also assumed to be constant. The angle the fiber makes with the tendon (the pennation angle, $\alpha$) is varied so that the muscle maintains a constant height $h$. Data reported by Randhawa et al. [35] indicate that biological pennated muscle becomes thinner under load, which suggests that the height of a pennated muscle model should vary. The fixed-height approximation is likely to introduce errors for muscles that bulge appreciably as they flex [36]. Nevertheless, the fixed-height approximation is used here (described in Sec. 2.4).

Fig. 1.

Simplified geometric representation of muscle fibers and tendon for musculotendon modeling. Muscle fibers are assumed to be straight, parallel, of equal length, coplanar, and attached to tendon at a pennation angle ($\alpha$). As the muscle shortens, the distance $h$ remains constant and the pennation angle increases. Adapted from Zajac [23].

In addition to these geometric simplifications, two assumptions are made to simplify the modeling of force generation. First, the tensile force developed by a muscle is assumed to be a scaled version of the force developed by a single representative fiber. This assumption allows us to represent musculotendon actuators with a wide range of architectures (e.g., fiber lengths, pennation angles, and maximum isometric forces) with a single dimensionless model [23,37]. Second, the force generated by a fiber is assumed to be a function of only its activation, length, and velocity, each of which is assumed to modulate force production independently. This assumption allows one to first compute the activation resulting from neural excitation (activation dynamics) and then use this result to compute the muscle force (contraction dynamics), as illustrated in Fig. 2.

Fig. 2.

Muscle-driven simulations use a model of musculotendon contraction dynamics to determine muscle lengths (${\ell }^{\mathrm{M}}$), velocities ($v^{\mathrm{M}}$), and forces ($f^{\mathrm{M}}$) from neural excitations ($u$), generalized coordinates ($q$), and generalized speeds ($\stackrel{·}{q}$). A model of activation dynamics determines muscle activations ($a$) from neural excitations ($u$). A musculoskeletal model determines musculotendon lengths and velocities (${\ell }^{\mathrm{MT}}$ and $v^{\mathrm{MT}}$) from the generalized coordinates and speeds ($q$ and $\stackrel{·}{q}$). The model of musculotendon contraction dynamics uses the results of the activation dynamics and the musculoskeletal model to produce a forward simulation of muscle length (${\ell }^{\mathrm{M}}$), velocity ($v^{\mathrm{M}}$), and force ($f^{\mathrm{M}}$).

2.1. Activation Dynamics

Our models use a simplified first-order activation dynamic model [38,39], though more detailed models of activation dynamics exist [40]. We compute activation $a$ from neural excitation $u$:

$$\stackrel{\wedge }{a}=\frac{a-a_{\min }}{1-a_{\min }}$$ (1)

$$\stackrel{·}{a}=\frac{u-\stackrel{\wedge }{a}}{\tau }$$ (2)

$$\tau =\{\begin{array}{c}\multicolumn{1}{c}{\begin{array}{cc}\multicolumn{1}{c}{{\tau }_{\mathrm{A}}(0.5+1.5\stackrel{\wedge }{a})}& \hfill \mathrm{if}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}u>\stackrel{\wedge }{a}\hfill \\ \multicolumn{1}{c}{\frac{{\tau }_{\mathrm{D}}}{0.5+1.5\stackrel{\wedge }{a}}}& \hfill \mathrm{otherwise}\hfill \end{array}}\end{array}$$ (3)

where ${\tau }_{\mathrm{A}}$ and ${\tau }_{\mathrm{D}}$ are, respectively, the activation and deactivation time constants, which are set to $10\hspace{1em}\mathrm{ms}$ and $40\hspace{1em}\mathrm{ms}$ by default [39]. We have modified the conventional activation state equation [23] so that activation smoothly approaches an adjustable lower bound ($a_{\min }$), which is necessary to avoid a numerical singularity in the equilibrium musculotendon model (see below).

2.2. Equilibrium Musculotendon Model

Musculotendon actuators consist of an active contractile element, a passive elastic element, and an elastic tendon (Fig. 3(a)). Active tension develops when the nervous system excites muscle. The maximum active force a muscle can develop varies nonlinearly with its length, represented by the active-force–length curve ${\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}})$ (Fig. 3(c)), peaking at a force of $f_{\mathrm{o}}^{\mathrm{M}}$ at a length of ${\ell }_{\mathrm{o}}^{\mathrm{M}}$ (the tilde is used to denote forces, velocities, muscle lengths, and tendon lengths that are normalized by $f_{\mathrm{o}}^{\mathrm{M}}$, $v_{\max }^{\mathrm{M}}$, ${\ell }_{\mathrm{o}}^{\mathrm{M}}$, and ${\ell }_{\mathrm{s}}^{\mathrm{T}}$, respectively). During non-isometric contractions, the force developed by muscle varies nonlinearly with its rate of lengthening, which is represented by the force–velocity curve ${\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})$ (Fig. 3(d)). Force is also developed when the muscle is stretched beyond a threshold length, regardless of whether the muscle is activated, which is represented by the passive-force–length curve ${\mathbf{f}}^{\mathit{PE}}({\tilde{\ell }}^{\mathrm{M}})$ (Fig. 3(c)). Muscle force ($f^{\mathrm{M}}$) is computed using these curves as follows:

Fig. 3.

Schematic of the equilibrium musculotendon model (a), tendon-force–length curve (b), active- and passive-force–length curves (c), and force–velocity curve (d). Experimental data for the tendon-force–length curve in panel (b) are illustrated as 95% confidence intervals [41,42]. Data points in panels (c) and (d) denote experimental data for the force–length [43,44] and force–velocity [45,46] curves. The default curves used in the musculotendon models are shown in comparison to these experimental data. Note that ${\tilde{f}}^{\mathrm{M}}$ and ${\tilde{f}}^{\mathrm{T}}$ represent, respectively, muscle force and tendon force normalized by $f_{\mathrm{o}}^{\mathrm{M}}$.

$$f^{\mathrm{M}}=f_{\mathrm{o}}^{\mathrm{M}}(a{\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}}){\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})+{\mathbf{f}}^{\mathrm{PE}}({\tilde{\ell }}^{\mathrm{M}}))$$ (4)

where $a$ is the muscle activation, which ranges from $a_{\min }$ to $1$.

Muscle attaches to bone through tendon. Since a long tendon may stretch appreciably beyond its slack length (${\ell }_{\mathrm{s}}^{\mathrm{T}}$) when under tension, tendon is modeled as a nonlinear elastic element developing force according to the tendon-force–length curve ${\mathbf{f}}^{\mathrm{T}}({\tilde{\ell }}^{\mathrm{T}})$ (Fig. 3(b)). Muscle fibers attach to tendon at a pennation angle ($\alpha$), scaling the force they transmit to the tendon. If the tendon is assumed to be elastic and the mass of the muscle is assumed to be negligible, then the muscle and tendon forces must be in equilibrium (i.e., $f^{\mathrm{M}}\cos \alpha -f^{\mathrm{T}}=0$):

$$f_{\mathrm{o}}^{\mathrm{M}}(a{\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}}){\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})+{\mathbf{f}}^{\mathrm{PE}}({\tilde{\ell }}^{\mathrm{M}}))\cos \alpha -f_{\mathrm{o}}^{\mathrm{M}}{\mathbf{f}}^{\mathrm{T}}({\tilde{\ell }}^{\mathrm{T}})=0$$ (5)

Muscle and tendon force development curves (boldface in Eqs. (4) and (5)) are expressed as functions of dimensionless length (${\tilde{\ell }}^{\mathrm{M}}$ and ${\tilde{\ell }}^{\mathrm{T}}$), velocity (${\tilde{v}}^{\mathrm{M}}$), and force (normalized by $f_{\mathrm{o}}^{\mathrm{M}}$) so they can be scaled to model a variety of human and animal muscles [23,37]. We have developed default force curves for the musculotendon model that have been fit to experimental data [41–46]. These curves can be adjusted to model muscle and tendon whose characteristics deviate from these default patterns. For example, the tendon strain developed at one normalized force can be adjusted by changing a single parameter, which proportionally scales the entire tendon-force–length curve along the horizontal axis (Fig. 3(b)). We used quintic Bézier splines [47] to represent the force development curves for three reasons: Bézier splines are $C_2$-continuous (i.e., continuous to the second derivative), which is required if a derivative-based algorithm (e.g., Newton's method) will be operating on the musculotendon models; Bézier splines respect the bounds defined by their control points; and Bézier splines are expressive yet straightforward to modify.

In a forward-dynamic simulation, the force generated by a musculotendon actuator must be calculated given the length (${\ell }^{\mathrm{M}}$), velocity ($v^{\mathrm{M}}$), and activation ($a$) of the muscle. Equation (5) alone cannot be used to solve for the muscle force because multiple combinations of muscle length and velocity will satisfy the equation. A unique solution can be found by solving Eq. (5) for the normalized muscle velocity (${\tilde{v}}^{\mathrm{M}}$) to obtain an ordinary differential equation, which can then be integrated to simulate muscle contraction [23]:

$${\tilde{v}}^{\mathrm{M}}={\mathbf{f}}_{\mathrm{inv}}^{\mathrm{V}}\left(\frac{{\mathbf{f}}^{\mathrm{T}}({\tilde{\ell }}^{\mathrm{T}})/\cos \alpha -{\mathbf{f}}^{\mathrm{PE}}({\tilde{\ell }}^{\mathrm{M}})}{a{\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}})}\right)$$ (6)

where ${\mathbf{f}}_{\mathrm{inv}}^{\mathrm{V}}$ is the inverse of the force–velocity curve. Although Eq. (5) is devoid of numerical singularities, Eq. (6) has four: as $\alpha \to 90\mathit{deg}$, as $a\to 0$, as ${\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}})\to 0$, and as $\partial {\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})/\partial {\tilde{v}}^{\mathrm{M}}\to 0$. Since these conditions are often encountered during a simulation, the quantities causing singularities in Eq. (6) are altered so that the singularities are approached but never reached: $\alpha <90\mathit{deg}$, $a>0$, ${\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}})>0$, and $\partial {\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})/\partial {\tilde{v}}^{\mathrm{M}}>0$. Although these modifications avoid numerical singularities, Eq. (6) becomes numerically stiff when these singularities are approached, which slows the process of numerical integration. The effect of these near-singularities on simulation time is so onerous that lower bounds of $a\ge 0.01$ [39] and ${\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}})>0.1$ [39,48] have been used, which deviate substantially from their physiological values of $0$.

Without modifying the formulation of the equilibrium model, the muscle is able to reach unrealistically short lengths [39] and cannot be simulated when fully deactivated. We use a unilateral constraint on muscle length to prevent the muscle from becoming unrealistically short:

$${\tilde{v}}^{\mathrm{M}}=\{\begin{array}{cc}\multicolumn{1}{c}{0}& \hfill \mathrm{if}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{\tilde{\ell }}^{\mathrm{M}}\le {\tilde{\ell }}_{\min }^{\mathrm{M}}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\mathrm{and}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{\tilde{v}}^{\mathrm{M}*}<0\hfill \\ \multicolumn{1}{c}{{\tilde{v}}^{\mathrm{M}*}}& \hfill \mathrm{otherwise}\hfill \end{array}$$ (7)

where ${\tilde{v}}^{\mathrm{M}*}$ is a candidate value for ${\tilde{v}}^{\mathrm{M}}$ computed using Eq. (6). We define the minimum permissible muscle length ${\tilde{\ell }}_{\min }^{\mathrm{M}}$ as the greater of the minimum active muscle length (defined by the active-force–length curve) and the length of the muscle when it is pennated by $84.26\mathit{deg}$ ($\mathit{arccos}(0.1)$). We use a maximum pennation angle of $84.26\mathit{deg}$ because higher pennation angles increase simulation time without improving accuracy. The muscle length and pennation angle constraints are important because they ensure that the muscle length has a realistic lower bound, and that Eq. (6) does not become numerically stiff as a pennation angle of $90\mathit{deg}$ is approached.

2.3. Damped Equilibrium Musculotendon Model

The singularities in Eq. (6) arise because Eq. (5) is formulated in such a way that prevents the muscle from satisfying the equilibrium equation when it is deactivated (i.e., $a=0$) or when a nonzero tendon force is applied to a maximally-pennated muscle (i.e., $f^{\mathrm{T}}>0$ and $\alpha =90\mathit{deg}$). We address these two problems by limiting the maximum pennation angle and introducing a damper in parallel with the contractile element, which results in the damped equilibrium musculotendon model. Though strong damping forces have not been observed during in vivo human experiments [49], it is reasonable to assume that muscle is lightly damped, given its high water content of $82.3\%$ [50]. The addition of the damper (with damping coefficient $\beta$) results in the following damped equilibrium equation:

$$f_{\mathrm{o}}^{\mathrm{M}}(a{\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}}){\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})+{\mathbf{f}}^{\mathrm{PE}}({\tilde{\ell }}^{\mathrm{M}})+\beta {\tilde{v}}^{\mathrm{M}})\cos \alpha -f_{\mathrm{o}}^{\mathrm{M}}{\mathbf{f}}^{\mathrm{T}}({\tilde{\ell }}^{\mathrm{T}})=0$$ (8)

Since muscle length ${\ell }^{\mathrm{M}}$ is a state, Eq. (8) can be readily and uniquely solved for ${\tilde{v}}^{\mathrm{M}}$ using a derivative-based root-finding algorithm such as Newton's method, provided all the force development curves (${\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}})$, ${\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})$, ${\mathbf{f}}^{\mathrm{PE}}({\tilde{\ell }}^{\mathrm{M}})$, and ${\mathbf{f}}^{\mathrm{T}}({\tilde{\ell }}^{\mathrm{T}})$) are $C_2$-continuous. The damped equilibrium musculotendon model of Eq. (8) should generate force profiles that are similar to those generated by the equilibrium model described by Eq. (5), but in a fraction of the simulation time because the damped equilibrium model is free of numerical singularities. We set the default damping coefficient to a value ($\beta =0.1$) that reduces simulation time without generating large damping forces (damping forces are $0.1f_{\mathrm{o}}^{\mathrm{M}}$ at $v_{\max }^{\mathrm{M}}$). Note that we use a constraint (as in Eq. (7)) to enforce a lower bound on the fiber length and to prevent Eq. (8) from becoming numerically stiff as a pennation angle of $90\mathit{deg}$ is approached.

2.4. Rigid-Tendon Musculotendon Model

Some tendons are so stiff that they can be treated as inextensible, effectively replacing the tendon spring in Fig. 3(a) with an inextensible cable. The tendon inextensibility assumption is appropriate only when the tendon does not stretch sufficiently to affect the normalized length of the contractile element; the validity of this assumption will be explored using a benchmark simulation in Sec. 3. This modeling simplification makes it possible to determine the muscle length (${\ell }^{\mathrm{M}}$) and velocity ($v^{\mathrm{M}}$) from the musculotendon length (${\ell }^{\mathrm{MT}}$) and velocity ($v^{\mathrm{MT}}$) using a kinematic model of the musculotendon actuator (Fig. 3(a)):

$${\ell }^{\mathrm{MT}}={\ell }^{\mathrm{T}}+{\ell }^{\mathrm{M}}\cos \alpha$$ (9)

Differentiating Eq. (9) with respect to time yields a relation between the muscle, tendon, and musculotendon actuator velocities:

$$v^{\mathrm{MT}}=v^{\mathrm{T}}+v^{\mathrm{M}}\cos \alpha -{\ell }^{\mathrm{M}}\stackrel{·}{\alpha }\sin \alpha$$ (10)

where $v^{\mathrm{T}}=0$ if the tendon is rigid. The length of the muscle (${\ell }^{\mathrm{M}}$) and its orientation ($\alpha$) are coupled by the fixed-height-parallelogram pennation model (Fig. 1):

$${\ell }^{\mathrm{M}}\sin \alpha =h$$ (11)

The constant height of the parallelogram ($h$) is computed using the optimal muscle length and pennation angle:

$$h={\ell }_{\mathrm{o}}^{\mathrm{M}}\sin {\alpha }_{\mathrm{o}}$$ (12)

Differentiating Eq. (11) with respect to time yields an expression that can be used to calculate the pennation angular velocity:

$$\stackrel{·}{\alpha }=-\frac{v^{\mathrm{M}}\sin \alpha }{{\ell }^{\mathrm{M}}\cos \alpha }$$ (13)

Since the tendon length and velocity are known (i.e., ${\ell }^{\mathrm{T}}={\ell }_{\mathrm{s}}^{\mathrm{T}}$ and $v^{\mathrm{T}}=0$), we use Eqs. (9) and (11) to solve for muscle length (${\ell }^{\mathrm{M}}$) given musculotendon length (${\ell }^{\mathrm{MT}}$), and Eqs. (10) and (13) to solve for muscle velocity ($v^{\mathrm{M}}$) given musculotendon velocity ($v^{\mathrm{MT}}$). As with the elastic-tendon models, we use the unilateral constraint of Eq. (7) to enforce a lower bound of ${\ell }_{\min }^{\mathrm{M}}$ on muscle length. We compute the force generated by the muscle directly:

$$f^{\mathrm{M}*}=f_{\mathrm{o}}^{\mathrm{M}}(a{\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}}){\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})+{\mathbf{f}}^{\mathrm{PE}}({\tilde{\ell }}^{\mathrm{M}})+\beta {\tilde{v}}^{\mathrm{M}})\cos \alpha$$ (14)

Light damping ($\beta =0.1$ by default) is included in this rigid-tendon muscle model. Since a muscle can generate only tensile force, we constrain Eq. (14) to remain positive:

$$f^{\mathrm{M}}=\{\begin{array}{cc}\multicolumn{1}{c}{f^{\mathrm{M}*}}& \hfill \mathrm{if}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{f}^{\mathrm{M}*}>0\hfill \\ \multicolumn{1}{c}{0}& \hfill \mathrm{otherwise}\hfill \end{array}$$ (15)

3. Computational and Biological Benchmarks

We performed four benchmarks to measure the speed and accuracy of each musculotendon model. Each musculotendon model implementation was confirmed to conserve energy during simulation. All benchmark simulations were performed on a 2.20-GHz, 64-bit laptop with 8.00 Gb of memory.

Elastic-Tendon Computational Benchmark

In the first benchmark simulation, we determined the differences in computational speed and force response between the equilibrium model and the damped equilibrium model over a range of activation values. The musculotendon actuator consisted of a short, pennated muscle (${\ell }_{\mathrm{o}}^{\mathrm{M}}=2\hspace{1em}\mathrm{cm}$ and ${\alpha }_{\mathrm{o}}=30\mathit{deg}$) and a long tendon (${\ell }_{\mathrm{s}}^{\mathrm{T}}=20\hspace{1em}\mathrm{cm}$) (Fig. 4). Eleven constant-activation, sinusoidal-displacement simulations were performed using each elastic-tendon musculotendon model, with activations varying from $0$ ($0.01$ for the equilibrium model) to $1$ in increments of $0.1$. The muscle and tendon force curves shown in Fig. 3 were used for each model; the initial length of the musculotendon actuator was ${\ell }_{\mathrm{s}}^{\mathrm{T}}+{\ell }_{\mathrm{o}}^{\mathrm{M}}\cos {\alpha }_{\mathrm{o}}$ (Fig. 4). Each muscle was initialized using the routine described in the Appendix, then lengthened and shortened by applying a sinusoidal displacement to the free end of the tendon. A period of $1\mathrm{s}$ and an amplitude of ${\ell }_{\mathrm{o}}^{\mathrm{M}}$ (i.e., ${\ell }^{\mathrm{MT}}(t)=({\ell }_{\mathrm{s}}^{\mathrm{T}}+{\ell }_{\mathrm{o}}^{\mathrm{M}}\cos {\alpha }_{\mathrm{o}})+{\ell }_{\mathrm{o}}^{\mathrm{M}}\sin 2\pi t$) resulted in a fiber length change of approximately $\pm 0.5{\ell }_{\mathrm{o}}^{\mathrm{M}}$ and fiber velocities of approximately $-0.55v_{\max }^{\mathrm{M}}$ to $0.75v_{\max }^{\mathrm{M}}$. Numerical simulations were performed using explicit (Runge–Kutta–Merson [51]) and implicit (CPODES [52]) integrators. Integrator tolerances were chosen for each combination of model and integrator to produce force profiles with mean absolute errors less than 0.1% of $f_{\mathrm{o}}^{\mathrm{M}}$ (at all activations) when compared to highly accurate (${10}^{-12}$ tolerance) simulation results obtained using the explicit integrator. The differences between the normalized force profiles generated by the equilibrium and damped equilibrium musculotendon models were recorded. We calculated the real-time fraction as the quotient of wall clock time and the amount of time simulated; a real-time fraction less than $1$ indicates that the simulation completed faster than real time.

Fig. 4.

Schematic of the musculotendon actuator used in the elastic-tendon and rigid-tendon computational benchmarks. In the simulations, the initial length of the musculotendon actuator was set to ${\mathrm{c}}_1\hspace{1em}=\hspace{1em}{\ell }_{\mathrm{s}}^{\mathrm{T}}+{\ell }_{\mathrm{o}}^{\mathrm{M}}\cos {\alpha }_{\mathrm{o}}$ and then the length was varied by ${\mathrm{c}}_2\sin 2\pi t$.

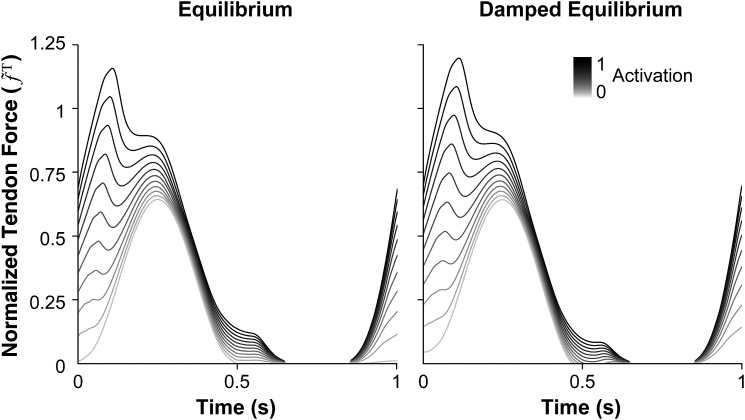
The damped equilibrium model produced force profiles that were within 2% of those produced by the equilibrium model (Fig. 5); however, the damped equilibrium model generally simulated faster at all activation levels and with either integrator (Fig. 6). The damped equilibrium model was 1–29 times faster than the equilibrium model when using the explicit integrator and 1–3 times faster when using the implicit integrator. The damped equilibrium model also exhibited simulation times with the lowest mean and standard deviation, completing in $92\hspace{1em}\pm \hspace{1em}10\hspace{1em}\mathrm{ms}$ and $73\hspace{1em}\pm \hspace{1em}12\hspace{1em}\mathrm{ms}$ when using the explicit and implicit integrators, respectively. In contrast, the equilibrium model required $315\hspace{1em}\pm \hspace{1em}539\hspace{1em}\mathrm{ms}$ (explicit) and $89\hspace{1em}\pm \hspace{1em}27\hspace{1em}\mathrm{ms}$ (implicit) to simulate. Thus, a system using the damped equilibrium musculotendon model can be expected to simulate in a consistent amount of time across a wide variety of operating conditions.

Fig. 5.

Normalized tendon force profiles of the equilibrium (left) and damped equilibrium (right) musculotendon models. Each muscle underwent constant-activation, sinusoidal-displacement simulations of 1-s duration with activations varying from 0 (0.01 for the equilibrium model) to 1 in increments of 0.1. The average absolute difference between normalized force profiles generated by the models was less than 0.3% at low activation and less than 2.5% at high activation.

Fig. 6.

Time required to generate the simulation results shown in Fig. 5 using explicit (left) and implicit (right) integrators. Wall clock time was divided by the amount of time simulated to obtain the real-time fraction; values below $1$ indicate that the simulations completed faster than real time.

Rigid-Tendon Computational Benchmark

Simulations of muscle with a rigid tendon were used to determine the differences in computational speed and force response between the damped equilibrium and rigid-tendon models over a range of tendon-to-fiber length ratios. The musculotendon actuator modeled in this benchmark was similar to that shown in Fig. 4, but consisted of a short, non-pennated muscle (${\ell }_{\mathrm{o}}^{\mathrm{M}}=2\hspace{1em}\mathrm{cm}$ and ${\alpha }_{\mathrm{o}}=0\mathit{deg}$). Ten maximal-activation, sinusoidal-displacement simulations were performed using each musculotendon model, with tendon slack lengths varying from only a small fraction of the optimal fiber length (${\ell }_{\mathrm{s}}^{\mathrm{T}}=10·2^{-9}{\ell }_{\mathrm{o}}^{\mathrm{M}}\approx 0.0195{\ell }_{\mathrm{o}}^{\mathrm{M}}$) to substantially longer than the optimal fiber length (${\ell }_{\mathrm{s}}^{\mathrm{T}}=10{\ell }_{\mathrm{o}}^{\mathrm{M}}$), with the tendon slack length doubling from one simulation to the next. A sinusoidal displacement of period $1\mathrm{s}$ and amplitude $0.5{\ell }_{\mathrm{o}}^{\mathrm{M}}$ was used, which resulted in a fiber length change of approximately $\pm 0.5{\ell }_{\mathrm{o}}^{\mathrm{M}}$. Numerical simulations were performed using the same integrators and accuracies used in the elastic-tendon computational benchmark, and the same metrics were computed.

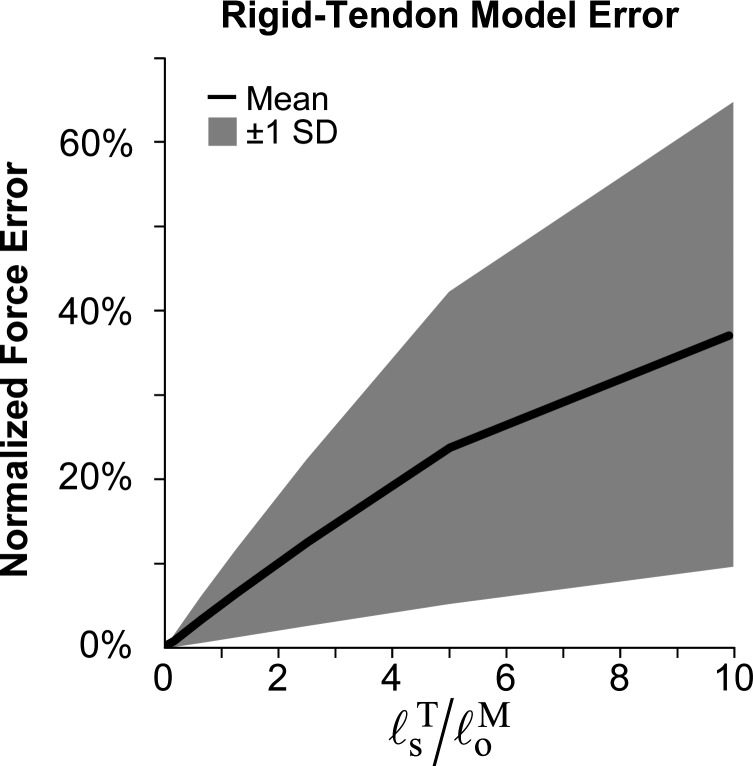
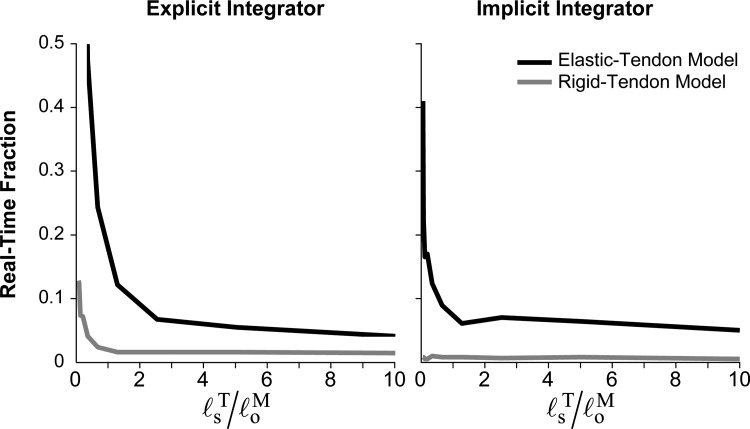
The rigid-tendon model generated force profiles that matched those generated by the damped equilibrium model to within $0.05f_{\mathrm{o}}^{\mathrm{M}}$ (on average) when ${\ell }_{\mathrm{s}}^{\mathrm{T}}<{\ell }_{\mathrm{o}}^{\mathrm{M}}$ (Fig. 7), and did so with greater computational speed (Fig. 8). As the tendon length increased beyond the optimal fiber length, however, the force profiles produced by the rigid- and elastic-tendon models diverged rapidly. In addition, Fig. 8 shows that the computational speed was largely dependent on the choice of integrator. The rigid-tendon model was 2–54 times faster than the elastic-tendon model when using the explicit integrator and 6–31 times faster when using the implicit integrator.

Fig. 7.

Differences in force profiles generated by rigid-tendon and damped equilibrium musculotendon models as a function of tendon slack length (${\ell }_{\mathrm{s}}^{\mathrm{T}}$) normalized by the optimal fiber length (${\ell }_{\mathrm{o}}^{\mathrm{M}}$). The force profiles were obtained using maximal-activation, sinusoidal-displacement simulations. The mean (solid curve) and standard deviation (shaded area) of the absolute difference in force profiles over the duration of each simulation show that errors in the rigid-tendon model increase rapidly as normalized tendon slack length increases.

Fig. 8.

Computational speed of the damped equilibrium (black curve) and rigid-tendon (gray curve) musculotendon models as functions of tendon slack length (${\ell }_{\mathrm{s}}^{\mathrm{T}}$) normalized by the optimal fiber length (${\ell }_{\mathrm{o}}^{\mathrm{M}}$) using explicit (left) and implicit (right) integrators. Wall clock time was divided by the amount of time simulated to obtain the real-time fraction; values below $1$ indicate that the simulations completed faster than real time.

Maximal-Activation Biological Benchmark

We compared the force profiles generated by the equilibrium, damped equilibrium, and rigid-tendon models to those produced by maximally-activated rat soleus muscle in vivo, using the experimental data of Krylow and Sandercock [29]. This data set consisted of six experimental trials, each beginning with the muscle deactivated and $2\hspace{1em}\mathrm{mm}$ shorter than its optimal length. The muscle was then maximally activated and stretched, displacing the muscle through a range that is consistent with ambulation (Fig. 9). The six trials were identical except for the amplitude of the displacement; the maximum amplitudes were $0.05$, $0.1$, $0.25$, $0.5$, $1.0$, and $2.0\hspace{1em}\mathrm{mm}$. While the optimal fiber length (${\ell }_{\mathrm{o}}^{\mathrm{M}}=17.1\hspace{1em}\mathrm{mm}$) and maximum isometric force ($f_{\mathrm{o}}^{\mathrm{M}}=1.17\hspace{1em}\mathrm{N}$) were reported by Krylow and Sandercock [29], several other parameters required by the musculotendon model were not. We assumed a pennation angle of ${\alpha }_{\mathrm{o}}=6\mathit{deg}$ and a tendon slack length of ${\ell }_{\mathrm{s}}^{\mathrm{T}}={\ell }_{\mathrm{o}}^{\mathrm{M}}$ based on measurements of rat soleus muscle architecture [53]; the muscle and tendon force curves shown in Fig. 3 were used. We used a Nelder–Mead [54] optimization algorithm to tune the maximum isometric force ($f_{\mathrm{o}}^{\mathrm{M}}$) and identify the maximum contraction velocity ($v_{\max }^{\mathrm{M}}$) and activation time constant (${\tau }_{\mathrm{A}}$) for each musculotendon model; the damping coefficient ($\beta$) was also identified for the damped equilibrium and rigid-tendon models. The force profile generated by each musculotendon model was fit to the experimental trial of amplitude $2.0\hspace{1em}\mathrm{mm}$ by minimizing the mean absolute error over the duration of the simulation, as specified by the objective function $J$:

Fig. 9.

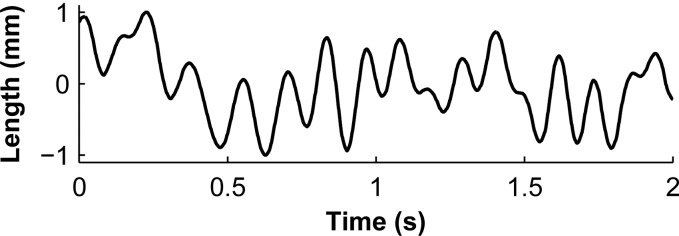
Waveform of the change in musculotendon length [29] used in the maximal-activation biological benchmark, shown here with a maximum length change of $1.0\hspace{1em}\mathrm{mm}$. This waveform was scaled by the appropriate maximum length change, added to ${\ell }_{\mathrm{s}}^{\mathrm{T}}+{\ell }_{\mathrm{o}}^{\mathrm{M}}\cos {\alpha }_{\mathrm{o}}-2\hspace{1em}\mathrm{mm}$, and then used to prescribe the displacement of the free end of the tendon.

$$J=\frac{1}{N}\sum _{i=1}^N|f_{i,\mathrm{model}}^{\mathrm{M}}-f_{i,\mathrm{experiment}}^{\mathrm{M}}|$$ (16)

where $N=2001$ is the number of data points, which were sampled at 1-ms intervals. We used the remaining five trials in this data set (corresponding to amplitudes between $0.05\hspace{1em}\mathrm{mm}$ and $1.0\hspace{1em}\mathrm{mm}$) to evaluate the performance of each musculotendon model using the optimized parameters.

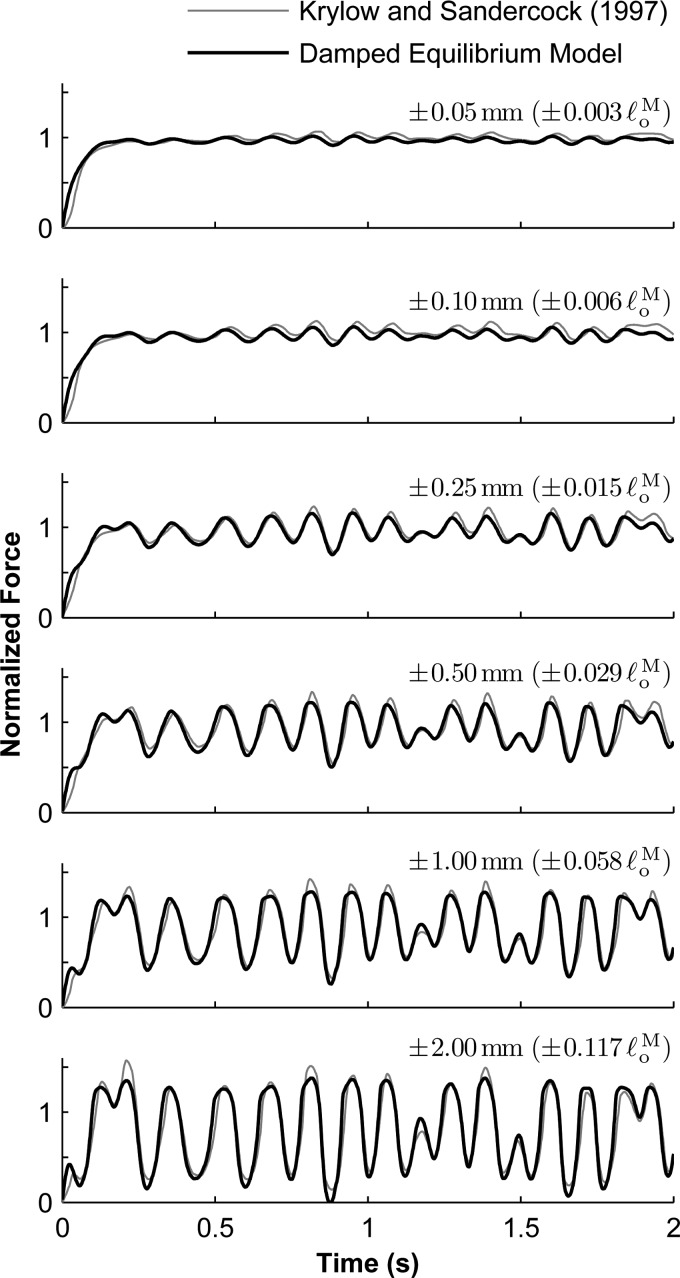
The damped equilibrium model produced forces that were similar to those produced by biological (rat soleus) muscle that was maximally activated. The force profile corresponding to a maximum amplitude of $2.0\hspace{1em}\mathrm{mm}$ (Fig. 10, bottom) was used to adjust the maximum isometric force ($1.27\hspace{1em}\mathrm{N}$) and identify the maximum contraction velocity ($5.50{\ell }_{\mathrm{o}}^{\mathrm{M}}/\mathrm{s}$), activation time constant ($22.8\hspace{1em}\mathrm{ms}$), and damping coefficient ($0.016$). The mean absolute error between the simulated and experimental force profiles corresponding to an amplitude of $2.0\hspace{1em}\mathrm{mm}$ was 8.9% (expressed as a percentage of $f_{\mathrm{o}}^{\mathrm{M}}$ measured experimentally), which is comparable to that obtained by Krylow and Sandercock (6.1%) [29]. The identified parameters resulted in simulations that compared favorably with experimental data collected using different amplitudes as well (Fig. 10). The mean absolute errors for the remaining trials were between 3.3% and 6.7%; Krylow and Sandercock [29] reported corresponding errors between 3.9% and 8.6%. The equilibrium model had similar optimal parameters ($f_{\mathrm{o}}^{\mathrm{M}}=1.28\hspace{1em}\mathrm{N}$, $v_{\max }^{\mathrm{M}}=5.32{\ell }_{\mathrm{o}}^{\mathrm{M}}/\mathrm{s}$, and ${\tau }_{\mathrm{A}}=24.0\hspace{1em}\mathrm{ms}$) and similar errors (8.9% for the trial of amplitude $2.0\hspace{1em}\mathrm{mm}$, and between 3.0% and 6.7% for the other trials). Using the rigid-tendon model, we obtained substantially different optimal parameters ($f_{\mathrm{o}}^{\mathrm{M}}=1.20\hspace{1em}\mathrm{N}$, $v_{\max }^{\mathrm{M}}=9.86{\ell }_{\mathrm{o}}^{\mathrm{M}}/\mathrm{s}$, ${\tau }_{\mathrm{A}}=37.8\hspace{1em}\mathrm{ms}$, and $\beta =0.024$) and larger errors (between 4.5% and 20.9%). Note that the mean absolute error obtained using the rigid-tendon model was approximately the sum of the equilibrium model error and the additional error introduced by the rigid-tendon assumption (Fig. 7). The agreement between our simulation results and the experimental data could be improved by fitting our model curves to the experimental data, as was done by Krylow and Sandercock [29].

Fig. 10.

Comparison of experimental [29] (gray curve) and simulated (black curve) force profiles from maximally-activated muscle undergoing length changes of maximum amplitude $0.05$ (top), $0.1$, $0.25$, $0.5$, $1.0$, and $2.0\hspace{1em}\mathrm{mm}$ (bottom). The maximum isometric force used in the model was $f_{\mathrm{o}}^{\mathrm{M}}\hspace{1em}=\hspace{1em}1.27\hspace{1em}\mathrm{N}$ and the optimal fiber length was ${\ell }_{\mathrm{o}}^{\mathrm{M}}\hspace{1em}=\hspace{1em}17.1\hspace{1em}\mathrm{mm}$.

Submaximal-Activation Biological Benchmark

We compared the force profiles generated by the equilibrium, damped equilibrium, and rigid-tendon models with forces measured from submaximally-activated cat soleus muscle in vivo [30]. In the first six experimental trials, the musculotendon actuator was held at a length of ${\ell }_{\mathrm{s}}^{\mathrm{T}}+{\ell }_{\mathrm{o}}^{\mathrm{M}}\cos {\alpha }_{\mathrm{o}}-4\hspace{1em}\mathrm{mm}$ and excited using constant-frequency stimulation rates of $10$, $20$, and $30\hspace{1em}\mathrm{Hz}$, and random stimulation signals with mean frequencies of $10$, $20$, and $30\hspace{1em}\mathrm{Hz}$, as described by Perreault et al. [30]. These six trials were then repeated while applying length changes with maximum amplitudes of $1.0\hspace{1em}\mathrm{mm}$ and $8.0\hspace{1em}\mathrm{mm}$ ($\pm 0.033{\ell }_{\mathrm{o}}^{\mathrm{M}}$ and $\pm 0.267{\ell }_{\mathrm{o}}^{\mathrm{M}}$, respectively) to the free end of the tendon (Fig. 11). The forces measured during the experimental isometric trials were filtered with a low-pass Butterworth filter of cut-off frequency $120\hspace{1em}\mathrm{Hz}$ and used to calculate the activation signals that must be applied to each musculotendon model to elicit the same response; we then used these activation signals in the 12 non-isometric simulations. Since it was not reported by Perreault et al. [30], we assumed a maximum isometric force of $f_{\mathrm{o}}^{\mathrm{M}}=25.1\hspace{1em}\mathrm{N}$, which resulted in a maximum activation signal of $1.0$ over the entire data set. We obtained estimates for the optimal fiber length (${\ell }_{\mathrm{o}}^{\mathrm{M}}=30\hspace{1em}\mathrm{mm}$), pennation angle (${\alpha }_{\mathrm{o}}=7.5\mathit{deg}$), and tendon slack length (${\ell }_{\mathrm{s}}^{\mathrm{T}}=65\hspace{1em}\mathrm{mm}$) from the measurements reported by Scott et al. [55]; the muscle and tendon force curves shown in Fig. 3 were used.

Fig. 11.

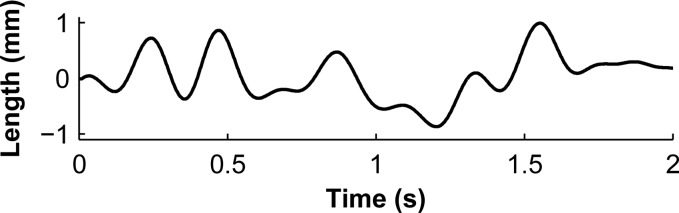
Waveform of the change in musculotendon length [30] used in the submaximal-activation biological benchmark, shown here with a maximum length change of $1.0\hspace{1em}\mathrm{mm}$. This waveform was scaled by the appropriate maximum length change (either $1.0\hspace{1em}\mathrm{mm}$ or $8.0\hspace{1em}\mathrm{mm}$), added to ${\ell }_{\mathrm{s}}^{\mathrm{T}}+{\ell }_{\mathrm{o}}^{\mathrm{M}}\cos {\alpha }_{\mathrm{o}}-4\hspace{1em}\mathrm{mm}$, and then used to prescribe the displacement of the free end of the tendon.

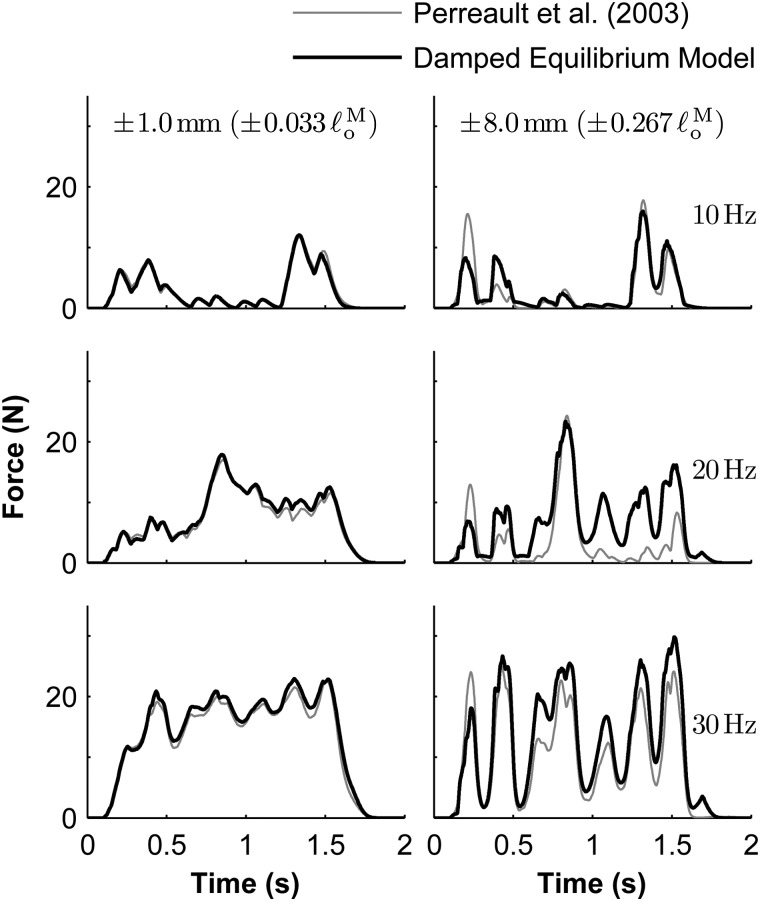
The damped equilibrium model was capable of producing a response that approximates the response of biological (cat soleus) muscle when submaximally activated, though the results were less accurate than those obtained in the maximal-activation biological benchmark. The mean absolute errors between the damped equilibrium model and experimental force profiles corresponding to amplitudes of $1.0\hspace{1em}\mathrm{mm}$ (left column in Figs. 12 and 13) and $8.0\hspace{1em}\mathrm{mm}$ (right column) were less than 3.2% and 16.2%, respectively, (expressed as a percentage of $f_{\mathrm{o}}^{\mathrm{M}}$). Perreault et al. [30] reported corresponding maximum mean absolute errors of 3.5% and 17.7% using their rigid-tendon Hill-type model. The corresponding errors obtained using the equilibrium model were 3.3% and 16.4%, which are very similar to those obtained using the damped equilibrium model. The rigid-tendon model produced errors of 5.5% and 18.5%.

Fig. 12.

Comparison of experimental [30] (gray curve) and simulated (black curve) force profiles from submaximally-activated muscle undergoing length changes of maximum amplitude $1.0\hspace{1em}\mathrm{mm}$ (left) and $8.0\hspace{1em}\mathrm{mm}$ (right). Constant-frequency stimulation rates of $10$ (top), $20$, and $30\hspace{1em}\mathrm{Hz}$ (bottom) were applied to the biological muscle. Force profiles measured experimentally during isometric trials were used to determine the corresponding activation signals that must be applied to the damped equilibrium musculotendon model. The maximum isometric force used in the model was $f_{\mathrm{o}}^{\mathrm{M}}\hspace{1em}=\hspace{1em}25.1\hspace{1em}\mathrm{N}$ and the optimal fiber length was ${\ell }_{\mathrm{o}}^{\mathrm{M}}\hspace{1em}=\hspace{1em}30\hspace{1em}\mathrm{mm}$.

Fig. 13.

Comparison of experimental [30] (gray curve) and simulated (black curve) force profiles from submaximally-activated muscle undergoing length changes of maximum amplitude $1.0\hspace{1em}\mathrm{mm}$ (left) and $8.0\hspace{1em}\mathrm{mm}$ (right). Random stimulation signals were applied to the biological muscle, with mean frequencies of $10$ (top), $20$, and $30\hspace{1em}\mathrm{Hz}$ (bottom), as described by Perreault et al. [30]. Force profiles measured experimentally during isometric trials were used to determine the corresponding activation signals that must be applied to the damped equilibrium musculotendon model. The maximum isometric force used in the model was $f_{\mathrm{o}}^{\mathrm{M}}\hspace{1em}=\hspace{1em}25.1\hspace{1em}\mathrm{N}$ and the optimal fiber length was ${\ell }_{\mathrm{o}}^{\mathrm{M}}\hspace{1em}=\hspace{1em}30\hspace{1em}\mathrm{mm}$.

4. Discussion

The development of muscle-driven simulations requires musculotendon models that are fast and accurate. This paper evaluates the computational speed and biological accuracy of musculotendon models and establishes benchmarks to accelerate future research. Our numerical results and the data required to replicate our benchmarks are available online3.

We developed and tested three musculotendon models: the equilibrium model, the damped equilibrium model, and the rigid-tendon model. The damped equilibrium model produced forces that compare favorably with those observed in maximally-activated biological muscle, and simulated faster than the equilibrium model regardless of whether an explicit or implicit integrator was used. The rigid-tendon model was fast and accurate when simulating a maximally-activated muscle with a short tendon (${\ell }_{\mathrm{s}}^{\mathrm{T}}\le {\ell }_{\mathrm{o}}^{\mathrm{M}}$). Since neither the damped equilibrium model nor the rigid-tendon model contains numerical singularities, it is possible to simulate deactivated muscle, use an active-force–length curve that reaches zero, and use a force–velocity curve that includes a slope of zero. We developed and tested another musculotendon model, named the acceleration model, that includes a small mass between the tendon and muscle. Despite improving a previous formulation of this model [56], the acceleration model was slower than the models presented above, so its results are not reported here. The source code for the acceleration musculotendon model is available online 3.

The fastest simulations of an elastic-tendon model were obtained by pairing the damped equilibrium model with the implicit integrator, though the explicit integrator was only marginally slower for these single-muscle simulations. The performance advantage of using an implicit integrator to simulate an equilibrium model is apparent from Fig. 6 and has been reported previously [48]. Note, however, that the number of function evaluations performed by an implicit integrator increases with system size [57], while the number of function evaluations required by an explicit integrator is independent of system size. Therefore, it is likely that an explicit integrator will outperform an implicit integrator when simulating a large number of muscles with the damped equilibrium model.

An important feature of our musculotendon models is that they can be scaled to represent muscles with different architectures based on experimental measurements of optimal muscle fiber lengths, pennation angles, and physiological cross-sectional areas [23,37]. We used this feature to scale the damped equilibrium musculotendon model to represent rat soleus and cat soleus muscles, and provided comparisons between simulated forces and forces measured experimentally. Since the force produced by a muscle depends on the muscle architecture, it is important to compare simulation results to experimental results obtained from muscles with different architectures. Our recommendation is to expand the repository of biological benchmarks that can be used to test the fidelity of musculotendon simulations.

Another feature of our musculotendon models is that they are implemented in OpenSim [31–33], an open-source software system for analyzing musculoskeletal dynamics. This feature allowed us to further test our models by simulating walking dynamics using a whole-body musculoskeletal model that includes over fifty muscles [3,18,58,59], which is freely distributed with OpenSim. We repeated the simulation using each of the three musculotendon models described here. We found that the time to simulate muscle-driven walking was dominated by the speed of the musculotendon model. A muscle-driven simulation of walking using the rigid-tendon model was $2.5$ times faster than that using the equilibrium model. An analogous simulation using the damped equilibrium model (which includes an elastic tendon) was $1.7$ times faster than a simulation using the equilibrium model.

The musculotendon models described here have important limitations. First, all of the models exhibit a region of negative stiffness on the descending limb of the active-force–length curve. This region of negative stiffness can cause a musculotendon length instability during forward-dynamic simulations. Second, although the damped equilibrium model was able to replicate the force profiles generated by biological muscle at maximal activation (Fig. 10), the comparisons between the model and experimental force profiles at submaximal activation revealed larger errors (Figs. 12 and 13). Third, the forces predicted by these models are dependent only on activation, length, and velocity, whereas the forces generated by biological muscle depend on past states [60] and other variables, such as temperature [61] and fatigue [62]. Fourth, the musculotendon models assume that all fibers within a musculotendon actuator are described by the same force–velocity curve, yet biological muscles are comprised of different fiber types that have different contractile speeds. Finally, our musculotendon actuators assume that the muscle fibers are straight, planar, parallel elements of equal length constrained to an area of constant height (Fig. 1). This assumption may limit the accuracy with which muscle forces can be simulated, especially for muscles that have variable fiber lengths and complex geometry.

We encourage researchers to develop musculotendon models that eliminate the limitations of our models and provide biological benchmark data that can be used as a standard for comparison. Musculotendon models published with software that implements the models will have the greatest impact. Providing software will enable others to reproduce and extend published results, and use the novel musculotendon models in muscle-driven simulations to gain insight into the dynamics of human and animal movement.

Glossary

Nomenclature

	Symbol Definition
${\ell }^{\mathrm{MT}}$ =	length of the musculotendon actuator (m)
${\ell }^{\mathrm{M}}$$\left\{{\tilde{\ell }}^{\mathrm{M}}\right\}$ =	muscle length (m)
${\ell }_{\mathrm{o}}^{\mathrm{M}}$ =	length at which the muscle develops peak isometric active force (m)
${\ell }_{\min }^{\mathrm{M}}$$\left\{{\tilde{\ell }}_{\min }^{\mathrm{M}}\right\}$ =	minimum permissible muscle length (m)
${\ell }^{\mathrm{T}}$$\left\{{\tilde{\ell }}^{\mathrm{T}}\right\}$ =	tendon length (m)
${\ell }_{\mathrm{s}}^{\mathrm{T}}$ =	length at which the tendon begins to develop a tensile force (m)
$v^{\mathrm{MT}}$ =	lengthening velocity of the musculotendon actuator (m/s)
$v^{\mathrm{M}}$$\left\{{\tilde{v}}^{\mathrm{M}}\right\}$ =	muscle lengthening velocity (m/s)
$v_{\max }^{\mathrm{M}}$ =	maximum muscle contraction velocity (m/s)
$v^{\mathrm{T}}$$\left\{{\tilde{v}}^{\mathrm{T}}\right\}$ =	tendon lengthening velocity (m/s)
$f^{\mathrm{M}}$$\left\{{\tilde{f}}^{\mathrm{M}}\right\}$ =	muscle force (N)
$f_{\mathrm{o}}^{\mathrm{M}}$ =	peak isometric muscle force (N)
$f^{\mathrm{T}}$$\left\{{\tilde{f}}^{\mathrm{T}}\right\}$ =	tendon force (N)
${\mathbf{f}}^{\mathrm{L}}({\tilde{\ell }}^{\mathrm{M}})$ =	normalized active-force–length curve of the muscle $(\mathrm{N}/f_{\mathrm{o}}^{\mathrm{M}})$
${\mathbf{f}}^{\mathrm{PE}}({\tilde{\ell }}^{\mathrm{M}})$ =	normalized passive-force–length curve of the muscle $(\mathrm{N}/f_{\mathrm{o}}^{\mathrm{M}})$
${\mathbf{f}}^{\mathrm{T}}({\tilde{\ell }}^{\mathrm{T}})$ =	normalized force–length curve of the tendon $(\mathrm{N}/f_{\mathrm{o}}^{\mathrm{M}})$
${\mathbf{f}}^{\mathrm{V}}({\tilde{v}}^{\mathrm{M}})$ =	normalized force–velocity curve of the muscle $(\mathrm{N}/f_{\mathrm{o}}^{\mathrm{M}})$
$\alpha$ =	muscle pennation angle (rad)
${\alpha }_{\mathrm{o}}$ =	muscle pennation angle when ${\ell }^{\mathrm{M}}={\ell }_{\mathrm{o}}^{\mathrm{M}}$ (rad)
$h$ =	pennated muscle height (m)
$u$ =	muscle excitation (–)
$a$ =	muscle activation (–)
$a_{\min }$ =	minimum permissible muscle activation (–)
${\tau }_{\mathrm{A}}$ =	activation time constant (s)
${\tau }_{\mathrm{D}}$ =	deactivation time constant (s)
$t$ =	time (s)

The braced symbols represent dimensionless quantities. Dimensionless forces, velocities, muscle lengths, and tendon lengths have been normalized by $f_{\mathrm{o}}^{\mathrm{M}}$, $v_{\max }^{\mathrm{M}}$, ${\ell }_{\mathrm{o}}^{\mathrm{M}}$, and ${\ell }_{\mathrm{s}}^{\mathrm{T}}$, respectively.

Appendix. Musculotendon Model Initialization

Model initialization describes the process of determining the length and velocity of the muscle, given its activation and the length and velocity of the musculotendon actuator. The ideal initial muscle state produces no artificial muscle-force transients at the beginning of a simulation. The equilibrium and damped equilibrium musculotendon models are initialized by determining the muscle state that achieves equilibrium between the muscle and tendon forces. The velocity of the musculotendon actuator is divided between the muscle and tendon in proportion to the linearized compliance of each element.

The derivation of the equation used to estimate muscle velocity begins with a substitution of variables:

$${\ell }^{\mathrm{S}}={\ell }^{\mathrm{M}}\cos \alpha$$ (A1)

$$f^{\mathrm{S}}=f^{\mathrm{M}}\cos \alpha$$ (A2)

where ${\ell }^{\mathrm{S}}$ and $f^{\mathrm{S}}$ are the length and force of the muscle projected onto the direction of the tendon, respectively. The equilibrium equation and the length of the musculotendon actuator are now expressed in more compact forms:

$$f^{\mathrm{S}}-f^{\mathrm{T}}=0$$ (A3)

$${\ell }^{\mathrm{MT}}={\ell }^{\mathrm{S}}+{\ell }^{\mathrm{T}}$$ (A4)

We now linearize Eq. (A3) with respect to the muscle length along the tendon and substitute for tendon length using Eq. (A4):

$$(f^{\mathrm{S}}+\frac{\partial f^{\mathrm{S}}}{\partial {\ell }^{\mathrm{S}}}\Delta {\ell }^{\mathrm{S}})-(f^{\mathrm{T}}+\frac{\partial f^{\mathrm{T}}}{\partial {\ell }^{\mathrm{T}}}(\Delta {\ell }^{\mathrm{MT}}-\Delta {\ell }^{\mathrm{S}}))=0$$ (A5)

Computing the time derivative of Eq. (A5), assuming that the partial derivatives are time-independent, yields the following:

$$\frac{\partial f^{\mathrm{S}}}{\partial {\ell }^{\mathrm{S}}}{v}^{\mathrm{S}}-\frac{\partial f^{\mathrm{T}}}{\partial {\ell }^{\mathrm{T}}}(v^{\mathrm{MT}}-v^{\mathrm{S}})=0$$ (A6)

Equation (A6) can now be solved for the muscle velocity in the direction of the tendon:

$$v^{\mathrm{S}*}=\frac{\frac{\partial f^{\mathrm{T}}}{\partial {\ell }^{\mathrm{T}}}}{\frac{\partial f^{\mathrm{S}}}{\partial {\ell }^{\mathrm{S}}}+\frac{\partial f^{\mathrm{T}}}{\partial {\ell }^{\mathrm{T}}}}{v}^{\mathrm{MT}}$$ (A7)

Unfortunately, Eq. (A7) cannot always be employed due to the region of negative stiffness (a result of the negative slope of the active-force–length curve in Fig. 3(c)), which can cause the denominator of Eq. (A7) to become zero. If the denominator of Eq. (A7) is within floating-point tolerance of zero ($\mathrm{\epsilon }$) or the tendon is slack, we assume that the muscle has zero velocity; otherwise, $v^{\mathrm{S}*}$ is used as the lengthening velocity of the muscle along the tendon:

$$v^{\mathrm{S}}=\{\begin{array}{cc}\multicolumn{1}{c}{0}& \hfill \mathrm{if}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}|\frac{\partial f^{\mathrm{S}}}{\partial {\ell }^{\mathrm{S}}}+\frac{\partial f^{\mathrm{T}}}{\partial {\ell }^{\mathrm{T}}}|<\mathrm{\epsilon }\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\mathrm{or}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{\tilde{\ell }}^{\mathrm{T}}<1.0\hfill \\ \multicolumn{1}{c}{v^{\mathrm{S}*}}& \hfill \mathrm{otherwise}\hfill \end{array}$$ (A8)

We compute the pennation angular velocity ($\stackrel{·}{\alpha }$) and tendon velocity ($v^{\mathrm{T}}$) using the kinematic model of the musculotendon actuator described in Sec. 2.4.