Complex Matrix Remodeling and Durotaxis Can Emerge From Simple Rules for Cell-Matrix Interaction in Agent-Based Models

Short abstract

Using a top-down approach, an agent-based model was developed within NetLogo where cells and extracellular matrix (ECM) fibers were composed of multiple agents to create deformable structures capable of exerting, reacting to, and transmitting mechanical force. At the beginning of the simulation, long fibers were randomly distributed and cross linked. Throughout the simulation, imposed rules allowed cells to exert traction forces by extending pseudopodia, binding to fibers and pulling them towards the cell. Simulated cells remodeled the fibrous matrix to change both the density and alignment of fibers and migrated within the matrix in ways that are consistent with previous experimental work. For example, cells compacted the matrix in their pericellular regions much more than the average compaction experienced for the entire matrix (696% versus 21%). Between pairs of cells, the matrix density increased (by 92%) and the fibers became more aligned (anisotropy index increased from 0.45 to 0.68) in the direction parallel to a line connecting the two cells, consistent with the “lines of tension” observed in experiments by others. Cells migrated towards one another at an average rate of ∼0.5 cell diameters per 10,000 arbitrary units (AU); faster migration occurred in simulations where the fiber density in the intercellular area was greater. To explore the potential contribution of matrix stiffness gradients in the observed migration (i.e., durotaxis), the model was altered to contain a regular lattice of fibers possessing a stiffness gradient and just a single cell. In these simulations cells migrated preferentially in the direction of increasing stiffness at a rate of ∼2 cell diameter per 10,000 AU. This work demonstrates that matrix remodeling and durotaxis, both complex phenomena, might be emergent behaviors based on just a few rules that control how a cell can interact with a fibrous ECM.

1. Introduction

The migration of cells on or through extracellular matrix (ECM) as well as cell-mediated remodeling of ECM underlie many biological processes including development [1], growth and remodeling [2], fibrotic pathologies [3], and wound healing [4] and are also important components of many tissue engineering applications [5,6]. In addition to chemical means such as the synthesis, modification, and degradation of the matrix, cells remodel (i.e., reorganize existing material) ECM using mechanical (or traction) forces. These traction forces develop as cells continuously interact with the matrix through the dynamic extension and retraction of pseudopodia [7]. The extent of mechanically mediated remodeling of ECM is clearly revealed in a number of in vitro models. Macroscopic compaction of ECM gels by fibroblasts and myofibroblasts in vitro can reduce initial volumes by more than 90% in models of the contraction of granulation tissue during wound healing [4,8–10]. Other cell types including endothelial [11,12], smooth muscle [6], and chondrocytes [13] also compact ECM gels. Compaction is spatially heterogeneous with greater compaction in the pericellular region [14] and the intercellular region between nearby adjacent cells [15]. Recent studies suggest that pericellular matrix densities, as opposed to regional average densities, regulate cellular behavior [11]. Coinciding with nonisotropic compaction, fibrous ECM proteins align between cells. The potential role of intercellular fiber density and alignment has been explored since the 1950 s [16]. Aligned fibers have been shown to allow for long-range stress transmission for cell-cell mechanical signaling [17] and may also create preferential axes for cell migration [18,19]. The paper by McLeod et al. [15] on capillary morphogenesis in this special issue quantifies the extent of macroscopic and pericellular compaction by endothelial cells within collagen gels. In addition, they note that cells initially within ∼100 μm apart efficiently compact and align the fibrous matrix in the intercellular space to form bundles of matrix connecting the cells before the cells migrate towards one another. In addition to remodeling the ECM, cells use mechanical forces to migrate within their environment. In the absence of soluble chemotactic factors, cells have been shown to migrate up an insoluble ECM concentration gradient (haptotaxis [20]) and in the direction of increasing substrate stiffness (durotaxis [21]).

A number of mathematical/computational models exist for studying mechanically mediated cell-ECM interactions. Many of these models focus on multicellular systems and the resulting macroscale changes such as compaction, average fiber alignment, or average mechanical properties [11,18]. In contrast, few models account for individual cellular-level mechanical forces [22,23] and interaction with individual ECM fibers [24,25]. One challenge of modeling cell-matrix interactions at the cellular length scale is that spatial heterogeneity (e.g., ECM fibers, cell versus extracellular space) excludes the continuum approximation needed for differential equation-based models. In addition, the dynamic binding and unbinding of the cell to the ECM requires a level of spatial and temporal flexibility not commonly found in finite element models. Agent-based modeling approaches are well suited to handle both spatial heterogeneity and frequently changing physical and spatial relationships between different components. Despite their potential utility, there have been few attempts to apply agent-based models to cell-matrix interactions. Dokukina et al. developed a 2D agent-based model of polarized cell migration by modeling the cell’s cytoskeleton as a network of nodes connected by elastic springs and viscous dashpots. Substrate-rigidity sensing was built into the model, however the matrix or the interaction of the cell with the matrix was not explicitly modeled. Instead a value for substrate rigidity determined by node location was substituted into the calculation for force generation at the front nodes of the cell [23]. Bauer et al. utilized a cellular Potts model to investigate the influence of ECM topography on the coordination of multicellular interactions during angiogenesis [26]. Although a fibrous matrix was explicitly modeled, it was static and therefore unable to be reorganized as a result of force exerted by the cells. Schlüter et al. explored the influence of ECM fiber orientation on cell migration representing the cell with a single agent. Although individual matrix fibers could be reoriented, they were not deformable, consisting only of rigid tubes with the farthest end as a fulcrum about which the fiber could be rotated. Consequently, matrix remodeling was severely limited, not allowing for fiber bending, force propagation, remodeling beyond a localized pericellular region, or matrix compaction [24]. Alberts developed an agent-based model to simulate realistic cytoskeletal filament bending dynamics [27], a model easily adaptable to filamentous ECM proteins. To our knowledge, no one has developed an agent-based model that considers ECM remodeling and cell migration on fibrous matrix containing cross links and capable of extensive force transmission and deformation. Here we develop an agent-based model that includes dynamic, mechanically mediated cell interaction with a fibrous ECM, deformation of cells and fibers, and cell migration. The predictions of our model are compared to known aspects of mechanically mediated ECM interactions including macroscopic, pericellular, and intercellular compaction of matrix, alignment of fibers between adjacent cells, and directional migration of cells towards one another.

2. Materials and Methods

2.1. Overview of NetLogo.

This agent-based model was developed using NetLogo 4.1.1 [28]. Our NetLogo code is available upon request from the corresponding author. In NetLogo there are four types of agents: turtles, patches, links, and the observer. The in silico world in which this model exists is 2D and divided up into a grid of square, stationary patches. Turtles, or nodes represented by user-defined shapes, can move within a single patch and to any other patch. Links are agents that connect two turtles. The observer gives instructions to the other agents. Turtles, patches, and links have properties that are user defined and subtypes of each can be defined with unique properties and rules governing their behavior. Herein, specific turtle subtypes will be denoted in quotes for clarity (e.g. “membrane,” “binding site,” and “nucleus”).

With the exception of four rules described below related to the initial fiber arrangement and cell-fiber interactions, all rules in our model were deterministic as opposed to probabilistic. The order of the agents to which the rules were applied during the simulation, however, was random. For example, during one iteration a specific rule might be applied to agent 1 before agent 2, while in the subsequent iteration the rule may or may not be applied to agent 2 first. Therefore, simulations with the same initial conditions may have different outcomes. The order of the agents on which rules were executed could have been explicitly defined, however there was concern that this may create unintended bias towards a particular outcome. Application of all the relevant rules to all the agents completes a single iteration of the simulation corresponding to the passing of one arbitrary unit (AU) of time.

2.2. General Model Components.

For all models in this study (described in more detail later), cells are composed of 30 “membranes,” which can be thought of as sections of a cell membrane arranged initially in a uniform circle around a single “nucleus” (Fig. 1(a)). Every “membrane” is linked to its immediate three neighbors on either side and its “nucleus” such that the cell resembles a wheel with a hub, rim, and spokes. While the intention was not to provide a realistic model of the cytoskeleton, this minimal structure was chosen to allow for intracellular force transmission and cell deformation while also preventing excessive local cell deformation.

Fig. 1.

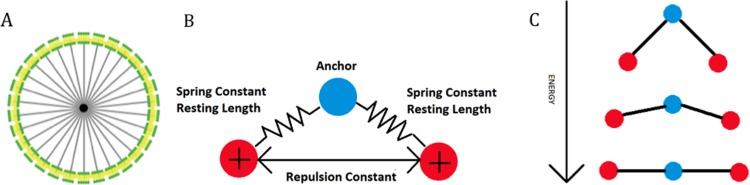
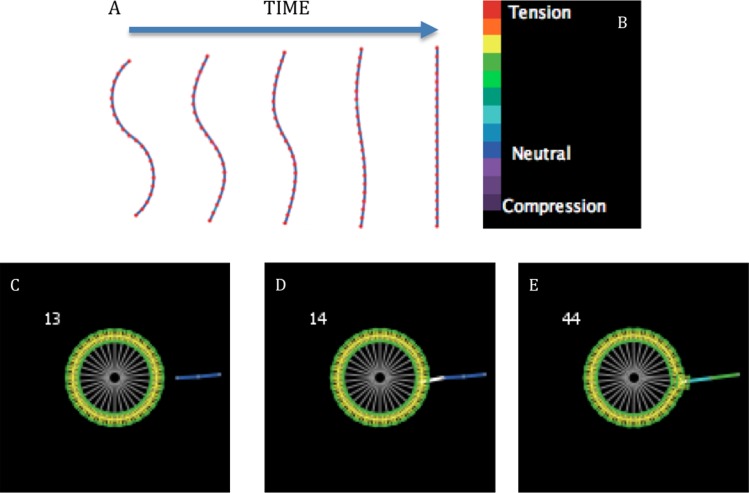
Graphical representations of model details. (a) Large view of a cell composed of 30 “membranes,” 1 “nucleus” (center), 30 membrane-nucleus links, and intermembrane links (not visible). (b) A graphical illustration of how the Fruchterman-Reingold algorithm is used to straighten fibers. Every “binding site” becomes an anchor (blue) once per iteration in random order and its neighboring “binding sites” (red) behave like charged particles. (c) As the neighbors repel each other, they pivot about the anchor and this section of the bent fiber straightens, reducing its potential energy. As each section of a fiber successively undergoes this process, the entire fiber straightens.

In order to allow for deformation and movement, all links are defined as “layout-spring” in NetLogo. Layout-spring is based on the Fruchterman-Reingold algorithm [29] where the link acts as a spring (Hooke’s law) and the turtles act as electrically charged particles (Coulomb’s law). Using this type of link, the user can define the spring constant, resting length, and repulsion constant. These forces are applied to the turtles, pulling them together or pushing them apart. A graphical representation of how the Fruchterman-Reingold algorithm is used in this model is shown in Figs. 1(b) and 1(c) for fibers, as an example, which are composed of a series of “binding sites” connected by links.

In some in vitro experiments, the perimeter of the ECM gel is bound to a solid surface (e.g., a gel attached to the bottom and wall of a tissue culture well plate). Cells on these bound (or constrained) gels exhibit different behavior than those on free-floating gels, able to resist macroscopic compaction [4,12]. To model the different boundary conditions experienced by constrained and free-floating gels, the “binding sites” of the ECM initially located at the perimeter of the world may either be infinitely weighted, such that they are immobile (constrained) or fractionally weighted (free-floating) so that there may be some mobility and macroscopic compaction.

In modeling, cell migration can be categorized as either random [30] or activated [23]. The type of cell migration presented in these models can be categorized as random in that a leading and trailing edge is not specified; migration occurs as the net effect of all the different forces between the cell and ECM. All “membranes” begin in an active state (green) (Fig. 2(c)), meaning that each has the ability to extend a pseudopodium (a type of link) and bind randomly to any “binding site” within proximity of ∼1/4 cell diameters (Fig. 2(d)). The resting spring length for this new link is set at ∼1/40 cell diameters, an order of magnitude smaller than the average link between “binding sites” on a fiber. The difference between a link’s current length and resting length determines the stored energy in the spring and force of contraction. Contraction pulls the fiber towards the cell and, to a lesser degree, the cell towards the fiber (Fig. 2(e)). After this “binding site” is pulled close to the cell, a cell will break this cell-fiber link and extend a new pseudopodium to an adjacent “binding site.” This adjacent “binding site” may either be a virgin site within ∼1/3 cell diameters or one previously pulled on. At sites of cross links the new pseudopodium will bind randomly to just one of the adjacent “binding sites” within ∼1/3 cell diameters. As with binding, there exist rules for unbinding from the matrix (Table 1). To control cell shape and restrict cell area only some of the “membranes” are allowed beyond a defined distance from their “nucleus” at any one time with preference for maintaining “membranes” that are farthest away. The preference for maintaining certain bonds between “membranes” and “binding sites” is motivated by the experimental observation that matrix stress increases cell-matrix adhesion strength [31], which we refer to here as force strengthening. When the number of “membranes” exceeds that allowed beyond a defined distance, the “membrane” closest to its “nucleus” and beyond the defined distance will unbind from the matrix and become inactivated (red “membranes” in Fig. 3) for 6 AU (a minimized value) to allow it to return towards its “nucleus.”

Fig. 2.

(a) A simulation of a single fiber straightening under the rules described in Fig. 1(b). The fiber is composed of 22 “binding sites” and is initially s-shaped (left, 0 AU). From left to right the following four frames are the same fiber at 250, 500, 1000, and 2500 AU. (b) Legend for the strain experienced by fiber segments. (c) At 13 AU a single proximal “binding site” on the unstrained fiber (blue) is just beyond the proximity within which a “membrane” on cell can interact with it. (d) At 14 AU the proximal “binding site” on the fiber falls just within the proximity of a single “membrane” that extends a pseudopod (white) to bind to the fiber. (e) After binding, the pseudopod retracts, pulling on the fiber inducing strain (represented by light blue and green) and causing the “membrane” to move in the direction of the fiber.

Table 1.

A list of parameter values

NetLogo Two-Cell Model Parameters (38)	Range	Value
World parameters (2)
Height	1–Max	33 Patches
Width	1–Max	57 Patches
ECM parameters (6)
Distance between “binding sites”		1.0 Patches
Max length of a fiber		100 Turtles
Initial fiber max deviation		15°
Degree of cross linking		100%
Fiber density	0–Max a	40
Edge weight	0–100%	100% or 99.5%
Cell parameters (5)
Cell radius		2 Patches
Number of cells		2
“Membranes” per cell		30
Distance between cells	0–Max a	16 Patches
Cell weight	0–100%	90%
Rules (7)
Force generation by pulling
Initial proximity for “membranes” to bind fibers		1.0 Patches
Proximity condition 1		0.5 Patches
Proximity condition 2		1.3 Patches
Cell shape and directional migration
“Pseudopodia” max length		Not defined
Number of “membranes”:
That can exceed 2.5 times radius		0
That can exceed 1.5 times radius		1
That can exceed 1.1 times radius		8
Other
Iterations to reset “inactive membranes”		6
Links (18)	Spring constant	Resting length	Repulsion constant
“Membranes”
Between first neighbors	1.000	0.418	0.000
Between second neighbors	1.000	0.832	0.000
Between third neighbors	1.000	1.236	0.000
Other
Between the “nucleus” and a “membrane”	0.900	1.800	0.005
Between a “membrane” and a fiber	1.000	0.100	0.000
About pivot points on a fiber	0.500	0.977	0.060

^aMaximum value undefined.

Fig. 3.

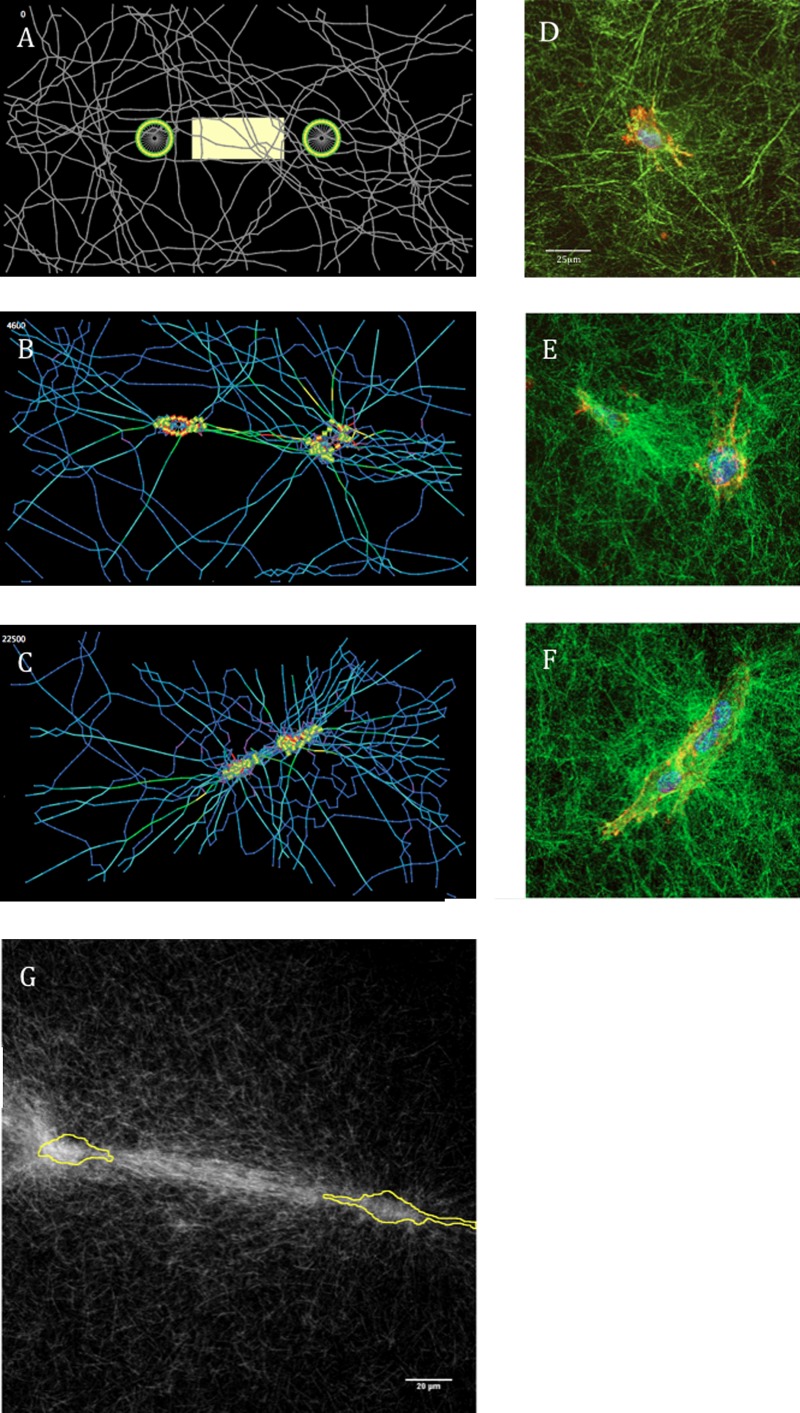
(a) The two-cell free-floating matrix model at initial conditions. The intercellular ROI (yellow box) is defined as being five patches in height (approximately 1 cell diameter) and having borders five patches from the “nuclei” of the two cells. (b) At 4600 AU aligned fibers between the cells show more strain compared to other regions and at (c) 22,500 AU fibers have pulled away from the edge allowing for macroscopic compaction. (d)–(f) Time course of collagen remodeling from McLeod et al. [15]. HUVEC cultured in 2 mg/ml collagen that were fixed and stained with phalloidin and DAPI, and collagen were imaged after (d) 0, (e) 4, and (f) 16 h of culture. Panels show overlay of collagen (green) with cells (red/blue). (d) Scale bar is 25 μm for images (d), (e), and (f) [15]. (g) A compressed z stack of confocal reflectance microscopy images of 3T3 cells (outlined in yellow) initially on collagen featuring prominent fiber alignment and increased matrix density between two cells. Scale bar is 20 μm.

2.3. Two Special Cases

2.3.1. Two-Cell Model.

The purpose of this model was to quantify ECM remodeling. In this model, the world is a 57 × 33 arrangement of patches. When the model initializes, fibers are formed by seeding a defined number of “binding sites” with a random location and orientation. These “binding sites” then propagate forwards and backwards by placing more “binding sites” one patch length (1/4 cell diameter) apart with successive “binding sites” connected by a link. Successive links are allowed to deviate a random value, with a maximum absolute value of 15 deg away from the axis of its neighbors. This value of 15 deg was chosen by trial and error to create fibers with a curvature visually similar to freshly made collagen gels [15]. Thus, fibers appear as wavy strands (Fig. 3(a)) and different simulations can vary at initial conditions in terms of overall matrix density, distribution, and anisotropy. All fiber segments (links between “binding sites”) that cross are cross linked by inserting a “binding site” on one fiber into the other fiber. This shared “binding site” is determined at random out of the four possibilities.

2.3.2. One-Cell Model.

The purpose of this model was to study the influence of a stiffness gradient on cell migration. The world is a 31 × 31 arrangement of patches. Every patch contains a “binding site” that is linked to its closest neighbors, forming a square lattice arrangement of fibers. This arrangement minimizes the potential contribution of fiber orientation or density to cell migration. Stiffness increases fourfold from the right edge of the world to the left linearly across the simulation space when a gradient is present with no gradient along the Y direction.

2.4. Analysis of Model Results

2.4.1. Fiber Density.

Average fiber density was calculated by dividing the number of “binding sites” by the number of patches in the matrix area. This area was determined by starting with the total number of patches in the world and excluding empty patches along the edge of the world along with all contiguous, empty patches. By this method, an empty patch or region within the matrix is considered part of the matrix area while an empty area bordering the edge of the matrix is not. The pericellular area was defined as the single layer of patches that circumscribes the cell but does not contain cell components. The density in this region was determined by dividing the number of “binding sites” on these patches by the number of these patches. Intercellular fiber density was also quantified because anisotropic compaction has been observed between pairs of cells [15,32] and because as the cells pull on fibers that loosely connect between them the fibers will be drawn into the intercellular region to form a bundle; thus increasing the density in that region. The intercellular region of interest (ROI) was defined as always five patches in height (approximately 1 cell diameter) and having borders five patches from the “nuclei” of the two cells (Fig. 3(a)). This region is purposely distant from the cell membranes to prevent compacted fibers in the pericellular region from disproportionately influencing fiber alignment and density calculations. The intercellular ROI is initially a rectangle between the two cells, but follows the movement of the cells throughout the simulation. If the cells migrate apart, the intercellular ROI lengthens. In cases where the cells migrate together, this region shortens. If the “nuclei” come within ten patches (∼2.5 cell diameters) from each other, the intercellular ROI shrinks to nothing and intercellular compaction and alignment cannot be calculated.

2.4.2. Fiber Alignment.

Fiber alignment was quantified in the intercellular ROI with two descriptors of the ECM, the anisotropy index (α), or extent of alignment, and principal angle (θ_p). First, the orientation (θ_s) and length (l_s) of each fiber segment along with a reference angle (0 deg ≤ θ_r ≤ 179 deg at 1 deg intervals) were substituted into Eq. (1) to find the reference angle that maximizes the x component of the orientation tensor (Ω_xx) [33–35]. That particular reference angle represents the principal angle of the fiber segments. To characterize the overall direction of fiber alignment relative to the intercellular axis, the difference between the principal angle and the angle of the intercellular axis (θ_i) was calculated, here called the angle of alignment (θ_a) [Eq. (2)]. The anisotropy index, with 1 corresponding with perfect alignment and 0 with no alignment, was calculated by substituting the maximum value of Ω_xx from Eq. (1) into Eq. (3):

$${\Omega }_{\mathit{xx}}=\frac{\sum l_s{\cos }^2({\theta }_s-{\theta }_r)}{\sum l_s}$$ (1)

$${\theta }_a=|{\theta }_p-{\theta }_i|$$ (2)

$$\mathrm{\alpha }=1-\frac{(1-{\Omega }_{\mathit{xx}\mathrm{MAX}})}{{\Omega }_{\mathit{xx}\mathrm{MAX}}}$$ (3)

2.4.3. Cell Migration.

Cell migration was quantified by tracking the location of the cells’ “nuclei” and using regression analysis to measure the speed of migration. In the two-cell model only, the distance between the “nuclei” was also measured throughout the simulation.

2.4.4. Statistics.

All data is reported as mean +/− standard error. Statistical differences were measured using the unpaired Student’s t test between groups and the paired Student’s t test with Bonferroni correction within groups. ANCOVA was used to compare slopes of the best-fit lines determined by linear regressions between conditions. P values below 0.05 were considered statistically significant.

3. Results

The selected rules for fiber mechanics gave individual fibers the ability to stretch and bend in response to loading, and after unloading, return to their unloaded conformation. For example, a single simulated fiber in isolation composed of 22 “binding sites” initially possessing an s-shape continuously straightened over 2500 AU (Fig. 2(a)). Qualitatively, simulations of cell-populated ECM gels exhibited many features previously reported in experimental studies. Cells exhibited pseudopodia extension and retraction, as reported by Meshel for fibroblasts in collagen [7], over a time scale of ∼3–30 AU (Figs. 2(c)–2(e)), depending on fiber orientation. Though initially circular (Fig. 3(a)), in a free-floating matrix after 4600 AU, the cells elongated, the major axes of the two cells co-aligned and were directed towards each other’s centroids (Fig. 3(b)) as reported for fibroblast on fibrin [36]. In the area between two adjacent cells, fiber density increased and fibers preferentially aligned parallel to the intercellular axis as has been observed for pairs of cells (Figs. 3(e) and 3(g)) [15] and cell clusters [37] on or within gels of fibrous ECM. The stresses carried by these bundles of intercellular fibers tended to be greater than that seen in other fibers, as indicated by the colors of the fibers in the intercellular region, consistent with the notion of “lines of tension” that Vernon and Sage proposed connect endothelial cells within collagen gels and mediated capillary morphogenesis [38]. In free-floating matrices, cells compacted the matrix and in both free-floating and constrained matrices the density of fibers in the pericellular region appeared to increase. In free-floating matrices, some of the pairs appeared to exhibit directed motion towards one another (Fig. 3(c)) as reported by others [36] and described by McLeod et al. [15] in this special issue (Fig. 3(f)).

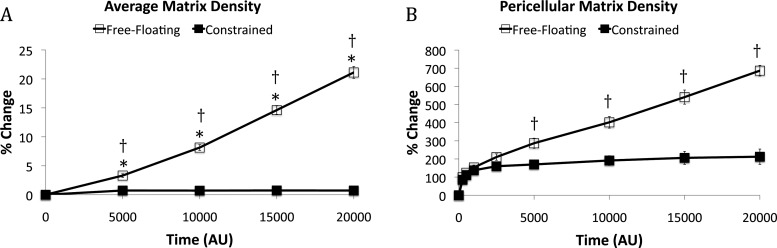
To further investigate these initially qualitative observations, quantitative assessments of matrix remodeling and cell migration were applied to the results from 10 simulations performed for each the free-floating and constrained matrices. Average fiber density increased 21.1% for the free-floating matrix from the initial conditions but did not change for the constrained matrix, as expected (Fig. 4(a)). The percent increase in pericellular matrix density (Fig. 4(b)) was (1) greater for the free-floating matrix than the constrained matrix and (2) was more than an order of magnitude greater than the percent increase in average matrix density. At 20,000 AU the pericellular matrix density increased 686% for the free-floating matrix compared to 212% for the constrained matrix. The pericellular matrix density for the constrained matrix appears to asymptote to a maximum value, perhaps resulting from the matrix’s ability to elastically resist the force exerted by the cell. This asymptotic behavior is not observed for the free-floating matrix that exhibits a linear increase in pericellular matrix density throughout the simulation.

Fig. 4.

(a) Average matrix density and (b) Pericellular matrix density. Free-floating matrices (edge weight = 0.995) have a perimeter of “binding sites” that move 0.5% of what they would were a weighting factor not to be included in the model. Constrained matrices (edge weight = 1.000) possess a perimeter of “binding sites” around the edge of the world that cannot move. The pericellular matrix density at all time points has increased significantly from 0 AU (p < 0.05) (significance not labeled on this graph). Confidence intervals signify the SEM. ^* p < 0.05 compared to 0 AU. ^† p < 0.05 between the free-floating and constrained matrices at a specific time point.

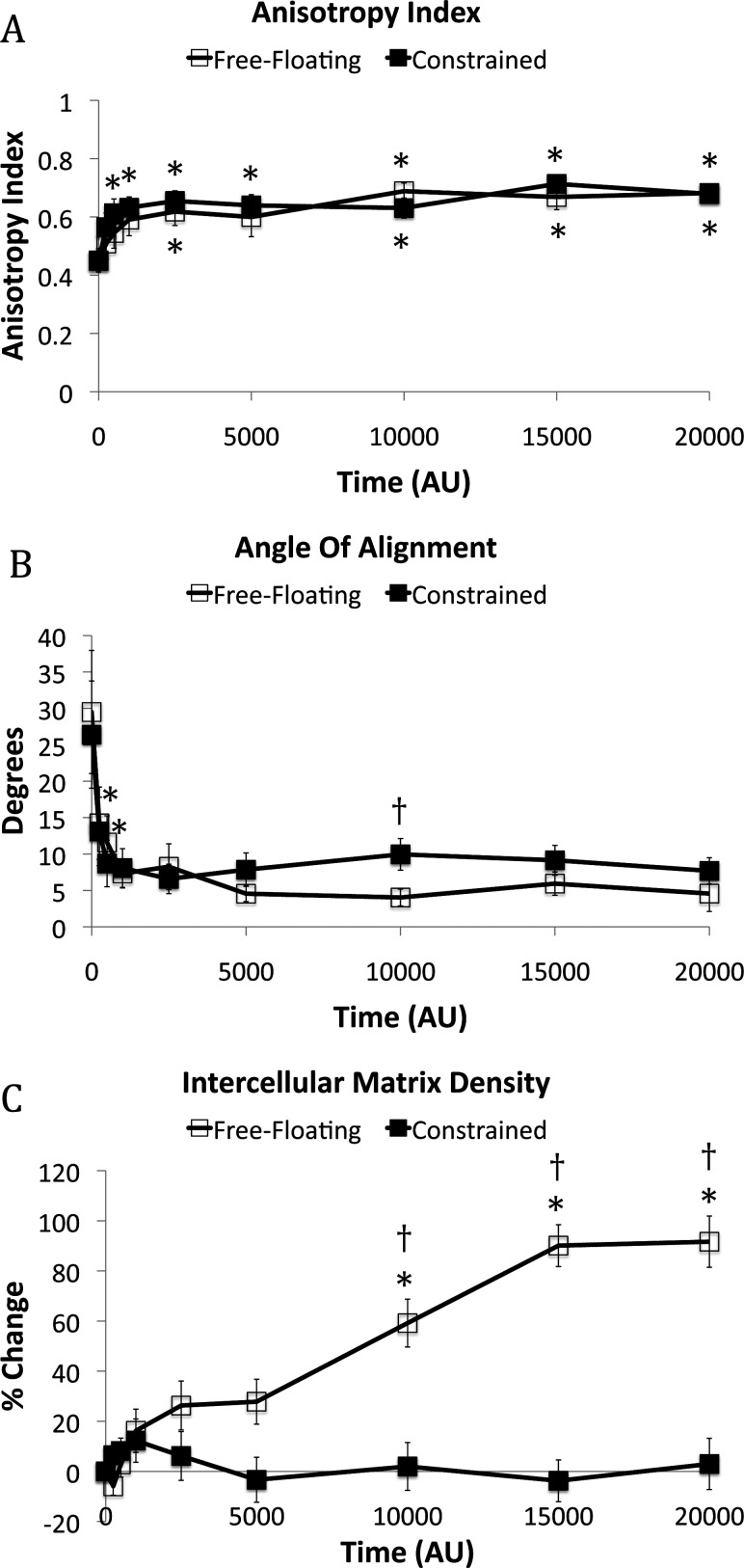
At initial conditions, anisotropy index, angle of alignment, and intercellular matrix density did not indicate preferential alignment of fibers nor were these metrics statistically different between free-floating and constrained matrices (Fig. 5). As the simulation progressed, each of these three descriptors for the microstructure indicated that fibers in the intercellular region aligned. Anisotropy index increased rapidly for both free-floating and constrained matrices within the first 500 AU and very little change in anisotropy index was observed after 1000 AU (Fig. 5(a)). Also by 1000 AU, the angle of alignment decreased from 29.5 deg to 7.3 deg for the free-floating matrix and from 26.4° to 8.1° for the constrained matrix (Fig. 5(b)). The density of fibers in the intercellular region increased 91.6% for the free-floating matrix and 3.0% for the constrained matrix compared to initial conditions (Fig. 5(c)).

Fig. 5.

(a) The anisotropy index, or extent of alignment, of the fibers in the intercellular region. (b) The angle of alignment represents the difference in angle between the principal angle of the fiber bundle and the intercellular axis. (c) The percent change in matrix density in the intercellular region. N = 10 for all time points except for the free-floating matrix at 15,000 AU (n = 9) and 20,000 AU (n = 7). Confidence intervals signify the SEM. ^* p < 0.05 compared to 0 AU. ^† p < 0.05 between the free-floating and constrained matrices at a specific time point.

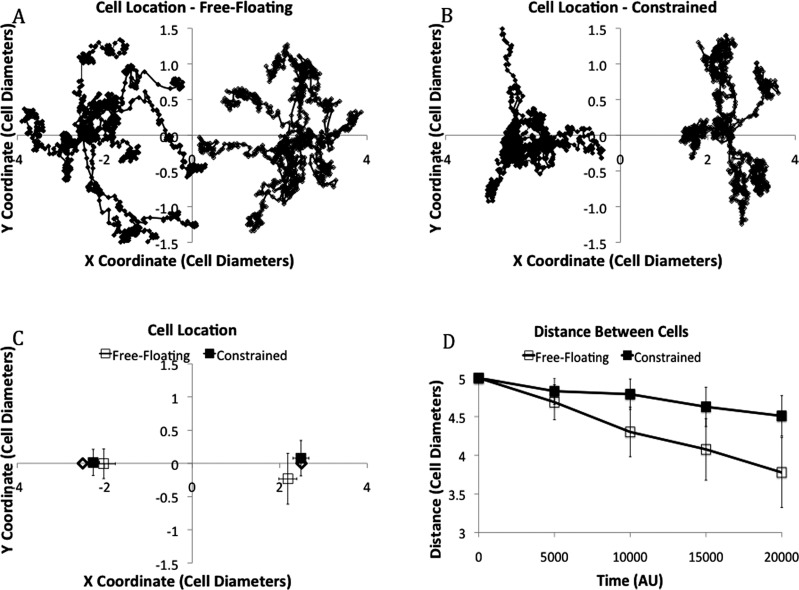
To quantify cell migration, the location of these cells was tracked at regular intervals throughout the simulations. The overlay of cell tracks (n = 10) shows that migration appears to consist of random, curlicue motion punctuated by periods of what appears to be coherent linear motion (Fig. 6(a) and 6(b)). A plot of the average distance between two cells as a function time (Fig. 6(d)) shows that cells on free-floating matrices migrated at roughly a constant rate towards each other of approximately 1 cell diameter per 20,000 AU. Cells on constrained matrices also migrated towards each other, but at a more modest rate of 0.45 cell diameters per 20,000 AU not achieving the criteria for statistical significance (p = 0.068).

Fig. 6.

Overlays of all cell tracks (n = 10) for (a) the free-floating matrix and (b) constrained matrix. Cell 1 is on the left and cell 2 is on the right. (c) Average location + / − SEM for the free-floating and constrained matrices. For (a)-(c), cells start with an X coordinate of + and – 2.5 cell diameters, marked with a ◊. (d) The distance between the two cells does not change significantly throughout the simulation. Cells on free-floating matrices migrated at roughly a constant rate towards each other of approximately 1 cell diameter per 20,000 AU (p = 0.003). Cells on constrained matrices migrated towards each other, but at a more modest rate of 0.45 cell diameters per 20,000 AU not achieving the criteria for statistical significance (p = 0.068).

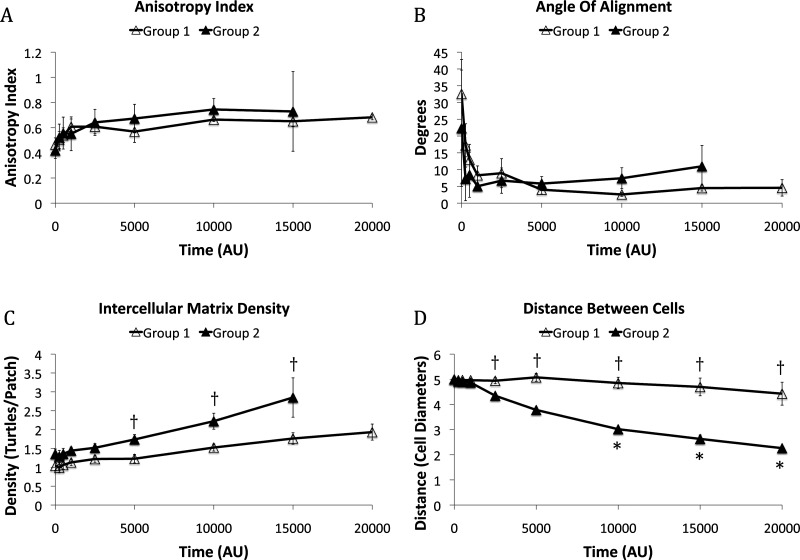
Given the large variation in the direction and distance cells migrated, we reasoned that some aspects of the initial conditions or conditions achieved early in the simulation might favor directed migration of the pair of cells towards one another. To explore this notion, simulation results for cells on free-floating gels were divided into two groups, those where cells’ “nuclei” did not come within 2.5 cell diameters at any time during the simulation (group 1) and those where the cells’ “nuclei” did come within 2.5 cell diameters at any time during the simulation (group 2). There was no significant difference in the anisotropy index, angle of alignment, or density of fibers in the intercellular ROI at initial conditions between groups 1 and 2. In addition, there was no significant difference in anisotropy index (Fig. 7(a)) or angle of alignment (Fig. 7(b)) between groups 1 and 2 throughout the simulation. Interestingly, the matrix density in the intercellular ROI was consistently higher for group 2 than group 1 and was initially ∼30% greater for group 2 (p = 0.168) than group 1. This difference increased with time and reached statistical significance at times greater than or equal to 5000 AU (Fig. 7(c)). Cells in group 2 had migrated closer together than those in group 1 by 2500 AU (Fig. 7(d)) suggesting that these cells might be responding to the initial or developing variations in intercellular density (i.e., exhibiting haptotaxis). Alternatively, since (1) increasing fiber density increases the stiffness of the matrix and (2) cells can exhibit durotaxis or migration in response to stiffness cues [20], we hypothesized that stiffness could be an important variable influencing cell migration in the simulations. To test this hypothesis we developed a single-cell model with a uniform matrix possessing a stiffness gradient.

Fig. 7.

(a) The anisotropy index of the fibers in the intercellular ROI. (b) The angle of alignment in the intercellular ROI. (c) The matrix density in the intercellular ROI. For all graphs, group 1 includes all simulations where cells do not migrate close together (n = 7) and group 2 includes all simulations where cells do migrate close together [n = 3, except at 15,000 AU (n = 2)]. Values for anisotropy index, angle of alignment, and intercellular matrix density for group 2 at 20,000 AU could not be calculated as the intercellular ROI had disappeared. (d) The distance between cells is significantly different between groups 1 and 2 from 2500 AU on. Confidence intervals signify the SEM. *p < 0.05 compared to AU. ^† p < 0.05 between group 1 and group 2 at a specific time point.

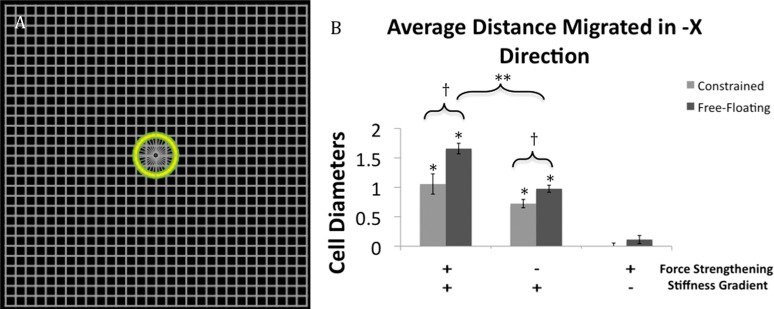
The single-cell, stiffness-gradient model (Fig. 8(a)) showed that when no stiffness gradient existed, average net migration did not achieve statistical significance. When a stiffness gradient was present, cells moved leftwards in the direction of increasing stiffness (Fig. 8(b)). Interestingly, cells on a free-floating matrix migrated 57% farther than cells on a constrained matrix. It is important to note here that there is no rule in our model for durotaxis; instead this behavior emerges from simpler rules governing cell-matrix interactions. The biological implication of these simulation results is that cells need not have specialized systems to detect stiffness gradients or to direct their migration up such gradients. Instead, relatively simple mechanical interactions between the cells and matrix can give rise to durotaxis. Furthermore, the model allows one to test the relative contribution of various aspects of the mechanical interactions on the response. For example, removing rules that correspond to the experimentally observed force strengthening of cell-matrix bonds reduces the extent of directional migration about 32% for the constrained matrix and 41% for the free-floating matrix. These results suggest that force strengthening of integrins likely contributes to, but does not fully account for, durotaxis. Average migration in the direction perpendicular to the stiffness gradient (i.e., Y direction) was not significant in any of the six cases and never exceeded 0.1 cell diameters.

Fig. 8.

(a) Single-cell model featuring a uniform square lattice arrangement of fibers. (b) Cells on this uniform matrix without a stiffness gradient do not migrate significantly in the –X direction regardless of whether the matrix is free-floating or constrained. When a stiffness gradient is present, decreasing from −X to +X, the cells move in the direction of greater stiffness in the −X direction with and without force strengthening of cell-matrix bonds. Cells on a matrix with a stiffness gradient migrate significantly farther when that matrix is free-floating than when the matrix is constrained. Cells never migrate more than 0.1 cell diameters in the Y direction. Data is presented as the mean +/− SEM. ^* p < 0.05 as compared to the same matrix type without a stiffness gradient. ^† p < 0.05 between the different matrices under the same conditions. **p < 0.05 between free-floating matrices with and without force strengthening.

4. Discussion

A top-down approach was adopted to create simplified representations of cells and fibers and implement a minimum set of rules providing for pseudopodia extension and retraction, cell-fiber adhesion, and deformation of cells and fibers. The model utilizes a gross simplification of the specific biological processes underlying cell and fiber behaviors and cell-fiber interactions leaving out mechanisms such as actin polymerization responsible for “membrane” protrusion, integrin mediated adhesion, and actin-myosin force generation. Instead, it is designed with simplified abstractions representing these biological mechanisms. For this reason, one can consider this model a “first step.” The model could be modified to fit a particular experimental system, by incorporating biologically relevant, “bottom-up” details and optimizing parameters.

The rationale for choosing many parameter values was to support a model that was reasonably realistic and visually appealing while not too computationally expensive. Cell size was arbitrarily chosen and the cornerstone around which this model was constructed. Height and width for this model had two constraints. The world had to be big enough surrounding these two cells such that the edge effects of fibers bound rigidly to the edge did not overly influence the outcome of the simulation. The upper limit was restricted by the processing time imposed by the additional agents. It was observed that the time to run a simulation increased proportionally to the square of the number of “binding sites.” As a result, the distance between “binding sites” on a fiber was restricted to a value corresponding to a few microns. The edge adhesion strength for the free-floating matrix was chosen to prevent rapid macroscopic compaction, while still allowing some compaction to occur. The number of “membrane” units was chosen such that the cell would be effective at interacting with nearby fibers without increasing the processing time for little benefit. Values for the spring parameters for each link type were chosen by trial and error to present a visually appealing model. Last, a 2D modeling approach was chosen due to the added complexity and computational cost associated with a 3D model with the implication that a 3D model would be very similar.

This work demonstrates the power of agent-based modeling by showing how complex biological phenomena might be emergent behaviors arising from just a few rules that control how a cell can interact with a fibrous ECM. For example, such rules were adequate to recreate many features of cells in fibrous gels observed experimentally such as migration of cells towards each other and in the direction of increasing stiffness (i.e., durotaxis). Furthermore, fiber densities in the pericellular region increased much more than in the regions further from the cell while fibers in the intercellular region became more anisotropic and oriented along the intercellular axis. Coinciding with fiber alignment, cells commonly adopted a spindle-shaped morphology and co-aligned. The fact that these behaviors emerged in our simulations from a simple set of rules suggests that the corresponding behaviors in real cells might also arise from an analogous set of simple processes. It is relatively easy to imagine how alignment of fibers in the intercellular area could emerge from a pair of cells pulling on a fibrous matrix without the cells having a mechanism to directly measure or alter the alignment of fibers. A less obvious implication from our simulation results is that durotaxis can arise from relatively simple rules for cell-matrix interactions and does not necessarily require the cell to directly sense matrix stiffness or have an explicit mechanism to migrate in a specific direction based on a stiffness cue.

In our simulations alignment and densification of fibers in the intercellular region occurred before cells began to migrate towards one another, which is consistent with the experimental observations of McLeod et al. [15] reported in this issue. The new experimental results from McLeod et al., especially their observed correlations between (1) the initial distance of cell separation and extent of intercellular densification and (2) initial matrix density and extent of intercellular densification suggest additional simulations that could be conducted to enable further avenues for comparing model predictions to experimental work. Conversely, our existing simulations make specific predictions that would require additional experimental results for validation. In our simulations, the initial and early concentration of the matrix in the intercellular area, but not the extent of alignment in this area, predicted the cells that would have greater directional migration. Additional experiments would be required to determine the validity of this prediction as well.

In summary, the results from this relatively simple agent-based model of cell-matrix interactions capture many behaviors observed experimentally, exhibit a number of emergent behaviors including durotaxis, and make new predictions that suggest new experimental work. The results also illustrate the potential for agent-based modeling in providing a greater understanding of biological processes with an important cell-matrix component (e.g., tissue morphogenesis and cancer metastasis) and could be used to guide the design of fibrous scaffolds for tissue engineering applications.