Short abstract
A nonlinear biphasic fiber-reinforced porohyperviscoelastic (BFPHVE) model of articular cartilage incorporating fiber reorientation effects during applied load was used to predict the response of ovine articular cartilage at relatively high strains (20%). The constitutive material parameters were determined using a coupled finite element-optimization algorithm that utilized stress relaxation indentation tests at relatively high strains. The proposed model incorporates the strain-hardening, tension-compression, permeability, and finite deformation nonlinearities that inherently exist in cartilage, and accounts for effects associated with fiber dispersion and reorientation and intrinsic viscoelasticity at relatively high strains. A new optimization cost function was used to overcome problems associated with large peak-to-peak differences between the predicted finite element and experimental loads that were due to the large strain levels utilized in the experiments. The optimized material parameters were found to be insensitive to the initial guesses. Using experimental data from the literature, the model was also able to predict both the lateral displacement and reaction force in unconfined compression, and the reaction force in an indentation test with a single set of material parameters. Finally, it was demonstrated that neglecting the effects of fiber reorientation and dispersion resulted in poorer agreement with experiments than when they were considered. There was an indication that the proposed BFPHVE model, which includes the intrinsic viscoelasticity of the nonfibrillar matrix (proteoglycan), might be used to model the behavior of cartilage up to relatively high strains (20%). The maximum percentage error between the indentation force predicted by the FE model using the optimized material parameters and that measured experimentally was 3%.
1. Introduction
In order to investigate the load bearing characteristics of articular cartilage and to predict the initiation of failure, the stresses and strains in the tissue must be determined. The most commonly used method is finite element analysis (FEA); however, such an analysis requires a constitutive material relationship that captures the unique behavior of cartilage incorporating all nonlinearities. Articular cartilage is composed of a porous solid matrix including proteoglycans and a fibrillar matrix embedded in interstitial fluid. Under an applied load, there is interaction between the solid and fluid phases that results in stress relaxation and creep behavior under displacement and force control compression tests, respectively. Cartilage exhibits tension-compression, permeability, finite deformation, and strain hardening nonlinearities. Capturing these nonlinearities has motivated the development of a number of novel constitutive models.
Several constitutive models have been proposed over the last three decades. These models originated from consolidation or poroelastic theory [1–3] and evolved to the biphasic theory (KLM) [4] to describe the rheological behavior of articular cartilage under compressive loads. Constitutive models have also been proposed to simulate its behavior in the framework of porous media theories such as biphasic poroelasticity (BPE) [5] and biphasic poroviscoelasticity (BPVE) [6–15].
The reorientation of collagen fibers during loading and its associated tension-compression nonlinearity, introduces additional complications for constitutive modeling of articular cartilage. In previous studies [16–24] the tension-compression nonlinearity was accounted for by using a fibril-reinforced model in which the mechanical stiffness of the material was affected by both a fibril network and an isotropic matrix. These previously proposed fibril-reinforced models calculated the total stress as a summation of the matrix and fiber stresses [16], and can be mainly classified into two groups, i.e., spring models and continuum models. The spring models utilized finite element (FE) analyses that represented fibers as spring elements between the element nodes, limiting their orientation to only the direction of the elements. For example, Li et al. [17–21] developed various models in which the stiffness of the fibrils was modeled using a linear spring in parallel with a nonlinear spring that had a stiffness that depended on the fibril strain. Fulin and Szeri [22] used springs to model fibrils and determined the Young's modulus and permeability of hydrated soft tissue using an FEA that was coupled to an optimization routine. The optimized material parameters were determined by calibrating the FE model using stress relaxation data obtained for ten ramps of an unconfined compression test. Recently Li et al. [23] proposed a fibril-reinforced model of cartilage in which fibrils were assumed to be viscoelastic. They proposed a theoretical continuum element to examine the fibril stiffening driven by fluid pressurization at different strain rates. They compared the proposed element with a spring-based element and did not observe any difference in the results. They also reported that the intrinsic viscoelasticity of the cartilage, which was not formulated in their model, may play an additional role in the mechanical response of articular cartilage.
Wilson et al. [24] proposed a fibril-reinforced poroviscoelastic model in which the total stress in the solid matrix was given as the sum of the stresses in the nonfibrilar matrix and all of the fibril stresses. They used a relatively simple linear and isotropic elastic model (Hooke's law) for the nonfibril matrix. Wilson et al. [25] also proposed a model of cartilage in which both the nonfibrillar and the fibrillar parts of the solid matrix were included in a single continuum element. These models; however, did not account for the intrinsic viscoelasticity of the solid matrix, and were tested against 5% strain experiments done by DiSilvestro and Suh [14]. Seifzadeh et al. [26] also used a nonlinear fiber-reinforced BPVE model to show the effect of friction when determining the material properties of human cartilage during indentation testing.
Previous investigators have found that nonlinear stress-strain relationship in soft tissue can be modeled by hyperelastic function which incorporates finite deformation nonlinearity [27,28]. Garcia et al. [29] proposed a linear biphasic viscohyperelastic fibril-reinforced model of articular cartilage, but it did not account for fiber reorientation and nonlinear permeability.
In summary, most of the above mentioned works proposed model simulations for relatively low strains. Moreover, in the previous fiber-reinforced FE models that were spring based, fiber directions could depend only on the element orientations [17–21]. In most of these studies, the intrinsic viscoelasticity of the solid matrix was not considered [16–18,21,24,25], and the ones that did (e.g., [29]), did not consider fiber reorientation and dispersion, and nonlinear permeability.
Thus, no previous study exists where cartilage was modeled as nonlinear biphasic using finite deformation, including the effects of fiber reorientation and dispersion, and the intrinsic viscoelasticity at high strains. The present work addresses this by utilizing a coupled FE/optimization scheme to determine the nonlinear fiber-reinforced biphasic porohyperviscoelastic (BFPHVE) material parameters of ovine cartilage using a series of indentation tests at strains up to 20%. The model used in this study includes the intrinsic viscoelasticity of the solid matrix, which was previously identified as being important in a number of studies [6,23,29], but has not been implemented in existing fiber-reinforced models such as those in Refs. [24,25]. It also incorporates a strain dependent permeability. Since the model is highly nonlinear with a large number of material parameters [30,31] to be determined, the optimization design space has many local minima. This will require use of the simulated annealing (SA) optimization algorithm scheme previously utilized by Seifzadeh et al. [26]. Because of the high strains encountered in the experiments, the total duration of the relaxation was very high compared to the time to ramp up to the peak forces. Thus, a new weighted error was introduced in order to magnify the effect of the peak magnitudes in the objective function.
2. Experiments
The indentation experimental setup and specimen preparation utilized in this study are based on those outlined in Kandel et al. [32].
Briefly, the knees of 3–6 month old sheep were exposed using a parapatellar incision and five 12.7 × 12.7 × 12.7 mm3 plugs of bone with attached articular cartilage were harvested from various sites on the trochlear ridge and the groove of the distal femur over an area of approximately 4 cm2, using a scalpel. The thicknesses of the cartilage on the five samples were measured in the range h = 0.41–0.6 mm by measuring the distance between the substrate bone and the top of cartilage, using X-ray fluoroscopy.
The specimens were prepared as described in detail in Kandel et al. [32], and their stress-relaxation response was determined using a 0.5 mm diameter cylindrical indenter to compressively indent the cartilage tissue in a Mach-1TM mechanical tester (Biosyntech, Laval, Quebec, Canada) fitted with a 10 N maximum load cell. Samples were not confined circumferentially, thereby allowing unconstrained lateral deformation during the testing. The compressive force was applied in 10 steps, each step corresponding to 1%–2% strain, estimated from taking thickness measurements of the indented and fully relaxed cartilage layer. The crosshead speed used was between 0.1 and 0.2 mm/min. After each deformation step to the prescribed level of strain, loading was stopped and the compressive force was allowed to relax until a steady-state (equilibrium) force level was reached. Equilibrium was defined as attained when the measured force change due to relaxation was less than 0.2 g/min. This was repeated for each of the 10 deformation steps for a total of 20% strain.
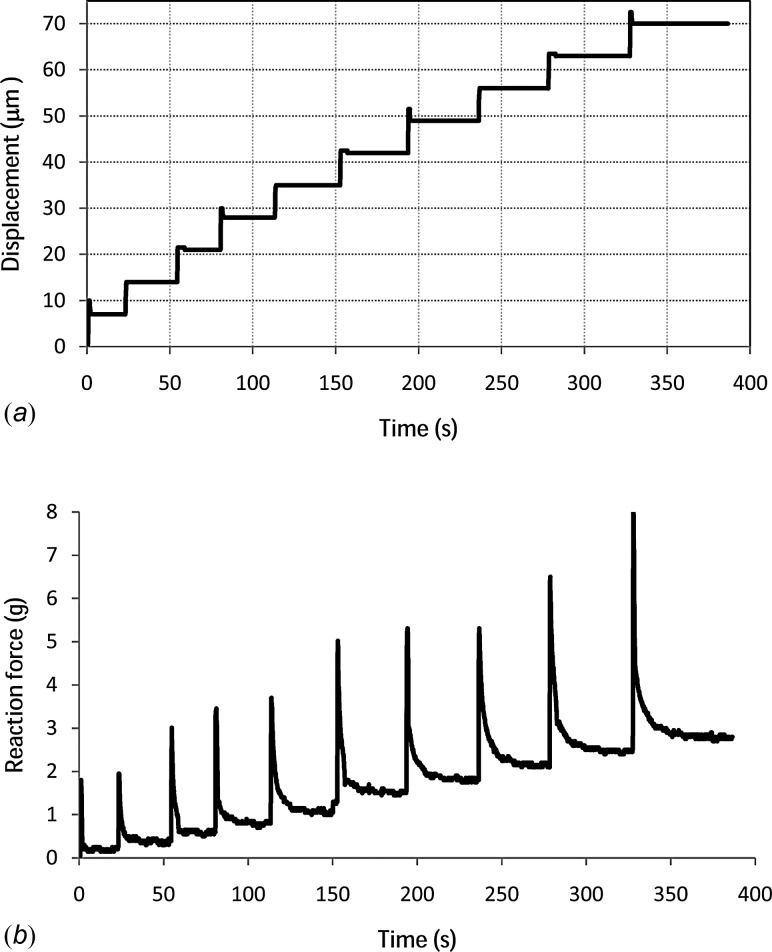
The applied displacement for one of the samples is shown in Fig. 1(a), and the resulting measured axial reaction force on the indenter is given in Fig. 1(b). This force data has not been previously published in [32] or elsewhere.
Fig. 1.
(a) Vertical displacement applied to the indenter. (b) Reaction force measured on the indenter.
3. Continuum Mechanical Framework
The nonlinear anisotropic hyperelastic constitutive model used in this work originated from the nonlinear continuum mechanics developed by Ogden [33] and employed by Holzapfel [34] to model anisotropic soft biological tissues [35–38].
Distributed Orientations of Embedded (Collagen) Fibers.
Two families of fibers were defined in ABAQUS, and collagen fibers were dispersed with rotational symmetry within each family. The level of dispersion in the fiber directions κ about a mean preferred direction is defined by an orientation density function [39] as follows:
| (1) |
where ρ(θ) is the normalized number of fibers with orientations in the range [θ, θ + dθ]. κ varies between 0, for perfectly aligned fibers (no dispersion), and 1/3 for randomly distributed (isotropic) fibers. It was also assumed that all families of fibers had the same mechanical properties and the same dispersion.
Strain Energy Function.
Using the continuum theory of fiber reinforced composites at finite strains [40], the strain energy function depends not only on the deformation gradient F but also on the fiber directions. and are the structural tensors of the two fiber directions, and C is the right Cauchy-Green deformation tensor [34,41]. For the two families of fibers this is written in terms of the invariants of the tensors C and the fiber vectors a 0 and b 0. Fibers are embedded in a continuum with an orientation that is characterized by the referential unit vectors a 0 and b 0 which denote the fiber directions. The vector a = F a 0 defines the spatial orientation, and the stretch in the direction of the fiber is |a|. Holzapfel et al. [42] and Gasser et al. [43] proposed a constitutive model for modeling arterial layers with distributed collagen fiber orientations as follows:
| (2) |
with
| (3) |
where U is the strain energy per unit of reference volume; C 10, D, , , and κ are temperature-dependent material parameters; N is the number of families of fibers (N ≤ 3); is the first invariant of , the modified Cauchy-Green deformation tensor [35–38]; J el is the elastic volume ratio; and are pseudoinvariants of and . Index α refers to different family of fibers (α = 1, 2 in this study).
The first two terms in Eq. (2) represent the distortional and volumetric contributions of the noncollagenous isotropic ground material; and the third term represents the contributions from the different families of collagen fibers, incorporated the effects of dispersion. Collagen fibers are assumed to support only tension, since they would buckle under compressive loading. Thus, the anisotropic contribution in the strain energy function appears only when the strain of the fibers is positive.
The stress is obtained from the derivative of the strain energy function U [Eq. (2)], and can be decomposed into deviatoric and hydrostatic components as follows [45]:
| (4a) |
| (4b) |
where dev(*) is the deviatoric component of (*), and the overdot denotes differentiation with respect to time. is the distortional deformation gradient of the state at relative to the state at t. G(τ) and K(τ) are relaxation shear and bulk moduli of viscoelasticity in terms of the Prony series:
| (5a) |
| (5b) |
where N is the number of terms in the Prony series, and are instantaneous shear and bulk modulus, respectively, are time constants, and and are the Prony series amplitude constants. and are long term dimensionless shear and bulk moduli, respectively.
At most three terms of the Prony series were required in the present case due to the constraint that N < log (t max /t min) [44]. In this study, t max = 350 s and t min = 0.3 s and therefore N = 2.
The permeability was assumed to vary through the tissue and with the tissue deformation. The soil analysis in ABAQUS, which assumes Darcy's law, was used to analyze the fluid flow through the porous media. The range of the void ratios was based on the water content through the cartilage thickness, with the highest amount near the joint surface and lowest in the deep zone, as described in Ref. [24]. The following dilatation-dependent permeability nonlinearity, developed by [8], was adopted in the present work.
| (6) |
where e is the deformation-dependent void ratio, e0 = 4 [22] is the initial void ratio, k 0 is the initial permeability at the initial void ratio, k is the corresponding permeability at e, and M is a constant. To define the permeability, a specific weight of the wetting liquid γ = 9.81 kN/m3 [26] was used. k 0 and M were determined as part of the optimization.
4. Finite Element Simulation
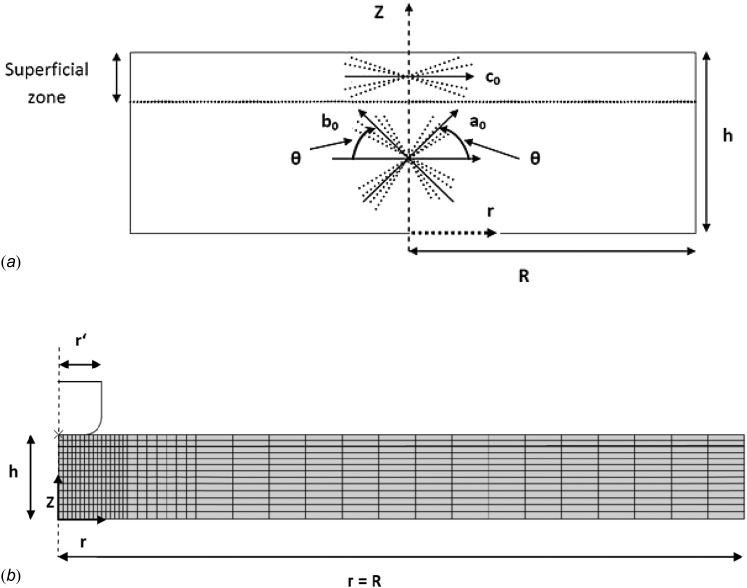
The indentation tests described in Sec. 2 were simulated for the five specimens using axisymmetric finite element analyses in ABAQUS (Version 6.9-1, Dassault Systems, Providence, RI, U.S.A). The cartilage specimen had a radius R = 6 mm, and was divided into two zones. The superficial zone represented the top 10% of the cartilage thickness, and had one family of fibers oriented in a radial direction. The rest of the cartilage thickness was assigned two families of fibers oriented at 45 and −45 deg to the radial direction [Fig. 2(a)]. The 0.5 mm indenter was modeled as a rigid body, and frictionless contact was assumed between it and the tissue. The cartilage was modeled with reduced 8-node axisymmetric biphasic porous CAX8PR elements, in which the total stress at each node is calculated by the summation of the solid and pore pressures. The finite element mesh was refined in the vicinity of the edge of the indenter as shown in Fig. 2(b). A mesh sensitivity analysis was performed, and it was found that a root-mean squared error (RMSE) in the reaction force of less than 2% could be obtained when using 602 elements.
Fig. 2.
(a) Approximation of the articular cartilage layer with one and two embedded families of fibers in the superficial and middle zones respectively. θ and κ characterize the mean orientations and the dispersion of the collagen fibers. (b) Example of undeformed finite element model of axisymmetric cartilage indentation. The indenter radius r’ = 0.25 mm, the cartilage radius R = 6 mm, and the thickness h varied in the range 0.41–0.6 mm. The heavy line indicates the boundary between the mesh for the superficial and middle zones.
The z displacements shown in Fig. 1(a) were applied to the indenter, and pore pressure at the free surface at Z = h [Fig. 2(b)] was assumed zero, an assumption which was also used by Li et al. [45]. The surface at Z = 0, representing the bone, was assumed to be fixed and impermeable. By symmetry, the surface at r = 0 was assumed impermeable and fixed in the radial direction. The pore pressure at the free surface at r = R [Fig. 2(b)] was assumed to be zero.
5. Optimization of Constitutive Parameters
The finite element (FE) model of Sec. 4 was coupled to a simulated annealing (SA) optimization algorithm to determine the material parameters that minimized the error between the experimental and predicted FE time-dependent indentation loads [e.g., Fig. 1(b)]. The general procedure is described in more detail in Seifzadeh et al. [26], but the high strains encountered in the present experiments required a novel cost function formulation that has not been previously employed. Initially, following Wilson et al. [25], the objective function based on the sum of error norms for the relaxation force used was
| (7) |
where Fi FEM and Fi EXP are the discrete relaxation force data for FE simulation and indentation experiments, respectively, xopt is the vector of optimized material parameters, and n is the number of observed points. Wilson et al. [25] utilized only one relatively short duration ramp compression and relaxation in their work. The present work; however, modeled many ramp compressions [Fig. 1(a)], and the total duration of the relaxation was thus very high compared to the time to ramp up to the peak forces. Thus, a new weighted error was added to Eq. (7) in order to magnify the effect of the peak magnitudes in the objective function:
| (8) |
in which m is the number of the peak value points (10 in all the present cases), and and are peak force values of the FE simulation and indentation experiments, respectively. is a weight function that was estimated based on the range of error calculated in Eq. (7), in order to scale Err2 to the order of magnitude of Err1. For each iteration, the measured reaction force was compared to the experimental every 0.3 s, resulting in n = 1256 compared data points. This procedure was repeated until the objective function, Err1 + Err2 was minimized to the desired accuracy.
6. Results and Discussion
6.1. Optimized Material Properties for Ovine Cartilage.
Under large deformations, soft biological tissues such as articular cartilage exhibit highly anisotropic and nonlinear elastic behavior due to rearrangements in their microstructure, such as reorientation of the fiber directions with deformation. The simulation of these nonlinear effects requires constitutive models formulated within the framework of anisotropic hyperelasticity. The present prediction of the tissue response at relatively high strains could not have been performed with the genetic algorithm (GA), differential evolution (DE), and nonlinear least squares (Lsqn) optimization algorithms proposed in previous studies because they require a very good estimate of the initial values to avoid converging to local minima. This necessitated the use of the presently utilized simulated annealing (SA) optimization algorithm with the presented augmented error function, which could account for both peak magnitude and relaxation errors in the stress relaxation indentation and converge to a unique global minimum.
There were 13 constitutive parameters that described the material behavior in the chosen nonlinear BFPHVE model: six to describe the viscoelastic behavior (gi, , ), two to describe the deformation-dependent permeability (k 0, M), and five to describe the anisotropic hyperelasticity (C 10, κ 1, κ 2, D, κ). The 13 independent material parameters that were determined with the maximum errors Err1 = 1.6%, Err2 = 1.39% using the finite element optimization scheme are shown in Table 1. The optimization was allowed to run for up to 750 iterations. The duration of each iteration was approximately 10 min with a Quad core Intel Xeon 2.9 GHz computer with 4 gigabytes of RAM.
Table 1.
Initial guess vector and average optimized material parameters of FBPHVE model considering both Err1 and Err2. The ± indicates the standard deviation for the five specimens that were harvested from different sites on the sheep knees. Maximum difference between optimized material parameters with three different initial guesses for each specimen is shown in the last column.
| Material parameters | Initial guesses | Optimized parameters | Max error (%) |
|---|---|---|---|
| C 10 (Pa) | 2 × 106 | 0.2 ± 0.09 × 106 | 0.009 |
| 2 × 104 | 0.68 ± 0.09 × 106 | 0.02 | |
| 1 × 105 | 0.45 ± 0.2 × 105 | 0.012 | |
| D (Pa−1) | 1 × 10−1 | 4 ± 1.8 × 10−6 | 0.06 |
| 0.1 | 0.242 ± 0.08 | 0.1 | |
| k 0 (m4/N s) | 0.1 × 10−10 | 2.4 ± 0.9 × 10−14 | 0.2 |
| M | 10 | 16 ± 8 | 0.01 |
| 0.3 | 0.618 ± 0.09 | 0.02 | |
| 0.1 | 0.15 ± 0.04 | 0.01 | |
| 100 | 5.2 ± 1.4 | 0.12 | |
| 0.1 | 25.1 ± 3 | 0.3 | |
| 0.01 | 0.495 ± 0.14 | 0.01 | |
| 0.001 | 0.143 ± 0.01 | 0.01 |
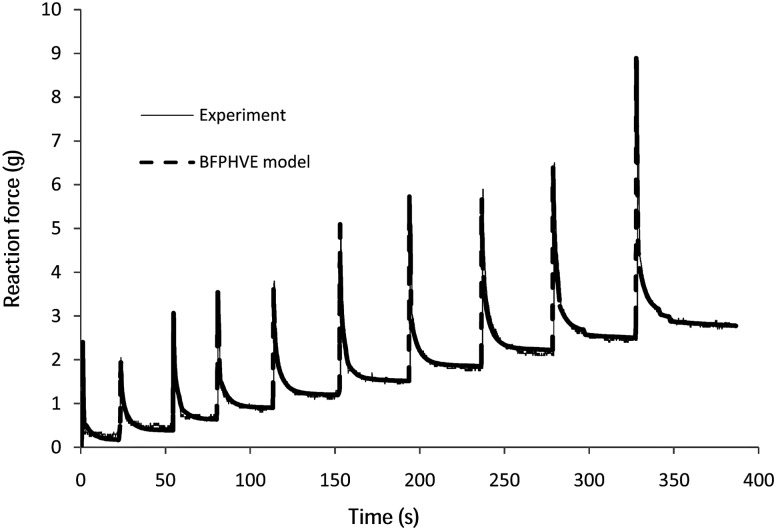
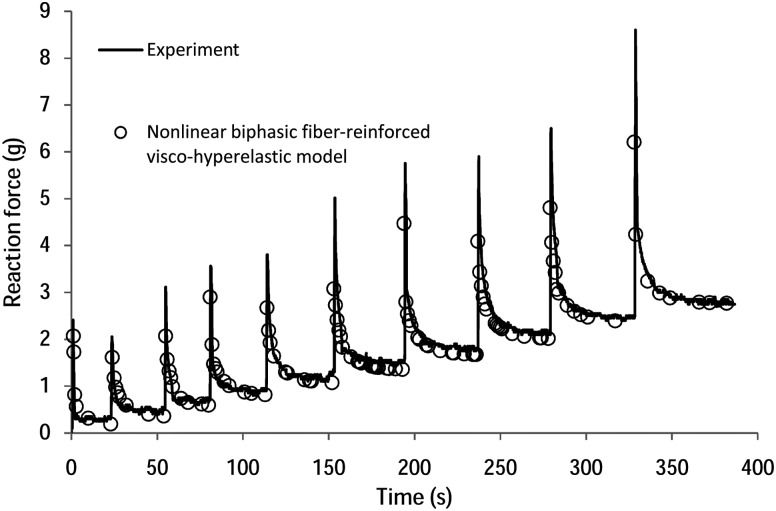
In Fig. 3 the FE-predicted response of the cartilage using the BFPHVE model with the final optimized material parameters is shown, together with the experimental indentation data for one of the samples. The model effectively captured both the maximum (instantaneous) and minimum (equilibrium) responses of the cartilage over most of the duration of the indentation stress relaxation test, for relatively high strains of up to 20%. Similarly good agreement between measured and predicted indentation forces was found for the other cases (not shown).
Fig. 3.
Measured and FE optimized reaction force using the BFPHVE model for one of the five samples considered in the study. Err1 = 1.2%, Err2 = 1.1%.
As depicted in Fig. 3, increasing the strain causes an increase in the peak response. This is an indication of the strain stiffening nonlinearity that the proposed model predicts due to fibril stiffening which produces a high pore pressure [23].
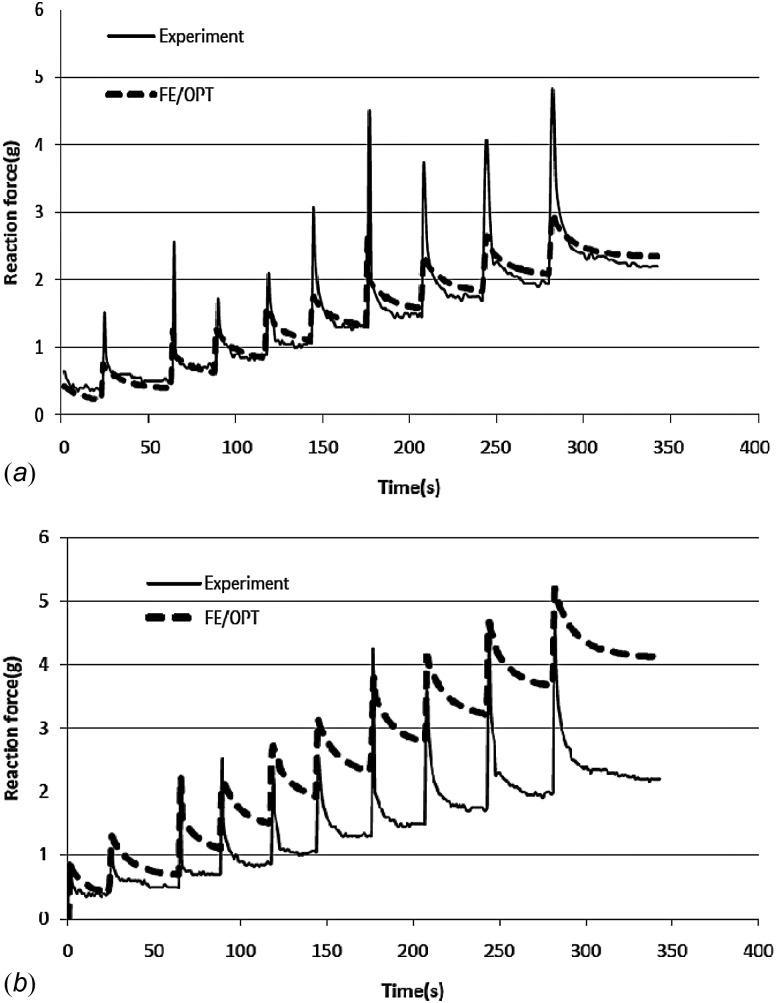
6.2. Use of Modified Objective Function.
Figures 4(a) and 4(b), resulting from optimizations (optimized parameters not shown) considering only Err1 and Err2, respectively, can be compared to Fig. 3, which considers both errors simultaneously. It is clear that while Err1 and Err2 can each be acceptable, using either solely results in an inproper prediction of the tissue response.
Fig. 4.
Comparison of measured force with that predicted by the BFPHVE model: (a) only considering Err1 = 1.3% [Eq. (7)]; (b) only considering Err2 = 1.3% [Eq. (8)]
6.3. Uniqueness of Optimized Parameters.
The optimization procedure was repeated with different initial guesses in order to test the uniqueness of the solution, i.e., whether the optimized parameters represent a global minimum in the solution space. Such a uniqueness test has been used by a number of different authors, e.g., [22,25,30]. For these runs, in each iteration, instead of comparing to the experimental reaction forces, the FE-predicted reaction forces were compared to the simulated reaction forces (e.g., Fig. 3) obtained using the optimized parameters in Table 1. The optimized parameters resulting from this uniqueness study converged to values that were very close to the values in the third column of Table 1, and the variation in material parameters was very small, despite using different initial guesses (last column in Table 1).
6.4. Comparison of Obtained Ovine Properties to Measured Properties From the Literature and Effect of Fiber Reorientation
Comparison to Measured Properties From the Literature.
Since there is no data available for ovine, the optimized hydraulic permeability k 0 given in Table 1 (2.4 × 10–14 m4/N s) was compared to previous findings (range of 10–14–10–16 m4/N s) for cartilage from other species, including human, bovine, rat, and rabbit [14,22,24,25,31,46]. The optimized value of the constant M given in Table 1 (16 ± 8) which indicates the degree of decrease in the tissue permeability with compressive strain [Eq. (6)] can be compared with previous work performed on bovine cartilage (i.e., M = 4.3 by Lai et al. [8], M = 5.6 in [25] and by Li et al., M = 23–30 in [20]). According to DiSilvestro et al. [13], most of the existing models in the literature have several limitations when applied to cartilage at high strains since they assume a linear stress-strain relationship. In the present study, a nonlinear stress-strain relation was used to account for the finite deformation of both the collagen fibrils and the nonfibrillar matrix. Therefore, the remaining material parameters in this study cannot directly be compared with the literature in the strict sense. However, the initial shear and bulk moduli [Eqs. (5a) and 5(b)] have been related to the coefficients in the first and second terms in Eq. (2), respectively, as and in Ref. [44]. In the present work, the initial aggregate modulus (HA = 2μ 0 + λ 0) was 1 MPa, which is close to the previously reported range of 0.1–2 MPa for bovine, canine, human, monkey, and rabbit cartilage [17,22,46–48]. Given the interspecies variability, the presently determined values of these material parameters for ovine cartilage agree reasonably well.
Fiber Reorientation Effects.
To elucidate the effect of fiber reorientation, a nonlinear biphasic viscohyperelastic fiber-reinforced model, i.e., without fiber dispersion and reorientation, was compared with the present model. Figure 5 indicates that using the model without fiber reorientation and dispersion yields an underestimation in the prediction of the transient maximum reaction force in each indentation ramp, but captures the equilibrium response well. The present model which considers fiber reorientation on the other hand captures both the transient and the equilibrium responses of the material well (Fig. 3). This is in agreement with the work by Li and Herzog [23] in which the interplay between fibril reinforcement and fluid pressurization in articular cartilage was discussed. They reported that they were not able to extend their results to strains greater than 15% because of limitations in their model formulation due to a linear representation of the nonfibrillar matrix and a neglect of fibril reorientation effects.
Fig. 5.
Comparison of predicted cartilage response for nonlinear biphasic fiber-reinforced viscohyperelastic model (i.e., without using fiber reorientation and dispersion) to experiments
6.5. Implementation of Model for Indentation and Unconfined Compression Tests on Bovine Cartilage.
DiSilvestro and Suh [14] performed indentation and unconfined compression tests on bovine cartilage samples at relatively low strains. It has been previously demonstrated that simpler infinitesimal deformation models, such as that in Ref. [14], utilizing less parameters than the present model can be used to fit this lower strain data. It was nevertheless of interest to confirm that the present larger strain model could also be used at these lower strain values, and the data of DiSilvestro and Suh [14] also provides an opportunity to test the ability of the present model to predict lateral displacements, albeit at low strains. A coupled finite element optimization procedure similar to that described in Secs. 4 and 5 was used to determine the BFPHVE model material properties using the indentation experiments of DiSilvestro and Suh [14] on bovine cartilage. The objective function was that presented in Eq. (7). The simulated indentation geometry was as described by DiSilvestro and Suh [14] (1.53 mm indenter), and three zones were modeled with different fiber orientations, as described in Sec. 4. An axisymmetric finite element mesh composed of 600 CAX4P elements was used. The nodes at the bottom were confined in all directions while those in the symmetry axis were restricted from radial movement [25]. A 10% compressive axial strain was applied to the indenter and then a full relaxation was allowed. Following that, a 5% strain was applied and held constant until equilibrium was reached. The axial reaction force was calculated during additional 5% indentation.
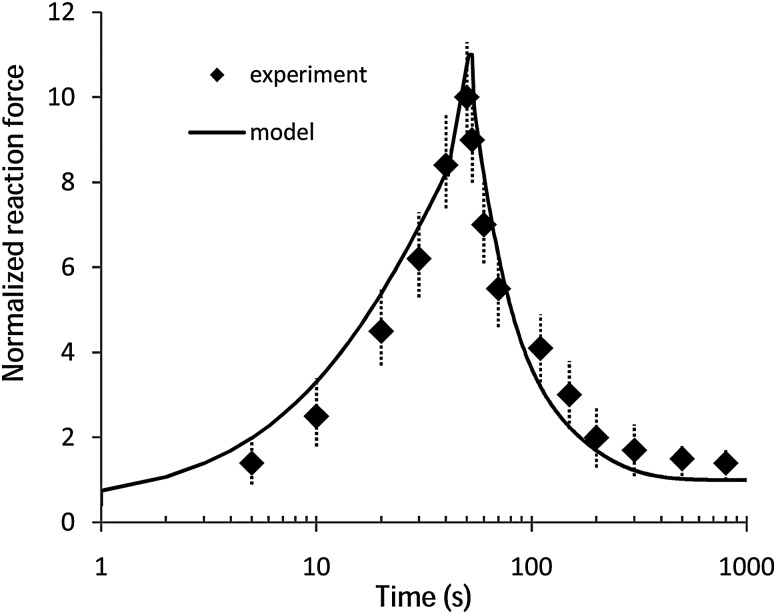
The coupled optimization-FE procedure determined the optimized material properties of the BFPHVE model as follows: C 10 = 0.355 MPa, κ 1 = 0.64 MPa, k2 = 0.191 × 105, D = 5 × 10−6 Pa−1, k = 0.195, = 0.75, = 0.18, = 0.219, = 0.017, = 2 s, = 70 s, k 0 = 3.1 × 10−15 m4/N s, M = 12, and e 0 = 4. The normalized reaction forces using the determined optimized material parameters were then compared to those measured by DiSilvestro and Suh [14] in Fig. 6.
Fig. 6.
Comparison of normalized (i.e., to the equilibrium value) indentation force measured by DiSilvestro and Suh [14] (r’ = 1.53 mm, h = 1.28 mm, r = 6.12 mm) with that predicted by the BFPHVE model using the optimized-FE material properties
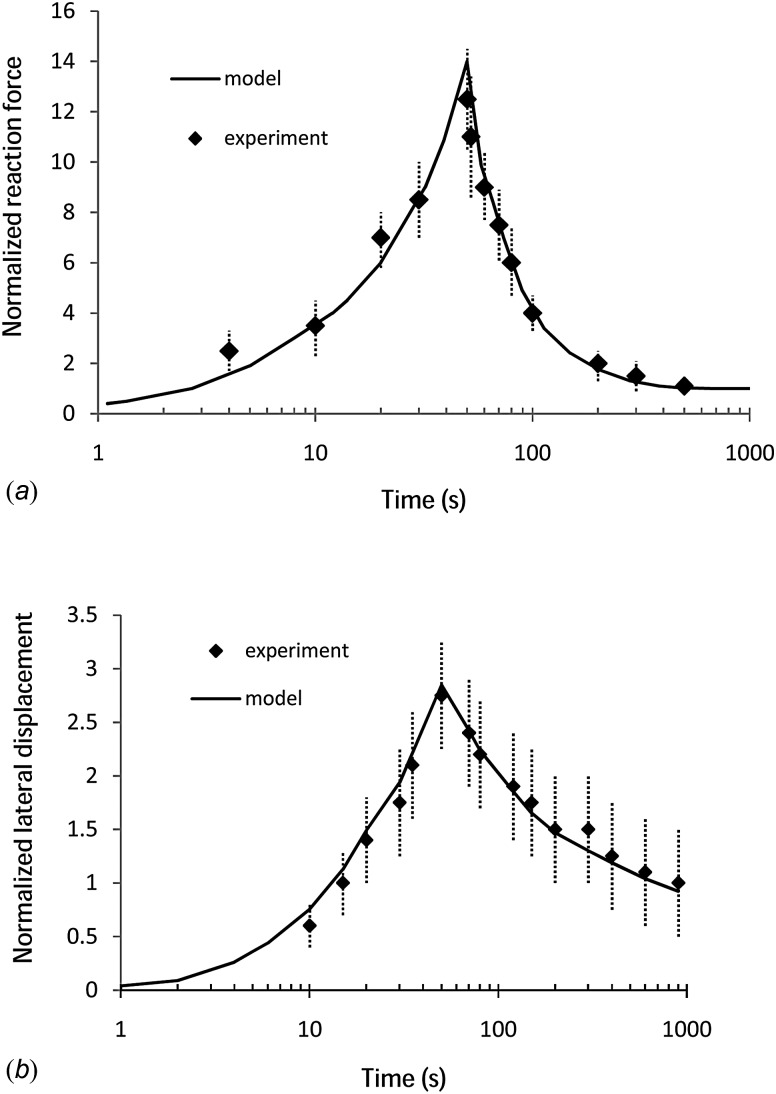
This set of material parameters, determined using the indentation data, was then used to predict the lateral displacement and the reaction force in the unconfined compression tests of DiSilvestro and Suh [14]. For these simulations, 800 linear axisymmetric pore pressure elements (CAX4P) were used, and the nodes at the bottom plate were restricted from vertical displacements [24]. The radial displacements of the nodes on the symmetric line were confined. The same compressive strain protocol used in the indentation test described above was applied to the top plate in the unconfined simulation. As is shown in Figs. 7(a) and 7(b), the finite element predictions using the optimized material parameters computed from the indentation experiment lie within both the experimental reaction force and lateral displacements of the unconfined compression experiments (R 2 = 0.98). In other words, a single set of optimized BFPHVE parameters was able to simulate both indentation and unconfined compression tests; thus lending further validity to the present model.
Fig. 7.
Comparison of (a) normalized (i.e., to the equilibrium value) reaction force and (b) lateral displacement (h = 1.28 mm, r = 1.5 mm) measured in the unconfined compression tests of DiSilvestro and Suh [14], with corresponding quantities predicted by the BFPHVE model using the same optimized-FE material properties as used in Fig. 5
The present BFPHVE model determined a lower initial (equilibrium) shear modulus for ovine samples ( MPa from Table 1) than what it predicted for the bovine samples of DiSilvestro and Suh [14] ( MPa from above). The discrepancy is expected because of the interspecies variability.
7. Conclusions
The present work demonstrated a model of fiber-reinforced biphasic porohyperviscoelastic (FBPHVE) that accounted for fiber reorientation and dispersion including the intrinsic viscoelasticity of cartilage at high strains. The BFPHVE model was found to be suitable for modeling both the fluid-flow dependent and fluid-flow independent responses of ovine articular cartilage to applied loads up to relatively high strains (20%) over ten compression ramps. The 13 material properties required for this model were determined by using an optimization scheme to calibrate a finite element model of a relatively simple stress relaxation indentation test. It was demonstrated that at such high strains where the total duration of the relaxation was very high compared to the time to ramp up to the peak forces, it was necessary to introduce a new weighted error into the objective function in order to magnify the effect of the peak magnitudes. With the utilized optimization scheme, the material parameters were optimized such that there was very good agreement between the measured indentation reaction loads and those predicted by the FEM (R 2 = 0.99). A single set of optimized BFPHVE parameters was also able to simulate both indentation and unconfined compression tests on bovine cartilage from the literature, further validating the present model.
Comparison of the models with and without fiber reorientation and dispersion showed the importance of using the fiber reorientation in the cartilage model, especially at higher strains. Finally, the presented finite element model accounts for anisotropic behavior of cartilage and the nonlinearities associated with tension compression identified in [36], the strain dependent elasticity and the finite deformation. It thus shows promise to be used in the future for modeling fibrillar collagen in human knee joint models undergoing large deformations.
Although this study accounts for fiber variations with zones and orientations consistent with those in [49,50], detailed microstructure measurements are needed to determine the precise orientation of the fibers in different zones. Furthermore, more experimental investigations of different conditions and configurations from different species, ages, and sites under different strain rates are necessary to objectively appraise the proposed model.
Acknowledgment
This work was supported through the Bioengineering of Skeletal Tissues Team (BESTT), funded by the Canadian Institutes of Health Research (CIHR). Thanks are also due to Ryerson University for additional funding.
Glossary
Nomenclature
- AC =
articular cartilage
- =
structural tensors of the fiber directions
- a0, b0,c0 =
fiber vector in mean direction
- BPE =
biphasic poroelastic
- BPVE =
biphasic poroviscoelastic
- C =
right Cauchy-Green deformation tensor
- =
modified right Cauchy-Green deformation tensor
- DE =
differential evolution algorithm
- =
elastic Young's modulus
- =
initial void ratio
- Err1 =
error between FE model and experimental data
- Err2 =
error between peak values in FE model and experimental data
- BFPHVE =
biphasic fiber-reinforced porohyperviscoelastic
- FE =
finite element
- FE/OPT =
coupled FE and optimization algorithm
- F =
deformation gradient
- =
instantaneous reaction force on the indenter
- =
peak reaction force on the indenter
- GA =
genetic algorithm
- =
instantaneous relaxation modulus
- g, =
dimensionless relaxation and bulk moduli
- , =
dimensionless relaxation and bulk amplitude constants of Prony series
- =
first invariant of
- =
pseudoinvariants of and
- Jel =
elastic volume ratio
- =
permeability of the undeformed state
- Lsqn =
least squares nonlinear algorithm
- m =
number of FE/experiment comparison peak points
- =
constant
- N =
number of Prony series term
- n =
number of data points for FE/optimization and experimental comparison
- R2 =
coefficient of determination
- RMSE =
root mean squared error
- =
stresslike parameter
- =
dimensionless parameter
- κ =
level of dispersion
- tmax =
total duration of the experiment
- tmin =
sampling time
- γ =
specific weight of wetting fluid
- =
relaxation time constant
Contributor Information
A. Seifzadeh, Department of Mechanical and Industrial Engineering, Ryerson University, 350 Victoria Street, Toronto, Ontario, M5B2K3, Canada
J. Wang, Faculty of Dentistry, University of Toronto, 124 Edwards St., Toronto, Ontario, M5G 1G6, Canada
D. C. D. Oguamanam, Department of Mechanical and Industrial Engineering, Ryerson University, 350 Victoria Street, Toronto, Ontario, M5B2K3, Canada
M. Papini, Department of Mechanical and Industrial Engineering, Ryerson University, 350 Victoria Street, Toronto, Ontario, M5B2K3, Canada; Canadian Institutes of Health Research, Bioengineering of Skeletal Tissues Team, e-mail: mpapini@ryerson.ca
References
- [1]. Terzaghi, K. , 1951, Theoretical Soil Mechanics, John Wiley and Sons, New York. [Google Scholar]
- [2]. Biot, M. A. , 1941, “General Theory of Three-Dimensional Consolidation,” J. Appl. Phys., 12, pp. 155–164. 10.1063/1.1712886 [DOI] [Google Scholar]
- [3]. Biot, M. A. , 1962, “Mechanics of Deformation and Acoustic Propagation in Porous Media,” J. Appl. Phys., 33, pp. 1482–1498. 10.1063/1.1728759 [DOI] [Google Scholar]
- [4]. Kuei, S. C. , Lai, W. M. , and Mow, V. C. , 1978, “A Biphasic Rheological Model of Articular Cartilage,” Advances in Bioengineering, R. C. Eberhardt and Burstein A. H., Eds., ASME, New York, p. 17. [Google Scholar]
- [5]. Mow, V. C. , Kuei, S. C. , Lai, W. M. , and Armstrong, C. G. , 1980, “Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments,” ASME J. Biomech. Eng., 102, pp. 73–84. 10.1115/1.3138202 [DOI] [PubMed] [Google Scholar]
- [6]. Mak, A. F. , 1986, “Unconfined Compression of Hydrated Viscoelastic Tissues: A Biphasic Poroviscoelastic Analysis,” Biorheology, 23, pp. 371–383. [DOI] [PubMed] [Google Scholar]
- [7]. Suh, J. K. F. , and DiSilvestro, M. R. , 1999, “Biphasic Poroviscoelastic Behavior of Hydrated Biological Soft Tissue,” J. Appl. Mech., 66, pp. 528–535. 10.1115/1.2791079 [DOI] [Google Scholar]
- [8]. Lai, W. M. , Mow, V. C. , and Roth, V. , 1981, “Effects of Nonlinear Strain Dependent Permeability and Rate of 34 Compressions on the Stress Behaviour of Articular Cartilage,” ASME J. Biomech. Eng., 103, pp. 61–66. 10.1115/1.3138261 [DOI] [PubMed] [Google Scholar]
- [9]. Soltz, M. A. , and Ateshian, G. A. , 1998, “Experimental Verification and Theoretical Prediction of Cartilage Interstitial Fluid Pressurization at an Impermeable Contact Interface in Confined Compression,” J. Biomech., 31, pp. 927–934. 10.1016/S0021-9290(98)00105-5 [DOI] [PubMed] [Google Scholar]
- [10]. Soltz, M. A. , and Ateshian, G. A. , 2000, “A Cone Wise Linear Elasticity Mixture Model for the Analysis of Tension Compression Nonlinearity in Articular Cartilage,” ASME J. Biomech. Eng., 122, pp. 576–586. 10.1115/1.1324669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Cohen, B. , Lai, W. M. , and Mow, V. C. , 1998, “A Transversely Isotropic Biphasic Model for Unconfined Compression of Growth Plate and Chondroepiphysis,” ASME J. Biomech. Eng., 120, pp. 491–496. 10.1115/1.2798019 [DOI] [PubMed] [Google Scholar]
- [12]. DiSilvestro, M. R. , Zhu, Q. , and Suh, J. K. , 2001, “Biphasic Poroviscoelastic Simulation of the Unconfined Compression of Articular Cartilage: II. Effect of Variable Strain Rates,” ASME J. Biomech. Eng., 123(2), pp. 198–200. 10.1115/1.1351887 [DOI] [PubMed] [Google Scholar]
- [13]. DiSilvestro, M. R. , Zhu, Q. , Wong, M. , Jurvelin, J. S. , and Suh, J. K. F. , 2001, “Biphasic Poroviscoelastic Simulation of the Unconfined Compression of Articular Cartilage: I. Simultaneous Prediction of Reaction Force and Lateral Displacement,” ASME J. Biomech. Eng., 123, pp. 191–197. 10.1115/1.1351890 [DOI] [PubMed] [Google Scholar]
- [14]. DiSilvestro, M. R. , and Suh, J. K. F , 2001, “A Cross-Validation of the Biphasic Poroviscoelastic Model of Articular Cartilage in Unconfined Compression, Indentation, and Confined Compression,” J. Biomech., 34, pp. 519–525. 10.1016/S0021-9290(00)00224-4 [DOI] [PubMed] [Google Scholar]
- [15]. Suh, J. K. F. , and Bai, S. , 1977, “Biphasic Poroviscoelastic Behaviour of Articular Cartilage in Creep Indentation Test,” Transactions of the 43rd Annual Meeting of the Orthopedic Research Society, San Francisco, CA, 22, p. 823. [Google Scholar]
- [16]. Soulhat, J. , Buschmann, M. D. , and Shirazi-Adl, A. , 1999, “A Fibril-Network Reinforced Biphasic Model of Cartilage in Unconfined Compression,” ASME J. Biomech. Eng., 121(3), pp. 340–347. 10.1115/1.2798330 [DOI] [PubMed] [Google Scholar]
- [17]. Li, L. P. , Soulhat, J. , Buschmann, M. D. , and Shirazi-Adl, A. , 1999, “Nonlinear Analysis of Cartilage in Unconfined Ramp Compression Using a Fibril Reinforced Poroelastic Model,” Clin. Biomech., 14(9), pp. 673–682. 10.1016/S0268-0033(99)00013-3 [DOI] [PubMed] [Google Scholar]
- [18]. Li, L. P. , Buschmann, M. D. , and Shirazi-Adl, A. , 2000, “A Fibril Reinforced Nonhomogeneous Poroelastic Model for Articular Cartilage: Inhomogeneous Response in Unconfined Compression,” J. Biomech., 33(12), pp. 1533–1541. 10.1016/S0021-9290(00)00153-6 [DOI] [PubMed] [Google Scholar]
- [19]. Li, L. P. , Buschmann, M. D. , and Shirazi-Adl, A. , 2001, “The Asymmetry of Transient Response in Compression Versus Release for Cartilage in Unconfined Compression,” ASME J. Biomech. Eng., 123, pp. 519–522. 10.1115/1.1388295 [DOI] [PubMed] [Google Scholar]
- [20]. Li, L. P. , Shirazi-Adl, A. , and Buschmann, M. D. , 2002, “Alterations in Mechanical Behaviour of Articular Cartilage Due to Changes in Depth Varying Material Properties—A Nonhomogeneous Poroelastic Model Study,” Comput. Methods Biomech. Biomed. Eng., 5(1), pp. 45–52. 10.1080/10255840290008088 [DOI] [PubMed] [Google Scholar]
- [21]. Li, L. P. , Buschmann, M. D. , and Shirazi-Adl, A. , 2003, “Strain-Rate Dependent Stiffness of Articular Cartilage in Unconfined Compression,” ASME J. Biomech. Eng., 125(2), pp. 161–168. 10.1115/1.1560142 [DOI] [PubMed] [Google Scholar]
- [22]. Fulin, L. , and Szeri, A. Z. , 2007, “Inverse Analysis of Constitutive Models: Biological Soft Tissues,” J. Biomech., 40, pp. 936–940. 10.1016/j.jbiomech.2006.03.014 [DOI] [PubMed] [Google Scholar]
- [23]. Li, L. P. , and Herzog, W. , 2004, “Strain-Rate Dependence of Cartilage Stiffness in Unconfined Compression: The Role of Fibril Reinforcement Versus Tissue Volume Change in Fluid Pressurization,” J. Biomech., 37(3), pp. 375–382. 10.1016/S0021-9290(03)00263-X [DOI] [PubMed] [Google Scholar]
- [24]. Wilson, W. , van Donkelaar, C. C. , van Rietbergen, C. , Ito, K. , and Huiskes, R. , 2004, “Stresses in the Local Collagen Network of Articular Cartilage: A Poroviscoelastic Fibril-Reinforced Finite Element Study,” J. Biomech., 37(3), pp. 357–366. 10.1016/S0021-9290(03)00267-7 [DOI] [PubMed] [Google Scholar]
- [25]. Wilson, W. , van Donkelaar, C. C. , van Rietbergen, B. , and Huiskes, R. , 2004, “A Fibril-Reinforced Poroviscoelastic Swelling Model for Articular Cartilage,” J. Biomech., 38(6), pp. 1195–1204. 10.1016/j.jbiomech.2004.07.003 [DOI] [PubMed] [Google Scholar]
- [26]. Seifzadeh, A. , Oguamanam, D. C. D. , Trutiak, N. , Hurtig, M. , and Papini, M. , 2011, “Determination of Nonlinear Fibre-Reinforced Biphasic Poroviscoelastic Constitutive Parameters of Articular Cartilage Using Stress Relaxation Indentation Testing and an Optimizing Finite Element Analysis,” Computer Methods and Programs in Biomedicine, doi:10.1016/j.cmpb.2011.07.004. [DOI] [PubMed] [Google Scholar]
- [27]. Holmes, M. H. , and Mow, V. C. , 1990, “The Non-linear Characteristics of Soft Gels and Hydrate Connective Tissues in Ultrafiltration,” J. Biomech., 23, pp. 1145–1156. 10.1016/0021-9290(90)90007-P [DOI] [PubMed] [Google Scholar]
- [28]. Limbert, G. , and Middleton, J. , 2004, “Atransversly Isotropic Viscohyperelastic Material; Application to the Modeling of Biological Soft Connecting Tissues,” Int. J. Solids Struct., 41, pp. 4237–4260. 10.1016/j.ijsolstr.2004.02.057 [DOI] [Google Scholar]
- [29]. Garcia, J. J. , and Cortés, D. H. , 2007, “A Biphasic Viscohyperelastic Fibril-Reinforced Model for Articular Cartilage: Formulation and Comparison With Experimental Data,” J. Biomech., 40, pp. 1737–1744. 10.1016/j.jbiomech.2006.08.001 [DOI] [PubMed] [Google Scholar]
- [30]. Olberding, J. E. , and Suh, J.-K. F. , 2006, “A Dual Optimization Method for the Material Parameter Identification of a Biphasic Poroviscoelastic Hydrogel: Potential Application to Hypercompliant Soft Tissues,” J. Biomech., 39, pp. 2468–2475. 10.1016/j.jbiomech.2005.07.019 [DOI] [PubMed] [Google Scholar]
- [31]. Cao, L. , Youn Inchan, I. , Guilak, F. , and Setton Lori, A. , 2006, “Compressive Properties of Mouse Articular Cartilage Determined in a Novel Micro-Indentation Test Method and Biphasic Finite Element Model,” ASME J. Biomech. Eng., 128(5), pp. 766–772. 10.1115/1.2246237 [DOI] [PubMed] [Google Scholar]
- [32]. Kandel, R. A. , Grynpas, M. , Pilliar, R. , Lee, J. , Wang, J. , Waldman, S. , Zalzal, P. , Hurtig, M. , 2006, “Repair of Osteochondral Defects With Biphasic Cartilage-Calcium Polyphosphate Constructs in a Sheep Model,” J. Biomater., 27, pp. 4120–4131. 10.1016/j.biomaterials.2006.03.005 [DOI] [PubMed] [Google Scholar]
- [33]. Ogden, R. W. , 1997, Non-linear Elastic Deformations, Dover, New York. [Google Scholar]
- [34]. Holzapfel, G. A. , 2000, Nonlinear Solid Mechanics, A Continuum Approach for Engineering, John Wiley & Son, Chichester: . [Google Scholar]
- [35]. Flory, P. J. , 1961, “Thermodynamic Relations for Highly Elastic Materials,” Trans. Faraday Soc., 57, pp. 829–838. 10.1039/tf9615700829 [DOI] [Google Scholar]
- [36]. Ogden, R. W. , 1978, “Nearly Isochoric Elastic Deformations: Application to Rubberlike Solids,” J. Mech. Phys. Solids, 26, pp. 37–57. 10.1016/0022-5096(78)90012-1 [DOI] [Google Scholar]
- [37]. Pena, E. , Calvo, B. , Martinez, M. A. , and Doblare, M. , 2007, “An Anisotropic Visco-hyperelastic Model for Ligaments at Finite Strains. Formulation and Computational Aspects,” Int. J. Solids Struct., 44, pp. 760–778. 10.1016/j.ijsolstr.2006.05.018 [DOI] [Google Scholar]
- [38]. Gasser, T. C. , Ogden, R. W. , and Holzapfel, G. A. , 2006, “Hyperelastic Modelling of Arterial Layers With Distributed Collagen Fibre Orientations,” J. R. Soc. Interface, 3, pp. 15–35. 10.1098/rsif.2005.0073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Lanir, Y. , Lichtenstein, O. , Imanuel, O. , 1996, “Optimal Design of Biaxial Tests for Structural Material Characterization of Flat Tissues,” ASME J. Biomech. Eng., 118(1), pp. 41–47. 10.1115/1.2795944 [DOI] [PubMed] [Google Scholar]
- [40]. Spencer, A. J. M. , 1984, “Constitutive Theory for Strongly Anisotropic Solids,” in Continuum Theory of the Mechanics of Fibre-Reinforced Composites, Spencer A. J. M., Ed., Springer, Wien, pp. 1–32. [Google Scholar]
- [41]. Holzapfel, G. A. , and Gasser, T. C. , 2001, “A Viscoelastic Model for Fiber-Reinforced Composites at Finite Strains: Continuum Basis, Computational Aspects and Applications,” Comput. Methods Appl. Mech. Eng., 190, pp. 4379–4430. 10.1016/S0045-7825(00)00323-6 [DOI] [Google Scholar]
- [42]. Holzapfel, G. A. , Gasser, T. C. , and Ogden, R.W. , 2000, “A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models,” J. Elast., 61, pp. 1–48. 10.1023/A:1010835316564 [DOI] [Google Scholar]
- [43]. Gasser, T. C. , Ogden, R. W. , and Holzapfel, G. A. , 2006, “Hyperelastic Modelling of Arterial Layers With Distributed Collagen Fibre Orientations,” J. R. Soc. Interface., 3(6), pp. 15–35. 10.1098/rsif.2005.0073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].ABAQUS Manual, 2006, ver. 6.3, Hibbit, Karlson, and Sorenson, Pawtucket, RI.
- [45]. Li, L. P. , Solhat, J. , Buschman, M. D. , and Shirazi-Adl, A. , 1999, “Nonlinear Analysis of Cartilage in Unconfined Ramp Compression Using a Fibril Reinforced Poroelastic Model,” Clin. Biomech., 14, pp. 673–682. 10.1016/S0268-0033(99)00013-3 [DOI] [PubMed] [Google Scholar]
- [46]. Spilker, R. L. , Suh J.-K., and Mow, V. C. , 1990, “Formulation and Evaluation of a Finite Element Model for the Biphasic Model of Hydrated Soft Tissues,” Comput. Struct., 35(4), pp. 425–439. 10.1016/0045-7949(90)90067-C [DOI] [Google Scholar]
- [47]. Athanasiou, K. A. , Rosenwasser, M. P. , and Buckwalter, J. A, 1991, “Interspecies Comparisons of In Situ Intrinsic Mechanical Properties of Distal Femoral Cartilage,” J. Orthop. Res., 9, pp. 330–340. 10.1002/jor.v9:3 [DOI] [PubMed] [Google Scholar]
- [48]. Hwang, N. H. C. , and Woo, S. L.-Y. , 2003, Frontiers in Biomedical Engineering, Kluwer Academic/Plenum, New York. [Google Scholar]
- [49]. Clark, J. M. , 1991, “Variation of Collagen Fiber Alignment in a Joint Surface: A Scanning Electron Microscope Study of the Tibial Plateau in Dog, Rabbit, and Man,” J. Orthop. Res., 9, pp. 246–257. 10.1002/jor.v9:2 [DOI] [PubMed] [Google Scholar]
- [50]. Clark, J. M. , 1990, “The Organization of Collagen Fibrils in the Superficial Zones of Articular Cartilage,” J. Anat., 171, pp. 117–130. [PMC free article] [PubMed] [Google Scholar]