Validation of an Empirical Damage Model for Aging and in Vivo Injury of the Murine Patellar Tendon

Short abstract

While useful models have been proposed to predict the mechanical impact of damage in tendon and other soft tissues, the applicability of these models for describing in vivo injury and age-related degeneration has not been investigated. Therefore, the objective of this study was to develop and validate a simple damage model to predict mechanical alterations in mouse patellar tendons after aging, injury, or healing. To characterize baseline properties, uninjured controls at age 150 days were cyclically loaded across three strain levels and five frequencies. For comparison, damage was induced in mature (120 day-old) mice through either injury or aging. Injured mice were sacrificed at three or six weeks after surgery, while aged mice were sacrificed at either 300 or 570 days old. Changes in mechanical properties (relative to baseline) in the three week post-injury group were assessed and used to develop an empirical damage model based on a simple damage parameter related to the equilibrium stress at a prescribed strain (6%). From the derived model, the viscoelastic properties of the 300 day-old, 570 day-old, and six week post-injury groups were accurately predicted. Across testing conditions, nearly all correlations between predicted and measured parameters were statistically significant and coefficients of determination ranged from R²= 0.25 to 0.97. Results suggest that the proposed damage model could exploit simple in vivo mechanical measurements to predict how an injured or aged tendon will respond to complex physiological loading regimens.

Introduction

Tendon injury and degeneration are common conditions that compromise proper tissue function. By altering tendon mechanical properties, these pathologies can lead to decreased joint stability [1,2], damage in adjacent tissues [3–5], pain [6,7], and disability [8–10]. Anticipating these unwanted side effects in an injured or aged tendon requires a detailed understanding of the induced mechanical changes. However, tendon is a complex tissue with time- and strain-dependent mechanical properties that are difficult to fully characterize, particularly in vivo. Therefore, a framework for modeling the effects of in vivo damage on the nonlinear, viscoelastic mechanical properties of tendon is necessary for predicting the mechanical consequences of injury or aging based on simple measurements.

Previous studies have proposed a variety of models to describe damage in tendon and other materials [11–18]. For example, a model described by Lemaitre [12] assumes that damage-induced structural discontinuities cause a reduction in the effective resisting area of a stretched material [12]. That is, a damage parameter D_σ can be defined by

$$A_{\mathrm{effective}}=A_{\mathrm{measured}}(1-D_{\sigma })$$ (1)

where nonzero damage leads to a decreased effective area A _effective relative to the overall (i.e., measured) area A _measured. Note that 0 ≤ D_σ ≤ 1. Equivalently, one can consider an effective stress and a measured stress defined by ${\sigma }_{\mathrm{effective}}=F/A_{\mathrm{effective}}$ and ${\sigma }_{\mathrm{measured}}=F/A_{\mathrm{measured}}$, yielding

$${\sigma }_{\mathrm{effective}}=\frac{{\sigma }_{\mathrm{measured}}}{1-D_{\sigma }}$$ (2)

In other words, a damaged tissue deforms in response to an applied stress as if the applied stress were higher due to a reduced effective area.

An alternative strain-based model described by Duenwald-Kuehl et al. [11] has recently been shown to accurately describe mechanical alterations in tendons overstretched in vitro. According to this useful model, a damaged tendon reacts to an applied strain as if the strain were lower. The strain “felt” by the material can be described as the effective strain, and the constitutive equation relating stress and effective strain are assumed to be unaltered after damage. That is, σ = σ(ε _effective) in both damaged and undamaged tendons. The damage-dependent effective strain is taken to obey the relation

$${\epsilon }_{\mathrm{effective}}={\epsilon }_{\mathrm{applied}}(1-D_{\epsilon })$$ (3)

where 0 ≤ D_ε ≤ 1 and D_ε is a parameter representing the extent of damage. Note that that the reduction in effective strain after damage can be thought of as arising from an increased effective tendon gauge length L ₀ [14] given by

$$L_0^{\mathrm{effective}}=\frac{L_0^{\mathrm{measured}}}{1-D_{\epsilon }}$$ (4)

since ${\epsilon }_{\mathrm{applied}}=\Delta L/L_0^{\mathrm{measured}}$ and ${\epsilon }_{\mathrm{effective}}=\Delta L/L_0^{\mathrm{effective}}$.

While the Duenwald-Kuehl model predicts the altered viscoelastic properties of tendons subject to subfailure overstretch in vitro quite well, the applicability of this and other damage models to in vivo injury, healing, and aging have not been investigated. In vivo, tendon injuries induce a complex, multiphase biological response that involves the degradation, deposition, and migration of extracellular matrix components in the wound site [19–22]. The resulting structural and mechanical alterations cannot be fully modeled in vitro. Similarly, mechanical changes in aging tendons are thought to be induced in part by biological factors that are difficult to recreate ex vivo. Therefore, the objective of this study was to build on previous work to develop and validate a simple damage model capable of predicting mechanical alterations over a range of loading conditions in mouse patellar tendons after aging, injury, and healing. We hypothesized that from undamaged properties and a single measurement of equilibrium stress at a given strain, viscoelastic parameters in damaged tendons can be accurately predicted across a wide range of frequencies and strain levels.

Methods

Study Design.

A total of 94 female C57 BL/6 wild-type mice were obtained with IACUC approval. Of these, 57 mice were sacrificed at 150, (n = 22), 300 (n = 15), or 570 (n = 20) days postnatal (denoted as P150, P300, and P570, respectively). Patellar tendon midsubstance injuries (see the following section) were performed on 37 additional mice at P120 as described previously [3] and these mice were sacrificed either 3 (n = 20) or 6 (n = 17) weeks post-injury. Tendons from uninjured P150 mice were considered healthy, while tendons from older and injured groups were considered to be damaged. A previous study demonstrated reduced mechanical properties in P300 and P570 mice as compared to P150 [23], motivating the use of mice at these ages to assess age-related damage. The uninjured P150 group was used to characterize baseline properties, the three week post-injury group was used to relate pre- and post-damage properties, and the six week post-injury and older (P300 and P570) groups were used to validate the damage model for healing and aging tendons.

Patellar Tendon Injury Model.

Bilateral patellar tendon injuries were performed on designated mice (n = 37) as described previously [24–26]. Briefly, mice were given buprenorphine (0.1 mg/kg) as a pre and postoperative analgesic. After anesthetization with a mixture of isofluorane and oxygen, both hindlimbs were shaved and sanitized. A small skin incision was made above the knee joint to expose the patellar tendon. The retinaculum was incised on both sides of the knee and jeweler's forceps were carefully positioned underneath the patellar tendon to facilitate the passage of a plastic-coated blade beneath the tendon. A small hemostat was clamped onto the end of the coated blade to provide further support and a full-thickness, partial-width circular defect was created in the center of the tendon using a 0.75 mm diameter biopsy punch corresponding to roughly 2/3 of the total tendon width. After closure of its skin wounds with sutures, each mouse was allowed to recover under a heat lamp before resuming normal cage activity.

Sample Preparation.

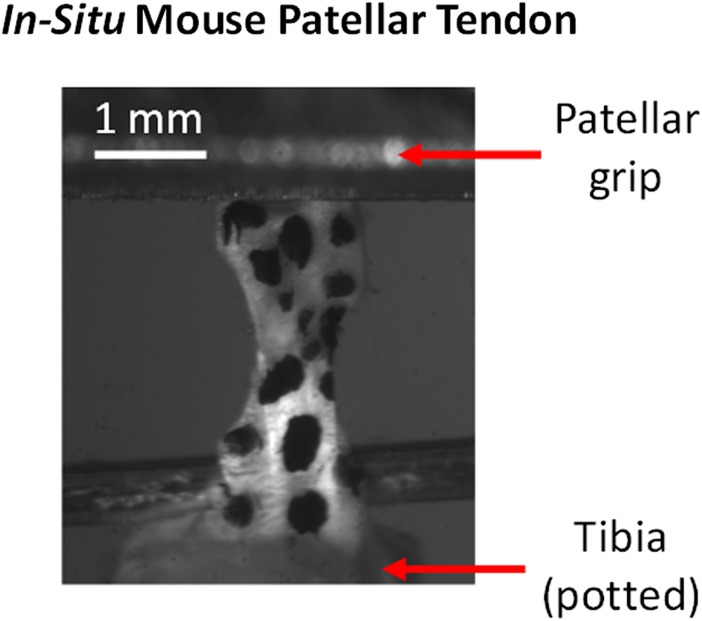
Patellar tendons were prepared and tested as described previously [23]. Briefly, patella-patellar tendon-tibia complexes were carefully dissected from a randomly chosen hindlimb (right or left). Tendons were then stamped into a dog-bone shape to isolate the injured region and tendon cross sectional area was measured using a custom, laser-based device [25,27]. Immediately prior to mechanical testing, the tibia was potted in PMMA and the patella was gripped with a custom aluminum fixture.

Mechanical Testing and Data Analysis.

Each specimen was loaded into a 37 °C PBS bath connected to an Instron 5848 materials testing system (Instron Corp., Norwood, MA). The aluminum fixture securing the patella was attached to the Instron actuator while the potted tibia was held fixed on the base of the PBS bath (Fig. 1). To fully characterize baseline properties, uninjured P150 specimens were tested across five frequencies and three strain levels according to the following protocol: (1) preload to 0.005 N, (2) preconditioning, (3) stress relaxation to 4% strain, (4) sinusoidal frequency sweep, and (5) repeat steps 3–4 to strain levels of 6 and 8%. For preconditioning, a ten-cycle triangle wave strain between 0% and 5% was imposed at 0.25 Hz. Each frequency sweep consisted of ten cycles of 0.125% amplitude sinusoidal strain at frequencies of 0.01, 0.1, 1, 5, and 10 Hz superimposed onto the baseline offset strain (4, 6, or 8%). According to preliminary tests in our laboratory, the average transition strain between toe and linear regions in uninjured, P150 mouse patellar tendons stretched to failure at 0.1% strain/s is 6% (data not shown). As such, 4% strain represents toe region behavior, 6% represents behavior near the toe-linear transition, and 8% strain represents linear region behavior. For comparison, physiological strains in the human patellar tendon are thought to span the range 0–6% [28].

Fig. 1.

Stamped P150 mouse patellar tendon prepared for mechanical testing. The dark spots are Verhoeff's stain for optical tracking, which was not used in this study.

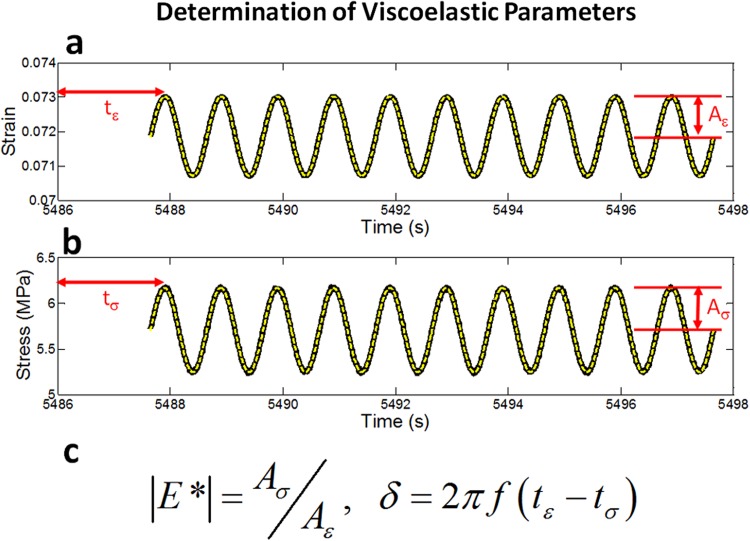
The equilibrium stress σ _eq, dynamic modulus |E*| and loss tangent tanδ were computed at each frequency f and strain level ε using a custom Matlab program. σ _eq was calculated from the measured stress 10 min after a 5% strain/s ramp; |E*| was defined as the stress amplitude divided by the strain amplitude and tanδ was given by the tangent of the phase difference between the stress and strain (Fig. 2). |E*| represents how resistant a material is to deformation while tanδ is a measure of viscoelasticity with high values reflecting fluid-like behavior and values near zero reflecting solid-like behavior.

Fig. 2.

(a) Strain and (b) stress versus time plots for a representative sample deformed at f = 1 Hz with an 8% strain offset. The solid black curves represent raw data, while the dashed lines represent sinusoidal fits. (c) The dynamic modulus |E*| is given by the ratio of the stress and strain amplitudes, while δ is computed from the phase difference between the stress and strain.

Development and Evaluation of the Damage Model.

To determine baseline (undamaged) properties, σ _eq, |E*|, and tanδ were first characterized as a function of ε for P150 uninjured tendons at each deformation frequency. Building directly on previous models [11,12], since damage decreases a tendon's equilibrium stress at a given strain level, a damage parameter D for each damaged tendon was defined according to

$$1-D=\frac{{\sigma }_{\mathrm{eq}}^{\mathrm{damaged}}(6\%)}{〈{\sigma }_{\mathrm{eq}}^{\mathrm{undamaged}}〉(6\%)}$$ (5)

where 〈 〉 denotes averaging across all tested tendons. In order to best characterize alterations in mechanical properties across 4, 6, and 8% based on a single parameter, the equilibrium stress at the intermediate strain level of 6% was chosen to define D (Eq. (5)). For each applied strain, |E*| and tanδ after damage were assumed to be functions of their mean undamaged values and the extent of damage D. Since damage was expected to be greater in three week post-injury tendons than in the other assessed groups, measured values of |E*| and tanδ for this group at all strains were plotted against $(1-D)\langle {\left|E^{*}\right|}_{\mathrm{undamaged}}\rangle$ and $(1-D)\langle \tan {\delta }_{\mathrm{undamaged}}\rangle$ to relate pre and post damage parameters. These plots were well-fit by the power law relations

$${\left|E^{*}\right|}_{\mathrm{damaged}}=A_1{\left[(1-D)\langle {\left|E^{*}\right|}_{\mathrm{undamaged}}\rangle \right]}^{n_1}$$ (6)

and

$$\tan {\delta }_{\mathrm{damaged}}=A_2{\left[(1-D)\langle \tan {\delta }_{\mathrm{undamaged}}\rangle \right]}^{n_2}$$ (7)

and values for A ₁, n ₁, A ₂, and n ₂ were determined by curve fitting the three week post-injury data with Eqs. (6) and (7). Note that while the empirical parameters A ₁, n ₁, A ₂, and n ₂ are not intended to correspond to specific physical properties of tendon, together they describe how |E*| and tanδ scale with their baseline values and the extent of damage. By applying Eqs. (6) and (7) to tendons in the other damage groups (i.e., the six week post-injury, P300 and P570 groups), predictions for |E*| and tanδ were made.

Comparisons of D after injury and during aging were performed using a one-way ANOVA with Bonferroni post hoc analysis. To validate and test the robustness of the damage model, predicted and measured values of |E*| and tanδ were compared by calculating the coefficient of determination (R ²) and the associated p-value. Significance was set at p ≤ 0.05.

Results

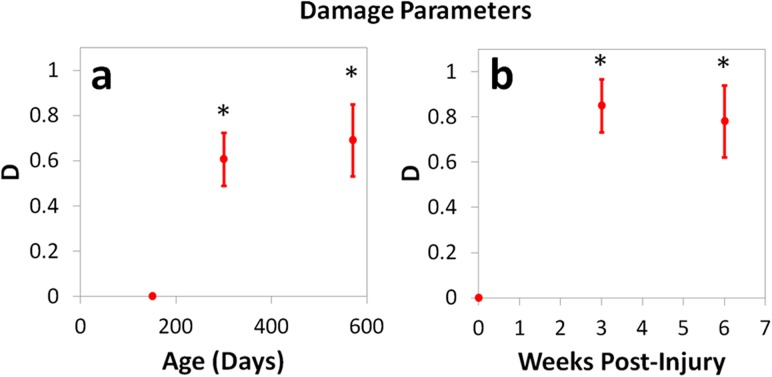
Damage parameters were greater than 0.6 and significantly higher than baseline (P150 uninjured) for all aged and injured groups (Table 1, Fig. 3). As expected, the highest damage parameter was measured in the three week post-injury group (D = 0.85). Changes in D from 300 to 570 days and from three to six weeks post-injury were not statistically significant.

Table 1.

Damage parameter D for each damage group assessed in the study (mean ± SD). D was significantly higher than baseline (D = 0) in all groups.

Damage Parameters
Damage Group	D
P300	0.61 ± 0.26
P570	0.69 ± 0.23
Three weeks post-injury	0.85 ± 0.12
Six weeks post-injury	0.78 ± 0.16

Fig. 3.

Damage parameter D during (a) aging and (b) the injury response. In all aging and injured groups, D was significantly increased compared to baseline (P150 uninjured). Mean ± SD, (*) p < 0.05/3 versus P150 uninjured.

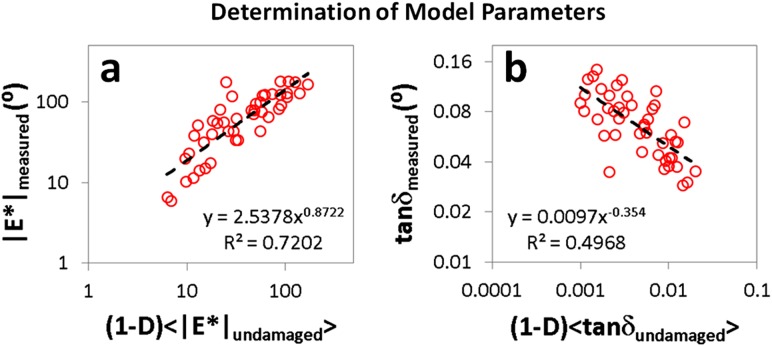
For f = 1 Hz, measurements of |E*| and tanδ plotted against $(1-D)\langle {\left|E^{*}\right|}_{\mathrm{undamaged}}\rangle$ and $(1-D)\langle \tan {\delta }_{\mathrm{undamaged}}\rangle$ for the three week post-injury group were closely fit by power laws (Fig. 4). Curve fitting of these data according to Eqs. (6) and (7) yielded values of 2.5, 0.87, 0.0097, and −0.35 for A ₁, n ₁, A ₂, and n ₂, respectively. The positive value of n ₁ and negative value of n ₂ indicate that |E*| decreased and tanδ increased with D. In all damage groups, predicted values of |E*| and tanδ based on these fit parameters and the sample-dependent damage parameter D (as described by Eqs. (6) and (7)) were consistent with measurements (Figs. 5, 6, and 7). Moreover, the correlation between measured and predicted values of both |E*| and tanδ was generally strong. Specifically, for |E*|, R ² was greater than 0.75 for nine out of 12 strain levels across all four damage groups while for tanδ, R ² was greater than 0.75 for seven out of 12 strain levels across all four damage groups (Table 2). Except for tanδ at 4% strain for the six week post-injury group, correlations between predictions and experimental data were significant for |E*| and tanδ at all strain levels, and coefficients of determination ranged from R ²= 0.25 to 0.92 (Table 2 ). Results were similar at all other frequencies (see Appendix).

Fig. 4.

Measured values of (a) |E*| and (b) tanδ plotted against (1 –D) < |E*|_damaged > and (1 – D) < tanδ_damaged > for mouse patellar tendons three weeks after injury at P120 tested at 4, 6, and 8% strain with f = 1 Hz. The dashed black lines represent power law fits of the acquired data. Relationships derived from these fits were used to predict |E*| and tanδ in other damage groups.

Fig. 5.

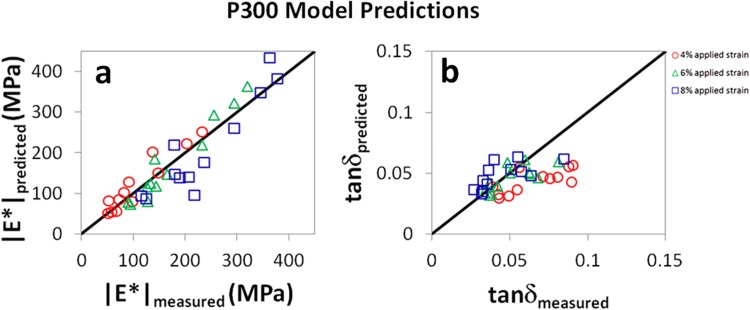
Measured and predicted values of (a) |E*| and (b) tanδ for P300 mouse patellar tendons tested at f = 1 Hz. The solid black lines are not fits of experimental data, but represent the expected relationship between predicted and measured parameters (e.g., |E*|_measured = |E*|_predicted). Agreement between model and experiment was strong for the dynamic modulus |E*|, but weaker for tanδ. For |E*|, R ²= 0.90, 0.95, and 0.85 at 4%, 6%, and 8% strain, respectively. For tanδ, R ²= 0.54, 0.55, and 0.46 at 4%, 6%, and 8% strain, respectively. Results were similar at other frequencies (see Appendix).

Fig. 6.

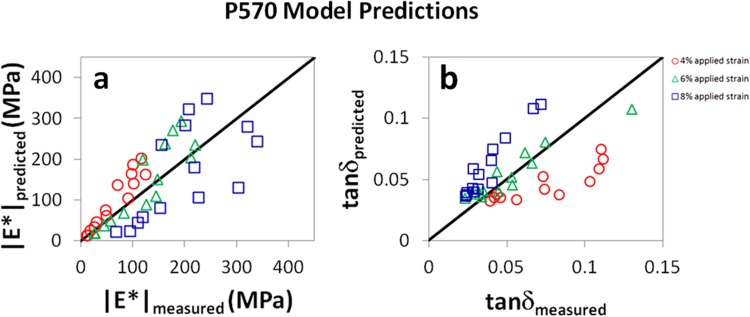
Measured and predicted values of (a) |E*| and (b) tanδ for P570 mouse patellar tendons tested at f = 1 Hz. The solid black lines are not fits of experimental data, but represent the expected relationship between predicted and measured parameters (e.g., |E*|_measured = |E*|_predicted). Agreement between model and experiment was evident for both parameters. For |E*|, R ²= 0.91, 0.80, and 0.42 at 4%, 6%, and 8% strain, respectively. For tanδ, R ²= 0.91, 0.85, and 0.91 at 4%, 6%, and 8% strain, respectively. Results were similar at other frequencies (see Appendix).

Fig. 7.

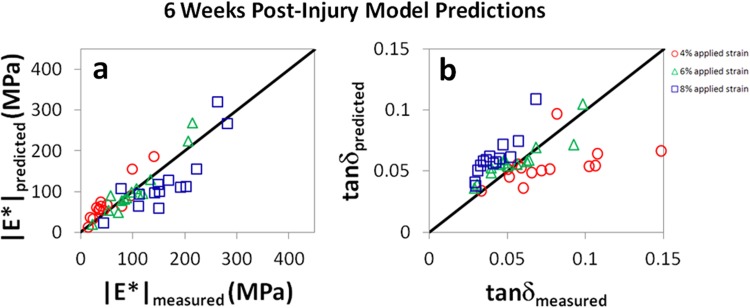
Measured and predicted values of (a) |E*| and (b) tanδ for mouse patellar tendons six weeks after injury at P120 tested at f = 1 Hz. The solid black lines are not fits of experimental data, but represent the expected relationship between predicted and measured parameters (e.g., |E*|_measured = |E*|_predicted). Agreement between model and experiment was strong for the dynamic modulus |E*|, but weaker for tanδ. For |E*|, R ²= 0.83, 0.92, and 0.71 at 4%, 6%, and 8% strain, respectively. For tanδ, R ²= 0.25, 0.82, and 0.82 at 4%, 6% and 8% strain, respectively. Results were similar at other frequencies (see Appendix).

Table 2.

Coefficients of determination and associated p-values for comparisons of measured and predicted values of |E*| and tanδ in aged (P300 and P570) and injured (three and six weeks post-injury at P120) tendons tested at 4%, 6%, and 8% with f = 1 Hz. Apart from the parameter tanδ at 4% strain for the six week post-injury group, in all groups, correlations were significant for both parameters at all strain levels. Results were similar at other frequencies (see Appendix).

Evaluation of Model Predictions at 1 Hz
P300 (uninjured)				P570 (uninjured)
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.90	< 0.0001	|E*|	4%	0.91	< 0.0001
	6%	0.95	< 0.0001		6%	0.80	< 0.0001
	8%	0.85	< 0.0001		8%	0.42	0.01
tanδ	4%	0.54	0.007	tanδ	4%	0.91	< 0.0001
	6%	0.55	0.006		6%	0.85	< 0.0001
	8%	0.46	0.02		8%	0.91	< 0.0001

Three weeks post-injury				Six weeks post-injury
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.91	< 0.0001	|E*|	4%	0.83	< 0.0001
	6%	0.84	< 0.0001		6%	0.92	< 0.0001
	8%	0.52	0.002		8%	0.71	0.0002
tanδ	4%	0.80	< 0.0001	tanδ	4%	0.25	0.07
	6%	0.90	< 0.0001		6%	0.82	< 0.0001
	8%	0.64	0.0003		8%	0.82	< 0.0001

Table 3.

Coefficients of determination and associated p-values for comparisons of measured and predicted values of |E*| and tanδ in aged (P300 and P570) and injured (three and six weeks post-injury at P120) tendons tested at 4%, 6%, and 8% with f = 0.01 Hz. Apart from the parameter tanδ at 4% strain for the six week post-injury and P300 groups, in all groups, correlations were significant for both parameters at all strain levels.

Evaluation of Model Predictions at 0.01 Hz
P300 (uninjured)				P570 (uninjured)
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.91	< 0.0001	|E*|	4%	0.92	< 0.0001
	6%	0.95	< 0.0001		6%	0.81	< 0.0001
	8%	0.87	< 0.0001		8%	0.44	0.009
tanδ	4%	0.42	0.02	tanδ	4%	0.48	0.006
	6%	0.32	0.06		6%	0.69	0.0002
	8%	0.34	0.05		8%	0.47	0.007

Three weeks post-injury				Six weeks post-injury
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.92	< 0.0001	|E*|	4%	0.83	< 0.0001
	6%	0.89	< 0.0001		6%	0.93	< 0.0001
	8%	0.50	0.002		8%	0.67	< 0.0001
tanδ	4%	0.69	0.0001	tanδ	4%	0.27	0.06
	6%	0.76	< 0.0001		6%	0.46	0.008
	8%	0.42	0.008		8%	0.45	0.008

Table 4.

Coefficients of determination and associated p-values for comparisons of measured and predicted values of |E*| and tanδ in aged (P300 and P570) and injured (three and six weeks post-injury at P120) tendons tested at 4%, 6%, and 8% with f = 0.1 Hz. In all groups, correlations were significant for both parameters at all strain levels.

Evaluation of Model Predictions at 0.1 Hz
P300 (uninjured)				P570 (uninjured)
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.92	< 0.0001	|E*|	4%	0.93	< 0.0001
	6%	0.95	< 0.0001		6%	0.84	< 0.0001
	8%	0.87	< 0.0001		8%	0.45	0.009
tanδ	4%	0.60	0.003	tanδ	4%	0.79	< 0.0001
	6%	0.68	0.0009		6%	0.85	< 0.0001
	8%	0.53	0.008		8%	0.78	< 0.0001

Three weeks post-injury				Six weeks post-injury
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.92	< 0.0001	|E*|	4%	0.85	< 0.0001
	6%	0.86	< 0.0001		6%	0.92	< 0.0001
	8%	0.53	0.002		8%	0.72	0.0001
tanδ	4%	0.76	< 0.0001	tanδ	4%	0.28	0.05
	6%	0.97	< 0.0001		6%	0.52	0.003
	8%	0.62	< 0.0001		8%	0.67	0.0003

Table 5.

Coefficients of determination and associated p-values for comparisons of measured and predicted values of |E*| and tanδ in aged (P300 and P570) and injured (three and six weeks post-injury at P120) tendons tested at 4%, 6%, and 8% with f = 5 Hz. In all groups, correlations were significant for both parameters at all strain levels.

Evaluation of Model Predictions at 5 Hz
P300 (uninjured)				P570 (uninjured)
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.89	< 0.0001	|E*|	4%	0.96	< 0.0001
	6%	0.95	< 0.0001		6%	0.90	< 0.0001
	8%	0.85	< 0.0001		8%	0.55	0.002
tanδ	4%	0.59	0.004	tanδ	4%	0.93	< 0.0001
	6%	0.53	0.007		6%	0.86	< 0.0001
	8%	0.43	0.02		8%	0.69	0.0002

Three weeks post-injury				Six weeks post-injury
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.91	< 0.0001	|E*|	4%	0.84	< 0.0001
	6%	0.84	< 0.0001		6%	0.92	< 0.0001
	8%	0.53	0.002		8%	0.70	0.0002
tanδ	4%	0.75	< 0.0001	tanδ	4%	0.57	0.002
	6%	0.89	< 0.0001		6%	0.83	< 0.0001
	8%	0.65	0.0003		8%	0.79	< 0.0001

Table 6.

Coefficients of determination and associated p-values for comparisons of measured and predicted values of |E*| and tanδ in aged (P300 and P570) and injured (three and six weeks post-injury at P120) tendons tested at 4%, 6%, and 8% with f = 10 Hz. In all groups, correlations were significant for both parameters at all strain levels.

Evaluation of Model Predictions at 10 Hz
P300 (uninjured)				P570 (uninjured)
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.89	< 0.0001	|E*|	4%	0.97	< 0.0001
	6%	0.94	< 0.0001		6%	0.89	< 0.0001
	8%	0.84	< 0.0001		8%	0.54	0.003
tanδ	4%	0.57	0.005	tanδ	4%	0.91	< 0.0001
	6%	0.56	0.005		6%	0.86	< 0.0001
	8%	0.41	0.03		8%	0.51	0.004

Three weeks post-injury				Six weeks post-injury
Parameter	Strain	R 2	p	Parameter	Strain	R 2	p
|E*|	4%	0.92	< 0.0001	|E*|	4%	0.85	< 0.0001
	6%	0.82	< 0.0001		6%	0.90	< 0.0001
	8%	0.50	0.003		8%	0.68	0.0003
tanδ	4%	0.92	< 0.0001	tanδ	4%	0.72	< 0.0001
	6%	0.94	< 0.0001		6%	0.86	< 0.0001
	8%	0.65	0.0003		8%	0.66	0.0004

Discussion

This study presents a simple damage model capable of describing and predicting mechanical changes in tendons due to aging or injury. According to these results, in vivo tendon damage can be characterized by a single parameter D that is easily calculated from a single simple measurement. Furthermore, D yields predictions for the viscoelastic parameters |E*| and tanδ across a wide range of frequencies (0.01–10 Hz) and strain levels (4–8%) that agree quantitatively with experiments.

According to the present study, the effects of aging and injury on patellar tendon mechanical properties are both well-described by the same damage models. That is, changes in viscoelastic properties due to these distinct biological processes scale similarly with the extent of damage. This surprising finding suggests that the same underlying biological and structural mechanisms of age-related changes in tendon mechanics may be responsible for alterations in tendon mechanics during the repair response. In fact, a number of biological and structural changes in tendon are common to both aging and the injury response including a decrease in collagen fibril diameter [29,30] and an increase in the presence of minor collagens [21,29]. Note that this analogy is limited by the fact that while aging tissue degrades over time, healing tissue improves over time.

In previously proposed damage models, the relationship between pre and post damage properties has been assumed. For example, Lemaitre [12] assumed that the effective stress on a material decreases linearly in proportion to the damage parameter D _s (Eq. (2)). Similarly, the model of Duenwald-Kuehl et al. [11] accurately predicted ex vivo tendon damage based on the assumption that the effective strain increases linearly in proportion to D_ε (Eq. (3)). In this study, to describe in vivo damage, a more flexible model was proposed in which a power law relationship between undamaged and damaged tendon properties was empirically derived (according to Eqs. (6) and (7)) from three week post-injury tendon properties. For f = 1 Hz, the measured power law exponents for |E*| and tanδ were n ₁ = 0.87 and n ₂ = –0.35, reflecting a complex, nonlinear relationship between pre and post damage parameters that incorporates the effects of both structural damage and the biological response.

The parameter D measured in this study provides an intuitive assessment of tendon damage as a result of aging, injury, and healing. High (i.e., close to 1) damage parameters reflect a larger extent of damage, while low (i.e., close to zero) damage parameters reflect near-baseline properties. Furthermore, changes in D were closely coupled with changes in |E*| and tanδ. |E*|, tanδ and D measured at a strain level of 6% did not change significantly from three to six weeks post-injury or from P300 to P570, while |E*| and D decreased significantly and tanδ increased significantly between baseline (P150 uninjured) and each aging or injury group (comparisons of |E*| and tanδ across injury and aging not shown). Therefore, D can be used to facilitate comparisons between groups when evaluating models of tendinopathy, healing, and the efficacy of treatment protocols. For example, the increase in D for both post-injury groups (Fig. 3) demonstrates that damage is still evident and baseline mechanical properties are still severely compromised after six weeks of healing.

While model predictions for both |E*| and tanδ were significant across nearly all conditions, the proposed damage model appears to be more accurate for |E*| than for tanδ (Figs. 5–7). This is likely due to the fact that the damage parameter D was defined according to the equilibrium stress measured at 6% strain, a parameter that is expected to relate more closely to the dynamic modulus (which is given by the stress amplitude divided by the strain amplitude for a small oscillatory displacement) than the tangent of the phase angle between stress and strain. It is possible that the model could be improved if the damage parameter were defined according to the stress relaxation time scale (for example) or another variable which may associate more closely with tanδ.

One limitation in this study was that for all groups, mechanical properties were assessed ex vivo after dissection of the patellar tendon and removal of surrounding tissue. As a result, changes in the same tendon after aging or injury could not be investigated and damage parameters for each tendon were instead determined by examining mechanical alterations with respect to the average baseline properties of tendons from uninjured, 150 day-old mice (Eq. (5)). Nevertheless, despite this limitation, close agreement between predicted and measured viscoelastic mechanical properties was observed. Future investigations deducing mechanical alterations in single tendons through in vivo measurements should yield even closer agreement between experiment and model predictions. In addition, it is possible that additional damage was induced during testing, particularly at 8% strain [11]. However, the model yielded predictions that closely mirrored experimental data at all three tested strain levels, suggesting that either damage did not occur or that the model is capable of describing tendon behavior at strain levels that correspond to damaged states. Importantly, mechanical testing was always performed in order of increasing strain. Therefore, we do not expect that the low-strain behavior of the tested tendons (or the model predictions at low strains) were impacted by possible damage.

The ability to predict the viscoelastic properties of damaged tendon across a range of conditions based on a single, simple measurement of equilibrium stress at a prescribed strain when baseline properties have been characterized has many potential applications both in the laboratory and in the clinic. For example, if the baseline properties of a particular tendon have been measured, investigators can fully describe mechanical changes in pathological tendon specimens without the sophisticated testing equipment typically required to characterize their complex strain- and rate-dependent mechanical response. In addition, while a number of ultrasound-, MRI- and implantable strain-gauge-based techniques capable of measuring tendon mechanical properties in vivo have been validated [31–34], these methods are typically limited in speed and resolution and are therefore better suited for simple measurements. However, according to the results of this study, only a single basic measurement is necessary to predict a broad range of viscoelastic properties in a damaged tendon. As a result, in combination with the proposed damage model, in vivo mechanical measurements may be used to diagnose tendon damage, guide rehabilitation protocols, assess the efficacy of treatment programs for injured or diseased tendons, and evaluate in vivo healing in surgically repaired tendons.