Multiscale Mechanical Simulations of Cell Compacted Collagen Gels

Short abstract

Engineered tissues are commonly stretched or compressed (i.e., conditioned) during culture to stimulate extracellular matrix (ECM) production and to improve the mechanical properties of the growing construct. The relationships between mechanical stimulation and ECM remodeling, however, are complex, interdependent, and dynamic. Thus, theoretical models are required for understanding the underlying phenomena so that the conditioning process can be optimized to produce functional engineered tissues. Here, we continue our development of multiscale mechanical models by simulating the effect of cell tractions on developing isometric tension and redistributing forces in the surrounding fibers of a collagen gel embedded with explants. The model predicted patterns of fiber reorganization that were similar to those observed experimentally. Furthermore, the inclusion of cell compaction also changed the distribution of fiber strains in the gel compared to the acellular case, particularly in the regions around the cells where the highest strains were found.

1. Introduction

Cell activity is controlled by a complex set of spatially and temporally varying environmental cues. Recently, it has been demonstrated that in addition to soluble biochemical factors, the properties of the surrounding extracellular matrix (ECM) and the local mechanical environment profoundly influence cell behavior [1–5]. The mechanical environment is controlled in part by the composition and stiffness of the local ECM and by the manner in which physical forces applied at the tissue-level propagate down to the cellular level. Forces are communicated to the cell through cell-cell and cell-ECM attachments via a number of signaling pathways that result in the conversion of mechanical signals into chemical signals (i.e., mechanotransduction) [6–8].

Changes in mechanical environment have been attributed to pathological remodeling in osteoporosis [9,10], glaucoma [11,12], atherosclerosis [13,14], and aneurysms [15], to cite just a few examples. Physical forces and changes in ECM stiffness have also been implicated in tumor metastasis [16–18]. The specifics on how such changes drive pathological tissue remodeling, however, remain unclear. Part of the confusion derives from the fact that the local mechanical environment is dynamic and dependent on the integrated and reciprocal response of the entire tissue.

In the field of tissue engineering, deformations applied to cell-seeded scaffolds have also been shown to modulate synthetic and enzymatic cell activity and differentiation [19–22]. As a result, engineered tissues are commonly conditioned mechanically by dynamic stretching, which improves mechanical properties beyond the level that can be derived solely from biochemical stimulants. The choice of a particular waveform and magnitude of stretch, however, is largely empirical because the precise relationships between the applied deformations and the cellular response are poorly understood. Furthermore, the amplitude and frequency of the conditioning protocols often does not change over the course of the culture period even though the remodeling process changes the local mechanical environment, ostensibly in an effort to drive it to a point of tensional homeostasis [23]. Recently, Syedain et al. found that fibrin-based engineered tissues had improved composition and mechanical properties when the magnitude of cyclic distension was incrementally increased every few days compared to those subjected to a constant magnitude over the duration of the experiment [24]. These results suggest that in order to maintain a synthetic response in growing constructs, the mechanical environment must change faster than the cells can adapt to it. Since the relationships between mechanical stimulation and ECM remodeling are complex, interdependent, and dynamic, theoretical remodels are required for understanding the underlying phenomena so that the conditioning process can be optimized to produce functional engineered tissues.

In order to understand and quantify how macroscopic forces affect cell activity, numerous mechanical models have been developed [25–27]. In these models, the microstructure is often represented as a continuum [26,28], or as a highly idealized periodic structure [25,29,30], but the heterogeneity of the actual scaffold limits the applicability of such an approach. Furthermore, the traction forces generated on the ECM by the cells that inhabit the scaffolds may be ignored due to the focus on macro-to-micro strain transfer and not micro-to-macro stress transfer. Yet, these forces can contribute substantially to the overall mechanical response of collagen gels [31]. It is unclear how active cell compaction of a gel changes force and strain transmission through it, which further limits our ability to engage in predictive tissue engineering. More advanced computational models, incorporating cell traction forces, are needed to resolve these complex relationships.

The purpose of this work is to lay the foundation for answering two questions: (1) how does cell compaction change the distribution of force and strain in a collagen or fibrin gel, (2) and what is the relationship between macroscopic tissue strain and microscopic tissue strain when these constructs are deformed? These are critical questions that must be answered in order to optimize mechanical conditioning procedures designed to produce engineered tissues with mechanical functionality similar to native tissues, particularly as the tissues and cells adapt to the mechanical environment. As an initial exploration into this area, we expand upon our previous work in modeling the multiscale mechanics of collagen gels [32–35] by incorporating the effect of cell tractions on developing isometric tension in the surrounding fibers of fiber-based scaffolds (e.g., collagen and fibrin gels).

2. Methods

2.1. Multiscale Model.

The multiscale modeling framework employed here was developed previously to examine mechanical coupling between scales in collagen gels [33,34,36] and other biomaterials [37,38]. The model treats the macroscopic domain of the material with the standard Galerkin finite element method and links it to a description of the microstructure via local microscopic fiber network problems and the theory of volume averaging [39,40]. The essential equations in the model include: (1) a constitutive equation describing the mechanical behavior of a single fiber, (2) an equation that provides the volume-averaged stress of a collection of cross-linked fibers that form a network, (3) and an equation for the balance of macroscopic stress. A detailed description of the equations in the model can be found in previous work [33,34]. Briefly, macroscopic displacements on the finite element (FE) mesh are mapped to the boundaries of the microscopic networks, each centered at the eight Gauss points within each element, through the use of tri-linear basis functions. The cross-linked fibers in the networks then reorganize and deform to satisfy force equilibrium. The volume-averaged stress from each network is then incorporated into the macroscopic stress balance, and an iteration is conducted until the positions of the FE nodes and the fiber reorganization combine to produce a state of equilibrium throughout the model. The constitutive equation of a fiber is

$$F=\frac{E_f{A}_f}{B}[\exp (B{\mathit{\varepsilon }}_f)-1]$$ (1)

where E_f is the Young's modulus at infinitesimal strain, A_f is the cross-sectional area of a fiber, B is a fitting parameter that controls the nonlinearity of the force response, and ε_f is the Green's strain of the fiber and is calculated as ${\varepsilon }_f=0.5({\lambda }_f^2-1)$, where λ_f is the fiber stretch ratio. In this study, a value of $E_f{A}_f=1.4\times {10}^{-8}\mathrm{N}$ and a value of B = 3.8 were used for both cellular and ECM networks based on our previous work [2]. The volume-averaged Cauchy stress of the fiber network, $〈{\sigma }_{\mathit{ij}}〉$, is calculated in discrete form as

$$〈{\sigma }_{\mathit{ij}}〉=\frac{1}{V}{\int }_V{\sigma }_{\mathit{ij}}\mathit{dV}=\frac{1}{V}\sum _{\mathrm{boundary}\mathrm{\hspace{1em}}\mathrm{nodes}}{x}_i{F}_j$$ (2)

where V is the volume of the network, σ_ij is the local microscopic stress, and x_i and F_j are the position and forces on the boundary nodes, respectively. The macroscopic stress balance is

$$〈{\sigma }_{\mathit{ij},i}〉=\frac{1}{V}{\oint }_{\delta V}({\sigma }_{\mathit{ij}}-〈{\sigma }_{\mathit{ij}}〉)u_{k,i}{n}_k\mathit{dA}$$ (3)

where u is the displacement of the network boundary δV, and n is the unit normal vector to the network surface.

2.2. Microscale Networks and Cell Compaction.

The collagen gel microstructure was approximated by a collection of 3D fiber networks that have been shown to resemble the structure and heterogeneity observed experimentally [1,2]. In this study, each element in the FE mesh was randomly assigned a 3D fiber network containing on average 323 ± 26 cross-linked fibers. The networks were created so that the fibers were preferentially aligned in the xy-plane (90% of the fibers were oriented within 10 deg of the xy-plane). In addition, the networks were created to be nearly isotropic (α = 0.15 ± 0.07 defined below) within the xy-plane. This configuration was chosen to help facilitate comparisons with experiments, in which information about fiber realignment through the thickness is often not available, and the subsequent analysis, which was conducted on the 2D projections of the 3D microstructures.

Network orientation and strength of alignment were quantified by the length-weighted 2D orientation tensor, Ω, which is given by

$$\Omega =\frac{\sum _{i=1}^{\mathit{NF}}{l}_i\left[\begin{array}{cc}\multicolumn{1}{c}{{\cos }^2{\theta }_i}& \hfill \cos {\theta }_i\sin {\theta }_i\hfill \\ \multicolumn{1}{c}{\cos {\theta }_i\sin {\theta }_i}& \hfill {\sin }^2{\theta }_i\hfill \end{array}\right]}{\sum _{i=1}^{\mathit{NF}}{l}_i}$$ (4)

where θ_i is the angle that fiber i makes with respect to the horizontal axis, l_i is the length of fiber i, and the sum is over all of the fibers in the network, NF. The eigenvectors and eigenvalues of this Ω represent the principal directions and magnitudes, respectively, of fiber orientation in the network. The strength of fiber alignment was quantified using an anisotropy index α, given by

$$\alpha =1-{\omega }_1/{\omega }_2$$ (5)

where ω₁ and ω₂ are the eigenvalues of Ω, and ω₁ ≤ ω₂. Under this convention, an isotropic network has an α value of 0, and a completely aligned network has an α value of 1 [41].

As a first step towards representing the physics of gel compaction and the development of internal tension, cell tractions were approximated by partitioning the networks in the model into either ECM (noncontractile) networks or cellular (contractile) networks. Therefore, elements designated as cells (or explants) contain only cellular networks, and elements designated as collagen gel only contain ECM networks. For this initial effort, cellular and ECM networks were assigned the same material properties and structure. The only difference between these types of networks was that during the compaction phase of the simulation, the reference length of fibers in the cellular networks was incrementally reduced, which created tension in surrounding fibers of the ECM networks. This approach to modeling cell compaction is only meant to simulate the effects of cell traction forces on the surrounding ECM. It is not meant to reflect the manner in which a cell actually exerts traction forces on the ECM.

2.3. Cell Compaction Case Studies.

In many applications that involve entrapping cells in gels, the cells are initially distributed homogeneously throughout the gel (e.g., [42]). The cells then compact the gel and produce a fiber alignment pattern that depends in part on cell traction forces, gel geometry, and gel mechanical constraints. In an effort to understand better the mechanisms involved within a less complex setting, several investigators have studied the development of fiber alignment, or “straps,” between clusters of cells, or explants [43–45]. The explant system allows easier arrangement of cells into simple geometric patterns and facilitates visualization of the mechanisms underlying cell-driven fiber realignment. Thus, the explant system provides a convenient system for understanding how alignment patterns form.

We simulated the development of fiber alignment in an explant system under similar conditions to those of Sawhney and Howard [44]. In that study, three mouse fibroblast explants (each consisting of approximately 4000 cells) were placed in a 1.7 mg/ml collagen gel in a triangular pattern spaced approximately 1 mm apart, and the development of fiber alignment between explants was monitored with time-lapse imaging over an 18 h period. To represent a typical experiment (Fig. 1(A)), a one-element thick square FE mesh consisting of 576 trilinear hexahedral elements and 1250 nodes was created to represent a spatial scale of 10 mm × 10 mm × 2 mm (length, width, thickness). The FE domain (Fig. 1(B)) was then partitioned into three triangularly arranged cellular domains, each consisting of four adjacent elements arranged as a square and containing only cellular networks. These cellular domains represent the explants, and they were embedded within a surrounding collagen gel domain consisting of ECM networks.

Fig. 1.

“Strap” formation between explants and the multiscale modeling strategy. (A) A triangular explant configuration develops strong fiber alignment between fibroblast explants after 60 h. Images are montages of sixty 20 × DIC images (images from Dr. Sander's lab). (B) Multiscale models consist of cellular networks (blue) that are configured in an analogous manner to the experiments and that contract to 40% of their original length to produce tension and reorganization in the surrounding ECM networks.

Three simulation cases were investigated for 40% cell-driven compaction by three triangularly arranged explants:

• case 1: four fixed boundaries (top, bottom, left, and right surfaces) during compaction

• case 2: two fixed boundaries (top and bottom surfaces) during compaction, followed by 50% uniaxial stretch

• case 3: three symmetry boundaries (bottom, left, and back surfaces) during compaction. For each scenario, unless specified above, the boundary was free.

We also repeated case 1 for 2 explants, 4 explants, and 5 explants to assess the role of explant geometry, and we repeated case 2 for no explants to assess the model mechanics without cell compaction.

To simulate cell compaction, the reference lengths of the fibers in the cellular networks were shortened either 4% (cases 1 and 2) or 2% (case 3) with each step, and the restructuring of fibers in both ECM and cell networks required to achieve mechanical equilibrium was determined iteratively. This process continued until the cellular network fiber reference lengths were 40% shorter than the original fiber lengths (i.e., either 10 or 20 steps). To apply uniaxial stretch (case 2), the top boundary was then displaced 0.5 cm over ten equally spaced steps (0.05 cm/step) while the bottom boundary remained fixed. Fiber stretch ratios were used to calculate the Lagrangian strain for the fibers. Fiber stretch ratios, which were defined relative to the original fiber length, were only calculated for the ECM networks due to difficulties with interpretation for the cellular networks, where the reference lengths were changed with each step to generate tension.

Since the FE domain contains 4608 networks and consists of approximately 1.5 × 10⁶ fibers, the computational demands for these simulations were large. Simulations were run using a custom parallelized C code with message passing interface (MPI) on high performance computing resources. All post processing was done using Matlab.

3. Results

The effect of cell compaction on microstructural reorganization, development of internal tension, and altered mechanical behavior in explants embedded in collagen gels was studied in a multiscale modeling framework for a number of different scenarios. Compaction was achieved by incrementally shrinking the reference length of cellular network fibers until it had been reduced by 40%, which we refer to as 40% compaction, for all simulations.

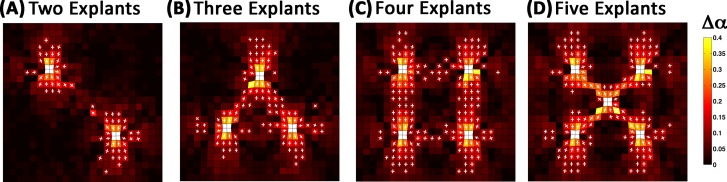
For case 1, four different explant configurations were simulated. Varying levels of fiber realignment were observed in the surrounding ECM networks for each configuration (Fig. 2). Fiber realignment increased with the amount of compaction, first in the networks nearest the explants. As the amount of compaction increased, fiber realignment spread outward on paths directed towards the other explants and towards the fixed boundaries. The change in ECM network fiber alignment with respect to the initial configuration (Δα) also increased with the number of explants. At the end of compaction, Δα reached values of 0.037 ± 0.048 (mean ± standard deviation, two explants), 0.051 ± 0.060 (three explants), 0.067 ± 0.064 (four explants), and 0.072 ± 0.071 (five explants). The Δα values are low because they were obtained by averaging over all ECM networks in the model, even though only a fraction of the ECM networks were impacted by cell compaction. As the number of explants increased, the fraction of ECM networks with Δα > 0.08 increased from approximately 11% to 30%. Within this subset, Δα values were as high as 0.40 for some ECM networks immediately adjacent to the explants.

Fig. 2.

Top-view of fiber network realignment after 40% compaction for case 1. ECM networks develop varying patterns of fiber alignment between explants in a configuration dependent manner. The color map indicates the change in the degree of fiber alignment (Δα) between the initial traction free configuration and 40% compaction. Also depicted are the principal directions of fiber alignment (white crosses). For clarity, directions are only shown for those elements with Δα > 0.08.

Among the different explant configurations examined above, the triangular configuration (Fig. 2(B)) was further explored to determine how boundary conditions affect model predictions of gel restructuring in response to cell compaction. As was observed with fiber realignment, cell compaction produced the largest strains in the networks immediately around and between the explants in a manner that depended on the boundary conditions (Fig. 3). For the case of four fixed boundaries (Figs. 3(A) and 3(D)), the direction of maximum principal strain was axially aligned between all three explants. When the left and right boundaries were freed (Figs. 3(B) and 3(E)), the strain in the 16 elements directly between the bottom two explants decreased from 0.062 ± 0.013 to 0.057 ± 0.019 and the strain pattern between explants switched from a triangular shape to an inverted V-shape. In contrast, when symmetry conditions were applied and the surfaces were allowed to freely translate with compaction (Figs. 3(C) and 3(F)), the direction of maximum principal strain changed and was generally perpendicular to the axis between explants. At the end of the 40% compaction, the average maximum principal strains were 0.051 ± 0.024, 0.044 ± 0.026, and 0.035 ± 0.032, for the fixed, uniaxial, and free boundary simulations, respectively.

Fig. 3.

Strain developed during 20% and 40% compaction for three explants. (A), (D) Top, bottom, left, and right boundaries are fixed, (B), (E) top and bottom are fixed, and (C), (F) symmetry boundary conditions are applied to the left, bottom, and back faces. Maximum principal strain patterns change in accord with the applied boundary conditions. White arrows show principal direction.

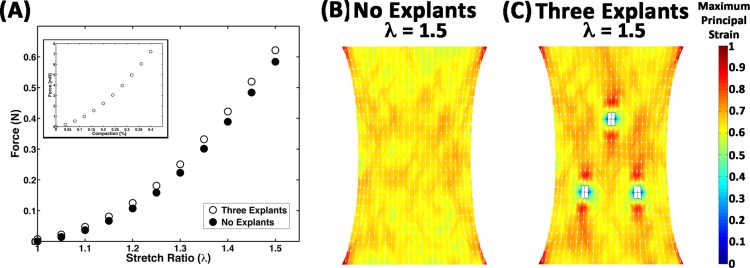
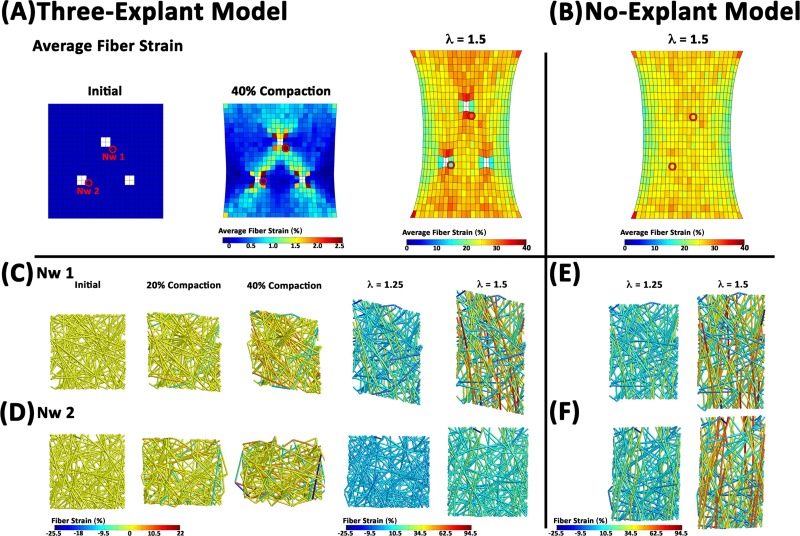
The effect of cell compaction on the mechanical response of the model construct was evaluated by comparing the response of the 40% compacted, three-explant model to an equivalent model without cellular networks (i.e., no explants), where both models were subjected to uniaxial extension (Fig. 4). Prior to stretch, 40% compaction resulted in the development of a small amount of isometric force (8 mN) on the surface perpendicular to the axis of stretch (Fig. 4(A)). The force then increased nonlinearly with stretch up to 0.62 N at a macroscopic stretch ratio of λ = 1.5 (i.e., 50% stretch). The force also increased with stretch in the explant-free model, but the force was always slightly lower (e.g., 0.58 N at λ = 1.5) than in the three-explant model. The average principal strain was also lower in the no-explant model (Fig. 4(B)) compared to the three-explant model (Fig. 4(C)), reaching values of 0.639 ± 0.048 and 0.649 ± 0.095, respectively, at λ = 1.5. Regional variations in strain were also more pronounced in the three-explant model, particularly around the explants, where regions of tension and compression were observed (Fig. 4(C)).

Fig. 4.

Comparison of mechanical response. (A) The force on the boundary during uniaxial extension for the case of 40% compaction for three explants (circles) is higher than the case where all of the networks are ECM networks (i.e., no explants). The inset plot shows the increase in force that develops on the boundary during the compaction process prior to uniaxial extension. (B), (C) Regional differences in strain, particularly around the explants, are apparent at full stretch (λ = 1.5).

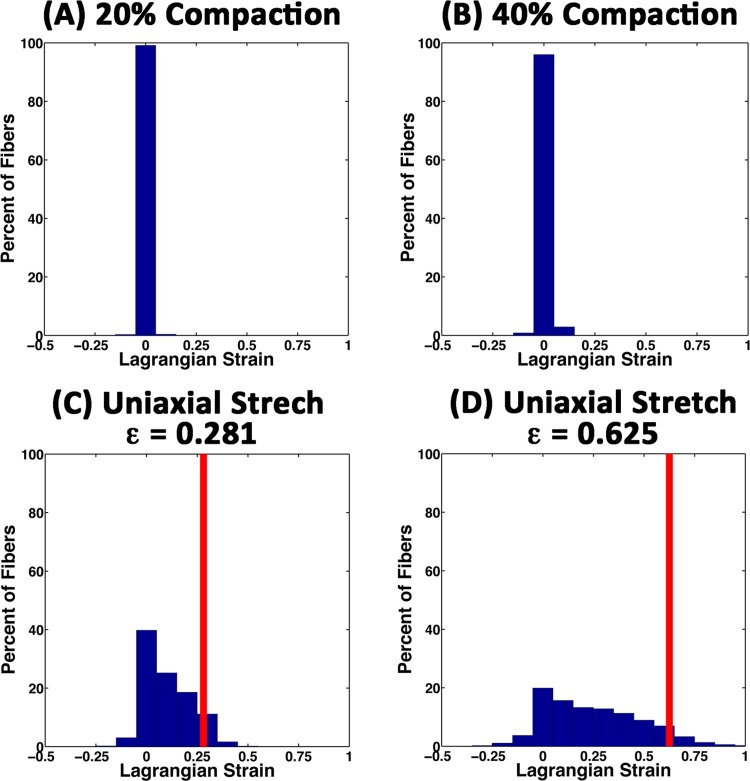
During the compaction phase of the simulations, the average ECM fiber strains were very small and increased from 0.001 ± 0.013 at 20% compaction (Fig. 5(A)) to 0.005 ± 0.021 at 40% compaction (Fig. 5(B)). The strains were small because the majority of fibers in the model were not strongly impacted by explant compaction. At 20% and 40% compaction, the fraction of fibers in the model with tensile strains exceeding 1% increased from 9.4% to 21.6%, respectively, and the fraction of fibers with compressive strains in excess of 1% increased from 3.2% to 5.4%, respectively. These fibers were primarily located in elements immediately around the explants and along the axes between explants.

Fig. 5.

Histograms of fiber strain in all ECM networks for uniaxial stretch of the three explant model. (A), (B) During the compaction phase of the simulations a small fraction of fibers developed small tensile and compressive strains. (C) 25% uniaxial stretch, (D) 50% uniaxial stretch. With uniaxial stretch a wide range of fiber strains were observed, most of which were below the amount of stretch applied macroscopically (red line). The distribution of fiber strains in the no-explant model (data not shown) were similar in shape to those in (C) and (D).

The average fiber strain increased with uniaxial extension from 0.101 ± 0.113 at 25% stretch (Fig. 5(C)) to 0.252 ± 0.241 at 50% stretch (Fig. 5(D)). By comparison, the average fiber strain in the no-explant model was slightly lower, 0.094 ± 0.103 at 25% stretch and 0.243 ± 0.230 at 50% stretch. The distribution of all fiber strains in the model was also similar in shape to the three-explant model (data not shown).

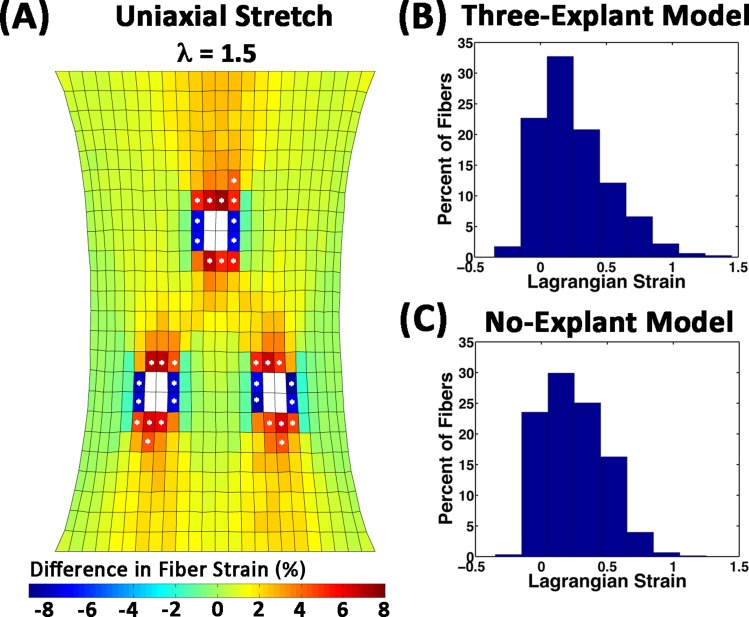
Even though the difference in the overall average fiber strain between the models was small, the presence of the compacting explants resulted in regional differences in average fiber strain, particularly near the explants (Figs. 6(A), 7(A), and 7(B)). For the three-explant model, average fiber strains were higher in elements above and below the explants, and lower in elements left and right of the explants than in the no-explant model. The starred elements in Fig. 6(A) indicate the locations where the difference in strain exceeded 4%. For the red/orange starred elements (22 elements) the average fiber strain was 0.311 ± 0.309 and 0.256 ± 0.229 in the three-explant and no-explant models, respectively. In the blue elements (12 elements) the average fiber strain was 0.170 ± 0.149 and 0.246 ± 0.227 in the three-explant and no-explant models, respectively. Histograms of fibers in this subpopulation of the elements revealed differences in the distribution profiles as a result of cell compaction (Figs. 6(B) and 6(C)). Regardless of the model or the location, the fiber strains tended to be much lower than the applied strain because fibers were able to rotate and realign towards the y-direction before stretching (Figs. 5(C) and 5(D)). A small number of fibers, however, experienced amplified strains, some as high as three times the applied strain. Network kinematics and individual fiber strains for two networks are depicted in Fig. 7. The first network (Fig. 7(C)) is from a region of high strain and fiber alignment. During compaction, the network sheared and aligned diagonally along the axis between explants. This diamond shape was maintained during stretch. The other network (Fig. 7(D)) also reorganized during compaction, but it shrank laterally with respect to the axis between the bottom explants. The fibers in this network also experience an increase in strain to accommodate the macroscopic stretch, but the reorganization differs markedly from its response to stretch in the no-explant model.

Fig. 6.

Differences in average fiber-level strain at 50% uniaxial stretch. (A) Regional variations in the average fiber-level strain in each element were apparent when the strains in the no-explant model were subtracted from those in the three-explant model. The largest differences were found in the elements around the explants (white). Differences in fiber strain that exceeded ± 4% are highlighted with a star. Histograms of the strains for all 88,728 fibers in the starred elements for the (B) three-explant model and (C) no-explant model.

Fig. 7.

Behavior of selected networks. (A), (B) Average fiber strains in each element are depicted at select instances for the (A) Three-explant model and the no-explant model (B). The red circles highlight the locations of two networks depicted below. (C) Top-view of network 1, which is associated with an area of high fiber strain. The individual fibers reorganize to satisfy force equilibrium and are color coded to indicate the level of fiber strain. (D) Network 2 is associated with an area low average fiber strain. Prior to uniaxial stretch the network volume shrinks and some fibers are under compression. The fiber strain and kinematics in these networks are compared with those developed in the no-explant model (E), (F).

4. Discussion

The models examined in this study were inspired by (but did not match exactly) the experiments of Sawhney and Howard (S&H) [44], who reported primarily on the reorganization of collagen fibers between explants in the triangular configuration. For example, the explants in the three-explant model were spaced farther apart (approximately 3.5 mm) than in S&H (approximately 1 mm). There were also differences between the model and the gels in S&H in terms of the geometry and dimensions. The model consisted of a rectangular geometry with a total volume of 0.2 cm³, whereas the gel was circular with a total volume of 1 cm³. Despite such differences, some qualitative comparisons can be made to provide some assessment of the model's predictive capabilities.

First, S&H reported that the anisotropy in collagen fiber alignment that materialized between explants developed simultaneously. The models (for all cases) also predicted an increase in network anisotropy and alignment along the axis between explants, but anisotropy in the models did not develop simultaneously between explants. Instead, alignment increased first in the ECM networks adjacent to the explants and then spread outward until meeting at the midpoint between explants, provided the distance between explants was not too far (e.g., the two-explant model in Fig. 2(A)). It is possible that the development of alignment between explants in the model proceeded gradually because the distance between explants in the model was greater than in the experiment. It is also possible that this discrepancy arose from some feature of the multiscale model, such as the ECM network geometry used. Finally, it may be that the growth of fiber alignment outward from the explants did happen in the experiment, but that the changes in fiber alignment were too small to resolve with phase contrast microscopy and a 10× objective until a sufficient amount of reorganization had occurred, which would give the appearance of simultaneous fiber alignment.

Second, the strains developed during compaction for the three-explant model were highly dependent on the boundary conditions (Fig. 3). For cases 1 and 2 where fixed boundaries were present, the maximum principal strains were directed parallel to the axis between explants. In contrast, for case 3 (Figs. 3(C) and 3(F)), where the surfaces were allowed to contract, the principal strains were generally directed perpendicular to the axis between explants. This strain pattern was consistent with the observations of S&H [44]. They found that there was significant lateral but not axial movement of glass beads embedded in the gel between explants. The qualitatively similar strain pattern for case 3 indicates that free boundary conditions better reflected the experimental conditions of a gel spread out over a coverslip than the fixed boundary simulations, and that a sufficient amount of translational freedom for the ECM network fibers was required to replicate the fiber restructuring of the experiment.

The model also predicted that a wide range of fiber strains developed in the ECM networks during uniaxial stretch. The inclusion of cell compaction changed the distribution of these strains, particularly in the regions around the cells where the highest strains were found, which could have important implications for predicting how macroscopic forces propagate down to the cellular level. In fact, the increasing use of mechanical stimulation to improve the mechanical properties of engineered tissues has necessitated the development of mechanical models that can predict the cellular mechanical environment as a function of the construct architecture, mechanical properties, and macroscopic loading conditions. Like this model, these models have generally found that incorporating microscopic heterogeneity is important and that wide range of microscopic strains can develop when a given amount of macroscopic stretch is applied to a construct [25,27,46].

A number of simplifications that were made in this model must be acknowledged. First, the same constitutive relationship, microstructure, and material properties were used for both the cellular and ECM networks as a matter of convenience, and because many of these parameters are not well defined experimentally, ECM proteins like collagen are formed and behave quite differently from intracellular cytoskeleton proteins like actin [47,48]. Other cellular details, including discrete cell attachments, cell proliferation, and cell migration, were omitted in this first-pass model (see [49–52] for models in this issue that incorporate some of these mechanisms). In addition, the method used here to simulate cell compaction was also chosen for its simplicity in implementation. It appears that uniform shrinking of fibers in the explants is sufficient for representing this aspect of the experimental system. It is far more probable, however, that cells pull on fibers until a homeostatic level of force is encountered, rather than waiting until a set level of displacement is achieved (i.e., force limited versus displacement limited) [53]. The next steps for developing this model involve modifying the details of the networks and the rules governing cell tractions so that they better reflect reality. For example, incorporating force-based rules for changing the fiber length based on target force should significantly change network restructuring and increase the development of anisotropy compared to the results presented here using uniform fiber shrinkage as a means to generate internal tension. To aid model development further, we are conducting new experiments (e.g., Fig. 1(A)) so that we can better assess model predictions and the physics we are incorporating (including aspects of these simulations, such as the different explant geometries). In conclusion, the model predictions were consistent with experiments and demonstrate the model's potential for predicting fiber reorganization in response to cell traction forces.