Short abstract
Advances in computational mechanics, constitutive modeling, and techniques for subject-specific modeling have opened the door to patient-specific simulation of the relationships between joint mechanics and osteoarthritis (OA), as well as patient-specific preoperative planning. This article reviews the application of computational biomechanics to the simulation of joint contact mechanics as relevant to the study of OA. This review begins with background regarding OA and the mechanical causes of OA in the context of simulations of joint mechanics. The broad range of technical considerations in creating validated subject-specific whole joint models is discussed. The types of computational models available for the study of joint mechanics are reviewed. The types of constitutive models that are available for articular cartilage are reviewed, with special attention to choosing an appropriate constitutive model for the application at hand. Issues related to model generation are discussed, including acquisition of model geometry from volumetric image data and specific considerations for acquisition of computed tomography and magnetic resonance imaging data. Approaches to model validation are reviewed. The areas of parametric analysis, factorial design, and probabilistic analysis are reviewed in the context of simulations of joint contact mechanics. Following the review of technical considerations, the article details insights that have been obtained from computational models of joint mechanics for normal joints; patient populations; the study of specific aspects of joint mechanics relevant to OA, such as congruency and instability; and preoperative planning. Finally, future directions for research and application are summarized.
Keywords: cartilage mechanics, finite element, subject-specific, osteoarthritis, surgical planning
1. Introduction and Motivation
1.1. Osteoarthritis.
Osteoarthritis (OA) is the symptomatic loss of cartilage in load-bearing areas of the joint, initiated by mechanical factors and sustained by the combination of mechanical and metabolic pathways. Radiographic OA is characterized by joint space narrowing, subchondral sclerosis, and osteophytes. Symptomatic OA is characterized by radiographic evidence along with persistent joint pain or stiffness [1,2].
The economic impact of arthritis has been estimated as 1%–2.5% of the gross national product in western nations, and OA accounts for approximately 85.5% of all arthritis-related costs [1,3,4]. Nearly 27 × 106 adults in the US [2], or 10% of the total population, have symptomatic OA [4]. An estimated 10% of the world population over 60 also suffers from OA [1]. OA is frequent in the knee, hip, hand, foot, and spine, but infrequent in the ankle, shoulder, wrist, and elbow [1]. There are currently no effective methods for preventing, slowing, or curing OA [1], making research important for easing the burden of this highly prevalent, chronic disease.
1.2. Mechanical Causes of OA.
OA is considered to be caused either by mechanical factors with secondary synovial inflammation [5] or by a complex interaction between mechanical and biological factors [6,7]. Therefore, the effects of mechanics at the microscale and the mechanics of cartilage at the macroscale are vital for understanding the initiation and progression of OA.
Microscale Mechanical Causes of OA.
Physiologic loading is required for maintenance of healthy cartilage, while altered loading can cause changes in cartilage structure and thereby changes in cartilage mechanical behavior [8–10]. The mechanical factors in cartilage degradation, metabolism, growth, and ossification will be reviewed briefly, and the reader is encouraged to consult other sources for more detailed reviews on this subject (e.g., Refs. [6–11]).
The effects of specific loading regimes on the physical integrity and metabolism of cartilage provide insight into mechanical loading of interest in the initiation of OA. Animal joints have been loaded to examine the effects of impact on the physical integrity and in vivo metabolic response of the articular cartilage. The effects of controlled mechanical loading on cartilage metabolism, cell viability, and cell proliferation have been studied using cartilage explants [8]. Changes in aggrecan synthesis and degradation are often used as an indication of anabolic/catabolic activity following mechanical loading [9]. An increase in aggrecan synthesis is considered a chondroprotective response to repair the extracellular matrix following damage, while a decrease in aggrecan synthesis indicates damage beyond the ability of chondrocytes to repair the extracellular matrix.
Traumatic impact loading that transfers sufficient amounts of energy (e.g., over 1 J for rabbit patellofemoral joints [12,13]) causes fissuring and softening of articular cartilage [12–16]. Impact loading in in vivo rabbit models as well as in vitro human and bovine tissue causes chondrocyte death [17–19] and changes in proteoglycan content [20]. Experimental and finite element analyses suggest that the mechanism of failure during impact loading is shear stress [21–24]. Following intra-articular fracture in a mouse model, decreases in proteoglycan content over time suggest that traumatic loading initiates a cascade of metabolic events [25]. The combination of initial gross damage and the following cascade of metabolic events is thought to result in posttraumatic OA following impact loading [26,27].
The effects of compression, tension, and shear are dose-dependent. Static compression is consistently detrimental to cartilage, with increasing inhibition of aggrecan synthesis with increasing load level [7,9]. Compression followed by release can cause increases, decreases, or no change in aggrecan synthesis, depending on the stress levels [9]. Further, compression followed by release at high stress levels may cause cell death [9]. Cyclic compression and intermittent static pressure also cause varying responses, depending on dose and frequency [9,28]. Cyclic compression above 1% strain and 0.01 Hz increases aggrecan synthesis [9]. Aggrecan synthesis is increased after cyclic tension at 5.5% at 0.2 Hz and at 10% at 1 Hz [9]. Additionally, 5% tensile loading at 1 Hz increases cell proliferation [9]. However, excessive tensile cyclic loading can also cause increased matrix metalloproteinase activity, which damages the extracellular matrix [9]. Shear loading is of particular interest, because it can be achieved while minimizing confounding factors, such as volume change and the resulting fluid and solute flow. Shear loading increases aggrecan synthesis at 1%–3% strain at 0.01–1 Hz [8,9]. Shear loading of cartilage explants above 5 MPa decreases cell viability in the superficial zone [29].
An understanding of the microscale mechanical causes of cartilage damage informs the selection of computational outputs. Further, coupling between microscale and macroscale mechanics via multiscale methods is an emerging field that can provide additional insight into the initiation of OA.
Proposed Macroscale Mechanical Causes of OA in the Hip, Knee, Shoulder, and Ankle.
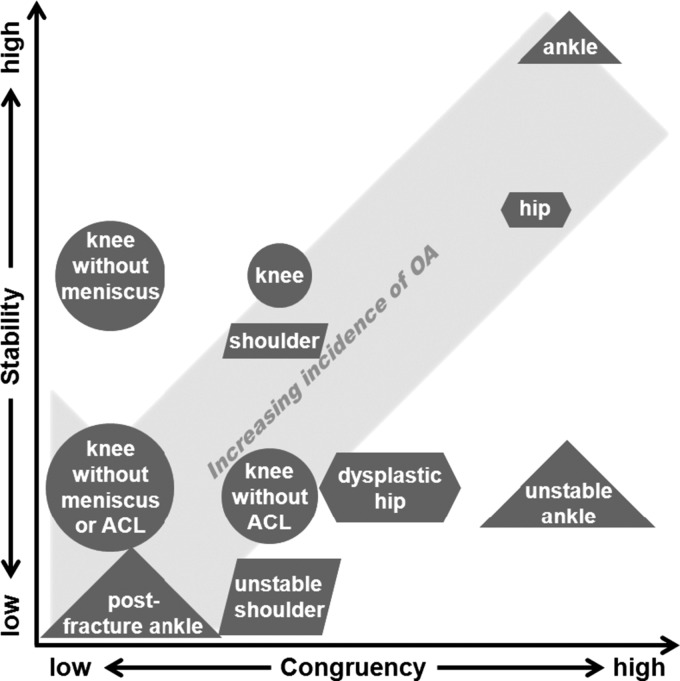
While all diarthrodial joints can develop OA, differences in the joint kinematics, cartilage thickness, cartilage mechanical properties, and articular morphology may result in variations in the pathogenesis of OA between joints. Therefore, broader insight can be obtained by examining joints that degenerate by different mechanisms. This review focuses on four joints, divided between two that frequently develop OA (hip and knee) and two that develop OA much less frequently (shoulder and ankle). Generally, the incidence of OA increases with decreases in joint stability and congruency (Fig. 1). Knee OA occurs in five percent of the population over 26 years old [4] and accounts for 67% of all OA [1]. There is a 50% chance of developing knee OA over any person's lifetime [30]. The chance of developing hip OA over any person's lifetime is lower, at 25% [31]. Estimates for ankle and shoulder OA are less widespread and reliable, as these joints are not typically included in epidemiological studies on OA. The prevalence of shoulder OA has been estimated between 0.4% and 4% [32–34]. The prevalence of ankle OA is approximately eight to ten times lower than knee OA [35].
Fig. 1.
The effect of congruency and stability on the development of OA in normal and pathologic hips, knees, shoulders, and ankles. Pathologies that make the joints less stable or less congruent tend to increase the incidence of OA. For example, removal of the meniscus in the knee primarily makes the joint less congruent, while removal of the ACL primarily makes the joint less stable.
Knee and hip OA are found in relatively large portions of the population and result from a variety of mechanical factors. Known causes of knee OA include increased loading (e.g., from obesity or manual labor), laxity, instability following ligament injury, meniscectomy, focal cartilage lesions, and malalignment [4,36–43]. Hip OA is generally thought to be secondary to bony abnormalities, such as femoroacetabular impingement and acetabular dysplasia, although some controversy remains [44–57]. The role of increased loading (i.e., obesity) in hip OA is still unclear [4,58].
Conversely, shoulder and ankle OA occur relatively infrequently. Therefore, the cause of OA in these joints has been the subject of less investigation. In the shoulder, the risk of OA increases over time with an unstable shoulder [59] and may increase with age [60]. Ankle OA is primarily caused by trauma, instability, and incongruity [3,61,62]. For instance, following tibial plafond fracture, 74% of patients develop OA [3]. Following recurrent sprain, ankle OA occurs in up to 78% of patients [3,61]. The native ankle joint is highly congruent and stable [35]. Therefore, injuries that cause ankle incongruency or instability are the primary causes of OA.
1.3. Computational Models for Examining the Mechanical Environment of the Joint.
The field of computational biomechanics offers a structured approach for studies of the mechanics of articular cartilage, providing information that would otherwise be difficult or impossible to obtain from experiments and clinical studies. Advances in the fields of constitutive modeling, computational mechanics, numerical method, and computer science have led to the widespread application of numerical procedures for the study of cartilage mechanics in basic scientific investigations (e.g., Refs. [63–72]). Using a large population, Segal et al. compared cartilage contact mechanics in 30 osteoarthritic knees with cartilage contact mechanics in 30 healthy knees [73]. This study leveraged the use of computational approaches to accomplish two things that experimental studies likely could not achieve: a large cohort size (cadaveric testing of 60 specimens would be challenging) and insight into a patient population (cadavers with specific symptoms can be difficult to obtain). Other studies have predicted cartilage mechanics through the depth of the cartilage (e.g., Ref. [74]), which is difficult to do via experiments.
To a lesser extent, the same approaches have been applied to translational research for surgical planning (e.g., Refs. [75] and [76]). Parametric analyses have evaluated variations in clinical treatments, such as perturbations in anterior cruciate ligament (ACL) graft tunnel orientation [77]. Subject-specific studies have suggested the importance of intersubject variability on preferred surgical intervention [75,78].
Depending on the physical scale of interest, several computational approaches are available and appropriate for the study of joint mechanics. Each of these approaches can lend insight to questions in basic and translational research related to OA. At the scale of multiple joints, multibody statics and dynamics can be used to predict motions, joint reaction forces and joint torques (e.g., OpenSim [79]). At the scale of the individual joint, cartilage contact mechanics can be evaluated with finite element analysis (FEA) and discrete element analysis (DEA). At the tissue and cell levels, FEA can resolve the stresses at any point in the structure. At the tissue level, variations in stress, strain, fluid flow, and solute flow through the articular cartilage thickness can be evaluated. At the cell level, stress, fluid flow, and pressure can be evaluated on the chondrocytes and in the extracellular matrix fibers. Further, coupling across scales is an emerging area in joint mechanics, with promising possibilities to offer additional insight [80].
2. Technical Considerations in Computational Models
2.1. Computational Methods for Joint Mechanics.
Computational methods can predict joint kinematics, reaction forces/torques, stresses, strains, fluid movement, ion movement, and solute movement within a continuum and thus provide insights that cannot be obtained experimentally or clinically. In general, computational approaches use numerical methods to approximate solutions to problems that do not have analytical solutions. The primary approaches that have been applied for computational modeling of cartilage mechanics are FEA, DEA, and multiscale modeling. Other types of computational methods (e.g., multibody dynamics) are common in biomechanics but are not typically used alone to predict mechanics at the cartilage level.
FEA uses basis functions with compact support to discretize a continuum structure into finite elements. The resulting discretization is used to obtain approximate solutions to the differential forms of the equations of motion and conservation laws. The continuum assumption requires that physical dimensions of structures in the tissue are much smaller than the finite elements (e.g., the size of the chondrocytes and collagen fibers in cartilage should be smaller than the elements for accurate representation as a continuum). The primary benefit of using FEA to study whole joint mechanics is the ability to accurately predict stress and strain at every point within the continuum. Although FEA is an established technique in engineering analysis, there remain many active areas of research and development, including contact algorithms, constitutive models, higher-order elements, and enhanced strain elements.
DEA, also called the rigid body spring method, represents deformable structures using discrete elements [81]. The implicit assumptions in DEA are that bones can be approximated as rigid and that deformable materials are approximated by one-dimensional discrete elements. Materials are commonly assumed to behave as linear elastic, modeled by linear springs. However, other types of discrete elements can be used, such as spring and dashpot combinations [82]. The main benefit of DEA is the drastic decrease in analysis time when compared to FEA. For example, in a hip model, the analysis with DEA took less than 1% of the time required for analysis with FEA [83]. This has led to the development and deployment of DEA methods to study large populations [73,84,85]. The main disadvantages of DEA are that results are not available at every point in the continuum, and the assumptions of linear elasticity and unidirectional deformation limit its utility to the prediction of only contact stress.
Multiscale modeling typically uses the methods of homogenization to concurrently produce stress and strain information across multiple physical scales, spanning from the macroscale to the microscale [86,87]. In the case of cartilage mechanics, the macroscale is typically the whole joint and the microscale is typically the scale of the chondrocytes and pericellular matrix. Kinematic measures (e.g., strain or the deformation gradient) are evaluated at the macroscale and passed as boundary conditions to a representative volume element at the microscale. The constitutive model at the microscale is then used to calculate stresses, which are passed back to the macroscale. This coupling is most commonly performed using first order homogenization [86]. The key assumption in multiscale modeling with first order homogenization is the principal of the separation of scales, which requires that the characteristic length at the microscale is much smaller than that at the macroscale [86]. The primary advantage of multiscale modeling is the additional information provided regarding the interactions between scales. The main disadvantage is the additional computational cost. Multiscale modeling using both homogenization methods and postprocessing macroscale kinematics as input to a separate microscale model has been employed in a limited number of studies of cartilage [86,88–91]. Multiscale methods are active areas of research and development and may allow greater understanding of the mechanobiology of cartilage in OA in the future [80,86].
2.2. Constitutive Models of Cartilage.
In continuum mechanics, the most basic material constitutive models relate kinematic measures (e.g., strain) to stress [10,92]. Therefore, constitutive models for articular cartilage are a fundamental requirement for application of computational mechanics to the study of OA. The earliest constitutive models used to describe articular cartilage were simple, due to the limited development of other models and the lack of alternative models in finite element codes [10,92,93]. Since then, cartilage constitutive models have grown in complexity and number. For example, a PubMed search for “cartilage and constitutive” yields 12 publications in the 1980s, versus 143 publications in the first decade of the new millennium. Many of these advanced constitutive frameworks are now available in both commercial and open-source finite element software (e.g., FEBio (www.febio.org) [94–97], COMSOL Multiphysics, COMSOL, Stockholm, Sweden; ABAQUS, Dassault Systèmes Simulia, Rhode Island, USA; ANSYS, ANSYS Inc., Pennsylvania, USA). The development of new constitutive models has been driven by the desire to predict new experimental observations of material behavior and to incorporate new information about material structure and symmetry.
This section briefly reviews cartilage structure and mechanics to provide background for the selection of cartilage constitutive models. In-depth coverage of these topics can be found in a previous review [10]. Because this section is intended to serve as a guide in selecting cartilage constitutive models for subject-specific analysis of joint contact mechanics relevant to OA and preoperative planning, it does not exhaustively list every constitutive model that has been proposed or applied. Instead, salient features and key developments are highlighted. More detailed reviews of cartilage constitutive models can be found elsewhere [5,98].
Review of Cartilage Structure and Mechanics.
Cartilage is a hydrated tissue composed primarily of water, collagen, and large proteoglycans (Fig. 2, left panel). Cartilage is 68%–85% water, 10%–20% collagen, 5%–10% proteoglycan, and < 5% other matrix molecules by wet weight [10]. Cartilage interstitial fluid contains dissolved electrolytes, predominantly Na+, Ca2+, Cl−, and K+ [10]. Chondrocytes account for less than 10% of the total volume of the tissue [88] and are responsible for the metabolic activity of cartilage. The chondrocytes themselves do not provide a significant contribution to the observed continuum level material behavior, although some multiscale constitutive models incorporate the effects of cell mechanics to understand stress and strain fields experienced by the chondrocytes (e.g., Ref. [99]). Collagen in cartilage is mainly fibril-forming type II collagen. The orientation of collagen varies through the depth of the tissue, with fibers oriented parallel to the articular surface in the superficial zone (top 10%–20%), fibers oriented randomly in the middle zone (middle 40%–60%), and fibers oriented perpendicular to the subchondral bone in the deep zone (bottom ∼30%). Aggrecan accounts for 80%–90% of all proteoglycan in cartilage. The primary glycosaminoglycan (GAG) side chains in cartilage are chondroitin sulfate, keratin sulfate, and hyaluronan. Chondroitin sulfate and keratin sulfate are anionic molecules, due to negatively charged sulfate and carboxyl groups. Hyaluronan is not sulfated and interacts with aggrecan and link proteins to form large aggregates that are immobilized in the extracellular matrix, thus stabilizing the extracellular matrix. Because of the anionic nature of the GAG side chains, proteoglycans control the fixed charge density of cartilage. The proteoglycan distribution, and therefore the fixed charge density distribution, varies through the cartilage depth. Aggrecan concentration is the lowest in the superficial zone and increases with depth [10].
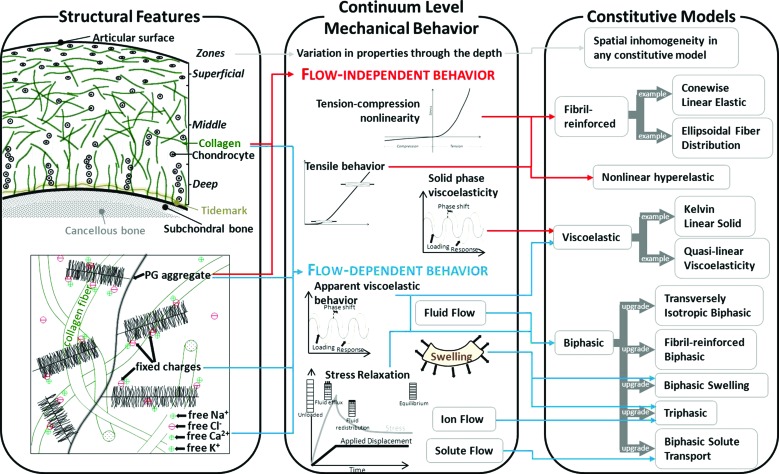
Fig. 2.
Cartilage structural features, continuum level mechanical behavior, and constitutive models. Left panel—The structure and orientation of collagen and proteoglycan aggregates drive continuum mechanical behavior. Middle panel—Key features of continuum mechanical behavior include tension-compression nonlinearity, anisotropy, viscoelastic material behavior, and swelling. Right panel—Constitutive models capture certain features of cartilage behavior. As a general rule, the simplest constitutive model that captures the behavior of interest should be chosen.
The structure of articular cartilage results in complex material behavior (Fig. 2, middle panel). Because cartilage structure and composition vary with depth, material properties also vary with depth [100–105]. The material behavior of cartilage varies between species within the same joint, between joints within species, and spatially within each joint within each species [106–111]. In theory, these variations can be captured by using inhomogeneous material coefficients with any constitutive model. Spatial variation should be used in the simplest manner required to capture the behavior of interest. For example, analysis with biphasic models demonstrated that variation in elastic moduli through the depth is necessary to predict fluid flow and stress distribution through the cartilage thickness, but depth-averaged properties can describe the overall load response [99,112,113].
Cartilage exhibits nonlinear behavior in both tension and compression. Under uniaxial tensile stress, cartilage material behavior is primarily determined by the collagen fibrils. The stress-strain curve in tension exhibits a toe region followed by an approximately linear region, due to the uncrimping of collagen fibers followed by loading of straightened fibers [10,114]. Under uniaxial compressive stress, the material response of cartilage is governed by the proteoglycan matrix and fluid flow. The modulus of cartilage in tension is approximately one or two orders of magnitude lower than in compression, a characteristic described as tension-compression nonlinearity [109]. This characteristic is important for most modes of cartilage deformation that are relevant to whole joint mechanics.
Cartilage exhibits time-dependent behavior and swelling as a result of flow-dependent viscoelasticity, due to fluid-solid interactions, intrinsic viscoelasticity of the solid phase, and fixed charge density. Time-dependent material behavior is due to the viscous drag of fluid moving through the porous solid matrix and to the intrinsic viscoelasticity of the solid matrix [10,115–118]. Cartilage swelling is caused by attraction of counterions in the interstitial fluid, due to the fixed charge density of the tissue as well as charge-charge repulsion between closely packed GAGs [10]. Collagen also has a role in swelling by constraining the matrix [119].
Solutes, including nutrients and metabolic byproducts, move through cartilage via diffusion. Solute diffusivity in cartilage is smaller than in an aqueous solution [10]. Diffusivity depends on tissue strain and decreases as the tissue is compressed [120–123]. Solute diffusivity also depends on the size of the solute. Diffusion can be enhanced by cyclic loading for large solutes, but not for small solutes [64].
A variety of constitutive models have been developed to capture the complex cartilage behavior under different loading conditions. As the complexity of constitutive models for cartilage increases, so too does the number of material coefficients and, therefore, the difficulty in determining a unique set of coefficients from experimental data. In some cases, the proposed constitutive model may be simplified to decrease the number of coefficients required to describe the model (e.g., Ref. [124]). The guiding principle in selecting cartilage constitutive models is to select the simplest model that accurately predicts the behavior of interest (Table 1) [125,126]. In addition, the reliability of the material coefficients should be considered when selecting a constitutive model.
Table 1.
Overview of cartilage material behavior as described by different constitutive models. Constitutive model features can be combined to capture specific behavior (e.g., by adding fibril-reinforcement to hyperelastic models). Refer to the text for additional detail on selecting constitutive model. For viscoelastic and multiphasic models, * denotes all behavior that can be captured (TC = tension-compression, SR = stress relaxation).
| Captured behavior → Constitutive model ↓ | Instantaneous loading | Quasistatic loading | Contact stress and area | TC nonlinear | Finite deformation | Creep and SR | Fluid flow | Ion flow | Solute flow | Swelling |
|---|---|---|---|---|---|---|---|---|---|---|
| Linear elastic | X | X | X | |||||||
| Hyperelasticity | X | X | X | X | ||||||
| Fibril-reinforcement | X | |||||||||
| Viscoelastic | * | * | * | * | * | |||||
| Discrete (spring/dashpot) | X | |||||||||
| Quasilinear viscoelasticity | X | X | X | X | ||||||
| Nonlinear viscoelastic | X | X | X | X | X | |||||
| Multiphasic/mixture | * | * | * | * | * | * | * | * | * | * |
| Linear biphasic | X | X | X | X | X | |||||
| Finite biphasic | X | X | X | X | X | X | ||||
| Triphasic | X | X | X | X | X | X | X | |||
| Biphasic with solute | X | X | X | X | X | X | X |
Elastic Constitutive Models.
For an elastic material, there is a one-to-one correspondence between deformation and stress (Fig. 2, right panel). The assumption of elasticity has been applied in many cases to describe and predict the material behavior of articular cartilage. Elasticity is appropriate for two loading regimes when modeling the material behavior of cartilage: very slow (quasistatic) and very fast (e.g., instantaneous) loading rates [98]. Therefore, the time frame or frequency of loading must be considered carefully when using elasticity to describe the material behavior of articular cartilage. Linear elastic constitutive models have been used to describe cartilage behavior, but these models are not objective (frame invariant) for large deformations. Since cartilage undergoes large deformation in vivo (e.g., Ref. [127]) and exhibits a nonlinear stress-strain response, nonlinear elastic or hyperelastic constitutive models are generally more appropriate than linear elastic constitutive models. Hyperelastic models have specific benefits over nonlinear elastic models for large deformations; for further discussion, see Ref. [128]. Compressible elastic behavior describes the response of cartilage under equilibrium conditions, as load is supported primarily by the solid matrix and fluid-solid interactions have subsided [10]. This is useful in computational models of the pathogenesis of OA, because the stress on the solid matrix can be used to evaluate when it may undergo damage. Nearly incompressible elastic and biphasic responses are equivalent under fast loading, when fluid does not have time to exude [129]. Specifically, elastic and biphasic behavior is equivalent for time steps of , where Δ is the characteristic length of the problem, is the 4th order elasticity tensor, and K is the permeability tensor. For one simplified articular cartilage contact problem where Δ was the radius of the contact patch, 5 seconds was determined, suggesting that incompressible elasticity is an appropriate approximation for loading that occurs in ∼0.5 seconds or less [129]. Incompressibility of cartilage under fast loading has been confirmed experimentally for adult bovine cartilage [130].
Linear elastic and nearly linear hyperelastic constitutive models can be used to predict cartilage contact stress and contact area, since these metrics are relatively insensitive to constitutive model descriptions (see Sec. 3 for further discussion) [131,132]. These outputs are relevant, because it has been suggested that the initiation of OA in pathologic groups results from low contact area and high contact stress [133,134].
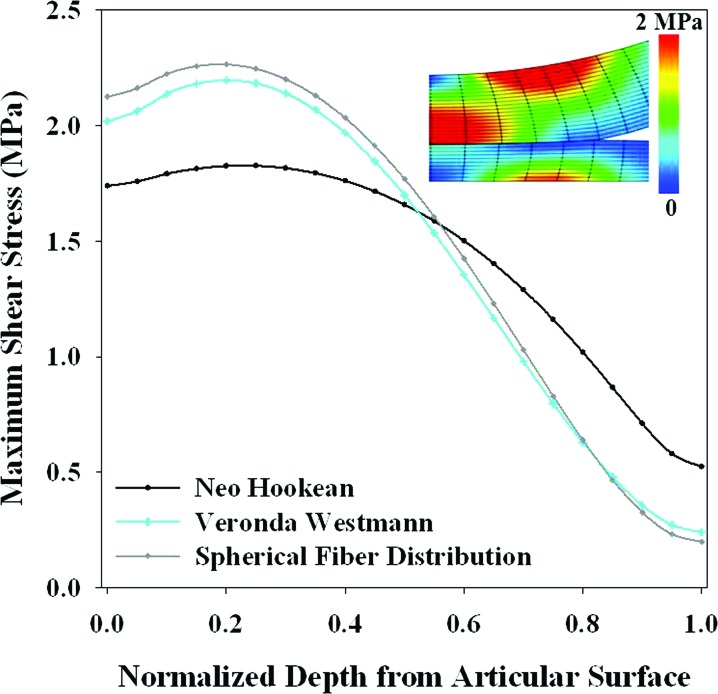
Additional features of elastic constitutive models required to accurately predict specific cartilage behavior have not been extensively explored. Therefore, parameter studies have an important role in the selection of the appropriate elastic constitutive model for subject-specific joint models. Nonlinear elastic constitutive models can be used to capture the nonlinear behavior of cartilage in tension and compression. Material anisotropy can be used to capture the anisotropy inherent in cartilage behavior. Fibril-reinforcement should be used to capture tension-compression nonlinearity [124,135–137]. Recent developments incorporating a continuous angular fiber distribution, which allows for fiber reorientation and changes in material symmetry under deformation, dramatically improve predictions when compared to discrete fiber bundles (e.g., ellipsoidal fiber distribution or EFD) [136–138]. This approach is both accurate and flexible, accommodating multiple possible material symmetries in a single framework.
In addition to describing instantaneous and quasistatic loading of articular cartilage, elasticity serves as the foundation for viscoelastic and multiphasic constitutive models, since these frameworks typically assume that a separate elastic response function exists or that the solid phase is elastic.
Viscoelastic Constitutive Models.
Viscoelastic constitutive models can be used to capture the time- and rate-dependent material behavior of articular cartilage when fluid flow, solute flow, and the separation of fluid and solid stresses are not important parameters to determine from the analysis (Fig. 2, right panel). In viscoelasticity, the current state of stress depends on both the current state of deformation and its history, which allows for energy dissipation. Because the time-dependent material behavior of articular cartilage changes during OA, viscoelasticity can be used to understand the effects of these changes [139]. Continuum viscoelastic representations have been developed using the superposition method, such as in quasilinear viscoelasticity [140], and using a Prony series expansion [141,142]. These models can describe the uniaxial tensile behavior of cartilage during stress relaxation and cyclic loading [143], as well as over the entire creep indentation series [141], and can be related to constituents in cartilage [142]. Viscoelastic models comprised of discrete elements (springs and dashpots) have limited utility in analysis of cartilage stress and strain because they are inherently one-dimensional and inconsistent with continuum deformation [98]. However, they have been used to represent fibers (e.g., Refs. [82] and [99]). In addition to describing the entire viscoelastic response of articular cartilage with a viscoelastic constitutive model, viscoelasticity of the solid matrix is sometimes incorporated in more advanced multiphasic constitutive models to yield improved description and prediction of experimental material response (e.g., Refs. [144–146]).
Multiphasic Constitutive Models.
Multiphasic, or mixture, constitutive models should be used when it is necessary to capture fluid, ion, or solute movement or when solid-phase stress and fluid-phase stress must be predicted separately (Fig. 2, right panel). These results are important in modeling the pathogenesis of OA from both a basic science and pharmacological perspective. The fluid phase supports a large portion of the load in healthy cartilage [147–149], so changes in the relative load support between the fluid and solid phases is important in the initiation of OA. Because cartilage is avascular, nutrient and drug movement occurs through diffusion from the interstitial fluid [150]. Tracking fluid and solute movement provides information regarding nutrient and drug movement, both of which can affect cartilage metabolism and therefore have a role in the initiation and progression of cartilage degeneration in response to mechanical loading.
The general framework for multiphasic models consists of several constituents: a charged or noncharged solid phase representing the proteoglycan and collagen matrix; a noncharged solvent phase representing the interstitial fluid; n charged ionic species representing free ions in the interstitium; and k noncharged solutes representing nutrients, drugs, or metabolic byproducts [64,151]. The solid phase can be described using any elastic or viscoelastic constitutive model. Permeability, diffusive drag, and solute diffusivity constants or rules govern fluid flow, ion transport, and solute transport [152]. Strain-dependent permeability and strain-dependent solute diffusivity are important considerations in cartilage undergoing large deformations [101,118,120–123,153–156]. Specific combinations of multiphasic constituents have been used to successfully describe specific sets of cartilage behavior.
Biphasic theory was the first multiphasic theory to be used for cartilage. It has been developed for infinitesimal strain as well as finite deformation, and it can describe many observed behaviors [118,153,157,158]. In biphasic theory, two immiscible, intrinsically incompressible phases are assumed: a noncharged solid phase and a fluid phase. In linear biphasic theory, the solid matrix is isotropic linear elastic and the permeability is constant [118]. Linear biphasic theory predicts compressive creep and stress relaxation behaviors under infinitesimal strain [10]. However, it cannot predict both with the same set of coefficients [157]. Additionally, linear biphasic theory cannot accurately describe time-dependent behavior in unconfined compression [159]. Therefore, the finite deformation version of biphasic theory is recommended in most cases over linear biphasic theory for capturing fluid flow and fluid-phase stress versus solid-phase stress as relevant to joint contact mechanics.
Triphasic theory builds on the biphasic theory by making the solid phase charged and including an ionic species as a third phase [154]. Triphasic theory should be selected when ionic movement is of interest. Triphasic theory has been expanded to account for anionic and cationic species, as well as more generally for n ionic species (with the inclusion of a second charged species, triphasic theory has also been called quadriphasic theory) [151,160]. Triphasic theory accounts for the time-dependent behavior and fluid flow captured in biphasic theory, as well as Donnan pressures, swelling, and ion transport through the tissues [151,154]. While triphasic theory provides information that biphasic theory does not, the two are equivalent in special cases [161]. Biphasic swelling is an alternative to triphasic theory that only accounts for the swelling behavior. The biphasic swelling model appropriately predicts tissue stresses and strains [162], but cannot predict ion transport.
Multiphasic models that include solute flow should be used to track the movement of solutes. The initial formulation included a noncharged solid matrix phase, a fluid solvent phase, and a fluid solute phase [64]. A finite deformation theory that includes the effects of solute interactions with the solid matrix has been implemented in FEBio [94]. In addition to the intrinsically incompressible assumptions made in biphasic theory, current solute mixture theory assumes isothermal conditions, negligible volume of solute, and negligible effects of solute and solvent viscosities [94]. Solute formulations can predict the effect of dynamic loading on solute uptake and the response under osmotic load [64,94]. The formulation can alternatively focus on other aspects of solute movement, including cartilage growth and biosynthesis (e.g., Ref. [163]).
The effects of fibril reinforcement on predictions with multiphasic cartilage have been explored extensively. Inclusion of anisotropy or fibril reinforcement improves predictions of time-dependent behavior in multiphasic models [125,159,164,165]. For example, a biphasic model with a transversely isotropic matrix predicts stress relaxation more accurately than a biphasic model with an isotropic matrix, and the former can also predict indentation behavior [166]. Stress predictions in the solid matrix are different in biphasic models with fibril reinforcement than in biphasic models without fibril reinforcement [165]. Other studies have added fibers as discrete elements, either as springs for elastic fibers in fibril-reinforced poroelastic models [113,167] or as spring and dashpot combinations for viscoelastic fibers in fibril-reinforced poroviscoelastic models [144,145]. While the same result can be achieved with continuum models to represent anisotropy from fibrils, discrete fibers decrease computational time and therefore can be used for efficiency after verification against the continuum description [144,146]. However, the coupling between matrix and fiber components is typically only at the nodes in finite element models. Thus, the mechanical interaction between the components is limited to simple load-sharing at the nodes.
Solid phase viscoelasticity should be included in multiphasic models when tensile loading dominates and highly accurate predictions of the transient behavior are important. Although the intrinsic viscoelasticity of collagen fibers is most important in tensile loading, it also affects the transient portion of stress relaxation and the lateral displacement in unconfined compression [144,145,159,168]. Further, biphasic poroviscoelasticity increases the types of loading that can be described using one set of coefficients, as the response of cartilage in indentation and confined compression can be predicted using coefficients fit from unconfined compression testing [159].
2.3. Model Generation.
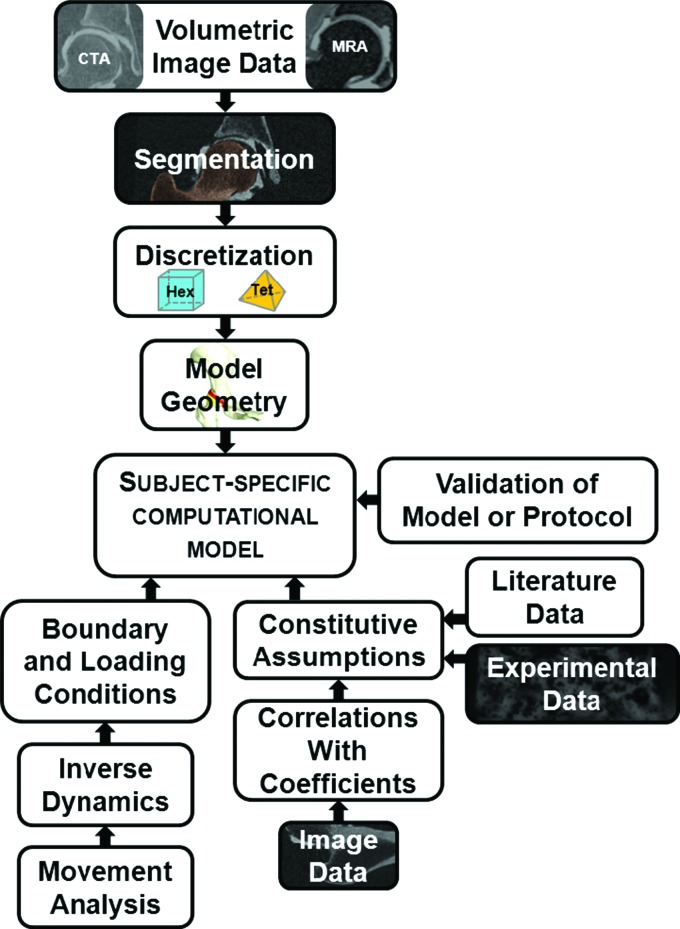
To generate subject-specific computational models of human joints, one must acquire and discretize geometry for the model, assign boundary and loading conditions and incorporate constitutive assumptions (Fig. 3). To help contextualize these requirements, this section discusses each aspect primarily with respect to the development of computational models of the hip. However, the information is pertinent to computational models of all diarthrodial joints.
Fig. 3.
High-level overview of methods for generating subject-specific computational models.
Idealized versus Subject-Specific Model Geometry.
Historically, models of human joints have used idealized geometry to describe the bone-cartilage and cartilage-cartilage interfaces (e.g., Ref. [169]). Besides providing a convenient means to define geometry, such assumptions substantially reduce the complexity of the contact interface and governing boundary conditions. As with other aspects of computational modeling, increases in computational power have enabled modeling more complex geometries. Some aspects of joint geometry can be described well via parameterized (i.e., idealized) shapes (e.g., [170–175]). However, most computational models that utilize idealized geometry do not predict realistic contact mechanics. For example, peak contact stress predictions from models with idealized hip geometry are in the range of 2–5 MPa [176,177], while peak contact stresses measured in vitro are in the range of 8–10 MPa [131,178–181]. Moreover, models that have used idealized geometry for the hip predict unicentric contact patterns, but contact patterns measured in vitro are generally complex and specimen-specific [131,177–182]. The differences in predictions of contact mechanics using idealized joint geometry likely arise due to small irregularities in subject-specific geometry being effectively “washed-out”.
Acquisition of Model Geometry.
Both in vitro and in vivo methods have been described to obtain subject-specific model geometry. In vitro methods, such as laser scanning and stereophotogrammetry, provide the most accurate modalities to reconstruct geometry [183], but they cannot be used in vivo. The advent and increased availability of volumetric imaging modalities and 3D segmentation software packages have made it possible to create detailed computational joint models of living subjects.
Subject-specific geometry can be obtained in vivo via volumetric computed tomography (CT) or magnetic resonance (MR) imaging. The cartilage-cartilage and subchondral bone-cartilage interfaces must be clearly delineated in these images to enable realistic predictions of cartilage contact stress from computational models [184]. While this task may seem trivial, imaging these interfaces is a major challenge. Joints are restricted in their movement and are often surrounded by thick musculature, ligaments, and tendons. Many joints are congruent, which helps to ensure that opposing layers of cartilage remain in contact, even when there are no external loads (besides gravity) present. Finally, the primary techniques utilized to image human joints, CT and MR, are based on entirely different physical principles, so different approaches to image acquisition are often necessary.
Clinical imaging techniques have been developed to diagnose cartilage damage or OA, but the technical considerations for acquiring image data that can be used for accurate 3D reconstructions are vastly different. For example, visualization of the entire joint contact interface is not necessary for an accurate diagnosis of cartilage damage, since the presence of a single cartilage lesion, finite region of cartilage thinning or delamination indicates that the cartilage is mechanically compromised. However, visualization of the entire joint contact interface is necessary for a faithful reconstruction of the joint geometry for modeling.
As an example of differences in protocols, consider our ongoing 3D FEA study of hip joint contact mechanics [185,186]. For CT arthrography, we routinely inject 15–25 ml of diluted contrast agent, followed directly by CT image acquisition while the hip is under traction. In contrast, clinicians typically use only 5–10 ml to detect cartilage lesions and delaminations. If less than 15 ml is injected, parts of the surface of the femoral cartilage will not be covered with contrast, rendering the scan essentially useless for generating 3D models.
High-resolution CT provides excellent delineation of bone and can be used to image opposing layers of cartilage with contrast enhancement [187–190]. CT is a popular imaging modality for modeling studies of the hip [50,76,131,134,186,191], knee [77,192–202], shoulder [203–205], and ankle [206–208]. The primary benefits of CT are excellent visualization of bone and cartilage and short scan times, which help to ensure minimal motion artifact. The primary drawbacks to CT are exposure to ionizing radiation and the invasive nature of the injection for arthrography. The benefits and risks of CT should be carefully considered when using volumetric image data to generate subject-specific models.
Many factors must be considered for generating computational models from CT image data to study OA. The most important factors are the estimated thickness of the tissue, the field of view (FOV), the slice thickness and resulting voxel size, the use of contrast and associated dilution factor for CT arthrography, the use of traction, the orientation of the joint in the scanner, and the energy settings.
The thickness of the tissue to be imaged is an important consideration, because CT is limited in its ability to visualize thin objects. This can affect the use of CT in joints with thinned cartilage or subchondral bone. A common belief is that thin tissues can be better resolved by reducing the FOV (e.g., to encompass only the joint) and improving the image resolution. Although this may sometimes be the case, narrowing the FOV may also cause the tissue to appear darker and the images to be grainier, since energy absorbed by each voxel is effectively less when the FOV is reduced and the acquisition matrix remains constant (typically 512 × 512) [209,210]. A secondary motivation for reducing the voxel size is to decrease stair-case artifact in the 3D segmented surfaces. However, this can also be achieved by resampling the image data postscan and thereby avoiding the issues that result from a narrowed FOV. The best method to establish the lower limit of resolution for CT is to quantify the full width at half maximum (FWHM) of a slice sensitivity profile [209,210]. Finally, the ability of CT to resolve thickness depends on the true thickness of the tissue. CT has a tendency to overestimate thickness when imaging thin objects, and to slightly underestimate thickness when imaging thick objects [187].
When choosing FOV and slice thickness, the goal is to achieve near-isotropic voxel resolutions and thereby ensure signal homogeneity within each voxel. The slice thickness should be chosen after the FOV is determined, taking into consideration the relationship between slice thickness and resulting radiation exposure. Most modern CT scanners can acquire images in a native slice increment of 0.7 mm or below (e.g., 0.6 mm of the pelvis in Ref. [211]).
The use of a radio-opaque contrast agent for CT is required to visualize opposing layers of cartilage in live subjects. Undiluted contrast agent appears extremely bright, which can interfere with the quantification of cartilage thickness, generally by artificial thinning due to volumetric averaging [187]. A mixture of saline and Lidocaine or Xylocaine is often used to dilute contrast agent [185]. Choosing the appropriate dilution factor involves tradeoffs between too much contrast agent, which makes the cartilage appear thinner due to volumetric averaging [187], and too little contrast agent, which makes the cartilage layers impossible to distinguish due to similar voxel intensities between the cartilage and contrast. [208]. To date, we have imaged nearly 90 human subjects with CT arthrography (both normal subjects [185] and those with bony pathologies [186]) and have found that a 33% contrast dilution (20 ml of lidocaine 2% to 10 ml of Isovue 300) provides a good compromise [185].
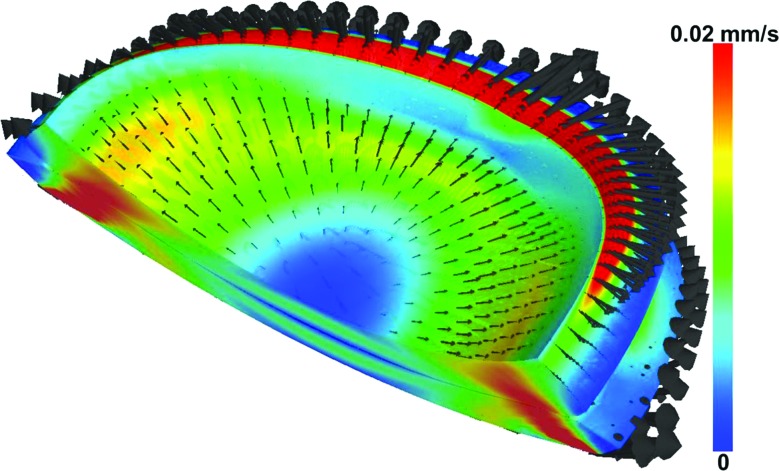
For more congruent joints, such as the hip, traction may be required to separate opposing layers of cartilage (Fig. 4). The application of moderate manual traction prior to imaging is recommended to initially “break the seal” of the hip [212]. Once this is performed, a minimal amount of traction will keep the joint space open. The amount of traction will vary on a per subject basis. Lower traction force is necessary to keep the hip distracted in patients with dysplasia (10–20 lb force), since dysplastic hips are more incongruent, exhibit poor femoral head coverage, and have lax capsules. For normal subjects [185], a greater degree of traction is required (>20 lb force), due to the high degree of congruency in normal hips.
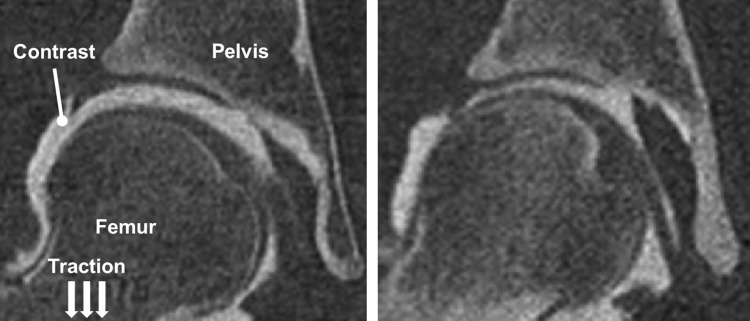
Fig. 4.
CT image data from female subjects with dysplastic (left) and normal (right) hip anatomy. Hips with dysplasia have reduced femoral head coverage and poor joint congruency. As a result, when traction is applied, greater separation is obtained between opposing layers of cartilage, thereby yielding more contrast in the joint space.
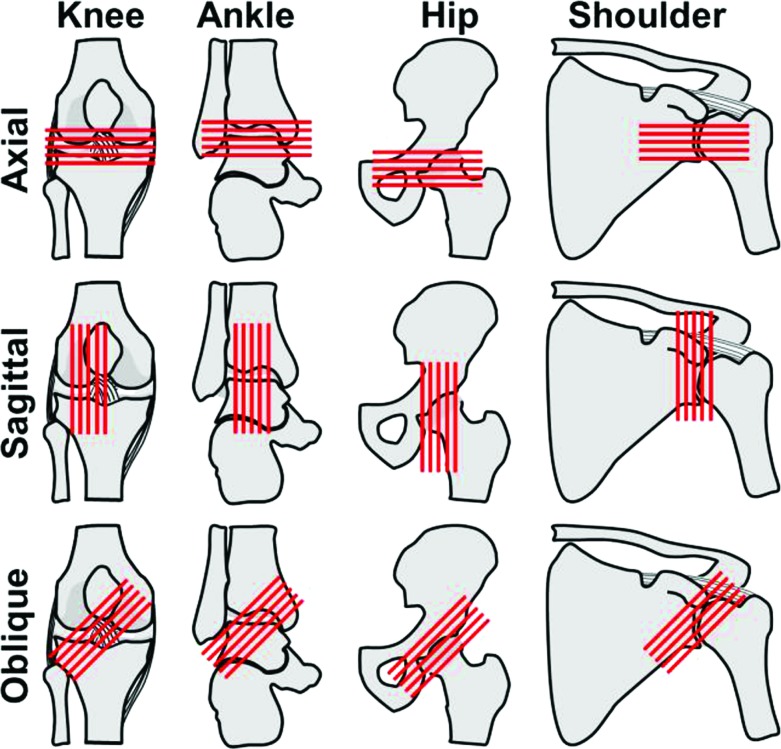
The position and orientation of the joint in the CT scanner can be adjusted for maximum signal and minimum stair-case artifact (Fig. 5). To maximize signal, the center of the joint or location of primary interest should be located as close to the center of the tube as possible. Once centered, the optimal orientation becomes a bit ambiguous. Clinical recommendations follow that the joint interface should be imaged oblique (i.e., 45 deg) to the long axis of the gantry to maximize the number of images defining the surface of the joint (i.e., “principle of obliquity”) [213]. However, this orientation produces images that exhibit large changes in cross-section between one another, causing stair-case artifact in the 3D reconstruction [214]. An alternative is to align the joint to minimize the change in cross-section between images. For the ankle and knee, this entails acquiring images in the coronal or sagittal planes, where the primary undulations are clearly shown [213]. For nearly spherical joints, such as the shoulder and hip, the stair-case artifact is unavoidable in any scan plane. Information on the expected location of cartilage contact can be helpful in choosing an orientation that provides the best image quality in that location.
Fig. 5.
Axial, sagittal, and oblique image acquisition direction in the knee, ankle, hip, and shoulder (lines represent individual slices). For both CT and MR, the chosen scan plane and orientation of the joint influences the degree in which cartilage can be visualized as well as the amount of staircase artifact that will be present in 3D reconstructions. Oblique slices (i.e., 45 deg) are preferred clinically for nonspherical joints, such as the knee and ankle, as they provide optimal visualization of the articulating surface. However, oblique slices may induce a larger degree of staircase artifact, resulting in unrealistic predictions of cartilage mechanics in subsequent contact models. Oblique slices can also be difficult or impossible to obtain and may not yield additional information for spherical joints. Images acquired axially provide worse stair-stepping artifact in the knee and ankle when compared to sagittal or coronal slices.
When using CT image data for computational modeling, energy settings should be guided by the ALARA philosophy (as low as reasonably achievable), due to ionizing radiation. Both tube voltage (kVp) and current (mAs) affect the estimated-dose-equivalent. Clinical settings should serve as a baseline for further optimization for the purpose of creating 3D models. Clinical scanners provide only a few options for tube voltage [215]. While the tube voltage is constant throughout a scan, tube current can be modulated. For example, the CARE Dose® by Siemens automatically adjusts the tube current according to the patient's anatomy to reduce unnecessary exposure. Small changes in tube voltage and current do not have an appreciable effect on thickness measurements of simulated cartilage, providing confidence that there is room to adjust energy settings to minimize exposure [216]. The size, relative location, and amount of surrounding soft tissue of a joint are the primary factors which influence energy settings. For example, the ankle has little surrounding soft tissue and therefore only requires tube currents of ∼75 mAs [189]. Conversely, tube currents exceeding 200 mAs are routinely necessary for the hip [185]. Analysts should consult with their local radiation safety board to develop CT protocols.
MR imaging without contrast provides a noninvasive alternative to CT arthrography. One of the major advantages of MR is that signal intensity is not tied to density alone. Tissues can be manipulated in many ways to generate a signal for MR imaging. Opposing cartilage layers in incongruent joints, such as the knee, can be differentiated fairly well without contrast [188]. In highly congruent joints, such as the ankle and hip, contrast may be necessary to delineate the entire cartilage-cartilage contact interface [185,187,217–220]. The limitations of MR have historically included low voxel resolution, long scan times that may result in motion artifact, the inability to image patients with certain types of metal, and the inherent complexity of MR (e.g., programmable pulse sequences). However, recent advances are starting to overcome some of these limitations, making MR imaging increasingly attractive for use in generating subject-specific computational models (e.g., Ref. [221]).
The most important factors to consider for creating 3D models of bone and cartilage from MR image data are signal to noise ratio (SNR), spatial resolution, field strength, scan protocol, use of coils, and orientation of scan plane [222–227]. High spatial resolution and adequate SNR must be balanced to obtain high-quality MR images [226]. Any increase in SNR affords the potential to increase the spatial resolution and thus improve MR image sensitivity [226]. Three-tesla (3-T) MR scanners offer improved SNR, higher spatial resolution, and, in many instances, yield shorter scan times than 1.5-T MR scanners [227]. For example, a 3-T system will double the SNR while maintaining the image resolution and scan time the same as a 1.5-T system. Similarly, a 3-T system will double the spatial resolution while maintaining the same SNR and imaging time as a 1.5-T system. A fourfold decrease in scan time can be achieved with a 3-T system while maintaining the same SNR and spatial resolution as a 1.5-T system.
Increased field strength may afford the ability to generate more physiologically realistic models to study OA, but there are also some down sides. Three-tesla MR can delineate cartilage lesions well [228], which analysts may wish to include in their biomechanical models. Variations in collagen orientation and in the concentrations of cartilage constituents can be captured in higher field systems from layers of varying signal intensity [126,226,229,230]. Although the fine details of collagen fiber orientation are not visible using 3-T MR, the general zones within cartilage can be resolved, which may be useful for assigning depth-dependent material properties. However, increasing field strength may also negatively impact image quality. T1 relaxation times must be increased by 14%–20% when doubling field strength from 1.5-to 3-T, which may increase off resonance effects, resulting in higher receiver bandwidth for some sequences, which, in turn, reduces SNR [227]. Chemical shift, fat saturation, and radio frequency power deposition can heavily influence image quality [227]. Additionally, complex tissue/field interactions can make it difficult to acquire high-quality images [227]. The precision error of volume and cartilage thickness measurements at 1.5-T (3.0% and 2.6%, respectively) are only slightly better than at 3-T (2.6% and 2.5%, respectively) [188]. Therefore, modeling requirements should be considered when selecting field strength.
The primary MR protocols to image cartilage are 3D, T1-weighted, spoiled gradient recalled acquisition (SPGR) and T2-weighted fast echo, both of which are routinely performed with and without fat suppression. The minimum T2 relaxation time in articular cartilage is short at ∼10 milliseconds [226]. As a result, T2 is the determinant of tissue contrast, even on T1-weighted and proton density–weighted images [226,231–233]. Accordingly, a moderate to fast low-angle shoot sequence with selective water excitation is frequently used to image articular cartilage [188]. For the hip, a moderate echo time fast spin echo sequencing with an effective echo of approximately 34 milliseconds at 1.5-T and 28 milliseconds at 3-T is recommended [225]. It may sometimes be desirable to obtain more uniform signal intensity in cartilage for autosegmentation. In this case, the influence of T2 relaxation can be minimized on short echo time images acquired with gradient-echo sequences or projection reconstruction techniques [226,234–236]. Numerous variations of these imaging techniques exist, due to differences in scanner hardware and user preference. Briefly, 3D, T1-weighted SPGR provides high-resolution images in relatively short scan times compared to regular spin-echo techniques. 3D, T1-weighted SPGR also shows excellent delineation between cartilage and adjacent fluids and structures, which is an important factor to consider when segmenting image data. T2-weighted fast echo sequences are faster than 3D, T1-weighted SPGR, which can result in reduced motion artifact. In T2-weighted protocols, cartilage exhibits a signal with an intermediate intensity, while surrounding fluids appear bright. The primary disadvantages of the T2-weighted protocols are that in-plane resolution may be limited and images may appear blurry.
Two types of coils are used in MR imaging: gradient coils and surface coils. Coils receive radio frequency radiation caused by direction changes in hydrogen nuclei. These direction changes are interpreted in the form of a grayscale image. Gradient coils are three orthogonal coils located within the MR magnetic field, designed to produce desired gradients in the magnetic field (i.e., transmitters). These fields are collectively and sequentially superimposed on the main field so that selective excitation occurs. Surface coils are placed directly on the patient in the region of interest as a means of increasing sensitivity to field changes. The center of the surface coil should be placed as close to the joint center as possible [237]. Purpose-built coils are available for the shoulder and knee, but a hip coil has yet to be developed. Torso coils are often used for the hip [225].
Unlike CT, MR can acquire native scans in all three anatomical planes. Like CT, the optimal scan plane depends on the joint to be imaged as well as the region where cartilage mechanics will be analyzed. As a basic rule, scans should be acquired in a plane perpendicular to the weight-bearing region of cartilage. 3D data reformations can certainly assist for clinical imaging, but generally need not be acquired, since most segmentation programs provide reformations within the segmentation mask windows.
CT arthography and MR or MR arthrography offer submillimeter accuracy for measurement of cartilage thickness. When compared to physical measurements, CT tends to underestimate cartilage thickness between 0.09 ± 0.24 mm and 0.13 ± 0.46 mm [187,189]. When compared to stereophotogrammetric measurements, measurements of cartilage thickness with CT had a mean error of 0.31 mm with 95% of the measurements within 0.62 mm, on average [238]. When compared to physical measurements, MR also underestimated the cartilage thickness by 0.14 ± 0.32 mm [239]. Direct comparison between CT and 1.5-T MR thickness measurements in the ankle demonstrated greater accuracy with CT [189]. However, additional studies are needed to clarify if higher MR field strength will result in more accurate measurements. In summary, the accuracies of MR and CT for imaging human joint geometry are comparable, but, risks aside, CT arthrography appears to have a slight advantage over MR [189,190].
Depending on the model, it may be necessary to reconstruct the shape and thickness of cortical bone. CT can clearly and accurately delineate the outside surface of cortical bone and the boundary between cortical bone and trabecular bone or marrow. Using a phantom, cortical bone thickness was measured down to 0.7 mm thick with less than 10% error [216]. Although less common, cortical bone geometry can also be obtained from MR. When compared to CT, MR was able to reconstruct 3D cortical bone geometry with maximum mean differences of ±0.23 mm and maximum standard deviations of ±0.81 mm [240]. To our knowledge, the accuracy of MR for measuring cortical bone thickness has not been determined.
Volumetric averaging is an imaging artifact that occurs due to variation in actual signal intensity within a single voxel and affects both CT and MR. Volumetric averaging is a well-known limitation of CT [187,208–210], affecting the accuracy of both cartilage and bone reconstructions [187,208,211]. Volumetric averaging in CT is affected by the use of contrast agent (for arthrography), intensity of the signal within a single pixel, as well as the size of the gradient between adjacent pixels, energy settings, spatial resolution, FWHM of the scanner, and, perhaps most importantly, thickness of the tissue. Volumetric averaging can artificially increase or artificially decrease the thickness of an object imaged in CT [187,189,208–211]. The most important factors influencing volumetric averaging in MR are the spin properties of the tissue, which dictate the intensity of any given pixel. The effects of volumetric averaging are reduced in both CT and MR with increased spatial resolution. In CT, the limitations in spatial resolution are based primarily on the FWHM of the scanner. In MR, the spatial resolution can be increased with stronger magnetic fields. To our knowledge, MR-based studies have not been performed to directly elucidate how volumetric averaging influences measurements of cartilage and bone thickness.
Segmentation and Discretization.
Segmentation is the process of identifying specific boundaries of interest in volumetric image data, and in the context of this article, discretization is the process of mesh generation. Specialized software programs, such as Amira (Visage Imaging, San Diego, CA), Mimics (Materialise, Leuven, Belgium), and Seg3D [241] enable 3D reconstruction of volumetric image data via automatic, semiautomatic, and manual segmentation. These programs vary substantially in price and layout, but all function primarily using methods such as thresholding, histogram-based segmentation, and manual segmentation of structures of interest. For 2D approaches, a segmentation mask is created for each 2D image. The 3D geometry can be reconstructed from the masks via several methods, and the result is often a triangulated surface [242]. Decimation and smoothing can be applied to refine the surface [243,244]. Accuracy of the segmented surfaces is an important consideration in both automatic and manual segmentation [187,208,238,245], as it will have an effect on the quality of model predictions. Automated methods can decrease the amount of time required for manual segmentation and can help to ensure uniformity between image datasets.
The quality of the image data dictates the amount of time that must be devoted to manual editing after segmentation. Segmentation masks that are obtained by automatic thresholding often require manual correction, which can be extremely time consuming. In a recent FEA study of cartilage contact mechanics in ten normal human hips, high-resolution CT arthrography images were segmented to define cortical and trabecular bone as well as the articular surfaces of the pelvis and the femur [185]. Each dataset required ∼60 h for segmentation and an additional 20–40 h for refinements.
An alternative approach to standard automatic and manual segmentation is active shape modeling, which has been employed to increase segmentation efficiency in soft tissue and in the knee, pelvis, and vertebrae [246–249]. In this method, an existing mask serves as a template, and it is warped to new images to provide a new mask [250]. A similar method has been used in the knee to leverage a library of segmented and discretized data to decrease the overall time for generating subject-specific models [251]. These methods are an active area of development for decreasing the time required to extract subject-specific geometry for studies of large cohorts.
Prior to use in FEA, polygonal surfaces segmented from volumetric image data must be discretized. Polygonal surfaces can serve directly as shell element geometry to discretize cortical bone and thin ligaments [131,185,186,252]. Hexahedral and tetrahedral elements are the most commonly used three-dimensional types of elements for computational biomechanics. There are many robust automatic tetrahedral mesh generation algorithms that can quickly discretize the complex shapes found in biomechanics [253–256]. Unfortunately, linear tetrahedral elements are overly stiff in large deformations and therefore are not suitable for most soft tissues [257]. Although new tetrahedral element formulations overcome many of the limitations of linear tetrahedral elements [258–262], these are not yet as available or robust as hexahedral elements. Because of the technical limitations with linear tetrahedral elements, hexahedral elements are preferred for soft tissue mechanics in general and for joint contact mechanics in particular (e.g., [78,131,185,186,206,263,264]). Hexahedral meshes are generated using the segmented surfaces in combination with user-defined splines and other boundaries and can be made using many different software packages. We have found that the commercial software packages TrueGrid (XYZ Scientific, Livermore, CA) and Cubit (Computational Simulation Software, LLC, American Fork, UT) both produce high-quality meshes. Even when using these software packages, hexahedral mesh generation can be a time-consuming task, because of the geometric complexity of many structures of interest (e.g., cartilage, meniscus, and labrum).
Boundary and Loading Conditions.
Boundary and loading conditions dictate the governing behavior of computational models. For models of human joints, examples of boundary conditions include joint orientation (i.e., “kinematic position”) and areas where the model is restricted in its movement (i.e., “kinematic constraints”). Loading conditions are generated by displacing one component relative to another (i.e., “displacement driven”), by specifying a direct force, or by using both methods. Boundary and loading conditions can be taken from the literature or estimated using methods described below.
Some degree of modeling error results from inaccuracies in the estimation of boundary and loading conditions. However, models of cartilage contact that are driven with even the simplest of boundary and loading conditions have the potential to yield considerable insight into the mechanisms of OA. If quantifying differences in cartilage mechanics between groups, using consistent boundary and loading conditions for all subjects can effectively isolate the contribution of pathology. Nevertheless, because many orthopedic pathologies include altered motion and force, it would follow that each should be incorporated into the model as accurately as possible.
In vivo joint kinematics and kinetics are most commonly determined using marker-based 3D motion capture and force-plates [265–267]. Markers are attached to the skin, most often at bony prominences. Joint kinematic models are used to represent raw marker trajectories as motion between rigid bodies (i.e., bones). This requires assumptions about the relationship between the segment coordinate system and the type of motion allowed between connecting rigid bodies. For example, the origin of the ankle may be defined as half the distance between a marker placed on the medial malleolus and one placed on the lateral malleolus. Frequently, the joint of interest is simplified in its allowable motion. Inverse kinematics compute joint angles from the captured motion data. Joint angles can be calculated in the motion analysis software or via programs with additional functionality (e.g., OpenSim [79]). One of the major limitations of standard motion capture techniques is that soft-tissue motion relative to bony landmarks can introduce errors up to 20 mm [268,269]. To gain an appreciation of the severity of this error, consider that, in patient-specific FEA of the hip, the femur only requires ∼1 to 2 mm of displacement to achieve a realistic joint reaction force of approximately three times body weight [131,185]. Soft tissue artifacts can be reduced with plate-mounted markers or marker trees [269]. However, the error may still be unacceptable for some modeling applications.
Other techniques can provide more accurate measurement of bony kinematics. Dual fluoroscopy measures joint kinematics in vivo with excellent accuracy and precision [198,270–283]. Dual fluoroscopy captures 3D joint kinematics through registration of volumetric image data and associated 3D surface reconstructions to the 2D images acquired using fluoroscopes. The technique has submillimeter accuracy for measuring kinematics of the ankle, shoulder, knee, and hip [270–277,279,281–287]. Dual fluoroscopy can provide joint angles [271] or displacements to use as boundary and loading conditions in joint models, such as those described by Wan et al. for the ankle [286]. The primary disadvantages of this technique are that it is technically challenging and includes radiation exposure. In addition, even submillimeter accuracy may be insufficient for kinematically driven joint contact models [264]. Single-plane fluoroscopy can also be used to quantify in vivo joint kinematics [240,288]. While this analysis is 2D, and out-of-plane motion is not considered, the error may be acceptable for some modeling applications where the primary movement is in a single plane [240]. Recent developments in 4D CT and open MR also offer the opportunity to quantify joint kinematics in vivo [78,289]. These techniques are in early development and are not yet widely available. However, as CT scanners become faster and MR scan acquisition times become shorter, there will likely be increased application of 4D CT and open MR in computational biomechanics.
Joint reaction forces are the net equivalent forces that act across the joint and are often used as loading conditions in joint-level computational models. Joint reaction forces include contributions from body mass, inertia, muscles, ligaments, tendons, capsule, and other tissues. Joint reaction forces can be obtained in vivo from instrumented implants in the nonnative joint or can be estimated with musculoskeletal modeling in the native joint [79,265]. Instrumented prostheses in the hip, knee, and shoulder have measured cartilage on metal joint reaction forces on the order of five times bodyweight or above, even during daily tasks of living [290–296]. While instrumented implants provide the only direct measurements of joint reaction forces in vivo, these data should be used with caution in joint-level models, since they are not a true measurement of cartilage-cartilage contact and the data were obtained from arthroplasty patients as treatment for end-stage OA.
Musculoskeletal models estimate individual muscles forces and joint reaction forces by solving the muscle redundancy problem, where there are more unknowns (i.e., forces for individual muscles) than there are knowns (i.e., ground reaction forces). Musculoskeletal models use rigid body dynamics to investigate how muscle forces produce movement of the rigid body segments via optimization methods, electromyography-driven methods or reduction methods [265,297,298]. Different optimization strategies are available, such as static optimization, dynamic optimization, and computed muscle control [299]. Although musculoskeletal modeling is predominately geared toward providing individual muscle forces, it is more appropriate to utilize an estimated joint reaction force that incorporates muscle contributions for joint-level models than it is to apply the individual muscle forces. Limitations inherent with the use of musculoskeletal models to estimate joint reaction forces are that they simplify the geometry, restrict the allowable motions, neglect cartilage, often represent muscles as single lines of action, often simplify the manner in which a muscle can generate force, and are often driven using inaccurate motion capture data. As a result, musculoskeletal models have a tendency to overestimate joint reaction forces when compared to those measured by instrumented prostheses [265].
Finally, consistent with the laws of physics, one must assign some level of kinematic constraint to computational models of joint contact mechanics this is implied. The type of constraint and the location of application will depend on the overall objective of the model. As an example, our group routinely utilizes joint angles and joint reaction forces from Bergmann and coworkers as boundary and loading conditions to estimate cartilage contact mechanics in human hips [185,186,290]. To avoid over-constraining the model, we fix the sacroiliac and pubis joints and allow the distal femur to move along a plane parallel to the shaft of the distal femur.
Constitutive Model Inputs.
In general, constitutive model coefficients must be obtained either from the literature or from laboratory experiments. Coefficients from the literature are the most common choice, but these data come with certain limitations. Because the analyst is not conducting the experiments, data from the literature should be used when there is sufficient evidence that the data are reliable and appropriate for the intended application. An additional challenge with using literature data is that the specific constitutive model of interest may not be characterized for the joint of interest. Material characterization specific to the joint is the most reliable way of obtaining coefficients, although it is more cumbersome and is rarely done in practice. This approach is required to obtain subject-specific properties [252,300], although average properties may sometimes be available in the literature.
Empirical relationships between imaging data and material coefficients have been established for the purpose of assigning site-specific properties to models of human joints. For example, the specification of bone material properties based on CT scan data is well described [211,301–303]. Although still an emerging field, measurements of cartilage anisotropy and site-specific material properties may also be obtained from MR images [229,304–308]. Using quantitative MR at 9.4-T, Nieminen et al. found that 87% of the variations in certain material properties could be explained by the MR images [305]. However, owing to the large field strengths used in these studies, the immediate impact MR may have on developing continuum level computational models to study OA remains to be seen. T1rho and dGEMRIC can provide information regarding proteoglycan content in cartilage, which can be tied to material coefficients or changes in material coefficients [223–225,227,229,305,306,309]. Collagen orientation and zonal delineations can be obtained from T2 mapping, which can then be used as inputs to the constitutive models [223,225–227,229,230,307,310]. T2* mapping has also been correlated with histological grades in cartilage [311,312], which could provide the basis for changes in cartilage structure as cartilage degenerates. The primary challenges associated with using these techniques are resolution required to obtain zonal information in cartilage, which is itself a thin tissue, and the effect of the orientation of fibers relative to the orientation of the magnetic field on the signal [226,313]. Most clinically available scanners (typically 1.5-T or 3-T) cannot obtain the same level of information as required for constitutive modeling inputs (e.g., 17.6-T MR used in Ref. [230]).
2.4. Validation.
Validation ensures that the computational model produces results that are consistent with reality. Validation and verification are separate aspects of computational modeling. Verification confirms that the equations implemented are solved correctly, while validation confirms that the correct equations are solved [314]. Most verification is part of software development, so the analyst has the responsibility to use code that has been verified. However, an additional verification step, mesh convergence, should be included in every modeling study. Previous review articles from our group have covered these topics in detail [132,315], so this section provides a brief overview of validation related to joint contact mechanics.
Validation is achieved via comparison of model predictions to experimental results. Direct validation, where the experimental and computational setups are as identical as possible, is the preferred method for validation. Indirect validation, where computational results are compared to existing experimental data, does not provide the confidence necessary for application to subject-specific modeling. Analysts must recognize the difference between model validation and model calibration. Model calibration is the process of perturbing model inputs to achieve a specific result (often to describe experimentally measured data).
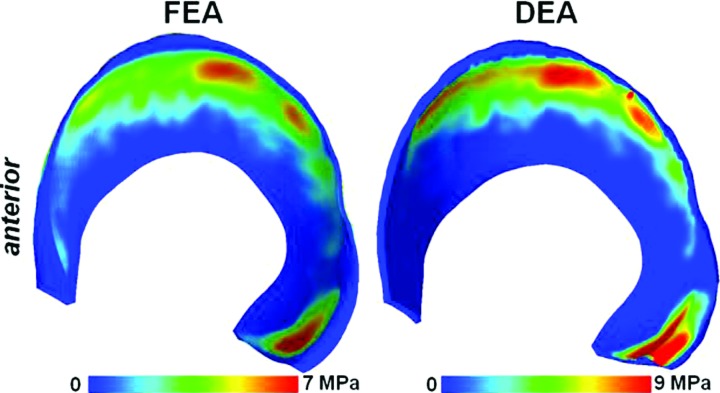
Validation should be done on the same physical scale that the model is expected to predict accurately. For joint contact analysis, there are three levels of model validation: overall displacement validation (kinematic); contact pattern (qualitative) validation; and contact stress and area (quantitative) validation. Validation on displacements of the patellofemoral joints have been used to assess the requirements of soft tissue constraints to predict accurate patellofemoral kinematics (e.g., Ref. [316]). While these models are appropriate for predicting kinematics, validation based on kinematics is not sufficient for providing confidence in cartilage contact predictions. To predict cartilage contact, model predictions should be validated against experimentally measured contact mechanics. The first step in comparing model and experimental results is qualitative comparison [131,206,317]. Preferably, validation should also compare the experimental and computational results quantitatively, either through peak and mean values or through pixel-wise comparison [131,206].
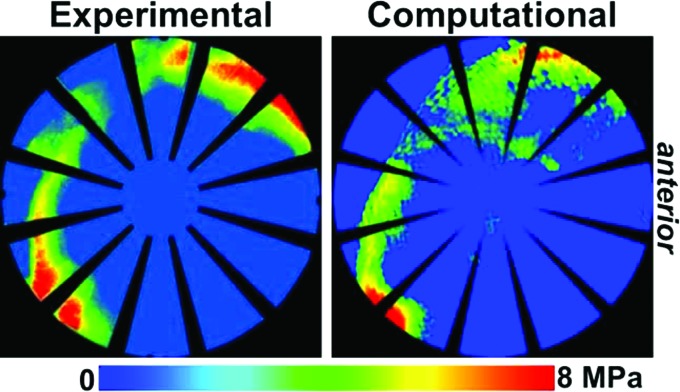
Direct validation of contact stress and area can be achieved through pressure-sensitive film and dynamic pressure sensors [318–321]. Pressure-sensitive film has been the gold standard method for experimental measurement of cartilage contact mechanics for decades, due to its reasonable accuracy and high spatial resolution [319] (Fig. 6). The primary drawbacks are the ability to only capture a single high point and the possibility for crinkle and shear artifacts [131,319]. Dynamic sensors, such as those produced by Tekscan (Boston, MA), overcome the limitation of film in their ability to capture contact pressure and area during dynamic motions. This dynamic capability is typically at the expense of spatial resolution [319]. There are several technical challenges associated with experimental testing of cadaveric joints. The joint should be kept moist throughout testing, which can conflict with the requirement for pressure-sensitive film and the electrical leads in dynamic sensors to stay dry. Further, the joint space must be opened to place the sensor between the cartilage layers, which may alter the mechanical environment of the joint [322]. Recent developments are aiming to overcome the challenge of opening the joint space by using in-fiber sensors [323]. In addition to the challenges presented by the joint, there are challenges with matching the boundary and loading conditions between the experimental and computational set-ups [131].
Fig. 6.
Validation of computational prediction of cartilage contact stress via direct comparison with experimental results indicates excellent agreement.
Because of the inherent variability within each population, validation should be completed on more than one specimen. Model results should be interpreted with the effects of experimental error and uncertainty understood, for which sensitivity studies are employed. Validation should be at least equal to the expected difference between patient populations. In the simulation of joint contact mechanics, direct validation has been reported for models of the ankle [206], hip [131,324], and knee [193]. The methods used to generate the validated models have subsequently been used to model live subjects [185,208].
2.5. Parametric Analysis, Factorial Design, and Probabilistic Analysis.
Computational models in biomechanics are not completely deterministic. Model inputs, including constitutive model coefficients and geometry, are associated with error and uncertainty [315,325,326]. Model inputs derived from experimentally measured data are described by statistical distributions (e.g., cartilage material coefficients are often represented as a Gaussian distribution) [132,327]. Uncertainty can be either aleatory (e.g., intersubject variability) or epistemic (e.g., incomplete material characterization or differences between experimental testing protocols) [315,326,328]. Parametric analysis, factorial design, and probabilistic analysis are methods for assessing the effects of error and uncertainty in model inputs on model outputs [132,315,329]. All three methods have the same goal: to quantify the effects of uncertainty in the input variables (also called factors or parameters) on the output variables (also called response variables or model results). To evaluate the effects of uncertainty, all three methods rely on repeated analysis of the computational model with varied input variables. Each model analysis with a different set of input variables is called a trial. Sensitivity factors describe the relative change in the output variable from the relative change in the input variable, and all three methods yield this information. Absolute sensitivity factors are calculated as nondimensional values and allow comparison between different variables in order to determine which input has the largest effects [327]. In addition to sensitivity factors, factorial design and probabilistic analysis quantify the interaction between multiple input variables. Probabilistic analysis can also be used to determine confidence intervals on the output variables as a result of uncertainty in the input variables.
The preferred approach to quantifying uncertainty in a particular application depends on the intended use of the model results, the ideal assessment of all possible uncertainties in input variables, and practical considerations regarding the number of trials that must be evaluated and the time to complete each trial. For example, when evaluating models for preoperative planning, the effects of uncertainty in the input variables should be rigorously assessed to provide a reliable prediction of expected surgical outcomes. One of the three methods can be employed individually or a combination can be used (e.g., factorial design to determine the most important parameters followed by probabilistic methods to obtain confidence intervals on the output variables [329]). The specimen-specific hip joint model developed by Anderson et al., which took approximately 2 h to analyze [131], will be used for timing comparisons between parametric analysis, factorial design, and probabilistic analysis to assess the uncertainty in the output variables arising from the uncertainty in three input variables (e.g., cartilage shear modulus, cartilage bulk modulus, and cartilage thickness).
Parametric analysis aims to examine the effect of uncertainty by probing the effects of variation in one input variable at a time. Selected input variables are varied from the baseline by some percentage, often in both directions. The change in output variable with each perturbation in input variable gives the sensitivity. The primary advantage of using parametric analysis is that it requires the fewest number of trials of the three methods presented here while still providing insight into the effects of uncertainty. Parametric analysis has been used in joint contact mechanics to provide insight into the effects of uncertainty in material parameters, boundary conditions, and model geometry [74,75,78,81,131,172,184,193,194,199,263,264,330–335]. To assess the effects of changing each of the three input variables in the hip model by ±10% would require the baseline model as well as six additional runs for a total analysis time of 14 h.
Factorial design is essentially a more systematic extension of parametric analysis, which includes varying multiple input variables simultaneously. The Taguchi method of factorial design has been used in subject-specific computational modeling of the knee [263,264]. This method assesses the outputs based on levels of the input variables. For example, in a two-level factorial design, models would be analyzed with each input variable at its minimum and maximum value, with all possible combinations between variables. So, for a two-level factorial design with three input variables, a total of 23 trials would be required. For a three-level factorial design, models would be analyzed with each input variable at its minimum, maximum, and midpoint value. Because variables are varied simultaneously in factorial design, the method yields insight into interaction effects. This is the primary advantage of factorial design over parametric analysis. The primary drawback is the increased number of trials. To complete a two-level factorial design on the hip model would require a total run time of 18 h. To complete a four-level factorial design on the hip model would require 130 h of run time. As an alternative method for decreasing the number of trials, a combination of levels could be used. For example, Yao et al. used two stages of factorial design to first evaluate the most important input variables and then evaluate the effects of those input variables in greater detail [263].
Probabilistic analysis provides forward uncertainty propagation by sampling statistical distributions of input variables to create statistical distributions of output variables [325,328]. In contrast to factorial design, where each level is sampled regardless of its probability of occurring, the input variables in probabilistic analysis are sampled based on the probability of a certain value occurring. The advantage of probabilistic analysis is that confidence bounds on the output variables can be generated [325]. The disadvantage is the drastically increased number of trials required [328]. Two types of probabilistic analysis methods that have been applied in computational biomechanics are the Monte Carlo method and the most probable point method [336–338]. Monte Carlo is the gold standard because, given sufficient trials, it will capture the variation in the output variables accurately. Monte Carlo analysis is typically required in the case of nonmonotonic functions, such as contact mechanics [325]. Further, it is recommended that Monte Carlo analysis be used for benchmarking any new solution [325]. Variations on Monte Carlo analysis aim to decrease the number of trials required by altering the sampling of input variables. Most probable point methods and variations (first-order reliability method, second-order reliability method, mean value, and advanced mean value) are approximate methods that reduce the number of trials compared to Monte Carlo methods [327,339]. Probabilistic analysis can be completed using commercial software (e.g., Nessus from Southwest Research Institute, Texas, USA and ANSYS from ANSYS Inc., Pennsylvania, USA), research software (e.g., DAKOTA from Sandia National Labs [328]), or custom software written by individual investigators. Monte Carlo analysis typically requires thousands of trials to achieve useful results [325]. To complete Monte Carlo analysis with 2000 trials in the Anderson et al. paper would take ∼4000 h (about 5½ months!). Monte Carlo analysis with Latin hypercube sampling has been used to assess the effects of material uncertainties in motion and load response predicted by subject-specific finite element models in the human cervical and lumbar spine [336,337] as well as to assess the effects of shape variations on intradiscal pressure, range of motion, and facet joint contact force [338]. For additional detail on background, implementation, and use of these methods, the reader is referred to standard texts (e.g., Refs. [340] and [341]). For additional detail on applying these methods specifically to computational biomechanics, the reviews and frameworks presented by Laz and Browne [325] and by Roy and Oberkampf are recommended [326].
2.6. Computational Model Outputs.
Computational models of joint mechanics provide a myriad of output parameters. Selecting, displaying, and reporting the appropriate values of interest are important components of the design and execution of modeling studies. Outputs can be scalars, vectors, or tensors. Scalar values include temperature, solute concentration, contact stress, fluid pressure, and solid pressure. Scalars are typically viewed as fringe plots, which allows visual assessment of patterns as well as for comparison between groups or parameters (e.g., for comparison between two constitutive models in parameter studies) (Fig. 7). The scale should be set such that the full range of colors or intensities is utilized. When comparing between fringe plots, the scales should be identical to ease interpretation. Maximum, minimum, and average scalar values can also be reported for numerical evaluation. Vectors, including displacement, fluid velocity, and solute flux, can be viewed using vector plots (Fig. 8). For symmetric second order tensors, such as stress and strain, decompositions or components can be viewed using fringe plots or vector plots. Decompositions into eigenvalues and eigenvectors can be viewed as scalars and vectors, respectively. Scalar invariants based on the eigenvalues of these tensors have utility, because they do not change under basis transformation. Commonly used invariants include the principal values (eigenvalues), pressure, maximum shear stress and strain, and effective (von Mises) stress.
Fig. 7.
Solute concentration over time in a 2D problem demonstrating the visualization of a scalar result using a fringe plot. The upper cylinder was initially at a uniform solute concentration of 0 mM, and the bottom plate was initially at a uniform solute concentration of 1 mM. The cylinder was displaced into the plate over the first second of analysis and then allowed to relax (based off analysis by Ateshian et al. [96]; solute solubility κ = 1, osmotic coefficient Φ = 1, diffusivity = 5 × 10–4 mm2s–1, free diffusivity = 10–3 mm2s–1, permeability 10–3 mm4N–1s–1, neo-Hookean solid matrix with E = 1 MPa and ν = 0.3, 3-mm radius of upper disk, displaced downward 1.5 mm, analyzed in FEBio).
Fig. 8.
Combination vector and fringe plot of fluid flux in a biphasic analysis (geometry from Ref. [97]). Contact between the two layers forces fluid out radially. The vector plot provides information regarding the direction of fluid flow, which is not clear from the fringe plot alone.
Results can be evaluated at any location in the cartilage in FEA models, and evaluation on both the articular surface and through the thickness may be important in understanding the pathogenesis of OA. For example, cartilage often fails at or near the boundary with subchondral bone [23,342]; therefore, results at the subchondral bone and through the cartilage thickness are of interest (Fig. 9).
Fig. 9.
Maximum shear stress through the thickness as a function of nearly incompressible hyperelastic constitutive model for a plane strain analysis of a cylinder (outer radius of 20 mm, thickness of 2 mm) contacting a plate (thickness of 1 mm). The fringe plot shows results for the spherical fiber distribution model, because minimal differences were visible in the fringe plot between constitutive models. Shear stress was evaluated in the cylindrical layer at the location of peak contact stress (left border of fringe plot). The neo-Hookean constitutive model has both a lower maximum value at the contacting surface and a smaller change in maximum shear stress through the thickness of the layer. The Veronda Westmann and spherical fiber distribution constitutive models both captured larger maximum shear stress below the contacting surface than on the contacting surface. The differences between the neo-Hookean constitutive model and the other two combined with the similarity between the Veronda Westmann and spherical fiber distribution models suggests that material nonlinearity, not fiber reinforcement, is a salient feature for capturing maximum shear stress gradients through the thickness with this simplified geometry.
Stress is of particular interest in models of OA, because stress above certain thresholds affects the physical integrity and metabolism of cartilage (see Sec. 2.2). Pressure, calculated as the average of the three principal stress components, is another useful stress invariant in understanding the pathogenesis of OA. Fluid and solid pressure can be evaluated separately in biphasic and multiphasic analysis. Stress results can also be integrated over time or across components (e.g., integrating first principal stress and maximum shear stress) to create a composite measurement. Postprocessing of contact stress via chronic-overload analysis has highlighted differences between normal and pathologic groups [134,207,343].
Kinematics variables are measurements of the deformation experienced by the tissue. Kinematics variables include displacements, velocities, and strains. Motion of bones is of interest in the context of joint stability [169] and has been employed extensively in the patellofemoral joint (e.g., [339,344]). Strain invariants, like stress invariants, can provide insight into the pathogenesis of OA via comparison with values that are expected to cause physical damage or metabolic change.
3. Insights From Computational Models
3.1. Understanding Normal Joints.
Understanding cartilage mechanics in normal or control populations is an essential first step in using computational models to study OA. Predictions in control populations serve two purposes. The first is to understand the variation in cartilage mechanics within the control population. The second purpose is to serve as a baseline for comparison against pathologic groups. Using a group of control subjects rather than an individual subject allows statistical comparisons between the two groups, greatly strengthening the insights provided by the models. Traditional statistical methods should be used to determine the required sample sizes. Because computational efficiency is an important consideration for modeling large groups, researchers have developed several efficient analysis methods. Anderson et al. developed DEA methods explicitly for the purpose of modeling large populations [84]. Rigid contact has been used to predict subject-specific contact mechanics in the patellofemoral joint, which were in reasonable agreement with deformable contact at a lower computational cost [344]. These methods have been applied in the knee [73,85] and can be used further in future studies.
Inclusion criteria for control populations should be carefully crafted. At a minimum, control subjects should be free of degenerative cartilage changes. This criterion alone provided a control group for comparison against subjects who did develop OA at 15-month follow-up [73]. Additional criteria for the control group should be clinically driven, depending on the pathology of interest and the patient population that will be used for comparison. For example, Harris et al. used subjects who had normal hip morphology on 2D radiographs for controls against which to compare subjects with pathologic hip morphology [185]. Yang et al. used a subject with normal varus-valgus alignment in the frontal plane for a control subject in studies of tibiofemoral contact [345,346]. In addition to the definition of pathology, which will be used to select the patient group, the control group should be selected to minimize other confounding factors. Specifically, age, gender, weight, height, and body mass index of the control population should be matched as closely as possible to the pathologic population. A second approach that has been used in the knee is comparing regions of each knee that did degenerate to those that remained healthy [85].
Studies examining groups of control subjects indicate that contact patterns are subject-specific, primarily due to geometric variability between subjects. A study of ten normal hips demonstrated intersubject variability in contact patterns (Fig. 10). While the anatomical position of the joint and the direction of the applied load had some effects on contact pattern, contact patterns were more consistent within each subject across loading scenarios than within each loading scenario across subjects. This study also elucidated regional differences in average contact stresses, providing numerical insight into the regions that support load during certain activities in normal hips [185]. Specimen-specific FEA models of the knee support the conclusion that subject-specific geometry is perhaps the single most important factor for predicting computational contact mechanics. Specifically, applying identical variations in the angle of applied quadriceps force caused different shifts in patellofemoral contact pattern for four different specimens in both experimental and computational trials, because each subject had unique geometry [317]. Variations in subject-specific geometry also influenced knee contact patterns in both the neutral position and the changes in cartilage stress following changes in femoral rotation [78]. Similarly, subject-specific FEA has demonstrated variation between subjects in normal ankles [206,207]. Additional studies have used single normal subjects for comparison to specific pathologic groups or for parameter studies and will be discussed in the following sections.
Fig. 10.
Contact pressure patterns in the human hip of ten normal subjects demonstrates large intersubject variability.
3.2. Understanding Patient Populations.
Similar to control populations, patient populations must be selected with care in an attempt to isolate the effects of pathologies of interest. Subjects with OA can be evaluated as a patient group, although probable changes in cartilage material properties should be addressed when modeling osteoarthritic subjects. Most orthopedic diseases, including those that predispose to OA, fall along a spectrum (e.g., hip dysplasia falls along a spectrum for both severity of undercoverage and incongruency [347]). As an example of selecting a patient population, hips with acetabular dysplasia can be characterized based on the lateral center-edge angle. Depending on the study, hips with lateral center-edge angles below 25 deg [348] or below 15 deg [349] could be considered dysplastic. Therefore, one approach in selecting patient populations would be to narrow the inclusion criteria to a specific portion of the spectrum of disease. In the case of dysplastic hips, inclusion criteria could be selected to evaluate subjects with borderline dysplasia characterized by center-edge angles between 20 deg and 25 deg or severe dysplasia with center-edge angles less than 5 deg. While both of these groups are within the broad category of patients with dysplastic hips, focusing on specific portions of the spectrum of disease would provide a more homogeneous patient group. An additional consideration in selecting patient populations is the reliability of radiological and clinical measurements. Measurements used to identify patients in the clinic may not be sufficiently reliable for selecting a homogeneous patient population (e.g., Refs. [350] and [351]). For example, bony pathologies of the hip have recently been characterized as complex three-dimensional morphologies [352], but diagnosis is typically done using 2D radiographic projections. When developing inclusion criteria for a patient population, the spectrum of disease and the reliability of measurements used to characterize the disease should be weighed against the expected outcomes of the study and the reality of how many patients can be recruited within certain criteria.
Studies comparing groups of pathologic and normal subjects demonstrate the power of subject-specific analysis in revealing differences between groups in cartilage contact mechanics. Russell et al. [134] and Hadley et al. [343] demonstrated elevated contact pressure in dysplastic hips after reduction. Specifically, there were differences in chronic overload for those hips with poor outcome and trends towards significant correlations with Severin score [134,343]. In congenital deformities, such as dysplasia, the control population should be recruited from another population, because the deformities are likely to exist in both joints. However, the contralateral joint can be used as a control in analyses of joints that rarely develop OA, except following injury. This principal was employed in the subject-specific ankle FEA of 11 subjects, each with one postfracture ankle and one normal ankle. Intact ankles had lower peak contact stress exposure and higher contact area [208]. The results of postfracture chronic overload in the ankle also correlated with outcomes at 2-year follow-up in three subjects [353]. Using computationally efficient DEA to examine knee contact mechanics in 60 knees, Segal et al. showed elevated contact pressures in 30 knees that developed OA at 15 months follow-up versus 30 knees that did not develop OA [73]. In a separate study, where both control and patient knees were evaluated as regions in the same 38 subjects, elevated contact pressures occurred in regions that had worsening bone marrow lesions and cartilage thinning at 30 months follow-up [85]. These studies of contact in the knee employ the DEA framework to study the largest populations to date.
While these studies provide powerful insight into the differences in cartilage contact stress and area, only one study that we are aware of has reported results for other measurements in a large group of patients. Farrokhi et al. [354] coupled subject-specific knee joint geometry with subject-specific kinematics and kinetics in a study comparing ten female subjects with patellofemoral pain to ten female subjects without patellofemoral pain. Similar to the results for groups above, subjects with patellofemoral pain had larger peak and mean contact stress on the patella than normal subjects. Additionally, subjects with patellofemoral pain had larger octahedral shear stress on the patella than normal subjects [354]. Both the coupling of subject-specific geometry with subject-specific kinematics and kinetics as well as the reporting of shear stress for a group of subjects represent important methodological advances that should be employed in future studies.
3.3. Effects of Joint Incongruency, Instability, and Focal Cartilage Damage.
Insight on the effects of joint congruency has primarily been provided by computational models of meniscus damage and removal. The meniscus in the knee functions to make the relatively incongruent tibiofemoral joint more congruent and thus distribute the loads transferred across the joint more efficiently [38,39,355–357]. Models are useful in understanding the effects of the meniscus, because they can examine more combinations of factors than are feasible experimentally and can provide results that cannot be measured experimentally, such as fluid pressure and shear stress through the cartilage layers. Removal of the meniscus decreases the fluid pressure in the cartilage immediately adjacent to the meniscectomy and causes slower overall fluid dissipation [358,359]. Consistent with experimental results, meniscus removal increases cartilage contact pressure [355,360]. As an extension from experimental results, computational modeling has also demonstrated that meniscus removal increases Tresca stress [199]. Model results have shown that, while the maximum stresses are on the medial tibia, the lateral tibia experiences larger changes in cartilage contact stress following meniscus removal than the medial tibia does [345,361]. Using subject-specific frontal plane alignment and kinematics in knee joint models with simulated meniscectomies, it was demonstrated that the precise effects of incongruency on contact mechanics varied between subjects with different varus/valgus alignment [362]. Taken together, these results show that the effects of induced incongruency are complex and include altered contact pressure, shear stress, and fluid movement in the joint.
The importance of soft tissue stabilization on joint contact mechanics has been demonstrated through subject-specific modeling of the knee, the shoulder, and dysplastic joints. The human knee joint is stabilized via soft tissue, including the menisci, ligaments, and tendons, and retinacula [363]. Parametric analyses have demonstrated that the constitutive assumptions regarding these soft tissues can drastically affect joint contact mechanics (see Sec. 3.4). Further, release of the lateral vasti moved patellofemoral contact medially [331]. The effect of the ACL has been evaluated in a 3D model of the knee joint. The peak pressure on the cartilage increased as the ACL stiffness decreased [208]. Additionally, ACL rupture caused increased tibial translation, highlighting the importance of the ACL on knee joint stability [364]. An FEA study of the shoulder demonstrated increased pressures in an OA shoulder compared to a normal shoulder, as well as more posterior contact in the OA shoulder. This shift may correspond to the posterior wear seen in OA shoulders, likely the result of instability [203]. In another study, the shoulder was stabilized fully through the surrounding soft tissue. This study provided additional evidence that the rotator cuff is the primary stabilizer in the joint [204] and can serve as a baseline for examining instability conditions, including rotator cuff tear. Dysplastic joints, including shallow acetabuli in the hip and shallow trochlear grooves in the patellofemoral joint, exhibit inherent bony instability. In a 2D DEA model of the knee, the effect of soft tissue constraint on various trochlear groove depths was assessed. This study demonstrated that, in a normal trochlear groove, the retinacula had no effect on patellar kinematics, but in a shallow trochlear groove, the retinacula were vital for maintaining stability [365]. Unstable dysplastic hips reduced at infancy have higher chronic overload stresses with decreased long-term outcome and in comparison to a normal hip [134,343]. In a single comparison of a normal hip to a dysplastic hip, the acetabular labrum was found to support more load in the dysplastic hip [186]. This suggests that soft tissues in the hip have an enhanced role in stability in dysplastic hips similar to that in dysplastic knees. Overall, these studies indicate that soft tissue is an important consideration for joint stability in joints that are inherently unstable and that damage to those stabilizing mechanisms can affect cartilage mechanics.
The relative influence of instability and incongruity in postfracture ankles with residual incongruity is unclear. To separate the effects of the two factors, Goreham-Voss et al. examined four cases of instability and incongruity in noncontact FEA, representing articular incongruity [62]. Contact pressure distributions determined experimentally were applied to a 2D plane strain model, and resulting fluid pressure, normal solid stress, and tangential solid stress were evaluated over time. A healthy ankle and an ankle with an anatomically reduced fracture were simulated for congruent, stable control cases. A postfracture ankle with a 2-mm step-off incongruity was simulated in one case with stable loading, where the load did not cross the incongruity, and in another case with unstable loading, where the load did cross the incongruity. The incongruous ankle without instability exhibited higher fluid pressure, normal stress, and tangential stress than the two congruent cases. The incongruous ankle with instability exhibited higher pressure and stress and drastically higher temporal gradients in fluid pressure, normal stress, and tangential stress. These results indicate that the incongruent ankle does have altered cartilage mechanics, but that greater variations from baseline occur as a result of instability. This study demonstrates the use of FEA in a controlled case to isolate the effects of instability versus the effects of incongruity.
The effects of focal lesions on cartilage contact mechanics depend on lesion size and location. In a 3D model of the knee, focal lesions 1.76 cm2 and larger created stress concentrations adjacent to the lesion [200]. Also, focal lesions on the medial condyle increased stress in the lateral condyle [200]. The effects of focal defects in a load-being region were more pronounced than in an unloaded region [200]. When comparing the effects of focal defects in each condyle in a 3D knee model, a defect of equal size in both condyles created larger peak contact pressure in the medial condyle than in the lateral condyle [197]. As with meniscus damage, computational models of focal cartilage defects are able to parametrically examine more cases than feasible experimentally. These additional variations demonstrated that lesion size and lesion location affect the changes in cartilage mechanics in the adjacent and distant cartilage.
While the importance of using subject-specific geometry has been demonstrated (see, e.g., Ref. [319] and the above paragraphs), there is a clear role for computational models with idealized geometry to understand the general effect of well-defined changes to geometry, material properties, and boundary conditions. Because of the challenges associated with separating individual influences, such as the relative effects of instability and incongruency in the pathogenesis of ankle OA, idealized models can be used to help interpret these effects. As an example, hips with acetabular dysplasia are often both unstable and incongruent, and congruency is an important factor in predicting the success of surgical intervention [52,366–370]. Using idealized spherical geometry, Chegini et al. were able to isolate the effects of instability on contact pressure elevations in dysplastic hips [371]. Similarly, Genda et al. used idealized geometry to demonstrate that the peak contact pressure correlated with femoral head coverage in spherical hip joints [176] and that the pressure tended to be on the anterior-lateral edge of spherical dysplastic hips [182]. Mathematical modeling has further corroborated these results in idealized hips (e.g., Refs. [372–375]). Idealized 2D models have also been used to demonstrate that peak fluid pressure and peak tensile strains increase without the labrum or meniscus [376,377] and that these effects depend on the congruency of the contacting layers [378].
3.4. Insights From Parametric Analysis in Whole Joint Models.
The assumptions of constant cartilage thickness and idealized joint geometry should be interpreted carefully, since these assumptions can lead to inaccurate predictions. In the human hip, spherical and ellipsoidal contact surfaces predicted lower contact pressures, higher contact areas, and contact patterns in poor agreement with subject-specific predictions [172,184]. Idealization of the subchondral bone geometry with subject-specific articular surfaces reduced contact stress, indicating that the geometry at both the articular and bony surface of the cartilage is important for accurate contact predictions [184]. The use of average cartilage thickness is an attractive simplifying assumption in computational models, because it allows the use of imaging modalities, such as noncontrast CT (see Sec. 2.5). FE predictions of contact area and pressure in the human ankle with constant cartilage thickness were in good agreement with experimental results [206]. However, these results were not compared directly to model results with subject-specific cartilage thickness. In parametric analyses of the human hip, constant cartilage thickness with subject-specific bones provided better predictions of contact than spherical or ellipsoidal joints, but did not provide contact that was consistent with subject-specific cartilage thickness [184]. Similarly, comparisons between subject-specific and constant cartilage thickness in the patellofemoral joint indicated that subject-specific cartilage thickness is preferred [75].
Sensitivity of model results to soft tissue boundary conditions has been explored extensively in the knee, because there are many soft tissue constraints. In several studies, both the stiffness and the material symmetry of menisci affected cartilage contact patterns [194,199]. The stiffness of the knee ligaments affected patellofemoral contact stress [330]. Additionally, the representation of the quadriceps muscles as just the rectus femoris resulted in different patellofemoral contact patterns than representation of the entire quadriceps [331]. Taken together, these results indicate that the required level of detail with which the soft tissue stabilizers are represented should be evaluated on a model-specific basis.
The assumption of rigid bones and the effect of subchondral bone thickening have been explored extensively in the hip and knee, with differing conclusions. Models of the hip have been fairly consistent in concluding that bones should be modeled as deformable and that the subchondral bone properties and thickness are important [74,131,184,335,379]. In comparisons with experimental measurements of hip contact pressure and area, rigid bones elevate predictions of contact pressure when compared to predictions made with deformable bones [184,131]. However, discretizing just the cortical shell with position-dependent thickness is sufficient, as the trabecular bone has minimal effects on contact patterns [131]. These results reiterate results found early in the use of FEA for joint contact analyses, where rigid bones were found to predict unrealistic pressure patterns in the human hip [335]. The effects of subchondral thickening have been assessed in 2D and 3D hip models. Subchondral thickening had minimal effects on cartilage contact pressure, but affected pressure near the bone [74] and affected the Tresca stress at the cartilage surface [379]. In the knee, using rigid bones changed results less than 2% when compared to predictions with deformable bones [193]; therefore, knee contact mechanics appear to be less sensitive to this modeling assumption.
The effects of other boundary conditions have been parametrically explored in the knee. When using kinematic positions derived from MR scans, variations on the order of uncertainty from MR image data resulted in large differences in contact predictions [264]. Similarly, constraining tibiofemoral varus/valgus and internal/external rotation changed contact parameters up to 19% in predictions of knee contact mechanics in single-leg stance [193]. Both the quadriceps force and the flexion angle influence contact force and contact area in the patellofemoral and tibiofemoral joints. However, the relative effect of quadriceps force varies depending on the tibiofemoral flexion angle [333]. Variations in femoral internal rotation from subject-specific alignment altered the contact mechanics in the patellofemoral joint [78]. These results suggest the need to examine the effects of boundary conditions on a model-specific basis.
Computational models employing linear elastic constitutive models have demonstrated that average cartilage contact pressure and contact area are fairly insensitive to material coefficients. In a validation study of a human hip finite element model, Anderson et al. demonstrated that changes of ±50% in the shear modulus of cartilage described with a neo-Hookean constitutive model only changed average pressure and contact area by around ±10% but changed peak contact pressure around ±30% [131]. Similarly, changes in cartilage Young's modulus and Poisson's ratio in the knee changed surface contact pressure more than von Mises stress [332]. Idealized and subject-specific comparisons between FEA and DEA demonstrated that DEA can be used to predict accurate contact mechanics, again reiterating the relative insensitivity to cartilage constitutive description [81,84,334] (Fig. 11).
Fig. 11.
Contact comparisons between a subject-specific FEA model (left) and a subject-specific DEA model (right) indicate good agreement in contact pattern, while the DEA model runs in less than 1% of the time required for the FEA model. This makes DEA an attractive option for analyzing large cohorts (adapted from Ref. [83]).
Recent analyses have demonstrated the large influence of fiber-reinforcement and assumed fiber orientation in cartilage constitutive models on cartilage strains in subject-specific 2D and 3D FEA. Strain and fluid displacement patterns vary as a function of the assumed fiber orientation, with fiber orientation held constant through the cartilage depth in the human knee [221,380]. Variations in the relative depth of the three zones of cartilage drastically affected model results in 2D FEA of the knee [307]. Subject-specific boundaries between the cartilage layers were obtained from MR with 0.322-mm spatial resolution, and a change of 2 pixels in the location of a zonal boundary caused the fibril strain to increase up to 136% [307]. Using a 3D model of the knee, the effects of vertical fibers in the deep zone and the effects of the tangential fibers in the superficial zone were assessed. The vertical fibers in the deep zone were important for reducing strains at the osteochondral interface, while the fibers in the superficial zone decreased tangential strains [381]. While some of these results may seem intuitive (e.g., tangential fibers decreasing tangential strain), the potential for interplay between subject-specific geometry and the effects of constitutive models requires the use of parametric analyses in whole joint models for determining the relative importance of constitutive model assumptions.
Fiber-reinforcement and transverse isotropy also affect shear stress and fluid pressure. In a 2D model of the knee, von Mises and pore stress were different in models with an isotropic poroelastic, a transversely isotropic poroelastic, and a fibril-reinforced poroviscoelastic cartilage constitutive model [304]. These results indicate that shear stress and fluid pressure in whole joints are sensitive to the implementation of anisotropy. In a separate 2D model of the human knee, differences in the location of peak maximum shear stress were found postmeniscectomy using two different cartilage-constitutive models. Before meniscectomy, both isotropic biphasic and transversely isotropic biphasic cartilage models predicted the largest maximum shear stress at the osteochondral interface. After meniscectomy, the largest maximum shear stress remained at the osteochondral interface in the isotropic biphasic analysis but shifted to the articular surface in the transversely isotropic biphasic analysis [382]. Overall, parametric analyses examining the effects of fibril reinforcement on whole joint cartilage mechanics indicate that the constitutive model is an important choice when evaluating fiber strains, fluid flow, and maximum shear stress.
3.5. Insights Into Preoperative Planning.
When using computational models for preoperative planning, the assumptions, effects of uncertainty, and limits of the model must be thoroughly characterized and understood so that results are applied appropriately to the clinic. Based on the effects of subject-specific geometry on model predictions in healthy and pathologic joints (see Sec. 3.4), it can be concluded that subject-specific geometry is generally required for preoperative planning. Sensitivity of model results to subject-specific varus/valgus alignment and kinematics in the knee also suggest that subject-specific anatomical alignment, kinematics, and kinetics should be incorporated when attempting to predict the effects of surgical intervention [78,345,346,361,362,383].
FE simulations of osteotomies have demonstrated the utility of subject-specificity for planning on the basis of contact pressure. When simulating four specific tibial tuberosity transfer surgeries on 20 patients, Cohen et al. demonstrated that the ideal surgery varied between patients as a result of subject-specific geometry [75]. In simulated periacetabular osteotomy for correction of acetabular dysplasia, Tsumura et al. found that the peak pressure initially decreased and then increased with rotation [76]. While both of these studies suggest that cartilage contact pressure can be used for optimization, other computational model outputs relevant to OA may be of interest in future preoperative planning based on computational models.
FE simulations of ligament and focal lesion repair in the knee indicate that the material properties and orientation of the repaired tissue are important surgical parameters. Several studies focused on the effects of ACL repair on tibial translation and graft deformations while ignoring the effects on joint contact mechanics [202,285]. With joint contact analysis included, ACL repair increased meniscus stress when compared to the reference configuration [77]. This analysis lends itself to future work using subject-specific modeling to optimize factors such as tunnel orientation and graft tension on a subject-specific basis. Evaluation of the offset of osteochondral plugs used in focal defect repair demonstrated stress discontinuities across the plug and native cartilage interface as well as increased stresses in the opposing cartilage layer [384]. Again, these methods can be employed to evaluate optimal repair of focal defects on a subject-specific basis. In another vein, Kelly and Prendergast [385] coupled a growth model with FEA to demonstrate the effects of loading on healing in a focal defect. Growth and differentiation depended on shear strain and fluid velocity, both parameters which can be obtained from biphasic and more complex constitutive models. The results of the growth model were used to iteratively update the mechanical properties of the finite element model [385]. These methods are an exciting new direction, coupling FEA and growth models for understanding the mechanical regulation in healing and in tissue-engineering applications.
Insights from computational models using constitutive models with specific collagen fiber orientation provide important guidance for cartilage tissue engineering. Two studies examined the effect of the superficial zone fibrillar organization in 2D models of the human knee joint. In a study where the menisci were included, the removal of superficial zone fibers reduced stresses at the center of contact but increased stresses in and under the menisci. Using simulated repair tissue with increased fibril stiffness and no surface zone tangential organization, this study also demonstrated that repair tissue that did not match the structure and properties of native tissue caused increased peak stress and large strain at the interface between repair and native tissue [304]. In a study without the meniscus, repair tissue, which included superficial zone fibers, decreased short-term axial compression and created flow patterns and strain levels closer to those in intact cartilage than repair tissue without superficial zone fibers [386]. These results indicate that the zonal structure of cartilage is an important consideration both in accurate models for understanding the pathogenesis of OA and for success with engineered cartilage constructs.
In summary, the insights provided thus far from computational modeling of whole joints include the effects of pathology on cartilage contact mechanics, the effects of instability in joints predisposed to degeneration, the effects of induced incongruency and focal lesions, the effects of many different parameters on computational model predictions, and the beginning of using subject-specific whole joint models for presurgical planning. Many of these insights have been provided by leveraging advances in computational methods with advances in imaging methods. However, in many ways, the field of subject-specific computational modeling of whole joints is just at the cusp of its potential for utility in understanding the pathogenesis of OA and for optimizing surgical procedures on a patient-specific basis.
4. Conclusions and Future Directions
While the existing literature provides a solid foundation for subject-specific computational modeling of joints, there are many exciting future directions. We propose five areas for focus in future studies: in addition to deterministic joint models, perform parametric and probabilistic analysis to characterize model uncertainty; determine the required levels of subject-specificity in model geometry, constitutive models, boundary conditions, and loading conditions; leverage the statistical advantage of large cohorts in computational modeling; couple joint-level models with those at other scales, including growth models; and apply subject-specific computational modeling to diagnosis and preoperative planning (Fig. 12).
Fig. 12.
Five key areas for future work for subject-specific computational modeling of joint contact mechanics
Parameter studies and probabilistic studies assessing the effects of uncertainty in input variables will provide more reliable model results that properly incorporate forward error propagation. The effects of uncertainty in constitutive models can be assessed at two levels: the preferred constitutive model and the error in constitutive model coefficients. The first level would include comparing different levels of material symmetry, hyperelastic versus viscoelastic versus multiphasic constitutive models, and spatial variation through the cartilage thickness and throughout the joint. Once the preferred constitutive model is selected, the effects of experimental uncertainty in that constitutive model should be assessed. Similar assessments should be used for the variability in other inputs (e.g., boundary and loading conditions). The effects of geometric error from imaging resolution and segmentation should also be evaluated via parametric or probabilistic analysis.
The required level of subject-specificity in model geometry, constitutive assumptions, boundary conditions, and loading conditions is an open area for evaluation. While assumptions concerning cartilage thickness and geometric idealization have been assessed in the hip [172,184], these results are unavailable in other joints. Direct comparisons between models with and without idealizations provide the most robust prediction of the effects of idealization. Direct comparisons between models results with subject-specific, population-averaged, and literature inputs for cartilage constitutive coefficients, anatomical alignment, kinematics, and kinetics should be made to determine what level of subject-specificity is required for accurate model predictions. While some of these areas are not currently ready for routine incorporation into subject-specific modeling (e.g., subject-specific cartilage properties), continued technical developments make them a prospect for the future.
The study of large populations using subject-specific modeling has recently started, with cohorts of up to 30 in each group [73]. The use of large populations allows more robust conclusions about groups of subjects and therefore provides more reliable insight into the pathogenesis of OA. There are several continued veins of further development and future work in this area: more efficient computational methods for predicting contact pressure and area (as started by Refs. [73], [84], [85], and [344]), more efficient methods that provide accurate predictions of results other than contact stress and area, and sharing data sets for model inputs (e.g., Osteoarthritis Initiative, which provides MR and other data for the knee, http://oai.epi-ucsf.org/datarelease/, and the Musculoskeletal Research Laboratories dataset, which provides CT arthrography image data for the hip, http://mrl.sci.utah.edu/software/hip-image-data). As an alternative to subject-specific analysis to capture the effects of geometry in large cohorts, the use of parameterized or statistical shape modeling should be explored further. This has been done previously in the spine and knee with promising results [338,387].
Coupling joint-level mechanics with other physical scales and with other models (e.g., growth models) is also an emerging field. Methods such as those used by Andriacchi et al. [388] to predict cartilage thinning and by Kelly and Prendergast [385] to predict healing in focal defects hold promise for modeling the effects of mechanical loading on cartilage growth and structural changes. Similarly, multiscale methods can be applied to understand the feedback loops between joint-level mechanics and cell-level mechanics and metabolism.
Finally, the use of computational methods in surgical planning and optimization is a largely open area. While the existing studies suggest promise in preoperative planning based on subject-specific modeling, additional work has to be done to actually apply those findings to clinical practice. Therefore, this area is an active area of development, both from the basic science side of developing models, which produce accurate predictions with well-characterized uncertainty, and from the translational science side of moving the resulting optimization into the clinic.
In conclusion, subject-specific computational modeling of joint contact mechanics has already provided insight into the mechanical causes of OA and has already demonstrated promise for presurgical planning, with many exciting advances and potential for additional insight on the near horizon.
Acknowledgment
Financial support from NIH grants # R01AR053344, R01GM083925, R01EB009643, and R01EB015133 is gratefully acknowledged. The authors thank Professor Gerard Ateshian (Columbia University) and Professor Thomas Brown (University of Iowa) for their continued collaboration and advice related to joint contact mechanics.
Contributor Information
Corinne R. Henak, Department of Bioengineering, University of Utah, Salt Lake City, UT 84112; Scientific Computing and Imaging Institute, University of Utah, Salt Lake City, UT 84112
Andrew E. Anderson, Department of Bioengineering, University of Utah, Salt Lake City, UT; Scientific Computing and Imaging Institute, University of Utah, Salt Lake City, UT; Department of Orthopaedics, University of Utah, Salt Lake City, UT 84108; Department of Physical Therapy, University of Utah, Salt Lake City, UT 84108
Jeffrey A. Weiss, Department of Bioengineering, University of Utah, Salt Lake City, UT 84108; Scientific Computing and Imaging Institute, University of Utah, Salt Lake City, UT 84108; Department of Orthopaedics, University of Utah, Salt Lake City, UT 84108, e-mail: jeff.weiss@utah.edu.
References
- [1]. Buckwalter, J. A. , Saltzman, C. , and Brown, T. , 2004, “The Impact of Osteoarthritis: Implications for Research,” Clin. Orthop. Relat. Res., (427 Suppl), pp. S6–S15. [DOI] [PubMed] [Google Scholar]
- [2]. Lawrence, R. C. , Felson, D. T. , Helmick, C. G. , Arnold, L. M. , Choi, H. , Deyo, R. A. , Gabriel, S. , Hirsch, R. , Hochberg, M. C. , Hunder, G. G. , Jordan, J. M. , Katz, J. N. , Kremers, H. M. , and Wolfe, F. , 2008, “Estimates of the Prevalence of Arthritis and Other Rheumatic Conditions in the United States—Part II,” Arthritis Rheum., 58(1), pp. 26–35. 10.1002/art.23176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Brown, T. D. , Johnston, R. C. , Saltzman, C. L. , Marsh, J. L. , and Buckwalter, J. A. , 2006, “Posttraumatic Osteoarthritis: A First Estimate of Incidence, Prevalence, and Burden of Disease,” J. Orthop. Trauma, 20(10), pp. 739–744. 10.1097/01.bot.0000246468.80635.ef [DOI] [PubMed] [Google Scholar]
- [4]. Murphy, L. , and Helmick, C. G. , 2012, “The Impact of Osteoarthritis in the United States: A Population-Health Perspective,” Am. J. Nurs., 112(3 Suppl 1), pp. S13–S19. 10.1097/01.NAJ.0000412646.80054.21 [DOI] [PubMed] [Google Scholar]
- [5]. Wilson, W. , van Donkelaar, C. C. , van Rietbergen, R. , and Huiskes, R. , 2005, “The Role of Computational Models in the Search for the Mechanical Behavior and Damage Mechanisms of Articular Cartilage,” Med. Eng. Phys., 27(10), pp. 810–826. 10.1016/j.medengphy.2005.03.004 [DOI] [PubMed] [Google Scholar]
- [6]. Carter, D. R. , Beaupre, G. S. , Wong, M. , Smith, R. L. , Andriacchi, T. P. , and Schurman, D. J. , 2004, “The Mechanobiology of Articular Cartilage Development and Degeneration,” Clin. Orthop. Relat. Res., (427 Suppl), pp. S69–S77. [DOI] [PubMed] [Google Scholar]
- [7]. Guilak, F. , Fermor, B. , Keefe, F. J. , Kraus, V. B. , Olson, S. A. , Pisetsky, D. S. , Setton, L. A. , and Weinberg, J. B. , 2004, “The Role of Biomechanics and Inflammation in Cartilage Injury and Repair,” Clin. Orthop. Relat. Res., (423), pp. 17–26. [DOI] [PubMed] [Google Scholar]
- [8]. Grodzinsky, A. J. , Levenston, M. E. , Jin, M. , and Frank, E. H. , 2000, “Cartilage Tissue Remodeling in Response to Mechanical Forces,” Annu. Rev. Biomed. Eng., 2, pp. 691–713. 10.1146/annurev.bioeng.2.1.691 [DOI] [PubMed] [Google Scholar]
- [9]. Guilak, F. , and Hung, C. T. , 2005, “Physical Regulation of Cartilage Metabolism,” Basic Orthopaedic Biomechanics and Mechano-Biology, Mow V. C. and Huiskes R., eds., Lippincott Williams & Wilkins, Philadephia. [Google Scholar]
- [10]. Mow, V. C. , Gu, W. Y. , and Chen, F. H. , 2005, “Structure and Function of Articular Cartilage and Meniscus,” Basic Orthopaedic Biomechanics and Mechano-Biology, Mow V. C. and Huiskes R., eds., Lippincott Williams & Wilkins, Philadephia. [Google Scholar]
- [11]. Setton, L. A. , Elliott, D. M. , and Mow, V. C. , 1999, “Altered Mechanics of Cartilage With Osteoarthritis: Human Osteoarthritis and an Experimental Model of Joint Degeneration,” Osteoarthritis Cartilage, 7(1), pp. 2–14. 10.1053/joca.1998.0170 [DOI] [PubMed] [Google Scholar]
- [12]. Haut, R. C. , Ide, T. M. , and De Camp, C. E. , 1995, “Mechanical Responses of the Rabbit Patello-femoral Joint to Blunt Impact,” ASME J. Biomech. Eng., 117(4), pp. 402–408. 10.1115/1.2794199 [DOI] [PubMed] [Google Scholar]
- [13]. Newberry, W. N. , Garcia, J. J. , Mackenzie, C. D. , Decamp, C. E. , and Haut, R. C. , 1998, “Analysis of Acute Mechanical Insult in an Animal Model of Post-traumatic Osteoarthrosis,” ASME J. Biomech. Eng., 120(6), pp. 704–709. 10.1115/1.2834882 [DOI] [PubMed] [Google Scholar]
- [14]. Li, X. , Haut, R. C. , and Altiero, N. J. , 1995, “An Analytical Model to Study Blunt Impact Response of the Rabbit P-F Joint,” ASME J. Biomech. Eng., 117(4), pp. 485–491. 10.1115/1.2794212 [DOI] [PubMed] [Google Scholar]
- [15]. Silyn-Roberts, H. , and Broom, N. D. , 1990, “Fracture Behaviour of Cartilage-on-Bone in Response to Repeated Impact Loading,” Connect. Tissue Res., 24(2), pp. 143–156. 10.3109/03008209009152430 [DOI] [PubMed] [Google Scholar]
- [16]. Atkinson, P. J. , and Haut, R. C. , 1995, “Subfracture Insult to the Human Cadaver Patellofemoral Joint Produces Occult Injury,” J. Orthop. Res., 13(6), pp. 936–944. 10.1002/jor.1100130619 [DOI] [PubMed] [Google Scholar]
- [17]. Borrelli, J., Jr. , Tinsley, K. , Ricci, W. M. , Burns, M. , Karl, I. E. , and Hotchkiss, R. , 2003, “Induction of Chondrocyte Apoptosis Following Impact Load,” J. Orthop. Trauma, 17(9), pp. 635–641. 10.1097/00005131-200310000-00006 [DOI] [PubMed] [Google Scholar]
- [18]. Tochigi, Y. , Buckwalter, J. A. , Martin, J. A. , Hillis, S. L. , Zhang, P. , Vaseenon, T. , Lehman, A. D. , and Brown, T. D. , 2011, “Distribution and Progression of Chondrocyte Damage in a Whole-Organ Model of Human Ankle Intra-articular Fracture,” J. Bone Jt. Surg., 93(6), pp. 533–539. 10.2106/JBJS.I.01777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Lewis, J. L. , Deloria, L. B. , Oyen-Tiesma, M. , Thompson, R. C., Jr. , Ericson, M. , and Oegema, T. R., Jr. , 2003, “Cell Death After Cartilage Impact Occurs Around Matrix Cracks,” J. Orthop. Res., 21(5), pp. 881–887. 10.1016/S0736-0266(03)00039-1 [DOI] [PubMed] [Google Scholar]
- [20]. Borrelli, J., Jr. , Zhu, Y. , Burns, M. , Sandell, L. , and Silva, M. J. , 2004, “Cartilage Tolerates Single Impact Loads of as Much as Half the Joint Fracture Threshold,” Clin. Orthop. Relat. Res., (426), pp. 266–273. [DOI] [PubMed] [Google Scholar]
- [21]. Atkinson, T. S. , Haut, R. C. , and Altiero, N. J. , 1998, “An Investigation of Biphasic Failure Criteria for Impact-Induced Fissuring of Articular Cartilage,” ASME J. Biomech. Eng., 120(4), pp. 536–537. 10.1115/1.2798025 [DOI] [PubMed] [Google Scholar]
- [22]. Atkinson, T. S. , Haut, R. C. , and Altiero, N. J. , 1998, “Impact-Induced Fissuring of Articular Cartilage: An Investigation of Failure Criteria,” ASME J. Biomech. Eng., 120(2), pp. 181–187. 10.1115/1.2798300 [DOI] [PubMed] [Google Scholar]
- [23]. Flachsmann, E. R. , Broom, N. D. , and Oloyede, A. , 1995, “A Biomechanical Investigation of Unconstrained Shear Failure of the Osteochondral Region Under Impact Loading,” Clin. Biomech., 10(3), pp. 156–165. 10.1016/0268-0033(95)93706-Y [DOI] [PubMed] [Google Scholar]
- [24]. Garcia, J. J. , Altiero, N. J. , and Haut, R. C. , 1998, “An Approach for the Stress Analysis of Transversely Isotropic Biphasic Cartilage Under Impact Load,” ASME J. Biomech. Eng., 120(5), pp. 608–613. 10.1115/1.2834751 [DOI] [PubMed] [Google Scholar]
- [25]. Furman, B. D. , Strand, J. , Hembree, W. C. , Ward, B. D. , Guilak, F. , and Olson, S. A. , 2007, “Joint Degeneration Following Closed Intraarticular Fracture in the Mouse Knee: A Model of Posttraumatic Arthritis,” J. Orthop. Res., 25(5), pp. 578–592. 10.1002/jor.20331 [DOI] [PubMed] [Google Scholar]
- [26]. Anderson, D. D. , Chubinskaya, S. , Guilak, F. , Martin, J. A. , Oegema, T. R. , Olson, S. A. , and Buckwalter, J. A. , 2011, “Post-Traumatic Osteoarthritis: Improved Understanding and Opportunities for Early Intervention,” J. Orthop. Res., 29(6), pp. 802–809. 10.1002/jor.21359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Furman, B. D. , Olson, S. A. , and Guilak, F. , 2006, “The Development of Posttraumatic Arthritis After Articular Fracture,” J. Orthop. Trauma, 20(10), pp. 719–725. 10.1097/01.bot.0000211160.05864.14 [DOI] [PubMed] [Google Scholar]
- [28]. Smith, R. L. , Carter, D. R. , and Schurman, D. J. , 2004, “Pressure and Shear Differentially Alter Human Articular Chondrocyte Metabolism: A Review,” Clin. Orthop. Relat. Res., (427 Suppl), pp. S89–S95. [PubMed] [Google Scholar]
- [29]. Martin, J. A. , and Buckwalter, J. A. , 2006, “Post-Traumatic Osteoarthritis: The Role of Stress Induced Chondrocyte Damage,” Biorheology, 43(3–4), pp. 517–521. [PubMed] [Google Scholar]
- [30]. Murphy, L. , Schwartz, T. A. , Helmick, C. G. , Renner, J. B. , Tudor, G. , Koch, G. , Dragomir, A. , Kalsbeek, W. D. , Luta, G. , and Jordan, J. M. , 2008, “Lifetime Risk of Symptomatic Knee Osteoarthritis,” Arthritis Rheum., 59(9), pp. 1207–1213. 10.1002/art.24021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Murphy, L. B. , Helmick, C. G. , Schwartz, T. A. , Renner, J. B. , Tudor, G. , Koch, G. G. , Dragomir, A. D. , Kalsbeek, W. D. , Luta, G. , and Jordan, J. M. , 2010, “One in Four People May Develop Symptomatic Hip Osteoarthritis in His or Her Lifetime,” Osteoarthritis Cartilage, 18(11), pp. 1372–1379. 10.1016/j.joca.2010.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Chard, M. D. , and Hazleman, B. L. , 1987, “Shoulder Disorders in the Elderly (a Hospital Study),” Ann. Rheum. Dis., 46(9), pp. 684–687. 10.1136/ard.46.9.684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Nakagawa, Y. , Hyakuna, K. , Otani, S. , Hashitani, M. , and Nakamura, T. , 1999, “Epidemiologic Study of Glenohumeral Osteoarthritis With Plain Radiography,” J. Shoulder Elbow Surg., 8(6), pp. 580–584. 10.1016/S1058-2746(99)90093-9 [DOI] [PubMed] [Google Scholar]
- [34]. van Schaardenburg, D. , Van den Brande, K. J. , Ligthart, G. J. , Breedveld, F. C. , and Hazes, J. M. , 1994, “Musculoskeletal Disorders and Disability in Persons Aged 85 and Over: A Community Survey,” Ann. Rheum. Dis., 53(12), pp. 807–811. 10.1136/ard.53.12.807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. Buckwalter, J. A. , and Saltzman, C. L. , 1999, “Ankle Osteoarthritis: Distinctive Characteristics,” Instr. Course Lect., 48, pp. 233–241. [PubMed] [Google Scholar]
- [36]. Zhang, Y. , and Jordan, J. M. , 2008, “Epidemiology of Osteoarthritis,” Rheum. Dis. Clin. North Am., 34(3), pp. 515–529. 10.1016/j.rdc.2008.05.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Jeong, H. J. , Lee, S. H. , and Ko, C. S. , 2012, “Meniscectomy,” Knee Surg. Relat. Res., 24(3), pp. 129–136. 10.5792/ksrr.2012.24.3.129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Tucker, B. , Khan, W. , Al-Rashid, M. , and Al-Khateeb, H. , 2012, “Tissue Engineering for the Meniscus: A Review of the Literature,” Open Orthop. J., 6, pp. 348–351. 10.2174/1874325001206010348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Crema, M. D. , Roemer, F. W. , Felson, D. T. , Englund, M. , Wang, K. , Jarraya, M. , Nevitt, M. C. , Marra, M. D. , Torner, J. C. , Lewis, C. E. , and Guermazi, A. , 2012, “Factors Associated With Meniscal Extrusion in Knees With or at Risk for Osteoarthritis: The Multicenter Osteoarthritis Study,” Radiology, 264(2), pp. 494–503. 10.1148/radiol.12110986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40]. Knoop, J. , Dekker, J. , Klein, J. P. , van der Leeden, M. , van der Esch, M. , Reiding, D. , Voorneman, R. E. , Gerritsen, M. , Roorda, L. D. , Steultjens, M. P. , and Lems, W. F. , 2012, “Biomechanical Factors and Physical Examination Findings in Osteoarthritis of the Knee: Associations With Tissue Abnormalities Assessed by Conventional Radiography and High Resolution 3.0 Tesla Magnetic Resonance Imaging,” Arthritis Res. Ther., 14(5), p. R212. 10.1186/ar4050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Lementowski, P. W. , and Zelicof, S. B. , 2008, “Obesity and Osteoarthritis,” Am. J. Orthop., 37(3), pp. 148–151. [PubMed] [Google Scholar]
- [42]. Suri, P. , Morgenroth, D. C. , and Hunter, D. J. , 2012, “Epidemiology of Osteoarthritis and Associated Comorbidities,” PM&R, 4(5 Suppl), pp. S10–S19. 10.1016/j.pmrj.2012.01.007 [DOI] [PubMed] [Google Scholar]
- [43]. Iliadis, A. D. , Jaiswal, P. K. , Khan, W. , and Johnstone, D. , 2012, “The Operative Management of Patella Malalignment,” Open Orthop. J., 6, pp. 327–339. 10.2174/1874325001206010327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44]. Bardakos, N. V. , and Villar, R. N. , 2009, “Predictors of Progression of Osteoarthritis in Femoroacetabular Impingement: A Radiological Study With a Minimum of Ten Years Follow-up,” J. Bone Jt. Surg., 91(2), pp. 162–169. 10.1302/0301-620X.91B2.21137 [DOI] [PubMed] [Google Scholar]
- [45]. Beck, M. , Kalhor, M. , Leunig, M. , and Ganz, R. , 2005, “Hip Morphology Influences the Pattern of Damage to the Acetabular Cartilage: Femoroacetabular Impingement as a Cause of Early Osteoarthritis of the Hip,” J. Bone Jt. Surg., 87(7), pp. 1012–1018. 10.1302/0301-620X.87B7.15203 [DOI] [PubMed] [Google Scholar]
- [46]. Cooperman, D. R. , Wallensten, R. , and Stulberg, S. D. , 1983, “Acetabular Dysplasia in the Adult,” Clin. Orthop. Relat. Res., (175), pp. 79–85. [PubMed] [Google Scholar]
- [47]. Croft, P. , Cooper, C. , Wickham, C. , and Coggon, D. , 1991, “Osteoarthritis of the Hip and Acetabular Dysplasia,” Ann. Rheum. Dis., 50(5), pp. 308–310. 10.1136/ard.50.5.308 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Ganz, R. , Leunig, M. , Leunig-Ganz, K. , and Harris, W. H. , 2008, “The Etiology of Osteoarthritis of the Hip: An Integrated Mechanical Concept,” Clin. Orthop. Relat. Res., 466(2), pp. 264–272. 10.1007/s11999-007-0060-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49]. Ganz, R. , Parvizi, J. , Beck, M. , Leunig, M. , Notzli, H. , and Siebenrock, K. A. , 2003, “Femoroacetabular Impingement: A Cause for Osteoarthritis of the Hip,” Clin. Orthop. Relat. Res., (417), pp. 112–120. [DOI] [PubMed] [Google Scholar]
- [50]. Harris, W. H. , 1986, “Etiology of Osteoarthritis of the Hip,” Clin. Orthop. Relat. Res., (213), pp. 20–33. [PubMed] [Google Scholar]
- [51]. Jessel, R. H. , Zurakowski, D. , Zilkens, C. , Burstein, D. , Gray, M. L. , and Kim, Y. J. , 2009, “Radiographic and Patient Factors Associated With Pre-radiographic Osteoarthritis in Hip Dysplasia,” J. Bone Jt. Surg., 91(5), pp. 1120–1129. 10.2106/JBJS.G.00144 [DOI] [PubMed] [Google Scholar]
- [52]. Klaue, K. , Durnin, C. W. , and Ganz, R. , 1991, “The Acetabular Rim Syndrome. A Clinical Presentation of Dysplasia of the Hip,” J. Bone Jt. Surg. Br., 73(3), pp. 423–429. [DOI] [PubMed] [Google Scholar]
- [53]. Lau, E. M. , Lin, F. , Lam, D. , Silman, A. , and Croft, P. , 1995, “Hip Osteoarthritis and Dysplasia in Chinese Men,” Ann. Rheum. Dis., 54(12), pp. 965–969. 10.1136/ard.54.12.965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54]. McWilliams, D. F. , Doherty, S. A. , Jenkins, W. D. , Maciewicz, R. A. , Muir, K. R. , Zhang, W. , and Doherty, M. , 2010, “Mild Acetabular Dysplasia and Risk of Osteoarthritis of the Hip: A Case Control Study,” Ann. Rheum. Dis., 69(10), pp. 1774–1778. 10.1136/ard.2009.127076 [DOI] [PubMed] [Google Scholar]
- [55]. Murphy, S. B. , Ganz, R. , and Muller, M. E. , 1995, “The Prognosis in Untreated Dysplasia of the Hip. A Study of Radiographic Factors That Predict the Outcome,” J. Bone Jt. Surg., 77(7), pp. 985–989. [DOI] [PubMed] [Google Scholar]
- [56]. Murray, R. O. , 1965, “The Aetiology of Primary Osteoarthritis of the Hip,” Br. J. Radiol., 38(455), pp. 810–824. 10.1259/0007-1285-38-455-810 [DOI] [PubMed] [Google Scholar]
- [57]. Solomon, L. , 1976, “Patterns of Osteoarthritis of the Hip,” J. Bone Jt. Surg. Br., 58(2), pp. 176–183. [DOI] [PubMed] [Google Scholar]
- [58]. Sulsky, S. I. , Carlton, L. , Bochmann, F. , Ellegast, R. , Glitsch, U. , Hartmann, B. , Pallapies, D. , Seidel, D. , and Sun, Y. , 2012, “Epidemiological Evidence for Work Load as a Risk Factor for Osteoarthritis of the Hip: A Systematic Review,” PLoS ONE, 7(2), p. e31521. 10.1371/journal.pone.0031521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59]. Cameron, M. L. , Kocher, M. S. , Briggs, K. K. , Horan, M. P. , and Hawkins, R. J. , 2003, “The Prevalence of Glenohumeral Osteoarthrosis in Unstable Shoulders,” Am. J. Sports Med., 31(1), pp. 53–55. [DOI] [PubMed] [Google Scholar]
- [60]. Oh, J. H. , Chung, S. W. , Oh, C. H. , Kim, S. H. , Park, S. J. , Kim, K. W. , Park, J. H. , Lee, S. B. , and Lee, J. J. , 2011, “The Prevalence of Shoulder Osteoarthritis in the Elderly Korean Population: Association With Risk Factors and Function,” J. Shoulder Elbow Surg., 20(5), pp. 756–763. 10.1016/j.jse.2011.01.021 [DOI] [PubMed] [Google Scholar]
- [61]. Bischof, J. E. , Spritzer, C. E. , Caputo, A. M. , Easley, M. E. , DeOrio, J. K. , Nunley, J. A., II , and DeFrate, L. E. , 2010, “ In Vivo Cartilage Contact Strains in Patients With Lateral Ankle Instability,” J. Biomech., 43(13), pp. 2561–2566. 10.1016/j.jbiomech.2010.05.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62]. Goreham-Voss, C. M. , McKinley, T. O. , and Brown, T. D. , 2007, “A Finite Element Exploration of Cartilage Stress Near an Articular Incongruity During Unstable Motion,” J. Biomech., 40(15), pp. 3438–3447. 10.1016/j.jbiomech.2007.05.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63]. Hughes, T. J. R. , and Liu, W. K. , 1981, “Nonlinear Finite Element Analysis of Shells: Part I—Three-Dimensional Shells,” Comput. Methods Appl. Mech. Eng., 26(3), pp. 331–362. 10.1016/0045-7825(81)90121-3 [DOI] [Google Scholar]
- [64]. Mauck, R. L. , Hung, C. T. , and Ateshian, G. A. , 2003, “Modeling of Neutral Solute Transport in a Dynamically Loaded Porous Permeable Gel: Implications for Articular Cartilage Biosynthesis and Tissue Engineering,” ASME J. Biomech. Eng., 125(5), pp. 602–614. 10.1115/1.1611512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65]. Puso, M. A. , 2000, “A Highly Efficient Enhanced Assumed Strain Physically Stabilized Hexahedral Element,” Int. J. Numer. Methods Eng., 49(8), pp. 1029–1064. [DOI] [Google Scholar]
- [66]. Puso, M. A. , 2004, “A 3D Mortar Method for Solid Mechanics,” Int. J. Numer. Methods Eng., 59(3), pp. 315–336. 10.1002/nme.865 [DOI] [Google Scholar]
- [67]. Puso, M. A. , and Laursen, T. A. , 2004, “A Mortar Segment-to-Segment Contact Method for Large Deformation Solid Mechanics,” Comput. Methods Appl. Mech. Eng., 193(6–8), pp. 601–629. 10.1016/j.cma.2003.10.010 [DOI] [Google Scholar]
- [68]. Simo, J. C. , and Taylor, R. L. , 1991, “Quasi-incompressible Finite Elasticity in Principal Stretches. Continuum Basis and Numerical Algorithms,” Comput. Methods Appl. Mech. Eng., 85(3), pp. 273–310. 10.1016/0045-7825(91)90100-K [DOI] [Google Scholar]
- [69]. Un, K. , and Spilker, R. L. , 2006, “A Penetration-Based Finite Element Method for Hyperelastic 3D Biphasic Tissues in Contact. Part II: Finite Element Simulations,” ASME J. Biomech. Eng., 128(6), pp. 934–942. 10.1115/1.2354203 [DOI] [PubMed] [Google Scholar]
- [70]. Un, K. , and Spilker, R. L. , 2006, “A Penetration-Based Finite Element Method for Hyperelastic 3D Biphasic Tissues in Contact: Part 1—Derivation of Contact Boundary Conditions,” ASME J. Biomech. Eng., 128(1), pp. 124–130. 10.1115/1.2133769 [DOI] [PubMed] [Google Scholar]
- [71]. Veronda, D. R. , and Westmann, R. A. , 1970, “Mechanical Characterization of Skin-Finite Deformations,” J. Biomech., 3(1), pp. 111–124. 10.1016/0021-9290(70)90055-2 [DOI] [PubMed] [Google Scholar]
- [72]. Weiss, J. A. , Maker, B. N. , and Govindjee, S. , 1996, “Finite Element Implementation of Incompressible, Transversely Isotropic Hyperelasticity,” Comput. Methods Appl. Mech. Eng., 135(1–2), pp. 107–128. 10.1016/0045-7825(96)01035-3 [DOI] [Google Scholar]
- [73]. Segal, N. A. , Anderson, D. D. , Iyer, K. S. , Baker, J. , Torner, J. C. , Lynch, J. A. , Felson, D. T. , Lewis, C. E. , and Brown, T. D. , 2009, “Baseline Articular Contact Stress Levels Predict Incident Symptomatic Knee Osteoarthritis Development in the MOST Cohort,” J. Orthop. Res., 27(12), pp. 1562–1568. 10.1002/jor.20936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74]. Brown, T. D. , and DiGioia, A. M., III , 1984, “A Contact-Coupled Finite Element Analysis of the Natural Adult Hip,” J. Biomech., 17(6), pp. 437–448. 10.1016/0021-9290(84)90035-6 [DOI] [PubMed] [Google Scholar]
- [75]. Cohen, Z. A. , Henry, J. H. , McCarthy, D. M. , Mow, V. C. , and Ateshian, G. A. , 2003, “Computer Simulations of Patellofemoral Joint Surgery. Patient-Specific Models for Tuberosity Transfer,” Am. J. Sports Med., 31(1), pp. 87–98. Available at: http://ajs.sagepub.com/content/31/1/87.short [DOI] [PubMed] [Google Scholar]
- [76]. Tsumura, H. , Kaku, N. , Ikeda, S. , and Torisu, T. , 2005, “A Computer Simulation of Rotational Acetabular Osteotomy for Dysplastic Hip Joint: Does the Optimal Transposition of the Acetabular Fragment Exist?,” J. Orthop. Sci., 10(2), pp. 145–151. 10.1007/s00776-004-0866-4 [DOI] [PubMed] [Google Scholar]
- [77]. Pena, E. , Calvo, B. , Martinez, M. A. , Palanca, D. , and Doblare, M. , 2006, “Influence of the Tunnel Angle in ACL Reconstructions on the Biomechanics of the Knee Joint,” Clin. Biomech., 21(5), pp. 508–516. 10.1016/j.clinbiomech.2005.12.013 [DOI] [PubMed] [Google Scholar]
- [78]. Besier, T. F. , Gold, G. E. , Delp, S. L. , Fredericson, M. , and Beaupre, G. S. , 2008, “The Influence of Femoral Internal and External Rotation on Cartilage Stresses Within the Patellofemoral Joint,” J. Orthop. Res., 26(12), pp. 1627–1635. 10.1002/jor.20663 [DOI] [PubMed] [Google Scholar]
- [79]. Delp, S. L. , Anderson, F. C. , Arnold, A. S. , Loan, P. , Habib, A. , John, C. T. , Guendelman, E. , and Thelen, D. G. , 2007, “OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement,” IEEE Trans. Biomed. Eng., 54(11), pp. 1940–1950. 10.1109/TBME.2007.901024 [DOI] [PubMed] [Google Scholar]
- [80]. Halloran, J. P. , Sibole, S. , van Donkelaar, C. C. , van Turnhout, M. C. , Oomens, C. W. , Weiss, J. A. , Guilak, F. , and Erdemir, A. , 2012, “Multiscale Mechanics of Articular Cartilage: Potentials and Challenges of Coupling Musculoskeletal, Joint, and Microscale Computational Models,” Ann. Biomed. Eng., 40(11), pp. 2456–2474. 10.1007/s10439-012-0598-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81]. Li, G. , Sakamoto, M. , and Chao, E. Y. , 1997, “A Comparison of Different Methods in Predicting Static Pressure Distribution in Articulating Joints,” J. Biomech., 30(6), pp. 635–638. 10.1016/S0021-9290(97)00009-2 [DOI] [PubMed] [Google Scholar]
- [82]. Akbar, M. , Farahmand, F. , Jafari, A. , and Foumani, M. S. , 2012, “A Detailed and Validated Three Dimensional Dynamic Model of the Patellofemoral Joint,” ASME J. Biomech. Eng., 134(4), p. 041005. 10.1115/1.4006403 [DOI] [PubMed] [Google Scholar]
- [83]. Abraham, C. L. , Maas, S. A. , Weiss, J. A. , Ellis, B. J. , Peters, C. L. , and Anderson, A. E. , 2012, “An Enhanced Discrete Element Analysis Method for Predicting Hip Contact Stresses,” International Symposium of Computer Methods in Biomechanics and Biomedical Engineering, Berlin, Germany. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84]. Anderson, D. D. , Iyer, K. S. , Segal, N. A. , Lynch, J. A. , and Brown, T. D. , 2010, “Implementation of Discrete Element Analysis for Subject-Specific, Population-Wide Investigations of Habitual Contact Stress Exposure,” J. Appl. Biomech., 26(2), pp. 215–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85]. Segal, N. A. , Kern, A. M. , Anderson, D. D. , Niu, J. , Lynch, J. , Guermazi, A. , Torner, J. C. , Brown, T. D. , and Nevitt, M. , 2012, “Elevated Tibiofemoral Articular Contact Stress Predicts Risk for Bone Marrow Lesions and Cartilage Damage at 30 Months,” Osteoarthritis Cartilage, 20(10), pp. 1120–1126. 10.1016/j.joca.2012.05.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86]. Geers, M. G. D. , Kouznetsova, V. G. , and Brekelmans, W. A. M. , 2010, “Multi-scale Computational Homogenization: Trends and Challenges,” J. Comput. Appl. Math., 234(7), pp. 2175–2182. 10.1016/j.cam.2009.08.077 [DOI] [Google Scholar]
- [87]. Yuan, Z. , and Fish, J. , 2008, “Toward Realization of Computational Homogenization in Practice,” Int. J. Numer. Methods Eng., 73(3), pp. 361–380. 10.1002/nme.2074 [DOI] [Google Scholar]
- [88]. Guilak, F. , and Mow, V. C. , 2000, “The Mechanical Environment of the Chondrocyte: A Biphasic Finite Element Model of Cell-Matrix Interactions in Articular Cartilage,” J. Biomech., 33(12), pp. 1663–1673. 10.1016/S0021-9290(00)00105-6 [DOI] [PubMed] [Google Scholar]
- [89]. Kim, E. , Guilak, F. , and Haider, M. A. , 2008, “The Dynamic Mechanical Environment of the Chondrocyte: A Biphasic Finite Element Model of Cell-Matrix Interactions Under Cyclic Compressive Loading,” ASME J. Biomech. Eng., 130(6), p. 061009. 10.1115/1.2978991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90]. Kim, E. , Guilak, F. , and Haider, M. A. , 2010, “An Axisymmetric Boundary Element Model for Determination of Articular Cartilage Pericellular Matrix Properties In Situ via Inverse Analysis of Chondron Deformation,” ASME J. Biomech. Eng., 132(3), p. 031011. 10.1115/1.4000938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91]. Sibole, S. C. , and Erdemir, A. , 2012, “Chondrocyte Deformations as a Function of Tibiofemoral Joint Loading Predicted by a Generalized High-Throughput Pipeline of Multi-Scale Simulations,” PLoS ONE, 7(5), p. e37538. 10.1371/journal.pone.0037538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92]. Lu, X. L. , and Mow, V. C. , 2008, “Biomechanics of Articular Cartilage and Determination of Material Properties,” Med. Sci. Sports Exercise, 40(2), pp. 193–199. 10.1249/mss.0b013e31815cb1fc [DOI] [PubMed] [Google Scholar]
- [93]. Stops, A. , Wilcox, R. , and Jin, Z. , 2012, “Computational Modelling of the Natural Hip: A Review of Finite Element and Multibody Simulations,” Comput. Methods Biomech. Biomed. Eng., 15(9), pp. 963–979. 10.1080/10255842.2011.567983 [DOI] [PubMed] [Google Scholar]
- [94]. Ateshian, G. A. , Albro, M. B. , Maas, S. , and Weiss, J. A. , 2011, “Finite Element Implementation of Mechanochemical Phenomena in Neutral Deformable Porous Media Under Finite Deformation,” ASME J. Biomech. Eng., 133(8), p. 081005. 10.1115/1.4004810 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95]. Maas, S. , Rawlins, D. , Weiss, J. A. , and Ateshian, G. A. , 2012, FEBio: Finite Elements for Biomechanics User's Manual. Available at http://help.mrl.sci.utah.edu/help/index.jsp [Google Scholar]
- [96]. Ateshian, G. A. , Maas, S. , and Weiss, J. A. , 2012, “Solute Transport Across a Contact Interface in Deformable Porous Media,” J. Biomech., 45(6), pp. 1023–1027. 10.1016/j.jbiomech.2012.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97]. Ateshian, G. A. , Maas, S. , and Weiss, J. A. , 2010, “Finite Element Algorithm for Frictionless Contact of Porous Permeable Media Under Finite Deformation and Sliding,” ASME J. Biomech. Eng., 132(6), p. 061006. 10.1115/1.4001034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98]. Taylor, Z. A. , and Miller, K. , 2006, “Constitutive Modeling of Cartilaginous Tissues: A Review,” J. Appl. Biomech., 22(3), pp. 212–229. [DOI] [PubMed] [Google Scholar]
- [99]. Federico, S. , Grillo, A. , La Rosa, G. , Giaquinta, G. , and Herzog, W. , 2005, “A Transversely Isotropic, Transversely Homogeneous Microstructural-Statistical Model of Articular Cartilage,” J. Biomech., 38(10), pp. 2008–2018. 10.1016/j.jbiomech.2004.09.020 [DOI] [PubMed] [Google Scholar]
- [100]. Buckley, M. R. , Gleghorn, J. P. , Bonassar, L. J. , and Cohen, I. , 2008, “Mapping the Depth Dependence of Shear Properties in Articular Cartilage,” J. Biomech., 41(11), pp. 2430–2437. 10.1016/j.jbiomech.2008.05.021 [DOI] [PubMed] [Google Scholar]
- [101]. Chen, A. C. , Bae, W. C. , Schinagl, R. M. , and Sah, R. L. , 2001, “Depth- and Strain-Dependent Mechanical and Electromechanical Properties of Full-Thickness Bovine Articular Cartilage in Confined Compression,” J. Biomech., 34(1), pp. 1–12. 10.1016/S0021-9290(00)00170-6 [DOI] [PubMed] [Google Scholar]
- [102]. Maroudas, A. , Bayliss, M. T. , and Venn, M. F. , 1980, “Further Studies on the Composition of Human Femoral Head Cartilage,” Ann. Rheum. Dis., 39(5), pp. 514–523. 10.1136/ard.39.5.514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [103]. Mow, V. C. , and Guo, X. E. , 2002, “Mechano-Electrochemical Properties of Articular Cartilage: Their Inhomogeneities and Anisotropies,” Ann. Rev. Biomed. Eng., 4(1), pp. 175–209. 10.1146/annurev.bioeng.4.110701.120309 [DOI] [PubMed] [Google Scholar]
- [104]. Schinagl, R. M. , Gurskis, D. , Chen, A. C. , and Sah, R. L. , 1997, “Depth-Dependent Confined Compression Modulus of Full-Thickness Bovine Articular Cartilage,” J. Orthop. Res., 15(4), pp. 499–506. 10.1002/jor.1100150404 [DOI] [PubMed] [Google Scholar]
- [105]. Setton, L. A. , Zhu, W. , and Mow, V. C. , 1993, “The Biphasic Poroviscoelastic Behavior of Articular Cartilage: Role of the Surface Zone in Governing the Compressive Behavior,” J. Biomech., 26(4–5), pp. 581–592. 10.1016/0021-9290(93)90019-B [DOI] [PubMed] [Google Scholar]
- [106]. Athanasiou, K. A. , Agarwal, A. , and Dzida, F. J. , 1994, “Comparative Study of the Intrinsic Mechanical Properties of the Human Acetabular and Femoral Head Cartilage,” J. Orthop. Res., 12(3), pp. 340–349. 10.1002/jor.1100120306 [DOI] [PubMed] [Google Scholar]
- [107]. Athanasiou, K. A. , Agarwal, A. , Muffoletto, A. , Dzida, F. J. , Constantinides, G. , and Clem, M. , 1995, “Biomechanical Properties of Hip Cartilage in Experimental Animal Models,” Clin. Orthop. Relat. Res., (316), pp. 254–266. [PubMed] [Google Scholar]
- [108]. Demarteau, O. , Pillet, L. , Inaebnit, A. , Borens, O. , and Quinn, T. M. , 2006, “Biomechanical Characterization and In Vitro Mechanical Injury of Elderly Human Femoral Head Cartilage: Comparison to Adult Bovine Humeral Head Cartilage,” Osteoarthritis Cartilage, 14(6), pp. 589–596. 10.1016/j.joca.2005.12.011 [DOI] [PubMed] [Google Scholar]
- [109]. Huang, C. Y. , Stankiewicz, A. , Ateshian, G. A. , and Mow, V. C. , 2005, “Anisotropy, Inhomogeneity, and Tension-Compression Nonlinearity of Human Glenohumeral Cartilage in Finite Deformation,” J. Biomech., 38(4), pp. 799–809. 10.1016/j.jbiomech.2004.05.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110]. Shepherd, D. E. , and Seedhom, B. B. , 1999, “The ‘Instantaneous’ Compressive Modulus of Human Articular Cartilage in Joints of the Lower Limb,” Rheumatology, 38(2), pp. 124–132. 10.1093/rheumatology/38.2.124 [DOI] [PubMed] [Google Scholar]
- [111]. Treppo, S. , Koepp, H. , Quan, E. C. , Cole, A. A. , Kuettner, K. E. , and Grodzinsky, A. J. , 2000, “Comparison of Biomechanical and Biochemical Properties of Cartilage From Human Knee and Ankle Pairs,” J. Orthop. Res., 18(5), pp. 739–748. 10.1002/jor.1100180510 [DOI] [PubMed] [Google Scholar]
- [112]. Li, L. , Shirazi-Adl, A. , and Buschmann, M. D. , 2003, “Investigation of Mechanical Behavior of Articular Cartilage by Fibril Reinforced Poroelastic Models,” Biorheology, 40(1–3), pp. 227–233. [PubMed] [Google Scholar]
- [113]. Li, L. P. , Buschmann, M. D. , and Shirazi-Adl, A. , 2000, “A Fibril Reinforced Nonhomogeneous Poroelastic Model for Articular Cartilage: Inhomogeneous Response in Unconfined Compression,” J. Biomech., 33(12), pp. 1533–1541. 10.1016/S0021-9290(00)00153-6 [DOI] [PubMed] [Google Scholar]
- [114]. Woo, S. L. , Akeson, W. H. , and Jemmott, G. F. , 1976, “Measurements of Nonhomogeneous, Directional Mechanical Properties of Articular Cartilage in Tension,” J. Biomech., 9(12), pp. 785–791. 10.1016/0021-9290(76)90186-X [DOI] [PubMed] [Google Scholar]
- [115]. DiSilvestro, M. R. , Zhu, Q. , Wong, M. , Jurvelin, J. S. , and Suh, J. K. , 2001, “Biphasic Poroviscoelastic Simulation of the Unconfined Compression of Articular Cartilage: I—Simultaneous Prediction of Reaction Force and Lateral Displacement,” ASME J. Biomech. Eng., 123(2), pp. 191–197. 10.1115/1.1351890 [DOI] [PubMed] [Google Scholar]
- [116]. Huang, C. Y. , Soltz, M. A. , Kopacz, M. , Mow, V. C. , and Ateshian, G. A. , 2003, “Experimental Verification of the Roles of Intrinsic Matrix Viscoelasticity and Tension-Compression Nonlinearity in the Biphasic Response of Cartilage,” ASME J. Biomech. Eng., 125(1), pp. 84–93. 10.1115/1.1531656 [DOI] [PubMed] [Google Scholar]
- [117]. Mak, A. F. , 1986, “The Apparent Viscoelastic Behavior of Articular Cartilage–the Contributions From the Intrinsic Matrix Viscoelasticity and Interstitial Fluid Flows,” ASME J. Biomech. Eng., 108(2), pp. 123–130. 10.1115/1.3138591 [DOI] [PubMed] [Google Scholar]
- [118]. Mow, V. C. , Kuei, S. C. , Lai, W. M. , and Armstrong, C. G. , 1980, “Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression? Theory and Experiments,” ASME J. Biomech. Eng., 102(1), pp. 73–84. 10.1115/1.3138202 [DOI] [PubMed] [Google Scholar]
- [119]. Setton, L. A. , Tohyama, H. , and Mow, V. C. , 1998, “Swelling and Curling Behaviors of Articular Cartilage,” ASME J. Biomech. Eng., 120(3), pp. 355–361. 10.1115/1.2798002 [DOI] [PubMed] [Google Scholar]
- [120]. Abazari, A. , Elliott, J. A. , McGann, L. E. , and Thompson, R. B. , 2012, “MR Spectroscopy Measurement of the Diffusion of Dimethyl Sulfoxide in Articular Cartilage and Comparison to Theoretical Predictions,” Osteoarthritis Cartilage, 20(9), pp. 1004–1010. 10.1016/j.joca.2012.04.023 [DOI] [PubMed] [Google Scholar]
- [121]. Burstein, D. , Gray, M. L. , Hartman, A. L. , Gipe, R. , and Foy, B. D. , 1993, “Diffusion of Small Solutes in Cartilage as Measured by Nuclear Magnetic Resonance (NMR) Spectroscopy and Imaging,” J. Orthop. Res., 11(4), pp. 465–478. 10.1002/jor.1100110402 [DOI] [PubMed] [Google Scholar]
- [122]. Evans, R. C. , and Quinn, T. M. , 2005, “Solute Diffusivity Correlates With Mechanical Properties and Matrix Density of Compressed Articular Cartilage,” Arch. Biochem. Biophys., 442(1), pp. 1–10. 10.1016/j.abb.2005.07.025 [DOI] [PubMed] [Google Scholar]
- [123]. Quinn, T. M. , Kocian, P. , and Meister, J. J. , 2000, “Static Compression is Associated With Decreased Diffusivity of Dextrans in Cartilage Explants,” Arch. Biochem. Biophys., 384(2), pp. 327–334. 10.1006/abbi.2000.2077 [DOI] [PubMed] [Google Scholar]
- [124]. Soltz, M. A. , and Ateshian, G. A. , 2000, “A Conewise Linear Elasticity Mixture Model for the Analysis of Tension-Compression Nonlinearity in Articular Cartilage,” ASME J. Biomech. Eng., 122(6), pp. 576–586. 10.1115/1.1324669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125]. Huang, C. Y. , Mow, V. C. , and Ateshian, G. A. , 2001, “The Role of Flow-Independent Viscoelasticity in the Biphasic Tensile and Compressive Responses of Articular Cartilage,” ASME J. Biomech. Eng., 123(5), pp. 410–417. 10.1115/1.1392316 [DOI] [PubMed] [Google Scholar]
- [126]. Pierce, D. M. , Trobin, W. , Trattnig, S. , Bischof, H. , and Holzapfel, G. A. , 2009, “A Phenomenological Approach Toward Patient-Specific Computational Modeling of Articular Cartilage Including Collagen Fiber Tracking,” ASME J. Biomech. Eng., 131(9), p. 091006. 10.1115/1.3148471 [DOI] [PubMed] [Google Scholar]
- [127]. Herberhold, C. , Faber, S. , Stammberger, T. , Steinlechner, M. , Putz, R. , Englmeier, K. H. , Reiser, M. , and Eckstein, F. , 1999, “In Situ Measurement of Articular Cartilage Deformation in Intact Femoropatellar Joints Under Static Loading,” J. Biomech., 32(12), pp. 1287–1295. 10.1016/S0021-9290(99)00130-X [DOI] [PubMed] [Google Scholar]
- [128]. Holzapfel, G. , 2000, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, Wiley, West Sussex. [Google Scholar]
- [129]. Ateshian, G. A. , Ellis, B. J. , and Weiss, J. A. , 2007, “Equivalence Between Short-Time Biphasic and Incompressible Elastic Material Responses,” ASME J. Biomech. Eng., 129(3), pp. 405–412. 10.1115/1.2720918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130]. Wong, M. , Ponticiello, M. , Kovanen, V. , and Jurvelin, J. S. , 2000, “Volumetric Changes of Articular Cartilage During Stress Relaxation in Unconfined Compression,” J. Biomech., 33(9), pp. 1049–1054. 10.1016/S0021-9290(00)00084-1 [DOI] [PubMed] [Google Scholar]
- [131]. Anderson, A. E. , Ellis, B. J. , Maas, S. A. , Peters, C. L. , and Weiss, J. A. , 2008, “Validation of Finite Element Predictions of Cartilage Contact Pressure in the Human Hip Joint,” ASME J. Biomech. Eng., 130(5), p. 051008. 10.1115/1.2953472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [132]. Anderson, A. E. , Ellis, B. J. , and Weiss, J. A. , 2007, “Verification, Validation and Sensitivity Studies in Computational Biomechanics,” Comput. Methods Biomech. Biomed. Eng., 10(3), pp. 171–184. 10.1080/10255840601160484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [133]. Creamer, P. , and Hochberg, M. C. , 1997, “Osteoarthritis,” Lancet, 350(9076), pp. 503–508. 10.1016/S0140-6736(97)07226-7 [DOI] [PubMed] [Google Scholar]
- [134]. Russell, M. E. , Shivanna, K. H. , Grosland, N. M. , and Pedersen, D. R. , 2006, “Cartilage Contact Pressure Elevations in Dysplastic Hips: A Chronic Overload Model,” J. Orthop. Surg. Res., 1, p. 6. 10.1186/1749-799X-1-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [135]. Korhonen, R. K. , Laasanen, M. S. , Toyras, J. , Lappalainen, R. , Helminen, H. J. , and Jurvelin, J. S. , 2003, “Fibril Reinforced Poroelastic Model Predicts Specifically Mechanical Behavior of Normal, Proteoglycan Depleted and Collagen Degraded Articular Cartilage,” J. Biomech., 36(9), pp. 1373–1379. 10.1016/S0021-9290(03)00069-1 [DOI] [PubMed] [Google Scholar]
- [136]. Ateshian, G. A. , 2007, “Anisotropy of Fibrous Tissues in Relation to the Distribution of Tensed and Buckled Fibers,” ASME J. Biomech. Eng., 129(2), pp. 240–249. 10.1115/1.2486179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137]. Ateshian, G. A. , Rajan, V. , Chahine, N. O. , Canal, C. E. , and Hung, C. T. , 2009, “Modeling the Matrix of Articular Cartilage Using a Continuous Fiber Angular Distribution Predicts Many Observed Phenomena,” ASME J. Biomech. Eng., 131(6), p. 061003. 10.1115/1.3118773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [138]. Seifzadeh, A. , Wang, J. , Oguamanam, D. C. , and Papini, M. , 2011, “A Nonlinear Biphasic Fiber-Reinforced Porohyperviscoelastic Model of Articular Cartilage Incorporating Fiber Reorientation and Dispersion,” ASME J. Biomech. Eng., 133(8), p. 081004. 10.1115/1.4004832 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [139]. Saarakkala, S. , Laasanen, M. S. , Jurvelin, J. S. , Torronen, K. , Lammi, M. J. , Lappalainen, R. , and Toyras, J. , 2003, “Ultrasound Indentation of Normal and Spontaneously Degenerated Bovine Articular Cartilage,” Osteoarthritis Cartilage, 11(9), pp. 697–705. 10.1016/S1063-4584(03)00154-7 [DOI] [PubMed] [Google Scholar]
- [140]. Fung, Y. C. , 1993, Biomechanics: Mechanical Properties of Living Tissues, Springer-Verlag, New York. [Google Scholar]
- [141]. Keenan, K. E. , Pal, S. , Lindsey, D. P. , Besier, T. F. , and Beaupre, G. S. , “A Viscoelastic Constitutive Model Can Accurately Represent Entire Creep Indentation Tests of Human Patella Cartilage,” J. Appl. Biomech., (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [142]. Thomas, G. C. , Asanbaeva, A. , Vena, P. , Sah, R. L. , and Klisch, S. M. , 2009, “A Nonlinear Constituent Based Viscoelastic Model for Articular Cartilage and Analysis of Tissue Remodeling Due to Altered Glycosaminoglycan-Collagen Interactions,” ASME J. Biomech. Eng., 131(10), p. 101002. 10.1115/1.3192139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [143]. Park, S. , and Ateshian, G. A. , 2006, “Dynamic Response of Immature Bovine Articular Cartilage in Tension and Compression, and Nonlinear Viscoelastic Modeling of the Tensile Response,” ASME J. Biomech. Eng., 128(4), pp. 623–630. 10.1115/1.2206201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [144]. Li, L. P. , and Herzog, W. , 2004, “The Role of Viscoelasticity of Collagen Fibers in Articular Cartilage: Theory and Numerical Formulation,” Biorheology, 41(3–4), pp. 181–194. [PubMed] [Google Scholar]
- [145]. Li, L. P. , Herzog, W. , Korhonen, R. K. , and Jurvelin, J. S. , 2005, “The Role of Viscoelasticity of Collagen Fibers in Articular Cartilage: Axial Tension Versus Compression,” Med. Eng. Phys., 27(1), pp. 51–57. 10.1016/j.medengphy.2004.08.009 [DOI] [PubMed] [Google Scholar]
- [146]. Suh, J. K. , and Bai, S. , 1998, “Finite Element Formulation of Biphasic Poroviscoelastic Model for Articular Cartilage,” ASME J. Biomech. Eng., 120(2), pp. 195–201. 10.1115/1.2798302 [DOI] [PubMed] [Google Scholar]
- [147]. Ateshian, G. A. , 2009, “The Role of Interstitial Fluid Pressurization in Articular Cartilage Lubrication,” J. Biomech., 42(9), pp. 1163–1176. 10.1016/j.jbiomech.2009.04.040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [148]. Bonnevie, E. D. , Baro, V. J. , Wang, L. , and Burris, D. L. , 2012, “Fluid Load Support During Localized Indentation of Cartilage With a Spherical Probe,” J. Biomech., 45(6), pp. 1036–1041. 10.1016/j.jbiomech.2011.12.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [149]. Krishnan, R. , Kopacz, M. , and Ateshian, G. A. , 2004, “Experimental Verification of the Role of Interstitial Fluid Pressurization in Cartilage Lubrication,” J. Orthop. Res., 22(3), pp. 565–570. 10.1016/j.orthres.2003.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [150]. O'Hara, B. P. , Urban, J. P. , and Maroudas, A. , 1990, “Influence of Cyclic Loading on the Nutrition of Articular Cartilage,” Ann. Rheum. Dis., 49(7), pp. 536–539. 10.1136/ard.49.7.536 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [151]. Gu, W. Y. , Lai, W. M. , and Mow, V. C. , 1998, “A Mixture Theory for Charged-Hydrated Soft Tissues Containing Multi-Electrolytes: Passive Transport and Swelling Behaviors,” ASME J. Biomech. Eng., 120(2), pp. 169–180. 10.1115/1.2798299 [DOI] [PubMed] [Google Scholar]
- [152]. Maas, S. , Rawlins, D. , Weiss, J. A. , and Ateshian, G. A. , 2012, FEBio: Finite Elements for Biomechanics, Theory Manual. Available at: http://help.mrl.sci.utah.edu/help/index.jsp [DOI] [PMC free article] [PubMed] [Google Scholar]
- [153]. Holmes, M. H. , and Mow, V. C. , 1990, “The Nonlinear Characteristics of Soft Gels and Hydrated Connective Tissues in Ultrafiltration,” J. Biomech., 23(11), pp. 1145–1156. 10.1016/0021-9290(90)90007-P [DOI] [PubMed] [Google Scholar]
- [154]. Lai, W. M. , Hou, J. S. , and Mow, V. C. , 1991, “A Triphasic Theory for the Swelling and Deformation Behaviors of Articular Cartilage,” ASME J. Biomech. Eng., 113(3), pp. 245–258. 10.1115/1.2894880 [DOI] [PubMed] [Google Scholar]
- [155]. Lai, W. M. , and Mow, V. C. , 1980, “Drag-Induced Compression of Articular Cartilage During a Permeation Experiment,” Biorheology, 17(1–2), pp. 111–123. [DOI] [PubMed] [Google Scholar]
- [156]. Lai, W. M. , Mow, V. C. , and Roth, V. , 1981, “Effects of Nonlinear Strain-Dependent Permeability and Rate of Compression on the Stress Behavior of Articular Cartilage,” ASME J. Biomech. Eng., 103(2), pp. 61–66. 10.1115/1.3138261 [DOI] [PubMed] [Google Scholar]
- [157]. Ateshian, G. A. , Warden, W. H. , Kim, J. J. , Grelsamer, R. P. , and Mow, V. C. , 1997, “Finite Deformation Biphasic Material Properties of Bovine Articular Cartilage From Confined Compression Experiments,” J. Biomech., 30(11–12), pp. 1157–1164. 10.1016/S0021-9290(97)85606-0 [DOI] [PubMed] [Google Scholar]
- [158]. Holmes, M. H. , 1986, “Finite Deformation of Soft Tissue: Analysis of a Mixture Model in Uni-Axial Compression,” ASME J. Biomech. Eng., 108(4), pp. 372–381. 10.1115/1.3138633 [DOI] [PubMed] [Google Scholar]
- [159]. DiSilvestro, M. R. , and Suh, J. K. , 2001, “A Cross-Validation of the Biphasic Poroviscoelastic Model of Articular Cartilage in Unconfined Compression, Indentation, and Confined Compression,” J. Biomech., 34(4), pp. 519–525. 10.1016/S0021-9290(00)00224-4 [DOI] [PubMed] [Google Scholar]
- [160]. Huyghe, J. M. , and Janssen, J. D. , 1997, “Quadriphasic Mechanics of Swelling Incompressible Porous Media,” Int. J. Eng. Sci., 35(8), pp. 793–802. 10.1016/S0020-7225(96)00119-X [DOI] [Google Scholar]
- [161]. Ateshian, G. A. , Chahine, N. O. , Basalo, I. M. , and Hung, C. T. , 2004, “The Correspondence Between Equilibrium Biphasic and Triphasic Material Properties in Mixture Models of Articular Cartilage,” J. Biomech., 37(3), pp. 391–400. 10.1016/S0021-9290(03)00252-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [162]. Wilson, W. , van Donkelaar, C. C. , and Huyghe, J. M. , 2005, “A Comparison Between Mechano-Electrochemical and Biphasic Swelling Theories for Soft Hydrated Tissues,” ASME J. Biomech. Eng., 127(1), pp. 158–165. 10.1115/1.1835361 [DOI] [PubMed] [Google Scholar]
- [163]. Sengers, B. G. , Oomens, C. W. , and Baaijens, F. P. , 2004, “An Integrated Finite-Element Approach to Mechanics, Transport and Biosynthesis in Tissue Engineering,” ASME J. Biomech. Eng., 126(1), pp. 82–91. 10.1115/1.1645526 [DOI] [PubMed] [Google Scholar]
- [164]. Fortin, M. , Soulhat, J. , Shirazi-Adl, A. , Hunziker, E. B. , and Buschmann, M. D. , 2000, “Unconfined Compression of Articular Cartilage: Nonlinear Behavior and Comparison With a Fibril-Reinforced Biphasic Model,” ASME J. Biomech. Eng., 122(2), pp. 189–195. 10.1115/1.429641 [DOI] [PubMed] [Google Scholar]
- [165]. Li, L. P. , Soulhat, J. , Buschmann, M. D. , and Shirazi-Adl, A. , 1999, “Nonlinear Analysis of Cartilage in Unconfined Ramp Compression Using a Fibril Reinforced Poroelastic Model,” Clin. Biomech., 14(9), pp. 673–682. 10.1016/S0268-0033(99)00013-3 [DOI] [PubMed] [Google Scholar]
- [166]. Cohen, B. , Lai, W. M. , and Mow, V. C. , 1998, “A Transversely Isotropic Biphasic Model for Unconfined Compression of Growth Plate and Chondroepiphysis,” ASME J. Biomech. Eng., 120(4), pp. 491–496. 10.1115/1.2798019 [DOI] [PubMed] [Google Scholar]
- [167]. Li, G. , Gil, J. , Kanamori, A. , and Woo, S. L. , 1999, “A Validated Three-Dimensional Computational Model of a Human Knee Joint,” ASME J. Biomech. Eng., 121(6), pp. 657–662. 10.1115/1.2800871 [DOI] [PubMed] [Google Scholar]
- [168]. DiSilvestro, M. R. , Zhu, Q. , and Suh, J. K. , 2001, “Biphasic Poroviscoelastic Simulation of the Unconfined Compression of Articular Cartilage: II—Effect of Variable Strain Rates,” ASME J. Biomech. Eng., 123(2), pp. 198–200. 10.1115/1.1351887 [DOI] [PubMed] [Google Scholar]
- [169]. An, K. N. , Himeno, S. , Tsumura, H. , Kawai, T. , and Chao, E. Y. , 1990, “Pressure Distribution on Articular Surfaces: Application to Joint Stability Evaluation,” J. Biomech., 23(10), pp. 1013–1020. 10.1016/0021-9290(90)90316-U [DOI] [PubMed] [Google Scholar]
- [170]. Menschik, F. , 1997, “The Hip Joint as a Conchoid Shape,” J. Biomech., 30(9), pp. 971–973. 10.1016/S0021-9290(97)00051-1 [DOI] [PubMed] [Google Scholar]
- [171]. Macirowski, T. , Tepic, S. , and Mann, R. W. , 1994, “Cartilage Stresses in the Human Hip Joint,” ASME J. Biomech. Eng., 116(1), pp. 10–18. 10.1115/1.2895693 [DOI] [PubMed] [Google Scholar]
- [172]. Gu, D. Y. , Hu, F. , Wei, J. H. , Dai, K. R. , and Chen, Y. Z. , 2011, “Contributions of Non-Spherical Hip Joint Cartilage Surface to Hip Joint Contact Stress,” Conference Proceedings: Annual International Conference of the IEEE Engineering in Medicine and Biology Society, pp. 8166–8169. [DOI] [PubMed] [Google Scholar]
- [173]. Soslowsky, L. J. , Flatow, E. L. , Bigliani, L. U. , and Mow, V. C. , 1992, “Articular Geometry of the Glenohumeral Joint,” Clin. Orthop. Relat. Res., (285), pp. 181–190. [PubMed] [Google Scholar]
- [174]. Huiskes, R. , Kremers, J. , de Lange, A. , Woltring, H. J. , Selvik, G. , and van Rens, T. J. , 1985, “Analytical Stereophotogrammetric Determination of Three-Dimensional Knee-Joint Geometry,” J. Biomech., 18(8), pp. 559–570. 10.1016/0021-9290(85)90011-9 [DOI] [PubMed] [Google Scholar]
- [175]. Cerveri, P. , Manzotti, A. , and Baroni, G. , “Patient-Specific Acetabular Shape Modelling: Comparison Among Sphere, Ellipsoid and Conchoid Parameterisations,” Comput. Methods Biomech. Biomed. Eng. pp. 1–8. [DOI] [PubMed] [Google Scholar]
- [176]. Genda, E. , Iwasaki, N. , Li, G. , MacWilliams, B. A. , Barrance, P. J. , and Chao, E. Y. , 2001, “Normal Hip Joint Contact Pressure Distribution in Single-Leg Standing–Effect of Gender and Anatomic Parameters,” J. Biomech., 34(7), pp. 895–905. 10.1016/S0021-9290(01)00041-0 [DOI] [PubMed] [Google Scholar]
- [177]. Yoshida, H. , Faust, A. , Wilckens, J. , Kitagawa, M. , Fetto, J. , and Chao, E. Y. , 2006, “Three-Dimensional Dynamic Hip Contact Area and Pressure Distribution During Activities of Daily Living,” J. Biomech., 39(11), pp. 1996–2004. 10.1016/j.jbiomech.2005.06.026 [DOI] [PubMed] [Google Scholar]
- [178]. Afoke, N. Y. , Byers, P. D. , and Hutton, W. C. , 1987, “Contact Pressures in the Human Hip Joint,” J. Bone Jt. Surg., 69(4), pp. 536–541. [DOI] [PubMed] [Google Scholar]
- [179]. Brown, T. D. , and Shaw, D. T. , 1983, “ In Vitro Contact Stress Distributions in the Natural Human Hip,” J. Biomech., 16(6), pp. 373–384. 10.1016/0021-9290(83)90071-4 [DOI] [PubMed] [Google Scholar]
- [180]. von Eisenhart, R. , Adam, C. , Steinlechner, M. , Muller-Gerbl, M. , and Eckstein, F. , 1999, “Quantitative Determination of Joint Incongruity and Pressure Distribution During Simulated Gait and Cartilage Thickness in the Human Hip Joint,” J. Orthop. Res., 17(4), pp. 532–539. 10.1002/jor.1100170411 [DOI] [PubMed] [Google Scholar]
- [181]. von Eisenhart-Rothe, R. , Eckstein, F. , Muller-Gerbl, M. , Landgraf, J. , Rock, C. , and Putz, R. , 1997, “Direct Comparison of Contact Areas, Contact Stress and Subchondral Mineralization in Human Hip Joint Specimens,” Anat. Embryol. (Berl), 195(3), pp. 279–288. 10.1007/s004290050047 [DOI] [PubMed] [Google Scholar]
- [182]. Genda, E. , Konishi, N. , Hasegawa, Y. , and Miura, T. , 1995, “A Computer Simulation Study of Normal and Abnormal Hip Joint Contact Pressure,” Arch. Orthop. Trauma Surg., 114(4), pp. 202–206. 10.1007/BF00444263 [DOI] [PubMed] [Google Scholar]
- [183]. Ateshian, G. A. , and Eckstein, F. , 2005, “Quantitative Anatomy and Imaging of Diarthrodial Joint Articular Layers,” Basic Orthopaedic Biomechanics and Mecho-Biology, Mow V. C. and Huiskes R., eds., Lippincott Williams & Wilkins, Philadelphia. [Google Scholar]
- [184]. Anderson, A. E. , Ellis, B. J. , Maas, S. A. , and Weiss, J. A. , 2010, “Effects of Idealized Joint Geometry on Finite Element Predictions of Cartilage Contact Stresses in the Hip,” J. Biomech., 43(7), pp. 1351–1357. 10.1016/j.jbiomech.2010.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [185]. Harris, M. D. , Anderson, A. E. , Henak, C. R. , Ellis, B. J. , Peters, C. L. , and Weiss, J. A. , 2012, “Finite Element Prediction of Cartilage Contact Stresses in Normal Human Hips,” J. Orthop. Res., 30(7), pp. 1133–1139. 10.1002/jor.22040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [186]. Henak, C. R. , Ellis, B. J. , Harris, M. D. , Anderson, A. E. , Peters, C. L. , and Weiss, J. A. , 2011, “Role of the Acetabular Labrum in Load Support Across the Hip Joint,” J. Biomech., 44(12), pp. 2201–2206. 10.1016/j.jbiomech.2011.06.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [187]. Allen, B. C. , Peters, C. L. , Brown, N. A. , and Anderson, A. E. , 2010, “Acetabular Cartilage Thickness: Accuracy of Three-Dimensional Reconstructions From Multidetector CT Arthrograms in a Cadaver Study,” Radiology, 255(2), pp. 544–552. 10.1148/radiol.10081876 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [188]. Eckstein, F. , Charles, H. C. , Buck, R. J. , Kraus, V. B. , Remmers, A. E. , Hudelmaier, M. , Wirth, W. , and Evelhoch, J. L. , 2005, “Accuracy and Precision of Quantitative Assessment of Cartilage Morphology by Magnetic Resonance Imaging at 3.0T,” Arthritis Rheum., 52(10), pp. 3132–3136. 10.1002/art.21348 [DOI] [PubMed] [Google Scholar]
- [189]. El-Khoury, G. Y. , Alliman, K. J. , Lundberg, H. J. , Rudert, M. J. , Brown, T. D. , and Saltzman, C. L. , 2004, “Cartilage Thickness in Cadaveric Ankles: Measurement With Double-Contrast Multi-Detector Row CT Arthrography versus MR Imaging,” Radiology, 233(3), pp. 768–773. 10.1148/radiol.2333031921 [DOI] [PubMed] [Google Scholar]
- [190]. Wyler, A. , Bousson, V. , Bergot, C. , Polivka, M. , Leveque, E. , Vicaut, E. , and Laredo, J. D. , 2009, “Comparison of MR-Arthrography and CT-Arthrography in Hyaline Cartilage-Thickness Measurement in Radiographically Normal Cadaver Hips With Anatomy as Gold Standard,” Osteoarthritis Cartilage, 17(1), pp. 19–25. 10.1016/j.joca.2008.05.015 [DOI] [PubMed] [Google Scholar]
- [191]. Bachtar, F. , Chen, X. , and Hisada, T. , 2006, “Finite Element Contact Analysis of the Hip Joint,” Med. Biol. Eng. Comput., 44(8), pp. 643–651. 10.1007/s11517-006-0074-9 [DOI] [PubMed] [Google Scholar]
- [192]. Beillas, P. , Papaioannou, G. , Tashman, S. , and Yang, K. H. , 2004, “A New Method to Investigate In Vivo Knee Behavior Using a Finite Element Model of the Lower Limb,” J. Biomech., 37(7), pp. 1019–1030. 10.1016/j.jbiomech.2003.11.022 [DOI] [PubMed] [Google Scholar]
- [193]. Donahue, T. L. , Hull, M. L. , Rashid, M. M. , and Jacobs, C. R. , 2002, “A Finite Element Model of the Human Knee Joint for the Study of Tibio-Femoral Contact,” ASME J. Biomech. Eng., 124(3), pp. 273–280. 10.1115/1.1470171 [DOI] [PubMed] [Google Scholar]
- [194]. Haut Donahue, T. L. , Hull, M. L. , Rashid, M. M. , and Jacobs, C. R. , 2003, “How the Stiffness of Meniscal Attachments and Meniscal Material Properties Affect Tibio-Femoral Contact Pressure Computed Using a Validated Finite Element Model of the Human Knee Joint,” J. Biomech., 36(1), pp. 19–34. 10.1016/S0021-9290(02)00305-6 [DOI] [PubMed] [Google Scholar]
- [195]. Haut Donahue, T. L. , Hull, M. L. , Rashid, M. M. , and Jacobs, C. R. , 2004, “The Sensitivity of Tibiofemoral Contact Pressure to the Size and Shape of the Lateral and Medial Menisci,” J. Orthop. Res., 22(4), pp. 807–814. 10.1016/j.orthres.2003.12.010 [DOI] [PubMed] [Google Scholar]
- [196]. McErlain, D. D. , Milner, J. S. , Ivanov, T. G. , Jencikova-Celerin, L. , Pollmann, S. I. , and Holdsworth, D. W. , 2011, “Subchondral Cysts Create Increased Intra-osseous Stress in Early Knee OA: A Finite Element Analysis Using Simulated Lesions,” Bone, 48(3), pp. 639–646. 10.1016/j.bone.2010.11.010 [DOI] [PubMed] [Google Scholar]
- [197]. Papaioannou, G. , Demetropoulos, C. K. , and King, Y. H. , 2010, “Predicting the Effects of Knee Focal Articular Surface Injury With a Patient-Specific Finite Element Model,” The Knee, 17(1), pp. 61–68. 10.1016/j.knee.2009.05.001 [DOI] [PubMed] [Google Scholar]
- [198]. Papaioannou, G. , Nianios, G. , Mitrogiannis, C. , Fyhrie, D. , Tashman, S. , and Yang, K. H. , 2008, “Patient-Specific Knee Joint Finite Element Model Validation With High-Accuracy Kinematics From Biplane Dynamic Roentgen Stereogrammetric Analysis,” J. Biomech., 41(12), pp. 2633–2638. 10.1016/j.jbiomech.2008.06.027 [DOI] [PubMed] [Google Scholar]
- [199]. Pena, E. , Calvo, B. , Martinez, M. A. , and Doblare, M. , 2006, “A Three-Dimensional Finite Element Analysis of the Combined Behavior of Ligaments and Menisci in the Healthy Human Knee Joint,” J. Biomech., 39(9), pp. 1686–1701. 10.1016/j.jbiomech.2005.04.030 [DOI] [PubMed] [Google Scholar]
- [200]. Pena, E. , Calvo, B. , Martinez, M. A. , and Doblare, M. , 2007, “Effect of the Size and Location of Osteochondral Defects in Degenerative Arthritis. A Finite Element Simulation,” Comput. Biol. Med., 37(3), pp. 376–387. 10.1016/j.compbiomed.2006.04.004 [DOI] [PubMed] [Google Scholar]
- [201]. Pena, E. , Calvo, B. , Martinez, M. A. , Palanca, D. , and Doblare, M. , 2005, “Finite Element Analysis of the Effect of Meniscal Tears and Meniscectomies on Human Knee Biomechanics,” Clin. Biomech., 20(5), pp. 498–507. 10.1016/j.clinbiomech.2005.01.009 [DOI] [PubMed] [Google Scholar]
- [202]. Pena, E. , Martinez, M. A. , Calvo, B. , Palanca, D. , and Doblare, M. , 2005, “A Finite Element Simulation of the Effect of Graft Stiffness and Graft Tensioning in ACL Reconstruction,” Clin. Biomech., 20(6), pp. 636–644. 10.1016/j.clinbiomech.2004.07.014 [DOI] [PubMed] [Google Scholar]
- [203]. Buchler, P. , Ramaniraka, N. A. , Rakotomanana, L. R. , Iannotti, J. P. , and Farron, A. , 2002, “A Finite Element Model of the Shoulder: Application to the Comparison of Normal and Osteoarthritic Joints,” Clin. Biomech., 17(9–10), pp. 630–639. 10.1016/S0268-0033(02)00106-7 [DOI] [PubMed] [Google Scholar]
- [204]. Favre, P. , Senteler, M. , Hipp, J. , Scherrer, S. , Gerber, C. , and Snedeker, J. G. , 2012, “An Integrated Model of Active Glenohumeral Stability,” J. Biomech., 45(13), pp. 2248–2255. 10.1016/j.jbiomech.2012.06.010 [DOI] [PubMed] [Google Scholar]
- [205]. Gatti, C. J. , Maratt, J. D. , Palmer, M. L. , Hughes, R. E. , and Carpenter, J. E. , 2010, “Development and Validation of a Finite Element Model of the Superior Glenoid Labrum,” Ann. Biomed. Eng., 38(12), pp. 3766–3776. 10.1007/s10439-010-0105-4 [DOI] [PubMed] [Google Scholar]
- [206]. Anderson, D. D. , Goldsworthy, J. K. , Li, W. , James Rudert, M. , Tochigi, Y. , and Brown, T. D. , 2007, “Physical Validation of a Patient-Specific Contact Finite Element Model of the Ankle,” J. Biomech., 40(8), pp. 1662–1669. 10.1016/j.jbiomech.2007.01.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [207]. Anderson, D. D. , Goldsworthy, J. K. , Shivanna, K. , Grosland, N. M. , Pedersen, D. R. , Thomas, T. P. , Tochigi, Y. , Marsh, J. L. , and Brown, T. D. , 2006, “Intra-articular Contact Stress Distributions at the Ankle Throughout Stance Phase-Patient-Specific Finite Element Analysis as a Metric of Degeneration Propensity,” Biomech. Model. Mechanobiol., 5(2–3), pp. 82–89. 10.1007/s10237-006-0025-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [208]. Li, W. , Anderson, D. D. , Goldsworthy, J. K. , Marsh, J. L. , and Brown, T. D. , 2008, “Patient-Specific Finite Element Analysis of Chronic Contact Stress Exposure After Intraarticular Fracture of the Tibial Plafond,” J. Orthop. Res., 26(8), pp. 1039–1045. 10.1002/jor.20642 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [209]. Prevrhal, S. , Engelke, K. , and Kalender, W. A. , 1999, “Accuracy Limits for the Determination of Cortical Width and Density: The Influence of Object Size and CT Imaging Parameters,” Phys. Med. Biol., 44(3), pp. 751–764. 10.1088/0031-9155/44/3/017 [DOI] [PubMed] [Google Scholar]
- [210]. Prevrhal, S. , Fox, J. C. , Shepherd, J. A. , and Genant, H. K. , 2003, “Accuracy of CT-Based Thickness Measurement of Thin Structures: Modeling of Limited Spatial Resolution in All Three Dimensions,” Med. Phys., 30(1), pp. 1–8. 10.1118/1.1521940 [DOI] [PubMed] [Google Scholar]
- [211]. Anderson, A. E. , Peters, C. L. , Tuttle, B. D. , and Weiss, J. A. , 2005, “Subject-Specific Finite Element Model of the Pelvis: Development, Validation and Sensitivity Studies,” ASME J. Biomech. Eng., 127(3), pp. 364–373. 10.1115/1.1894148 [DOI] [PubMed] [Google Scholar]
- [212].Llopis, E., Cerezal, L., Kassarjian, A., Higueras, V., and Fernandez, E., 2008, “Direct MR arthrography of the hip with leg traction: feasibility for assessing articular cartilage,” AJR, Am. J. Roentgenol., 190(4), pp. 1124–1128. [DOI] [PubMed] [Google Scholar]
- [213]. Buckwalter, K. A. , Rydberg, J. , Kopecky, K. K. , Crow, K. , and Yang, E. L. , 2001, “Musculoskeletal Imaging With Multislice CT,” AJR, Am. J. Roentgenol., 176(4), pp. 979–986. [DOI] [PubMed] [Google Scholar]
- [214]. Wang, G. , and Vannier, M. W. , 1994, “Stair-Step Artifacts in Three-Dimensional Helical CT: An Experimental Study,” Radiology, 191(1), pp. 79–83. [DOI] [PubMed] [Google Scholar]
- [215]. Jun, B. R. , Yong, H. S. , Kang, E. Y. , Woo, O. H. , and Choi, E. J. , 2012, “64-Slice Coronary Computed Tomography Angiography Using Low Tube Voltage of 80 kV in Subjects With Normal Body Mass Indices: Comparative Study Using 120 kV,” Acta Radiol., 53(10), pp. 1099–1106. [DOI] [PubMed] [Google Scholar]
- [216]. Anderson, A. E. , Ellis, B. J. , Peters, C. L. , and Weiss, J. A. , 2008, “Cartilage Thickness: Factors Influencing Multidetector CT Measurements in a Phantom Study,” Radiology, 246(1), pp. 133–141. 10.1148/radiol.2462070082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [217]. Czerny, C. , Hofmann, S. , Neuhold, A. , Tschauner, C. , Engel, A. , Recht, M. P. , and Kramer, J. , 1996, “Lesions of the Acetabular Labrum: Accuracy of MR Imaging and MR Arthrography in Detection and Staging,” Radiology, 200(1), pp. 225–230. [DOI] [PubMed] [Google Scholar]
- [218]. Petersilge, C. A. , 2001, “MR Arthrography for Evaluation of the Acetabular Labrum,” Skeletal Radiol., 30(8), pp. 423–430. 10.1007/s002560100386 [DOI] [PubMed] [Google Scholar]
- [219]. Petersilge, C. A. , Haque, M. A. , Petersilge, W. J. , Lewin, J. S. , Lieberman, J. M. , and Buly, R. , 1996, “Acetabular Labral Tears: Evaluation With MR Arthrography,” Radiology, 200(1), pp. 231–235. [DOI] [PubMed] [Google Scholar]
- [220]. Steinbach, L. S. , Palmer, W. E. , and Schweitzer, M. E. , 2002, “Special Focus Session. MR Arthrography,” Radiographics, 22(5), pp. 1223–1246. [DOI] [PubMed] [Google Scholar]
- [221]. Mononen, M. E. , Mikkola, M. T. , Julkunen, P. , Ojala, R. , Nieminen, M. T. , Jurvelin, J. S. , and Korhonen, R. K. , 2012, “Effect of Superficial Collagen Patterns and Fibrillation of Femoral Articular Cartilage on Knee Joint Mechanics-A 3D Finite Element Analysis,” J. Biomech., 45(3), pp. 579–587. 10.1016/j.jbiomech.2011.11.003 [DOI] [PubMed] [Google Scholar]
- [222]. Gold, G. E. , Chen, C. A. , Koo, S. , Hargreaves, B. A. , and Bangerter, N. K. , 2009, “Recent Advances in MRI of Articular Cartilage,” AJR, Am. J. Roentgenol., 193(3), pp. 628–638. 10.2214/AJR.09.3042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [223]. Gold, S. L. , Burge, A. J. , and Potter, H. G. , 2012, “MRI of Hip Cartilage: Joint Morphology, Structure, and Composition,” Clin. Orthop. Relat. Res., 470(12), pp. 3321–3331. 10.1007/s11999-012-2403-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [224]. Potter, H. G. , Black, B. R. , and Chong le, R. , 2009, “New Techniques in Articular Cartilage Imaging,” Clin. Sports Med., 28(1), pp. 77–94. 10.1016/j.csm.2008.08.004 [DOI] [PubMed] [Google Scholar]
- [225]. Potter, H. G. , and Schachar, J. , 2010, “High Resolution Noncontrast MRI of the Hip,” J. Magn. Reson. Imaging, 31(2), pp. 268–278. 10.1002/jmri.22025 [DOI] [PubMed] [Google Scholar]
- [226]. Recht, M. P. , Goodwin, D. W. , Winalski, C. S. , and White, L. M. , 2005, “MRI of Articular Cartilage: Revisiting Current Status and Future Directions,” AJR, Am. J. Roentgenol., 185(4), pp. 899–914. 10.2214/AJR.05.0099 [DOI] [PubMed] [Google Scholar]
- [227]. Shapiro, L. , Harish, M. , Hargreaves, B. , Staroswiecki, E. , and Gold, G. , 2012, “Advances in Musculoskeletal MRI: Technical Considerations,” J. Magn. Reson. Imaging, 36(4), pp. 775–787. 10.1002/jmri.23629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [228]. Mamisch, T. C. , Bittersohl, B. , Hughes, T. , Kim, Y. J. , Welsch, G. H. , Dudda, M. , Siebenrock, K. A. , Werlen, S. , and Trattnig, S. , 2008, “Magnetic Resonance Imaging of the Hip at 3 Tesla: Clinical Value in Femoroacetabular Impingement of the Hip and Current Concepts,” Semin. Musculoskeletal Radiol., 12(3), pp. 212–222. 10.1055/s-0028-1083105 [DOI] [PubMed] [Google Scholar]
- [229]. Julkunen, P. , Korhonen, R. K. , Nissi, M. J. , and Jurvelin, J. S. , 2008, “Mechanical Characterization of Articular Cartilage by Combining Magnetic Resonance Imaging and Finite-Element Analysis: A Potential Functional Imaging Technique,” Phys. Med. Biol., 53(9), pp. 2425–2438. 10.1088/0031-9155/53/9/014 [DOI] [PubMed] [Google Scholar]
- [230]. Pierce, D. M. , Trobin, W. , Raya, J. G. , Trattnig, S. , Bischof, H. , Glaser, C. , and Holzapfel, G. A. , 2010, “DT-MRI Based Computation of Collagen Fiber Deformation in Human Articular Cartilage: A Feasibility Study,” Ann. Biomed. Eng., 38(7), pp. 2447–2463. 10.1007/s10439-010-9990-9 [DOI] [PubMed] [Google Scholar]
- [231]. Mlynarik, V. , Degrassi, A. , Toffanin, R. , Vittur, F. , Cova, M. , and Pozzi-Mucelli, R. S. , 1996, “Investigation of Laminar Appearance of Articular Cartilage by Means of Magnetic Resonance Microscopy,” Magn. Reson. Imaging, 14(4), pp. 435–442. 10.1016/0730-725X(96)00025-2 [DOI] [PubMed] [Google Scholar]
- [232]. Xia, Y. , 1998, “Relaxation Anisotropy in Cartilage by NMR Microscopy (muMRI) at 14-Microm Resolution,” Magn. Reson. Med., 39(6), pp. 941–949. 10.1002/mrm.1910390612 [DOI] [PubMed] [Google Scholar]
- [233]. Xia, Y. , Farquhar, T. , Burton-Wurster, N. , and Lust, G. , 1997, “Origin of Cartilage Laminae in MRI,” J. Magn. Reson. Imaging, 7(5), pp. 887–894. 10.1002/jmri.1880070518 [DOI] [PubMed] [Google Scholar]
- [234]. Brossmann, J. , Frank, L. R. , Pauly, J. M. , Boutin, R. D. , Pedowitz, R. A. , Haghighi, P. , and Resnick, D. , 1997, “Short Echo Time Projection Reconstruction MR Imaging of Cartilage: Comparison With Fat-Suppressed Spoiled GRASS and Magnetization Transfer Contrast MR Imaging,” Radiology, 203(2), pp. 501–507. [DOI] [PubMed] [Google Scholar]
- [235]. Rand, T. , Imhof, H. , Czerny, C. , Breitenseher, M. , Machold, K. , Turetschek, K. , and Trattnig, S. , 1999, “Discrimination Between Fluid, Synovium, and Cartilage in Patients With Rheumatoid Arthritis: Contrast Enhanced Spin Echo Versus Non-contrast-Enhanced Fat-Suppressed Gradient Echo MR Imaging,” Clin. Radiol., 54(2), pp. 107–110. 10.1016/S0009-9260(99)91070-X [DOI] [PubMed] [Google Scholar]
- [236]. Recht, M. P. , Kramer, J. , Marcelis, S. , Pathria, M. N. , Trudell, D. , Haghighi, P. , Sartoris, D. J. , and Resnick, D. , 1993, “Abnormalities of Articular Cartilage in the Knee: Analysis of Available MR Techniques,” Radiology, 187(2), pp. 473–478. [DOI] [PubMed] [Google Scholar]
- [237]. Rakhra, K. S. , Lattanzio, P. J. , Cardenas-Blanco, A. , Cameron, I. G. , and Beaule, P. E. , 2012, “Can T1-Rho MRI Detect Acetabular Cartilage Degeneration in Femoroacetabular Impingement?: A Pilot Study,” J. Bone Jt. Surg. Br., 94(9), pp. 1187–1192. [DOI] [PubMed] [Google Scholar]
- [238]. Cohen, Z. A. , McCarthy, D. M. , Kwak, S. D. , Legrand, P. , Fogarasi, F. , Ciaccio, E. J. , and Ateshian, G. A. , 1999, “Knee Cartilage Topography, Thickness, and Contact Areas From MRI: In-Vitro Calibration and In-Vivo Measurements,” Osteoarthritis Cartilage, 7(1), pp. 95–109. 10.1053/joca.1998.0165 [DOI] [PubMed] [Google Scholar]
- [239]. McGibbon, C. A. , Bencardino, J. , Yeh, E. D. , and Palmer, W. E. , 2003, “Accuracy of Cartilage and Subchondral Bone Spatial Thickness Distribution From MRI,” J. Magn. Reson. Imaging, 17(6), pp. 703–715. 10.1002/jmri.10309 [DOI] [PubMed] [Google Scholar]
- [240]. Moro-oka, T. A. , Hamai, S. , Miura, H. , Shimoto, T. , Higaki, H. , Fregly, B. J. , Iwamoto, Y. , and Banks, S. A. , 2007, “Can Magnetic Resonance Imaging-Derived Bone Models Be Used for Accurate Motion Measurement With Single-Plane Three-Dimensional Shape Registration?,” J. Orthop. Res., 25(7), pp. 867–872. 10.1002/jor.20355 [DOI] [PubMed] [Google Scholar]
- [241]. Scientific Computing and Imaging Institute, £Seg3D, “Volumetric Image Segmentation and Visualization. Scientific Computing and Imaging Institute (SCI),” http://www.seg3d.org.
- [242]. Boissonnat, J.-D. , 1988, “Shape Reconstruction From Planar Cross Sections,” Comput. Vis. Graph. Image Process., 44(1), pp. 1–29. 10.1016/S0734-189X(88)80028-8 [DOI] [Google Scholar]
- [243]. Schneider, E. , Nevitt, M. , McCulloch, C. , Cicuttini, F. M. , Duryea, J. , Eckstein, F. , and Tamez-Pena, J. , 2012, “Equivalence and Precision of Knee Cartilage Morphometry Between Different Segmentation Teams, Cartilage Regions, and MR Acquisitions,” Osteoarthritis Cartilage, 20(8), pp. 869–879. 10.1016/j.joca.2012.04.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [244]. Taubin, G. , Zhang, T. , and Golub, G. , 1996, “Optimal Surface Smoothing as Filter Design Computer Vision — ECCV’96,” Buxton B. and Cipolla R., eds., Springer, Berlin/Heidelberg, pp. 283–292. [Google Scholar]
- [245]. Stammberger, T. , Eckstein, F. , Michaelis, M. , Englmeier, K. H. , and Reiser, M. , 1999, “Interobserver Reproducibility of Quantitative Cartilage Measurements: Comparison of B-Spline Snakes and Manual Segmentation,” Magn. Reson. Imaging, 17(7), pp. 1033–1042. 10.1016/S0730-725X(99)00040-5 [DOI] [PubMed] [Google Scholar]
- [246]. Al-Helo, S. , Alomari, R. S. , Chaudhary, V. , and Al-Zoubi, M. B. , 2011, “Segmentation of Lumbar Vertebrae From Clinical CT Using Active Shape Models and GVF-Snake,” Conf. Proc. IEEE Eng. Med. Biol. Soc., 2011, pp. 8033–8036. [DOI] [PubMed] [Google Scholar]
- [247]. Fripp, J. , Crozier, S. , Warfield, S. K. , and Ourselin, S. , 2007, “Automatic Segmentation of the Bone and Extraction of the Bone-Cartilage Interface From Magnetic Resonance Images of the Knee,” Phys. Med. Biol., 52(6), pp. 1617–1631. 10.1088/0031-9155/52/6/005 [DOI] [PubMed] [Google Scholar]
- [248]. Lamecker, H. , Seebass, M. , Hege, H. C. , and Deuflhard, P. , 2004, “A 3D Statistical Shape Model of the Pelvic Bone for Segmentation,” Proc. SPIE, Medical Imaging: Image Processing, 5370, pp. 1341–1351. [Google Scholar]
- [249]. Tameem, H. Z. , Selva, L. E. , and Sinha, U. S. , 2007, “Morphological Atlases of Knee Cartilage: Shape Indices to Analyze Cartilage Degradation in Osteoarthritic and Non-osteoarthritic Population,” Conf. Proc. IEEE Eng. Med. Biol. Soc., 2007, pp. 1310–1313. [DOI] [PubMed] [Google Scholar]
- [250]. Heimann, T. , and Meinzer, H. P. , 2009, “Statistical Shape Models for 3D Medical Image Segmentation: A Review,” Med. Image Anal., 13(4), pp. 543–563. 10.1016/j.media.2009.05.004 [DOI] [PubMed] [Google Scholar]
- [251]. Baldwin, M. A. , Langenderfer, J. E. , Rullkoetter, P. J. , and Laz, P. J. , 2010, “Development of Subject-Specific and Statistical Shape Models of the Knee Using an Efficient Segmentation and Mesh-Morphing Approach,” Comput. Methods Programs Biomed., 97(3), pp. 232–240. 10.1016/j.cmpb.2009.07.005 [DOI] [PubMed] [Google Scholar]
- [252]. Weiss, J. A. , Gardiner, J. C. , Ellis, B. J. , Lujan, T. J. , and Phatak, N. S. , 2005, “Three-Dimensional Finite Element Modeling of Ligaments: Technical Aspects,” Med. Eng. Phys., 27(10), pp. 845–861. 10.1016/j.medengphy.2005.05.006 [DOI] [PubMed] [Google Scholar]
- [253]. Lo, S. H. , 1991, “Volume Discretization Into Tetrahedra—I. Verification and Orientation of Boundary Surfaces,” Computers & Structures, 39(5), pp. 493–500. 10.1016/0045-7949(91)90058-T [DOI] [Google Scholar]
- [254]. Lo, S. H. , 1991, “Volume Discretization Into Tetrahedra—II. 3D Triangulation by Advancing Front Approach,” Comput. Struct., 39(5), pp. 501–511. 10.1016/0045-7949(91)90059-U [DOI] [Google Scholar]
- [255]. Shephard, M. S. , and Georges, M. K. , 1991, “Automatic Three-Dimensional Mesh Generation by the Finite Octree Technique,” Int. J. Numer. Methods Eng., 32(4), pp. 709–749. 10.1002/nme.1620320406 [DOI] [Google Scholar]
- [256]. Wrazidlo, W. , Brambs, H. J. , Lederer, W. , Schneider, S. , Geiger, B. , and Fischer, C. , 1991, “An Alternative Method of Three-Dimensional Reconstruction From Two-Dimensional CT and MR Data Sets,” Eur. J. Radiol., 12(1), pp. 11–16. 10.1016/0720-048X(91)90125-F [DOI] [PubMed] [Google Scholar]
- [257]. Zienkiewicz, O. C. , and Taylor, R. L. , 2000, The Finite Element Method: The Basis, Butterworth-Heinemann, Oxford. [Google Scholar]
- [258]. Beissel, S. R. , and Johnson, G. R. , 2000, “Large-Deformation Triangular and Tetrahedral Element Formulations for Unstructured Meshes,” Comput. Methods Appl. Mech. Eng., 187(3-4), pp. 469–482. 10.1016/S0045-7825(99)00336-9 [DOI] [Google Scholar]
- [259]. Bonet, J. , Marriott, H. , and Hassan, O. , 2001, “An Averaged Nodal Deformation Gradient Linear Tetrahedral Element for Large Strain Explicit Dynamic Applications,” Commun. Numer. Methods Eng., 17(8), pp. 551–561. 10.1002/cnm.429 [DOI] [Google Scholar]
- [260]. Gee, M. W. , Dohrmann, C. R. , Key, S. W. , and Wall, W. A. , 2009, “A Uniform Nodal Strain Tetrahedron With Isochoric Stabilization,” Int. J. Numer. Methods Eng., 78(4), pp. 429–443. 10.1002/nme.2493 [DOI] [Google Scholar]
- [261]. Puso, M. A. , and Solberg, J. , 2006, “A Stabilized Nodally Integrated Tetrahedral,” Int. J. Numer. Methods Eng., 67(6), pp. 841–867. 10.1002/nme.1651 [DOI] [Google Scholar]
- [262]. Taylor, R. L. , 2000, “A Mixed-Enhanced Formulation for Tetrahedral Finite Elements,” Int. J. Numer. Methods Eng., 47(1-3), pp. 205–227. [DOI] [Google Scholar]
- [263]. Yao, J. , Funkenbusch, P. D. , Snibbe, J. , Maloney, M. , and Lerner, A. L. , 2006, “Sensitivities of Medial Meniscal Motion and Deformation to Material Properties of Articular Cartilage, Meniscus and Meniscal Attachments Using Design of Experiments Methods,” ASME J. Biomech. Eng., 128(3), pp. 399–408. 10.1115/1.2191077 [DOI] [PubMed] [Google Scholar]
- [264]. Yao, J. , Salo, A. D. , Lee, J. , and Lerner, A. L. , 2008, “Sensitivity of Tibio-Menisco-Femoral Joint Contact Behavior to Variations in Knee Kinematics,” J. Biomech., 41(2), pp. 390–398. 10.1016/j.jbiomech.2007.08.015 [DOI] [PubMed] [Google Scholar]
- [265]. Fregly, B. J. , Besier, T. F. , Lloyd, D. G. , Delp, S. L. , Banks, S. A. , Pandy, M. G. , and D'Lima, D. D. , 2012, “Grand Challenge Competition to Predict In Vivo Knee Loads,” J. Orthop. Res., 30(4), pp. 503–513. 10.1002/jor.22023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [266]. Kennedy, M. J. , Lamontagne, M. , and Beaule, P. E. , 2009, “Femoroacetabular Impingement Alters Hip and Pelvic Biomechanics During Gait Walking Biomechanics of FAI,” Gait and Posture, 30(1), pp. 41–44. 10.1016/j.gaitpost.2009.02.008 [DOI] [PubMed] [Google Scholar]
- [267]. Rau, G. , Disselhorst-Klug, C. , and Schmidt, R. , 2000, “Movement Biomechanics Goes Upwards: From the Leg to the Arm,” J. Biomech., 33(10), pp. 1207–1216. 10.1016/S0021-9290(00)00062-2 [DOI] [PubMed] [Google Scholar]
- [268]. Fuller, J. , Liu, L. J. , Murphy, M. C. , and Mann, R. W. , 1997, “A Comparison of Lower-Extremity Skeletal Kinematics Measured Using Skin- and Pin-Mounted Markers,” Hum. Mov. Sci., 16(2-3), pp. 219–242. 10.1016/S0167-9457(96)00053-X [DOI] [Google Scholar]
- [269]. Garling, E. H. , Kaptein, B. L. , Mertens, B. , Barendregt, W. , Veeger, H. E. , Nelissen, R. G. , and Valstar, E. R. , 2007, “Soft-Tissue Artefact Assessment During Step-Up Using Fluoroscopy and Skin-Mounted Markers,” J. Biomech., 40(Suppl 1), pp. S18–S24. 10.1016/j.jbiomech.2007.03.003 [DOI] [PubMed] [Google Scholar]
- [270]. Anderst, W. J. , Les, C. , and Tashman, S. , 2005, “ In Vivo Serial Joint Space Measurements During Dynamic Loading in a Canine Model of Osteoarthritis,” Osteoarthritis Cartilage, 13(9), pp. 808–816. 10.1016/j.joca.2005.04.019 [DOI] [PubMed] [Google Scholar]
- [271]. Bey, M. J. , Zauel, R. , Brock, S. K. , and Tashman, S. , 2006, “Validation of a New Model-Based Tracking Technique for Measuring Three-Dimensional, In Vivo Glenohumeral Joint Kinematics,” ASME J. Biomech. Eng., 128(4), pp. 604–609. 10.1115/1.2206199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [272]. Bingham, J. T. , Papannagari, R. , Van de Velde, S. K. , Gross, C. , Gill, T. J. , Felson, D. T. , Rubash, H. E. , and Li, G. , 2008, “ In Vivo Cartilage Contact Deformation in the Healthy Human Tibiofemoral Joint,” Rheumatology, 47(11), pp. 1622–1627. 10.1093/rheumatology/ken345 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [273]. Boyer, P. J. , Massimini, D. F. , Gill, T. J. , Papannagari, R. , Stewart, S. L. , Warner, J. P. , and Li, G. , 2008, “ In Vivo Articular Cartilage Contact at the Glenohumeral Joint: Preliminary Report,” J. Orthop. Sci., 13(4), pp. 359–365. 10.1007/s00776-008-1237-3 [DOI] [PubMed] [Google Scholar]
- [274]. Fu, E. , Li, G. , Souer, J. S. , Lozano-Calderon, S. , Herndon, J. H. , Jupiter, J. B. , and Chen, N. C. , 2009, “Elbow Position Affects Distal Radioulnar Joint Kinematics,” J. Hand Surg., 34(7), pp. 1261–1268. 10.1016/j.jhsa.2009.04.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [275]. Kozanek, M. , Fu, E. C. , Van de Velde, S. K. , Gill, T. J. , and Li, G. , 2009, “Posterolateral Structures of the Knee in Posterior Cruciate Ligament Deficiency,” Am. J. Sports Med., 37(3), pp. 534–541. 10.1177/0363546508325664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [276]. Li, G. , Papannagari, R. , Nha, K. W. , Defrate, L. E. , Gill, T. J. , and Rubash, H. E. , 2007, “The Coupled Motion of the Femur and Patella During In Vivo Weightbearing Knee Flexion,” ASME J. Biomech. Eng., 129(6), pp. 937–943. 10.1115/1.2803267 [DOI] [PubMed] [Google Scholar]
- [277]. Li, G. , Van de Velde, S. K. , and Bingham, J. T. , 2008, “Validation of a Non-invasive Fluoroscopic Imaging Technique for the Measurement of Dynamic Knee Joint Motion,” J. Biomech., 41(7), pp. 1616–1622. 10.1016/j.jbiomech.2008.01.034 [DOI] [PubMed] [Google Scholar]
- [278]. Moynihan, A. L. , Varadarajan, K. M. , Hanson, G. R. , Park, S. E. , Nha, K. W. , Suggs, J. F. , Johnson, T. , and Li, G. , 2010, “ In Vivo Knee Kinematics During High Flexion After a Posterior-Substituting Total Knee Arthroplasty,” Int. Orthop., 34(4), pp. 497–503. 10.1007/s00264-009-0777-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [279]. Nha, K. W. , Papannagari, R. , Gill, T. J. , Van de Velde, S. K. , Freiberg, A. A. , Rubash, H. E. , and Li, G. , 2008, “ In Vivo Patellar Tracking: Clinical Motions and Patellofemoral Indices,” J. Orthop. Res., 26(8), pp. 1067–1074. 10.1002/jor.20554 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [280]. Suggs, J. F. , Kwon, Y. M. , Durbhakula, S. M. , Hanson, G. R. , and Li, G. , 2009, “ In Vivo Flexion and Kinematics of the Knee After TKA: Comparison of a Conventional and a High Flexion Cruciate-Retaining TKA Design,” Knee Surg. Sports Traumatol. Arthrosc., 17(2), pp. 150–156. 10.1007/s00167-008-0637-4 [DOI] [PubMed] [Google Scholar]
- [281]. Tashman, S. , and Anderst, W. , 2003, “In-Vivo Measurement of Dynamic Joint Motion Using High Speed Biplane Radiography and CT: Application to Canine ACL Deficiency,” ASME J. Biomech. Eng., 125(2), pp. 238–245. 10.1115/1.1559896 [DOI] [PubMed] [Google Scholar]
- [282]. Tashman, S. , Anderst, W. , Kolowich, P. , Havstad, S. , and Arnoczky, S. , 2004, “Kinematics of the ACL-Deficient Canine Knee During Gait: Serial Changes Over Two Years,” J. Orthop. Res., 22(5), pp. 931–941. 10.1016/j.orthres.2004.01.008 [DOI] [PubMed] [Google Scholar]
- [283]. Van de Velde, S. K. , Bingham, J. T. , Gill, T. J. , and Li, G. , 2009, “Analysis of Tibiofemoral Cartilage Deformation in the Posterior Cruciate Ligament-Deficient Knee,” J. Bone Jt. Surg., 91(1), pp. 167–175. 10.2106/JBJS.H.00177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [284]. Bey, M. J. , Kline, S. K. , Tashman, S. , and Zauel, R. , 2008, “Accuracy of Biplane X-ray Imaging Combined With Model-Based Tracking for Measuring In-Vivo Patellofemoral Joint Motion,” J. Orthop. Surg. Res., 3, p. 38. 10.1186/1749-799X-3-38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [285]. Suggs, J. , Wang, C. , and Li, G. , 2003, “The Effect of Graft Stiffness on Knee Joint Biomechanics After ACL Reconstruction–A 3D Computational Simulation,” Clin. Biomech., 18(1), pp. 35–43. 10.1016/S0268-0033(02)00137-7 [DOI] [PubMed] [Google Scholar]
- [286]. Wan, L. , de Asla, R. J. , Rubash, H. E. , and Li, G. , 2008, “ In Vivo Cartilage Contact Deformation of Human Ankle Joints Under Full Body Weight,” J. Orthop. Res., 26(8), pp. 1081–1089. 10.1002/jor.20593 [DOI] [PubMed] [Google Scholar]
- [287]. You, B. M. , Siy, P. , Anderst, W. , and Tashman, S. , 2001, “ In Vivo Measurement of 3-D Skeletal Kinematics From Sequences of Biplane Radiographs: Application to Knee Kinematics,” IEEE Trans. Med. Imaging, 20(6), pp. 514–525. 10.1109/42.929617 [DOI] [PubMed] [Google Scholar]
- [288]. Acker, S. , Li, R. , Murray, H. , John, P. S. , Banks, S. , Mu, S. , Wyss, U. , and Deluzio, K. , 2011, “Accuracy of Single-Plane Fluoroscopy in Determining Relative Position and Orientation of Total Knee Replacement Components,” J. Biomech., 44(4), pp. 784–787. 10.1016/j.jbiomech.2010.10.033 [DOI] [PubMed] [Google Scholar]
- [289]. Wassilew, G. I. , Janz, V. , Heller, M. O. , Tohtz, S. , Rogalla, P. , Hein, P. , and Perka, C. , 2013, “Real Time Visualization of Femoroacetabular Impingement and Subluxation Using 320-Slice Computed Tomography,” J. Orthop. Res., 31(2), pp. 275–281. 10.1002/jor.22224 [DOI] [PubMed] [Google Scholar]
- [290]. Bergmann, G. , Deuretzbacher, G. , Heller, M. , Graichen, F. , Rohlmann, A. , Strauss, J. , and Duda, G. N. , 2001, “Hip Contact Forces and Gait Patterns From Routine Activities,” J. Biomech., 34(7), pp. 859–871. 10.1016/S0021-9290(01)00040-9 [DOI] [PubMed] [Google Scholar]
- [291]. Bergmann, G. , Graichen, F. , Rohlmann, A. , and Linke, H. , 1997, “Hip Joint Forces During Load Carrying,” Clin. Orthop. Relat. Res., (335), pp. 190–201. [PubMed] [Google Scholar]
- [292]. Hodge, W. A. , Fijan, R. S. , Carlson, K. L. , Burgess, R. G. , Harris, W. H. , and Mann, R. W. , 1986, “Contact Pressures in the Human Hip Joint Measured In Vivo ,” Proc. Natl. Acad. Sci. U.S.A., 83(9), pp. 2879–2883. 10.1073/pnas.83.9.2879 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [293]. Varadarajan, K. M. , Moynihan, A. L. , D'Lima, D. , Colwell, C. W. , and Li, G. , 2008, “ In Vivo Contact Kinematics and Contact Forces of the Knee After Total Knee Arthroplasty During Dynamic Weight-Bearing Activities,” J. Biomech., 41(10), pp. 2159–2168. 10.1016/j.jbiomech.2008.04.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [294]. Westerhoff, P. , Graichen, F. , Bender, A. , Halder, A. , Beier, A. , Rohlmann, A. , and Bergmann, G. , 2011, “Measurement of Shoulder Joint Loads During Wheelchair Propulsion Measured In Vivo ,” Clin. Biomech., 26(10), pp. 982–989. 10.1016/j.clinbiomech.2011.05.017 [DOI] [PubMed] [Google Scholar]
- [295]. Westerhoff, P. , Graichen, F. , Bender, A. , Rohlmann, A. , and Bergmann, G. , 2009, “An Instrumented Implant for In Vivo Measurement of Contact Forces and Contact Moments in the Shoulder Joint,” Med. Eng. Phys., 31(2), pp. 207–213. 10.1016/j.medengphy.2008.07.011 [DOI] [PubMed] [Google Scholar]
- [296]. Zhao, D. , Banks, S. A. , D'Lima, D. D. , Colwell, C. W., Jr. , and Fregly, B. J. , 2007, “ In Vivo Medial and Lateral Tibial Loads During Dynamic and High Flexion Activities,” J. Orthop. Res., 25(5), pp. 593–602. 10.1002/jor.20362 [DOI] [PubMed] [Google Scholar]
- [297]. Erdemir, A. , McLean, S. , Herzog, W. , and van den Bogert, A. J. , 2007, “Model-Based Estimation of Muscle Forces Exerted During Movements,” Clin. Biomech., 22(2), pp. 131–154. 10.1016/j.clinbiomech.2006.09.005 [DOI] [PubMed] [Google Scholar]
- [298]. Pandy, M. G. , Anderson, F. C. , and Hull, D. G. , 1992, “A Parameter Optimization Approach for the Optimal Control of Large-Scale Musculoskeletal Systems,” ASME J. Biomech. Eng., 114(4), pp. 450–460. 10.1115/1.2894094 [DOI] [PubMed] [Google Scholar]
- [299]. Anderson, F. C. , and Pandy, M. G. , 2001, “Static and Dynamic Optimization Solutions for Gait Are Practically Equivalent,” J. Biomech., 34(2), pp. 153–161. 10.1016/S0021-9290(00)00155-X [DOI] [PubMed] [Google Scholar]
- [300]. Gardiner, J. C. , and Weiss, J. A. , 2003, “Subject-Specific Finite Element Analysis of the Human Medial Collateral Ligament During Valgus Knee Loading,” J. Orthop. Res., 21(6), pp. 1098–1106. 10.1016/S0736-0266(03)00113-X [DOI] [PubMed] [Google Scholar]
- [301]. Viceconti, M. , and Taddei, F. , 2003, “Automatic Generation of Finite Element Meshes From Computed Tomography Data,” Crit. Rev. Biomed. Eng., 31(1-2), pp. 27–72. 10.1615/CritRevBiomedEng.v31.i12.20 [DOI] [PubMed] [Google Scholar]
- [302]. Dalstra, M. , Huiskes, R. , Odgaard, A. , and van Erning, L. , 1993, “Mechanical and Textural Properties of Pelvic Trabecular Bone,” J. Biomech., 26(4-5), pp. 523–535. 10.1016/0021-9290(93)90014-6 [DOI] [PubMed] [Google Scholar]
- [303]. Dalstra, M. , Huiskes, R. , and van Erning, L. , 1995, “Development and Validation of a Three-Dimensional Finite Element Model of the Pelvic Bone,” ASME J. Biomech. Eng., 117(3), pp. 272–278. 10.1115/1.2794181 [DOI] [PubMed] [Google Scholar]
- [304]. Mononen, M. E. , Julkunen, P. , Toyras, J. , Jurvelin, J. S. , Kiviranta, I. , and Korhonen, R. K. , 2011, “Alterations in Structure and Properties of Collagen Network of Osteoarthritic and Repaired Cartilage Modify Knee Joint stresses,” Biomech. Model. Mechanobiol., 10(3), pp. 357–369. 10.1007/s10237-010-0239-1 [DOI] [PubMed] [Google Scholar]
- [305]. Nieminen, M. T. , Toyras, J. , Laasanen, M. S. , Silvennoinen, J. , Helminen, H. J. , and Jurvelin, J. S. , 2004, “Prediction of Biomechanical Properties of Articular Cartilage With Quantitative Magnetic Resonance Imaging,” J. Biomech., 37(3), pp. 321–328. 10.1016/S0021-9290(03)00291-4 [DOI] [PubMed] [Google Scholar]
- [306]. Nissi, M. J. , Rieppo, J. , Toyras, J. , Laasanen, M. S. , Kiviranta, I. , Nieminen, M. T. , and Jurvelin, J. S. , 2007, “Estimation of Mechanical Properties of Articular Cartilage With MRI - dGEMRIC, T2 and T1 Imaging in Different Species With Variable Stages of Maturation,” Osteoarthritis Cartilage, 15(10), pp. 1141–1148. 10.1016/j.joca.2007.03.018 [DOI] [PubMed] [Google Scholar]
- [307]. Räsänen, L. P. , Mononen, M. E. , Nieminen, M. T. , Lammentausta, E. , Jurvelin, J. S. , and Korhonen, R. K. , 2013, “Implementation of Subject-Specific Collagen Architecture of Cartilage Into a 2D Computational Model of a Knee Joint-Data From the Osteoarthritis Initiative (OAI),” J. Orthop. Res., 31(1), pp. 10–22. 10.1002/jor.22175 [DOI] [PubMed] [Google Scholar]
- [308]. Jobke, B. , Bolbos, R. , Saadat, E. , Cheng, J. , Li, X. , and Majumdar, S. , 2013, “Mechanism of Disease in Early Osteoarthritis: Application of Modern MR Imaging Techniques - A Technical Report,” Magn. Reson. Imaging, 31(1), pp. 156–161. 10.1016/j.mri.2012.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [309]. Tang, S. Y. , Souza, R. B. , Ries, M. , Hansma, P. K. , Alliston, T. , and Li, X. , 2011, “Local Tissue Properties of Human Osteoarthritic Cartilage Correlate With Magnetic Resonance T(1) Rho Relaxation Times,” J. Orthop. Res., 29(9), pp. 1312–1319. 10.1002/jor.21381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [310]. Pierce, D. M. , Ricken, T. , and Holzapfel, G. A. , “A Hyperelastic Biphasic Fibre-Reinforced Model of Articular Cartilage Considering Distributed Collagen Fibre Orientations: Continuum Basis, Computational Aspects and Applications,” Comput. Methods Biomech. Biomed. Eng., (in press). [DOI] [PubMed] [Google Scholar]
- [311]. Bittersohl, B. , Miese, F. R. , Hosalkar, H. S. , Herten, M. , Antoch, G. , Krauspe, R. , and Zilkens, C. , 2012, “T2* Mapping of Hip Joint Cartilage in Various Histological Grades of Degeneration,” Osteoarthritis Cartilage, 20(7), pp. 653–660. 10.1016/j.joca.2012.03.011 [DOI] [PubMed] [Google Scholar]
- [312]. Bittersohl, B. , Hosalkar, H. S. , Hughes, T. , Kim, Y. J. , Werlen, S. , Siebenrock, K. A. , and Mamisch, T. C. , 2009, “Feasibility of T2* Mapping for the Evaluation of Hip Joint Cartilage at 1.5T Using a Three-Dimensional (3D), Gradient-Echo (GRE) Sequence: A Prospective Study,” Magn. Reson. Med., 62(4), pp. 896–901. 10.1002/mrm.22096 [DOI] [PubMed] [Google Scholar]
- [313]. Xia, Y. , 2007, “Resolution ‘Scaling Law’ in MRI of Articular Cartilage,” Osteoarthritis Cartilage, 15(4), pp. 363–365. 10.1016/j.joca.2006.12.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [314].ASME Committee (PT60) on Verification and Validation in Computational Solid Mechanics, 2006, “Guide for Verification and Validation in Computational Solid Mechanics,“ America Society of Mechanical Engineers, New York. [Google Scholar]
- [315]. Henninger, H. B. , Reese, S. P. , Anderson, A. E. , and Weiss, J. A. , 2010, “Validation of Computational Models in Biomechanics,” Proc. Inst. Mech. Eng., Part H: J. Eng. Med., 224(7), pp. 801–812. 10.1243/09544119JEIM649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [316]. Baldwin, M. A. , Clary, C. , Maletsky, L. P. , and Rullkoetter, P. J. , 2009, “Verification of Predicted Specimen-Specific Natural and Implanted Patellofemoral Kinematics During Simulated Deep Knee Bend,” J. Biomech., 42(14), pp. 2341–2348. 10.1016/j.jbiomech.2009.06.028 [DOI] [PubMed] [Google Scholar]
- [317]. Elias, J. J. , Wilson, D. R. , Adamson, R. , and Cosgarea, A. J. , 2004, “Evaluation of a Computational Model Used to Predict the Patellofemoral Contact Pressure Distribution,” J. Biomech., 37(3), pp. 295–302. 10.1016/S0021-9290(03)00306-3 [DOI] [PubMed] [Google Scholar]
- [318]. Brand, R. A. , 2005, “Joint Contact Stress: A Reasonable Surrogate for Biological Processes?,” Iowa Orthop. J., 25, pp. 82–94. [PMC free article] [PubMed] [Google Scholar]
- [319]. Brown, T. D. , Rudert, M. J. , and Grosland, N. M. , 2004, “New Methods for Assessing Cartilage Contact Stress After Articular Fracture,” Clin. Orthop. Relat. Res. (423), pp. 52–58. 10.1097/01.blo.0000132633.38338.8b [DOI] [PubMed] [Google Scholar]
- [320]. Rudert, M. J. , Ellis, B. J. , Henak, C. R. , Stroud, N. J. , Pedersen, D. R. , Weiss, J. A. , and Brown, T. D. , “A New Sensor for Measurement of Dynamic Contact Stress in the Hip,” ASME J. Biomech. Eng., (submitted). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [321]. Rudert, M. J. , Ellis, B. J. , Henak, C. R. , Stroud, N. J. , Weiss, J. A. , and Brown, T. D. , 2011, “A New Sensor for Measurement of Dynamic Contact Pressure in the Hip,” Orthopaedic Research Society Meeting, Abstract No. 936571. [Google Scholar]
- [322]. Wu, J. Z. , Herzog, W. , and Epstein, M. , 1998, “Effects of Inserting a Pressensor Film Into Articular Joints on the Actual Contact Mechanics,” ASME J. Biomech. Eng., 120(5), pp. 655–659. 10.1115/1.2834758 [DOI] [PubMed] [Google Scholar]
- [323]. Dennison, C. R. , and Wild, P. M. , 2010, “Sensitivity of Bragg Gratings in Birefringent Optical Fiber to Transverse Compression Between Conforming Materials,” Appl. Opt., 49(12), pp. 2250–2261. 10.1364/AO.49.002250 [DOI] [PubMed] [Google Scholar]
- [324]. Pawaskar, S. S. , Grosland, N. M. , Ingham, E. , Fisher, J. , and Jin, Z. , 2011, “Hemiarthroplasty of Hip Joint: An Experimental Validation Using Porcine Acetabulum,” J. Biomech., 44(8), pp. 1536–1542. 10.1016/j.jbiomech.2011.02.140 [DOI] [PubMed] [Google Scholar]
- [325]. Laz, P. J. , and Browne, M. , 2010, “A Review of Probabilistic Analysis in Orthopaedic Biomechanics,” Proc. Inst. Mech. Eng., Part H: J. Eng. Med., 224(8), pp. 927–943. 10.1243/09544119JEIM739 [DOI] [PubMed] [Google Scholar]
- [326]. Roy, C. J. , and Oberkampf, W. L. , 2011, “A Comprehensive Framework for Verification, Validation, and Uncertainty Quantification in Scientific Computing,” Comput. Methods Appl. Mech. Eng., 200(25-28), pp. 2131–2144. 10.1016/j.cma.2011.03.016 [DOI] [Google Scholar]
- [327]. Easley, S. K. , Pal, S. , Tomaszewski, P. R. , Petrella, A. J. , Rullkoetter, P. J. , and Laz, P. J. , 2007, “Finite Element-Based Probabilistic Analysis Tool for Orthopaedic Applications,” Comput. Methods Programs Biomed., 85(1), pp. 32–40. 10.1016/j.cmpb.2006.09.013 [DOI] [PubMed] [Google Scholar]
- [328]. Adams, B. , Bohnhoff, W. , Dalbey, K. , Eddy, J. , Eldred, M. , Gay, D. , Haskell, K. , Hough, P. , and Swiler, L. , 2011, “DAKOTA, A Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis: Version 5.0 User's Manual,” Sandia Technical Report SAND2010-2183.
- [329]. Dar, F. H. , Meakin, J. R. , and Aspden, R. M. , 2002, “Statistical Methods in Finite Element Analysis,” J. Biomech., 35(9), pp. 1155–1161. 10.1016/S0021-9290(02)00085-4 [DOI] [PubMed] [Google Scholar]
- [330]. Dhaher, Y. Y. , Kwon, T.-H. , and Barry, M. , “The Effect of Connective Tissue Material Uncertainties on Knee Joint Mechanics Under Isolated Loading Conditions,” J. Biomech., 43(16), pp. 3118–3125. 10.1016/j.jbiomech.2010.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [331]. Fernandez, J. W. , and Hunter, P. J. , 2005, “An Anatomically Based Patient-Specific Finite Element Model of Patella Articulation: Towards a Diagnostic Tool,” Biomech. Model. Mechanobiol., 4(1), pp. 20–38. 10.1007/s10237-005-0072-0 [DOI] [PubMed] [Google Scholar]
- [332]. Li, G. , Lopez, O. , and Rubash, H. , 2001, “Variability of a Three-Dimensional Finite Element Model Constructed Using Magnetic Resonance Images of a Knee for Joint Contact Stress Analysis,” ASME J. Biomech. Eng., 123(4), pp. 341–346. 10.1115/1.1385841 [DOI] [PubMed] [Google Scholar]
- [333]. Mesfar, W. , and Shirazi-Adl, A. , 2005, “Biomechanics of the Knee Joint in Flexion Under Various Quadriceps Forces,” The Knee, 12(6), pp. 424–434. 10.1016/j.knee.2005.03.004 [DOI] [PubMed] [Google Scholar]
- [334]. Miller, E. J. , Riemer, R. F. , Haut Donahue, T. L. , and Kaufman, K. R. , 2009, “Experimental Validation of a Tibiofemoral Model for Analyzing Joint Force Distribution,” J. Biomech., 42(9), pp. 1355–1359. 10.1016/j.jbiomech.2009.03.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [335]. Rapperport, D. J. , Carter, D. R. , and Schurman, D. J. , 1985, “Contact Finite Element Stress Analysis of the Hip Joint,” J. Orthop. Res., 3(4), pp. 435–446. 10.1002/jor.1100030406 [DOI] [PubMed] [Google Scholar]
- [336]. Lee, K. K. , and Teo, E. C. , 2005, “Material Sensitivity Study on Lumbar Motion Segment (L2-L3) Under Sagittal Plane Loadings Using Probabilistic Method,” J. Spinal Disord. Tech., 18(2), pp. 163–170. 10.1097/01.bsd.0000147658.60961.51 [DOI] [PubMed] [Google Scholar]
- [337]. Ng, H. W. , and Teo, E. C. , 2004, “Probabilistic Design Analysis of the Influence of Material Property on the Human Cervical Spine,” J. Spinal Disord. Tech., 17(2), pp. 123–133. 10.1097/00024720-200404000-00009 [DOI] [PubMed] [Google Scholar]
- [338]. Niemeyer, F. , Wilke, H. J. , and Schmidt, H. , 2012, “Geometry Strongly Influences the Response of Numerical Models of the Lumbar Spine–A Probabilistic Finite Element Analysis,” J. Biomech., 45(8), pp. 1414–1423. 10.1016/j.jbiomech.2012.02.021 [DOI] [PubMed] [Google Scholar]
- [339]. Baldwin, M. A. , Laz, P. J. , Stowe, J. Q. , and Rullkoetter, P. J. , 2009, “Efficient Probabilistic Representation of Tibiofemoral Soft Tissue Constraint,” Comput. Methods Biomech. Biomed. Eng., 12(6), pp. 651–659. 10.1080/10255840902822550 [DOI] [PubMed] [Google Scholar]
- [340]. Logothetis, N. , and Wynn, H. P. , 1989, Quality Through Design: Experimental Design, Off-line Quality Control and Taguchi's Contributions, Clarendon Press, Oxford. [Google Scholar]
- [341]. Rao, S. S. , 1992, Reliability-Based Design, McGraw-Hill, New York. [Google Scholar]
- [342]. Meachim, G. , and Bentley, G. , 1978, “Horizontal Splitting in Patellar Articular Cartilage,” Arthritis Rheum., 21(6), pp. 669–674. 10.1002/art.1780210610 [DOI] [PubMed] [Google Scholar]
- [343]. Hadley, N. A. , Brown, T. D. , and Weinstein, S. L. , 1990, “The Effects of Contact Pressure Elevations and Aseptic Necrosis on the Long-Term Outcome of Congenital Hip Dislocation,” J. Orthop. Res., 8(4), pp. 504–513. 10.1002/jor.1100080406 [DOI] [PubMed] [Google Scholar]
- [344]. Fitzpatrick, C. K. , Baldwin, M. A. , and Rullkoetter, P. J. , 2010, “Computationally Efficient Finite Element Evaluation of Natural Patellofemoral Mechanics,” ASME J. Biomech. Eng., 132(12), p. 121013. 10.1115/1.4002854 [DOI] [PubMed] [Google Scholar]
- [345]. Yang, N. H. , Canavan, P. K. , and Nayeb-Hashemi, H. , 2010, “The Effect of the Frontal Plane Tibiofemoral Angle and Varus Knee Moment on the Contact Stress and Strain at the Knee Cartilage,” J. Appl. Biomech., 26(4), pp. 432–443. [DOI] [PubMed] [Google Scholar]
- [346]. Yang, N. H. , Nayeb-Hashemi, H. , Canavan, P. K. , and Vaziri, A. , 2010, “Effect of Frontal Plane Tibiofemoral Angle on the Stress and Strain at the Knee Cartilage During the Stance Phase of Gait,” J. Orthop. Res., 28(12), pp. 1539–1547. 10.1002/jor.21174 [DOI] [PubMed] [Google Scholar]
- [347]. Larson, A. N. , Rabenhorst, B. , De La Rocha, A. , and Sucato, D. J. , 2012, “Limited Intraobserver and Interobserver Reliability for the Common Measures of Hip Joint Congruency Used in Dysplasia,” Clin. Orthop. Relat. Res., 470(5), pp. 1414–1420. 10.1007/s11999-011-2136-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [348]. Troelsen, A. , 2009, “Surgical Advances in Periacetabular Osteotomy for Treatment of Hip Dysplasia in Adults,” Acta Orthop. Suppl., 80(332), pp. 1–33. 10.1080/17453690610046585 [DOI] [PubMed] [Google Scholar]
- [349]. Wenger, D. E. , Kendell, K. R. , Miner, M. R. , and Trousdale, R. T. , 2004, “Acetabular Labral Tears Rarely Occur in the Absence of Bony Abnormalities,” Clin. Orthop. Relat. Res., (426), pp. 145–150. 10.1097/01.blo.0000136903.01368.20 [DOI] [PubMed] [Google Scholar]
- [350]. Clohisy, J. C. , Carlisle, J. C. , Trousdale, R. , Kim, Y. J. , Beaule, P. E. , Morgan, P. , Steger-May, K. , Schoenecker, P. L. , and Millis, M. , 2009, “Radiographic Evaluation of the Hip Has Limited Reliability,” Clin. Orthop. Relat. Res., 467(3), pp. 666–675. 10.1007/s11999-008-0626-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [351]. Anderson, L. A. , Gililland, J. , Pelt, C. , Linford, S. , Stoddard, G. J. , and Peters, C. L. , 2011, “Center Edge Angle Measurement for Hip Preservation Surgery: Technique and Caveats,” Orthopedics, 34(2), p. 86. 10.3928/01477447-20101221-17 [DOI] [PubMed] [Google Scholar]
- [352]. Hansen, B. J. , Harris, M. D. , Anderson, L. A. , Peters, C. L. , Weiss, J. A. , and Anderson, A. E. , 2012, “Correlation Between Radiographic Measures of Acetabular Morphology With 3D Femoral Head Coverage in Patients With Acetabular Retroversion,” Acta Orthop., 83(3), pp. 233–239. 10.3109/17453674.2012.684138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [353]. Masrouha, K. Z. , Anderson, D. D. , Thomas, T. P. , Kuhl, L. L. , Brown, T. D. , and Marsh, J. L. , 2010, “Acute Articular Fracture Severity and Chronic Cartilage Stress Challenge as Quantitative Risk Factors for Post-traumatic Osteoarthritis: Illustrative Cases,” Iowa Orthop. J., 30, pp. 47–54. [PMC free article] [PubMed] [Google Scholar]
- [354]. Farrokhi, S. , Keyak, J. H. , and Powers, C. M. , 2011, “Individuals With Patellofemoral Pain Exhibit Greater Patellofemoral Joint Stress: A Finite Element Analysis Study,” Osteoarthritis Cartilage, 19(3), pp. 287–294. 10.1016/j.joca.2010.12.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [355]. Kelly, M. A. , Fithian, D. C. , Chern, K. Y. , and Mow, V. C. , 1990, “Structure and Function of the Meniscus: Basic and Clinical Implications,” Biomechanics of Diarthrodial Joints, Mow V. C., Ratcliffe A., and Woo S. L., eds., Springer-Verlag, New York. [Google Scholar]
- [356]. Krause, W. R. , Pope, M. H. , Johnson, R. J. , and Wilder, D. G. , 1976, “Mechanical Changes in the Knee After Meniscectomy,” J. Bone Jt. Surg., 58(5), pp. 599–604. [PubMed] [Google Scholar]
- [357]. Ahmed, A. M. , and Burke, D. L. , 1983, “In-Vitro Measurement of Static Pressure Distribution in Synovial Joints–Part I: Tibial Surface of the Knee,” ASME J. Biomech. Eng., 105(3), pp. 216–225. 10.1115/1.3138409 [DOI] [PubMed] [Google Scholar]
- [358]. Kazemi, M. , Li, L. P. , Buschmann, M. D. , and Savard, P. , 2012, “Partial Meniscectomy Changes Fluid Pressurization in Articular Cartilage in Human Knees,” ASME J. Biomech. Eng., 134(2), p. 021001. 10.1115/1.4005764 [DOI] [PubMed] [Google Scholar]
- [359]. Kazemi, M. , Li, L. P. , Savard, P. , and Buschmann, M. D. , 2011, “Creep Behavior of the Intact and Meniscectomy Knee Joints,” J. Mech. Behav. Biomed. Mater., 4(7), pp. 1351–1358. 10.1016/j.jmbbm.2011.05.004 [DOI] [PubMed] [Google Scholar]
- [360]. Bae, J. Y. , Park, K. S. , Seon, J. K. , Kwak, D. S. , Jeon, I. , and Song, E. K. , 2012, “Biomechanical Analysis of the Effects of Medial Meniscectomy on Degenerative Osteoarthritis,” Med. Biol. Eng. Comput., 50(1), pp. 53–60. 10.1007/s11517-011-0840-1 [DOI] [PubMed] [Google Scholar]
- [361]. Yang, N. , Nayeb-Hashemi, H. , and Canavan, P. K. , 2009, “The Combined Effect of Frontal Plane Tibiofemoral Knee Angle and Meniscectomy on the Cartilage Contact Stresses and Strains,” Ann. Biomed. Eng., 37(11), pp. 2360–2372. 10.1007/s10439-009-9781-3 [DOI] [PubMed] [Google Scholar]
- [362]. Yang, N. H. , Canavan, P. K. , Nayeb-Hashemi, H. , Najafi, B. , and Vaziri, A. , 2010, “Protocol for Constructing Subject-Specific Biomechanical Models of Knee Joint,” Comput. Methods Biomech. Biomed. Eng., 13(5), pp. 589–603. 10.1080/10255840903389989 [DOI] [PubMed] [Google Scholar]
- [363]. Markolf, K. L. , Mensch, J. S. , and Amstutz, H. C. , 1976, “Stiffness and Laxity of the Knee–The Contributions of the Supporting Structures. A Quantitative In Vitro Study,” J. Bone Jt. Surg., 58(5), pp. 583–594. [PubMed] [Google Scholar]
- [364]. Li, G. , Suggs, J. , and Gill, T. , 2002, “The Effect of Anterior Cruciate Ligament Injury on Knee Joint Function Under a Simulated Muscle Load: A Three-Dimensional Computational Simulation,” Ann. Biomed. Eng., 30(5), pp. 713–720. 10.1114/1.1484219 [DOI] [PubMed] [Google Scholar]
- [365]. Jafari, A. , Farahmand, F. , and Meghdari, A. , 2008, “The Effects of Trochlear Groove Geometry on Patellofemoral Joint Stability–A Computer Model Study,” Proc. Inst. Mech. Eng., Part H: J. Eng. Med., 222(1), pp. 75–88. 10.1243/09544119JEIM255 [DOI] [PubMed] [Google Scholar]
- [366]. Hartig-Andreasen, C. , Troelsen, A. , Thillemann, T. M. , and Soballe, K. , 2012, “What Factors Predict Failure 4 to 12 Years After Periacetabular Osteotomy?,” Clin. Orthop. Relat. Res., 470(11), pp. 2978–2987. 10.1007/s11999-012-2386-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [367]. Matheney, T. , Kim, Y. J. , Zurakowski, D. , Matero, C. , and Millis, M. , 2010, “Intermediate to Long-Term Results Following the Bernese Periacetabular Osteotomy and Predictors of Clinical Outcome: Surgical Technique,” J. Bone Jt. Surg., 92(Suppl 1 Pt 2), pp. 115–129. 10.2106/JBJS.J.00646 [DOI] [PubMed] [Google Scholar]
- [368]. Okano, K. , Enomoto, H. , Osaki, M. , and Shindo, H. , 2009, “Joint Congruency as an Indication for Rotational Acetabular Osteotomy,” Clin. Orthop. Relat. Res., 467(4), pp. 894–900. 10.1007/s11999-008-0443-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [369]. Okano, K. , Yamada, K. , Takahashi, K. , Enomoto, H. , Osaki, M. , and Shindo, H. , 2010, “Joint Congruency in Abduction Before Surgery as an Indication for Rotational Acetabular Osteotomy in Early Hip Osteoarthritis,” Int. Orthop., 34(1), pp. 27–32. 10.1007/s00264-009-0734-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [370]. Yasunaga, Y. , Yamasaki, T. , and Ochi, M. , 2012, “Patient Selection Criteria for Periacetabular Osteotomy or Rotational Acetabular Osteotomy,” Clin. Orthop. Relat. Res., 470(12), pp. 3342–3354. 10.1007/s11999-012-2516-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [371]. Chegini, S. , Beck, M. , and Ferguson, S. J. , 2009, “The Effects of Impingement and Dysplasia on Stress Distributions in the Hip Joint During Sitting and Walking: A Finite Element Analysis,” J. Orthop. Res., 27(2), pp. 195–201. 10.1002/jor.20747 [DOI] [PubMed] [Google Scholar]
- [372]. Iglič, A. , Kralj-Iglič, V. , Daniel, M. , and Maček-Lebar, A. , 2002, “Computer Determination of Contact Stress Distribution and Size of Weight Bearing Area in the Human Hip Joint,” Comput. Methods Biomech. Biomed. Eng., 5(2), pp. 185–192. 10.1080/10255840290010300 [DOI] [PubMed] [Google Scholar]
- [373]. Ipavec, M. , Brand, R. A. , Pedersen, D. R. , Mavcic, B. , Kralj-Iglic, V. , and Iglic, A. , 1999, “Mathematical Modelling of Stress in the Hip During Gait,” J. Biomech., 32(11), pp. 1229–1235. 10.1016/S0021-9290(99)00119-0 [DOI] [PubMed] [Google Scholar]
- [374]. Mavčič, B. , Pompe, B. , Antolič, V. , Daniel, M. , Iglič, A. , and Kralj-Iglič, V. , 2002, “Mathematical Estimation of Stress Distribution in Normal and Dysplastic Human Hips,” J. Orthop. Res., 20(5), pp. 1025–1030. 10.1016/S0736-0266(02)00014-1 [DOI] [PubMed] [Google Scholar]
- [375]. Pompe, B. , Daniel, M. , Sochor, M. , Vengust, R. , Kralj-Iglič, V. , and Iglič, A. , 2003, “Gradient of Contact Stress in Normal and Dysplastic Human Hips,” Med. Eng. Phys., 25(5), pp. 379–385. 10.1016/S1350-4533(03)00014-6 [DOI] [PubMed] [Google Scholar]
- [376]. Haemer, J. M. , Carter, D. R. , and Giori, N. J. , 2012, “The Low Permeability of Healthy Meniscus and Labrum Limit Articular Cartilage Consolidation and Maintain Fluid Load Support in the Knee and Hip,” J. Biomech., 45(8), pp. 1450–1456. 10.1016/j.jbiomech.2012.02.015 [DOI] [PubMed] [Google Scholar]
- [377]. Haemer, J. M. , Song, Y. , Carter, D. R. , and Giori, N. J. , 2011, “Changes in Articular Cartilage Mechanics With Meniscectomy: A Novel Image-Based Modeling Approach and Comparison to Patterns of OA,” J. Biomech., 44(12), pp. 2307–2312. 10.1016/j.jbiomech.2011.04.014 [DOI] [PubMed] [Google Scholar]
- [378]. Adeeb, S. M. , Sayed Ahmed, E. Y. , Matyas, J. , Hart, D. A. , Frank, C. B. , and Shrive, N. G. , 2004, “Congruency Effects on Load Bearing in Diarthrodial Joints,” Comput. Methods Biomech. Biomed. Eng., 7(3), pp. 147–157. 10.1080/10255840410001710885 [DOI] [PubMed] [Google Scholar]
- [379]. Wei, H. W. , Sun, S. S. , Jao, S. H. , Yeh, C. R. , and Cheng, C. K. , 2005, “The Influence of Mechanical Properties of Subchondral Plate, Femoral Head and Neck on Dynamic Stress Distribution of the Articular Cartilage,” Med. Eng. Phys., 27(4), pp. 295–304. 10.1016/j.medengphy.2004.12.008 [DOI] [PubMed] [Google Scholar]
- [380]. Gu, K. B. , and Li, L. P. , 2011, “A Human Knee Joint Model Considering Fluid Pressure and Fiber Orientation in Cartilages and Menisci,” Med. Eng. Phys., 33(4), pp. 497–503. 10.1016/j.medengphy.2010.12.001 [DOI] [PubMed] [Google Scholar]
- [381]. Shirazi, R. , Shirazi-Adl, A. , and Hurtig, M. , 2008, “Role of Cartilage Collagen Fibrils Networks in Knee Joint Biomechanics Under Compression,” J. Biomech., 41(16), pp. 3340–3348. 10.1016/j.jbiomech.2008.09.033 [DOI] [PubMed] [Google Scholar]
- [382]. Wilson, W. , van Rietbergen, B. , van Donkelaar, C. C. , and Huiskes, R. , 2003, “Pathways of Load-Induced Cartilage Damage Causing Cartilage Degeneration in the Knee After Meniscectomy,” J. Biomech., 36(6), pp. 845–851. 10.1016/S0021-9290(03)00004-6 [DOI] [PubMed] [Google Scholar]
- [383]. Besier, T. F. , Gold, G. E. , Beaupre, G. S. , and Delp, S. L. , 2005, “A Modeling Framework to Estimate Patellofemoral Joint Cartilage Stress In Vivo ,” Med. Sci. Sports Exercise, 37(11), pp. 1924–1930. 10.1249/01.mss.0000176686.18683.64 [DOI] [PubMed] [Google Scholar]
- [384]. Wu, J. Z. , Herzog, W. , and Hasler, E. M. , 2002, “Inadequate Placement of Osteochondral Plugs May Induce Abnormal Stress-Strain Distributions in Articular Cartilage –Finite Element Simulations,” Med. Eng. Phys., 24(2), pp. 85–97. 10.1016/S1350-4533(01)00122-9 [DOI] [PubMed] [Google Scholar]
- [385]. Kelly, D. J. , and Prendergast, P. J. , 2005, “Mechano-regulation of Stem Cell Differentiation and Tissue Regeneration in Osteochondral Defects,” J. Biomech., 38(7), pp. 1413–1422. 10.1016/j.jbiomech.2004.06.026 [DOI] [PubMed] [Google Scholar]
- [386]. Owen, J. R. , and Wayne, J. S. , 2011, “Contact Models of Repaired Articular Surfaces: Influence of Loading Conditions and the Superficial Tangential Zone,” Biomech. Model. Mechanobiol., 10(4), pp. 461–471. 10.1007/s10237-010-0247-1 [DOI] [PubMed] [Google Scholar]
- [387]. Fitzpatrick, C. K. , Baldwin, M. A. , Laz, P. J. , FitzPatrick, D. P. , Lerner, A. L. , and Rullkoetter, P. J. , 2011, “Development of a Statistical Shape Model of the Patellofemoral Joint for Investigating Relationships Between Shape and Function,” J. Biomech., 44(13), pp. 2446–2452. 10.1016/j.jbiomech.2011.06.025 [DOI] [PubMed] [Google Scholar]
- [388]. Andriacchi, T. P. , Briant, P. L. , Bevill, S. L. , and Koo, S. , 2006, “Rotational Changes at the Knee After ACL Injury Cause Cartilage Thinning,” Clin. Orthop. Relat. Res., 442, pp. 39–44. 10.1097/01.blo.0000197079.26600.09 [DOI] [PubMed] [Google Scholar]