Viscoelastic Material Properties of the Myocardium and Cardiac Jelly in the Looping Chick Heart

Short abstract

Accurate material properties of developing embryonic tissues are a crucial factor in studies of the mechanics of morphogenesis. In the present work, we characterize the viscoelastic material properties of the looping heart tube in the chick embryo through nonlinear finite element modeling and microindentation experiments. Both hysteresis and ramp-hold experiments were performed on the intact heart and isolated cardiac jelly (extracellular matrix). An inverse computational method was used to determine the constitutive relations for the myocardium and cardiac jelly. With both layers assumed to be quasilinear viscoelastic, material coefficients for an Ogden type strain-energy density function combined with Prony series of two terms or less were determined by fitting numerical results from a simplified model of a heart segment to experimental data. The experimental and modeling techniques can be applied generally for determining viscoelastic material properties of embryonic tissues.

1. Introduction

During embryonic development, stress plays an important role in controlling growth, remodeling, and morphogenesis [1]. Embryonic tissues as viscoelastic materials exhibit time-dependent stress during deformation. Therefore, the viscoelastic response of tissues may have a significant effect on the timing and regulation of embryonic development. Here, using microindentation experiments and nonlinear finite element (FE) modeling, we determine the viscoelastic properties of the embryonic chick heart during the morphogenetic process of c-looping, as the relatively straight heart tube bends and twists toward the right side of the embryo [2]. Abnormalities that arise during looping can lead to severe congenital defects of the heart and cardiovascular system [3].

The chick embryo, in which heart development parallels that in the human embryo, undergoes c-looping during Hamburger and Hamilton (HH) stages 10 to 12 (approximately 36 to 48 h of incubation) [4]. At this time, the heart tube is composed of a two-cell-thick outer layer of myocardium (MY), a thick middle layer of extracellular matrix known as cardiac jelly (CJ), and a single-cell-thick endocardium (Fig. 1(a)). The present study focuses on the MY and CJ, which are the primary load-bearing layers. Previous studies of the looping heart have focused on pseudoelastic properties [5]. Viscoelastic properties of MY have been measured at later stages [6–8], but the microstructure changes considerably as cardiomyocytes differentiate [9], suggesting that these data do not apply to earlier stages. Our data are useful for studies of the physical mechanisms that drive and regulate looping.

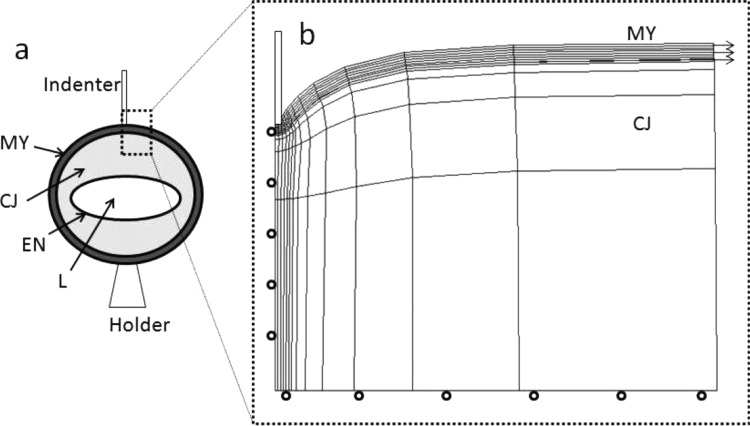
Fig. 1.

(a) Schematic of heart cross section showing indentation of the side of the heart (MY: myocardium; CJ: cardiac jelly; EN: endocardium; L: lumen). (b) Axisymmetric cylindrical model with 8-node quadratic hybrid elements was used to represent the indentation experiment. Roller boundary conditions were specified along the bottom edge of the CJ, and the outer boundary was free. The mesh was refined near the indenter, and the mesh density was determined by a convergence test. The residual stress in MY was modeled as a radial stretch applied to the MY layer. During the initial stretch, interaction between the MY and CJ was frictionless. Then, the MY was tied to the CJ so that there was no relative motion between the two layers during indentation. The contact between the indenter and the heart was modeled as frictionless hard contact with no penetration allowed between the contacting surfaces.

2. Methods

2.1. Microindentation Testing.

Fertilized, white Leghorn chicken eggs were incubated at 38 °C for approximately 48 h in a humidified, forced draft incubator to yield embryos at HH stage 12. Whole embryos were harvested from the eggs using a filter paper carrier method [10], and placed ventral side up in 35 mm culture dishes filled with phosphate buffered saline (PBS). Under a Leica MZ8 dissecting microscope, c-looped hearts were excised from the embryos using micro-scissors and needles fashioned from pulled glass micropipettes.

To obtain CJ isolates, intact hearts were transferred to a 24-well plate (presoaked in 1% bovine serum albumin (BSA)) and incubated on a shaker at 38 °C in 10 mM EDTA in PBS for 1 h to disrupt cadherin-dependent cell contacts. The hearts were then placed in a 0.1% solution of deoxycholic acid in PBS and incubated for 1 h to lyse the cells. Trypan blue (Sigma) staining was used to confirm that all cellular material had been removed from the isolates.

To characterize the viscoelastic response of the MY and CJ, we conducted (1) hysteresis and (2) ramp-hold microindentation experiments on both intact hearts and CJ isolates. The hearts (or isolates) were transferred to a bath of PBS, held in place via suction by a micropipette holder, and indented at the side of the heart near the midventricular region (Fig. 1(a)) using a custom-built microindentation device. Briefly, the microindenter is attached to the end of a calibrated cantilever beam, whose motion is driven by a piezoelectric motor; the beam deflection is used to calculate the applied indentation force (see details in Ref. [11]). The tissue loading/unloading rate was varied by modifying the voltage signal sent to the motor. Prior to each CJ isolate experiment, the bath, pipette holder, and microindenter were all presoaked in 1% BSA to prevent excessive adhesion between the CJ and glass. For the hysteresis experiments (intact hearts, n = 6; CJ isolates, n = 6), while the indenter was in contact with tissue the deformation rate ranged from 27 to 66 μm/s for intact hearts, and 19 to 38 μm/s for CJ isolates. (The stage-12 heart tube is approximately 300 μm in diameter, and the MY is about 20 μm thick.) The difference between the loading and unloading force-deflection curves provided a measure of viscous energy dissipation.

In a separate set of experiments (intact hearts, n = 9; CJ isolates, n = 6), we specified an input voltage to the motor that, after a quick (<2 s) initial ramp phase, was held constant for approximately 10 min. Since the motor controls only the motion of the fixed end of the cantilevered indenter, neither the applied force nor the tissue deflection was held constant (after the ramp phase) during these experiments (Figs. 2(c) and 2(d)). The resulting ramp-hold test was therefore a hybrid of the paradigmatic stress-relaxation and creep viscoelastic material tests. For intact hearts (n = 4), ramp-hold tests were conducted at different tissue deflection depths, varying from 32 to 55 μm, to test our assumption of quasilinear viscoleasticity.

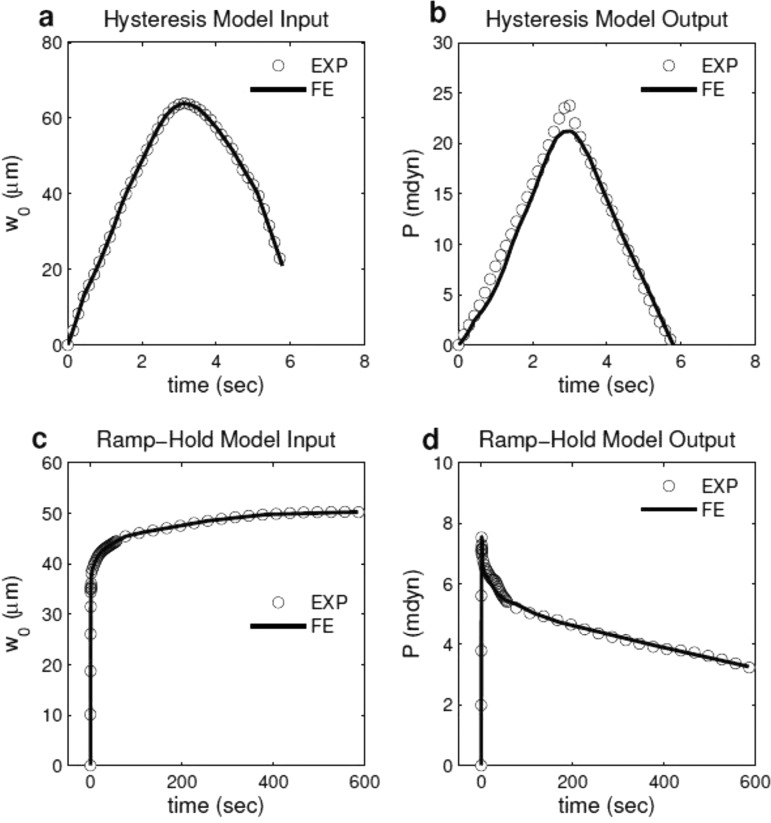
Fig. 2.

Experimentally measured displacement-time data were prescribed as displacement history of the rigid indenter in the finite element models of (a) hysteresis and (c) ramp-hold tests. Viscoelastic material properties of the indented tissue were inversely computed by fitting the FE predictions (solid line) in force-time responses to experimental measurements from (b) hysteresis and (d) ramp-hold tests.

2.2. FE Modeling for Microindentation Experiments.

Because early embryonic heart tissues are extremely soft, deformation was confined to a relatively small region near the indenter tip (Fig. 1). Using the nonlinear FE code Abaqus (Dassault Systemes), a local region of the heart near the indenter tip was modeled as a bilayered axisymmetric cylindrical structure composed of a thin circular plate (MY) with an underlying soft foundation (CJ) (Fig. 1(b)) [5]. Residual stress in the MY was included by prescribing radial displacements along the edge to give an initial stretch ratio (λ_MY) in both circumferential and radial directions. The experimentally measured tissue deflection versus time curves were smoothed using the matlab smooth function (The Mathworks, Inc.) (Figs. 2(a) and 2(c)), and applied as a displacement boundary condition for the rigid indenter. The model-predicted reaction force at the indenter was used to generate force-time curves (Figs. 2(b) and 2(d)), and material properties were inversely computed thereafter as described later.

2.3. Inverse Computational Method.

Both MY and CJ were modeled as isotropic nearly incompressible viscoelastic materials. We selected the Ogden (N = 1) function [12], as it best-fit the nonlinear force-displacement curves for the MY with significant residual strain. The function only requires two parameters, μ and α. Additionally, the stability condition of Ogden material is straightforward to enforce, i.e., μα ≥ 0 [13]. This function is written as

$$W^0\hspace{1em}=\hspace{1em}\frac{2\mu }{{\alpha }^2}({\overline{\lambda }}_1^{\alpha }+{\overline{\lambda }}_2^{\alpha }+{\overline{\lambda }}_3^{\alpha })+\frac{1}{D}{(J-1)}^2$$ (1)

where μ is the small-strain shear modulus, the ${\overline{\lambda }}_i$ is the deviatoric component of the principal stretch ratios, J = det(F) is the volume ratio, with F being the deformation gradient tensor, and α and D are constants. To compare our results to hyperelastic results from a previous study [5], we also used the exponential strain-energy density function

$$W^0\hspace{1em}=\hspace{1em}\frac{A}{B}\{\mathit{exp}\left[B({\overline{I}}_1-3)\right]-1\}+\frac{1}{D}{(J-1)}^2$$ (2)

where A and B are material constants and ${\overline{I}}_1=\mathit{trace}\left(\overline{\mathit{C}}\right)$ is the first principal invariant of the deviatoric right Cauchy-Green deformation tensor.

The Cauchy stress tensor is written in the quasilinear form [14,15]

$$\mathbf{\sigma }\left(t\right)={\int }_{t_0}^{t}G(t-\tau )\frac{d{\mathbf{\sigma }}^0\left(\tau \right)}{d\tau }d\tau$$ (3)

where the current stress $\mathbf{\sigma }\left(t\right)$ can be regarded as a linear summation of all previous instantaneous elastic stresses ${\mathbf{\sigma }}^0\left(t\right)$ multiplied by the relaxation function $G(t-\tau )$. The instantaneous elastic stress ${\mathbf{\sigma }}^0$ is given by [14,16]

$${\mathbf{\sigma }}^0=J^{-1}\mathit{F}\frac{\partial W^0}{\partial E}{\mathit{F}}^T$$ (4)

where $W^0$ is the strain energy density function defined in Eqs. (1) and (2), and $\mathit{E}=\frac{1}{2}({\mathit{F}}^T\mathit{F}-I)$ is the Green-Lagrange strain tensor. The relaxation function is taken as a Prony series

$$G\left(t\right)={\gamma }_{\infty }+\sum _{i=1}^N{\gamma }_i\hspace{1em}\mathit{exp}\hspace{1em}(-\frac{t}{{\tau }_i})$$ (5)

where ${\gamma }_i$ and ${\tau }_i$ define the nondimensional moduli and relaxation times, respectively. In addition, $G\left(\infty \right)={\gamma }_{\infty }=1-{\sum }_{i=1}^N{\gamma }_i$ defines the equilibrium modulus as $t\to \infty$. Preliminary studies indicated that using two terms or less in the Prony series was sufficiently accurate in this work. This formulation was implemented in Abaqus (Dassault Systemes, version 6.9) through a user material subroutine UMAT.

We used a least-squares objective function to fit the force-time curves measured during experiments to reaction force data given by the FE model through fminsearch in the matlab Optimization Toolbox (Fig. 2). Mathematically, the objective was to minimize the error written as

$$\mathit{err}=\sum _{i=1}^N\sqrt{\sum _{j=1}^{n_i}{(F_j^{\mathit{FE}}-F_j^{\mathit{EXP}})}^2\hspace{1em}\frac{1}{n_i}}$$ (6)

where N is the number of experiments, n_i is the number of time points for the ith experiment, and $F_j^{\mathit{FE}}$ and $F_j^{\mathit{EXP}}$ are values of the force predicted by the FE model and measured by the experiment for the jth time point, respectively.

Due to experimental difficulties, we used two sets of hearts to test the intact heart and isolated CJ. We first obtained the CJ parameters using microindentation experiments on CJ isolates, and then we determined the MY parameters individually from experiments on intact hearts using the average material properties of the CJ. Because CJ is much softer than MY [5], using average or representative elastic properties of CJ should not significantly affect the predicted elastic properties of the MY. In addition, although the contribution of CJ to the viscous response of the whole heart may be significant, the average Prony series properties are similar to those of several individual samples (Table 1). The prestretch ratio of the MY (λ_MY) was set as 1.2 for the optimization precedure. Our preliminary study indicated that although residual stress can strongly influence the measured elastic properties of the MY, it did not significantly affect the viscoelastic parameter values (data not shown).

Table 1.

Material parameters of the CJ determined by fitting hysteresis and ramp-hold tests using both Ogden and exponential strain energy density functions

	Exponential				Ogden
No.	A (Pa)	B	γi	τi (s)	μ (Pa)	α	γi	τi (s)
1	2.67	0.39	0.44, 0.30	0.97, 112	8.73	2.93	0.41, 0.30	1.02, 117
2	2.15	0.40	0.42, 0.37	1.04, 68.7	7.83	2.87	0.43, 0.31	1.08, 57.5
3	10.0	0.38	0.49, 0.28	0.84, 48.7	30.8	3.25	0.44, 0.31	0.86, 44.7
4	11.6	0.37	0.36, 0.49	1.26, 22.7	39.2	3.30	0.37, 0.49	0.67, 16.8
5	3.45	0.48	0.55, 0.36	0.98, 62.8	9.50	3.11	0.40, 0.35	1.06, 59.5
6	2.39	0.41	0.44, 0.34	1.03, 61.9	9.05	2.89	0.43, 0.34	1.01, 61.9
Mean	5.38	0.41	0.45, 0.36	1.02, 62.8	17.5	3.06	0.41, 0.35	0.95, 59.5
S.D.	3.88	0.04	0.06, 0.08	0.13, 32.7	12.6	0.17	0.02, 0.08	0.14, 36.5
Median	3.06	0.40	0.44, 0.34	1.01, 61.9	9.28	3.02	0.42, 0.31	1.02, 57.5

3. Results

3.1. General Behavior.

Both CJ and MY exhibited characteristic viscoelastic behavior, including hysteresis (Figs. 3(a), 4(a)) and stress relaxation (Figs. 3(b), 4(b)). The viscoelastic FE models captured these responses correctly (Figs. 3 and 4).

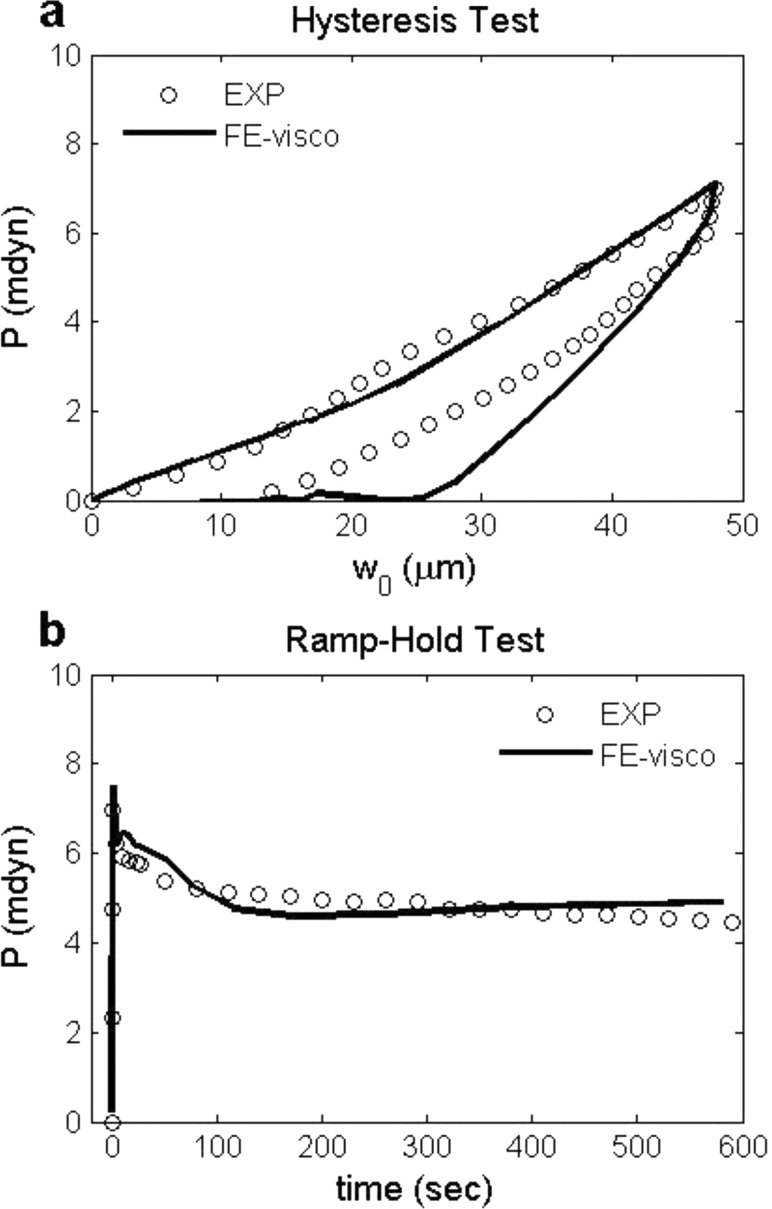
Fig. 3.

(a) Force-displacement curves of hysteresis test and (b) force-time curves of ramp-hold test for one representative CJ isolate (No. 3 in Table 1). Viscoelastic FE models (solid lines) generally agree with experimental measurements (circles).

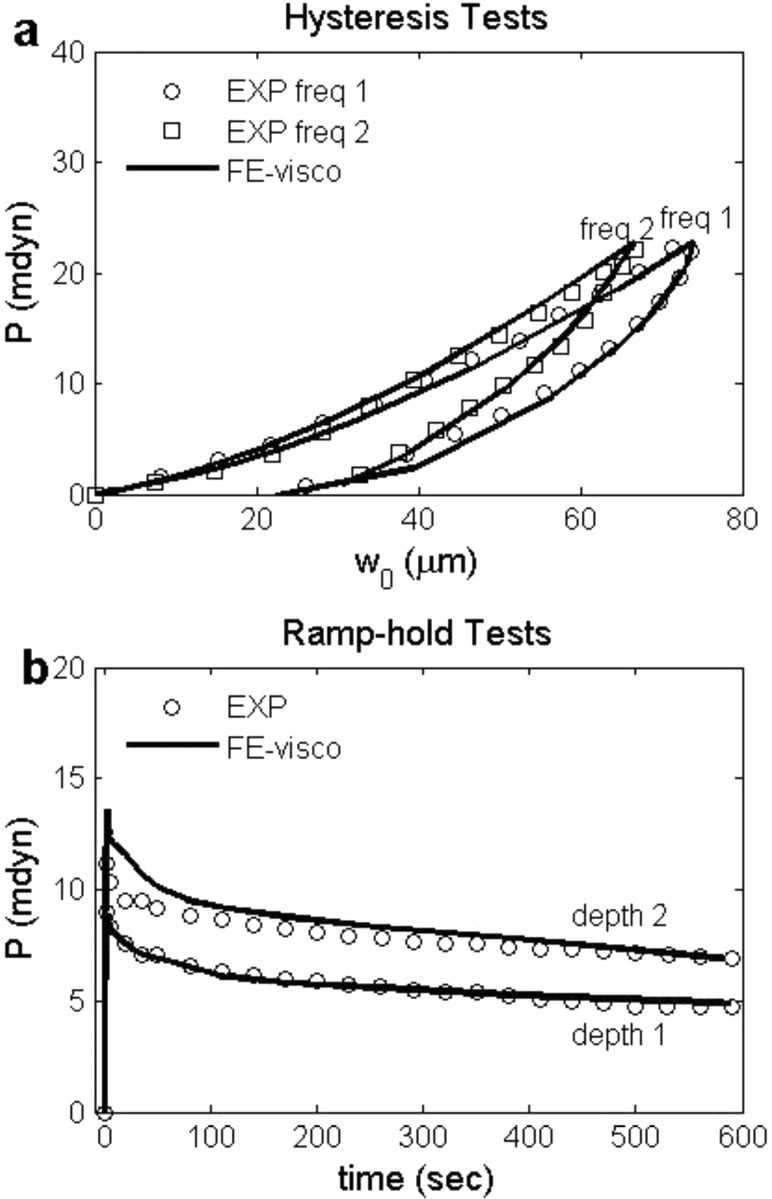
Fig. 4.

(a) Force-displacement curves of hysteresis tests with two representative loading/unloading rates for one representative intact heart (No. 1 in Table 2). (b) Force-time curves of ramp-hold tests with two indentation depths for another representative intact heart (No. 11 in Table 2). Best-fit viscoelastic finite element solutions (solid lines) using Ogden strain energy density function are shown together with experimental data (circles and squares).

3.2. Material Parameters for Cardiac Jelly.

CJ material parameters (${\mu }_{\mathit{CJ}},{\alpha }_{\mathit{CJ}},{\gamma }_{\mathit{CJ}},{\tau }_{\mathit{CJ}}$ were determined for the exponential and the Ogden strain-energy density functions using both hysteresis and ramp-hold tests on each CJ isolate (Table 1). The difference between the results given by the two strain-energy density functions was less than 0.05 in the predicted relaxation function (Fig. 5(a)). Therefore, only the Ogden strain-energy density function was used to obtain the MY material parameters for individual hearts (Table 2).

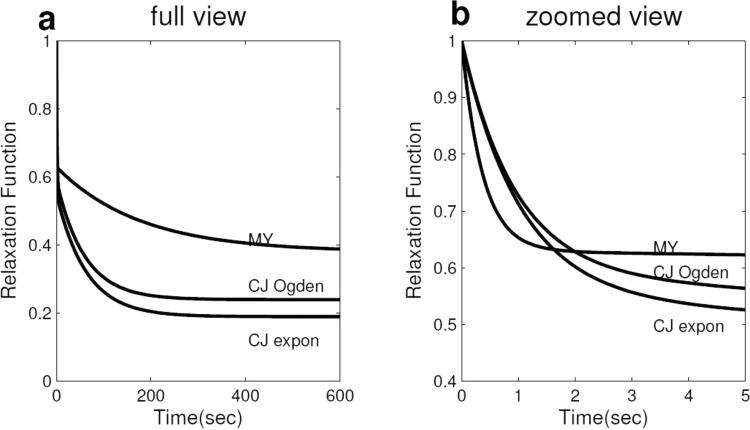
Fig. 5.

Mean relaxation functions versus time for CJ (both exponential and Ogden strain energy density functions) and MY in (a) full view and (b) zoomed view. These relaxation functions were plotted using the mean Prony series parameters in Tables 1 and 2.

Table 2.

Material parameters of MY determined using Ogden strain energy density function, MY has a residual stretch ratio of 1.2. Hysteresis tests (HY) were performed on samples 1 to 6, ramp-hold tests (RH) were performed on samples 7 to 15. Mean, standard deviation and median are calculated for all tests. The hysteresis test, due to its short duration (0 to 6 s), gave only one Prony series term and this was characterized by a small relaxation time, while the ramp-hold test, due to its long duration (0 to 600 s), gave two Prony series terms.

Type	No.	μ (Pa)	α	γi	τi (s)	G (∞)	Residual Stress (Pa)
HY	1	10.2	16.8	0.63	0.23	0.37	25.9
	2	7.03	13.9	0.58	0.66	0.42	12.8
	3	14.9	24.6	0.35	0.64	0.65	10.7
	4	11.0	19.7	0.61	0.19	0.39	40.3
	5	11.9	19.8	0.49	0.20	0.51	44.0
6	11.3	10.4	0.24	0.21	0.76	14.4
RH	7	6.20	19.1	0.50, 0.35	0.27, 248	0.15	24.4
	8	8.43	16.7	0.59, 0.14	0.18, 118	0.27	14.8
	9	6.13	25.7	0.32, 0.35	0.40, 100	0.33	51.4
	10	6.62	15.9	0.49, 0.49	0.32, 219	0.02	15.1
	11	10.4	22.9	0.17, 0.39	0.55, 84.7	0.44	53.4
	12	8.24	7.51	0.34, 0.17	0.44, 162	0.49	8.50
	13	7.93	12.6	0.02, 0.01	0.43, 37.1	0.97	12.5
	14	8.38	13.2	0.01, 0.15	0.44, 600	0.84	14.1
15	6.37	27.0	0.28, 0.20	0.42, 47.8	0.52	64.9
Mean		9.0	17.7	0.37, 0.25	0.37, 177	0.48	27.2
S.D.		2.54	5.72	0.20, 0.15	0.16, 176	0.25	18.6
Median		8.38	16.8	0.35, 0.20	0.40, 118	0.44	15.1

In Fig. 3, an experimental force-displacement curve of a hysteresis test and a force-time curve of a ramp-hold test for one representative CJ isolate are shown along with the best-fit viscoelastic model solutions. Note that one set of viscoelastic parameters was used to fit both hysteresis and ramp-hold tests.

3.3. Material Parameters for Myocardium.

We determined the MY material parameters (${\mu }_{\mathit{MY}},{\alpha }_{\mathit{MY}},{\gamma }_{\mathit{MY}},{\tau }_{\mathit{MY}}$ from 15 embryonic hearts (Table 2). The initial rate of stress relaxation was very rapid; for example, $G(0.5s)=0.71\pm 0.19$ and $G\left(\infty \right)=0.46\pm 0.26$ (Fig. 6(b)), meaning that 54% of the relaxation occurred within 0.5 s of loading.

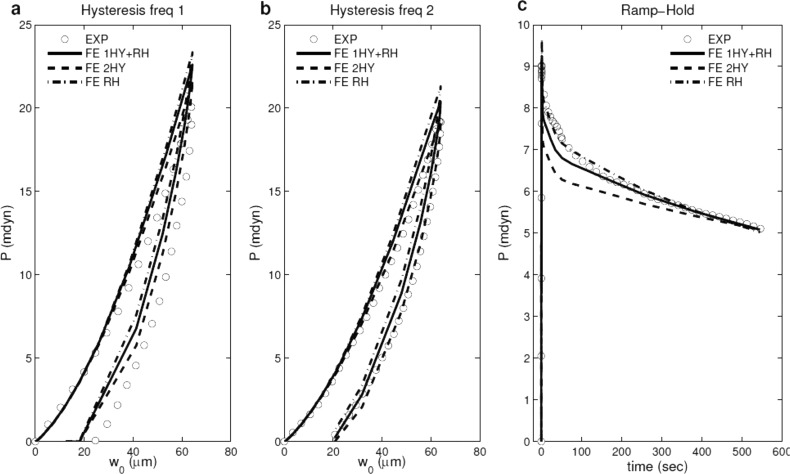
Fig. 6.

Force-displacement curves of hysteresis tests with (a and b) two representative loading/unloading rates and (c) force-time curve of ramp-hold test for the MY average experimental data (dotted lines). The solid lines represent the best-fit curves when the objective is to fit one hysteresis rate and ramp-hold curve only; the dash lines represent the best-fit curves when the object is to fit two hysteresis curves only; the dashed-dotted lines represent the best-fit curves when the object is to fit ramp-hold curve only.

Figure 4 shows experimental force-displacement curves of hysteresis tests with two loading rates for one representative intact heart and force-time curves of ramp-hold tests with two indentation depths for another representative intact heart, along with the best-fit viscoelastic model solutions. Note that one set of viscoelastic parameters was used to fit the two hysteresis tests, and another set of viscoelastic parameters was used to fit the two ramp-hold tests.

Mean MY relaxation functions are shown together with mean CJ relaxation functions in Fig. 5. Compared to CJ, MY had a larger mean equilibrium modulus (0.46 for MY versus 0.25 for CJ) (Fig. 5(a)), and a quicker mean relaxation rate (e.g., $G(0.5s)$ was 0.71 for MY versus 0.82 for CJ) (Fig. 5(b)).

3.4. Predictive Capability of Proposed Constitutive Relations.

To evaluate the ability of the proposed constitutive relations to make predictions, we performed the following tests (Fig. 6): (1) use material properties from hysteresis data (Fig. 6(a), 6(b)) to predict ramp-hold behavior (Fig. 6(c)); (2) use properties from ramp-hold data (Fig. 6(c)) to predict hysteresis behavior (Fig. 6(a), 6(b)); (3) use properties from one hysteresis (Fig. 6(a)) and ramp-hold (Fig. 6(c)) tests to predict the second hysteresis loading rate (Fig. 6(b)). As expected, using properties obtained from only hysteresis data resulted in larger error in predicting ramp-hold behavior compared to using properties obtained by considering ramp-hold data as well (Fig. 6(c)). Similarly, using properties obtained from only ramp-hold data resulted in larger error in predicting hysteresis behavior compared to using properties obtained by considering hysteresis data as well (Fig. 6(a), 6(b)). However, the error of using one type of test to predict the behavior of another test was less than 10%. In addition, using properties obtained from fitting one hysteresis test and one ramp-hold test resulted in smaller error in predicting the second hysteresis loading rate compared to using properties obtained from only ramp-hold data (Fig. 6(b)). Therefore, although it may be sufficient to use only one type of test to obtain the material properties, performing both hysteresis and ramp-hold tests can improve the predictive capabilities of the constitutive relations.

4. Discussion

In this study, we quantified the viscoelastic material properties of the HH stage 12 chick heart using microindentation and an inverse computational method based on nonlinear FE modeling. We measured the properties for two different layers of the heart and identified the separate contribution of MY and CJ to the global viscoelastic response.

4.1. Remarks on the Instantaneous Properties of CJ and MY.

The elastic constants of the CJ ($A_{\mathit{CJ}}=5.28\hspace{1em}\pm \hspace{1em}3.81$ Pa, $B_{\mathit{CJ}}=0.39\hspace{1em}\pm \hspace{1em}0.07$) were relatively close to the values ($A_{\mathit{CJ}}=3.2\hspace{1em}\pm \hspace{1em}1.0\hspace{1em}$ Pa, $B_{\mathit{CJ}}=0.39\hspace{1em}\pm \hspace{1em}0.51$) reported in Ref. [5]. However, our values described the instantaneous properties, while Zamir and Taber [5] did not consider the energy dissipation during indentation.

To compare our results to MY hyperelastic parameters in Ref. [5] (i.e., $A_{\mathit{MY}}=13\hspace{1em}\pm \hspace{1em}5.6$ Pa, ${\mathrm{B}}_{\mathit{MY}}=0.57\hspace{1em}\pm \hspace{1em}0.34$, ${\lambda }_{\mathit{MY}}=1.3\pm 0.04$), we set the myocardium stretch ratio as 1.3, and fit the average experimental data from hysteresis tests and ramp-hold tests at the same time. This yielded parameters for the exponential strain energy density function ($A_{\mathit{MY}}=22$ Pa, $B_{\mathit{MY}}=0.5$, for ${\lambda }_{\mathit{MY}}=1.3$), which were consistent with those previously reported.

4.2. Remarks on the Transient Properties of CJ and MY.

The current stage 12 MY (Table 2) had a nondimensional modulus $G\left(\infty \right)$ of $0.46\pm 0.26$, which was similar to those determined previously for HH stages 18 (0.39) [7], 24 (0.36) [8], and 27 (0.52) [6]. Thus, if the equilibrium behavior is dominated by solid matrix viscoelasticity [8], the intrinsic viscoelasticity of the solid matrix may be similar for different stages in the embryonic heart. This result may be somewhat surprising, as sarcomere density increases considerably during these stages [17,18]. However, it should be noted that $G\left(\infty \right)$ is the percentage of instantaneous stress remaining at equilibrium. Although it is possible that the absolute magnitude of the equilibrium modulus does increase with development; currently, there are no data on the instantaneous modulus reported for later stage hearts.

Our results on the rapid initial relaxation rate of stage 12 MY (i.e., $G(0.5s)=0.71\pm 0.19$ and $G\left(\infty \right)=0.46\pm 0.26$) were comparable to those of stage 16 ($G(0.5s)=0.81$ for $G\left(\infty \right)$ of 0.4) and stage 24 ($G(0.5s)=0.66$ for $G\left(\infty \right)$ of 0.36) [8]. Because the filtration of extracellular fluid from the elastic matrix may be one of the major reasons for viscoelastic behavior of passive MY [19], this rapid relaxation rate suggests little friction between fluid and solid phases during short times after loading for embryonic MY. The difference in equilibrium modulus and relaxation rate between MY and CJ may be related to the microstructures of MY and CJ. At HH stage 12, MY is an epithelial tissue with myocytes firmly attached to each other by desmosomes and intercalated discs [9]. The extracellular CJ contains a microfibrillar network with a high content of hydrophilic glycosaminoglycans (GAGs) [20]. Therefore, it is very likely that besides of instantaneous behavior [5], MY and CJ also have distinctly different fluid resistance and viscoelasticity for the solid phase.

The standard deviations of some of the material parameters are on the same order of the parameters themselves (Tables 1 and 2). Much of this variation is likely due to the individual differences between subjects, because we obtained similar sets of parameters when multiple starting points were used in the optimization procedure. Subject variation is expected to be large for embryonic tissues, because every heart develops somewhat differently. Similar subject variations have been found in previous mechanical studies of embryonic tissues [6].

5. Conclusion

In summary, our results provide for the first time the viscoelastic constitutive relations for the MY and CJ for the HH stage 12 embryonic chick heart. These data can be used to extend the current understanding of the mechanical processes of early cardiac looping. The use of microindentation experiments provides multiaxial characterization of the viscoelasticity of embryonic tissue, which is more robust than uniaxial tests on excised tissue samples [21,22]. The methods used in this study are generally applicable to embryonic tissues, the small size of which makes traditional testing techniques difficult. The combination of hysteresis and ramp-hold tests improves the predictive capabilities of the proposed viscoelastic constitutive relations.