Short abstract
The foot consists of many small bones with complicated joints that guide and limit motion. A variety of invasive and noninvasive means [mechanical, X-ray stereophotogrammetry, electromagnetic sensors, retro-reflective motion analysis, computer tomography (CT), and magnetic resonance imaging (MRI)] have been used to quantify foot bone motion. In the current study we used a foot plate with an electromagnetic sensor to determine an individual subject's foot end range of motion (ROM) from maximum plantar flexion, internal rotation, and inversion to maximum plantar flexion, inversion, and internal rotation to maximum dorsiflexion, eversion, and external rotation. We then used a custom built MRI-compatible device to hold each subject's foot during scanning in eight unique positions determined from the end ROM data. The scan data were processed using software that allowed the bones to be segmented with the foot in the neutral position and the bones in the other seven positions to be registered to their base positions with minimal user intervention. Bone to bone motion was quantified using finite helical axes (FHA). FHA for the talocrural, talocalcaneal, and talonavicular joints compared well to published studies, which used a variety of technologies and input motions. This study describes a method for quantifying foot bone motion from maximum plantar flexion, inversion, and internal rotation to maximum dorsiflexion, eversion, and external rotation with relatively little user processing time.
Introduction
The foot is a complex structure with many small bones and intricate joints. Consequently, tracking foot bone motion is technically challenging, but it is necessary to better understand normal and pathological foot function. Foot bone kinematics have been studied with cadavers using mechanical means [1,2] or with living subjects using X-ray stereophotogrammy and implanted markers [3,4], electromagnetic sensors [5,6], and retro-reflective markers on the skin [7–9] or on bone pins [10]. These methods are either invasive or require ionizing radiation or rely on indirect tracking of bones.
More recently medical imaging technology [computed tomography (CT) and magnetic resonance imaging (MRI)] has been employed for the noninvasive investigation of foot bone kinematics. However, some of these studies moved all subjects through the same positions, i.e., an average subtalar joint axis [11–13]. Recently Beimers et al. [14] applied forces onto feet in eight specific positions in a CT scanner, while Sheehan [15] used cine phase contrast MRI of the foot during dorsiflexion/plantar flexion. However both studies applied forces in predefined directions that were the same for all subjects. Finally, biplane fluoroscopy has been used to study nonweight-bearing range of motion (ROM) from maximum plantar flexion, inversion, and internal rotation to maximum dorsiflexion, eversion, and external rotation [16]. However, only the end ROM positions were used and radiation exposure was required.
The purpose of our study was to scan subjects in foot positions ranging from maximum plantar flexion, inversion, and internal rotation to maximum dorsiflexion, eversion, and external rotation using a modified MRI-compatible loading frame that had been previously been used to apply inversion and anterior drawer loads on the ankle [17]. Our method was noninvasive, did not require radiation, and included intermediate positions. Additionally, we were able to image the entire foot while minimizing user processing time.
Methods
Ten subjects (five males and five females, age 51.8 ± 7.3 years) were enrolled in this institutional review board (Human Subject Division, University of Washington) approved study. All subjects had a neutrally aligned foot (based on examination by an orthopaedic surgeon) and were free of any lower-extremity pathology. Exclusion criteria included the inability to self ambulate, current ulceration, and partial foot amputation.
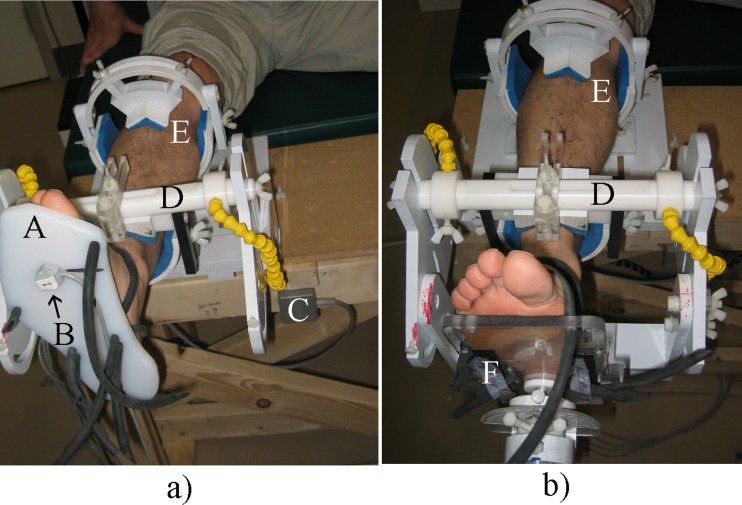
Foot end ROM was measured with the Polhemus Liberty electromagnetic motion analysis system (Polhemus Inc., Colchester, VT). The subject's foot was strapped to a plate that had an electromagnetic sensor attached (Fig. 1(a)). Each subject's foot was measured in three orientations: maximum plantar flexion, inversion, and internal rotation (position 1); anatomical neutral (position 5); and maximum dorsiflexion, eversion, and external rotation (position 8). Direction cosines were recorded and converted to the desired Cardan angle system (XY′Z″ sequence). The Cardan angles (α, β, γ) correspond to rotations about the x axis (dorsiflexion/plantar flexion), the y axis (inversion/eversion), and the z axis (internal/external rotation). To immobilize the lower leg, the back portion of a modified ankle loading device (ALD) [17] was employed (Fig. 1(a)).
Fig. 1.
(a) Foot in back portion of modified ankle loading device (ALD) with Polhemus sensor on the plate. (A) foot plate, (B) Polhemus sensor, (C) Polhemus transmitter, (D) distal leg holder, and (E) proximal leg holder. (b) Foot in modified ALD with (F) foot positioning device.
Prior to the MRI, the remaining scanning positions were linearly interpolated between positions 1, 5, and 8. The two extreme positions were tested on the subject with the ALD (Fig. 1(b)) to check for interference. Position 1 had to be slightly backed off in all three angles for most subjects because of a physical limitation in the amount of plantar flexion allowed by the ALD design resulting in new orientations 1 through 4 (Table 1).
Table 1.
The desired position was obtained with a free floating foot plate attached to a subject's foot. Actual positions accounted for a limitation in the ALD which prevented the full plantar flexion that most subjects could obtain during passive movement. When this limit was determined with the foot positioning device of the ALD reattached the other two angles were backed off by the same percentage of their maximum and this new position 1 was used to determine positions 2–4. Note that left and right feet had different signs for γ and β.
| Subject |
Desired |
Percent |
Actual |
||||
|---|---|---|---|---|---|---|---|
| α | β | γ | α | β | γ | ||
| NA01R | −58.2 | 50.3 | 30.8 | 83 | −48.3 | 41.7 | 25.6 |
| NA02L | −63.7 | −55.9 | −36.7 | 75 | −47.7 | −41.9 | −27.5 |
| NA03L | −44.8 | −45.2 | −35.0 | 100 | −44.8 | −45.2 | −35.0 |
| NA04R | −72.5 | 54.6 | 35.0 | 60 | −43.5 | 32.7 | 21.0 |
| NA05L | −78.1 | −66.0 | −34.1 | 54 | −42.2 | −35.7 | −18.4 |
| NA06R | −82.2 | 60.1 | 33.7 | 61 | −50.1 | 36.7 | 20.5 |
| NA07L | −69.1 | −53.1 | −32.9 | 65 | −44.9 | −34.5 | −21.4 |
| NA09L | −80.1 | −55.6 | −31.2 | 56 | −44.8 | −31.1 | −17.5 |
| NA14R | −69.7 | 53.8 | 29.3 | 90 | −49.8 | 38.5 | 20.9 |
| NA18R | −73.8 | 54.9 | 30.2 | 71.5 | −48.0 | 35.7 | 19.6 |
Each subject's foot was scanned in the eight positions using an MRI (Phillips Intera Gyroscan 1.5 T) scanner running a 3D volume sequence (slice thickness 1 mm, slice spacing 0.5 mm, repetition time 5.87 ms, echo time 1.83 ms, flip angle 25°). Scanning took approximately 1.5 h per subject; in all cases the smallest possible volume was scanned to minimize scan time.
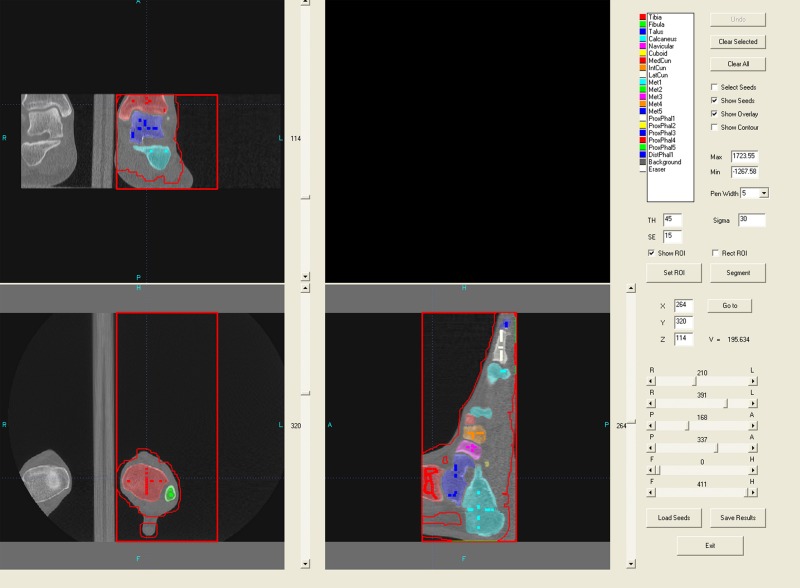
Data was segmented, registered, and visualized in Multi-Rigid, a custom software program [18]. Segmentation was accomplished via graph cuts by drawing initial seeds in the neutral position (position 5, see Fig. 2) which the software uses as a starting point for segmentation. During processing the segmented volume expands until it comes to a bone's edge (recognized as a change in image intensity). This was done for all 14 bones of interest (tibia, fibula, calcaneus, talus, navicular, cuboid, three cuneiforms, and five metatarsals). Following segmentation, results were refined using a level set algorithm. If necessary, the user could add additional seeds and repeat the segmentation process.
Fig. 2.
Segmented bones using Multi-Rigid. Darker lines represent the initial seeds used to begin the segmentation process, while the lighter colors show the resulting segmented bone volumes.
Once segmentation of the base level scan was satisfactory, registration was performed automatically by software that located the segmented bones in each of the seven remaining volumes, using the segmented results from the base position as a guide. This step uses mutual information maximization to determine the transformation matrix that defines each bone's change in position from its neutral orientation to its position in each of the non-neutral orientations. To initialize the automatic registration process one point was selected manually within three hindfoot bones (talus, calcaneus, and tibia) in the neutral orientation and the seven other orientations.
After the 3D motion of each bone in each position was determined, finite helical axes (FHA) were calculated using an embedded coordinate system based on the principal axes of the bones at the neutral position and the transformation matrixes for the other positions [19]. The numerical outputs from each FHA calculation are: (1) orientation, (2) rotation about the axis, (3) translation along the axis, and (4) a location point on each axis. Ten FHAs were calculated for each bone to bone relationship; 1→2 (position 1 to position 2), 2→3, 3→4, 4→5, 5→6, 6→7, 7→8, 1→5, 5→8, and 1→8. Data processing was carried out on a Dell Precision 470 computer with dual 3.2 GHz processors and 2 GB of RAM.
Results
For each foot, preprocessing and segmentation took approximately 30 min, split evenly between user and computer time. The ensuing registration took approximately 5 h 30 min after 10 min of user time. Position 1 of subject NA18R was excluded because the tibia and fibula were not oriented similar to the neutral position.
The 3D anatomy of the bones was different for each subject; however, the general distribution and orientation of the axes were similar (Table 2). Position data were collected and analyzed for all the bones of interest; however, only the data from three representative joints are presented here.
Table 2.
Data summarized over all subjects (n = 10) for talocrural (talus relative to tibia), talocalcaneal (calcaneus relative to talus), and talonavicular (navicular relative to talus)
| Position |
Axis orientation |
Rotation about (deg) |
Translation along (mm) |
|||
|---|---|---|---|---|---|---|
| Dorsiflexion in sagittal plane, relative to transverse plane (deg) | Inversion in coronal plane, relative to transverse plane (deg) | External rotation in transverse plane, relative to coronal plane (deg) | ||||
| Talocrural | 1→2 | 23.75 ± 23.57 | 8.00 ± 7.28 | 17.08 ± 8.01 | 6.94 ± 1.81 | 0.55 ± 0.26 |
| 2→3 | 39.04 ± 18.45 | 10.96 ± 6.46 | 12.51 ± 5.52 | 8.69 ± 2.44 | 0.22 ± 0.11 | |
| 3→4 | 48.48 ± 15.13 | 13.06 ± 4.76 | 12.15 ± 6.37 | 8.62 ± 1.73 | 0.19 ± 0.13 | |
| 4→5 | 49.83 ± 12.38 | 15.96 ± 3.17 | 14.03 ± 5.62 | 8.99 ± 1.68 | 0.21 ± 0.10 | |
| 5→6 | 37.41 ± 56.38 | 33.58 ± 45.85 | 37.30 ± 38.51 | 3.06 ± 1.63 | 0.20 ± 0.15 | |
| 6→7 | 41.47 ± 51.09 | 11.68 ± 58.02 | 34.59 ± 51.12 | 4.69 ± 2.67 | 0.19 ± 0.15 | |
| 7→8 | 54.44 ± 13.59 | 22.89 ± 8.69 | 16.26 ± 4.89 | 5.83 ± 1.75 | 0.21 ± 0.16 | |
| 1→5 | 43.47 ± 11.59 | 12.67 ± 2.97 | 13.85 ± 5.87 | 32.57 ± 6.09 | 0.93 ± 0.36 | |
| 5→8 | 64.78 ± 13.30 | 36.33 ± 20.52 | 33.49 ± 50.91 | 11.46 ± 3.76 | 0.25 ± 0.24 | |
| 1→8 | 48.79 ± 10.83 | 17.61 ± 3.27 | 16.05 ± 6.21 | 42.94 ± 4.41 | 0.99 ± 0.59 | |
| Position | Dorsiflexion in sagittal plane, relative to transverse plane (deg) | Inversion in coronal plane, relative to transverse plane (deg) | Internal rotation in transverse plane, relative to sagittal plane (deg) | Rotation about (deg) | Translation along (mm) | |
|---|---|---|---|---|---|---|
| Talocalcaneal | 1→2 | 46.70 ± 12.89 | 80.39 ± 6.91 | 11.42 ± 7.94 | 3.37 ± 0.40 | 0.32 ± 0.22 |
| 2→3 | 49.17 ± 8.20 | 78.04 ± 7.32 | 13.78 ± 8.54 | 4.91 ± 2.07 | 0.23 ± 0.13 | |
| 3→4 | 46.34 ± 6.63 | 73.42 ± 7.05 | 17.26 ± 8.23 | 5.23 ± 1.45 | 0.22 ± 0.18 | |
| 4→5 | 48.48 ± 6.69 | 62.46 ± 5.39 | 31.05 ± 8.44 | 3.70 ± 1.19 | 0.28 ± 0.21 | |
| 5→6 | 36.69 ± 7.88 | 63.73 ± 7.01 | 20.65 ± 6.57 | 5.65 ± 2.46 | 0.78 ± 0.50 | |
| 6→7 | 32.76 ± 9.54 | 54.08 ± 6.62 | 24.75 ± 6.07 | 2.80 ± 1.05 | 0.41 ± 0.15 | |
| 7→8 | 33.36 ± 15.33 | 53.77 ± 16.62 | 26.60 ± 21.05 | 1.56 ± 0.81 | 0.16 ± 0.13 | |
| 1→5 | 47.28 ± 6.91 | 73.39 ± 5.21 | 17.90 ± 5.38 | 17.18 ± 4.19 | 0.52 ± 0.31 | |
| 5→8 | 34.58 ± 7.92 | 59.61 ± 5.15 | 22.30 ± 5.93 | 9.97 ± 3.81 | 1.36 ± 0.69 | |
| 1→8 | 42.80 ± 5.97 | 68.17 ± 5.10 | 20.52 ± 5.22 | 26.95 ± 4.74 | 1.18 ± 0.61 | |
| Talonavicular | 1→2 | 25.82 ± 11.29 | 70.81 ± 18.76 | 8.17 ± 4.19 | 5.59 ± 0.97 | 0.33 ± 0.19 |
| 2→3 | 37.67 ± 6.50 | 74.04 ± 11.86 | 13.59 ± 12.26 | 7.69 ± 2.96 | 0.47 ± 0.52 | |
| 3→4 | 45.94 ± 12.09 | 73.52 ± 9.90 | 20.20 ± 15.06 | 8.51 ± 1.98 | 0.48 ± 0.34 | |
| 4→5 | 48.49 ± 9.37 | 71.47 ± 5.64 | 22.12 ± 11.50 | 6.67 ± 1.68 | 0.27 ± 0.21 | |
| 5→6 | 31.86 ± 9.91 | 82.70 ± 19.64 | 6.35 ± 8.03 | 10.11 ± 4.36 | 0.74 ± 0.46 | |
| 6→7 | 29.14 ± 15.42 | 96.60 ± 39.57 | 4.01 ± 15.19 | 5.38 ± 1.48 | 0.39 ± 0.20 | |
| 7→8 | 28.37 ± 16.18 | 67.49 ± 86.05 | −2.39 ± 13.22 | 3.23 ± 1.48 | 0.26 ± 0.26 | |
| 1→5 | 40.23 ± 7.14 | 74.59 ± 5.88 | 14.21 ± 7.70 | 28.14 ± 5.58 | 1.25 ± 0.61 | |
| 5→8 | 30.39 ± 9.59 | 87.39 ± 19.94 | 4.08 ± 8.55 | 18.32 ± 6.69 | 1.36 ± 0.55 | |
| 1→8 | 34.80 ± 6.33 | 76.67 ± 6.99 | 10.08 ± 5.09 | 46.16 ± 7.51 | 2.67 ± 0.59 |
1→2: position 1 to position 2.
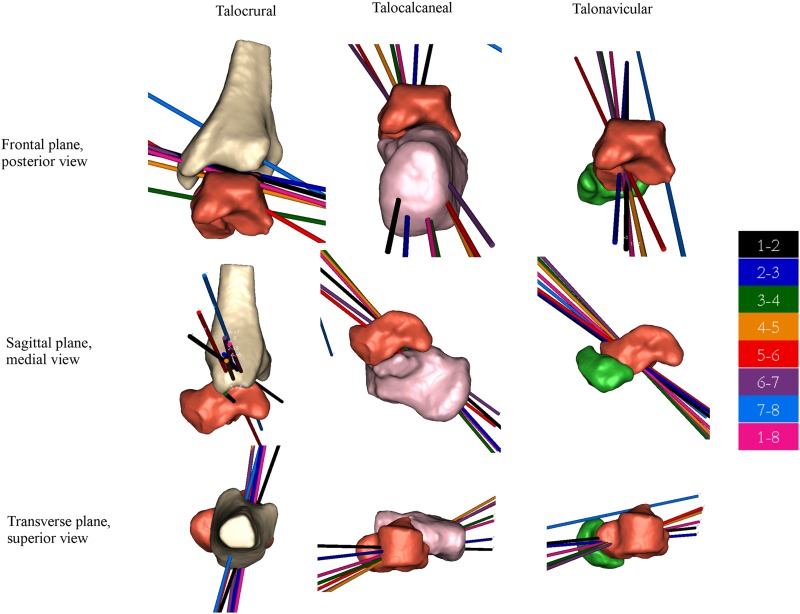
For the talocrural joint the FHA from position 1 to position 8 were oriented primarily in the medial-lateral direction, rotated externally 16.1°, and dorsiflexed 48.8° with an average of 42.9° of rotation about the talocrural joint axis. The orientation of the talocalcaneal joint's FHA from position 1 to position 8 was very consistent between subjects. This joint axis was dorsiflexed 42.8° with 20.5° of average internal rotation and 27.0° of rotation about the joint axis. The talonavicular FHA from position 1 to 8 had an average dorsiflexion of 34.8° with internal rotation of 10.1° and 46.2° of average rotation about the axis.
Discussion
We have presented a methodology for objective, noninvasive quantification of foot bone kinematics with relatively little user interaction time. This methodology allowed for patient-specific positions and analysis, while the use of FHAs provided clinically useful information that was reproducible between patients while retaining quantitative bone-to-bone kinematics.
Many studies have measured joint axes orientation; for feet, the talocrural, talocalcaneal, and talonavicular joints are among those most often studied due to their significance in foot function. While each study has used different methods, the resultant axes are similar to our work indicating general agreement. This is apparent both quantitatively (Table 3) and qualitatively (Fig. 3) for the talocalcaneal [1,3–5,7,14,15,20–22] and talonavicular [3,4] joints (Fig. 3). The consistency with other studies is likely high for these joints because the input foot end-ROM positions used here (maximum plantar flexion, inversion, and internal rotation and maximum dorsiflexion, eversion, and external rotation) are similar to the natural motion of the joints.
Table 3.
FHA orientation relative to Cardan planes for the axis of rotation of the talocrural (talus relative to tibia), talocalcaneal (calcaneus relative to talus), and talonavicular joint (navicular relative to talus) compared between multiple studies. PF: plantar flexion, DF: dorsiflexion, IN: inversion, EV: eversion, IR: internal rotation, ER: external rotation, NP: neutral position, and FHA: finite helical axes, 1→8: position 1 to position 8.
| Talocrural joint | Motion | Year | Dorsiflexion in sagittal plane, relative to transverse plane (deg) | Inversion in coronal plane, relative to transverse plane (deg) | External rotation in transverse plane, relative to coronal plane (deg) | Rotation about axis (deg) |
|---|---|---|---|---|---|---|
| Isman | varied | 1968 | – | 10 ± 4 | 6 ± 7 | – |
| Inman | PF → DF | 1976 | – | 7.3 ± 3.6 | – | – |
| Lundberg | NP → PF | 1989 | – | −2 ± 5 | – | 28.5 ± 7.5 |
| van den Bogert | varied | 1994 | – | 4.6 ± 7.4 | 1 ± 15.1 | – |
| Kitaoka a | NP → PF | 1997 | 4.1 | 0.6 | 8.1 | – |
| Sheehan | PF → DF | 2010 | 22 ± 41.7 | 5.5 ± 12.9 | 15.8 ± 12.2 | 31.7 ± 11.3 |
| Current (FHA 1→8) | IR + IN + PF → ER + EV + DF | 2010 | 48.8 ± 10.8 | 17.6 ± 3.3 | 16.1 ± 6.2 | 42.9 ± 4.4 |
| Talocalcaneal joint | Dorsiflexion in sagittal plane, relative to transverse plane (deg) | Inversion in coronal plane, relative to transverse plane (deg) | Internal rotation in transverse plane, relative to sagittal plane (deg) | |||
|---|---|---|---|---|---|---|
| Manter | IR + IN + PF → ER + EV + DF | 1941 | 29 to 47 | – | 15 to 31 b | – |
| Inman | IR + IN + PF → ER + EV + DF | 1976 | 42 ± 9 | – | 23 ± 11 | – |
| van Langelaan | Leg ER relative to foot | 1983 | 41.5 ± N/A | – | 25.8 ± N/A | – |
| Lundberg | NP → PF | 1989 | 32 ± 16 | – | 34 ± 16 | 4.3 ± 1.6 |
| van den Bogert | varied | 1994 | 35.3 ± 4.8 | – | 18 ± 16.2 | – |
| Kitaoka a | NP → IR + IN + PF | 1997 | 37.5 | 57.3 | 26.3 | – |
| Lewis | IN → EV | 2005 | 38.2 ± 6.2 | – | 21.3 ± 3.6 | – |
| Beimers | EV + DF → IN + PF | 2008 | 50.9 ± 4 | – | 11.8 ± 8 | 29.7 ± 5.1 |
| Goto | DF → PF | 2009 | 39 ± 8 | – | 46 ± 7 | 16 ± 3 |
| Sheehan | PF → DF | 2010 | variable | variable | variable | 15.1 ± 9.7 |
| Current (FHA 1→8) | IR + IN + PF → ER + EV + DF | 2010 | 42.8 ± 6.0 | 68.2 ± 5.1 | 20.5 ± 5.2 | 27.0 ± 4.7 |
| Talonavicular joint | ||||||
|---|---|---|---|---|---|---|
| van Langelaan | Leg ER relative to foot | 1983 | 38.5 | – | 14.1 | – |
| Lundberg | NP → PF | 1989 | 34 ± 12 | – | 42 ± 19 | 7.8 ± 3.2 |
| Current (FHA 1→8) | IR + IN + PF → ER + EV + DF | 2010 | 34.8 ± 6.3 | 76.7 ± 7.0 | 10.1 ± 5.1 | 46.2 ± 7.5 |
Calculated from reported unit vectors.
7° offset was added to the results of Manter due to differences in how the sagittal plane was defined.
Fig. 3.
Joints of the foot from a representative subject (NA01R) with eight finite helical axes (FHA), color coded by change in position (e.g., 1→8 is the FHA describing motion between the two end positions)
While our set of positions did not take place in a single plane for the talocrural joint as do most [4,5,15,22] but not all [7,23] related studies, the resultant axes are more consistent (lower standard deviations) than other studies. This is likely due to our choice of ROM positions keeping the foot in a more mechanically stable position. Taking a foot through a purely sagittal plane excursion could allow more freedom of motion, especially in the plantar flexed position.
There are a few limitations to this study. Although the foot positions were customized to each subject, the foot still followed a very specific “path” resulting in a particular subset of possible joint axes. Nevertheless, this path was optimized for each subject. Additionally during scanning only a small force was applied (to secure the plate to the foot) rather than weight bearing loads. However, along our path of positions, high loads would only be realistic near the neutral position. Nevertheless, it should be noted that the axes determined in this study might be different from the functional axes during walking. Furthermore comparisons presented show FHAs oriented relative to the cardinal planes. These planes are coincident with the MRI scanner coordinate system and not specific to a subject's anatomy. Finally registration was found to have problems if not enough of the tibia and fibula was included in the MRI scan or if a position does not have the tibia and fibula in a similar position to the neutral position scan.
We have presented a technique requiring relatively little user interaction time that describes the motion of bones of the foot while the foot is exercised from maximum plantar flexion, inversion, and internal rotation to maximum dorsiflexion, eversion, and external rotation. The ability to use a customized ROM prevents possible inaccuracies or truncation of subject motion that can occur when requiring subject to go through an unnatural ROM.
Acknowledgment
This work was supported in part by the Department of Veterans Affairs, Rehabilitation Research & Development Service Grant No. A3030R.
Contributor Information
Eric S. Rohr, RR&D Center of Excellence for Limb, Loss Prevention and Prosthetic Engineering, VA Puget Sound Heath Care System, Seattle, WA 98108
Yangqiu Hu, Department of Bioengineering, University of Washington, Seattle, WA 98195.
David R. Haynor, Departments of Bioengineering and Radiology, University of Washington, Seattle, WA 98195
Sorin Siegler, Department of Mechanical Engineering, and Mechanics, Drexel University, Philadelphia, PA 19104.
Bruce J. Sangeorzan, RR&D Center of Excellence for Limb, Loss Prevention and Prosthetic Engineering, VA Puget Sound Heath Care System, Seattle, WA 98108; Orthopaedics and Sports Medicine, University of Washington, Seattle, WA 98195
William R. Ledoux, RR&D Center of Excellence for Limb, Loss Prevention and Prosthetic Engineering, VA Puget Sound Heath Care System, Seattle, WA 98108; Orthopaedics and Sports Medicine and, Department of Mechanical Engineering, University of Washington, Seattle, WA 98195, e-mail: wrledoux@u.washington.edu
References
- [1]. Manter, J. T. , 1941, “Movements of the Subtalar and Transverse Tarsal Joints,” Anat. Rec., 80(4), pp. 397–410. 10.1002/ar.v80:4 [DOI] [Google Scholar]
- [2]. Elftman, H. , 1960, “The Transverse Tarsal Joint and Its Control,” Clin. Orthop., 16, pp. 41–45. [PubMed] [Google Scholar]
- [3]. Van Langelaan, E. J. , 1983, “A Kinematic Analysis of the Tarsal Joints, an X-Ray Photogrammetric Study,” Acta Orthop. Scand. Suppl., 204, pp. 1–269. [PubMed] [Google Scholar]
- [4]. Lundberg, A. , 1989, “Kinematics of the Ankle and Foot. In Vivo Roentgen Stereophotogrammetry,” Acta Orthop. Scand. Suppl., 233, pp. 1–24. 10.3109/17453678909154185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Kitaoka, H. B. , Luo, Z. P. , and An, K. N. , 1997, “Three-Dimensional Analysis of Normal Ankle and Foot Mobility,” Am. J. Sports Med., 25(2), pp. 238–242. 10.1177/036354659702500218 [DOI] [PubMed] [Google Scholar]
- [6]. Cornwall, M. W. , and Mcpoil, T. G. , 2002, “Motion of the Calcaneus, Navicular, and First Metatarsal During the Stance Phase of Walking,” J. Am. Podiatr. Med. Assoc., 92(2), pp. 67–76. [DOI] [PubMed] [Google Scholar]
- [7]. van den Bogert, A. J. , Smith, G. D. , and Nigg, B. M. , 1994, “In Vivo Determination of the Anatomical Axes of the Ankle Joint Complex: An Optimization Approach,” J. Biomech., 27(12), pp. 1477–1488. 10.1016/0021-9290(94)90197-X [DOI] [PubMed] [Google Scholar]
- [8]. Leardini, A. , Benedetti, M. G. , Catani, F. , Simoncini, L. , and Giannini, S. , 1999, “An Anatomically Based Protocol for the Description of Foot Segment Kinematics During Gait,” Clin. Biomech. (Bristol, Avon), 14(8), pp. 528–536. 10.1016/S0268-0033(99)00008-X [DOI] [PubMed] [Google Scholar]
- [9]. Kidder, S. M. , Abuzzahab, F. S. , Harris, G. F. , and Johnson, J. , 1996, “A System for the Analysis of Foot and Ankle Kinematics During Gait,” IEEE Trans. Rehabil. Eng., 4(1), pp. 25–32. 10.1109/86.486054 [DOI] [PubMed] [Google Scholar]
- [10]. Lundgren, P. , Nester, C. , Liu, A. , Arndt, A. , Jones, R. , Stacoff, A. , Wolf, P. , and Lundberg, A. , 2008, “Invasive in Vivo Measurement of Rear-, Mid- and Forefoot Motion During Walking,” Gait Posture, 28(1), pp. 93–100. 10.1016/j.gaitpost.2007.10.009 [DOI] [PubMed] [Google Scholar]
- [11]. Stindel, E. , Udupa, J. K. , Hirsch, B. E. , and Odhner, D. , 2001, “An In Vivo Analysis of the Motion of the Peri-Talar Joint Complex Based on MR Imaging,” IEEE Trans. Biomed. Eng., 48(2), pp. 236–247. 10.1109/10.909645 [DOI] [PubMed] [Google Scholar]
- [12]. Udupa, J. K. , Hirsch, B. E. , Hillstrom, H. J. , Bauer, G. R. , and Kneeland, J. B. , 1998, “Analysis of in Vivo 3-D Internal Kinematics of the Joints of the Foot,” IEEE Trans. Biomed. Eng., 45(11), pp. 1387–1396. 10.1109/10.725335 [DOI] [PubMed] [Google Scholar]
- [13]. Wolf, P. , Luechinger, R. , Boesiger, P. , Stuessi, E. , and Stacoff, A. , 2007, “A MR Imaging Procedure to Measure Tarsal Bone Rotations,” J. Biomech. Eng., 129(6), pp. 931–936. 10.1115/1.2805400 [DOI] [PubMed] [Google Scholar]
- [14]. Beimers, L. , Maria Tuijthof, G. J. , Blankevoort, L. , Jonges, R. , Maas, M. , and Van Dijk, C. N. , 2008, “In-Vivo Range of Motion of the Subtalar Joint Using Computed Tomography,” J. Biomech. Eng., 41(7), pp. 1390–1397. 10.1016/j.jbiomech.2008.02.020 [DOI] [PubMed] [Google Scholar]
- [15]. Sheehan, F. T. , 2010, “The Instantaneous Helical Axis of the Subtalar and Talocrural Joints: A Non-Invasive In Vivo Dynamic Study,” J. Foot Ankle Surg., 3 (13), pp. 1–10. 10.1186/1757-1146-3-13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Asla, R. J. D. , Wan, L. , Rubash, H. E. , and Li, G. , 2005, “Six DoF In Vivo Kinematics of the Ankle Joint Complex: Application of a Combined Dual-Orthogonal Fluoroscopic and Magnetic Resonance Imaging Technique,” J. Orthop. Res., 24 (5), pp. 1019–1027. [DOI] [PubMed] [Google Scholar]
- [17]. Siegler, S. , Udupa, J. K. , Ringleb, S. I. , Imhauser, C. W. , Hirsch, B. E. , Odhner, D. , Saha, P. K. , Okereke, E. , and Roach, N. , 2005, “Mechanics of the Ankle and Subtalar Joints Revealed through a 3D Quasi-Static Stress MRI Technique,” J. Biomech. Eng., 38(3), pp. 567–578. 10.1016/j.jbiomech.2004.03.036 [DOI] [PubMed] [Google Scholar]
- [18]. Hu, Y. , Ledoux, W. R. , Fassbind, M. , Rohr, E. S. , Sangeorzan, B. J. , and Haynor, D. R. , 2011, “Multi-Rigid Image Segmentation and Registration for the Analysis of Joint Motion from 3D MRI,” J. Biomech. Eng., in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Beggs, J. S. , 1983, Kinematics, Hemisphere, Washington, D.C. [Google Scholar]
- [20]. Lewis, G. S. K. , Kevin A., and Piazza, Stephen, J. , 2007, “Determination of Subtalar Joint Axis Location by Restriction of Talocrural Joint Motion,” Gait Posture, 25, pp. 63–69. 10.1016/j.gaitpost.2006.01.001 [DOI] [PubMed] [Google Scholar]
- [21]. Goto, A. , Moritomo, H. Itohara, T. Watanabe, T. , and Sugamoto, K. , 2009, “Three-Dimensional In Vivo Kinematics of the Subtalar Joint During Dorsi-Plantarflexion and Inversion-Eversion,” Foot Ankle Int., 30(5), pp. 432–438. 10.3113/FAI.2009.0432 [DOI] [PubMed] [Google Scholar]
- [22]. Inman, V. T. , 1976, The Joints of the Ankle, Williams and Wilkins, Baltimore. [Google Scholar]
- [23]. Isman, R. E. , and Inman, V. T. , 1968, “Anthropometric Studies of the Human Foot and Ankle,” Technical Report No. Technical Report 58, Biomechanics Laboratory, University of California, San Francisco and Berkeley, San Francisco. [Google Scholar]