Effect of the Intra-Abdominal Pressure and the Center of Segmental Body Mass on the Lumbar Spine Mechanics – A Computational Parametric Study

Short abstract

Determination of physiological loads in human lumbar spine is critical for understanding the mechanisms of lumbar diseases and for designing surgical treatments. Computational models have been used widely to estimate the physiological loads of the spine during simulated functional activities. However, various assumptions on physiological factors such as the intra-abdominal pressure (IAP), centers of mass (COMs) of the upper body and lumbar segments, and vertebral centers of rotation (CORs) have been made in modeling techniques. Systematic knowledge of how these assumptions will affect the predicted spinal biomechanics is important for improving the simulation accuracy. In this paper, we developed a 3D subject-specific numerical model of the lumbosacral spine including T12 and 90 muscles. The effects of the IAP magnitude and COMs locations on the COR of each motion segment and on the joint/muscle forces were investigated using a global convergence optimization procedure when the subject was in a weight bearing standing position. The data indicated that the line connecting the CORs showed a smaller curvature than the lordosis of the lumbar spine in standing posture when the IAP was 0 kPa and the COMs were 10 mm anterior to the geometric center of the T12 vertebra. Increasing the IAP from 0 kPa to 10 kPa shifted the location of CORs toward the posterior direction (from 1.4 ± 8.9 mm anterior to intervertebral disc (IVD) centers to 40.5 ± 3.1 mm posterior to the IVD centers) and reduced the average joint force (from 0.78 ± 0.11 Body weight (BW) to 0.31 ± 0.07 BW) and overall muscle force (from 349.3 ± 57.7 N to 221.5 ± 84.2 N). Anterior movement of the COMs from −30 mm to 70 mm relative to the geometric center of T12 vertebra caused an anterior shift of the CORs (from 25.1 ± 8.3 mm posterior to IVD centers to 7.8 ± 6.2 mm anterior to IVD centers) and increases of average joint forces (from 0.78 ± 0.1 BW to 0.93 ± 0.1 BW) and muscle force (from 348.9 ± 47.7 N to 452.9 ± 58.6 N). Therefore, it is important to consider the IAP and correct COMs in order to accurately simulate human spine biomechanics. The method and results of this study could be useful for designing prevention strategies of spinal injuries and recurrences, and for enhancing rehabilitation efficiency.

1. Introduction

Determination of the physiological loads in the human lumbar spine is critical for understanding the mechanisms of lumbar injuries and diseases as well as for designing surgical techniques for treatment of lumbar pathologies, such as disc replacement and spinal fusion [1–4]. Numerous experimental studies, both in vitro and in vivo, have attempted to investigate the biomechanics of the spinal system [5–10]. However, it is always difficult to mimic the physiological conditions in in vitro experiments such as including muscle forces [5,6]. On the other hand, due to technical limitations, there are only few in vivo studies that tried to measure the joint forces directly using telemeterized implant techniques [5–8] and indirectly from the measurement of intra-discal pressure using pressure transducer [9,10].

Many computational models have been proposed to provide an alternative way to estimate the physiological loads of the spine during various functional activities [1,2,4,11–20]. For example, Stokes and Gardner-Morse investigated the activation synergies of the lumbar spinal muscle using an inverse dynamic optimization method [19]. Kim et al. reported lumbar joint and muscle forces using a finite element model [15–17]. Shirazi-Adl et al. reported changes of spinal joint and muscle forces, and stability in various standing and loading postures using a finite element model and an optimization algorithm [1,2,4,11,12]. Han et al. reported that the joint forces, which correspond to the same direction as the spinal lordosis (i.e., a follower load), could be generated by spinal muscles using a static numerical model [13]. These modeling studies made various assumptions on physiological factors of the spinal system, such as the intra-abdominal pressure (IAP) [12,20,21], centers of mass (COMs) of the upper body and the lumbar segments [1,2,4,11–20], as well as the vertebral centers of rotation (CORs) [13,17]. A widely used mathematical model of the lumbar spine [18] has assumed a “ball and socket” joint between two vertebral bodies to calculate the spinal joint and muscle forces. When a “ball and socket” joint is used, no moment was transmitted through the joint center. Generally, joint reaction forces and moments were calculated at the midpoint of the intervertebral disc (IVD) in the human articular joint models [18,22]. However, if the selected geometric center is not a real COR, the reaction joint moments are not actually zero at the selected center [22]. A systematic knowledge of how these assumptions affect the prediction of the spinal biomechanics is important for improved accuracy of computational spine biomechanics.

In this study, we developed a subject-specific numerical model of the healthy lumbosacral spine to calculate the lumbar joint forces and muscle forces using a global convergence optimization procedure [22,23]. A parametric study was performed to examine the effects of the changing IAP magnitude and the COMs locations on the spine biomechanical responses. Further, we calculated the locations of the CORs of the lumbar spinal motion segments using a global convergence optimization procedure when the spine was under different loading conditions.

2. Materials and Methods

2.1. A Subject-Specific Model of the Lumbosacral Spine.

Coronal and sagittal x-ray images of the lumbosacral spine including the T12 in weight bearing upright standing posture were obtained from three healthy subjects (one male and two females). The detailed information of the subjects was shown in Table 1. The subjects had no history of spinal diseases. The x-ray images were carefully reviewed by an orthopaedic spine surgeon to ensure that there was no abnormality in the lumbosacral spine.

Table 1.

Information of the three subjects who participated in this study including the lordosis and Cobb's angle between the upper planes of L1 vertebra and sacrum and the piecewise linear length of lumbosacral spines from T12 and S1 measured by an orthopaedic spinal surgeon

No.	Sex	Age	Weight (kg)	Height (cm)	Lordosis angle (°)	Cobb angle (°)	L-spine length (mm)
1	Male	43	80	175	54.1	1.6	264
2	Female	27	53	163	54.4	0.7	234
3	Female	35	58	165	52.2	0.0	238

A three dimensional (3D) subject-specific model of the lumbosacral spine was developed based on the coronal and sagittal x-ray images of the subject (Fig. 1) using an inhouse code that was developed using MATLAB ^TM 2010 a (MathWorks Inc., Natick, MA, USA). A general model that represented the average positions of the vertebrae, and the attachment points of the spinal muscles was created based on the previously published data by Stokes et al. [18,24] and Bogduk et al. [25]. The general model included 7 vertebrae (from T12 to S1) and 90 pairs of spinal muscles (5 longissimus pars lumborum, 4 iliocostalis pars lumborum, 12 longissimus pars thoracis, 8 iliocostalis pars thoracis, 11 psoas, 5 quadratus lumborum, 12 thoracic multifidus, 20 lumbar multifidus, 6 external oblique, 6 internal oblique, and 1 rectus abdominis). For each subject, the lines connecting the geometric centers of the adjacent vertebrae from T12 to S1 were created using the information on the coronal and sagittal x-ray images (Fig. 1). The lengths of these lines were used to scale the general model to a subject-specific model along all directions. In addition, the lordosis angles were defined from x-ray images. In the scaling, linear and rotational transformation of vertebrae were also considered to make the subject specific models have the same lordosis angle with the x-ray image. Thus, a subject-specific model, including the bony geometry, the attachment points of the spinal muscles and the lordosis angle, could be obtained.

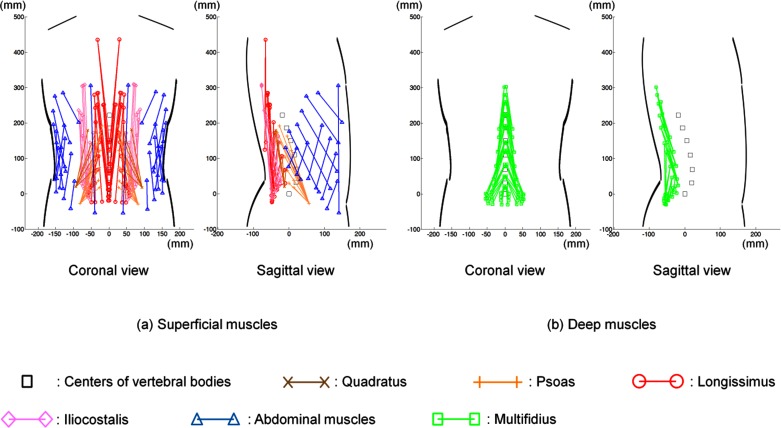
Fig. 1.

Subject specific musculoskeletal models of lumbosacral spine of subject #2 based on her coronal and sagittal X-ray images. Only right side muscles are shown in the sagittal view; (a) 58 pairs of superficial muscles (5 longissimus pars lumborum, 4 iliocostalis pars lumborum, 12 longissimus pars thoracis, 8 iliocostalis pars thoracis, 11 psoas, 5 quadratus lumborum, 6 external oblique, 6 internal oblique, and 1 rectus abdominis) and (b) 32 pairs of deep muscles (12 thoracic multifidus, 20 lumbar multifidus).

A local coordinate system was defined to calculate the COR in each IVD (Fig. 2(c)). The origin of the coordinate system was assumed to be at the mid-axial plane of the IVDs and the midpoint of the line connecting the geometric centers of the corresponding upper and lower vertebrae in this study. This definition was based on the studies using “ball and socket” joints [13,18], and based on the fact that the CORs have been determined to be in the IVDs in literature [26–29]. The z axis was defined along this line. The x axis pointing to the anterior direction was in the sagittal plane and perpendicular to the z direction. The y axis was perpendicular to the x-z plane.

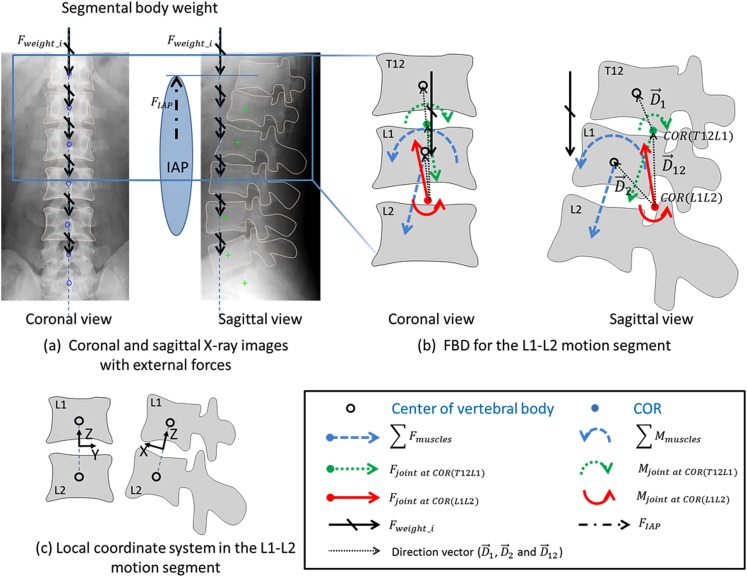
Fig. 2.

Free body diagram (FBD) for force and moment equilibrium equations of L1-L2 motion segment; (a) coronal and sagittal x-ray images with external forces (segmental body weight and IAP force); (b) FBD for the L1-L2 motion segment and (c) the local coordinate system of the L1-L2 motion segment

2.2. Inverse Dynamics.

A free body diagram (FBD) was established in each motion segment from T12 to S1. Figure 2 shows the FBD of L1-L2 motion segment. In this study all spinal joint forces were normalized to body weight (BW). A joint force was defined as the total force of the IVD, ligaments, and facet joints in each motion segment that counterbalanced the external forces and muscle forces. The muscle forces were represented using muscle groups. The COR was defined as the location where the joint moment was zero and represented using a vector in x-y plane of the local coordinate system for each IVD. An equal distribution of segmental body weights from T12 to L5 was assumed [15]. Therefore, we applied 44.0% BW on T12 (head and trunk were considered as one rigid body) as the upper body weight and 2.7% BW on each vertebra from L1 to L5 [30,31]. The COMs of the upper body and of all segments were assumed to lie along the same vertical line in the coronal and sagittal planes (Fig. 2). The force generated by the IAP was calculated as a multiplication of the IAP magnitude and the diaphragm area, assumed to be 20 cm² [32] because of a limitation of the range of the x-ray images. The superiorly-directed force simulating the effect of the IAP was applied at the point located 40 mm anterior to the geometric center of T12 vertebra [12].

In this study, the static model using a “ball and socket” joint was adapted to the spinal joint. Therefore, force and moment equilibrium equations at the geometric centers of the vertebrae could be established using the FBD for T12-L1,

$$\begin{array}{c}\multicolumn{1}{c}{{\overrightarrow{F}}_{\mathit{weight}\_i}+\sum {\overrightarrow{F}}_{\mathit{muscles}}+{\overrightarrow{F}}_{\mathit{IAP}}+{\overrightarrow{F}}_{\mathit{joint}\hspace{1em}\hspace{1em}\mathit{at}\hspace{1em}\hspace{1em}\mathit{COR}(T12L1)}=0{\overrightarrow{M}}_{\mathit{weight}\_i}+\sum {\overrightarrow{M}}_{\mathit{muscles}}+{\overrightarrow{M}}_{\mathit{IAP}}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+{\overrightarrow{D}}_1·({\overrightarrow{F}}_{\mathit{weight}\_i}+\sum {\overrightarrow{F}}_{\mathit{muscles}}+{\overrightarrow{F}}_{\mathit{IAP}})=0}\end{array}$$ (1)

and for L1-L2 (Fig. 2(b)),

$$\begin{array}{c}\multicolumn{1}{c}{{\overrightarrow{F}}_{\mathit{weight}\_i}+\sum {\overrightarrow{F}}_{\mathit{muscles}}-{\overrightarrow{F}}_{\mathit{joint}\hspace{1em}\mathit{at}\hspace{1em}\mathit{COR}(T12L1)}+{\overrightarrow{F}}_{\mathit{joint}\hspace{1em}\mathit{at}\hspace{1em}\mathit{COR}(L1L2)}=0{\overrightarrow{M}}_{\mathit{weight}\_i}+\sum {\overrightarrow{M}}_{\mathit{muscles}}+{\overrightarrow{D}}_2·(\sum {\overrightarrow{F}}_{\mathit{muscles}}+{\overrightarrow{F}}_{\mathit{weight}\_i})\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+{\overrightarrow{D}}_{12}·(-{\overrightarrow{F}}_{\mathit{joint}\hspace{1em}\mathit{at}\hspace{1em}\mathit{COR}(T12L1)})=0}\end{array}$$ (2)

The equations contain unknown joint forces $({\overrightarrow{F}}_{\mathit{joint}\hspace{1em}\mathit{at}\hspace{1em}\mathit{COR}(T12L1)}$ and ${\overrightarrow{F}}_{\mathit{joint}\hspace{1em}\mathit{at}\hspace{1em}\mathit{COR}(L1L2)})$, muscle forces (${\overrightarrow{F}}_{\mathit{muscles}}$), and CORs (${\overrightarrow{D}}_1$, ${\overrightarrow{D}}_2$ and ${\overrightarrow{D}}_{12}$ represented the vectors from the COR of T12-L1 motion segment to the geometric center of T12 vertebra, from the COR of L1-L2 motion segment to the geometric center of L1 vertebra, and from the COR of L1-L2 motion segment to the COR of T12-L1 one, respectively). The given variables were external forces (${\overrightarrow{F}}_{\mathit{weight}\_i}$ and ${\overrightarrow{F}}_{\mathit{IAP}}$) and moments (${\overrightarrow{M}}_{\mathit{weight}\_i}$ and ${\overrightarrow{M}}_{\mathit{IAP}}$) representing the effects of the ith segmental body weight and the IAP, respectively on the vertebral geometric center. ${\overrightarrow{M}}_{\mathit{muscles}}$ represented the moments exerted by the muscle forces on the geometric center of a vertebral body. Joint reaction moments were calculated at the geometric centers of the vertebrae by the products of the joint reaction forces and the COR vectors ${\overrightarrow{D}}_1$, ${\overrightarrow{D}}_2$ and ${\overrightarrow{D}}_{12}$. Equations similar to Eq. (2) could be derived for each motion segment. Thus, a total of 36 equilibrium equations (three forces and three moments in each motion segment; and six motion segments from T12 to S1) were established. The muscles were assumed to generate only tensile forces. The stress of a muscle was defined as the muscle forces divided by its physiological cross sectional area (PCSA) and constrained between 0 kPa and 460 kPa [25]. The COR of each motion segment was assumed to be located in the mid-axial (x-y) plane of the IVD. It could move in x-y plane, but not beyond the anterior edge of the disc [26,33,34]. The positions of the CORs were calculated in the local coordinate systems, and the positive “x” value represents the anterior direction.

There were total 216 unknowns (18 for joint forces, 18 for CORs and 180 muscle forces). Since there were more unknowns than the equilibrium equations, this was an indeterminant problem and an optimization procedure was used to solve this problem. Intervertebral disc can sustain much higher compressive forces than shear forces. We therefore chose a cost function that minimizes both muscle stress and the shear forces applied on the motion segments. The normal direction of the joint force was defined as the z-direction in each predefined local coordinate system. We used the sum of two sub-objective functions, the normalized joint shear forces and muscle stresses, as the cost function for the optimization procedure [19,20],

$$f=W_1·\sum _1^{\mathit{ns}}{({\mathit{FS}}_i/F_i)}^2+W_2·\sum _1^{\mathit{nm}}{({\sigma }_j/{\sigma }_{max})}^3$$ (3)

where FS _i and F _i represented the shear joint force and resultant joint force of the ith motion segment, σ_j and σ_max represented the stress in the jth muscle and the maximum muscle stress of 460 kPa, respectively, and ns and nm were the numbers of spinal motion segments and muscles. Weight factors W ₁ was assumed ten times of W ₂ [20]. Therefore, the inverse dynamic optimization procedure was formulated as

$$\delta =\underset{f_j^M,{\overrightarrow{D}}_i}{\mathrm{Min}}\hspace{1em}f$$ (4)

where the muscle force ($f_i^M$) and the vector from a vertebral geometric center to the real COR (${\overrightarrow{D}}_i$) were optimization variables. For the parametric study, we investigated the human lumbosacral spine biomechanics during a weight-bearing standing position. The magnitude of the IAP and the locations of the COMs were varied independently. The IAP was changed from 0 kPa to 10 kPa in 1 kPa increments based on the experimental measurements of Essendrop and Schibye [35] and Mueller et al. [36]. In the previous studies, the locations of COMs varied from about 10 mm to 70 mm anterior to the T12 vertebra [2,4,13–16,20]. In this study, the COMs were chosen from 30 mm posterior and 70 mm anterior to the geometric center of T12 vertebra in 10 mm increments for the parametric study. The optimization problem was solved using Excel 2010 (Microsoft, USA) and the What'sBEST! software (LINDO system Inc., Chicago, USA).

3. Results

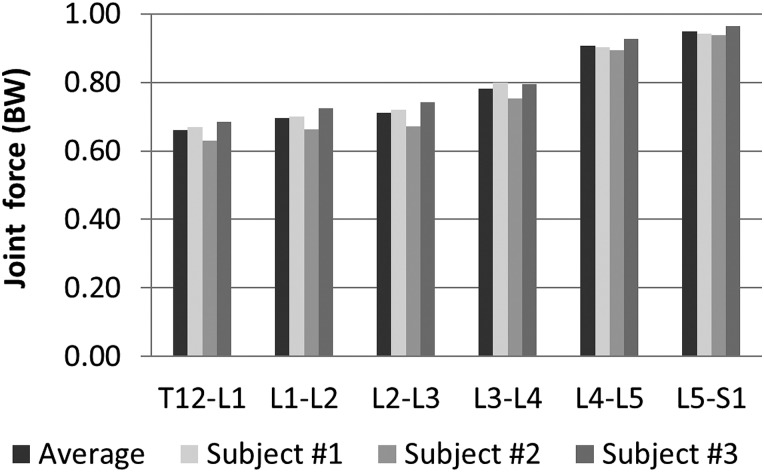
At standing position, when no IAP was applied and the COMs were 10 mm anterior to the geometric center of T12 vertebra, CORs in the anterior-posterior directions of the local coordinate systems of IVDs were 16.58 ± 0.70 mm, 8.00 ± 2.60 mm, 1.30 ± 4.22 mm, −5.95 ± 4.44 mm, −10.44 ± 2.88 mm and −1.23 ± 1.77 mm, from T12-L1 to L5-S1, respectively. The positions changed slightly (0.56 ± 2.60 mm) in the left and right direction of the vertebra. Joint forces were 0.66 ± 0.03, 0.70 ± 0.03, 0.71 ± 0.04, 0.78 ± 0.02, 0.91 ± 0.02 and 0.95 ± 0.01 of BW for the six motion segments, respectively (Fig. 3). Only six muscles groups, thoracic multifidus (39.39 ± 4.23 N), lumbar multifidus (35.11 ± 3.14 N), logissimus pars lumbroum (68.17 ± 2.10 N), iliocostalis pars lumborum (83.48 ± 12.63 N), quadratus lumborum (2.55 ± 2.21 N) and external oblique (120.58 ± 47.75 N), were activated in the standing position.

Fig. 3.

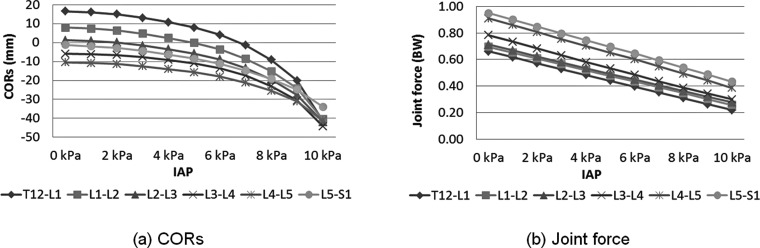
Normalized joint forces of all motion segments from T12-L1 to L5-S1 in standing posture with an IAP of 0 kPa and a COMs of 10 mm anterior to the geometric center of T12 vertebra

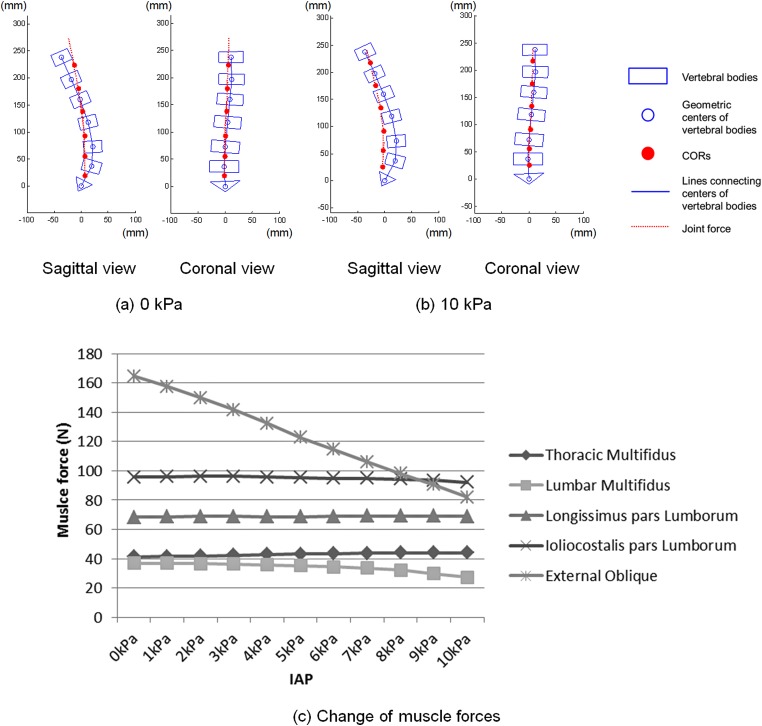
When the IAP increased from 0 kPa to 10 kPa with the COMs at 10 mm anterior to the geometric center of T12 vertebral body, CORs in all motion segments moved toward the posterior direction. The largest change was at T12-L1 (from 16.58 ± 0.70 mm to − 41.31 ± 41.80 mm), and the smallest change was at L5-S1 (from −1.23 ± 1.77 mm to −33.98 ± 16.24 mm) (Fig. 4(a) and 4(b) and Fig. 5(a)). Joint forces and muscle forces also decreased with increasing IAP (Fig. 4(a) and 4(b) and Fig. 5(b)). Joint forces decreased linearly (R²≥ 0.9995) with an average of 28.55 ± 3.39 N decrease for every 1 kPa increase of the IAP. Under a 10 kPa IAP, the normalized joint forces decreased when compared to those under no IAP by 67%, 63%, 61%, 62%, 57%, and 54% in all motion segments from T12-L1 to L5-S1, respectively. External oblique muscle force showed a significant decrease of 80 N (66%) when the IAP increased from 0 kPa to 10 kPa, while the other muscle forces showed slightly decrease of 1.84 N – 26.34 N (Fig. 4(c)).

Fig. 4.

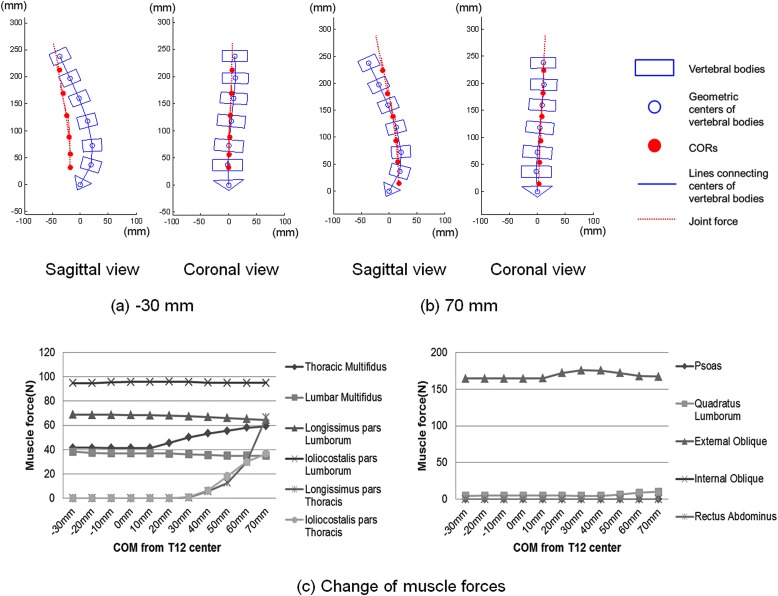
Comparison of the joint force directions and CORs with (a) 0 kPa and (b) 10 kPa of IAP in sagittal and coronal views, and (c) the change of muscle forces with variation of IAPs in subject #1; only the activated muscles were shown

Fig. 5.

Change of average (a) CORs and (b) joint forces of the three subjects when the IAP varies from 0 kPa to 10 kPa; When the IAP increased from 0 kPa to 10 kPa, CORs in all motion segments moved toward the posterior direction and joint forces decreased. The largest COR change was at the T12-L1 segment, and the smallest change was at the L5-S1. The positions of CORs were calculated in the local coordinate systems of the IVDs (origin: the geometric center point of each IVD), and the positive value represents the anterior position.

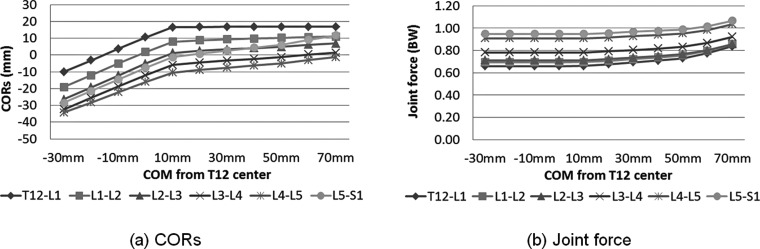
When the COMs shifted from 30 mm posterior to 10 mm anterior to the geometric center of T12 under 0 kPa of IAP, the CORs moved 26.45 ± 1.76 mm toward the anterior direction (Fig. 6(a) and 6(b) and Fig. 7(a)). The joint forces and muscle forces showed slight change (Fig. 6 and Fig. 7(b)). In the case when the COMs were 10 mm anterior from the geometric center of T12, the COR of T12-L1 motion segment was constrained to the anterior edge of the IVD. When the COMs moved further anteriorly, the COR of T12-L1 motion segment was constrained to the anterior disc edge and the CORs of the other segments moved slightly anteriorly with increase of joint forces. At the same time, thoracic multifidius and external oblique muscles forces started to increase. Longissimus pars thoracis, iliocostalis pars thoracis, and quadratus lumbrorum muscles were activated when the COMs were at 40 mm or 50 mm (Fig. 6(c)). At the extreme case when the COMs were at 70 mm anterior to the geometric center of T12 vertebra, joint forces were 27 ± 4%, 23 ± 3%, 21 ± 3%, 18 ± 2%, 14 ± 2%, and 12 ± 1% higher (from T12-L1 to L5-S1) than those when the COMs were 10 mm anterior to the geometric center of T12 vertebra (Fig. 6(a) and 6(b), and Fig. 7(b)). Data of each individual subject was presented in Table 2 through 5.

Fig. 6.

Comparison of the joint force directions and the CORs with (a) −30 mm and (b) 70 mm of COMs in sagittal and coronal views, and (c) the change of muscle forces with different COMs positions of subject #1; Initially CORs shifted anteriorly with anterior shift of the COMs. When the COMs moved to 10 mm position, the COR of the T12-L1 reached the anterior boundary. Muscle forces and joint forces increased with further anterior shift of the COMs.

Fig. 7.

Changes of the average (a) CORs and (b) joint forces of the three subjects when the COMs shifts from −30 mm to 70 mm; The CORs shifted anteriorly with anterior shift of the COMs. In the case when the COMs was 10 mm anterior from the geometric center of the T12, the COR of T12-L1 motion segment reached the anterior edge of the IVD in all three subjects. When the COMs moved further anteriorly, the COR in T12-L1 motion segment was constrained to the anterior disc edge and the CORs of the other segments moved slightly anteriorly while joint forces and muscle forces increased.

Table 2.

Change of CORs of the three subjects when the IAP shifts from 0 kPa to 10 kPa

Sub.	MSU	0 kPa	1 kPa	2 kPa	3 kPa	4 kPa	5 kPa	6 kPa	7 kPa	8 kPa	9 kPa	10 kPa
#1	T12L1	15.78	15.38	14.74	14.11	13.64	13.02	11.75	10.31	8.23	4.86	0.69
	L1L2	5.02	4.75	4.23	3.73	3.37	2.88	1.81	0.63	−1.13	−4.09	−7.77
	L2L3	−3.57	−3.67	−4.00	−4.29	−4.39	−4.60	−5.40	−6.32	−7.80	−10.42	−13.69
	L3L4	−11.03	−11.17	−11.51	−11.82	−11.98	−12.22	−12.95	−13.77	−15.02	−17.16	−19.81
	L4L5	−13.45	−13.74	−14.22	−14.69	−15.06	−15.52	−16.39	−17.33	−18.63	−20.62	−23.04
L5S1	−3.10	−3.63	−4.38	−5.15	−5.86	−6.68	−7.93	−9.25	−10.96	−13.37	−16.24
#2	T12L1	16.98	15.64	13.36	10.32	6.46	1.36	−5.31	−15.32	−28.83	−47.82	−82.91
	L1L2	9.08	7.76	5.55	2.72	−0.83	−5.52	−11.58	−20.56	−32.08	−47.05	−72.41
	L2L3	3.96	2.87	0.90	−1.63	−4.83	−9.12	−14.70	−23.07	−33.70	−47.21	−69.49
	L3L4	−2.84	−3.69	−5.13	−6.94	−9.40	−12.71	−17.26	−24.22	−33.87	−46.66	−68.16
	L4L5	−7.70	−8.61	−10.03	−11.80	−14.03	−16.89	−20.58	−25.83	−32.79	−41.95	−57.26
L5S1	0.42	−0.85	−2.72	−4.92	−7.57	−10.85	−14.90	−20.33	−27.06	−35.34	−48.11
#3	T12L1	16.99	17.00	16.90	14.96	12.04	9.26	5.85	0.55	−6.68	−17.16	−41.73
	L1L2	9.88	9.76	9.52	7.54	4.68	2.04	−1.14	−5.97	−12.44	−21.51	−41.33
	L2L3	3.52	3.47	3.27	1.40	−1.28	−3.71	−6.63	−11.07	−17.03	−25.25	−42.34
	L3L4	−3.97	−3.56	−3.00	−4.08	−5.90	−7.88	−10.52	−14.62	−20.20	−27.97	−44.50
	L4L5	−10.17	−10.06	−9.84	−11.02	−12.78	−14.64	−16.96	−20.36	−24.81	−30.75	−43.46
L5S1	−1.00	−1.26	−1.44	−3.19	−5.53	−7.95	−10.81	−14.68	−19.49	−25.55	−37.59
Avg.	T12L1	16.58	16.01	15.00	13.13	10.71	7.88	4.10	−1.49	−9.09	−20.04	−41.32
	L1L2	7.99	7.42	6.43	4.66	2.41	−0.20	−3.64	−8.63	−15.22	−24.22	−40.50
	L2L3	1.30	0.89	0.06	−1.51	−3.50	−5.81	−8.91	−13.49	−19.51	−27.63	−41.84
	L3L4	−5.95	−6.14	−6.55	−7.61	−9.09	−10.94	−13.58	−17.54	−23.03	−30.60	−44.16
	L4L5	−10.44	−10.80	−11.36	−12.50	−13.96	−15.68	−17.98	−21.17	−25.41	−31.11	−41.25
L5S1	−1.23	−1.91	−2.85	−4.42	−6.32	−8.49	−11.21	−14.75	−19.17	−24.75	−33.98

Table 3.

Average change of joint forces (BW) of the three subjects when the IAP shifts from 0 kPa to 10 kPa

Sub.	MSU	0 kPa	1 kPa	2 kPa	3 kPa	4 kPa	5 kPa	6 kPa	7 kPa	8 kPa	9 kPa	10 kPa
#1	T12L1	0.67	0.64	0.60	0.57	0.53	0.50	0.46	0.43	0.39	0.36	0.33
	L1L2	0.70	0.67	0.63	0.60	0.56	0.53	0.49	0.46	0.42	0.39	0.36
	L2L3	0.72	0.69	0.65	0.62	0.58	0.54	0.51	0.47	0.44	0.41	0.37
	L3L4	0.80	0.76	0.73	0.69	0.65	0.62	0.58	0.54	0.51	0.47	0.43
	L4L5	0.90	0.87	0.84	0.80	0.76	0.72	0.69	0.65	0.61	0.57	0.53
L5S1	0.94	0.91	0.87	0.84	0.80	0.76	0.73	0.69	0.65	0.62	0.58
#2	T12L1	0.63	0.58	0.53	0.49	0.44	0.39	0.35	0.30	0.25	0.20	0.14
	L1L2	0.66	0.62	0.57	0.52	0.48	0.43	0.38	0.34	0.29	0.24	0.19
	L2L3	0.67	0.63	0.58	0.53	0.49	0.44	0.40	0.35	0.30	0.25	0.20
	L3L4	0.75	0.70	0.65	0.60	0.54	0.49	0.43	0.36	0.30	0.25	0.20
	L4L5	0.89	0.84	0.78	0.73	0.67	0.61	0.55	0.48	0.41	0.35	0.28
L5S1	0.94	0.89	0.83	0.78	0.72	0.66	0.60	0.53	0.46	0.40	0.33
#3	T12L1	0.68	0.63	0.58	0.53	0.48	0.43	0.38	0.34	0.29	0.23	0.19
	L1L2	0.72	0.67	0.62	0.57	0.52	0.47	0.42	0.38	0.33	0.28	0.23
	L2L3	0.74	0.69	0.64	0.59	0.54	0.49	0.44	0.40	0.35	0.30	0.26
	L3L4	0.79	0.73	0.67	0.61	0.55	0.50	0.45	0.40	0.36	0.31	0.27
	L4L5	0.93	0.86	0.80	0.73	0.67	0.62	0.57	0.51	0.46	0.40	0.34
L5S1	0.97	0.90	0.84	0.77	0.71	0.66	0.61	0.56	0.50	0.45	0.39
Avg.	T12L1	0.66	0.62	0.57	0.53	0.48	0.44	0.40	0.36	0.31	0.26	0.22
	L1L2	0.69	0.65	0.61	0.56	0.52	0.48	0.43	0.39	0.35	0.30	0.26
	L2L3	0.71	0.67	0.62	0.58	0.54	0.49	0.45	0.41	0.36	0.32	0.28
	L3L4	0.78	0.73	0.68	0.63	0.58	0.54	0.49	0.43	0.39	0.34	0.30
	L4L5	0.91	0.86	0.81	0.75	0.70	0.65	0.60	0.55	0.49	0.44	0.38
L5S1	0.95	0.90	0.85	0.80	0.74	0.69	0.65	0.59	0.54	0.49	0.43

Table 4.

Average change of CORs of the three subjects when the COMs shifts from −30 mm to 70 mm

Sub.	MSU	−30 mm	−20 mm	−10 mm	0 mm	10 mm	20 mm	30 mm	40 mm	50 mm	60 mm	70 mm
#1	T12L1	−11.83	−4.87	2.09	9.13	15.78	16.34	16.69	16.87	16.95	17.00	17.00
	L1L2	−23.06	−15.99	−8.90	−1.75	5.02	6.14	6.95	7.44	7.68	7.91	8.04
	L2L3	−31.93	−24.75	−17.61	−10.43	−3.57	−2.15	−1.13	−0.26	0.39	0.87	1.13
	L3L4	−37.74	−30.98	−24.27	−17.51	−11.03	−9.41	−8.18	−7.06	−6.13	−5.25	−4.66
	L4L5	−38.34	−32.05	−25.79	−19.49	−13.45	−11.66	−10.22	−8.84	−7.52	−6.22	−5.17
L5S1	−31.27	−24.16	−17.07	−9.94	−3.10	−0.85	0.95	2.86	4.75	6.67	8.43
#2	T12L1	−10.81	−3.71	3.39	10.50	16.98	16.97	16.95	16.95	16.91	16.95	16.95
	L1L2	−18.96	−11.81	−4.67	2.48	9.08	9.75	10.21	10.63	11.00	11.86	12.26
	L2L3	−25.02	−17.64	−10.26	−2.88	3.96	4.96	5.76	6.47	7.15	9.46	10.41
	L3L4	−29.94	−23.05	−16.17	−9.28	−2.84	−1.46	−0.41	0.57	1.52	4.11	5.62
	L4L5	−31.73	−25.63	−19.53	−13.43	−7.70	−6.21	−4.96	−3.77	−2.62	0.49	2.63
L5S1	−26.38	−19.58	−12.77	−5.96	0.42	2.28	4.02	5.66	7.26	11.73	14.89
#3	T12L1	−7.56	−0.97	5.64	12.27	16.99	16.98	16.97	16.95	16.91	16.82	16.75
	L1L2	−15.03	−8.40	−1.75	4.93	9.88	10.57	11.12	11.57	11.98	12.54	12.87
	L2L3	−22.23	−15.41	−8.57	−1.70	3.52	4.62	5.54	6.32	7.06	8.40	9.32
	L3L4	−29.21	−22.55	−15.87	−9.16	−3.97	−2.61	−1.43	−0.36	0.69	2.21	3.39
	L4L5	−32.84	−26.87	−20.89	−14.89	−10.17	−8.65	−7.31	−6.09	−4.89	−3.19	−1.28
L5S1	−27.48	−20.53	−13.56	−6.57	−1.00	1.07	2.92	4.60	6.28	8.85	11.82
Avg.	T12L1	−10.07	−3.18	3.71	10.63	16.58	16.76	16.87	16.92	16.92	16.92	16.90
	L1L2	−19.02	−12.07	−5.11	1.89	8.00	8.82	9.43	9.88	10.22	10.77	11.06
	L2L3	−26.39	−19.27	−12.15	−5.00	1.30	2.48	3.39	4.18	4.87	6.24	6.95
	L3L4	−32.29	−25.53	−18.77	−11.98	−5.95	−4.49	−3.34	−2.28	−1.31	0.35	1.45
	L4L5	−34.30	−28.18	−22.07	−15.94	−10.44	−8.84	−7.50	−6.23	−5.01	−2.97	−1.27
L5S1	−28.38	−21.42	−14.47	−7.49	−1.23	0.83	2.63	4.37	6.09	9.08	11.71

Table 5.

Change of joint forces of the three subjects when the COMs shifts from −30 mm to 70 mm

Sub.	MSU	−30 mm	−20 mm	−10 mm	0 mm	10 mm	20 mm	30 mm	40 mm	50 mm	60 mm	70 mm
#1	T12L1	0.67	0.67	0.67	0.67	0.67	0.69	0.70	0.72	0.75	0.79	0.84
	L1L2	0.70	0.70	0.70	0.70	0.70	0.71	0.73	0.74	0.77	0.81	0.86
	L2L3	0.72	0.72	0.72	0.72	0.72	0.73	0.75	0.76	0.78	0.82	0.88
	L3L4	0.80	0.80	0.80	0.80	0.80	0.81	0.82	0.83	0.86	0.89	0.94
	L4L5	0.91	0.90	0.90	0.90	0.90	0.92	0.92	0.93	0.95	0.98	1.04
L5S1	0.94	0.94	0.94	0.94	0.94	0.95	0.96	0.97	0.99	1.01	1.06
#2	T12L1	0.63	0.63	0.63	0.63	0.63	0.64	0.66	0.68	0.70	0.76	0.82
	L1L2	0.66	0.66	0.66	0.66	0.66	0.67	0.69	0.70	0.72	0.77	0.84
	L2L3	0.67	0.67	0.67	0.67	0.67	0.68	0.70	0.71	0.73	0.77	0.83
	L3L4	0.76	0.76	0.76	0.76	0.75	0.76	0.77	0.79	0.80	0.85	0.90
	L4L5	0.90	0.90	0.90	0.90	0.89	0.89	0.91	0.92	0.94	0.98	1.03
L5S1	0.94	0.94	0.94	0.94	0.94	0.93	0.95	0.97	0.98	1.01	1.06
#3	T12L1	0.68	0.68	0.68	0.68	0.68	0.70	0.72	0.73	0.75	0.78	0.85
	L1L2	0.72	0.72	0.72	0.72	0.72	0.74	0.75	0.76	0.77	0.81	0.87
	L2L3	0.74	0.74	0.74	0.74	0.74	0.75	0.77	0.78	0.79	0.81	0.87
	L3L4	0.79	0.79	0.79	0.79	0.79	0.81	0.82	0.83	0.84	0.86	0.92
	L4L5	0.92	0.93	0.92	0.92	0.93	0.94	0.95	0.96	0.96	0.99	1.04
L5S1	0.96	0.96	0.96	0.96	0.97	0.98	0.99	1.00	1.00	1.03	1.07
Avg.	T12L1	0.66	0.66	0.66	0.66	0.66	0.68	0.69	0.71	0.73	0.77	0.84
	L1L2	0.69	0.69	0.69	0.69	0.70	0.71	0.72	0.74	0.76	0.80	0.86
	L2L3	0.71	0.71	0.71	0.71	0.71	0.72	0.74	0.75	0.77	0.80	0.86
	L3L4	0.78	0.78	0.78	0.78	0.78	0.79	0.80	0.82	0.83	0.87	0.92
	L4L5	0.91	0.91	0.91	0.91	0.91	0.92	0.93	0.94	0.95	0.98	1.04
L5S1	0.95	0.95	0.95	0.95	0.95	0.96	0.97	0.98	0.99	1.02	1.07

4. Discussion

Computational models and optimization techniques have been used widely to estimate spinal joint and muscle forces. In this study, we investigated the effect of the magnitude of the IAP and locations of the COMs on the CORs, joint and muscle forces of the lumbosacral motion segments from T12-L1 to L5-S1. The results of this study showed that increases of the IAP shifted the location of CORs toward the posterior direction of the IVDs and reduced joint and muscle forces (external oblique, iliocostalis pars lumborum, and lumbar multifidus muscles). Anterior shift of the COMs resulted in an anterior movement of the CORs and small changes in joint and muscle forces. When the CORs were not able to move more anteriorly at the anterior boundaries of the IVDs, further anterior shift of the COMs increased joint forces and muscle forces mainly in the external oblique, longissimus pars thoracis, iliocostalis pars thoracis, external oblique and thoracic multifidus muscles.

The joint forces were calculated at the geometric centers of vertebrae or IVDs in most previous computational simulation studies [1,2,4,11,12,14–16,18–20]. In several recent reports, “follower load concept” has been suggested where the CORs in the lumbar spinal motion segments were assumed to locate along the parallel path of the spinal lordosis [13,17], i.e., the distances between the CORs and the geometric centers of every vertebrae were the same at all vertebral segments [37,38]. However, Pierce et al. and Li et al. [22,23] have verified that a global convergence optimization procedure is necessary to determine the CORs of the joints in order to accurately calculate the joint and muscle forces, since the rotation center is not known a priori. Because the human spine consists of a multiple motion segments, individual COR should be considered in each level of the motion segment due to different loading conditions at these segments. Therefore, we formulated an optimization problem with changing CORs in each motion segment of the lumbosacral spine using a global convergence optimization procedure.

In the numerical analyses of the spine mechanics, the validations were usually performed indirectly due to the limitation of experimental measurements [15]. At standing posture, facet joint forces have been thought negligible and most of compressive forces applied on the lumbar spine are transmitted through the IVDs in the intact lumbar spine [39]. Therefore, similar to other studies, we compared the calculated intra-discal pressure to the in vivo measurement at the upright standing posture [15]. The intra-discal pressure at the standing posture was reported between 0.48 MPa to 0.5 MPa [9,10]. Taking the L4-L5 motion segment of the male subject as an example, when the cross-sectional area of IVD was assumed to be 1300 mm², the pressure was 0.55 MPa in the initial condition (0 kPa IAP, anterior 10 mm COMs), decreased to 0.32 MPa when the IAP increased to 10 kPa. Similar intra-discal pressure values (about 0.55 MPa) were calculated when the COMs shifted from 30 mm posterior to 20 mm anterior to the geometric center of T12 vertebra.

The calculated CORs or the path of joint forces were different at different motion segments and showed an overall path not parallel but had smaller curvature than the spinal lordosis. The COR of T12-L1 motion segment located most anteriorly from the geometric center of its IVD, while the COR of L4-L5 motion segment located most posteriorly from the center of its IVD. The second most anterior COR was calculated in L1-L2 motion segment. Consistently with previous in vivo studies [25,26,40], we found that in the L2-L5 motion segments the CORs located posterior to the center of each IVD. The COR in L5-S1 motion segment was calculated at the geometric center or slightly posterior site to the geometric center of the IVD. Similar findings have been reported by Pearcy and Bogduk [26]. When the upper depth of the vertebra was 34 mm [34], the COR in L1-L2 motion segment located relatively more anteriorly than the other segments by 1−2 mm, 3−6 mm and 0−2 mm in flexion from upright, extension from upright and flexion from extension, respectively.

The Generation of the IAP, that contributes an overall extension moment to the upper human body, is still unclear [35,41–48]. Several in vivo studies have assumed that the IAP was generated mainly by transverse abdominal muscles [43], but the rectus abdominal muscles did not contributed to IAP generation [35]. Hodges et al. has reported that the IAP could be generated without any overt activity of the abdominal or back muscles [46]. The maximal IAP was assumed at around 10 kPa in previous experimental studies [35,42,46]. In this study, the IAP, changing from 0 kPa to 10 kPa, was applied as an independent parameter without any correlation to abdominal muscles activation. Therefore, compressive force and flexion moment due to segmental body weight were deducted by the superiorly-directed IAP load and corresponding extension moment. As a result, increase of the IAP reduced joint and muscle forces, and the moved CORs posteriorly. In consistence with our results, Arjmand et al. reported that the IAP reduced spinal joint forces when the IAP was applied without abdominal muscles co-activation [12]. Stokes et al. also reported that the IAP, generated by the activation of the abdominal muscles, caused decreases of the spine joint and muscle forces [20].

When the COMs shifted from the posterior toward the anterior portion of the vertebra, we observed an anterior movement of CORs and an increase of muscle and joint forces. This could be explained by the fact that the anterior shift of COMs increased the flexion moment applied to the geometric center of T12 vertebra. To counterbalance this flexion moment, either the moment arms of the muscle forces or the muscle force magnitude should be increased. Increasing the moment arms corresponded to a shift of the CORs anteriorly. Thus, initial CORs shifted anteriorly with anterior movement of the COMs. When the COR of T12-L1 reached the anterior boundary, muscle forces and joint forces had to increase. Interestingly, the increased muscle forces slowed down the anterior shift of the CORs in the other motion segments (L1 to S1). Han et al. have shown the similar results that an increase of joint moments led to anterior movements of the CORs and the increase of joint forces in their computational simulation study [13].

In this study, we investigated the effects of the variations of the IAP and COMs on spine biomechanics using three subject-specific models and with independent CORs in every motion segment. The COR concept in this paper were adopted from a global convergence optimization procedure [22,23]. It is a point where the overall net moment is zero. It is an instantaneous point corresponding to the standing position, and changes not only with different loading conditions, but also with different spinal positions such as flexion and extension. Pearcy and Bogduk have measured in vivo rotation centers of lumbar spine using lateral radiographs between upright standing and full flexion, between upright standing and full extension, and between full extension and full flexion [26]. The determined CORs in the in vivo study are close to the upper endplates of the lower vertebral bodies. The CORs are also determined around mid-axial plane of the IVD in computational studies [27,28]. The location of CORs can vary with defined motions. Therefore we calculated the CORs in the mid-axial planes of IVDs and focused on the anterior-posterior movement of CORs in this parametric analysis.

The simplified superiorly-directed load and the corresponding extension moment of the IAP were used to study the biomechanical effect of the IAP. Correlations between the IAP and abdominal muscle activation, and antagonistic muscle activation were not included. In this study the spinal curvature was assumed to be the same with the variation of the COMs or IAP since this is a parametric study and the actual relation of the spine curvature and the COMs or IAP is unknown. In the future, the spinal curvature change due to change of IAP should be investigated using accurate x-ray image techniques during flexion and extension of the body. Despite the above mentioned limitations, this parametric study did reveal the importance of accurate simulation of the IAP and COMs in spine biomechanics.

In summary, we analyzed the joint, muscle forces and CORs of human lumbosacral spine system in a parametric study of the IAP and COMs. The data indicated that an increase of the IAP shifted the CORs posteriorly and reduced the joint and muscle forces. Anterior shift of the COMs led to an anterior movement of the CORs and further increased the joint and muscle forces. Therefore, it is necessary to include the IAP and the correct COMs in computational spinal models in order to accurately simulate human spine biomechanics. The method and results of this study could be useful for designing prevention strategies of spinal injuries and recurrences, and for enhancing rehabilitation efficiency. Furthermore, the results of this study could be useful for recommendation of safe working posture in occupational biomechanics.