Short abstract
Treatments for coarctation of the aorta (CoA) can alleviate blood pressure (BP) gradients (Δ), but long-term morbidity still exists that can be explained by altered indices of hemodynamics and biomechanics. We introduce a technique to increase our understanding of these indices for CoA under resting and nonresting conditions, quantify their contribution to morbidity, and evaluate treatment options. Patient-specific computational fluid dynamics (CFD) models were created from imaging and BP data for one normal and four CoA patients (moderate native CoA: Δ12 mmHg, severe native CoA: Δ25 mmHg and postoperative end-to-end and end-to-side patients: Δ0 mmHg). Simulations incorporated vessel deformation, downstream vascular resistance and compliance. Indices including cyclic strain, time-averaged wall shear stress (TAWSS), and oscillatory shear index (OSI) were quantified. Simulations replicated resting BP and blood flow data. BP during simulated exercise for the normal patient matched reported values. Greatest exercise-induced increases in systolic BP and mean and peak ΔBP occurred for the moderate native CoA patient (SBP: 115 to 154 mmHg; mean and peak ΔBP: 31 and 73 mmHg). Cyclic strain was elevated proximal to the coarctation for native CoA patients, but reduced throughout the aorta after treatment. A greater percentage of vessels was exposed to subnormal TAWSS or elevated OSI for CoA patients. Local patterns of these indices reported to correlate with atherosclerosis in normal patients were accentuated by CoA. These results apply CFD to a range of CoA patients for the first time and provide the foundation for future progress in this area.
1. Introduction
Coarctation of the aorta (CoA) accounts for 8%–11% of congenital heart defects affecting ∼3000–5000 patients annually in the United States. Surgical or catheter-based treatments can alleviate the blood pressure (BP) gradient across a coarctation with low morbidity. However, despite this success and the clinical view of CoA as a simple disease, long-term results have revealed decreased life expectancy and substantial morbidity in the form of hypertension, early coronary artery disease (CAD), stroke, and aneurysm formation.
Several decades ago, O’Rourke and Cartmill suggested the majority of morbidity for CoA can be explained on the basis of abnormal hemodynamics through the ascending aorta and its branches by showing that its conduit (blood flow) and cushioning (capacitance) functions were altered by CoA [1]. The authors described how the presence of CoA introduces a BP wave reflection site near the heart causing drastic reductions in aortic capacitance and elevated pulse BP. These findings are consistent with hypertension often observed during rest and exercise. Furthermore, the observed reduction in diastolic BP [1] can alter coronary artery perfusion thereby accentuating the likelihood for adverse hemodynamics associated with premature CAD such as wall shear stress (WSS). Concomitant increases in afterload also offer an explanation for heart failure in these patients.
Recent CoA clinical literature has lost sight of this hemodynamic basis for morbidity. Currently, the putative treatment guideline is a BP gradient ≥20 mmHg at rest, which was originally based on the best results possible by surgical repair or angioplasty without increased risk of additional procedures [2]. Reports using this guideline commonly compare BP gradients and rates of mortality, hypertension, aneurysm formation and recoarctation to those of previous studies. Still, morbidity persists and studies have hinted that altered biomechanical properties may be a contributing factor [3].
Investigation into the hemodynamic and biomechanical basis of morbidity in CoA is intriguing considering recent advancements in computational modeling. Patient-specific anatomy can now be extracted, and representative models of the vasculature can be created, using data obtained during a routine clinical imaging session. This anatomic data, together with physiological data such as phase-contrast MRI (PC-MRI) and BP, can be used to create 3D patient-specific representations of hemodynamics that consider vascular properties associated with the current patient state. This paradigm has been applied with single ventricle congenital defects where computational fluid dynamics (CFD) simulations of the Fontan procedure have led to several technical modifications demonstrated to be hemodynamically superior to previous surgical techniques [4]. Similar outcomes may be realized if this approach is applied to CoA, but few studies to date have used CFD for this purpose. The complexity of aortic flow patterns, selecting appropriate boundary conditions, replicating vascular compliance, including collateral arteries and vascular tethering, and the motion of the aorta all contribute to the difficulty of the problem and, likely, the scarcity of such studies.
The objective of this investigation is to introduce a procedure that combines clinical imaging data and CFD tools to further understand hemodynamic alterations under resting and nonresting blood flow conditions, uniquely investigate potential sources of morbidity, and evaluate treatment outcomes and coarctation severity in a manner not possible using current imaging modalities solely. This objective is realized through several examples of native and postoperative CoA patients. It is our intention that this work will stimulate further collaboration between engineers and physicians and serve as the first step toward advancing the field in a manner similar to that which has occurred in the Fontan procedure. In this way, we may be able to understand the consequences of treatments for CoA and identify processes that could lead to morbidity long before they are clinically apparent.
2. Methods
2.1. Magnetic Resonance Imaging.
Magnetic resonance imaging was performed as clinically ordered or as follow-up to surgical or interventional treatment after Institutional Review Board approval. Prior to protocol enrollment, verbal and written information was provided and informed consent or assent was obtained from participants or their parents/guardians. Gadolinium-enhanced MR angiography (MRA) was performed with the participant in the supine position inside a 1.5-T GE Signa TwinSpeed MRI scanner (GE Medical Systems, Milwaukee, WI) using a T1-weighted, half k-space, 3D spoiled gradient recalled echo sequence (slice thickness: 2.0–2.2 mm; 40–44 slices interpolated to 80–88 slices/volume; acquisition matrix: 384 × 192 reconstructed to 512 × 512; field of view: 30 × 30 to 40 × 40 cm2; in-plane spatial resolution: 0.78–2.08 mm; TR: 3.3–3.9 ms; TE: 0.78–0.92 ms; flip angle: 25°). A test bolus of 1 ml gadopentetate dimeglumine (Magnevist, Bayer Healthcare Pharmaceuticals, Wayne, NJ) was injected to determine the optimal contrast timing to enhance the aorta. For the actual MRA, a 2 ml/kg dose of gadopentetate was injected at a rate of 2 ml/s into a peripheral intravenous access. Participants were instructed to hold their breath during the MRA data acquisition period (∼20 s) when age and ability permitted.
Blood flow information was acquired using a cardiac-gated, 2D, respiratory-compensated, phase-contrast (PC) cine sequence with through-plane velocity encoding (slice thickness: 10 mm, field-of-view: 24 × 24 cm2, acquisition matrix: 256 × 160, spatial resolution: 0.94–1.5 mm, TR: ∼5 ms, TE: 2–3 ms, flip angle: 15°, velocity encoding: 150–400 cm/s, temporal resolution: 10 ms). Each scan lasted ∼3 min as participants breathed freely. Cine images were reconstructed at 16–20 cardiac phases. PC images were obtained at planes transverse to the aortic root, the cervical arteries, the coarctation, and the descending aorta at the diaphragm. After each study, upper and lower extremity BP was measured using a sphygmometer cuff with the subject in a supine position.
2.2. CFD Model Construction.
The MRA imaging data were processed using specialized software to correct for known gradient nonlinearities [5]. Computational representations of the aorta and arteries of the head and neck were then created using Simvascular (Simtk.org) software that facilitates volume visualization and conversion of the MRA imaging data into geometrically representative computer models, as demonstrated in Fig. 1 [6] and discussed previously [7]. Models were discretized using a commercially available, automatic mesh generation program (MeshSim, Simmetrix, Clifton Park, NY). When collateralization was extensive (e.g., for the severe native CoA) the collateral network was represented by vessels extending from their origin at the subclavian arteries to their insertion distal to the coarctation and their caliber was selected to match the BP gradient measured clinically thereby replicating the conduit function of these vessels.
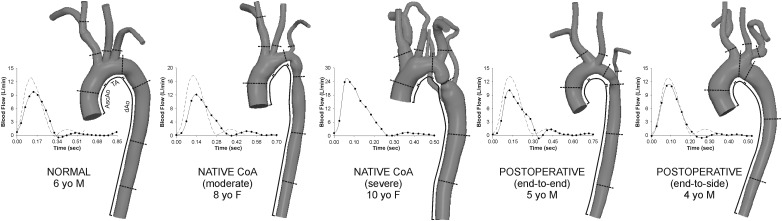
Fig. 1.
Computational models of the patients analyzed and their inflow waveforms (rest = solid lines; simulated exercise = dashed lines). Lines on each model indicate where cyclic strain calculations were performed and the approximate center of 5 mm bands used to quantify WSS indices. Regions of the ascending aorta (AscAo), transverse arch (TA), and descending aorta (dAo) are also depicted.
2.3. Inflow Boundary Conditions.
PC-MRI data were used to calculate time-resolved volumetric blood flow as previously described [7,8]. Ascending aorta (AscAo) PC-MRI waveforms were mapped to the inlet of CFD models using a temporally varying parabolic flow profile. Flow from the innominate (IA), left carotid, and left subclavian (LSA) arteries and descending aorta (dAo) were used, together with BP data, to prescribe outflow boundary conditions as discussed in the following. For the normal patient, resting cardiac output (CO) was determined from body surface area (BSA) and a normal cardiac index (CI) of 3.5 l/min/m2 as PC-MRI data was not available. The inflow waveform contour was obtained by ensemble averaging PC-MRI data from healthy children [9] and scaling by BSA [8], whereas flow to branches was estimated from a known relationship between their diameter and AscAo flow [10]. Nonresting conditions were simulated by modifying resting conditions to reflect increases in flow and heart rate (by 50%) during moderate exercise [9], resulting in CI within the expected normal range [11]. Figure 1 shows inflow waveforms for resting and simulated exercise conditions.
2.4. Outflow Boundary Conditions and Wall Deformation Parameters.
To replicate the impact of vessels distal to CFD model branches, a three-element Windkessel model was imposed using a coupled-multidomain method [12]. This method represents arterial networks using three parameters with physiologic meaning: characteristic resistance (Rc), capacitance (C), and distal resistance (Rd). Under resting conditions, the total arterial capacitance (TAC) for each patient was determined from inflow and BP measurements assuming a characteristic to total resistance ratio of 6% [13]. The TAC was then distributed among outlets according to their blood flow distributions [14]. Once the capacitance term for each branch was assigned, the terminal resistance (Rt = Rc + Rd) was calculated from mean BP and PC-MRI flow measurements and distributed between the remaining resistance parameters by adjusting Rc to Rt ratios (6%–10%) for each outlet using the pulse pressure method [15,16] thereby replicating BP values shown in Table 1. BP measurements during moderate exercise were not available for patients. Values of Rt, Rc, C, and Rd for each model outlet were therefore adjusted consistent with reported changes during exercise at an equivalent heart rate [15,17] to replicate changes, particularly systolic BP, typically observed in normal patients [18,19]. These methods were then applied to the coarctation patients to elucidate the severity of native or residual coarctation and associated vascular alterations. The amount of blood flow delivered to the carotid arteries during moderate exercise remained unchanged [20], but was decreased by 43% to the arms [21]. Associated increases in resistance primarily impact Rd and resting capacitance values in the subclavian arteries were adjusted based on clinical measurements for an equivalent change in heart rate [17]. Rt, Rd, and C were similarly adjusted for the dAo outlet. An augmented-Lagrangian formulation [22] for constraining the shape of the velocity profiles at model outlets was used to mitigate instabilities often occurring during flow deceleration and diastole.
Table 1.
Patient data, measured hemodynamics and simulation blood pressure characteristics
| Pressure indices | Flow indices from PC-MRI | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Measurements-rest | Simulations-rest | Simulations-exercise | ||||||||||||||||||||||||
| Age (yrs) | BSA (m2) | SBP | DBP | Mean BP grad | SBP | SBP error (%) | DBP | DBP error (%) | Mean BP grad | Mean BP grad error (mmHg) | Peak BP grad | SBP | DBP | Mean BP grad | Peak BP grad | Resting QAscAo (l/min) | Resting Cardiac index (l/min/m2) | QIA | QLCCA | QLSA | QDAo | |||||
| Normal | 6 | 0.66 | 91 | 53 | 0 | 91 | 0 | 56 | 6 | 1 | 1 | 3 | 106 | 59 | 8 | 23 | 2.3 | 3.5 | 22.7 | 11.5 | 10.7 | 55 | ||||
| Native CoA (moderate) | 8 | 0.94 | 115 | 65 | 12 | 115 | 0 | 67 | 3 | 7 | -5 | 22 | 154 | 65 | 31 | 73 | 3.25 | 3.45 | 25.6 | 11.3 | 4.26 | 58.8 | ||||
| Native CoA (severe) | 10 | 0.93 | 145 | 68 | 25 | 148 | 2 | 74 | 9 | 27 | 2 | 69 | - | - | - | - | 6.48 | 6.97 | 11.7 | 5.56 | 7.87 | 73.9 | ||||
| Postoperative (end-to-end) | 5 | 0.69 | 106 | 72 | 0 | 106 | 0 | 73 | 1 | 1 | 1 | 6 | 128 | 75 | 9 | 29 | 2.43 | 3.51 | 25.6 | 9.97 | 3.38 | 61.1 | ||||
| Postoperative (end-to-side) | 4 | 0.72 | 112 | 69 | 0 | 111 | -1 | 69 | 0 | 3 | 3 | 20 | 123 | 65 | 9 | 38 | 2.36 | 3.28 | 10.9 | 4.81 | 6.04 | 78.3 | ||||
Note: Blood flow distributions are provided as a percentage of QAscAo. Severe CoA patient had an anomalous vertebral artery originating from the transverse arch receiving 1% of QAscAo.
Coupled blood flow and vessel wall dynamics were solved using a coupled-momentum method [23] formulation. A membrane model was used for the vessel wall that considers physiologic material properties based on published data [24], including a wall thickness of 0.15 cm [25]. Briefly, the computer model was first prestressed using linear elastic theory. The prestress was derived by loading the vessel wall with the diastolic pressure, assuming that the geometry given by the MRA corresponds approximately to a low diastolic configuration. This defines the diastolic geometry as the reference configuration for the model. The Young’s modulus was then adjusted iteratively until the AscAo mean luminal displacement was within 5% of the values obtained from PC-MRI magnitude measurements (values are presented in Table 2). This approach was found to provide reasonable wall displacement in simulations when compared to spatially equivalent locations from PC-MRI.
Table 2.
Young's modulus of the vessel wall
| Patient | E (dyn/cm2) |
|---|---|
| Normal | 2.57 × 106 |
| Native CoA (moderate) | 3.17 × 106 |
| Native CoA (severe) | 5.54 × 106 |
| Postoperative (end-to-end) | 9.03 × 106 |
| Postoperative (end-to-side) | 5.54 × 106 |
Note: The same E was used for resting and non-resting simulations.
A viscoelastic boundary condition was also used to account for tissue surrounding the aorta [26]. This external tissue support condition provides physiologically realistic dissipation that damps the high-frequency fluttering modes of the vessel wall motion that are likely to occur during moderate exercise simulations. The numerical values for elastic and viscoelastic response of the external tissue implemented were 100 g/mm3/s2 and 100 g/mm3/s, respectively.
2.5. CFD Simulations.
Simulations were performed using a novel stabilized finite element method to solve the conservation of mass (continuity), balance of fluid momentum (Navier–Stokes) and vessel wall elastodynamics equations [23]. Meshes contained 2–3 × 106 tetrahedral elements and localized refinement was performed using an adaptive technique [27,28] to deposit more elements near the luminal surface and in anatomical regions prone to flow disruption [28]. Simulations were run for four to six cardiac cycles until the flow rate and pressure fields yielded periodic solutions.
Blood flow velocity, BP and wall displacement were visualized using ParaView (Kitware, Clifton Park, NY). Time-averaged WSS (TAWSS) and oscillatory shear index (OSI) were then calculated [7]. Low TAWSS is thought to promote atherogenesis, as is elevated OSI, an index of directional changes in WSS. Low OSI indicates WSS is unidirectional, whereas a value of 0.5 is indicative of bidirectional WSS with a time-average value of zero. These indices were determined in 5 mm bands of the AscAo, transverse arch (TA), coarctation, mid-dAo, and diaphragm levels of the aorta, as well as one diameter distal to the origin of branch vessels. Average values for each location in the normal patient were used as thresholds for low TAWSS or elevated OSI.
Previous imaging studies found local low TAWSS and elevated OSI values that were statistically different from circumferential averages [29], motivating the need to report detailed local WSS maps in CFD studies. To visualize TAWSS locally, the surface of each vessel was unwrapped and mapped into a θ, l rectangular domain, where θ and l are the circumferential and longitudinal coordinates of each point on the vessel wall.
Wall displacement results were used to estimate the principal component of cyclic strain at nine vascular locations. Green–Lagrange strain, Eθθ, and maximum strain, Eθθ ,max, were calculated as Eθθ = 0.5((D current/D diastolic)2 − 1) and Eθθ ,max = 0.5((D systolic/D diastolic)2 − 1), where D = diameter and D diastolic is its reference value [30]. The position of the surface nodes was updated with the displacement components at each time point before cyclic strain was calculated to be consistent with calculations from PC-MRI magnitude data, and values were expressed as a percentage.
3. Results
Anatomy and hemodynamics reflective of surgical treatment were observed and captured in CFD simulations. All CoA patients exhibited systolic BP exceeding normal for their age and gender regardless of whether surgery had been performed. AscAo PC-MRI revealed variations in CO and flow to branches (Fig. 1, Table 1). CI was similar for all patients except the severe CoA subject where it resembled moderate exercise.
Simulations replicated resting clinical BP gradients (Table 1) with a maximum error of 5 mmHg and relative systolic and diastolic BP errors <10%. Under moderate exercise conditions, simulation systolic BP increased 15 mmHg and mean and peak BP gradients increased from 1 and 3 mmHg at rest, respectively, to 8 and 23 mmHg for the normal patient. Systolic BP increased by 12 and 22 mmHg for the end-to-side and end-to-end patients, respectively, and mean BP gradients were similar to the normal patient. However, peak BP gradients in treated CoA patients were higher than the normal patient (end-to-end = 29 and end-to-side = 38 versus 23 mmHg). Substantial increases in systolic BP and mean and peak BP gradients were observed in the untreated moderate CoA patient. For this patient with a simulated resting systolic BP of 115 and a 7 mmHg gradient at rest, systolic BP increased to 154 mmHg, and the mean and peak BP gradients increased to 31 and 73 mmHg, respectively, during simulated moderate exercise.
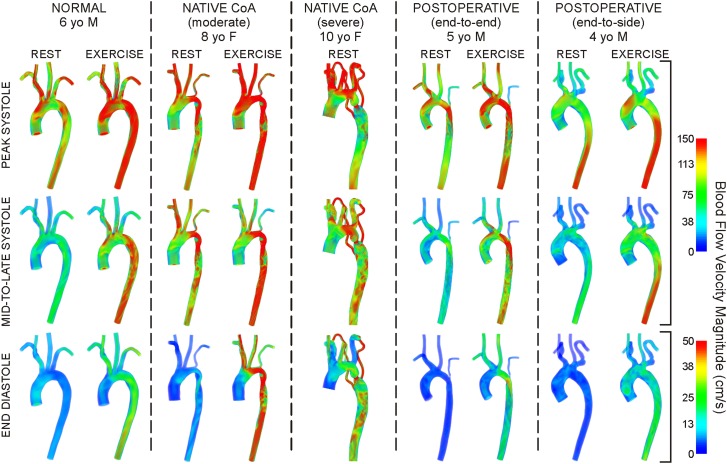
Volume-rendered velocity patterns during peak systole, mid-to-late systole and end diastole are shown in Fig. 2. Elevated velocity was observed near coarctations at rest for all simulations except for the 4 year old (yo) with end-to-side repair. Blood acceleration across these regions produced complex downstream swirling and recirculation, often with a jet impinging on the posterior dAo wall. These complex patterns were accentuated during exercise. Patterns at rest and exercise were similar for the normal and end-to-side patients.
Fig. 2.
Volume-rendered velocity during peak systole (top row), mid-to-late systole (middle row) and end diastole (bottom row) under resting and simulated moderate exercise conditions. Note the difference in scale for end diastole.
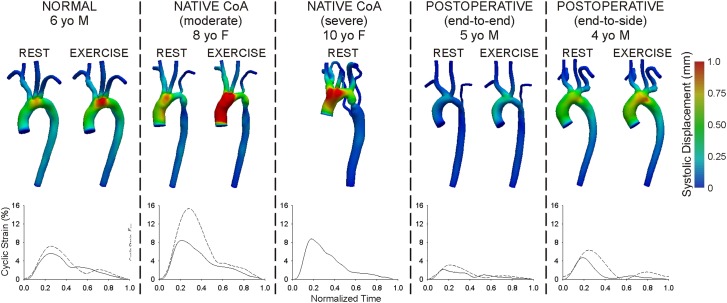
Biomechanics indices (Eθθ, TAWSS, OSI) are listed in Table 3. Peak systolic wall displacement is shown in Fig. 3 with plots of temporal Eθθ at AscAo locations. In general, Eθθ ,max within the AscAo and branch vessels was greater for native CoA patients than for the normal patient, but smaller for treated CoA patients. Eθθ , max was smaller than in the normal patient near or distal to narrow areas such as hypoplastic TA and coarctation regions. Changes in Eθθ ,max with exercise were more pronounced in CoA patients proximal to these narrowed regions, but decreased in the dAo for all patients due to reduced downstream vascular resistance and elevated BP gradients.
Table 3.
Indices of vascular biomechanics
| AscAo | TA | Ductus | Mid dAo | dAo | IA | RCCA | LCCA | LSA | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rest | Exer | Rest | Exer | Rest | Exer | Rest | Exer | Rest | Exer | Rest | Exer | Rest | Exer | Rest | Exer | Rest | Exer | |||||||||||||
| Maximum Circumferential Strain (%) | ||||||||||||||||||||||||||||||
| Normal | 5.6 | 7.2 | 5.9 | 7.0 | 4.7 | 5.3 | 4.3 | 4.3 | 3.8 | 3.1 | 4.0 | 5.5 | 2.8 | 3.4 | 5.5 | 6.4 | 3.9 | 5.5 | ||||||||||||
| Native CoA (moderate) | 8.4 | 15.3 | 5.6 | 9.8 | 1.4 | 3.2 | 2.8 | 2.5 | 2.6 | 2.0 | 4.4 | 8.4 | 2.9 | 5.3 | 3.2 | 5.7 | 1.8 | 3.3 | ||||||||||||
| Native CoA (severe) | 8.8 | – | 7.6 | – | 3.4 | – | 1.6 | – | 1.0 | – | 8.3 | – | 4.5 | – | 4.6 | – | 3.9 | – | ||||||||||||
| Postop (end-to-end) | 2.2 | 3.1 | 1.3 | 1.7 | 1.0 | 1.1 | 1.2 | 1.3 | 1.2 | 1.3 | 1.2 | 1.8 | 0.9 | 1.3 | 1.1 | 1.7 | 0.8 | 1.0 | ||||||||||||
| Postop (end-to-side) | 4.7 | 6.3 | 5.1 | 5.9 | 4.8 | 6.4 | 2.7 | 3.2 | 1.8 | 1.6 | 2.6 | 3.5 | 1.8 | 2.3 | 1.8 | 2.3 | 2.4 | 3.7 | ||||||||||||
| TAWSS - 5 mm bands (dyn/cm2) | ||||||||||||||||||||||||||||||
| Normal | 39 | 77 | 42 | 108 | 29 | 85 | 24 | 70 | 24 | 70 | 59 | 77 | 48 | 60 | 40 | 66 | 46 | 59 | ||||||||||||
| Native CoA (moderate) | 32 | 77 | 92 | 289 | 179 | 618 | 40 | 124 | 36 | 118 | 67 | 104 | 75 | 127 | 47 | 79 | 58 | 99 | ||||||||||||
| Native CoA (severe) | 33 | – | 147 | – | 529 | – | 45 | – | 57 | – | 100 | – | 87 | – | 74 | – | 96 | – | ||||||||||||
| Postop (end-to-end) | 28 | 58 | 52 | 146 | 50 | 148 | 11 | 39 | 17 | 51 | 54 | 93 | 27 | 39 | 20 | 41 | 33 | 21 | ||||||||||||
| Postop (end-to-side) | 18 | 31 | 18 | 38 | 11 | 25 | 23 | 54 | 27 | 60 | 22 | 30 | 13 | 16 | 10 | 12 | 13 | 9 | ||||||||||||
| OSI-5 mm bands (dimensionless) | ||||||||||||||||||||||||||||||
| Normal | 0.11 | 0.09 | 0.07 | 0.05 | 0.07 | 0.03 | 0.06 | 0.02 | 0.06 | 0.02 | 0.08 | 0.16 | 0.06 | 0.12 | 0.12 | 0.13 | 0.08 | 0.19 | ||||||||||||
| Native CoA (moderate) | 0.11 | 0.10 | 0.04 | 0.03 | 0.08 | 0.11 | 0.05 | 0.06 | 0.02 | 0.02 | 0.10 | 0.21 | 0.05 | 0.23 | 0.11 | 0.22 | 0.08 | 0.15 | ||||||||||||
| Native CoA (severe) | 0.20 | – | 0.07 | – | 0.12 | – | 0.20 | – | 0.03 | – | 0.09 | – | 0.17 | – | 0.19 | – | 0.09 | – | ||||||||||||
| Postop (end-to-end) | 0.13 | 0.11 | 0.07 | 0.03 | 0.09 | 0.09 | 0.20 | 0.14 | 0.08 | 0.02 | 0.10 | 0.10 | 0.09 | 0.13 | 0.17 | 0.17 | 0.02 | 0.18 | ||||||||||||
| Postop (end-to-side) | 0.19 | 0.16 | 0.24 | 0.18 | 0.27 | 0.20 | 0.10 | 0.04 | 0.10 | 0.06 | 0.19 | 0.20 | 0.19 | 0.25 | 0.22 | 0.28 | 0.14 | 0.24 | ||||||||||||
| Amount exposed to subnormal | ||||||||||||||||||||||||||||||
| TAWSS (%) | AscAo | TA | Entire dAo | IA | RCCA | LCCA | LSA | |||||||||||||||||||||||
| Normal | 60 | 32 | 63 | 3 | 49 | 3 | 80 | 78 | 42 | 35 | 79 | 70 | 46 | 53 | ||||||||||||||||
| Native CoA (moderate) | 74 | 34 | 34 | 6 | 11 | 1 | 75 | 55 | 22 | 20 | 52 | 28 | 39 | 54 | ||||||||||||||||
| Native CoA (severe) | 57 | – | 28 | – | 7 | – | 36 | – | 28 | – | 16 | – | 12 | – | ||||||||||||||||
| Postop (end-to-end) | 66 | 41 | 48 | 7 | 80 | 6 | 85 | 73 | 96 | 91 | 96 | 69 | 88 | 87 | ||||||||||||||||
| Postop (end-to-side) | 95 | 63 | 93 | 73 | 47 | 9 | 99 | 96 | 98 | 98 | 97 | 92 | 97 | 95 | ||||||||||||||||
| Amount of region exposed to elevated OSI (%) | ||||||||||||||||||||||||||||||
| Normal | 24 | 18 | 41 | 25 | 48 | 10 | 26 | 84 | 35 | 87 | 31 | 61 | 17 | 86 | ||||||||||||||||
| Native CoA (moderate) | 45 | 35 | 29 | 32 | 34 | 38 | 51 | 93 | 50 | 97 | 25 | 82 | 9 | 90 | ||||||||||||||||
| Native CoA (severe) | 48 | – | 61 | – | 58 | – | 75 | – | 97 | – | 73 | – | 51 | – | ||||||||||||||||
| Postop (end-to-end) | 39 | 24 | 47 | 21 | 75 | 42 | 31 | 81 | 81 | 99 | 49 | 77 | 9 | 59 | ||||||||||||||||
| Postop (end-to-side) | 72 | 61 | 89 | 84 | 64 | 31 | 83 | 94 | 100 | 100 | 89 | 92 | 82 | 95 | ||||||||||||||||
Fig. 3.
Color contours of systolic wall displacement mapped to the reference diastolic configuration and examples of associated cyclic strain plots in the ascending aorta during rest (solid lines) and simulated moderate exercise (dashed lines)
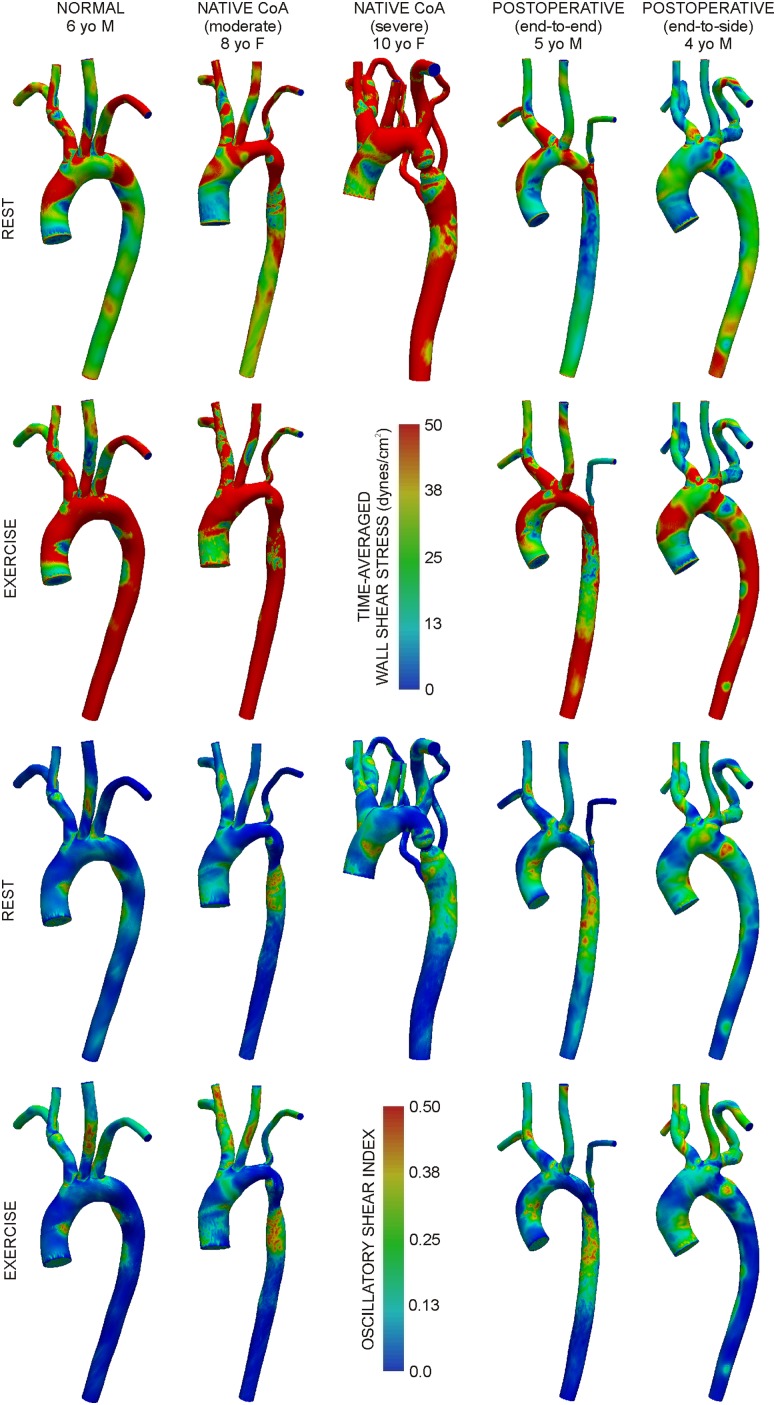
Figure 4 shows TAWSS and OSI under resting and exercise conditions. TAWSS in 5 mm bands (Table 3) within the AscAo of the normal patient were higher than those in treated and untreated CoA patients (e.g., 39 dyn/cm2 versus moderate native CoA: 32 dyn/cm2 and end-to-end: 28 dyn/cm2). Narrow areas in TA and coarctation regions caused higher TAWSS relative to the normal patient that persisted throughout the dAo and were pronounced for the severe native CoA patient. Resting TAWSS was higher for untreated CoA patients in the head and neck vessels (e.g., IA: normal = 59 dyn/cm2 versus moderate = 67 dyn/cm2 and severe CoA = 100 dyn/cm2) and smaller for the treated CoA patients (e.g., IA: end-to-end = 54 dyn/cm2; end-to-side = 22 dyn/cm2). Simulated moderate exercise resulted in a substantial increase in TAWSS for the normal patient (approximately one- to twofold). This increase was similar for all CoA patients except the end-to-side patient whose changes in TAWSS values were smaller by 17-71%. Similar trends were observed in the head and neck vessels, but changes were less pronounced within and between patients.
Fig. 4.
Distributions of time-averaged wall shear stress under resting (first row) and simulated moderate exercise (second row) conditions. Distributions of oscillatory shear index under resting (third row) and simulated moderate exercise (fourth row) conditions.
OSI was elevated in the AscAo of CoA patients and slightly greater than in other locations. OSI decreased throughout the aorta during exercise for all cases except for the moderate native CoA where it was unchanged or moderately higher beyond the TA. Conversely, OSI increased in branch arteries of all patients during exercise.
A greater percent of the AscAo was exposed to subnormal TAWSS or elevated OSI for CoA patients (Table 3). Simulated moderate exercise reduced this percentage for all patients. Narrowed aortic regions for native CoA patients generally resulted in smaller regions of the downstream lumen exposed to subnormal TAWSS, but larger distal areas of elevated OSI. Adverse hemodynamics were mitigated during simulated moderate exercise with the exception of the moderate native CoA patient where elevated OSI increased by 12%–14% distal to the coarctation. Exercise-induced reductions in the area exposed to subnormal TAWSS or elevated OSI were less pronounced in branch vessels. Simulated exercise caused a substantial increase in the amount of the lumen exposed to elevated OSI in all models except for the end-to-side patient where changes were <16%. Patients with small caliber LSA typically had lower values of TAWSS and larger regions of the lumen exposed to subnormal TAWSS during rest and exercise.
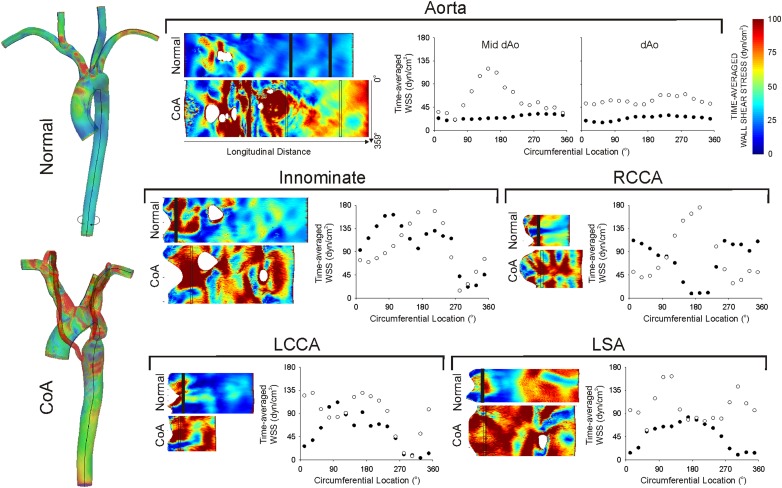
TAWSS values were also plotted on patches corresponding to the endothelial surface unwrapped about longitudinal axes along the inner curvature of the aorta, and anterior surface of branch vessels (Fig. 5). Circumferential TAWSS contours in the dAo and branch vessels are provided for the normal and severe native CoA patients. Plots in the dAo of the normal patient clearly show low TAWSS spiraling down the dAo. This pattern is also supported by the solid circles shown in plots generated by averaging TAWSS values every 22.5°. TAWSS values were elevated for the patient with severe CoA (e.g., mean = 1777 dyn/cm2; max ∼6000 dyn/cm2). The coarctation also interrupted helical TAWSS patterns down the dAo, particularly near the insertion of collateral vessels (Fig. 5, solid circles). Similarly, circumferential plots in branch arteries were elevated relative to the normal patient and suggest that velocity profiles and TAWSS patterns are altered as blood flows from the aorta to the brain and upper extremities.
Fig. 5.
TAWSS results were unwrapped about longitudinal axes along the inner curvature of the aorta, and anterior surface of the head and neck arteries (shown in black on the left-most side). Unwrapped plots are provided for the aorta and innominate, right (RCCA) and left carotid (LCCA), and left subclavian (LSA) arteries. Circumferential TAWSS plots in the descending aorta and in vessels one diameter distal to their branching from the aorta are also provided for the patient with severe native CoA (empty circles) as compared to the normal patient (solid circles).
4. Discussion
Morbidity from CoA persists with current guidelines that ignore the ramifications of a particular treatment on local hemodynamics or vascular mechanics. The current investigation introduces a coupled computational and imaging technique to increase our understanding of detailed alterations in related indices such as distributions of WSS and strain that are associated with CoA under resting and nonresting blood flow conditions, uniquely investigate potential sources of morbidity, and evaluate treatment options. The methods are based on data obtained at rest as part of a routine clinical imaging session and used in conjunction with CFD tools to generate temporally and spatially varying indices that are difficult to obtain using conventional methods including TAWSS, OSI and Eθθ in the portions of the vasculature where long-term morbidity seems to be manifested. Specifically, this investigation offers several key findings discussed in detail in the following.
4.1. CFD Tools Can Replicate the Pathophysiology Typically Observed for Patients With CoA.
The present results confirm and extend those of O’Rourke and Cartmill [1]. Their physiologic observations were manifested in simulations of the native CoA patient where the aorta’s conduit function is maintained through collateral vessels, but its cushioning function was reduced by the coarctation and limited pressure pulse transmission through small caliber and tortuous collateral vessels [1].
Patterns of velocity in the normal patient were similar to those obtained with 3D and 4D PC-MRI techniques [31,32]. Velocity patterns during early systole were completely attached to the luminal surface, right-handed helical flow developed in the AscAo and TA at peak systole and flow during diastole included swirling and rotational patterns throughout the aorta and its branches. These patterns are altered with varying severity in CoA patients.
A previous study showed thoracic cyclic strain decreased from ∼9% at age 41 to ∼2.5% at age 68 [30]. The current results provide the first known reports of strain in coarctation patients derived from CFD. While strain in the AscAo of native CoA patients is largely impacted by the downstream coarctation, treated CoA patients had values closer to older patients reported in the previous study. The strain results in Table 2 not only demonstrate the ability of CFD tools to quantify this index, but are also consistent with studies suggesting deleterious changes in vascular properties can persist despite treatment [3].
4.2. CFD Tools Can Quantify the Severity of Hemodynamic Alterations in Borderline CoA Patients and Under Blood Flow Conditions Representative of Daily Activity.
Cases similar to the native moderate CoA patient presented here are often difficult to evaluate clinically. The resting BP gradient is modest (12 mmHg) and the question arises as to whether treatment should be performed if cardiac function is acceptable. Currently, there is only limited data to influence this decision. BP, hemodynamics, and Eθθ results from simulated exercise suggest this patient may have benefited from treatment to restore lumen caliber. Similarly, CoA treatment often acutely alleviates resting BP gradients, but there is conflicting data concerning residual gradients during ambulatory or exercise conditions reflecting daily activity [33]. These conditions can be generated by exercise testing, but the tests are not routinely ordered and imaging is difficult under such conditions. The current results indicate CFD is a useful tool for simulating the severity of hemodynamic alterations in patients with moderate CoA and under elevated flow conditions.
Presently there is no technique to assess detailed hemodynamic and biomechanic ramifications of a treatment a priori. CFD modeling is applied to native or surgically corrected CoA patients for this purpose here, but can also be conducted after simulated or actual interventions including angioplasty and stenting to facilitate virtual catheterization within the patient-specific model during resting or exercise conditions.
4.3. CoA Disturbs Normal Patterns of TAWSS and OSI Throughout the Thoracic Aorta.
Imaging studies quantifying TAWSS in the thoracic aorta of normal patients reported findings consistent with those revealed here. Low TAWSS and elevated OSI were found in a rotating pattern down the dAo [29,34], and these sites correlated with those prone to atherosclerotic plaque development. Treated or untreated CoA patients with even modest narrowing areas are likely exposed to unique patterns of WSS [35], which may influence the location and magnitude of plaque formation. Thus, the current approach may be used to determine sites of atherosclerotic susceptibility based on local hemodynamic alterations in longitudinal studies. Values in the native coarctation region are concerning as they are within the range of hemolysis. Additionally, potentially deleterious WSS indices established in CoA patients are only partially mitigated by exercise after repair. Differences in these indices between the aorta and branch arteries are interesting given the frequency of cerebrovascular events in CoA patients. Interestingly, a number of recent investigations report that intima-media thickness thought to be associated with altered distributions of WSS and stroke were pronounced in the carotid arteries of postoperative CoA patients [36,37].
4.4. Restoring Favorable Anatomy May Not Restore Normal Hemodynamics.
The end-to-side repair presented here established arch anatomy most closely resembling normal by alleviating TA hypoplasia. However, CFD indicated that this favorable arch anatomy may introduce lower TAWSS in the aorta thereby causing larger fractions of the lumen to be exposed to deleterious WSS. These results must be verified in more patients, but highlight how CFD can offer important additional functional information regarding the severity of vascular pathologies, or be used to evaluate different treatment options.
The current results should be interpreted within the constraints of several potential limitations. BP was obtained from brachial artery cuff measurements, but may differ from central BP. In many MRI studies portions of the intercostal arteries can be delineated in the MRA volume. These vessels are thought to take between 7% and 11% of the flow from the level of the coarctation to the diaphragm under normal conditions, and are often recruited to serve as collateral vessels in patients with native CoA. These vessels were not included in all models as localized PC-MRI measurements can only provide a summed estimate of the total flow through the collection of these vessels and appropriate boundary conditions for these arteries are not presently known. Two intercostal arteries serving as collateral vessels were included for the native patient with severe CoA. The caliber of these vessels was adjusted to replicate conduit function and the measured BP gradient. Although improved imaging resolution would facilitate including more detailed collateral or intercostal vessels, these benefits would be offset by current limitations in accurately assessing coarctation BP gradients from cuff measurements or a modified Bernoulli’s estimation.
A single elastic modulus and thickness value was used for respective CFD models, but vascular tissue properties vary spatially. While the results produced AscAo wall motion similar to PC-MRI, they may be less accurate at other locations.
Although the concept of patient-specific CFD modeling was reported in 1999 [38], this investigation marks the first full-scale application with a sampling of CoA patients. Although observations between patients are reported here, the goal of this work is really to demonstrate utility of the methods described with a variety of CoA patient populations to be studied further in future investigations. One of the patients featured here, the 10 yo female subject with severe CoA, presented clinically with elevated cardiac output. Similar cases have been reported for severe native CoA in the absence of heart failure to meet an apparent metabolic need beyond the stenosis. Nonetheless, an exercise simulation was not conducted because such a test would not be clinically ordered for this patient presenting in a hyperdynamic state and in obvious need of treatment.
The procedure used to assess the severity of hemodynamic alterations under moderate exercise generated inflow waveforms, flow distributions to aortic branches, and BP changes consistent with those previously reported in response to supine stationary ergometer exercise at a 50% change in heart rate for normal patients [18,19]. However, it is important to note that none of the subjects in this investigation underwent exercise testing for direct comparison to simulation results. Although exercise testing can be done in the setting of CoA, it is not commonly implemented. Moreover, if data from exercise testing were available, it is highly unlikely that blood flow distributions to branch arteries, indices of vascular capacitance, and four extremity blood pressure readings would have been obtained for use in determining the Windkessel parameters required for CFD. Thus, the approach described here, which is rooted in documented physiological changes, was implemented with CoA patients. Future studies are currently underway to elucidate changes in outlet boundary conditions at a number of exercise levels for use with CFD of CoA patients and preliminary results are in good agreement with the trends reported here.
Results presented would not have been possible without several technical advancements including realistic outflow boundary conditions, fluid–structure interaction, substantial computational power and a number of additional seminal advancements in CFD. Nonetheless, the results are exciting and will likely lead to similar studies in short order. Many important considerations were included in the CFD procedure, but the addition of several factors could add further realism to the results (Table 4) and will be the focus of future work.
Table 4.
Summary of computational considerations, associated physiological references, and applicable computational studies related to patient-specific modeling for CoA
| Consideration | Physiologic reference(s) | Applicable computational reference(s) | Currently implemented |
|---|---|---|---|
| Replication of physiologic flow patterns and aortic root motion | 32 | 39 | partially |
| Outflow boundary conditions that replicate the distal vasculature to reproduce flow splits and BP | 40 | 12 | yes |
| Compliance of the aorta, variable tissue properties and support structures for the arterial system | 41, 42 | 23, 26, 43 | partially |
| Inclusion of intercostal, internal mammary and collateral vessels | 44, 45 | 46 | partially |
| Ability to provide unique, clinically applicable data | 47 | 4 | yes |
5. Conclusions
The current results demonstrate the applicability of a procedure combining clinical imaging data and novel computational modeling tools for a range of patients with CoA and provide the foundation for future progress in this area. We are optimistic that applying these computational techniques to CoA will ultimately help to reduce the long-term morbidity currently observed in these patients by identifying associated processes before they are clinically apparent.
Acknowledgment
This work was supported by the Dean’s Postdoctoral Fellowship and Vera Moulton Wall Center for Pulmonary Vascular Disease at Stanford University, and NIH Award No. R15HL096096-01. Material presented is based upon work supported by NSF Grant No. 0205741. The authors gratefully acknowledge Dr. Nathan Wilson and Timothy Gundert for technical assistance.
Contributor Information
John F. LaDisa, Jr., Department of Biomedical Engineering, Marquette University, Milwaukee, WI 53233; Department of Pediatrics, Children’s Hospital of Wisconsin, Milwaukee, WI 53226, e-mail: john.ladisa@mu.edu.
C. Alberto Figueroa, Department of Bioengineering, Stanford University, Stanford, CA 94305.
Irene E. Vignon-Clementel, INRIA Paris-Rocquencourt BP 105, 78153 Le Chesnay Cedex, France
Hyun Jin Kim, Aerospace Engineering Sciences, University of Colorado at Boulder, Boulder, CO 80309.
Nan Xiao, Department of Bioengineering, Stanford University, Stanford, CA 94305.
Laura M. Ellwein, Department of Biomedical Engineering, Marquette University, Milwaukee, WI 53233
Frandics P. Chan, Department of Radiology, Stanford University, Stanford, CA 94305
Jeffrey A. Feinstein, Department of Bioengineering, Department of Pediatrics, Stanford University, Stanford, CA 94305; Lucile Packard Children’s Hospital, Palo Alto, CA 94304
Charles A. Taylor, Department of Bioengineering, Department of Radiology, Stanford University, Stanford, CA 94305
References
- [1]. O’Rourke, M. F. , and Cartmill, T. B. , 1971, “Influence of Aortic Coarctation on Pulsatle Hemodynamics in the Proximal Aorta,” Circulation, 44(2), pp. 281–292. [DOI] [PubMed] [Google Scholar]
- [2]. Rosenthal, E. , 2001, “Stent Implantation for Aortic Coarctation: The Treatment of Choice in Adults?,” J. Am. Colloid Cardiol., 38(5), pp. 1524–1527. 10.1016/S0735-1097(01)01573-X [DOI] [PubMed] [Google Scholar]
- [3]. Ong, C. M. , Canter, C. E. Gutierrez, F. R. Sekarski, D. R. , and Goldring, D. R. , 1992, “Increased Stiffness and Persistent Narrowing of the Aorta after Successful Repair of Coarctation of the Aorta: Relationship to Left Ventricular Mass and Blood Pressure at Rest and with Exercise,” Am. Heart J., 123(6), pp. 1594–1600. 10.1016/0002-8703(92)90815-D [DOI] [PubMed] [Google Scholar]
- [4]. Pizarro, C. , and De Leval, M. R. , 1998, “Surgical Variations and Flow Dynamics in Cavopulmonary Connections: A Historical Review,” Semin. Thorac. Cardiovasc. Surg. Pediatr. Card. Surg. Annu., 1, pp. 53–60. [DOI] [PubMed] [Google Scholar]
- [5]. Draney, M. T. , Alley, M. A. , Tang, B. T. , Wilson, N. M. , Herfkens, R. J. , and Taylor, C. A. , 2002, “Importance of 3D Nonlinear Gradient Corrections for Quantitative Analysis of 3D Mr Angiographic Data,” Conference Proceedings of the International Society for Magnetic Resonance in Medicine, Honolulu, HI. [Google Scholar]
- [6]. Wilson, N. , Wang, K. , Dutton, R. , and Taylor, C. A. , 2001, “A Software Framework for Creating Patient Specific Geometric Models from Medical Imaging Data for Simulation Based Medical Planning of Vascular Surgery,” Lect. Notes Comput. Sci., 2208, pp. 449–456. 10.1007/3-540-45468-3_54 [DOI] [Google Scholar]
- [7]. Les, A. S. , Shadden, S. C. , Figueroa, C. A. , Park, J. M. , Tedesco, M. M. , Herfkens, R. J. , Dalman, R. L. , and Taylor, C. A. , 2010, “Quantification of Hemodynamics in Abdominal Aortic Aneurysms During Rest and Exercise Using Magnetic Resonance Imaging and Computational Fluid Dynamics,” Ann. Biomed. Eng., 38(4), pp. 1288–1313. 10.1007/s10439-010-9949-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8]. Tang, B. T. , Cheng, C. P. , Draney, M. T. , Wilson, N. M. , Tsao, P. S. , Herfkens, R. J. , and Taylor, C. A. , 2006, “Abdominal Aortic Hemodynamics in Young Healthy Adults at Rest and During Lower Limb Exercise: Quantification Using Image-Based Computer Modeling,” Am, J, Physiol, Heart, Circ, Physiol, 291(2), pp. H668–H676. [DOI] [PubMed] [Google Scholar]
- [9]. Cheng, C. P. , Herfkens, R. J. , Lightner, A. L. , Taylor, C. A. , and Feinstein, J. A. , 2004, “Blood Flow Conditions in the Proximal Pulmonary Arteries and Vena Cavae in Healthy Children During Upright Seated Rest and Cycling Exercise, Quantified with MRI,” Am. J. Physiol. Heart. Circ. Physiol., 287(2), pp. H921–H926. 10.1152/ajpheart.00022.2004 [DOI] [PubMed] [Google Scholar]
- [10]. Zamir, M. , Sinclair, P. , and Wonnacott, T. H. , 1992, “Relation between Diameter and Flow in Major Branches of the Arch of the Aorta,” J. Biomech., 25(11), pp. 1303–1310. 10.1016/0021-9290(92)90285-9 [DOI] [PubMed] [Google Scholar]
- [11]. Seear, M. , Webber, S. , and Leblanc, J. , 1994, “Descending Aortic Blood Flow Velocity as a Noninvasive Measure of Cardiac Output in Children,” Pediatr. Cardiol., 15(4), pp. 178–183. 10.1007/BF00800672 [DOI] [PubMed] [Google Scholar]
- [12]. Vignon-Clementel, I . E. , Figueroa, C. A. , Jansen, K. E. , and Taylor, C. A. , 2006, “Outflow Boundary Conditions for Three-Dimensional Finite Element Modeling of Blood Flow and Pressure in Arteries,” Comput. Methods Appl. Mech. Eng., 195, pp. 3776–3796. 10.1016/j.cma.2005.04.014 [DOI] [Google Scholar]
- [13]. Laskey, W. K. , Parker, H. G. , Ferrari, V . A. , Kussmaul, W. G. , and Noordergraaf, A. , 1990, “Estimation of Total Systemic Arterial Compliance in Humans,” J. Appl. Physiol., 69(1), pp. 112–119. [DOI] [PubMed] [Google Scholar]
- [14]. Stergiopulos, N. , Young, D. F. , and Rogge, T. R. , 1992, “Computer Simulation of Arterial Flow with Applications to Arterial and Aortic Stenoses,” J. Biomech., 25(12), pp. 1477–1488. 10.1016/0021-9290(92)90060-E [DOI] [PubMed] [Google Scholar]
- [15]. O’Rourke, M. F. , and Safar, M. E. , 2005, “Relationship between Aortic Stiffening and Microvascular Disease in Brain and Kidney: Cause and Logic of Therapy,” Hypertension, 46(1), pp. 200–204. 10.1161/01.HYP.0000168052.00426.65 [DOI] [PubMed] [Google Scholar]
- [16]. Stergiopulos, N. , Segers, P. , and Westerhof, N. , 1999, “Use of Pulse Pressure Method for Estimating Total Arterial Compliance in Vivo,” Am. J. Physiol. Heart. Circ. Physiol., 276(45), pp. H424–H428. [DOI] [PubMed] [Google Scholar]
- [17]. Naka, K. K. , Tweddel, A. C. , Parthimos, D. , Henderson, A. , Goodfellow, J. , and Frenneaux, M. P. , 2003, “Arterial Distensibility: Acute Changes Following Dynamic Exercise in Normal Subjects,” Am. J. Physiol. Heart. Circ. Physiol., 284(3), pp. H970–H978. [DOI] [PubMed] [Google Scholar]
- [18]. Calbet, J. A. , Gonzalez-Alonso, J. , Helge, J. W. , Sondergaard, H. , Munch-Andersen, T. , Boushel, R. , and Saltin, B. , 2007, “Cardiac Output and Leg and Arm Blood Flow During Incremental Exercise to Exhaustion on the Cycle Ergometer,” J. Appl. Physiol., 103(3), pp. 969–978. 10.1152/japplphysiol.01281.2006 [DOI] [PubMed] [Google Scholar]
- [19]. Markham, L. W. , Knecht, S. K. , Daniels, S. R. , Mays, W. A. , Khoury, P. R. , and Knilans, T. K. , 2004, “Development of Exercise-Induced Arm-Leg Blood Pressure Gradient and Abnormal Arterial Compliance in Patients with Repaired Coarctation of the Aorta,” Am. J. Cardiol., 94(9), pp. 1200–1202. 10.1016/j.amjcard.2004.07.097 [DOI] [PubMed] [Google Scholar]
- [20]. Hellstrom, G. , Fischer-Colbrie, W. , Wahlgren, N. G. , and Jogestrand, T. , 1996, “Carotid Artery Blood Flow and Middle Cerebral Artery Blood Flow Velocity during Physical Exercise,” J. Appl. Physiol., 81(1), pp. 413–418. [DOI] [PubMed] [Google Scholar]
- [21]. Green, D. , Cheetham, C. , Reed, C. , Dembo, L. , and O’Driscoll, G. , 2002, “Assessment of Brachial Artery Blood Flow across the Cardiac Cycle: Retrograde Flows during Cycle Ergometry,” J. Appl. Physiol., 93(1), pp. 361–368. [DOI] [PubMed] [Google Scholar]
- [22]. Kim, H. J. , Figueroa, C. A. , Hughes, T. J. R. , Jansen, K. E. , and Taylor, C. A. , 2009, “Augmented Lagrangian Method for Constraining the Shape of Velocity Profiles at Outlet Boundaries for Three-Dimensional Finite Element Simulations of Blood Flow,” Comput. Methods Appl. Mech. Eng., 198, pp. 3551–3566. 10.1016/j.cma.2009.02.012 [DOI] [Google Scholar]
- [23]. Figueroa, C. A. , Vignon-Clementel, I . E. , Jansen, K. E. , Hughes, T. J. R. , and Taylor, C. A. , 2006, “A Coupled Momentum Method for Modeling Blood Flow in Three-Dimensional Deformable Arteries,” Comput. Methods Appl. Mech. Eng., 195, pp. 5685–5706. 10.1016/j.cma.2005.11.011 [DOI] [Google Scholar]
- [24]. Figueroa, C. A. , Ladisa, J. F., Jr. , Vignon-Clementel, I. E. , Jansen, K. C. , Hughes, T. J. R. , Feinstein, J. A. , and Taylor, C. A. , 2005, “A Coupled-Momentum Method for Fluid-Structure Interaction: Applications to Aortic Co-arctation,” Second International Conference on Computational Bioengineering, Lisbon, Portugal: . [Google Scholar]
- [25]. Westerhof, N. , Bosman, F. , De Vries, C. J. , and Noordergraaf, A. , 1969, “Analog Studies of the Human Systemic Arterial Tree,” J. Biomech., 2(2), pp. 121–143. 10.1016/0021-9290(69)90024-4 [DOI] [PubMed] [Google Scholar]
- [26]. Moireau, P. , Xiao, N. , Astorino, M. , Figueroa, C. A. , Chapelle, D. , Taylor, C. A. , and Gerbeau, J. F. , 2011, “External Tissue Support and Fluid-Structure Simulation in Blood Flows,” Biomech. Model. Mechanobiol. (in press). 10.1007/s10237-011-0289-z [DOI] [PubMed] [Google Scholar]
- [27]. Sahni, O. , Muller, J. , Jansen, K. E. , Shephard, M. S. , and Taylor, C. A. , 2006, “Efficient Anisotropic Adaptive Discretization of the Cardiovascular System,” Comput. Methods Biomech. Biomed. Eng., 195, pp. 5634–5655. [Google Scholar]
- [28]. Muller, J. , Sahni, O. , Li, X. , Jansen, K. E. , Shephard, M. S. , and Taylor, C. A. , 2005, “Anisotropic Adaptive Finite Element Method for Modelling Blood Flow,” Comput. Methods Biomech. Biomed. Engin., 8(5), pp. 295–305. 10.1080/10255840500264742 [DOI] [PubMed] [Google Scholar]
- [29]. Frydrychowicz, A. , Stalder, A. F. , Russe, M. F. , Bock, J. , Bauer, S. , Harloff, A. , Berger, A. , Langer, M. , Hennig, J. , and Markl, M. , 2009, “Three-Dimensional Analysis of Segmental Wall Shear Stress in the Aorta by Flow-Sensitive Four-Dimensional-MRI,” J. Magn. Reson. Imaging, 30(1), pp. 77–84. 10.1002/jmri.21790 [DOI] [PubMed] [Google Scholar]
- [30]. Morrison, T. M. , Choi, G. , Zarins, C. K. , and Taylor, C. A. , 2009, “Circumferential and Longitudinal Cyclic Strain of the Human Thoracic Aorta: Age-Related Changes,” J. Vasc. Surg., 49(4), pp. 1029–1036. 10.1016/j.jvs.2008.11.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Markl, M. , Draney, M. T. , Hope, M. D. , Levin, J. M. , Chan, F. P. , Alley, M. T. , Pelc, N. J. , and Herfkens, R. J. , 2004, “Time-Resolved 3-Dimensional Velocity Mapping in the Thoracic Aorta: Visualization of 3-Directional Blood Flow Patterns in Healthy Volunteers and Patients,” J. Comput. Assist. Tomog., 28(4), pp. 459–468. 10.1097/00004728-200407000-00005 [DOI] [PubMed] [Google Scholar]
- [32]. Kilner, P. J. , Yang, G. Z. , Mohiaddin, R. H. , Firmin, D. N. , and Longmore, D. B. , 1993, “Helical and Retrograde Secondary Flow Patterns in the Aortic Arch Studied by Three-Directional Magnetic Resonance Velocity Mapping,” Circulation, 88(5 Pt 1), pp. 2235–2247. [DOI] [PubMed] [Google Scholar]
- [33]. Sigurdardottir, L. Y. , and Helgason, H. , 1996, “Exercise-Induced Hypertension after Corrective Surgery for Coarctation of the Aorta,” Pediatr. Cardiol., 17(5), pp. 301–307. 10.1007/s002469900066 [DOI] [PubMed] [Google Scholar]
- [34]. Wentzel, J. J. , Corti, R. , Fayad, Z. A. , Wisdom, P. , Macaluso, F. , Winkelman, M. O. , Fuster, V . , and Badimon, J. J. , 2005, “Does Shear Stress Modulate Both Plaque Progression and Regression in the Thoracic Aorta? Human Study Using Serial Magnetic Resonance Imaging,” J. Am. Coll. Cardiol., 45(6), pp. 846–854. 10.1016/j.jacc.2004.12.026 [DOI] [PubMed] [Google Scholar]
- [35]. LaDisa, J. F., Jr. , Dholakia, R. J. , Figueroa, C. A. , Vignon-Clementel, I . E. , Chan, F. P. , Samyn, M. M. , Cava, J. R. , Taylor, C. A. , and Feinstein, J. A. , 2011, “Computational Simulations Demonstrate Altered Wall Shear Stress in Aortic Coarctation Patients Previously Treated by Resection with End-to-End Anastomosis,” Congen. Heart Dis. 10.1111/j.1747-0803.2011.00553.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Vriend, J. W. , De Groot, E. Bouma, B. J. Hrudova, J. Kastelein, J. J. Tijssen, J. G. and Mulder, B. J. , 2005, “Carotid Intima-Media Thickness in Post-Coarctectomy Patients with Exercise Induced Hypertension,” Heart, 91(7), pp. 962–963. 10.1136/hrt.2004.045245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Carallo, C. , Lucca, L. F. , Ciamei, M. , Tucci, S. , and De Franceschi, M. S. , 2006, “Wall Shear Stress Is Lower in the Carotid Artery Responsible for a Unilateral Ischemic Stroke,” Atherosclerosis, 185(1), pp. 108–113. 10.1016/j.atherosclerosis.2005.05.019 [DOI] [PubMed] [Google Scholar]
- [38]. Taylor, C. A. , Draney, M. T. , Ku, J. P. , Parker, D. , Steele, B. N. , Wang, K. , and Zarins, C. K. , 1999, “Predictive Medicine: Computational Techniques in Therapeutic Decision-Making,” Comput. Aided Surg., 4(5), pp. 231–247. 10.3109/10929089909148176 [DOI] [PubMed] [Google Scholar]
- [39]. Jin, S. , Oshinski, J. , and Giddens, D. P. , 2003, “Effects of Wall Motion and Compliance on Flow Patterns in the Ascending Aorta,” J. Biomech. Eng., 125(3), pp. 347–354. 10.1115/1.1574332 [DOI] [PubMed] [Google Scholar]
- [40]. O’Rourke, M. F. , and Taylor, M. G. , 1967, “Input Impedance of the Systemic Circulation,” Circ. Res., 20(4), pp. 365–380. [DOI] [PubMed] [Google Scholar]
- [41]. Wolinsky, H. , and Glagov, S. , 1969, “Comparison of Abdominal and Thoracic Aortic Medial Structure in Mammals. Deviation of Man from the Usual Pattern,” Circ. Res., 25(6), pp. 677–686. [DOI] [PubMed] [Google Scholar]
- [42]. Patel, D. J. , and Fry, D. L. , 1966, “Longitudinal Tethering of Arteries in Dogs,” Circ. Res., 19(6), pp. 1011–1021. [DOI] [PubMed] [Google Scholar]
- [43]. Holzapfel, G. A. , and Weizsacker, H. W. , 1998, “Biomechanical Behavior of the Arterial Wall and Its Numerical Characterization,” Comput. Biol. Med., 28(4), pp. 377–392. 10.1016/S0010-4825(98)00022-5 [DOI] [PubMed] [Google Scholar]
- [44]. Steffens, J. C. , Bourne, M. W. , Sakuma, H. , O’Sullivan, M. , and Higgins, C. B. , 1994, “Quantification of Collateral Blood Flow in Coarctation of the Aorta by Velocity Encoded Cine Magnetic Resonance Imaging,” Circulation, 90(2), pp. 937–943. [DOI] [PubMed] [Google Scholar]
- [45]. Riehle, T. J. , Oshinski, J. N. , Brummer, M. E. , Favaloro-Sabatier, J. , Mahle, W. T. , Fyfe, D. A. , Kanter, K. R. , and Parks, W. J. , 2006, “Velocity-Encoded Magnetic Resonance Image Assessment of Regional Aortic Flow in Coarctation Patients,” Ann. Thorac. Surg., 81(3), pp. 1002–1007. 10.1016/j.athoracsur.2005.07.002 [DOI] [PubMed] [Google Scholar]
- [46]. Engvall, J. , Karlsson, M. , Ask, P. , Loyd, D. , Nylander, E. , and Wranne, B. , 1994, “Importance of Collateral Vessels in Aortic Coarctation: Computer Simulation at Rest and Exercise Using Transmission Line Elements,” Med. Biol. Eng. Comput., 32(4), pp. S115–S122. 10.1007/BF02523337 [DOI] [PubMed] [Google Scholar]
- [47]. Steinman, D. A. , and Taylor, C. A. , 2005, “Flow Imaging and Computing: Large Artery Hemodynamics,” Ann. Biomed. Eng., 33(12), pp. 1704–1709. 10.1007/s10439-005-8772-2 [DOI] [PubMed] [Google Scholar]