Multiple Genetic Variant Association Testing by Collapsing and Kernel Methods With Pedigree or Population Structured Data

Abstract

Searching for rare genetic variants associated with complex diseases can be facilitated by enriching for diseased carriers of rare variants by sampling cases from pedigrees enriched for disease, possibly with related or unrelated controls. This strategy, however, complicates analyses because of shared genetic ancestry, as well as linkage disequilibrium among genetic markers. To overcome these problems, we developed broad classes of “burden” statistics and kernel statistics, extending commonly used methods for unrelated case-control data to allow for known pedigree relationships, for autosomes and the X chromosome. Furthermore, by replacing pedigree-based genetic correlation matrices with estimates of genetic relationships based on large-scale genomic data, our methods can be used to account for population-structured data. By simulations, we show that the type I error rates of our developed methods are near the asymptotic nominal levels, allowing rapid computation of P-values. Our simulations also show that a linear weighted kernel statistic is generally more powerful than a weighted “burden” statistic. Because the proposed statistics are rapid to compute, they can be readily used for large-scale screening of the association of genomic sequence data with disease status.

Introduction

Large-scale genomic technologies, such as assays used for genome wide association studies (GWAS), whole exome sequencing, or whole genome sequencing, provide rich resources to screen for genetic variants associated with complex diseases. Recent efforts have focused on the potential role of rare variants influencing disease, such as variants with minor alleles having a frequency of less than 5%. Rare variants are likely to have a prominent role in the etiology of some complex traits, a role found true for a number diseases [Azzopardi et al., 2008; Cohen et al., 2004; Hershberger et al., 2010] and supported by population genetic principles [Bodmer and Bonilla, 2008; Dickson et al., 2010; Pritchard, 2001]. To enrich for affected subjects likely to carry rare variants, pedigrees with multiple affected subjects are a good choice [Bodmer and Bonilla, 2008; Teng and Risch, 1999], particularly because of widely available resources from past linkage mapping efforts. Many of such collections have multiple affected pedigree members, perhaps with some unaffected members. It is not unusual to use these types of collections as a source for sampling cases (one per family), to compare with a set of unrelated controls. To make full use of such pedigree data with multiple cases, and possibly unrelated controls, we developed broad classes of statistics to account for pedigree relationships, allowing a mixutre of related and unrelated cases and controls. To understand our proposed methods, it is worthwhile to review recent developments of “burden” tests and kernel tests for association testing of multiple genetic variants with disease status.

Because they are sparse, it is nearly impossible to evaluate individual rare variants. Hence, a popular strategy is to combine rare variants into groups, to increase the group sizes and hence power. The grouping could be at the gene level, or a set of genes composing a biochemical pathway. Most strategies are based on combining the minor alleles across multiple variant sites into a single test statistic, either without weighting [Li and Leal, 2008; Morgenthaler and Thilly, 2007; Zawistowski et al., 2010], or with fixed weights based on allele frequencies [Madsen and Browning, 2009; Sun et al., 2011], or with data-adaptive weights [Lin and Tang, 2011; Liu and Leal, 2010]. Variations on these strategies are data-adaptive thresholds to include or exclude some variants [Hoffmann et al., 2010; Pan and Shen, 2011; Price et al., 2010]. The strengths and weaknesses of these methods have been reviewed and compared [Asimit and Zeggini, 2010; Bansal et al., 2010; Basu and Pan, 2010]. A simplistic view of this overall strategy is the creation of a variant-sum “burden” for each subject, where the variant-sum is the total, across all variant sites, of the minor allele dosages (possibly weighting each variant site with either fixed weights or data-adaptive weights, and possibly weights of zero to exclude some variants). The variant-sum can be used in regression models, possibly as a score-statistic, to test the association of the variant-sum with a trait. From this perspective, these methods can be viewed as testing whether the variant-sum influences the mean of the trait. For case-control studies, this is analogous to testing the difference in the mean of the variant-sums between cases and controls. These combined approaches are sensitive to when the minor alleles across all sites have effects in the same direction (i.e., all risk variants or all protective variants).

Although testing of the variant-sum on the mean of a trait has significant advantages in a regression framework, allowing for covariate adjustment (such as eigenvectors for population stratification), it will have limited power when the variants are a mixture of both risk and protective variants. Methods to overcome this limitation have been proposed [Ionita-Laza et al., 2011; Neale et al., 2011], with powerful methods that allow covariate adjustment based on kernel regression [Kwee et al., 2008; Lee et al., 2012a, b; Wu et al., 2011]. Some important aspects of the kernel regression approach are: (1) kernel regression can be formulated as a mixed model, with the adjusting covariates treated as fixed effects and the genetic factors treated as random effects; (2) the random effects are assumed to have a covariance structure that is determined by σ²H, where H is an n × n kernel matrix of specified structure that summarizes the genetic similarity between pairs of subjects; (3) under the null hypothesis of no association of the genetic data with a trait, the genetic similarity between pairs of subjects is not associated with trait similarity between pairs of subjects, so the scalar parameter σ² = 0 under the null hypothesis of no association. The resulting score statistic for testing H_o : σ² = 0 can be efficiently computed by the quadratic form Q = (Y – Ŷ)′ H(Y – Ŷ), where Y is a vector of length n for the trait values of n subjects, and Ŷ is the covariate-fitted value of Y. Note that for quantitative traits, Q is typically scaled by dividing by $2{\widehat{\sigma }}_e^2$, where ${\widehat{\sigma }}_e^2$ is the maximum likelihood estimate of the residual variance [Kwee et al., 2008].

A key assumption of the kernel association test, when applied to unrelated subjects, is that the residuals, (Y – Ŷ), are assumed to be uncorrelated. To extend the kernel association test for autosomes to quantitative traits of pedigree data, Schifano et al. [2012] and Chen et al. [2012] allowed for residual correlations among family members by assuming that the random effects, denoted by the vector b, have a multivariate normal distribution under the null hypothesis of no genetic-trait associations, with mean 0 and covariance matrix $V\left(b\right)={\sigma }_b^{2}K$. The matrix K contains diagonal elements K_ii = 1 + h_i, where h_i is the inbreeding coefficient for subject i, and off-diagonal elements K_ij = 2ϕ_ij . The parameter ϕ_ij is the kinship coefficient between individuals i and j, the probability that a randomly chosen allele at a given locus from individual i is identical by descent to a randomly chosen allele from individual j, conditional on their ancestral relationship. For autosomes, the genetic correlation between subjects i and j is K_ij = 2ϕ_ij. By combining variation from the random effects with the residual error variation, they were able to construct a null variance matrix that accounts for correlations induced by pedigree relationships: $V={\sigma }_b^{2}K+{\sigma }_e^{2}I$. The unknown parameters are replaced with their maximum likelihood estimates, $\widehat{V}={\widehat{\sigma }}_b^{2}K+{\widehat{\sigma }}_e^{2}I$, and this is used in the quadratic association statistic to account for correlations induced by pedigree relationships: Q = (Y – Ŷ)′ V̂^–1 HV̂^–1 (Y – Ŷ). The mixed model provides a framework to separate the variance components into a part attributed to pedigree relationships and a part due to random error. This is especially useful for quantitative traits, but statistically more challenging for binary traits due to complications with generalized linear mixed models [Breslow and Lin, 1995; Lin and Breslow, 1996]. An important assumption of these methods is that the pedigrees were randomly ascertained. Without random sampling, it is critically important to account for the ascertainment process (e.g., sampling according to trait values of some pedigree members) [Epstein et al., 2002]. Without proper adjustment for ascertainment, the estimated variance components are biased, influencing the Q statistic.

Recently, Ionita-Laza et al. [2013] developed a family-based association test (FBAT) for the kernel statistic, following the approach of others [Rabinowitz and Laird, 1999] by specifying the distribution of offspring genotypes conditional on their phenotypes and their parental genotypes (or the sufficient statistic when parental genotypes are not available), treating the offspring genotypes as random. Although this approach is robust to population stratification, there is a high price in terms of loss in power by the conditioning process. For example, moderate-sized pedigrees sampled for multiple affected subjects with older age of onset often have little information for the sufficient statistic because only affected subjects in the lowest generation are available. Furthermore, this approach ignores between-family information, which dramatically decreases power [Ionita-Laza et al., 2007; Van Steen et al., 2005], and makes it impossible to use unrelated controls.

We developed statistical methods to analyze pedigree data for binary traits, which could include unrelated subjects (e.g., multiple cases from pedigrees and unrelated controls), for both the kernel statistic and the burden statistic. To do so, we took the perspective that the ascertainment process for pedigrees enriched for multiple affected subjects is difficult to define and model, leading us to a retrospective view that treats the traits as fixed and the genotypes as random, in contrast to others who consider prospective random sampling, treating the trait as random and the genotypes as fixed. This allowed us to account for complex and undefined ascertainment of pedigrees [Kraft and Thomas, 2000; Schaid et al., 2010], typical of pedigrees selected for linkage studies. We then evaluated the type I error rates of our developed methods by simulations, as well as compared the power of the burden and kernel statistics. Based on our simulations, we propose guidelines on choice of statistic for testing the association of multiple variants with disease status.

Methods

To derive the kernel association statistic and the burden statistic for data that includes related subjects, we take a retrospective view of sampling, with the genotypes considered random. Key aspects of our derivations are the first two moments of the random matrix of genotypes. First consider genotypes measured on the autosomes. We use G to denote an n × m matrix of genotype scores with elements g_il having values of 0, 1, or 2 for the number of minor alleles for the lth marker (l = 1, . . . , m) of the ith subject. Under the null hypothesis of no association of genotypes with traits, the expectation of matrix G has elements E_o[g_il] = 2p_l, where p_l is the minor allele frequency for the lth marker. The null covariance of elements of matrix G, Cov_o(g_ik, g_jl), are influenced by how subjects are related (captured by identity by descent coefficients) and how the genetic markers are correlated within subjects due to linkage disequilibrium. We assume that we can obtain unbiased estimates of the correlations among markers, perhaps from unrelated subjects or through use of estimating equations with related subjects [Olson, 1994]. Let R denote an m × m correlation matrix of genotype scores, with item R_kl for markers k and l, and let Ω denote an n × n matrix of genetic correlations for all n subjects. For autosomes, the elements of Ω are twice the kinship coefficients, Ω_ij = 2ϕ_ij. For outbred pedigrees, the diagonal elements of Ω are 1, but for inbreeding, the diagonal elements are Ω_ii = 1 + h_i, where h_i is the inbreeding coefficient for subject i. For the X chromosome, discussed later, the genetic correlations are not as simple. The covariance of the genotype codes in matrix G for subjects i and j, and markers k and l, can be expressed as

$${\mathrm{Cov}}_o(g_{i,k},g_{j,l})=2R_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)}{\Omega }_{ij}.$$ (1)

A compact way to express the entire covariance structure of G is to stack the columns of the matrix G on top of each other, into an nm × 1 vector, $G_{\mathrm{vec}}^{\prime }=(G_1^{\prime },\dots ,G_m^{\prime })$, so that $V_o\left(G_{\mathrm{vec}}\right)=V_p\otimes \Omega$ where V_p is an m × m matrix with elements $V_{p,kl}=2R_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)}$ and the symbol ⊗ denotes the Kronecker matrix product. When there are no cryptic relationships among subjects from different pedigrees, the matrix Ω is block diagonal, with pedigree-specific kinship matrices filling in the blocks.

Kernel Statistic for Pedigree Data

Let Y′ = (y₁, . . . , y_n) denote a vector of disease status indicators for n subjects, with y_i having values of 1 or 0 for affected and unaffected, respectively. The quadratic kernel association statistic can be expressed as Q = (Y – Ŷ) H(Y – Ŷ), where (Y – Ŷ) is the vector of residuals, after adjusting for covariates, perhaps by use of logistic regression models, and H is an n × n kernel matrix H (assumed to be positive semidefinite). Although the kernel matrix, used to measure genetic similarity between all pairs of subjects, can be formulated in many different ways [Schaid, 2010a, b; Wu et al., 2011], we derive the moments of Q under the null hypothesis of no association based on a weighted linear kernel. The weighted linear kernel has the form H = GWWG′, where G is the matrix of genotype scores, described earlier, and W is a diagonal matrix with weights for each marker along the diagonal. We make this restriction because of the wide use of the linear kernel [Lee et al., 2012a, b; Wu et al., 2011], and the straight-forward way this kernel is amenable to the derivations we present.

By assuming a weighted linear kernel, the elements of the kernel matrix can be expressed as $H_{ij}={\sum }_{l=1}^m{w}_l^2{g}_{il}{g}_{jl}$, where w_l is the weight for marker l, and the quadratic statistic can be expressed as

$$\begin{array}{cc}\hfill Q& =\sum _{l=1}^m{\left[w_l\sum _{i=1}^n(y_i-{\widehat{y}}_i)g_{il}\right]}^2,\hfill \\ \hfill & =Z^{\prime }Z\hfill \end{array}$$

where vector Z has elements $Z_l=w_l{\sum }_{i=1}^n(y_i-{\widehat{y}}_i)g_{il}$. By the central limit theorem, Z has an asymptotic multivariate normal distribution (although we should divide Z by n for this asymptotic result, n would cancel in later derivations so we ignore it here). An advantage of the multivariate normal distribution is that the moments of a quadratic form are well known. That is, if Z ~ N(μ, V_Z), then E [Z′ AZ] = tr(AV_Z) + μ′ Aμ and Var(Z′ AZ) = 2tr(AV_ZAV_Z) + 4μ′ AV_ZAμ, where tr(A) is the trace of matrix A (sum of diagonal elements). We use this to derive the moments of Q under the null hypothesis (using subscript o to denote null hypothesis). The first moment of vector Z has elements $E_o\left[Z_l\right]=w_{l}2p_l{\sum }_{i=1}^n(y_i-{\widehat{y}}_i)=0$. The elements of the covariance matrix of Z can be expressed as

$${\mathrm{Cov}}_o(Z_k,Z_l)=w_k{w}_l\sum _{i=1}^n\sum _{j=1}^n(y_i-{\widehat{y}}_i)(y_j-{\widehat{y}}_j){\mathrm{Cov}}_o(g_{ik},g_{jl}),$$

where Cov_o(g_ik, g_jl) is obtained from expression (1). This makes it clear that Cov_o(Z_k, Z_l) depends on how the genotype scores are correlated, both within subjects (due to linkage disequilibrium) and between subjects (due to kinship).

If the data contains pedigrees of known structure, including pedigrees of size 1 for singleton subjects (e.g., unrelated controls or unrelated cases), then Ω is block-diagonal with block sizes depending on the size of each pedigree. For this situation, the calculation of Cov_o(Z_k, Z_l) simplifies because we only need to sum over the contributions from each pedigree. For example, with D pedigrees, and the size of the dth pedigree denoted n_d,

$${\mathrm{Cov}}_o(Z_k,Z_l)=w_k{w}_l\sum _{d=1}^D\sum _{i=1}^{n_d}\sum _{j=1}^{n_d}(y_i-{\widehat{y}}_i)(y_j-{\widehat{y}}_j)2R_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)}{\Omega }_{ij}.$$

By rearranging terms, this covariance can be expressed as

$${\mathrm{Cov}}_o(Z_k,Z_l)=c_Z{w}_k{w}_l{R}_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)},$$

where

$$c_Z=2\sum _{d=1}^D\sum _{i=1}^{n_d}\sum _{j=1}^{n_d}(y_i-{\widehat{y}}_i)(y_j-{\widehat{y}}_j){\Omega }_{ij}.$$

The factor c_Z depends only on relationships among subjects, and is constant over all markers. This means that the covariance matrix for vector Z can be expressed as V_Z = c_Z * ff′ ○ R, where f is a vector with elements $f_l=w_l\sqrt{p_l(1-p_l)}$, matrix R is the correlation matrix of the m markers, the symbol * denotes multiplication of the scalar c_Z times all elements in the adjacent matrix, and the symbol ○ denotes element-wise matrix multiplication. By computing V_Z in this manner, the factor c_Z only needs to be computed once, making efficient computation of matrix V_Z when the number of markers is large.

Now, because Q = Z′Z, we can use the null moments of Z to determine the null moments of Q: E_o[Q] = tr(V_Z), Var_o(Q) = 2tr(V_ZV_Z). Asymptotically, the Q statistic is distributed as a mixture of independent χ² statistics. Alternatively, the distribution of Q can be approximated by a Satterwaite approximation for the distribution of quadratic forms [Kwee et al., 2008; Liu et al., 2008; Wu et al., 2011]. We estimate the distribution of Q by a scaled χ² distribution with the scale and degrees of freedom estimated by the first two moments of Q. That is, the scale was estimated as δ = Var_o(Q)/(2E_o[Q]), the degrees of freedom as d = 2E_o[Q]²/Var_o(Q), and P-values were computed by assuming $Q_{\text{scaled}}=Q∕\delta \sim {\chi }_d^2$.

Burden Test for Pedigree Data

A burden test can be formulated as follows. For the ith subject, compute a weighted average of the genotype scores, $S_i={\sum }_{l=1}^m{w}_l{g}_{il}$. Under the null hypothesis, these summed scores are not correlated with the trait, so a burden test can be constructed as L′S, where L is a mean-zero function of the trait. For example, as discussed elsewhere [Thornton and McPeek, 2010], the Armitage trend test uses the contrast vector L = (Y – Ȳ). To adjust for covariates, one could use L = (Y – Ŷ), the vector of residuals, after adjusting for covariates. The statistic for this type of burden test is

$$T=\frac{{\left[{(Y-\widehat{Y})}^{\prime }S\right]}^2}{{(Y-\widehat{Y})}^{\prime }{V}_{\mathrm{S}}(Y-\widehat{Y})}.$$

The elements of matrix V_S depend on Cov_o(g_ik, g_jl), resulting in

$\mathrm{Cov}(S_i,S_j)={\Omega }_{ij}{c}_{\mathrm{S}},$

where

$$c_{\mathrm{S}}=\sum _{k=1}^m\sum _{l=1}^m{w}_k{w}_{l}2R_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)}.$$

Because c_S is constant over all pairs of subjects, it needs to be computed only once. This means that V_S = c_SΩ. Hence,

$$T=\frac{{\left[(Y-\widehat{Y}){}^{\prime }S\right]}^2}{c_{\mathrm{S}}{(Y-\widehat{Y})}^{\prime }\Omega (Y-\widehat{Y})}.$$

For large samples, T has an approximate χ² distribution with 1 degree of freedom.

Our proposed T statistic is similar in form to the statistics derived by Thornton [Thornton and McPeek, 2010], yet with some notable differences. First, Thornton's statistic was for a single marker at a time, not a burden test. Second, Thornton et al. considered pedigrees of known structure as well as relationships estimated from large-scale genomic data. This would be simple to do for our proposed statistic, by replacing the genetic correlation matrix Ω with a matrix of estimated relationships. For example, if a large number of genetic markers are available on the subjects, say m markers, then an estimate of the elements of Ω proposed by Thornton et al. is

$${\widehat{\Omega }}_{ij}=\frac{1}{m}\sum _{l=1}^m\frac{(g_{il}-2p_l)(g_{jl}-2p_l)}{2p_l(1-p_l)}.$$

If markers are missing on some subjects, Thornton et al. adjusted this estimate by summing over nonmissing pairs of subjects and dividing by the number of terms in the sum. Alternative ways to estimate ${\widehat{\Omega }}_{ij}$ could be based on estimated probabilities of identical by descent (IBD) sharing, with ${\widehat{\Omega }}_{ij}={\widehat{P}}_2+{\widehat{P}}_1∕2$, where P̂_j is an estimate of the probability of sharing j alleles IBD. Both moment-based [Purcell et al., 2007] and maximum likelihood estimation [Sun et al., 2002; Weir et al., 2006] procedures have been developed. We have found maximum likelihood estimates to be closer to pedigree-based expected IBD probabilities, particularly for third-degree and higher relationships, despite the more time it takes to compute them. Which procedure is best is worthy of future research, but nonetheless this estimated genetic correlation matrix would be a way to account for cryptic relationships for both the kernel association statistic and the burden statistic.

Extensions to the X Chromosome

Because of the asymmetry of males and females with respect to the X chromosome, a number of modifications are needed to extend the kernel and burden association tests to the X chromosome. First, expression (1) for the null covariances of elements in the G matrix changes because of the need to consider the sex of the members of each pair of relatives. Second, because of X chromosome dosage compensation in females, the power for association testing with the X chromosome can be improved by coding males as homozygous females (i.e., 0, 2 instead of 0, 1) [Clayton, 2008; Ozbek, 2012]. To develop our methods in a general way to code male genotypes for the X chromosome, we use d to represent the code for males that carry the minor allele, so that males are coded as 0 or d (d might be 1 or 2), whereas females are coded as 0, 1, or 2 (as for autosomes). Assuming Hardy-Weinberg equilibrium, the null expected value of the code for females is ${\mu }_o^F=2p$, and the null variance for females is ${\nu }_o^F=2p(1-p)$. For males, the null mean is ${\mu }_o^M=dp$ and the null variance is ${\nu }_o^F=d^{2}p(1-p)$. The genetic correlation for the X chromosome for a pair of relatives can be expressed in terms of the probability of sharing 0, 1, or 2 alleles IBD, denoted k_o, k₁, k₂, respectively [Li, 1976]. The genetic correlations are

$${\Omega }_{ij}=\{\begin{array}{cc}{k}_1∕2+k_2\hfill & \text{if female}-\text{female},\hfill \\ k_1\hfill & \text{if male - male},\hfill \\ k_1∕\sqrt{2}\hfill & \text{if female}-\text{male}.\hfill \end{array}\phantom{\}}$$ (2)

Note that the genetic correlation for a pair of females is computed in the same manner as for autosomes, because the kinship coefficient is ϕ_ij = k₁/4 + k₂/2. However, the values of k₁ and k₂ differ between autosomes and the X chromosome. For example, for a pair of outbred sisters, the values for autosomes are k₁ = 0.5 and k₂ = 0.25, yet for the X chromosome the values are k₁ = 0.5 and k₂ = 0.5, because sisters must share the X chromosome from their father. The genetic correlation for a pair of males depends on the probability of sharing 1 allele IBD, which can be nonzero when there are no males in the ancestral line connecting the pair of males. The genetic correlation for a female-male pair also depends on sharing 1 allele IBD, but the divisor of $\sqrt{2}$ originates from dividing the genetic covariance by the square-root of the product of genetic variances, and only females have a factor of 2 for their binomial variance (males have a factor of 1 due to one X chromosome). Note that these genetic correlations do not change if we code males as 0, d, because the genetic covariance (numerator) and the square-root of the product of genetic variances (denominator) both depend on d, which cancels in the correlation. Finally, similar to Thornton et al. [2012], we define the diagonal terms to be Ω_ii = 1 + h_i for females, where h_i is the inbreeding coefficients for females based on pedigree relationships, and Ω_ii = 2 for males regardless of inbred.

With the genetic correlations in expression (2), the elements of the null covariance matrix of the genotype codes can be expressed as follows, for subjects i and j and markers k and l;

$${\mathrm{Cov}}_o(g_{i,k},g_{j,l})=\{\begin{array}{cc}2R_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)}{\Omega }_{ij}\hfill & \text{if female}-\text{female},\hfill \\ d^2{R}_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)}{\Omega }_{ij}\hfill & \text{if male}-\text{male},\hfill \\ d\sqrt{2}{R}_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)}{\Omega }_{ij}\hfill & \text{if female}-\text{male}.\hfill \end{array}\phantom{\}}$$

As for the case of autosomes, the above null covariance matrix of the genetic codes can be used to express the covariance matrix for vector Z as V_Z = c_Z * ff′ ○ R, but now the coefficient c_Z for the X chromosome is,

$$c_Z=\sum _{d=1}^D\sum _{i=1}^{n_d}\sum _{j=1}^{n_d}(y_i-{\stackrel{‒}{y}}_i)(y_j-{\stackrel{‒}{y}}_j){\Omega }_{ij}{\alpha }_{ij},$$

where

$${\alpha }_{ij}=\{\begin{array}{cc}2\hfill & \text{if female}-\text{female},\hfill \\ d^2\hfill & \text{if male}-\text{male},\hfill \\ d\sqrt{2}\hfill & \text{if female}-\text{male}.\hfill \end{array}\phantom{\}}$$

With the above changes for the X chromosome, the other methods to compute the kernel association statistic and its approximate asymptotic distribution remain the same as for autosomes.

For the burden test, the computation of the numerator remains the same, (Y – Ŷ)′S]², but the variance in the denominator, (Y – Ŷ)′V_S(Y – Ŷ) is slightly altered. The matrix V_S has elements

$$\mathrm{Cov}(S_i,S_j)={\alpha }_{ij}{\Omega }_{ij}{c}_{\mathrm{S}},$$

where

$$c_{\mathrm{S}}=\sum _{k=1}^m\sum _{l=1}^m{w}_k{w}_l{R}_{kl}\sqrt{p_k(1-p_k)p_l(1-p_l)}.$$

To extend the above methods to situations for which relationships are estimated from genomic data, we propose replacing the genetic correlation matrix Ω with a matrix of estimated relationships, tailored for the X chromosome. Following ideas from Yang et al. [2011], the estimated correlations take the form

$$\begin{array}{cc}\hfill {\widehat{\Omega }}_{ij}& =\frac{1}{m}\sum _{l=1}^m\frac{(g_{il}-2p_l)(g_{jl}-2p_l)}{2p_l(1-p_l)}\text{for female}-\text{female pair},\hfill \\ \hfill {\widehat{\Omega }}_{ij}& =\frac{1}{m}\sum _{l=1}^m\frac{(g_{il}-p_l)(g_{jl}-p_l)}{p_l(1-p_l)}\text{for male}-\text{male pair},\hfill \\ \hfill {\widehat{\Omega }}_{ij}& =\frac{1}{m}\sum _{l=1}^m\frac{(g_{il}-p_l)(g_{jl}-2p_l)}{\sqrt{2}{p}_l(1-p_l)}\text{for male}-i\text{and female}-j\text{pair}.\hfill \end{array}$$

Simulation Methods

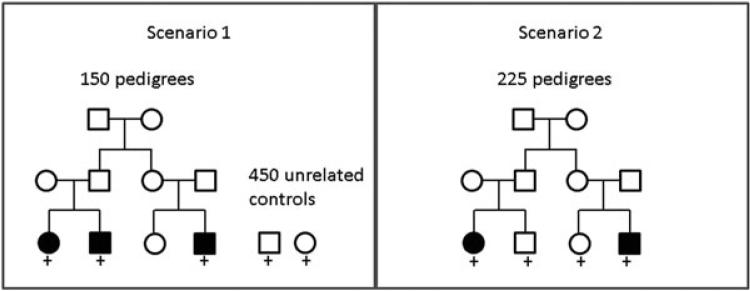
To evaluate the type I error rates and power of our developed statistics, we simulated genotype data for subjects in pedigrees, as well as unrelated control subjects, as illustrated in Figure 1. For scenario 1, we simulated genetic markers for 150 pedigrees, each composed of 10 members, and included in the analyses the 3 affected members in the third generation. These 450 affected subjects were compared with 450 unrelated controls. This scenario represents a common study design that uses multiple cases of older onset disease from pedigrees, and compares them with unrelated controls. In contrast, scenario 2 uses only cases and controls from pedigrees, also from the third generation. These two scenarios represent extremes, whereas in practice cases and controls are likely to be a mix of unrelated and related subjects.

Figure 1.

Scenarios for simulations. Each scenario has 450 affected subjects and 450 unaffected subjects with simulated genotype data. The “+” symbol indicates subjects included in analyses.

To simulate genetic marker data, we first simulated haplotypes, and then randomly sampled haplotypes to assign to founders of pedigrees (or to unrelated controls). The haplotypes were randomly assigned to the nonfounders of pedigrees by Mendelian “gene-dropping,” assuming no recombination within haplotypes, as one would expect for small genomic regions. For simulations under the null of no associations, the populations of haplotypes were the same for pedigrees and unrelated controls (scenario 1). For power evaluations (restricted to scenario 1), separate haplotype populations were created for pedigrees (with three affected cases per pedigree) and for unrelated controls.

Because we anticipated that a number of features of the haplotypes could influence either type I error rates or power, we designed a simulation process that would allow us to rapidly simulate haplotypes, while specifying the number of markers, the minor allele frequencies (MAF), the amount of correlations among the markers, and—for power—the number of risk and protective markers, along with their relative risks. To achieve this, we used the methods of Basu [Basu and Pan 2010], which are based on multivariate normal simulations. For m markers, a latent vector Z of standard normal random variables was simulated. The latent vector was transformed to have a specified correlation structure by X = AZ, where the Cholesky decomposition is given by AA′ = R, and R is an m × m matrix of specified correlation structure. The latent vector X was transformed to a haplotype vector having alleles of 0 or 1 by using quantiles of a standard normal distribution based on the MAF of the genetic markers. For correlation structure, we used a compound symmetric matrix (all off-diagonal correlations equal to common value of ρ). We chose this to evaluate the impact of extremes in linkage disequilibrium, with values of ρ = 0, 0.5, and 0.9. For rare variants, we do not expect large values of ρ, yet we wanted to force extremes to fully test our methods. For the total number of markers, we simulated m = 50 and 100. For MAF, we chose values of MAF = 0.01, 0.05, and 0.10, keeping MAF constant across all m markers for each evaluation. Each simulation was based on 1,000 simulated datasets. For the weights, we used the Madsen-Browning weights [Madsen and Browning, 2009], $w_l=1∕\sqrt{{\widehat{p}}_l(1-{\widehat{p}}_l)}$, where p̂_l was the naïve minor allele frequency estimate based on gene counting. Because p̂_l can be unstable for rare variants, we estimated it by the pool of all simulated data, not just the controls, as suggested by others [Lin and Tang, 2011]. The elements of the correlation matrix, R, were also based on gene-counting, a method that has been shown to provide consistent estimates even when relationships among pedigree members are ignored [Olson, 1994].

To compare the power of the kernel Q statistic vs. the burden T statistic, we simulated a total of m = 50 markers. In one set of simulations, we set the number of risk variants to be 10, 20, or 40, with no protective variants (all risk variants having the same relative risk). In another set of simulations, we set an equal number of risk and protective variants, with risk:protective counts of variants as 5:5, 10:10, and 20:20.

We recognize that our simulations might not reflect real population data, as one might simulate by a coalescent process, such as the popular COSI software [Schaffner et al., 2005]. Our intent, however, was to have more control over parameters that might influence the properties of our statistical tests, such as MAF, number of variants, and correlation structure, primarily because these features differ across the genome, and a population average model of simulation might not reveal critical aspects of our methods.

Results

Simulation results for the type I error are presented in Table 1 for scenario 1 with autosomal markers, which included 150 pedigrees, each with three affected members, and 450 unrelated controls. These results show that both the kernel Q statistic and the burden T statistic control the type I error rates at the nominal levels of 0.05 and 0.01. The type I error rates for scenario 2 with autosomal markers, which used both cases and controls from pedigree data, are presented in Table 2. In general, the empirical type I error rates are close to the nominal, yet with a few exceptions that were slightly above the nominal (for 1,000 simulations, the upper 99th binomial percentile of the nominal type I error rates are 0.067 for α = 0.05 and 0.018 for α = 0.01). The results in Tables 1 and 2 were for equal MAF across all markers. We repeated simulations allowing the MAFs to have an exponential distribution, truncated to the range of 0.01 to 0.1, so that the MAFs were skewed toward small values, as one would expected for rare variants. Similar to results in Tables 1 and 2, the type I error rates were close to the nominal values (results not shown).

Table 1.

Type I error rates for scenario 1

			Type I error rate
			Nominal 0.05		Nominal 0.01
MAF	No. markers	ρ	Q (kernel)	T (burden)	Q (kernel)	T (burden)
0.01	50	0	0.038	0.053	0.004	0.010
		0.5	0.041	0.052	0.012	0.011
		0.9	0.050	0.052	0.021	0.012
	100	0	0.035	0.063	0.006	0.012
		0.5	0.034	0.052	0.009	0.010
		0.9	0.042	0.045	0.006	0.005
0.05	50	0	0.044	0.042	0.006	0.008
		0.5	0.046	0.041	0.013	0.006
		0.9	0.048	0.048	0.011	0.006
	100	0	0.047	0.049	0.011	0.013
		0.5	0.047	0.049	0.015	0.008
		0.9	0.054	0.052	0.013	0.012
0.1	50	0	0.044	0.060	0.007	0.009
		0.5	0.044	0.049	0.015	0.009
		0.9	0.042	0.043	0.010	0.007
	100	0	0.032	0.046	0.006	0.010
		0.5	0.050	0.045	0.022	0.010
		0.9	0.043	0.044	0.006	0.005

Table 2.

Type I error rates for scenario 2

			Type I error rate
			Nominal 0.05		Nominal 0.01
MAF	No. markers	ρ	Q (kernel)	T (burden)	Q (kernel)	T (burden)
0.01	50	0	0.076	0.048	0.019	0.013
		0.5	0.058	0.052	0.019	0.011
		0.9	0.051	0.047	0.014	0.011
	100	0	0.072	0.052	0.021	0.011
		0.5	0.053	0.050	0.012	0.009
		0.9	0.064	0.062	0.026	0.016
0.05	50	0	0.040	0.050	0.007	0.017
		0.5	0.045	0.039	0.014	0.005
		0.9	0.060	0.056	0.024	0.013
	100	0	0.061	0.055	0.012	0.009
		0.5	0.050	0.044	0.016	0.009
		0.9	0.059	0.055	0.013	0.013
0.1	50	0	0.043	0.044	0.012	0.006
		0.5	0.052	0.046	0.018	0.008
		0.9	0.049	0.047	0.016	0.013
	100	0	0.045	0.044	0.009	0.009
		0.5	0.049	0.047	0.020	0.005
		0.9	0.057	0.056	0.014	0.010

For the X chromosome, simulation results for scenario 2 are presented in Table 3. The empirical type I error rates are close to the nominal for the kernel Q statistic for all the different parameter settings. The burden T statistic had empirical type I error rates close to the nominal in most situations, with the exception that it tended to be very conservative when the MAF was not small (e.g., MAF = 0.10), and genetic markers were simulated without correlations (ρ = 0). We suspect that this is caused by sampling errors that cause nonzero estimates of elements of the correlation matrix, making the statistic conservative by overcorrecting for estimated correlations that would approach zero with larger sample sizes. This suspicion was validated by using the assumed correlation (identity matrix, because ρ = 0), in place of the estimated correlation, which resulted in simulated type I error rates near the nominal (results not shown). This suggests that methods to “shrink” small correlations [Wen and Stephens, 2010] might prove useful when correlations are small. Overall, these results suggest that the null distributions of both the kernel Q and burden T statistics are reasonably approximated by our asymptotic derivations.

Table 3.

Type I error rates for scenario 2, X chromosome. Males scored 0 or 2

			Type I error rate
			Nominal 0.05		Nominal 0.01
MAF	No. markers	ρ	Q (kernel)	T (burden)	Q (kernel)	T (burden)
0.01	50	0	0.044	0.040	0.010	0.013
		0.5	0.052	0.047	0.012	0.010
		0.9	0.047	0.046	0.012	0.008
	100	0	0.048	0.033	0.005	0.005
		0.5	0.047	0.052	0.013	0.008
		0.9	0.058	0.061	0.020	0.012
0.05	50	0	0.057	0.018	0.010	0.001
		0.5	0.051	0.047	0.017	0.008
		0.9	0.051	0.049	0.013	0.009
	100	0	0.044	0.011	0.007	0.000
		0.5	0.054	0.050	0.024	0.009
		0.9	0.053	0.051	0.009	0.006
0.1	50	0	0.044	0.006	0.004	0.000
		0.5	0.045	0.034	0.018	0.012
		0.9	0.054	0.052	0.014	0.008
	100	0	0.045	0.000	0.004	0.000
		0.5	0.057	0.045	0.024	0.013
		0.9	0.041	0.039	0.012	0.007

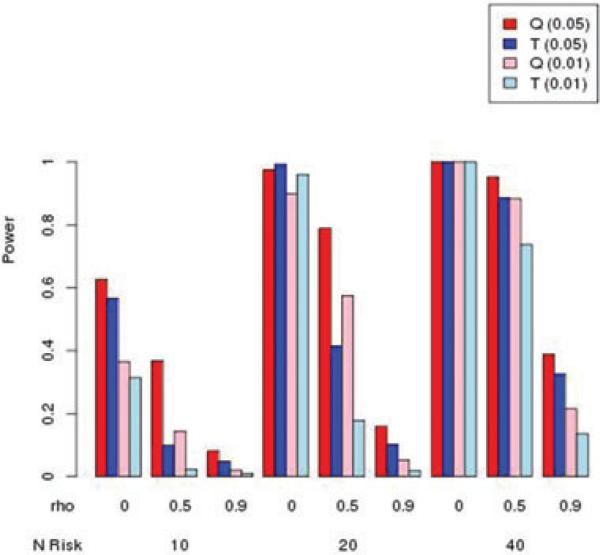
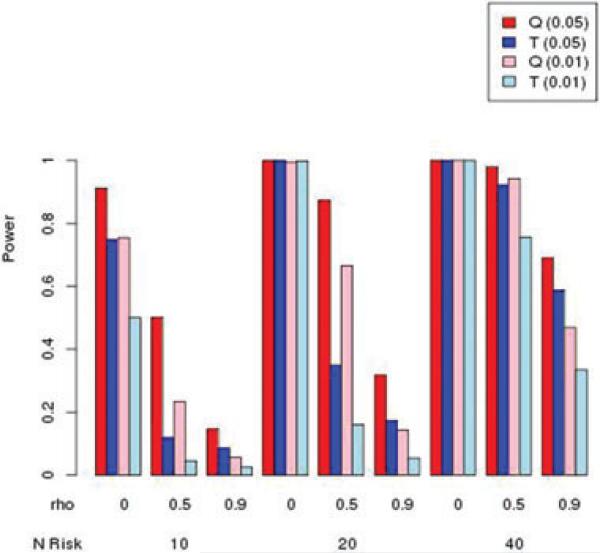
Simulation results for power for autosomal markers are summarized in Figures 2–5. For each of these figures, we present the Q and T statistics, each evaluated at nominal type I error rates of 0.05 and 0.01. Each figure shows simulations for different values of ρ = 0, 0.5, and 0.9, as well as the number of risk and protective variants. In Figure 2, the results for only risk variants with MAF of 0.01, it can be seen that power increases with the number of risk variants, but decreases as correlation ρ increases. Figure 3 illustrates similar patterns, for MAF = 0.05. Surprisingly, the burden T statistic has little power advantage over the kernel Q test, even as the number of risk variants increases.

Figure 2.

Simulated power for MAF = 0.01 with risk variants having relative risk of 2, and no protective variants. Nominal type I error rate in parentheses.

Figure 5.

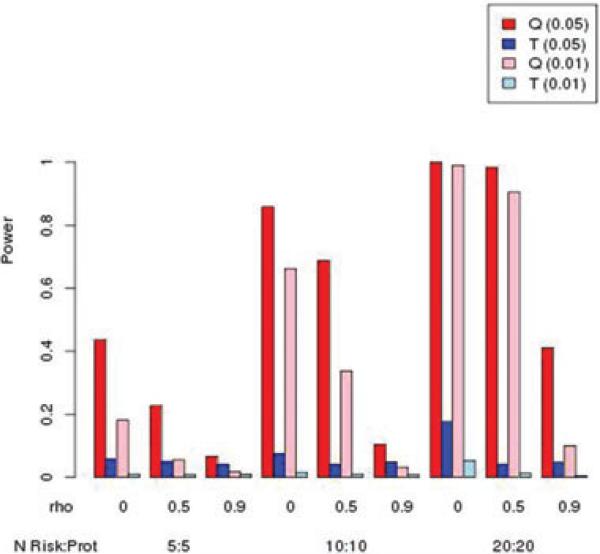
Simulated power for MAF = 0.05 with an equal mix of risk:protective variants. Relative risk for risk variants was 1.5, and relative risk for protective variants was 0.67. Nominal type I error rate in parentheses.

Figure 3.

Simulated power for MAF = 0.05 with risk variants having relative risk of 1.5, and no protective variants. Nominal type I error rate in parentheses.

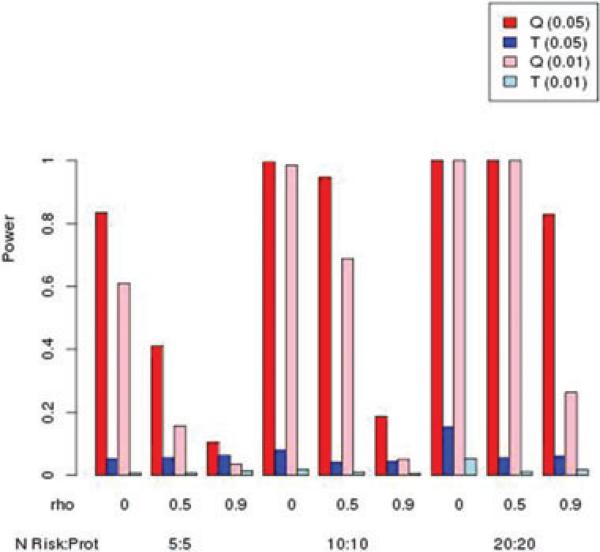
Figures 4 and 5 illustrate power when there are an equal number of risk and protective variants. Not surprisingly, the burden T statistic performs poorly, due to the canceling of effects in the weighted sum of variants per subject. Because the magnitude of relative risk for the protective variants was set as the inverse of the relative risk for the risk variants, we can compare Figures 4 and 5 with Figures 2 and 3, to see that power results are similar for the kernel Q statistic, indicating that the direction of effect has little impact on power, as expected.

Figure 4.

Simulated power for MAF = 0.01 with an equal mix of risk:protective variants. Relative risk for risk variants was 2, and relative risk for protective variants was 0.5. Nominal type I error rate in parentheses.

Discussion

Our proposed methods to evaluate the association of multiple genetic variants with disease status when subjects are related provide a sound basis for analyzing pedigree data, with particular emphasis on rare genetic variants that benefit from analyzing groups of variants, instead of individual variants. Because our statistical methods are simple to compute, and the nominal type I error rates are reasonably approximated by our developed methods, it is feasible to use the proposed statistics on large scale data, such as whole exome sequence data.

A critical feature of our approach was viewing the sample collection as a retrospective study, which means conditioning on phenotypes, treating the genotype data random. This approach seems reasonable for pedigrees sampled because of multiple affected members, such as those collected for past linkage studies. This overcomes the problem of modeling the ascertainment process, which would be particularly challenging for highly enriched pedigrees. Although conditioning on traits in a retrospective likelihood tends to be less efficient than treating traits as random variables in a prospective likelihood, there tends to be little loss in efficiency for binary traits [Kraft and Thomas, 2000]. In principal, this approach could be extended to quantitative traits, by conditioning on the quantitative traits of all pedigree members. This might be of value when pedigrees are highly selected according to quantitative traits of the pedigree members, or when subjects to sequence are sampled according to extreme phenotypes to increase power to detect rare variants [Barnett et al., 2012].

Through simulations, we showed that the linear weighted kernel Q statistic had more power than the weighted burden T statistic, even in situations that would seem to favor the burden statistic. This suggests that the kernel Q statistic would be the method of choice. An advantage of the weighted kernel is that a wide variety of weights could be used, such as those based on the β density function or based on functional information [Wu et al., 2011]. Although our methods were based on additive allele dosage, scoring genotypes as 0, 1, and 2 for the number of minor alleles, it is possible to generalize the scoring, such as for dominant effects (scores of 0, 1, and 1) or for recessive effects (scores of 0, 0, and 1). However, it can be shown that the genetic correlations for dominant and recessive scoring are no longer as simple as twice the kinship coefficient (for autosomes), but rather depend on the minor allele frequencies. Furthermore, because our methods were proposed to analyze multiple genetic markers for a gene, it is not clear that scoring all markers as dominant, or all as recessive, or even a mix of these scores, would offer much advantage over the simple additive scoring for all markers.

We chose a linear kernel, which is rapid to compute and facilitated our derivations. It might be worthwhile to evaluate other types of kernels (e.g., Gaussian kernels, or a kernel-based local identical by descent for the evaluated gene), although nonlinear kernels complicate the computations of the moments of the Q statistic. To illustrate the complications, consider the popular Gaussian radial basis kernel [Schaid, 2010a], which has the form $H_{ij}=\exp \{-\frac{1}{{\sigma }^2}{\sum }_{l=1}^m{(g_{il}-g_{jl})}^2\}$, where σ² is a specified scale parameter that governs how rapid the kernel function diminishes to 0. An approach to derive the moments of Q would be to use Taylor-series expansion to “linearize” the kernel into a polynomial function of the genotype scores. Expanding this function about 0 (assuming that the scale parameter σ² is chosen large enough), this kernel can be approximated as $H_{ij}=1-\frac{1}{{\sigma }^2}{\sum }_{l=1}^m{(g_{il}-g_{jl})}^2$. With this in hand, the Q statistic can be expressed in terms of g_il, $g_{il}^2$, g_jl, and $g_{jl}^2$, and product terms, g_ilg_jl. The covariances among these pieces can be determined in a manner similar to our derivations for Cov_o(g_i,k, g_j,l), but requiring third and fourth moments, because of terms like $g_{il}^2$. The third and fourth null moments for pedigree data can be challenging to compute, because they no longer depend solely on kinship coefficients. Rather, pedigree-based simulations by “gene-dropping” would likely be required. At this computational cost, it would seem better to use gene dropping (including random assignment of alleles to unrelated controls) to compute P-values for nonlinear kernels. For these reasons, and the computational speed of the weighted linear kernel, we favored the linear kernel.