Abstract
Tumor hypoxia develops heterogeneously and affects radiation sensitivity and development of metastases. Prognostic information derived from the in vivo characterisation of the spatial distribution of hypoxic areas in solid tumors can be of value for radiation therapy planning and for monitoring early treatment response. Tumor hypoxia is caused by an imbalance between the supply and consumption of oxygen. Tumor oxygen supply is inherently linked to its vasculature and perfusion which can be evaluated by dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) using the contrast agent Gd-DTPA. Thus we hypothesize that DCE-MRI data may provide surrogate information regarding tumor hypoxia. In this study, DCE-MRI data from a rat prostate tumor model were analysed with a Gaussian Mixture Model (GMM)-based classification to identify perfused, hypoxic, and necrotic areas for a total of ten tumor slices from six rats, of which one slice was used as training data for GMM classifications. The results of pattern recognition analyses were validated by comparison to corresponding Akep maps defining the perfused area (0.84±0.09 overlap), hematoxylin/eosin (H&E) stained tissue sections defining necrosis (0.64±0.15 overlap), and pimonidazole-stained sections defining hypoxia (0.72±0.17 overlap), respectively. Our preliminary data indicate the feasibility of a GMM-based classification to identify tumor hypoxia, necrosis, and perfusion/permeability from non-invasively acquired, in vivo DCE-MRI data alone, possibly obviating the need for invasive procedures, such as biopsies, or exposure to radioactivity, such as in PET exams.
Keywords: DCE-MRI, hypoxia, Gaussian mixture model, preclinical prostate model, tumor microenvironments, radiation therapy
INTRODUCTION
In vivo imaging of the tumor microenvironment provides critical and detailed prognostic information about the response to treatment. Non-invasive methods for the detection and localisation of hypoxic areas in tumors are of great interest, as hypoxia is related to prognostic outcome due to the resistance of these cancer cells to treatment [1–3] and their inherently poorer outcome. Thus, non-invasive imaging of the tumor microenvironment could provide critical information for treatment planning, and facilitates the early assessment of treatment response before actual tumor shrinkage occurs.
A conventional method for detecting tumor hypoxia involves the invasive insertion of polarographic electrodes to measure the partial pressure of oxygen (pO2). The development of non-invasive hypoxia imaging methods is an active research area, as these methods will enable total volume coverage as well as longitudinal studies of tumor oxygenation before and after treatment [4–14]. Positron Emission Tomography (PET) using 18F-fluoromisonidazole (18F-Fmiso) is a potential method to detect tumor hypoxia, as 18F-Fmiso binds selectively to hypoxic regions, and its uptake in cells can be detected with in vivo PET [15–17]. A recent study in an animal tumor models suggests that the initial 18F-Fmiso uptake may be dominated by perfusion of the tumor, necessitating the dynamic monitoring of uptake for accurate assessment of tumor hypoxia [18, 19]. However, the longer acquisition time required for dynamic monitoring of tracer uptake (when compared to static image acquisition) is a hindrance for practical application in the clinic along with poorer image resolution compared to MRI. Measurements of pO2 using electron paramagnetic imaging and Overhauser-enhanced MRI are other candidate methods [20–23]; the former requires a high frequency microwave source, has low resolution, requires a magnet of appropriate size and field strength and a injection of an expensive EPR tracer, which may limit its clinical applicability.
Tumor hypoxia is caused by an imbalance between the supply and the consumption of oxygen [24]. Therefore, the structure and functionality of tumor vasculature as well as the degree of angiogenesis can be significant factors in the development of hypoxia in solid tumors [25–27]. Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is used clinically and preclinically to investigate leaky tumor vasculature [28, 29]. This technique enables the dynamic measurement of signal changes after bolus administration of a T1 contrast agent (CA). The T1 values of tissue water decrease when the paramagnetic CA, such as Gd-DTPA, leaks through the vessel wall into the interstitium. The CA diffuses at a faster rate and in larger concentrations in well-perfused permeable regions. Thus, the MR image displays a characteristic time signal intensity change related to the contrast agent concentration in the tumor tissue. The DCE-MRI data measures tumor vasculature/perfusion and permeability and can be acquired in ~10 min without the need for ionizing radiation.
Recently, a combination of in vivo DCE-MRI, 18F-Fmiso PET and ex vivo immunohistochemical and histological information validated that the Akep value, which is a measure of tumor perfusion/permeability derived from DCE-MRI data analysis, is able to distinguish well-perfused from necrotic tumor tissue [19]. However, the in vivo identification of hypoxic areas required the additional acquisition of dynamic 18F-Fmiso PET [19] in the animal model. An inverse relationship between the hypoxic fraction of a tumor and its microvessel density has been shown in studies using histologically-based methods [30, 31]. In a rat prostate cancer model, a negative correlation between the perfusion parameter (Akep) obtained from DCE-MRI data and the tumoral uptake of the hypoxia PET tracer 18F-Fmiso has also been shown [19]. Thus, DCE-MRI may have the potential to provide valid surrogate information regarding tumor hypoxia and may complement existing dynamic PET methods.
Conventional interpretations of uptake curves in DCE-MRI are based on various parameters obtained from multi-parameter, non-linear fittings of contrast agent uptake curves. Fitted parameters, such as tumor perfusion, microvascular vessel wall permeability and extravascular-extracellular volume fraction are obtained from fittings using pharmacokinetic models [32–37]. Pharmacokinetic models are advantageous because they enable the fitted parameters to be assigned to model-based physiological parameters and offer valuable information regarding tumor microenvironments. However, the non-linear fittings of multiple parameters based on a specific model may be limited by underlying assumptions, or may restrict the ability to relate a voxel-specific contrast uptake curve in an in vivo DCE-MRI voxel to its characteristic tumor microenvironment. The latter is probably because thresholding a specific, model-based parameter is limited in differentiating the tumor microenvironments when the parameter values between tumor microenvironments overlap significantly. In addition, the requirement for an arterial input function (AIF) in various models is demanding, as reliable AIF measurement is well known to be challenging both clinically and preclinically [38–40].
In this study, we used a Gaussian Mixture Model (GMM)-based classification scheme to identify the diverse tumor microenvironments from the time-signal uptake curves of individual DCE-MRI voxels. The advantage of this approach is that it is simple and data-driven which does not involve the complicated physical modelings, those are typically used in quantitative analyses of DCE-MRI data. Heterogeneous uptake curves in DCE-MRI datasets were classified into three representative categories based on GMM classification. Each category was then assigned to a specific tumor microenvironment and maps of spatially resolved regions featuring perfused, hypoxic and necrotic areas were generated. The results were compared to previously obtained results in which necrotic and hypoxic areas were identified respectively from hematoxylin/eosin (H&E)- and pimonidazole-stained tissue sections, while well-perfused areas were identified from Akep maps of in vivo DCE-MRI data [19, 33].
This paper reports the feasibility of the in vivo identification of tumor microenvironments, including but not limited to areas of hypoxia, based on the GMM classification of voxel-wise DCE-MRI uptake curves.
Materials and Methods
A. Tumor model, in vivo DCE-MRI, and ex vivo Tissue processing
The experiments were performed as described in detail previously[19].
Briefly, animal studies were carried out in compliance with protocols approved by the Institutional Animal Care and Use Committee of Memorial Sloan-Kettering Cancer Center (MSKCC). The R3327-AT rat prostate cancer cell line was cultured in DME (Dulbecco’s Modified Eagle’s) medium, supplemented with penicillin and streptomycin (1%), under sterile conditions at 37°C in a humidified atmosphere (95% air and 5% CO2). The cells were harvested when they reached around 70% confluence. A concentration of 2×106 per 0.1 mL was injected subcutaneously in the right hind leg of 6- to 8-week-old Copenhagen rats.
When the tumor size reached 500–2500 mm3, the rat tail-vein was catheterized to facilitate the i.v. injection of the contrast agent (CA) Gd-DTPA (0.2 mM Gd/kg, 0.045ml/s, 10~12s injection time, Magnevist; Berlex Laboratories, Inc., Wayne, NJ) for the DCE-MRI study. The animal was anesthetized with isoflurane (2.5%) mixed in with oxygen and placed in the magnet with the tumor-bearing leg positioned in the MR coil, as previously described[19].
A series of T1-weighted, i.e., fast low-angle shot (FLASH), MR images were acquired to monitor the rapid increase in signal intensity due to the shortened T1, caused by the uptake of paramagnetic Gd-DTPA into the extracellular-extravascular space (EES) of the tumor. DCE-MRI data were acquired using the FLASH sequence, with the repetition interval (TR) = 41.775 ms, echo time (TE) = 3.1 ms, number of repetitions (NR) = 256, number of averages (NA) = 4, slice thickness (ST) = 0.79 mm, field of view (FOV) = 3.5 cm × 3.5 cm, matrix size = 128 × 128, flip angle = 30°, resulting in an in-plane resolution of 273 μm × 273 μm and a temporal resolution of 5.347s [19]. T2-weighted MR images (RARE, TR = 2000 milliseconds, TE = 30 milliseconds, NR = 1, NA = 1, ST = 0.79 mm, FOV = 3.5 cm x 3.5 cm, matrix = 128 × 128) were acquired for the boundary visualization of the tumor.
After the in vivo DCE-MRI scan, the hypoxia marker pimonidazole was injected i.v. and the tumor was excised, embedded in OCT (Tissue-Tek O.C.T. Compound, Sakura Finetek U.S.A., Inc., Torrance, CA) and frozen at −80°C until processed [19].
The frozen OCT-embedded tumors were sectioned on a Microm HM500 cryostat microtome (Microm International GmbH, Walldorf, Germany) into 8-μm thick sections at 0.79-mm increments across the tumor using the fiduciary markers to align the tissue sections with the in vivo MR image slices of the tumor [19]. Tissue sections were stained with a fluoroscein isothiocyanate conjugated anti-pimonidazole monoclonal antibody (Chemicon, Temecula, CA) as well as Hematoxylin and Eosin (H&E) [19] Images of stained tumor sections were acquired using an Olympus BX40 fluorescence microscope (Olympus, America, Inc., Melville, NY) [19].
To validate the ability of classified GMM mixtures of DCE-MRI uptake curves to characterize different tumor microenvironments, necrotic, hypoxic, and perfused regions were identified using relative thresholding on tissue sections (necrotic, hypoxic) and in vivo Akep maps (perfused), respectively.
Briefly, pimonidazole-positive (hypoxic) areas were selected by setting the threshold at 5–6 fold of the background level (necrotic area) and a binary hypoxia mask (black/white) was generated from the RGB-converted image of pimonidazole-stained section. For necrotic area, the image of H&E stain was also converted to RGB and a separate binary mask for tumor necrosis was generated by thresholding elevated intensity area in the same manner, where the level of the background staining intensity was set based on levels in well-perfused areas. Perfused tumor areas were identified in vivo from the dynamic build-up curves in the DCE-MR images that were fitted for each voxel using the Hoffmann model [33]. The Hoffmann model is a two-compartment model that assumes a linear relationship between the MR signal and the concentration of the CA in the tissue. In the model, an amplitude (A) corresponds to the relative signal enhancement while the exchange rate (kep) corresponds to the velocity of signal increase. The magnitude of Akep is proportional to the slope of the MR signal over time and thus reflects the vascular flow or perfusion and vascular permeability of the tumor tissue. Akep values were calculated for each individual voxel from the dynamic build-up curves. Binary perfusion masks were obtained for each tumor slice by setting a threshold of the corresponding Akep maps. Voxels with Akep values larger than ~0.006 (1/s) were defined as well-perfused regions of the tumor area, and assigned to 1 in the binary perfusion masks, otherwise voxels were considered ill-perfused and assigned to 0 in the binary perfusion masks.
B. GMM classification of DCE-MRI data
The GMM classification was applied to the analysis of DCE-MRI uptake curves with the aim of separating tumor microenvironments based on the characteristics of contrast agent uptake curves alone without having to revert to ex vivo analyses.
A GMM classification is a well-known statistical tool for approximating any arbitrary probability density function (pdf) by a weighted sum of multiple Gaussian densities with several parameters, such as the mean vector, covariance matrix, and mixture weight [41–44]. Let M be the number of groups (classes) in the data. The target mixture density function can be defined as
| (1) |
where x⃗ is a D-dimensional measurement or observation vector, wi, i=1,…, M are the mixture weights that satisfy 0 ≤ wi ≤1 and , and Pi,(x⃗) is a D-variate Gaussian density for the ith mixture as given by the equation:
| (2) |
where μ⃗i is the ith mean vector and Ci is the ith covariance matrix of size M × M. The complete Gaussian mixture density function is parameterised by the mixture weights, mean vectors and covariance matrices from all Gaussian densities, and is represented by the notation:
| (3) |
This set of parameters, i.e., λ, are estimated for the GMM-based classification by the expectation-maximisation (EM) algorithm [45], which is further explained in the Appendix section.
Here, using a representative tumor (training tumor 3, slice 1), we tested first the applicability of the GMM classification system to the heterogeneous DCE-MRI contrast uptake curves resulting in a set of Gaussian component probability density functions (pdfs) categorizing tumoral contrast uptake behavior. The analysis of the training tumor using vector quantization and the EM algorithm (Appendix) led to multiple pdfs. This set of pdfs was assigned to either the hypoxia, perfused, or necrotic tumor area based on the respective binary maps created from pimonidazole, Akep and H&E maps, respectively, and an assignment rule was developed. To reduce the computation time for the GMM classification as well as the observation errors, the images of every five time points were averaged for the entire time resolved data points (256 time points), reducing the time resolution from 5.347 s to 26.735 s per image set (4 slices). Signal time curves were corrected for baseline signal intensity before CA injection, as described previously[19]. For optimal GMM categorization, the baseline-corrected signal time curves were normalized using SN = (S−Smin/Smax−Smin), with Smin defining the minimum signal, Smax the maximum signal intensity value within each voxel, and S the signal intensity value. Starting at time of CA injection, the normalized signal time curves (SN(t)) served as multi-dimensional input vector to GMM and optimized classification was achieved.
Based on the training data set, the contrast uptake curves for each of the remaining tumors were classified into different mixtures and attributed to its respective tumor microenvironment using the developed assignment rule described in detail in the result section. Finally, spatially-resolved, GMM classified tumor microenvironments from DCE-MRI data were compared directly to corresponding masks of perfused, hypoxic and necrotic areas obtained from the analysis of Akep, pimonidazole, and H&E maps used as the ‘gold- standard’.
Results
A T2-weighted MR image of a tumor slice and representative, regional contrast agent uptake curves that illustrate the spatial heterogeneity of CA uptake in tumors are shown in Fig. 1. (The signal (S) is normalized with respect to the maximum signal (Smax) in the slice). The variations in the contrast agent uptake across the solid tumor indicate the presence of a diversity of tumor microenvironments, which are not readily distinguishable in the T2-weighted 1H MR image alone. Specifically, in region (a), the small signal increase resulting from the minimal uptake of CA is characteristic for tumor necrosis [46]. Region (b) shows delayed CA uptake signal build-up due to reduced vascularisation and permeability, and is likely to be a hypoxic area. Region (c) shows a fast signal increase with a fast contrast agent washout, representing a well-perfused area.
Fig. 1.
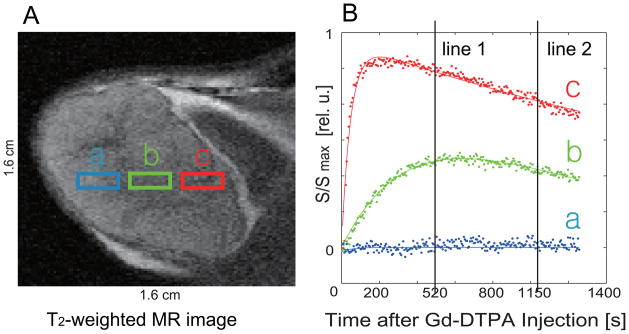
(A) T2 – weighted MR image of a tumor slice. The color boxes marked with (a), (b) and (c) depict three different regions of tumor. (B) Representative uptake curves from voxels within the three regions (a), (b), and (c) in (A). Each curve was normalized with the maximum signal within the image slice. The vertical lines mark 2 time points on the signal curves for the three representative, normalized CA uptake curves.
A. Number of classifiers and Gaussian density functions
The normalized signal SN(t) at two different time points (vertical lines 1 and 2 in Fig 1B) for all the voxels in a tumor slice after the injection of Gd-DTPA are shown in Fig. 2C. Each curve was normalized within tissue segmentation, and thus, the signals of necrotic areas appear to be centered around 0.5. Perfused (red,’x’), hypoxic (green,’o’) and necrotic (blue.’+’) areas were selected from the analysis of Akep, pimonidazole, and H&E maps, as described in the Materials and Methods and corresponding masks were applied to the DCE-MRI data to generate the scatterplot and histograms shown in Fig. 2. The histograms of SN(t) at these two time points after CA injection are shown in Fig. 2A and 2B, respectively. The necrotic voxels (blue points) show low signal intensities for both the earlier and later time point (520 s and 1150 s respectively). Two time points were chosen to reflect the rising and falling region of dynamic data. The green points (hypoxic voxels) show an intermediate signal enhancement at 520 s after CA injection with no significant washout of the CA detected at the later time point, i.e. 1150 s. The red points (perfused voxels) show the highest signal intensity at the earlier time point and decreasing signal intensity (representing CA washout) at 1150 s. Three clusters with some overlap are observed in both the scatterplot and the histograms. The identified clusters are of skewed and elliptical shapes with corresponding skewed histograms as shown in Fig. 2C. The skewed elliptical data distributions in each histogram can be approximated by the mixing of a minimum of two bivariate Gaussian pdfs that are weighted to accommodate their respective contributions to fit the corresponding histogram. The asymmetry in the histograms leading to the overlap of histograms representative of the three different tumor microenvironments implies that there are voxels which have predominantly one feature (e.g. necrosis) and still a measurable contribution from a second feature (e.g. hypoxia) resulting in vivo in a volume-averaged CA uptake curve.
Fig. 2.
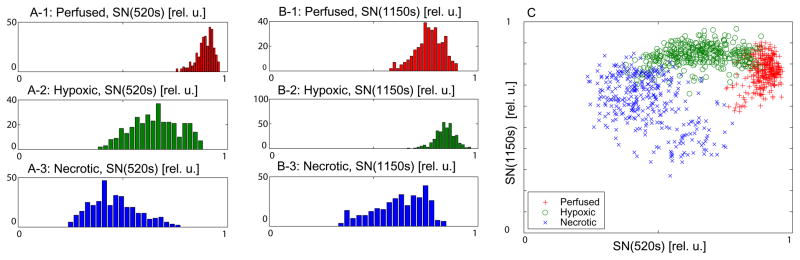
(A) and (B) show the histogram distributions of normalized image intensities in perfused, hypoxic, and necrotic regions at two different time points (520 s, 1150 s), respectively. The assignments of each region as necrotic, hypoxic, or well-perfused has been based on masks generated from the corresponding histology slices and Akep map as described in the method section. (C) 2D scatter-plot of signal magnitude at two time points, i.e., 520 s and 1150 s after the injection of the contrast agent. Each curve was normalized within tissue segmentation, and thus, the signals of necrotic area appear to be centered around 0.5.
Initially, all the DCE-MRI data were normalized for each voxel and classified using a mixture of 3,4, and 6 Gaussian pdfs, respectively. Having 6 pdfs captured transitional pattern between three representative pattern, whereas 3 and 4 pdfs showed many outliers in each classified mixture. Based on these observations, DCE-MRI data were classified using a mixture of 6 pdfs to model the boundary data distributions between neighboring classes, for GMM study presented here.
B. Assignment rule of classifiers to tumor microenvironment
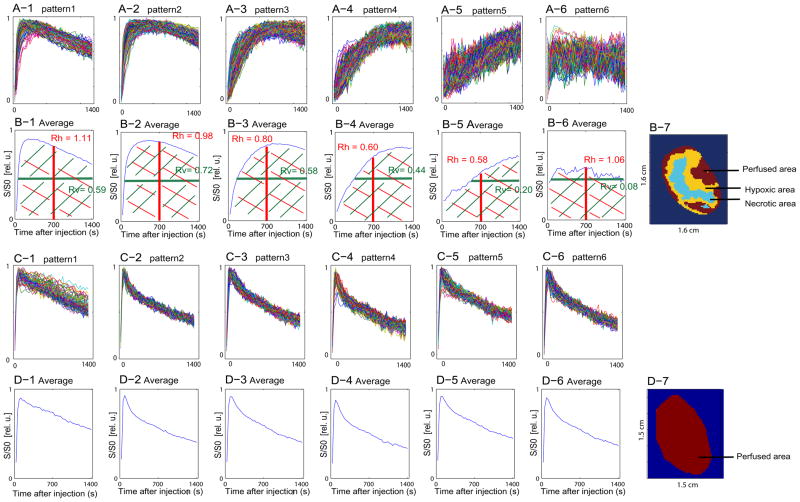
The results of the GMM-based classification using six pdfs are summarized for two representative slices of two separate tumors in Fig. 3. One tumor slice represents a heterogenous tumor with hypoxic, necrotic and well-vascularized areas (Fig. 3A, B), while the second tumor slice is from a homogeneous, well-vascularized tumor (Fig. 3C, D). While the heterogenous tumor was used to develop the assignment rule, the homogeneous tumor demonstrates the validity of the model for tumors presenting only one of the three micro-environmental features.
Fig. 3.
(A-1)~ (A-6) Classified uptake curves of each image voxel in a heterogeneous tumor slice. (B-1)~ (B-6) Average uptake curves for each pattern in A-1 to A-6, respectively. (B-7) Corresponding pattern mask as a result of GMM-classification for this heterogeneous tumor slice (same tumor slice as depicted in Fig. 1, 2). (C-1)~ (C-6) Classified uptake curves of each image voxel in a well-perfused, homogeneous tumor slice. (D-1)~ (D-6) Average uptake curves for each pattern in C-1 to C-6, respectively. (D-7) Pattern mask as a result of classification of homogeneous tumor. Each curve was normalized within tissue segmentation, and thus the signals of necrotic area appear to be centered around 0.5.
In these tumors, the signal time curve for each voxel is assigned to one of six patterns (Fig. 3A, C) using the GMM-based classification. For each pattern (1–6), the corresponding average signal time curves were calculated from the mean vector of the respective Gaussian component density (Fig. 3B, D). For the assignment of each pattern to one of the three tumor micro-environmental features, i.e., perfused, hypoxic or necrotic areas, we developed an assignment rule based on the area under the mean signal time curve (AUC). The AUC was divided into 4 quadrants with the lines set at 50% of total time after injection (Fig. 3B-1, red line) and 50% of Smax (Fig. 3B-1, green line). The ratio of the area of the two left quadrants to the two right quadrants is defined as Rh, while the ratio of the area of the two upper quadrants to the two lower quadrants is defined as Rv.
Predominantly perfused areas in the tumor are characterized by a fast uptake of the contrast agent followed by a fast washout (Fig. 3B-1, B-2), resulting in Rh values close to or larger than 1. In hypoxic tissues induced by poor perfusion, the CA uptake is slower and demonstrates very little washout of the CA during the acquisition time because of poor perfusion (Fig. 3B-3, B-4), resulting in lower Rh values than for well-perfused areas.
Necrotic areas are typically characterized by no CA uptake (Fig. 3B-6) or slowly increasing CA uptake (Fig. 3B-5), the first resulting in Rh values close to 1, the latter in Rh values below 0.5 (i.e., when the area of the left two quadrants is smaller than that of the right two quadrants by a factor of 2 or more). Necrotic areas characterized by a lack of CA uptake (Fig. 3B-6) cannot be distinguished from perfused areas by the Rh value alone. However in such cases, SN(t) does not change significantly over time, resulting in low Rv values, while perfused and hypoxic areas with their SN(t) changing over time demonstrate larger Rv values.
Based on these characteristics, we categorized each voxel depending on its Rh or Rv value of the corresponding average signal time curve as summarized in Table 1.
TABLE 1.
The criteria of classification of DCE-MRI data
| Rh | Rv | |
|---|---|---|
| Perfused voxel | Rh > 0.9 | Rv > 0.2 |
| Hypoxic voxel | 0.5 ≤ Rh ≤ 0.9 | Rv > 0.2 |
| Necrotic voxel | Rh < 0.5 or | Rv < 0.2 |
Based on Table 1, the patterns in Fig. 3B-1 and 3B-2 are classified as being perfused, patterns in 3B-3 and 3B-4 as being hypoxic, and patterns in Fig. 3B-5 and 3B-6 as being necrotic. The resulting spatial distribution of the perfused (red), hypoxic (yellow), and necrotic (blue) areas are depicted for the heterogeneous tumor in Fig. 3B-7.
The specificity of the assignment rule to identify correctly the predominant tumor characteristics for tumors presenting only one of the three micro-environmental features is demonstrated on a well-perfused tumor (Fig. 3C, D). Here the GMM analysis with six pdfs resulted in six similar patterns that all fell into the same micro-environmental category (perfused voxels) and the resulting spatial distribution is shown in Fig. 3D-7.
C. Validation & Specificity of GMM-based classification of the tumor microenvironment
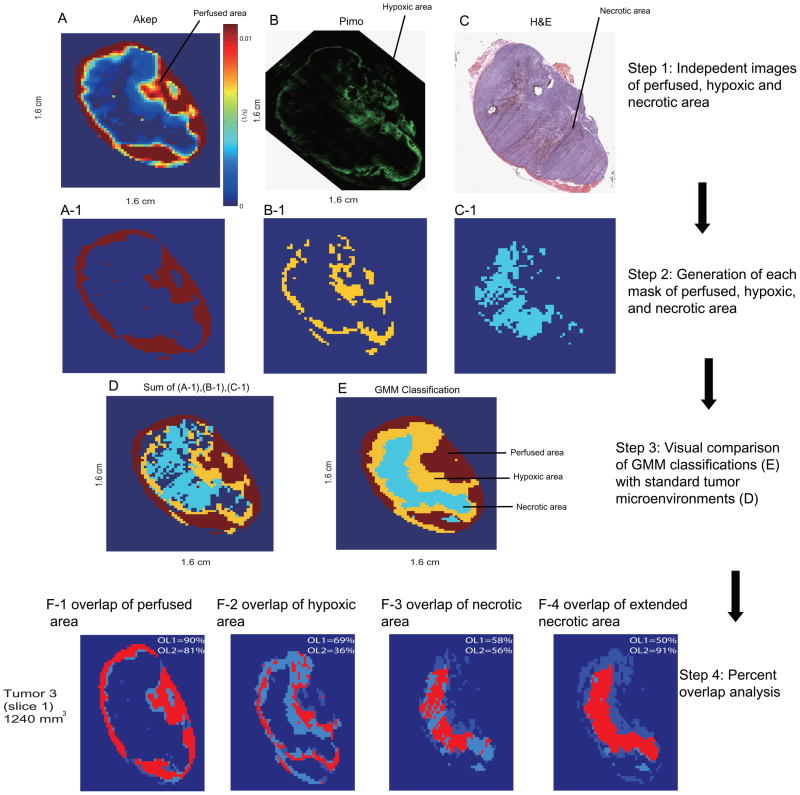
In Fig. 4 A-C, Akep, pimonidazole, and H&E maps are shown for the same heterogeneous tumor slice as shown in Fig. 1, 2, and 3A, 3B (Same slice is shown for the consistency of the procedure description in this work). This slice data has been presented previously [47] and are reproduced with permission for the new analyses. Based on the relative threshold method described in Materials & Methods, perfused, hypoxic, and necrotic areas were identified and the resulting spatial distributions are displayed in Fig. 4A-1,4B-1 and 4C-1. An overlay image combining the spatial distributions obtained by thresholding is shown in Fig. 4D. For comparison, the spatial distributions of the perfused, hypoxic, and necrotic areas identified from the GMM analysis are displayed again in Fig. 4E, and which resemble qualitatively areas identified by masks from the corresponding immunohistochemistry and histology slices.
Fig. 4.
(A) Akep map from DCE-MRI with, corresponding (B) pimonidazole and (C) H&E images. (D) The combined mask of well-perfused(red), hypoxic(yellow) and necrotic(blue) areas of this tumor slice obtained based on the binary masks from (A-1), (B-1), and (C-1). (E) displays for the same tumor slice the spatial distribution of perfused, hypoxic, and necrotic areas obtained from GMM-categorization of DCE-MRI uptake curves. An overlap analysis between each compartmentation from GMM-classified and threshold methods is shown for perfused (F-1), hypoxic (F-2), necrotic (F-3) and extended necrotic (F-4) areas. For each segmentation: OL1=(number of overlapping voxels)/(total number of thresholded voxels from standard images). OL2=(number of overlapping voxels)/(total number of GMM-classified voxels) Data (A–C) are re-derived from [47] with permission from Neoplasia.
To evaluate the efficacy of the GMM-based classification, we compared the spatial overlap between perfused, hypoxic, and necrotic regions identified by the GMM-based classification with the corresponding spatial distribution identified from ‘standard’ methods, i.e. from Akep, pimonidazole, and H&E images (Figs. 4F-1,4F-2 and 4F-3). The percent overlaps between DCE-GMM classifications and standard (thresholding) methods have been calculated for each segmentation, i.e. perfusion, hypoxia and necrosis as follows: The number of overlapping voxels for each segmentation was divided by the total number of voxels covering the segmented area either obtained by thresholding from ‘standard images’ (overlap 1, OL1) or obtained by GMM classification (overlap 2, OL2). It is noted that tumor voxels that were not assigned to any of the three microenvironments by the relative threshold methods (Fig. 4D, dark blue within the tumor) demonstrate typically very low Akep values (no significant CA uptake) and no significant pimonidazole staining, indicative of tumor necrosis or dying cells that could not be clearly identified on the corresponding H&E-stained section by thresholding methods. This unassigned region based on thresholding reduces the overlap between the necrotic area obtained by DCE-GMM classification and the one obtained by thresholding methods of ‘standard’ images (Fig. 4D, 4F-3). Based on these observations, unassigned voxels from perfusion (Akep) and pimonidazole images were designated to be necrotic and an extended necrotic area was used for the following overlap analysis (Fig. 4F-4).
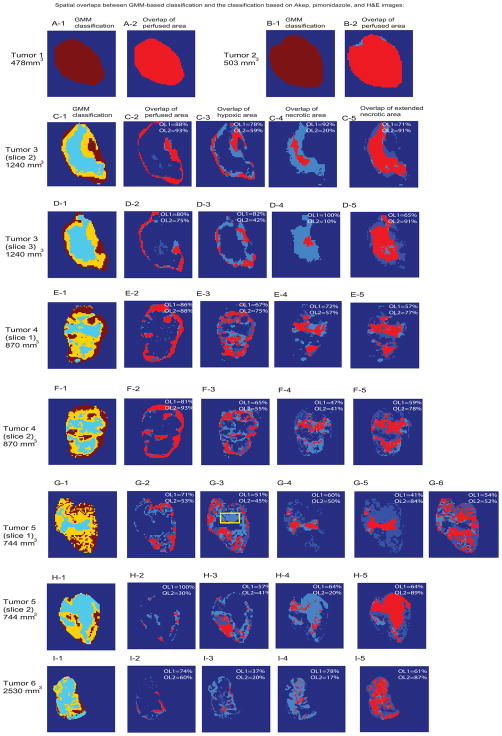
The same overlap analysis was performed for nine slices out of six rats, whose tumor size ranged from 500~2500 mm3 and encompassed the whole range of tumor manifestations from well-perfused (Fig. 5A, 5B) across heterogeneous (Fig. 5D-H) to predominantly necrotic (Fig. 5I) tumors. The resulting percent overlaps are summarized in Table 2. The mean OL1 (number of overlapping voxels for each mask)/(total number of thresholded voxels from standard images for each mask)) values between the GMM-based classification and the thresholding methods of Akep, pimonidazole, and H&E images were 0.83±0.09,0.64±0.16, 0.72±0.17, respectively. These values represent how well the GMM-classified masks matched expected tumor microenvironments obtained from standard thresholding methods. Corresponding mean OL2 (number of overlapping voxels for each mask)/(total number of GMM-classified voxels for each mask)) were 0.72±0.23–0.48±0.16–0.34±0.19, respectively. The lower overlaps, i.e. overestimations of GMM-classified area, were observed for both hypoxia and necrosis, and were due to the significant contributions of unassigned regions (voxels) from standard thresholding methods. When unassigned voxels from perfusion and pimonidazole thresholding were designated for necrosis, the numbers of overlapping voxels were seen to increases for necrosis, as shown in Fig. 5C-5~5I-5. This observation suggests that the unassigned voxels from the thresholding methods are likely to be from dying cells in areas without significant functional vascular supply and not yet apparent as necrosis on H&E. On the other hand, for slice1 of tumor 5, GMM-classification was seen to overestimate hypoxia that was in close vicinity to a perfused region, where negligible pimonidazole staining is observed as marked with a yellow box in Fig. G-3. When unassigned voxels from thresholding method were designated as hypoxia in this case, the number of overlapping voxels was seen to increase for hypoxia, as shown in Fig G-6. This observation suggests that the overestimated region from GMM-classifications in this slice may represent a hypoxic area lacking trapping of sufficient amounts of pimonidazole to be identified as hypoxic areas.
Fig. 5.
(A-1)~(I-1) Delineated tumor microenvironments of well-perfused (red), hypoxic (yellow) and necrotic (blue) areas from the GMM categorisation of DCE-MRI uptake curves. The spatial overlap between the perfused, hypoxic, and necrotic areas obtained from the GMM-categorization and the same areas obtained with thresholding from Akep, pimonidazole, and H&E maps, respectively, are depicted for the perfused areas in (A-2) ~ (I-2), for the hypoxic areas in (C-3) ~ (I-3), for the necrotic areas without unassigned voxel correction in (C-4) ~ (I-4), and for the extended necrotic areas, including voxels unassigned by thresholding of ‘standard’ images in (C-5)~ (I-5). Unassigned voxels from thresholding method were designated as hypoxia for tumor 5 (slice 1) as shown in Fig. G-6. Yellow box in Fig. G-3 highlights less prominent hypoxic area. Areas obtained from GMM categorization are colored in light blue, while areas obtained from thresholding segmentation based on Akep, pimonidazole, or H&E masks are depicted in darker blue and overlapping voxels are shown in pink. Corresponding percent overlap values for each segmentation are listed on their respective image. For each segmentation: OL1=(number of overlapping voxels)/(total number of thresholded voxels from standard images). OL2=(number of overlapping voxels)/(total number of GMM-classified voxels))
TABLE 2.
The spatial percentage overlap of perfused, hypoxic, and necrotic tumor areas obtained by GMM-based classification with those obtained from Akep, pimonidazole, and H&E images
| Tumor slices | % overlap of perfused area (OL1, OL2) | % overlap of hypoxic area (OL1, OL2) | % overlap of necrotic area | |||||
|---|---|---|---|---|---|---|---|---|
| H&E (OL1, OL2) | Extended (OL1, OL2) | |||||||
| Tumor 1 (478 mm3) | 1 | 1 | - | - | - | - | - | - |
| Tumor 2 (503 mm3) | 1 | 0.98 | - | - | - | - | - | - |
| Tumor 3 (sl.1, 1240 mm3):Training | 0.90 | 0.81 | 0.70 | 0.36 | 0.58 | 0.56 | 0.50 | 0.91 |
| Tumor 3 (sl.2, 1240 mm3) | 0.88 | 0.93 | 0.78 | 0.59 | 0.92 | 0.20 | 0.71 | 0.91 |
| Tumor 3 (sl.3, 1240 mm3 mm3) | 0.80 | 0.75 | 0.82 | 0.42 | 1 | 0.10 | 0.65 | 0.91 |
| Tumor 4 (sl.1, 870 mm3) | 0.86 | 0.88 | 0.67 | 0.75 | 0.72 | 0.57 | 0.57 | 0.77 |
| Tumor 4 (sl.2, 870 mm3) | 0.81 | 0.93 | 0.65 | 0.55 | 0.47 | 0.41 | 0.59 | 0.78 |
| Tumor 5 (sl.1, 744 mm3) | 0.71 | 0.53 | 0.51 | 0.45 | 0.60 | 0.50 | 0.41 | 0.84 |
| Tumor 5 (sl.2, 744 mm3) | 1 | 0.30 | 0.57 | 0.41 | 0.64 | 0.20 | 0.64 | 0.89 |
| Tumor 6 (2530 mm3) | 0.74 | 0.60 | 0.37 | 0.20 | 0.78 | 0.17 | 0.61 | 0.87 |
| Mean±SD | 0.84± 0.09 | 0.72± 0.23 | 0.64± 0.15 | 0.48± 0.16 | 0.72± 0.17 | 0.34± 0.19 | 0.58± 0.09 | 0.86± 0.09 |
Necrotic areas identified based on GMM-classification were compared to necrotic areas identified from H&E images alone or to necrotic areas corrected for unassigned voxels with no significant CA uptake and pimonidazole staining (Extended).
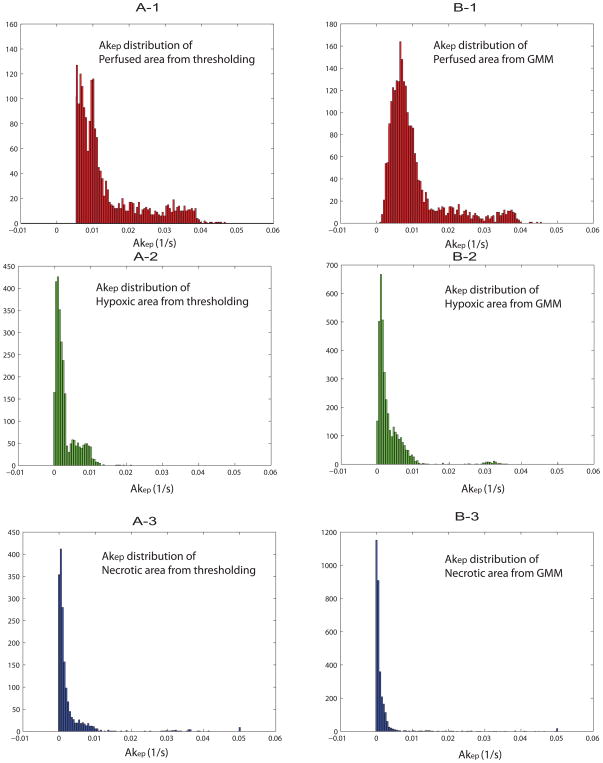
Next, the distribution of Akep values of the three different tumor microenvironments was evaluated. The Akep distribution of the perfused, hypoxic and necrotic areas from both, standard thresholding methods and GMM classifications, are shown in Figs. 6A-1~6A-3 and Figs. 6B-1~6B-3, respectively. The distribution patterns of Akep for each segmentation were similar for the two methods (thresholding vs. GMM classifications), confirming the accuracy/consistency of GMM classifications with respect to independent thresholding from immunohistochemistry and histology. Median Akep values of the perfused, hypoxic and necrotic areas were 0.010/0.0037/0.0017 (p<0.00001, Student’s T test) respectively, based on GMM classification and were 0.012/0.0030/0.0018 (p<0.00001, Student’s T test), respectively, based on thresholding from ‘standard’ images as summarized in Table 3. On the other hand, significant overlap of Akep values between each segmentation distribution, highlights the difficulty in setting relevant threshold Akep values to solely distinguish different tumor microenvironments from a single parameter.
Fig. 6.
Akep distributions of each tumor segmentation for perfused (A-1), hypoxic (A-2) and necrotic (A-3) regions from thresholding methods are shown. Corresponding Akep distribution from GMM classification of perfused (B-1), hypoxic (B-2) and necrotic (B-3) regions are shown as well. Data from six rats were combined for the analysis.
TABLE 3.
Median Akep (1/s) values of GMM-classified and thresholded tumor microenvironments of perfused, hypoxic and necrotic areas.
| Tumor slices | Perfused area from DCE-GMM | Perfused area from thresholding of standard images | Hypoxic area from DCE- GMM | Hypoxic area from thresholding of standard images | Necrotic area from DCE- GMM | Necrotic area from thresholding of standard images |
|---|---|---|---|---|---|---|
| Tumor 3(sl.1, 1240 mm3):Training | 0.0168±0. 0079 | 0.0174±0. 0138 | 0.0036±0 .0114 | 0.004±0. 0.0027 | 0.0020±0 .0092 | 0.0018±0. 0022 |
| Tumor 3(sl.2, 1240 mm3) | 0.0121±0. 0068 | 0.0123±0. 0161 | 0.0024±0 .0124 | 0.0015±0. 0.0007 | 0.0015±0 .0087 | 0.0007±0. 0007 |
| Tumor 3(sl.3, 1240 mm3 mm3) | 0.0065±0. 0029 | 0.0090±0. 0096 | 0.0021±0 .0009 | 0.0013±0. 0009 | 0.0020±0 .0085 | 0.0004±0. 0006 |
| Tumor 4 (sl.1,870 mm3) | 0.0095±0. 0100 | 0.0122±0. 0130 | 0.0028±0 .0060 | 0.0013±0. 0008 | 0.0024±0 .0100 | 0.0009±0. 0008 |
| Tumor 4(sl.2,870 mm3) | 0.0088±0. 0089 | 0.0105±0. 0110 | 0.0036±0 .0073 | 0.0013±0. 0009 | 0.0007±0 .0050 | 0.0008±0 0008. |
| Tumor 5(sl.1,720 mm3) | 0.0089±0. 0029 | 0.0107±0. 0020 | 0.0065±0 .0021 | 0.0064±0. 0036 | 0.0017±0 .0009 | 0.0051±0. 0036 |
| Tumor 5(sl.2,720 mm3) | 0.0081±0. 0020 | 0.0106±0. 0014 | 0.0048±0 .0015 | 0.0045±0. 0023 | 0.0016±0 .0011 | 0.0029±0. 0022 |
| Median±S D | 0.0101±0. 0059 | 0.0118±0. 0096 | 0.0037±0 .006 | 0.0030±0. 0017 | 0.0017±0 .0062 | 0.0018±0. 0016 |
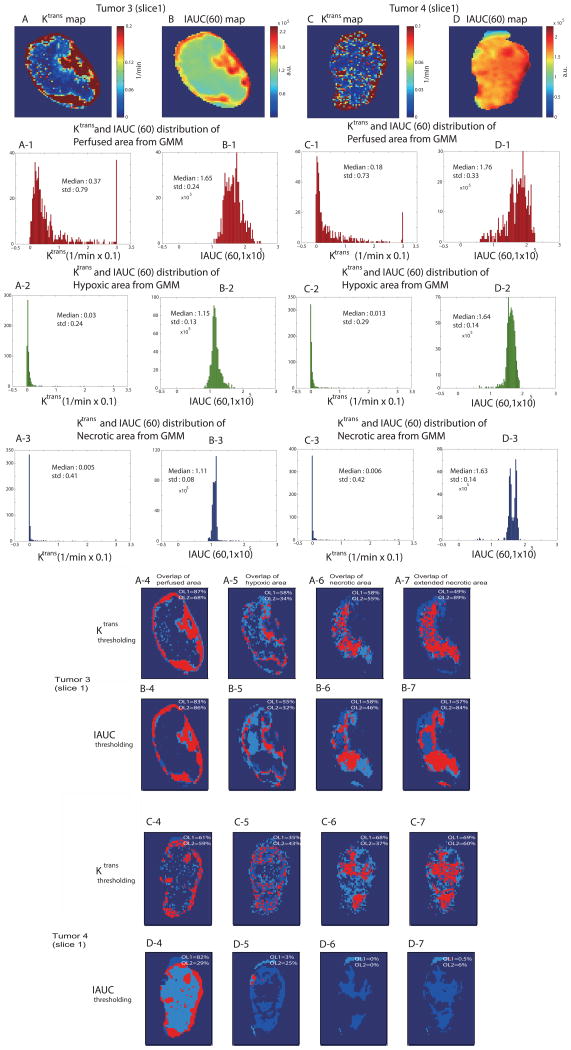
Standard parameters of DCE-MRI such as Ktrans and IAUC(60) (IAUC of the first 60s after contrast agent arrival) maps [48, 49] were generated and corresponding distributions were evaluated for GMM-classified tumor segmentations of perfused, hypoxic and necrotic areas. Ktrans and IAUC (60) maps of tumor 3 (slice1) are shown in Figs. 7A, 7B, and those of tumor 4 (slice1) are shown in Figs. 7C,7D, respectively. For the Ktrans calculations, an arterial input function (AIF) curve shape was taken from a direct measurement in another DCE-MRI study [50] and temporally resampled to match the time resolution of the current DCE-MRI data. The AIF amplitude was then adjusted using a muscle ROI as a reference tissue region [50]. Different Ktrans distributions with overlap of parameter values between each GMM-classified segmentation were observed. Especially, larger overlap of Ktrans values between hypoxic and necrotic areas for tumor 4 (slice1) was observed, in consistency with significant overlap trend of Akep values in Table 3 for the same tumor slice. IAUC(60) distributions showed more severe overlap between hypoxic and necrotic area as characterized by close median values between hypoxic and necrotic areas for both tumors.
Fig. 7.
Ktrans map (A) and IAUC(60) map (B) of tumor 3(slice1) are shown. Corresponding distribution of Ktrans and IAUC(60) values for GMM-classified perfused (A-1, B-1), hypoxic (A-2, B-2) and necrotic (A-3, B-3) regions are shown, respectively. The Ktrans map (C) and IAUC(60) map (D) of tumor 4 (slice1) are shown. Corresponding distribution of Ktrans and IAUC(60) values for GMM-classified perfused (C-1, D-1), hypoxic (C-2, D-2) and necrotic (C-3, D-3) region are shown, respectively as well. An overlap analysis between each compartmentation from Ktrans thresholding and ‘standard’ methods (i.e, pimonidazole, H&E) is shown for perfused (A-4, C-4), hypoxic (A-5, C-5), necrotic (A-6, C-6) and extended necrotic (A-7, C-7) areas for both tumors. An overlap analysis between each compartmentation from IAUC thresholding and ‘standard’ methods is shown for perfused (B-4, D-4), hypoxic (B-5, D-5), necrotic (B-6, D-6) and extended necrotic (B-7, D-7) areas for both tumors as well. For each segmentation: OL1=(number of overlapping voxels)/(total number of thresholded voxels from standard images). OL2=(number of overlapping voxels)/(total number of Ktrans/IAUC thresholding classified voxels).
To further verify the possibility of simple thresholding of standard Ktrans and IAUC(60) for the spatial segmentation of tumor microenvironments, midpoint values between the three peaks of the distributions in Figs. 7A-1,-2,-3 were set as two thresholds. Two threshold values were then used to classify maps into 3 (perfused, hypoxic and necrotic) regions, and the spatial overlap of each region with respect to corresponding ‘standard’ segmentation (such as pimonidazole and H&E) was shown in Figs. 7A-4~7A-7 and Figs. 7C-4~7C-7, respectively for two different tumors. Reasonable overlaps of tumor 3 (slice1) suggest that with relevant threshold values (obtained from GMM-classification in this case) and with minimal overlap of Ktrans values, a simple thresholding method of standard Ktrans parameter may spatially classify different tumor microenvironmental regions reasonably well. However, observed lower overlap values (OL1, OL2) of maps from Ktrans thresholding method compared to those from GMM classification for both tumors, especially for hypoxic and necrotic regions for tumor4 (slice1), suggest that a simple thresholding method may be problematic when the overlap of Ktrans parameter is large. The data-driven GMM classification utilizes the dynamic behavior of DCE-MRI data in its entirety and appears to provide larger overlap values (OL1, OL2) with respect to ‘standard’ images (such as pimonidazole and H&E) for both tumors, in distinguishing subtle hypoxic regions where significant overlap of physical parameters exist. Overlap studies from IAUC(60) thresholding method resulted in much worse overlap values (OL1, OL2) compared to those from Ktrans thresholding and were shown in Figs. 7B-4~7B-7 and Figs. 7D-4~7D-7 for both tumors for the comparisons. The results of overlap comparisons of GMM classifications and Ktrans/IAUC thresholding methods to ‘standard’ maps of perfused, hypoxic and necrotic areas were summarized in Table 4.
TABLE 4.
The spatial percentage overlap of perfused, hypoxic, and necrotic tumor areas obtained by GMM-based classification, Ktrans and IAUC thresholding with those obtained from Akep, pimonidazole, and H&E images for tumor 3 (slice1) and tumor 4 (slice1).
| Classification methods and tumor slices | % overlap of perfused area | % overlap of hypoxic area | % overlap of necrotic area | % overlap of extended necrotic area | |||||
|---|---|---|---|---|---|---|---|---|---|
| OL1 | OL2 | OL1 | OL2 | OL1 | OL2 | OL1 | OL2 | ||
| GMM classification | Tumor 3 (slice1) | 0.90 | 0.81 | 0.70 | 0.36 | 0.58 | 0.56 | 0.50 | 0.91 |
| Tumor 4 (slice1) | 0.86 | 0.88 | 0.67 | 0.75 | 0.72 | 0.57 | 0.57 | 0.77 | |
| Ktrans thresholding | Tumor 3 (slice1) | 0.87 | 0.68 | 0.58 | 0.34 | 0.58 | 0.55 | 0.49 | 0.89 |
| Tumor 4 (slice1) | 0.61 | 0.59 | 0.35 | 0.43 | 0.68 | 0.37 | 0.69 | 0.60 | |
| IAUC thresholding | Tumor 3 (slice1) | 0.83 | 0.86 | 0.55 | 0.32 | 0.58 | 0.46 | 0.57 | 0.84 |
| Tumor 4 (slice1) | 0.82 | 0.29 | 0.03 | 0.25 | 0.00 | 0.00 | 0.01 | 0.06 | |
Conclusions and discussion
This study shows the feasibility of applying a GMM-based classification of tumor microenvironments using spatially-resolved uptake curves from DCE-MRI data. Heterogeneous uptake curves of DCE-MRI data for solid tumors may be categorised with pattern recognition techniques, because a characteristic uptake curve inside the tumor should reflect similar microenvironments. Direct comparisons with respect to immunohistochemistry and histology data confirm the feasibility of GMM classifications of DCE-MRI data for the characterisation of tumor microenvironments such as perfusion, hypoxia and necrosis. The micro-environmental characteristics could be reliably identified in homogeneous and heterogeneous tumors from in vivo DCE-MRI data using a GMM-based classification.
Another advantage of using the GMM for this application is that it is based on unsupervised learning. Other classifiers such as artificial neural networks (ANNs) and support vector machine (SVM) require supervised learning, as training data with true class labels are necessary to learn the model parameters. However, true class labels are usually unavailable. In most medical pattern recognition problems, class labels are usually provided by well-trained physicians. However, measured patterns for the diagnosis are not clear when they are close to the decision boundary. The performance of classifiers with supervised learning is strongly dependent on the accuracy of the given class labels. The GMM does not require any labelled training data, and minimises human intervention. As a result, optimised GMM classification performance was obtained for DCE-MRI data by combining the ability to discriminate multiple dimensions with minimal intervention.
In summary, the present study showed that uptake curves of Gd-DTPA in a prostate tumor model can be categorised by a simple GMM-based classification from very homogeneous to heterogeneous tumors. The similarities between the tumor microenvironments identified GMM categorization of DCE-MRI uptake curves and the independent histology-based classification are promising. Moreover, significant correlations were found between the histology-based categorisation and the GMM-based categorisation, including the identification of hypoxic tumor areas. Apparent overestimations of hypoxic and necrotic areas from GMM-classifications were observed in comparison with standard thresholding methods from pimonidazole and H&E images. Our data indicate that unassigned regions from thresholding methods may represent less prominent necrotic or hypoxic regions without significant H&E or pimonidazole stainings, respectively. The differences in the size of slices used for DCE-MRI (0.79 mm) and pimonidazole and H&E (8 μm) should also be taken into consideration when considering regional mismatch. To estimate the tumor microenvironmental changes in a region equal in size to the slice thickness of the DCE-MR images, two adjacent H&E images for different tumors were taken at interval of 0.8 mm, as shown in the Supplementary Fig. 1. General characteristics of necrotic area remain consistent, while local shift, enlargement, or reduction of necrosis are apparent between the adjacent slices in both tumors. These variations in the slice thickness of DCE-MRI studies may also contribute to volume averaging effects, decreasing the percent overlap between GMM classifications and the thresholding method from standard histology images. A possible limitation of this classification approach is that it may not distinguish the contributions of the different tumor microenvironments on a sub-voxel level due to limited resolution of MR images, compared to cellular dimensions. Future advances may be focused on disentangling different contributions within a tumor voxel of DCE-MRI data to distinguish mildly-hypoxic region penetrating well-perfused areas, which may be signature result of acute hypoxia.
For the further verifications of GMM classification method of DCE-MRI data, increased sample sizes with different tumor models should be performed considering inherent biological heterogeneity of tumors. Longitudinal studies for multiple time points across tumor progression and treatment response will also shed light on the rigorous validation of the proposed method as well.
The imaging of tumor hypoxia clincally may provide prognostic information useful for therapy planning and for the monitoring of early treatment response, possibly reducing the need for invasive procedures. Since DCE-MRI is routinely performed clinically, the method proposed in this study could have a direct application in the clinic with fast, simple, and data-driven analysis.
Supplementary Material
Supplementary Fig. H&E images of two tumor slices that are 0.8 mm apart for two different tumors (A, B). These images demonstrate the variability in the extent of tumor necrosis across tumor slices and tumors.
Acknowledgments
This work was supported in part by the National Research Foundation of Korea Grants funded by the Korean Government (No. 2011-0000886 and No. 2011-0005711) and NIH grants P50 CA092629 and The Research and Therapeutics Program in Prostate Cancer. We thank Mihai Coman for his excellent technical assistance and Dr. Xin Li for his help in generating the Ktrans maps.
ABBREVIATIONs
- AIF
Arterial Input Function
- ANN
Artificial Neural Networks
- AUC
Area Under the Curve
- CA
Contrast Agent
- DCE-MRI
Dynamic Contrast Enhanced - Magnetic Resonance Imaging
- DME
Dulbecco’s Modified Eagle’s
- EES
Extracellular-Extravascular Space
- EM
Expectation-Maximisation
- EPR
Electron Paramagnetic Resonance
- FLASH
Fast Low Angle SHot
- FOV
Field Of View
- 18F-Fmiso
18F-fluoromisonidazole
- GMM
Gaussian Mixture Model
- H&E
Hematoxylin/Eosin
- IAUC
Integrated Area Under the Curve
- IHC
Immunohistochemistry
- LBG
Linde-Buzo-Gray
- MSKCC
Memorial Sloan Kettering Cancer Center
- NA
Number of Averages
- NR
Number of Repetitions
Probability Density Function
- PET
Positron Emission Tomography
- RARE
Rapid Acquisition with Refocused Echoes
- ST
Slice Thickness
- SVM
Support Vector Machine
- TE
Echo time
- TR
Repetition interval
- VQ
Vector Quantisation
Appendix
The expectation-maximisation (EM) algorithm is an iterative procedure that maximises the data likelihood generated by the GMM. It begins with an initial model λ and estimates a new model λnew, and then the new model becomes the initial model for the next iteration such that p(X∣λnew)≥p(X∣λ), where , and X={x1,…, xT} is a set of training vectors. This adaptation process is repeated until a predefined convergence threshold is reached and the selected parameters become their own GMM parameters. The initial model is derived by using VQ (vector quantisation) estimation using the LBG (Linde-Buzo-Gray) split strategy in our implementation [51, 52].
The expectation step is composed of computing the likelihood of the training vectors by the following equation:
| (5) |
In the maximization step, the likelihood value is increased until the convergence threshold is reached and three parameters are estimated:
| (6) |
| (7) |
| (8) |
where the a posteriori probability for the ith component is given by,
| (9) |
References
- 1.Varlotto J, Stevenson MA. Anemia, tumor hypoxemia, and the cancer patient. International Journal of Radiation Oncology* Biology* Physics. 2005;63(1):25–36. doi: 10.1016/j.ijrobp.2005.04.049. [DOI] [PubMed] [Google Scholar]
- 2.Vaupel P. Tumor microenvironmental physiology and its implications for radiation oncology: 2004. Elsevier; 2004. pp. 198–206. [DOI] [PubMed] [Google Scholar]
- 3.Vaupel P, Mayer A. Hypoxia in cancer: significance and impact on clinical outcome. Cancer and Metastasis Reviews. 2007;26 (2):225–239. doi: 10.1007/s10555-007-9055-1. [DOI] [PubMed] [Google Scholar]
- 4.Dewhirst MW, Secomb TW, Ong ET, Hsu R, Gross JF. Determination of local oxygen consumption rates in tumors. Cancer Research. 1994;54(13):3333. [PubMed] [Google Scholar]
- 5.Evans SM, Judy KD, Dunphy I, Jenkins WT, Nelson PT, Collins R, Wileyto EP, Jenkins K, Hahn SM, Stevens CW. Comparative measurements of hypoxia in human brain tumors using needle electrodes and EF5 binding. Cancer Research. 2004;64(5):1886. doi: 10.1158/0008-5472.can-03-2424. [DOI] [PubMed] [Google Scholar]
- 6.Brizel DM, Sibley GS, Prosnitz LR, Scher RL, Dewhirst MW. Tumor hypoxia adversely affects the prognosis of carcinoma of the head and neck. International Journal of Radiation Oncology* Biology* Physics. 1997;38(2):285–289. doi: 10.1016/s0360-3016(97)00101-6. [DOI] [PubMed] [Google Scholar]
- 7.Gulledge C, Dewhirst M. Tumor oxygenation: a matter of supply and demand. Anticancer research. 1996;16(2):741–750. [PubMed] [Google Scholar]
- 8.Raleigh JA, Dewhirst MW, Thrall DE. Measuring tumor hypoxia. Elsevier; 1996. pp. 37–45. 1996. [DOI] [PubMed] [Google Scholar]
- 9.Sorg BS, Moeller BJ, Donovan O, Cao Y, Dewhirst MW. Hyperspectral imaging of hemoglobin saturation in tumor microvasculature and tumor hypoxia development. Journal of biomedical optics. 2005;10:044004. doi: 10.1117/1.2003369. [DOI] [PubMed] [Google Scholar]
- 10.Yuan H, Schroeder T, Bowsher JE, Hedlund LW, Wong T, Dewhirst MW. Intertumoral differences in hypoxia selectivity of the PET imaging agent 64Cu (II)-diacetyl-bis (N4-methylthiosemicarbazone) Journal of Nuclear Medicine. 2006;47(6):989. [PubMed] [Google Scholar]
- 11.Zhang G, Palmer GM, Dewhirst MW, Fraser CL. A dual-emissive-materials design concept enables tumour hypoxia imaging. Nature materials. 2009;8(9):747–751. doi: 10.1038/nmat2509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vikram DS, Zweier JL, Kuppusamy P. Methods for noninvasive imaging of tissue hypoxia. Antioxid Redox Sign. 2007;9 (10):1745–1756. doi: 10.1089/ars.2007.1717. [DOI] [PubMed] [Google Scholar]
- 13.Bache M, Kappler M, Said HM, Staab A, Vordermark D. Detection and specific targeting of hypoxic regions within solid tumors: Current preclinical and clinical strategies. Curr Med Chem. 2008;15(4):322–338. doi: 10.2174/092986708783497391. [DOI] [PubMed] [Google Scholar]
- 14.Tatum JL, Kelloff GJ, Gillies RJ, Arbeit JM, Brown JM, Chao KSC, Chapman JD, Eckelman WC, Fyles AW, Giaccia AJ, et al. Hypoxia: Importance in tumor biology, noninvasive measurement by imaging, and value of its measurement in the management of cancer therapy. Int J Radiat Biol. 2006;82(10):699–757. doi: 10.1080/09553000601002324. [DOI] [PubMed] [Google Scholar]
- 15.Casciari J, Graham M, Rasey J. A modeling approach for quantifying tumor hypoxia with [F-18] fluoromisonidazole PET time-activity data. Medical Physics. 1995;22:1127. doi: 10.1118/1.597506. [DOI] [PubMed] [Google Scholar]
- 16.Koh WJ, Rasey JS, Evans ML, Grierson JR, Lewellen TK, Graham MM, Krohn KA, Griffin TW. Imaging of hypoxia in human tumors with [F-18] fluoromisonidazole. International Journal of Radiation Oncology* Biology* Physics. 1992;22(1):199–212. doi: 10.1016/0360-3016(92)91001-4. [DOI] [PubMed] [Google Scholar]
- 17.Serganova I, Humm J, Ling C, Blasberg R. Tumor hypoxia imaging. Clin Cancer Res. 2006;12(18):5260. doi: 10.1158/1078-0432.CCR-06-0517. [DOI] [PubMed] [Google Scholar]
- 18.Krause BJ, Beck R, Souvatzoglou M, Piert M. PET and PET/CT studies of tumor tissue oxygenation. Q J Nucl Med Mol Im. 2006;50(1):28–43. [PubMed] [Google Scholar]
- 19.Cho HJ, Ackerstaff E, Carlin S, Lupu ME, Wang Y, Rizwan A, O’Donoghue J, Ling CC, Humm JL, Zanzonico PB, et al. Noninvasive Multimodality Imaging of the Tumor Microenvironment: Registered Dynamic Magnetic Resonance Imaging and Positron Emission Tomography Studies of a Preclinical Tumor Model of Tumor Hypoxia. Neoplasia. 2009;11(3):247–U245. doi: 10.1593/neo.81360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gallez B, Baudelet C, Jordan BF. Assessment of tumor oxygenation by electron paramagnetic resonance: principles and applications. NMR in Biomedicine. 2004;17(5):240–262. doi: 10.1002/nbm.900. [DOI] [PubMed] [Google Scholar]
- 21.Kuppusamy P, Afeworki M, Shankar RA, Coffin D, Krishna MC, Hahn SM, Mitchell JB, Zweier JL. In vivo electron paramagnetic resonance imaging of tumor heterogeneity and oxygenation in a murine model. Cancer Research. 1998;58 (7):1562. [PubMed] [Google Scholar]
- 22.Matsumoto K, Subramanian S, Devasahayam N, Aravalluvan T, Murugesan R, Cook JA, Mitchell JB, Krishna MC. Electron paramagnetic resonance imaging of tumor hypoxia: enhanced spatial and temporal resolution for in vivo pO2 determination. Magnetic resonance in medicine. 2006;55(5):1157–1163. doi: 10.1002/mrm.20872. [DOI] [PubMed] [Google Scholar]
- 23.Ahn KH, Scott G, Stang P, Conolly S, Hristov D. Multiparametric Imaging of Tumor Oxygenation, Redox Status, and Anatomical Structure Using Overhauser-Enhanced MRI-Prepolarized MRI System. Magnetic resonance in medicine. 2011;65 (5):1416–1422. doi: 10.1002/mrm.22732. [DOI] [PubMed] [Google Scholar]
- 24.Vaupel P, Kallinowski F, Okunieff P. Blood flow, oxygen and nutrient supply, and metabolic microenvironment of human tumors: a review. Cancer Research. 1989;49(23):6449. [PubMed] [Google Scholar]
- 25.Dachs GU, Chaplin DJ. Microenvironmental control of gene expression: Implications for tumor angiogenesis, progression, and metastasis* Elsevier; 1998. pp. 208–216. [DOI] [PubMed] [Google Scholar]
- 26.Haroon Z, Peters K, Greenberg C, Dewhirst M. Antiangiogenic agents in cancer therapy. Totowa, NJ: Humana Press Inc; 1999. Angiogenesis and oxygen transport in solid tumors; pp. 3–21. [Google Scholar]
- 27.Neeman M, Provenzale JM, Dewhirst MW. Magnetic resonance imaging applications in the evaluation of tumor angiogenesis* Elsevier; 2001. pp. 70–82. [DOI] [PubMed] [Google Scholar]
- 28.Egeland TAM, Gaustad JV, Benjaminsen IC, Hedalen K, Mathiesen B, Rofstad EK. Assessment of fraction of hypoxic cells in human tumor xenografts with necrotic regions by dynamic contrast-enhanced MRI. Radiation research. 2008;169(6):689–699. doi: 10.1667/RR1311.1. [DOI] [PubMed] [Google Scholar]
- 29.Hylton N. Dynamic contrast-enhanced magnetic resonance imaging as an imaging biomarker. Journal of Clinical Oncology. 2006;24(20):3293. doi: 10.1200/JCO.2006.06.8080. [DOI] [PubMed] [Google Scholar]
- 30.Secomb TW, Hsu R, Ong ET, Gross JF, Dewhirst MW. Analysis of the effects of oxygen supply and demand on hypoxic fraction in tumors. Acta Oncologica. 1995;34(3):313–316. doi: 10.3109/02841869509093981. [DOI] [PubMed] [Google Scholar]
- 31.Secomb T, Hsu R, Beamer N, Coull B. Theoretical simulation of oxygen transport to brain by networks of microvessels: effects of oxygen supply and demand on tissue hypoxia. Microcirculation. 2000;7(4):237–247. [PubMed] [Google Scholar]
- 32.Gerlowski LE, Jain RK. Physiologically based pharmacokinetic modeling: principles and applications. Journal of Pharmaceutical Sciences. 1983;72(10):1103–1127. doi: 10.1002/jps.2600721003. [DOI] [PubMed] [Google Scholar]
- 33.Hoffmann U, Brix G, Knopp MV, Heβ T, Lorenz WJ. Pharmacokinetic mapping of the breast: a new method for dynamic MR mammography. Magnetic resonance in medicine. 1995;33(4):506–514. doi: 10.1002/mrm.1910330408. [DOI] [PubMed] [Google Scholar]
- 34.Tofts PS. Modeling tracer kinetics in dynamic Gd-DTPA MR imaging. Journal of Magnetic Resonance Imaging. 1997;7 (1):91–101. doi: 10.1002/jmri.1880070113. [DOI] [PubMed] [Google Scholar]
- 35.Yankeelov TE, Cron GO, Addison CL, Wallace JC, Wilkins RC, Pappas BA, Santyr GE, Gore JC. Comparison of a reference region model with direct measurement of an AIF in the analysis of DCE-MRI data. Magnetic resonance in medicine. 2007;57 (2):353–361. doi: 10.1002/mrm.21131. [DOI] [PubMed] [Google Scholar]
- 36.Li X, Huang W, Yankeelov TE, Tudorica A, Rooney WD, Springer CS. Shutter-speed analysis of contrast reagent bolus-tracking data: Preliminary observations in benign and malignant breast disease. Magnetic resonance in medicine. 2005;53 (3):724–729. doi: 10.1002/mrm.20405. [DOI] [PubMed] [Google Scholar]
- 37.Egeland TAM, Gulliksrud K, Gaustad JV, Mathiesen B, Rofstad EK. Dynamic contrast-enhanced-MRI of tumor hypoxia. Magnetic Resonance in Medicine. 2012;67(2):519–530. doi: 10.1002/mrm.23014. [DOI] [PubMed] [Google Scholar]
- 38.Fan XB, Haney CR, Mustafi D, Yang C, Zamora M, Markiewicz EJ, Karczmar GS. Use of a Reference Tissue and Blood Vessel to Measure the Arterial Input Function in DCEMRI. Magnetic Resonance in Medicine. 2010;64(6):1821–1826. doi: 10.1002/mrm.22551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ivancevic MK, Zimine I, Montet X, Hyacinthe JN, Lazeyras F, Foxall D, Vallee JP. Inflow effect correction in fast gradient-echo perfusion imaging. Magnetic Resonance in Medicine. 2003;50(5):885–891. doi: 10.1002/mrm.10633. [DOI] [PubMed] [Google Scholar]
- 40.Hansen AE, Pedersen H, Rostrup E, Larsson HBW. Partial Volume Effect (PVE) on the Arterial Input Function (AIF) in T-1-Weighted Perfusion Imaging and Limitations of the Multiplicative Rescaling Approach. Magnetic Resonance in Medicine. 2009;62(4):1055–1059. doi: 10.1002/mrm.22098. [DOI] [PubMed] [Google Scholar]
- 41.Roweis S, Ghahramani Z. A unifying review of linear Gaussian models. Neural computation. 1999;11(2):305–345. doi: 10.1162/089976699300016674. [DOI] [PubMed] [Google Scholar]
- 42.Fraley C, Raftery AE. Model-based clustering, discriminant analysis, and density estimation. Journal of the American Statistical Association. 2002;97(458):611–631. [Google Scholar]
- 43.Paalanen P, Kamarainen JK, Ilonen J, Kalviainen H. Feature representation and discrimination based on Gaussian mixture model probability densities--Practices and algorithms. Pattern Recognition. 2006;39(7):1346–1358. [Google Scholar]
- 44.Minati L, Węglarz WP. Physical foundations, models, and methods of diffusion magnetic resonance imaging of the brain: A review. Concepts in Magnetic Resonance Part A. 2007;30(5):278–307. [Google Scholar]
- 45.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society Series B (Methodological) 1977:1–38. [Google Scholar]
- 46.Egeland TAM, Gaustad JV, Galappathi K, Rofstad EK. Magnetic resonance imaging of tumor necrosis. Acta Oncologica. 2011:1–8. doi: 10.3109/0284186X.2010.526633. [DOI] [PubMed] [Google Scholar]
- 47.Cho H, Ackerstaff E, Carlin S, Lupu M, Wang Y, Rizwan A, O’Donoghue J, Ling C, Humm J, Zanzonico P. Noninvasive multimodality imaging of the tumor microenvironment: Registered dynamic magnetic resonance imaging and positron emission tomography studies of a preclinical tumor model of tumor hypoxia. Neoplasia (New York, NY) 2009;11(3):247. doi: 10.1593/neo.81360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.O’Connor JPB, Jackson A, Parker GJM, Roberts C, Jayson GC. Dynamic contrast-enhanced MRI in clinical trials of antivascular therapies. Nat Rev Clin Oncol. 2012;9(3):167–177. doi: 10.1038/nrclinonc.2012.2. [DOI] [PubMed] [Google Scholar]
- 49.Huang W, Li X, Morris EA, Tudorica LA, Seshan VE, Rooney WD, Tagge I, Wang Y, Xu JG, Springer CS. The magnetic resonance shutter speed discriminates vascular properties of malignant and benign breast tumors in vivo. P Natl Acad Sci USA. 2008;105(46):17943–17948. doi: 10.1073/pnas.0711226105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Li X, Rooney WD, Varallyay CG, Gahramanov S, Muldoon LL, Goodman JA, Tagge IJ, Selzer AH, Pike MM, Neuwelt EA, et al. Dynamic-contrast-enhanced-MRI with extravasating contrast reagent: Rat cerebral glioma blood volume determination. J Magn Reson. 2010;206(2):190–199. doi: 10.1016/j.jmr.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Franc V, Hlavác V. Statistical pattern recognition toolbox for Matlab. Center for Machine Perception, Czech Technical University; [Google Scholar]
- 52.Huang Y, Englehart KB, Hudgins B, Chan ADC. A Gaussian mixture model based classification scheme for myoelectric control of powered upper limb prostheses. Biomedical Engineering, IEEE Transactions on. 2005;52(11):1801–1811. doi: 10.1109/TBME.2005.856295. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Fig. H&E images of two tumor slices that are 0.8 mm apart for two different tumors (A, B). These images demonstrate the variability in the extent of tumor necrosis across tumor slices and tumors.