Abstract
We present a fluctuating hydrodynamics approach and a hybrid approach combining fluctuating hydrodynamics with generalized Langevin dynamics to resolve the motion of a nanocarrier when subject to both hydrodynamic interactions and adhesive interactions. Specifically, using these approaches, we compute equilibrium probability distributions at constant temperature as well as velocity autocorrelation functions of the nanocarrier subject to thermal motion in a quiescent Newtonian fluid medium, when tethered by a harmonic spring force mimicking a tether due to a single receptor-ligand bond. We demonstrate that the thermal equipartition of translation, rotation, and spring degrees of freedom are preserved by our formalism while simultaneously resolving the nature of the hydrodynamic correlations. Additionally, we evaluate the potential of mean force (or free energy density) along a specified reaction coordinate to faciltate extensive conformational sampling of the nanocarrier motion. We show that our results are in excellent agreement with analytical results and Monte Carlo simulations, thereby validating our methodologies. The frameworks we have presented provide a comprehensive platform for temporal multiscale modeling of hydrodynamic and microscopic interactions mediating nanocarrier motion and adhesion in vascular targeted drug delivery.
1 Introduction
Multiscale modeling can complement experimental technologies in order to access the mesoscale (10–100 nm). Traditional multiscale modeling involves bottom-up approaches of systematically coarse-graining the atomistic description. Bridging techniques that seamlessly integrate two distinct length scales in this category include mixed quantum mechanics/molecular mechanics (QM/MM) [1], and integrated molecular mechanics/coarse-grained or MM/CG approaches [2]. Alternatively, a top-down approach can be pursued, in which models are constructed at the mesoscale based on phenomenological interaction potentials; in prior work published in the literature, such an approach has been extensively employed, and specific choices of the governing equations have been validated based on experimental studies [3]. The top-down strategy is already proven to be a viable avenue for pursuing models that provide physical insight as well as for enabling direct comparison with experiments. Such methods involve continuum scale formalisms and often incorporate finer length scales by considering spatial heterogeneities as inhomogeneous fields [4]. Bridging methods integrating molecular mechanics or coarse-grained models with continuum approaches have been achieved in two limits: (1) hierarchical bridging which involves computing a property or a constitutive relationship at one (typically the molecular) scale and employing (either pre- or on-the-fly-) computed values in the other (typically the continuum scale) [5, 6, 7]; (2) domain decomposition bridging which involves performing molecular scale modeling in one (typically a small domain) and integrating it with continuum modeling in an adjoining (larger) domain, such that certain constraints (boundary conditions) are satisfied self-consistently at the boundary separating the two domains. Such approaches have been shown to be effective for various problems involving contact lines or points [8, 9, 10, 11, 12, 13, 14, 15, 16].
In situations where molecular interactions (due to biomolecular recognition) and hydrodynamic interactions (due to fluid flow and boundary effects) are both significant, the integration of disparate length- and time- scales does not fit the traditionally available multiscale methods outlined above. The main source of complexity lies in integrating fluid flow and memory for multiphase flow in complex and arbitrary geometries, while simultaneously including thermal and stochastic effects to correctly simulate quasi-equilibrium distributions to enable biomolecular (receptor-ligand) binding/unbinding interactions at the physiological temperature. Such a scenario is ubiquitous in multivalent binding or adhesive interactions between nanocarriers and cells or between two cells in the vasculature. The former application, namely, the computational modeling of nanocarrier binding to endothelium, is the subject of this article. The use of nanocarriers functionalized with specific targeting antibodies enables precise and effcacious delivery of drugs to diseased or inflamed target endothelial cells which often have a distinct pattern of expression of biomarkers (such as increased intracellular adhesion molecule-1, ICAM-1, or platelet endothelial cell adhesion molecule, PECAM, expression levels) [17, 18]. In order to more broadly integrate this technology into clinical medicine, a model-based design and optimization of nanocarrier transport in the vasculature and adhesion to target cells can prove effective. Towards achieving this goal, an important step is to determine the motion of a nanocarrier subject to hydrodynamic effects in the vasculature while simultaneously being subject to a constant temperature; this is crucial to accurately model the biological reactions (receptor-ligand interactions) mediating the adhesion of nanocarrier to the endothelial cell surface lining the vasculature [19, 20, 21, 22].
In prior work, we have combined novel computational methodologies with experimental (in vivo and in vitro) measurements in order to develop mesoscale continuum models for nanocarrier motion and nanocarrier adhesion. We developed a computational methodology to calculate the absolute binding free energy between functionalized nanocarriers and endothelial cell surfaces based on Metropolis Monte Carlo and the weighted histogram analysis method. We calculated nanocarrier binding free energy landscapes, which yielded binding affinities that agreed quantitatively when directly compared with analogous measurements of specific antibody-coated nanocarriers (100 nm diameter) to ICAM-1 expressing endothelial surfaces in in vitro cell-culture experiments as well as with in vivo targeting of the anti-ICAM-1 coated nanocarriers to pulmonary endothelium in mice [22]. This model for nanocarrier binding was also extended and comprehensively validated to predict the effects of multivalent binding under shear flow [23]; our results indicate that the interplay between multivalent binding and shear force can reproduce the shear-enhanced binding phenomenon suggesting that under certain conditions this phenomenon can also occur in systems that do not show a catch-bond behavior.
With the objective of developing a computational framework for nanocarrier Brownian motion and hydrodynamic interactions in the presence of flow fields, in a recent study [24] we employed the fluctuating hydrodynamics approach in an incompressible Newtonian fluid medium. This is an inherently multi-scale problem in its own right with multiple macroscopic and mesoscopic time scales governing the problem, including (i) a hydrodynamic time scale; (ii) a Brownian relaxation time scale and (iii) a Brownian diffusion time scale. Our formalism considers situations where both the Brownian motion as well as the hydrodynamic interactions are important and our results for thermal equilibrium were validated by comparing the predictions for the temperatures of the particle with those obtained from the equipartition theorem. The nature of the hydrodynamic interactions was verified by comparing the velocity autocorrelation functions and mean square displacements with analytical [25] and experimental results where available [24]. In a recent study [26], we extended our hydrodynamic model to include Brownian effects using the generalized Langevin dynamics frame-work, where the hydrodynamic memory effects of the nanocarrier fluid interactions and their relationship to thermal equipartition and equilibrium distributions were delineated.
While the fluctuating hydrodynamics framework [24] captured the correct hydrodynamic correlations, it conserved thermal equipartition (for a nanocarrier in an incompressible fluid) only after the added mass correction was applied [25]; the generalized Langevin dynamics method on the other hand yielded the correct thermal equipartition (without any corrections), but modified the nature of the hydrodynamics correlations (due to the coupling of the fluid equations with the thermostat degrees of freedom). Hence, in a recent study, we have proposed a hybrid formalism combining fluctuating hydrodynamics and generalized Langevin dynamics [27], where we have implemented a novel hybrid computational scheme based on Markovian fluctuating hydrodynamics of the fluid and a non-Markovian Langevin dynamics with the Ornstein-Uhlenbeck noise perturbing the translational and rotational equations of motion of the nanocarrier. Using this approach, we validated the thermal equilibrium between the particle and the fluid by comparing the numerically predicted temperature of the nanocarrier with that obtained from the equipartition theorem. More significantly, we have simultaneously verified the nature of the hydrodynamic correlations (interactions) by comparing the velocity autocorrelation function (VACF) and mean square displacement (MSD) with well-known analytical results [25]. Hence, our simulations performed with this hybrid approach simultaneously satisfy the equipartition theorem and the (short- and long-time) hydrodynamic correlations. This framework effectively produces a thermostat that also simultaneously preserves the true hydrodynamic correlations [27].
The importance and significance of this result is that our hybrid algorithm provides a robust computational approach to explore nanocarrier motion in arbitrary geometries and flow fields, while simultaneously enabling us to study carrier adhesion mediated by biological reactions (receptor-ligand interactions) at the vessel wall at a specified finite temperature [22, 23]. In this article, we demonstrate that our fluctuating hydrodynamics approach [24] and our hybrid approach [27] can indeed be employed when both hydrodynamic interactions and adhesive interactions are present simultaneously. In section 2, we present the details of our model and simulation methodologies. In section 3, we consider the equilibrium and hydrodynamic correlations for a nanocarrier subject to thermal motion in a quiescent Newtonian fluid medium, when tethered by a spring force (mimicking a single tether due to one receptor-ligand bond). Since the tethering localizes the nanocarrier very close to the cylindrical wall, significant hydrodynamic interactions between the nanocarrier and the wall are also resolved in our model. We demonstrate that the thermal equipartition of translation, rotation, and spring degrees of freedom are preserved by our formalism while simultaneously resolving the nature of the hydrodynamic correlations. Since the timescale of integration of the fluid and particle (nanocarrier) equations needs to be smaller than the fastest inherent timescale of our system (in order to achieve linear stability during numerical integration) [28], the choice for the timestep of integration is limited to Δt < 10−10s (for a nanocarrier of size 100–500 nm). This limits the total amount of time to be simulated in our simulations to ten micro seconds (for 100000 timesteps). Leveraging the conservation of thermal equipartition of our formalism, in section 3, we also demonstrate that we can perform temporal multiscaling by evaluating the potential of mean force (or free energy density) along a specified reaction coordinate. This enables the determination of probability distributions and extensive conformational sampling of nanocarrier motion which is prohibitive by conventional dynamics. In section 4, we present outlook for future extensions of our approach in the broader context of temporal multiscale modeling and targeted drug delivery.
2 Methods
A nanocarrier suspended in a fluid undergoes random motion due to the thermal fluctuations in the fluid. In determining the translational and rotational motions of the nanocarrier in an incompressible Newtonian fluid, there exist two methods to couple the thermal fluctuations with the hydrodynamic interactions: the fluctuating hydrodynamics method and the generalized Langevin dynamics method. The fluctuating hydrodynamics method essentially consists of adding stochastic stresses (random stress) to the stress tensor in the momentum equation of the fluid [29]. The stochastic stress tensor depends on the temperature and the transport coefficients of the fluid medium [25, 30]. Numerical simulations of the fluctuating hydrodynamics approach have been carried out employing the finite volume method [31, 30, 32, 33], lattice Boltzmann method (LBM) [34, 35, 36, 37, 38, 39, 40], finite element method [41, 42, 24] and stochastic immersed boundary method [43]. In contrast, in the Langevin dynamics method, the effect of thermal fluctuations are incorporated as random forces and torques in the particle equation of motion [44, 45, 46, 47, 48, 49, 26]. The properties of these forces depend on the grand resistance tensor. The tensor in turn depends on the fluid properties, particle shape, and its instantaneous location such as its proximity to a wall or a boundary.
Brownian particle trapped in a harmonic potential in an incompressible Newtonian stationary fluid medium contained in a horizontal circular vessel (see Figure 1) is considered. The fluid and particle equations are formulated in an inertial frame of reference with the origin coinciding with the center of the cylindrical vessel (Figure 1). The diameter, D, and the length, L, of the vessel are very large compared to the nanocarrier diameter, d. Antigen of length 19nm is attached to the wall of the cylindrical tube (R = 2.5μm) containing a quiescent Newtonian fluid and antibody of length 15nm is attached to the surface of the neutrally buoyant solid spherical nanocarrier of radius a = 250nm. The nanocarrier is placed close to the antigen such that the direction of antibody is initially pointing towards the antigen and the distance between them is 2Å. The tips of the antigen and the antibody are tethered by a simple harmonic (spring) potential with spring constant k. Initially, the fluid and particle are at rest. No body force is assumed to be applied either on the particle or in the fluid domain. Starting at time t = 0, the nanocarrier experiences Brownian motion and harmonic motion. The motion of the nanocarrier is determined by the hydrodynamic and spring forces and torques acting on the particle. The numerical results are obtained from simulations of the fluid-particle system with physical parameters μ = 10−3 kg/ms; ρ(f) = 103 kg/m3; ρ(p) = 103 kg/m3; kB = 1.3806503 × 10−23 kgm2/s2K; k = 1N/m. The temperature of the fluid is initially set to T = 310K.
Figure 1.
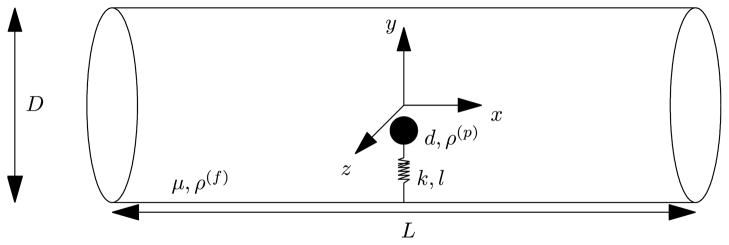
Schematic representation of a nanocarrier in a cylindrical vessel (tube) (not to scale). Diameter of the tube: D = 5 μm; Length of the tube: L = 10 μm; Diameter of the nanocarrier: d = 500 nm; Viscosity of the fluid: μ = 10−3kg/ms; Density of the fluid and the nanocarrier: ρ(f) = ρ(p) = 103kg/m3; Spring constant: k = 1N/m.
2.1 Fluctuating Hydrodynamics Method
The motion generated in the incompressible Newtonian fluid satisfies the conservation of mass and momentum as given by
| (1) |
| (2) |
where u and ρ(f) density of the fluid respectively. The stress tensor σ, for Newtonian fluid is given by
| (3) |
where p is the pressure, J is the identity tensor, μ is the dynamic viscosity, and S is the random stress tensor. S is assumed to be a Gaussian with
| (4) |
where 〈 〉 is the ensemble average, kB is the Boltzmann constant, T is the absolute temperature, and δ(x–x′) denotes that the components of the random stress tensor are spatially uncorrelated (Markovian). The right hand side of equation (4) denotes the mean and variance of the thermal fluctuations chosen to be consistent with the fluctuation-dissipation theorem [29, 25, 50, 51]. By including this stochastic stress tensor due to the thermal fluctuations in the governing equations, the macroscopic hydrodynamic theory is generalized to include the mesoscopic scales ranging from tens of nanometers to a few microns.
For a rigid Brownian particle trapped in a harmonic potential in an incompressible Newtonian fluid, the translational motion of the particle satisfies Newton’s second law,
| (5) |
and the roational motion satisfies the Euler equation,
| (6) |
where m is the mass of the particle, I is its moment of inertia, and U and ω are the translational and angular velocities of the particle, respectively. The hydrodynamic force F and the torque T acting on the particle are given by
| (7) |
where X is the position of the centroid of the particle, (x – X) is a vector from the center of the particle to a point on its surface, ∂Σp denotes the particle surface, and n∩ is the unit normal vector on the surface of the particle pointing into the particle. The spring force Sf and torque St acting on the particle are given by
| (8) |
where k is the spring constant, l is the length of the spring, d∩ is the unit vector pointing towards the tip of the antigen attached to the wall.
The initial conditions for the problem are
| (9) |
and the boundary conditions are given by
| (10) |
| (11) |
| (12) |
where Σ0 is the domain occupied by the fluid and ∂Σi and ∂Σo are the inlet and outlet boundaries, respectively. It is assumed that there is no body torque acting at any point in the fluid and the viscous stress tensor, σ, is symmetric. The fluctuation-dissipation theorem for the random stress tensor of the fluid requires that S is symmetric as well [51, 52].
2.2 Hybrid Formalism
Recently, we formulated a hybrid method where we combined Markovian fluctuating hydrodynamics for the fluid with non-Markovian generalized Langevin approach for the nanocarrier to show that the approach can simultaneously satisfy equipartition of energy (and equilibrium probability distributions) in a thermal environment, as well as hydrodynamic interactions imposed by the flow field [27]. This formalism was based on modifying the particle equations of motion (5) and (6) similar to the generalized Langevin equation [53, 54] resulting in
| (13) |
| (14) |
where the random force ξ and torque η are given by
| (15) |
| (16) |
for the Ornstein-Uhlenbeck process. The time integral in equations (13) and (14) excludes the frictional force and torque at the time instant t since it has already been accounted for in the hydrodynamic force and torque terms, respectively. The characteristic memory time for translational, τ1 = n1·Δt, and rotational, τ2 = n2·Δt, motions of the nanocarrier add certain amounts of memory from the previous history of fluctuations to the system. Here, n1 and n2 correspond to the number of time steps required to adequately represent the memory effects. These are variable quantities and are determined on the basis of satisfying the equipartition theorem. The amount of memory required by translational and rotational motions of the nanocarrier in order to satisfy the equipartition theorem are different. Hence τ1 = τ2 is not a necessary condition for the temperature of the particle to attain the preset temperature of the fluid. Equations (15) and (16) are the random force and torque acting on the nanocarrier at time t′ (a previous time instant). Since the random stress S(x, t) is Gaussian, ξ(t′) and η(t′) are also Gaussian with variance equivalent to the strength of the white noise in the Langevin equation. In the limit of the characteristic memory times τ1, τ2 → 0 (i.e. in the absence of memory), equations (13) and (14) reduce to the equations (5) and (6), respectively, which correspond to the Markovian fluctuating hydrodynamics.
2.3 Numerical Discretization
The stochastic governing equations (1) – (6) (for hybrid method: equations (1) – (4), (13), (14)) along with the initial and boundary conditions (9) – (12) are solved numerically. A numerical simulation at a mesoscopic scale involving a particle in a fluid could be based on a discretization of the equations (1) – (6). However, the discrete forms have to satisfy the fluctuation-dissipation theorem [50, 51, 30, 32, 55, 31, 56]. Español and Zúñiga [41] and Español et al. [42] have shown that a well behaved set of discrete equations obtained in terms of the finite element shape functions based on the Delaunay triangulation conserves mass, momentum and energy while ensuring thermodynamic consistency. Furthermore, Español et al. [42] have cast their discrete hydrodynamic equations in the GENERIC structure and observed that the resulting reversible matrix does not satisfy the Jacobi identity and the degeneracy conditions of GENERIC structure [50, 51]. But, these conditions are of the order of the cell size and vanish in the continuum limit [42]. In effect, Español et al. [42] have shown that the finite element discretization procedure based on Delaunay triangulation is an appropriate procedure for discretizing the compressible fluctuating Navier-Stokes equations. In the present study, we obtain the discrete hydrodynamic equations using finite element shape functions based on the Delaunay-Voronoi tetrahedrizations. The details of combined fluid-solid weak formulation, generating random stress tensor for the tetrahedral finite element mesh, spatial discretization, mesh movement techniques, and temporal discretization of time derivatives are discussed in [24, 26]. These details will not be repeated here for brevity. Briefly, the fluid domain is approximated by quadratic tetrahedral finite-elements (10 nodes defined per tetrahedron with 10 basis functions that are second-order polynomials). The discrete solution for the fluid velocity is approximated in terms of piecewise quadratic functions, and is assumed to be continuous over the domain (P2 elements). The discrete solution for the pressure is taken to be piecewise linear and continuous (P1 element). This P1/P2 element for the pressure and velocity is consistent with the Ladyzhenskaya-Babuska-Brezzi (LBB) or inf-sup condition and yields convergent solutions [57, 58].
2.4 Time-scale Analysis
The time scales involved in this study are (i) τb = m/ζ(t) the Brownian relaxation time over which velocity correlations decay in the Langevin equation, (ii) τd = a2ζ(t)/kBT, the Brownian diffusive time scale over which the nanocarrier diffuses over a distance equal to its own radius, (iii) τν = a2/ν, the hydrodynamic time scale for momentum to diffuse over a distance equal to the radius of the nanocarrier, and (iv) , the harmonic time for a single oscillation of spring, where ζ(t) = 6πμa is the Stokes dissipative friction force coefficient for a sphere, a is the radius of the nanocarrier, and ν is the kinematic viscosity of the fluid. The time scale Δt for the numerical simulation has been chosen to be smaller than all the relevant physical time scales described above. The simulations presented in this study have been carried out for long enough durations to allow for the temperature of the particle to equilibrate; i.e., if N is the number of simulated time steps then N·Δt = t ≫ τν.
2.5 Potential of Mean Force
In order to determine average properties corresponding to a given equilibrium distribution at a finite (fixed) temperature, we compute the potential of mean force (PMF) for the harmonic (spring) interactions between antibodies and antigens. We choose a reaction coordinate y, which is the vertical displacement between the tips of the antigen and the antibody; increase in y allows the nanocarrier to be displaced away from the wall while still being bound by the spring. Since, the maximum (and hence the average) displacements along y are limited by temperature and by the total time of the simulation, we perform umbrella sampling in multiple windows with harmonic biasing potentials to facilitate extensive sampling along y. The window size of the umbrella sampling is chosen as Δy = 0.05nm and the harmonic biasing potential in each window is chosen to be 0.5ku(y − y0,i)2, where 0.5ku(Δy)2 = 1.0 × 10−20J, ku is the harmonic force constant and y0,i is the vertical coordinate of the center of window i. By updating y0,is, the tip of the antibody (on the average) is slowly varied relative to the antigen reaction tip. The weighted histogram analysis method (WHAM) algorithm [59] is used to unbias and combine the histograms in different windows to form a complete PMF (W(y)) profile using a tolerance factor of 10−6 in the WHAM method. For determining the PMF profile using fluctuating hydrodynamics method, 3 realizations in each window have been computed with up to 100, 000 time steps per realization, (hence yielding a total of 3 ×100, 000 = 300, 000 time steps per window). All the relevant parameters including the window size Δy, strength of the biasing potential ku and the sampling size in each window have been tested to ensure convergence.
2.6 Monte Carlo Simulations
Even though the PMF described above is being computed using a method that preserves hydrodynamic correlations, the PMF itself is an equilibrium property which is independent of dynamics. Therefore, as a check, we perform Monte Carlo simulations of the nanocarrier bound to the wall by a harmonic spring to determine the equilibrium distributions in an independent fashion. In our method, the spring interaction (mediated by a single antibody bound to an antigen) is accounted for by the same harmonic potential as described above, i.e., using the Bell model [60]: , where l is the distance between the tips of the interacting antibody and antigen, k is the interaction bond force constant and ΔG0 the free energy change at equilibrium state (l = 0). In our model, these parameters are chosen to mimic the interactions between murine anti-ICAM-1 antibody and ICAM-1. From the experimental measurements from Muro et al. [61], the equilibrium free energy change between antibody and ICAM-1 is found to be −7.98 × 10−20 J, which we set as ΔG0 in our simulations. We also set the bond spring constant k = 1N/m by fitting rupture force distribution data reported from single-molecule force spectroscopy [62, 63]. In this work, for simplicity (and to conform to the model employed in the fluctuating hydrodynamics above), we neglect the ICAM-1 flexural movement; therefore the ICAM-1s are always in upright conformations. We also do not allow the antigen-antibody bond to rupture. However, as discussed in our previous work [22, 23, 5], the flexural movement of the antigens and bond formation/breaking can be easily implemented using orientational biased Monte Carlo (MC) sampling technique [64]. Metropolis Monte Carlo steps are employed for nanocarrier translation and rotation with an adaptive step size to ensure a Metropolis acceptance rate of 50%. In order to determine the PMF (W(y)), we divide up the windows using the same exact specifications (and at the same temperature) as described above (for the fluctuating hydrodynamics method). A total of 200 million Monte Carlo steps are performed in each window and the histogram is saved. The PMF is independently computed by using the WHAM algorithm as outlined above and compared with the previous estimate.
3 Results and Discussion
For a given nanocarrier of radius a, and tube radius R, a ‘realization’ consists of N time steps (approximately 10s of wall-clock time is required for each time step). The number of time steps for equilibration of particle temperature, and determination of VACFs is in the range of 100,000 per realization, requiring a wall-clock time of ~11.5 days. In order to ensure the uniqueness of the realizations, different initial seeds are chosen for a Gaussian random number generator. In our simulations, we predict (i) the translational and rotational temperatures of the nanocarrier, where the temperature calculation is carried out until thermal equilibration is obtained for the particle; (ii) the translational and rotational velocity distributions of the nanocarrier motion; (iii) the translational and rotational VACFs; (iv) temperature of the spring. We compare the various numerical predictions with known analytical results.
3.1 Thermal Equipartition
At thermal equilibrium, the probability density distribution of the velocity of the fluctuating nanocarrier follows the Maxwell-Boltzmann distribution:
where, m* = m + m0/2 for the fluctuating hydrodynamics method and m* = m for the hybrid method. The equilibrium statistics of the other two components Uy, Uz are the same as Ux, and those for the components of ω are independent of each other.
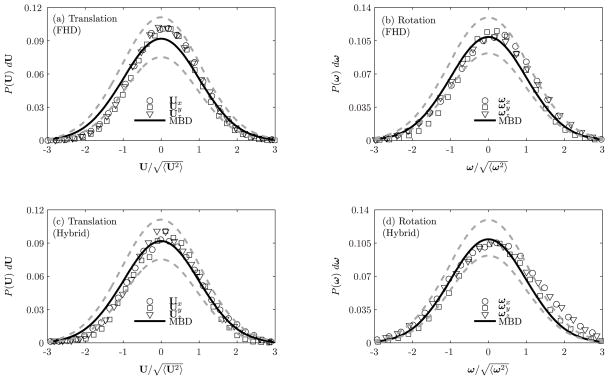
In Figure 2, we plot the velocity distributions of the particle for each component of U (Figures 2(a) and (c)) and ω (Figures 2(b) and (d)) using fluctuating hydrodynamics ((Figures 2(a) and (b))) and hybrid (Figures 2(c) and (d)) methods. For determining the velocity distribution of the nanocarrier, 5 realizations in each coordinate direction consisting of 5×100, 000 = 500, 000 time steps have been computed. Thus, a total of 1, 500, 000 time steps have been computed. It is observed that each degree of freedom individually follows a Gaussian distribution. In particular, the mean and the variance obtained by using the fluctuating hydrodynamics approach agrees to within 5% to 11% statistical error with that of the analytical Maxwell-Boltzmann distribution, whereas using hybrid scheme agrees to within 6% error relative to that of the analytical Boltzmann distribution. The main difference between the results of the fluctuating hydrodynamics method and the hybrid method is the effective mass: in the case of the fluctuating hydrodynamics, we employ the added mass correction, i.e. M = m + m0/2, where m0 is the mass of the fluid displaced by the particle; in the case of the hybrid method, the added mass correction is not required and we simply use the mass of the particle m.
Figure 2.
Equilibrium probability density of the (a,c) translational and (b,d) rotational velocities of the neutrally buoyant nanocarrier (a = 250 nm) trapped in a harmonic potential in a Newtonian fluid using fluctuating hydrodynamics and the hybrid methods. MBD: Maxwell-Boltzmann distribution; FHD: fluctuating hydrodynamics.
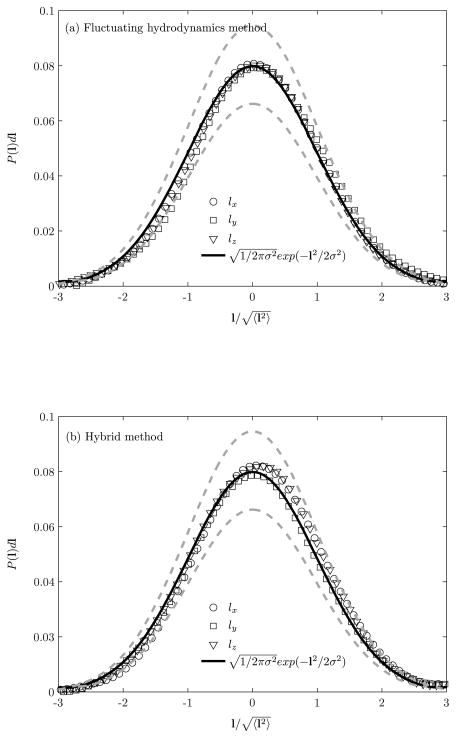
Figure 3 shows the probability distribution of spring length using fluctuating hydrodynamics and hybrid methods. The equilibrium probability density of the displacement of spring in each Cartesian direction follows a Gaussian distribution. The agreement with the analytical Gaussian distribution with the mean zero and the variance kBT/k is to within 6% of statistical error using both the methods. These results demonstrate that our dynamic formalisms conserve the equilibrium distributions of the canonical (constant temperature) ensemble. In the case of translational temperature, the fluctuating hydrodynamics requires the added mass correction to satisfy the analytical Maxwell-Boltzmann distribution, whereas in the case of the hybrid method, the Maxwell-Boltzmann distribution is satisfied based on the actual mass of the particle m (i.e., without the added mass correction). In the case of rotational and spring temperatures, there is no need for the added mass correction in both methods.
Figure 3.
Equilibrium probability density of the displacement of spring length using (a) fluctuating hydrodynamics and (b) hybrid methods, where the standard deviation .
3.2 Hydrodynamic Correlations
A nanocarrier experiencing Brownian motion in a fluid is influenced by the hydrodynamic interactions. The fluid around the particle is dragged in the direction of motion of the particle. On the other hand, the motion of the particle is resisted by viscous forces arising due to its motion relative to the surrounding fluid. The momentum of the fluid surrounding the particle at any instant is related to its recent history. The friction coefficient is time dependent and is no longer given by the constant Stokes value. Zwanzig and Bixon [65] have shown that for constant friction coefficient, the VACF of the particle in a simple fluid obeys exponentially decaying behavior, which is valid at short times:
| (17) |
| (18) |
Here, ζ(t) = 6πμa, ζ(r) = 8πμa3 are the Stokes dissipative friction force and torque coeffcients, respectively. Hauge and Martin-Löf [25] have analytically shown that the decay of the translational and rotational VACFs at long time obeys a power-law:
| (19) |
| (20) |
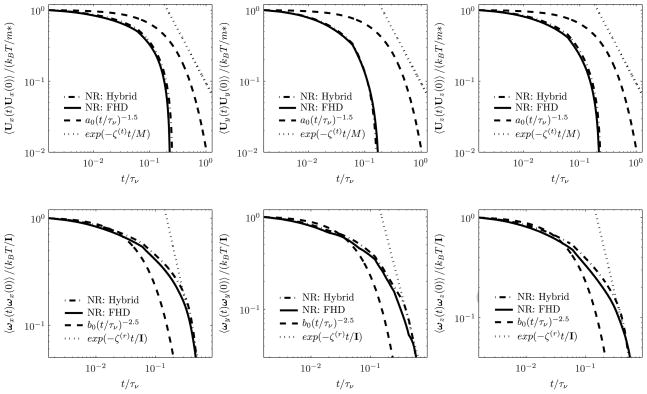
where the values of constants a0 and b0 are 0.094 and 0.014, respectively; we note that M = m + m0/2, where m0 is the mass of the fluid displaced by the particle. For determining the VACF of the nanocarrier, 5 realizations in each coordinate directions have been employed with total computation of 15 × 100, 000 = 1, 500, 000 time steps. Figure 4 shows the VACF of the translational and rotational motions of a nanocarrier (a = 250 nm) in a quiescent fluid medium in a circular vessel as obtained from our numerical simulations. It may be observed that the translational and rotational VACFs of the Brownian particle have exponential and power-law decays (~ t−5/2) over long times, respectively. We note that the exponential decay of the translational velocity of the nanocarrier over long times is due to its proximity to the wall (due to the confining harmonic potential), again indicating that hydrodynamic correlations are correctly captured by our model. For a free nanocarrier the long-time behavior of the translational and rotational VACFs both follow algebraic decays with time, as shown by us in previous studies [24, 27].
Figure 4.
Translational ((a), (b), (c)) and rotational ((d), (e), (f)) VACFs of the Brownian particle of radius a = 250 nm through a circular vessel of radius R = 2.5 μm obtained using fluctuating hydrodynamics and hybrid methods. Here m* = M for the FHD method and m* = m for the hybrid method. The constants a0 = 0.094 and b0 = 0.014 are determined from analytical expressions [25]. Abbreviations, NR: numerical results; FHD: fluctuating hydrodynamics
3.3 Comparison of Potential of Mean Force
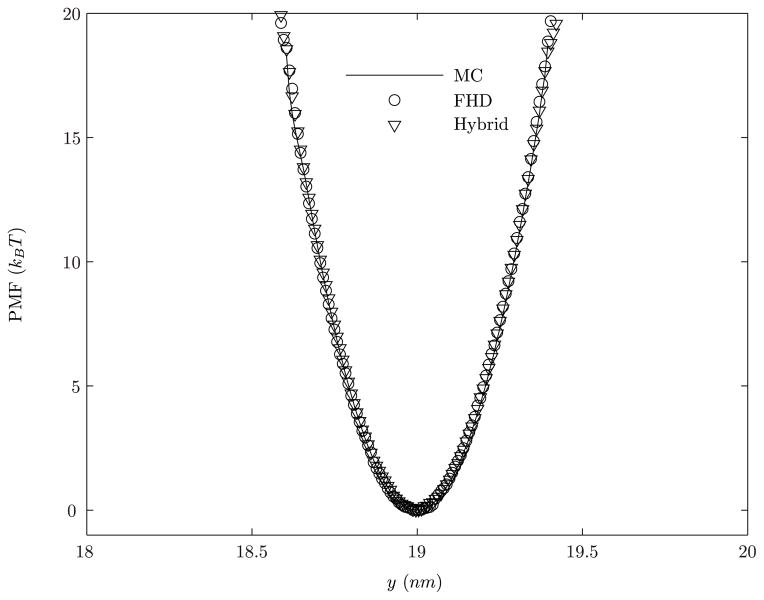
Figure 5 shows the comparison of calculated PMF profile along y using MC and fluctuating hydrodynamics methods at a temperature of 310 K. The excellent agreement between the two methods reiterates the preservation of equilibrium distribution of the canonical ensemble by our dynamics method. The successful validation of the computed PMF using our fluctuating hydrodynamics method also highlights a concrete path for temporal multiscaling; namely, to reach a y-coordinate value of 0.4nm corresponds to a PMF of W(y) = 19kBT, requires a time-scale of ~ 0.1s, which is currently much outside the scope of conventional dynamics; however, the umbrella sampling strategy enables us to evaluate equilibrium probability distributions associated with rare-events.
Figure 5.
The calculated PMF W(y) at a temperature of 310 K. Abbreviations, MC: Monte Carlo method; FHD: fluctuating hydrodynamics method.
4 Conclusions and Future Outlook
For a Brownian particle trapped in a harmonic potential in an incompressible Newtonian stationary fluid medium contained in a horizontal circular vessel, we demonstrate that the thermal equipartition of translation, rotation, and spring degrees of freedom are preserved by our fluctuating hydrodyamics and hybrid formalisms, while simultaneously resolving the nature of the hydrodynamic correlations. We also successfully demonstrate that we can perform temporal multiscaling by evaluating the potential of mean force (or free energy density) along a specified reaction coordinate. This enables the determination of probability distributions and extensive conformational sampling of nanocarrier motion which is prohibitive by conventional dynamics. The framework we have presented in this article provides a comprehensive platform for temporal multiscale modeling of hydrodynamic and microscopic interactions mediating nanocarrier motion in vascular targeted drug delivery. The formalism integrates three distinct regimes: a macroscopic regime (nanocarrier transport occurs in the flowing fluid medium subject to Brownian collisions); a lubrication regime (the nanocarrier approaches the vessel wall); and an adhesion regime (ligands on the carrier interact with cell surface receptors to mediate arrest). Possible extensions to our model to represent more realistic interactions in each of the three regimes are outlined below. (1) Macroscopic regime: while we have shown that the correct equipartition and hydrodynamic correlations can be correctly captured using the fluctuating hydrodynamics and hybrid formalisms, the hybrid formalism is more generally applicable for incorporating pre-programmed memory into the nanocarrier motion. Several modeling approaches to hemodynamics [66] have been proposed in the literature [67, 68, 69, 70]. These models take into account the geometry of the blood particulates, the compliance of blood cells, the flow field and the flow geometry. However, approaches that simultaneously resolve the stochastic nature of the particulate collisions and the hydrodynamic interactions are limited. Towards this objective, the hybrid formalism can be extended such that the random stresses are modified as S = Sthermal + Sathermal in equation 4, where the temperature for the athermal component can be adjusted iteratively to match the experimentally determined collision characteristics under different conditions [21]. Therefore, this method enables us to incorporate pre-programmed dynamic correlations and memory in nanocarrier transport due to stochastic collisions with particulates of the blood plasma in a mean-field fashion, while remaining consistent with experimental conditions. (2) Lubrication regime: It is possible to incorporate the effect of glycocalyx through viscoelastic resistance models, and porous media flow for the fluid in the glycocalyx layer for nanocarrier interaction with the endothelium [22, 23]. The fluctuating hydrodynamics formalism will include the glycocalyx layer by appropriately modifying the stochastic stress tensors to treat the non-Newtonian nature of the fluid medium at the glycocalyx interface. In the presence of the glycocalyx layer and/or to better model the hematocrit as a non-Newtonian fluid (such as using the Casson model), the fluctuating hydrodynamics equations need to be modified by incorporating the desired constitutive equations for the viscosity in the weak formulation as well as when evaluating the random stress tensors. (3) Adhesion regime: to mimic multivalent interactions in the adhesion regime mediated by receptor-ligand bonds, more realistic potentials such as the Bell model and flexural rigidity of the receptors [22, 23] can be incorporated. The potential of mean force using these realistic potentials follow the same strategy as the one we outlined in section 3 and can be employed to quantify the nanocarrier binding affinity, which is experimentally observable [22, 23]. Moreover, this free energy approach can be employed to probe nanocarrier binding under transient flow conditions because our formalism captures the true hydrodynamic correlations. This framework is important in the design of nanocarriers in order to define the adhesion landscape and to determine effects of control variables such as receptor density, antibody density, antibody type, and nanocarrier size/shape, on nanocarrier binding affinity.
The binding affinity is defined based on the probability for the nanocarrier to be bound to the endothelium relative to being unbound. Hence, a potential of mean force approach to compute the absolute binding free energy directly yields the binding affinity. Phenomenon such as rolling, however, can be viewed as connecting two bound states of the nanocarrier under steady or unsteady flow conditions. Since the process of rolling depends on the rate of transitions between successive bound states, a formalism that is reaction coordinate free and that is applicable in unsteady dynamic conditions is more appropriate for addressing rolling behavior. Besides, the reaction coordinate mediating rolling can be quite complex and multi-dimensional, involving multiple receptors and ligands. Such transient processes can be readily treated by combining our methodology with methods for rare-events. Examples include transition path sampling [71, 72], which aims to capture rare events (excursions or jumps between metastable basins in the free energy landscape) in dynamic processes by essentially performing Monte Carlo sampling of symplectic dynamics trajectories. These methodological extensions can easily be integrated with our dynamics framework, thereby vastly expanding the scope of our approach to study adhesive interactions in both steady and unsteady flow conditions.
Acknowledgments
This work was sponsored by National Institute of Health (NIH) Grant R01 EB006818 (D.M.E.); National Science Foundation (NSF) Grant CBET-0853389. Computational resources were provided in part by the National Partnership for Advanced Computational Infrastructure under Grant No. MCB060006.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Warshel A, Levitt M. Theoretical studies of enzymic reactions: dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. Journal of Molecular Biology. 1976;103(2):227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- 2.Klein ML, Shinoda W. Large-scale molecular dynamics simulations of self-assembling systems. Science. 2008;321(5890):798–800. doi: 10.1126/science.1157834. [DOI] [PubMed] [Google Scholar]
- 3.Liu J, Agrawal NJ, Eckmann DM, Ayyaswamy PS, Radhakrishnan R. Top-down mesoscale models and free energy calculations of multivalent protein-protein and protein-membrane interactions. In: Schlick Tamar., editor. Innovations in Biomolecular Modeling and Simulation. Royal Society of Chemistry; 2011. page in press. [Google Scholar]
- 4.Chaikin PM, Lubensky TC. Principles of Condensed Matter Physics. 2. Cambridge University Press; 2000. [Google Scholar]
- 5.Liu J, Bradley R, Eckmann DM, Ayyaswamy PS, Radhakrishnan R. Multiscale modeling of functionalized nanocarriers in targeted drug delivery. Current Nanoscience. 2011;7(5):727–735. doi: 10.2174/157341311797483826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yasuda S, Yamamoto R. Multiscale modeling and simulation for polymer melt flows between parallel plates. Phys Rev E. 2010;81:036308. doi: 10.1103/PhysRevE.81.036308. [DOI] [PubMed] [Google Scholar]
- 7.Kevrekidis IG, Gear CW, Hyman JM, Kevrekidis PG, Runborg O, Theodoropoulos C. Equation-free, coarse-grained multiscale computation: enabling microscopic simulations to perform system-level analysis. Communications in Mathematical Sciences. 2003;1:715–762. [Google Scholar]
- 8.Engquist WEB, Li X, Ren W, Vanden-Eijnden E. Heterogeneous multiscale methods: A review. Communications in Computational Physics. 2007;2:367–450. [Google Scholar]
- 9.Hadjiconstaninou NG, Patera AT. Heterogeneous atomistic-continuum representations for dense fluid systems. International Journal of Modern Physics C. 1997;8:967–976. [Google Scholar]
- 10.Liu WK, Qian D, Gonella S, Li S, Chen W, Chirputkar S. Multiscale methods for mechanical science of complex materials: Bridging from quantum to stochastic multiresolution continuum. International Journal for Numerical Methods in Engineering. 2010;83:1039–1080. [Google Scholar]
- 11.Luan BQ, Hyun S, Molinari JF, Bernstein N, Robbins MO. Multiscale modeling of two-dimensional contacts. Physical Review E. 2006;74:046710. doi: 10.1103/PhysRevE.74.046710. [DOI] [PubMed] [Google Scholar]
- 12.Nie X, Chen S, Robbins WEMO. A continuum and molecular dynamics hybrid method for micro- and nano-fluid flow. Journal of Fluid Mechanics. 2004;500:55–64. [Google Scholar]
- 13.Flekkoy EG, Wagner G, Feder J. Hybrid model for combined particle and continuum dynamics. Europhysics Letters. 2000;52:271–276. [Google Scholar]
- 14.Abraham FF, Broughton JQ, Bernstein N, Kaxiras E. Concurrent coupling of length scales: Methodology and application. Physical Review B. 1999;60:2391–2402. [Google Scholar]
- 15.Shenoy VB, Miller R, Tadmor EB, Phillips R, Ortiz M. Quasicontinuum models of interfacial structure and deformation. Physical Review Letters. 1998;80:742–745. [Google Scholar]
- 16.O’Connell ST, Thompson PA. Molecular dynamics-continuum hybrid computations: A tool for studying complex fluid flows. Phys Rev E. 1995;52:R5792–5795. doi: 10.1103/physreve.52.r5792. [DOI] [PubMed] [Google Scholar]
- 17.Swaminathan TN, Liu J, Uma B, Ayyaswamy PS, Radhakrishnan R, Eckmann DM. Dynamic factors controlling carrier anchoring on vascular cells. IUBMB Life. 2011;63(8):640–647. doi: 10.1002/iub.475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Muzykantov VR, Radhakrishnan R, Eckmann DM. Dynamic factors controlling targeting nanocarriers to vascular endothelium. Current Drug Metabolism. 2011 doi: 10.2174/138920012798356916. page (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Calderon AJ, Muzykantov V, Muro S, Eckmann DM. Flow dynamics, binding and detachment of spherical carriers targeted to icam-1 on endothelial cells. Biorheology. 2009;46:323–341. doi: 10.3233/BIR-2009-0544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Calderon Andres J, Bhowmick Tridib, Leferovich John, Burman Bharat, Pichette Benjamin, Muzykantov Vladimir, Eckmann David M, Muro Silvia. Optimizing en-dothelial targeting by modulating the antibody density and particle concentration of anti-icam coated carriers. Journal of Controlled Release. 2011;150(1):37–44. doi: 10.1016/j.jconrel.2010.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Munn LL, Melder RJ, Jain RK. Role of erythrocytes in leukocyte-endothelial interactions: mathematical model and experimental validation. Biophysical Journal. 1996;71(1):466– 478. doi: 10.1016/S0006-3495(96)79248-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu J, Weller GER, Zern B, Ayyaswamy PS, Eckmann DM, Muzykantov VR, Radhakrishnan R. A computational model for nanocarrier binding to endothelium validated using in vivo, in vitro, and atomic force microscopy experiments. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:16530–16535. doi: 10.1073/pnas.1006611107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu J, Agrawal NJ, Calderon A, Ayyaswamy PS, Eckmann DM, Radhakrishnan R. Multivalent binding of nanocarrier to endothelial cells under shear flow. Biophysical journal. 2011;101(2):319–326. doi: 10.1016/j.bpj.2011.05.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Uma B, Swaminathan TN, Radhakrishnan R, Eckmann DM, Ayyaswamy PS. Nanoparticle Brownian motion and hydrodynamic interactions in the presence of flow fields. Phys Fluids. 2011;23:073602. doi: 10.1063/1.3611026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hauge EH, Martin-Löf A. Fluctuating hydrodynamics and Brownian motion. Journal of Statistical Physics. 1973;7(3):259–281. [Google Scholar]
- 26.Uma B, Swaminathan TN, Ayyaswamy PS, Eckmann DM, Radhakrishnan R. Generalized Langevin dynamics of a nanoparticle using a finite element approach: Thermostating with correlated noise. The Journal of Chemical Physics. 2011;135:114104. doi: 10.1063/1.3635776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Uma B, Eckmann DM, Ayyaswamy PS, Radhakrishnan R. A hybrid formalism combining fluctuating hydrodynamics and generalized langevin dynamics for the simulation of nanoparticle thermal motion in an incompressible fluid medium. Molecular Physics. 2011 doi: 10.1080/00268976.2012.663510. page (under review) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schlick T. Molecular modeling and simulation: an interdisciplinary guide. Springer; Netherlands: 2010. [Google Scholar]
- 29.Landau LD, Lifshitz EM. Fluid Mechanics. Pergamon Press; London: 1959. [Google Scholar]
- 30.Serrano M, Espñnol P. Thermodynamically consistent mesoscopic fluid particle model. Phys Rev E. 2001;64(4):046115. doi: 10.1103/PhysRevE.64.046115. [DOI] [PubMed] [Google Scholar]
- 31.Sharma N, Patankar NA. Direct numerical simulation of the Brownian motion of particles by using fluctuating hydrodynamic equations. Journal of Computational Physics. 2004;201(2):466– 486. [Google Scholar]
- 32.Serrano M, Gianni DF, Español P, Flekkøy EG, Coveney PV. Mesoscopic dynamics of voronoi fluid particles. Journal of Physics A: Mathematical and General. 2002;35(7):1605–1625. [Google Scholar]
- 33.Donev A, Vanden-Eijnden E, Garcia AL, Bell JB. On the accuracy of explicit finite-volume schemes for fluctuating hydrodynamics. Communications in Applied Mathematics and Computational Science. 2010;5(2):149–197. [Google Scholar]
- 34.Ladd AJC. Short-time motion of colloidal particles: Numerical simulation via a fluctuating Lattice-Boltzmann equation. Phys Rev Lett. 1993 Mar;70(9):1339–1342. doi: 10.1103/PhysRevLett.70.1339. [DOI] [PubMed] [Google Scholar]
- 35.Ladd AJC. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. part 1. theoretical foundation. Journal of Fluid Mechanics. 1994;271:285–309. [Google Scholar]
- 36.Ladd AJC. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. part 2. numerical results. Journal of Fluid Mechanics. 1994;271:311–339. [Google Scholar]
- 37.Patankar NA. Technical Proceedings of the 2002 International Conference on Computational Nanoscience and Nanotechnology. Vol. 2. Nano Science and Technology Institute; 2002. Direct numerical simulation of moving charged, flexible bodies with thermal fluctuations; pp. 93–96. [Google Scholar]
- 38.Adhikari R, Stratford K, Cates ME, Wagner AJ. Fluctuating lattice–Boltzmann. EPL (Europhysics Letters) 2005;71(3):473–479. [Google Scholar]
- 39.Dünweg B, Ladd AJC. Lattice–Boltzmann simulations of soft matter systems. Advances in Polymer Science. 2008;221:89–166. [Google Scholar]
- 40.Nie D, Lin J. A fluctuating lattice-Boltzmann model for direct numerical simulation of particle Brownian motion. Particuology. 2009;7(6):501–506. [Google Scholar]
- 41.Español P, Zúñiga I. On the definition of discrete hydrodynamic variables. J Chem Phys. 2009;131:164106. doi: 10.1063/1.3247586. [DOI] [PubMed] [Google Scholar]
- 42.Español P, Anero1 JG, Zúñiga I. Microscopic derivation of discrete hydrodynamics. J Chem Phys. 2009;131:244117. doi: 10.1063/1.3274222. [DOI] [PubMed] [Google Scholar]
- 43.Atzberger PJ, Kramer PR, Peskin CS. A stochastic immersed boundary method for fluid-structure dynamics at microscopic length scales. Journal of Computational Physics. 2007;224(2):1255–1292. [Google Scholar]
- 44.Ermak DL, McCammon JA. Brownian dynamics with hydrodynamic interactions. The Journal of Chemical Physics. 1978;69(4):1352–1360. [Google Scholar]
- 45.Brady JF, Bossis G. Stokesian dynamics. Annual Review of Fluid Mechanics. 1988;20(1):111–157. [Google Scholar]
- 46.Foss DR, Brady JF. Structure, diffusion and rheology of Brownian suspensions by Stokesian dynamics simulation. Journal of Fluid Mechanics. 2000;407:167–200. [Google Scholar]
- 47.Banchio AJ, Brady JF. Accelerated Stokesian dynamics: Brownian motion. The Journal of Chemical Physics. 2003;118(22):10323–10332. [Google Scholar]
- 48.Iwashita T, Nakayama Y, Yamamoto R. A numerical model for Brownian particles fluctuating in incompressible fluids. Journal of the Physical Society of Japan. 2008;77(7):074007. [Google Scholar]
- 49.Iwashita T, Yamamoto R. Short-time motion of Brownian particles in a shear flow. Phys Rev E. 2009 Mar;79(3):031401. doi: 10.1103/PhysRevE.79.031401. [DOI] [PubMed] [Google Scholar]
- 50.Grmela M, Ottinger HC. Dynamics and thermodynamics of complex fluids. i. development of a general formalism. Phys Rev E. 1997;56(6):6620–6632. [Google Scholar]
- 51.Ottinger HC, Grmela M. Dynamics and thermodynamics of complex fluids. ii. illustrations of a general formalism. Phys Rev E. 1997;56(6):6633–6655. [Google Scholar]
- 52.Español P, Serrano M, Ottinger HC. Thermodynamically admissible form for discrete hydrodynamics. Phys Rev Lett. 1999;83(22):4542–4545. [Google Scholar]
- 53.Kubo R. The fluctuation-dissipation theorem. Reports on Progress in Physics. 1966;29(1):255–284. [Google Scholar]
- 54.Zwanzig R. Nonequilibrium Statistical Mechanics. Oxford University Press; 2001. [Google Scholar]
- 55.Patankar NA, Singh P, Joseph DD, Glowinski R, Pan TW. A new formulation of the distributed Lagrange multiplier/fictitious domain method for particulate flows. International Journal of Multiphase Flow. 2000;26:1509–1524. [Google Scholar]
- 56.Chen Y, Sharma N, Patankar NA. Fluctuating immersed material (fimat) dynamics for the direct numerical simulation of the Brownian motion of particles. In: Balachandar S, Prosperetti A, editors. Proceedings of the IUTAM Symposium on Computational Multiphase Flow. Springer Verlag; 2006. pp. 119–129. [Google Scholar]
- 57.Hu HH. Direct simulation of flows of solid-liquid mixtures. International Journal of Multiphase Flow. 1996;22(2):335– 352. [Google Scholar]
- 58.Hu HH, Patankar NA, Zhu MY. Direct numerical simulations of fluid-solid systems using the arbitrary langrangian-Eulerian technique. J Comput Phys. 2001;169(2):427–462. [Google Scholar]
- 59.Roux B. The calculation of the potential of mean force using computer simulations. Computer Physics Communications. 1995;91(1–3):275– 282. [Google Scholar]
- 60.Bell GI, Dembo M, Bongrand P. Cell adhesion. competition between nonspecific repulsion and specific bonding. Biophysical Journal. 1984;45(6):1051– 1064. doi: 10.1016/S0006-3495(84)84252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Muro S, Dziubla T, Qiu W, Leferovich J, Cui X, Berk E, Muzykantov VR. Endothelial targeting of high-affinity multivalent polymer nanocarriers directed to intercellular adhesion molecule. Journal of Pharmacology and Experimental Therapeutics. 2006;317:1161–1169. doi: 10.1124/jpet.105.098970. [DOI] [PubMed] [Google Scholar]
- 62.Agrawal NJ, Radhakrishnan R. The role of glycocalyx in nanocarrier-cell adhesion investigated using a thermodynamic model and monte carlo simulations. The Journal of Physical Chemistry C. 2007;111(43):15848–15856. doi: 10.1021/jp074514x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Zhang X, Wojcikiewicz E, Moy VT. Force spectroscopy of the leukocyte function-associated antigen-1/intercellular adhesion molecule-1 interaction. Biophysical Journal. 2002;83(4):2270– 2279. doi: 10.1016/S0006-3495(02)73987-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Frenkel D, Smit B. Molecular simulation: from algorithms to applications. Orlando, FL: Academic; 2001. [Google Scholar]
- 65.Zwanzig R, Bixon M. Hydrodynamic theory of the velocity correlation function. Phys Rev A. 1970;2(5):2005–2012. [Google Scholar]
- 66.Goldsmith HL, Skalak R. Hemodynamics. Annual Review of Fluid Mechanics. 1975;7(1):213–247. [Google Scholar]
- 67.Pan W, Caswell B, Karniadakis GEM. A low-dimensional model for the red blood cell. Soft Matter. 2010;6:4366–4376. doi: 10.1039/C0SM00183J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Singh V, Koch DL, Stroock AD. Ideal rate of collision of cylinders in simple shear flow. Langmuir. 2011;27(19):11813–11823. doi: 10.1021/la202138t. [DOI] [PubMed] [Google Scholar]
- 69.Boryczko K, Dzwinel W, Yuen AD. Dynamical clustering of red blood cells in capillary vessels. Journal of Molecular Modeling. 2003;9:16–33. doi: 10.1007/s00894-002-0105-x. [DOI] [PubMed] [Google Scholar]
- 70.Chesnutt JKW, Marshall JS. Effect of particle collisions and aggregation on red blood cell passage through a bifurcation. Microvascular Research. 2009;78(3):301– 313. doi: 10.1016/j.mvr.2009.09.003. [DOI] [PubMed] [Google Scholar]
- 71.Dellago C, Bolhuis PG, Geissler PL. Transition Path Sampling. John Wiley & Sons, Inc; 2003. pp. 1–78. [Google Scholar]
- 72.Bolhuis PG, Chandler D, Dellago C, Geissler PL. Transition path sampling: throwing ropes over dark mountain passes. Annual Review of Physical Chemistry. 2002;51:291–318. doi: 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]