Abstract
We introduce a novel algorithm to reconstruct dynamic MRI data from under-sampled k-t space data. In contrast to classical model based cine MRI schemes that rely on the sparsity or banded structure in Fourier space, we use the compact representation of the data in the Karhunen Louve transform (KLT) domain to exploit the correlations in the dataset. The use of the data-dependent KL transform makes our approach ideally suited to a range of dynamic imaging problems, even when the motion is not periodic. In comparison to current KLT-based methods that rely on a two-step approach to first estimate the basis functions and then use it for reconstruction, we pose the problem as a spectrally regularized matrix recovery problem. By simultaneously determining the temporal basis functions and its spatial weights from the entire measured data, the proposed scheme is capable of providing high quality reconstructions at a range of accelerations. In addition to using the compact representation in the KLT domain, we also exploit the sparsity of the data to further improve the recovery rate. Validations using numerical phantoms and in-vivo cardiac perfusion MRI data demonstrate the significant improvement in performance offered by the proposed scheme over existing methods.
I. Introduction
The imaging of dynamically evolving phenomena is central to several magnetic resonance imaging (MRI) applications, including cardiac, perfusion, functional, and gastro-intestinal imaging. Achieving high spatio-temporal resolutions is challenging in dynamic MRI due to the hardware limitations and the risk of peripheral nerve stimulation. Several model based image reconstruction schemes were introduced to improve the spatio-temporal resolution and to minimize the acquisition time in breath-held cardiac MRI [1]–[6]. These methods exploit the banded structure or sparsity of the data in x – f space to recover the dynamic images from under-sampled measurements. Such methods have been observed to perform poorly in the presence of respiratory motion [7], which is often difficult to avoid in several cardiac imaging applications. For example, the dynamic contrast variations in the myocardium are typically imaged for 40–60 seconds in cardiac perfusion imaging; most patients cannot maintain a breath-hold for such long durations, especially during hyperemia. The respiratory motion and contrast variations due to bolus passage severely degrade the structure and sparsity in x-f space, which makes the above model-based schemes ineffective. The current clinical practice of using small image matrices and restricting the temporal resolution and spatial coverage (typically three slices are acquired) present several challenges in the interpretation of cardiac perfusion MRI data. It is also not straight-forward to extend the current model-based schemes to general dynamic imaging applications.
Several researchers have recently proposed to exploit the compact signal representation in the Karhunen Louve transform (KLT) domain as an alternative to x-f space sparsity/structure [8]–[11]. Since KLT is a data-derived transform, the resulting adaptive scheme is capable of exploiting the correlations in the data, even when the temporal profiles of the voxels are not periodic. This property makes these methods applicable to a range of dynamic imaging problems. Current KLT-based algorithms rely on a two-step approach to recover the data [9]–[12]. Specifically, they estimate the temporal basis functions using the singular value decomposition (SVD) of a training dataset; the training dataset is an image time series with low spatial resolution and Nyquist temporal samping rate. The training dataset is obtained as the IFFT of the central phase encodes, which is collected along with higher k-space samples at sub-Nyquist temporal sampling rates. The estimated temporal basis functions are then used to reconstruct the data with high spatio-temporal resolution from sub-Nyquist sampled k-space data. These schemes rely on the implicit assumption that the temporal basis functions estimated from the training data closely approximate the principal components of the entire data. Clearly, this approximation is heavily dependent on the number of phase encodes in the training data. For example, if only a single phase encode is used in the training stage, the estimated temporal functions will fail to capture the dynamics due to intermediate vertical shifts resulting from respiratory motion. Moreover, this may also result in the scheme failing to capture small details such as perfusion defects. These problems can be minimized by acquiring more phase-encodes in the training data. However, this comes at the expense of the number of higher k-space encodes that can be acquired at a specified acceleration factor, resulting in significant spatial aliasing artifacts.
We propose a novel algorithm to significantly accelerate dynamic MRI by exploiting the correlations between the temporal profiles of the voxels. In contrast to the classical KLT-based schemes that use the above two-step approach [9]–[12], we propose to simultaneously estimate the temporal basis functions and its spatial weights directly from the entire k – t space data. This approach is enabled by the re-interpretation of the KLT based reconstruction as a spectrally regularized matrix recovery scheme. Specifically, we pose the joint estimation of the bases and the signal as the recovery of a low-rank matrix, obtained by stacking the temporal dynamics of the voxels, from the measured data. This approach provides more accurate estimates of the temporal basis functions and hence result in reconstructions with better quality at a specified acceleration.
The recovery of a low-rank matrix using nuclear norm minimization has been rigorously studied by several researchers [13]–[17]. Motivated by the recent results in the use of non-convex penalties in compressed sensing [18], [19], we introduce novel non-convex spectral penalties to minimize the number of measurements required to recover a low-rank matrix. By suppressing the singular vectors that correspond to aliasing artifacts, this approach can considerably improve the reconstructions. Moreover, the images in dynamic time series themselves can be assumed to have sparse wavelet coefficients or gradients. We propose to additionally exploit the sparsity of the matrix in pre-determined domains to further improve the recovery rate. Since the degrees of freedom in representing sparse and low-rank matrices are significantly lower than the class of arbitrary low-rank matrices, this approach enables us to improve the recovery rate. We do not promote joint sparsity as done in [20]. In our work, the temporal basis functions themselves are not constrained to be sparse in any bases; enforcing the sparsity in a specified space (eg. Fourier) may introduce significant bias in the presence of motion (and/or perfusion) (see Fig. 1). Moreover, we observe that different temporal basis functions play dominant roles in different spatial regions. Since the sparsity properties of these functions may be very different, we expect the use of joint sparsity penalty to smooth subtle motion/perfusion induced variations.
Fig. 1.

Utility of KLT in compactly representing the dynamic image time series: The numerical simulation of breath held cine data (top row) and ungated free breathing data (bottom row), along with their corresponding representations in the x – f and x–KLT spaces are shown. The x –f space coefficients are highly sparse/structured in the context of breath-held acquisitions due to the pseudo-periodic nature of heart-beats. The structure and sparsity of the x –f space is disturbed in the presence of breathing motion. In contrast, the free breathing data is compact in the x–KLT space. The few significant singular values implies that the dataset can be efficiently approximated as a low rank matrix, described by (1).
The preliminary version of this work was reported in our conference paper [21]. The work of Haldar et. al. [22], which was also published in the same proceedings, is conceptually similar to the proposed scheme. However, they do not use sparsity priors and their optimization scheme is drastically different from the proposed scheme.
Most of the existing convex matrix recovery algorithms are based on iterative singular value thresholding [14], [23], [24]. Since it is not straightforward to extend these schemes to our problem with both sparsity and low-rank penalties, we introduce a novel variable splitting algorithm for the fast minimization of the optimization criterion. This approach is the generalization of similar algorithms used for total variation minimization [25], [26] to matrix recovery. We demonstrate the utility of the proposed scheme in the context of clinical cardiac perfusion MRI. Validations using numerical phantoms and in-vivo data demonstrate the significant improvement in performance over state of the art methods. Although we focus on cardiac perfusion imaging in this paper, the algorithm is readily applicable to most dynamic MRI applications.
II. Background
A. Dynamic MRI using KLT
We denote the spatio-temporal signal as γ(x, t), where x is the spatial location and t denotes time. The dynamic MRI measurements correspond to the samples of the signal in k – t space, corrupted by noise:
Here, (ki, ti) indicates the ith sampling location. We denote the set of sampling locations as Ξ = {(ki, ti), i = 0, .., s − 1}. The above expression can be rewritten in the vector form as b =
 (γ) + n, where,
(γ) + n, where,
 is the Fourier sampling operator. The goal is to recover the signal γ(x, t) from the measured k-t space samples.
is the Fourier sampling operator. The goal is to recover the signal γ(x, t) from the measured k-t space samples.
In dynamic imaging applications, the temporal profiles of the voxels, indicated by the n-dimensional vectors
are highly correlated/linearly dependent. Here, m is the number of voxels. Liang et. al., proposed to re-arrange the spatio-temporal signal γ(x, t) in a matrix form to exploit the correlations [8], [9]:
| (1) |
The rows of Γ correspond to the voxels, while the columns represent the temporal samples. Since the rows of this m × n matrix are linearly dependent, the rank of Γ, is given by r < min (m, n). An arbitrary m × n matrix of rank r can be decomposed as
| (2) |
This decomposition implies that the spatio-temporal signal γ(x, t) can be expressed as a weighted linear combination of r temporal basis functions [8], [9]:
| (3) |
The temporal basis functions vi(t) are the columns of the matrix V in (2) while the spatial weights ρi(x) are the row vectors of UΣ (often termed as spatial weights). The utility of this scheme in compactly representing the dynamic time series data is illustrated in Fig. 1. Most of the KLT-based algorithms use the below-mentioned two-step strategy to reconstruct the spatio-temporal signal [8]–[12].
Estimate the temporal basis functions vi(t); i = 0, .., r − 1 using SVD of the training image time-series. The training data consists of dynamic image data, acquired with low-spatial resolution and high temporal sampling rate; it is obtained as the IFFT of the central phase encodes, acquired at the Nyquist temporal sampling rate.
Use the linear model specified by (3) to recover the cardiac data from sub-Nyquist sampled measurements, using the pre-determined temporal basis functions vi(t). This involves the estimation of the spatial weight images ρi(x); i = 0, .., r − 1 from the under-sampled measurements. Since r ≪ n, this approach provides a significant reduction in the number of unknowns and hence the number of measurements.
These schemes implicitly assume that the principal basis functions estimated from the low-resolution data to closely approximate the original KLT basis functions. As discussed previously, this assumption is violated when the number of phase encodes in the training data are too few, resulting in the loss of subtle details and reconstructions with inaccurate temporal dynamics. While the acquisition of more training data can minimize these problems, this comes at the expense of the number of high-frequency encodes that can be acquired at a specified acceleration rate; this can often result in aliasing artifacts. In summary, the performance of the two-step schemes requires a fine balance between the amount of training data and the number of high-frequency encodes. To overcome these problems, we introduce the single-step spectrally regularized reconstruction scheme in Section III.
B. Matrix recovery using nuclear norm minimization
The recovery of a low-rank matrix Γ from few of its linear measurements is currently a hot topic in signal processing. The recent theoretical results indicate that a matrix Γ ∈ ℝm×n of rank r; r ≤ min(m, n) can be perfectly recovered from its measurements b =
 (Γ) by solving the constrained optimization problem [15], [27]:
(Γ) by solving the constrained optimization problem [15], [27]:
| (4) |
The rank constraint is an effective means of regularizing the inverse problem since it significantly reduces the number of degrees of freedom. Specifically, the number of degrees of freedom in representing m × n matrices of rank r is r(m+n−r), which is much smaller than mn. Recht et. al. have shown that this approach perfectly recovers the matrix with a high probability, if the random measurement ensemble is used and the number of measurements exceeds a constant (two to four) times the number of degrees of freedom [27]. Reformulating the above constrained optimization problem using Lagrange’s multipliers, we get
| (5) |
Since the rank penalty is non-convex, it is often replaced with the nuclear norm, which is the closest convex relaxation. The nuclear norm of an r-rank matrix Γ = UΣV*, denoted by ||Γ||*, is the sum of the singular values of . With this relaxation, the recovery of the matrix is simplified as
| (6) |
III. k-t SLR: Formulation
We introduce the proposed algorithm in two steps to facilitate its easy understanding. We will first introduce the reconstruction of the spatio-temporal signal as a spectrally regularized matrix recovery problem in Section III-A. This scheme is then further constrained using additional sparsity priors to improve the recovery rate in Section III-B.
A. Regularized matrix recovery using spectral priors
We recover the matrix Γ from the undersampled k–t space data as a spectrally regularized optimization problem, similar to (6):
| (7) |
where ϕ(Γ) is an appropriate spectral penalty1. We use the general class of Schatten p-functionals, specified by
| (8) |
Here, Γ = UΣV* is the singular value decomposition of Γ and Σ = diag ([σ0, σ1, ..σr−1]). The above spectral penalty simplifies to the nuclear norm for p = 1. When p ≤ 1, this penalty ceases to be a norm and is non-convex. The use of similar non-convex semi-norms are well-studied in the context of vector recovery; they are found to significantly improve the reconstruction of the signal from fewer measurements, in comparison to the standard ℓ1 semi-norms [28]–[32]. During the review of this paper, we were made aware of the recent work of Majumdar et. al [33], where they introduced the non-Convex Schatten p-norm for denoising and 2D MRI. The optimization algorithm in [33] is very different from our approach. In addition to providing rapid convergence, our algorithm is also capable of using sparsity penalties.
Note that the cost function, specified by (8), does not depend explicitly on the temporal basis functions or its spatial weights as in the case of current two-step KLT schemes. However, the optimization algorithm to minimize (8) iteratively updates the temporal basis functions and spatial weights, which are essentially the column vectors of V and U respectively. The optimization algorithm is discussed in detail in Section IV.
B. Regularized matrix recovery using spectral and sparsity priors
In dynamic imaging applications, the images in the time series may have sparse wavelet coefficients or sparse gradients. In addition, if the intensity profiles of the voxels are periodic (eg. cardiac cine), the columns of Γ may be sparse in the Fourier domain. We propose to additionally exploit the sparsity of the signal in specified basis sets along with the low-rank property to further improve the recovery rate. Specifically, we consider the simple example of recovering an r-rank matrix Γ ∈ ℝm×n that has atmost N non-zero entries in a specified basis: ||ΦHΓΨ||ℓ0 ≤ N. Here, Φ and Ψ are transformations or operators that sparsify the row-space and column space of Γ, respectively. For example, Φ can be chosen to be the 2-D wavelet transform to sparsify each of the images in the time series, while Ψ can be a 1-D Fourier transform to exploit the pseudo-periodic nature of motion. The set of matrices that satisfy both the rank and the sparsity constraints are far smaller in dimension than the class of matrices that satisfy only one of the constraints. For example, consider an r-rank matrix Γ whose right and left singular vectors are k1 and k2 sparse. The number of degrees of freedom of such r-rank matrices is given by r(k1 + k2 − r). If k1 ≪ m and k2 ≪ n, the use of this prior knowledge, along with the low-rank constraint, can significantly reduce the number of measurements required to recover the matrix. To exploit the sparsity and low-rank properties of the matrix, we formulate the problem as
| (9) |
Rewriting the above constrained optimization problem using Lagrange’s multipliers and relaxing the penalties, we obtain
| (10) |
where ψ (Γ) = ||ΦHΓΨ||ℓ1 is a surrogate for the ℓ0 term and . When p ≥ 1, the cost function is convex and hence will have a unique minimum.
While it is straight-forward to use this scheme to exploit the sparsity in different transform domains, it cannot be used for non-separable total variation (TV) penalties. Exploiting the sparsity of the gradient has proven to be very powerful in various image recovery application and is shown to provide comparable or better performance than most other transform domain schemes [34]. To adapt this scheme for TV regularization, we consider a collection of transforms/operators on Γ, indicated by , i = 0, .., q − 1, and specify the non-separable penalty as
| (11) |
The total variation norm of the entire volume can be obtained by setting q = 3, Φ0 = Dx; Ψ0 = I, Φ1 = Dy; Ψ1 = I, and Φ2 = I; Ψ2 = Dt, where Dx, Dy and Dt are the finite difference matrices along x, y, and t respectively. Note that the above expression simplifies to the standard ℓ1 penalty, when the number of transforms/operators is q = 1.
The proposed scheme is well posed since the sparsifying transforms/operators Φi, Ψi; i = 0, .., q−1 are incoherent with the Fourier sampling operator. We do not need the additional assumption of the right and the left singular vectors of Γ to be in-coherent with the operator that picks the samples/matrix entries of Γ as in [13]to make the problem well posed.
IV. Optimization Algorithm
It is not straightforward to extend the current nuclear norm minimization schemes [14], [23], [24] to solve (10), since it uses both sparsity and spectral penalties. We introduce a novel variable splitting algorithm for the efficient recovery of the matrix using (10).We pose the regularized matrix recovery scheme as a constrained minimization problem using variable splitting:
| (12) |
Here, R and Si; i = 0, .., q −1 are auxiliary variables, which are also determined during the optimization process. The rationale behind the above decomposition is that the constrained optimization problem is simpler to solve than its unconstrained version, specified by (10). We solve (12) using the penalty method, where we minimize
| (13) |
with respect to Γ, R and Si; i = 0, .., q − 1. The second row of (13) are the penalties introduced to enforce the constraints Γ = R and ; i = 0, .., q − 1. The solution of the above problem tends to that of (12), when β1, β2 → ∞. We solve (13) using a three-step alternating minimization scheme below (14,15,16), where we solve a variable of interest assuming the rest to be known:
| (14) |
| (15) |
| (16) |
Similar alternating directions methods are widely used in compressed sensing and TV minimization [26], [35]. The first sub-problem (14) is quadratic and hence can be solved analytically as
| (17) |
where the operator
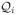 is defined as
; i = 0, .., q − 1 This step can be efficiently evaluated in the Fourier domain, if the measurements are Fourier samples on a Cartesian grid [25], [26]. We instead rely on solving (14)using a few conjugate gradient steps, since we are dealing with non-Cartesian sampling problems.
is defined as
; i = 0, .., q − 1 This step can be efficiently evaluated in the Fourier domain, if the measurements are Fourier samples on a Cartesian grid [25], [26]. We instead rely on solving (14)using a few conjugate gradient steps, since we are dealing with non-Cartesian sampling problems.
The second sub problem is of the similar form of standard nuclear norm minimization problems. The iterative singular value thresholding (IST) scheme used in nuclear norm minimization can be generalized to the case that has non convex spectral penalties. The generalization in this regard, would lead to obtaining Rn+1 as a singular value thresholding of Γn+1, specified by
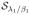 :
:
| (18) |
where the singular value shrinkage is specified by,
| (19) |
Here, ui, vi and σi are the singular vectors and values of Γn+1, respectively. The thresholding function is defined as
| (20) |
Note that, when p = 1, the expression in (19) simplifies to the shrinkage scheme used for nuclear norm minimization problems.
The solution to the third sub problem (16) requires the joint processing of all the terms
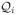 (Γn+1); i = 0, .., q −1, such that the magnitude, specified by
, is reduced:
(Γn+1); i = 0, .., q −1, such that the magnitude, specified by
, is reduced:
| (21) |
This approach is termed as multidimensional shrinkage of {
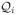 (Γn+1), i = 0, .., q − 1} [26], [35].
(Γn+1), i = 0, .., q − 1} [26], [35].
The convergence of the above three step alternating minimization scheme as the penalty parameters β1, β2 → ∞ is well known [36]. The three-step optimization scheme involves update rules based on the operators
 ,
,
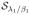 , κλ2/β2. Clearly, we are interested in the convergence of this iterative scheme to its fixed point, specified by R*,
; i = 0, .., q−1. Following the proofs in [25], it can be shown that the three-step scheme converges to the global minimum of
, κλ2/β2. Clearly, we are interested in the convergence of this iterative scheme to its fixed point, specified by R*,
; i = 0, .., q−1. Following the proofs in [25], it can be shown that the three-step scheme converges to the global minimum of
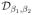 (Γ,
R,
Si)for any fixed β1
> 0, β2
> 0. The argument proceeds by showing that the operator
(Γ,
R,
Si)for any fixed β1
> 0, β2
> 0. The argument proceeds by showing that the operator
 and the shrinkage operations
and the shrinkage operations
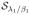 , κλ2/β2 are non-expansive; (i.e, ||
, κλ2/β2 are non-expansive; (i.e, ||
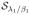 (Γ1) −
(Γ1) −
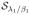 (Γ2)||2 ≤ ||Γ1 − Γ2||2)2 and (||κλ2/β2(Γ1) − κλ2/β2(Γ2)||2 ≤ ||Γ1 − Γ2||2). Since these operators are non-expansive, the above iterative algorithm to update the auxiliary variables R and Si will decrease the distances ||Rn − R*||F,
respectively at each iteration; here (R*,
; i = 0, ..q − 1) is the optimal solution. This implies that Rn → R* and
as n → ∞.
(Γ2)||2 ≤ ||Γ1 − Γ2||2)2 and (||κλ2/β2(Γ1) − κλ2/β2(Γ2)||2 ≤ ||Γ1 − Γ2||2). Since these operators are non-expansive, the above iterative algorithm to update the auxiliary variables R and Si will decrease the distances ||Rn − R*||F,
respectively at each iteration; here (R*,
; i = 0, ..q − 1) is the optimal solution. This implies that Rn → R* and
as n → ∞.
High values of β1, β2 are needed for the solution of
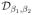 (Γ,
R,
Si) to yield a good approximation for the original minimization scheme in (12), as discussed before. However, the quadratic problem specified by (14) will become ill-conditioned for high values of β1, β2, resulting in poor convergence. We propose to use a continuation strategy to overcome the tradeoff between computational complexity and accuracy. Specifically, we will start with very small values of β1, β2, when the algorithm converges very fast to {Γ,
R,
Si}(β1,β2)n; i = 0, .., q − 1, which is the solution of
(Γ,
R,
Si) to yield a good approximation for the original minimization scheme in (12), as discussed before. However, the quadratic problem specified by (14) will become ill-conditioned for high values of β1, β2, resulting in poor convergence. We propose to use a continuation strategy to overcome the tradeoff between computational complexity and accuracy. Specifically, we will start with very small values of β1, β2, when the algorithm converges very fast to {Γ,
R,
Si}(β1,β2)n; i = 0, .., q − 1, which is the solution of
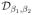 . To improve the quality of the approximation, we will then increase (β1, β2)n to obtain (β1, β2)n+1 and initialize the algorithm with {Γ,
R,
Si}(β1β2)n+1 = {Γ,
R,
Si}(β1β2)n; i = 0, .., q − 1. We observe that the continuation strategy significantly improves the convergence of the algorithm. Similar continuation strategies are widely used in similar algorithms for total variation minimization and compressed sensing [26], [35].
. To improve the quality of the approximation, we will then increase (β1, β2)n to obtain (β1, β2)n+1 and initialize the algorithm with {Γ,
R,
Si}(β1β2)n+1 = {Γ,
R,
Si}(β1β2)n; i = 0, .., q − 1. We observe that the continuation strategy significantly improves the convergence of the algorithm. Similar continuation strategies are widely used in similar algorithms for total variation minimization and compressed sensing [26], [35].
To summarize, the regularized matrix recovery scheme as a constrained minimization problem using variable splitting framework involves the following three step algorithm with a continuation strategy:
| Variable splitting with continuation: Set p = 0; (β1)0, (β2)0 > 0; R = 0; Si = 0; i = 0, .., q − 1; Γ = 0 |
| Repeat |
| Repeat |
| Update Γ by solving (14) using the CG scheme; |
Shrinkage: R =
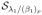 (Γ); (Γ); |
| Shrinkage: Si = κλ2/(β2)p(Γ) ; i = 0, .., q − 1; |
| Until stopping criterion is satisfied. |
| (β1)p+1 = (β1)p * INC_FACTOR1; (β2)p+1 = (β2)p * INC_FACTOR2; |
| p = p + 1 |
| Until R ≈ Γ and ; i = 0, .., q − 1 |
Note that the above algorithm involves two loops. The parameters β1, β2 are incremented in the outer loop, while the minimization of
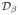 (Γ,
R,
Si); i = 0, .., q − 1 is performed in the inner loop. We terminate the inner iteration when the stopping criterion, specified by
(Γ,
R,
Si); i = 0, .., q − 1 is performed in the inner loop. We terminate the inner iteration when the stopping criterion, specified by
| (22) |
is satisfied.
The above discussed theoretical guarantees on the convergence are not valid for the non-convex spectral penalties (i.,e when p < 1). However, we did not experience issues with convergence in our practical experiments; we obtained monotonic reduction in the cost function and the algorithm converged to a good minimum, independent of the initialization. The main reason for the good convergence performance may be attributed to the continuation scheme.
A. Implementation
The computationally expensive component of the algorithm is the singular value decomposition required for (15). The usual dynamic MRI data sizes are 128x128x70, resulting in the matrix Γ of size 16384 x 70. To minimize the computational complexity, we first determine the right singular vectors and the singular values as the eigen decomposition of ΓHΓ. The eigen decomposition of this 70x70 matrix takes less than 0.1 seconds in MATLAB. The left singular vectors are then obtained using a simple least squares scheme, using the known singular values and left singular vectors. We realized the entire algorithm, described by (14)–(16), in MATLAB using Jacket [37] on a Linux workstation with eight cores and a NVDIA Tesla graphical processing unit. We observe that the execution time for the reconstruction of the largest data (128x128x70) is approximately eight to ten minutes. We focus on the total variation sparsity prior as explained in Section III-B. However, the proposed algorithm is general enough to exploit the sparsity in any transform/operator domain.
V. Materials and Methods
A. Datasets
We study the utility of the proposed k-t SLR scheme in accelerating cardiac perfusion MRI. To validate the method, we use (a) the physiologically improved non uniform cardiac torso (PINCAT) numerical phantom [38], [39] and (b) in-vivo cardiac perfusion MRI data. We set the parameters of the PINCAT phantom to obtain realistic cardiac perfusion dynamics and contrast variations due to bolus passage, while accounting for respiration with variability in breathing motion. The contrast variations due to bolus passage are realistically modeled in regions of the right ventricle (RV), left ventricle (LV) and the left ventricle myocardium. To obtain a realistic model, we use the Biot-Savart’s law to simulate the spatial distribution of the magnetic flux of the receiver coil [40]. We consider a single coil that is placed on the chest and has the maximum sensitivity to the FOV containing the heart. Here, we use a single slice and assume a temporal resolution of one heart-beat, acquired during the diastolic phase (where the cardiac motion is minimal). The time series data consists of 70 time frames. We observe that the predominant motion (due to respiration) is in the superior-inferior direction with a low degree of through plane motion in the anterior-posterior direction. The spatial matrix size is 128 x 128, which corresponds to a spatial resolution of 1.5 x 1.5 mm2. A few slices of this dataset are shown in Figure 2.
Fig. 2.

The PINCAT phantom used to validate the proposed scheme. Three distinct spatial frames at different instances of the contrast uptake are shown in (a)–(c). The x – t cross section of the dataset corresponding to the arrow in (c) is shown in (d). The temporal location of the frames shown in (a) – (c) are marked by dotted lines in (d).
The in-vivo data was acquired on a 3T Siemens scanner with a saturation-recovery sequence (TR/TE=2.5/1 ms, saturation recovery time=100 ms) at the University of Utah. The study was approved by the institutional review board and written consent was obtained from the subject before the acquisition. The data from a single slice was acquired on a Cartesian grid with a k-space matrix of 90 ×190 (phase-encodes x frequency encodes) at a temporal resolution of one heart-beat. The subject was instructed to hold the breath for as long as possible. However, the data had significant motion as the subject was not capable of holding the breath for the entire imaging duration.
B. Comparisons against different methods
We compare the k-t SLR scheme against (a) two-step KLT schemes with different number of phase encodes in the training data (b) the k-t FOCUSS scheme, which relies on sparsity in the x-f space, and (c) variants of the k-t SLR scheme, which rely on only the TV penalty and the spectral penalty alone. Using these comparisons, we mainly seek to verify the following claims:
Posing the dynamic reconstruction problem as a spectrally regularized matrix recovery problem provides improved reconstructions over two-step KLT schemes. To verify this claim, we focus on the comparisons between the spectrally regularized matrix recovery scheme (only low rank prior; p = 0.1; λ2 = 0) and the two step KLT method [8]–[11] with different training data settings at different accelerations.
The exploitation of the sparsity priors, along with the low rank structure, can improve the reconstructions. To verify this claim, we focus on the comparisons of the k-t SLR scheme against regularized schemes that rely only on the spectral (λ2 = 0) or TV (λ1 = 0) penalty.
The k-t SLR scheme can outperform regularized schemes that rely on the sparsity in x-f space. The k-t FOCUSS scheme is known to provide comparable or better performance over all dynamic imaging schemes that use the sparsity in x-f space. We hence compare the k-t SLR scheme against k-t FOCUSS.
The reconstructions are evaluated at a range of acceleration factors denoted by A, which is defined as PEs in fully sampled dataset
| (23) |
it is the ratio of the number of acquired phase encodes in the fully sampled dataset to the number of phase encodes used to reconstruct the dataset. We quantify the performance of the algorithms using the signal to error ratio (SER) specified as
| (24) |
where ||·||F is the Frobenius norm. While this measure provides a quantitative index of performance, it is notorious in being insensitive to artifacts and other distortions. Hence, we also show specific reconstructed frames and the time series data to enable visual comparisons.
The two-step KLT schemes assume a dual density Cartesian sampling pattern. Specifically, the central k-space samples are acquired at the Nyquist temporal sampling rate, while the outer k-space are sampled with a lower-density as shown in Figure 5. We consider the KLT scheme with different number of phase encodes in the training data to analyze the performance dependence of the scheme on the number of samples in the training data. Here, we denote the size of the training data by Nt. The regularized reconstruction schemes such as k-t FOCUSS, k-t SLR, and its variants (spectral penalty alone, TV penalty alone) are capable of accounting for arbitrary non-Cartesian sampling patterns. For these schemes, we consider a radial trajectory with uniform angular spacing; the angular spacing between the spokes is chosen to obtain the specified acceleration factor. The trajectory is rotated by a small random angle in each temporal frame to make the measurements incoherent. By using the equi-angular spacing within each frame, we ensure that the entire k-space is covered uniformly. By considering a small random angle rotation, we not only maintain incoherency, which is required for k-t SLR, spectral penalty and k-t FOCUSS schemes; but also ensure that there are not any sudden jumps across the samples acquired over time, as these jumps could not be optimal for the reconstruction based on only the TV penalty.
Fig. 5.
Comparison of the two-step KLT schemes (two top rows) with the spectrally regularized reconstruction scheme (p = 0.1, λ2 = 0), shown in the bottom row. The sampling pattern, the peak LV frame of the reconstructed dataset, the corresponding error image (shown at the same scale in all the insets), and the estimated temporal basis functions (vi(t), i = 0 to 3) overlaid on the actual temporal basis functions are shown in each column. Note that the classical KLT based schemes experience a tradeoff between spatial aliasing and accuracy of temporal modeling. The first row correspond to Nt = 41, where the basis functions are estimated correctly. However, the sparse sampling of outer k-space regions results in spatial aliasing, indicated by the dotted arrow. When the number of phase encodes in training data is reduced to Nt = 5 in the second row, the temporal basis functions fail to capture the dynamics; this often results in inaccurate temporal modeling of the cardiac motion, especially in regions with significant respiratory motion (denoted by the solid arrow). The spectrally regularized reconstruction scheme, along with the radial sampling pattern, is capable of accurately estimating the temporal bases and spatial weights directly from the undersampled data. The significantly decreased errors with the spectral regularization scheme proves the utility in jointly estimating the temporal basis functions and its spatial weights.
We use the NUFFT approximation [41] to realize the
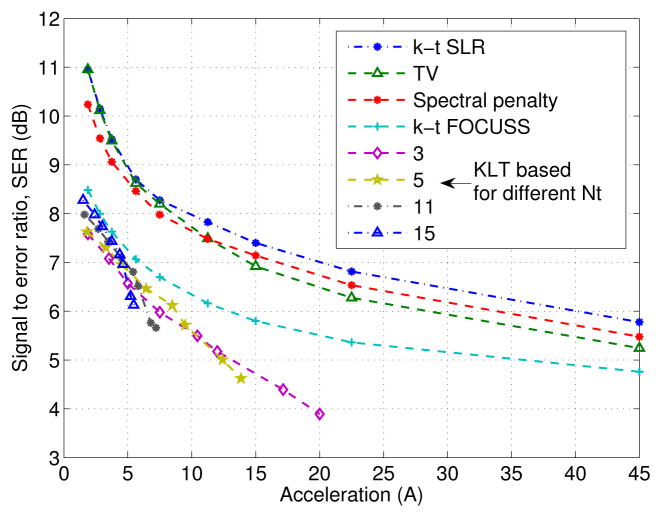
 operator. See Figure 5 for an illustration. We add zero mean Gaussian random noise to the measurements in the PINCAT comparisons such that the signal to noise ratio is 46 dB. In the in-vivo comparisons, we resample the uniformly sampled Cartesian data. Hence, we approximate the above radial trajectory with its closest Cartesian trajectory. Specifically, we approximate each k-space location with its nearest neighbor on the Cartesian grid. We chose to use the non convex (p = 0.1) spectral penalty to exploit the low rank structure because of its superior performance of suppressing singular values associated with artifacts as opposed to the (p = 1), nuclear norm penalty; (See figure (4), where the spectral penalty obtains a consistent increase in the SER over nuclear norm at a range of accelerations).
operator. See Figure 5 for an illustration. We add zero mean Gaussian random noise to the measurements in the PINCAT comparisons such that the signal to noise ratio is 46 dB. In the in-vivo comparisons, we resample the uniformly sampled Cartesian data. Hence, we approximate the above radial trajectory with its closest Cartesian trajectory. Specifically, we approximate each k-space location with its nearest neighbor on the Cartesian grid. We chose to use the non convex (p = 0.1) spectral penalty to exploit the low rank structure because of its superior performance of suppressing singular values associated with artifacts as opposed to the (p = 1), nuclear norm penalty; (See figure (4), where the spectral penalty obtains a consistent increase in the SER over nuclear norm at a range of accelerations).
Fig. 4.
Decay of SER as a function of acceleration on the PINCAT data. Note that the k-t SLR scheme provides an improvement of around 2–4 dB over k-t FOCUSS and two-step KLT based schemes at most accelerations. It is seen that the TV scheme provides reconstructions that are similar in SER to the k-t SLR scheme at low accelerations (A < 4). However, at higher accelerations, the TV reconstructions exhibit significant over-smoothing and loss of spatial details as seen from Figure 6.
The regularization parameters of the penalized schemes (k-t FOCUSS, k-t SLR, low rank penalty alone, and TV penalty alone) have to be optimized to enable fair comparisons between the different methods. We determine the optimal regularization parameters such that the SER of the reconstructions are maximized. Similarly, the model order (number of temporal basis functions) of the two-step KLT schemes are chosen such that the SER is maximized. We rely on the fully sampled dataset to compute the SER. Alternate risk functions, which closely approximate the signal to error ratio, have been introduced by [42] for cases when ground truth is not available. We plan to use such risk functions for the selection of the regularization parameters and model-order in the future. We initialize the regularized reconstruction schemes with the gridding solution and iterate the algorithms until convergence.
VI. Results
We initially demonstrate the utility of the continuation scheme in accelerating the convergence. We then perform quantitative and qualitative comparisons of the proposed scheme with the different methods listed in section V-B on the PINCAT and invivo cardiac perfusion data sets to verify our claims.
A. Convergence of the algorithm
We first study the convergence of the optimization algorithm in the context of the PINCAT phantom, sampled with 20 k-space spokes/frame; A = 6.4 in Figure 3. Here, we plot the decrease in the cost function, specified by (10), and the improvement in SER of the reconstructed data as a function of the number of iterations. It is seen that for lower values of β1 and β2, the algorithm converges quite fast to the solution of
 . However, this corresponds to a low SER since the constraints in (12) are not satisfied. Increasing the parameters β1 and β2 ensures that the constraints are satisfied, but results in slow convergence. We observe that the continuation scheme, where β1 and β2 are gradually increased starting from low values, provides a significantly improved convergence rate with good accuracy. In our experiments, we set the TOLERANCE=10−6 to ensure good convergence.
. However, this corresponds to a low SER since the constraints in (12) are not satisfied. Increasing the parameters β1 and β2 ensures that the constraints are satisfied, but results in slow convergence. We observe that the continuation scheme, where β1 and β2 are gradually increased starting from low values, provides a significantly improved convergence rate with good accuracy. In our experiments, we set the TOLERANCE=10−6 to ensure good convergence.
Fig. 3.
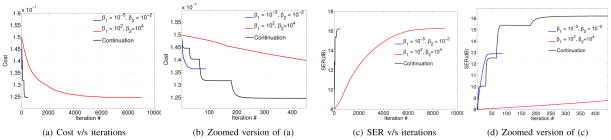
Convergence of the proposed continuation scheme as a function of β1 and β2. (a) indicates the evolution of the cost function specified by (10), while (b) is zoomed version of (a). The change in signal to error ratio as a function of the iterations is shown in (c) with its zoomed version in (d). Note that the convergence of the algorithm is very slow if these parameters are chosen as high values, which is needed for the constraints in (12) to be satisfied. In contrast, the algorithm converges very fast, when these parameters are set to low values. However, the solution of
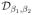 is a poor approximation for the solution of (10). We observe that by properly selecting a continuation scheme, it is possible to significantly improve the convergence rate, while maintaining the accuracy.
is a poor approximation for the solution of (10). We observe that by properly selecting a continuation scheme, it is possible to significantly improve the convergence rate, while maintaining the accuracy.
B. Comparisons on the PINCAT phantom
We plot the SER v/s acceleration (A) for the various reconstruction schemes in Figure 4. It is seen that k-t SLR method consistently out-performs k-t FOCUSS and the classical KLT-based algorithms by 2–4 dB at most accelerations. We observe that the TV regularization scheme provides comparable SER to k-t SLR at lower acceleration factors, but the performance of the TV algorithm degrades significantly as the acceleration increase. To enable visual comparisons, we show the reconstructions of the different approaches at A ≈ 5 in Figure 6. The improved reconstructions offered by k-t SLR can be easily appreciated. We now specifically focus on verifying our claims.
Fig. 6.
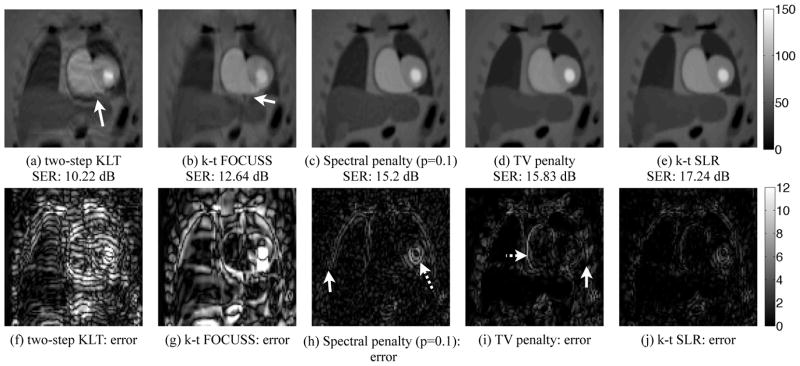
Performance evaluation of k-t SLR in comparison with different schemes on the PINCAT phantom: We compare the k-t SLR (fifth column) against the best two-step KLT scheme (first column), k-t FOCUSS (second column) and its own variants i.e, using the spectral penalty alone and the TV penalty alone (third and fourth columns respectively). The two-step KLT scheme assumes A = 5.28, while all the other methods provides an acceleration of A = 5.33. The reconstructed peak LV uptake frame and the corresponding error images shown in the top and bottom rows respectively. The two-step KLT scheme exhibits incorrect temporal modeling and spatial aliasing, indicated by the arrow in (a)). Since the sparsity in the x – f space is disturbed in the presence of respiratory motion, the k-t FOCUSS reconstructions results in aliasing in regions with significant inter frame motion (see arrow in (b)). The use of the spectral penalty alone resulting in temporal smoothing (dotted arrow in (h)) and residual streaking artifacts due to aliasing (solid arrow in (h)). The use of the TV scheme alone suppresses the spatial aliasing artifacts, while it loses important spatial details due to over smoothing. For instance, the border between the myocardium and the blood pool are smeared, indicated by the dotted arrow in (i) and the details of the ribs are smeared (solid arrow in (i)). By combining the benefits of both low rank and TV schemes, the k-t SLR scheme provides more accurate reconstructions.
1) Utility of the proposed spectrally regularized scheme over two-step KLT methods
We compare the reconstructions of the spectrally regularized algorithm (p = 0.1; λ2 = 0) with the two-step KLT approach in Figure 5. We set A ≈ 3 and consider two different choices of the training data. Note that the accuracy of the temporal basis functions estimated with the two-step KLT schemes are dependent on the number of phase encodes in the training data. It is seen from the second row of Figure 5 that the estimate of the temporal basis functions are poor when the number of phase encodes in the training data is less, resulting in degradations in the temporal dynamics. While the accuracy of the temporal basis functions is improved when the number of phase-encodes in the training data are increased, it comes at the expense of lower density in outer k-space; the lower k-space density results in significant spatial aliasing artifacts in the reconstructions, as seen from the first row of Figure 5. Since the spectrally regularized reconstruction algorithm estimates the temporal bases and the spatial weights directly from the undersampled data, the estimates are more accurate as seen from the last row of Figure 5.
2) Advantage of exploiting total variation prior, along with the spectral penalty
We direct the readers attention to the last three columns of Figure 6 where we study the regularized schemes with TV penalty only, spectral penalty only, and k-t SLR at A = 5.33. It is seen that the TV algorithm over smoothes the edges of the myocardium in (d)). In contrast, the use of spectral penalty alone results in reconstructions with unsuppressed spatial aliasing and temporal smoothing (see the residual streaking artifacts in (c) and errors due to the temporal smoothing in (h)). The k-t SLR method, which relies on both spectral and sparsity penalties, significantly reduces these artifacts. It provides a 2 dB improvement in SER over the methods that rely on only spectral or sparsity penalties.
3) Comparison of k-t SLR with k-t FOCUSS (model based x – f scheme)
The second and fourth columns of Figure 6 shows the reconstructions of k-t FOCUSS and k-t SLR at A = 5.33, using the same k-space trajectory. Since k-t FOCUSS relies on the x – f space sparsity that is degraded in the presence of breathing motion and contrast variations due to bolus passage, the reconstructions exhibits significant aliasing artifacts in regions with high interframe motion.
C. Comparisons on the invivo data
We plot the SER of the in-vivo reconstructions as a function of the acceleration in Figure 7. The trend is consistent with the PINCAT comparisons. Specifically, the k-t SLR scheme provides a consistent 1–2 dB performance improvement over classical KLT based method and k-t FOCUSS at most acceleration factors. The visual comparisons of all the methods at A ≈ 11 is shown in Figure 8. In figure 8, the time profiles of regions within the blood pool and the myocardium are routinely studied and form the basis for perfusion quantification. To evaluate the accuracy in determining these profiles, we also show the plots of the time series of specific regions within the blood pool and the myocardium; For consistently plotting these time series, we initially perform a registration step on the fully sampled data, such that the chosen regions are stationary across the time frames. The deformations from the registration step are then used to wrap the reconstructions. Next, we plot the average signal intensity of the regions at each time frame and obtain the plots in figure8(e),(f).
Fig. 7.
Quantitative comparison of the different schemes at a range of accelerations on in-vivo data. It is seen that the k-t SLR consistently provides significantly higher SER over classical KLT based schemes and k-t FOCUSS at all accelerations. The trend of all the methods are similar to the PINCAT comparisons. The use of TV penalty alone is seen to provide comparable SER to k-t SLR until A ≈ 7. However, note that the SER of the TV scheme is observed to drop at higher accelerations due to over-smoothing, as seen from Figure 8.
Fig. 8.
Comparisons on in-vivo data: The first column shows the reconstructions of the fully sampled data. Columns 2 to 6 show the reconstructions using the best two-step KLT scheme, k-t FOCUSS method, spectrally regularized (only low rank prior), TV regularized (only sparsity prior), and the k-t SLR scheme, respectively. We choose A = 11.2 for all the methods except the two-step KLT, which is at an acceleration of A = 10.2. We studied several two-step KLT schemes (see Fig. 7) with different number of phase encodes in the training data and picked the one with the best SER. Rows (a), (b) and (c) respectively show a frame at peak LV uptake, peak myocardial uptake and post contrast during breathing. The row (d) shows the image time series plot corresponding to the arrow in (c); the location of (a)–(c) are also marked in (d). Rows (e) and (f) respectively show the averaged signal intensity of the blood pool and myo-caridal regions (denoted in (b)) for the registered reconstructions overlaid on the registered fully sampled data. We observe that the reconstructions with the two-step KLT scheme exhibit significant spatial aliasing due to which the time series in (e and f) are inaccurate. The k-t FOCUSS reconstructions exhibit significant shape distortions and motion inaccuracies. These artifacts can be appreciated from the time series plots in (d–f), shown in the third column. The spectrally regularized scheme with only the low rank constraint has residual aliasing artifacts as pointed by the arrows in (a), 4th column. This has smoothing along time as well, which can be seen from smoothening of the perfusion peaks in (e) and (f) in the fourth column. The TV penalty based scheme has over spatial smoothing and blurring of important structures like the myocardium (see (b), fifth column), due to which the myocardial time series are inaccurate as seen in (f), fifth column. In contrast, k-t SLR in the last column provides efficient reconstructions, with good correlations of the blood and myocardial region time series with the fully sampled data.
Similar to our findings with the PINCAT phantom, we find significant performance improvement of k-t SLR in comparison to the other methods in figure (8) that verify our claims in V.B. Specifically, the utility of k-t SLR in obtaining close to accurate time profiles in the blood pool and myocardial regions is of great clinical importance. Any inaccuracies here, could lead to false analysis in the subsequent quantification stages. For instance, the blood pool region time profiles are used to determine the arterial input function, which forms the key component of the model fitting stage in the perfusion quantification. The methods of KLT, k-t FOCUSS and spectral penalty provide inaccurate time profiles in this regard. While TV provides good blood pool curves, it loses its accuracy in determining the time profiles within the clinically relevant myocardial region due to over smoothing; In contrast, k-t SLR provides a close match of its time profiles with that of the fully sampled data.
VII. Discussion
The quantitative comparisons of the different algorithms on numerical simulations and in-vivo perfusion MRI data clearly demonstrates the ability of the k-t SLR scheme in significantly accelerating cardiac perfusion MRI, while introducing few artifacts. Specifically, it provides consistently improved results over current state-of-the art approaches such as two-step KLT algorithm and the k-t FOCUSS method, which relies on sparsity in x-f space. Since the proposed scheme learns the temporal basis functions from the data itself, and does not make any assumptions on the x-f space structure; it is capable of exploiting the correlations in the data, even when the dynamics are not periodic. This property makes the proposed framework applicable to arbitrary dynamic imaging problems.
We have cast the low rank property in a non convex form, while the TV sparsity in the convex form. The non convex spectral penalty in our experiments have shown to provide consistently better performance over the convex nuclear norm at a range of accelerations. The main reason of using the convex TV norm is to be relatively robust to stair case like artifacts that are usually dominant, when one uses the non convex TV norm. The non convex TV sparsity penalty introduce these artifacts in locally smooth regions; and the voxel time series in our application of perfusion MRI are usually smooth along time.
From our results, it is observed that using spectral penalty alone results in significant aliasing artifacts, while the use of TV penalty alone results in considerable spatial smoothing. By constraining the reconstructions, the proposed scheme is capable of providing improved reconstructions. In our results, we observe that the performance of the TV scheme is comparable to that of k-t SLR at lower accelerations. However, the SER of the TV scheme drops significantly at higher accelerations due to excessive spatial smoothing. This behavior is reported by earlier myocardial perfusion MRI schemes that only rely on the TV penalty [43].
In this work, the trade-off between the problem fidelity and convergence rate in the variable splitting strategy is addressed by the use of a continuation scheme. The continuation scheme can have some numerical instabilities at high values of β1, β2. To address this instability, we plan to investigate an augmented Lagrangian strategy as proposed in [44] in the future.
We considered the reconstruction of perfusion dynamics from a single slice of the heart in this paper. We expect to obtain significantly improved results by jointly recovering multiple slices from 3-D k-space acquisitions. The main reason is the significant redundancy in the temporal profiles between slices, which the k-t SLR scheme is capable of exploiting. We also plan to address the recovery using multichannel data. Several authors have used the spatial diversity of the coil sensitivity profiles to accelerate cardac MRI [45], [46]. We expect that these extensions will enable k-t SLR to provide robust high-resolution perfusion MRI data from 8–12 slices with a temporal resolution of upto 2–3 frames per second.
VIII. Conclusion
We introduced a novel algorithm to reconstruct dynamic MRI data from under-sampled k-t space data. The proposed scheme exploits the correlations in the dynamic imaging dataset by modeling the data to have a compact representation in the Karhunen Louve transform (KLT) domain. The use of the adaptive scheme makes our approach ideally suited for a range of dynamic imaging problems. In contrast to current KLT-based methods that rely on two-step approaches to first estimate the basis functions and then use it for reconstruction, we posed the problem as a regularized matrix recovery problem. The proposed scheme uses both sparsity and spectral priors to significantly improve the recovery rate. Quantitative and qualitative comparisons on numerical phantoms and in-vivo cardiac perfusion MRI data clearly demonstrated a significant improvement in performance over existing methods.
Acknowledgments
This work is supported by NSF award CCF-0844812 and in part by NIH R01EB006155.
Footnotes
Such cost functions are termed as spectral penalties since they are functions of the singular values of the matrix.
The shrinkage operation is non-expansive if the spectral norm is convex.
Contributor Information
Sajan Goud Lingala, Departments of Biomedical Engineering and Imaging Sciences, University of Rochester, NY, USA.
Yue Hu, Departments of Biomedical Engineering and Imaging Sciences, University of Rochester, NY, USA.
Edward DiBella, Department of Radiology at the University of Utah.
Mathews Jacob, Departments of Biomedical Engineering and Imaging Sciences, University of Rochester, NY, USA.
References
- 1.Liang Z, Jiang H, Hess C, Lauterbur P. Dynamic imaging by model estimation. International Journal of Imaging Systems and Technology. 1997;8(6):551–557. [Google Scholar]
- 2.Madore B. Using UNFOLD to remove artifacts in parallel imaging and in partial-Fourier imaging. Magn Reson Med. 2002 Sep;48(3):493–501. doi: 10.1002/mrm.10229. [DOI] [PubMed] [Google Scholar]
- 3.Tsao J, Boesiger P, Pruessmann K. kt BLAST and kt SENSE: dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magnetic Resonance in Medicine. 2003;50(5):1031–1042. doi: 10.1002/mrm.10611. [DOI] [PubMed] [Google Scholar]
- 4.Sharif B, Bresler Y. Adaptive real-time cardiac mri using PARADISE: Validation by the physiologically improved ncat phantom,” in. ISBI. 2007 doi: 10.1109/ISBI.2007.357028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sharif B, Derbyshire JA, Faranesh AZ, Bresler Y. Patient-adaptive reconstruction and acquisition in dynamic imaging with sensitivity encoding (PARADISE) Magnetic Resonance in Medicine. 2010:501–513. doi: 10.1002/mrm.22444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lustig M, Santos J, Donoho D, Pauly J. kt SPARSE: High frame rate dynamic MRI exploiting spatio-temporal sparsity. Proceedings of the 13th Annual Meeting of ISMRM; Seattle Citeseer. 2006. p. 2420. [Google Scholar]
- 7.Adluru G, Awate S, Tasdizen T, Whitaker R, DiBella E. Temporally constrained reconstruction of dynamic cardiac perfusion MRI. Magnetic Resonance in Medicine. 2007;57(6):1027–1036. doi: 10.1002/mrm.21248. [DOI] [PubMed] [Google Scholar]
- 8.Liang Z. Spatiotemporal imaging with partially separable functions. ISBI. 2007:181–182. [Google Scholar]
- 9.Brinegar C, Wu Y, Foley L, Hitchens T, Ye Q, Ho C, Liang Z. Real-time cardiac MRI without triggering, gating, or breath holding; International Conference of the IEEE Engineering in Medicine and Biology Society, 2008. EMBS 2008; 2008. pp. 3381–3384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Brinegar C, Zhang H, Wu Y, Foley L, Hitchens T, Ye Q, Pocci D, Lam F, Ho C, Liang Z. Real-time cardiac MRI using prior spatial-spectral information. International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference; 2009. p. 4383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pedersen H, Kozerke S, Ringgaard S, Nehrke K, Kim WY. k-t PCA: temporally constrained k-t BLAST reconstruction using principal component analysis. Magn Reson Med. 2009 Sep;62(3):706–716. doi: 10.1002/mrm.22052. [DOI] [PubMed] [Google Scholar]
- 12.Jung H, Park J, Yoo J, Ye JC. Radial k-t FOCUSS for high-resolution cardiac cine MRI. Magnetic Resonance in Medicine. 2009 Oct; doi: 10.1002/mrm.22172. [DOI] [PubMed] [Google Scholar]
- 13.Candes E, Recht B. Exact matrix completion via convex optimization. Foundations of Computational Mathematics. 2009;9(6):717–772. [Google Scholar]
- 14.Cai J, Candes E, Shen Z. A singular value thresholding algorithm for matrix completion. preprint. 2008 [Google Scholar]
- 15.Candes EJ, Recht B. Exact matrix completion via convex optimization. Foundations of Computational Mathematics. 2009 [Google Scholar]
- 16.Lee K, Bresler Y. Admira: Atomic decomposition for minimum rank approximation. arXiv. 2009;905 [Google Scholar]
- 17.Lee K, Bresler Y. Guaranteed minimum rank approximation from linear observations by nuclear norm minimization with an ellipsoidal constraint. Arxiv preprint arXiv:0903.4742. 2009 [Google Scholar]
- 18.Chatrand R. Fast algorithms for nonconvex compressive sensing: Mri reconstruction from very few data. IEEE ISBI. 2009 [Google Scholar]
- 19.Trzasko J, Manduca A. Highly undersampled magnetic resonance image reconstruction via homotopic ell0 -minimization. IEEE Transactions on Medical Imaging. 2009;28(1):106–121. doi: 10.1109/TMI.2008.927346. [DOI] [PubMed] [Google Scholar]
- 20.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2006;68(1):49–67. [Google Scholar]
- 21.Goud S, Hu Y, Jacob M. Real-time cardiac MRI using low-rank and sparsity penalties. Proceedings of the ISBI. 2010 [Google Scholar]
- 22.Haldar J, Liang Z-P. Spatiotemporal Imaging With Partially Separable Functions: A Matrix Recovery Approach. Proceedings of the ISBI. 2010 [Google Scholar]
- 23.Toh K, Yun S. An accelerated proximal gradient method for nuclear norm regularized least squares. Preprint. 2009 [Google Scholar]
- 24.Ma S, Goldfarb D, Chen L. Fixed point and bregman iterative methods for matrix rank minimization. Preprint. 2009;05 [Google Scholar]
- 25.Wang Y, Yang J, Yin W, Zhang Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J Imaging Sciences. 2008;1(3):248–272. [Google Scholar]
- 26.Yang J, Zhang Y, Yin W. A fast TVL1-L2 minimization algorithm for signal reconstruction from partial Fourier data. IEEE J Special Topics Signal Processing, to appear [Google Scholar]
- 27.Recht B, Fazel M, Parrilo P. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. preprint. 2007 [Google Scholar]
- 28.Trzasko J, Manduca A. Relaxed conditions for sparse signal recovery with general concave priors. IEEE Trans SP. 2009;57(11):4347–4354. [Google Scholar]
- 29.Wipf D, Nagarajan S. SPARS09. Rennes, France: 2009. Iterative reweighted l1 and l2 methods for finding sparse solutions. [Google Scholar]
- 30.Gorodnitsky I, Rao B. Sparse signal reconstruction from limited data using focuss: A re-weighted minimum norm algorithm. IEEE Transactions on Signal Processing. 1997;45(3) [Google Scholar]
- 31.Candes E, Wakin M, Boyd S. Enhancing sparsity by reweighted 1 minimization. Journal of Fourier Analysis and Applications. 2008;14(5):877–905. [Google Scholar]
- 32.Chartrand R. Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Processing Letters. 2007;14(10):707–710. [Google Scholar]
- 33.Majumdar A, Ward R. An algorithm for sparse mri reconstruction by schatten p-norm minimization. Magnetic Resonance Imaging. 2010 doi: 10.1016/j.mri.2010.09.001. [DOI] [PubMed] [Google Scholar]
- 34.Chambolle A, Lions P. Image recovery via total variation minimization and related problems. Numerische Mathematik. 1997;76(2):167–188. [Google Scholar]
- 35.Yang J, Zhang Y. Alternating direction algorithms for l1-problems in compressive sensing. preprint. 2009 [Google Scholar]
- 36.Wright S, Nocedal J. Numerical optimization. Springer; 2006. [Google Scholar]
- 37.Accelereyes Jacket. 2010 [Online]. Available: http://www.accelereyes.com/
- 38.Segars W, Tsui B. Study of the efficacy of respiratory gating in myocardial spect using the new 4-d ncat phantom. IEEE Transactions on Nuclear Science. 2002;49(3):675. [Google Scholar]
- 39.Sharif B, Bresler Y. Adaptive real-time cardiac MRI using PARADISE: validation by the physiologically improved ncat phantom. 4th IEEE International Symposium on Biomedical Imaging. 2007:1020–1023. doi: 10.1109/ISBI.2007.357028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lin F-H. B1 simulator : simulate b1 field for mri rf coils. [Online]. Available: http://www.nmr.mgh.harvard.edu/~fhlin/
- 41.Jacob M. Optimized least-square nonuniform fast fourier transform. IEEE Transactions on Signal Processing. 2009;57(6):2165–2177. [Google Scholar]
- 42.Ramani S, Blu T, Unser M. Monte-carlo sure: A black-box optimization of regularization parameters for general denoising algorithms. IEEE Transactions on Image Processing. 2008;17(9):1540–1554. doi: 10.1109/TIP.2008.2001404. [DOI] [PubMed] [Google Scholar]
- 43.Adluru G, McGann C, Speier P, Kholmovski E, Shaaban A, DiBella E. Acquisition and reconstruction of undersampled radial data for myocardial perfusion magnetic resonance imaging. Journal of Magnetic Resonance Imaging. 2009;29(2):466–473. doi: 10.1002/jmri.21585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Afonso M, Bioucas-Dias J, Figueiredo M. An augmented lagrangian approach to the constrained optimization formulation of imaging inverse problems. Arxiv preprint arXiv:0912.3481. 2009 doi: 10.1109/TIP.2010.2076294. [DOI] [PubMed] [Google Scholar]
- 45.Guttman MA, Kellman P, Dick AJ, Lederman RJ, McVeigh ER. Real-time accelerated interactive MRI with adaptive TSENSE and UNFOLD. Magnetic Resonance in Medicine. 2003 Aug;50(2):315–21. doi: 10.1002/mrm.10504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kellman P, Epstein FH, McVeigh ER. Adaptive sensitivity encoding incorporating temporal filtering (tsense) Magn Reson Med. 2001 May;45(5):846–52. doi: 10.1002/mrm.1113. [DOI] [PubMed] [Google Scholar]