Three-Component Cure Rate Model for Non-Proportional Hazards Alternative in the Design of Randomized Clinical Trials

Abstract

BAKGROUND

Cure rate models have been extensively studied and widely used in time-to-event data in cancer clinical trials.

PURPOSE

Although cure rate models based on the generalized exponential distribution have been developed, they have not been used in the design of randomized cancer clinical trials, which instead have relied exclusively on two-component exponential cure rate model with a proportional hazards alternative. In some studies, the efficacy of the experimental treatment is expected to emerge some time after randomization. Since this does not conform to a proportional hazards alternative, such studies require a more flexible model to describe the alternative hypothesis.

METHODS

In this article, we report the study design of a phase III clinical trial of acute myeloid leukemia using a three-component exponential cure rate model to reflect the alternative hypothesis. A newly developed power calculation program that does not require proportional hazards assumption was used.

RESULTS

Using a custom-made three-component cure rate model as an alternative hypothesis, the proposed sample size was 409, compared with a sample size of 209 under the assumption of exponential distribution, and 228 under the proportional hazards alternative. A simulation study was performed to present the degree of power loss when the alternative hypothesis is not appropriately specified.

LIMITATIONS

The power calculation program used in this study is for a single analysis and does not account for group sequential tests in phase III trials. However, the loss in power is small and this was handled by inflating the sample size by 5%.

CONCLUSION

Misspecification of the alternative hypothesis can result in a seriously underpowered study. We report examples of clinical trials that required a custom-made alternative hypothesis to reflect a later indication of experimental treatment efficacy. The proposed three-component cure rate model could be very useful for specifying non-proportional hazards alternative.

INTRODUCTION

One important aspect of designing a randomized clinical trial comparing two treatments is the determination of an adequate sample size so that the study will be properly powered to test the main hypothesis of treatment difference between the two arms. A typical primary endpoint in randomized phase III cancer clinical trials is overall survival or disease-free survival, and an exponential distribution is often assumed in the sample size calculation. That is, survival is assumed to be continuously decreasing and a uniform hazard rate applies to all patients. If the underlying survival distribution is known to be non-exponential or if the survival distributions of the two arms are not proportional hazards, the use of a standard sample size calculation may significantly overestimate the number of events, underestimate time to completion of the study, and thus underestimate the required sample size.

With rapid improvement in the treatment of cancer, for certain cancers such as leukemia, lymphoma, melanoma, or many pediatric cancers, some patients are considered cured in that the disease does not come back for a long period of time. Thus, a cure rate model is frequently employed in the sample size calculation for these cancers. Indeed, irrespective of the proportion of patients who are cured, the sample size would be underestimated if a constant hazard rate (exponential model) were assumed, when in fact there is reasonable a priori evidence that the survival curve would be non-exponential with a long and stable plateau.

When cure rate model is considered in designing a clinical trial, a two-component exponential cure rate model is typically used in sample size calculation and the alternative hypothesis is expressed as either a proportional hazards alternative or a two-component cure rate model with different improvement rates for the cured and non-cured groups. However, if the efficacy of the experimental treatment is expected to emerge some time after randomization, neither of these alternative hypotheses (proportional hazards or two component cure rate) will be able to accommodate this complexity. Examples of such cases may include studies comparing vaccination with non-vaccination or comparing allogeneic hematopoietic stem cell transplant with the standard chemotherapy in randomized clinical trials. In these examples, there is a wait time for patients randomized to the vaccination or to the transplant arm to get vaccinated or to get transplanted, and thus the effect of the experimental treatment would be expected to be non-proportional hazards.

In this article, we first describe the design of a phase III clinical trial when the null hypothesis is based on the Berkson-Gage exponential cure-rate model, based on the results of a previous clinical trial, and the alternative hypothesis is based on a custom made three-component cure rate model. The three-component cure rate model was constructed as an ad hoc solution to account for the anticipated delay before the superiority of the experimental treatment might emerge. The projected efficacy of the experimental treatment was provided by the corporate sponsor based on outcomes of their phase I and II clinical trials. Although we report our design of a two- vs. three-component cure rate model, this approach is flexible and can be easily modified for other settings. In addition, to further demonstrate the applicability of this model, we include two more trials that used the three-component cure rate model to specify the alternative hypothesis. The power calculation program (called ‘powlgrnk’) used in the design of these trials was developed independently at the time of the design of the phase III trial. This program computes the power of the two-group log-rank test for arbitrary failure time distributions. Unlike other sample size formulas in survival analysis, it does not assume a proportional hazards alternative. The description and source codes of this program are attached in the Appendix.

CURE RATE MODEL

Parametric and semi-parametric cure rate models have been extensively studied in the literature and can be found elsewhere [1,2]. In this section, we briefly introduce two cure rate models that are related to the study design of the trial. The simplest cure rate model for a survival time T, also known as the standard cure rate model or mixture model, is the one proposed by Berkson and Gage [3].

$$\text{S}(\text{t})=\text{P}(\text{T}>\text{t})=\pi +(1-\pi )\text{H}(\text{t}),$$

where π denotes the population proportion of patients cured, 1− π denotes the population proportion of patients not cured, and H(t) is the survival function for the patients not cured. If H(t) is exponential, then the exponential cure rate model is

$$\text{S}(\text{t})=\text{P}(\text{T}>\text{t})=\pi +(1-\pi )exp(-\lambda \text{t}).$$ (1)

The hazard function of (1) is

$$\text{h}(\text{t};\pi ,\lambda )=\frac{\lambda (1-\pi )exp(-\lambda t)}{\pi +(1-\pi )exp(-\lambda t)}.$$

When π=0, S(t) = exp(−λt), is an exponential survival model with h(t; π, λ)= λ. This two-component cure rate model is widely used in sample size consideration in many clinical trials. The model, however, can be extended further into three groups to reflect a more complex patient population.

$$\text{S}(\text{t})=\text{P}(\text{T}>\text{t})={\pi }_0+{\pi }_1{\text{H}}_1(\text{t})+(1-{\pi }_0-{\pi }_1){\text{H}}_2(\text{t}).$$

If H₁(t) and H₂(t) are exponential, then

$$\text{S}(\text{t})=\text{P}(\text{T}>\text{t})={\pi }_0+{\pi }_{1}exp(-{\lambda }_1\text{t})+(1-{\pi }_0-{\pi }_1)exp(-{\lambda }_2\text{t})$$ (2)

where λ₁ is the hazard rate of the non-cured group 1 and λ₂ is the hazard rate of the non-cured group 2. (2) is the basis of our alternative hypothesis even though the exact classification of patients into these groups may not be possible at the time the study is designed.

A PHASE III DESIGN OF ACUTE MYELOID LEUKEMIA: Eastern Cooperative Oncology Group (ECOG) Clinical Trial, E3999

Study Design

The median age of onset for acute myeloid leukemia (AML) in the United States is around 65 years. Conventional induction chemotherapy in older patients with AML is associated with a lower complete remission rate (<50%) and a shorter median disease-free survival time compared to younger patients. One possible mechanism of this poor outcome is more frequent multidrug resistance (MDR) in older patients. MDR is an extensively studied phenomenon, relating to the ability of cancer cells to survive exposure to a wide variety of drugs. It is therefore reasonable to hypothesize that modulation of MDR might improve treatment outcome for older patients with newly diagnosed AML.

ECOG study, E3999, was a double-blind phase III trial of a multi-drug resistant modulator, Zosuquidar Trihydrochloride, in patients over the age of 60 with newly diagnosed AML or advanced myelodysplastic syndrome (MDS) (refractory anemia with excess blasts or refractory anemia with excess blasts in transformation ). The primary objective of this randomized phase III trial was to compare the overall survival (OS) between the MDR modulator and placebo given in conjunction with the standard ‘3+7’ chemotherapy (i.e., A+B vs. A design). Patients were randomized 1:1 between the two arms prior to the induction treatment.

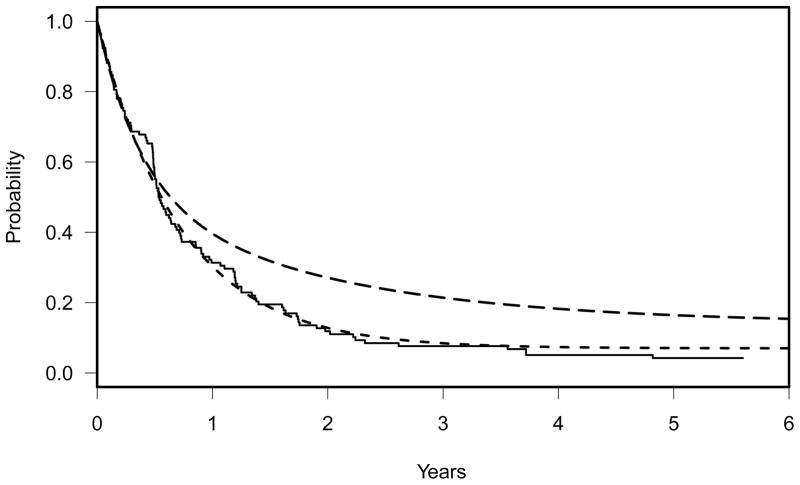
Because long-term cures had been observed in the previous ECOG study with the same patient population, we used a cure rate model to compute the sample size for the primary endpoint. Based on the data from the previous study, we assumed that the long-term cure rate in the placebo arm would be 7% with a median survival time of 6 months for the non-cured group (Figure 1). With the modulator, it was anticipated that there would be no improvement in the survival curve during the first 6 months since the primary effect of the modulator should be in delaying or overcoming resistance for patients who are benefiting from the chemotherapy. Survival improvement, however, would begin to show after the first 6 months, and it was hypothesized that the long-term cure rate would be doubled to 14%. To model this specific alternative hypothesis, we used a three-component mixture model, partitioning the non-cured patients into two groups: early failures with no improvement expected and non-cured but with some improvement expected. This assumption led to the following two survival models for the null (H₀: S_p(t)=S_m(t)=S₀) and alternative (H_A: S_p(t)<S_m(t) ) hypotheses for the sample size calculation. Here S₀ denotes an unspecified survival function, S_p(t) denotes the survival distribution of the placebo arm, and S_m(t) denotes the survival distribution of the modulator arm. Specifically,

Figure 1.

Solid line: Kaplan-Meier curve of the previous ECOG trial, E3993. Dashed line: two component-cure rate model, S_p(t) = 0.07 + 0.93 exp(−t log(2)/6), representing the null hypothesis. Long dashed line: three-component cure rate model, S_m(t) = 0.14 + 0.39 exp(−t log(2)/15) + 0.47 exp(−t log(2)/3.1), representing the alternative hypothesis(H_A: S_p(t) < S_m(t)).

$${\text{S}}_{\text{p}}(\text{t})=0.07+0.093exp(-\text{t}log(2)/6),$$ (3)

and under the alternative,

$${\text{S}}_{\text{m}}(\text{t})=0.14+0.39exp(-\text{t}log(2)/15)+0.47exp(-\text{t}log(2)/3.1).$$ (4)

(3) and (4) are depicted graphically in Figure 1. The solid line in Figure 1 represents the Kaplan-Meier curve of the previous ECOG trial, E3993, on which the null hypothesis was based. With this design, a sample size of 409 eligible patients was proposed to achieve approximately 80% power to detect a difference in OS between the two treatment arms at the one-sided significance level of 0.025. This power was calculated using the two-group log rank test for arbitrary failure time distributions using our ‘powlgrnk’ program and assumed an accrual rate of 99 eligible patients per year with an additional two years of follow-up after the completion of accrual. The projected accrual rate for the power calculation was estimated from the previously conducted ECOG study. The description, R source code, and manual of powlgrnk are attached in the Appendix. This program was developed and written by Robert Gray at the time of designing the trial, but independently of the trial.

The study design also included two planned interim analyses for early detection of superiority of the investigational arm using truncated O’Brien-Fleming boundaries [4] or for early detection of non-superiority using conditional power [5]. One limitation of the program, powlgrnk, is that it computes power and the expected number of events for a single analysis and does not consider group sequential tests. To account for the sequential testing as well as ineligibility (~5%), the final sample size was inflated by 10% to 450, accruing over 4.1 years. It is well known that with multiple interim analyses, critical values must be adjusted to control the overall type I error rate. However, with the O’Brien-Fleming boundaries, loss of power associated with the number of looks is fairly small (e.g., 1.3% loss in power if nine analyses are planned throughout the study compared to a single analysis at the end of the study) as demonstrated in Freidlin et al (1999) [4]. Thus, our conservative and practical guideline for a unique study design such as E3999 was either to reduce the power by 2% or to increase the sample size by 5%.

Based on the total expected number of events (354), the two interim analyses were scheduled to take place when 117 and 238 events had been observed, which corresponds to 33% and 67% of the expected total information. The interim analyses were anticipated to take place at 3.4 and 4.8 years after the study began active accrual with the final analysis occurring at 6.1 years. Of note, this trial was designed and activated for accrual prior to the NCI guideline for semi-annual interim monitoring [4], although this trial might not be a good candidate for frequent interim looks. We refer to Freidlin et al (1999) for detailed discussion on advantages and disadvantages of frequent interim looks. A formal statistical test for futility would be executed by computing conditional power under the alternative of rejecting the null hypothesis at a future analysis. If at one of the scheduled interim analyses, this conditional power is less than 0.1, then the study would be stopped in favor of the null hypothesis. This rule is relatively conservative for futility stopping and adding it has little effect on power. For the recent developments on conditional power, we refer to Lachin [6,7]. An alternative to using conditional power for futility stopping is to use repeated confidence intervals [8], but here the alternative hypothesis cannot be expressed as a single parameter.

Proportional Hazards and Exponential Alternatives

Alternative hypotheses in phase III studies are usually assumed to follow proportional hazards. That is, λ_A(t) = θ λ₀(t), where λ_A(t) denotes the hazard of the experimental treatment arm and λ₀(t) denotes the hazard of the standard treatment arm. θ is often expressed in terms of percent reduction in the hazard rate, percent improvement in the median failure time or percent increase in the proportion of failure-free at a specified time. Proportional hazards can also be applied to cure rate model as S_A(t) = [S₀(t)]^θ, where S_A(t) and S₀(t) denote the survival distribution of the experimental and standard treatment arm, respectively.

If S₀(t) is a two-component exponential cure rate model as shown in (1), the proportional hazards alternative can be expressed as

$${\text{S}}_{\text{A}}(\text{t})={[{\text{S}}_0(\text{t})]}^{\theta }={[\pi +(1-\pi )exp(-\lambda \text{t})]}^{\theta }$$ (5)

which is algebraically identical to

$${\text{S}}_{\text{A}}(\text{t})={\pi }^{\theta }+(1-{\pi }^{\theta })\text{H}(\text{t})$$ (6)

where

$$\text{H}(\text{t})=\frac{{[\pi +(1-\pi )exp(-\lambda t)]}^{\theta }-{\pi }^{\theta }}{1-{\pi }^{\theta }}.$$

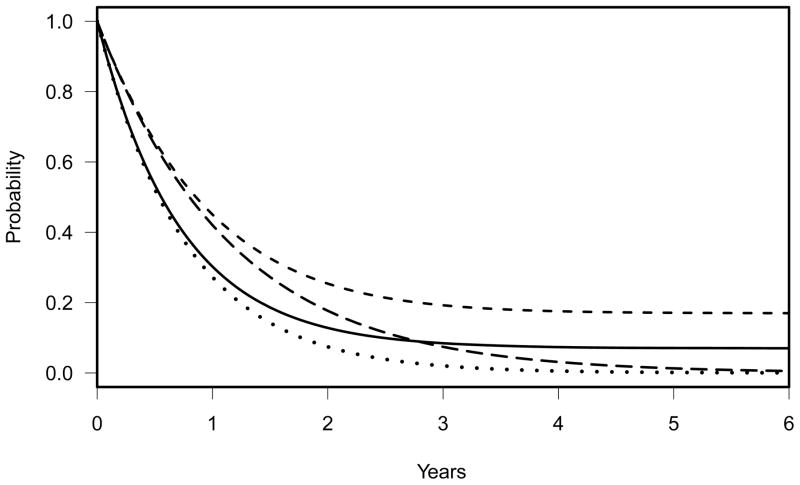
The model (6) is a two-component non-exponential cure rate model. The dashed line in Figure 2 reflects this proportional hazards alternative with θ=0.667. While it is difficult to say what a similar effect size to the alternative (4) would be in this model, this hazard ratio makes the resulting alternative equal to (4) at 1.62 and 4.46 years, although it should be noted that the long term cure fraction is almost 0.17, which is larger than in (4). This curve can be compared with the null hypothesis of two component exponential cure rate model, (3), shown in the solid line in Figure 2. For this alternative, the required sample size to achieve 80% power would be 228 with 196 events expected assuming the same accrual rate and an additional two-years of follow-up. This power calculation is calculated using powlgrank. By definition, this alternative assumes that the study population would respond uniformly to the experimental treatment and would not be appropriate if the experimental treatment efficacy is anticipated to take some time to result in beneficial outcome. If the study had been planned with a sample size of 228 and if the true survival distribution of the experimental treatment were (4), the study would have had a 57% power for the alternative hypothesis (4).

Figure 2.

Solid line: two-component cure rate model, S₀(t) = 0.07 + 0.93 exp(−t log(2)/6), representing a null hypothesis. Dashed line: S_A(t)=[S₀(t)]^0.667, representing a proportional hazards alternative hypothesis (H_A: S₀(t) < S_A(t)) with a 33% reduction in hazard. Dotted line: exponential null hypothesis with a median survival time of 6.4 months. Long dashed line: exponential alternative hypothesis with a median survival time of 9.6 months.

Alternatively, since the failure rate in this patient population is fairly rapid, one could assume exponential distributions for S₀(t) and S_A(t). The median survival time of the previous ECOG study, E3993, was 6.4 months. Using this as a null hypothesis, a 33.3% reduction in hazard translates into a 50% improvement of the median survival time to 9.6 months in the experimental treatment arm. i.e., S₀(t) = exp(−t log(2)/6.4) and S_A(t)= exp(−t log(2)/9.6). The dotted and long dashed lines in Figure 2 graphically illustrate these two exponential distributions for the alternative hypothesis H_A: S₀(t) < S_A(t). With this design, the required sample size would be 209 with 198 events to achieve 80% power at the one-sided 0.025 level with the same accrual rate and two-years of additional follow up. This design, however, ignores the small portion of patients in the previous ECOG trial who were still alive at the time that the successor study E3999 was launched (6–8 years after the termination of the previous study). The exponential design assumes that the probability of surviving beyond 5 years is nearly zero in both standard and experimental arms and anticipates an early beneficial effect of the experimental treatment. The study thus would be significantly underpowered if a portion of patients are cured. If the study were planned with a sample size of 209, and if the true survival distributions under H_o and H_A were as given in (3) and (4), the study would have had a 54% power for testing the alternative hypothesis with the final analysis at two years after completion of accrual. However, the expected number of deaths at that time point is only 177; even with substantially longer follow-up the expected number of deaths increases to 187, at which point the power is only 46.5% (the power decreases at longer follow-up due to crossing hazards in the alternative (4)).

SIMULATION

To verify the calculations above and to examine the effect of interim monitoring, simulations were performed. Survival times were generated from the distribution (3) for the control arm and (4) for the experimental arm. The three designs discussed above were considered with N denoting total sample size and D denoting number of deaths:

1. N=409 and D=354 based on the alternative (4);

2. N=228 and D=196 based on the proportional hazards alternative to (3); and

3. N=209 and D=198 based on the exponential model.

Entry times were generated from a uniform (0, N/99) distribution. Interim analyses were performed at calendar times when D/3 and 2D/3 deaths had been observed (rounded to the nearest integer) with the final analysis at D deaths. If the total number of deaths in the trial was < D, then all deaths available at a long follow-up time were included in the final analysis. The null hypothesis was rejected if the Lan-DeMets error spending function boundary corresponding to the O’Brien-Fleming boundary was crossed, with early stopping for futility if the conditional power for the design alternative was < 10%. Ten thousand trials were run for each case, which gives a standard error for the estimated power of 0.4% when the power is 80% and 0.5% when the power is 50%. All calculations were done in R version 2.10.1 using the Mersenne Twister random number generator. The results are summarized in Table 1. As expected, due to the effect of the interim analyses, the power for each design was slightly lower than the calculations shown above: 78.7%, 52.5%, 45.0% for the three-component, proportional hazards (PH), and exponential model, respectively. Without interim stopping rules, however, the percent of trials where a single analysis at full information would reject the null hypothesis was 80.1%, 55.4% and 46.5%, respectively. The first is consistent with the power of 80.3% given by powlgrnk, the last is the same as given by powlgrnk at longer follow-up, and the decrease in the PH model case is largely because the analyses are often at later follow-up times here than in the powlgrnk calculation, and the crossing hazards under the alternative (4) lead to lower power as follow-up increases. The proportion of trials that were stopped early for futility was 6.6%, 22.3%, and 20.8% for the three alternatives, respectively (Table 1), but only a very small proportion would have become positive later (0.6%, 1.5%, 0.4%, respectively), so the impact of this futility stopping rule on the power is minimal.

Table 1.

Estimated power for the logrank test from 10,000 simulated trials generated under the 3 component cure rate model. Total sample size (N) and number of events (D) for full information was calculated for 80% power when each of 3 alternative hypothesis models was assumed to be true. Estimated power was the percent of trials that reject the null hypothesis using the N and D from each alternative model

	Alternative hypothesis model
	3 component cure rate	Proportional hazards cure rate	Exponential model
Total sample size (N)	409	228	209
Total number of deaths (D)	354	196	198
Estimated power with 2 interim looks	78.7%	52.5%	45.0%
Estimated power without interim looks	80.1%	55.4%	46.5%
% of trials stopped early for futility	6.6%	22.3%	20.8%

OTHER EXAMPLES

In this section, we include our recent study designs that used a three-component curer rate model as an alternative.

Example 1. A Randomized Phase II Trial of GVAX After Allogeneic HSCT

Because many factors influence outcomes after allogeneic hematopoietic stem cell transplantation (HSCT), single-arm phase II vaccine studies have been of little benefit in evaluating vaccines specifically designed for enhancing graft-versus-leukemia effect after transplant and subject to selection bias. We thus designed a randomized phase II study of GM-CSF secreting leukemia cell vaccines (GVAX) given early after HSCT to patients with high risk acute myeloid leukemia (AML) or myelodysplastic syndrome (MDS) compared with a standard transplant control arm. The primary endpoint of this study is progression-free survival (PFS) at 18 months post-randomization. PFS is defined as time from randomization to progression of disease or death whichever occurs first. Patients are randomized 1:1 between the GVAX arm (Arm A) and the standard transplant arm (Arm B). The target accrual goal is 106 patients accruing over a 3 year period with an additional 18 months of follow-up after the completion of accrual.

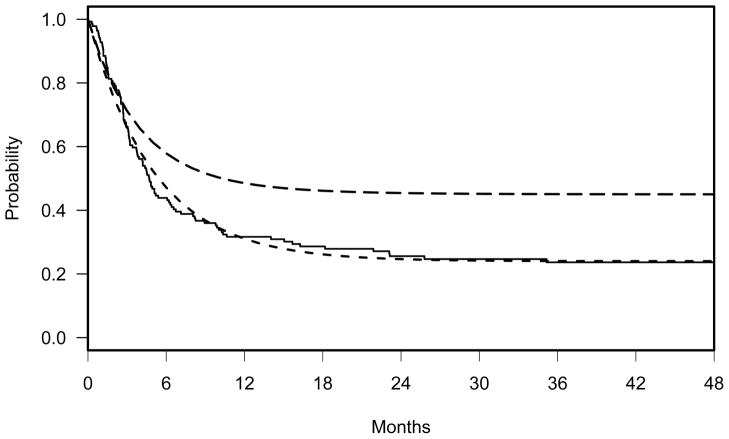
In our previous report on the GVAX study [17], the 2-year PFS for 15 patients who received at least one vaccination was 46%. This estimate compared to 18% 2-year PFS from our concurrent control cohort that was most similar to those patients in the previous GVAX trial. This retrospective analysis of high risk AML/MDS patients with active disease who underwent allogeneic HSCT at the same period of the GVAX study at the Dana-Farber Cancer Institute (DFCI) showed that a portion of patients were cured from the underlying disease after allogeneic HSCT and the distribution of PFS followed a two-component exponential cure rate model (the solid line in Figure 3 represents the Kaplan-Meier curve). Basing the fitted curve in Figure 3 as the null hypothesis, we hypothesize that the PFS will be increased by 75% from 26% to 46% by 18 months post HSCT in Arm A. More specifically, the proposed alternative hypothesis is H_a: S_A>S_B where S_A and S_B denote the distributions of PFS in Arm A and B, shown in (5) and (6), respectively.

Figure 3.

Solid line: Kaplan-Meier curve of the previous study. Dashed line: two-component cure rate model, S_B = 0.24+ 0.76*exp(−t*(log(2)/3.5)), representing the null hypothesis. Long dashed line: three-component cure rate model, S_A = 0.45+0.45*exp(−t*(log(2)/2.5))+ 0.1*exp(−t*(log(2)/4.5)), representing the alternative hypothesis (H_A: S_B(t) < S_A(t)).

$${\text{S}}_{\text{A}}=0.45+{0.45}^{\ast }exp(-{\text{t}}^{\ast }(log(2)/2.5))+{0.1}^{\ast }exp(-{\text{t}}^{\ast }(log(2)/4.5))$$ (5)

$${\text{S}}_{\text{B}}=0.24+{0.76}^{\ast }exp(-{\text{t}}^{\ast }(log(2)/3.5))$$ (6)

This projection incorporates approximately 30–45 days of wait time from randomization to the start of vaccination for patients randomized to the GVAX arm (Arm A) and additional ~40 days for the administration of a serial of 6 vaccinations. During this period, we expect little difference in PFS between two arms. With this design, 106 patients with 69 events are required to achieve approximately 80% power with one-sided significance level of 0.15. Since this is a direct but non-definitive randomized comparison to a standard treatment control, we follow the recommendations made by Rubinstein et al[18,19] and use a one-sided type I error rate of 0.15 with 80% power[18–20]. Of note, designing a phase III trial is prohibitive considering the current accrual of high risk AML/MDS patients at our institution. To verify the power calculation, a simulation is performed as above. Without interim looks, the estimated power is 79.2%. There are no formal interim stopping rules in the protocol. However, if two interim looks with O’Brien-Fleming boundaries were proposed, the estimated power would have been 77%.

Example 2. The Myelodysplasia Transplantation-Associated Outcomes (MDS-TAO) Study

Myelodysplastic syndrome primarily affects elderly people with the average age at diagnosis around 65 years. Although allogeneic HSCT is the only known curative therapy for patients with MDS, until recently the procedure with full intensity conditioning has been withheld from older patients due to concerns about excessive transplant related complications. Reduced-intensity conditioning transplant, on the other hand, is safe and has proven much less transplant related complications, and thus offered to many older patients with MDS. However, the Centers for Medicare & Medicaid Services (CMS)—the main health insurer for adults 65 and older in the United States— recently announced that CMS would in general decline coverage for allogeneic HSCT of MDS. Motivated by this decision and given the fact that the vast experience and volume of the Dana-Farber/Harvard Cancer Center with respect to both HSCT and other treatments for older adults with MDS, we launched the MDS TAO study for high-risk MDS patients aged 60–75 who are at baseline considered reasonable candidates for imminent transplantation and meet criteria for consideration of allogeneic HSCT with reduced intensity conditioning.

The study is a prospective, observational trial comparing overall survival (OS) between patients who undergo HSCT for MDS (Arm A) and patients who do not undergo HSCT but who have disease of sufficiently high enough risk to warrant HSCT and who are also fit enough to undergo HSCT (Arm B). 290 eligible patients will be enrolled between the two arms over a period of 5 years with an additional 5 years of follow-up. The primary endpoint of this study is 5-year OS. OS is defined as time from the study entry to death from any cause. Based on our current practice, we anticipate that the enrollment will be 1:2 ratio for Arm A to Arm B. The survival distribution in Arm A is projected based on our experience at DFCI and the recent report of Alessandro et al [21] on the outcome of MDS patients who underwent allogeneic HSCT. i.e., a portion of patients will be cured with HSCT from the underlying disease and the 5-year OS will be 25%. The survival distribution for Arm B is based on the recent report of Malcovati et al [22] on the outcome of high risk MDS patients with standard treatment. In addition, we expect that there will be approximately 4–6 months wait time for patients enrolled in Arm A from enrollment to the actual HSCT, thus no difference in OS between two arms is expected for some period after the start of the study. Based on this information and assumptions, the proposed alternative hypothesis is

$${\text{H}}_{\text{a}}:{\text{S}}_{\text{A}}>{\text{S}}_{\text{B}}$$

where S_A and S_B denote the survival distributions of Arm A and B, respectively. Specifically,

$$\begin{array}{l}{\text{S}}_{\text{A}}=0.19+{0.4}^{\ast }exp(-{\text{t}}^{\ast }(\text{log}2/10))+{0.41}^{\ast }exp(-{\text{t}}^{\ast }(log(2)/20)),\text{and}\\ {\text{S}}_{\text{B}}=exp(-{\text{t}}^{\ast }(log(2)/18).\end{array}$$

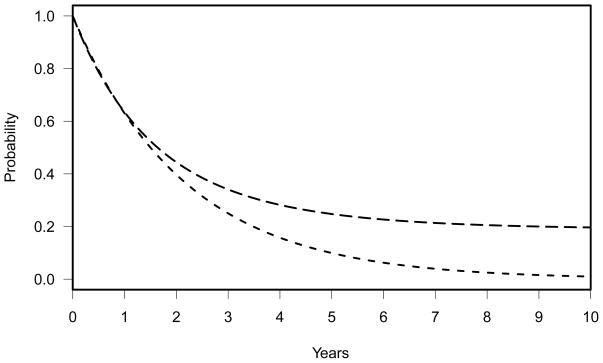
Figure 4 depicts these two survival distributions graphically. With this design, 290 patients will be required to achieve 85% power with one-sided significance level of 0.025. This power calculation is calculated using the R program, Powlgrnk. To verify the power calculation, a simulation is performed as above. Without interim looks, the estimated power is 83.0%. Since this is an observational study, there are no formal interim stopping rules incorporated in the protocol. However, if two interim looks with O’Brien-Fleming boundaries were assumed, the estimated power would have been 82.3%.

Figure 4.

Dashed line: exponential model, S_B = exp(−t*(log(2)/18)), representing the null hypothesis. Long dashed line: three-component cure rate model, S_A = 0.19+0.4*exp(−t*(log(2)/10))+ 0.41*exp(−t*(log(2)/20)), representing the alternative hypothesis (H_A: S_B(t) < S_A(t)).

CONCLUSIONS

Many cancer clinical trials are underpowered due to the inaccurate specification of the alternative hypothesis. The most common choice of an alternative hypothesis is a proportional hazards (PH) alternative, whether the underlying null distribution is assumed to be exponential or two-component cure rate model. However, when the PH assumption is inappropriate, as occurs when there is a delay in the emergence of the treatment effect in the experimental arm, this will result in a significant loss of power. In our study design of E3999, the use of a three-component cure rate model reflected the alternative hypothesis more accurately. Our simulation study confirmed that inappropriate specification of the alternative or null hypothesis would have resulted in an accrual goal of approximately 200 fewer patients, a power loss of 25%–35%, and approximately 15% higher chance of stopping early for futility, compared with a design based on a correctly specified alternative.

To further demonstrate the applicability of the proposed cure rate model, we included two more examples with simulation results. In these studies, the PH assumption would be inappropriate since there is a wait time from the study entry to the administration of the experimental treatment (vaccination or transplant). The simulation results indicate that if two interim analyses were planned, the power loss using Powlgrnk would have been within 3%.

One limitation of our approach is the accurate estimation of parameters in the projected alternative hypothesis at the time the study is designed. This issue, however, is not unique in our study. Since data from phase II studies are often limited, it is difficult to project the exact distribution of patients for a non-proportional hazards alternative, regardless of the choice of statistical model. Nonetheless, we acknowledge that the performance and applicability of this model needs to be further investigated. The other limitation is that the power calculation program, Powlgrnk, is for a single analysis and does not account for group sequential tests. Thus, this program needs further development to reach its full utility.

Our simulation results are consistent with those presented in Barthel et al [15], who proposed the piecewise exponential distribution for testing non-proportional hazards in the event of changing hazard after a certain time period. Using a simulation study, they showed that poor specification of the alternative hypothesis significantly impacts sample size. Another approach for non-proportional hazards alternatives is a lag-time model proposed by Zhang and Quan [14]. To account for an expected 1-year delay in the emergence of efficacy for a treatment of cardiovascular disease in a placebo-controlled clinical trial, they proposed a lag-time model using a two-step function with the first hazard being 1 and the second hazard being less than one. Their method is an extension of Schoenfeld’s [12, 16] sample size formula for two different hazards to reflect the non-proportional hazards alternative hypothesis. Both of the above scenarios could be expressed in terms of a mixture of patient population and handled using our approach. Furthermore, even though we report a three-component cure rate model, our approach is very flexible and can be easily modified for testing a mixture model of any arbitrary failure time distributions. The use of our approach in the design of clinical trials could lead to a significant improvement in the power to detect a treatment benefit, especially when such a benefit is expected to be delayed from the time of randomization.

Glossary

AML

Acute myeloid leukemia

DFCI

Dana-Farber Cancer Institute

ECOG

Eastern Cooperative Oncology Group

MDR

Multidrug resistance

MDS

Myelodysplastic syndrome

MDS-TAO

Myelodysplasia Transplantation-Associated Outcomes

OS

Overall survival

PFS

Progression-free survival

NCI

National Cancer Institute

Appendix

A. Sample Size Formula of two-group logrank test for arbitrary failure distributions

The power program used in the design of E3999 was developed by Stephenson and Gray [19]. In this section, we briefly describe the relevant sample size formula presented in Stephenson and Gray [19]. Sample size formulas for the logrank test are usually based on asymptotic approximations and assume a proportional hazards alternative [17, 20–22]. In their unpublished manuscript, Stephenson and Gray (2005) used a more accurate approximation that does not rely on the proportional hazards assumption. Let T_i be the failure time and C_i be the censoring time for subject i. Using the counting process of survival analysis, de ne U_i = min(T_i, C_i), I(.) as the indicator function with value 1 if the statement is true and 0 if it is false, δ_i = I (T_i ≤ C_i), Y_i(t) = I(U_i ≥ t), N_i(t) = I(U_i ≤ t, δ_i = 1), $Y_i(t)=I(U_i\ge t),N_i(t)=I(U_i\le t,{\delta }_i=1),\overline{Y}(t)={\sum }_{i=1}^n{Y}_i(t),{\overline{Y}}_j(t)={\sum }_{i=1}^{n}I(z_i=j)Y_i(t)$, j = A, B, and ${\overline{N}}_j(t)={\sum }_{i=1}^{n}I(z_i=j)N_i(t)$ where z_i is the indicator for group membership. Also, define

$$Q_{lr}^n={\left(\frac{n}{n_A{n}_B}\right)}^{\frac{1}{2}}\left[\underset{0}{\overset{\infty }{\int }}\frac{{\overline{Y}}_B(t)}{\overline{Y}(t)}d{\overline{N}}_A(t)-\underset{0}{\overset{\infty }{\int }}\frac{{\overline{Y}}_A(t)}{\overline{Y}(t)}d{\overline{N}}_B(t)\right]$$

and

$${\widehat{\sigma }}^2=\frac{n}{n_A{n}_B}{\int }_0^{\infty }\left(\frac{{\overline{Y}}_A(t){\overline{Y}}_B(t)}{\overline{Y}(t)}\right)\frac{d{\overline{N}}_A(t)+d{\overline{N}}_B(t)}{\overline{Y}(t)},$$

where n_A, n_B are total number of patients in treatment A and B, respectively, and n = n_A + n_B. $Q_{lr}^n$ is then the numerator of the logrank statistic and σ̂² is the standard pooled variance. Applying the large sample theory,

$$\frac{Q_{lr}^n}{\widehat{\sigma }}\approx N\left(\frac{{\xi }_n}{{\sigma }_n},\frac{V_n^2}{{\sigma }_n^2}\right),$$ (7)

where ξ_n, ${\sigma }_n^2$, and $V_n^2$ are approximations to $E(Q_{lr}^n)$, E(σ̂²), and $\mathit{Var}(Q_{lr}^n)$, respectively with moments calculated under the hypothesized alternative. Similar formulas have been given elsewhere, and the main difference from the general result in [17] is separately approximating E(σ̂²) and $\mathit{Var}(Q_{lr}^n)$. Applying (7) to the common sample size formula, the total number of events, d, to achieve power 1−β with size α for a one-sided test is

$$d=\frac{{\left[{\sigma }_n{z}_{\alpha }+V_n{z}_{\beta }\right]}^2}{{\mu }^2}P(d)$$ (8)

where z_α and z_β are the α-th and β-th percentile of standard normal distribution, $\mu ={\xi }_n/\sqrt{n}$, and $P(d)={\int }_0^{T+\tau }[1-G(t)][p{f}_A(t)+(1-p)f_B(t)]dt$ is the overall probability of having an event during the time of study with f_j, j = A, B, the densities of the event time distributions and G(.) the CDF of the censoring distribution. (8) is more accurate approximation to sample size than the existing formulas and does not assume proportional hazards alternative.

B. R program powlgrnk

powlgrnk {desmon}                                    R Documentation

Computes the power of the logrank test

Description

Computes the power of the two-group logrank test for arbitrary failure time distributions in a standard clinical trials setting

Usage

powlgrnk (acc.per, acc.rate, add.fu, alpha = 0.025, p.con = 0.5,
      hazcon=function (x,lc,pc,…) {u <- (1−pc)*exp(−lc*x); lc*u/(pc+u)},
     survcon=function(x,lc,pc,…) pc+(1−pc)*exp(−lc*x),
     haztst=function(x,lt,pt,…) {u <- (1−pt)*exp(−lt*x); lt*u/(pt+u)},
     survtst=function(x,lt,pt,…) pt+(1−pt)*exp(−lt*x),
     control.rate=NULL, test.rate=NULL, control.cure=0, test.cure=0, …)

Arguments

acc.per: Planned duration of accrual
acc.rate: Number of patients expected to be entered per time unit
  add.fu: Additional follow-up between the end of accrual and the time of analysis
  alpha: The one-sided type I error of the test
  p.con: The proportion randomized to the control arm
  hazcon: A function evaluating the control group hazard function at a vector of times
 survcon: A function evaluating the control group survivor function at a vector of times
  haztst: A function evaluating the experimental or test group hazard function at a vector of times
 survtst: A function evaluating the experimental or test group survivor function at a vector of times
control.rate: Exponential hazard rate in control group for non-cured
test.rate: Exponential hazard rate in test group for non-cured
control.cure: Cure fraction in control group
test.cure: Cure fraction in test group
   …: additional arguments passed to survival and hazard functions

Details

The calculations assume that n=acc.rate*acc.per patients are entered uniformly over the period [0,acc.per], with follow-up continuing for an addition add.fu time units, so censoring will be uniform on [add.fu,add.fu+acc.per]. The failure probability under the specified failure distribution is then computed, as is the expected number of failures, n*fail.prob.

hazcon must be the hazard function corresponding to the survivor function in survcon (and similarly for haztst and survtst). The program does not check for consistency of these functions, though. One way to check would be to compare survcon(x) to exp( integrate(hazcon,0,x)$value) for various values x. The default functions are for the exponential cure rate model, which reduces to the two-sample exponential when the cure fractions are 0.

The calculations are performed by using the integrate function to approximate the expectations of the logrank score and the logrank variance estimator and the variance of the logrank score under the specified conditions, and then using a normal approximation to the distribution of the logrank statistic.

This function only computes power for a single analysis, and does not consider group sequential tests.

Caution: consistent time units must be used for all quantities; eg if the accrual rate is given in patients/month, then the hazard rates must be in units of events/month and acc.per and add.fu must be in months.

Value

Returns a vector giving the power of the test under the specified conditions (power), the total sample size (n) and the expected number of events (nd).

Examples

# Exponential distributions
lc <- .1
lt <- .1*.75
hc <- function(x) lc
ht <- function(x) lt
sc <- function(x) exp(−lc*x)
st <- function(x) exp(−lt*x)
powlgrnk(5, 200, 3, hazcon=hc,survcon=sc,haztst=ht,survtst=st)
#      power           n         nd
#   0.7925548 1000.0000000 375.5712999
# Exponential cure-rate distributions
pic <- .3
pit <- .4
lc <- log(2)/3
lt <- log(2)/4
sc <- function(x) pic+(1−pic)*exp(−lc*x)
st <- function(x) pit+(1−pit)*exp(−lt*x)
hc <- function(x) {u <- (1−pic)*exp(−lc*x); lc*u/(pic+u)}
ht <- function(x) {u <- (1−pit)*exp(−lt*x); lt*u/(pit+u)}
powlgrnk(3, 200, 3, hazcon=hc,survcon=sc,haztst=ht,survtst=st)
#     power          n         nd
#  0.8962665 600.0000000 230.7956591
# Exponential cure-rate with proportional hazards alternative
ht <- function(x) .75*hc(x)
st <- function(x) sc(x)^.75
powlgrnk(5, 200, 3, hazcon=hc,survcon=sc,haztst=ht,survtst=st)
#       power           n          nd
#   0.8564817 1000.0000000 446.0797311

C. R source code

powlgrnk <- function(acc.per,acc.rate,add.fu,alpha=.025,p.con=.5,
hazcon=function(x,lc,pc,…) {u <- (1−pc)*exp(−lc*x); lc*u/(pc+u)},
survcon=function(x,lc,pc,…) pc+(1−pc)*exp(−lc*x),
haztst=function(x,lt,pt,…) {u <- (1−pt)*exp(−lt*x); lt*u/(pt+u)},
survtst=function(x,lt,pt,…) pt+(1−pt)*exp(−lt*x),
control.rate=NULL,test.rate=NULL,control.cure=0,test.cure=0,…) {
  risk <- function(t,c.rng,surv,…) ifelse (t<=c.rng[1],1,ifelse(
    t>=c.rng[2],0,(c.rng[2]-t)/((c.rng[2]-c.rng[1]))))*surv(t,…)
    #P(still at risk at t)
  mn <- function(t,p.con,c.rng,risk,survcon,hazcon,survtst,haztst,
      lc,lt,pc,pt,…) {#mean of logrank score
   y1 <- p.con*risk(t,c.rng,survcon,lc=lc,pc=pc,…)
   y2 <- (1-p.con)*risk(t,c.rng,survtst,lt=lt,pt=pt,…)
   y <- y1+y2
   ifelse(y>0,y1*y2*(hazcon(t,lc=lc,pc=pc,…)-
haztst(t,lt=lt,pt=pt,…))/y,0)
  }
  vs <- function(t,p.con,c.rng,risk,survcon,hazcon,survtst,haztst,
     lc,lt,pc,pt,…) {#expected value of null variance estimator
   y1 <- p.con*risk(t,c.rng,survcon,lc=lc,pc=pc,…)
   y2 <- (1-p.con)*risk(t,c.rng,survtst,lt=lt,pt=pt,…)
   y <- y1+y2
   ifelse(y>0,(y1*y2/y)^2*(hazcon(t,lc=lc,pc=pc,…)/y2+haztst(t,lt=lt,pt=pt,
    …)/y1),0)
  }
  sig2 <- function(t,p.con,c.rng,risk,survcon,hazcon,survtst,haztst,
     lc,lt,pc,pt,…) {#variance of logrank score
   y1 <- p.con*risk(t,c.rng,survcon,lc=lc,pc=pc,…)
   y2 <- (1-p.con)*risk(t,c.rng,survtst,lt=lt,pt=pt,…)
   y <- y1+y2
   ifelse(y>0,(y1*y2/y)^2*(haztst(t,lt=lt,pt=pt,…)/y2+hazcon(t,lc=lc,pc=pc,
     …)/y1),0)
  }
  pf <- function(t,c.rng,risk,surv,haz,…) {
   haz(t,…)*risk(t,c.rng,surv,…)}
  c.rng <- c(add.fu,acc.per+add.fu)
  r1 <- integrate(mn,0,c.rng[2],p.con=p.con,c.rng=c.rng,risk=risk,
   survcon=survcon,survtst=survtst,hazcon=hazcon,haztst=haztst,
   lc=control.rate,lt=test.rate,pc=control.cure,pt=test.cure,…)[[1]]
  r2 <- integrate(vs,0,c.rng[2],p.con=p.con,c.rng=c.rng,risk=risk,
   survcon=survcon,survtst=survtst,hazcon=hazcon,haztst=haztst,
   lc=control.rate,lt=test.rate,pc=control.cure,pt=test.cure,…)[[1]]
  r3 <- integrate(sig2,0,c.rng[2],p.con=p.con,c.rng=c.rng,risk=risk,
   survcon=survcon,survtst=survtst,hazcon=hazcon,haztst=haztst,
   lc=control.rate,lt=test.rate,pc=control.cure,pt=test.cure,…)[[1]]
  r4 <- integrate(pf,0,c.rng[2],c.rng=c.rng,risk=risk,surv=survcon,
   haz=hazcon,lc=control.rate,pc=control.cure,…)[[1]]
  r5 <- integrate(pf,0,c.rng[2],c.rng=c.rng,risk=risk,surv=survtst,
   haz=haztst,lt=test.rate,pt=test.cure,…)[[1]]
  crit <- qnorm(1-alpha)
  n <- acc.rate * acc.per
  power <- 1-pnorm(crit*sqrt(r2/r3)−r1*sqrt(n/r3))
  c(power=power,n=n,nd=n*(p.con*r4+(1-p.con)*r5))
}