Continuous development of schemes for parallel computing of the electrostatics in biological systems: Implementation in DelPhi

Abstract

Due to the enormous importance of electrostatics in molecular biology, calculating the electrostatic potential and corresponding energies has become a standard computational approach for the study of biomolecules and nano-objects immersed in water and salt phase or other media. However, the electrostatics of large macromolecules and macromolecular complexes, including nano-objects, may not be obtainable via explicit methods and even the standard continuum electrostatics methods may not be applicable due to high computational time and memory requirements. Here, we report further development of the parallelization scheme reported in our previous work (J Comput Chem. 2012 Sep 15; 33(24):1960–6.) to include parallelization of the molecular surface and energy calculations components of the algorithm. The parallelization scheme utilizes different approaches such as space domain parallelization, algorithmic parallelization, multi-threading, and task scheduling, depending on the quantity being calculated. This allows for efficient use of the computing resources of the corresponding computer cluster. The parallelization scheme is implemented in the popular software DelPhi and results in speedup of several folds. As a demonstration of the efficiency and capability of this methodology, the electrostatic potential and electric field distributions are calculated for the bovine mitochondrial supercomplex illustrating their complex topology which cannot be obtained by modeling the supercomplex components alone.

INTRODUCTION

Electrostatic potential and energies originating from the charge distribution within biomolecules greatly impact intra- and inter-molecular interactions. Various explicit (treating the solvent as individual water molecules) and implicit (treating the water phase as a continuum media) models have been developed to calculate electrostatic potential and corresponding energies of biomolecules and nano-objects immersed in water and salt phase. Implicit models are usually considered to be more computationally efficient and suitable for calculating the electrostatic potential of large objects and systems ^1–5. One of the most recognized implicit models is the nonlinear elliptic Poisson-Boltzmann equation (PBE) ^6–8

$$\nabla ·\left(\epsilon (x)\nabla \phi (\text{x})\right)-k{(x)}^{2}sinh(\phi (\text{x}))=-4\pi \rho (x),$$ (1)

where φ is the electrostatic potential, ε is the spatial dielectric function, k is a modified Debye-Huckel parameter, and ρ is the charge distribution function.

Due to the important role of PBE in molecular biology, numerous PBE solvers have been developed independently in various laboratories to solve the PBE by a number of numerical methods, including finite difference (FDM), finite element (FEM), and boundary element (BEM) methods, etc. ⁹. A short list of PBE solvers includes AMBER ^2,10–12, CHARMM ¹³, ZAP ¹⁴, MEAD ¹⁵, UHBD ¹⁶, AFMPB ¹⁷, MIBPB ^18,19, ACG-based PBE solver ²⁰, Jaguar ²¹, APBS ^22,23 and DelPhi ^24–26. Despite their differences, all these solvers consist of three major components: determination of the molecular surface ^27–30 or dielectric coefficient map ^31,32, calculation of the potential, and acquirement of the corresponding electrostatic energies. It is outside of the scope of this work to compare the performance of the above mentioned PBE solvers, but they all become very slow if applied to large systems such as viruses ^33,34, molecular motors ³⁵ and systems made of nano-objects and biomolecules ³⁶. For such large systems, for example the adeno-associated virus ³⁴, even one of the fastest solvers, the DelPhi program, takes more than half of a day to complete the calculations at minimum requirements for the grid resolution = 0.5 Å/grid ³⁷. For many of the other mentioned PBE solvers more precise resolution may be needed to achieve stable results, and this may take days to calculate. Obviously significant speedup is required to make these serial algorithms applicable to the study of large macromolecular assemblages, as it was done by parallelizing APBS ²³, FDPB ³⁸, UHBD ³⁹ etc..

Inspired by the development of high performance scientific computing techniques, in this paper we introduce several techniques, resulting in parallelization scheme for solving the PBE. To illustrate the effectiveness of this approach and provide concrete examples, it was implemented in the DelPhi program. The method is graphically demonstrated in Figure 1 and is described in detail in the methods section. Using Delphi as an example, the execution flow chart consists of 3 major tasks: surface construction, iteration, and energy calculation as shown in Figure 2. Each task is then divided into subtasks which are carried out in parallel by slave processors (green ovals in Figure 2). Enhanced by the computational power of multiple processors, the method reduces the computational time of the parallelized DelPhi program several folds. It should be clarified that the reported method is not based on standard spatial domain decomposition only; instead, the proposed algorithm delivers the solutions by applying specific techniques to each of the three major tasks and reflects the physical nature of the quantities being modeled. Thus, the construction of the molecular surface, being a geometrical problem, is parallelized via the methods of geometrical clustering and duplicated calculations at extended boundaries. The iterations of calculating the electrostatic potential, being long-range, are parallelized via a combination of numerical techniques and specific software design but without invoking any assumptions, and finally, the calculations of the corresponding electrostatic energies, being independent of the geometry, are parallelized via multi-threading. The resulting solutions obtained with the parallelized code, in terms of the electrostatic potential and energies, track the solutions obtained with the serial algorithm to double precision. Although such accuracy may not be biologically relevant for many current applications, keeping the parallelized and serial code consistent is important for future code development.

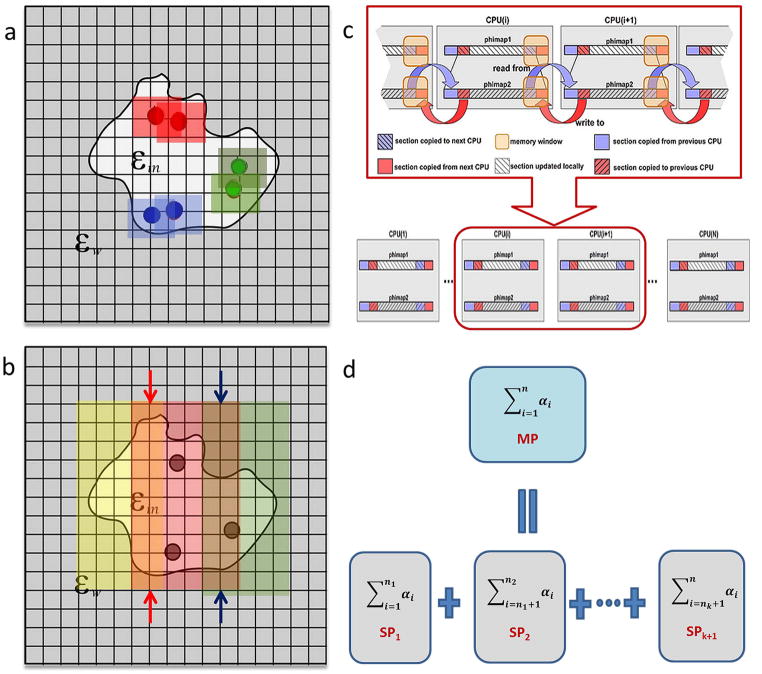
Figure 1.

Parallelization techniques involved: a) Geometric clustering b) Duplicated calculations at extended boundary grids. Regions disputed to different processors are demonstrated by their colors. “Boundaries” of regions are indicated by arrows. Calculations on each processor are extended to the left and right one more grid so that two successive regions share a common region of 3 grids. c) Parallelization of GS/SOR iterations using one-sided Direct Remote Memory Access operations provided in MPI-2 library. Network communication between two processors using MPI-2 one-sided operations is shown in upper half of the graph. d) Mimic of multithreading programming: a sum of n numbers on the master processor (MP) is broken into k+1 partial sum, each of which is calculated on a single slave processor (SP) simultaneously.

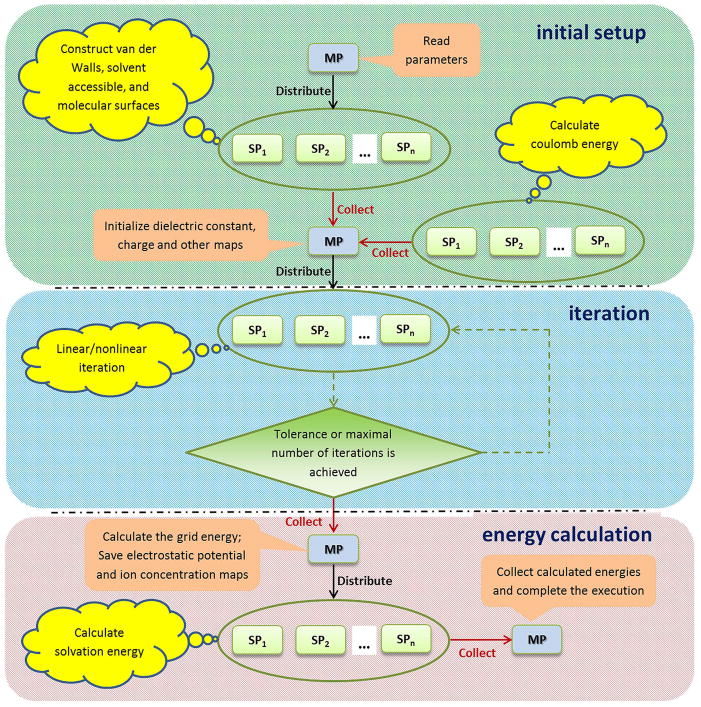
Figure 2.

Demonstration of the parallelization scheme for parallel computing. The execution flowchart of the DelPhi program for calculating electrostatic potential and energies is split into three tasks (initial setup, iteration and energy calculation). Tasks performed by the master processor (MP) and slave processors (SP₁, SP₂, …, SP_n) are described in pink rectangle and yellow cloud callouts, respectively. Green oval indicates parallel computing performed on multiple slave processors. Levels of the algorithm are divided by black broken lines. Network communication between the master and slaves is demonstrated by either black arrow (master distributes job to slaves) or red arrow (master collects results from slaves).

It should be emphasized that the reported parallelization techniques are equally applicable for solving the linearized and nonlinear PBEs. Moreover, these techniques are not restricted to the DelPhi program. They can be easily modified and recruited by other software to parallelize the surface construction, iteration algorithms, and energy calculations.

To illustrate the capabilities of the proposed parallelization method, it was applied to model a large super molecular complex: the mitochondrial supercomplex ⁴⁰. Here we take advantage of a recently reported 3D structure of mitochondrial supercomplex I₁III₂IV₁ ⁴⁰ to demonstrate the complexity of the distribution of the electrostatic potential and field in large systems with very complicated shape placed in a model of biological membrane.

PARALLELIZATION SCHEME

In this section, we describe in detail the parallelization scheme and its implementation in the DelPhi program. The goal of our method’s design is to reduce the computational cost time noticeably without losing “accuracy”, meaning we will not sacrifice the ability to reproduce the same results obtained by sequential calculations up to double precision. This is required in order to assure that the error will not propagate in future code developments. However, it should be clarified that such accuracy may not be crucial for most biological applications, since the errors associated with the model and the parameters chosen are much larger.

The DelPhi execution flowchart (Figure 2) consists of 3 major steps: (I) The “initial setup” step initializes the dielectric constant map, as well as several other maps, and generates the van der Waals, solvent accessible, and molecular surfaces by a rapid construction method described in ⁴¹. (II) The “iteration” step utilizes the Gauss-Seidel (GS) or Successive Over Relaxation (SOR) algorithms to iteratively update the 3D electrostatic potential map at grids until the pre-defined tolerance or the maximum number of iterations is achieved ²⁵. (III) The “energy calculation” step calculates the user-specified energies, such as the grid energy, the coulomb energy, and the reaction field energy. If desired, the dielectric, electrostatic potential, and ion concentration maps are saved in standard files, which can be easily rendered by visualization software like VMD ⁴², CHIMERA ⁴³, etc.

Most of sequential PBE solvers, including DelPhi, are practically limited to solving the PBE for molecules and complexes of size less than couple of hundred Angstroms; this is true no matter which numerical methods are carried out due to the high computational time and memory requirements when the system’s size is large. After carefully benchmarking the execution time cost of each step in the DelPhi program, our numerical experiments revealed that the most expensive procedures, which consequently must be carried out in parallel, are indeed the procedures mentioned above: the surface construction, the “iteration” step, and the calculations of electrostatic energies. Since these procedures involve different methods and deal with different quantities, specific techniques must be taken into consideration in order to increase the performance of parallel computing. We shall describe the parallelization techniques as follows.

Initial setup

Parallelizing the surface construction in the “initial setup” step can be achieved via the standard space domain decomposition method. In addition, two techniques are designed to improve the performance without losing accuracy: one is called “geometric clustering” (Figure 1a), which reduces duplicated calculations and network communication among processors during the construction of the van der Waals and molecular surfaces, and the other is called “duplicated calculations at extended boundary grids” (Figure 1b), which carries out additional calculations on grids located on the extended boundary in order to maintain consistency between the results obtained by parallel and sequential calculations.

Geometric clustering

By considering each atom a “hard ball” with a certain radius, the van der Waals surface can be viewed as the composition of the surface of these “hard balls”. DelPhi utilizes a fast van der Waals surface construction method ⁴¹, which reduces computational cost by restraining calculations on grids inside boxes centered at those atoms. The grids inside each box are classified as follows: external grid points, internal grid points, boundary grid points, and internal boundary grid points, each based on their six nearest midpoint positions ⁴¹ in order to determine the boundary grids approximating the van der Waals surface of the object. One can see that these boxes may share large overlapping area if the atoms are located within close proximity to each other in space (boxes of the same color shown in Figure 1a).

A straightforward approach for the parallelization of the construction of the van der Waals surface is to group the atoms according to their sequential appearance in the structural file, and then dispatch them to different processors for calculating the surface in parallel. However, we must bear in mind that the atoms read from the PDB files are usually geometrically unsorted; therefore, it is highly possible that adjacent atoms are dispatched to different processors by chance. In the worst case scenario, two or more slave processors may repeat the same calculations in a large overlapping area at the same time and return to the master processor large amounts of redundantly computed values. This would result in a significant waste of the computational power of the processors and unnecessarily increase the demand of network traffic between master and slave processors. It is therefore advised to spend some computational time to sort the atoms on the master processor before dispatching them to the slave processors. Taking advantage of the simplicity and efficiency of the Quicksort method ⁴⁴ and other various existing algorithms for parallelizing (see ^45–47 for example), we parallelized the surface construct as follows and consider our implementation to be one geometric clustering ^48,49 by nature.

The following method was developed to sort the atoms in 3D space before dispatching them to slave processors. For the sake of simplifying the description of this method, we make the following two hypotheses which, indeed, are not mandatory to implement the method. We first assume the number of available processors N_CPU = n_x · n_y · n_z for positive integers n_x, n_y, and n_z. These integers indicate how many segments the computational domain is partitioned into in x-, y-, and z-direction, respectively. These integers usually are chosen to be as close as possible to each other in order to treat x-, y-, and z-direction equally. Next, we assume the number of atoms N_atom is a multiple of N_CPU and N_atom ≫ N_CPU so that each processor is given N_atom/N_CPU atoms to work on. Given that the above two assumptions are satisfied, we intend to split the computational domain into n_x, n_y, and n_z segments in x-, y-, and z-direction respectively so that each subdomain, consisting of N_atom/N_CPU atoms, is given to one slave processor for parallel computing.

First, the atoms are sorted by their x-coordinates, using a fast sorting method, and are evenly broken into n_x groups. The sorting method we chose to use is the quicksort method ⁴⁴, which makes O(nlog(n)) comparisons to sort n items on average. Next, the atoms in each of these n_x groups are sorted by their y-coordinates and are split into n_y groups, resulting in n_x · n_y groups of atoms in total. Applying the same sorting-splitting methodology one more time in z-direction yields n_x · n_y · n_z groups of atoms of equal number N_atom/N_CPU. Finally, each group of atoms is given to one individual slave processor for calculation. A detailed description of implementing the geometric clustering is provided in Table 2 and a pseudo-code implemented in DelPhi can be found in the supplementary material.

Table 2.

A detailed description for implementing geometric clustering

Given NCPU available processors (NCPU = nx · ny · nz for positive integer nx, ny, and nz) and Natom atoms, we assume Natom is a multiple of NCPU and Natom ≫ NCPU. The following steps intend to distribute each processor Natom/NCPU atoms for parallel computing. Step 1All atoms are sorted according to their x-coordinates either by the regular (sequential) Quicksort method on the master processor, or by a parallel Quicksort method on all processors. Then all processors are split into nx groups, each of which consists of ny · nz processors. Processors in the 1st group keep the 1st Natom/nx sorted (in x-direction) atoms and discard the rest atoms; processors in the 2nd group keep the 2nd Natom/nx sorted (in x-direction) atoms and discard the rest atoms; …, and so on. Step 2Each processor sorts its own atoms according to their y-coordinates by the Quicksort method independently, or all processors in the same group together adopt a parallel Quicksort method to sort the same set of atoms. Then each group of ny · nz processors is split into ny subgroups, each of which consists of nz processors. In each group, processors in the 1st subgroup keep the 1st Natom/(nx · ny) atoms and discard the rest; processors in the 2nd subgroup keep the 2nd Natom/(nx · ny) atoms and discards the rest; …, and so on. Step 3After sorting its atoms according to their z-coordinates in the same fashion, the 1st processor in each subgroup keeps the 1st Natom/(nx · ny· nz) atoms; the 2nd processor keeps the 2nd Natom/(nx · ny· nz) atoms; …, and so on. Each processor now has Natom/(nx · ny· nz) atoms geometrically staying close to each other. Step 4After each processor performs calculations on its own atoms, the results are collected and assembled on the master processor.

The above method is designed to balance the workload of processors. In addition, this method can be easily parallelized due to its divide-and-conquer nature by applying the Quicksort method to sort each group on one individual processor simultaneously. One can view this method as a dynamical space decomposition method in the sense that the whole computational domain is dynamically partitioned into multiple exclusive subdomains of various lengths in x-, y-, and z-directions, according to the density of the atoms in the subdomains: a higher density of atoms results in a smaller subdomain, and vice versa.

Duplicated calculations at extended boundary grids

After the van der Waals surface is obtained, the molecular surface is generated by the Smoothed Numerical Surface (SNS) method ⁴¹ in the DelPhi program by running a water probe with a user-specified radius (usually is set to be 1.4 Å) on the van der Waals surface. The “out” mid-points that surround external boundary grid points are dispatched to slave processors in order to perform the SNS method in parallel. However, the resulting molecular surface obtained by parallel computing could be different from that obtained from sequential computing when aggregated mid-points are dispatched to different slave processors. These mid-points share same neighboring grid points, whose status is changed by the SNS method across multiple processors at the same time. Parallel computing can be achieved, yet very inefficiently, by synchronizing the status of the mid-points and their neighbors across processors during calculations.

Stimulated by the previous strategy for constructing the van der Waals surface, we developed a second method to obtain the molecular surface. This time, the mid-points are sorted only in one direction, e.g. z-direction. Then all mid-points with the same z-coordinate are given to one processor. In order to handle the mid-points of atoms with adjacent z-coordinates but given to different processors, each processor extends its calculations to all mid-points with one less z-coordinate on the left boundary and one more z-coordinate on the right boundary as demonstrated in Figure 1b. By doing so, two processors share a common region consisting of mid-points with two successive z-coordinates such that previous “boundary” mid-points become “internal” together with their neighbors which have been calculated on the same processor. Calculations in the common region are performed independently on these two processors with no synchronization. When calculations on all processors finish, results obtained at the “internal” points are sent back to the master processor for assembling. A step-by-step description is given in Table 3 and the associated pseudo-code is shown in the supplementary material.

Table 3.

A detailed description for implementing duplicated calculations at extended boundary grids

Given NCPU available and Nmidpt mid-points, we assume Nmidpt ≫ NCPU. Step 1All atoms are sorted according to their z-coordinates either by the regular (sequential) Quicksort method on the master processor, or by a parallel Quicksort method on all processors. Step 2Many midpoints may have the same z-coordinates. Count the number of different z-coordinates that the mid-points have (for example, say p different z-coordinates in total) and save the number of mid- points with the same z-coordinate in an array named counts (for example, say counts={k1, k2, …, kp} such that ${\sum }_{i=1}^p{k}_i=N_{\mathit{midpt}}$. Step 3Each processor intends to perform calculations on the number of midpoints as close as possible in order to balance the workload on each processor as much as possible. Because of this, first of all, the smallest number q1 satisfying ${\sum }_{i=1}^{q_1}{k}_i\ge N_{\mathit{midpt}}/N_{\mathit{CPU}}$ is searched and obtained. Then all mid-points with their z- coordinates belonging to the subset {k1, k2, …, kq1, kq1+1} are given to the 1st processor for future parallel computing. Notice that all mid-points with z-coordinates equal to kq1+1 serve as the “extended right boundary grids”, especially in the case of kq1+1 = kq1 + 1. The results on them are calculated in case they may have impact on the calculations on the rest of points. However, these results are not collected by the master processor for the final assemblage. Similarly, starting from kq1 + 1, the smallest number q2 satisfying ${\sum }_{i=q_{1+1}}^{q_2}{k}_i\ge N_{\mathit{midpt}}/N_{\mathit{CPU}}$ is searched and obtained. Then all mid-points with their z-coordinates belonging to the subset {kq1, kq1+1, …, kq2, kq2+1} are given to the 2nd processor for future parallel computing. All mid-points with z-coordinates equal to kq1 or kq2+1 serve as the “extended left/right boundary grids”, respectively, and the results obtained on them are not collected. Repeat the same procedure until all mid-points are assigned to one processor. It is possible that there are more processors left. In such case, these processors are marked “idle” and not involved in the next step parallel computing. Step 4All processors perform calculations of constructing surface on its own mid-points independently. The obtained results are sent back to the master processor for the final assemblage.

Iteration

After the surfaces are constructed, PBE solvers utilize various numerical methods to calculate the potentials at grids. For example, DelPhi utilizes the GS/SOR algorithms to iteratively update the electrostatic potentials at grids. The technique implemented to parallelize these iteration methods has been reported in Ref.³⁷. For consistency, we only outline the idea here.

The GS/SOR methods are iteration algorithms to solve a system of equations numerically. Though they usually enjoy a faster convergence rate when compared to the Jacobi method, the standard implementation of these methods restricts their utilization for parallel computing due to the sequential nature of a requirement of using the most recently updated values in current iteration as soon as they are available. A variety of parallelization techniques ^50–54 have been developed to parallelize the GS/SOR methods. In the DelPhi program, special techniques, namely the “checkerboard” ordering (also known as the “black-red” ordering) and contiguous memory mapping ²⁵, have been implemented previously in order to achieve better performance than the standard implements of the GS/SOR methods. Based on these techniques, we chose to implement the algorithm similar to that described in ⁵³ and utilize the Master-Slave paradigm to parallelize the iterations using one-sided Direct Remote Memory Access (DRMA) operations provided in the Message Passing Interface library MPI-2 ³⁷ (Figure 1C). The multi-processor parallelization of the GS/SOR methods in the DelPhi program is so highly efficient that the computational time is reduced as a linear/nearly-linear function of the number of processers on the protein 3KIC. Interested readers are directed to Ref. ³⁷ for more details.

Energy calculation

Three energies are usually of users’ interests: (I) the grid energy which is obtained from the product of the potential and the charge at each grid point, summed over all points on the grid; (II) the coulomb energy which is calculated using Coulomb’s law and demonstrates the energy required to bring charges from infinite distance to their resting positions within the dielectric specified for the molecule; (III) the reaction field energy (also known as the solvation energy) obtained from the product of the potential due to induced surface charges with all fixed charges of the solute molecule.

The parallel calculation of energy is more straightforward and less complicated than the previous two calculation methods. The first technique is based on the observation that calculating the coulomb energy, by definition, does not require that the potentials be obtained by iterations. Therefore, the coulomb energy can be calculated either before the “iteration” step by slave processors while the master processors is still performing initial setups, or by the master processor while the slave processors are iteratively updating the potentials. By implementing either of above two techniques, we expect to significantly reduce the cost of calculating the coulomb energy in the overall program execution time.

The second technique, based on the observation that the desired energies are approximated by summing values computed over all grids, follows a commonly adopted simple, yet effective, trick in multi-threading programming: a summation is split into multiple partial sums, each of which is calculated by one thread (processor in our case) simultaneously (Figure 1d). The final result is obtained by summing those partial sums by one thread (master processor). Again, see the supplementary material for a pseudo-code.

RESULTS

PDB preparation

We used the large mitochondrial complex to test the performance of the proposed parallelization scheme. To make it suitable for the modeling, the original coordinate file (PDB ID: 2YBB) was subjected to several procedures: (a) the m, n, o and p chains in the original PDB file had only Ca atoms and no residue assignment. For this reason they were manually substituted by analogical L, M, N and (K+J) chains respective to the membrane domain of respiratory complex I of Escherichia coli BL21(DE3) (PDB ID: 3ROK) as previously described in Ref. ⁴⁰. In order to relax plausible structural clashes in the modified structure, the complex was subjected to relaxation by energy minimization using Chimera software ⁵⁵; (b) the final corrected structure was subjected to the profix program from the JACKAL package (http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software website: JACKAL) ⁵⁶ developed in Dr. B. Honig’s lab in order to add missing atoms and/or sequence fragments; (c) the protonation of macromolecule was performed with Chimera software ⁵⁵; (d) a model of the membrane was built by ProNO Integrator ⁵⁷ and was added to the structural file. The entire structural file, including the membrane model, is available for download from the website http://compbio.clemson.edu/downloadDir/2YBB_H-MEM.pdb.

Computational environment

The numerical experiments reported below were performed by a dedicated queue on the Palmetto cluster at Clemson University (http://citi.clemson.edu/palmetto). This computational queue consists of 1 master node (Model: HP DL980G7) equipped with Intel Xeon 7542 @ 2.7 GHz CPU and 50 GB memory, and 200 slave nodes (Model: Sun X6250) equipped with Intel Xeon E5420 @2.5 GHz CPU and 32 GB memory. Only one CPU per node participated in each run in order to avoid possible memory competition on the same node. Both sequential and parallel code were compiled with GNU compiler GCC version 4.5.1 (http://gcc.gnu.org/) and the parallel code was executed using MPICH2 version 1.4 (http://www.mcs.anl.gov/research/projects/mpich2/). Myrinet 10G is used for network interconnect.

Both sequential and parallel calculations were performed on processors with identical hardware configurations and were provided enough memory to avoid possible slow-downs caused by additional data exchanges between the memory and hard disk. All identical runs were repeated 5 times and their averages are reported here in order to reduce random fluctuations caused by temporary system workload and network communication.

Numerical experiments and performance analysis

In order to compare the parallel experiments quantitatively to the sequential ones, we are particularly interested in a standard quantity, the speedup (more precisely, the absolute speedup): $S_N=\frac{T_1}{T_N}$, where T₁ is the execution time of the sequential program and T_N is the execution time of parallel program running on N processors. In principle, the higher speedup implies a better mapping of the molecule onto the grid. The achieved speedups at grid resolution=1, 2/3 and 1/2 Å/grid, resulting in the total number of grids= 373³, 559³ and 747³, are selected to demonstrate the performance of the parallel DelPhi at various grid resolutions. Other quantities commonly used in performance analysis of parallel computing, such as efficiency and scalabilities, will be defined and used as well in analyzing the performance of the proposed parallelization scheme.

Numerical experiments

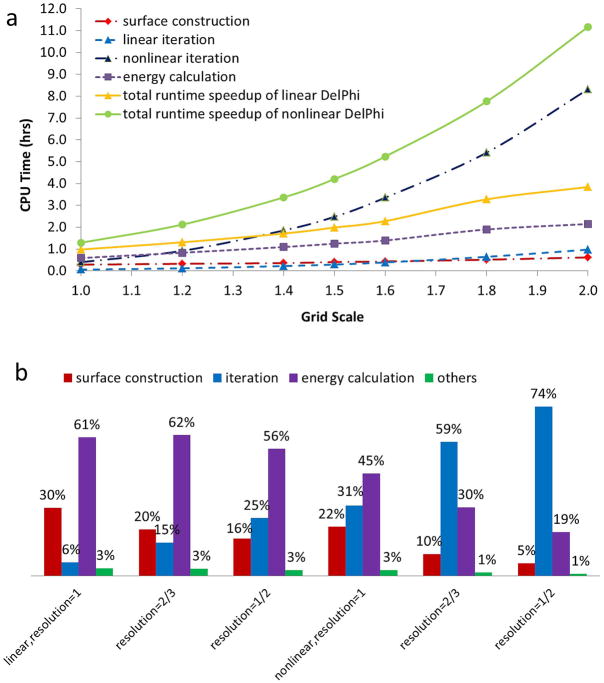
The first series of experiments were performed to solve the PBE (linear and nonlinear) for the protein 2YBB using the sequential DelPhi program in order to determine the computational cost on various grid resolutions and grid dimensions. All parameters, shown in Table 1, except the resolution were fixed in all experiments. Notice that the parameter ionrad is set to be 4.0Å (twice as large as the default value 2.0Å) in order to reduce the time cost for solving the nonlinear PBE and to make it similar to the time cost of the linear calculations and to make the three components of the calculations: the surface construction, potential interaction and energy calculations carrying similar weight in the total speedup. Thus at 10 CPUs, the surface construction takes about 14min, the energy calculations about 15min and the SOR interactions about 56min with ionrad = 4.0Å or 10h and 14min with ionrad = 2.0Å. Obviously in the case of ionrad = 2.0Å, the speedup will be almost entirely due to the speedup of SOR algorithm, an investigation already reported in our previous work. Because of that, the ionrad was selected to be 4.0Å to allow the speedup to be assessed having contributions from the three parallelized components mentioned above. The resulting CPU time (in hours) of individual calculations (broken lines) and total execution time (solid lines), by varying the grid resolution are shown in Figure 3a (notice that smaller resolution results in more grids and better approximation). It is obvious that all CPU time increases dramatically in both linear and nonlinear cases when using finer (smaller) resolution; especially, the time for solving the nonlinear PBE (solid light-green line), which requires significantly more iterations to achieve the given tolerance, increases rapidly from about 1 hour when grids= 373³ (resolution=1.0 Å/grid) to more than 11 hours when grids= 747³ (resolution=0.5 Å/grid) primarily due to the increase of time cost by iterations (broken dark blue line). Figure 3b demonstrates the percentages contributed by individual calculations at grid resolution = 1, 2/3 and 1/2 Å/grid. One can see that the three major components (surface construction, iteration, and energy calculation) mentioned in the Introduction section together contribute over 97% of the overhead in all cases, which reemphasizes the importance of parallelizing them in order to substantially reduce the computational cost. The rest of the calculations (green bars) do not contribute much and therefore are not parallelized and remain identical in both sequential and parallel codes.

Table 1.

Parameters used in numerical experiments of protein 2YBB

Parameter	Value	Meaning and Unit
perfil	80	A percentage of the object longest linear dimension to the lattice linear dimension.
grid resolution	0.5–1.0	one grid spacing (Å/grid).
indi	4.0	The internal (molecules) dielectric constant.
exid	80.0	The external (solution) dielectric constant.
prbrad	1.4	A radius (Å) of probe molecule that will define solvent accessible surface in the Lee and Richard’s sense.
salt	0.1	The concentration of first kind of salt,(moles/liter).
bndcon	2	Dipolar boundary condition. The boundary potentials are approximated by the Debye-Huckel potential of the equivalent dipole to the molecular charge distribution.
ionrad	4	The thickness of the ion exclusion layer around molecule (Å).
relpar	0.9	A manually assigned value for relaxation parameter in non-linear iteration convergence process.
maxc	0.0001	The convergence threshold value based on maximum change of potential.
linit	2000	An integer number (> 3) of iterations for solving linear PBE.
ninit	2000	An integer number (>= 0) of iterations for solving non-linear PBE.
energy(s,c,g)	---	Grid, solvation and coulombic energies are calculated.

Figure 3.

Increasing CPU time of the DelPhi program when calculating electrostatic potential and energies for protein 2YBB. a) CPU time cost by individual calculations and overall execution time at various grid resolutions b) Individual percentage contributed by each parallel calculation when solving linear and nonlinear PBE at 3 selected grid resolution=1, 2/3, and 1/2 Å/grid.

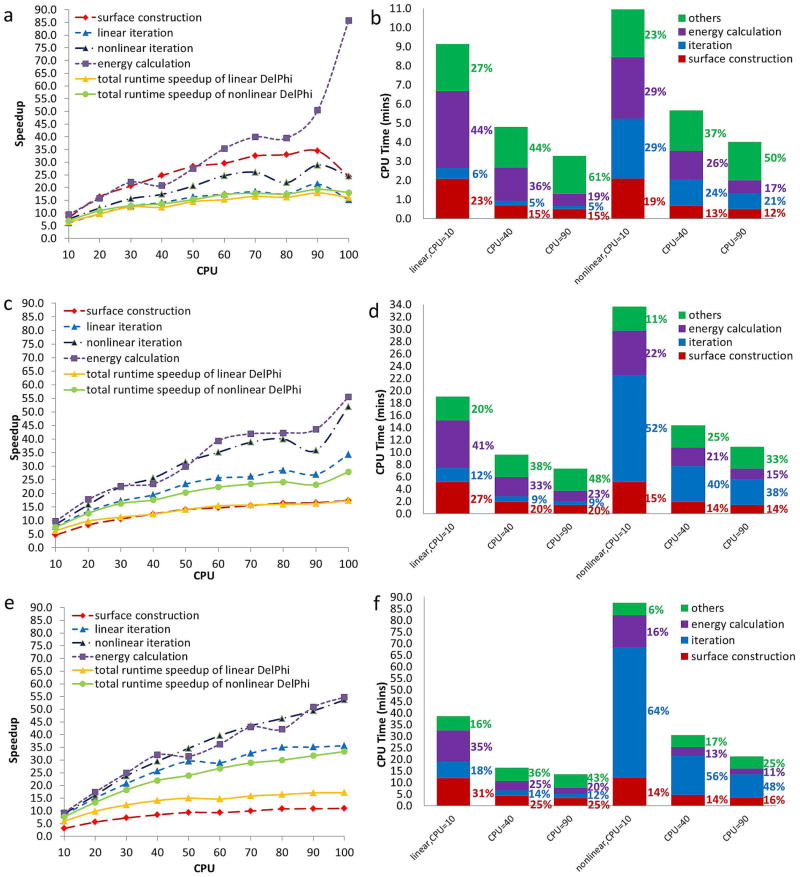
In the next series of experiments the number of adopted slave processors ranges from 10 to 100 in increments of 10. The results obtained by our computational experiments are shown in Figure 4. The achieved speedups for grid resolution = 1, 2/3 and 1/2 Å/grid in parallel computing on various CPUs are shown in Figure 4a, c and e on the left panel, respectively. In order to have better insight and compare the performance of sequential and parallel implementations, three examples at CPU=10, 40, 90 are chosen for detailed demonstration. The CPU time (in minutes) of individual calculations of these three examples are demonstrated by the height of the colored columns, as well as the contributed percentages of individual calculations in the overall execution time are labeled next to the columns on the right, in Figure 4b, d and f on the right panel for each grid resolution.

Figure 4.

Speedups obtained by the MLIPB method at grid resolution=1, 2/3, and 1/2 Å/grid and results obtained for selected examples at CPU=10, 40, 90. a)–b) Results obtained at grid resolution=1 Å/grid. c)–d) Results obtained at grid resolution=2/3 Å/grid. e)–f) Results obtained at grid resolution=1/2 Å/grid).

Performance analysis

From Figure 4a, c and e, it is easy to see that the proposed parallelization scheme is able to achieve better performance (higher speedups) for solving both linear and nonlinear PBEs when more CPUs (up to 100 CPUs) are utilized by observing that the speedup lines of overall execution time (solid yellow and light-green lines) increase monotonically from CPU=10 to CPU=100 and reach their peaks at CPU=100. It is also clear that the problem size and complexity have great impact on the achieved speedups. Taking the performance of the parallelization scheme implemented in DelPhi at 100 CPUs as an instance, the method achieved 16-time speedup (solid yellow line in Figure 4a) for solving the linear PBE at grid resolution=1 Å/grid, and achieved 33-time speedup (solid light-green line in Figure 4e) for solving the nonlinear PBE at grid resolution=1/2 Å/grid. However, in light of Amdahl’s Law, the speedup lines, which are not flattened at their peaks when CPU=100, imply that the MLIPB method has the potential to achieve higher speedups when more than 100 CPUs are used or when the problem size is larger.

Efficiency, which is defined as $E_N=\frac{T_1}{N\ast T_N}=\frac{S_N}{N}$, is another quantity which is closely related to speedup and gauges the performance of parallel computing from another aspect. Its value equals 1 in the ideal case of linear speedup. Efficiency determines how much computational power of each processor is utilized in solving the problem, as compared to how much effort is wasted in communication and synchronization. In our case, efficiency, by its definition, can be easily calculated from the results shown in Figure 4a, c and e. For instance, when solving the nonlinear PBE at grid resolution=2/3 Å/grid, the method achieved 75% efficiency at 10 CPUs, and achieved less efficiency, down to 28% at 100 CPUs (solid light-green line in Figure 4c) due to increasing network communication.

Above, the speedup and efficiency analysis is discussed in strong scaling sense where the problem size (grid resolution) stays fixed while the number of processing units is increased in terms of parallel scaling. Weak scaling is another case in which the problem size assigned to each processing unit stays constant and additional units are used to solve a larger total problem. A discussion of weak scaling efficiency is not applicable in this work due to the large size of the problem. Numerically solving the PBE for the 2YBB protein at minimal requirement (grid resolution=1 Å/grid) yields the total number of grids= 373³, which can be done on 10 slave processors. However, to keep the problem size the same on the slave processors and to increase the number of the slave processors involved in the calculations, it will require a dramatic increase in the size of the problem on the master node. For example, to complete the benchmarking on 10 slave processors it will require grid size on the master processor to be 803³. While this is still doable, the next increments to 20 and more slave processors will make the problem too big to be handled by the master processor because of the limits of its memory capacity.

It should be pointed out here that the speedups shown in Figure 4a, c and e, as well as the efficiencies calculated above, are achieved based on the total program execution time, including the time consumed by the non-parallelized calculations after applying the parallelization scheme in the DelPhi program. The same amount of time cost by non-parallelized calculations (green columns) contributes a little to the execution time in sequential experiments, but contributes increasingly more notable fractions in all parallel experiments as the number of CPUs increases due to the significantly reduced time cost by parallelized calculations (purple, blue and red columns). For instance, the non-parallelized calculations for solving the linear PBE at grid resolution=1 Å/grid contributes 3% (the first green column in Figure 3b) in the overall execution time, but contributes 27%, 44%, and 61% (the green portions of the left three stacked columns in Figure 4b) when the number of employed CPUs in parallel computing was 10, 40, and 90, respectively. The same results can be observed for all other cases in Figure 3b, d and e.

The following observations are made in order to understand how much the non-parallelized calculations slow down the speedups at various grid resolutions. One can see that the overall execution time (the solid yellow and green lines) stays beneath (in Figure 4a), or in between (in Figure 3c and e) the broken lines for each individual calculations. This indicates that the non-parallelized calculations (the same as those demonstrated by the green columns in Figure 3b) in the parallel code have a smaller slow-down impact on the speedups of the program execution as the number of grids increases. This result is consistent with the observation of decreasing percentage contributions by the non-parallelized calculations (green columns) when the resolution decreases in Figure 4b, d and f.

Due to the notable impact of the non-parallelized routines on calculations of speedup and efficiency, additional attention is required to investigate the individual performance of each parallel calculation in order to fully understand the performance of the parallelization scheme.

The individual speedup, in the strong scaling sense, achieved by each parallelized calculation is demonstrated by broken lines in Figure 4a, c and e. One can use the definition of efficiency to calculate corresponding efficiencies as well. For example, it is observed that the techniques for parallelizing surface construction, which perform best and complete calculations 34 times faster when using 90 CPUs (38% efficiency) at coarse grid resolution=1 Å/grid (broken red lines in Figure 4a), achieve much less maximal speedup, about 18 times faster, on 100 CPUs (17% efficiency) at finer grid resolution=2/3 Å/grid (broken red lines in Figure 4c) and about 11 times faster on 100 CPUs (11% efficiency) at finest grid resolution=1/2 Å/grid (broken red lines in Figure 4e). On the other hand, the technique for parallelizing iterations, which achieves maximal speedup of 21 in linear case (broken light-blue lines in Figure 4a) and speedup of 29 in nonlinear case (broken dark-blue lines in Figure 4a) on 90 CPUs (23% and 32% efficiency, respectively), is surpassed by the techniques for parallelizing surface construction at coarse grid resolution=1 Å/grid, but outperforms the techniques for parallelizing surface construction by achieving speedup of 34 in linear case (broken light-blue lines in Figure 4c) and speedup of 52 in nonlinear case on 100 CPUs (broken dark-blue lines in Figure 4c) on 100 CPUs (34% and 52% efficiency, respectively) at finer grid resolution=2/3 Å/grid, and speedup of 36 in linear case (broken light-blue lines in Figure 4e) and speedup of 54 in nonlinear case (broken dark-blue lines in Figure 4e) on 100 CPUs (36% and 54% efficiency, respectively) at finest grid resolution=1/2 Å/grid (see also Ref ³⁷).

The techniques for parallelizing energy calculations, which achieve maximal speedups of 86, 55 and 55 at grid resolution=1, 2/3, 1/2 Å/grid, outperform all other parallelization techniques in terms of speedup and become the most effective methods in the parallelization scheme. The same conclusion can also be drawn from the concrete examples in Figure 4b, d and f by noticing that the percentages made by the parallel energy calculations decrease while the percentages made by the other techniques increase provided that the number of adopted CPUs is fixed.

The reported parallelization scheme is an alternative to the standard space domain parallelization. We compared the efficiency achieved by the MLIPB method to the parallelization method implemented in APBS^22,23,58 and observed that, though these two methods have very different approaches and emphasize different aspects to parallelize the corresponding numerical method for solving PBE, they are essentially equally efficient.

Memory requirement

Another major limitation, aside from the computational time, is the memory requirement for parallel computing. It is true that in our parallel implementation, the master process requires extra memory to maintain the data arising from the MPI framework in addition to the same amount of memory for the data required by the sequential implementation due to the master-slave paradigm we chose to use. The memory could be the leading limitation, for example, when the master process, as well as several slave processes, run on the same computer node. As mentioned in the section of computational environment, we circumvented this issue by requiring one process per node, and especially, the master process be assigned to the master node with larger memory.

Memory usage is important, however, it was not our primary concern to reduce memory usage of every process, including the master process, when the parallelization scheme was development. Our goal was to reduce the memory usage of the slave processes so that either multiple slave processes can be run on one computer node with enough memory, or so that the slave process can be run on a computer node with less memory. Taking the Palmetto cluster as an example, more than 90% of computer nodes on this cluster have less than 32GB memory and only 5 computer nodes have memory larger than 500GB (http://desktop2petascale.org/resources/159). This implementation strategy reduces the burden on the cluster’s architecture because only the master node is required to have large memory.

Electrostatic potential and field distributions in large protein complex

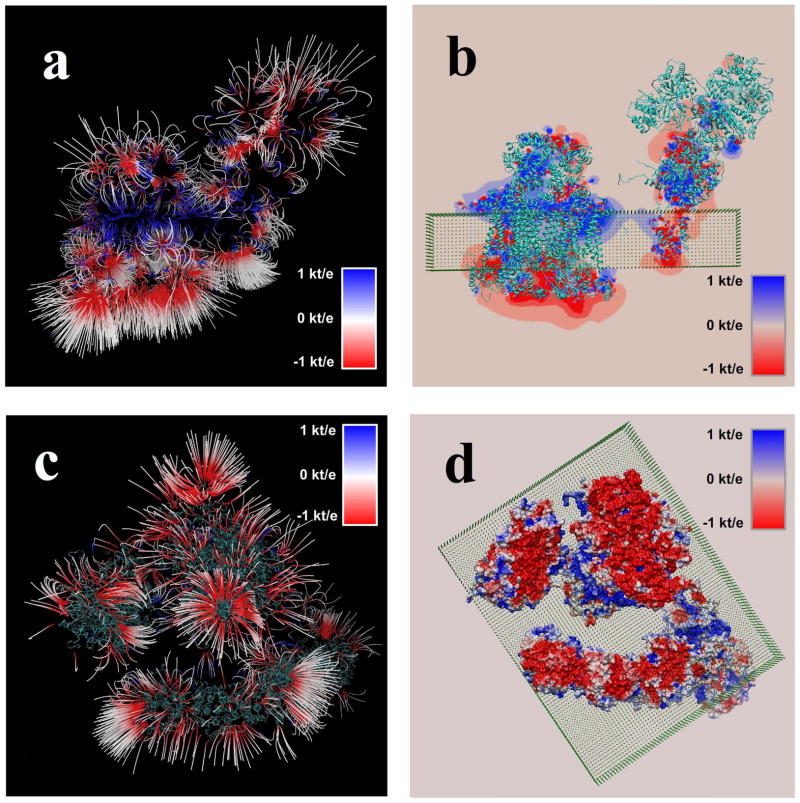
Recent work ⁴⁰ revealed the 3D structure of bovine mitochondrial supercomplex and indicated that the arrangement of the components within the complex supports the solid state model of organization ⁵⁹. The same investigation ⁴⁰ suggested the binding sites for various cofactors (ubiquinones and hemes) and a small protein electron carrier: cytochrome c. However, the specific pathways guiding the electron from one site to another are still under debate. Here we use the electrostatic potential and field maps calculated with parallelized DelPhi to demonstrate the complexity of their 3-Dimensional (3D) topology, a topology which cannot be obtained by modeling the individual components alone. Such electrostatic potential and field map would be essential component in understanding the role of electrostatics in the electron transport processes, and in analysis of plausible pathways among the electron donor and acceptor sites.

The potential map was calculated as described above and visualized using VMD viewer ⁴². Figure 5a, b shows the electrostatic field lines and the potential distribution in the case of the membrane being oriented perpendicular to the view. One can appreciate the complexity of a 3D distribution and the fact that electrostatic potential forms distinctive patterns between the subunits of the complex,

Figure 5.

Resulting electrostatic field and potential maps of the bovine mitochondrial supercomplex. Membrane is shown as a slab made of pseudo atoms. (a) Electrostatic field distribution in case of side-view; (b) Potential distribution in a plane at the center of the supercomplex, side-view. The protein moiety is shown as well; (c) Electrostatic field distribution in case of membrane-view; and (d) Electrostatic potential mapped onto molecular surface of the supercomplex, membrane-view. The protein moiety is shown as well.

Figure 5c,d shows electrostatic potential and field distributions at the opposite side of the membrane. Similarly to the Figure 5a,b, one can see that electrostatic field forms well-defined pockets and these pockets are connected to each other via electrostatic interactions across the interface of the components of the complex. It should be reiterated that these results cannot be obtained by modeling individual subunits within the supercomplex, but require the entire structure to be used in the Poisson-Boltzmann calculations; a task for which the parallelized DelPhi is particularly well suited.

DISCUSSION

In this work, we present a set of techniques to parallelize existing numerical methods for solving PBE, and accelerate calculations of electrostatic potentials and energies of large proteins and complexes. This parallelization method has been implemented in a popular PBE solver, the DelPhi program, and it was demonstrated that the parallelization scheme dramatically reduces the time for calculations. A reduced time is critical for large systems for which the modeling cannot be done by parts; as is the typical case when dealing with the electrostatic properties due to the long-ranged nature of electrostatic potentials (as demonstrated on bovine mitochondrial complex). With the progress of the development of methods for structural determination and prediction, it is anticipated that more and more structures of macromolecular assemblages will be available and their modeling will require parallelized techniques to solve the Poisson-Boltzmann equation.