Abstract
Habituation is a common form of non-associative learning in which the organism gradually decreases its response to repeated stimuli. The decrease in exploratory activity of many animal species during exposure to a novel open field arena is a widely studied habituation paradigm. However, a theoretical framework to quantify how the novelty of the arena is learned during habituation is currently missing. Drosophila melanogaster display a high mean absolute activity and a high probability for directional persistence when first introduced to a novel arena. Both measures decrease during habituation to the arena. Here, we propose a phenomenological model of habituation for Drosophila exploration based on two principles: Drosophila form a spatial representation of the arena edge as a set of connected local patches, and repeated exposure to these patches is essential for the habituation of the novelty. The level of exposure depends on the number of visitations and is quantified by a variable referred to as “coverage.” This model was tested by comparing predictions against the experimentally measured behavior of wild type Drosophila. The novelty habituation of wild type Canton-S depends on coverage and is specifically independent of the arena radius. Our model describes the time dependent locomotor activity, ΔD, of Canton-S using an experimentally established stochastic process Pn(ΔD) which depends on the coverage. The quantitative measures of exploration and habituation were further applied to three mutant genotypes. Consistent with a requirement for vision in novelty habituation, blind no receptor potential A7 mutants display a failure in the decay of probability for directional persistence and mean absolute activity. The rutabaga2080 habituation mutant also shows defects in these measures. The kurtz1 non-visual arrestin mutant demonstrates a rapid decay in these measures, implying reduced motivation. The model and the habituation measures offer a powerful framework for understanding mechanisms associated with open field habituation.
Keywords: Drosophila, habituation, exploration, computational modeling
1. Introduction
Habituation is a common form of non-associative learning in which an organism decreases its response to repeated stimuli [1]. One of the most widely studied forms of habituation is the decrease in exploration observed during an exposure to a novel open field arena. Exploratory behavior is defined as a collection of acts and postures that allows an animal to gather information on a new environment [2]. A novel arena acts as a stimulus that elicits exploration behaviors, which in turn leads to the waning of the exploration as the novelty is abated. Although habituation is considered as one of the most elementary forms of behavioral plasticity, it is mechanistically quite complex because it involves dynamic interactions between the environment, the animal’s sensory systems, learning and memory. Consequently, decomposing the behavioral rules underlying habituation is a non-trivial task. Here, we outline an approach that combines experimental data and phenomenological modeling to address this problem.
Open field activity of Drosophila melanogaster is emerging as a strong model to study habituation and exploration [2–7]. Drosophila adults exhibit non-linear time-dependent activity when introduced into a novel open field arena. Specifically, flies exhibit three stages during exploration: (1) an initial stage of high activity, (2) an intermediate stage during which the activity decays, and (3) a final stage with a stable level of spontaneous activity [7,8]. It has been demonstrated that the initial stage is a response to the arena and not to handling. Specifically, the level of initial activity scales linearly with arena circumference and it is genetically separable from spontaneous activity [7]. These results strongly suggest that the foremost component of the elevated activity during the initial stage is specific exploration induced by the novelty of the arena. Furthermore, the decay in activity in the spontaneous phase is most likely a result of habituation to the arena’s novelty through visual learning [7]. This conjecture is based on observations that flies with poor sensory acuity are defective in attenuating the initial activity; completely blind flies exhibit greatly reduced activity decay and a very significant extension of the initial activity period. The increase in arena boundary contrast specifically rescues the habituation defect of the visually impaired w1118 mutants, further supporting a role for vision in habituation [7].
Hypotheses concerning habituation include stimulus satiation [9], afferent neuronal inhibition [10], and classical conditioning [11]. Associated mathematical models of habituation based on differential equations [12–15], neural networks [16,17], and circuit models [18,19] have been introduced. Even though these models can generate decay in the response function as a result of habituation, they are not directly related to stochastic locomotor activity in animals. A habituation model, which inputs novel stimuli and reproduces both realistic spatial trajectories of flies locomotion and the decay in exploratory activity is still lacking.
Other studies of spatial exploration have indicated that (1) animals form an internal representation of a novel environment, and (2) repeated exposure to the same stimulus is required to habituate novelty [1,7]. Based on these principles, we develop a phenomenological model of habituation in Drosophila during arena edge exploration. It describes temporal pattern of Drosophila behavior that depends on habituation and helps identify how habituation can be characterized. The characterization aids in disentangling potential phenotypes between mutants; for example, those that fail to learn or may not be motivated for exploration.
To build the phenomenological model of novelty habituation, we assume that a fly forms and maintains a spatial internal representation or map of the arena boundary as a set of connected lattice patches or sites and gathers information about the arena by proximally visiting these sites. Changes in exploratory behavior are caused by “coverage,” which is a function of the number of such visits and hence the strength of the spatial memory. These changes in exploratory behavior are quantified using “activity,” which is the mean absolute step size at a time t following its introduction to the arena. The activity is largest immediately following an animal’s introduction to the arena and reduces in time to its smallest value at large times. The rate of decay in activity from the initial to the spontaneous phase is quantified using the “habituation index.” The parameters of this model are extracted from the trajectories of wild type Drosophila close to the arena boundary where a large majority of the fly’s exploration is directed. From these analyses, we infer that the primary difference in the fly’s motion between the exploratory and spontaneous stages is an altered determination for forward motion. Specifically, during the initial stage of a trajectory a fly will strive to maintain persistent forward motion while during the latter stages the choice of its direction will be essentially random. Moreover, we find that in wild type Drosophila the decay in activity and the transition from directionally persistent motion to random motion and occurs at different rates in arenas of different sizes, indicating these habituation measures are not simply time dependent. Consistent with our model, the decay in activity and persistent forward motion in arenas of two different sizes are dependent on coverage. We have thus identified, through the analysis of trajectories in multiple arenas, how the animal’s motion changes from the exploratory phase to the spontaneous phase.
One of the applications of our framework is to search for differences in the exploratory behaviors in mutant genotypes with habituation defects. Our analysis suggests that impaired visual learning lead to a failure in decay of forward probability and mean absolute activity, while a rapid decay in mean absolute activity and forward motion is due to a lack of motivation for exploration.
2. Materials and Methods
2.1. Fly stocks and husbandry
All stocks of flies were raised and maintained on standard yeast-cornmeal agar food at room temperature. They were 2–5 day old males raised on standard food at 25°C, 60% humidity, with a 12 hr light/dark cycle. The norpA7 mutants were obtained from the Bloomington Stock Center. The rut2080 mutants were obtained from Ronald Davis (Scripps FL). The kurtz1 homozygotes are as previously described [20], and have the following genotype: w+; UAS-krz.T12/+; krz1, hs-Gal4/krz1. These krz1 homozygotes flies were raised from embryogenesis through the wandering third instar larval stage with one 1.5 hr 37°C heat shock every 12 hours. This heat shock provides krz expression, rescuing the developmental lethality of the krz1 mutation. The Krz protein decays through metamorphosis, and upon eclosion, the krz1 homozygotes lack detectable Krz protein within the nervous system [7].
2.2. Behavior Assays
The arenas used in our study were made of transparent Plexiglas by the University of Houston Physics Machine shop. Two circular arenas of radii 4.2 cm and 2.5 cm were used to collect the trajectories of wild type flies. The experimental data of Canton-S, norpA7 and rut2080 flies from circular arena of radius 4.2 cm were previously used in Ref. [21]. All arenas were 0.7 cm in height. The stochastic motion was studied using 136 independent wild type flies in the 2.5 cm arena and 275 independent wild type flies in the 4.2 cm arena. We used a larger number of flies in the larger arena to develop a highly accurate quantitative description of movement since this is the arena that is used most frequently to compare genotypes. As previously described by Ref. [21], the base and walls of all the open field arenas were made of clear polycarbonate. The ceiling of the arena was made from the lid of a 15-cm polystyrene petri plate (Fisher Scientific). Flies were typically aspirated into the arena approximately 2–3 cm from the boundary through a 2-mm hole in the top of the arena, close to the side. The starting positions of the flies were carefully distributed between the four quadrants of the arena. The arenas were illuminated by two 23W compact fluorescent flood lights (R40, 1200 lumens, 5100K) located 1.15 meters above them. They were set up in a laboratory that was maintained between 22°C and 24°C.The movement of the fly within the arena was tracked with Ethovision XT v5.0 (Noldus Information Technology, Leesburg VA). The recording duration was 10 minutes and the recording rate of the tracker was set to 30 frames per second. krz1 flies show a low initial activity and reach a stable activity faster than the other genotypes [7]. Consequently, the recording duration for krz1 flies was set to 5 minutes.
Trajectories obtained from the tracking software were smoothened using a running line regression with a window of 5 data points (0.2 s) and a 1-point step size (0.04 s) [22]. They were reconstructed using a sampling time interval of δt = 1 s. The noise threshold was set to 0.1 cm by visual inspection. Therefore, movement displacements which were reported by the tracking software to be less than 0.1 cm during 1 s were set to 0.
2.3. Model
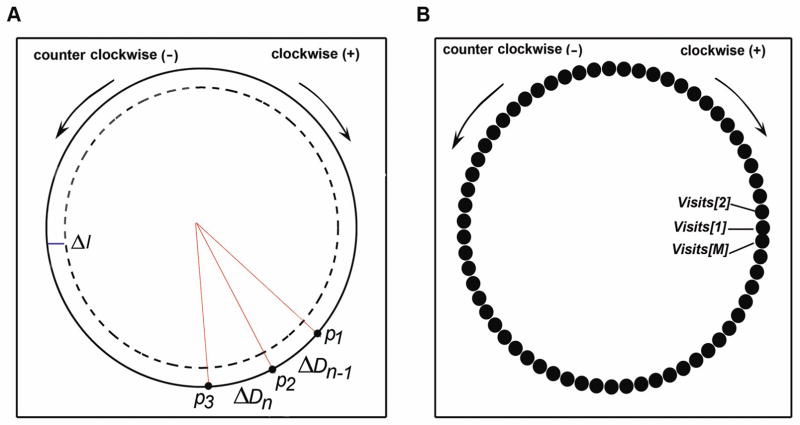
The analysis and modeling outlined in this paper are limited to motion at the arena edge. Habituation will lead to decay in the level of movement during exploration of the edge. Thus, we model the movement of a fly in a thin annular boundary region of width of Δl as shown in Figure 1A. The movement is equivalent to a one-dimensional motion along a circle as shown in Figure 1. It has been demonstrated that Drosophila are capable of forming and retaining visual place memories [23], and that normal sighted flies can learn and accurately recall spatial locations in a complex visual arena [23,24]. During exploration, flies are repeatedly exposed to the novel stimuli offered by the arena edge. As the exposure increases, flies begin to habituate the novelty of the arena edge resulting in a decrease in their activity [7]. In concordance with these previous studies, we propose a phenomenological model of habituation of Drosophila melanogaster based on two principles: (1) Drosophila form a spatial representation of the arena edge as a set of M connected patches (Figure 1), and (2) repeated exposure to these patches is essential for the habituation to the novel arena.
Figure 1. Modeling movements along the boundary of a circular arena.
A. The motion within the annular region of width Δl along the circular boundary is considered. The motion can be either clockwise (+) or counter-clockwise (-). In this illustration, the fly moves in a clockwise direction and traverses a displacement of ΔDn−1 from position p1 to p2 during the (n−1)th time step, while a displacement of ΔD n from p2 to p3 during the nth time step. Since the fly is moving in a clockwise direction, ΔDn−1 and ΔD n are greater than zero. B. The annular region of width Δl along the circular boundary was partitioned into M connected lattice patches. The width of each patch was set to the noise threshold of the tracking software. The set of patches was represented by a one-dimensional array, Visits.
Previous studies have indicated that flies actively explore the arena boundary through proximate investigation [25–27]. In our habituation model, the fly gathers information about the entire arena by visiting the individual patches. The cumulative number of visits from all local patches contributes to the global information acquired by the fly. We quantify this information using coverage, C. Habituation is the result of repeated exposure to novel stimuli. In our model, repeated exposure corresponds to an increase in coverage. In order to quantify coverage, we begin by defining the patches. The width of each patch is set to the noise threshold of tracking. We define a one-dimensional array, Visits, which contains M cells. The ith cell in Visits, denoted Visits[i], contains the number of visits to the ith patch. If the fly stays in the ith patch for two consecutive time points, Visits[i] remains unchanged. Visits[i] is incremented by 1 when the fly returns to the ith patch after visiting others. Habituating the entire arena requires the fly to visit each boundary patch a sufficiently large number of times. The animal’s familiarity, or the amount of information it gathers, is quantified through “coverage,” defined as follows: during initial times, when the fly has not visited all patches, it is the fraction of patches visited by step n. As long as the fly has not visited all sites the coverage is smaller than 1. When it has visited all sites we find Min, the number of times it has visited all patches, and supplement it with the fraction of patches it has visited more than Min times. Thus, coverage Cn at the nth step is defined as
| (1) |
where the function f(x) = 0 when x = 0 and f(x) = 1 when x > 0, and Min is the minimum of the values in the M cells of Visits. The time step n in our model is meant to represent 1 sec.
As examples, a coverage of Cn = 0.5 indicates that the fly has visited 50% of all the patches at least once and not visited some of the patches, while a coverage of Cn = 1.5 implies that the fly has visited all patches at least once (but not all of them twice) and 50% of the patches at least two times. It is important to note that the fly might have to visit a patch more than once before entirely abating the arena’s novelty. It is also possible to define an alternative to coverage that depends on the time spent within the patches. We chose to use Visits since the time-dependent “learning” of a patch is likely to have a non-linear decaying component where the fly learns less with time, complicating the modeling. Nevertheless, since flies do not generally stop for extended periods during exploration and hence generally spend similar time visiting each patch, we do not expect that consideration of time would make a significant change in our conclusions.
We assume that the displacement ΔD of the fly at time step n is stochastic and is distributed on a function Pn(ΔD). We emphasize that the time dependence of the probability distribution is expected from habituation. In this paper, ΔD is defined as the activity and each time step is 1 second. ΔD > 0 if the fly maintains its direction and ΔD < 0 if it reverses its direction; ΔD = 0 if the fly is dormant during the time interval. The mean absolute activity is given by 〈|ΔD|〉. Due to the symmetry of the circular arena, clockwise (+) and anti-clockwise (−) motions are considered equivalent.
In our habituation model, Pn(ΔD), depends on the coverage. When the fly is completely ‘ignorant’ about the arena (i.e., when coverage is 0), its motion is described by a stochastic process Pa(ΔD). In contrast, when the fly has habituated the entire arena and reaches the spontaneous activity stage, its motion is given by Pb(ΔD). Stochastic motion of the fly during intermediate times is a function of a habituation index, W, which is assumed to be a function of coverage. W quantifies the amount by which a fly has transitioned from its high initial activity [Pa(ΔD)] to the steady state spontaneous activity [Pb(ΔD)]. It is expressed as
| (2) |
When W=0, Pn(ΔD)= Pa(ΔD) and when W=1, Pn(ΔD)= Pb(ΔD). It is clear that the movement of the fly, Pn(ΔD), depends on W, which in turn is assumed to depend on coverage.
2.4. Estimation of model parameters
Sections of trajectories of Canton-S flies during the first five seconds of the experiments in the circular arena of 2.5 cm were used to estimate Pa(ΔD), while movements during the last five seconds (of the 10-minute trajectories) were used to compute Pb(ΔD). Only motions within an annular region of width Δl near the boundary were considered and displacements smaller than the noise threshold (of the tracking) were set to 0. The functional relationship between the habituation index W and the coverage C is obtained as follows. The mean displacement at a coverage C, 〈ΔD(C)〉, can be obtained from the trajectories in a single arena. However, if W is a function of C, it can be computed from Equation (2). Equating them gives
| (3) |
where 〈ΔD〉a is the mean displacement of the distribution Pa(ΔD), and 〈ΔD〉b is that of Pb(ΔD). It thus follows that
| (4) |
2.5. Directional persistence
Directional persistence, the tendency to continue moving in a forward direction, has been reported as a vital feature of animal locomotion [21,28–30]. A fly with high initial speed might have a strong directional persistence. The degree of directional persistence might change as the fly habituates to the arena’s novelty. Here, we explored this potential correlation between habituation and directional persistence during exploration of the arena edge. If the habituation model is accurate, it should give similar temporal behavior of directional persistence as the experiments. Directional persistence is quantified using the probabilities of forward motion (P++), stopping (P+o) and reversal (P+−). They were defined as
| (5) |
| (6) |
| (7) |
where, ‘Prob’ denotes ‘probability’. Since, there is no difference between clockwise (+) and counter clockwise (−) motions, we have
| (8) |
| (9) |
Clearly, P++(n) + P+−(n) + P+o(n) = 1 and P−+(n) + P−−(n) + P−o(n) = 1 Strong directional persistence corresponds to P++ close to 1..
3. Results
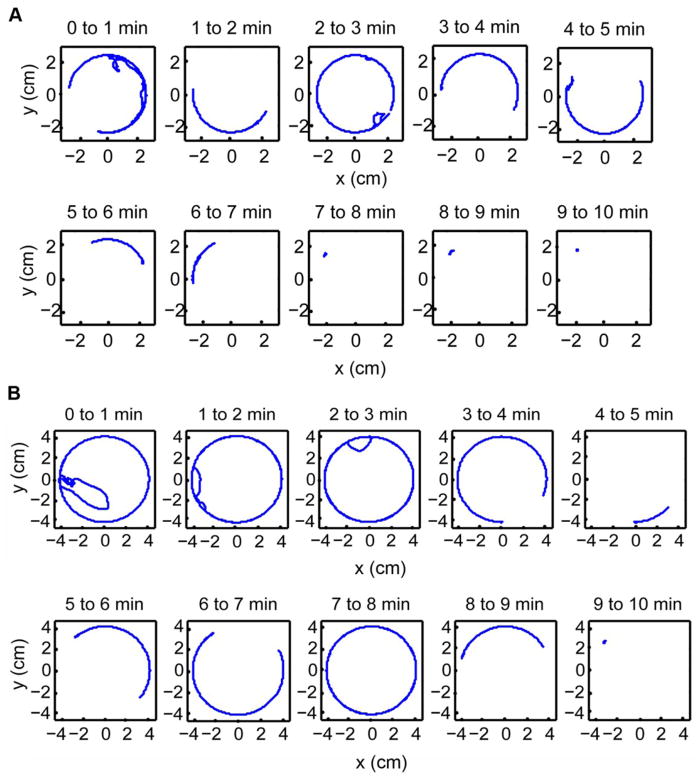
Trajectories of a wild type fly inside a circular arena of radii 2.5 cm and 4.2 cm are shown in Figures 2A and 2B, respectively. The trajectories were broken into 1 minute intervals as represented in the panels. The plots clearly indicate that the flies spent most of their time executing motions along the boundary. The fly is less active in the last few minutes of the experiments.
Figure 2. Drosophila movement decays with time and is largely limited to the arena boundary.
Representative wild type fly trajectories inside a circular arena of radii 2.5 cm and 4.2 cm are shown in panels A and B, respectively. The trajectories were broken into 1 minute intervals as represented in the panels. The plots clearly indicate that the flies spent most of their time executing motions along the boundary. The flies are less active in the last few minutes of the experiments.
In the habituation model, the movement along the boundary within an annular width of Δl was considered. The Δl was estimated from the spatial densities of Canton-S flies inside the 2.5 cm and 4.2 cm arena as shown in Figure 3. Since these flies spent about 90% of their time within an annular region of width 0.6 cm along the boundary in both the arenas, a Δl of 0.6 cm was selected.
Figure 3. Spatial densities of wild type flies inside circular open field arenas.
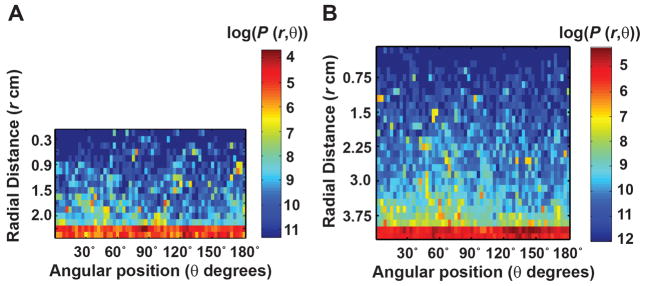
Panels A and B show the spatial densities of Canton-S flies inside two circular arenas of radius 2.5 cm and 4.2 cm, respectively in logarithmic scale. The position of a fly inside the circular arena is defined by polar coordinates, (r,θ), where r is the radial position and θ is the angular position. The two dimensional distribution was computed with a bin size of 0.15 cm along radial distance, r, and a bin size of 6° along angular position, θ. More than 90% of the trajectories were within the annular region of width 0.6 cm along the boundary in both the circular arenas.
3.1. Activity Decay
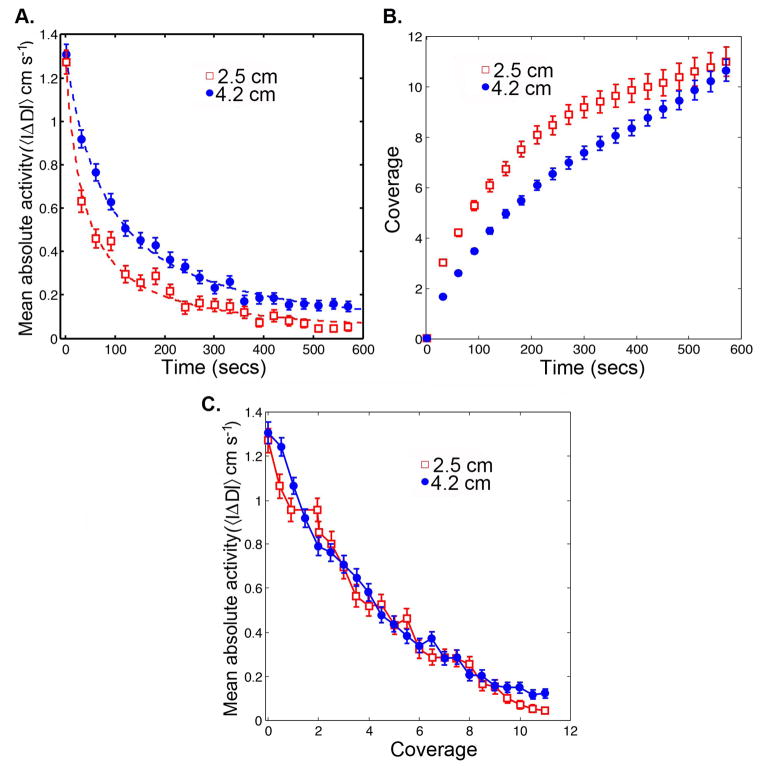
Habituation of an open field arena is indicated by the decrease of ambulation inside the arena within the first several minutes. We computed the mean absolute activity, 〈|ΔD|〉, of Canton-S flies in two circular arenas of radii 4.2 and 2.5 cm. The behaviors of 〈|ΔD|〉 in circular arenas of radius 4.2 cm and 2.5 cm are shown in Figure 4A with 21 data points representing the decay in 〈|ΔD|〉 for visualization purposes. The plots indicate that speed decreases in time as 〈|ΔD|〉 = 〈|ΔDo|〉 (1 + n/T)h, where T is a relaxation constant, h is a scaling index, 〈|ΔDo|〉 is mean absolute activity during the first time step, and n is time in seconds The corresponding values of T in 4.2 and 2.5 cm arenas were 98.92 and 107.7, respectively. The values of h for 4.2 cm and 2.5 cm arenas were −1.170 and −1.240, respectively. The reduction in 〈|ΔD|〉 began immediately after the fly was introduced inside the arena and there was no sharp transition between initial and spontaneous activities. The speed in the first one second was similar in both the arenas (4.2 cm: 1.307 ± 0.049 cm s−1, 2.5 cm: 1.272 ± 0.055 cm s−1); however, the decay in 〈|ΔD|〉 was dependent on the arena size (Figure 4A). By the end of 10 minutes, the speed decreased to 0.147 ± 0.024 cm s−1 in the 4.2 cm arena compared to 0.048 ± 0.01 cm s−1 in the 2.5 cm arena. The rate of increase in arena coverage was also dependent on the arena radius (Figure 4B). As expected, flies explored the smaller arena faster than the larger arena. In both arenas, coverage reached an approximate maximum value of 11. This means that Canton-S flies visited all the patches along the boundary 11 times. Interestingly, the behavior of 〈|ΔD|〉 as a function of coverage was independent of radius of the arena (Figure 4C), therefore, coverage appears to be the more appropriate variable to study habituation of a novel open field arena.
Figure 4. Mean absolute activity and coverage in two circular arenas are time dependent.
A. The behavior of mean absolute activity, 〈|ΔD|〉, in two circular arenas of radii 4.2 cm and 2.5 cm are shown as a function of time, n. For visualization purposes, 21 time points are shown. The interval between any two consecutive time points in the plots is 30 seconds. The decay in 〈|ΔD|〉 for 2.5 cm is faster than that of 4.2 cm arena. B. The coverage, for two circular arenas of radii 4.2 cm and 2.5 cm, as a function of time are shown. Flies explore the smaller arena faster than the bigger arena. C. The behavior of 〈|ΔD|〉 in two circular arenas of radii 4.2 cm and 2.5 cm are shown as a function of arena coverage. When plotted as a function of coverage, 〈|ΔD|〉 from the two different circular arenas are similar (p = 0.624, F(2,594) = 0.472).
3.2. Model parameters and simulation
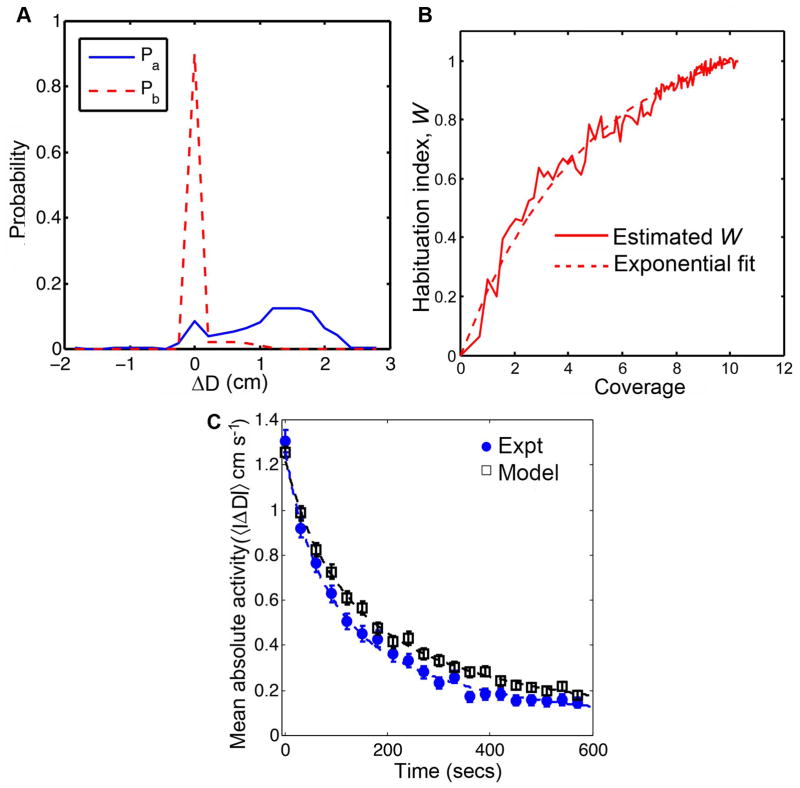
As a function of coverage, 〈|ΔD|〉 exhibited nearly identical decay in the two arenas. The movements of Canton-S flies along the boundary of a circular arena of radius 2.5 cm were used to estimate the parameters (Pa, Pb, and W) in the habituation model. The estimated probability distributions, Pa and Pb are shown in Figure 5A. The estimated Pa, which represents the movements when the arena is completely novel to the fly, indicates that flies execute forward motion during the initial stage of exploration 5A. The estimated density Pb peaks near ΔD = 0, indicating that the flies are more likely to be stationary during the later stage of habituation with small probabilities of forward or reverse motions (Figure 5A). The characterization of the habituation index, W, is reminiscent of nonlinear performance or learning curves related to practice trials [31, 32]. Such learning curves are considered to obey a power or an exponential law [31,32]. Therefore, for habituation index, we examined a power law fit of the form 1 − (1 + C)−ηand an exponential fit of the form σ (1 − exp(−μC)), where the σ, μ and η are fitting parameters. The exponential fit was found to be more appropriate than a power law fit (in supplementary file Text S1). Figure 5B shows the estimated form of W using the experimental data for Canton-S flies in a circular arena of radius 2.5 cm. The estimated values of σ and μ in W were 1.120 and 0.206, respectively. The parameters: W, Pa and Pb, estimated using trajectories in the 2.5 cm arena were used to simulate the movements of flies along the boundary of a circular arena of radius 4.2 cm. The simulation algorithm is shown in Algorithm 1 in the supplementary file, Text S1. There was no significant difference between the mean absolute activity, 〈|ΔD(n)|〉, obtained from experiments and simulations (Figure 5C, p = 0.910, F(2,594) = 0.095). The similar temporal decay in 〈|ΔD|〉 between experiments and simulations confirms our hypothesis that habituation is a function of arena coverage.
Figure 5. The habituation model gives an accurate form for the mean absolute activity in Drosophila in the 4.2 cm arena.
The estimated distributions Pa and Pb are shown in panel A while the estimated habituation index W is shown in B. The two densities were estimated from the trajectories of wild type flies in the circular arena of radius 2.5 cm. The distribution Pb peaks at ΔD =0, indicating that flies are more likely to pause during the later stages of exploration. Panel C shows 〈|ΔD|〉 obtained from experiments with Canton-S flies in circular arena of radius 4.2 cm and simulations using the memory model. For visualization purposes, 21 time points are shown in panel C. The interval between any two consecutive time points in the plots is 30 seconds. There was no statistical difference between the experiments and the simulations for 〈|ΔD|〉 (p = 0.9097, F(2,594) = 0.095). These results confirm (along with Figure 4C) that W(C) is independent of the arena.
3.3. Directional Persistence
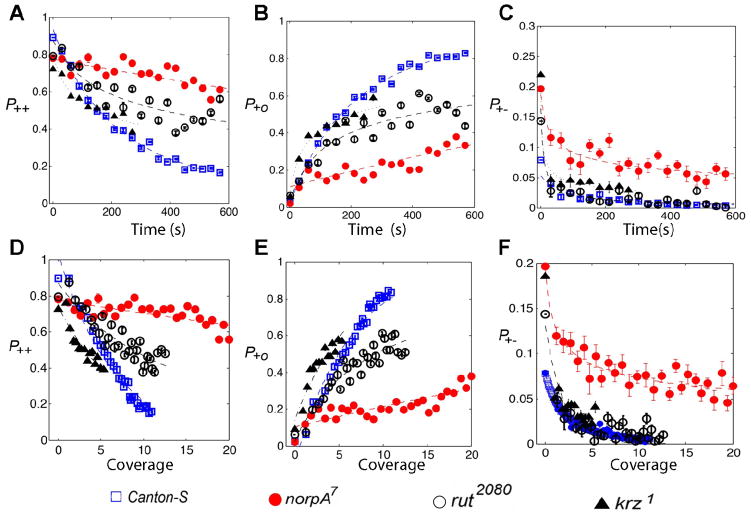
A motivated fly is expected to exhibit strong directional persistence, which is investigated using P++(n), P+−(n) and P+o(n) in two circular arenas (Figure 6). P++(n) and P+−(n) had the same functional form as 〈|ΔD|〉 (Figure 6). Also, P+o(n) is P+o(n) = 1−P++(n)−P+−(n). The behavior of P++ shared two important properties with 〈|ΔD|〉: (1) the decay in P++, began immediately following the introduction of the fly into the arena and, (2) the decay in P++ was faster in the smaller arena. Initially, the fly exhibited a high probability of moving forward (4.2 cm: P++(n = 0) = 0.912, 2.5 cm: P++(n = 0) = 0.883). The likelihood of persistence decreased with increased habituation to the novelty (4.2 cm: P++(n = 600) = 0.155, 2.5 cm: P++(n = 600) = 0.114). The stopping probability of the fly increased with time (4.2 cm: P+o(n = 0) = 0.024, P+o(n = 600) = 0.841, 2.5 cm: P+o(n = 0) = 0.072, P+o(n = 600) = 0.878). There was a small probability of direction reversal during the 10 minute duration (4.2 cm: P+−(n = 0) = 0.064, P+−(n = 600) = 0.004, 2.5 cm: P+−(n = 0) = 0.045, P+−(n = 600) = 0.008). These results show that flies maintain a strong directional persistence in the beginning of exploration, representing a motivated behavior to explore novelty. However, as habituation increases, so does the stopping probability. To check if the habituation model predicts a similar time-dependent directional persistence as Canton-S flies, we compared the behaviors of P++(n), P+o(n) and P+−(n) between habituation model and experiments with the circular arena of radius 4.2 cm. There were no statistical differences between the experiments and simulations (Figure 6; P++ : p = 0.731, F(2,594) = 0.314; P+o : p = 0.892, F(2,594) = 0.115; P+− : p = 0.128, F(2,594) = 2.060). The similarities between experiments and the habituation model indicate that decay in the forward persistent motion is dependent on the increase of coverage or the habituation to novelty.
Figure 6. The habituation model accurately reproduces the directional persistence behavior in Drosophila.
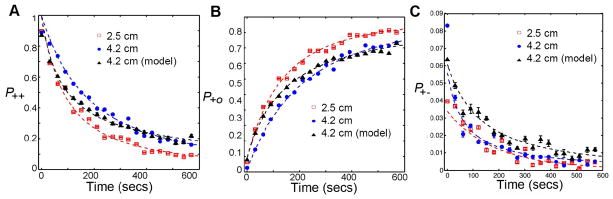
The probabilities P++, P+o and P+o for wild type flies along the boundary of two circular arenas of radii 4.2 cm and 2.5 cm are shown. P++, P+o and P+o are shown in panels A, B and C, respectively as a function of time. Simulations were performed on the circular arena of radius 4.2 cm using the parameters estimated from 2.5 cm arena. P++, P+o and P+o obtained from the simulations and experiments (both from 4.2 cm arena) are also shown. There were no statistical differences between the experiments and the simulations in the behaviors of directional persistence (P++ : p = 0.7308, F(2,594) = 0.314; P+o : p = 0.892, F(2,594) = 0.115; P+− : p = 0.128, F(2,594) = 2.060).
3.4. Examination of activity and directional persistence of mutant genotypes
Decay of directional persistence and mean absolute activity depend on habituation. To further test this, we examined three other genotypes of flies: norpA7, rut2080, and krz1, which have defects in exploration, habituation or positional preference within an arena [7, 33]. The norpA7 mutant flies are defective in phospholipase Cβ, fail to perform a receptor potential, and are completely blind [34]. These flies show a prolonged high exploratory activity indicating a deficit in habituation of the open field novelty [7]. The krz1 mutation is a lethal, loss-of-function mutation in the kurtz non-visual arrestin. The lethality of this insertional mutation is rescued through the heat shocked induced expression of krz twice daily through development [20, 35]. The heat shock ends after pupation and the krz1 homozygotes lack krz protein in the central nervous system [7]. These homozygotes fail to display the elevated exploratory activity phase within the open field arena [7].
The rut2080 mutants are defective in a type I adenylyl cyclase and display a reduced preference for the arena boundary in an open field arena [33]. These mutants also have pleiotropic learning defects, including poor habituation to different stimuli [36–38]. We collected at least 100 different trajectories of each of the mutants in a circular arena of radius 4.2 cm. Each trajectory of norpA7 and rut2080 flies lasted for 10 minutes. Since krz1 flies show a low initial exploratory activity and reaches a stable state very quickly [7], each experiment with krz1 flies was conducted only for 5 minutes.
Initially, we analyzed the behavior of mean absolute activity versus time for the mutant flies in an annular region of width 0.6 cm along the edge of the circular arena of radius 4.2 cm. Each of the mutant genotypes exhibited significantly different pattern of absolute activity, 〈|ΔD|〉, from Canton-S flies during the 10 minute duration (Canton-S vs norpA7: F(2,595) = 336, p < 0.001, Canton-S vs krz1: F(2,296) = 213, p < 0.001 and Canton-S vs rut2080: F(2,595) = 677.450, p < 0.001). The norpA7 flies maintained a higher speed than Canton-S flies during the entire 10 minute duration (Figure 7A). These results support a role for visual learning in activity decay. The movement speeds of krz1 started low, decayed very rapidly and did not change significantly after the first one and half minutes (Figure 7A, F(2,209) = 0.147, p = 0.147). This kind of behavior reflects a lack of motivation for exploration. Even though the rut2080 flies had a lower initial speed than Canton-S flies, their movement failed to decay as much as that of Canton-s flies (Figure 7A). This is consistent with a role of the learning defects in rut2080 in decay of mean absolute activity.
Figure 7. Differences in mean absolute activity are found in mutants with defects in exploration or habituation.
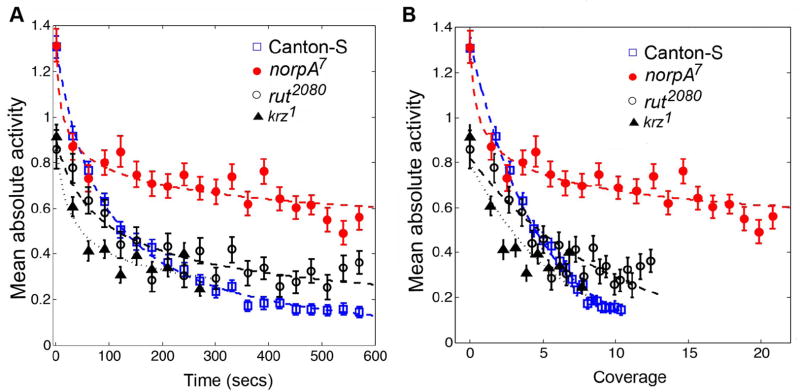
The 〈|ΔD|〉 of four genotypes: Canton-S, norpA7, rut2080 and krz1, along the boundary of a circular arena of radius 4.2 cm are shown. For all the four genotypes, 〈|ΔD|〉 are plotted as a function of time and arena coverage in panels A and B, respectively. For visualization purposes, 21 time points are shown. The interval between any two consecutive time points in the plots is 30 seconds. norpA7, rut2080 and krz1, which are known to have exploratory or habituation defects, display different patterns of mean absolute activity from Canton-S flies. Coverage had the least effect in the decay of 〈|ΔD|〉 in the blind norpA7 flies, consistent with a role of visual learning in habituation. The krz1 flies show a low initial ambulation which decreases rapidly to a stable state before habituation could occur, consistent with a reduced motivation to respond to novelty. The decay in rut2080 lies between non-habituating blind norpA7 and wild type Canton-S flies.
We also analyzed changes in directional persistence in time for the mutant flies along the edge of the circular arena of radius 4.2 cm. The mutant genotypes also exhibited significantly different patterns of directional persistence (P++, P+o, and P+−) from Canton-S flies (Figure 8, Canton-S vs norpA7: F(2,594) = 3274.2, p < 0.001, Canton-S vs krz1: F(2,295) = 428.717, p < 0.001 and Canton-S vs rut2080: F(2,594) = 2725.2, p < 0.001). As was the case for mean absolute activity, the norpA7 flies had the lowest decay in P++ among the genotypes. This suggests that visual learning is essential for the decay of forward persistent motion. The krz1 flies had a significantly lower P++ than Canton-S during the first two minutes of exploration (Figure 8A, F(2,197) = 480.043, p < 0.001), which indicates that a low P++ may also represent a lack of motivation for exploration. The rut2080 flies began with a lower P++ than Canton-S, but the decay in P++ was between Canton-S and norpA7 flies indicating a possible role of the learning defects in the failure in P++. All the genotypes exhibited small probabilities of direction reversal (Figure 8C). This measure decreases to values less than 0.1 by the end of one minute (Figure 8C) in all the genotypes. All the genotypes increased in their stopping probabilities. These data indicate that flies are more likely to persist in forward motion during the initial stages of exploration, the strong forward motion decays depending on the amount of habituation to novelty, and the decay in forward motion is replaced by movement stops.
Figure 8. Mutant genotypes with exploration or habituation defects also exhibit differences in directional persistence.
Directional persistence is studied using P++, P+o and P+o. The behaviors of P++, P+o and P+o of four genotypes: Canton-S, norpA7, rut2080 and krz1, along the boundary of a circular arena of radius 4.2 cm are shown. norpA7, rut2080 and krz1 are known to have exploratory or habituation defects. The behaviors of P++, P+o and P+o are shown in panels A, B and C, respectively as a function of time. The behaviors of P++, P+o and P+o are shown in panels D, E and F, respectively as a function of coverage. For visualization purposes, 21 time points are shown. The interval between any two consecutive time points in the plots is 30 seconds. norpA7, rut2080 and krz1 display different patterns of P++, P+o and P+o from Canton-S flies. Among the four genotypes, the blind norpA7 flies benefitted the least from the increase in coverage. P++ decreased to 0.1595 in Canton-S, 0.6 in norpA7, 0.509 in rut2080, respectively at the end of the 10th minute. In krz1 flies, P++ decreased to 0.4 approximately by the end of the 5th minute.
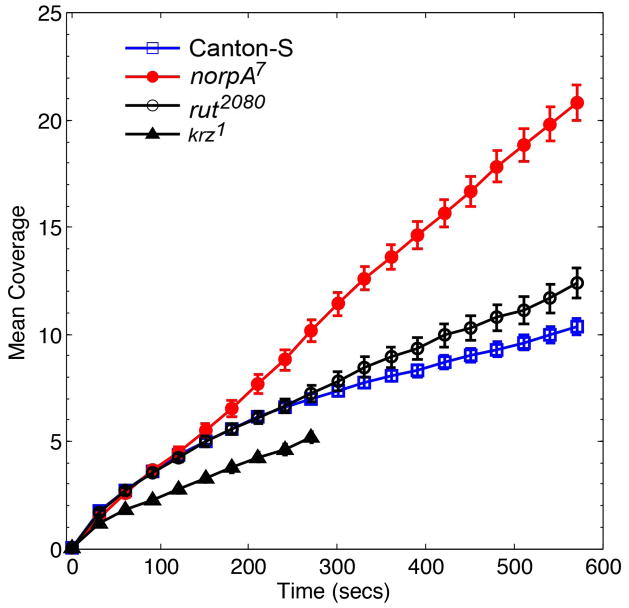
Our analysis indicated that coverage is a more appropriate variable than time to analyze habituation. To further examine the effect of increase in coverage on habituation among the mutants, we explored the relationship between coverage, probability of forward motion and mean absolute activity in the mutant genotypes. Both the norpA7 and rut2080 mutant flies reached a higher arena coverage compared to the Canton-S flies during the 10 minute duration (approximately 11 in Canton-S, 22 in norpA7 and 13 in rut2080; Figure 7B). During the entire 5 minutes of exploration, krz1 flies attained the least amount of coverage (Figure 9) indicating very little exploration of the novel arena. This indicates that norpA7 flies were exposed the most to the novelty of the arena followed by rut2080, Canton-S and krz1.
Figure 9. Coverage increases differently with time between Drosophila and mutant genotypes.
The coverage attained by wild type flies and three mutant flies, norpA7, rut2080 and krz1, with habituation defects are shown. During the 10-min duration, the blind norpA7 flies attained the highest increase in the coverage. The krz1 flies with reduced exploratory drive attained the least coverage during the 5 minute duration. The rut2080 displayed similar increase in coverage to Canton-S for the first 4 minutes, but their increase rate exceeded that of Canton-S during the rest of exploration.
Even though the blind flies had the largest increase in coverage, this increase had the least effect on the decay of mean absolute activity and P++ (Figure 7B). Even with the increase in coverage, norpA7 flies maintained a high 〈|ΔD|〉 and P++ most likely due to their visual inability to learn the arena. A similar increase in coverage was associated with a very rapid decay in 〈|ΔD|〉 and P++ of krz1 flies compared to Canton-S flies. The rapid decay of 〈|ΔD|〉 and P++ to a stable state with a low increase in coverage is consistent with a lack of motivation in krz1 flies to explore the novel arena. The rut2080 benefitted less than Canton-S but more than norpA7 flies by the increase in coverage in decay of P++, indicating that learning deficits in rut2080 play a role in the failure of the decay (Figure 7B). We draw three main conclusions from these analyses: (1) the likelihood of forward motion and mean absolute activity represent motivated movements to explore, (2) the failure in decay of forward persistent motion and mean absolute activity, which can be caused by inadequate visual learning, may correspond to a failure in habituation to the arena’s novelty, and (3) a rapid decay in these two measures will represent deficits in motivation for exploration or habituation.
3.5. Habituation index of mutant genotypes
The habituation index, W, in our habituation model quantifies the rate at which the high initial activity reduces to a final steady activity as coverage increases. As coverage quantifies the amount of exposure to the arena edge, the habituation index indicates the rate of habituation to novelty. W was estimated using two probability distributions: Pa(ΔD) and Pb(ΔD), which correspond to initial and final movement behaviors of wild type flies during exploration.
To estimate the habituation index of a mutant genotype with different activity pattern from wild type flies, our habituation model requires that the mutant genotype exhibits similar initial speed to wild type flies. To check if the three mutant flies displayed similar speeds from Canton-S flies in the beginning of exploration, we compared the first one minute portions of curves of mean absolute activity between the mutants and Canton-S flies (Figure 7). The norpA7 flies had similar speed to Canton-S (F(2,57) = −18.810, p > 0.05), while krz1 and rut2080 flies had lower movement speeds than Canton-S during the first one minute (rut2080: F(2,57) = 214.345, p < 0.001, krz1: F(2,57) = 986.087, p < 0.001). This means that among the three mutant flies, only the blind flies exhibited speeds similar to Canton-S flies in the first minute of exploration. The behaviors of a fly along the boundary are not characterized by the absolute speed only; a fly can be in three different states near the boundary: clockwise motion, anti-clockwise motion and stationary. To check if the behaviors of the norpA7 flies were similar to that of wild type flies during the initial stage of exploration, we compared the displacements, ΔD, of norpA7 flies during the first five seconds to that of Canton-S flies. Note that ΔD can be positive, negative or zero. There was no statistical difference between the movement behaviors of norpA7 and Canton-S flies (Figure 7A, F(2,4) = 1.19, p = 0.312). This indicates that the foremost initial response to a novel circular arena is similar in Canton-S and blind flies. Therefore, the habituation index of the blind flies, denoted by Wblind, can be estimated using the habituation model. To estimate Wblind, we used the same functional form as the habituation index of wild type flies, i.e, Wblind = σblind (1−exp(−μblind C)). We used a genetic algorithm (using MATLAB) to estimate the parameters: μblind and σblind. To do so, the following fitness function was minimized,
| (11) |
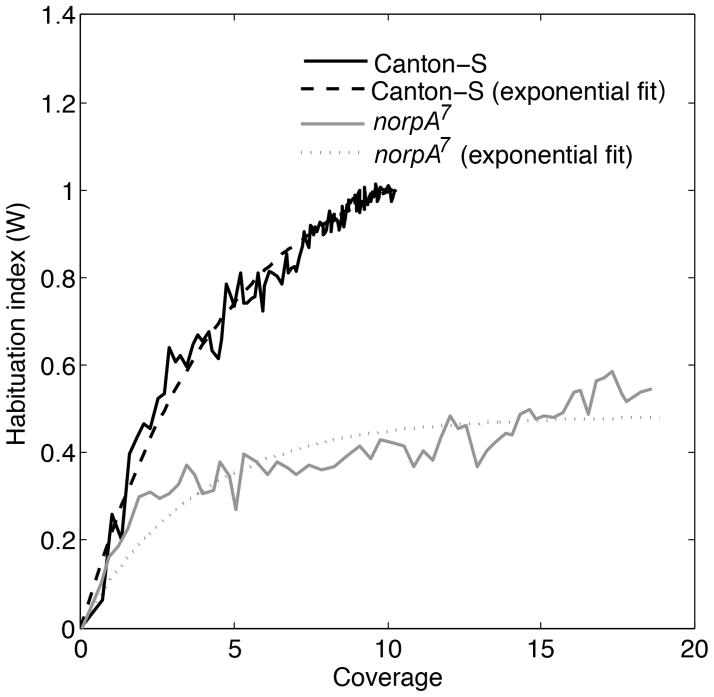
Here, 〈|ΔD(C)| 〉blind =〈|ΔD|〉a − Wblind (〈|ΔD|〉a − 〈|ΔD|〉b) and 〈|ΔD(C)|〉expt was estimated from the trajectories of blind flies in the thin annular region of width 0.6 cm along the edge of the circular arena of radius 4.2 cm. The estimated Wblind is shown in Figure 10, where σblind = 0.4835 and μblind = 0.2633, which are different from the parameters in the habituation index of Canton-S flies (for Canton-S flies: σ = 1.120 and μ = 0.206). Even though coverage of blind flies increased more rapidly than that of Canton-S flies (Figure 9), Wblind increased at a slower rate (Figure 10) than the Canton-S flies during the 10 minutes of exploration. This shows that the blind flies require a higher amount of exposure to the arena edge for habituating to novelty of the arena. Our analysis shows that habituation index differentiates between habituation responses to novelty of blind and Canton-S flies. In the habituation model, the parameters σ and μ describe the form of habituation response in a genotype. Specifically, σ indicates the amount of habituation achieved by a genotype and μ nonlinearity in the habituation response from initial high activity to reach the end habituation. A smaller σ and larger μ in blind flies than Canton-S flies indicate that blind flies exhibit a lower amount of habituation to novelty and a more nonlinear rate of habituation response.
Figure 10. The habituation index discriminates between wild type and non-habituating blind flies.
This figure shows the habituation indices of Canton-S and norpA7 blind flies. As coverage increases the habituation index of the Canton-S flies increases, while the blind flies fails to do so. The habituation index of the blind flies increases to a value of 0.5 when coverage increases to a value of 18 approximately. While in Canton-S flies, the habituation index reaches the value of 1 when coverage attains a value of 11 approximately. This indicates that the blind flies require a significantly higher amount of exploration than Canton-S flies to habituate the arena.
4. Discussion
In this paper, we addressed the nature of Drosophila novelty habituation through a quantitative description of the behavior and phenomenological modeling. We first introduced two new important variables: (1) probability of forward motion, P++, which corresponds to the motivation to abate the novelty and (2) habituation index, W, which models the acquisition and memory of the habituation. We further introduce coverage or the amount of visits to different areas of the arena boundary as an important variable for habituation. We show that in wild type Drosophila, the habituation index depends on coverage and the functional form is independent of the radius of the arena. Furthermore temporal variation of mean absolute activity and forward persistent movement of Canton-S flies along the edge depend only on the coverage of the arena during a trajectory.
We next introduced a novel approach of modeling habituation based on two principles: (1) when introduced into an environment, animals form a spatial internal representation of their surroundings and (2) habituation results from repeated exposure to a novel stimulus. The novelty drives exploration, which results in habituation to the novel stimulus, reducing and finally eliminating the specific exploration [39]. Our model, which uses P++ and W, accurately replicates the time dependent decreases in activity that occur during novelty habituation. The ability to phenomenologically model habituation supports the conclusion that Drosophila learn each portion of the arena independently and that habituation depends on the number of visits. Together the model and the new measures of behavior provide a framework for understanding variations in habituation found in additional genotypes.
Previous habituation studies at neurophysiological and psychological levels have also attempted to understand the mechanisms underlying habituation through mathematical models of habituation [9–11,14,17,19]. These models take an input in the form of one or multiple stimuli repeatedly applied to a system and generate an output in the form of a response function which decays from a high to a stable level with the decrease in novelty of the stimuli. The input is transferred to output response through differential equations [12–15], neural networks [16,17,40], and network circuits [18,19]. For example, a model proposed in Ref.[40] describes habituation to two stimuli using neural networks representing different physiological layers. This model requires information about the stimuli such as intensity and frequency of the stimuli. Our habituation model is different from these existing models for three reasons: (1) prior models are not capable of generating spatial trajectories of animals from input stimuli, (2) most models generate a deterministic output of the response function; however, movement of flies are not deterministic and each trajectory is different, and (3) most models do not provide any characteristics of the stimuli the animal is exposed to.
Although the underlying mechanism used by flies to learn, store information, and navigate in an environment is still to be elucidated, our habituation model resonates with previous theories of mechanisms of spatial exploration. When placed inside a novel environment, a rodent visits different portions of the environment a sufficient number of times before decreasing its exploratory behavior [41]. Hence, repeated exposure to novel stimuli is a prerequisite for habituation of novelty. Similarly in our habituation model, an increase in coverage, which quantifies the amount of exposure to the novel stimuli, results in the habituation to the novel arena and decay in exploratory activity. Notably, each area of the arena boundary represents a separable novel stimulus that is required to be habituated for decay in exploration. We have successfully modeled the effect of this increase in exposure on locomotor activity. In our habituation model, we assume that flies form a spatial representation of the arena boundary as a set of connected patches. Using this array, the fly is able to store and retrieve information of the boundary. This kind of modeling is reminiscent of previous indications that the information collected during visual exploration is mainly of a spatial nature [41]. In mammals, the presence of place, grid and head direction cells indicates the existence of a ‘cognitive map’ [41]; this map allows the animals to construct an internal representation of the spatial properties of their environment in their hippocampus [41]. Since invertebrates are capable of solving similarly challenging navigational feats as mammals, we do not negate such correlation between the flies and mammals [23]. Similar to the behavior displayed by rats with hippocampal lesions, flies with silenced ellipsoid body neurons have a basic circling search routine [23]. Likewise in flies, a neural structure might exist that allows flies to identify novelty in an environment that motivates them to collect more information about that environment.
4.1. Directional persistence as motivated movement
We hypothesize that directional persistence in movement within an open field arena represents movement motivated by novelty and the decay in probability of continued forward motion in flies is dependent on habituation of this novelty. Our hypothesis is supported by different probabilities for forward motion, P++, in wild type, norpA7, krz1, and rut2080 flies. Both the wild type and the blind flies displayed a high persistent forward motion in the beginning of exploration of a novel arena. As exploration and habituation increased, the likelihood of forward motion decreased in wild type flies. Our model accurately replicates this behavior; however there was a significantly reduced rate of decay in likelihood of forward motion, P++, for blind flies compared to normally sighted flies with the same increase in coverage in the two genotypes. On the other hand, we also observe that krz1 flies began with a lower P++ than wild type flies and showed a rapid decay in P++, maintaining a lower P++ than the wild type flies during exploration. The rut2080mutants began with a P++ that was lower than Canton-S flies, possibly because they were not fully motivated by novelty to explore, but attained a lesser decay in P++ compared to Canton-S flies.
A strong directional persistence during the initial stages of exploration in Canton-S and blind flies is consistent with movements motivated by the novelty of the arena. Previous theoretical studies have shown that there is a strong correlation between persistence in movement direction and efficacy of search strategies by animals in a novel environment [29,42,43]. A strong persistent forward motion can lead to faster habituation of the novel arena edge. In mammals, a strong persistent forward motion can increase the encounter rates of targets in a novel environment [42]. Likewise, strong directional persistence during the initial stages of exploration might reflect motivation to attain faster exploration and habituation to the arena’s novelty.
The initially high P++ decayed as exploration or habituation increased in wild type flies. However, mutant blind flies exhibited high initial motivated movements and habituation defects caused by visual learning defects, failed to exhibit a decay in P++. This observation suggests that the decay in P++ is dependent on habituation to novelty. Thus the wild type flies can learn the environment as exploration increases; they are less ‘motivated’ to exhibit strong forward motion. Since the blind norpA7 flies failed to habituate, the motivation to explore and the P++ remained high for a longer period of time. Studies have demonstrated that, during open field activity, normal sighted flies can learn and accurately recall spatial locations in a complex visual arena [23, 24]. Normally sighted flies can store the position of, or path towards, different sites inside an arena for several seconds [24]. Flies learn an environment either through visual or non-visual cues. It has been demonstrated that flies can use non-visual cues such as path integration and idiothetic cues while navigating; however, this experience is not sufficient for the formation of a place memory [23]. Specifically, normal-sighted flies were unable to form visual place memories of a dark environment (which contains non-visual cues) [23]. Therefore, the failure in decay in P++ in the blind flies is most consistent with defects in habituation to novelty caused by inadequate visual learning.
Our hypothesis of forward persistent motion as an indicator of motivated movement is also supported by the behavior of krz1 flies. Unlike the blind norpA7 and rut2080 mutants, krz1 flies began with a lower P++ than wild type flies but showed a rapid decay in P++ maintaining a lower P++ than the wild type flies during exploration (when P++ was studied as a function of coverage). This kind of behavior is more consistent with a low motivated movement than faster habituation by the flies because the krz1 flies exhibited low speeds and high stopping probabilities during the initial stage of exploration. Moreover, the krz1 homozygotes have reduced olfactory acuity that would lead to slower habituation [35]. In the case of krz1 flies, low motivated movement might be closely tied with depression. The krz gene encodes the only nonvisual arrestin in Drosophila and is required within the nervous system for the motivated movement in an open field arena [7, 20]. Similar to the krz1 mutants, different mouse models of depression exhibit significant decreases in locomotor activity [44]. Interestingly, a decrease in the expression of non-visual arrestins, which are necessary for signaling the effects of antidepressants, has also been observed in depression models [45–47]. Therefore, the krz1 reduced initial absolute activity and P++ are most consistent with a defect in motivated movement elicited by novelty in these mutants.
We also suspect that the rut2080 failure in decay of forward persistent motion may be due to a failure in habituation and hence may support our hypothesis that decay in P++ is dependent on habituation. The Rutabaga adenylyl cyclase is required for learning of various tasks including operant spatial conditioning [37], learning and memory, sensory habituation [48,49], and habituation of startle and escape circuits [38,50]. Experiments with rodents have indicated a role of learning and memory component in habituation [51]. A failure to habituate with repeated exposure to a novel environment is a powerful indicator of learning and memory deficits [51]. We found that these rut2080 mutants began with a lower P++ and mean absolute activity compared to Canton-S flies. This may mean rut2080 mutants exhibit a lower initial motivation to explore, yet after similar amount of exposure to the arena edge as Canton-S flies, rut2080 exhibited a reduced decay in forward persistent motion compared to Canton-S flies. This suggests that rut2080 flies might carry a more complex habituation response to novelty. Since learning mechanisms can be independent, a role in rut2080 in the habituation to other stimuli doesn’t necessarily mean it will also be required for novelty habituation. Nevertheless, there remains a strong possibility that rut activity is required for habituation to novelty.
4.2. Quantifying Habituation
We also propose that habituation index, W, can serve as a measure of habituation in flies. It quantifies the rate at which a highly motivated movement evolves to a low motivated movement as habituation increases. Our quantitative formulation of habituation index, W, is reminiscent of previous forms of learning indices related to human performance in psychophysics and skill acquisition [31, 32]. In such studies, the success in a certain task depends on the amount of exposure or practice as a power or exponential law, though which functional form best describes the empirical observation has not been resolved [31]. In flies, W depends on coverage, C, or the amount of exposure to a novel stimuli as an exponential law of the form σ(1−exp(−μC)). The parameters μ and σ control the form of W as a function of coverage, C. Through the two parameters μ and σ, habituation index can serve as a measure to disentangle potential phenotypes in habituation mutants. σ reflects the degree of end habituation a genotype achieves during the period of exposure to a novel stimuli and μ indicates the amount of nonlinearity in transitioning from complete ‘ignorance’ of an environment to the end habituation. Between genotypes with different habituation responses, the genotype with higher habituation deficits will exhibit lower σ. On the other hand, genotypes which exhibit a more nonlinear behavior in reaching end habituation will exhibit a higher μ. In our study, blind flies had a lower σ than Canton-S flies because the habituation index of blind flies stabilized approximately to 0.5. This is consistent with lesser habituation to novelty in blind flies compared to Canton-S flies. The blind flies exhibited a higher μ than Canton-S flies indicating that they obey a more nonlinear habituation response to novelty to attain their end habituation phase.
Vision, memory and learning defects play important roles in habituation responses in flies. It is difficult to ascertain how the effects of poor vision, memory and learning are embedded in μ and σ. Flies with these defects may achieve lesser amount of habituation compared to the Canton-S flies; this will be reflected by a lower σ compared to Canton-S flies. Simultaneously, a slower rate of learning or abrogating novelty in these flies will alter μ. Thus, it is most likely that the effects of habituation defects on μ and σ are coupled. To accurately understand the effects of learning, memory and vision on habituation, μ and σ may be further described by separable components representing these factors. Nevertheless, our study shows that W is an accurate measure to differentiate between the habituation response in blind and normally sighted flies. Specifically, the blind flies exhibited a lower value of W at any value of coverage compared to the wild type flies. Between two genotypes with different degrees of habituation defects, the genotype with lesser defects will exhibit a habituation index closer to that of Canton-S flies.
To compare the habituation index of a given mutant genotype to wild type controls, our model requires that these mutant flies exhibit similar initial movement behavior as wild type flies. The habituation response of mutants with different initial movement speed from Canton-S might represent a low initial motivation to explore, and hence W may be different for reasons other than differences in habituation. For such mutants, the habituation processes represent a more complex phenotype (e.g., rut2080 mutants have reduced initial activity, but also show reduced levels of activity attenuation). A different mathematical formulation of W is needed to achieve a comparison between Canton-S flies and these mutants. Similar approaches of handling flies with different initial exploratory activity indicated in previous studies of habituation (percent change [52], activity ratio change [53–55]) might achieve such goals. Nevertheless, the habituation index in our model can compare different phenotypes of habituation responses to novelty provided the flies have similar initial exploratory activity.
5. Conclusions
Habituation to a novel open field arena during exploration depends on visitations to each area of the arena, referred to as coverage, and not specifically time in the area. Each area of the novel area boundary represents a unique stimulus, and each is required to be learned for habituation. Habituation can be phenomenologically modeled using two principles: (1) when introduced into a novel environment, animals form a spatial internal representation of their surroundings and (2) habituation results from repeated exposure to a novel stimulus. The novelty drives exploration, which results in habituation of the novelty stimulus, reducing and finally eliminating the specific exploration. For our habituation model, two new important variables are also introduced: (1) probability of forward motion, P++, which corresponds to the motivation to abate the novelty and (2) habituation index, W, which quantifies the acquisition and memory of the habituation. These two variables can serve as metrics to differentiate between distinct habituation phenotypes.
Supplementary Material
Highlights.
We develop new quantitative measures for open field behavior.
Open field habituation requires repeated exposure to each section of the arena boundary.
We phenomenologically model habituation of novelty in open field arenas.
Our model accurately reflects Drosophila habituation behavior.
Mutant Drosophila are used to show the effect of changes in habituation parameters.
Acknowledgments
We are grateful to C. Manson-Bishop, R. Gamblin, and R. Goldfeder for technical assistance and helpful discussions. This work was funded by the grant MH091304 from the National Institute of Mental Health to GR.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may *be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Harris J. Habituatory response decrement in the intact organism. Psychological Bulletin. 1943;40:385–422. [Google Scholar]
- 2.Soibam B, Goldfeder RL, Manson-Bishop C, Gamblin R, Pletcher SD, Shah S, Gunaratne GH, Roman GW. Modeling Drosophila positional preferences in open field arenas with directional persistence and wall attraction. PLoS ONE. 2012;7(10):e46570. doi: 10.1371/journal.pone.0046570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wolf FW, Rodan AR, Tsai LT, Heberlein U. High-resolution analysis of ethanol-induced locomotor stimulation in Drosophila. J Neurosci. 2002;22:11035–44. doi: 10.1523/JNEUROSCI.22-24-11035.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rodan AR, Kiger JA, Heberlein U. Functional dissection of neuroanatomical loci regulating ethanol sensitivity in Drosophila. J Neurosci. 2002;22:9490–501. doi: 10.1523/JNEUROSCI.22-21-09490.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Engel JE, Wu CF. Neurogenetic approaches to habituation and dishabituation in Drosophila. Neurobiol Learn Mem. 2009;92:166–75. doi: 10.1016/j.nlm.2008.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Martin JR. A portrait of locomotor behaviour in Drosophila determined by a video-tracking paradigm. Behav Processes. 2004;67:207–219. doi: 10.1016/j.beproc.2004.04.003. [DOI] [PubMed] [Google Scholar]
- 7.Liu L, Davis RL, Roman G. Exploratory activity in Drosophila requires the kurtz nonvisual arrestin. Genetics. 2007;175:1197–1212. doi: 10.1534/genetics.106.068411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Connolly K. Locomotor activity in Drosophila. 3. A distinction between activity and reactivity. Anim Behav. 1967;15:149–152. doi: 10.1016/s0003-3472(67)80026-5. [DOI] [PubMed] [Google Scholar]
- 9.Glanzer M. Stimulus satiation: an explanation of spontaneous alternation and related phenomena. Psychol Rev. 1953;60:257–68. doi: 10.1037/h0062718. [DOI] [PubMed] [Google Scholar]
- 10.Hernndez-Pen R. Neurophysiological correlates of habituation and other manifestations of plastic inhibition. Electroencephalography and Clinical Neurophysiology. 1960;13:101–114. [Google Scholar]
- 11.Stein L. Habituation and stimulus novelty: a model based on classical conditioning. Psychol Rev. 1966;73:352–6. doi: 10.1037/h0023449. [DOI] [PubMed] [Google Scholar]
- 12.Wang D, Arbib MA. Modeling the dishabituation hierarchy: the role of the primordial hippocampus. Biol Cybern. 1992;67:535–544. doi: 10.1007/BF00198760. [DOI] [PubMed] [Google Scholar]
- 13.Wang D. A neural model of synaptic plasticity underlying short-term and long-term habituation. Adapt Behav. 1993;2:111–129. [Google Scholar]
- 14.delRosal E, Alonso L, Moreno R, Vazquez M, Santacreu J. Simulation of habituation to simple and multiple stimuli. Behav Processes. 2006;73:272–277. doi: 10.1016/j.beproc.2006.06.007. [DOI] [PubMed] [Google Scholar]
- 15.Marsland S. Using habituation in machine learning. Neurobiol Learn Mem. 2009;92:260–266. doi: 10.1016/j.nlm.2008.05.014. [DOI] [PubMed] [Google Scholar]
- 16.Schmajuk NA, Gray JA, Lam YW. Latent inhibition: a neural network approach. J Exp Psychol Anim Behav Process. 1996;22:321–349. doi: 10.1037//0097-7403.22.3.321. [DOI] [PubMed] [Google Scholar]
- 17.Schmajuk NA, Larrauri JA. Experimental challenges to theories of classical conditioning: application of an attentional model of storage and retrieval. J Exp Psychol Anim Behav Process. 2006;32:1–20. doi: 10.1037/0097-7403.32.1.1. [DOI] [PubMed] [Google Scholar]
- 18.Groves PM, Thompson RF. Habituation: a dual-process theory. Psychol Rev. 1970;77:419–450. doi: 10.1037/h0029810. [DOI] [PubMed] [Google Scholar]
- 19.Stanley JC. Computer simulation of a model of habituation. Nature. 1976;261:146–148. doi: 10.1038/261146a0. [DOI] [PubMed] [Google Scholar]
- 20.Roman G, He J, Davis RL. kurtz, a novel nonvisual arrestin, is an essential neural gene in Drosophila. Genetics. 2000;155:1281–1295. doi: 10.1093/genetics/155.3.1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Soibam B, Mann M, Liu L, Tran J, Lobaina M, et al. Open-field arena boundary is a primary object of exploration for Drosophila. Brain and Behavior. 2012;2:97–108. doi: 10.1002/brb3.36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Valente D, Golani I, Mitra PP. Analysis of the trajectory of Drosophila melanogaster in a circular open field arena. PLoS ONE. 2007;2(10):e1083. doi: 10.1371/journal.pone.0001083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ofstad TA, Zuker CS, Reiser MB. Visual place learning in Drosophila melanogaster. Nature. 2011;474:204–207. doi: 10.1038/nature10131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Neuser K, Triphan T, Mronz M, Poeck B, Strauss R. Analysis of a spatial orientation memory in Drosophila. Nature. 2008;453:1244–1247. doi: 10.1038/nature07003. [DOI] [PubMed] [Google Scholar]
- 25.Gotz K. Visual guidance in Drosophila. Basic Life Sci. 1980;16:391–407. doi: 10.1007/978-1-4684-7968-3_28. [DOI] [PubMed] [Google Scholar]
- 26.Schuster S, Strauss R, Gotz KG. Virtual-reality techniques resolve the visual cues used by fruit flies to evaluate object distances. Curr Biol. 2002;12:1591–1594. doi: 10.1016/s0960-9822(02)01141-7. [DOI] [PubMed] [Google Scholar]
- 27.Robie AA, Straw AD, Dickinson MH. Object preference by walking fruit flies, Drosophila melanogaster, is mediated by vision and graviperception. J Exp Biol. 2010;213:2494–2506. doi: 10.1242/jeb.041749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nossal R, Weiss GH. A descriptive theory of cell migration on surfaces. Journal of Theoretical Biology. 1974;47:103–113. doi: 10.1016/0022-5193(74)90101-5. [DOI] [PubMed] [Google Scholar]
- 29.Viswanathan GM, Buldyrev SV, Havlin S, da Luz MG, Raposo EP, et al. Optimizing the success of random searches. Nature. 1999;401:911–914. doi: 10.1038/44831. [DOI] [PubMed] [Google Scholar]
- 30.DVN, Armitage JP, Maini PK. Directional persistence and the optimality of run-and-tumble chemotaxis. Computational Biology and Chemistry. 2009;33:269–274. doi: 10.1016/j.compbiolchem.2009.06.003. [DOI] [PubMed] [Google Scholar]
- 31.Cousineau D, Helie S, Lefebvre C. Testing curvatures of learning functions on individual trial and block average data. Behav Res Methods Instrum Comput. 2003;35:493–503. doi: 10.3758/bf03195528. [DOI] [PubMed] [Google Scholar]
- 32.Murre JM, Chessa AG. Power laws from individual di erences in learning and forgetting: mathematical analyses. Psychon Bull Rev. 2011;18:592–597. doi: 10.3758/s13423-011-0076-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lebreton S, Martin JR. Mutations a ecting the cAMP transduction pathway disrupt the centrophobism behavior. J Neurogenet. 2009;23:225–234. doi: 10.1080/01677060802509160. [DOI] [PubMed] [Google Scholar]
- 34.Harris WA, Stark WS. Hereditary retinal degeneration in Drosophila melanogaster. A mutant defect associated with the phototransduction process. J Gen Physiol. 1977;69:261–291. doi: 10.1085/jgp.69.3.261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ge H, Krishnan P, Liu L, Krishnan B, Davis RL, et al. A Drosophila nonvisual arrestin is required for the maintenance of olfactory sensitivity. Chem Senses. 2006;31:49–62. doi: 10.1093/chemse/bjj005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tully T, Quinn WG. Classical conditioning and retention in normal and mutant Drosophila melanogaster. J Comp Physiol A. 1985;157:263–277. doi: 10.1007/BF01350033. [DOI] [PubMed] [Google Scholar]
- 37.Zars T, Wolf R, Davis R, Heisenberg M. Tissue-specific expression of a type I adenylyl cyclase rescues the rutabaga mutant memory defect: in search of the engram. Learn Mem. 2000;7:18–31. doi: 10.1101/lm.7.1.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cho W, Heberlein U, Wolf FW. Habituation of an odorant-induced startle response in Drosophila. Genes Brain Behav. 2004;3:127–137. doi: 10.1111/j.1601-183x.2004.00061.x. [DOI] [PubMed] [Google Scholar]
- 39.Berlyne DE. Curiosity and exploration. Science. 1966;153:25–33. doi: 10.1126/science.153.3731.25. [DOI] [PubMed] [Google Scholar]
- 40.Wang D. Modeling neural mechanisms of vertebrate habituation: Locus specificity and pattern discrimination. Journal of Computational Neuroscience. 1994;1:285–299. doi: 10.1007/BF00961877. [DOI] [PubMed] [Google Scholar]
- 41.O’Keefe J, Nadel L. The Hippocampus as a Cognitive Map. Oxford: Oxford University Press; p. 197. [Google Scholar]
- 42.Bartumeus F, Catalan J, Viswanathan GM, Raposo EP, da Luz MG. The influence of turning angles on the success of non-oriented animal searches. J Theor Biol. 2008;252:43–55. doi: 10.1016/j.jtbi.2008.01.009. [DOI] [PubMed] [Google Scholar]
- 43.Bartumeus F, Levin SA. Fractal reorientation clocks: Linking animal behavior to statistical patterns of search. Proc Natl Acad Sci USA. 2008;105:19072–19077. doi: 10.1073/pnas.0801926105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chkhartishvili E, Maglakelidze N, Babilodze M, Chijavadze E, Nachkebia N. Changes of open field behavior in animal model of depression. Georgian Med News. 2011;11:107–112. [PubMed] [Google Scholar]
- 45.Golan M, Schreiber G, Avissar S. Antidepressants, beta-arrestins and GRKs: from regulation of signal desensitization to intracellular multifunctional adaptor functions. Curr Pharm Des. 2009;15:1699–1708. doi: 10.2174/138161209788168038. [DOI] [PubMed] [Google Scholar]
- 46.Schreiber G, Golan M, Avissar S. Beta-arrestin signaling complex as a target for antidepressants and as a depression marker. Drug News Perspect. 2009;22:467–480. [PubMed] [Google Scholar]
- 47.Golan M, Schreiber G, Avissar S. Antidepressants increase -arrestin 2 ubiquitinylation and degradation by the proteasomal pathway in C6 rat glioma cells. J Pharmacol Exp Ther. 2010;332:970–976. doi: 10.1124/jpet.109.160218. [DOI] [PubMed] [Google Scholar]
- 48.Duerr JS, Quinn WG. Three Drosophila mutations that block associative learning also affect habituation and sensitization. Proc Natl Acad Sci USA. 1982;79:3646–3650. doi: 10.1073/pnas.79.11.3646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Asztalos Z, Arora N, Tully T. Olfactory jump reflex habituation in Drosophila and effects of classical conditioning mutations. J Neurogenet. 2007;21:1–18. doi: 10.1080/01677060701247508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Engel JE, Wu CF. Altered habituation of an identified escape circuit in Drosophila memory mutants. J Neurosci. 1996;16:3486–3499. doi: 10.1523/JNEUROSCI.16-10-03486.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Leussis MP, Bolivar VJ. Habituation in rodents: a review of behavior, neurobiology, and genetics. Neurosci Biobehav Rev. 2006;30:1045–1064. doi: 10.1016/j.neubiorev.2006.03.006. [DOI] [PubMed] [Google Scholar]
- 52.Fraley SM, Springer AD. Memory of simple learning in young, middle-aged, and aged C57/BL6 mice. Behav Neural Biol. 1981;31:1–7. doi: 10.1016/s0163-1047(81)90986-9. [DOI] [PubMed] [Google Scholar]
- 53.Cook MN, Bolivar VJ, McFadyen MP, Flaherty L. Behavioral differences among 129 substrains: implications for knockout and transgenic mice. Behav Neurosci. 2002;116:600–611. [PubMed] [Google Scholar]
- 54.Bolivar VJ, Manley K, Messer A. Exploratory activity and fear conditioning abnormalities develop early in R6/2 Huntington’s disease transgenic mice. Behav Neurosci. 2003;117:1233–1242. doi: 10.1037/0735-7044.117.6.1233. [DOI] [PubMed] [Google Scholar]
- 55.Bolivar VJ, Manley K, Messer A. Early exploratory behavior abnormalities in R6/1 Huntington’s disease transgenic mice. Brain Res. 2004;1005:29–35. doi: 10.1016/j.brainres.2004.01.021. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.