Power of Single- vs. Multi-Marker Tests of Association

Abstract

Current genome-wide association studies still heavily rely on a single-marker strategy, in which each single nucleotide polymorphism (SNP) is tested individually for association with a phenotype. Although methods and software packages that consider multimarker models have become available, they have been slow to become widely adopted and their efficacy in real data analysis is often questioned. Based on conducting extensive simulations, here we endeavor to provide more insights into the performance of simple multimarker association tests as compared to single-marker tests. The results reveal the power advantage as well as disadvantage of the two- vs. the single-marker test. Power differentials depend on the correlation structure among tag SNPs, as well as that between tag SNPs and causal variants. A two-marker test has relatively better performance than single-marker tests when the correlation of the two adjacent markers is high. However, using HapMap data, two-marker tests tended to have a greater chance of being less powerful than single-marker tests, due to constraints on the number of actual possible haplotypes in the HapMap data. Yet, the average power difference was small whenever the one-marker test is more powerful, while there were many situations where the two-marker test can be much more powerful. These findings can be useful to guide analyses of future studies.

INTRODUCTION

In a typical genome-wide association studies (GWAS) analysis pipeline, a single-marker test is used first, such as the allelic frequency contrast test, the Cochran-Armitage trend test, and the Hardy-Weinberg Disequilibrium (HWD) contrast test [Li et al., 2009; Sasieni, 1997; Song and Elston, 2006]. The SNPs are then ranked based on their P-values, and a threshold is set (e.g., the genome-wide significance level 5 × 10^–8) such that SNPs with a P-value below that threshold receive highest priority for replication or other downstream analyses. Single-marker tests examine association between a trait and one SNP at a time, while the linkage disequilibrium (LD) structure of the markers is ignored. On the other hand, multimarker tests that examine association between a trait and multiple SNPs simultaneously have the potential to yield more robust, powerful, and informative results [Kim et al., 2010; Slavin et al., 2011; Wang et al., 2007; Wu and Lin, 2008].

A number of multimarker-based approaches have been suggested. One major strategy is based on haplotype information, which preserves the LD structure across a set of markers [Akey et al., 2001; Schaid, 2004; Schaid et al., 2002]. Evidence of association can also be evaluated by contrasting the extent of LD across multiple markers between case and control groups [Nielsen et al., 2004; Wang et al., 2007]. For unphased genotype data, which is what we focus on here, we can consider a natural multivariate generalization—contrasting a profile/vector of allele frequencies for several markers between cases and controls—by using Hotelling's T-squared test or related procedures [Clayton et al., 2004; Fan and Knapp, 2003; Xiong et al., 2002], or we can consider the composite LD contrast test [Zaykin et al., 2006]. Nevertheless, these multimarker methods have been slow to be adopted widely. In a literature survey of all GWAS published in high impact journals, the initial step in most studies was restricted to single-marker analysis [Becker and Herold, 2009]. In addition to implementation difficulties, there is a major concern about the performance of these multimarker methods in real data analysis. Indeed, it is known that the power of an association test depends on a complex balance among many factors, such as degrees of freedom (df), multiplicity of tests, and the correlation pattern among the risk and tagging SNPs [Cordell and Clayton, 2005; Li et al., 2011; Morris and Elston, 2011; Pan et al., 2010]. Owing to their increased degrees of freedom (df), multi-marker tests may have similar or reduced power relative to single-marker tests. Difficulties also arise in determining an optimal multimarker test. Some researchers have found that analyses using multivariate marker data that do not require resolution of gametic phase were often more powerful than analyses based on haplotypes, while others reached different conclusions [Becker and Herold, 2009; Clayton et al., 2004]. In fact, a uniformly most powerful test does not exist for the analysis of either unphased or haplotype data, albeit some methods are frequent winners under certain conditions or simulations [Pan et al., 2010].

Recently, Kim et al. [2010] derived single- and two-marker statistics to compare cases and controls according to allele frequencies, HWD, and composite LD scores. The three distinct sources of information about case-control differences may be tested jointly in a framework where the retrospective contrast test and the prospective logistic regression model are unified. Simulation studies carried out by Kim et al. found that power can differ for single- versus vs. two-marker tests, and that this difference in power can depend on the LD pattern among the measured markers. We might expect 2-df tests to be less powerful than 1-df tests, but that paper suggested otherwise for markers in high LD. In this study, we explore the power differences of a single- vs. a multimarker test numerically by computing the asymptotic power for both approaches. Our strategy was to focus directly on the correlation patterns of the measured SNPs and the unmeasured causal SNP, rather than attempt to simulate different LD patterns based on population genetic assumptions. We chose this strategy because the power depends directly on the correlation patterns—different simulation parameters could give the same correlation pattern, and hence the same power. Although our multimarker calculations focus only on two SNPs, our methods are general enough to be applied to a larger number of SNPs. Through extensive simulations, we examine whether it is possible, by prescreening the correlation patterns of the markers, to predict which will be the best test to perform.

METHODS

To explain the asymptotic power calculations, we first give our notation. Let p_c be the population minor allele frequency of the causal SNP, and assume that the causal allele acts multiplicatively on the genotype relative risks (RRs), such that R₂ = γ² and R₁ = γ, where R_i is the risk of disease for subjects carrying i copies of the causal allele relative to homozygous noncarriers. We also assume Hardy-Weinberg equilibrium in the population. Under these assumptions, the frequency of the causal allele among cases is $p_c^D=\gamma p_c∕(\gamma p_c+1-p_c)$ [Clayton, 1999]. If the disease is rare, the frequency of the causal allele among controls, $p_c^C$, is approximately the same as the population allele frequency, $p_c^C\approx p_c$. If the causal SNP were measured, the test statistic to compare allele frequencies between cases and controls (assuming equal numbers of cases and controls) would be $z_c=\sqrt{N}(p_c^D-p_c^C)∕\sqrt{2{\stackrel{‒}{p}}_c(1-{\stackrel{‒}{p}}_c)}$, where ${\stackrel{‒}{p}}_c=(p_c^D+p_c^C)∕2$. This z-statistic has an asymptotic normal distribution, $N(\sqrt{N}{\lambda }_c,1)$, where ${\lambda }_c=(p_c^D-p_c^C)∕\sqrt{2{\stackrel{‒}{p}}_c(1-{\stackrel{‒}{p}}_c)}$.

When m marker SNPs are measured, but not the causal SNP, the corresponding vector statistic Z = (Z₁, Z₂, ..., Z_m) asymptotically follows a multivariate normal distribution: $Z\sim MVN(\sqrt{N}\lambda ,\Sigma )$, where $\sqrt{N}\lambda =\sqrt{N}{\lambda }_c({\rho }_{1c},{\rho }_{2c},\dots ,{\rho }_{mc})$; the statistic for the ith marker (coded as the number of susceptibility alleles in the genotype) is $z_i=\sqrt{N}(p_i^D-p_i^C)∕\sqrt{2{\stackrel{‒}{p}}_i(1-{\stackrel{‒}{p}}_i)}$, its asymptotic mean is λ_i = ρ_icλ_c, Σ is the correlation matrix of the measured markers, and ρ_ic is the correlation of the ith marker with the causal SNP. These asymptotic results are further discussed elsewhere [Zaitlen et al., 2010].

Based on the asymptotic multivariate normal distribution of the vector Z, the power of using either the maximum of the single-marker tests or the multivariate T-test can be evaluated as follows. For the maximum of the single-marker tests, power is the probability that at least one of the marker z-statistics exceeds the critical value threshold, which can be expressed as 1 – P(–c < z₁ < c, ..., –c < z_m < c). The critical value c gives the desired type I error and P(–c < z₁ < c, ..., –c < z_m < c) is evaluated by numerical integration of the multivariate normal distribution. For the multivariate T-test, asymptotic power can be calculated from the noncentral chi-square distribution with m df. The noncentrality parameter is ncp = Nλ′Σ^–1λ, where λ = (λ_cρ_1c, λ_cρ_2c, ..., λ_cρ_mc).

We conducted simulation studies to compare two- and single-marker analyses. In the first simulation, we set the type I error rate to 0.05, the causal allele frequency to 0.2, the causal allele RR to 1.2, and we simulated 1,000 cases and 1,000 controls. We then let each of the values of ρ₁₂, ρ_1c, and ρ_2c range over –0.995 to 0.995, with a fixed increment of 0.05 (40 × 40 × 40 combinations) and 0.01 (200 × 200 × 200 combinations), respectively. The generated correlations that did not satisfy the constraint that the correlation matrix be positive definite were removed, i.e., the correlation combinations had to satisfy the constraint: $1-{\rho }_{1c}^2-{\rho }_{2c}^2-{\rho }_{12}^2+2{\rho }_{1c}{\rho }_{2c}{\rho }_{12}>0$. We further evaluated more scenarios, setting the type I error at 0.001 and a genome-wide significance level 5 × 10^–8, increasing the causal allele RR to 1.25 and 1.3, and increasing the sample sizes to 4,000 and 8,000 (equal numbers of cases and controls), respectively. Since the power (and noncentrality parameter) depends only on the standardized effect size $z_c=\sqrt{N}(p_c^D-p_c^C)∕\sqrt{2{\stackrel{‒}{p}}_c(1-{\stackrel{‒}{p}}_c)}$ and type I error rate α, in the second simulation, we performed tests varying only z_c (2–8) and α (0.05, 0.005, . . . ,5 × 10^–8).

Lastly, instead of assuming a uniform correlation distribution, we generated the correlation space by using the SNP data on chromosome 11 of the HapMap CEU (Phase 3) population data. We split the chromosome into mutually exclusive consecutive regions containing three SNPs each. For each region, we chose the disease SNP to be the one in the middle—to simulate the ideal case that a causal SNP is tagged by two flanking marker SNPs. We excluded regions where the minor allele frequency of either of the two flanking markers was less than 0.1, leaving 14,022 regions. For each region, we computed the power of single- and two-marker tests based on the correlation coefficients among three SNPs. For those regions with ρ₁₂ = 1 or –1 (where the noncentrality parameter for the two-marker test becomes invalid), we set the power of the two tests to be equal to the value based on the univariate normal distribution, i.e., power = 1 – P(–c < z < c), where c controls the desired type I error.

RESULTS

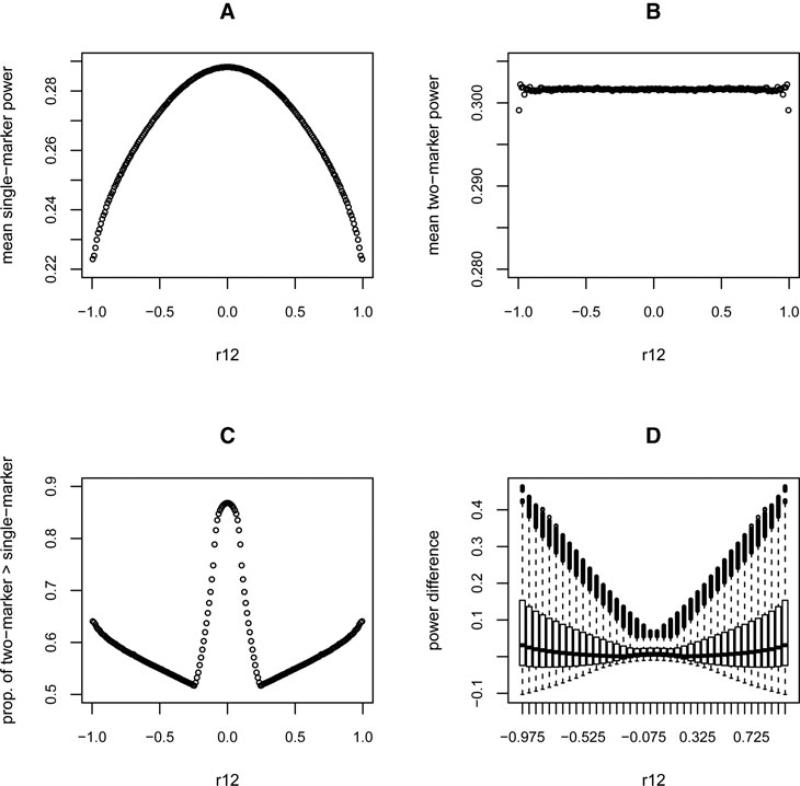
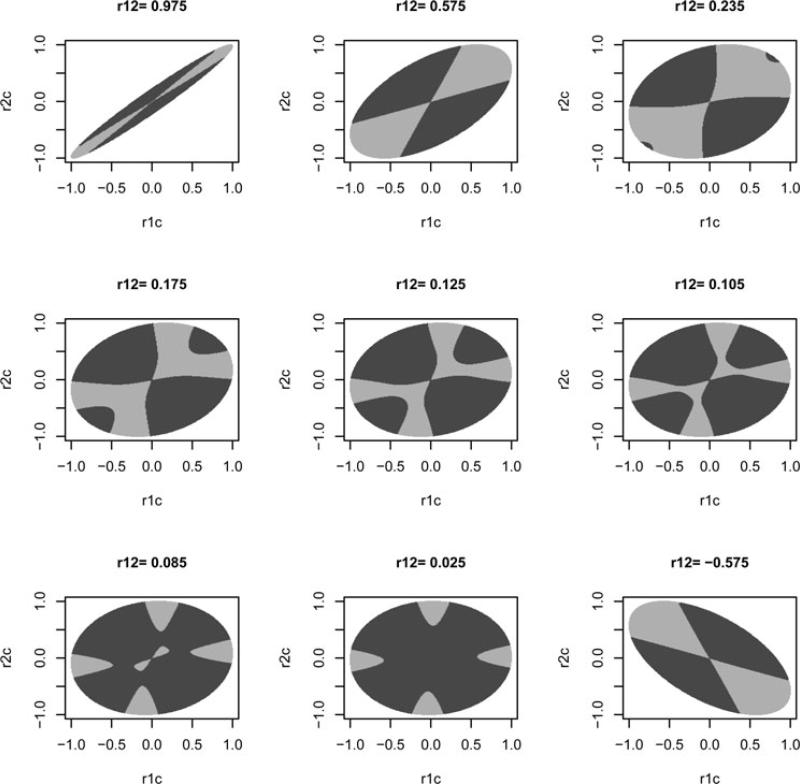
As shown in the scatter plot of the power (Supplementary Fig. S1) and Figure 1D, the two-marker test had greater power for most of the correlation space in the first simulation. Because we are most interested in determining whether the known correlations between marker SNPs (ρ₁₂) can guide us in choosing an optimal test, we depicted the contrast in power of the two tests as a function of ρ₁₂ (Fig. 1). As shown in Figure 1A and B, the mean values of the power, i.e., averaged over sets of correlations corresponding to a particular value of ρ₁₂, for single-marker tests increases when |ρ₁₂| decreases, while the mean power of the two-marker tests is almost invariant with respect to change in ρ₁₂ and is always greater than that of the single-marker tests. Figure 1C shows a trend that differs from the mean results: the proportion of tests where the two-marker test is more powerful reaches its highest point when ρ₁₂ is close to zero but is lowest when |ρ₁₂| is around 0.23. As shown in Supplementary Figure S2, this turning point depends on the sample size, causal allele RR, and significance level. From the results of the second simulation (Supplementary Fig. S3), we see that the distance between the two symmetrically placed turning points increases with increased standardized effect size and decreased significance level. Additional information from the correlations between the marker SNPs and the causal SNP must be considered to explain these findings. Figure 2 depicts the correlation space of ρ_1c and ρ_2c when ρ₁₂ is fixed. It shows that two-marker tests always have greater power than single-marker tests when ρ_1c and ρ_2c are extreme and in opposite directions if ρ₁₂ > 0, and when ρ_1c and ρ_2c are extreme and in the same directions if ρ₁₂ < 0. This can be understood graphically by considering the difference in the shape of the acceptance regions of the two tests (an elliptical region for the two-marker test and a square region for the single-marker test). However, the power of the two-marker test will be less sensitive to the directions of the correlations when ρ₁₂ is small (the elliptical acceptance region will approach a circle). When ρ₁₂ is between –0.23 and +0.23, the two-marker test can also be more powerful even when ρ_1c and ρ_2c are extreme and in the same direction when ρ₁₂ > 0, or extreme and in opposite directions when ρ₁₂ < 0. Figure 2 shows that the region where the two-marker test is more powerful tends to dominate the correlation space when ρ₁₂ is close to zero, which explains the trend we observed in Figure 1C.

Fig. 1.

Summary of power from the first simulation (with type I error 0.05, causal RR 1.2, and sample size 2,000). The x-axis is the correlation between the two markers (ρ₁₂). (A) The mean of the test power for each set of correlations corresponding to a small bin of ρ₁₂ values using single-marker tests. (B) The mean power using two-marker tests. (C) The proportion of tests where two-marker tests have greater power than single-marker tests for each ρ₁₂ bin. (D) Box plots showing the distribution of the difference in power between the two-marker and single-marker tests for each ρ₁₂.

Fig. 2.

Power comparison of two-marker vs. single-marker tests and their relationship with the correlation space in the first simulation. Each plot has a fixed ρ₁₂ (correlation between markers). The gray regions are the possible space of ρ_1c and ρ_2c (correlations between markers and causal SNPs) for a specific value of ρ₁₂. The dark/light area indicates those correlation combinations where the two-marker test is more/less powerful than the single-marker test.

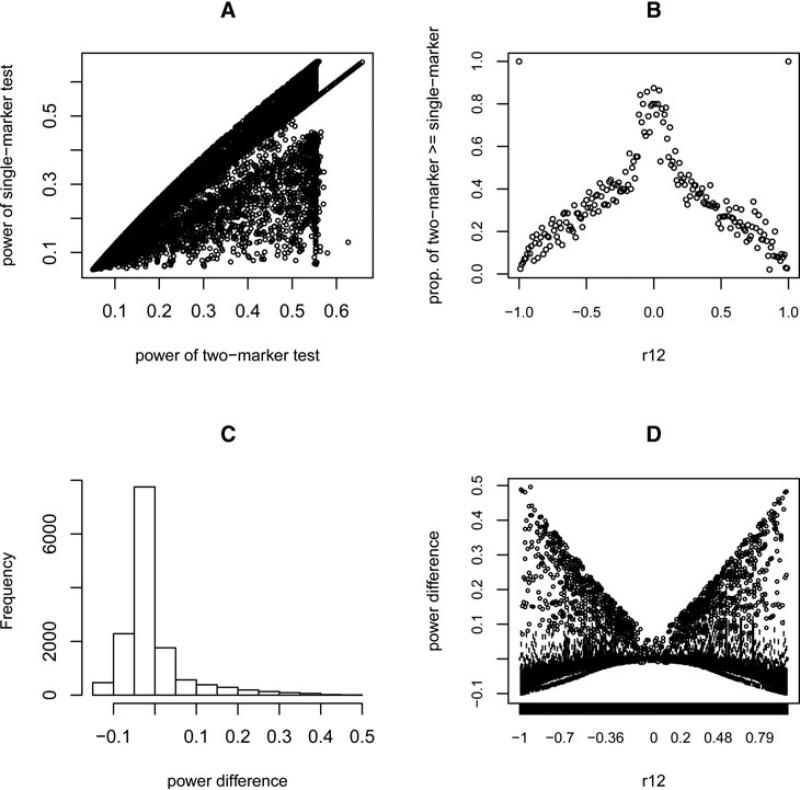
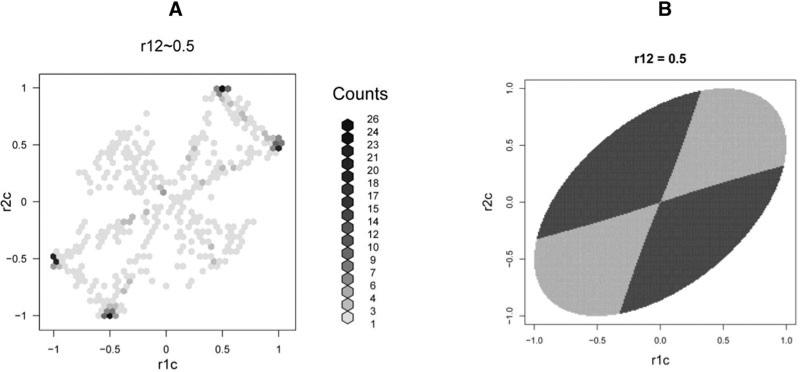
Figure 3 shows the results obtained using the HapMap correlation pattern, in which the effect size and type I error rate were set identical to the first simulation (α = 0.05, causal allele RR = 1.2, and sample size = 1,000 + 1,000). Similar to what we found for uniformly distributed correlations, there are many cases where the two-marker test is much more powerful than the single-marker test. However, a finding that seems to contradict the previous results is that there are actually more cases in total where using a single-marker test is more powerful than using a two-marker one, although the power difference is then small (Fig. 3C). More surprisingly, the proportion of cases where the two-marker test is more powerful—when ρ₁₂ is fixed in a small range—always decreases as |ρ₁₂| increases, and comes down to zero when is close to 1 or –1 (Fig. 3B). To understand how the special correlation structure of the HapMap data can cause this phenomenon, we again plotted the empirical two-dimensional (2D) correlation space of ρ_1c and ρ_2c while fixing ρ₁₂ (Fig. 4A). This shows that most of the correlation points group around an empty bow-tie shaped region (or lines) and, more interestingly, this region is in the correlation space where the two-marker test is the more powerful (Fig. 4C). There is also a proportion of points scattered in another, smaller bow-tie shaped region. This pattern remained consistent when we tried using different ethnic populations, releases, SNP panels, or chromosomes in the HapMap data. We surmised this pattern to be caused by the limited number of actual possible haplotypes. This was confirmed by enumerating the possible haplotype structures, which reproduced a similar correlation pattern (Supplementary Fig. S4).

Fig 3.

Results of a power comparison using the correlations calculated from HapMap data. (A) Scatter plot of power of two-marker tests vs. single-marker tests (each point represents an individual simulated case). (B) The proportion of tests where the two-marker test has greater power than the single-marker test for each fixed range of ρ₁₂. (C) Histogram of power difference between the two-marker test and the single-marker test over all simulated cases. (D) Box plots showing the distribution of the difference in power between the two tests for each small fixed range of ρ₁₂.

Fig. 4.

The empirical (HapMap data) and theoretical correlation space with fixed ρ₁₂. (A) Hexagon binning plot showing the distribution of the correlations ρ_1c and ρ_2c (ρ₁₂ is fixed around 0.5) based on the SNPs chosen from HapMap data. (B) The theoretical two-dimensional correlation space when we fix ρ₁₂ at 0.5. The dark/light gray area indicates the two-marker test is more/less powerful than the single-marker test.

DISCUSSION

It is widely acknowledged that the success and cost-effectiveness of a GWAS depends principally on the appropriate choice of tagging markers and sample size. Comparatively little attention appears to have been given to the determination of a sensible analysis strategy. To reduce the computational burden, a multistage testing is often applied in a typical analysis pipeline. Single-marker methods have become the “gold standard” in GWAS because they are easy and fast to implement, straightforward to interpret, and involve a simple (but often too stringent) multiple testing adjustment. On the other hand, multimarker association testing methods, though widely available, have had very limited use in the initial stage of the analysis. One major concern that statisticians may have had is that the increased number of df involved might negate the benefits achieved from the joint modeling of multiple markers. In this study, we have endeavored to provide more insights into the performance of the two types of methods in practical analysis—particularly for the first stage. Specifically, we have conducted extensive simulations to investigate the power of a two-marker association test vs. a single-marker test. The simulation scenarios were created by varying effect size related parameters (sample size, causal allele RR), type I error rate and, most importantly, the correlation pattern among the markers. Earlier studies based on simulated data have shown that the power of an indirect association test—and also results from comparing between different testing methods—relies on the correlation structure among tag SNPs, as well as that between tag SNPs and causal variants [Kim et al. 2010; Roeder et al., 2005]. In real data analysis, however, we have no way of obtaining information about the correlations between tag SNPs and causal SNPs, as we do in simulation studies. This is why it becomes important to learn—and we have aimed to find out—whether one can in any way determine or narrow down the optimal tests to perform by simply prescreening the correlation pattern of the markers.

Four major conclusions can be drawn from the results obtained, assuming a uniform distribution over the correlation space. First, for the major part of the correlation space, the two-marker test has greater power and the power difference is small in situations where the single-marker test is the more powerful. Second, the mean power of the single-marker test, for a fixed value of the correlation between adjacent marker SNPs (ρ₁₂), is always smaller than that of the two-marker test—a result that is invariant to change of ρ₁₂. Third, two interesting turning points show up when we plot the proportion of tests where the two-marker test is more powerful as a function of values of ρ₁₂. These points move toward –1 and +1 as the effect size increases or the significance level decreases. We have given a graphic explanation of this phenomenon by examining the profiles of the power change in a 2D correlation space. Last, the distribution of the power difference at each value of ρ₁₂ suggests that the two-marker test has relatively better performance when the correlation of the two adjacent markers is high.

However, some different, even opposite, conclusions were revealed by simulations based on the correlation patterns abstracted from HapMap CEU population data. A major difference is that, using HapMap data, overall two-marker tests have higher probability of being less powerful than single-marker tests. We have found that this difference is caused by a special bow-tie shaped region for the correlation between two markers, which is invariant to different ethnic groups and SNP panels. We have further shown that such a pattern is due to constraints on the number of actual possible haplotypes. This result seems to suggest that in general the one-marker test has the better performance for real HapMap data. But we have further discovered that, as demonstrated in Figure 3A and C, the average power difference is small whenever the one-marker test is more powerful, while there are many situations where the two-marker test can be much more powerful. For example, Figure 3D shows that, when the correlation between marker SNPs ρ₁₂ is very high, there are situations where two-marker tests are 50% more powerful than one-marker tests. In summary, our results indicate that overall—though not on average—the two-marker test provides a valuable supplement to the one-marker test, and in fact the two-marker test should be preferred when ρ₁₂ is known to be small (Fig. 3B). A meaningful implication of our findings is that they provide a plausible explanation for why some methods are frequent winners in some studies, and why researchers have often reached different conclusions with different simulation designs.

As pointed out by Kim et al. [2010], an advantage of the two-marker test framework in comparison with single-marker tests is that it enables the potential use of the joint Allelic-LD contrast test, which is equivalent to including a first-order interaction term as well as linear terms in the (prospective) regression model. Their results suggested that this method provides robust power under various disease models. Nevertheless, caution must be taken in using this model for the purpose of detecting a biological interaction and one may refer to Wang et al. [2010a] for a more detailed discussion of this point. What has so far been given less recognition is that the two-marker test can capture additional haplotype information even when an interaction term is not included in the model. A recent real data example of the two-marker association test discussed here is given in Slavin et al. [2011], who detected multiple new putative associated variants for coronary artery disease and hypertension by using by using it. Surprisingly, many of the significant SNP pairs they found are in high LD, which means that their interaction terms can hardly be significant and that these SNPs should, intuitively, have already been detected in a single-marker analysis. After excluding factors such as multicollinearity, they concluded that the extra power is provided by the inclusion of haplotype information when the markers are both heterozygous and in high enough LD.

In this work, we have focused on the case of an additive disease model. For dominant/recessive models, it is known that assuming additive when recessive is true results in large loss in power, but there is not much loss if the true model is dominant. This has been demonstrated by results in Kim et al. [2010]. Therefore, results of power comparisons may change under different disease models. However, by using the true penetrance model, Kim et al. [2010] showed that any difference becomes very minor as the LD between the disease and marker SNP decreases. In the case of marker SNPs that are extremely close and hence in perfect LD with the causal SNP, we would not want to consider haplotypes at all as a single-marker test would then always give the best power.

Collectively, this study provides evidence that the two-marker association test can be superior to the single-marker test and, in particular, suitable for the initial stage of a GWAS analysis to prioritize markers. It is easy to implement and yet offers reliable power to detect risk variants across various circumstances. Moreover, it is less computationally demanding because our aim is not to search for statistical interaction, and thus there is no need to conduct an exhaustive search of all pairwise combinations of markers across the genome [Evans et al., 2006; Marchini et al., 2005; Wang et al., 2010b]. For the first-stage scan, we propose to search over only all the consecutive marker pairs, for which the total number of tests will be the number of markers minus the number of chromosomes. Consequently, the adjustment for multiple testing can be based on a level similar to that used in single-marker analysis. A possible extension, to be investigated in the future, is to test three consecutive markers at a time, in which case we need to examine issues such as its reliability, as well as whether the power increase, if any, is worth the additional complexity.