Black-White Differences in Maternal Age, Maternal Birth Cohort, and Period Effects on Infant Mortality in the U.S. (1983-2002)

Abstract

We investigate three interrelated sources of change in infant mortality rates over a 20 year period using the National Center for Health Statistics (NCHS) linked birth and infant death cohort files. The effects of maternal age, maternal birth cohort, and time period of childbirth on infant mortality are estimated using a modified age/period/cohort (APC) model that identifies age, period, cohort effects. We document black-white differences in the patterning of these effects and find that maternal age effects follow the predictable U-shaped pattern, net of period and cohort, but with a less steep gradient in the black population. The largest relative maternal age-specific disparity in IMR occurs among older African American mothers. Cohort effects, while considerably smaller than age and period effects, present an interesting pattern of a modest decline in IMR among later cohorts of African American mothers coupled with an increasing IMR among the same cohorts of non-Hispanic whites. However, period effects dominate the time trends, implying that period-related technologies overwhelmingly shape U.S. infant survival in today’s population. These general findings are mirrored in APC analyses carried out for several leading underlying causes of infant mortality.

Introduction

Temporal change in infant mortality involves period-driven technological advances in the face of changing childbearing contexts experienced by different birth cohorts of mothers, in combination with changes in the maternal age patterns of childbearing. We argue that age-period-cohort (APC) analysis could prove useful to disentangle these interrelated effects in a study of infant mortality, and that this kind of analysis can provide insight into the temporal components of black-white differences in infant mortality rates. In particular, a cohort analysis can uncover differences that would not be revealed by consideration of age and period alone, or by approaches that fail to account for the inherent dependence of these temporal dimensions.

APC analysis is a well known approach to gain insight into the unique contribution of age, birth cohort, and time period in mortality research. Age typically represents variation associated with different age groups and attributable to differences in physiological changes, life experiences and changes in social roles. Period effects represent variation over time that simultaneously affects all age groups. Cohort effects represent variation associated with groups of individuals having different formative experiences at successive ages in successive years. A common goal is to assess the effects of one of these temporal dimensions net of the effects of the other two (Yang et al. 2005; Yang and Land. 2008).

With regard to mortality processes, biological age accounts for considerable variation. Yet, some of this variation is shaped by the historical period in which death occurs and by a cohort’s unique experience of history. Although the most straightforward application of APC is in the analysis of adult mortality, the APC analytic approach may offer insights about aspects of infant mortality, which have not thus far been explored in past research. In particular, the historical time period in which infant death occurs, the age of the mother at the time of childbirth, and the mother’s birth cohort may play important distinct roles in infant mortality. As such, maternal age, mother’s birth cohort, and time period of infant death potentially tap distinct dimensions of change which are not easily separable due to the perfect linear dependence of mother’s birth cohort on maternal age and time period in which infant death occurs.

This paper is organized as follows. Section 1 provides background about the contributors to change in infant mortality and their relevance for race/ethnic comparisons. Section 2 describes the data and methodology with particular attention to the statistical underpinnings of the widely-used intrinsic estimator (IE) for APC analysis. Section 3 provides results on the APC analysis of overall infant mortality in addition to analyses of several leading underlying causes of infant mortality and Section 4 summarizes the main findings.

1. Background

Significant declines in U.S. infant mortality have occurred over the past several decades (Mathews and MacDorman 2007). Much of this decline reflects decreases in specific causes of death and has been attributed to innovations in perinatal care and technology. We can attribute some share of the decline to medical innovations targeting specific leading underlying causes of infant death such as congenital anomalies, sudden infant death syndrome (SIDS), and respiratory distress syndrome (RDS). Reductions in these causes would be reflected in period changes in infant mortality. No efficacious interventions emerged during the period under study for other leading causes, which include disorders leading to short gestation and low birth weight and maternal complications. We briefly review three leading causes of infant mortality that have responded to period-related interventions and innovations from 1983-2002 along with evidence of racial differences in responses to these interventions and innovations.

Congenital anomalies have been the leading underlying cause of neonatal infant death since the 1980s and medical innovations have played a significant role in reducing mortality due to this cause. In the mid and late 1990s, congressional appropriations provided to the centers of disease control and prevention (CDC) went to several states to establish or improve pre-natal screening (Erickson 2000). In 1998 the FDA mandated folic acid supplements in all enriched grain products as a population strategy targeted to reach a broad population of women while requiring minimal changes in behavior for compliance (Lawrence 2005; Rader 2002). The emerging evidence from a number of studies points to growing disparities between the white (specifically the non-Hispanic white) majority and some minorities (notably non-Hispanic blacks) after notable medical advances, and argues that growing disparities are largely the result of inequality in access to perinatal care advances (Dowd and Aiello 2008, Gortmaker and Wise 1997; Nsiah-Jefferson 1993; Wise 1999, 2003). Race differences in the IMR from congenital anomalies may also reflect selection processes. For example, Velie and Shaw (1996) find that in a sample of neural-tube-defect (NTD)-affected pregnancies, women who electively terminated pregnancies were more likely to be white, tended to have higher levels of education and household income, and were more likely to be using folic acid supplements. They attribute the difference in rates of elective termination to variation in access and utilization of prenatal screening and choices regarding elective termination procedures.

Sudden Infant Death Syndrome (SIDS) was the second leading cause of death into the early 1990s, and the leading cause of postneonatal death in the 1980s and 1990s (Black et al. 1986; Pollack and Frohna 2001, 2002). A specific low-tech innovation recommended by American Academy of Pediatrics (AAP) that infants be put to sleep in a supine as opposed to a prone position had a large beneficial impact on SIDS survival (Gibson et al. 2000; Li et al. 2003; Pollack and Frohna 2001, 2002; Ottolini et al. 1999; Willinger et al. 1998.) The “back to sleep” campaign was mounted nationwide in 1994. SIDS mortality dropped by more than one-third between 1989 and 1996 (Pollack and Frohna 2001). Using data from the 1989 and 1996 linked birth and infant death files—points in time that are respectively, before and after the “back to sleep” initiative—Pollack and Frohna (2001) found that net of several risk factors, non-Hispanic African American infants were at 24% greater risk of SIDS death when compared to the non-Hispanic white reference group.

Respiratory Distress Syndrome is primarily a disease of preterm (<26 weeks gestation) or low birth weight (<2500gm) newborns resulting from the inability of the lungs to naturally produce a sufficient amount of surfactant required for gas exchange to occur (British Columbia Reproductive Care Program 1993; Halliday 1997; Malloy and Freeman 2000). RDS was the 2nd leading cause of neonatal mortality through the mid 1980s and dropped to the 4^th or 5^th leading cause by 1995. Despite large absolute declines in RDS among blacks and whites, the black-white neonatal rate ratios rose from 1.7 to 2.8 from 1980-1995 (Charmichael et al. 1998), while overall black-white RDS rate ratios rose from 1.8 to 2.9 from 1983-2002 (Frisbie et al. 2010; Powers and Song 2009).

The FDA approved the use of surfactant replacement therapy in 1990 and RDS responded well to medical innovations during the period under study leading to substantial mortality declines (Frisbie et al. 2010; Frisbie et al. 2004; Halliday 1997; Hamvas et al. 1996; Malloy and Freeman 2000; Ranganathan et al. 2000). The availability of data on variation in risk of death from RDS in the periods before and after FDA approval of surfactant replacement therapy in 1990 provides an opportunity to gain insight into the possible differential impact of advances in perinatal health care produced by social and other factors. Several studies have taken advantage of this natural experiment with regard to change in black-white RDS differentials. Following approval of surfactant replacement therapy, RDS mortality declined substantially among both blacks and whites. Absolute declines were greater for blacks than for whites, but in relative terms (i.e., in terms of rate ratios), the black/white gap increased substantially (Frisbie et al. 2010; Frisbie et al. 2004; Halliday 1997; Hamvas et al. 1996; Malloy and Freeman 2000; Powers and Song 2009; Ranganathan et al. 2000).

No efficacious innovations emerged during the period under study for other leading causes of infant mortality, including disorders leading to short gestation and low birth weight and maternal complications (e.g., incompetent cervix, premature rupture of membranes, ectopic pregnancies, plural pregnancies, and maternal death). In the absence of specific technological innovations we would expect weaker period effects in APC analysis when compared to other leading causes. However, this does not rule out other dimensions of change. In particular, while there is a clear expectation for the role of historical period in light of significant advances in medical technologies, we would expect that some portion of the decline in infant mortality is impacted by the changing maternal age structure of childbearing, perhaps affected by offsetting trends toward older ages of childbearing and changes in teenage childbearing rates. This component of change would be captured by maternal age effects in an APC analysis.

A third temporal component reflects secular changes in the experience of various cohorts of women. Cohort effects may tap the tendency toward smaller families in later birth cohorts or may reflect secular trends in teen pregnancy rates or may reflect distributional changes in the correlates of mortality such as education. The extent that these components of change are mirrored across distinct populations is also of interest. For example, later birth cohorts of African American women may have benefitted in important ways from the Civil Rights movement and the accompanying changes in racial attitudes and the change in the degree of discrimination towards racial and ethnic minorities in ways that non-Hispanic white women did not, whereas both the African American and non-Hispanic white populations would be expected to benefit by cohort change in the distribution of education. A comparative analysis by race could be informative in isolating these cohort effects, net of changes in the maternal age distribution and with respect to the historical period in which childbearing and infant mortality occurs.

Other trends in known risk factors may have different impacts depending on time period and mother’s birth cohort. In particular, trends in infant mortality may be responsive to increasing obesity prevalence and declines in smoking in the U.S. population. Maternal obesity is associated with a number of maternal complications as well as long term risks for the fetus (Kim et al. 2007). Covering roughly the same period as the present study, Kim et al. 2007 show a 69% increase in the prevalence of pre-pregnancy obesity, with the highest prevalence among black mothers and women between the ages of 20-29. Unfortunately, their data were not suited to addressing cohort differences in pre-pregnancy obesity prevalence.

Smoking during pregnancy is associated with low birth weight, intrauterine growth retardation, and infant mortality (Mathews 2004). Overall, smoking during pregnancy declined by about one-third during the 1990s, with the largest declines reported by mothers aged 25-34. More muted declines were reported among 15-19 year old mothers resulting from recent increases maternal smoking in that age group (Mathews 2004). Maternal smoking rates were higher for non-Hispanic white mothers (15.7% in 1999) compared with non-Hispanic blacks (9.1). During the 1990s, maternal smoking declined by 25% and 43% for whites and blacks, respectively. Ananth et al. (2005) were able to more fully account for secular trends of smoking prevalence using an APC approach, with period effects likely suggesting the role of intervention programs to reduce maternal smoking, maternal age effects suggesting a role for lifestyle and socioeconomic influences, and cohort effects suggesting the influence of culture or better compliance or access to smoking cessation programs (Ananth et al. 2005). Race differences in cohort trends in maternal smoking were noteworthy. In particular, the most dramatic changes in smoking decline occurred for cohorts of women born before 1965. But little change in smoking prevalence was evident for cohorts of black women born in 1970 or later (Ananth et al. 2005).

The conceptual framework underlying the present work stems from the proposition that as advances in health care occur, the ability of individuals to reduce the risk of disease and death is shaped by social inequality. Social resources, such as income, power, prestige, and social networks are relevant for all aspects of health, and pertain directly or indirectly to infant mortality via their effects on maternal health and via their effects on access to and benefit from health interventions (see e.g., Link and Phelan 1995, 2002). Despite the growth in technological innovations aimed at preserving the lives of infants, there is evidence that access to these innovations is much more limited for “low income women and women of color” (Nsiah-Jefferson 1993: 308). Among the limitations in black access to preventative and curative interventions are: lack of adequate prenatal care and screening, lower levels of education and knowledge about the health care system, and insufficient economic resources and health insurance (Dowd and Aiello 2008, Nsiah-Jefferson 1993). Focusing directly on infant mortality, Gortmaker and Wise (1997) suggest that, due to social inequality, growing disparities in infant mortality between the white majority and disadvantaged minorities are likely to occur following beneficial innovations in perinatal care.

2. Data and Methods

The NCHS linked birth and infant death cohort files from 1983-2002 provide a series of data consisting of millions of births per year, with an exceptional match rate. About 98% of the infant death records were successfully linked to birth certificates in any given year (U.S. Department of Health and Human Services 1995). However, no linked birth/infant death cohort files were produced by the NCHS from 1992-94. The resulting study population consists of individual-level records for 62,878,862 live births and 530,635 infant deaths. As is customary in this research, race of mother, as indicated on the birth certificate is used to ascertain race of infant. This yields an analytic sample of 10,054,428 births and 152,793 infant deaths in the non-Hispanic black population and 51,767,843 births and 351,221 infant deaths in the non-Hispanic white population.

We carry out an APC analysis of the NCHS cohort-linked birth death files from 1983 to 2002 to examine infant mortality using information on mother’s age (reported on the birth certificate) and year of infant death. Data are arranged in seven 5-year maternal age groupings (A) ranging from age 15 or less to age 45 and older, as well as four 4-year periods (P) spanning the period from 1983 to 2002.² This yields ten 5-year maternal birth cohorts ranging from 1940 to 1985. It should be noted that certain cohorts might be incompletely represented as the NCHS linked file data are not available from 1992-1994. Most problematic would be the failure to capture the relatively few later births that occurred to earlier cohorts during this period.

These data adhere to the assumptions of APC analysis insofar as mother’s birth cohort (C) is linearly dependent on period and age C = P − A. As is well known, data in this form suffer from an identification problem that renders conventional estimation of all the age-period-cohort effects impossible without imposing constraints on at least 1 of the model parameters. Yang et al. (2004) proposed an estimator that yields estimates of all quantities that we implement here. We also examine some alternative approaches.

Descriptive Summary

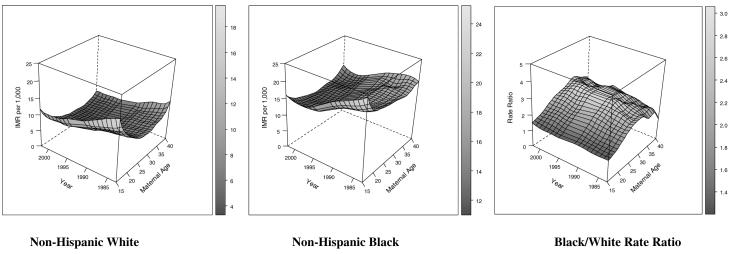
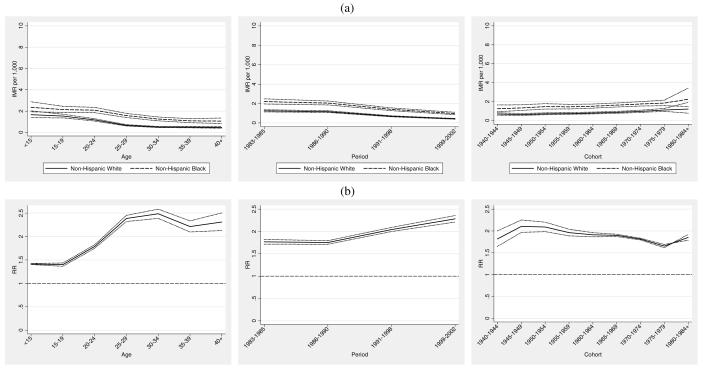
Tables 1 and 2 present the data arrayed by maternal age and maternal birth cohort in terms of number of births and infant mortality rates for non-Hispanic whites and non-Hispanic blacks in the NCHS data. Figure 1 shows the smoothed empirical IMRs by maternal age and year for each group along with the black/white rate ratios using a finer measurement scale than was used in Tables 1 and in the analytic models discussed later. Maternal birth cohort specific rates are reflected along the diagonals of Figure 1. We notice somewhat different maternal age profiles of risk depending on racial group, with non-Hispanic whites exhibiting markedly steeper infant mortality gradients at younger and older ages than non-Hispanic blacks. Each group experiences a flattening of the generally U-shaped pattern of infant mortality associated with maternal age. We also observe a somewhat more dramatic absolute reduction in infant mortality over time among non-Hispanic blacks when compared to non-Hispanic whites. However, the empirical black/white rate ratios in the rightmost panel of Figure 1 demonstrate the increasing relative black-white disparity occurring throughout the past several decades documented in past research (Frisbie et al. 2004; Frisbie et al. 2010). The 3-dimensional depiction by maternal-age and time period reveals that this widening relative disparity is quite obvious over the 25-35 maternal age range and less obvious for women under 20 and over 35. The two leftmost panels of Figure 1 suggest that the source of this relative increase is the combination of steeper declines in maternal age specific infant mortality among non-Hispanic whites in later decades coupled with a stagnating decline from the mid-1990s to 2002 among non-Hispanic blacks.

Table 1.

Number of live births and infant deaths by maternal age and maternal birth cohort among non-Hispanic whites (NCHS cohort linked files)

Live Births Non-Hispanic Whites
Maternal Age
Maternal Birth Cohort	<15	15-19	20-24	25-29	30-34	35-39	40+	Total
1940							64,741	64,741
1945						474,653	159,806	634,459
1950					1,635,236	1,096,974	96,954	2,829,164
1955				2,899,837	3,299,577	577,166	486,641	7,263,221
1960			2,690,494	5,044,245	1,465,898	2,426,426		11,627,063
1965		966,368	4,099,337	1,840,702	5,175,650			12,082,057
1970	11,709	1,609,930	1,542,453	5,956,100				9,120,192
1975	21,115	686,381	5,139,852					5,847,348
1980	10,662	2,257,686						2,268,348
1985	31,252							31,252
Total	74,738	5,520,365	13,472,136	15,740,884	11,576,361	4,575,219	808,142	51,767,845
Infant Deaths
Maternal Age
Maternal Birth Cohort	<15	15-19	20-24	25-29	30-34	35-39	40+	Total
1940							722	722
1945						3,980	1,534	5,514
1950					12,138	7,888	713	20,739
1955				21,643	21,502	3,498	3,362	50,005
1960			25,153	33,073	7,684	12,782		78,692
1965		12,425	34,274	9,981	23,210			79,890
1970	261	18,598	10,868	28,665				58,392
1975	395	6,535	31,398					38,328
1980	166	18,314						18,480
1985	459							459
Total	1,281	55,872	101,693	93,362	64,534	28,148	6,331	351,221

Table 2.

Number of live births and infant deaths by maternal age and maternal birth cohort among non-Hispanic blacks (NCHS cohort linked files)

Live Births Non-Hispanic Blacks
Maternal Age
Maternal Birth Cohort	<15	15-19	20-24	25-29	30-34	35-39	40+	Total
1940							11,249	11,249
1945						65,950	23,495	89,445
1950					203,251	148,055	13,53 1	364,837
1955				406,179	427,145	76,383	68,642	978,349
1960			570,353	766,879	187,795	314,418		1,839,445
1965		383,154	1,012,102	285,051	629,935			2,310,242
1970	16,301	685,136	388,456	925,853				2,015,746
1975	29,599	274,746	1,292,597					1,596,942
1980	11,846	809,046						820,892
1985	27,281							27,281
Total	85,027	2,152,082	3,263,508	2,383,962	1,448,126	604,806	116,917	10,054,428
Infant Deaths
Maternal Age
Maternal Birth Cohort	<15	15-19	20-24	25-29	30-34	35-39	40+	Total
1940							203	203
1945						1,183	449	1,632
1950					3,445	2,496	236	6,177
1955				6,884	7,083	1,209	1,022	16,198
1960			10,267	12,576	2,743	4,127		29,713
1965		7,462	17,047	4,012	8,000			36,521
1970	437	12,119	5,700	11,456				29,712
1975	703	4,074	16,305					21,082
1980	249	10,819						11,068
1985	487							487
Total	1,876	34,474	49,319	34,928	21,271	9,015	1,910	152,793

Figure 1.

IMR per 1,000 by Infant Birth/Death Period, Maternal Age, and Race and Black/White Rate Ratios (smoothed estimates). The maternal age label 15 denotes the interval [< 15) and the maternal age label of 40 denotes the interval [40+), otherwise age is measured in single years.

APC Model

The APC model conditions on the marginal distributions of age and period. The cohort distribution may be viewed as an age × period interaction along the diagonals of an age by period contingency table. In a conventional generalized linear model (glm), the linear dependence of the cohort effects requires equating two model coefficients. In this case, the usual dummy-variable constraints are used to identify the remaining age and period effects. Alternatively, one could constrain age or period effects in the same manner and estimate all but two of the cohort effects. We ruled out constrained models using a number of fit criteria, including the model −2 log likelihood (−2logL), and the Bayesian and Akaike information criteria (BIC and AIC). For both racial groups, the full APC model produced the smallest values of −2logL, BIC, and AIC and was judged the preferred model. Although these checks provide evidence that the full APC model is preferred, this does not rule out the existence of plausible constraints on one or more APC parameters that would lead to a simpler model. Estimates of the APC parameters can be sensitive to the choice of equality constraints, and these types of constraints generally require external information for justification (Glenn 2005).

The APC model is specified as

$$\log \mathrm{E}\left(r_{\mathit{ij}}\right)=\log \mathrm{E}\left(\frac{d_{\mathit{ij}}}{n_{\mathit{ij}}}\right)={\beta }_0+{\beta }_i^A+{\beta }_j^P+{\beta }_k^C,$$ (1)

where log E(r_ij) is the logarithm of the expected IMR based on d_ij deaths and n_ij births pertaining to cell i j of a cross-classification of infant deaths and births in maternal age interval i (for i = 1,…, I age groups) and time period j (for j = 1,…, J periods). Age and period effects are denoted by ${\beta }_i^A$ and ${\beta }_j^P$, respectively. ${\beta }_k^C$ denotes the kth (diagonal) maternal birth cohort effect (for k = 1,…, I + J − 1 birth cohorts) , and where the index k = I − i + j. For this study, I = 7, J = 4 for N = I × J = 28 age by period cells covering 10 maternal birth cohorts.

The following ANOVA, centered-effects (or sigma constraint) normalization is imposed on the effects $\sum {\beta }_i^A=\sum {\beta }_j^P=\sum {\beta }_k^C=0$. Alternatively, the model can be cast terms of multiplicative effects,

$$\mathrm{E}\left(r_{\mathit{ij}}\right)={\tau }_0{\tau }_i^A{\tau }_j^P{\tau }_k^C,$$ (2)

where $\prod {\tau }_i^A=\prod {\tau }_j^P=\prod {\tau }_k^C=1$. The τ parameters under the APC model are multiplicative effects whose product is 1 over the levels of each factor. This normalization ensures that the constant term in the model (τ₀) is the scaled grand mean IMR (or central IMR). The APC estimates therefore reflect the maternal age, maternal birth cohort and time period departures from the central mean IMR for each population, net of the other APC effects.

Estimating the APC Model

Yang et al. (2004) propose an estimator that decomposes the less-than full-rank design matrix to provide a solution to the APC identification problem via principal components regression. This yields the “intrinsic estimator” (IE). Although we refer to the IE as an estimator, it is more appropriately viewed as an estimable function.³ We forego the description of the underlying vector geometry of the solution for the IE—which is described elsewhere—and focus on the mechanics of estimation. The IE is easily implemented for a linear model using well known procedures for dealing with ill-conditioning arising from collinear predictors, which involve finding characteristic roots and orthonormal vectors that are linear transformations of the model design matrix. Formally, let Q be the p× p orthogonal matrix of eigenvectors of the X’X matrix based on the N × p design matrix X composed of an intercept term, I −1 age terms, J −1 period terms, and I + J − 2 cohort terms subject to the ANOVA normalization above. Let l₁,…,l_p denote the eigenvalues of X’X and L be the p× p diagonal matrix containing these eigenvalues. Because QLQ’ = X’X, the IE can be obtained as the solution to the following principle components regression

$${\mathbf{b}}_{\mathrm{IE}}=\left({\mathbf{QL}}_0^{-1}{\mathbf{Q}}^{\prime }\right)\left({\mathbf{X}}^{\prime }\mathbf{y}\right),$$ (3)

where y is the N ×1 response vector—which is typically in the form of log rates—and ${\mathbf{L}}_0^{-1}$ is the p× p diagonal matrix containing $l_1^{-1},\dots ,l_{p-1}^{-1},0$ on the main diagonal and zeros elsewhere. In this case ${\mathbf{QL}}_0^{-1}{\mathbf{Q}}^{\prime }$ plays the role of [X’X]⁻¹ in the usual linear regression model.

Yang et al.’s 2004 approach is one of several strategies to obtain estimates from under-identified models, of which the APC model is a special case. More generally, we can view the IE as the limit of a coefficient vector from a penalized regression where the shrinkage penalty λ → 0⁺ (see e.g., Fu 2000), in which case we may dispense with the step of computing eigenvalues/vectors and work directly with X . The estimator then takes the form of a ridge regression (Hoerl 1962; Hoerl and Kennard 1970)

$${\mathbf{b}}_{\mathrm{R}}={({\mathbf{X}}^{\prime }\mathbf{X}+\lambda \mathbf{I})}^{-1}\left({\mathbf{X}}^{\prime }\mathbf{y}\right),$$ (4)

where I is the p× p identity matrix. This model may also be motivated from a Bayesian perspective in which case prior data X₀ and Y₀ is brought to bear in the estimation. In this case, Y₀ = 0, X₀’X₀ = I and λ → 0⁺ constitutes non-informative prior information (Marquardt 1970; Draper and Smith 1981).

It is well known that the ridge estimator is biased. However, there is a tradeoff between bias and variance, with the variance in the ridge estimator decreasing as λ → ∞. Typically, a cross-validation strategy is employed to find the optimal λ value for a particular set of data. The resulting standard errors of b_R when λ > 0 are smaller than those of b_IE (i.e., b_R has lower mean square error than b_IE). In applied work, one may use the ridge estimator for APC analysis and set λ to a very small number (i.e., 1.e-8) so that b_R ≈ b_IE. However, cross-validation may reveal a more suitable λ for the data.

Finally, perhaps a more straightforward approach in contrast to Yang et al.’s 2004 exposition, the IE may be computed using an OLS estimator that employs a “pseudo”, Moore-Penrose, or generalized inverse of X’X denoted by (X’X)⁺ (Fu and Hall 2006; Marquardt 1970; Searle 1971),

$${\mathbf{b}}_{\mathrm{IE}}={\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}^{+}\left({\mathbf{X}}^{\prime }\mathbf{y}\right).$$ (5)

Employing the generalized inverse obviates computing eigenvalues/vectors as these steps are subsumed in the generalized inverse (Marquardt 1970).

In summary, a number of equivalent numerical methods (i.e., principal components, singular value decomposition, generalized inverse, etc.) may be employed in various ways to provide solutions to problems where the design matrix is rank deficient (i.e., X’X is ill-conditioned). These methods are not new, and date back at least 50 years. In the case of APC analysis, the problem is simplified because the there is only one collinear predictor (i.e., one too many columns in the design matrix) yielding a single zero eigenvalue of X’X, which gives X an effective rank of p−1.

Maximum Likelihood Estimation

Least squares-type solutions outlined above require one matrix inverse operation. In the case of the generalized linear models used here (i.e., loglinear models for rates based on counts of deaths and exposure to risk), we require iterative updating of the estimates in order to maximize a log likelihood function of the form

$$\log L=\sum _{i=1}^N{d}_i\mathbf{X}{\beta }_{\mathrm{ML}}-n_i{e}^{\mathbf{x}{\beta }_{\mathrm{ML}}},$$ (6)

where d and n pertain to the number of deaths and exposures in each age by period “cell,” respectively. The most straightforward optimization approach employs the Moore-Penrose inverse to the matrix of second derivatives of log L with respect to β_ML in Eq. (6) in the updating equations for a generalized linear model using a Newton-Raphson algorithm, where at iteration t + 1, the estimator is updated as

$${\mathbf{b}}_{\mathrm{ML}}^{t+1}={\mathbf{b}}_{\mathrm{ML}}^t-{\left[{\mathbf{H}}^t\right]}^{+}{\mathbf{g}}^t,$$ (7)

where g^t is the p×1 vector of 1^st derivatives of the log likelihood function with respect to the APC parameters (i.e., the gradient), H^t is the p× p matrix of 2^nd derivatives (i.e., the Hessian), each of which is evaluated at iteration t. That is, in a nonlinear estimation H assumes the role that X’X plays in the linear case (Marquardt 1970).

As mentioned earlier, the results from the model adopted here are normalized using an ANOVA-type or “centered-effects” coding, thus providing estimates for all the APC effects and the grand mean (or central log rate). Like dummy variable regression, an omitted category must be chosen to identify the model. Under the sigma constraint normalization, this effect is simply minus the sum of the effects of the included categories for a particular APC factor. Thus, obtaining the omitted category effects is straightforward. Obtaining their standard errors is a technical aspect of the model that is not well documented, so we discuss this in some detail. Using the last level of each APC factor as the omitted category, we obtain the excluded category effects as follows:

$$b_I^A=-\sum _{i=1}^{I-1}{b}_i^A,b_J^P=-\sum _{j=1}^{J-1}{b}_j^P,\text{and}{b}_{I+J-1}^C=-\sum _{k=1}^{I+J-2}{b}_k^C.$$ (8)

Following the usual rule for the variance of a sum, the variances of the omitted category effects may be computed as

$$\mathrm{var}\left(b_I^A\right)=\sum _{j=1}^{I-1}\sum _{k=1}^{I-1}\mathrm{cov}\left(b_{\mathit{jk}}^A\right),\mathrm{var}\left(b_J^P\right)=\sum _{j=1}^{J-1}\sum _{k=1}^{J-1}\mathrm{cov}\left(b_{\mathit{jk}}^P\right),\text{and}\mathrm{var}\left(b_{I+J-1}^C\right)=\sum _{j=1}^{I+J-2}\sum _{k=1}^{I+J-2}\mathrm{cov}\left(b_{\mathit{jk}}^C\right),$$ (9)

where $\left(b_{\mathit{jk}}^{\mathit{APC}}\right)$ denotes element j k of the variance/covariance matrix pertaining to the APC effects, and is obtained at the final optimization iteration as cov(b_ML) = [−H]⁺.

A Stata program apc_ie (Schulhofer-Wohl and Yang 2006) is available for fitting APC models using IE. A somewhat more flexible program ie_rate (Powers 2012) offers more possibilities for outputting fitted rates and does not require perfect APC dependence.

3. Results from the APC Model

All Causes

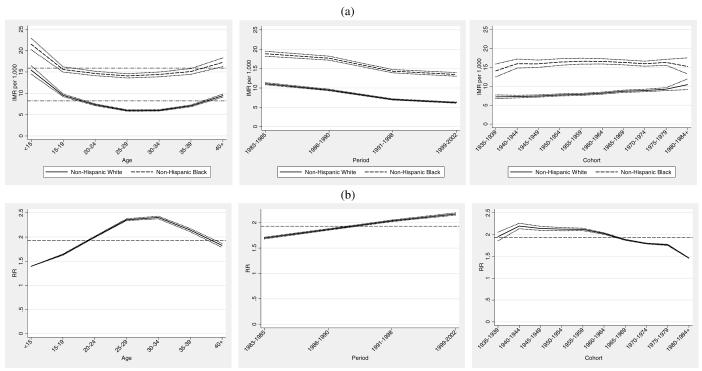
Combining relevant model terms, we generate the maternal age, maternal birth cohort and period specific IMRs as shown in the top panel of Figure 2 (Figure 2a) from each model as ${\widehat{\tau }}_0{\widehat{\tau }}_i^A{\widehat{\tau }}_j^P{\widehat{\tau }}_k^C\times 1,000$, where two of the ${\widehat{\tau }}_i^A,{\widehat{\tau }}_j^P$, and ${\widehat{\tau }}_k^C$ terms are set to 1.0 in order to generate age, period, or cohort IMRs that would prevail at the average maternal age, maternal birth cohort, or period. The central mean IMR—denoted by the dashed line appearing through each group’s plot in Figure 2a— is ${\widehat{\tau }}_0$. We can see for example, that the estimated IMR in the population of women in the under age 15 and over 40 age groups is higher than the grand mean IMR. This pattern is consistent with the U-shaped infant mortality pattern, with relatively higher infant mortality associated with both younger and older maternal ages. Figure 2a shows a steeper age gradient in IMR in the non-Hispanic white population and a somewhat steeper period gradient in the non-Hispanic black population, which is also consistent with the empirical patterns given in Figure 1. The lower maternal age gradient in the black population is well known and consistent with the conceptual framework of weathering (Geronimus 1992). Consistent with Figure 1, the bottom panel of Figure 2 (Figure 2b) shows that the largest relative black-white infant mortality gap occurs for women aged 30-40.

Figure 2.

Infant Mortality Attributed to All Causes: (a) maternal age, infant birth/death period, and maternal birth cohort-specific IMR and 95% confidence intervals. (b) black/white age, period, and cohort relative rate ratios and 95% confidence intervals.

Figure 2a also shows that period effects are monotonically decreasing in each population. The span of the reduction among non-Hispanic blacks is on the order of 5.37 infant deaths per 1,000 births compared to a reduction of 4.78 deaths per 1,000 births among non-Hispanic whites. Thus, in an absolute sense, a somewhat larger decline is observed in the non-Hispanic black population. This is consistent with the observed pattern in Figure 1, which shows a somewhat steeper period gradient in the non-Hispanic black population. We may attribute this component to technological changes occurring during the time period under study. However, we tentatively conclude that these changes appear to have about equal impact on the decline in infant mortality for both non-Hispanic whites and non-Hispanic blacks.

Cohort change in IMR is less pronounced, as illustrated by the relatively flat curves in Figure 2a. However, the cohort patterns are considerably more interesting from a comparative standpoint. Among non-Hispanic whites, there is a moderate increase in IMR by birth cohort, with evidence of increasing infant mortality in later cohorts of mothers, net of maternal age and period. There is somewhat less precision in the estimates for the oldest and youngest cohorts, particularly in the non-Hispanic black population. Nevertheless, patterns of cohort change in infant mortality among non-Hispanic blacks are notably distinct from those of non-Hispanic whites. Cohort change in IMR among non-Hispanic blacks reveals a moderate shift toward lower infant mortality for younger cohorts of African American women. This pattern is in sharp contrast to the cohort patterns evident among non-Hispanic whites, where earlier cohorts of women experience relatively lower infant mortality compared to more recent cohorts. The fact that a main portion of cohort decline in IMR occurs for the population of African American women born after the civil rights movement leads to speculation that a modest survival benefit accrued to the infants whose mothers were the likely beneficiaries of positive social change occurring during this period. However, this benefit appears to be overwhelmingly overshadowed by period changes.

The bottom panel of Figure 2 (Figure 2b) shows the black/white age, period, and cohort specific rate ratios based on the APC specific rates for each population. We calculate the age, period, and cohort-specific rates from each model as ${\widehat{r}}_{\mathit{ijk}}={\widehat{\tau }}_0{\widehat{\tau }}_i^A{\widehat{\tau }}_j^P{\widehat{\tau }}_k^C$ then form the ratio of the black and white IMRs. The dashed horizontal lines appearing in Figure 2b depict the central black/white rate ratio of 1.93, from which the other rate ratios depart. This may be viewed as an “expected” relative disparity of about 2 infant deaths in the black population for each infant death in the white population, evaluated at the average maternal age at birth, time period, and maternal birth cohort. Rate ratios lower than 1.93 denote smaller than expected relative black/white disparities in specific APC effects, whereas those that are higher indicate larger than expected disparities in specific APC effects. Relative disparities in IMR by maternal age exhibit narrower than expected black/white gaps at younger maternal ages, a widening black/white relative gap over the prime childbearing years (25-35), and moderate narrowing at later ages. Period effects show the increasing relative black/white gaps over the 20-year period. Both the age and period effects mirror the empirical depiction of Figure 1. More interestingly, consistent with earlier results, cohort effects exhibit narrowing of the relative black/white gap for later cohorts of women. The leftmost panel in Figures 2a suggest that this is due to higher infant mortality experienced in later cohorts (1965 and onward) of non-Hispanic white mothers rather than to the relatively modest declines in infant mortality that occurred among the same cohorts of non-Hispanic black women.

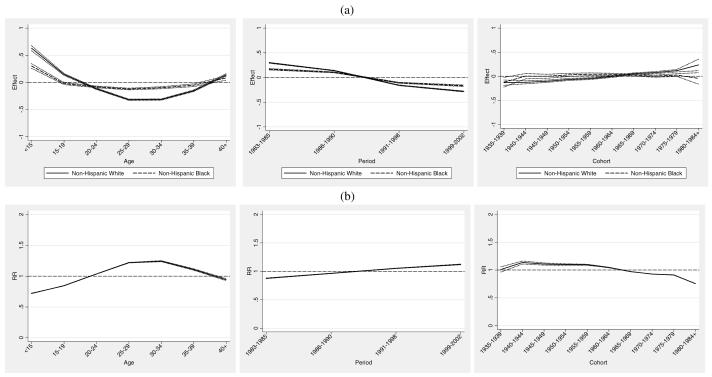
Thus far we have considered results based on predicted rates from the APC models. We now compare the estimated APC effects by group and assess their relative magnitude. These results permit a direct comparison of absolute and relative race-specific APC effects. The top panel (a) of Figure 3 (Figure 3a) shows the age, period and cohort effects (b^A , b^P , and b^C) for each group plotted against age, period and cohort respectively. The lower panel (b) of Figure 3 (Figure 3b) shows the black/white relative risk ratios, $e^{b_B^A}∕e^{b_W^A},e^{b_B^P}∕e^{b_W^P}$, and $e^{b_B^C}∕e^{b_W^C}$.

Figure 3.

Infant Mortality Attributed to All Causes: (a) maternal age, infant birth/death period, and maternal birth cohort estimates (bA , bP , and bC ) and 95% confidence intervals. (b) black/white age, period, and cohort relative risk ratios and 95% confidence intervals.

We see from Figure 3a that the maternal age effects for non-Hispanic whites exhibit more variation and reveal both higher effects at younger maternal ages and lower effects in the prime childbearing years when compared with non-Hispanic blacks. This is highlighted in panel (b) which shows that maternal age effects for non-Hispanic blacks are relatively lower than those of whites at younger ages and relatively higher in the prime childbearing years. Period effects show similar patterns but are somewhat stronger for non-Hispanic whites. A modest crossover is evident in the relative effect (i.e., the period effect for blacks is initially lower from 1983 to 1990 and then moderately higher thereafter), which suggests that high-tech and low-tech interventions in the post 1990 period benefitted non-Hispanic whites to a somewhat greater extent than non-Hispanic blacks (Frisbie et al. 2010; Frisbie et al. 2004; Powers and Song 2009; Nsiah-Jefferson 1993; Gortmaker and Wise 1997). Cohort effects show modest increases for whites coupled with a level tendency and slight decline for blacks. The relative differences in these effects reveal a clearer picture of a modest increasing infant survival advantage for cohorts of African women born after 1965. However, given the flat profile of cohort effects for non-Hispanic blacks, this partially reflects an infant survival disadvantage accruing to non-Hispanic whites born cohorts.

Results from Cause-Specific Models

We now present results based on separate analyses by cause-of-death groupings. This allows us to more squarely address change in IMR for underlying causes of death that may exhibit different age-period-cohort patterns by race in response to period-level interventions and innovations. The first grouping combines congenital anomalies (CA) and respiratory distress syndrome (RDS)—the two leading causes of neonatal mortality. Each of these conditions responded to interventions and medical innovations in the form of federally mandated supplements and improvement in screening technology (CA) and FDA approval of surfactant therapy (RDS). These two causes together account for 28.2% (white 31.8%, black 19.7%) of infant deaths over the period under study.⁴ A second analysis is carried out for sudden infant death syndrome (SIDS), the leading cause of post-neonatal infant mortality, which responded to a low-tech intervention in the form of the back-to-sleep campaign. SIDS accounts for 12.8% of the infant mortality during the period under study (white 12.9%, black 11.9%). A third grouping considers short gestation/low birth weight (SG/LBW) and maternal complications (MC), leading causes for which no efficacious interventions or innovations emerged during the period under study. These causes account for 15.1% of infant deaths during the period under study (white 12.7%, black 20.6%).

Congenital Anomalies and Respiratory Distress Syndrome

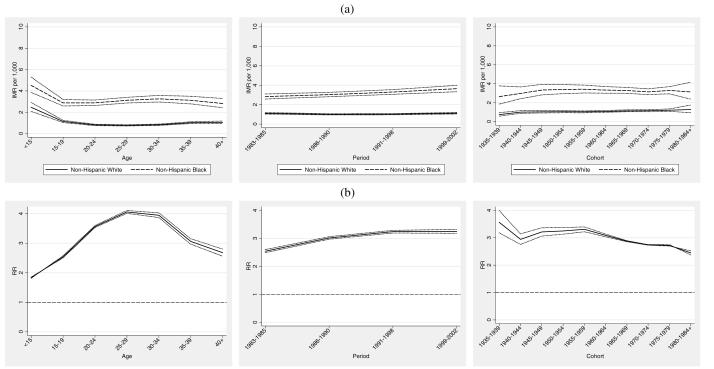
The top panel of Figure 4 (Figure 4a) shows age, period, and cohort IMRs for congenital anomalies and respiratory distress syndrome. Maternal age-specific IMRs are increasing for African American women 20 and older in contrast to the pattern for non-Hispanic whites, which remain relatively flat until age 35 and older. Panel b (Figure 4b) highlights this increasing relative disparity. Mortality due to CA/RDS declines in both populations over the time period under study. Figure 4b shows a modestly increasing relative disadvantage for blacks over time, and is consistent with past observations of increasing relative racial disparities on a variety of measures in the face of technological advances (Dowd and Aiello 2009; Frisbie et al. 2010; Frisbie et al. 2004; Powers and Song 2009; Nsiah-Jefferson 1993; Gortmaker and Wise 1997). Cohort changes are similar for both groups, but reveal a slight closing of the IMR gap for later cohorts. This is a combination of lower CA/RDS mortality among recent cohorts of African American women coupled with increasing CA/RDS IMRs for non-Hispanic whites.

Figure 4.

Infant Mortality Attributed to Congenital Anomalies (CA) and Respiratory Distress Syndrome (RDS): (a) maternal age, infant birth/death period and maternal birth cohort IMRs and 95% confidence intervals. (b) Black/white age, period, and cohort rate ratios and 95% confidence intervals.

Sudden Infant Death Syndrome

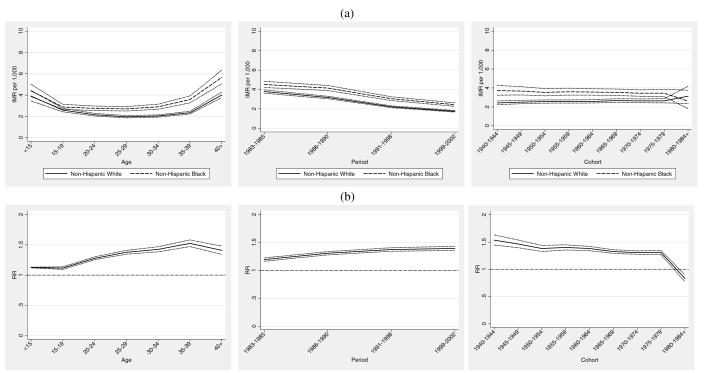
The top panel of Figure 5 (Figure 5a) shows the age, period, and cohort IMRs for SIDS. SIDS rates generally decline with maternal age for both groups. However, maternal age-specific SIDS IMR among non-Hispanic black women age 19 to 29 showed a less steep decline compared with non-Hispanic whites, reflected by the increasing relative gap over that age range shown in Figure 5b. Period trends exhibit a monotonic decrease in SIDS IMR along with a somewhat narrowing racial gap. The bottom panel of Figure 5 (Figure 5b) shows an increasing relative black-white gap in SIDS IMRs from the late 1980s onward, which is consistent with previous research (Frisbie et al. 2010; Frisbie et al. 2004; Powers and Song 2009). Cohort trends are slightly increasing, with a slight closing of the relative SIDS IMR gap for cohorts of women born after 1954.

Figure 5.

Infant Mortality Attributed to Sudden Infant Death Syndrome (SIDS): (a) maternal age, infant birth/death period, and maternal birth cohort IMRs and 95% confidence intervals. (b) black/white age, period, and cohort rate ratios and 95% confidence intervals.

Short Gestation/Low Birth Weight and Maternal Complications

The top panel of Figure 6 (Figure 6a) shows age, period, and cohort IMRs attributed to short gestation/low birth weight and maternal complications. Maternal age profiles are relatively flat after age 19, with evidence of increasing relative black disadvantage until age 29 (Figure 6b). Period IMR profiles are relatively flat for non-Hispanic whites and moderately increasing for non-Hispanic blacks, which is expected given the lack of specific technologies to reduce these underlying causes of infant mortality. Conditions related to short gestation and low birth weight are the leading causes of death among non-Hispanic blacks in the period under study. Moreover, the black infant mortality rate from maternal complications has been about two and one-half times that of whites (Mathews et al. 2002). This increasing relative disadvantage is reflected in Figure 6b. Cohort patterns are flat for non-Hispanic whites and more variable for non-Hispanic blacks. As with the other depictions of cohort change in IMR, we find a moderate decrease in relative disparities for cohorts of women born after the 1960s.

Figure 6.

Infant Mortality Attributed to Low Birth Weight/Short Gestation and Maternal Complications: (a) maternal age, infant birth/death period, and maternal birth cohort IMR and 95% confidence intervals. (b) black/white age, period, and rate ratios and 95% confidence intervals.

4. Summary

This paper applies APC modeling to disentangle maternal age, time period and maternal birth cohort effects in 17 years of cross-sectional longitudinal data on infant mortality in the U.S. based on the NCHS linked birth-infant death files from 1983 to 2002. While it is common to apply APC analysis to adult mortality where age at death, time period of death, and birth cohort are the relevant interrelated temporal dimensions, this paper is the first that we are aware of to apply an APC analytic strategy to the study of infant mortality and to the study of white-black racial disparities in infant mortality. In this case, time period is the year that infant death occurs, while in any given year this event can be experienced by different birth cohorts of U.S. women and at different points in the life course. The estimation method produces components of change in IMR over 2 decades. We find that, whereas period effects dominate change in infant mortality over this time frame, cohort effects reveal a modest closing of the absolute black-white infant mortality gap. Whereas some narrowing of the gap may be attributable to lower mortality occurring to non-Hispanic black infants whose mothers grew up in the post-civil rights era, a larger contributor to the narrowing gap appears to be the increasing infant mortality experienced by later cohorts of non-Hispanic whites. These general findings tend to be mirrored in APC analyses carried out for several leading underlying causes of infant mortality.

Our results indicate that period-related technologies are overwhelmingly shaping U.S. infant survival in today’s population. The finding that period effects outweigh cohort effects in IMR highlights the dramatic improvements in U.S. infant survival across historical time. Because our data are limited to a 20-year time frame, we may be unable to fully assess the significance of maternal birth cohort. The lack of life-saving technologies coupled with poor maternal nutrition and/or poor maternal health may have produced significant IMR variation across maternal cohorts in earlier time periods and this might have significantly and substantively affected infant survival in the past.

A more complete understanding the sources of age, period, and cohort change will require additional data beyond the 3 measures used here. In particular, a fruitful area of further research would be to compare the black-white IMR differentials by level of education, as this may reveal potentially interesting cohort differentials. In this case, separate APC model would be fit to each population within each educational stratum, yielding APC effects that are conditional on race and education. A noteworthy limitation of the foregoing analysis is the failure to control for a number of confounding factors that may alter the associations between infant mortality and maternal age, time period and cohort. While it is “statistically” straightforward to include controls in the APC specifications described above as components of the design matrix, the APC specification adopted here is less flexible than hierarchical APC models which break the linear dependency by treating period and cohort as crossed random effects at level-2 nested in age at level-1 (Yang and Land 2008). Generalized linear mixed models and Bayesian simulation (Markov-Chain-Monte-Carlo [MCMC]) methods are the widely recommended choice when fitting multivariate APC models as they allow mediation of cohort and period specific effects through the inclusion of relevant predictors in the level-2 submodels, and permit flexible specifications of fixed effects in the level-1 submodel. Finally, in addition to the substantive findings presented here, we hope to show that there are a variety of analytical methods for dealing with the singular design that is characteristic of APC analysis. The intrinsic estimator, while seemingly offering something new and improved, has roots in methodologies developed over a half century ago.

Highlights.

• We examine sources of black-white differences in change in infant mortality over time

• APC analysis helps to disentangles interrelated age, period, and cohort effects

• Period effects dominate change in specific causes of death over time

• Higher infant mortality is observed for more recent cohorts of whites

• The Intrinsic Estimator for APC effects has roots in much older methods