Abstract
A protein is a biopolymer that self-assembles through the process of protein folding. A cell is a crowded space where the surrounding macromolecules of a protein can limit the number of ways of folding. These crowding macromolecules can also affect the shape and the size of a physically malleable, or “soft, squishy”, protein with regulatory purposes. In this review, we focus on the in silico approaches of coarse-grained molecular simulations that enable the investigation of protein folding in a cell-like environment. When these simulation results were compared with experimentally measured properties of a protein, such joint effort has yielded new ideas on the specific function of a protein in cells. We also highlight the recent developments of computer modeling and simulations that encompass the importance of the shape of a macromolecule, the interactions between macromolecules, and the hydrodynamic interactions on the kinetics and thermodynamics of a protein in a high concentration of protein solution and in cytoplasmic environments.
Introduction -- Proteins are soft living matter
The concentration of a cell can reach up to 400mg/ml [1], which corresponds to a volume fraction of macromolecules of 20–40% of the total cellular volume [2]. These macromolecules exert volume exclusion [3] upon each other, which impacts the behavior of biopolymers inside a cell. This effect is the “macromolecular crowding effect” [4], which is a term coined by Minton [5]. It has been difficult to experimentally examine the protein dynamics in living species. Experimentalists have developed clever methods to mimic the macromolecular crowding effects by adding inert synthetic polymers (crowders) such as PEG, Ficoll, and dextran into a test tube [6]. Several theorists have used simple analytical calculations based on the scaled particle theory (SPT; references in reviews [7]) that model macromolecules as simple hard spheres or rods. The assumption of crowders as hard cores is an acceptable approach because experiments suggest that artificial crowders, such as Ficoll 70, can be modeled as semi-hard spheres [8]. SPT has provided the foundation of successful predictions on the thermodynamic behavior of a globular protein with high stability by assuming that the folded and unfolded states of a test protein are rigid objects in solution.
The scope of this article focuses on the polymeric behavior of a protein in a crowded medium. Starting from a pool of unstructured conformations, protein folding involves a large-scale structural fluctuation encompassing multiple orders of magnitude in both space and time. The complexity of this problem is beyond the scope of the analytical calculation such that the computer simulation must be used. Instead of the computationally demanding all-atomistic protein models, we focused on the simulations built on the coarse-grained protein models in which amino acids were represented by a few beads (reviews in [9–11]). Such a “low-resolution” polymeric model, which lacks the chemically atomistic details, can provide valuable insights into the analysis of the dominant influences on protein folding in a complex system.
We begin this review of recent in silico developments on protein structure, stability, and folding in the cell by asking several questions as the following: First, how can we extend the theories and the ideas for the understanding of protein folding in vitro (reviews in [12–14]) to protein folding in vivo? Second, how can we simulate and model a large and a physico-chemically complex system? Third, what are the prominent intracellular conditions that are not represented in dilute solution (reviews in [15])? To address these questions, the approaches that we have used are (1) to strip away the complex details of macromolecules through coarse-graining (Fig 1); (2) to collaborate with the experimentalists who can test our predictions by using different methods; and (3) to revisit the theories of protein folding and to include the necessary details wherever a prediction would fail, implying that a new algorithm or a physical model is required. It is important to understand the physical principle of how a protein folds from an unstructured conformation to a biologically meaningful one in a cell, because such knowledge will facilitate the manipulation of the specific functions of a protein through the change of its surrounding environment.
Fig 1.
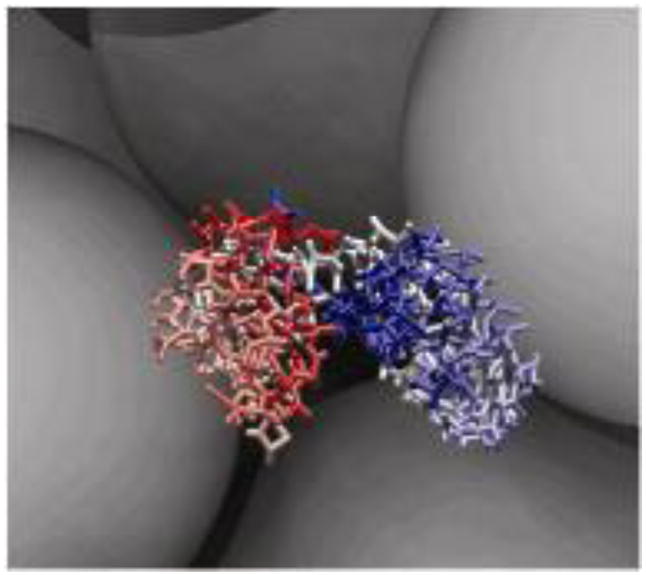
Snapshot of phosphoglycerate kinase (PGK) and hard spheres of Ficoll 70 models in coarse-grained molecular simulations.
Simplicity out of complexity
Coarse-graining is a valuable approach because it provides an efficient venue to evaluate the dominant influence on a protein due to the macromolecular crowding effect. When we addressed the impact of the volume exclusion, we modeled the crowding agents or crowders as hard cores so that they cannot spatially overlap. The density fluctuation of the hard cores generates void spaces that can accommodate a compact protein. In the presence of these hard cores, an extended protein conformation is permitted but not statistically favored. This effect is referred to as the “deplete-induced attraction” [16–19], which the stability of a compactly folded protein is relevantly enhanced (Fig 2). In contrast, under confinement an extended configuration of a protein greater than the size of the pore is not allowed. This marks the distinction between the confinement and the macromolecular crowding effect.
Fig 2.
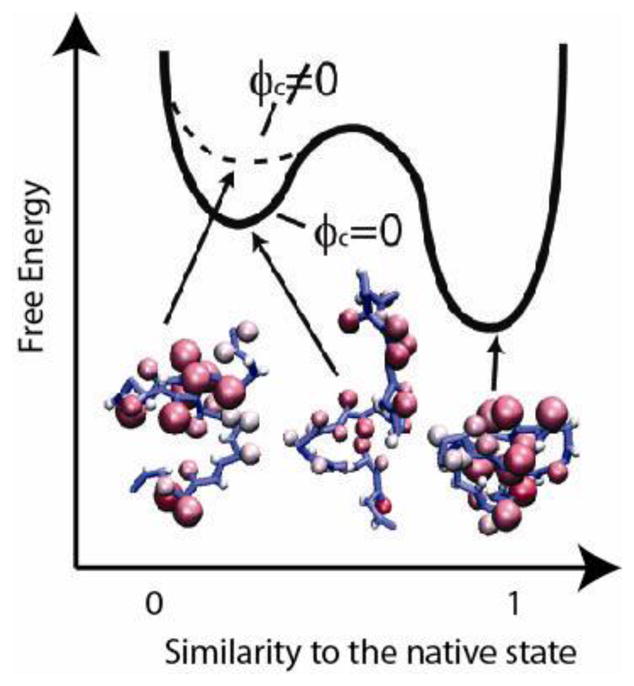
Fig 2[20]. To illustrate the macromolecular crowding effect on the folding energy landscape, we plot a schematic diagram of the free energy against an order parameter, such as the fraction of native contact formation Q. When Q is close to l, the corresponding basin represents the folded state; when Q is close to 0, the corresponding basin represents the unfolded state. Upon the addition of hard-core crowders, the ensemble of unfolded states become compact and the free energy of the unfolded states are destabilized. As a result, the folded state of a protein is relatively stabilized. This shift in free energy is entropically driven.
Coarse-grained molecular simulations
The investigation performed by Cheung, Klimov and Thirumalai was the first to employ the coarse-grained molecular simulation on protein folding in a crowded medium [20]. A structure-based protein model (or G -like model [12]) that renders a minimally frustrated folding energy landscape was used to address the folding and the unfolding of a small protein in a medium of crowders that were modeled as hard spheres. They predicted the protein folding rates to be non-monotonically enhanced by the volume fraction of crowders. In addition, their study showed a rather modest enhancement of the folding stability due to the macromolecular crowding effect than the ones previously calculated according to the SPT formalism [21]. Later Cheung employed the coarse-grained molecular simulations on several large proteins. The range of the folding stabilities obtained from simulations agrees well with the experimentally measured values [22,23].
A thorough investigation that compares the coarse-grained molecular simulations with the SPT calculation was performed by Mittal and Best [24] on the study of three two-state proteins (folded-unfolded) with high stability. When the folded and unfolded states of a protein were both modeled as hard cores, it was found that the size of the folded state of an all-β protein (Protein G) was independent on the content of crowders. However, a 20% reduction in the effective radius of a hard core for the unfolded states was required to match the calculation using Minton’s SPT [21]. Cheung and Wittung-Stafshede have investigated the folding stability of cytochrome c in crowded media by a combined in vitro and in silico approach. The change in the enhanced folding stability (ΔΔGfu) in the presence of crowders was experimentally measured by the far-UV circular dichroism (CD). The changes in the folding temperature at a range between 5 and 10 °C were quantitatively in accordance with the results obtained by the coarse-grained molecular simulation [22]. They have also compared ΔΔGfu with two prominent SPT calculations: It was found that Minton’s SPT calculation overestimates ΔΔGfu by an order of magnitude and Zhou’s SPT calculation underestimates ΔΔGfu by an order of magnitude. Such discrepancies are attributed to the insufficient modeling of the “softness” of the unfolded states. In Minton’s SPT calculation, the unfolded state of a protein was treated as impenetrable hard cores, which results in a lower stability of the unfolded states. In Zhou’s SPT calculation, the overly soft protein chains can overlap themselves and pass through the space of the crowders, leading to a greater stability of the unfolded state. To address an adequate configurational space of a protein ensemble in the presence of crowders, it is important to include the softness of a protein in a model by the consideration of the excluded volume of the polymeric chain that permits the structure of a protein to fluctuate in solution.
The energy landscape for protein folding in a cell-like environment
The configurational space of the unfolded and folded proteins can be described by an energy landscape [25] where a protein folds from a wide range of unfolded configurations on the top of the energy landscape to a few native states near the bottom of a global minimum. The folding energy landscape in a cell-like environment was explored for apoflavodoxin (an α/β protein) in the presence of Ficoll 70 by a combined approach of the far-UV CD experiment by the Wittung-Stafshede group and the coarse-grained molecular simulations by the Cheung group [23]. What was surprising is that the amount of experimentally measured helical content at a high concentration of Ficoll 70 was greater than that in aqueous solution. The computer simulation showed that more formation of native contacts appear at the loops, loose ends, and the regions between the helices and the central β sheet upon the addition of inert Ficoll crowders. The folded states of apoflavodoxin are better packed in the presence of crowders than in solution; they are structurally similar to the crystal structure.
The macromolecular crowding effect can also alter the folding routes of apoflavodoxin [26]. It is shown by the coarse-grained molecular simulations that the folding pathway of apoflavodoxin is topologically frustrated: this protein has an inherent packing problem during the course of folding. An addition of anisotropic crowders relieved the topological frustration at the early stage of folding by favorably populating the globular conformations over extended ones in the unfolded states. In a joint in silico and in vitro study, the kinetic folding experiments confirmed that the time-resolved folding pathways of apoflavodoxin were modulated by the geometry of crowders. This study suggests that the folding pathways of a protein under a heterogeneous intracellular condition may be distinct from those in a test tube.
Thermal denaturation is often used as a tool to populate the unfolded states of a protein in the computer simulations. However, the chemical denaturation is often used in experiments [27]. There is lack of a quantitative comparison of the energy landscapes acquired by the two different denaturation methods. This problem complicates the data analysis of protein folding in crowded conditions. The Cheung group has developed an in silico approach using the coarse-grained molecular simulations for the investigation of urea denaturation on protein folding [28]. The effect of urea was incorporated into an energy function derived from the all-atomistic molecular dynamics simulations through a Boltzmann inversion method. This approach allows the development of a linear relationship between the concentration of denaturants and the temperature based on thermodynamics [29]. Experiments verified the in silico predictions by testing the thermal and chemical denaturation effects on three different proteins (apoazurin, cytochrome c and apoflavodoxin). Coarse-grained molecular simulations further produced the m-value of Trp-cage and created an in silico Chevron plot in a crowded medium that can be tested experimentally [30]. Coarse-grained molecular simulation provides a framework of understanding protein-folding dynamics and the folding energy landscape in a complex environment that involves both the chemical influences and the macromolecular crowding effect.
Effect of macromolecular crowding on the conformation and the specific function of a protein
The macromolecular crowding effect has been most studied on the proteins that can fold and unfold in two states. What happens to the anisotropic proteins whose folded conformations are structurally malleable (soft) and can appear in several compact states? Instead of a single basin on the energy landscape that represents a unique “native” conformation, there could exist several shallow basins separated by a low barrier that is within the same order of magnitude as the thermal fluctuation. A shift in the populations among these basins can occur upon a slight change in the environment as demonstrated through the simulations using a simple homopolymer model [31,32].
Modeling-wise, a protein model has to go beyond a “structure-based” one that has been useful for the investigation of protein folding toward a single folded state. The Cheung group used a statistical potential for the interactions among the amino acids that allows the contact formation according to their chemical characteristics. In collaboration with several experimentalists who employed a wide range of biophysics techniques, the folding thermodynamics of a few aspherical proteins with marginal stability, such as Borrelia burgdorferi VlsE (olive-shaped) [27], calmoduin (CaM, dumbbell-shaped)[33,34], and phosphoglycerate kinase (PGK, pacman-shaped) [35], was investigated under cell-like conditions. A short summary on the study of each protein is provided in the following paragraphs. These studies have yielded surprising results on protein folding in a crowded environment that are not found in dilute condition, which rendered indication on the specific function of a protein in cells.
Borrelia burgdorferi VlsE
The macromolecular crowding effect impacts the folding and the overall shape of the compacted folded states of VlsE [27]. In a crowded milieu, distinct conformations vary from an olive-shape, a bent, to a collapsed-spherical form, which are accompanied by the alteration of secondary structures that lead to the exposure of its hidden antigenic region.
CaM
The macromolecular crowding effect stabilizes several compactly folded conformations of CaM varying from a dumbbell-like shape to a globular one, which reflects its inherent plasticity in the structures [33]. A multiscale solution of charges was further developed to represent the charge distribution on CaM in the transition from apoCaM to holoCaM upon the calcium binding in a coarse-grained representation [34]. Increased levels of macromolecular crowding, in addition to calcium binding and ionic strength, can impact the conformation and the secondary structure of CaM, which may provide unique insight into understanding the promiscuous behavior of CaM in target binding and selection inside cells.
PGK
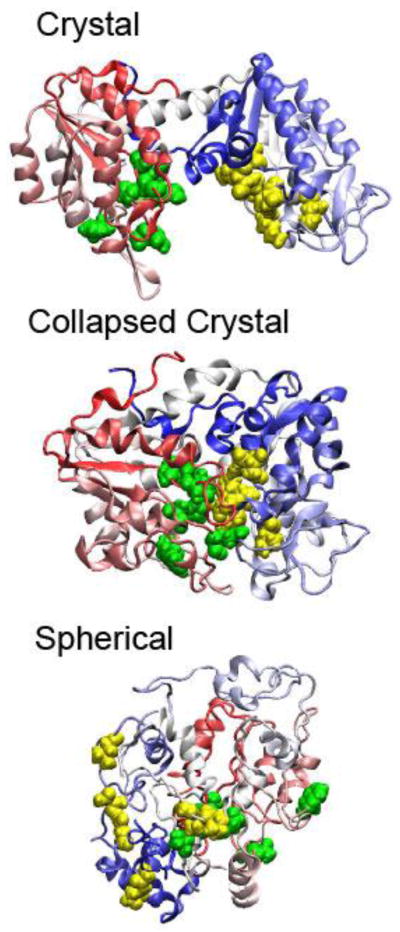
Experiments suggested that the appearance of several PGK conformations along the concentrations of Ficoll 70 is distinct from those in dilute solution [35]. The experimentally measured enzymatic activity of PGK is approximately 15-fold or greater in Ficoll 70 solution than in dilute solution. Coarse-grained molecular simulations suggested three possible compactly folded conformations of PGK in Fig 3. It was found by the in silico studies that the binding sites at the inner parts of two domains of PGK are already located in proximity in the compact forms of PGK under crowded conditions. Such a new finding obtained by a joint in silico and in vitro approach opposes a prior hypothesis that the enzymatic activity of PGK relies on a hinge motion that brings the two domains together.
Fig 3.
Several dominant compactly folded structures of PGK in cartoon representation. (A) Crystal state, (B) collapsed crystal state, and (C) spherical state. The Mg-ATP and 3PG binding sites are colored in yellow and green.
Beyond artificial crowding agents
Several in vivo experiments observed a lower protein stability inside cells [36–38], which disagrees with other in vitro and in silico studies that assumed the dominance of the macromolecular crowding effect in a crowded environment. It implies that the inert artificial crowders are poor approximations to the protein crowders because the former lack the chemical details necessary for a correct description of macromolecular interactions in cells. Secondly, these artificial crowders are not adequate to represent the macromolecules in a poly-dispersive environment of a cell because their sizes are often much larger than the size of an average protein[22]. Therefore, there is a need to develop an in silico framework for the investigation of the impact of the intracellular environment on the macromolecular dynamics.
In the past two years, there has been a rapid growth in the modeling of the macromolecular dynamics in an intracellular environment. The Elcock group [39] created an atomistically detailed model of an E. coli cytoplasmic model that includes 50 of the most abundant types of macromolecules at experimentally measured concentrations. Although these macromolecules are rigid objects in the model, they parameterized the energy functions between the macromolecules (including electrostatic and van der Waals interactions) by matching the translational diffusion coefficients of a green fluorescence protein (GFP) in a cytoplasmic model with the experimentally measured values inside bacteria. Their simulations showed accordance with the experimentally measured folding stability of protein λ6–85 and CRABP in the cytoplasm of E.coli. The Skolnick group[40] included the hydrodynamic interactions (HI) into the simulations of diffusivity of a GFP in an E. coli cytoplasmic model that consists of 15 different types of most abundant macromolecules. They have shown that hydrodynamic interactions, together with the excluded volume effect, can account for a ~10-fold reduction in the GFP’s translational diffusion coefficient without the need of non-specific interactions. The Wade group [41] has further pointed out that the weak protein-protein interactions, the shape of a protein, and the rotational and translational hydrodynamic interactions at a high concentration of protein solution can affect the rotational diffusion coefficient.
The number of atoms limits the capacity of the all-atomistic molecular dynamics simulation. The approach of coarse-grained molecular simulations is valuable because a low-resolution model offers a comprehensive understanding of the complex system, which provides a qualitative insight into problem solving. The Feig group used a mixed coarse-grained/all-atom model to create a protein solution with a box of 8 Protein G’s [42]. Their peptide of interest is represented in an atomistic detail while Protein G’s are represented by coarse-grained models. A Generalized Born (GB)-type implicit solvent is used to facilitate the dielectric investigation of the cellular content. They used this system as an example to show the significance of the enthalpic interactions (the van der Waals and the electrostatic interactions), which dominates over the volume exclusion in a protein milieu. The Cheung group studied the folding of apoazurin in a coarse-grained E coli cytoplasmic model. They developed a self-assembled clustering algorithm (CGCYTO) [43] that uses the size of a test protein as a criterion (particle insertion method) to coarse-grain the macromolecules of an E. coli cytoplasm. The macromolecules represented by a few beads not only retain the geometry of a macromolecule, but also capture over 90 percent of the excluded volume effect relative to an all-atomistic model. It was computationally shown that the folding temperature of protein apoazurin in a polydisperse cytoplasmic model is higher than that of apoazurin in solution of monodisperse Ficoll 70 by approximately 5 degrees, indicating that the excluded volume effect due to macromolecules inside cells may not genuinely captured by inert artificial crowders.
Conclusion
We attempt to treat a protein-folding problem inside cells through the approach of coarse-graining from a physicist’s perspective. The coarse-grained molecular simulations are able to reveal the interesting behavior of a protein in a complex system, particularly due to the physical softness of a fluctuating polymer. Together with experiments, it is possible to explore the connection between the protein conformations and their specific functions in a cellular content. One of the next challenges is to develop a comprehensive intracellular model that reflects the functional states of a cell for the investigation and prediction of protein folding in vivo. Coarse-grained molecular simulations can be useful for studying protein folding inside cells on other aspects involving post-translational modification [44], chaperone-assisted folding (reviews in [45]) and co-translational folding [46], which are beyond the length of this review. I apologize to any author whose work is not individually cited.
Highlights.
Coarse-grained molecular simulations are used to investigate proteins under cell-like conditions.
Macromolecular crowding effects can impact protein folding under cell-like conditions.
Malleable proteins can sample several compact conformations driven by crowding effects.
The function of a protein inside a cell may not be represented as that in a test tube.
Modeling of cytosolic solution can be the next challenge.
Acknowledgments
MSC thanks Drs. Qian Wang, Antonios Samiotakis, and Dirar Homouz for their comments on the manuscript and grants from the National Science Foundation (MCB 0919974) and the National Institutes of Health (1R01GM097553) for the support.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Zimmerman SB, Trach SO. Estimation of macromolecular concentrations and excluded volume effects for the cytoplasm of escherichia coli. J Mol Biol. 1991;222:599–620. doi: 10.1016/0022-2836(91)90499-v. [DOI] [PubMed] [Google Scholar]
- 2.Ellis RJ, Minton AP. Cell biology: Join the crowd. Nature. 2003;425(6953):27–28. doi: 10.1038/425027a. [DOI] [PubMed] [Google Scholar]
- 3.Laurent TC, Ogston AG. The interaction between polysaccharides and other macromolecules. 4. The osmotic pressure of mixtures of serum albumin and hyaluronic acid. Biochem J. 1963;89:249–253. doi: 10.1042/bj0890249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ellis RJ. Macromolecular crowding: An important but neglected aspect of the intracellular environment. Curr Opin Struct Biol. 2001;11:114–119. doi: 10.1016/s0959-440x(00)00172-x. [DOI] [PubMed] [Google Scholar]
- 5.Minton A. Excluded volume as a determinant of macromolecular structure and reactivity. Biopolymers. 1981;20:2093–2120. [Google Scholar]
- 6.Zimmerman SB, Minton AP. Macromolecular crowding: Biochemical, biophysical, and physiological consequences. Annu Rev Biophys Biomol Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 7.Zhou HX, Rivas G, Minton AP. Macromolecular crowding and confinement: Biochemical, biophysical and potential physiological consequences. Annual Review of Biophysics. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Venturoli D, Rippe B. Ficoll and dextran vs. Globular proteins as probes for testing glomerular permselectivity: Effects of molecular size, shape, charge, and deformability. Am J Physiol Renal Physiol. 2005;288:F605–F613. doi: 10.1152/ajprenal.00171.2004. [DOI] [PubMed] [Google Scholar]
- 9.Cheung MS, Chavez LL, Onuchic JN. The energy landscape for protein folding and possible connections to function. Polymer. 2004;45:547–555. [Google Scholar]
- 10.Hyeon C, Thirumalai D. Capturing the essense of folding and function of biomolecules using coarse-grained models. Nature Communications. 2011;2:1–11. doi: 10.1038/ncomms1481. [DOI] [PubMed] [Google Scholar]
- 11.Tozzini V. Coarse-grained models for proteins. Curr Opin Struct Biol. 2005;15:144–150. doi: 10.1016/j.sbi.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 12.Onuchic JN, Wolynes PG. Theory of protein folding. Curr Opin Struct Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 13.Shea JE, Brooks CL., 3rd From folding theories to folding proteins: A review and assessment of simulation studies of protein folding and unfolding. Annu Rev Phys Chem. 2001;52:499–535. doi: 10.1146/annurev.physchem.52.1.499. [DOI] [PubMed] [Google Scholar]
- 14.Dill KA. Polymer principles and protein folding. Protein Sci. 1999;8:1166–1180. doi: 10.1110/ps.8.6.1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gershenson A, Gierasch LM. Protein folding in the cell: Challenges and progress. Curr Opin Struct Biol. 2011;21(1):32–41. doi: 10.1016/j.sbi.2010.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Asakura S, Oosawa F. Interaction between particles suspended in solutions of macromolecules. J Polymer Science. 1958;33:183–192. [Google Scholar]
- 17.Asakura S, Oosawa F. On interaction between two bodies immersed in a solution of macromolecules. J Chem Phys. 1954;22:1255–1256. [Google Scholar]
- 18.Shaw MR, Thirumalai D. Free polymer in a colloidal solution. Physical Review A. 1991;44:R4797–R4800. doi: 10.1103/physreva.44.r4797. [DOI] [PubMed] [Google Scholar]
- 19.Vrij A. Polymers at interfaces and the interactions in colloidal dispersions. Pure Appl Chem. 1976;48:471–483. [Google Scholar]
- 20.Cheung MS, Klimov D, Thirumalai D. Molecular crowding enhances native state stability and refolding rates. Proc Natl Acad Sci U S A. 2005;102:4753–4758. doi: 10.1073/pnas.0409630102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Minton AP. Models for excluded volume interaction between an unfolded protein and rigid macromolecular cosolutes: Macromolecular crowding and protein stability revisited. Biophys J. 2005;88:971–985. doi: 10.1529/biophysj.104.050351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- •22.Christiansen A, Wang Q, Samiotakis A, Cheung MS, Wittung-Stafshede P. Factors defining effects of macromolecular crowding on protein stability: An in vitro/in silico case study using cytochrome c. Biochemistry. 2010;49:6519–6530. doi: 10.1021/bi100578x. Using a combined approach of the far UV-circular dichroism experiment and the coarse-grained molecular simulations, the authors demonstrated the range of enhanced stability of cytochrome c in solution of inert crowders. The authors compared them with the calculations using different flavors of the scaled particle theory. They concluded that the modeling of softness of the unfolded states is necessary for the correct description of protein folding in crowded solution. [DOI] [PubMed] [Google Scholar]
- 23.Stagg L, Zhang S-Q, Cheung MS, Wittung-Stafshede P. Molecular crowding enhances native structure and stability of alpha/beta protein flavodoxin. Proc Natl Acad Sci U S A. 2007;104:18976–18981. doi: 10.1073/pnas.0705127104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mittal J, Best RB. Dependence of protein folding stability and dynamics on the density and composition of macromolecular crowders. Biophys J. 2010;98:315–320. doi: 10.1016/j.bpj.2009.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Onuchic JN, LutheySchulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 26.Homouz D, Stagg L, Wittung-Stafshede P, Cheung MS. Macromolecular crowding modulates folding mechanism of α/β protein apoflavodoxin. Biophys J. 2009;96:671–680. doi: 10.1016/j.bpj.2008.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Homouz D, Perham M, Samiotakis A, Cheung MS, Wittung-Stafshede P. Crowded, cell-like environment induces shape changes in aspherical protein. Proc Natl Acad Sci U S A. 2008;105:11754–11759. doi: 10.1073/pnas.0803672105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Samiotakis A, Homouz D, Cheung MS. Multiscale investigation of chemical interference in proteins. J Chem Phys. 2010;132:175101. doi: 10.1063/1.3404401. [DOI] [PubMed] [Google Scholar]
- 29.Wang Q, Christiansen A, Samiotakis A, Wittung-Stafshede P, Cheung MS. Part ii. Comparison of chemical and thermal protein denaturation by combination of computational and experimental approaches. J Chem Phys. 2011;135:175102. doi: 10.1063/1.3656692. [DOI] [PubMed] [Google Scholar]
- 30.Samiotakis A, Cheung MS. Part i. Folding dynamics of trp-cage in the presence of chemical interference and macromolecular crowding. J Chem Phys. 2011;135:175101. doi: 10.1063/1.3656691. [DOI] [PubMed] [Google Scholar]
- 31.Kudlay A, Cheung MS, Thirumalai D. Crowding effects on the structural transitions in a flexible helical homopolymer. Phys Rev Lett. 2009;102:118101. doi: 10.1103/PhysRevLett.102.118101. [DOI] [PubMed] [Google Scholar]
- 32.Kudlay A, Cheung MS, Thirumalai D. Influence of the shape of crowding particles on the structural transitions in a polymer. J Phys Chem B. 2012;116:8513–8522. doi: 10.1021/jp212535n. [DOI] [PubMed] [Google Scholar]
- 33.Homouz D, Sanabria H, Waxham MN, Cheung MS. Modulation of calmodulin plasticity by the effect of macromolecular crowding. J Mol Biol. 2009;391:933–943. doi: 10.1016/j.jmb.2009.06.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang Q, Liang KC, Czader A, Waxham MN, Cheung MS. The effect of macromolecular crowding, ionic strength and calcium binding on calmodulin dynamics. Plos Computational Biology. 2011;7(7) doi: 10.1371/journal.pcbi.1002114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ••35.Dhar A, Samiotakis A, Ebbinghaus S, Nienhaus L, Homouz D, Gruebele M, Cheung MS. Structure, function and folding of phosphoglycerate kinase are strongly perturbed by macromolecular crowding. Proceedings of the National Academy of Sciences U S A. 2010;107:17586–17591. doi: 10.1073/pnas.1006760107. Using the temperature-jump laser experiment and the coarse-grained molecular simulations, the authors probed the structural distribution of the phosphoglycerate kinase in crowded solution that are different from that in dilute solution. This is the first study that showed an increase of enzymatic activity enhanced by the macromolecular crowding effect. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ghaemmaghami S, Oas TG. Quantitative protein stability measurement in vivo. Nature Structural Biology. 2001;8(10):879–882. doi: 10.1038/nsb1001-879. [DOI] [PubMed] [Google Scholar]
- 37.Schlesinger AP, Wang YQ, Tadeo X, Millet O, Pielak GJ. Macromolecular crowding fails to folding a globular protein in cells. JACS. 2011;133:8082–8085. doi: 10.1021/ja201206t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ignatova Z, Krishnan B, Bombardier JP, Marcelino AMC, Hong J, Gierasch M. From the test tube to the cell: Exploring the folding and aggregation of a beta-clam protein. Biopolymers. 2007;88:157–163. doi: 10.1002/bip.20665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ••39.McGuffee SR, Elcock AH. Diffusion, crowding and protein stability in dynamic molecular model of bacterial cytoplasm. PloS Comput Biol. 2010;6:e1000694. doi: 10.1371/journal.pcbi.1000694. The authors generated an atomistic cytoplasmic model using the top 50 most abundant macromolecules in the E. coli bacteria. They simulated the diffusion of a green fluorescent protein by assuming that the macromolecules in the cytoplasmic model are rigid-body and their interactions are beyond the steric effect. The authors showed the attraction between macromolecules are sufficient to reproduce the folding stability of several test proteins in cells. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ••40.Ando T, Skolnick J. Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc Natl Acad Sci USA. 2010;107:18457–18462. doi: 10.1073/pnas.1011354107. The authors included the hydrodynamic interactions into the intramolecular dynamics and examined its impact and several other dominant factors that contributed to the reduction of diffusion coefficient of a protein in a cytoplasmic model. The authors concluded that without the nonspecific attraction between macromolecules, the use of the hydrodynamic interaction and the macromolecular crowding effect is sufficient to account for the 10-fold reduction of the diffusion coefficient of a protein inside a cell. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mereghetti P, Wade RC. Atomic detail brownian dynamics simulations of concentrated protein solutions with a mean field treatment of hydrodynamic interactions. J Phys Chem B. 2012;116:8523–8533. doi: 10.1021/jp212532h. [DOI] [PubMed] [Google Scholar]
- •42.Predeus AV, Gul S, Gopal SM, Feig M. Conformational sampling of peptides in the presence of protein crowders from aa/cg-multiscale simulations. J Phys Chem B. 2012;116:8610–8620. doi: 10.1021/jp300129u. The authors used a mixed scaled of protein models to investigate the conformations of a peptide in solution with varying dielectric constants and in protein solution. They suggested that the dielectric properties of solution is one of the important factors, that opposes the macromolecular crowding effect, influencing on protein folding in the cell. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wang Q, Cheung MS. A physics-based approach of coarse-graining the cytoplasm of E. Coli (cgcyto) Biophys J. 2012;102:2353–2361. doi: 10.1016/j.bpj.2012.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shental-Bechor D, Levy Y. Communication: Folding of glycosylated proteins under confinement. J Chem Phys. 2011;135:141104. doi: 10.1063/1.3650700. [DOI] [PubMed] [Google Scholar]
- 45.Jewett AI, Shea J-E. Reconciling theories of chaperonin accelerated folding with experimental evidence. Cell Mol Life Sci. 2010;67:255–276. doi: 10.1007/s00018-009-0164-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.O’Brien EP, Christodoulou J, Vendruscolo M, Dobson CM. Trigger factor slows co-translational folding through kinetic trapping while sterically protecting the nascent chain from aberrant cytosolic interactions. J Am Chem Soc. 2012;134:10920–10932. doi: 10.1021/ja302305u. [DOI] [PubMed] [Google Scholar]