Compositional sorting dynamics in coexisting lipid bilayer phases with variations in underlying e-beam formed curvature pattern

Abstract

Nanometer-scale curvature patterns of an underlying substrate are imposed on lipid multibilayers with each pattern imparting distinctly different sorting dynamics to a metastable pixilation pattern of coexisting liquid ordered (L_o) – liquid disordered (L_d) lipid phases. Therefore, this work provides pathways toward mechanical energy-based separations for analysis of biomembrane-associate species. The central design concept of the patterned sections of the silica substrate is a square lattice pattern of 100 nm projected radius poly(methyl methacrylate) (PMMA) hemispherical features formed by electron beam lithography which pixelates the coexisting phases in order to balance membrane bending and line energy. In one variation, we surround this pattern with three PMMA walls/fences 100 nm in height which substantially slows the loss of the high line energy pixelated L_o phase by altering the balance of two competing mechanism (Ostwald ripening vs. vesiculation). In another walled variation, we form a gradient of the spacing of the 100 nm features which forces partitioning of the L_o phase toward the end of the gradient with the most open (400 nm spacing) lattice pattern where a single vesicle could grow from the L_o phase. We show that two other variations distinctly impact the dynamics, demonstrating locally slowed loss of the high line energy pixelated L_o phase and spontaneous switching of the pixel location on the unit cell, respectively. Moreover, we show that the pixilation patterns can be regenerated and sharpened by a heating and cooling cycle. We argue that localized variations in the underlying curvature pattern have rather complex consequences because of the coupling and/or competition of dynamic processes to optimize mechanical energy such as lipid diffusion, vesiculation and growth, and phase/compositional partitioning.

Introduction

Cells appear to be able to sort lipids to the membranes of various organelles by including mechanisms that do not involve specific lipid transport proteins.^1,2,3 Membrane curvature variation has been implied as an important mechanism involved in lipid and protein sorting with curvature generated by different classes of curvature-generating proteins. ^2,4,5 This sorting mechanism takes advantage of the compositional coupling of the membrane bending modulus and/or intrinsic curvature that control curvature partioning.⁴ Cells also appear to be capable of aggregating certain proteins and lipids together in their membranes, for example to form signalling complexes involved in signal transduction.^6,7 This process has brought attention to the mechanistic importance of line tension at the boundary of a membrane heterogeneity in controlling its dynamics.^8,9,10,11 The interfacial nature of these processes presents a great opportunity for chip-based separations of biomembrane species driven solely by differences in mechanical energy followed by analysis of the separated species.

Curvature-based sorting of coexisting lipid bilayer phases of differing compositions has been studied using substrate imposed curvature, i.e. periodic channels, ridges, and surface wrinkles.^12,13,14,15 Sorting patterns of these systems were dominated by the bending energy difference of the lipid phases and line tension did not play a major role because the imposed pattern periodicity was similar to the scale of phase separated domains on a completely flat substrate, i.e. micrometer-scale. More recently, curvature thresholds were demonstrated for curvature sensing proteins using membrane-coated channel patterns created by photolithography.¹⁶ The influence of line tension in kinetics and size of lipid domains in coexisting phases has been demonstrated using supported and unsupported systems.^10,11,17,18 Additionally, line tension between two phases plays an important role in 3-dimensional transformations such as the spontaneous formation of curvature in phase-separated domains to reduce line energy.^8,9

We demonstrated recently that both bending energy and line energy play an important role in the sorting pattern of coexisting lipid phases when the imposed periodicity of the curvature features is in the sub-micrometer scale, i.e. less than the scale of phase separation. We imposed curvature on the membranes using an underlying substrate containing a square lattice pattern of hemispherical features, “bumps”, formed by standard e-beam lithography of a poly(methyl methacrylate) (PMMA) layer on silica.¹⁹ We showed that the high-bending modulus L_o phase formed the fundamental units (or “pixels”) of the pattern by being confined to and centred on the flat region between the unit cell of 4 bumps and that the “domain pixels” connect up to form linear and rectangular 2 dimensional shapes surrounded by the lower bending modulus L_d phase. Moreover, these domain pixilation patterns are metastable, presumably because of the substantial line energy generated at the large and curved L_o-L_d phase interface of the pixilation pattern, resulting in separation of the L_o phase from the patterned regions.

Here we demonstrate that the sorting/separation dynamics of this mechanical energy-based metastability can be controlled by implementing some simple variations to this underlying curvature pattern. We include PMMA walls/fences to surround the lattice that substantially slow the kinetics by changing the mechanism that the system uses to reduce the L_o area fraction on the curvature patterned regions of these substrates. We create a gradient in lattice spacing that results in directional partitioning of each phase, and their corresponding compositions, and we demonstrate the possibility to use this substrate to localize the growth of giant vesicles of a single phase. We demonstrate that although these pixilation patterns are metastable, they can be regenerated/refreshed by a short heating and cooling cycle that sharpens the definition of the patterns. In addition, we demonstrate two other variations on the underlying lattice pattern that change the sorting dynamics of the pixilation pattern. These results provide multiple new strategies for guiding the separation and dynamics of biomembrane-associated species using curvature patterned substrates.

Experimental

Materials

1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), cholesterol and 1-palmitoyl-2-(6-((7-nitro-2-3,1-benzoaxidazol-4-yl)amino) hexanoyl)-sn-glycero-3-phosphocholine (NBD-PC) were purchased in chloroform (10 mg/ml) from Avanti Polar Lipids, Inc. Milli-Q water (18 MΩ cm) was used for all the steps involving water. The hexane (ACS reagent ≥= 98.5%) and the methanol (HPLC grade) used in the lipid spin coating solvent mixture, were purchased from Sigma-Aldrich Inc. and Fisher Scientific, respectively. The silicon wafers used for the production of the 1cm × 1cm substrates were purchased from Silicon Valley Group (San Jose CA) and the poly(methyl methacrylate) (PMMA) 950k 2% dissolved in Anisole from MicroChem (Newton MA).

Preparation of the Substrates

Substrates were produced in the Northern California Nanotechnology Center, University of California, Davis. A stock solution of PMMA 950k 2% dissolved in Anisole was spin coated onto pre-cleaned 4-inch silicon wafers in a Silicon Valley Group (SVG, San Jose CA) 8100 spin coater at 3,000 rpm for 45 s and then proximity baked 1cm above a hotplate at 190 °C for 5 mins. 2 nm uniformity was recorded at 5 points around the wafer using a NanoSpec 210 film thickness measurement tool and Veeco Dektak 3030 Profilometer to verify reaching the target PMMA thickness of 100 nm. Then individual 1 cm² sections were subjected to electron beam writing in an FEI 430 NanoSEM (FEI, Hillsboro, OR) equipped with a Nabity Pattern Generating System (NPGS v.9.0) and high speed beam blanker. Since PMMA is a positive electron beam resist, the bumps, which were patterned in a squared lattice arrangement, were formed by the removal of the PMMA from the silicon wafer. The patterned chips were immersed in 1:3 methyl isobutyl ketone:isopropyl alcohol (MIBK:IPA) developer solution for 90 seconds.²⁰ The final inspection of the samples was performed in a FEI 430 NanoSEM. Scanning electron microscope (SEM) images were used to determine the projected radius and lattice spacing of the patterned bumps. Atomic force microscopy (AFM) (Veeco Metrology, Inc., Santa Barbara, CA) using contact mode imaging was used to confirm that the bumps were of hemispherical shape.

Preparation of the supported lipid multibilayers

The lipid mixture used for this study was (6:4, mol:mol) DPPC: DOPC and 20 mol % cholesterol. In order to use fluorescence microscopy, NBD-PC (2 mol %) was added to the mixture. The lipids were mixed in a 1 mL conical vial and dried with nitrogen. The dried lipid film was combined with a spin coating solvent, 97:3 (v/v) hexane/methanol, in order to completely dissolve the lipids. The volume of the solvent was the amount necessary to have a 5mM solution of lipids. 30 μl of this solution was dispersed onto the 1cm × 1cm substrate which was place on a spin coater (Chemat Technology, Inc., Northridge, CA) set for 3000 rpm for 40 s. After spin coating, each sample was placed under mild vacuum (while in the dark) for 24 hr in order to evaporate the solvents. The lipid multibilayer of each sample was hydrated (while in the dark) by immersing each sample in a 70°C buffer bath (10mM Tris-HCl, 150 mM NaCl and 2mM CaCl₂-H2O at pH 7.4) for 30 minutes. Once each sample reached room temperature (22°C ± 1°C) it was imaged with a 60x water immersion lens on a Nikon TE400 fluorescence microscope, using a FITC filter set (Chroma Technology. Bellows Falls, VT). Further sample cooling was achieved using a Bionomic Controller, 20/20 Technology, Inc., Wilminton, NC. The software used for image analysis was ImageJ/Micromanager (National Institutes of Health).

Results and Discussion

Electron beam lithography of 100 nm thickness PMMA-coated silicon wafers was used to form curvature patterns that included hemispherical PMMA features, “bumps”, projecting from a flat silica surface in the form of a square lattice pattern. The projected radius of each bump was approximately 100 nm as measured by SEM. The out-of-plane curvature of each bump was 9.7±0.8 μm⁻¹ as measured previously by atomic force microscopy.¹⁹ This is well above the curvature threshold range necessary for sorting the stiffer L_o phase lipid from softer L_d phase lipid.12 Note that each pattern was imprinted multiple times into a PMMA-coated silicon wafer (Fig. S1) allowing for statistical analysis. A multibilayer of (6:4, mol:mol) DPPC: DOPC and 20 mol % cholesterol, doped with 2% of a fluorescent dye - NBD PC, was spin-coated onto each curvature patterned substrate, hydrated at 70 ± 1 °C, and cooled to 22 ± 1 °C. Phase separation resulted in the formation of pixilation patterns of coexisting dark L_o and bright L_d phases visualized by fluorescence microscopy (see Fig. 1a), as shown in our previous work.¹⁹ Typically we spin coat 2 to 3 bilayers and the distal 1 or 2 bilayers display microscopically visible L_o phase, giving potentially two shades of grey for overlapped and non-overlapped domains.^13,19

Fig. 1.

a) Pixilation pattern of coexisting dark Lo and bright Ld phase lipid multibilayers supported by a square lattice pattern of PMMA features (bumps) on silica surrounded by 3 PMMA walls; imaging by fluorescence microscopy. b) SEM image demonstrating that the underlying square lattice of bumps has a spacing of 200 nm and the 3 walls/fences (arrows) are 180 nm in thickness spaced 250 nm apart as produced by e-beam lithography. c) Alignment and elongation of dark Lo phase domains (e.g. arrow), supported by this wall pattern, along the long axis of the walls.

Walls slow dissolution of the pixilation pattern

In the first curvature pattern, we included three PMMA walls/fences of 100 nm in height and 180 nm in thickness surrounding each square 50 μm × 50 μm lattice of bumps. The spacing between the walls was 250 nm and the square lattice spacing between the bumps was approximately 200 nm as shown by the SEM images in Fig. 1b and Fig. S2. There was noticeable alignment and elongation of dark L_o phase domains, supported by this wall pattern, along the long axis of the walls as shown in Fig. 1 (a and c, arrow). It is very possible that domains also exist on the flat sides of these walls. However we could not image them because the microscope is situated above the sample. Similar alignment of L_o domains had been observed by Parthasarathy et al. in phase separated lipid bilayers supported by a larger-scale repetitive pattern of aligned channels approximately 1 micrometer in width.¹² In comparison, elongation of the L_o domains is more pronounced here because, given similar domain growth conditions, the width of the walls and their spacing is nearly an order of magnitude smaller (~100 nm), forcing domains to grow in the direction of the long axis of the walls.

The area fraction of the dark L_o phase of the pixilation pattern viewed initially is noticeably high and nearly the same as that in multibilayers supported by the flat PMMA outside of the pattern, 0.59 ± 0.01 and 0.64 ± 0.01 respectively. The similarity in the flat and unpatterned L_o phase area fractions indicates that we attained a relatively homogenous spin coated layer across the entire substrate, i.e. both patterned and unpatterend regions. At such a high area fraction, it is primarily the bright L_d phase, rather than dark L_o phase that is isolated and forms pixelated elongated and rectangular shapes as shown in Fig. 1a. In comparison, without walls, we showed in previous work that the initial L_o area fraction supported by the same curvature lattice was significantly less, 0.43 ± 0.01.¹⁹

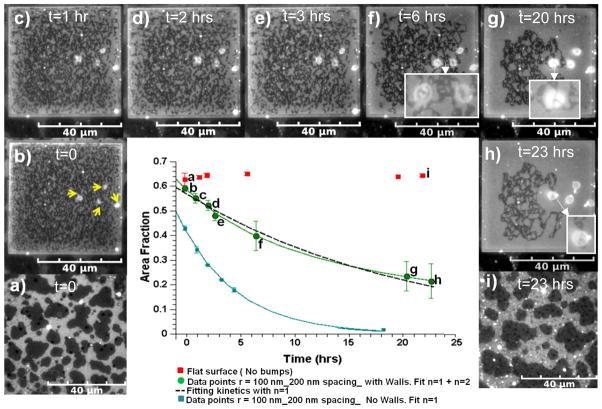
The area fraction of the dark L_o phase supported by the lattice pattern decreased to about half of the initial observation value over a period of 23 hrs as can be observed by fluorescence microscopy in Fig. 2 (b–h). Measurements of these area fractions averaged from 5 patterned regions are plotted in the centre of Fig. 2 (green circles) and show that area fraction decreased more rapidly in the first few hours and appeared to be heading toward a plateau at 23 hrs. By comparison, in previous work without walls, we observed that the area fraction of the L_o phase decreased in 18 hrs to approximately 5% of the initial observation value.²¹ This previous data is replotted for comparison in the centre of Fig. 2 (blue squares). The area fraction of L_o phase on unpatterned PMMA remains constant over 23 hours as shown in Fig. 2a, Fig. 2i, and the centre plot (red squares) of Fig. 2.

Fig. 2.

Fluorescence microscopy images showing that the area fraction of the dark Lo phase supported by the walled 200 nm lattice pattern decreased over time in comparison to the Lo phase on the unpatterned sections of PMMA. a and i) Lo-Ld coexisting phases on unpatterned PMMA at t = 0 and t = 23 hrs respectively. b–h) Vesicles (yellow arrows) grow accompanying the loss of Lo phase area fraction supported by walled lattice pattern. Insets in f–h show 5 that the vesicles are transparent to the underlying pixilation pattern. The centre graph shows the area fraction vs. time data (green circles) fit to equation (1) by the green line, and a first order fit (dAf/dt = −kAf) by the dashed line. The blue data points correspond to area fraction vs. time data for the same underlying lattice pattern without walls and a first order fit, blue line, from our previous work²¹ reproduced by permission of The Royal Society of Chemistry (RSC)

There were less than 10, and at least two, large vesicles growing from the pixelation pattern to reach approximately 10 microns each in diameter as demonstrated by Fig. 2 (b - arrows and h). The L_o area fraction noticeably decreased more rapidly in the vicinity of the vesicles as demonstrated in Fig. 2 (f–h) where the L_o area fraction is noticeably lower on the right side of the image containing growing vesicles. The vesicles were entirely transparent as evidenced by the observation of the underlying pixilation pattern superimposed on vesicles that were large enough to have a viewing area through their centers (see Fig. 2 (f–h insets)). This is evidence that they are of a single phase. In addition the total surface area of the growing spherical vesicles is, on average, large enough to account for approximately half of the decrease in L_o area fraction of a pixilation pattern, assuming the vesicles are unilamellar. In comparison, without walls, we observed in previous work no vesicle growth for this lattice pattern.²¹ Therefore, the walls have caused a significant shift in the kinetics and the mechanism of the decrease in L_o phase area fraction in the lattice patterned regions.

We showed in previous work,²¹ that the L_o area fraction (A_f) loss could be fit by a kinetic equation of the type, dA_f/dt =-kA_fn, where n describes the order of the kinetics. The uptake of pixelated L_o domain lipids into vesicles was best fit by cooperative second order kinetics, dA_f/dt =-kA_f2. However, if the area fraction loss was not accompanied by vesicle formation, it was best fit with first order kinetics, dA_f/dt =-kA_f, associated with diffusion-limited (Ostwald ripening) migration of L_o phase lipids to the surrounding flat multibilayers.21 Here, when walls surround the underlying lattice pattern, we visibly observed vesicles growing from the pixelated multibilayer, but they do not completely account for the total loss in L_o phase area. Therefore, we assume that both second- and first- order processes are taking place by fitting the A_f vs. time data shown in the graph in Fig. 2 with equation (1) that takes into account both processes,

$$\frac{{dA}_f}{dt}=-k_1{A}_f-k_2{A_f}^2,$$ (1)

where k₁ and k₂ are the kinetic rate constants. The experimental data in the centre of Fig. 2 was regressed using the method of least squares, where the residual error between the experimental data and the objective function, the integral form of equation (1), was minimized. We determined that the best fit (green line) is primarily second-order based on the relative magnitude of k₂ to k₁, k₂=0.12 ± 0.02 h⁻¹ and k_{1 =}0.0032 ± 0.0082 h⁻¹. However, because A_f vs. t is a weakly decaying function for the walled pattern, a purely first-order best fit (k₁ is 0.0475 ± 0.003) is also within the error bars as shown by the dashed line in the centre of Fig. 2. In comparison, without walls, a first order fit to our previously obtained data (blue line) gave a k₁ of 0.219 ± 0.007 h⁻¹, i.e. 4 times larger than the value with walls.

Based upon the evidence, we speculate that the presence of the 3 walls markedly slowed the migration of L_o lipids from the pixilation pattern to the surrounding flat multibilayers. The presence of elongated L_o domains that were forced to grow along the long axis of the walled portion of the pattern, as discussed earlier, would have resulted in severely obstructed diffusion at the walls, slowing the diffusion limited dissolution of the L_o pattern. The high curvature ridges of the walls also present multiple continuous bending energy barriers to diffusing L_o lipids, if they were re-clustering at the sub-micron level, as they migrated from the pixelated area. Because the first-order diffusion process was so slowed, the slow second-order process of vesiculation of the pixelated L_o phase served as an observable competing mechanism for achieving a lower energy state. In contrast, we did not observe growing vesicles without walls for this underlying lattice pattern in our previous work.²¹

In order to understand why the L_o phase area fraction was significantly higher upon initial observation with walls, we extrapolated the best fit curves with walls and without walls in Fig. 2 backwards from t = zero of observation as shown. We do this because approximately one hour before viewing the temperature dropped below the miscibility temperature (T_m), of approximately 32°C ⁹ when the metastable pixelated pattern would have first formed. Viewing was delayed to allow for temperature equilibration to room temperature. The curve with walls extrapolates correctly to the area fraction of the L_o phase on flat PMMA at t = zero indicating that the same kinetics were followed from the time that domains appeared. However, without walls, the extrapolated area fraction is significantly below the area fraction on flat PMMA indicating that faster kinetics took place during the cool-down phase, perhaps reflecting the temperature dependence of k₁ which is a function of the diffusion coefficient of DPPC dissolved in the L_d phase. ²¹

Gradient of lattice spacing confers directionality to phase partitioning and vesicle growth

Next, we fabricated curvature patterned areas with a gradient in lattice spacing between the bumps while maintained the same wall geometry to separate and concentrate the L_o phase to one end of the gradient. The lattice spacing controls the domain pixel size¹⁹ and therefore, this substrate creates a gradient in line energy with the smallest line energy associated with the largest lattice spacing. On one end of the substrate the lattice spacing was 75 nm, while in the middle section it was 200 nm, and on the other end it was 400 nm as shown in Fig. 3a and Fig. S3. Strong partitioning of the L_o phase to the 400 nm, low line energy, end was evident upon initial observation by its uniformly dark appearance as demonstrated in Fig. 3b. Based upon its uniformly dark appearance, we assume that the area fraction of L_o phase at the 400 nm end is at its maximum, A_f = 0.91, i.e. completely occupying the flat regions between bumps. The area fraction in the 200 nm centre section is measured to be approximately 0.55. The 75 nm pixel size was chosen in order to provide a very high line energy, low partitioning of L_o phase, to that end. This pixel size is below the resolution of the microscope so we did not measure the area fraction, but it appears to be less than in the 200 nm section. A Boltzmann distribution applied to the two measured area fractions gives a free energy difference of approximately 0.5 kT, a reflection of the difference in total bending and line energy associated with L_o phase in the 400 nm section and 200 nm sections. This calculation should be viewed with caution since the system is not at equilibrium.

Fig. 3.

Gradient in the lattice pattern of underlying bumps imparts directionality to the partitioning and dynamics of the Lo phase in Lo-Ld multibilayer. a) SEM images showing the variation in lattice spacing from top to bottom and presence of surrounding walls in the underlying patterned area. b) Vesicle (circle) has formed at the 400 nm end of the underlying lattice where there is strong partitioning of the Lo phase evidenced by the dark appearance. c) The border of the Lo phase migrates toward the 400 nm end. The vesicle grows from the Lo phase at the 400 nm end as shown at d) 201 min and e) 271 min, reaching a diameter of approximately 40 μm. Scale bars 10 μm unless indicated otherwise.

Similar to our observation above, at least one vesicle grew from the pixelated pattern, and these tended to initiate in the vicinity of the walls as demonstrated in Fig. 3b (circle). Similarly, these vesicles tended to take up all of the interconnected L_o phase in their vicinity. However since they were fewer in number, they were not in competition and therefore, one vesicle could take up L_o phase extending for tens of microns. This is demonstrated in Fig. 3 (b–e) where a vesicle (red circle) at the 400 nm-end takes up the interconnected L_o phase from both the 400 nm and 200 nm sections. The vesicle began to grow between 1.5 and 3 hours, causing the border of the L_o phase to migrate toward the growing vesicle as shown by the arrows in Fig. 3c. The L_o phase in the 200 nm middle section was cleared by this growing giant vesicle in approximately 30 minutes. At 5 hours, the giant vesicle had grown to a diameter of approximately 40 μm and only a small section of L_o phase remained at the 400 nm-end as shown in Fig. 3e. The vesicle tether and L_o phase subsequently became separated, ending the more rapid loss of the L_o phase.

Heating/cooling cycle regenerates/refreshes pixilation pattern

Next we heated these samples above the miscibility temperature (32 ± 1 °C)²² to put the multibilayers completely into the L_d phase, at which point there should be free exchange of the three species between the regions with underlying PMMA and the patterned regions. Subsequently, we cooled to room temperature as a means of testing the potential to regenerate/refresh the pixelated domain pattern for future reusable devices that might display proteins in the L_o phase.

After heating the multibilayer on the first walled pattern up to T = 34°C for 10 min, we cooled (~1°C/min) until reaching room temperature. At 34 ± 1 °C there were no L_o domains as demonstrated in Fig. 4a (34 °C). At 21 ± 1 °C branched chains of domain pixels as much as 10 micrometers in length had grown (Fig. 4a, 21 °C). The area fraction of the domains at 21 ± 1 °C was 0.24 ± 0.02 based upon the evaluation of 4 patterned regions in comparison to an area fraction of 0.09±0.02 before the heating/cooling cycle. Therefore, we can regenerate a pixilation pattern by heating and cooling, but the relatively short time (10 min) we held the temperature above the miscibility temperature probably resulted in incomplete mixing and an incomplete recovery of the area fraction.

Fig. 4.

A heating/cooling cycle regenerates/refreshes the pixilation pattern of coexisting Lo-Ld phases. a) Multibilayer from Fig. 2 heated to 34 °C and then cooled to 29 °C and 21 °C demonstrating nucleation and growth of the pixilation pattern. b) Left - multibilayer on the gradient pattern at 35 °C. Right –multibilayer (from Fig. 3) on the gradient pattern that had been heated to 35 °C and then cooled to 22 °C demonstrating a sharp Lo phase pixilation pattern.

We heated the multibilayers on the second walled pattern to 35 ± 1 °C for 10 min and cooled at the same rate (~1°C/min) to room temperature. At 35 °C there was no L_o phase as demonstrated in Fig. 4b (35 °C). Upon cooling to 22 ± 1 °C, a domain pixilation pattern was present on the 200 nm and 400 nm lattice spacing (Fig. 4b, 22°C) with A_f values of 0.20 ± 0.03 and 0.32 ± 0.02 respectively with 4 different patterend areas evaluated to obtain these area fractions. Although the pixel size in the 75 nm section is below the resolution of the microscope, the lack of any dark shading there may indicate a very low area fraction due to partitioning of the L_o phase into the sections supported by the 200 nm and 400 nm lattices as observed in the previous section. The pixilation pattern of the multibilayer supported by the 400 nm section is particularly well-defined, with minimum line widths clearly defined by the lattice spacing and the presence of sharp (90 degree) bends. Therefore heating and cooling serves as a method to both regenerate and sharpen these pixilation patterns.

Flat region (dead pixels) slows dissolution of surrounding pixilation pattern

Non-uniformities in the e-beam patterning process occasionally resulted in regions of the substrate where the lattice pattern was absent either because the PMMA was completely removed or not removed at all in a section. In the terminology of liquid crystal displays, this type of a defect is termed as “dead pixels”. Interestingly, the stability of the L_o phase directly surrounding any flat region was enhanced. As an example, in Fig. 5a a dark 3μm × 3μm square, void of pixilation, exists in the center of the pixilation pattern imposed by a defect in the center of the underlying 200 nm lattice. A high density of pixelated L_o phase can be observed in a 5 μm, roughly square, border around the central dark square as shown in Fig. 5a. 23 hours later, the square dark patch and 5 μm pixelated border remained largely in tact. While the remainder of the pixelated L_o phase pattern has disappeared over the same period of time as shown in Fig. 5 (b and c). A calculation shows that this overall border geometry can achieve a reasonably low energy by minimizing line energy through its compactness. The total perimeter associated with the bordering L_o phase is approximately 400 μm which takes into account its outer and inner edges and the perimeter around each bump in the border area, where L_o/L_d interface exists. If the same L_o phase existed in an elongated geometry of one pixel in width, similar to the remainder of the L_o phase, its perimeter would be approximately 730 μm. The line energy of the compact geometry is substantially lower, by approximately 8 × 10⁻¹⁶ J or 2 × 10⁵ kT assuming a line tension of ~2.5 pN.⁸ After 33 hours only the central square patch primarily existed and it was lighter in appearance (Fig. S4) except for a small border indicating that the darker appearance of the central square in Fig. 5 resulted from the presence of L_o phase in more than one bilayer of the multilayer.

Fig. 5.

Altered partitioning of the Lo phase and dynamics associated with a flat region in the centre of the lattice pattern of bumps. The dark square in the centre of the patterned region (dead pixels) at t = 0 indicates strong partitioning to the flat region. Area fraction of the pixelated Lo phase decreased with time, but remained higher in a border around the dead pixels at t = 1 hr and t = 23 hrs.

Open lattice confined to small area associated with spontaneous switching of pixel location on the lattice

Our final e-beam formed pattern was a smaller walled-in area (15 μm × 50 μm) containing a square lattice of bumps with a more open lattice of 600 nm between the bumps (Fig. S5). Interestingly, as the area fraction of this pattern decreased, the interface between the L_o and L_d phase noticeably switched from a wavy geometry (Fig. 6a, t=0) to a smooth geometry (Fig. 6b, t=3.3 hr). Upon closer inspection, it can be observed that each domain pixels is centred and confined inside of a unit cell of 4 bumps at t=0 as expected, but at t=3.3 hrs each pixels is larger and appears to form an annulus around a bump confined by 4 unit cells. Moreover, the pixels have switched back to being centred inside of a unit cell at 23 hrs. We show evidence for this in Fig. 6a where we outline some domain pixels at t=0 and 23 hrs to show that they correspond to the size and spacing of a circle centred on a unit cell of bumps. (The bumps are visible in the bright L_d regions due to interference contrast.) We outline domain pixels at t=3.3 hrs and it can be seen in the figure that they correspond to the size of a circle centered on a bump with its size limited by the 4 unit cells. The geometry of these larger pixels affords that they overlap each other significantly which presumable creates a smooth interface which would lower line energy. However, each of these L_o phase pixels actually has the shape of an annulus as can be observed by their brighter centre which creates line energy at this L_o-L_d interface. The switching behavior was associated with every imprint of the underlying 600 nm pattern as demonstrated by two more time sequences in Fig. S6. We speculate that this behaviour is related to the relatively small number of bumps in this pattern, particularly that there are only about 20 rows of bumps.

Fig. 6.

Demonstration of dynamic behaviour associated with smaller walled-in area (15 μm × 50 μm) containing a square lattice of bumps with a more open lattice of 600 nm between the bumps. a) Spontaneous switching of the Lo pixel location and size on the lattice as the area fraction decreases. At t=0, each domain pixels is centred and confined inside of a unit cell of 4 bumps (solid circles), at t=3.3 hrs each pixels is larger and appears to form an annulus around a bump confined by 4 unit cells (dashed circles), and at t=23 hrs the pixels have switched back to being centred inside of a unit cell (solid circles). We use the visibility of the lattice in the bright Ld regions to prove that these geometries correspond to 1 and 4 unit cells. b and c) Images demonstrating the mobility of these pixels where the arrows show spontaneous pixel motion over very short periods of time (seconds).

The pixels in this pattern are more mobile in comparison to any of our previous observations as we demonstrate in Fig. 6 (b and c) where the arrows show evidence of spontaneous pixel motion over very short periods of time (seconds). The higher mobility of this pattern may be attributed to the open nature of the underlying substrate where bumps take up only 5% of the area. Note that a pixilation pattern emerged in this particular patterned region which resembles a swan as shown in Fig. 6b. It may be possible in the near future to use electric fields to create patterns in these pixelated platforms, which would be particularly useful for screening applications if proteins were associated with the pixelated phase, a direction that we are beginning to explore.

Conclusions

This study provides proof-of-concept that chip-based systems with nanometer-scale features can be used to impart distinct dynamic sorting behaviours by manipulating bending and line energy of phase-separated lipid bilayers. Simple variations in an underlying e-beam formed lattice pattern of curved features imparted distinctly different dynamics to a metastable pixilation pattern of L_o-L_d lipid phases. This was possible because each pattern had a distinct impact on phase/compositional partitioning and the rates of competing dynamic processes, particularly lipid diffusion/Ostwald ripening vs. vesiculation and growth. These results are suggestive of future refreshable analytic devices that separate and/or control the dynamics of biomembrane species using differences in mechanical energy.