Nanocarrier Hydrodynamics and Binding in Targeted Drug Delivery: Challenges in Numerical Modeling and Experimental Validation

Short abstract

This review discusses current progress and future challenges in the numerical modeling of targeted drug delivery using functionalized nanocarriers (NC). Antibody coated nanocarriers of various size and shapes, also called functionalized nanocarriers, are designed to be injected in the vasculature, whereby they undergo translational and rotational motion governed by hydrodynamic interaction with blood particulates as well as adhesive interactions mediated by the surface antibody binding to target antigens/receptors on cell surfaces. We review current multiscale modeling approaches rooted in computational fluid dynamics and nonequilibrium statistical mechanics to accurately resolve fluid, thermal, as well as adhesive interactions governing nanocarrier motion and their binding to endothelial cells lining the vasculature. We also outline current challenges and unresolved issues surrounding the modeling methods. Experimental approaches in pharmacology and bioengineering are discussed briefly from the perspective of model validation.

1. Introduction

In the treatment of diseases, drugs are often injected directly into the circulation. However, only a minor fraction of injected drugs get to, and act in, the diseased tissue site. Suboptimal drug delivery represents an especially acute challenge in case of interventions using biotherapeutics (enzymes, genetic materials), which are labile and require specific addressing to given sub-cellular compartments: plasmalemma, vesicular bodies, cytosol or the nucleus. Furthermore, the complexity of many diseases substantiates a need for novel and effective disease treatments. Such novel treatments may be based on predictions made possible by original theoretical and computational approaches that dovetail with innovative experimental methods. Targeted drug delivery using functionalized nanocarriers (NCs) coated with specific targeting ligands is such an approach in therapeutic and diagnostic applications in many medical diseases [1,2,3,4].

In particular, monolayer of endothelial cells lining vascular lumen represents the key target for delivery of drug nanocarriers. The vasculature is a highly accessible and convenient route and target for drug delivery [5,6,7,8,9]. In order to achieve targeted delivery to endothelial compartments, drugs or their carriers are conjugated with molecules having affinity to specific endothelial determinants, providing optimal anchoring and subsequent sub-cellular delivery—this is the basic concept in targeted drug delivery. Targeting of NCs to vascular endothelial cells (ECs) remains an important design challenge in pharmacological and biomedical sciences. ECs represent the first tissue barrier encountered by circulating drugs and drug carriers en route to extravascular therapeutic targets including tumor cells, neurons and cardiomyocytes. In order to facilitate extravasation, one strategy is to anchor drug carriers specifically to endothelial molecules involved in processes that transfer blood components into tissues [5,10,11,12].

It is now realized that the vascular administration of targeted NCs may indeed enable precise delivery of drugs to endothelial cells [2]. From a drug delivery standpoint, EC adhesion molecules, either constitutive or inducible, represent a good target for anchoring carriers of anti-inflammatory and antithrombotic agents. In particular, determinants up-regulated or selectively expressed on pathologically altered endothelial cells, such as intracellular adhesion molecule-1 (ICAM-1) are attractive targets for therapeutic drug delivery to pathological sites [2,13,14,15,16]. Molecules expressed in tumors and sites of angiogenesis are excellent targets for diagnosis and treatment of these conditions [17]. On the other hand, molecules exposed on the surface of both normal and abnormal endothelium, such as platelet endothelial cell adhesion molecule (PECAM) can be employed for both prophylactic and therapeutic drug delivery [2,4].

Theoretically, the clinical goal of targeted delivery can be achieved by coating drug carriers with affinity ligands providing anchoring to the endothelial surface molecules, such as antibodies to ICAM-1 or PECAM-1 [12,18,19,20,21,22]. This approach permits increasing the binding specificity of delivered therapeutic agents to enhance drug delivery while minimizing potential toxicity [2,3,4,16,23,24,25,26]. Use of functionalized drug NCs offers a variety of tunable design parameters (e.g., size, shape, type, method of functionalization, instillation concentration, drug packaging, drug offloading) [13,14,20,27,28]. Currently, the impact of tuning these parameters is characterized empirically for each given case, which requires massive experimentation in a high-dimensional tunable parameter space to optimize treatment design in drug delivery applications [3,29,30]. A physiologically sound, computationally tractable model, which is both quantitative and predictive, will be most useful for rational design of NCs for drug delivery.

The challenge of designing functionalized drug NCs includes inherent complexities of multiple underlying interactions. These include (i) molecular and geometric parameters surrounding receptor-ligand interactions and NCs [13,31,32,33]; (ii) lack of accurate characterization of hydrodynamics and (iii) physicochemical barriers for NC uptake/arrest [34,35,36,37]; (iv) incomplete characterization of nanoparticle-cell membrane force interactions and their influence on particle trafficking [38]; (v) extreme complexity and variability of targeting environment in vivo [39,40,41] and (vi) incomplete tracking of transported cargo delivery and losses in transit. Among the factors impacting the design of nanocarriers and therapeutic agents are: (a) binding affinity [42,43]; (b) multivalency or the average number of receptor-ligand bonds per bound NC and their spatial orientation [43,44,45,46,47]; (c) in vivo targeting, measured as percentage of injected dose accumulated after intravenous injection [48,49,50], and (d) hemodynamics [51,52,53,54,55,56,57,58,59,60].

For example, binding avidity is a direct measure of the efficiency of NC targeting, but not drug delivery efficiency. The binding avidity of anti-ICAM-1 coated NCs to ECs can be two orders of magnitude higher than affinity of anti-ICAM-1 binding to ICAM-1 [42]. Studies of the kinetic rate constants of attachment and detachment of NCs as a function of receptor density, ligand density on the surface, and flow shear rate have identified a time dependence of the detachment rate due to multivalent binding [18,19]. A linear dependence of binding avidity on antibody surface coverage has been observed in experiments of the effect of antibody surface coverage on equilibrium binding constants by measuring fractional coverage of bound NCs as a function of NC concentration [61].

However, despite the apparent wealth of studies on NC binding, a detailed understanding of the determinants of NC binding to ECs, let alone drug delivery, is still limited. This fact is further amplified by researchers who acknowledge that such lack of specific experimental data limit computational tool development for model-based analysis because current data are insufficient to identify the underlying process model [61]. In order to transition and integrate simulation technology for targeted drug delivery into clinical medicine, model-based design and optimization of NC transport in the vasculature and adhesion to target cells must be achieved first.

Targeted drug delivery is inherently a multiscale problem: A large range of length and time scales are important to hydrodynamic, microscopic, and molecular interactions mediating NC motion in bloodflow and cell binding. Therefore, research in this area must be focused on deriving detailed information that will guide rational NC design via a computational model: What size nanocarriers should be used, and in what concentration? What is the optimal ligand density and how should the ligand be tethered to yield optimal NC avidity? The importance of some of these factors has already been experimentally demonstrated. For example, it has been shown that for small targeting ligands, nanoparticle avidity is highest at intermediate ligand densities and that differences in cell binding can be on the order of several-fold [62]. It has also been shown that antibody on and off rates affect nanoparticle specificity [19].

A computational throughput for NC optimization may be expected to lead to more than an order of magnitude improvement in tissue targeting efficiency with great rapidity. It is important to emphasize that the development of computational methods bridging relevant molecular dynamics, mesoscale binding interactions and hydrodynamics influencing NC transport and cellular adhesion is essential to access design optimization parameters for NCs used in targeted drug delivery. This is achievable through integration of concepts and technologies from molecular dynamics, Monte Carlo simulations, statistical mechanics, biofluid dynamics, pharmacology, materials science, synthetic chemistry and vascular cell biology. Some of the significant challenges in numerical simulation are: parameters which are unavailable in the literature must be estimated de novo using computational techniques such as molecular dynamics simulation; quantities such as binding affinities require determination of absolute binding free energies. This necessitates extensive sampling over conformational degrees of freedom and determination of various entropy changes upon binding. As an illustrative example, inspired by the framework in Ref. [63], a mesoscale model of NCs functionalized with antibodies which bind to antigens on the EC surface amid fluid flow and glycocalyx interactions has been developed, validated, and the absolute binding free energy has been computed [29,64,65,66]. Specific computational methodology to reveal NC Brownian motion and relevant hydrodynamic interactions have been developed and validated [51,52,53,64,65], and this further expands both time and length scales involved for bridging the transit phase of NC motion in blood flow, subsequent near wall interactions and resultant binding at the target site. Clearly, much more remains to be done in this area.

Traditional multiscale modeling involves bottom-up approaches of systematically coarse-graining the atomistic description. Bridging techniques that seamlessly integrate two distinct length scales in this category include mixed quantum mechanics/molecular mechanics (QM/MM) [67], and integrated molecular mechanics/coarse-grained or MM/CG approaches [68]. Alternatively, a top-down approach may be used, in which models are constructed at the mesoscale based on phenomenological interaction potentials, with specific choices of governing equations then validated by experiment [64]. Such methods involve continuum scale formalisms and often incorporate finer length scales by considering spatial heterogeneities as inhomogeneous fields [69]. Bridging methods integrating molecular mechanics or coarse-grained models with continuum approaches have been achieved in two limits: (1) hierarchical bridging which involves computing a property or a constitutive relationship at one (typically the molecular) scale and employing (either pre- or on-the-fly-) computed values in the other (typically the continuum scale) [65,70,71]; (2) domain decomposition bridging which involves performing molecular scale modeling in one (typically a small domain) and integrating it with continuum modeling in an adjoining (larger) domain, such that certain constraints (boundary conditions) are satisfied self-consistently at the boundary separating the two domains. Such approaches have been shown to be effective for various problems involving contact lines or points [72,73,74,75,76,77,78,79,80,81].

For vascular drug targeting, both molecular interactions (due to biomolecular recognition) and hydrodynamic interactions (due to fluid flow and boundary effects) are significant. The integration of disparate length and time scales does not fit traditional multiscale methods. Complexity lies in integrating fluid flow and memory for multiphase flow in complex and arbitrary geometries, while simultaneously including thermal and stochastic effects to simulate correctly quasi-equilibrium distributions to enable receptor-ligand binding at the physiological temperature. This is ubiquitous in multivalent binding or adhesive interactions between NCs and cells or between two cells in the vasculature. An important step in computational modeling of NC binding to endothelium is to determine the motion of a NC subject to vascular hydrodynamic effects while simultaneously being subject to a constant temperature; this is crucial to model accurately the receptor-ligand interactions mediating NC adhesion to the endothelium [46,47,48,49]. Bridging the multiple length scales (from meso to molecular) and the associated time scales relevant to the problem is essential to success herein. Multiple macroscopic and mesoscopic time scales governing the problem include (i) hydrodynamic time scale; (ii) viscous/Brownian relaxation time scale and (iii) Brownian diffusion time scale.

Multiscale modeling must complement experimental technologies. Novel computational methods [1,29,52,54,55,56,57,58,82,83,84,85] may be combined with in vivo and in vitro experiments [14,46,47,55] to model NC motion and adhesion. Brownian motion and hydrodynamic interactions are both important. Brownian effects may be included using the generalized Langevin dynamics framework, where the hydrodynamic memory effects of the NC-fluid interactions and their relationship to thermal equipartition and equilibrium distributions are delineated. The fluctuating hydrodynamics framework described in Ref. [82] captures hydrodynamic correlations and conserves thermal equipartition (for a NC in an incompressible fluid) only after the added mass correction is applied [83]. The generalized Langevin dynamics method yields the correct thermal equipartition without any corrections, but modifies the nature of the hydrodynamics correlations due to the coupling of the fluid equations with the thermostat degrees of freedom [59]. Therefore, each procedure has its shortcomings. In this context, it is therefore useful to consider the development of a developed a hybrid formalism that combines fluctuating hydrodynamics and generalized Langevin dynamics, resulting in a hybrid scheme based on Markovian fluctuating hydrodynamics of the fluid and a non-Markovian Langevin dynamics with the Ornstein–Uhlenbeck noise perturbing the translational and rotational equations of NC motion [51]. In this formulation, comparing the predicted NC temperature with that obtained from the equipartition theorem validates the thermal equilibrium between the particle and the fluid. Furthermore, the nature of the hydrodynamic correlations (interactions) is verified by comparing the time-dependence of the velocity autocorrelation function and mean square displacement with analytical predictions [83].

Validated multiscale models of NC dynamics that mechanistically handle events at multiple distinct scales (e.g., the macroscopic regime, the lubrication regime and the adhesion regime), and which couple directly with the associated transport mechanics of cargo loss and intracellular offloading should be able to provide the algorithmic methodology for rapid and accurate in silico determination of optimal NC design and delivery parameters. In turn, these are required to invoke safe and effective clinical therapies. The dependence of drug delivery on these parameters may be culled in computations from the myriad of tunable physical options otherwise reachable only through the conduct of enormous quantities of in vitro and in vivo experimentation. This will, in effect, establish simulation methodology for fast tracking of translation from carrier design to clinical medical practice in disease treatment by drawing on the wide ranging expertise from the relevant fields of engineering, biology and clinical medicine.

2. Types of Cargo Carriers

Ideally, the NC for drug delivery must be nontoxic, biocompatible, biodegrdable and nonimmunogenic. The common drug delivery vehicles include liposomes, polymeric micelles and dendrimers, artificial DNA structures, and biodegradable scaffolds [84]. Liposomes are sufficiently nontoxic and biocompatible to grant clinical use. Polymeric micelles prepared from copolymers consisting of both hydrophilic and hydrophobic monomer units represent an alternative to liposomes, especially useful to carry drugs that have poor solubility [85]. Dendrimers based on polymers or natural biomolecules and nanodevices based on DNA as a structural material may be used for drug delivery and these may be designed such that drug is released specifically in response to stimulus from a specific mRNA. Hydrogels are biocompatible and swellable polymeric materials, which are useful for drug delivery. Hydrogel carriers swell in an aqueous medium and have sensitivity to pH, temperature and other stimuli. They are suitable carriers for bioactive drugs with tissue specificity. They are noted to function as drug protectors for peptides and proteins in an in vivo environment [86].

Solid, biodegradable particles are stable and may be designed for controlled release. Among these, this review will primarily concern itself with biodegradable solid nano particles. These are usually nanoparticles bearing ligands to P-selectin, endothelial selectin (E-selectin) and ICAM-1, and adhere to inflamed endothelium. Biodegradable nanoparticles, in general, can deliver a wide range of drugs to different areas of the body and over long durations of time. Biodegradable polymer nanoparticles for drug delivery and targeting are discussed in detail by Hans and Lowman [87], who note that the most widely used polymers for this purpose are polylactic acid (PLA), polyglycolic acid (PGA), and their copolymers polylactide-co-glycolide, which are all known for biocompatibility and resorbability through natural pathways. Furthermore, with these particles the drug release rate for a specific purpose can be adjusted by varying the ratio of PLA (increased hydrophobicity) to PGA (increased hydrophilicity).

3. Multiscale Modeling of Hydrodynamic and Microscopic Interactions Mediating NC Motion

3.1. Brownian Motion and Hydrodynamic Interactions in the Presence of Flow Fields.

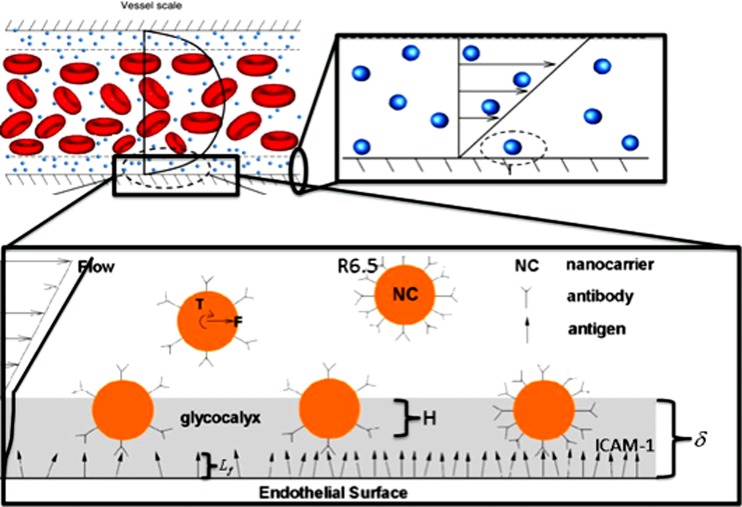
Prior studies of the NC in the bulk flow medium (hydrodynamic regime) in regard to targeted drug delivery have considered blood as Newtonian, either stationary or with an established Poiseuille parabolic profile flowing in a circular tube. Simultaneously, Brownian interactions (microscopic regime) have been fully considered [51,54,56,57,58,59]. The treatments of the resistance of the glycocalyx and adhesion interactions mediated by multivalent antigen-antibody binding/unbinding events using molecular dynamics have been bridged with the macroscopic regime so evaluated [1,29,51,66,82,85], see Fig. 1. These studies have to be comprehensively modified to obtain realistic predictions. The macroscopic regime described there must be modified by taking into account the non-Newtonian nature of blood caused by the presence of particulates, Fahraeus–Lindqvist effect and realistic flow profiles with cell free layers (see, for example, [88,89,90,91,92,93,94,95] for studies in another context). The complex microrheology of blood using complimentary modeling techniques has been described in Ref. [96] and this may also be pursued. The multiple length scales must be bridged in order to rigorously treat both hydrodynamic and near-wall effects simultaneously. The complex rheology due to the particulate nature of blood, the effect of glycocalyx, and NC adhesion to cells mediated by receptor-ligand bonds under various hydrodynamic conditions have to be integrated in the procedure.

Fig. 1.

Schematic of different length scales of NC dynamics. Top: at the micron length-scale, the hydrodynamics of particulate nature of blood and near-wall margination of NC is described. Bottom: at the 50–200 nm length scale, the near-wall adhesion of NC and resistance due to glycocalyx is described.

For evaluating the multiphase stochastic dynamics of NC and cells in plasma subject to Brownian and hydrodynamic forces, the recently described hybrid model combining Markovian fluctuating hydrodynamics for the fluid with non-Markovian generalized Langevin approach for the NC within a finite element [51,54,56] may be employed. The hybrid approach has been demonstrated to simultaneously satisfy the equipartition of energy in an isothermal environment, as well as hydrodynamic interactions imposed by the flow field [1,29,51,56,66]. If the choice is to use an ab initio approach for the non-Newtonian fluid description, the bulk fluid may be modeled as a Newtonian fluid of viscosity μ_NF. Hematocrit and platelets may be explicitly modeled at the appropriate volume fraction (Hematocrit 45%, plasma 54.3%, and platelets 0.7%). Because of the ab initio nature of the model description, the hydrodynamic forces will ensure the appropriate margination into a “three-layer” flow (Fig. 1) consisting of a cylindrical core of red blood cell (RBC) suspension surrounded by a less viscous, thin cell-free layer together with the glycocalyx [88,89,97,98].

In such a model, for the particle, the governing equation for translation of the NC would be:

$$\begin{array}{c}\multicolumn{1}{c}{md\mathbf{U}/\mathit{dt}=-{\int }_{\partial {\mathbf{\Sigma }}_p}\mathbf{\sigma }·\stackrel{\wedge }{\mathbf{n}}\mathit{ds}+{\mathbf{S}}_f+{\int }_{-\infty }^{t_{-}}\mathbf{\xi }(t\text{'})e^{-|t-t\text{'}|/{\tau }_1}\mathit{dt}\text{'}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\hspace{1em}+{\mathbf{F}}_{\mathrm{adhesive}}+{\mathbf{F}}_{\mathrm{cell}-\mathit{NC}}+{\mathbf{F}}_{\mathit{NC}-\mathit{NC}}}\end{array}$$

The fluid equation and the term ξ are given by

$$\begin{array}{c}\multicolumn{1}{c}{{\int }_{{\Sigma }_o}({\rho }^{\left(f\right)}\frac{D\mathit{u}}{\mathit{Dt}}·\stackrel{\wedge }{\mathit{u}}-p(\nabla ·\stackrel{\wedge }{\mathit{u}})+\{\mu [\nabla \mathit{u}+{(\nabla \mathit{u})}^T]+\mathit{s}\}:\nabla \stackrel{\wedge }{\mathit{u}})\mathit{dV}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}=\stackrel{\wedge }{\mathit{U}}·[-m\frac{d\mathit{U}}{\mathit{dt}}+\sum _{i=1}^{n_1}\xi (t-i\Delta t)e^{-i\Delta t/{\tau }_1}]}\end{array}$$

and

$$\mathbf{\xi }(t\text{'})={\int }_{\partial {\mathbf{\Sigma }}_p}\mathbf{S}(\mathbf{x}\text{'},t\text{'})·\stackrel{\wedge }{\mathbf{n}}\hspace{1em}\mathit{ds}$$

Here $m,\mathbf{U}$ are the mass, and linear velocity of the NC, respectively, u is the velocity field of the fluid, Σ₀ is the fluid boundary and Σ_p is the particle boundary, S is the random stress field in the fluid within the fluctuating hydrodynamics approach. The corresponding rotational equation of motion for the particle is given by:

$$Id\omega /\mathit{dt}=-{\int }_{\partial {\Sigma }_p}(x-X)\times \sigma ·\stackrel{\wedge }{\mathbf{n}}\hspace{1em}\mathit{ds}+{\mathbf{S}}_t+{\int }_{-\infty }^{t_{-}}\eta (t\text{'})e^{-|t-t\text{'}|/{\tau }_1}\mathit{dt}\text{'}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\hspace{1em}+T_{\mathrm{adhesive}}+T_{\mathrm{cell}-\mathit{NC}}+T_{\mathit{NC}-\mathit{NC}}$$

Here, I is the moment of inertia and ω, (x-X) is a vector from the centeroid of the particle and the particle surface, S_t is the random torque, T terms represent specific torques, and

$$\mathit{\eta }(t\text{'})={\int }_{\partial {\Sigma }_p}(x-X)\times [\mathbf{S}(\mathbf{x}\text{'},\mathit{t}\text{'})·\stackrel{\wedge }{\mathbf{n}}]\mathit{ds}$$

For NC undergoing Brownian motion under flow, S should be treated as a Gaussian with 〈S_ij(x,t)〉 = 0 and 〈S_ik(x,t)S_lm(x′,t′)〉 = 2k_BTμ(δ_ilδ_km + δ_imδ_kl)δ(x − x′)δ(t − t′), and it must be confirmed that this can simultaneously preserve the equilibrium thermal distribution and the short and long-time hydrodynamic correlations. The viscosity of the flow which has a direct bearing on the magnitude of the functuating stress S may be expressed as: μ(r,z,t) = μ_NF in 0 ≤ r ≤ (1 − δ)R; = μ_gly in (1 − δ)R ≤ r ≤ R. Here t is time, μ_gly is the viscosity in the glycocalyx layer, and δ is the dimensionless thickness of the glycocalyx normalized with respect to vessel radius R. The ab initio modeling of the multiphase flow will then definitely ensure that the core viscosity is shear-dependent. The three terms F_adhesive, F_cell-NC and F_NC−NC above represent external forces on the NC. The treatment of these terms within the same equation of motion for the NC involves bridging of length scales. This bridging procedure for F_cell-NC and F_NC−NC can be described here (see below) but the bridging for F _adhesive that is associated with binding can be discussed later. To solve the above set of equations with specified boundary conditions at the inlet, outlet, closed boundaries of the wall and the moving particles, an arbitrary Lagrangian–Eulerian based finite element method may be employed to solve the fluid equation [51,53,54,57,58,59]. Such a numerical approach should also be able to capture arbitrary flow fields and flow geometries (including boundary conditions), the noncontinuum nature of the stress because in this formalism an allowance has been made for the stress to fluctuate in the fluid domain. Moreover, with this formalism, the equations of motions incorporate temporal memory in NC dynamics [51,53,54,56,57,58,59], adhesive force from ligand-receptor bonds [56,58], cell-NC, cell-cell, and NC-NC interaction forces [99]. The dominant factors in nonspecific NC-NC, NC-cell, and cell-cell (this term occurs in the equations of motion of the cells, not provided in this article for the sake of brevity) interactions in this model will be the fluid-mediated hydrodynamic interactions. Further, the short-range interactions between these particulate bodies have to be resolved through predefined expressions for the interaction potential [98,100,101,102,103]. These expressions usually treated as Lennard–Jones or Morse potentials (see, e.g., Ref. [104]) will yield the near-field interaction terms for F_NC-NC and F_Cell-NC; for NC-cell and NC-NC interactions, a Lennard–Jones potential will be introduced. As stated earlier, the evaluation of the adhesive interactions involves an entirely different length-scale and may be performed only when the point force on the NC due to each receptor-ligand interaction (S _f) is available. The integrated adhesion force F_adhesive, on particle surface may then be calculated as

$${\mathrm{F}}_{\mathrm{adhesive}}·\stackrel{\wedge }{\mathbf{n}}=\int N_b{\mathbf{S}}_{f}d\sum _{\mathrm{p}}$$

In regard to the flow in the glycocalyx (see Fig. 1), the dynamics of NC in the glycocalyx has to be treated as an entirely different length-scale following [34,105,106], where the gap between the NC and the endothelium surface is locally approximated as a smooth microchannel (x-y coordinate system) coupled with a layer of glycocalyx filaments (and the receptor-ligand bonds) of uniform length, L_l. The flow regime in the glycocalyx may be divided into two parts: one outside the layer (L_f ≤ y ≤ H) and one within the glycocalyx layer (0 ≤ y ≤ L_l) where H is the height of the penetration of the NC in the glycocalyx layer. The flow equation within the glycocalyx layer may be approximated using the Brinkman equation

$$\partial p/\partial x={\mu }_{\mathit{NF}}\hspace{1em}\partial /\partial y(\partial U/\partial y)-{\mu }_{\mathit{NF}}/K_{p}U$$

in which U is the fluid velocity, the expression

$$\begin{array}{c}\multicolumn{1}{c}{K_p=r_f^2(\ln (c^{-0.5})-0.745+c-c^2/4/4c),c=2\pi r_f^2/\sqrt{3}(2r_f+\Delta ){\hspace{0.17em}}^2}\end{array}$$

is the Darcy permeability of the glycocalyx, r_f is the glycocalyx fiber radius, Δ is the fiber gap. For example, we could have r_f = 6 nm, Δ = 8 nm and L_f = 150 nm. The bridging between the bulk flow and the glycocalyx regime may be done through the boundary conditions: at y = 0, U = 0 and at y = L_f, U = u, ∂U/∂t = ∂U/∂t, where u is the fluid velocity in the bulk. The first condition enforces no-slip at the bottom of the glycocalyx and the second enforces the continuity of the velocity and shear stress across the interface at y = L_f for the bulk and glycocalyx flow.

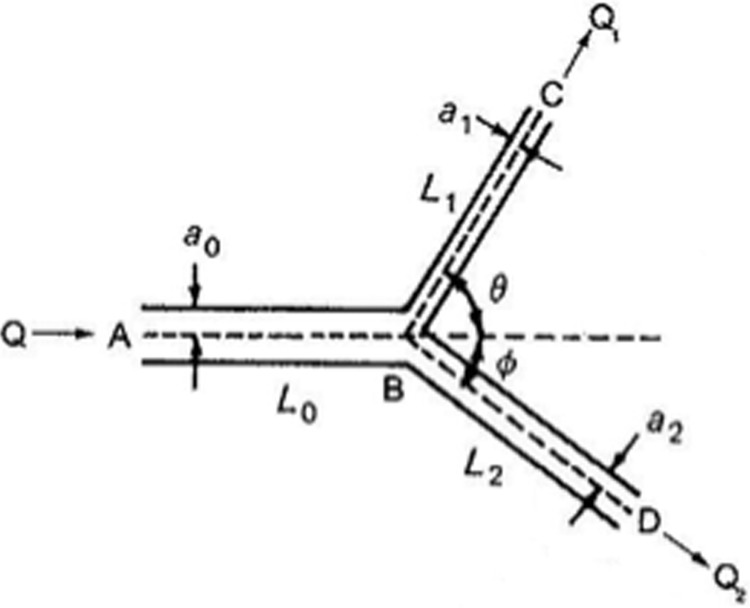
Branched flows are a common occurrence in the vasculature and can serve to be important in the targeted drug delivery problem. This, of course introduces additional complicating issues for modeling. Following Refs. [89,107,108,109,110,111] for flow of pure fluids in branched vessels, at a minimum, there is a need to investigate NC dynamics in branched geometries in which a parent vessel branches into two daughter vessels at angles θ and ϕ relative to the parent axis (Fig. 2). For pure fluids, based on optimization theories, the parent vessel inner radius, a ₀ = [16μ/(π² k[ρ _tube(c ²+ 2c) + ρ _blood])]^1/6 Q ^1/3. Here, k is the pump mass index, c is the ratio of wall thickness to inner radius, and Q is the volumetric flow rate. In the nth generation of a bifurcating network, there will be 2ⁿ vessels, each having an inner radius a _n = a ₀/2^{n /3} and a volumetric flow rate Q _n = Q/2ⁿ. Bifurcation angles are given by $\cos \theta =\{a_0^4+a_1^4-(a_0^3-a_1^3){\hspace{0.17em}}^{4/3}\}/2a_0^2{a}_1^2$ and a similar expression for ϕ will apply. Similar relationships must be developed for the particulate-fluid model; in particular, the rate of NC collision with the vessel wall in linear versus branched geometries for differing branching angles, flow rates and hematocrits must be evaluated and compared to ascertain the role of branching on drug delivery.

Fig. 2.

Branching vessel geometry. The flow rates in the two branches are functions of the geometric variables describing the branch.

It may be noted that many of the parameters for cell-NC and NC-NC, and cell-cell interactions are only known in an approximate sense from the information that is currently available in the literature. Even though the fluid-mediated hydrodynamic interactions are expected to be the dominant factor in shaping such interactions, there is a need to continually update the near-field interactions based on experimental and modeling advances in the literature. Further, sensitivity analysis techniques must be employed to constrain the values of parameters which are not directly available from the literature [1,58].

3.2. Multiscale Modeling of Multivalent Adhesive Interactions of NCs Binding to Endothelial Cells.

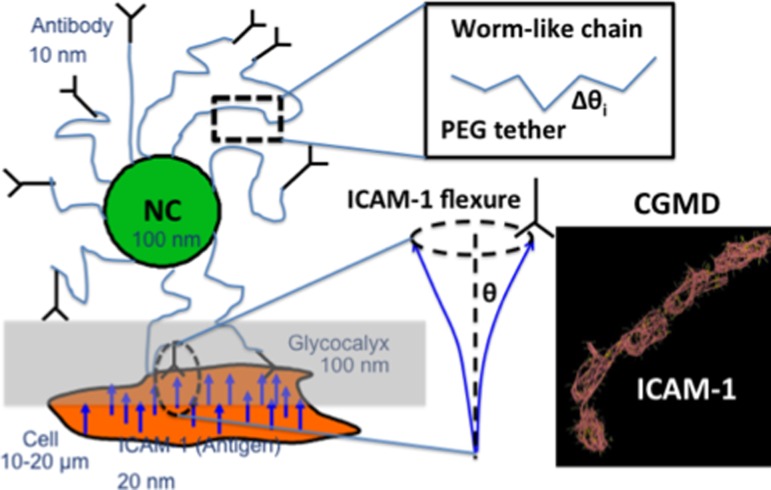
The near wall multivalent receptor-ligand interactions must be incorporated [1,29,51,56,66,82] for an accurate treatment of adhesive interactions. Models proposed in recent studies explore NC translation and rotation, and receptor translation using Metropolis Monte Carlo (MC) moves [1,29,51,56,66,82]. Interactions between ligands (antibody fragments) and receptors (intracellular adhesion molecule 1 or ICAM-1) on the cell surface have been considered through the Bell model through the reaction free energy: ΔG_r(d) = ΔG₀ + 0.5kd ², where d represents the distance between the reaction sites of the interacting antibody and antigen, ΔG₀ is the free energy change at equilibrium state (d = 0) and k is the interaction bond force constant. The receptor flexure is accounted for by allowing them to bend relative to their normal upright conformation. Under the assumption of small flexural deformations, the flexure of an antigen has been modeled as bending a beam from equilibrium (upright) position (Fig. 3); for small deformations, bending energy can be expressed as: ΔG_f(θ) = (2EI/L)θ ²; this assumption may, in fact, be relaxed in coarse-grained/continuum Monte Carlo (CG/CM) simulations which will be discussed below. The effects of flow and resistance due to glycocalyx, captured by the modeling described in the earlier section may now be incorporated by computing the incremental work done against flow and glycocalyx between the old and new trial configurations and accepting the move through the aforementioned Metropolis criterion. One can also consider the effect of mediating tethers for enhanced conformational accessibility and multivalency in receptor-ligand interaction through a wormlike chain model [112]. For the sake of illustration (see Fig. 3), if we consider discretizing each tether of length l into N rigid links, each of length Δs (such that Δs ≪ ξ_P, where ξ_P is the persistence length of tether), then the potential energy that is associated with the tether conformation is given by:

Fig. 3.

Multiscale model for NC adhesion interactions with molecular specificity. NC with functionalized antibodies attached via tethers. The tether dynamics is described using a wormlike chain model (see inset). The antigens on the cell surface are treated with flexural dynamics, which are resolved using coarse-grained molecular dynamics or CGMD simulations.

$$E\left[\theta \left(s\right)\right]=\sum _{i=1}^N\frac{\xi p{\left(\Delta {\theta }_i\right)}^2{\mathit{k}}_B\mathit{T}}{2\Delta s}+{\overrightarrow{f}}_{\iota }·\overrightarrow{\Delta }{r}_{\iota }+{\mathit{T}}_i·\overrightarrow{\Delta }{\psi }_{\iota }$$

where Δθ_i is the relative angle formed between the i and i + 1 links and the terms comprising of f_i (hydrodynamic force on link i) and T_i (hydrodynamic torque on link i) are the work done in translating (by displacement Δr_i) and rotating (by angular displacement ΔΨ_i ) the center of mass of the ith link against the fluid; these terms may be determined from the stress and velocity distributions in the fluid obtained from solving the fluid equations discussed in the earlier section and also provided; for example, in Ref. [113]. The explicit coupling of hydrodynamic stress of the flow descriptions of the earlier section (through the computation of the force and torque terms) to the tether (link) dynamics through the definition of the energy function (Hamiltonian) E[θ(s)] represents an explicit bridging of length-scales. This enables the simultaneous treatment (bridging) of F_adhesive and hydrodynamic forces on the NC within a single equation (described in the earlier section). MC link moves may be used to conformationally sample fluctuations of each tether in the flow-field [114].

The models for NC motion, tether dynamics, and adhesive interactions described so far collectively account for the multivalent interactions between NC and cell in the presence of flow. In order to translate this model to output experimentally accessible quantities, the partial/full dissociation of NC from the bound state needs to be modeled. This may be achieved through the calculation of the free energy landscape or the potential of mean force (PMF); this procedure yields the experimentally measurable binding association constant K_a [29,66]. The computation of the free energy landscape represents a temporal multiscale approach through which it should be able to translate 1–100 ns dynamics of the NC into a NC association/dissociation landscape that happens in a O(10⁻³) s to O(1) s timescale. The free energy landscape approach [29,56,66] may be extended to the NC Monte Carlo simulations outlined above, in order to compute and define the adhesion free energy landscapes subject to flow conditions and hydrodynamic interactions. In particular, the absolute free energy of binding of NC to the endothelial cell lining the wall may be computed by calculating the association constant, K_a. This may be achieved by computing the potential of mean force or PMF, W(z), where z is the distance between the NC and the cell surface by performing umbrella sampling in multiple windows with harmonic biasing constraints, see Refs. [29,56,66]. For NC binding to planar, nondeformable cell surface, the form of the binding affinity for interactions between NC and cell surface may be expressed as:

$$\begin{array}{c}\multicolumn{1}{c}{K_a=\frac{1}{\left[\mathbf{L}\right]}\times T_1\times T_2\times T_3,\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{T}_1=\frac{A_{R,b}^{(1)}\times A_{R,b}^{(2)}\times \dots \times A_{R,b}^{(N_b)}}{A_{R,\mathit{ub}}^{(1)}\times A_{R,\mathit{ub}}^{(2)}\times \dots \times A_{R,\mathit{ub}}^{(N_b)}},T_2=\frac{(N_{\mathit{ab}}/N_b)\Delta \omega }{8{\pi }^2},\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{T}_3=\frac{A_{\mathit{NC},b}\int e^{-\beta W\left(z\right)}\mathit{dz}}{A_{\mathit{NC},\mathit{ub}}{l}_z}}\end{array}$$

where T ₁ represents the entropy loss from the bounded receptors, $A_{R,b}^{(n)}$ is the accessible surface area to the nth receptor in the bound state and $A_{R,\mathit{ub}}^{(n)}$ is the area in the unbound state. The term T ₂ accounts for the NC rotational entropy loss due to binding, where N_ab is the number of antibodies per NC, N_b is the total number of bonds in equilibrium state, $\Delta \omega$ is the rotational volume of the NC in the bound state which can be determined from the distributions of Euler angles. The term T ₃ accounts for NC translational entropy loss, where A_NC,b is the area for the NC translational movement in the bound state, A_NC,ub and A_NC,ubl_z are the area and volume accessible to the NC in the unbound state.

As is evident from the discussion thus far, several parameters that go into characterizing this model have to be chosen based on independent experiments and from the literature. In the event it is foreseen that there is an uncertainty in a given parameter, sensitivity analysis has to be applied for constraining the parameter values and for estimation of error bars in nonlinear relationships. In the event that parameters are unavailable (such as values of EI for ICAM-1 or k for ICAM-1/antibody interactions), they have to be modeled and estimated ab initio using coarse-grained molecular dynamics (CGMD) simulations. Another potential issue impacting the approach described approach is that the binding affinity (K_a) is defined by connecting the bound with the unbound state of NC only under steady (equilibrium) conditions for which a PMF approach is valid. For unsteady situations (such as NC rolling), a reaction-coordinate independent path formalism (using the transition path sampling method) has to be employed [115,116].

3.3. Membrane Mobility in Live Cells.

Cell membrane deformation and undulation is crucial to delineating binding and arrest characteristics of NC in fixed versus live cells. The differences are primarily due to the interplay between receptor-ligand interactions and physicochemical processes such as membrane dynamics, and the lateral diffusion of receptors. Hydrodynamic effects caused by the shear flow can accentuate these differences in binding in both fixed and live cells. Accounting for the effects of membrane undulations and the lateral diffusion of receptors, and quantifying how their effects along with physicochemical and hydrodynamic interactions influence NC binding and arrest are important components of the multiscale model. While a rigid cell surface assumption is adequate for fixed cells with arrested membrane motility, binding and arrest characteristics of NC to fixed versus live cells can be primarily attributable to the interplay between receptor-ligand interactions and physicochemical processes such as membrane dynamics, lateral diffusion of receptors. It can further be hypothesized that hydrodynamic effects caused by the shear flow can accentuate these differences in binding in fixed and live cells. Localized membrane deformation and curvature of the cell can be coupled with the receptor-ligand bond breaking and formation, in the regime where the NC is close to the cell membrane. The length-dependent receptor-ligand forces couple to the membrane tension because the membrane has to deform in order to accommodate the receptor-ligand bond formation. Since the receptors on the membrane are diffusible species, and the ligands are fixed on the carriers, strong local deformation of the membrane, in turn, can act as a pressure gradient driving the motion of the receptor-ligand pairs in such a way to relieve the membrane tension. The competition between the energetic advantage of receptor-ligand pairing and the energetic penalty of strong membrane deformation modulated by thermal effects; therefore, determines the local deformation of the membrane when the NC is attached to the cell surface via receptor-ligand bonds. These coupled effects can be treated as follows. Based on recent studies of coupling lateral protein dynamics on the membrane and membrane dynamics [117,118], we describe the vesicle membrane dynamics in the near-wall limit via a time-dependent Ginzburg–Landau (TDGL) equation [117,118,119,120]:

$$\frac{\partial z}{\partial t}=-M\otimes \frac{\delta F}{\delta z}+\zeta$$

where z = z(x,y,t) is the separation between the NC and the cell surface, M is a generalized mobility factor associated with the membrane dynamics, ς is white (thermal) noise, and F is the free energy functional associated with membrane elasticity. F is given by [121]:

$$\begin{array}{c}\multicolumn{1}{c}{F=\int \int \mathit{dxdy}[\gamma {(\nabla z)}^2+{\left(\kappa {\nabla }^{2}z\right)}^2]\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+{\lambda }_{\mathit{TM}}\int \int {\mathit{dxdyC}}_{\mathit{TM}}(x,y){(z(x,y)-Z_{\mathit{TM}})}^2}\end{array}$$

Here, free-receptors are denoted as T, free-ligands as M, and bound receptor-ligand pairs TM, γ is the membrane tension, κ is the bending rigidity, and λ_TM is the receptor-ligand binding energy well for the TM pair. In the elastic free energy equation above, the first term (integrand) on the right accounts for elastic energy associated with membrane bending and membrane tension, and the second term accounts the local membrane deformation at the site of receptor-ligand pairing and represents a coupling between the concentration field C_TM(x,y,t) and the nanocarrier-cell separation distance z(x,y,t). The above TDGL equation is solved for a given concentration profile of C_TM on the EC membrane surface using a finite difference scheme as outlined in our recent published [82,121]. The noise term is generated by drawing a random number from a Gaussian distribution with zero mean and with variance depending on the temperature and the viscosity of the surrounding medium. The simulation results in a constant temperature dynamics for the membrane, where the separation distance between the nanocarrier surface and the cell membrane at each time step is given by the value of the z coordinate at each grid point in x and y dimensions. For a numerically stable integration of the TDGL equation, the maximal allowed temporal step size is related to the spatial grid-size by the Courant–Friedrich–Levy condition [118].

3.4. Lateral Diffusion of Receptors on the EC Membrane.

Receptors and ligands can be modeled as occupying lattice points and protein-protein interactions are considered as size exclusions, (i.e., repulsive interactions on the scale of the size of the solvated protein). The three-dimensional space is discretized into a lattice using a rectilinear grid with grid-size corresponding to the size exclusion parameter, a₀. Thus, in our model, each lattice site can accommodate at most one protein molecule. If a lattice-site i on the EC membrane has an occupied species (either of type T or TM), then the concentration at that lattice site is C_T,TM(x_i,y_i,t) = $1/a_0^3$. This relationship establishes the instantaneous concentration profiles. The profiles to be used in the above TDGL equation are the time-averaged profiles, i.e., 〈C_T,TM(x_i,y_i,t)〉_t which are described below: The diffusion of free receptors T is treated via a kinetic Monte Carlo (KMC) scheme on the discretized grid or lattice, (the discretization scheme is kept the same as the Ginzburg–Landau treatments above), using the Gillespie algorithm, this procedure is demonstrated in recent studies [118]. Namely, each hop (diffusive or convective) to a neighboring lattice-site is treated as an elementary chemical reaction. The diffusion process involving free receptors is a random-walk on the lattice, which is decoupled from the membrane deformation; the rate of hopping to a neighboring lattice-site is determine as k_T = D_T/a ${\hspace{0.17em}}_0^2$, where, a ₀ is the grid spacing. Diffusive and convective transport receptor-ligand bound pairs coupled with membrane and nanocarrier motion. The transport of bound receptor-ligand pairs TM is also treated via a kinetic Monte Carlo (KMC) scheme on a discretized grid or lattice. Each hop of a TM species can either be diffusive or convective. The diffusive hops to neighboring lattice points are random walks with bare rates equal $k_{\mathit{TM}}^{\mathrm{bare}}=D_{\mathit{TM}}/a_0^2$. The convective hops are biased hops to neighboring lattice-sites with bare rates $k_{\mathit{TM}}^{\mathrm{bare}}={\nu }_i/a_0$, if the neighboring lattice lies along the v_i, the projection of the velocity vector of the receptor on the membrane surface. Here, we assume that the nanocarrier, the ligand and the bound receptor translate as a rigid body. For neighboring lattice-sites not on this path of translation, the bare hop is set to zero. For TM pairs, since the diffusive and convective motion are coupled to the membrane, we have derived the correction over the bare rates in Refs. [117,118]: the timescale for lateral diffusion on the membrane is corrected by [$a_0^2$/D_i]/[δF/δC] and that for lateral convection is corrected by [a ₀/v_i]/[δF/δC]. This, in turn, renormalizes the bare rate constants used in the KMC moves. This renormalization of kinetic constants for each KMC move has to be performed on the fly, as dictated by the instantaneous conformation of the membrane.

Multiscale Integration of the NC Trajectory: based on a scaling analysis, one can determine that the method of integration depends on the Deborah number, De, i.e., competition between time-scales of lateral diffusion and membrane motion: De = [$a_0^2$ /D_a]/[$Z_{\mathit{TM}}^2$ /M]. The relevant timescales are, [$a_0^2$ /D_a] (diffusion of species a = T,M,TM on the membrane), and [$Z_{\mathit{TM}}^2$ /M] (membrane motion). The physical properties dictate that the Deborah number De ≪ 1. In this (adiabatic) limit the diffusion occurs much faster than membrane deformation. In the adiabatic limit KMC simulations can be carried out for N ∼ Δt/(a${\hspace{0.17em}}_0^2$/D_i) steps (such that the total time elapsed in the KMC simulations is equal to Δt, the time step of TDGL integration). We can then determine the steady state profiles 〈C_TM(x,y)〉_N (determined by averaging the protein locations on the membrane in the course of the N steps of the KMC simulations) at every timestep of integration involving the membrane dynamics (TDGL) equations. Thus, the TDGL equations are propagated in time based on time-averaged interactions dictated by 〈C_TM〉_N resulting from KMC simulations. The temperature T in the TDGL and KMC schemes has to be made equal to ensure thermal equilibration. Therefore, the KMC simulations become decoupled from the membrane and flow equations in the temporal sense; however, a two-way coupling exists through the free energy functional as described by the normalization of the bare rates and by the averaging of the C_TM field. In the implementation of the multiscale algorithm, the time-averaged receptor-ligand forces from the KMC-TDGL simulations have to be fed back to the hydrodynamic model to determine the NC trajectory.

3.5. Multiscale Modeling of Nanocarrier Vascular Transport and Controlled Drug Release.

The formulations related to hydrodynamics and binding kinetics must be coupled with mass transport formulations to establish a mass (cargo) transport model of targeted drug delivery that will provide estimates of the drug composition needed and optimal carrier shape/size to deliver the drug in an efficient manner. This coupled formulation will reveal release mechanisms and enhance drug safety [123,124,125,126]. The most significant processes governing cargo transport are diffusion, dissolution, erosion (bulk or surface), swelling, deformation, and convection [127,128,129,130,131,132,133,134]. The modeling must systematically cover all of these processes. Porous and encapsulated biodegradable carriers including hydrogels may also have to be considered. Modeling has to be carried out in an interactive way with experiments where possible. Validation of the model may be made by using on going experimental results supplemented with relevant literature-based results [135,136,137,138,139,140,141,142].

Consider bulk and surface erosion, with diffusion and dissolution. For semipermeable coatings or porous carriers, swelling and deformation must also be considered. The numerically estimated numerical release rates will serve as the requisite boundary conditions for the associated convective mass transport problem in the bulk medium. Repeated iterations between diffusive and convective processes throughout the duration of targeting has to be carried out to predict the cumulative actual release rate. With bulk erosion, three distinct patterns have been observed and may be modeled as linear erosion, S erosion, and hyperbolic erosion. All three patterns may be required and, for illustration here, let us consider the linear erosion model with liquid, virtual solid and effective solid phases. In the liquid phase, together with diffusion, drug enters by dissolution and erosion. The time rate of change of drug concentration is: ∂C_L/∂t = 1/r ² ∂/∂r (Dr ²∂C_L/∂r) + C_SeK _Lero − ∂C_Se/∂t (1−K _Lero t). In the virtual solid phase, C_S decreases due to erosion and dissolution and is equal to the amount of drug accumulated in the liquid phase. Therefore, ∂C_L/∂t = ∂C_Se/∂t (1−K _Lero t) − C_sK _Lero, C_s = C_SeV ₁/V ₀ = (C_Se/V ₀) (V ₀ ^1/3 – K _Hero t/3)³ dissolution is the difference between actual and saturation concentrations; ∂C_Se/∂t = −k _dis(εC _Sat−C_L), where C_L is the concentration in the liquid phase (kg/m³), C_Se is the concentration in the effective solid phase (kg/m³), D is the diffusion coefficient (m²/s), K _Lero is the linear erosion rate constant for bulk erosion (m/day), k _dis is the dissolution rate constant (s ⁻¹), C _Sat is the saturation concentration (kg/m³), V₀ is the initial volume of the carrier (m ³), V ₁ is the effective volume of the carrier (m ³) in the virtual solid phase, and ε is the porosity. The equations will be subject to the following boundary conditions (see Table 1).

Table 1.

Boundary conditions

	Liquid phase	Virtual solid phase	Effective solid phase
t = 0	CL = C Sat	CS = C0−C Sat	CSe = C0 − C Sat
t > 0	∂CL/∂r = 0	∂CS/∂r = 0	∂CSe/∂r = 0
r = 0	C is finite
t > 0, r = R0	−D∂CL/∂r|r=Ro =h(CL−C∞)	CS = C∞CSe = C∞

Similar formulations will govern S and hyperbolic erosion models. Next, with surface erosion, the external fluid may penetrate the nanocarrier. Dissolution from the solid phase, diffusion of dissolved drug, and erosion of the matrix must then be modeled. Concentration in the liquid phase is mainly determined by diffusion and dissolution.

When C_∞, C_L, εC _Sat and C_S ≥ C_∞, C_L is governed by ∂C_L/∂t = 1/r ² ∂/∂r (Dr ²∂C_L/∂r) + k _dis(εC _Sat−C_L), where C_∞ is the concentration in the external fluid, C _Sat is the drug saturation concentration, εC _Sat is the effective saturation concentration in porous region with porosity ε, and D is the effective diffusion coefficient (D = D ₀ε/λ). Boundary conditions for surface erosion are given by t = 0, 0 ≤ r ≤ R ₀, C_L = C _∞; r = 0, ∂C_L/∂r = 0; r = R ₀(1−k _ero t), C_L = C_∞. Here, the nanocarrier has been considered to shrink at a constant linear rate as evidenced in experiments, and the radius of the carrier at any time may be expressed as r = R ₀(1 − k _ero t), where R₀ is the initial radius of the carrier and k _ero is the surface erosion constant (s ⁻¹). Governing equation for the drug concentration in the solid phase is given by ∂C_Se/∂t = − k _dis(εC _Sat-C_L), subject to t = 0, 0 ≤ r ≤ R ₀, C_S = C ₀; where C ₀ is the loading concentration in the solid phase. Solutions to such formulations provide the controlled release rate.

Next, consider particles coated with semipermeable membrane. Swelling and deformation have to be considered. Release from porous carriers (with or without semipermeable coating) will experience external bulk convection. With semipermeable coatings, main release occurs during the lag phase. Influx of solvent, followed by dissolution, swelling due to solvent accumulation, pressure build-up, and efflux into the bulk medium. The model must predict the lag time since this is fundamental to optimizing carrier design, especially for time-delayed drug delivery. During the lag phase, due to solvent accumulation the particle swells and the coating is subjected to tensile stress which may lead to fracture or cracking of the coating. This can lead to drug release by diffusion and convection. Release rate prediction will require simultaneous solution of equations governing the instantaneous mass balance for the particle, the rate of change of the drug mass in the dissolved phase within the carrier, and the mass balance for the release medium before crack formation. Pressure build-up and tensile stresses acting on the coating have to be simultaneously evaluated, and the stress could be related to the strain by Hooke's law (which may not be valid throughout the swelling process, so it may be necessary to consider a strain dependent modulus of elasticity). Swelling may cause particle deformation. For simplicity, if the carrier is approximated by an ellipsoid with semiaxis a, b and c = a, the principal radii may be taken as R ₁(Ψ) and R ₂(Ψ), where Ψ is the angle between the normal to the surface and the axis of rotation. If the hydrostatic loading is assumed symmetric, shear is absent and only normal forces N_Ψ and N_ϕ, where ϕ is the azimuthal angle will arise. The tensile stresses σ_ϕ and σ_Ψ may be deduced. The coating displacements at surface locations (top, equator) may be calculated, and the new shape determined. There are many ways of doing this. Once the new shape is determined, surface boundary conditions for the governing equations will have to be prescribed based on the new shape. This has to be done in a very judicious manner during the simulation process. Other shapes may be handled similarly.

In regard to hydrogel systems, models may be based on the rate limiting step for controlled release and can be treated under (1) diffusion-controlled (reservoir system: estimate release by Fick's first law, matrix system: use Fick's second law, swollen system: use free volume approach), (2) swelling-controlled (for Deborah number, De ≪ 1, use Fick's law, and for De ≫ 1, have to consider both the velocity of swelling front and the swelling interface number), and (3) chemically-controlled delivery may be modeled under two categories: (1) kinetic-controlled release (surface eroding) where polymer degradation (bond-cleavage) is the rate-determining step and diffusion term is negligible. Key point in modeling: for hydrophobic polymer networks, surface erosion occurs when the rate of water transport into the polymer is much slower than the rate of bond hydrolysis. Due to high water content of hydrogels, surface erosion only occurs in enzymatic degrading systems, and (2) reaction-diffusion-controlled release in which both reaction (e.g., polymer degradation, protein–drug interaction) and diffusion terms have to be included since release profiles are governed by both network degradation and molecule diffusion.

Convective mass transfer associated with targeted drug delivery have to be considered when there is bulk motion involved. Where bulk convection is present, the total pressure at particle surface will be “osmotic” pressure plus the prevailing bulk fluid field pressure. This enhanced pressure causes faster swelling and early crack formation. There is a need to accurately evaluate this pressure profile. A very efficient model for determining the flow field pressure and velocity under similar circumstances but in the absence of cargo are available. This has been achieved by simultaneously solving the fluid and particle equations, taking into account Brownian interactions. The drug transfer flux due to convective flow may be evaluated from solving the species equation for concentration, ∂C_k/∂t + V•∇C_k = •∇(D_k∇C_k), where V is the carrier instantaneous velocity determined by fluctuating hydrodynamics approach. Modeling of convective transport may be treated as a “conjugate” problem. The species concentration profiles at the carrier surface obtained from solving the diffusion problem could be employed as boundary conditions for the convection problem. Once the local flux is evaluated, the total amount of transport may be obtained by integrating the flux over the surface of the carrier and time duration involved. In any numerical model for cargo transport, property values such as diffusivities, porosities, pore geometry/topology, erosion and dissolution rate constants, saturation concentration of drug in the solvent and polymer phases, etc., are inputs. These will have to rely on generating required data for the specific systems through independent characterization experiments (AFM, flow chamber, microscopy, radiolabeled tagging, flow cytometry, dynamic light scattering, biodistribution, etc.).

3.6. A Brief Discussion of Some Results From Published Literature.

The comprehensive modeling formalisms described in earlier sections have not been solved in their complete forms as evident from a review of existing literature at this time. There have been partial solutions that have been published. In the following, we will concentrate on results in papers published by the authors, which solve and discuss some of the aspects described earlier.

In Ref. [53], the Brownian motion of a NC in an incompressible Newtonian fluid medium (quiescent or fully developed Poiseuille flow) has been addressed with the fluctuating hydrodynamics approach. The formalism considers situations where both the Brownian motion and hydrodynamic interactions are important. Nanoparticles of different sizes have been considered as well as nearly neutrally buoyant particle densities. Tracked particles are initially located at various distances from the bounding wall to delineate wall effects. Comparing the predictions for the temperatures of the particle with those obtained from the equipartition theorem has validated results for thermal equilibrium. The nature of the hydrodynamic interactions has been verified by comparing the velocity autocorrelation functions (VACF) and mean square displacements (MSD) with analytical and experimental results where available. The equipartition theorem for a Brownian particle in Poiseuille flow has been verified for a range of low Reynolds numbers. Numerical predictions of wall interactions with the particle in terms of particle diffusivities are shown to be consistent with perturbation solution results [143,144].

In Ref. [59], another multiscale study, direct numerical simulation (DNS) has been employed to investigate nanoparticle thermal motion in an incompressible Newtonian fluid using the generalized Langevin approach. Both the Markovian (white noise) and non-Markovian (Ornstein–Uhlenbeck noise (OUP) and Mittag–Leffler noise (MLN)) processes have been considered. Particle position at various distances from the bounding wall is included to delineate wall effects. At thermal equilibrium, comparing the calculated translational and rotational temperatures of the particle with those obtained from the equipartition theorem has validated the results. The nature of the hydrodynamic interactions has been verified by comparing the velocity autocorrelation functions and mean square displacements with analytical results. Numerical predictions of wall interactions with the particle in terms of mean square displacements are compared with analytical results. It is demonstrated that for the non-Markovian Langevin approach, an appropriate choice of colored noise is required to satisfy the power-law decay in the velocity autocorrelation function at long times. Results obtained using non-Markovian MLN simultaneously satisfy the equipartition theorem and the long-time behavior of the hydrodynamic correlations for a range of memory correlation times. The OUP does not yield appropriate hydrodynamic correlations. The DNS results have been compared to results of a one-dimensional generalized Langevin equation and it is observed that where the thermostat adheres to the equipartition theorem, the characteristic memory time in the noise is consistent with the inherent time scale of the memory kernel. An important conclusion is that the performance of the thermostat with respect to equilibrium and dynamic properties for various noise schemes must be carefully considered for NC motion to be predicted correctly.

In Refs. [51,54,56], a novel hybrid computational scheme based on Markovian fluctuating hydrodynamics of the fluid and a non-Markovian Langevin dynamics with the OUP noise perturbing the translational and rotational equations of motion of the nanoparticle has been implemented. The nanocarrier motion in the bloodstream has been modeled using DNS of the thermal motion of the nanoparticle in an incompressible Newtonian fluid in a tube. An arbitrary Lagrangian–Eulerian (ALE) based finite element method (FEM) has been adopted. Comparing the numerically predicted nanoparticle temperature with that obtained from the equipartition theorem has validated results for thermal equilibrium between the particle and the fluid. The nature of the hydrodynamic interactions is verified by comparing the VACF and MSD with well-known analytical results. The simulations are noted to simultaneously satisfy the equipartition theorem and (short- and long-time) hydrodynamic correlations for a range of memory correlation times in the OUP. The numerical scheme effectively produces a thermostat that also simultaneously preserves the true hydrodynamic correlations. In Ref. [54] the hybrid approach has been extended using DNS to further analyze the thermal motion of a nearly neutrally buoyant nanoparticle in an incompressible Newtonian fluid medium. The instantaneous flow around the particle and the particle motion are fully resolved. The numerical results show that (a) the calculated temperature of the nearly neutrally buoyant Brownian particle in a quiescent fluid satisfies the equipartition theorem; (b) the translational and rotational decay of the velocity autocorrelation functions result in algebraic tails, over long time; (c) the translational and rotational mean square displacements of the particle obey Stokes–Einstein and Stokes–Einstein–Debye relations, respectively; and (d) the parallel and perpendicular diffusivities of the particle closer to the wall are consistent with the analytical results, where available.

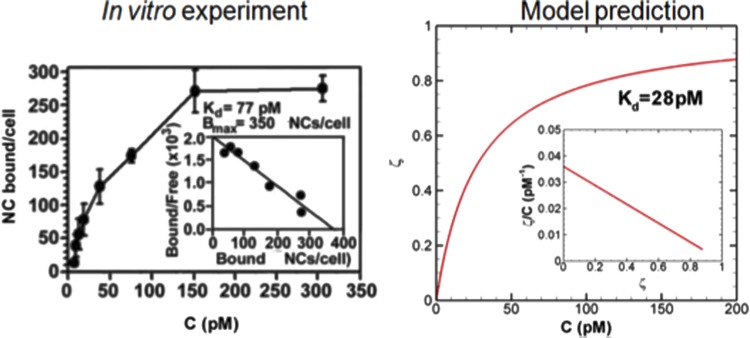
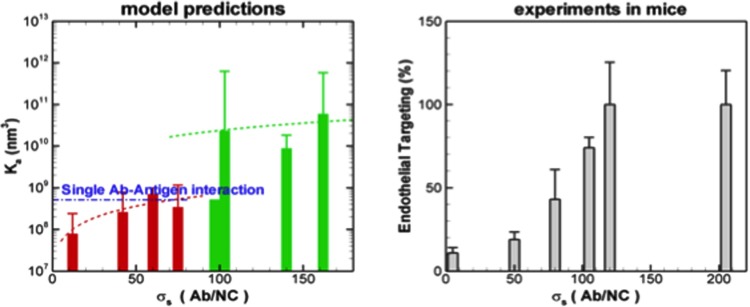
In Ref. [66], a computational methodology has been introduced to calculate the absolute binding free energy between functionalized nanocarriers (NC) and endothelial cell (EC) surfaces based on Metropolis Monte Carlo and the weighted histogram analysis method. The NC binding free energy landscapes have been calculated, which yield binding affinities that agree quantitatively when directly compared with analogous measurements of specific antibody-coated NCs (100 nm diameter) to intracellular adhesion molecule-1 (ICAM-1) expressing EC surfaces in cell culture experiments (Fig. 4, reproduced with permission from Ref. [66]). The effect of antibody surface coverage (σ_s) of NC on binding simulations reveal a threshold σ_s value below which the NC binding affinities reduce drastically and drop lower than that of single anti-ICAM-1 molecules to ICAM-1. This model further suggests that the dominant effect of changing σ_s around the threshold is through a change in multivalent interactions; however, the losses in translational and rotational entropies are also important. Consideration of shear flow and glycocalyx does not alter the computed threshold of antibody surface coverage. The computed trend describing the effect of σ_s on NC binding is noted to agree with experimental results of in vivo targeting of anti-ICAM-1 coated NCs to pulmonary endothelium in mice (Fig. 5, reproduced with permission from [66]). Model results have been further validated through close agreement between computed NC rupture-force distribution (230 ± 41 pN) and measured values in AFM experiments (316 ± 48 pN). This three-way quantitative agreement with AFM, in vitro (cell-culture), and in vivo (murine) experiments establishes the thermodynamic, mechanical and physiological consistency of the model, which provides a quantitative, predictive approach for model-driven optimization of functionalized NCs in targeted drug delivery.

Fig. 4.

Binding affinity (association constant or K_a) in vitro (a) and in silico (b) showing excellent agreement between simulation and experiment

Fig. 5.

Threshold binding of NCs in silico (a) and in vivo (b) showing excellent agreement between model and experiment. The in silico prediction (a) describes the association constant K_a versus antibody density, while the in vivo results describe lung endothelial targeting of NC versus antibody density.

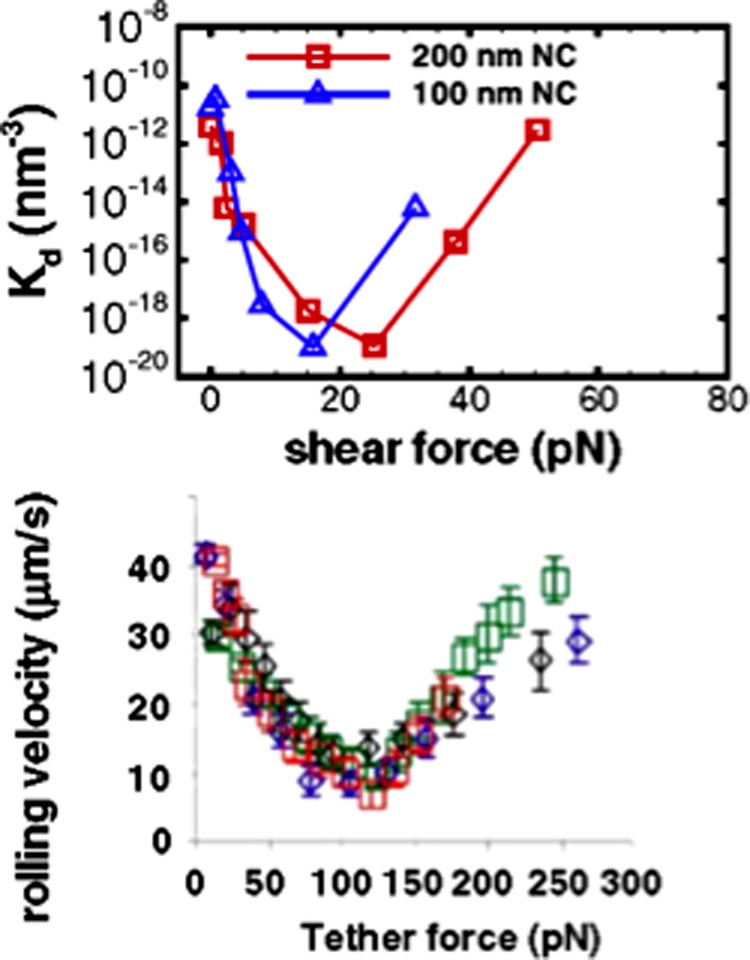
In Ref. [29], the effects of particle size, shear flow, and resistance due to the glycocalyx on the multivalent binding of functionalized NCs to ECs have been investigated. The binding free-energy landscapes of NC binding to the EC surface when the system is subjected to shear have been computed. The binding affinities calculated based on the free-energy profiles is shown to be in excellent agreement with experimental measurements for different sized NCs. The model shows that increasing NC size significantly increases the multivalency but only moderately enhances the binding affinities due to the entropy loss associated with bound receptors on the EC surface. The model predicts that under flow conditions, the binding free energies of NCs are a nonmonotonic function of the shear force. A well-defined minimum occurs at a critical shear value, which quantitatively mimics the shear-enhanced binding behavior observed experimentally. The results indicate that the interplay between multivalent binding and shear force can reproduce the shear-enhanced binding phenomenon (Fig. 6, reproduced with permission from Ref. [29]), suggesting that under certain conditions this can also occur in systems that do not show a catch-bond behavior. The model also suggests an exponential impact of the glycocalyx thickness on NC binding affinity, implying a highly nonlinear effect of the glycocalyx on binding.

Fig. 6.

Shear enhanced binding in silico (a) and in vitro (b) showing excellent agreement between model and experiment. Both panels depict shear-enhanced binding behavior below a shear threshold.

Predictions based on the foregoing modeling haves to be compared with experiments. The comparison will require investigations of NC of different sizes at different flow and physiological conditions (varying flow rates, hematocrit concentration, antibody density, receptor expression, etc.). Using the simulations of the kinematics, dynamics, and binding of the NC described earlier, it should be possible to l resolve the NC dynamics under various flow geometries (linear versus branched flows), hydrodynamic (different flow rates) and physiological (different hematocrit densities) conditions, and NC design (different tether configurations and targeting epitopes); in addition, through the free energy landscape (or PMF), it should be possible to quantify the balance between gain in favorable binding energy and loss of translational and rotational entropy, which will enable direct comparison of binding affinities between model and experiment for different experimental conditions [29,66]. The effects of control variables such as receptor density, antibody density and antibody type, tether length, NC size, on NC binding and hydrodynamics have to be determined and compared to in vitro and in vivo experiments. In particular, the binding affinity (K_a) versus shear rate for varying receptor expression, antibody coverage, and hematocrit concentration has to be compared between model and experiment. For larger NCs (d > 300 nm, where the NC dynamics in any experiment can be resolved by fluorescence microscopy), the rolling velocity versus shear rate may also be compared between model and experiment. In order to achieve meaningful comparison between theory and experiment, sensitivity and error analysis may be combined with parameter optimization using the Levenberg–Marquardt procedure.

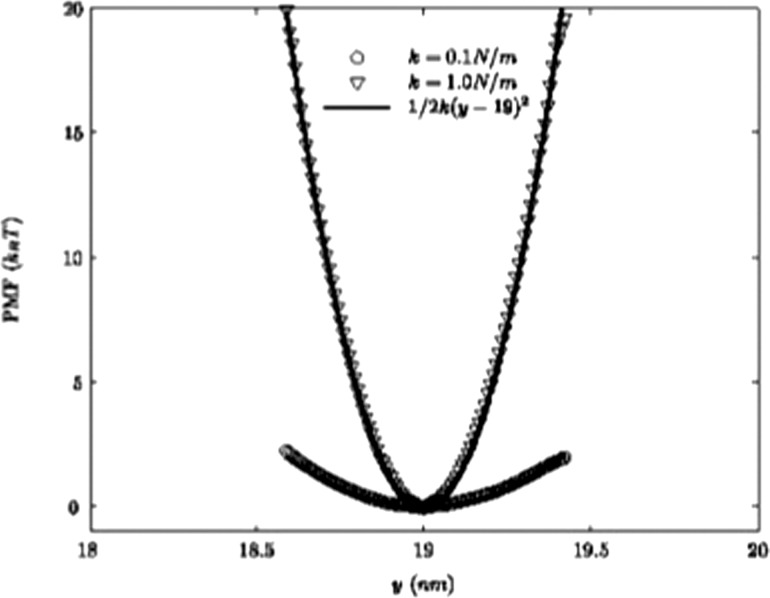
A hybrid algorithm to explore NC motion in arbitrary geometries and flow fields, while simultaneously enabling us to study carrier adhesion mediated by biological reactions (receptor-ligand interactions) at the vessel wall at a specified finite temperature has been developed in Refs. [51,54,56]. The fluctuating hydrodynamics approach and the hybrid approach can be employed when both hydrodynamic interactions and adhesive interactions are present simultaneously. In Ref. [56] the equilibrium and hydrodynamic correlations for a NC subject to thermal motion in a quiescent Newtonian fluid medium have been considered, when tethered by a spring force (mimicking a single tether due to one receptor-ligand bond). Since the tethering localizes the NC very close to the wall, significant hydrodynamic interactions between the NC and the wall are also resolved. Figure 7 (reproduced with permission from Ref. [58]) shows the calculated potential of mean force (PMF) profile for two values of the bond constant k along the reaction coordinate y at T = 310 °K. The numerical results agree with the appropriate analytical solution. The bond constant relevant for biological applications has been taken to be in the range 0.4–2.5 N/m [145,146,147]. For k > 0.1 N/m, the PMF is insensitive to the bond constant. For k > 1.0 N/m, only 10% of PMF values lies within the biological range. The hybrid algorithm is noted to provide a robust computational approach to explore NC motion in arbitrary geometries and flow fields, while simultaneously enabling us to study carrier adhesion mediated by receptor-ligand interactions as in Refs. [53,66] and at the vessel wall.

Fig. 7.

Calculated PMF at T = 310 °K for different values of the bond constant, k

4. In Vitro and In Vivo Experiments of Targeted NC Binding

Factors controlling NC motion and its interactions with molecular targets on the EC surface are studied experimentally in Ref. [90]. Spherical 1 μm beads coated with ICAM-1 monoclonal antibody (mAb) at 370, 1100, or 4100 mAb/μm² surface density have been employed. Carriers were perfused at two shear rates in a parallel plate flow chamber over coverslips on which were grown to confluence resting or tumor necrosis factor-α (TNF-α) activated human umbilical vein endothelial cells (HUVECs) expressing minimum versus maximum ICAM-1 levels.

Using fluorescence microscopy NC rolling, binding and detachment events have been quantified. Even at 1 dyn/cm² shear stress and with 4100 mAb/μm² surface coverage, carriers are noted to attach only to activated cells (21-fold increase over resting cells). This is ideal for specific drug targeting to sites of pathology. Binding was increased by raising the mAb surface density on the carrier as a consequence of decreased rolling velocity. Carrier binding is noted to be firmly arrested on endothelial surface even under a high shear stress: carriers with 1100 and 4100 mAb/μm² have withstood shear stress over 30 dynes/cm² without detaching. Figure 8 (reproduced with permission from Ref. [90]) shows a plot of time-dependent targeting as a function of targeting molecule density (including controls). Such results provide important data for tuning multiscale modeling.

Fig. 8.

NC binding to HUVECs in flow under various antibody densities in cell culture experiments

4.1. An Attempt for Optimizing EC.

Targeting by modulating anti-ICAM Ab density and particle concentration has been described in Ref. [148]. The influence of two carrier design parameters—carrier dose and surface density of targeting molecules has been further explored—on specific and efficient endothelial targeting in vitro and in vivo. The role of these parameters on the biodistribution of model polymer carriers targeted to ICAM-1 (¹²⁵I-anti-ICAM carriers) in mice has been assessed by using radioisotope tracing. Increasing the carrier dose is noted to enhance specific accumulation in the lung vasculature (a preferential endothelial target) and decrease the nonspecific hepatic and splenic uptake [66]. Increasing the Ab density enhances lung accumulation with minimally reduced liver and spleen uptake.

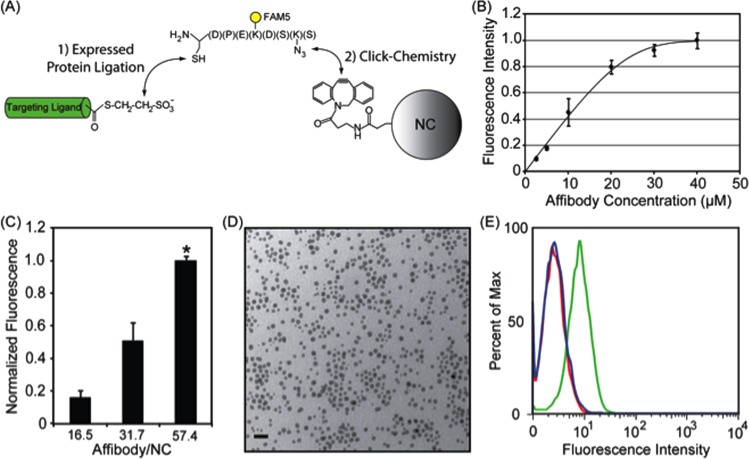
Site-specific click conjugation for highly controlled NC functionalization has been examined in Refs. [149,150]. To overcome limitations of conventional bioconjugate chemistry techniques (e.g., low efficiency, nonspecific ligand orientation), click chemistry has been combined and expressed protein ligation (EPL) to produce a highly efficient, site-specific reaction. Expressed protein ligation between an expressed targeting ligand, which contains a C-terminal thioester, and an azido fluorescent peptide (AzFP) containing an N-terminal cysteine results in the chemoselective attachment of a “clickable” azide group onto the targeting ligand (Fig. 9, reproduced with permission from [149,150]). Subsequent copper-free click chemistry between dibenzocyclo-octyne (DIBO) modified NCs and the targeting ligand-AzFP ligation product results in site-specific attachment of the targeting ligand onto the NCs. The 1:1 stoichiometric ratio of targeting ligand and fluorescent moiety allows for the quantification of ligands per nanoparticle. This method is noted to be effective to be effective with a range of different targeting ligands, as well as various NCs. As shown in Fig. 9, as the reaction ratio of the targeting ligand to NC is increased, the degree of NC functionalization also increases, in a highly controllable manner—as assessed by fluorescence intensity at a constant NC concentration. Data are for NCs functionalized with anti-Her2/neu affibodies. SPIO NCs with different ligands densities were subsequently incubated with Her2/neu-positive T6-17 cells. As noted in Fig. 9, increasing ligand density results in an increase in cell labeling—at a constant NC concentration. Results shown represent the mean fluorescent intensity of cells as assessed by flow cytometry. All measurements have been normalized against fluorescence per particle. To confirm specificity, control studies have been conducted with Her2/neu-negative NIH3T3 cells and via competitive inhibition. In these studies, it has also been shown that gold NCs may be functionalized using the same EPL-click conjugation strategy. Specifically, 5 nm gold nanoparticles (representative TEM shown in Fig. 9) have been pegylated and functionalized with anti-HER2/neu affibodies. Flow cytometric analysis of Her2/neu-positive cells incubated in the presence of the Her2/neu-targeted gold NCs is shown in Fig. 9(e) (green). Histograms of unlabeled cells (blue) and cells incubated with targeted gold NCs in the presence of excess free affibodies (red), i.e., competitive inhibition, are also seen.

Fig. 9.

Schematic and data of EPL-click conjugation strategy, control of NC. (a) Schematic of the conjugation chemistry; (b) NC binding quantification; (c) effect of antibody density on NC; and (d)–(e) cell labeling and flow-cytomentry experiments, see main text.

To confirm the targeting capabilities and assess the relative avidity of each NC composition, increasing concentrations of NCs may be incubated with endothelial cells for requisite number of hours and analyzed by flow cytometry and fluorescence microscopy. The specificity of NCs may be established by evaluating the nonspecific association of targeted NCs with NIH/3T3 (fibroblast) cells and nontargeted ‘control’ NCs with endothelial cells. Competitive inhibition studies may also be performed by incubating targeted NCs with endothelial cells in the presence of excess free antibodies. Confocal microscopy may be used to evaluate cell uptake carefully controlling for cell internalization. Targeted NC binding may be visualized as detailed above under defined shear stress conditions [90,94]. Steps must be taken to synchronize binding and uptake phases in the pulse-chase manner, to exclude endocytosis in negative control and to characterize the kinetics of endocytosis and trafficking during controlled shear exposure [13,151]. Surface-bound NCs have to be identified [152,153]. Cells may be inspected by wide field or confocal microscopy [8,90,91,95,96,98]. Discrete time point imaging will enable determination of affinity for binding cells, rolling velocities, and shear effects on binding and their dependence on NC size, targeting molecule and its surface density, tether length and bulk concentration. Data so obtained may be used to validate modeling simulations and predictions of time-dependent multivalency. The model may then be used to predict parameters (e.g., NC size, tether length) for optimal binding. The characterization of NC delivery to the endothelium may be achieved by characterizing pharmacokinetics, biodistribution and specific and intended location targeting in intact animals [5,6,153,154,155]. The data so obtained has to be used to validate the modeling described earlier for NC binding in vivo. The model may then be used to predict parameters (e.g., NC size, tether length) for optimal biodistribution. Fluorescence microscopy methods may lead to misleading results, especially with NCs in the 100 nm size-range due to optical limitations. Confirmation through other imaging techniques having greater resolution may also be pursued as needed.

5. Concluding Remarks

The success of the modeling procedures described above depend on the accessibility of experimental data which may be used both to validate the modeling and provide insights for additional model predictions. In vitro and in vivo experiments using a range of targeting molecules attached to NCs of various sizes with (using a range of PEG tether lengths) and without tethers over a range of surface densities are needed for this purpose. The dependence of NC binding avidity on the parameters may be determined using (i) live flow adapted and fixed endothelial cells and (ii) intravascular delivery in rodents for similar ranges of tunable and experimentally controllable parameters explored computationally (e.g., bulk concentration, shear stress). The data for the different variables tested has to be directly compared between modeling and experiment. For NCs of various sizes (say, monodisperse, 100, 200 nm diameter), the effects of NC size and PEG lengths on cell targeting and binding have to be evaluated. Importantly, although measurements of the number of targeting ligands per NC will represent an ensemble average, past modeling data have revealed that narrow ligand distributions can be achieved if large particle systems (>100 reactive sites) and efficient modification reactions are employed. A large number of parameters such as antibody density, carrier concentration, receptor expression level, shear stress level, and tether length studied in the experiments can be used to validate the performance of the models [156]. Once model has been validated using test data, experiments can become selective with conditions, especially based on the computational model sensitivity analysis. This can be important as a feedback mechanism to focus on only those conditions where “optimization” is shown to be tunable.