Integrating DNA strand-displacement circuitry with DNA tile self-assembly

Abstract

DNA nanotechnology has emerged as a reliable and programmable way of controlling matter at the nanoscale through the specificity of Watson–Crick base pairing, allowing both complex self-assembled structures with nanometer precision and complex reaction networks implementing digital and analog behaviors. Here we show how two well-developed frameworks, DNA tile self-assembly and DNA strand-displacement circuits, can be systematically integrated to provide programmable kinetic control of self-assembly. We demonstrate the triggered and catalytic isothermal self-assembly of DNA nanotubes over 10 μm long from precursor DNA double-crossover tiles activated by an upstream DNA catalyst network. Integrating more sophisticated control circuits and tile systems could enable precise spatial and temporal organization of dynamic molecular structures.

DNA tile self-assembly and DNA strand displacement circuits are well-developed frameworks in DNA nanotechnology. Here, the two approaches are combined to give programmable kinetic control of DNA nanotube self-assembly.

Biological cells are self-organized information-based molecular systems that acquire material and information, make molecules and decisions, and take actions that regulate their internal functions and their interactions with the environment1. The mechanisms underlying such behaviors involve an interplay between biochemical control circuitry and self-assembly processes. For example, in contrast to viruses that self-assemble from constitutively expressed proteins2, pathogenic bacteria often actively regulate construction of organelles such as flagella to escape immune responses, conserve resources and improve assembly yield3. Even more sophisticated examples exist in eukaryotic cells, where biochemical circuits modulate microtubule growth for tasks such as separating chromosomes during mitosis4, determining cell shape and polarity5,6, probing the environment with filopodia7, and directing cellular motility with lamellipodia7. These biological systems illustrate the potential of regulated self-assembly for complex molecular construction and dynamic behavior; it follows that engineering regulated self-assembly is a promising approach for expanding the capabilities of molecular nanotechnology8 and could facilitate the construction of synthetic cells9,10 and nanoscale robotic systems11,12,13.

Structural DNA nanotechnology offers a promising approach to constructing nanoscale components14. The specificity of Watson–Crick hybridization of oligonucleotides and the geometric predictability of the double helix enables precise rational design of primary sequence to achieve reliable self-assembly of target molecular structures. Often synthetic oligonucleotides are designed so as to hierarchically self-assemble first into nanometer-scale building blocks, which subsequently assemble into micron- or even millimeter-scale structures15,16. Cooperative self-assembly of building blocks can result in complex ‘algorithmically’ patterned structures that construct different objects based on information present in a ‘seed’ structure, conferring a degree of self-regulation to the systematically programmed self-assembly reactions17,18,19.

Thermal annealing is frequently used as an easy and robust way to coordinate the desired sequence of self-asembly events in structural DNA nanotechnology. In contrast, self-assembled biological components grow, reconfigure and shrink isothermally in response to cellular or environmental signals. Conditional and isothermal assembly of DNA structures may also be desirable for applications in biomedical technology and materials science, for example. While isothermal tile-based self-assembly has been demonstrated20,21, controlling desired and undesired nucleation19,22 can make the temporal and spatial regulation of these processes difficult.

In dynamic DNA nanotechnology23, isothermal DNA strand-displacement reactions24,25 are systematically used to design complex autonomous behaviors26,27,28,29,30. In a strand-displacement reaction, complementary short single-stranded regions (toeholds) colocalize separate DNA molecules to facilitate branch migration processes, which can reconfigure the molecule or release a previously sequestered single-stranded species into solution. Single-stranded products can then participate in downstream strand-displacement reactions, allowing complex cascaded circuits to be constructed, including digital circuits that evaluate boolean logic26 as well as analog circuits that modulate oligonucleotide concentrations27,28. Recently, mixed analog/digital strand-displacement circuits involving >100 different strands have been demonstrated30. In principle, arbitrary well-mixed chemical reaction network dynamics can be systematically implemented using DNA strand-displacement circuits29. Such DNA circuits could potentially act as control elements for other molecular processes, such as DNA self-assembly reactions.

In order to combine the structural and dynamic aspects of DNA nanotechnology, it is necessary to identify features that allow self-assembly to proceed robustly at a constant temperature and to engineer mechanisms whereby the control signals trigger specific self-assembly reactions or structural changes. For non-autonomous systems, assembly steps, disassembly steps and conformational changes within structures formed by annealing can be effected by subsequent manual addition of control strands under isothermal conditions13,24,25,26,27,28,29,30,31,32,33; assembly can also be used for read-out34. Such isothermal self-assembly reactions could, in principle, be controlled autonomously by more complex transcriptional circuitry35,36. Additionally, isothermal self-assembly of DNA nanostructures have been demonstrated using hairpin opening reactions28,37,38,39, and one hairpin-based self-assembly design has even been demonstrated to function inside living cells20.

Here, we integrate two molecular programming paradigms–DNA tile self-assembly15,17,18,19,40,41,42 and DNA strand-displacement circuits25,26,27,29,30,43,44,45–that have each been well characterized theoretically and experimentally. Our specific goal here is to show that in an autonomous isothermal reaction, an upstream strand-displacement control circuit can release a single-stranded signal molecule that activates specific tiles in a downstream self-assembly reaction, thus allowing control over the composition and timing of a fabrication process. For the upstream circuit, we chose an entropy-driven catalyst that releases its output at a rate controlled by an input catalyst strand27, while for downstream self-assembly, we chose a double-crossover tile that polymerizes to form a DNA nanotube structurally analogous to biological microtubules40. The integrated system demonstrates effective control over the assembly process: in the absence of the input catalyst strand, the mixture of circuit components and precursor tiles does not produce DNA nanotubes, while with the addition of even a sub-stoichiometric amount of input, the precursor tiles are fully converted. The resulting DNA nanotubes can be >10 μm long, as visualized in real-time through total internal reflection fluorescence (TIRF) microscopy. These structures are estimated to incorporate >4,000 DNA monomer tiles with a total mass of >200 MDa.

Results

DNA tile-based nanotube self-assembly

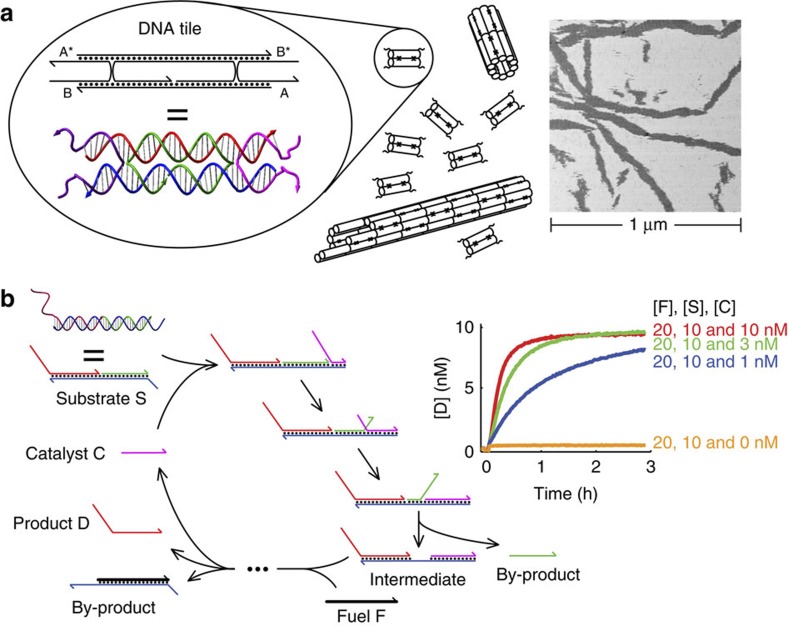
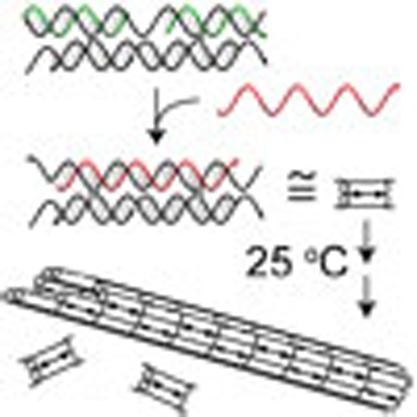
DNA double-crossover tiles (schematically shown in Fig. 1a) were the first motifs used to demonstrate large-scale DNA self-assembly15,46. The tile consists of a rigid core containing two parallel DNA duplex helices that display four short ‘sticky ends’ (labeled A, A*, B and B* in Fig. 1). The sticky ends allow multiple copies of the tile to self-assemble into periodic lattices or nanotubes. Owing to the rigidity of the tile, complementary sticky ends on a single tile will not interact.

Figure 1. Structural and dynamic DNA nanotechnology.

(a) Double-crossover DNA complexes (tiles) self-assemble into DNA nanotubes. Each tile possesses four single-stranded regions, known as ‘sticky ends’, each 5 nt long. Here, they are labeled A, A*, B and B*, with A being complementary to A* and B being complementary to B*. Owing to the intrinsic curvature at the positions where different tiles join, the tiles self-assemble into a one-dimensional DNA nanotube18,40. The nanotubes are typically observed to be between five to seven tiles wide (five-tile wide nanotubes are shown). Inset shows an atomic force microscopy (AFM) image of DNA nanotubes formed through a thermal annealing process; tubes break open upon adsorption to the mica surface. (b) A DNA catalyst expedites the release of multiple identical product oligonucleotides from a multi-stranded reactant complex. Inset shows a 25 °C fluorescence assay of the kinetics of product release at three different substrate-to-catalyst ratios, using a fluorescent reporter that stoichiometrically reacts with the product D (see Supplementary Fig. S3 for more details).

Several related double-crossover tile motifs have been designed and experimentally demonstrated; these vary in the details of the crossover spacing and oligonucleotide orientations15,46. We use a particular type of tile motif known as DAE-E. In addition to its simplicity (previously shown to self-assemble into DNA nanotubes with just a single tile type18,40), this motif also possesses an architecture amenable to integration with strand-displacement circuits. The DAE-E motif determines the lengths and complementarities of the oligonucleotide domains, but the exact sequences of the core and the sticky ends can be varied according to design. Here, we used the core sequences from the ‘UE’ tile in the study by Rothemund et al.18, but with different sticky-end sequences.

Self-assembly is typically achieved through a thermal annealing process, in which a solution containing all requisite strands are heated to ~95 °C, then cooled slowly (over the course of ~1.5 h) to room temperature. The tile itself assembles at ~60 °C, while the higher-order structures assemble at ~40 °C (see ref. 18 and Supplementary Figs S1 and S2 for polyacrylamide gel electrophoresis and UV absorbance melting curves); this separation of formation temperature and the slow annealing processes ensures that tiles are formed before lattices, and is thought to facilitate reliable self-assembly. In contrast, mixture of strands at room temperature does not yield well-formed nanotubes, consistent with predictions of kinetic traps in similar molecules47. However, if tiles can be pre-formed and kept at room temperature, but prevented from hierarchical self-assembly, then subsequent isothermal activation of these tiles could lead to room temperature self-assembly.

DNA strand-displacement-based catalysis

Strand-displacement reactions can be systematically engineered to form biomolecular circuits that exhibit digital26 or analog27 logic. Figure 1b shows the reaction cycle for a hybridization catalyst system that serves as an analog signal amplifier27. A multi-stranded DNA molecule, called the substrate S, and a single-stranded molecule, called the fuel F, are initially in a metastable mixture in which it is thermodynamically favorable for them to react, but, lacking toeholds, they do so at a negligible rate. However, the S and F can react with the help of another single-stranded molecule, called the catalyst C, which is not consumed in the reaction. C first binds to S and releases a by-product while simultaneously revealing a single-stranded toehold in the intermediate species. The single-stranded toehold provides an initiation site for reaction between the intermediate and F, and then F displaces both C and a single-stranded product D. The sequence of D is independent of that of C. The released C can subsequently react with other molecules of S and engage in multiple turnover events; the concentration of C is effectively amplified into a larger concentration of product D. One important feature of the catalytic system is that the sequence of D is independent of that of C—given desired sequences for D and C, S and F can be systematically constructed to allow C to catalyze the release of D.

The catalytic reaction proceeds isothermally with kinetics within an order of magnitude of standard hybridization (Fig. 1b)27. Each catalyst molecule, on average, yields the release of >100 product molecules (Supplementary Fig. S3), and functions robustly in the presence of other nucleic acids48. There is a slight amount of uncatalyzed (leak) reaction (that is, reaction between F and S in absence of C, as characterized by the accumulation of D); at the 10 nM concentrations, the half-life of the leak reaction is expected to be ~2 months27.

In solution, long single-stranded regions (such as F and part of D in the catalyst system) could potentially interact due to spurious sequence complementarity. Consequently, careful sequence design is necessary in order to ensure that few unintended hybridization reactions occur (Table 1). Software such as NUPACK or DD49,50 can be used to design sequences and/or verify the lack of interaction between orthogonal sequences.

Table 1. Domain sequences.

Domain	Sequence	Length (nt)
1	5′-ATAGATCC-3′	8
2	5′-TGATAGC-3′	7
3	5′-GAGACCT-3′	7
4	5′-AGCAACC-3′	7
5	5′-TGAAACCA-3′	8
6	5′-CGTTAAGG-3′	8
7	5′-ACGACGCAATTCT-3′	13
8	5′-CACATCGG-3′	8
9	5′-ACGAGTAG-3′	8
A	5′-ATACC-3′	5
B	5′-GAATT-3′	5
11	5′-CCCTC-3′	5
12	5′-ATACAATACCC-3′	11
13	5′-TCACCATG-3′	8

Integration challenges

Our approach to isothermal self-assembly relies on integrating tile-based assembly and DNA strand-displacement circuits: the product of the DNA catalyst circuit triggers the formation of active double-crossover tiles competent for self-assembly from inactive precursor tiles. We consider three methods for triggering inactive precursor tiles. Precursor tiles could be unable to self-assemble because (1) they lack a component necessary for self-assembly, or because (2) they contain an extra protecting group that prevents self-assembly. In the former case, the DNA circuit must provide the lacking component, and in the latter, the DNA circuit must provide a deprotector that removes the protecting group. These two approaches may also be combined by constructing a precursor tile that (3) both lacks a component and possesses a protecting group.

Tile activation design and experiments

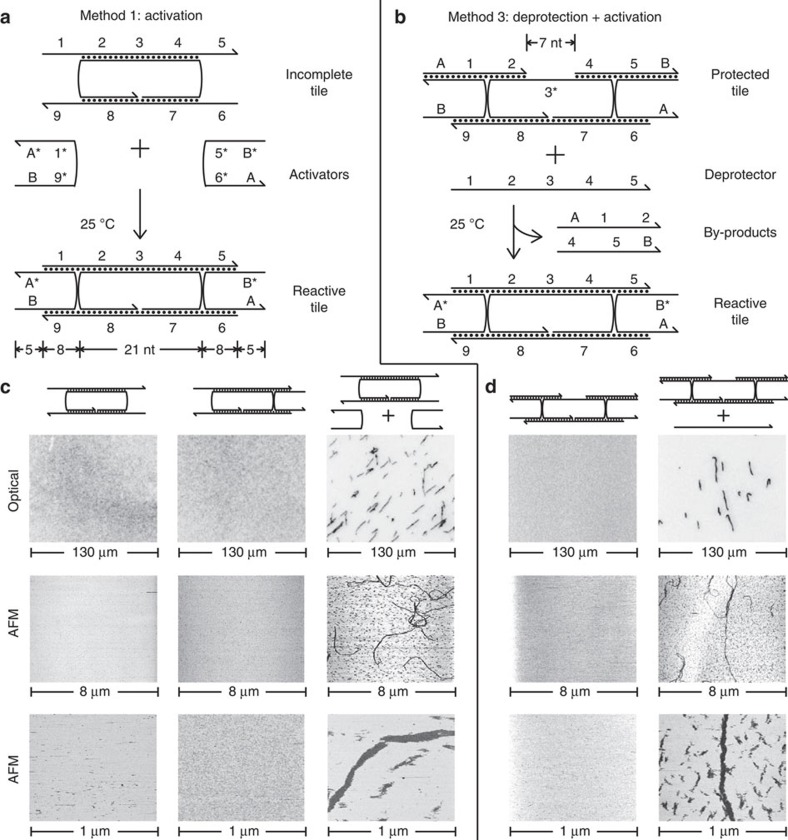
The DAE-E double-crossover tile is composed of five different strands; the three central ones contribute structural rigidity, while the outer two contain sticky ends that effect assembly logic. Removal of either or both of the two sticky-end-bearing strands would result in an incomplete precursor tile with no designed mechanism for self-assembly (Fig. 2a). When these sticky-end-bearing strands are subsequently introduced as activators, they hybridize to the incomplete tile to form the standard double-crossover structure (see Supplementary Note 1). This approach to isothermally triggering DNA nanotube growth is known as method 1: activation.

Figure 2. Methods for isothermal triggering of DNA nanotube self-assembly.

(a) Method 1: when the two sticky-end-bearing strands are absent, the three-stranded complex forms an incomplete tile that does not self-assemble. When the two missing strands (activators) are subsequently introduced, they hybridize to the incomplete tile to form the complete (reactive) tile, which then self-assembles into DNA nanotubes. (b) Method 3: an alternative method of isothermally triggering DNA self-assembly involves a protected tile in which the top two sticky ends are pre-hybridized to protector strands. Exogeneous deprotector will react with the protected tile via strand-displacement24,25 and yield the reactive tile as well as two by-product strands. (c) Experimental results on method 1 using TIRF microscopy or AFM. In all experiments, the concentrations of all species were 200 nM and reactions were performed at room temperature (25 °C). For all TIRF experiments, a Cy3-modified version of the central tile strand was used. Both activators are needed for the reactive tile to form and for DNA nanotubes to self-assemble. (d) Experimental results on method 3. Addition of the deprotector causes self-assembly of DNA nanotubes.

We verified by AFM and TIRF microscopy that incomplete tiles lacking either sticky-end-bearing strand do not self-assemble (Fig. 2c). When both activator strands are present, DNA nanotubes of >10 μm long are observed to assemble over the course of 2 h. These results were further verified by native polyacrylamide gel electrophoresis (Supplementary Fig. S1) and additional AFM and TIRF (Supplementary Figs S4 and S5) experiments.

Tile deprotection design

The sticky ends of the double-crossover tile hybridize to the sticky ends of other tiles to enable hierarchical self-assembly. Pre-hybridization of one or more protector strands to these sticky ends should result in a protected tile that is incapable of self-assembly. Introduction of complements to displace the protecting strands reveals the sticky ends and enables the deprotected tile to self-assemble (Supplementary Fig. S6). This approach to isothermally triggering DNA nanotube growth is known as method 2: deprotection.

However, the short lengths of the sticky ends in the standard DAE-E tile (5 nt) do not bind stably to their complements at room temperature; thus, implementation of this method would require either operation at low temperatures (for example, 4 °C) or revision to the tile architecture. Consequently, we chose not to experimentally pursue this approach here.

Tile deprotection and activation design and experiments

Figure 2b shows the design of a precursor tile that reacts with its trigger via both activation and deprotection. The protected tile lacks one of the three central structural strands of the double-crossover tile, so that each of the two protectors can stably bind to their respective sticky-end targets. The missing tile strand serves as the deprotector that displaces the protectors via a process of toehold exchange25,27. This approach to isothermally triggering DNA nanotube growth is known as method 3: deprotection and activation.

In order for the deprotector to displace the two protector species, it is necessary for it to hybridize to the central 3* domain and subsequently undergo two independent branch migration processes that end in the spontaneous dissociation of both protectors. In doing so, the deprotector strand must wind around the central tile strand twice within the tile’s 21-base-pair central region between the crossovers. The kinetics of the deprotection process thus was not known a priori: on one hand, this threading process could be sterically and electrostatically hindered; on the other, the threading is a unimolecular process and could be faster than the bimolecular toehold initiation process at reasonably low concentrations (see Supplementary Note 2).

Figure 2d shows that the system functions as designed: DNA nanotubes are observed only when the protected tile reacts with the deprotector. Over the course of 2 h, DNA nanotubes over 10 μm long are observed to assemble. Any kinetic slowdown of the strand-displacement process due to the threading was not observable on this time scale. Native polyacrylamide gel electrophoresis (Supplementary Fig. S1) and melt curves (Supplementary Fig. S2) further support the claim that protected tiles are functionally and structurally distinct from the deprotected tiles.

AFM images in Fig. 2d showed that there were a number of small assemblies in addition to the DNA nanotubes after the protected tile was deprotected. Possibly, these assemblies were too small to ‘wrap around’ and form a tube, and thus the DNA nanotube elongation could not occur. Alternatively, these small structures may form only on the surface of the mica during imaging, and are not present in solution. Yet another possibility is that these small assemblies are fragments of DNA nanotubes that broke off as the nanotubes deposited on mica.

Catalyzed tube formation using method 3

Modularity is the primary challenge in integrating the DNA strand-displacement catalysis system with either of our two methods for isothermally triggering DNA nanotube self-assembly. While it is relatively easy to independently design a catalyst system and a triggered nanotube assembly system, combining the two so that the former feeds forward into the latter requires additional consideration for potential side reactions. In the original catalyst system27, half of the product strand is single-stranded even as part of the substrate complex, while the single-stranded fuel shares the sequence of the other half of the product strand. When this product strand is also the trigger for the precursor tiles, there is a potential for the single-stranded domains of the substrate or the fuel to spuriously interact with the precursor tiles.

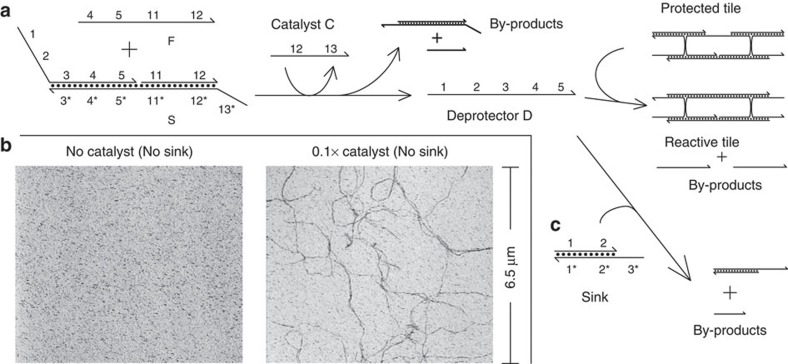
The sequences of the activators for method 1 necessarily include the sticky ends that enable self-assembly of the DAE-E tile, and Supplementary Fig. S7 shows designs that illustrate the difficulty of integrating method 1 and upstream circuits, due to expected remote toehold interactions51. In contrast, the sequence of the deprotector for method 3 is independent in sequence of the sticky ends. Consequently, we judged that the latter would be less likely to exhibit unwanted interactions between different components, and chose to experimentally pursue the latter (Fig. 3a).

Figure 3. Upstream control circuit.

(a) A non-covalent catalytic system that produces the deprotector for method 3 as a product, based on the study by Zhang et al.27 The catalyst, an oligonucleotide with sequence independent of the deprotector, speeds up the strand-displacement reaction between reactants F and S to release of the deprotector. As part of the complex, the deprotector is mostly double-stranded and will not react with the protected tile. (b) AFM results on the integrated reaction network. The left panel shows the network in absence of catalyst (2-day reaction time), and the right panel shows the network in the presence of 20 nM catalyst (2 h reaction time). In both panels, the initial concentration of the protected tile was 200 nM, of F was 440 nM, of S was 220 nM. The concentration of the catalyst in the right panel was 20 nM, 0.1 × of the limiting reagent (protected tile). DNA nanotubes form in the presence of catalyst, and do not form in the absence of catalyst. (c) The sink complex serves as a competitive threshold for the deprotector to prevent small amounts of released deprotector from causing DNA nanotube assembly.

Figure 3b shows AFM microscropy results for the integrated system; fuel, substrate and protected tile do not react significantly in the absence of the catalyst, and no DNA nanotubes are observed. With a sub-stoichiometric quantity of catalyst (20 nM, compared with ≥200 nM of other reagents), DNA nanotubes in excess of 10 μm in length are observed.

Previous characterization of the upstream catalyst system found that there can be a small amount of uncatalyzed reaction (leak) between the fuel and substrate that will spontaneously produce D even in absence of catalyst C (refs 27,48). To prevent this from resulting in spontaneous assembly of DNA nanotubes, we constructed a ‘sink’ complex that acts as a competitive threshold to absorb a stoichiometric quantity of deprotector (Fig. 3c). In the experiments reported here, the sink may not have been necessary, both because (1) the leak of the catalyst reaction was low, (2) a low concentration of active tiles resulting from residual leak would be kinetically hindered from self-assembly due to the nucleation barrier (c.f. ref. 22, Supplementary Figs. S5, S8, and S9), and (3) our modeling, described in the next section, suggests that absorption by the sink may not have been faster than deprotection, to our surprise.

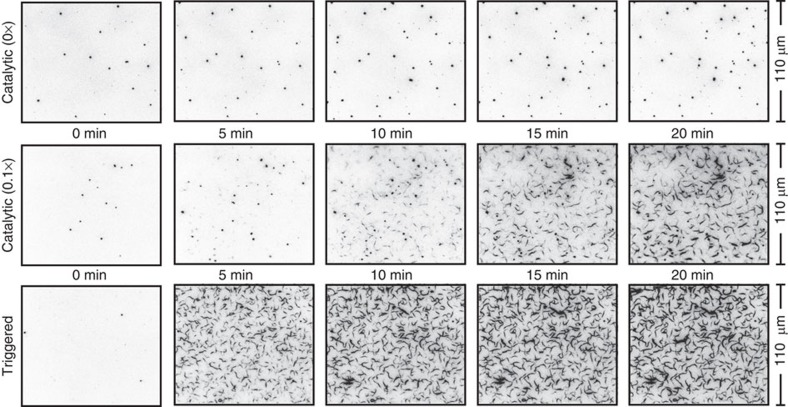
To directly observe the dynamics of triggered and catalyzed self-assembly, we took movies of several samples using optical (TIRF) microscopy (Fig. 4 and Supplementary Movies 1–3). Samples were prepared in the presence of methylcellulose as a crowding agent to help confine DNA tubes to the surface where they can be seen by TIRF. As a consequence, tubes that nucleate and grow in solution to a large enough size will subsequently settle on the surface, often (thanks to the crowding agent) forming bundles with other deposited tubes that appear as increasing the length and fluorescence brightness of filaments during the course of the movies. When the inactive tiles and the catalytic subsystem is prepared in the absence of the catalyst strand, no tube formation is observed (Fig. 4, top, and Supplementary Movie 1). The same preparation, followed by addition of a sub-stoichiometric concentration of catalyst (0.1 × ), results in a substantial amount of DNA tubes within 20 min (Fig. 4, middle, and Supplementary Movie 2). Movies of direct triggering of inactivated tiles (Fig. 4, bottom, and Supplementary Movie 3) indicate the fastest rate for tube nucleation, growth, and deposition under these experimental conditions, suggesting a roughly 10 min delay for the catalytic subsystem to produce a sufficient amount of deprotector.

Figure 4. Time-lapse TIRF microscopy images.

These images are timepoints of TIRF movies (see Supplementary Movies 1–3). The bright circular spots correspond to fluorescent beads used for position and focus reference; the number of bright spots increase through the course of the experiments because beads continue to deposit on the surface of the slide. For the top two rows, the initial reagents present were [protected tile]=200 nM, [F]=440 nM, [S]=220 nM, and [sink]=40 nM; 20 nM catalyst was introduced at time t≈0. For the bottom row, only [protected tile]=200 nM was initially present; 220 nM deprotector was introduced at time t≈0. No DNA nanotubes form within the time frame of the experiment when no catalyst was present. When a small amount (20 nM) of catalyst was added, DNA nanotubes formed slowly, initially limited by nucleation due to low active tile concentration. From this, it can be inferred that the upstream catalyst system possesses multiple turnover, because the catalyst concentration is lower than the sink concentration. This multiple turnover is consistent with fluorimeter assay of the upstream catalyst (see Supplementary Fig. S3). When a super-stoichiometric quantity of trigger was added, DNA nanotubes formed immediately.

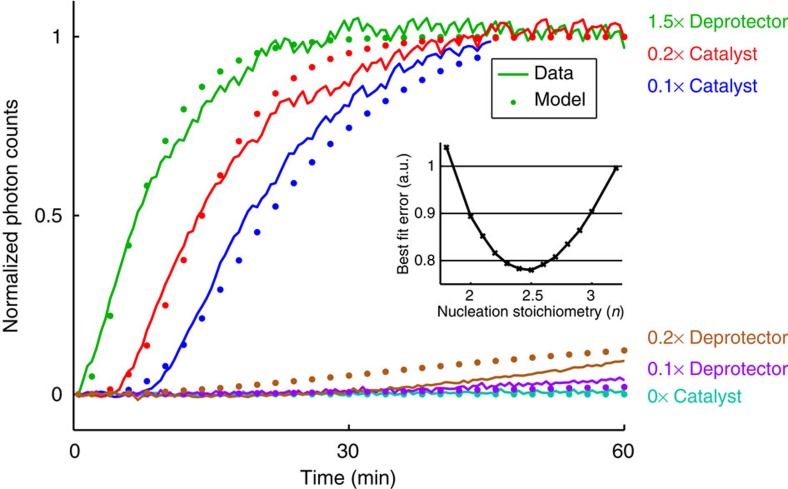
To investigate the kinetics in greater detail, we performed a similar set of experiments but with six different experimental conditions (Supplementary Movie 4). From each movie, we estimated the total amount of DNA in tube form as a function of time (Fig. 5) by assuming that normalized photon counts in each movie image are linearly related to the amount of deprotected monomer incorporated into tubes (see Supplementary Methods for details).

Figure 5. Modeling and quantitation of DNA nanotube growth.

Normalized photon counts of time for time-lapse TIRF microscopy images and control experiments shown as Supplementary Movie 4 (these are distinct from experiments shown in Figure 4); this value corresponds to the amount of deprotected monomers incorporated into tubes. In all experiments shown here, [protected tile]=200 nM (1 × ) and [sink]=40 nM (0.2 × ). For the green, brown, and purple traces, the listed quantity of deprotector was introduced at time t≈0. For the red and blue traces, [fuel]=600 nM (3 × ) and [substrate]=300 nM (1.5 × ) were present in solution initially, and the listed quantity of catalyst was introduced at time t=0. Shown in dotted lines are the expected kinetic behaviors predicted by our model using a best-fit nucleation stoichiometry value of n=2.5; the inset shows the relative sum of squared error for different values of n (with corresponding best-fit k_nuc, k_deprot and k_sink rate constants). The model captures the qualitative differences of the different traces; quantitative agreement is limited due to many uncharacterized parameters and the simplicity/incompleteness of model reactions.

Kinetic models of catalyzed tube formation

To determine whether the TIRF movies of the integrated catalytic DNA nanotube system are consistent with our understanding of the various sub-processes, we constructed a simplified kinetic model of the system. The reactions suggested here, and their rate constants, are intended only as a ‘sanity check’ for our qualitative mechanistic interpretation of the catalyzed DNA nanotube formation process, and should not be overinterpreted. The model reactions can be divided into two groups, one set for the catalysis subsystem:

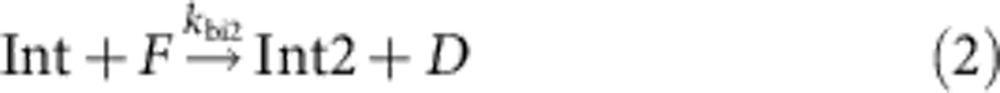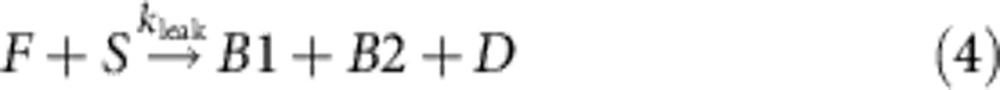and the other for the nucleation of DNA nanotubes and their subsequent elongation:

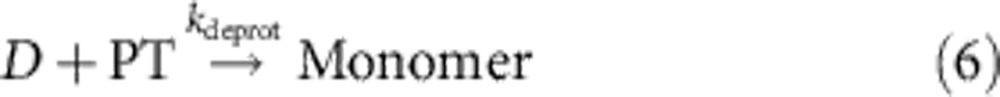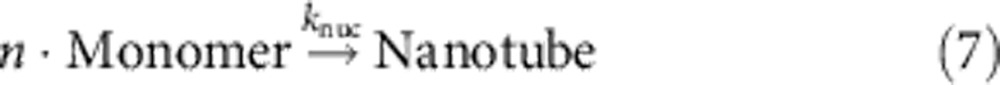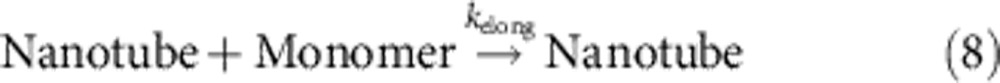Int and Int2 correspond to two intermediates of the catalytic reaction, B1 and B2, respectively, refer to the single-stranded and double-stranded by-products of the catalytic cycle. PT denotes the protected tile, Monomer denotes the reactive tile, n is the phenomenological nucleation stoichiometry, and [Nanotube] denotes the concentration of the DNA ‘nanotubes’ that have successfully nucleated.

For the integrated system, we used the best-fit catalysis rate constants, previous literature-reported rate constant of DNA nanotube elongation52, and fitted the remaining parameters to the data shown in Fig. 5 (Table 2, see Supplementary Note 4). The value of k_elong for a related, but not identical, DNA nanotube was experimentally measured in the study of Hariadi et al.52 to be 5.7 × 10⁵ layers per M per s; our DNA nanotubes appear to have a mean circumference of six tiles, so we estimate k_elong=3.4 × 10⁶ M⁻¹ s⁻¹. We then fit k_deprot, k_sink and k_nuc for different values of n to five of the data traces shown in Fig. 5 (the 0 × catalyst control trace shown in cyan, being almost completely flat, was not fitted). For the best fit, n=2.5 (Fig. 5 inset), k_deprot=10⁷ M⁻¹ s⁻¹, k_sink=10⁵ M⁻¹ s⁻¹ and k_nuc=2.0 × 10⁵ M⁻¹ s⁻¹.

Table 2. Model parameters values.

Parameter	Description	Value
kbi1	S+C rate constant; rxn (1) and (3); fitted	5.5 × 105 M−1 s−1
kbi2	F+Int rate constant; rxn (1) and (2); fitted	6.2 × 106 M−1 s−1
kuni	Int2→C+B2 rate constant; rxn (3); fitted	4.2 × 10−2 s−1
kleak	F+S leakage rate constant; rxn (4); fitted	7.4 M−1 s−1
ksink	D+sink rate constant; rxn (5); fitted	105 M−1 s−1
kdeprot	D+PT rate constant; rxn (6); fitted	107 M−1 s−1
n	Phenomenological stoichiometry of nucleation; fitted	2.5
knuc	n ˙ monomer nucleation rate constant; rxn (7); fitted	2.0 × 105 M1−n s−1
kelong	Nanotube+Monomer rate constant; rxn (8); assumed	3.4 × 106 M−1 s−1

The parameters of the catalysis subsystem were fitted only to the catalytic data shown in Supplementary Fig. S3, which includes fluorescence reporter characterization, the data shown in Figure 1b with 10 nM precursors, and catalytic behavior at 100 nM precursor concentrations (see Supplementary Methods for fitting details). We initially attempted to use more simplified reaction models for the catalysis subsystem, but these models failed to qualitatively capture its kinetic behavior over the relevant range of times and concentrations. Specifically, reaction (3) is essential for capturing both the unimolecular rate-limiting nature of the catalytic reaction at high substrate concentrations, and the product inhibition (due to reverse reaction) that slows the catalysis as the reaction approaches completion. Reactions (2) and (4) are modeled as irreversible, whereas in reality some amount of reverse reaction may occur (see Supplementary Note 3). A similar model was previously explored in the study by Zhang et al.48, and rate parameters reported in that work are all within one order of magnitude of corresponding rate constants here (with differences likely attributed to differences in DNA sequence).

In the course of our fitting, we constrained the values of k_deprot and k_sink to be between 10⁵ M⁻¹ s⁻¹ and 10⁷ M⁻¹ s⁻¹, consistent with our expectations for strand-displacement reactions with toeholds of this length25. The best-fit values of these two parameters were at the limits (k_deprot=10⁷, k_sink=10⁵), with k_deprot significantly higher than k_sink. This seems to indicate that the sink is not effective in reducing the leak reaction. However, the model is sensitive to changes in nucleation stoichiometry: slightly higher or lower concentrations of certain species can result in significantly different parameter values.

The model captures the qualitative features of the different traces, including (1) the characteristic shapes of the 1.5 × deprotector, 0.2 × catalyst and 0.1 × catalyst traces (shown in green, red and blue, respectively) that are affected by the nucleation barrier and the slowdown of the catalytic system, (2) the separation of these three traces corresponding to the delayed release of deprotector molecules, and (3) the eventual rise of the 0.2 × deprotector trace (brown), due to both catalytic leakage and the competition between the protected tile and the sink. We hypothesize that the quantitative fitting could be improved via (1) more detailed modeling of the tube nucleation and elongation processes, (2) modeling of surface adsorption kinetics and (3) improved characterization of the catalytic system for this particular set of sequences. Based on the time-lapse TIRF results and our model predictions, we conclude that our experimental data is consistent with and supports our rationally designed mechanism for the kinetic control of isothermal DNA nanotube assembly using a modular upstream catalyst system. In particular, multiple turnover of the catalyst is unambiguously shown by the 0.1 × catalyst trace (blue) that yields significantly higher photon counts than the 0.2 × deprotector trace (brown).

Discussion

By designing inert precursor double-crossover tiles that are activated through isothermal strand-displacement processes, and by using an upstream strand-displacement circuit to control the timing of DNA nanotube self-assembly, we have demonstrated room-temperature self-assembly of DNA nanotubes over 10 μm long from nanometer-scale components. It is reasonable to believe that the methods and results here may be robust to a variety of temperatures and environmental conditions, because we did not fine-tune any part of the design process for optimal function at room temperature; previous DNA strand-displacement systems exhibit temperature and salinity robustness27,48,53. More fundamentally, we have established a link between the well-studied molecular programming paradigms of strand-displacement circuits and tile-based self-assembly. As the former paradigm enables complex dynamical behavior and the latter enables complex spatial structure formation, their integration has the potential to enable a rich class of isothermal molecular systems with complex spatiotemporal behaviors.

To go beyond the particular example demonstrated here and to establish the generality of our approach, a systematic method of coupling DNA tile systems and DNA strand-displacement circuits must be developed. This could be challenging because, on the one hand, there are many distinct DNA tile motifs (for example, several variants of double-crossover molecules15,46, multi-crossover molecules17,54, rigid-junction tiles55, single-stranded tiles56,57) and RNA tiles58. On the other hand, systematic methods to compile abstract biochemical circuit specifications into DNA strand-displacement systems employ a variety of standardized domain architectures to avoid unintentional interactions between dynamic species29,43,45,59, and it will be necessary to verify that undesired interactions can be systematically avoided when arbitrary tile sets are interfaced to arbitrary circuits. Although these challenges do not appear insurmountable, especially with the aid of automated software tools43, they will require care.

A theoretical framework is needed to characterize what molecular behaviors can or cannot be achieved by integrated DNA tile and strand-displacement systems. The foundations of such a framework already exist in the extensive theoretical characterization of both tile systems (for example, arbitrary computable shapes can be self-assembled using small tile sets41,42) and strand-displacement systems (for example, arbitrary formal chemical reaction network dynamics can be implemented but suffer certain logical limitations29,60). Nonetheless, there is considerable flexibility to consider distinct mechanisms for coupling tile systems and strand-displacement systems, and these choices may have significant implications for the theoretical capabilities of the class of molecular programs obtained. For example, here we showed that signals from a strand-displacement system to a tile system can control the timing of tile activation. It is not hard to imagine that a feedback signal from the tile system—such as a ‘by-product’ of method 3—could be used to trigger further strand-displacement circuit events. A feedback signal that is released only when a tile is successfully assembled into a growing structure (rather than just when it is activated) would be even more powerful, though more difficult to implement. By further allowing strand-displacement signals to trigger and report disassembly events as well as assembly events, remarkably efficient Turing-universal computation is theoretically possible, even using just one-dimensional structures59.

Beyond allowing for a theoretical characterization, systematic architectures and formal models maximally leverage experimental advances, in that lessons learned from specific experimental implementations can be applied to a wide range of potential systems whose behaviors can be formally characterized. For example, DNA tile self-assembly was proposed as an abstract model of computation and shown to be Turing-universal for both computation and for construction41,42, guiding experimental demonstrations to rapidly increasing complexity15,18,19. Analogously, DNA strand-displacement circuits have been formalized as a programming language and shown to be capable of implementing arbitrary chemical reaction network dynamics, including arbitrary digital and analog circuits29,43, facilitating the experimental advance from tens of strands to hundreds26,30. Key to both work is that generic molecular components can be conceptualized as motifs whose behavior is largely independent of specific (well-designed) sequence choices—conceptual design can be performed at the domain level, then implemented systematically. These properties make it meaningful to discuss full-fledged programming languages and compilers43,50 for molecular programming architectures.

Molecular programming paradigms that combine solution-phase circuitry with structural self-assembly are not limited to the combination of tile systems and strand-displacement cascades. Indeed, interacting hairpin systems28,37,38,39 naturally and seamlessly integrate circuitry, assembly, and disassembly reactions, and have been experimentally demonstrated for tasks such as triggered and catalytic assembly, signal amplification circuitry and molecular motors. However, theoretical characterization of what can and cannot be achieved using interacting hairpin systems lags behind the experimental demonstrations. Thus, an important target for future research will be to develop theory, software and experimental practice that integrates all three molecular programming paradigms. Such advances will facilitate the application of molecular programming technologies to real-world problems38,44.

Methods

DNA oligonucleotides

DNA oligonucleotides used in this study were purchased from Integrated DNA Technologies (IDT), and HPLC purified by IDT. Where applicable, fluorophores were attached by IDT as well.

Buffer conditions

Individual DNA oligonucleotides were resuspended and stored in TE buffer (10 mM Tris–HCl pH balanced to 8.0, with 1 mM EDTA˙Na₂, purchased as 100 × stock from Sigma-Aldrich) at 4 °C. Directly preceding experiments, TE buffer with 62.5 mM MgCl₂ was added at 1:4 ratio to the sample, achieving a final MgCl₂ concentration of 12.5 mM. As roughly 1 mM of the Mg²⁺ is chelated by the EDTA present in solution, the free concentration of Mg²⁺ is estimated to be 11.5 mM. All experiments and purifications were performed at 25 °C.

Complex purifications

Multi-stranded complexes (namely the incomplete tile, the protected tile, the catalytic substrate, and the trigger sink) were purified in-house by non-denaturing PAGE as follows: oligonucleotides needed for each sample were prepared with nominally correct stoichiometry at 20 μM and annealed with an Eppendorf Mastercycler Gradient thermocycler. The solutions were brought down from 95 °C to 20 °C at a constant rate over the course of 75 min. The solution were then run on 12% non-denaturing PAGE at 180 V for 6 h. The proper bands were cut out and eluted in 1 ml TE/Mg²⁺ buffer for 2 days. Typical yields ranged from 40 to 60%. The concentrations of purified complexes were estimated by measuring absorbance at 260 nm using an Eppendorf Biophotometer, and dividing by extinction coefficients for single- and double-stranded DNA predicted by nearest-neighbor models.

Atomic force microscopy

AFM images were acquired using tapping mode on a Nanoscope IIIa (Veeco Instruments) under 1 × TAE/Mg²⁺ (TAE=40 mM Tris base, 20 mM acetic acid, and 1 mM EDTA, pH 8.0 with 12.5 mM Mg-acetate–4H₂O) buffer equipped with nanoAnalytics Q-control III (Asylum Research) and 110 μm, 0.38 N m⁻¹ spring constant SNL silicon nitride cantilever (Veeco Instruments).

Following (potential) self-assembly in the centrifuge tubes, the samples were diluted by a factor of two with 1 × TAE/Mg²⁺. Five microlitre of this diluted sample was deposited on a freshly cleaved piece of V1 grade mica (Ted Pella), ~1 cm × 1 cm in size, affixed to a 15-mm diameter magnetic stainless steel puck (Ted Pella) using a hot glue gun. The presence of Mg²⁺ ions and other multivalent cations in the buffer facilitates the formation of salt bridges between the DNA species and negatively charged mica surface. Once the DNA nanotubes are immobilized on the mica, no further reactions (assembly, end-to-end joining, disassembly, and so on) are expected to occur. An additional 30 μl of 1 × TAE/Mg²⁺ was added to both sample and cantilever holder before imaging.

We imaged each sample at three or more random locations, each at least 75 μm apart. At each scan location, we imaged at the 8, 2 and 1 μm scales. We used custom-written Matlab and Mathematica code to flatten the images by subtracting a linear fit from each scan line and matching intensity histograms between scan lines.

Total internal reflection fluorescence optical microscopy

We used fluorescence microscopy with a 130 × 130 μm field of view to visualize self-assembly reactions in real-time using a custom-built prism-based TIRF microscope equipped with autofocus and temperature controller, as previously described52.

For fluorescence microscopy imaging only, the tile’s central strand (with sequence 7*4*3*2*8*) was 5′-end-labeled with a Cy3 fluorophore. The samples were excited by a 532-nm solid-state laser (CrystaLaser) weakly focused on the surface of a suprasil prism (CVI Melles Griot) upon which the microscope slide was mounted. The emitted photons were collected by a 60 × ,1.2 NA water immersion objective (Nikon), 20 cm lens tube (CVI Melles Griot) and a C9100-02 electron multiplier CCD camera (Hamamatsu). The images were analyzed using the ImageJ software (NIH) and Mathematica.

For static imaging (for example, Fig. 2c), a 5-μl drop of typically 10-fold diluted sample was deposited between a clean microscope slide and a coverslip. The dilution factor of the static fluorescence assay is higher than that of the AFM imaging to facilitate visualization of individual nanotubes. Under 1 × TAE/Mg²⁺ buffer, DNA nanotubes were immobilized on negatively charged clean glass surfaces.

For fluorescence movies, snapshots of which appear in Fig. 4, we flowed 6 μl of the sample into a flow chamber made from a glass capillary tube (Vitrotubes) and subsequently sealed both ends of the chamber with Vaseline. DNA nanotubes were observed to interact minimally with the capillary tube; therefore, no glass passivation protocol was necessary for real-time observation of self-assembly. Owing to the brightness and slow photobleaching rate of Cy3, the sample reaction does not contain an oxygen scavenger mix. To guide the autofocus process, 100 nm fluorescent beads (Polyscience, Inc) were added at roughly 1 pM. To confine the DNA nanotubes within the evanescence field near the surface, a crowding agent (0.3% w/v of methylcellulose, Sigma-Aldrich) was added to the solution mix. In the presence of crowding agents, the entropy of the system is maximized when all long structures are close to another surface, such as the capillary tube walls.

A side effect of this confinement strategy is that the same entropic force also favors confining DNA nanotubes to any surface, such as the surfaces of other DNA nanotubes. Consequently, at high concentrations, DNA nanotubes are observed to exhibit side-to-side joining and lateral aggregation. The increasing intensity of tubes corresponds to the lateral ‘bundling’ of multiple DNA nanotubes.

Author contributions

D.Y.Z., R.F.H. and H.M.T.C. conceived and designed the experiments; D.Y.Z. and R.F.H. performed the experiments and analyzed the data; D.Y.Z. and E.W. wrote the paper; E.W. guided the research.

Additional information

How to cite this article: Zhang, D. Y. et al. Integrating DNA strand-displacement circuitry with DNA tile self-assembly. Nat. Commun. 4:1965 doi: 10.1038/ncomms2965 (2013).

Supplementary Material

Supplementary Figures, Methods and Notes

Supplementary Figures S1-S9, Supplementary Methods and Supplementary Notes 1-4.

Supplementary Movie 1

Lack of nanotube growth in absence of catalyst. Reagents present were [Protected Tile] = 200 nM, [F] = 440 nM, [S] = 220 nM, and [Sink] = 40 nM. Snapshots of this movie were used to generate the top row of images in Fig. 4.

Supplementary Movie 2

Nanotube growth in presence of substoichiometric catalyst. Reagents initially present were [Protected Tile] = 200 nM, [F] = 440 nM, [S] = 220 nM, and [Sink] = 40 nM, and 20 nM catalyst was introduced at time t ≈ 0. Snapshots of this movie were used to generate the middle row of images in Fig. 4.

Supplementary Movie 3

Nanotube growth in presence of stoichiometric excess of trigger. Only [Protected Tile] = 200 nM was initially present; 220 nM Deprotector was introduced at time t ≈ 0. Snapshots of this movie were used to generate the bottom row of images in Fig. 4.

Supplementary Movie 4

Montage of growth and control movies. These were used to generate the fluorescence counts used in Fig. 5. Importantly, these movies are distinct experiments from those shown in Movies 1-3.