Comparison of Logistic Regression and Artificial Neural Network Models in Breast Cancer Risk Estimation

A study is described in which a logistic regression model and an artificial neural network, the two most commonly used computer models in medical diagnosis, are reviewed and compared, with emphasis on their application in an estimation of breast cancer risk on the basis of mammographic descriptors and demographic risk factors.

Abstract

Computer models in medical diagnosis are being developed to help physicians differentiate between healthy patients and patients with disease. These models can aid in successful decision making by allowing calculation of disease likelihood on the basis of known patient characteristics and clinical test results. Two of the most frequently used computer models in clinical risk estimation are logistic regression and an artificial neural network. A study was conducted to review and compare these two models, elucidate the advantages and disadvantages of each, and provide criteria for model selection. The two models were used for estimation of breast cancer risk on the basis of mammographic descriptors and demographic risk factors. Although they demonstrated similar performance, the two models have unique characteristics—strengths as well as limitations—that must be considered and may prove complementary in contributing to improved clinical decision making.

Introduction

Accurate prediction of clinical outcomes is integral to successful decision making and can lead to better patient care. For example, in breast cancer diagnosis, accurately predicting which women should undergo biopsy on the basis of mammographic findings may prevent missing a breast cancer or performing biopsy of a noncancerous lesion.

Although clinical prediction might prove valuable, it is challenging for physicians who must balance the relative contributions of numerous (and possibly interacting) risk factors. Physicians often predict the outcome of a disease or adverse event by using probabilities calculated with heuristic methods on the basis of training and experience. Although these heuristic methods may be necessary and useful, they can be biased and lead to systematic errors (1,2). For instance, estimation of breast cancer risk may involve integration of over 100 risk factors simultaneously to estimate a single posttest probability, a nearly impossible task if based solely on memory and experience. Computer models can provide assistance in processing a large number of variables and in bridging the gap between risk factors and risk estimation (3).

A variety of computer models have been developed in the area of machine learning and statistics that can be used for predicting clinical outcomes, such as logistic regression, decision trees, artificial neural networks (ANNs), and Bayesian networks. Logistic regression was developed by the statistics community, whereas the remaining methods were developed by the machine-learning community. Logistic regression, a statistical fitting model, is widely used to model medical problems because the methodology is well established and coefficients can have intuitive clinical interpretations (4,5). Decision trees are graphical models that contain rules for predicting the target variable. ANNs and Bayesian networks are graphical models consisting of nodes interconnected with arcs. However, these last two models are intrinsically different. The arcs of a Bayesian network represent the conditional dependence relationships between the variables as defined with probability theory, and each node represents a variable of interest. The arcs and nodes of an ANN admit of no such interpretation; their values are discovered during “training,” and they do not have any underlying meaning. In general, ANNs have more complex structures with many extra nodes (called hidden nodes) compared with Bayesian networks, and this complexity provides ANNs with the power to classify any data with complex relationships. Among the computer models that are used in risk estimation, logistic regression and ANNs enjoy the most widespread use, mainly because they are relatively easy to build and often have excellent predictive ability (6).

ANNs and logistic regression have been applied in various domains in medical diagnosis. To date, ANNs have been used for estimating risk in a variety of cancers, including (but not limited to) breast, prostate, liver, ovarian, cervical, bladder, and skin cancer (7,8). Logistic regression has been used to estimate disease risk in coronary heart disease (9), breast cancer (10), prostate cancer (11), postoperative complications (12,13), and stroke (14).

Retrospective studies have shown both ANNs and logistic regression to be useful tools in medical diagnosis. The ultimate aim is to incorporate these analytic tools into clinical practice to provide a second opinion in real time for case management (see the Discussion section).

In this article, we discuss and illustrate logistic regression models and ANNs and the application of these models in estimating breast cancer risk on the basis of mammographic descriptors and demographic risk factors. In addition, we discuss the advantages and disadvantages of each model, provide criteria for model selection, and compare the two models in terms of ease of model building, ability to detect complex relationships between predictor variables and outcome, ability to detect implicit interactions among predictor variables, generalizability to external data sets, discrimination ability, computational considerations, ease of sharing the models with other researchers, generation of confidence intervals, and ease of clinical interpretation.

Logistic Regression

Logistic regression examines the relationship between a binary outcome (dependent) variable such as presence or absence of disease and predictor (explanatory or independent) variables such as patient demographics or imaging findings (15). For example, the presence or absence of breast cancer within a specified time period might be predicted from knowledge of the patient’s age, breast density, family history of breast cancer, and any prior breast procedures. The outcome variables can be both continuous and categoric. If X₁, X₂,…, X_n denote n predictor variables (eg, calcification types, breast density, patient age, and so on), Y denotes the presence (Y = 1) or absence (Y = 0) of disease, and p denotes the probability of disease presence (ie, the probability that Y = 1), the following equation describes the relationship between the predictor variables and p:

$$\text{Log}\left(\frac{p}{1-p}\right)={\beta }_0+{\beta }_1{X}_1+\dots +{\beta }_n{X}_n,$$ (1)

where β₀ is a constant and β₁, β₂, …, β_n are the regression coefficients of the predictor variables X₁, X₂, …, X_n. The regression coefficients are estimated from the available data. The probability of disease presence p can be estimated with this equation.

Each regression coefficient describes the size of the contribution of the corresponding predictor variable to the outcome. The effect of the predictor variables on the outcome variable is commonly measured by using the odds ratio of the predictor variable, which represents the factor by which the odds of an outcome change for a one-unit change in the predictor variable. The odds ratio is estimated by taking the exponential of the coefficient (eg, exp[β₁]). For example, if β₁ is the coefficient of variable X_FH (“family history of breast cancer”), and p represents the probability of breast cancer, exp(β₁) is the odds ratio corresponding to the family history of breast cancer. The odds ratio in this case represents the factor by which the odds of having breast cancer increase if the patient has a family history of breast cancer and all other predictor variables remain unchanged. In other words, if the odds ratio corresponding to the family history of breast cancer is 2, then breast cancer occurs twice as often in women with a family history of breast cancer in comparison with women in the study population with no such family history.

Logistic regression models generally include only the variables that are considered “important” in predicting an outcome. With use of P values, the importance of variables is defined in terms of the statistical significance of the coefficients for the variables. The significance criterion P ≤ .05 is commonly used when testing for the statistical significance of variables; however, such criteria can vary depending on the amount of available data. For example, if the number of observations is very large, predictors with small effects on the outcome can also become significant. To avoid exaggerating the significance of these predictors, a more stringent criterion (eg, P ≤ .001) can be used.

Significant variables can be selected with various methods. In forward selection, variables are sequentially added to an “empty” model (ie, a model with no predictor variables) if they are found to be statistically significant in predicting an outcome. In contrast, backward selection starts with all of the variables in the model, and the variables are removed one by one as they are found to be insignificant in predicting the outcome. The stepwise logistic regression method is a combination of these two methods and is used to determine which variables to add to or drop from the model in a sequential fashion on the basis of statistical criteria. Although different techniques can yield different regression models, they generally work similarly. Sometimes, clinically important variables may be found to be statistically insignificant with the selection methods because their influence may be attenuated by the presence of other strong predictors. In such cases, these clinically important variables can still be included in the model irrespective of their level of statistical significance.

Artificial Neural Networks

ANNs are computer models inspired by the structure of biologic neural networks. They consist of highly interconnected nodes, and their overall ability to help predict outcomes is determined by the connections between these neurons (16). ANNs simulate neural processes by summing negative (inhibitory) and positive (excitatory) inputs to produce a single output (17). Although ANNs differ in the way the neurons are connected and inputs are processed, we will focus on “feedforward” networks, the most commonly used ANNs in medical research.

Figure 1 illustrates the generic structure of an ANN. A typical ANN consists of a series of nodes arranged in three layers (input, hidden, and output layers). Each node in the input layer is called an input node and represents an input variable (eg, an imaging feature such as calcification or breast density) that is used as a predictor of the outcome. The single node in the output layer (output node) represents the predicted outcome (eg, probability of malignancy). The inputs and the output of an ANN correspond to the predictor variables and the outcome variable Y, respectively, in a logistic regression model. The nodes in the hidden layer (hidden nodes) contain intermediate values calculated by the network that do not have any physical meaning. The hidden nodes allow the ANN to model complex relationships between the input variables and the outcome. The ANN in Figure 1 has N input nodes, K hidden nodes, and only one output node.

Figure 1.

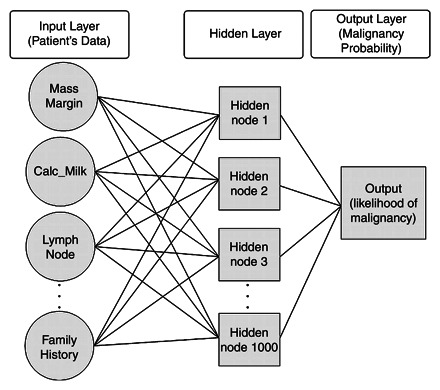
Chart illustrates the generic structure of an ANN.

The nodes in different layers are connected by means of connection weights, represented by arcs (Fig 1). The connection weights contain the “knowledge” representing the relationships between variables and correspond to the coefficients in a logistic regression model. ANNs “learn” the relationships between input variables and the effects they have on outcome by strengthening (increasing) or weakening (decreasing) the values of these connection weights on the basis of known cases. The procedure of estimating the optimal weights that generate the most reliable outcomes is called learning or training (18). Training an ANN is analogous to estimating parameters in a logistic regression model; however, an ANN is not an automated logistic regression model because the two models use different training algorithms for parameter estimation. There are several algorithms for training ANNs, the most popular of which is backpropagation. The backpropagation algorithm is based on the idea of adjusting connection weights to minimize the discrepancy between real and predicted outcomes by propagating the discrepancy in a backward direction (ie, from the output node to the input nodes).

Case Study: Breast Cancer Risk Estimation

The models and data used in this case study have been presented elsewhere (19,20) and are summarized here for the convenience of the reader.

Data

The institutional review boards at our institutions exempted this HIPAA (Health Insurance Portability and Accountability Act)–compliant retrospective study from requiring informed consent. We collected structured reports from 48,744 consecutive mammography examinations (477 malignant and 48,267 benign) in 18,269 patients (17,924 female and 345 male) performed from April 1999 to February 2004. We extracted 62,219 mammographic findings and matched them to the Wisconsin Cancer Reporting System, which served as our reference standard.

The data were entered using a PenRad mammography reporting-tracking data system (PenRad, Colorado Springs, Colo), which records clinical data in a structured format (ie, point-and-click entry of information populates the clinical report and the database simultaneously).

We mapped the mammographic descriptors, demographic risk factors (patient age, family and personal history of breast cancer, and administration of hormone replacement therapy), and Breast Imaging Reporting and Data System (BI-RADS) assessment categories collected in the National Mammography Database format (21) to 36 discrete variables (Fig 2). We trained a mammography logistic regression model and a mammography ANN to predict breast cancer risk using these 36 variables.

Figure 2.

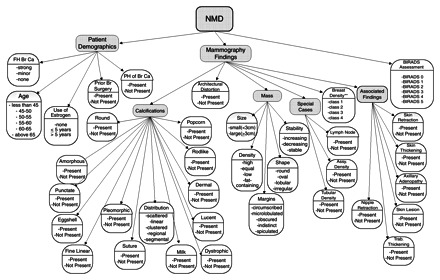
Chart illustrates the descriptors from the National Mammography Database (NMD) used to build the mammography ANN and the mammography logistic regression model. Assy. = asymmetric, Br = breast, Ca = cancer, FH = family history, PH = personal history, Trab = trabecular.

Mammography Logistic Regression Model

We constructed our mammography logistic regression model by using SPSS statistical software (SPSS, Chicago, Ill). We used a forward selection method to select significant predictors of breast cancer, with a cutoff value of P < .001 for adding new terms. This stringent criterion was used to avoid including clinically less important predictors that may have become statistically significant because of the large amount of data used in our study.

Mammography ANN

We built our mammography ANN as a three-layer feedforward network with use of MATLAB 7.4 (Mathworks, Natick, Mass). The layers included an input layer of the 36 discrete variables shown in Figure 2, a hidden layer with 1000 hidden nodes, and an output layer with a single node. The output node generated a number between 0 and 1 that represented the risk of malignancy. We trained our mammography ANN using the back-propagation algorithm.

Training and Testing of the Models: Cross-Validation

To train and test our mammography logistic regression model and mammography ANN with independent data validation, we used a standard machine-learning technique called k-fold (10-fold in our case) cross-validation. In k-fold cross-validation, the whole data set is divided into k approximately equal and distinct subsets. k−1 of these subsets are combined and used for training, and the remaining set is used for testing (Fig 3). The algorithm continues iteratively until each fold is used exactly once for testing. The results from all test sets are then combined and used to evaluate model performance. In k-fold cross-validation, every data point is used exactly one time for testing and k−1 times for training.

Figure 3.

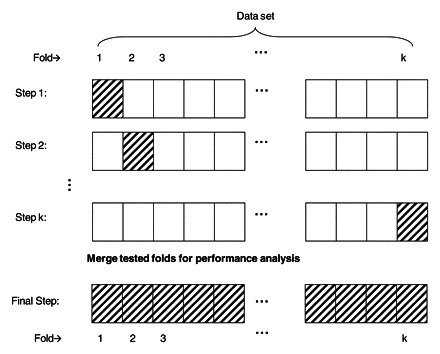
Drawing illustrates the steps used in k-fold cross-validation to train and test the mammography logistic regression model and the mammography ANN on an independent data set. Empty boxes = training folds, hatched boxes = test folds.

Evaluation of the Models

We measured and compared the discriminative performances of interpreting radiologists and of our mammography logistic regression model and mammography ANN in classifying breast lesions as malignant or benign with use of receiver operating characteristic (ROC) curves. The area under an ROC curve (AUC) indicates how well a prediction model discriminates between healthy patients and patients with disease. The value of an AUC varies between 0.5 (ie, random guess) and 1.0 (perfect accuracy) (22).

We plotted the ROC curve for the two models using the probabilities generated for all findings by means of the 10-fold cross-validation technique. We constructed the ROC curves for all radiologists’ assessments by using BI-RADS final assessment categories assigned by the radiologists after ordering the categories according to likelihood of malignancy (1<2<3<0<4<5). We used the DeLong method (23) to measure and compare the AUCs, since this method accounts for correlation between ROC curves obtained from the same data.

Results

The radiologists achieved an AUC of 0.939 ± 0.011 as measured with the BI-RADS assessment categories assigned to each record. Our mammography logistic regression model and mammography ANN achieved AUCs of 0.963 ± 0.009 and 0.965 ± 0.001, respectively. Both models performed significantly better (P < .001) than the radiologists working unaided. No statistically significant difference (P = .607) was found between the AUCs of the mammography logistic regression model and mammography ANN (Fig 4).

Figure 4.

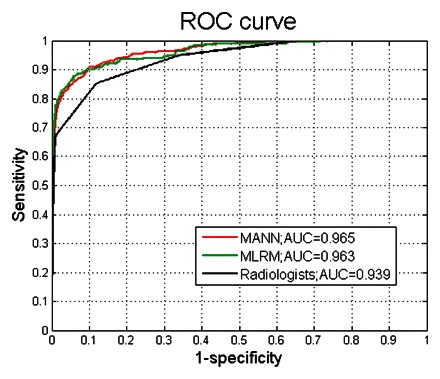
Graph shows ROC curves constructed from the output probabilities of the mammography ANN (MANN), the mammography logistic regression model (MLRM), and radiologists’ assessments.

Unlike the ANN, the mammography logistic regression model allowed us to determine the most predictive explanatory variables as well. The most important predictors associated with breast cancer as determined with the odds ratio (a high odds ratio implies that a variable is a strong predictor of breast cancer) were BI-RADS assessment codes 0, 4, and 5; segmental calcification distribution; and history of invasive carcinoma. Although a family history of breast cancer and the use of hormones were clinically relevant, our mammography logistic regression model did not find them to be significant predictors of malignancy. Similarly, the imaging descriptors, breast density, architectural distortion, and amorphous calcification morphologic features were shown not to be significant predictors of malignancy, perhaps because their influence might have been attenuated by other strong predictors of breast cancer such as BI-RADS assessment categories.

Case Example

Mammography performed in a 52-year-old woman with a family history of breast cancer demonstrated an oval-shaped mass less than 3 cm in size with an ill-defined margin. This abnormality was assigned a BI-RADS 4 assessment code. Using the β coefficients estimated by our mammography logistic regression model and Equation 1, we can easily estimate the probability of cancer in this patient as follows:

$$\text{Log}\left(\frac{p}{1-p}\right)=-8.95+0.76+1.13+0.02+2.40+5.21=0.57,$$ (2)

where −8.95 is a constant and 0.76, 1.13, 0.02, 2.40, and 5.21 correspond to the coefficients “Mass margins: ill-defined,” “Mass size: small (less than 3 cm),” “Age 51–54,” “History of breast cancer,” and “BIRADS Category 4,” respectively, in our mammography logistic regression model. Algebraic transformation yielded a probability of breast cancer of 0.64. Because it was not feasible to estimate the risk of cancer by using algebraic transformation with our mammography ANN, we applied our mammography ANN to the data in this case and obtained a probability of breast cancer of 0.60.

Discussion

In our study, we reviewed logistic regression models and ANNs and illustrated an application of these algorithms in predicting the risk of breast cancer with use of a mammography logistic regression model and a mammography ANN. We showed how statistical and machine-learning models can help physicians better understand cancer risk factors and make an accurate diagnosis. The mammography logistic regression model and the mammography ANN demonstrated high discrimination accuracy and similar performance, with the mammography ANN yielding a slightly higher AUC. Both models yielded a higher AUC at all threshold levels compared with the radiologists working unaided, which suggests that the models possess greater discrimination ability than do the radiologists.

Both models have the potential to be used as decision support tools once they are integrated into clinical practice. Such models could be directly linked to structured reporting software that radiologists use in daily practice to collect relevant variables. Radiologists can then use the probability calculations made by these integrated computer models to aid in clinical decision making.

Several other studies have also compared the use of ANNs and logistic regression models on specific data sets and reported varying results depending on the data set that was used. To our knowledge, the two most recent review articles in the literature reported on 28 and 72 studies, respectively, comparing ANNs and logistic regression models with respect to medical data classification tasks (5,6). Although the majority of these studies reported similar performance results for the two models, some reported that one or the other model performed better. It is hard to draw general conclusions regarding the superiority of one model over the other on the basis of findings from published studies, since the results for each of these studies are based on the specific data set used. Each model has its advantages, and the selection of a model should be based on these advantages and the intended purpose of the study. The advantages and disadvantages of these models can be categorized according to nine different criteria: ease of model building, ability to detect complex relationships between predictor variables and outcome, ability to detect implicit interactions among predictor variables, generalizability and overfitting, discrimination ability, computational considerations, ease of sharing the models with other researchers, generation of confidence intervals, and ease of clinical interpretation (Table).

Comparison of Logistic Regression and ANN Models

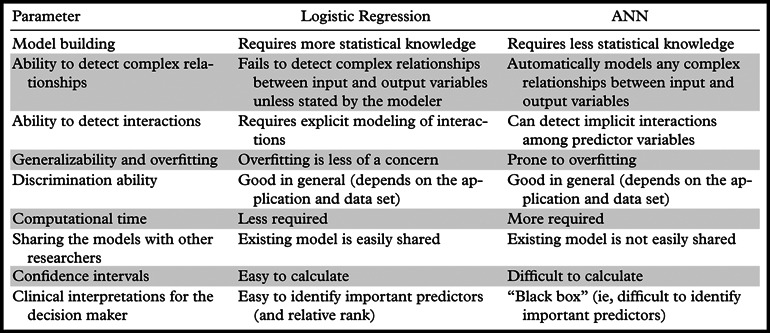
Ease of Model Building

Building an ANN requires less domain knowledge than does building a logistic regression model. A variety of available software with user-friendly interfaces exists that can be used to quickly build an ANN without the need to understand the inherent structure of the network. Logistic regression models are more challenging to construct because they require expert domain knowledge, including an understanding of statistical concepts such as odds ratios, statistical significance, interactions, and confounding (24).

Ability to Detect Complex Relationships between Predictor Variables and Out come

Medical outcomes, such as the presence of malignancy, are generally dependent on a variety of factors such as patient age and family history. However, these dependencies might be based on complex relationships that are difficult to detect and model explicitly. ANNs are ideally suited to modeling such relationships because they require no a priori knowledge about the underlying data. ANNs can automatically detect and model any arbitrary relationships between the input and output variables (5,6,25,26). In contrast, a logistic regression model can incorporate complex relationships only if they are explicitly identified and included in the model.

Ability to Detect Implicit Interactions among Predictor Variables

Similarly, ANNs have the ability to model any possible implicit interactions among input variables, which are commonly encountered in medical data. Often, the interactions among input variables are difficult to detect (eg, the relationship between mass margin and personal history of breast cancer). ANNs can handle these complex interactions through the use of hidden nodes, which act as interaction detectors and increase the capacity of the network to learn complex relationships among the predictor variables. In contrast, logistic regression models usually consider only up to two-way interactions (ie, interactions between two predictor variables) and miss others unless they are explicitly stated by the model builder (5,25,26).

We included only significant predictors when building our mammography logistic regression model; we did not include any interaction terms. On the other hand, our mammography ANN automatically detected various possible implicit interactions among the predictor variables and complex relationships between the predictors and the outcome variable.

Generalizability and Overfitting

The term generalizability refers to the ability of a model to perform well on future as-yet-unseen data. The generalizability of a model depends heavily on the way the model is built. k-fold cross-validation is one of the methods used during training to assess and improve generalizability. However, the cross-validation does not guarantee generalizability. One common issue with all risk estimation models that causes low generalizability is overfitting (18), a phenomenon in which the model is highly adjusted specifically to the available data set but performs poorly on unseen data. In general, logistic regression models are less prone to overfitting than are ANNs because they involve simpler relationships between the outcome variable and predictor variables (6). ANNs are more prone to overfitting due to their complex structures. Large networks with more hidden nodes often tend to overfit more because these hidden nodes detect almost any possible interaction, with the result that the model becomes too specific to the training data set.

Numerous techniques have been used to prevent overfitting in risk estimation modeling (5). When building our mammography ANN, we had to use an advanced technique called early stopping to prevent overfitting. In early stopping, the training of the model is stopped when the model starts to overlearn the training data set. In contrast, because our mammography logistic regression model used only significant predictors and did not include any interaction terms, we did not have to implement any special techniques to deal with the overfitting issue.

Discrimination Ability

Studies in the literature have reported varying performance results for logistic regression models versus ANNs. Although the majority of investigators have reported similar performance results for the two models, some have reported that one or the other model performed better on their data set (5,6). However, the results from these studies are specific to the data sets from which the models were built, as are the results from our study. So far, neither of these algorithms has been shown to always perform better than the other for any given data set and application area.

Computational Considerations

Logistic regression models are usually computationally less complicated to build and require less computation time to train compared with ANNs. For instance, the total building time (ie, the time required for training and to perform the 10-fold cross-validation) for our mammography ANN on a 2.4-GHz Intel Core 2 Duo computer (Intel, Santa Clara, Calif) was 39 minutes, whereas the total building time for our mammography logistic regression model was 8 minutes. However, once it is built, either model can be tested on a new case very quickly (usually in only seconds). Because of increasing computing power, computational time may not be an issue in the future.

Ease of Sharing the Models with Other Researchers

Logistic regression models have a distinct advantage over ANNs in terms of the sharing of an existing model with other researchers. One need only know the coefficients of the logistic regression model and perform simple calculations to predict an outcome. On the other hand, to share an existing ANN, one needs to provide either a copy of the trained ANN or the connection weight matrices, which might be extremely large. If the aim of the user is to share a decision support tool that embeds a logistic regression model or an ANN in the background, sharing of the two tools would be treated equivalently.

Generation of Confidence Intervals

Although point estimates of risk (eg, “65% malignant”) are useful in clinical decision making, these numbers by themselves without confidence intervals create a false sense of certainty (27). To use the risk estimate in decision making, one should also know the confidence intervals of the predicted probabilities. We acknowledge that the formal definition “95% confidence interval” might be difficult to use in clinical practice; however, this statistic may be used in clinical practice by considering the upper and lower bounds of the interval in decision making (27). Because logistic regression models are statistical methods, confidence intervals of the predicted probabilities can easily be calculated. The majority of the statistical software packages used to create logistic regression models provide the confidence intervals along with the probability of the outcome as standard output. In contrast, ANNs, which are not built primarily for statistical use, cannot easily generate confidence intervals of the predicted probabilities and usually require extensive computations to do so.

Ease of Clinical Interpretation

Logistic regression models have better clinical or real-life inferences than do ANNs. Logistic regression models easily determine the variables that are most predictive of outcome on the basis of the coefficients and the corresponding odds ratios (6,26). The odds ratios can be interpreted as the relative increase or decrease in the probability of an outcome given a change in the predictor variables. In contrast, parameters of ANNs do not carry any real-life interpretation. In ANNs, inputs and outputs are not related in a form that the human user can understand, which is why ANNs are commonly called black boxes.

Conclusions

In general, ANNs can be thought of as a generalization of logistic regression models (26,28,29). The main advantage of ANNs over logistic regression models lies in their hidden layers of nodes. In fact, a special ANN with no hidden node has been shown to be identical to a logistic regression model (29). ANNs are particularly useful when there are implicit interactions and complex relationships in the data, whereas logistic regression models are the better choice when one needs to draw statistical inferences from the output. In medical diagnosis, neither model can replace the other, but the two may be used complementarily to aid in decision making. Both models have the potential to help physicians with respect to understanding cancer risk factors, risk estimation, and diagnosis.