Abstract
Purpose: Kinetic modeling is widely used to analyze dynamic imaging data, estimating kinetic parameters that quantify functional or physiologic processes in vivo. Typical kinetic models give rise to nonlinear solution equations in multiple dimensions, presenting a complex fitting environment. This work generalizes previously described separable nonlinear least-squares techniques for fitting serial compartment models with up to three tissue compartments and five rate parameters.
Methods: The approach maximally separates the linear and nonlinear aspects of the modeling equations, using a formulation modified from previous basis function methods to avoid a potential mathematical degeneracy. A fast and robust algorithm for solving the linear subproblem with full user-defined constraints is also presented. The generalized separable parameter space technique effectively reduces the dimensionality of the nonlinear fitting problem to one dimension for 2K-3K compartment models, and to two dimensions for 4K-5K models.
Results: Exhaustive search fits, which guarantee identification of the true global minimum fit, required approximately 10 ms for 2K-3K and 1.1 s for 4K-5K models, respectively. The technique is also amenable to fast gradient-descent iterative fitting algorithms, where the reduced dimensionality offers improved convergence properties. The objective function for the separable parameter space nonlinear subproblem was characterized and found to be generally well-behaved with a well-defined global minimum. Separable parameter space fits with the Levenberg-Marquardt algorithm required fewer iterations than comparable fits for conventional model formulations, averaging 1 and 7 ms for 2K-3K and 4K-5K models, respectively. Sensitivity to initial conditions was likewise reduced.
Conclusions: The separable parameter space techniques described herein generalize previously described techniques to encompass 1K-5K compartment models, enable robust solution of the linear subproblem with full user-defined constraints, and are amenable to rapid and robust fitting using iterative gradient-descent type algorithms.
Keywords: kinetic modeling, compartment modeling, dynamic imaging, positron emission tomography (PET)
INTRODUCTION
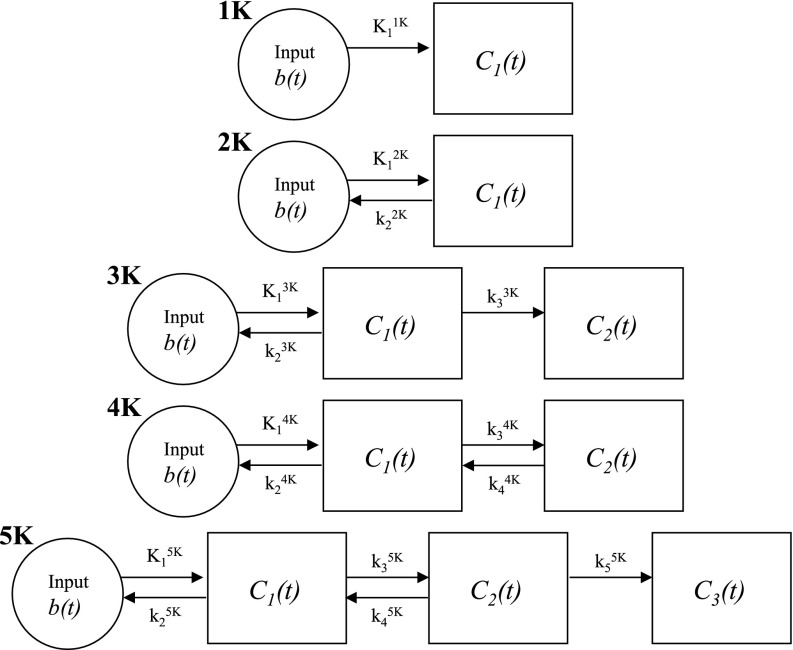
Dynamic imaging techniques can measure and characterize temporal changes in imaging signals for many modalities, providing more indepth functional information than static images that provide a snapshot or time-average over the acquisition period. Analysis of dynamic images usually involves applying a kinetic model that describes the temporal behavior of image voxels or regions in terms of a set of unknown scalar parameters. Many types of kinetic models exist, most involving a combination of scalar coefficients that weight temporal terms. These temporal terms are functions of time and may also depend on additional scalar parameters. The archetypal example kinetic model is the compartment model,1, 2, 3, 4 which comprises a series of homogenous compartments driven by an input function, and where temporal exchange between compartments is governed by rate parameters and simple linear differential equations. The solutions to such equations, however, are nonlinear and present a complex fitting environment. Figure 1 presents several generic serial compartment models in order of increasing complexity, along with a shorthand nomenclature that will be used in this paper to quickly reference each generic model. This paper is focused on the mathematical problem of fitting compartment model equations to dynamic imaging data in order to estimate best-fit kinetic rate parameters for a predetermined fitting criterion (e.g., weighted least-squares). Other related issues, such as measurement of the input function or selection of fitting weights, fall outside the scope of this work and are not discussed.
Figure 1.
Generic serial compartment models, each consisting of an input driving 1–3 tissue compartments in series that exchange according to the labeled rate parameters. We use a shorthand nomenclature to quickly reference each generic model as shown. For example, the “3K” model refers to the model with input plus two additional compartments and three rate parameters.
Exchange of tracer between connected compartments is governed by linear differential equations of the form
| (1) |
where the subscripts in and out refer to rate parameters that describe exchange into (from compartment Cin) or out of compartment Ci, respectively. The input function, b(t), drives the system; it is assumed in this work that the input function is known a priori from direct measurement or some other estimation technique. We also assume that all tracer activity concentrations are decay corrected, although the effects of radioactive decay could also easily be included in the modeling equations with a few simple modifications. The imaging measurement R(t) typically cannot measure each compartment individually; rather, the imaging signal comprises the sum over all compartments, C(t; b(t), {ki}), often with the addition of a vascular term due to imaging signal from whole-blood, B(t),
| (2) |
where fB is the fractional contribution of B(t) to the imaging measurement. The rate parameters {ki}, along with fB, comprise the unknown parameters of the model to be estimated. While the differential equations are linear in these unknowns, the solution equations are nonlinear, containing weighted sums of exponentials convolved with the input function. As such, fitting compartment models to measured datasets involves a nonlinear minimization problem.
A large body of work has been performed in addressing the compartment model fitting problem. Perhaps the most robust—but also most computationally demanding—approaches for estimating individual rate parameters for multicompartment models involve nonlinear least-squares estimation (NLLS) in a variety of forms. Numerous nonlinear curve-fitting algorithms have been investigated, including gradient-based algorithms such as Levenberg-Marquardt,5, 6 ridge-regression,7, 8, 9, 10, 11 and simulated annealing methods.12, 13, 14, 15 When using conventional compartment model formulations, the multidimensional fitting space can be large and complex, and it often contains local minima and/or broad shallow valleys that slow or confound iterative minimization routines. The result is sensitive to initial conditions, and one can never be certain that the true global optimum has been reached.
One of the most promising approaches to improving robustness and fitting speed is to reformulate the compartment model solution equations into separable linear and nonlinear components prior to fitting. Separable nonlinear least-square techniques16, 17, 18, 19 can then be used, either directly or indirectly, to simplify and accelerate the fitting problem. This approach has been used for years in fitting 2K compartment models,9, 20, 21, 22, 23, 24 and more recently has been extended to 3K and 4K models.25, 26, 27, 28 The nonlinear components of the reformulated equations have largely been interpreted as forming basis functions for the kinetic model, and the fitting algorithm searches among these bases to identify (weighted sums of) curves that best-match the measured data. The best-fit basis functions and linear weighting parameters are then used to compute corresponding kinetic rate parameters (and/or macroparameters) of the compartment model. We collectively refer to these approaches as basis function methods throughout this paper.
Basis function methods bring the advantage of simplifying the nonlinear compartment model fitting problem by effectively separating the nonlinear aspects of the fit (i.e., identification of the best-fit basis functions) from the linear aspects (i.e., finding best-fit scalar weights for a given set of basis functions). However, current basis function methods have a few limitations. The basis function formulations for 4K models exhibit a potential degeneracy in the nonlinear parameters of the fit (see Sec. 2A below), which can lead to indeterminate results. Similarly, full implementation of boundary conditions and user-definable constraints on kinetic rate parameter estimates has not yet been described. Moreover, the algorithms employed for identifying the best-fit basis functions have largely been based on exhaustive search or simplex strategies, and fast iterative gradient-descent algorithms have not been broadly applied in this context.
In this work, we describe an alternate mathematical formulation of basis function methods that generalizes separable parameter space techniques for serial compartment models with up to three tissue compartments and five rate parameters. The alternate formulation avoids a potential degeneracy that may arise for previously described basis function formulations. A theoretical perspective of interpreting the resulting equations as effectively reducing the dimensionality of the solution space of the fitting problem is then discussed, followed by a description of a rigorous method for solving the linear subproblem with full user-defined constraints. The reformulated modeling equations are validated against conventional model formulations, and we demonstrate that both formulations provide identical time-activity curves and have the same least-squares global minimum. The application of fast iterative gradient descent algorithms for solving the nonlinear subproblem is then explored by characterizing separable parameter space objective functions. Finally, the performance of both exhaustive search and the iterative Levenberg-Marquardt algorithms are studied for separable parameter space fits and compared to fits using the conventional model formulations.
THEORY
Without loss of generality, the theory for the generalized separable parameter space modeling formulation is presented in the context of kinetic modeling in dynamic nuclear medicine imaging, e.g., positron emission tomography (PET) and single-photon emission computed tomography (SPECT). As such, quantities are described as tracer radioactivity concentrations. The concepts and mathematics, however, are generalizable to other dynamic imaging modalities and nonimaging applications of kinetic modeling.
Generalized kinetic modeling formulation
Let κB, κb, κ1, κ2, υ1, and υ2 be scalar parameters that will be further described below, and let B(t) be the whole-blood activity concentration. Further, define the following temporal terms that depend on the input function, b(t), as well as scalar parameters υ1 and υ2,
| (3) |
| (4) |
| (5) |
Note that the temporal terms S1(t; υ1; b(t)) and S2(t; υ1, υ2; b(t)) are convolutions of exponentials with the input function. We can now write a generalized modeling equation
| (6) |
which is linear in {κB, κb, κ1, κ2} and nonlinear in {υ1, υ2}. Defining κB, κb, κ1, κ2, υ1, and υ2 as listed in Tables 1, 2, it can easily be shown that this general formulation encompasses the solution equations for well known 1K-4K serial compartment models,1, 2, 29, 30 as well as the lesser-used 5K serial compartment model.31
Table 1.
Nonlinear parameter definitions for 1K-5K compartment models.
| Model | υ1 | υ2 | Constraint |
|---|---|---|---|
| 1K | 0 | 0 | n/a |
| 2K | k2 | 0 | 0 < υ1 |
| 3K | k2 + k3 | 0 | 0 < υ1 |
| 4K | 0 < υ2 < υ1 | ||
| 5K | 0 < υ2 < υ1 |
Table 2.
Linear parameter definitions for 1K-5K compartment models.
| Model | κB | κb | κ1 | κ2 | Constraints |
|---|---|---|---|---|---|
| 1K | fB | (1 − fB)K1 | 0 | 0 | 0 ⩽ κB ⩽ 1; 0 < κb |
| 2K | fB | 0 | (1 − fB)K1 | 0 | 0 ⩽ κB ⩽ 1; 0 < κ1 |
| 3K | fB | 0 | 0 ⩽ κB ⩽ 1; 0 < κb; 0 < κ1 | ||
| 4K | fB | 0 | (1 − fB)K1 | 0 ⩽ κB ⩽ 1; 0 < κ2 < κ1 | |
| 5K | fB | 0 ⩽ κB ⩽ 1; 0 < κb; 0 < κ2 < κ1 |
We refer to Eq. 6 as the “generalized separable parameter space formulation.” For 2K models, the formulation presented above is equivalent to that previously used with the application of separable nonlinear least-squares for these models.20 Similarly, for 3K models it is identical to the basis function for plasma input compartment (BAFPIC) method of Hong et al.28 The proposed generalized formulation extends the approach to include the 5K compartment model, and for ≥4K models, there is a subtle difference as compared to previously described basis function methods.27 The difference lies in our definition of the S2 term, which in previous approaches was defined as . Subtracting in the S2 term as in Eq. 5 ensures that S1 and S2 are determinant and distinguishable (i.e., S1 ≠ S2 for all nonzero values of υ1, 2), which avoids the potential degeneracy in the previous approach that could arise for υ1 ≈ υ2. Further, our formulation of S2 immediately leads to the constraint 0 < υ2 < υ1 in order to ensure positivity for this temporal term, which is required in order to limit Eq. 6 to represent valid compartment model solutions. Similarly, the special case of υ1 = υ2 in our formulation implies that both k4 and k5 must be zero in order to represent a valid compartment model, which corresponds to simplification to a 3K model (see below). Analogous constraints and boundary conditions could be applied when using previously described basis function formulations,27 for example, by implementing a constraint to ensure that υ1 and υ2 differ by some minimum value. However, we find that the description and interpretation of these cases may be more straightforward when using the formulation described in Eq. 5.
The constraints listed in Tables 1, 2 limit the generalized formulation to valid compartment model solutions with positivity constraints on the conventional kinetic rate parameters K1, k2 − k5. For 4K and 5K models, the constraint 0 < υ2 < υ1 is equivalent to requiring k2 to be positive and k3 and k4 to be non-negative, and 0 < κ2 < κ1 ensures positivity for k2 − k4. Of note, we have used positivity constraints here (except for the vascular term κB) rather than non-negativity constraints, thus the constraints preclude solutions with rate parameters equal to zero. Solutions where a rate parameter is zero are encompassed via model simplification, e.g., a 4K model with k4 = 0 simplifies to a 3K model. This approach also ensures that the modeling formulation does not attempt to compute inestimable rate parameters. For example, if k3 = 0, then no information is available regarding k4 and k5 (as there is no tracer exchange with the unobservable compartment), and the estimable model reduces to a 2K model.
Construction of the WSSE objective function
For dynamic imaging, the measured data are generally discrete samples in time. Depending on the modality and other factors, two discretization schemes are commonly encountered—instantaneous samples, and samples averaged over time-frame durations. For each case we define the following discretizations, where j = 1…M represents the time (time-frame) index:
Instantaneous samples:
| (7) |
Averaged over time-frame durations:
| (8) |
In addition, we distinguish between modeled values and noisy measurements using a carat and tilde, respectively.
Using either discretization, the generalized kinetic model at each time sample j is written
| (9) |
The model fitting problem amounts to finding the values of the parameters κB, κb, κ1, κ2, υ1, and υ2 that minimize some objective function. We consider the weighted least-squares (WLS) criterion, and write the weighted sum-squared error objective function as
| (10) |
where wj are the weights for each time sample j.
Application of separable nonlinear least-squares
The generalized formulation of Eq. 6 has 6 degrees-of-freedom (κB, κb, κ1, κ2, υ1, υ2), as does the conventional model formulation for the 5K model (fB, K1, k2 − k5); however, the generalized formulation is written to be explicitly linear in κB, κb, κ1, and κ2, and nonlinear in υ1 and υ2 (which appear as exponents in the convolutions of temporal terms S1 and S2). Inspection of the 2K and 3K models (see, e.g., Tables 1, 2) reveals that there is inherently one convolution integral containing a single free parameter in the exponent (υ1), resulting in one nonlinear degree-of-freedom; the remaining degrees-of-freedom are linear. Likewise, inspection of the 4K and 5K models reveals two inherent convolution integrals with differing exponents. The free parameters in the exponents, υ1 and υ2, are independent parameters: υ1 cannot be written in terms of (κB, κb, κ1, κ2, υ2), and likewise υ2 cannot be written in terms of (κB, κb, κ1, κ2, υ1). As such, two separate free parameters are required to represent these convolution integrals, and these models inherently have two nonlinear degrees-of-freedom. Since the generalized formulation of Eq. 6 is written explicitly to have the minimum number of nonlinear free parameters (one for 2K-3K models, two for 4K-5K models), and likewise the maximum number of linear free parameters (the κs), this formulation can be considered to maximally separate the linear and nonlinear parameters.
Separating the linear and nonlinear parameters in this manner provides for the full benefit of separable nonlinear least-squares techniques.16, 17, 18, 19 The fitting problem is essentially separated into two problems: a nonlinear fit in (υ1, υ2), coupled simultaneously with a linear fit in (κB, κb, κ1, κ2). Previous basis function methods have largely used exhaustive search or downhill simplex algorithms to search among the (υ1, υ2) “basis functions,” analytically solving the linear subproblem to find the best-fit (κB, κb, κ1, κ2) for each point (υ1, υ2) encountered along the way. In this section, we show that the linear subproblem can also be directly incorporated into the nonlinear fit, providing a “Reduced Parameter Space Reformulation” with interesting theoretical perspectives that illustrate the value of separable parameter space fitting techniques.
Consider the linear subproblem that arises at each iteration/step of the nonlinear fit: finding (κB, κb, κ1, κ2) that minimizes WSSE given the current value of (υ1, υ2). For the moment, we ignore constraints on the κs and consider the unconstrained linear subproblem. Taking the derivative of WSSE [Eq. 10] with respect to each linear parameter and setting the result to zero, we obtain the linear subproblem
where
| (11) |
and “.” denotes symmetric matrix elements.
The conventional approach, as used with previously described basis function methods, is to analytically invert the linear subproblem () to directly compute the best-fit κs that minimize WSSE given the current values of υ1 and υ2. The estimated κs are then fed back to the nonlinear fitting algorithm, and the fit in (υ1, υ2) progresses accordingly.
Consider an alternative approach, however, where the inverted linear subproblem (which computes best-fit κs as functions of υ1, υ2, and measured/known quantities) is substituted back into the original modeling Eq. 6. The result is a reformulated modeling equation, which we call the Unconstrained Generalized Reduced Parameter Space Reformulation, which effectively removes the linear parameters from the model:
Unconstrained generalized reduced parameter space reformulation:
| (12) |
In essence, the reformulated model equation has been constrained to only permit solutions that minimize the WSSE objective function in the linear sense. Inspection of each term in Eq. 12 reveals that the reformulated model depends on υ1, υ2, and the measurements; however, no linear free parameters (κs) remain. One interpretation of this is that the application of separable nonlinear least-squares can be considered to constrain the solution space to only include solutions that minimize the objective function in the linear sense, effectively reducing the dimensionality of the fit to only the nonlinear free parameters. More specifically, the dimensionality of the “reduced” fitting space for 1K-5K serial compartment models becomes:
| Model | Conventional formulation | Reduced parameter space reformulation |
|---|---|---|
| 1K | 2D (fB, K1) | 0D (no free parameters) |
| 2K | 3D (fB, K1, k2) | 1D (υ1) |
| 3K | 4D (fB, K1, k2 − k3) | 1D (υ1) |
| 4K | 5D (fB, K1, k2 − k4) | 2D (υ1, υ2) |
| 5K | 6D (fB, K1, k2 − k5) | 2D (υ1, υ2) |
While of limited practical interest (due to difficulty in constraining the κs with this approach), this theoretical perspective illustrates the value of separable parameter space fitting techniques (including basis function methods). The effective dimensionality of the nonlinear fitting problem is greatly reduced, simplifying and speeding the fit. Of note, any iterative minimization procedure employed to solve the nonlinear subproblem would act effectively the same regardless of whether it uses Eq. 11 or 12, except for approaches which implement constraints on the κs.
Constraining fitted parameters in the linear subproblem
The constraints listed in Tables 1, 2 ensure that the generalized separable parameter space formulation [Eq. 6] represents valid compartment models with positivity constraints on all kinetic parameters (plus 0 ⩽ fB ⩽ 1). In practice, one may well wish to impose additional constraints on parameter estimates for the particular application at hand. In either case, constraints on the nonlinear parameters (υ1, υ2) can be imposed in the standard fashion for whichever nonlinear fitting algorithm is employed. Implementing constraints on the linear subproblem, however, is less straightforward. Direct inversion of the linear subproblem of Eq. 11 does not account for any constraints on the κs, and the direct analytical solution to the linear subproblem is unconstrained. Ad hoc approaches to implementing a certain level of constraint for the linear subproblem have been proposed;32 however, these approaches do not guarantee that the resulting fitted parameters minimize the objective function within the parameter ranges allowed.
The Appendix describes a pseudo-code algorithm for solving the linear subproblem with full user-defined constraints on the estimated parameter values (κs). The algorithm first computes the direct inversion solution. If any parameter is out of range, then an exhaustive search over that parameter is performed, analytically computing the direct inverse for the remaining parameters at each step. When more than one parameter goes out of range, nested loops are used to exhaustively search among those parameters whose analytical solution is out of range while computing analytical solutions for those parameters remaining in range. While this algorithm can require a large number of steps (i.e., when exhaustive searches are required for more than one κ), each step is extremely fast as no new convolution integrals need be performed and many of the sums can be reused for each step. The resulting computational cost per step is orders-of-magnitude lower than the cost per step (or iteration) of the nonlinear subproblem [where changing υ1 and/or υ2 requires recalculation of convolution integral(s)].
One may also desire to apply physiologic equality constraints to certain parameters, e.g., setting K1/k2 to some fixed value known a priori. A number of different such scenarios could arise for different tracers and modeling applications, and discussion of each falls outside the scope of this work. However, separable parameter space fitting approaches could still be used by applying the equality constraint to the original modeling equations and rederiving the separable parameter space formulation. Depending on the equality constraint(s) applied, the resultant formulations may have fewer linear and/or nonlinear free parameters than shown in this work for the generalized formulations.
Fitting algorithms for the nonlinear subproblem
Two fitting algorithms for solving the nonlinear subproblem were used in this work. The first algorithm, exhaustive search, is equivalent to the basis function search algorithms used with much of the prior work on basis function modeling methods (with some slight differences in the details of implementation). In some sense, this algorithm can be considered as searching among the temporal terms (“basis functions”) that correspond to each nonlinear model parameter (υ1, υ2). Taking a somewhat different perspective, one can also treat the nonlinear parameters themselves as parameters of the fit and apply iterative gradient-descent fitting approaches. In this work, we study the Levenberg-Marquardt algorithm for this purpose.
Exhaustive search algorithm
The dimensionality of the separable parameter space nonlinear subproblem—only one or two free parameters for 2K-3K and 4K-5K compartment models, respectively—is small enough that the entire solution space (within appropriate parameter ranges) can be exhaustively searched to an arbitrary precision with a reasonable amount of computational effort. Such brute-force exhaustive search guarantees identification of the global minimum to within the selected search precision and parameter ranges. As such, exhaustive search provides the most robust fit for the given data, weights, and input functions. In this work, we implemented exhaustive search routines in C for solving the nonlinear subproblem (finding best-fit υ1 and υ2). The routine loops over υ1 from 0.0 to 2.0 min−1 in 1000 steps, sampling υ1 at a precision of 0.002 min−1. Here, we chose uniformly spaced sampling in order to simplify discussion of the precision of the algorithm; for practical application, logarithmic spacing would likely be more appropriate as used in most previous implementations of these algorithms. For the 4K and 5K models, a nested loop over υ2 was likewise included for each value of υ1. Recalling that υ2 should be constrained less than υ1 in order to represent a valid compartment model, this inner loop ranged from 0.0 up to the current value of υ1 in steps of 0.002 min−1. This resulted in 1000 total steps for the 2K-3K models, and ∼500 000 steps for the 4K-5K models. For comparison, consider that exhaustive search with conventional compartment model formulations would require 109, 1012, and 1015 steps for 2K, 3K, and 4K models, respectively—becoming computationally intractable.
Levenberg-Marquardt algorithm
Nonlinear minimization with the Levenberg-Marquardt algorithm was also implemented in C for both the generalized separable parameter space formulation and for conventional 1K-5K compartment model formulations. Single-threaded coding was used with no parallelization. Close attention was paid to code optimization for both model formulations, and all concurrent routines applicable to both algorithms were shared in order to match the implementations as closely as possible and to ensure valid comparisons between the two implementations could be performed. For the conventional implementation, the vascular fraction (fB) and all applicable rate parameters (K1, k2 − k5) were estimated by the fitting algorithm, whereas only the nonlinear parameters υ1, υ2 were fit for the separable parameter space implementation. The algorithm was implemented as described in Press et al.,33 where the second derivative term of the Hessian matrix was ignored. Iterations were stopped after a successful update when the fractional change in WSSE reached 0.0001 or less, indicating convergence to a (possibly local) minimum. The magnitude of the update vector was bound to fall within the range [0.01,1.00] in order to avoid wild steps as well as to reduce the number of steps required to traverse a shallow valley of complicated topology. Various initial conditions were used for the evaluation studies as described in Sec. 4.
Recovery of individual rate parameters K1-k5
After completing the fit, the kinetic rate parameters K1, k2 − k5, as well as fB, are easily calculated from the best-fit parameters κB, κb, κ1, κ2, υ1, and υ2. The calculation does merit some discussion of parameter estimability, however. Table 3 provides conversions for the 1K-5K serial compartment models. In all cases fB = κB. When macro parameters such as the volume of distribution or net influx are desired, they can either be computed using the individual rate parameters, or more directly in some cases (e.g., the net influx parameter for the 3K model is more directly calculated as Ki = κb/(1 − fB)).
Table 3.
Recovery of kinetic rate parameters.
| Model | fB | K1 | k2 | k3 | k4 | k5 |
|---|---|---|---|---|---|---|
| 1K | κB | 0 | 0 | 0 | 0 | |
| 2K | κB | υ1 | 0 | 0 | 0 | |
| 3K | κB | 0 | 0 | |||
| 4K | κB | 0 | ||||
| 5K | κB |
The above equations provide one-to-one correspondence between any set of separable parameter space variables and a set of conventional rate parameters, provided that divide-by-zero singularities are not encountered. The majority of such potential singularities are avoided through application of the constraints listed in Tables 1, 2, which concurrently ensure that the generalized modeling equations represent valid 1K-5K compartment models. The remaining potential singularities are avoided through model simplification (as described in Sec. 2A). For example, consider the potential singularity of fB = 1.0, affecting all K1 calculations. If the best-fit value of fB is 1.0, this means the best-fit time-activity curve is pure whole-blood and there is no extravascular tissue uptake. In that case, K1 is zero and all higher order rate parameters (k2 − k5) are undefined and not meaningful (one could consider this a “0K” model).
EVALUATION METHODS
Separable parameter space modeling techniques, which are generalized in this work, have already been thoroughly evaluated in the research literature for both 2K models9, 20, 21, 22, 23, 24 and more complex models with a basis function methods.25, 26, 27, 28 As such, the evaluation provided in this work is designed to first broadly characterize separable parameter space model formulations vs conventional compartment model formulations, and then to evaluate the applicability and receptiveness of the generalized separable parameter space formulations to fast gradient-descent fitting algorithms. Sections 3A, 3B, 3C, 3D describe the evaluations performed in this work. The emphasis of this evaluation is focused on 2K, 3K, and 4K serial compartment models, as these represent the most commonly used compartment models in dynamic PET imaging and cover both 1D (3K) and 2D (4K) separable parameter space solution equations.
Simulation of time-activity curves
A set of 24 typical input functions and whole-blood curves were selected from dynamic PET exams using 15O-water (2K model), 18F-fluorodeoxyglucose (FDG; 3K model), and 11C-acetate (4K model) in patients with malignant solid tumors at our institution. Populations of kinetic parameters were then generated with a pseudorandom number generator to be randomly distributed within the following ranges: 0.001 ⩽ fB ⩽ 0.2, 0.02 ⩽ K1 ⩽ 0.5, 0.02 ⩽ k2 ⩽ 0.7, 0.002 ⩽ k3 ⩽ 0.4, and 0.002 ⩽ k4 ⩽ 0.4. Here, each parameter was independently and uniformly distributed over the given range except for k2, which was set according to a uniform distribution of 0.7 ⩽ K1/k2 ⩽ 1.1. These distributions were not designed to represent any particular tracer or target organ, but rather were set to cover a broad range of values that might be encountered in a variety of applications. The input functions and rate parameter ranges were used to simulate populations of 200–1000 time-activity curves each for the 2K, 3K, and 4K models using the conventional model formulations. The number of curves in each population was heuristically selected to include enough datapoints such that “outlier” points (representing best-fit differences between the separable parameter space and conventional model fits—see, e.g., results Figs. 67) presented themselves for study. Progressive temporal sampling schemes were used, for example, 18 × 10, 6 × 20, 4 × 30, 5 × 60, 5 × 120, 4 × 300, 3 × 600 s for a total duration of 72 m for the 18F 3K model simulations.
Figure 6.
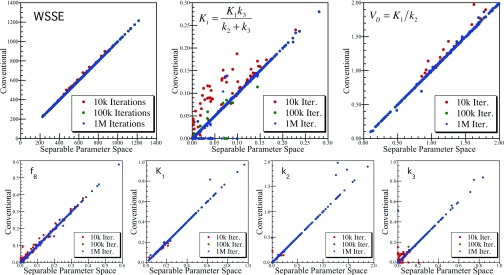
Scatter plots of the 3K model WSSE objective function, macroparameters, and individual rate parameters comparing conventional versus separable parameter space fit results for noisy populations of time-activity curves. In each case, results for three different numbers of iterations are shown for the conventional fits with simulated annealing, demonstrating convergence effects as progressively higher numbers of iterations produced successively better fits (lower WSSE) for some curves. Note that in all cases the separable parameter space fits with exhaustive search produced equal or lower WSSE than the conventional model fits to within the numerical precision of the search (approximately 1 part in 10−3). As a population, the conventional model fits approached the separable parameter space fits as the number of iterations increased.
Figure 7.
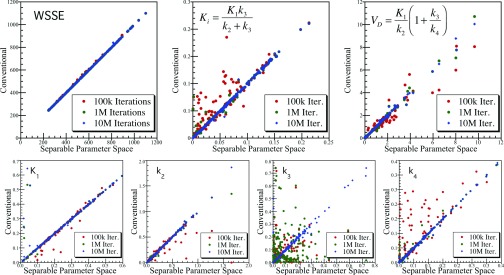
Scatter plots of the 4K model WSSE objective function, macroparameters, and individual rate parameters (fB not shown) comparing conventional vs separable parameter space fit results for noisy populations of time-activity curves. The conventional model results are shown for 105, 106, and 107 iterations of simulated annealing, showing convergence effects similar to those shown in Fig. 6 for the 3K model (but at 10× more iterations due to the increased complexity of the 4K model). Again, the separable parameter space exhaustive search fits provided the lowest WSSE for all cases to within the precision of the search, and the conventional model fits progressive convergence toward these global minima across the full population of curves with increasing iteration.
Noise-free curves were first simulated for each case. Statistical noise was then added using a noise model that approximates the noise characteristics of iteratively reconstructed PET images. Here, Gaussian deviates were simulated for each datapoint with variance inversely proportional to the time-frame durations, and scaled to five different noise levels. When a noisy sample went negative, however, the absolute value was used—providing an asymmetric non-negative distribution roughly approximating the statistical distribution of iteratively reconstructed PET values. The resulting noisy curves had Gaussian-like non-negative statistics that varied with time-frame duration, providing more realistic test cases than simulating curves that were consistent with either Gaussian or Poisson noise. The noise model did not account for other factors, such as differences due to radioactive decay, deadtime, randoms rates, or reconstruction algorithm, that would be encountered in practice. Note that this noise model is inconsistent with the L2-norm criterion typically used in model fitting (which essentially assumes a Gaussian noise model); however, such inconsistency is a real and present challenge for actual dynamic PET data. Five different noise levels were used, covering the approximate range encountered in the dynamic PET datasets—ranging from high noise in individual voxels to lower noise curves representative of larger tumor ROIs.
Characterization of separable parameter space WSSE objective functions
Given the reduction in the number of free parameters offered by the separable parameter space formulations, the objective functions reside within 1D (2K-3K models) or 2D (4K-5K models) solution spaces. Thus, they can be plotted and analyzed much more easily than conventional objective functions in three to six dimensions. Using the exhaustive search routines just described, the WSSE objective functions were characterized for a number of noisy 3K-5K time-activity curves by storing and plotting the WSSE at each value of υ1 (3K) or υ1, υ2 (4K-5K). The resulting objective functions were analyzed for the presence/absence of local minima or other confounding structures that could affect the performance of curve fits using the separable parameter space formulations with various minimization algorithms.
Characterization of global minimums for both conventional and separable parameter space formulations
In order for the separable parameter space formulations to be a viable alternative for kinetic modeling, the reformulated modeling equations must provide the same global minimum and best-fit rate parameters as the conventional model equations. In order to perform this study, fits to both model formulations need to correctly reach the true global minimums. Identification of the true global minimum is not straightforward, however, as commonly used fitting algorithms may be sensitive to initial conditions and converge to local minima (see Sec. 4D, for example, data regarding convergence for the Levenberg-Marquardt algorithm for conventional model fits). To overcome these shortcomings, the simulated annealing algorithm13, 14, 15, 33 was selected for the conventional model fits. As implemented, the simulated annealing algorithm was independent of starting conditions (aside from the set parameter ranges used for all fits in this paper) and included means for escaping local minima and progressing toward the true global minimum provided that enough iterations and a slow enough relaxation schedule were used. We progressively applied simulated annealing with 104–108 iterations, increasing the number of iterations by 10× each step and observing the number of cases in each population where the best-fit solution did not change versus those that continued moving toward a better fit. While this approach does not guarantee that the true global minimum was reached for all fits (only exhaustive search could so guarantee), it did allow visualization of the progression of the population of fits toward the true global minima as will be shown in Figs. 67 below. As such, the simulated annealing algorithm was used with the conventional model formulations in order to identify the true global minimum fits for the simulated population studies. The exhaustive search algorithm was used to identify the global minimum fits for the separable parameter space formulations, where the reduced dimensionality of the separable parameter space nonlinear subproblem makes such exhaustive search computationally feasible (guaranteeing identification of the true global minimum to within the search range and precision for all cases).
Performance of Levenberg-Marquardt algorithm
The performance of the Levenberg-Marquardt algorithm for solving the nonlinear subproblem of the separable parameter space formulations was studied and compared to fitting performance of the same algorithm for conventional compartment model formulations. Iterative fitting performance was evaluated in terms of convergence to the true global minimum (as opposed to local minima), sensitivity to initial values, and number of iterations and fitting time required to reach convergence. Here the populations of noisy time-activity curves for 2K-4K models described above were fit again using the Levenberg-Marquardt algorithm with both model formulations. Three sets of fits were performed with differing initial conditions. First, each curve was fit repeatedly using 100 randomly generated sets of rate parameters as initial estimates. These fits provide a measure of sensitivity of the iterative fits to the initial parameters. In practice, the initial parameter estimates for conventional model Levenberg-Marquardt fits would be selected manually by the user to be a reasonably close match to the measured curve. In addition to introducing a level of subjectivity into the final result, the manual intervention adds significantly to the real-world fitting time. Rather than replicating this subjective process, randomly selected initial parameters were studied in order to characterize the sensitivity of the fits to these initial conditions. In the second set of fits, the initial parameter values were each set to the minimum value (e.g., 0.001), which results in the Levenberg-Marquardt algorithm finding the (possibly local) minimum closest to the minimum parameter values. Finally, in the third set of fits, the initial parameter values were set to midrange values, defined as being 1/4th the way between the minimum and maximum value for each parameter (e.g., for a parameter ranging from 0.0 to 2.0, the initial value was set at 0.5). The number of iterations and CPU times were recorded for each fit, and the best-fit results were analyzed relative to the true global minimum fits for each case (determined as described in Sec. 3C above).
RESULTS
Verification that the conventional and reformulated equations provide the same time-activity curves
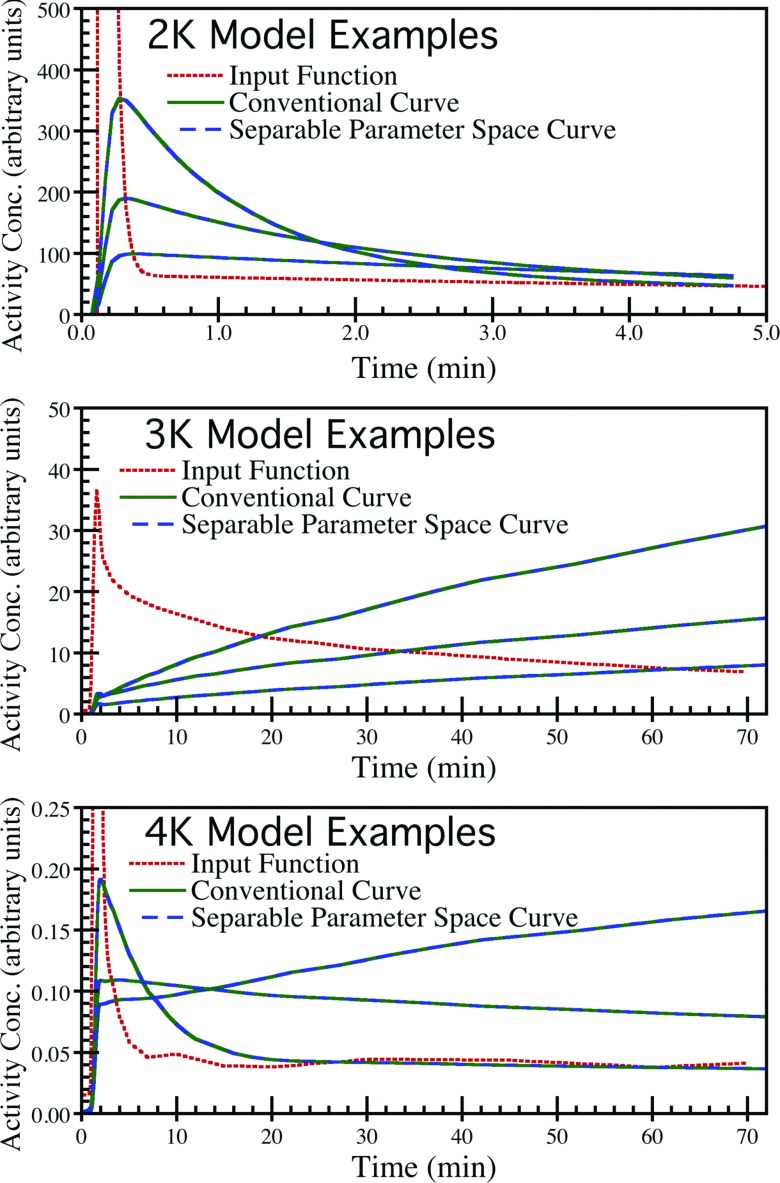
Figure 2 shows example time-activity curves for 2K (based on 15O-water), 3K (based on 18F-FDG), and 4K (based on 11C-acetate) compartment models. For each model, three representative sets of rate parameters were selected and curves were simulated using both conventional compartment model formulations and the separable parameter space formulation of Eq. 6. For the latter case, the values of κB, κb, κ1, κ2, υ1, and υ2 were computed from the conventional rate parameters according to the conversions described in Sec. 2A. The curves for each case were identical up to the numerical precision of the computer, confirming that the separable parameter space formulations correctly represent valid compartment models for these data.
Figure 2.
Example time-activity curves for 2K-4K serial compartment models simulated using the conventional and separable parameter space model formulations. Three example curves are shown for each model. The curves for the conventional and reformulated models were identical up to the numerical precision of the computer, and overlap exactly in the plots.
Characterization of objective functions
The separable parameter space reformulations reduce the dimensionality of the nonlinear fitting problem to only one free parameter for 2K-3K compartment models, and to only two free parameters for 4K-5K compartment models. The resultant 1D and 2D objective functions can be plotted and analyzed more easily than conventional objective functions in three to six dimensions. Figure 3 shows a representative WSSE objective function for a 3K compartment model fit to a noisy time-activity curve modeled on dynamic FDG PET tumor imaging. This typical objective function is well behaved, having a single well-defined minimum and no other confounding structures such as local minima or shelves. The plot also shows how the values of κB, κb, and κ1 vary as functions of υ1 to keep WSSE minimized according to the linear subproblem [Eq. 11]; the corresponding values of fB and the conventional rate parameters are also shown in the lower panel for comparison.
Figure 3.
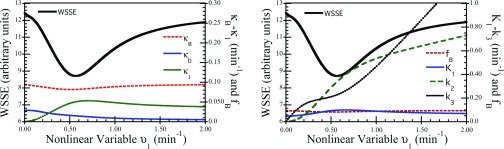
Plots of the separable parameter space WSSE objective function for an example noisy time-activity curve with 3K compartment model. The left plot shows how the values of κB, κb, and κ1 that minimize WSSE change as a function of υ1 (recall υ1 = k2 + k3 for the 3K model). Similarly, the plot at right shows the same objective function with the corresponding values of fB, K1, k2, and k3 at each point. The objective function is well behaved, having a single clearly defined minimum with no other local minima, shelves, or confounding structures.
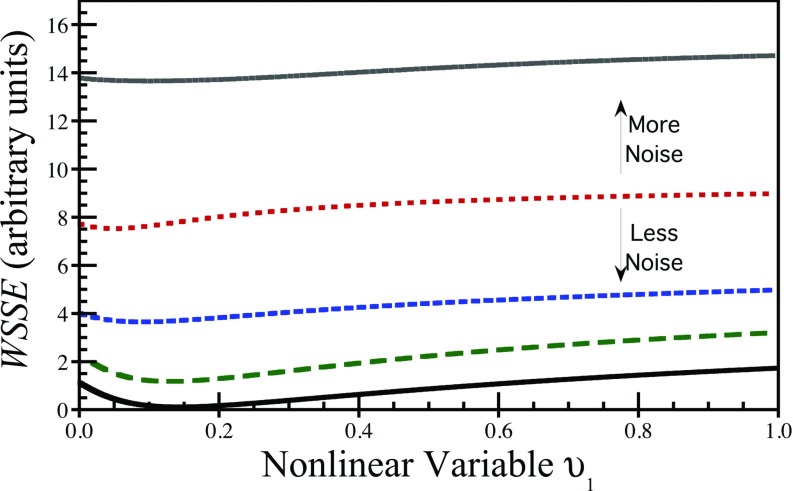
Figure 4 shows example separable parameter space WSSE objective functions for another representative 3K model curve at five different noise levels. The minimum is deepest for the lowest noise curve, and becomes shallower with increasing noise—consistent with the observation that the best-fit parameters will have greater statistical variability for noisier data. However, the objective function remained well behaved for all noise levels studied. Upon reviewing hundreds of 3K model objective functions for the separable parameter space formulation, the majority of functions are well behaved with only a single minimum and little or no complicated topology; however, shallow local minima were present in a minority of cases that could affect descent-type iterative fitting algorithms. In each of these cases, the local minimum occurred at relatively large values of υ1—often larger than the physiologically meaningful range—and furthermore the local minima were shallow relative to the global minimum. The potential presence of such local minima has implications for descent-type fitting algorithms, but do not affect best-fit results when the exhaustive search algorithm is used. One potential solution for handling such local minima would be to provide an upper bound constraint on the value of υ1 during the fitting procedure.
Figure 4.
Example separable parameter space WSSE objective functions for fitting a 3K compartment model to curves at five different noise levels. The minimum is deeper and better-defined for lower noise data, and becomes shallower as noise increases. However, for all noise levels the reformulated objective function remained well-behaved, and no complex topological features appeared with increasing noise levels.
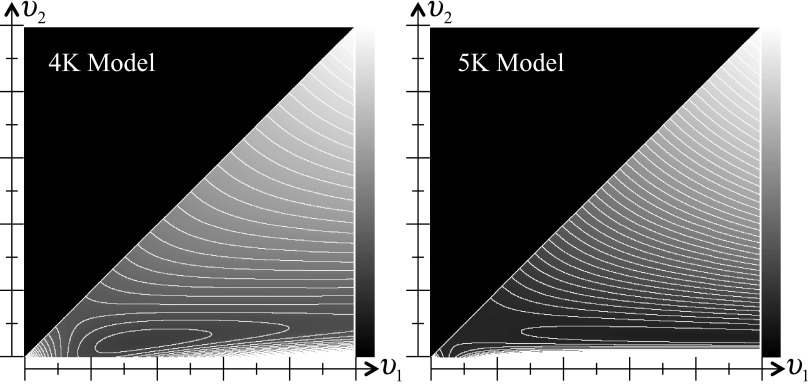
Representative objective functions in two dimensions for 4K and 5K compartment models using the separable parameter space formulation are provided in Fig. 5. Here the reformulation has two nonlinear unknowns, υ1 and υ2, both of which are constrained to be non-negative, and further the solution space was constrained to values υ2 < υ1 in order to limit the solution space to regions that represent valid compartment models. The majority of these 2D objective functions were again generally well-behaved, with only a single minimum, although some complexity was present for lower values of υ1 that may be considered a “side valley.” These curvatures in the objective function arise from imaginary “poles” in the excluded regions υ2 > υ1 and υ2 < 0 (corresponding to values where the reformulated equations do not represent value compartment models—giving rise to rate parameters with either negative or imaginary values). The potential for local minima again cannot be ruled out, although empirical evidence suggests that the prevalence of local minima is low, and also that such minima are shallow and occur at relatively large values of υ1 or υ2. Overall, least-squares objective functions for the separable parameter space formulations were generally well-behaved with topology considerably less complex than that for the conventional model formulations, providing a simpler and potentially more robust environment for fast iterative nonlinear fitting.
Figure 5.
Contour plots of two examples separable parameter space WSSE objective functions for 4K (left) and 5K (right) compartment models. The grayscale represents WSSE values, and contour lines are drawn at regular intervals. Recall that the separable parameter space formulation for 4K-5K models has two nonlinear unknowns (υ1, υ2), and also that υ2 is constrained to be less than υ1 (hence the plots are only defined for regions υ2 < υ1). The objective functions are generally well behaved and do not show complex topological features. However, some complex structure exists in the lower-left corner near υ1 = υ2 line and near υ2 = 0 which could slow convergence of gradient-descent type algorithms in these regions. These structures arise from “attraction” due to imaginary poles in the excluded υ2 > υ1 and υ2 < 0 regions of the solution space.
Verification that the conventional and reformulated model equations have the same global minimum
Populations of 200–1000 noisy time-activity curves representative of dynamic PET tumor imaging with 15O-water (2K model), 18F-FDG (3K model), and 11C-acetate (4K model) were simulated using methods described in Sec. 3A. Each noisy curve was fit to the separable parameter space formulation using the exhaustive search algorithm with the constraints listed in Tables 1, 2. The curves were also fit to the conventional model formulations using simulated annealing, where the fits were repeated using 104–108 iterations progressively in 10× increments in order to progressively approach the true global minimum fits across the population of curves as the number of iterations increased.
Figure 6 shows scatter plots of the best-fit WSSE and rate parameters for the 3K model comparing conventional versus separable parameter space fit results. Analogous results for the 4K model are provided in Fig. 7. These figures also include results for macroparameters Ki and VD for each model. In all cases, the separable parameter space fits with exhaustive search produced equal or lower WSSE than the conventional fits with simulated annealing to within the numerical precision of the exhaustive search algorithm (approximately 1 part in 10−3). This result is consistent with the prediction that exhaustive search identifies the true global minimum to within the selected precision for all fits. In addition, the conventional model fits with simulated annealing progressively approached the separable parameter space exhaustive search results, further confirming that both model formulations provide the same best-fit global minimums.
Linear regression analysis between the conventional (maximum no. iterations) and separable parameter space fits revealed slopes of 1.000 ± 0.001 and Pearson correlation coefficients greater than 0.999 for all individual rate parameters and macroparameters. These results confirm that both the conventional and reformulated model equations provided identical best-fit results across these populations of curves to within the precision of the search. Small differences on the order of 10−4 were observed in the final rate parameters, consistent with a precision on the order of 10−3 for the exhaustive search algorithm [note that this precision is applicable to the nonlinear parameters υ1 and υ2; calculation of the linear (κ) parameters and then conversion to kinetic rate parameters K1 − k4 were computed at full floating point double- precision].
Performance of Levenberg-Marquardt algorithm
Table 4 summarizes the performance of the Levenberg-Marquardt algorithm for fitting both the conventional and separable parameter space model formulations. The number of iterations required to attain the stopping criterion provide a measure of iterative convergence properties. Here, the separable parameter space fits required significantly fewer iterations to converge than did the conventional model fits, suggesting that the reduced dimensionality of the nonlinear fitting space simplified the iterative fit. In order to determine whether or not each fit converged to the global minimum, as opposed to a local minimum, the true global minimum fit for each case was identified from the simulated annealing and exhaustive search results from Sec. 4C. For each Levenberg-Marquardt fit, the difference in best-fit WSSE between the Levenberg-Marquardt fit and the global minimum was computed. The median value and range are shown in the table. Similarly, the best-fit kinetic parameters (fB, K1 − k4) for the Levenberg-Marquardt fits were evaluated versus those for the global minimum fits by computing the magnitude of the error vector (root sum-square error in parameter estimates). Again, the median value and range of the error vector magnitude are listed in the table.
Table 4.
Levenberg-Marquardt fit results.
| Conventional model fits |
Separable parameter space fits |
||||||
|---|---|---|---|---|---|---|---|
| Model | Initial condition | Number of iterations (mean ± SD) | WSSE difference (median [range]) | Magnitude error vector (median [range]) | Number of iterations (mean ± SD) | WSSE difference (median [range]) | Magnitude error vector (median [range]) |
| 2K | Random | 314 ± 390 | 314 [0–76705] | 5.300 [0–6.97] | 19 ± 16 | 0.00 [0–76706] | 0.001 [0.00–4.97] |
| Minimum | 205 ± 349 | 205 [0–814] | 1.900 [0–2.88] | 20 ± 24 | 0.00 [0–18.9] | 0.001 [0.00–1.99] | |
| Midrange | 123 ± 250 | 167 [0–1045] | 1.100 [0–1.32] | 20 ± 6 | 0.00 [0–0] | 0.000 [0.00–0.11] | |
| 3K | Random | 117 ± 260 | 3214 [0–136933] | 2.990 [0.0–6.05] | 15 ± 14 | 26 [0–695] | 0.084 [0.00–7.14] |
| Minimum | 906 ± 234 | 107 [0–1393] | 1.909 [0.062–4.82] | 15 ± 18 | 32 [0–285] | 2.881 [0.00–4.38] | |
| Midrange | 117 ± 178 | 155 [10–2566] | 1.008 [0.065–3.56] | 28 ± 18 | 0.00 [0.0–0.0] | 0.000 [0.00–0.002] | |
| 4K | Random | 287 ± 389 | 1593 [0–56568] | 2.357 [0.01–5.39] | 130 ± 177 | 282 [0–16545] | 1.550 [0.00–3.23] |
| Minimum | 723 ± 422 | 460 [0–54330] | 1.894 [0.02–2.94] | 62 ± 171 | 0.00 [0–796] | 0.004 [0.00–2.79] | |
| Midrange | 483 ± 460 | 16 [0–245] | 1.478 [0.00–2.01] | 80 ± 124 | 0.00 [0.0–0.0] | 0.000 [0.00–0.01] | |
The fit results were sensitive to the initial conditions for both the conventional and separable parameter space model formulations, indicating that local minima may be present (at least some of the time) for both cases. However, the separable parameter space fits were less sensitive to initial conditions than were the conventional model fits. In particular, initializing the fit with midrange parameter values provided excellent results. When using these initial values, the separable parameter space fits attained the true global minimum fit for all parameters (defined as magnitude of the best-fit error vector < 0.01) in 96% of cases for the 2K model, 98% of cases for the 3K model, and 94% of cases for the 4K model. In contrast, the conventional model fits attained the true global minimum fit for all parameters in 53% of cases for the 2K model, in 4.8% of cases for the 3K model, and in 1.5% of cases for the 4K model. These results demonstrate the importance of manually selecting good initial conditions for the Levenberg-Marquardt algorithm with the conventional model formulation. Conversely, the Levenberg-Marquardt fits for the separable parameter space formulation were much less sensitive to initial conditions, which can be seeded within midrange initial values and converge to the true global minimum in the majority of cases.
Fitting times
Table 5 shows the CPU times for fitting noisy time-activity curves with 2K, 3K, and 4K models using both the conventional and separable parameter space model formulations. Times were computed for single-threaded code run on a 2.80 GHz Intel Xeon workstation, and no acceleration via multithreading was implemented. Each algorithm was implemented in C, sharing routines when possible, and with identical attention to optimizing the code for computational efficiency. The CPU time per iteration was similar for both model formulations, on the order of 0.04–0.07 ms for 2K-3K models and 0.09–0.10 ms for 4K models. Overall, the separable parameter space fits required approximately 10 ms for 2K-3K models and 1.1 s for 4K models; these times were reduced to about 1 and 7 ms, respectively, using the Levenberg-Marquardt algorithm.
Table 5.
CPU times for fits.
| 2K |
3K |
4K |
||||
|---|---|---|---|---|---|---|
| Model | Number of iterations | CPU time (ms) | Number of iterations | CPU time (ms) | Number of iterations | CPU time (ms) |
| Conventional model formulations | ||||||
| Simulated annealing | 104 | 326 ± 22 | 105 | 2227 ± 163 | 106 | 24056 ± 4508 |
| Levenberg-Marquardt | 123 ± 250 | 6.87 ± 13.97 | 117 ± 178 | 8.79 ± 13.39 | 483 ± 460 | 48.80 ± 46.19 |
| Separable parameter space reformulations | ||||||
| Exhaustive search | 103 | 10.2 ± 1.5 | 103 | 10.1 ± 0.9 | 106 | 1109 ± 172 |
| Levenberg-Marquardt | 20 ± 6 | 0.90 ± 0.27 | 28 ± 18 | 1.32 ± 0.85 | 80 ± 124 | 7.34 ± 11.38 |
DISCUSSION AND CONCLUSIONS
The separable parameter space techniques discussed in this paper generalize previously proposed methods for applying separable nonlinear least-squares to the compartment model fitting problem. The formulation described herein encompasses 1K-5K serial compartment models, including a modified formulation for higher order models that avoids a potential degeneracy present in previously proposed reformulations for these models. As a theoretical exercise, the linear subproblem of the reformulated equations was solved analytically and substituted back into the remaining nonlinear fitting equations. The resultant system can be interpreted as effectively reducing the dimensionality of the fitting space to only one dimension for 2K-3K compartment models, and to two dimensions for 4K-5K models—providing a nonlinear fitting problem that is both simpler and easier to solve than that of the original model formulation. This illustrates the value of the separable parameter space technique, but is not amenable to imposing constraints on the linear parameters. When keeping the linear subproblem separate, a fast and robust algorithm was presented for solving the linear subproblem with complete user-defined constraints on the fitted parameters. The generalized technique also treats the nonlinear unknowns as fittable parameters, rather than treating their corresponding temporal terms as basis functions. The receptiveness of the technique to fast gradient-descent type nonlinear fitting algorithms was explored by characterizing the objective functions, and by studying the performance of the Levenberg-Marquardt algorithm for solving the nonlinear subproblem.
The work focused specifically on the topic of performing the mathematical fit according to a preestablished fitting criterion—the WLS criterion. In order to retain focus upon the mathematical fitting approach, we did not explore other issues such as consideration of other fitting criteria, selection of the fitting weights, or identification of the input function. While these issues affect the bias and noise properties of the fitted parameters, they are distinct from issues regarding the mathematical fit—the fitting algorithm is a mathematical procedure for attaining the fitting solution that minimizes the fitting criterion, whereas the criterion, weights, and input function determine the properties of the fit at the global minimum.
When using the Levenberg-Marquardt algorithm, it is a common practice to estimate the covariance matrix of the standard errors in the fitted parameters by inverting the Hessian matrix used by the fitting algorithm33 (typically with second derivatives ignored). When using separable parameter space techniques, the Hessian matrix used in the nonlinear subproblem corresponds to only the nonlinear free parameters [as well as being subject to the constraint of minimizing the linear subproblem, as per Eq. 12]. In order to estimate the covariance matrix of the fitted kinetic rate parameters, one should compute and invert the Hessian matrix of the conventional full-parameter space model formulation using the best-fit rate parameters obtained from the separable parameter space fit. This approach is viable since both the conventional and separable parameter space formulations have the same global minimum, and requires a small degree of additional computation after completing the fit.
The generalized separable parameter space technique was found to provide identical time-activity curves as conventional compartment model formulations, and both the conventional and reformulated equations give rise to the same global minima. As such, fitting the reformulated equations (with appropriate constraints) and calculating conventional rate parameters from the best-fit reformulated parameters effectively finds the best-fit to the conventional model equations. However, the reduced dimensionality of the reformulated nonlinear fitting subproblem greatly simplifies separable parameter space fits. This reduced dimensionality makes exhaustive search algorithms feasible (and indeed computationally rapid), providing fits that guarantee the true global minimum to within the search precision in as little as 10 ms for 2K-3K models and 1.1 s for 4K models. For applications in which more rapid fitting is desired, e.g., voxelwise parametric imaging, fast iterative fitting algorithms, such as Levenberg-Marquardt, can be used to reduced the fitting times to approximately 1 ms for 2K-3K models and 7 ms for 4K models. Such fits were found to be less sensitive to initial conditions than comparable iterative fits with the conventional model formulations, and to converge in fewer iterations. In conclusion, the separable parameter space techniques described in this work generalize previously described techniques to encompass 1K-5K compartment models, enable robust solution of the linear subproblem with full user-defined constraints, and are amenable to rapid and robust fitting using iterative gradient-descent type algorithms.
ACKNOWLEDGMENTS
This work was supported by Grant No. R01CA135556 from the National Cancer Institute, and was made possible through seed funding from the Ben B. and Iris M. Margolis Foundation. The content is solely the responsibility of the authors and does not necessarily represent the views of the National Cancer Institute. The authors would like to thank Larry Zeng, Ph.D., Frederic Noo, Ph.D., and Thomas Rust, Ph.D. for many helpful discussions and assistance in proofreading the paper.
NOMENCLATURE
- b(t)
Input function
Temporal term (integral of b(t)); used in 1K, 3K, and 5K models
- B(t)
Tracer concentration in whole-blood
- fB
Fractional contribution of B(t) to the imaging measurement
- Ki
Net influx macroparameter, Ki = K1k3/ (k2 + k3)
- K1, k2 − k5
Rate constants for 1K-5K serial compartment models
- κB, κb, κ1, κ2
Linear parameters of the separable parameter space formulations
- R(t)
Modeled time-activity curve
- S1(t; υ1; b(t))
Temporal term present in 2K-5K compartment models
- S2(t; υ1, υ2; b(t))
Temporal term present in 4K-5K compartment models
- υ1, υ2
Nonlinear parameters of the separable parameter space formulations
- VD
Volume of distribution
APPENDIX: PSEUDOCODE ALGORITHM FOR COMPUTING CONSTRAINED LINEAR SUBPROBLEM
Let and be arbitrary user-defined minimum and maximum values for each linear parameter κi.
The linear subproblem described in Sec. 2C can be rapidly solved subject to these constraints using the following pseudocode algorithm:
| (1) Analytically invert the linear subproblem directly to obtain unconstrained best-fit values of all κs. |
| (2) If any κi is out of range, where i ∈ {B, 2, 1, b}, then: |
| Loop over with step size Δi: (i.e., exhaustively search over κi; typical Δi = 0.001 min−1) |
| Fixing κi, analytically invert the remaining linear subproblem for the remaining free κs. |
| If any κj is out of range, where j ∈ {B, 2, 1, b} and j ≠ i, then: |
| Loop over with step size Δj: (i.e., exhaustively search over κj) |
| Fixing κj, analytically invert the remaining linear subproblem for the remaining free κs. |
| If any κk is out of range, where k ∈ {B, 2, 1, b} and k ≠ i and k ≠ j, then: |
| Loop over with step size Δk: (i.e., exhaustively search over κk) |
| Analytically compute κl, where l ∈ {B, 2, 1, b} and l ≠ i, l ≠ j, and l ≠ k. |
| If κl is out of range, then: |
| Loop over with step size Δl: (i.e., exhaustively search over κl) |
| Find κl that maximizes WSSE for the current values of κi, κj, and κk. |
| End loop. |
| End if. |
| Find κk that maximizes WSSE for the current values of κi, κj, and κl. |
| End loop. |
| End if. |
| Find κj that maximizes WSSE for the current values of κi, κk, and κl. |
| End loop. |
| End if. |
| Find κi that maximizes WSSE for the current values of κj, κk, and κl. |
| End loop. |
| End if. |
References
- Carson R. E., “Tracer kinetic modeling in PET,” in Positron Emission Tomography, edited by Bailey D. L., Townsend D. W., Valk P. E., and Maisey M. N. (Springer-Verlag, London, 2005). [Google Scholar]
- Cherry S. R., Sorenson J. A., and Phelps M. E., Physics in Nuclear Medicine (Saunders, Philadelphia, 2003). [Google Scholar]
- Schmidt K. C. and Turkheimer F. E., “Kinetic modeling in positron emission tomography,” Q. J. Nucl. Med. 46, 70–85 (2002). [PubMed] [Google Scholar]
- Watabe H., Ikoma Y., Kimura Y., Naganawa M., and Shidahara M., “PET kinetic analysis–Compartmental model,” Ann. Nucl. Med. 20, 583–588 (2006). 10.1007/BF02984655 [DOI] [PubMed] [Google Scholar]
- Urien S., “MicroPharm-K: A microcomputer interactive program for the analysis and simulation of pharmacokinetic processes,” Pharm. Res. 12, 1225–1230 (1995). 10.1023/A:1016280430580 [DOI] [PubMed] [Google Scholar]
- Zhang X., Andrews J. N., and Pedersen S. E., “Kinetic modeling and fitting software for interconnected reaction schemes: VisKin,” Anal. Biochem. 361, 153–161 (2007). 10.1016/j.ab.2006.11.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Sullivan F. and Saha A., “Use of ridge regression for improved estimation of kinetic constants from PET data,” IEEE Trans. Med. Imaging 18, 115–125 (1999). 10.1109/42.759111 [DOI] [PubMed] [Google Scholar]
- Zhou Y., Sung-Cheng H., and Bergsneider M., “Linear ridge regression with spatial constraint for generation of parametric images in dynamic positron emission tomography studies,” IEEE Trans. Nucl. Sci. 48, 125–130 (2001). 10.1109/23.910842 [DOI] [Google Scholar]
- Zhou Y., Endres C. J., Brasic J. R., Huang S. C., and Wong D. F., “Linear regression with spatial constraint to generate parametric images of ligand-receptor dynamic PET studies with a simplified reference tissue model,” Neuroimage 18, 975–989 (2003). 10.1016/S1053-8119(03)00017-X [DOI] [PubMed] [Google Scholar]
- Byrtek M., O’Sullivan F., Muzi M., and Spence A. M., “An adaptation of ridge regression for improved estimation of kinetic model parameters from PET studies,” IEEE Trans. Nucl. Sci. 52, 63–68 (2005). 10.1109/TNS.2004.843094 [DOI] [Google Scholar]
- Dai X., Chen Z., and Tian J., “Performance evaluation of kinetic parameter estimation methods in dynamic FDG-PET studies,” Nucl. Med. Commun. 32, 4–16 (2011). 10.1097/MNM.0b013e32833f6c05 [DOI] [PubMed] [Google Scholar]
- Eftaxias A., Font J., Fortuny A., Fabregat A., and Stuber F., “Nonlinear kinetic parameter estimation using simulated annealing,” Comput. Chem. Eng. 26, 1725–1733 (2002). 10.1016/S0098-1354(02)00156-4 [DOI] [Google Scholar]
- Wong K. P., Meikle S. R., Feng D., and Fulham M. J., “Estimation of input function and kinetic parameters using simulated annealing: Application in a flow model,” IEEE Trans. Nucl. Sci. 49, 707–713 (2002). 10.1109/TNS.2002.1039552 [DOI] [Google Scholar]
- Yaqub M., Boellaard R., Kropholler M. A., and Lammertsma A. A., “Optimization algorithms and weighting factors for analysis of dynamic PET studies,” Phys. Med. Biol. 51, 4217–4232 (2006). 10.1088/0031-9155/51/17/007 [DOI] [PubMed] [Google Scholar]
- Marsh R. E., Riauka T. A., and McQuarrie S. A., “Use of a simulated annealing algorithm to fit compartmental models with an application to fractal pharmacokinetics,” J. Pharm. Pharm. Sci. 10, 168–179 (2007). [PubMed] [Google Scholar]
- Lawton W. H. and Sylvestre E. A., “Elimination of linear parameters in nonlinear regression,” Technometrics 13, 461–467 (1971). 10.1080/00401706.1971.10488810 [DOI] [Google Scholar]
- Kaufman L. and Pereyra V., “A method for separable nonlinear least squares problems with separable nonlinear equality,” SIAM J. Numer. Anal. 15, 12–20 (1978). 10.1137/0715002 [DOI] [Google Scholar]
- Golub G. H. and Pereyra V., “The differentiation of pseudo-inverses and nonlinear least squares problems whose variables separate,” SIAM J. Numer. Anal. 10, 413–432 (1973). 10.1137/0710036 [DOI] [Google Scholar]
- Golub G. and Pereyra V., “Separable nonlinear least squares: The variable projection method and its applications,” Inverse Probl. 19, R1–R26 (2003). 10.1088/0266-5611/19/2/201 [DOI] [Google Scholar]
- Koeppe R. A., Holden J. E., and Ip W. R., “Performance comparison of parameter estimation techniques for the quantitation of local cerebral blood flow by dynamic positron computed tomography,” J. Cereb. Blood Flow Metab. 5, 224–234 (1985). 10.1038/jcbfm.1985.29 [DOI] [PubMed] [Google Scholar]
- Huesman R. H., Reutter B. W., Zeng G. L., and Gullberg G. T., “Kinetic parameter estimation from SPECT cone-beam projection measurements,” Phys. Med. Biol. 43, 973–982 (1998). 10.1088/0031-9155/43/4/024 [DOI] [PubMed] [Google Scholar]
- Reutter B. W., Gullberg G. T., and Huesman R. H., “Kinetic parameter estimation from attenuated SPECT projection measurements,” IEEE Trans. Nucl. Sci. 45, 3007–3013 (1998). 10.1109/23.737657 [DOI] [Google Scholar]
- Boellaard R., Knaapen P., Rijbroek A., Luurtsema G. J., and Lammertsma A. A., “Evaluation of basis function and linear least squares methods for generating parametric blood flow images using 15O-water and positron emission tomography,” Mol. Imaging Biol. 7, 273–285 (2005). 10.1007/s11307-005-0007-2 [DOI] [PubMed] [Google Scholar]
- Watabe H., Jino H., Kawachi N., Teramoto N., Hayashi T., Ohta Y., and Iida H., “Parametric imaging of myocardial blood flow with 15O-water and PET using the basis function method,” J. Nucl. Med. 46, 1219–1224 (2005). [PubMed] [Google Scholar]
- Gunn R. N., Lammertsma A. A., Hume S. P., and Cunningham V. J., “Parametric imaging of ligand-receptor binding in PET using a simplified reference region model,” Neuroimage 6, 279–287 (1997). 10.1006/nimg.1997.0303 [DOI] [PubMed] [Google Scholar]
- Gunn R. N., Gunn S. R., Turkheimer F. E., Aston J. A., and Cunningham V. J., “Positron emission tomography compartmental models: A basis pursuit strategy for kinetic modeling,” J. Cereb. Blood Flow Metab. 22, 1425–1439 (2002). 10.1097/00004647-200212000-00003 [DOI] [PubMed] [Google Scholar]
- Hong Y. T. and Fryer T. D., “Kinetic modelling using basis functions derived from two-tissue compartmental models with a plasma input function: General principle and application to [18F]fluorodeoxyglucose positron emission tomography,” Neuroimage 51, 164–172 (2010). 10.1016/j.neuroimage.2010.02.013 [DOI] [PubMed] [Google Scholar]
- Hong Y. T., Beech J. S., Smith R., Baron J. C., and Fryer T. D., “Parametric mapping of [18F]fluoromisonidazole positron emission tomography using basis functions,” J. Cereb. Blood Flow Metab. 31, 648–657 (2011). 10.1038/jcbfm.2010.141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng D., Ho D., Chen K., Wu L. C., Wang J. K., Liu R. S., and Yeh S. H., “An evaluation of the algorithms for determining local cerebral metabolic rates of glucose using positron emission tomography dynamic data,” IEEE Trans. Med. Imaging 14, 697–710 (1995). 10.1109/42.476111 [DOI] [PubMed] [Google Scholar]
- Phelps M. E., PET: Molecular Imaging and Its Biological Applications (Springer Science, New York, NY, 2004). [Google Scholar]
- Bertoldo A., Peltoniemi P., Oikonen V., Knuuti J., Nuutila P., and Cobelli C., “Kinetic modeling of [(18)F]FDG in skeletal muscle by PET: A four-compartment five-rate-constant model,” Am. J. Physiol. Endocrinol. Metab. 281, E524–E536 (2001). [DOI] [PubMed] [Google Scholar]
- Tomasi G., Bertoldo A., Bishu S., Unterman A., Smith C. B., and Schmidt K. C., “Voxel-based estimation of kinetic model parameters of the L-[1-(11)C]leucine PET method for determination of regional rates of cerebral protein synthesis: Validation and comparison with region-of-interest-based methods,” J. Cereb. Blood Flow Metab. 29, 1317–1331 (2009). 10.1038/jcbfm.2009.52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press W. H., Flannery B. P., Teukolsky S. A., and Vetterling W. T., Numerical Recipes in C (Cambridge University Press, Cambridge, 1988). [Google Scholar]