Integrating Event- and Trend-based Analyses to Improve Detection of Glaucomatous Visual Field Progression

Abstract

Purpose

To present and evaluate a new method of integrating event- and trend-based analyses of visual field progression in glaucoma.

Design

Observational cohort study

Participants

The study included 711 eyes of 357 glaucoma patients or suspects followed for an average of 5.0 ± 2.0 years with an average of 7.7 ± 2.3 standard automated perimetry visual fields. An additional group of 55 eyes of 55 glaucoma patients had repeated tests over a short-period of time to test the specificity of the method.

Methods

Event-based analysis of progression was performed using the Guided Progression Analysis (GPA). Trend-based assessment used the Visual Field Index (VFI). A hierarchical Bayesian model was built to incorporate results from the GPA in the prior distribution for the VFI slopes, allowing the event-based method to influence the inferences made for the trend-based assessment.

Main Outcome Measures

The Bayesian method was compared to the conventional ordinary least squares (OLS) regression method of trend-based assessment.

Results

From the 711 eyes followed over time, 64 (9%) had confirmed progression with GPA. Bayesian slopes of VFI change were able to detect 63 of these eyes (98%). An additional group of 49 eyes (7%) had progression by Bayesian slopes but not by GPA. Slopes of VFI change calculated by the OLS method were able to identify only 32 (50%) of the 64 eyes with GPA progression. The agreement with GPA was significantly better for the Bayesian compared to the OLS method (kappa of 0.68 vs. 0.43, respectively; P<0.001). Eyes progressing only by the Bayesian method had faster rates of change than those progressing only by the OLS method. When applied to the 55 eyes in the stable glaucoma group, both the Bayesian and the OLS methods had a specificity of 96%.

Conclusion

A Bayesian hierarchical modeling approach for integrating event- and trend-based assessments of visual field progression performed better than either method used alone. Estimates of rates of change obtained from the Bayesian model had increased precision and may be superior to the conventional OLS method for providing information on the risk of development of functional impairment in the disease.

INTRODUCTION

Detection of progression plays a central role in the clinical diagnosis and management of glaucoma and standard automated perimetry (SAP) remains the method of choice for monitoring functional changes in the disease. In addition to its role in clinical care, visual field assessment has traditionally been chosen as the primary endpoint in most clinical trials evaluating disease progression and, therefore, determination of what constitutes true visual field change over time is essential in order to validate their results.^1–4 Nevertheless, accurate and precise identification of visual field progression in glaucoma remains one of the most challenging tasks facing both clinicians and researchers.

Several algorithms have been proposed to identify visual field progression over time using different approaches to separate true change from test-retest variability. These approaches can be broadly divided into two categories: event- versus trend-based methods.⁵ In event-based methods, the differences in visual field sensitivities of the current tests are compared to those of previously established baseline exams and if they exceed a certain threshold in a specific number of test locations, significant visual field progression is declared to have occurred. The thresholds are usually based on test-retest variability levels obtained from patients followed over relatively short periods of time in whom there is reasonable assurance that the disease has not progressed. This approach is used by the commercially available Guided Progression Analysis (GPA) software from the Humphrey Field Analyzer (HFA, Carl-Zeiss Meditec, Inc., Dublin, CA).^6–8

In trend-based analyses, visual field sensitivities of all tests available during the follow-up period of interest are analyzed for the presence of statistically significant change over time, usually employing a linear regression approach.^9–11 Unlike the event-based method, trend analysis relates the magnitude of change over time to the long-term variability observed within the individual data series and does not rely on previously established thresholds. A potential advantage of trend-based methods is that they can provide estimates of rates of visual field progression over time.^12–14 These estimates are essential in order to identify those patients with fast disease progression that could be at higher risk for developing functional impairment from the disease. In addition to the GPA analysis, the current HFA software also provides a trend-based assessment of progression based on linear regression of the Visual Field Index (VFI) over time.¹⁵ The VFI represents a global measure of visual function that is intended for use in calculating rates of progression and staging glaucomatous functional damage.

Previous studies have compared event- and trend-based approaches to detect visual field progression and have found substantial disagreements among them.^{1, 7, 16–18} Recently, Casas-Llera et al¹⁸ found only a fair agreement between the GPA event-based and the VFI trend-based assessments of progression. Such disagreements generate confusion among clinicians who are challenged to interpret apparently conflicting results coming from different tests. If they decide to declare as progressing an eye that has significant change in either one of the tests, this will likely increase the chance of false positives. This occurs because, in the conventional approach, the nominal levels of statistical significance employed by the event-based method do not take into account those of the trend-based assessment, and vice-versa. However, as the data is coming from the same eye, results of trend- and event-based analyses should be allowed to correlate and this correlation should be taken into account when deciding whether or not progression has occurred with either method.

In the current study, we propose a new methodology for combining the results of event-and trend-based analysis of visual field progression based on Bayesian hierarchical models. These models allow the correlation between results of both methods to be formally taken into account in the model decision framework, which helps solve potentially conflicting results. Using a Bayesian approach, information derived from one method is allowed to influence the inferences obtained from the other method. For example, a visual field change that would otherwise be declared non-statistically significant by analysis of trend-based assessment alone may be declared significant after taking into consideration the results of the event-based approach. We apply our methodology to the investigation of longitudinal changes in SAP using the event-based GPA and the trend-based VFI approaches.

METHODS

This was an observational cohort study. Participants from this study were included in two prospective longitudinal studies designed to evaluate optic nerve structure and visual function in glaucoma (the African Descent and Glaucoma Evaluation Study [ADAGES] and the Diagnostic Innovations in Glaucoma Study [DIGS]). The 3-site ADAGES collaboration includes the Hamilton Glaucoma Center at the Department of Ophthalmology, University of California-San Diego (UCSD) (data coordinating center), the New York Eye and Ear Infirmary and the Department of Ophthalmology, University of Alabama, Birmingham (UAB). Although the DIGS includes only patients recruited at UCSD, the protocols of the two studies are identical. The institutional review boards at all 3 sites approved the study methodology, which adhered to the tenets of the Declaration of Helsinki and to the Health Insurance Portability and Accountability Act. Methodological details have been described previously.¹⁹

At each visit during follow-up, subjects underwent a comprehensive ophthalmologic examination including review of medical history, best-corrected visual acuity, slit-lamp biomicroscopy, intraocular pressure (IOP) measurement, gonioscopy, dilated fundoscopic examination, stereoscopic optic disc photography, and automated perimetry using Swedish Interactive Threshold Algorithm (SITA Standard 24-2). Only subjects with open angles on gonioscopy were included. Subjects were excluded if they presented with a best-corrected visual acuity less than 20/40, spherical refraction outside ± 5.0 diopters and/or cylinder correction outside 3.0 diopters, or any other ocular or systemic disease that could affect the optic nerve or the visual field.

The study included 711 eyes of 357 patients diagnosed with glaucoma or suspected of having the disease, as determined on the baseline visit. Eyes were classified as glaucomatous if they had repeatable (two consecutive) abnormal visual field test results on the baseline visits, defined as a pattern standard deviation (PSD) outside of the 95% normal confidence limits, or a Glaucoma Hemifield Test result outside normal limits. Eyes were classified as glaucoma suspects if they had a history of elevated intraocular pressure (>21 mmHg) and/or glaucomatous or suspicious appearance of the optic nerve but normal and reliable visual field results on the baseline visits.

We also included an additional group of 55 eyes of 55 stable glaucoma patients to evaluate the specificity of our method. This set consisted of eyes with five weekly serial visual fields collected within four weeks from individuals seen at the Department of Ophthalmology, University of Miami Miller School of Medicine. The assumption was made that the glaucomatous defects in these eyes were not progressing over such a short time, and that any change noted would be due to the variability in the visual fields measured in stable glaucoma. Each eye in the stable dataset was tested 5 times and was required to have reliable visual fields at all 5 visits. Each eye also had to have evidence of glaucoma at baseline based on ocular examination and the presence of repeated visual field loss as defined above. These eyes had median (first quartile, third quartile) MD and PSD of −6.3dB (−12.5dB, −3.4dB) and 6.7dB (3.5dB, 11.6dB). For evaluation of rates of change in these eyes, the visits were annualized.

Standard Automated Perimetry

A minimum of 5 SAP visual fields during follow-up was required for inclusion in the study. All visual fields were evaluated by the UCSD Visual Field Assessment Center (VisFACT).²⁰ Visual fields with more than 33% fixation losses or false-negative errors, or more than 15% false-positive errors were excluded. The only exception was the inclusion of visual fields with false-negative errors of more than 33% when the field showed advanced disease (MD lower than −12dB). Visual fields exhibiting a learning effect (i.e., initial tests showing consistent improvement on visual field indexes) were also excluded. Visual fields were further reviewed for the following artifacts: lid and rim artifacts, fatigue effects, inappropriate fixation, evidence that the visual field results were due to a disease other than glaucoma (such as homonymous hemianopia), and inattention. The VisFACT requested repeats of unreliable visual field test results, and these were obtained whenever possible.

Event-based Analysis

Event-based analysis of visual field progression was performed using the Guided Progression Analysis from the Humphrey Field Analyzer. Progression by SAP GPA was defined as a significant decrease from baseline (2 examinations) pattern deviation at 3 or more of the same test points on 3 consecutive tests, which is classified by the software as Likely Progression. We recorded the number of points that showed repeatable consecutive change compared to baseline for eyes that showed progression on the GPA. Trend- and event-based analyses were performed using all visual fields available during follow-up. However, for eyes that were classified as Likely Progression by the GPA, we used only the visual fields up to the date of confirmation of Likely Progression.

Bayesian Model for Assessment of Progression

Trend-based analysis was performed using the VFI provided by the Humphrey perimeter. Details of the calculation of the VFI have been described elsewhere.¹⁵ In brief, the VFI represents the percent of normal age-corrected visual function and it is intended for use in calculating rates of progression and staging glaucomatous functional damage. Evaluation of rates of functional loss in glaucoma eyes with the VFI has been proposed to be less susceptible than the mean deviation to the effects of cataract or diffuse media opacities.^24,50,57 The VFI can range from 100% (normal visual field) to 0% (perimetrically blind field).

For the Bayesian analysis of trend in the visual fields over time, we fitted a random-intercept random-slope Bayesian hierarchical model for the VFI data. In these models, the average evolution of VFI values was described using a linear function of time, and subject-specific deviations from this average evolution were introduced by random intercepts and random slopes, allowing for different baseline values and different rates of change for each eye.^21–23 In our application, the Bayesian models incorporated results from the event-based GPA method in the prior distribution for the slopes, which allowed the GPA results to influence the VFI slopes, therefore integrating event- and trend-based analyses.

The model can be written as:

$${\mathrm{y}}_{\mathrm{i}}={\alpha }_{\mathrm{j}\left[\mathrm{i}\right]}+{\beta }_{\mathrm{j}\left[\mathrm{i}\right]}\ast {\mathrm{time}}_{\mathrm{i}}+{\epsilon }_{1,}{\epsilon }_1~\mathrm{N}(0,{{\sigma }_{\mathrm{y}}}^2)\mathrm{for}\mathrm{i}=1,2,3,4,\dots ,\mathrm{n}$$ (1)

Where y_i represents the VFI data and the α_j's and β_j's represent the intercepts and slopes for each one of the j eyes, respectively. Each eye had n_j visual field tests over time. Equation (1) is called the data model or the likelihood. The α_j's and β_j's were modeled using a bivariate t distribution, that is, in Bayesian inference, the bivariate t distribution was used as the “prior” distribution for the pairs of slopes and intercepts. In order to allow GPA results to influence inferences made on VFI slopes, we added a group-level regression on the slopes using the number of points that showed repeatable consecutive change on the GPA as a covariate. This can be written as:

$${\beta }_{\mathrm{j}}={\gamma }_0+{\gamma }_1{\mathrm{u}}_{\mathrm{j}}$$ (2)

Equation (2) is called the prior model, where u_j represents the number of points that showed repeatable consecutive change on GPA for each eye. By doing that, we are allowing different prior distributions for the slope of VFI change for each eye. For any particular eye, its slope β_j has a prior distribution with mean ${\widehat{\beta }}_{\mathrm{j}}={\gamma }_0+{\gamma }_1{\mathrm{u}}_{\mathrm{j}}$. The parameters γ₀ and γ₁ are called hyperparameters and are estimated from the data. In Bayesian inference, all the hyperparameters along with unmodeled parameters, also need prior distributions which were set to noninformative or diffuse prior distributions in this application. We used Normal (0,1000) for γ₀ and γ₁ and Uniform (0,100) for variance paramaters.²⁴ An exponential (0.1) prior was used for the degrees of freedom in the t distribution,²⁵ but restricted to greater than 2.5 to prevent problems with undefined variance.

Hierarchical models can also easily handle the correlation structure arising from data coming from both eyes of the same patient.²⁶ However, fitting a more complex model with eyes nested within patient did not provide any overall improvement in our model and, therefore, we report here only the results of the simpler model.

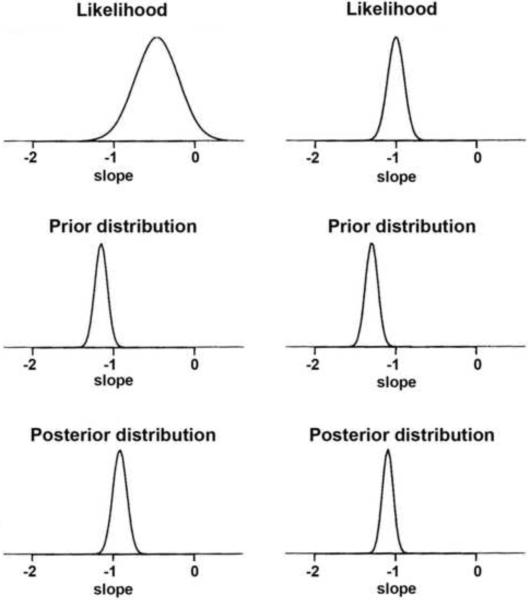
Inferences on the VFI slopes were made by analyzing their posterior distributions. In Bayesian inference, the likelihood is multiplied by the prior distribution and inferences are summarized by random draws from this product, the posterior distribution (Figure 1).²⁷ For each eye j, the likelihood for the VFI slope indicates the range of values of β_j that are most consistent with the data available for that eye. The likelihood is more informative as the sample size increases, i.e., the larger the number of VFI measurements available for a particular eye, the more informative the likelihood will be. The prior distribution conveys information about the distribution of the VFI slopes (β_j's) among the eyes in the population and the influence of GPA. As shown in Figure 1, the posterior distribution is centered at a point between the maximum likelihood estimate and the maximum of the prior distribution – a weighted average of the likelihood and prior estimates – falling closer to the prior when the number of measurements per eye is small or have a large variance, and closer to the likelihood when the number of measurements is large or there is a small variance. Therefore, the influence of the prior is greater when there is less information to estimate the slope based on the fact that only a few VFI measurements are available over time. When there are many measurements available over time for a particular eye, its slope of change can be estimated with great precision and, therefore, the prior exerts less influence.

Figure 1.

Conventional random-intercept random-slope models assume a normal distribution of random effects. However, previous studies have shown that the general assumption of normally distributed random effects may lead to biased estimates of individual change parameters when there is heterogeneity in the population.^{28, 29} In the present application, heterogeneity is to be expected as only a proportion of eyes will show progression over time. Further, in the progressing group, only a small proportion is expected to have relatively fast progression. This can induce considerable non-normality in the random effects distribution. In order to address this we used a multivariate t distribution to model random effects, as indicated above.³⁰

Estimates of the posterior distributions of the parameters of interest, i.e., the random effects, were obtained by Markov chain Monte Carlo (MCMC) procedures. The MCMC sampler was implemented in WinBUGS software³¹ and the code is available from the authors upon request. We used 10000 iterations after discarding the initial 5000 iterations for burn-in. Convergence of the generated samples was assessed by standard tools in WinBUGS (trace plots, autocorrelation function [ACF] plots) as well as Gelman-Rubin convergence diagnostics. After the posterior distributions were estimated, summary measures were calculated such as mean and credible intervals. For the Bayesian VFI slope, we considered that progression had occurred if the upper limit of the 95% credible interval for the slope was less than zero.

We compared our Bayesian algorithm for trend-based assessment of progression to the current algorithm used by the Humphrey Field Analyzer. The HFA analyzes the rate of VFI change over time using ordinary least squares (OLS) regression, also known as simple linear regression, and the printout shows a message indicating whether or not the slope of the regression line is statistically significant based on an alpha level of 0.05.

RESULTS

The main study group included 711 eyes of 357 participants with a mean ± SD age of 58 ± 12 years at baseline. Two-hundred nineteen (61%) patients were female. From the 711 eyes, 331 (47%) had glaucomatous visual field loss at the baseline visit and 380 (53%) were considered as glaucoma suspects. From the 380 glaucoma suspects, 84 (22%) had ocular hypertension and 296 (78%) had suspicious or glaucomatous appearance of the optic disc. Median (first quartile, third quartile) MD and PSD of the visual field closest to the baseline imaging test date in glaucomatous eyes were −3.09dB (−5.61dB, −1.72dB) and 3.52dB (2.44dB, 6.33dB), respectively. Corresponding values for glaucoma suspect eyes were −0.37dB (−1.41dB, 0.50dB) and 1.60dB (1.40dB, 1.88dB), respectively. There was a large variation in the baseline MD of the eyes included in the study, with values ranging from −29.8dB to 2.91dB. The average follow-up time was 5.0 ± 2.0 years and the average number of visual fields available during follow-up was 7.7 ± 2.3.

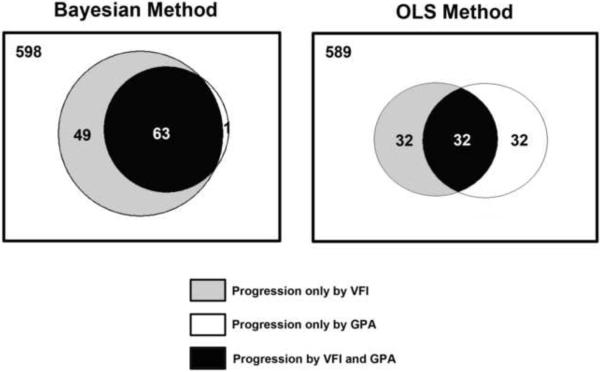
From the 711 glaucoma and glaucoma suspect eyes followed over time, 64 (9%) had progression with the GPA (48 had glaucomatous visual field defects at baseline and 16 were glaucoma suspects at baseline). From the 64 eyes progressing by GPA, Bayesian slopes of change for VFI were able to detect 63 eyes (98%) as progressing, that is, only 1 eye was detected as progressing by GPA but not by the Bayesian trend-based assessment of change. Rates of change for VFI calculated by the Bayesian method were significantly faster for eyes that progressed by GPA than for eyes that did not (−2.08 ± 2.16%/year vs. −0.04 ± 0.58%/year; P<0.001). An additional group of 49 of the 711 eyes (7%) were identified as progressing by Bayesian slopes of change but not by the GPA. These eyes had an average rate of change of −1.25%/year (range: − 8.20 to −0.32%/year). The 49 eyes that progressed by the Bayesian method but not by GPA had significantly lower baseline VFI values (i.e., more severe disease) compared to the 63 eyes that progressed by both the Bayesian and GPA analyses (81.6 ± 19.0% vs. 92.4 ± 9.1%; P<0.001). Figure 2 shows a Venn diagram illustrating the number of eyes detected by GPA and Bayesian slopes of change for VFI. The agreement between GPA and the Bayesian trend-based assessment was strong with kappa of 0.68 ± 0.04.

Figure 2.

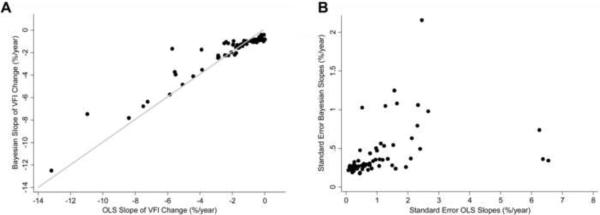
Rates of change for VFI calculated by the OLS method were also significantly faster for eyes that progressed by GPA than for eyes that did not (−2.35 ± 2.63%/year vs. −0.07 ± 0.87 %/year; P<0.001). However, only 32 (50%) of the 64 eyes identified as progressing by the GPA were also identified as progressing by the OLS method, i.e, had statistically significant slopes that were below zero. An additional number of 32 eyes were identified as progressing by OLS VFI slopes but not by GPA. Figure 2 also shows a Venn diagram illustrating the number of eyes detected by GPA and OLS VFI slopes. The agreement between the two methods in detecting visual field progression had a kappa of 0.45 ± 0.04. Agreement with GPA, as measured by the kappa index, was significantly better for the Bayesian method compared to the OLS method (P<0.001). The Bayesian method showed a superior agreement compared to OLS both in eyes with glaucoma at baseline (0.64 ± 0.05 vs. 0.52 ± 0.05, respectively) as well as in eyes that were suspected of having the disease at baseline (0.78 ± 0.06 vs. 0.31 ± 0.06, respectively). Figure 3a shows scatterplots for the rates of change of VFI calculated using Bayesian and OLS methods for the 64 eyes showing progression by the GPA. Figure 3b shows the corresponding plots for the standard errors of the slopes. Although there was a very strong relationship in the values of the slopes (Spearman's ρ = 0.91), there were large discrepancies in the standard errors of the slopes. Standard errors for the slopes calculated using the Bayesian method were lower than those for the OLS method (0.43 ± 0.34 vs. 1.13 ± 1.36; P<0.001).

Figure 3.

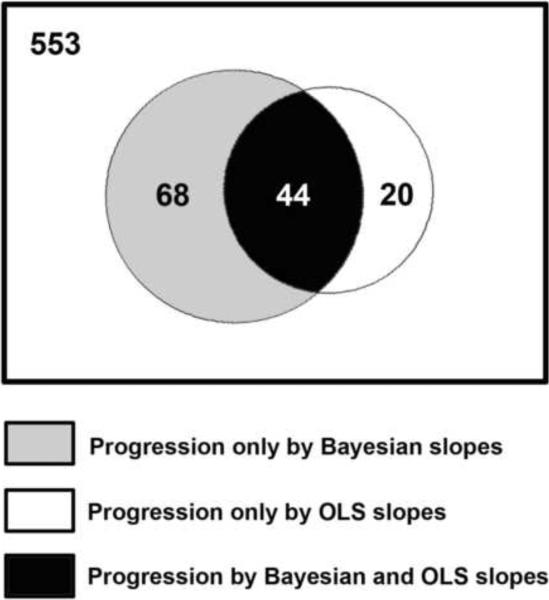
We also examined the factors related to the differences between detection of progression by the Bayesian and OLS methods. Figure 4 shows a Venn diagram representing the agreement between these two methods for detection of progression. Sixty-eight eyes were detected as progressing only by the Bayesian method, whereas 20 eyes were detected as progressing only by the OLS method. Table 1 shows average slopes of change for the Bayesian and OLS methods, along with average standard error of the slopes of change, which indicate the variability of measurements over time and precision in the estimation of the slopes. In general, eyes progressing only by the Bayesian method had faster rates of change than those progressing only by OLS, but the large standard errors of the slopes precluded their identification as progressing by the OLS method. The use of information from event-based progression in these eyes along with the information on the slopes and intercepts from the whole sample allowed the Bayesian method to declare the trend as significant. Eyes progressing only by the OLS method had relatively slow and almost insignificant rates of visual field loss that were not supported by concomitant changes in the GPA and, therefore, were declared as non-progressors by the Bayesian method.

Figure 4.

Table 1.

Differences in slopes of change and standard errors of the slopes between eyes that progressed according to the Bayesian versus ordinary least squares linear regression methods.

	Progression only by the Bayesian Method (n = 68)	Progression only by the OLS Method (n = 20)	P
Average Bayesian slope (%/year)	−1.19 ± 0.94	−0.07 ± 0.13	<0.001
Average standard error of the Bayesian slopes (%/year)	0.37 ± 0.17	0.22 ± 0.05	<0.001
Average OLS slope (%/year)	−1.46 ± 1.33	−0.56 ± 0.61	<0.001
Average standard error of the OLS slopes (%/year)	1.16 ± 1.32	0.13 ± 0.11	<0.001

OLS: Ordinary least squares

From the 55 eyes of the stable glaucoma group with repeated visual fields within 1 month, the OLS method identified 2 as progressing, resulting in a specificity of 96%. The Bayesian method also identified 2 eyes from this group as progressing, with a specificity of 96%.

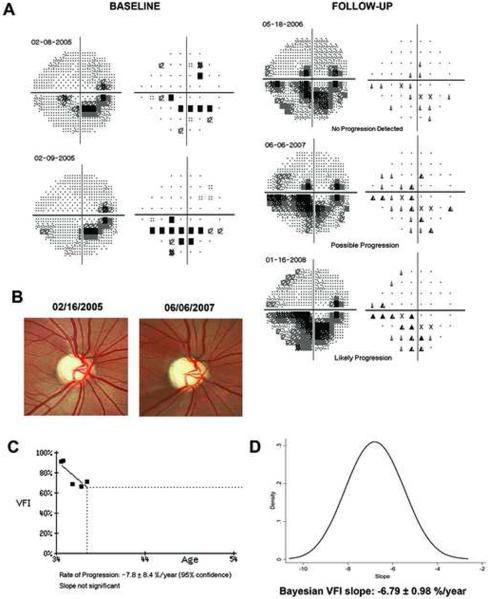
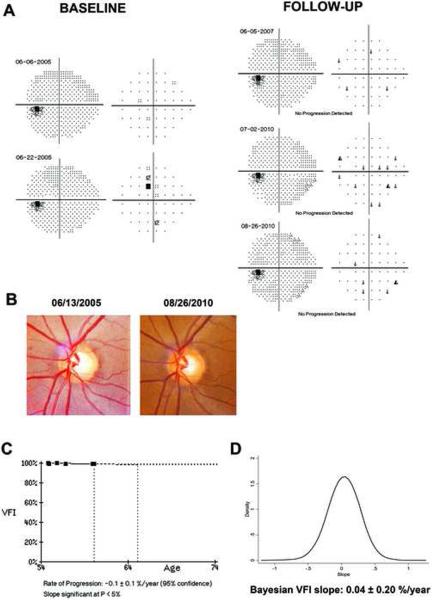
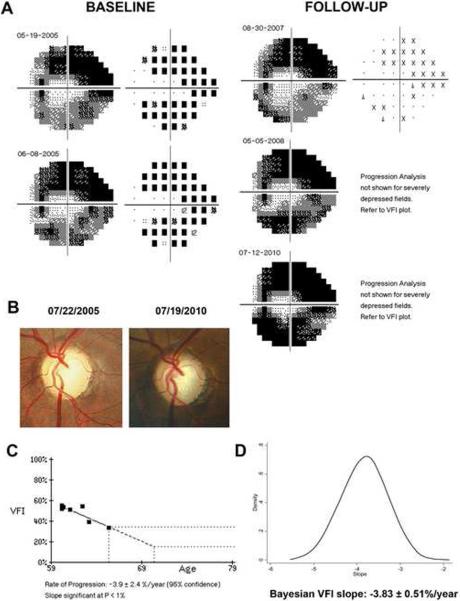
Figure 5 illustrates a case of glaucoma progression detected by the Bayesian method but not by OLS. This eye also had progressive visual field loss detected by the GPA and progressive glaucomatous optic neuropathy on stereophotographs. Figure 6 (available at http://aaojournal.org) illustrates a case where the OLS slope was significant, but the Bayesian slope was not. This eye had a very slow rate of change of −0.1%/year, did not show any consistent pattern of visual field loss over time, and had no evidence of progressive optic disc change on stereophotographs.

Figure 5.

Figure 6.

DISCUSSION

In the current study, we proposed an innovative methodology for the combination of event- and trend-based assessments of visual field progression in glaucoma. Our approach resulted in better agreement between these two methods compared to the conventional approach employed by the software of commercially available instruments. To our knowledge, this is the first study to report a successful method for combining event- and trend-based assessments of glaucomatous progression.

The use of a Bayesian approach for combining event- and trend-based analyses of visual field change provides several advantages compared to the analysis performed separately by either technique. Our Bayesian model allowed the results of GPA to influence the inferences made on the slopes of VFI change over time. This is likely to explain the improved agreement observed between these two analytical methods. In fact, only 1 eye was detected as progressing by GPA but not by Bayesian slopes of change for VFI. Although the 95% credible interval for the slope in this eye did not exclude zero, the analysis of its posterior distribution revealed a high probability of 92% that the slope would be less than zero. In contrast to the Bayesian method, the OLS method detected only 50% of the eyes with confirmed change by the GPA. This large disagreement can be challenging for clinicians, who are frequently uncertain about how to interpret apparently conflicting results coming from different tests. It has been suggested that the GPA could be a more sensitive method to detect localized progressive changes than trend-based assessment using a global index, such as the VFI.^6–8 This could perhaps explain the disagreements between the two methods. However, our study shows that trend-based assessment can in fact detect most of the cases progressing by the GPA, once the event-based results are incorporated as prior information into the Bayesian model. The use of prior information leads to posterior distributions that are more informative than the likelihoods and, therefore, allow better inferences on the slopes of change. A visual field change that would otherwise be declared non-statistically significant by the trend analysis alone could be declared significant after taking into consideration the event-based assessment in the same eye.

Both the Bayesian and OLS slopes detected a significant number of eyes as progressing that were not detected by the GPA. Also, the Bayesian and OLS methods showed significant disagreement in determining which cases had statistically significant slopes. In fact, the Bayesian method detected 68 eyes as progressing that were not detected by the OLS slopes, whereas the OLS method detected 20 eyes that were not declared as progressing by the Bayesian method. In general, eyes progressing only by the Bayesian method had faster rates of change than those progressing only by OLS, but the large standard errors of the slopes precluded their identification by the OLS method, i.e., the likelihood was weakly informative. The use of event-based progression in the prior distribution for these eyes allowed the Bayesian method to declare the trend as significant. On the other hand, eyes progressing only by OLS had relatively slow (Table 1) and mostly clinically irrelevant rates of change, which were not supported by concomitant GPA progression. It is interesting to note that eyes progressing by the Bayesian trend-based assessment but not by GPA had more severe disease at baseline compared to eyes that progressed by both the Bayesian and GPA analyses. This could be due to the inability of the GPA to evaluate progression in cases of severe visual field damage at baseline (Figure 7, available at http://aaojournal.org). Due to the inexistence of a perfect independent reference standard for glaucoma progression, it is not possible to exclude the possibility that some of the eyes identified as progressing by the Bayesian method are actually false positives. However, the very high specificity of the Bayesian method when applied to the stable glaucoma group suggests that the significant changes were indeed representative of true disease deterioration.

Figure 7.

According to the Consensus on Medical Treatment from the World Glaucoma Association, glaucoma treatment would be indicated for patients whose rates of progression will most likely result in loss in vision-related quality of life over the projected remaining years of life.³² Therefore, accurate and precise estimation of rates of change are essential in order to determine the need and/or aggressiveness of treatment. For this purpose, rates of change in structural and functional tests in glaucoma have traditionally been estimated using OLS regression of the measurements obtained for an individual eye over time.^{15, 17, 33–37} The true rate of change, however, is actually a latent or unobservable variable and the slope of change obtained from OLS is just an imprecise estimate that is confounded by noise and influenced by the number and intervals of measurements during follow-up. The greater precision in the estimation of the slopes of change with the Bayesian model may improve the assessment of risk for development of functional impairment over time, as the Bayesian slopes are more likely to be closer to the “true” unobservable slope of change. In fact, many eyes with relatively fast rates of visual field loss were declared as non-progressing by the OLS method in our study due to the variability of measurements over time (i.e., large standard error of the OLS regression slope), as exemplified in Figure 5. In these cases, one frequently has to obtain more tests in order to attempt to more precisely estimate the slope of OLS regression. However, in clinical practice, there is a cost associated with obtaining more measurements over time, including the expense of the test itself, the cost in patient time, and the cost related to delaying detection of change. Although different techniques have been used in an attempt to decrease the impact of variability in the detection of visual field progression, to our knowledge, no previous method has been reported combining event- and trend-based assessments using Bayesian methodology. It is important to note, however, that a statistically significant slope does not necessarily mean a clinically relevant deterioration in the visual field. In order to assess clinical relevance, clinicians also need to consider other factors, such as life expectancy. By providing more precise estimates of rates of change, however, the Bayesian approach potentially improves the determination of the clinical relevance of the slopes of change over time.

Bayesian estimates of slopes of change depend not only on the actual data for the eye being evaluated, but also on data available from the overall population of eyes. This represents another potential advantage of the method compared to OLS regression. OLS estimates are obtained taking into account only the measurements of an individual patient, without considering the influence of the population where the patient comes from. The Bayesian hierarchical modeling approach, however, improves the precision of an individual patient's estimate of slope of change by using previously longitudinally collected data from other patients. For example, it is reasonable to assume that the best estimator of the rate of change in a patient in whom we do not have any measurements collected over time is the average rate of change in the overall population from where he/she comes from. As measurements are acquired for this patient, however, his/her rate of change will most likely deviate from the population average. For patients with fewer measurements, the precision of the estimates can be increased by “borrowing strength” from the population, whereas for patients with large number of measurements, precise estimates can be obtained relying almost only on the individual data and the need to borrow strength from the population decreases. It is important to note, however, that this approach requires an adequate and sufficiently large sample of patients similar to the patients in whom we want to make predictions. In our study, we used a large group of glaucoma and glaucoma suspect patients that have been longitudinally studied according to pre-specified protocols for many years. Construction of similar built-in databases would be required to implement this methodology into currently available instruments. Another potential advantage of our methodology is that data from patients tested over time can be continuously incorporated into the Bayesian model, leading to improved estimates that would more likely reflect the progression rates in a particular clinical setting, generating a “customized” database for comparison. It is important to note, however, that our methodology should be further validated on external datasets including patients followed under different conditions.

Although we applied our methodology to VFI and GPA, it is likely that it will also perform well for combining other event- and trend- based methods of evaluation of functional and structural losses in glaucoma. In fact, we recently applied a similar approach to combine structural and functional tests for detecting glaucoma progression which performed significantly better than either method alone.³⁸

Our study has limitations. The Bayesian model was designed so that GPA results could influence trend-based assessment with VFI. However, a potentially better model would also allow information to flow in the other way as well, i.e., for results of trend-based analysis to influence event-based assessments. We were not able to design such a model, however, as the GPA is proprietary software and the details of its calculation, including thresholds and normative database, were not available to us. Future studies should address whether improvements can be obtained with such models. Another limitation is that we assumed a linear rate of functional change over time. Previous studies using cross-sectional data suggest that functional changes over the whole course of the disease would probably not be linear.³⁹ However, the assumption of linear change is probably a reasonable one when evaluating change in periods of short- to medium term follow-up, as performed in clinical practice. It should be noted, however, that extensions of our methodology in order to incorporate non-linear change are also possible, but their evaluation will likely require populations with longer follow-up times. Another limitation of our study is that we had only a relatively small dataset of stable eyes tested only 5 times in order to test the specificity. Further evaluations of specificity should also be performed in other datasets of stable eyes with greater number of tests obtained during follow-up.

In conclusion, a Bayesian hierarchical modeling approach for integrating event- and trend-based assessments of visual field change detected more eyes as progressing than either method alone, at the same specificity. Additionally, it resulted in much better agreement than that obtained by conventional methods of trend- and event-based assessment of change. Estimates of rates of change obtained from the Bayesian model had increased precision and may be superior to the conventional OLS method for providing information on the risk of development of functional impairment in the disease.