Abstract
There is no generally accepted account of the function of the second visual cortical area (V2), partly because no simple response properties robustly distinguish V2 neurons from those in primary visual cortex (V1). We constructed synthetic stimuli replicating the higher-order statistical dependencies found in natural texture images, and used them to stimulate macaque V1 and V2 neurons. Most V2 cells responded more vigorously to these textures than to control stimuli lacking naturalistic structure; V1 cells did not. fMRI measurements in humans revealed differences between V1 and V2 that paralleled the neuronal measurements. The ability of human observers to detect naturalistic structure in different types of texture was well predicted by the strength of neuronal and fMRI responses in V2 but not in V1. Together, these results reveal a novel and particular role for V2 in the representation of natural image structure.
Introduction
The perception of complex visual patterns emerges from neuronal activity in a cascade of areas in the primate cerebral cortex. Neurons in the primary visual cortex (V1) represent information about basic image features like local orientation and spatial scale. Downstream areas contain neurons sensitive to more complex properties, especially those found in behaviorally-relevant, natural images. But sensitivity to these naturalistic structures requires transformations of basic visual signals, which have been difficult to characterize in computational or physiological terms.
The role of the second visual area (V2) has been particularly enigmatic. V2 is the largest extrastriate visual cortical area in primates, and its responses depend on feedforward input from V11,2. Neurons in V2 presumably combine and elaborate signals from V1 to encode image features that V1 does not, but the responses of V2 neurons to most “artificial” stimuli, including gratings, angles, curves, anomalous contours, and second-order patterns are largely similar to the responses of neurons in V13-11. Reliable responses to border ownership and relative disparity are more prevalent in V2 than in V112,13, and V2 neurons exhibit stronger tuned suppression14, but neither of these properties reliably and robustly distinguish V1 and V2 neurons.
We wondered whether the responses of V2 cells encode aspects of natural image structure. A ubiquitous property of natural images is that they contain orderly structures which create strong statistical dependencies across the outputs of filters — similar to the responses of V1 cells — tuned to different positions, orientations, and spatial scales15-17. Dependencies across scale, for example, occur in the vicinity of abrupt changes in luminance, and dependencies across orientation and position arise from spatially extended contours18,19. The character and extent of these dependencies varies for different classes of images. Many artificial stimuli lack them; in photographs of scenes and objects, they are present but sparse, non-uniform, and difficult to control. But a sub-class of natural images — visual textures — contain these dependencies in a form that can be captured parametrically20, and previous psychophysical investigations suggest that V2 may be the locus for representing them21.
We found a novel and distinctive property of V2 cells by measuring their responses to controlled naturalistic texture stimuli. We first captured the statistical dependencies in natural texture photographs by computing correlations among the outputs of V1-like filters tuned to different positions, orientations, and spatial scales. We then generated families of homogenous textures containing the same statistical dependencies. There was a unique response to these texture stimuli in V2 but not V1, in both macaque and human, that reliably predicted perceptual sensitivity to the same stimuli. A large-scale crowdsourced psychophysics experiment revealed the statistical dependencies most relevant for perception and — by extension — selective responses in V2. Together, these findings situate V2 along a cascade of computations that lead to the representation of naturally-occurring patterns and objects.
Results
Generating naturalistic texture stimuli
For each of several original photographs of visual texture, we transformed samples of Gaussian noise to synthesize new images with the statistical properties of the original20,22 (Fig. 1 and Supplementary Fig. 1). For each original texture, we generated two sets of stimuli using different statistics: “spectrally-matched noise images” and “naturalistic texture images”. Spectrally-matched noise images were synthesized using phase randomization, i.e., by computing the Fourier transform, randomizing the phase values, and then inverting the Fourier transform. This is approximately equivalent to measuring and matching the spatially-averaged responses of linear and energy filters (akin to V1 simple and complex cells, respectively) selective for different orientations, positions, and spatial scales. The resulting synthetic images had the same overall orientation and spatial-frequency content as the original (i.e., the same spectral properties) but lacked its higher-order statistical dependencies (Fig. 1a). Naturalistic texture images were generated by additionally matching correlations between filter responses (and their energies) across orientations, positions, and spatial scales (Fig. 1b). We used an iterative procedure (Fig. 1c) to match the spatially-averaged filter responses, the correlations between filter responses, and also the mean, variance, skewness, and kurtosis of the pixel luminance distribution (“marginal statistics”). Synthetic images matched for these properties contain many complex naturalistic structures seen in the original photograph20, readily recognizable by human observers23.
Figure 1.
Analysis and synthesis of naturalistic textures. (a) Original texture photographs. (b) Spectrally-matched noise images. The original texture is analyzed with linear filters and energy filters (akin to V1 simple and complex cells, respectively) tuned to different orientations, spatial frequencies, and spatial positions. Noise images contain the same spatially-averaged orientation and frequency structure of the original, but lack many of the more complex features. (c) Naturalistic texture images. Correlations are computed by taking products of linear and energy filter responses across different orientations, spatial frequencies, and positions. Images are synthesized to match both the spatially-averaged filter responses and the spatially-averaged correlations between filter responses. The resulting texture images contain many more of the naturalistic features of the original. See more examples in Supplementary Figure 1. (d) Synthesis of naturalistic textures begins with Gaussian white noise, and the noise is iteratively adjusted using gradient descent until analysis of the synthetic image matches analysis of the original (see Portilla & Simoncelli, 2001). Initializing with different samples of Gaussian noise yields distinct but statistically-similar images.
We synthesized images based on 15 original texture photographs, yielding 15 different “texture families”; for each original, we made ensembles of self-similar naturalistic texture samples, each different in detail but all having identical statistical dependencies and containing similar visual properties (Supplementary Fig. 1). Since each of these 15 texture families was based on a different original photograph, they varied in their appearance, and in the form and extent of their higher-order statistical dependencies.
Differentiating V2 from V1 in macaque
We recorded the responses of 102 V1 and 103 V2 neurons in 13 anesthetized macaque monkeys to a sequence of texture stimuli, presented in suitably vignetted 4 deg patches centered on each neuron's receptive field. The sequence, which was identical for all cells, included 20 repetitions, each of 15 samples of naturalistic and 15 samples of noise stimuli from 15 different texture families (9000 stimuli in total). The textures were each presented for 100 ms and were separated by 100 ms of a blank gray screen, so the entire sequence lasted 30 min.
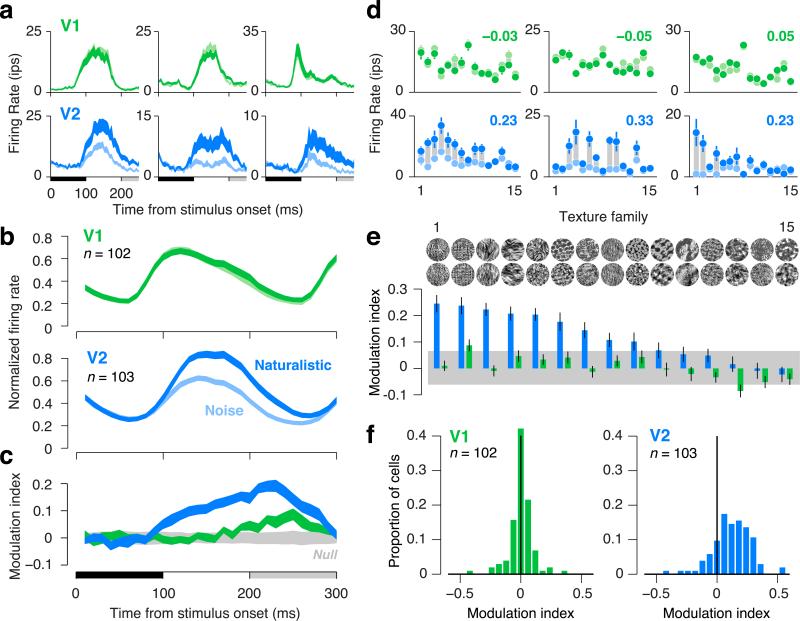
V1 neurons responded similarly to both stimulus types, while V2 neurons often responded more vigorously to naturalistic textures than to spectrally-matched noise. This distinction between V2 and V1 was evident when examining individual responses as a function of time from stimulus onset (averaged over all samples of all texture families) (Fig. 2a), and when the responses were averaged over the cell populations (Fig. 2b). We use the term “modulation” to capture the differential responses to textures and noise, and index its magnitude by taking the difference of responses divided by the sum (Fig. 2c). The average modulation index of neurons in V1 was near zero for most of the response time course, except for a modest late positive modulation (Fig. 2c). Neurons in V2 showed a substantial modulation that was evident soon after response onset and maintained throughout the duration of the response (Fig. 2c). The late modulation in V1 might reflect feedback from V2 or other higher areas24.
Figure 2.
Neuronal responses to naturalistic textures differentiate V2 from V1 in macaques. (a) Time course of firing rate for three single units in V1 (green) and V2 (blue) to images of naturalistic texture (dark) and spectrally-matched noise (light). Thickness of lines indicates s.e.m. across texture families. Black horizontal bar indicates the presentation of the stimulus; gray bar indicates the presentation of the subsequent stimulus. (b) Time course of firing rate averaged across neurons in V1 and V2. Each neuron's firing rate was normalized by its maximum before averaging. Thickness of lines indicates s.e.m. across neurons. (c) Modulation index, computed as the difference between the response to naturalistic and the response to noise, divided by the sum. Modulation was computed separately for each neuron and texture family, then averaged across all neurons and families. Thickness of blue and green lines indicates s.e.m. across neurons. Thickness of gray shaded region indicates the 2.5th and 97.5th percentiles of the null distribution of modulation expected at each time point due to chance. (d) Firing rates for three single units in V1 (green) and V2 (blue) to naturalistic (dark dots) and noise (light dots), separately for the 15 texture families. Families are sorted according to the ranking in panel e. Gray bars connecting points are only for visualization of the differential response. Modulation indices (averaged across texture families) are reported in the upper right of each panel. Error bars indicate s.e.m. across the 15 samples of each texture family. (e) Diversity in modulation across texture families, averaged across all neurons. Error bars indicate s.e.m. across neurons. Gray bar indicates 2.5th and 97.5th percentiles of the null distribution of modulation expected due to chance. (f) Distributions of modulation indices across single neurons in V1 and V2. For each neuron, the modulation index for each texture family was computed on firing rates averaged within an 100 ms window following response onset, and modulation was then averaged across families.
V2 responses were significantly modulated by naturalistic structure on average, but the modulation was typically more pronounced for some texture families than for others. We examined responses as a function of texture family, averaged over all samples. There was a consistent trend across the V2 population for some texture families to evoke stronger modulation than others, although the most effective families varied from cell to cell (Fig. 2de). By contrast, all families yielded negligible modulation of V1 responses (Fig. 2de). In V2, the modulation strength across texture families was not significantly correlated with the response magnitude (r = 0.42, P = 0.12, correlation computed after averaging across cells). An analysis of the distribution and ranking of modulation across individual neurons ruled out the possibility that modulation in V1 was present but concealed by the process of taking means (Supplementary Fig. 2).
Some neurons were more sensitive overall to naturalistic structure than others. We computed a modulation index for each neuron, averaged over the response duration and over all samples of all texture families (Fig. 2f). Significant positive modulation was observed in 15% of V1 neurons, and 63% of V2 neurons (P < 0.05, randomization test for each neuron). The difference in modulation between V1 and V2 was significant (P < 0.0001, t-test on signed modulation; P < 0.0001, t-test on modulation magnitude, ignoring sign). Results were similar when examining firing rates instead of the modulation index (Supplementary Fig. 3).
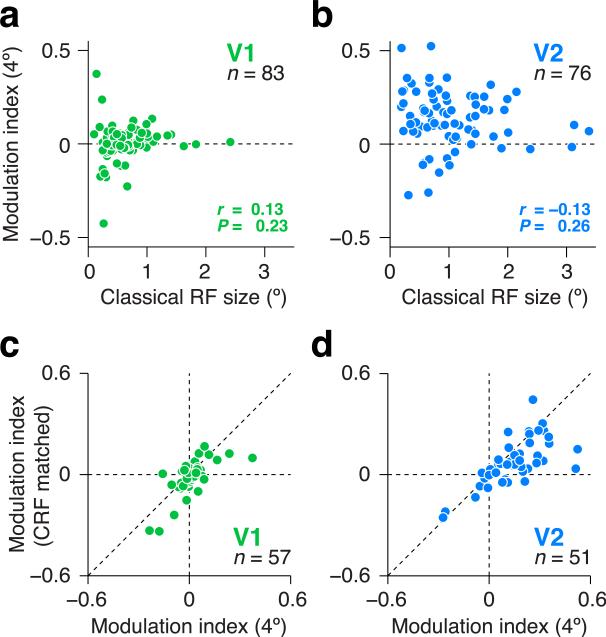
The receptive fields of V2 neurons are larger than those of V1, but this distinction did not explain the observed differences in sensitivity to naturalistic structure (Fig. 3). The stimuli presented to V1 and V2 cells were of the same size (diameter), roughly twice that of a typical V2 receptive field, and 4 times that of a typical V1 receptive field. There was no evidence for a correlation between receptive field size and modulation in either visual area (V1: r = 0.13, V2: r = –0.13, P > 0.05, Fig. 3ab). When we restricted our analysis to subsets of neurons matched for average receptive field size, the difference in modulation index between areas was reduced by only 9% and remained significant (P < 0.0001, randomization test).
Figure 3.
Receptive field size does not explain differential responses to naturalistic texture stimuli in V2. (a,c) V2 neurons (blue). (b,d) V1 neurons (green). (a,b) Modulation index (difference in response to naturalistic and noise stimuli, divided by the sum) measured using stimuli presented within a 4° aperture (ordinate) versus classical receptive field size (abscissa). Each data point represents a neuron. There was no evidence for a relationship between modulation index and classical receptive field size in either V1 or V2. (c,d) Comparison of modulation indices measured using stimuli presented in an aperture matched in size to the classical receptive field (ordinate) versus indices measured using stimuli presented within a 4° aperture (abscissa). Each data point represents a neuron. Diagonal dashed line is the line of equality. Modulation in V1 was near 0 for both stimulus sizes. Modulation in V2 was positive for both stimulus sizes, but there was significantly less modulation in V2 for the smaller size.
We also made measurements on a subset of cells in which the stimuli were confined to each neuron's classical receptive field (CRF). In V1, the modulation was near 0 for both CRF-matched and large stimuli, though there was a small but significant reduction in modulation for the smaller stimuli (P < 0.05, t-test, Fig. 3c). In V2, there was a robust but incomplete reduction in modulation for the smaller stimuli (P < 0.0001, t-test, Fig. 3d), suggesting that the modulation in V2 depended partly, but not entirely, on interactions between receptive field center and surround. We found no evidence for a relationship in V2 between the modulation and commonly characterized properties of early visual neurons, including surround suppression, orientation tuning bandwidth, preferred spatial frequency, spatial frequency tuning bandwidth, or parameters of the contrast sensitivity function (c50 and exponent) (all P > 0.05, correlation). We therefore believe that our measurements reveal a hitherto unrecognized dimension of visual processing in macaque V2.
Differentiating V2 from V1 in human
Given the reliable effect of higher-order image statistics on the responses of V2 neurons, we wondered if similar effects could be observed in humans using functional magnetic resonance imaging (fMRI), which can capture large-scale differential responses across visual areas25. We presented alternating blocks of naturalistic and noise stimuli — one texture family at a time — in the near-peripheral visual field while measuring blood-oxygenation level dependent (BOLD) fMRI responses in visual cortex. Subjects performed a demanding task at the center of gaze to divert their attention from the peripheral stimulus. Responses were visualized on a flattened representation of the occipital lobe, and boundaries between V1 and V2 were derived from independent retinotopic mapping25,26.
In all three subjects, there were strong differential fMRI responses to naturalistic texture throughout V2, and weaker ones in V1 (Fig. 4a). We captured differential fMRI responses evoked by naturalistic texture and noise stimuli with a modulation index analogous to that used for single-unit physiology (see Methods). Differences in modulation between V2 and V1 were significant in each subject (Fig. 4b; P < 0.0001, paired t-test comparing responses in V1 and V2 across the 15 texture families). The much weaker modulation in V1 was nevertheless significantly greater than 0 in two of three subjects (Fig. 4b; P < 0.05). Modulation was also evident in V3, and to some extent in V4, though weaker in higher object-selective areas like the lateral occipital complex. The modulation in V3 and V4 might be inherited from V2. These results complement the single-cell findings by showing that the same response differences were evident over all of V2, and were sufficiently robust to manifest at the coarse spatial scale of fMRI.
Figure 4.
fMRI responses to naturalistic textures differentiate V2 from V1 in humans. (a) Responses to alternating blocks of naturalistic texture images and spectrally-matched noise shown on a flattened representation of the occipital pole. Color indicates coherence, which captures the extent to which the fMRI responses to naturalistic and noise stimuli differ, computed voxel by voxel after averaging responses to all texture families. White lines indicate boundaries between visual areas identified in an independent retinotopic mapping experiment. (b) A measure of fMRI modulation (see Methods) averaged across voxels and texture families in V1 and V2 for three subjects. Error bars indicate s.e.m. across texture families. (c) Responses from an example subject to two individual texture families, only one of which evoked robust differential responses in V2. Same format as panel a. (d) Correlation between fMRI and single-unit modulation for V1 (green) and V2 (blue). Each data point represents a different texture family.
As for the single-cell responses, some texture families elicited more robust fMRI modulation in V2 than others (see examples in Fig. 4c). We compared, across texture families, the fMRI and single-unit modulation indices (averaged across neurons). fMRI and electrophysiological measures were significantly correlated in V2 (Fig. 4d; r = 0.55, P < 0.05), but this was not evident in V1 (r = 0.30, P = 0.28). We also correlated the modulation indices from each individual neuron with the fMRI response modulation, and found that correlations were significantly higher in V2 than in V1 (P < 0.005, t-test on Z-transformed correlations). The presence and diversity of the differential responses to naturalistic textures in V2 are thus similar when measured in macaque neurons and human fMRI.
Linking V2 physiology to perception
If this distinctive feature of V2 responses has a perceptual correlate, then texture families that evoke larger differential responses (Fig. 2,4) should be those for which the naturalistic textures are more perceptually distinct from spectrally-matched noise. To test this hypothesis, we built textures with varying degrees of “naturalness” (Fig. 5a), by titrating the inclusion of higher-order correlations in the synthesis process. We measured perceptual sensitivity to naturalness for each texture family using a three-alternative forced choice discrimination task (Fig. 5b,c) suitable for studying stochastic stimuli like textures27.
Figure 5.
Neuronal responses to naturalistic textures in V2 predict perceptual sensitivity. (a) Stimuli were generated along an axis of “naturalness” by gradually introducing higher-order correlations (Fig. 1b). (b) Observers performed a 3AFC “oddity” task in which they viewed three images, two naturalistic and one noise (or vice versa), and indicated which looked different from the other two. All three images were synthesized independently (e.g., starting with statistically independent samples of Gaussian white noise). (c) Psychometric function: performance as a function of naturalness. Solid curves, best-fit cumulative Weibull function. Chance performance is 1/3. The two panels show two different texture families (same as in Fig. 4c) with different thresholds (defined as the level of naturalness required to obtain ~75% correct). (d) Correlation between psychophysical sensitivity (1/threshold) and single-unit modulation in V1 (green) and V2 (blue). Each data point represents a texture family. (e) Correlation between psychophysical sensitivity and fMRI modulation. Same format as panel d.
Across 15 texture families, perceptual sensitivity was significantly correlated with electrophysiological response modulations, averaged across neurons in V2 (Fig. 5d; r = 0.62, P < 0.05), but not in V1 (r = 0.21, P = 0.45), and the correlation was significantly larger for V2 than V1 (P < 0.0001, t-test on Z-transformed correlations). We also found that perceptual sensitivity was significantly correlated with the fMRI modulation in V2 (Fig. 5e; r = 0.70; P < 0.005) but not in V1 (r = 0.40; P = 0.13), and that this correlation was again significantly larger for V2 than V1 (P < 0.01, paired t-test on Z-transformed correlations). These relationships suggest a functional role for V2 in the perception of these naturalistic stimuli.
Predicting diversity in neuronal and perceptual sensitivity
The texture families we used varied in the form and extent of their statistical dependencies. We wondered which of the many possible dependencies were most important for perception and — by extension — for evoking responses in V2. Identifying the relevant subset requires a large number of stimuli, but making biological measurements – neuronal or fMRI – for such an ensemble would be unfeasible. We therefore measured perceptual sensitivity for nearly 500 texture families using Amazon.com's Mechanical Turk service to “crowdsource” our measurements28 and expand their range 30-fold. This approach yielded a total of 300 hours of behavioral data from thousands of human observers (Fig. 6ab, see Methods). We developed analysis procedures to combine data from this large number of observers, and to evaluate the reliability of the results.
Figure 6.
Crowdsourced psychophysical estimates of sensitivity for hundreds of texture families. (a) Example psychometric functions for two texture families (same as Fig. 4c and 5c), each based on observers recruited from Amazon.com's Mechanical Turk performing a 3AFC task in a web browser. Each colored line corresponds to one observer. The black line indicates the best-fitting psychometric function, estimated using a mixture model that re-weighted observers based on their reliability (see Supplementary Analysis); thickness of the colored lines indicates the weight assigned to each observer. Chance performance is 1/3. (b) Perceptual sensitivity (1/threshold) was significantly correlated when measured in the laboratory (abscissa) and in the crowd (ordinate). Dashed line is the line of equality. (c) The distribution of perceptual sensitivities across 494 texture families was used to pick 20 families spanning the range of sensitivities, emphasizing the extremes (light gray regions). (d) Correlations between single-unit modulation and sensitivity (measured in the crowd) for the chosen families, in V1 (green) and V2 (blue). Only 17 of the 20 families were included due to experimental time constraints. (e) Correlations between fMRI modulation and sensitivity. All 20 families were included. Same format as panel d.
We related our crowdsourced measurements to our previous results in two ways. First, we confirmed for the original 15 texture families (Fig. 5) that perceptual sensitivity measured in the crowd was reliably correlated with, albeit lower than, sensitivity measured in the laboratory (r = 0.92, P < 0.0001, Fig. 6b). Second, we used the 494 new texture families to link the crowdsourced sensitivity estimates back to physiological responses. We selected 20 texture families spanning a range of crowd-estimated sensitivities, emphasizing the extremes (Fig. 6c). We used images from these families as stimuli in additional single-unit and fMRI experiments. Both the single-unit modulation in V2 (r = 0.74, P < 0.001, 16 cells) and fMRI modulation in V2 (r = 0.77, P < 0.0001, 2 subjects) were significantly correlated with crowd-estimated sensitivity (Fig. 6de), confirming with novel stimuli the relationship found in our earlier experiments (Fig. 5). In V1, single-unit modulation showed no evidence for a correlation with sensitivity (r = –0.25, P = 0.33, 11 cells). fMRI modulation in V1 to these new stimuli revealed a significant correlation (r = 0.49, P < 0.05). This was weaker than the correlation found for V2, and similar to our results using the original 15 textures (Fig. 5e).
The crowdsourced psychophysical data for the complete ensemble of texture families allowed us to identify which statistical dependencies of the images explained diversity in perceptual sensitivity to naturalistic structure. Recall that our textures were synthesized to match correlations among V1-like responses — both linear filter responses, and energies — at different orientations, positions and scales (Fig. 7a,b). Through a combination of principal components analysis and multiple linear regression (see Methods), we used these correlations, along with spectral and marginal statistics, to predict more than half of the variance in perceptual sensitivity (Fig. 7a, R2 = 66%). To ensure that results were not a result of overfitting, we confirmed that accuracy was still high (R2 = 60%) with 10-fold cross-validation. To identify the relative importance of different synthesis parameters, we decomposed the total R2 using the “averaging over orderings” technique (see Methods)29. The largest share of variance was accounted for by the cross-scale correlations among the energy filter responses; second and third most important were the cross-position and cross-orientation energy-filter correlations (Fig. 7b). Correlations among linear filter responses were less important. Spectral properties had a small amount of predictive power, but this likely reflected how spectra control visibility, e.g., insensitivity to high spatial frequencies. The contribution of marginal statistics (skewness and kurtosis) was negligible, indicating that perceptual sensitivity is driven by the higher-order correlations rather than basic image properties. Together, these results link perceptual sensitivity — and, we infer, neuronal sensitivity in V2 — to the particular kinds of higher-order statistical dependencies found in our visual textures.
Figure 7.
Using higher-order correlations to predict perceptual sensitivity. (a) Cross-scale, cross-position, and cross-orientation correlations are computed by taking products of localized V1-like filter responses. Each circle represents an image location. Filters at each location are tuned to orientation and frequency, and compute either linear or energy responses (see panel b). (b) Linear filters are sensitive to phase, akin to V1 simple cells; energy filters compute the square root of the sum of squared responses of two phase-shifted filters (in quadrature pair) and are thus insensitive to phase, akin to V1 complex cells (Adelson & Bergen, 1985). For both filter types, products (as in panel a) are averaged across spatial locations to yield correlations. (c) We used multiple linear regression to predict perceptual sensitivity to naturalistic textures based on higher-order correlations and other image statistics used in texture synthesis. Each data point corresponds to a texture family; black dots indicate all texture families used in physiological experiments (from Figs. 2e, 5de, 6de). Black dashed line is the line of equality. (d) Wedges indicate the fractional R2 assigned to each group of texture synthesis parameters from the regression analysis. See Portilla & Simoncelli (2001) and Balas (2008) for example images demonstrating the role of some of these parameters in texture synthesis.
Discussion
We have discovered that naturalistic texture stimuli modulate the responses of neurons in area V2, while having only a minimal effect on neurons in area V1. These modulations were similar and substantial in both anesthetized macaques and awake humans. The diversity of modulation across different texture families predicted the perceptual salience of their naturalistic structure. We capitalized on this diversity to reveal the importance of correlations across scale, and to a lesser extent across position and orientation, for driving V2 activity. The combination of human and monkey physiology, and crowdsourced psychophysics, provide mutually reinforcing evidence that V2 plays a direct functional role in representing naturalistic structures.
Previous studies have identified specialized response properties in subpopulations of V2 neurons8,9,14, but the differences between V2 and V1 were usually small3,5-7,11. Some of these may reflect special cases of the properties identified here, such as tuning for angles reflecting sensitivity to cross-orientation correlations. The attribute that has most robustly distinguished V2 from V1 is “border ownership”12, which may also depend on the receptive field surround in V219,30. Border ownership signaling, however, may rely on attentional feedback31,32, whereas the response pattern we have discovered probably does not, as it is evident in both awake humans with diverted attention and anesthetized macaques.
Our fMRI measurements robustly differentiated human V2 from V1. However, unlike in our single-unit recordings, there was a weak, significant correlation between fMRI measurements in V1 and perceptual sensitivity (Fig. 5e, 6e). These V1 signals may reflect the influence of modulatory feedback24. Such an influence was hinted by the late component of modulation in the V1 single-unit response time course (Fig. 2c), and could be more readily evident with fMRI33. Establishing a more direct relationship would require further study of the late V1 single-unit response — by recording from more neurons, and thus more reliably measuring the weak signal, or employing techniques, like cooling, capable of isolating feedback signals34.
We compared responses to naturalistic texture stimuli with responses to spectrally-matched noise images, similar to the globally phase-randomized images that have been used previously in fMRI35, psychophysics36, and physiology37 experiments. Presentation of intact and phase-randomized objects, for example, reveals differential fMRI responses throughout the human lateral occipital cortex35. But none of these studies reported differences between V1 and V2. This may be due to the use of uncontrolled images of natural objects or scenes38,39, which obscures the influence of the higher-order statistical dependencies upon which we have focused, and instead emphasizes responses in downstream object-selective areas. A previous study of V1 and V2 used natural photographs as stimuli14, but this study had different goals and did not relate neuronal responses to the particular statistical dependencies considered here. The spatial homogeneity of our stimuli, coupled with a synthesis method that enforced a particular set of higher-order statistical dependencies, facilitated robust and specific links between neuronal responses in V2, image statistics, and perception. Our ability to generate multiple images from each texture family also facilitated comparisons between neurophysiology (averaging across neurons with different receptive field locations) and human fMRI40. Synthetic naturalistic stimuli like ours thus offer a balance between natural and artificial that may prove useful in physiological characterization in other sensory domains41.
We used a large-scale, crowdsourced psychophysical experiment to show that particular subsets of higher-order statistical dependencies predicted diversity in perceptual sensitivity — and, by extension, neuronal responses in V2. Correlations among energy filter responses (akin to V1 complex cells) were more important than among linear filter responses (akin to V1 simple cells), which is notable given that V2 neurons receive input from both simple and complex cells42. The particular computation implied by the responses to our stimuli may depend primarily on complex cell input. This hypothesis could be further explored by combining our stimulus protocol with measures of V1-to-V2 connectivity43. Our analysis of crowdsourced data also revealed the importance of dependencies across scale, followed by dependencies across position and orientation. Most studies of V2 thus far have emphasized interactions across orientation, e.g., by measuring responses to curvature or angles4,5,8-10. These visual elements are salient in man-made environments, but may play an outsized role in our intuitions about how the visual system begins the process of parsing natural scenes.
Instead, we infer that V2 neurons might be particularly sensitive to dependencies across scale, which are equally fundamental to natural image structure.
The statistical dependencies in our texture stimuli are readily computable from the responses of V1 neurons. Given our results, it is tempting to hypothesize that V2 neurons directly encode correlations of their V1 afferents. However, a variety of nonlinear computations, similar in function but differing in detail, can effectively capture the same information, and could enable the sensitivity to naturalistic stimuli that we found in V2. For example, selectivity for different kinds of correlations could be achieved by combining squared and spatially pooled linear combinations of appropriate V1 inputs, analogous to the way “motion energy” computations can express the correlations of the Reichardt model44. Such “complex cells” in V2 would give enhanced responses to stimuli containing higher-order correlations, unlike V2 “simple cells” which would linearly combine the responses of orientation-tuned filters9,10,14. In this framework, the larger receptive field sizes of V2 cells would allow them to compute correlations of V1 inputs across distinct spatial positions, as well as across different orientations and scales; our analyses revealed an important role for all three factors (Fig. 7d). Individual V2 “complex cells” could be sensitive only to particular subsets of higher-order correlations, explaining both why some texture families were more effective on average (Fig. 2e), and also that there was a diversity of selectivity across individual neurons (Fig. 2d). The idea of a V2 complex cell is conceptually satisfying because it suggests that nonlinear computations of identical form reappear at multiple stages of the cortical hierarchy45,46, and could be further explored in V2 by measuring responses to naturalistic or artificial stimuli containing specific higher-order correlations and predicting their responses with hierarchical models47,48.
The transformation of visual information as it ascends the cortical hierarchy enables the perception of scenes and objects. A common view is that early computations encode the primitive elements of which scenes are made, and that subsequent stages of processing assemble these elements into larger and more complex combinations, capturing the structural relationships that determine the visual world. This constructionist view has stumbled on the problem of V2, whose neurons have stubbornly refused to reveal the form of their preferred elementary feature combinations3-11. We have found it useful to attack this problem with well-controlled texture stimuli that emphasize the statistical regularities of natural images, as well as with stimuli containing more conventional visual features. Our findings suggest that two fundamental constituents of visual scenes — the specific feature combinations that comprise objects, and the statistics that define textures — may both be represented in V249.
Online Methods
Model and synthesis of stimuli
Model
Here we describe aspects of the model and stimulus generation common to all experiments. Further details of stimulus presentation for each experimental method are presented separately, below. Stimuli in all experiments were generated using the texture analysis-synthesis procedure described in Portilla and Simoncelli (2000) (code and examples available at http://www.cns.nyu.edu/~lcv/texture/). We began with an ensemble of diverse natural homogenous black and white photographs of visual textures, drawn from both commercial and personal databases. Each original texture photograph served as the basis for a “texture family.” Most of our experiments used 15 texture families, selected to vary in the extent to which each texture differed from an image of spectrally-matched noise. The crowdsourced psychophysical experiments (Fig. 6, 7) used an additional 479 texture families, selected only to avoid duplicates and images with entirely blank regions (e.g. clouds). For each texture family, we computed the model parameters on the original photograph, by processing the image with a multi-scale multi-oriented bank of filters with 4 orientations and 4 spatial scales. For each filter, we computed the real, linear output and the energy (square root of sum of squared quadrature pair outputs), analogous to the responses of simple and complex V1 cells. We then computed pairwise products across filter responses at different positions (within each orientation and scale), across different orientations, and across different scales. All of these pairwise products were averaged across the spatial extent of the image, yielding correlations. We additionally computed spectral statistics (average energy within each band of the pyramid) and marginal pixel statistics (skew and kurtosis).
Synthesis
After computing the model responses on an original image, we synthesized 15 new samples by initializing 15 different images of Gaussian white noise, and adjusting each using gradient descent (specifically, gradient projection) until it matched the model parameters computed on the original image. Because the dimensionality of the image was larger than the number of parameters, this process yielded multiple random high-entropy samples that were statistically identical in terms of the model parameters. Convergence of all parameter groups was monitored and ensured, and the number of synthesis iterations used (50) was far more than typically required. For each texture family, we also generated spectrally-matched “noise” images by randomizing the phase but matching the complete two-dimensional power spectra. This procedure yielded nearly identical results to iteratively matching the power averaged within each band of the multi-scale multi-oriented filter bank, and was performed for speed of computation. We performed noise synthesis separately on each naturalistic texture sample to generate 15 samples. For psychophysical experiments, we generated stimuli that spanned a “naturalness” axis between naturalistic and noise. For each texture family we computed the model parameters on the original natural photograph and parameters on a spectrally-matched noise image, and then linearly interpolated the model parameters between the two endpoints, . For each interpolated parameter vector, we used the same synthesis procedure to generate 15 samples. Pilot experiments suggested that the distribution of thresholds across texture families was approximately normally distributed in the log domain, so we sampled the naturalness axis with 10 values of Δ equally spaced on a logarithmic scale. For laboratory psychophysics, we used a range of 0.04–0.8; for crowdsourced psychophysics, we used a range of 0.1–1.0 (see below).
Physiology
Recording
We recorded from 13 anesthetized, paralyzed, adult macaque monkeys (2 M. Nemestrina and 11 M. Cynomolgus). Our standard methods for surgical preparation have been documented in detail previously50. We maintained anesthesia with infusion of sufentanil citrate (6-30 μg kg-1 hr-1) and paralysis with infusion of vecuronium bromide (Norcuron; 0.1 mg kg-1 hr-1) in isotonic dextrose-Normosol solution. We monitored vital signs (heart rate, lung pressure, EEG, body temperature, urine volume and specific gravity, and and end-tidal pCO2) and maintained them within the appropriate physiological range. The eyes were protected with gas permeable contact lenses and refracted with supplementary lenses chosen through direct ophthalmoscopy. At the conclusion of data collection, the animal was killed with an overdose of sodium pentobarbital. All experimental procedures were conducted in compliance with NIH Guide for the Care and Use of Laboratory Animals and with the approval of the New York University Animal Welfare Committee. We made a craniotomy and durotomy centered approximately 2-4 mm posterior to the lunate sulcus and 10-16 mm lateral and individually advanced several quartz-platinum-tungsten microelectrodes (Thomas Recording) into the brain at an angle 20° from vertical. We distinguished V2 from V1 on the basis of depth from the cortical surface and changes in the receptive field location of recorded units. In an effort to obtain an unbiased sample of single units, we made extracellular recordings in V1 and V2 from every single unit with a spike waveform that rose sufficiently above noise to be isolated, and we fully characterized every unit that demonstrated a measurable visually-evoked response to gratings or naturalistic texture. Data are reported from every unit for which we completed characterization (see below). The receptive fields of most units were between 2 and 5 deg eccentricity, but our estimates of eccentricity were not sufficiently precise to include in analyses.
Visual stimulation
We presented visual stimuli on a gamma-corrected CRT monitor (Eizo T966; mean luminance, 33 cd/m2) at a resolution of 1280 × 960 with a refresh rate of 120Hz. Stimuli were presented using Expo software on an Apple Macintosh computer. For each isolated unit, we first determined its ocular dominance and occluded the non-preferred eye. We used drifting sinusoidal gratings to characterize the basic receptive field properties of each unit, including tuning for orientation and direction, spatial and temporal frequency, size, and contrast. We then presented the texture stimuli. We used a set of 15 texture families, and generated 15 samples for each texture family for a total of 225 images. 15 spectrally-matched noise samples of the 15 families were also presented. The 450 unique images making up our stimulus ensemble were presented in pseudo-random order for 100 ms each, separated by 100 ms of mean luminance. Each image was presented 20 times. Images were presented to every unit at the same scale and at a size of 4° within a raised cosine aperture. We chose a 4° aperture to be larger than all the receptive fields at the eccentricities from which we typically record. Nearly all recorded units had receptive fields smaller than 4°, and the majority were less than 2°. For a subset of V1 and V2 neurons we additionally presented stimuli in a smaller aperture matched to the receptive field size of that unit. The aperture diameter was set to be the grating summation field as measured with full contrast drifting gratings50. We ran the full texture stimulus ensemble within this aperture although typically with only 5-10 repeats per image.
Analysis
The full stimulus ensemble consisted of 450 images presented 20 times each. All analyses were performed after averaging spiking responses across those 20 repeats, and also averaging responses across the 15 samples. Depending on the analysis, responses were further averaged across texture family, neurons, and/or a temporal window. Response time courses were computed by counting spikes within a sliding, non-overlapping 10 ms window. Time courses were always averaged across texture families (Fig. 2ab). For the population average plot (Fig. 2b), time courses for each neuron were first normalized by dividing by each neuron's maximum response across all texture families and time points, but after averaging responses evoked by the 20 repeats of each of the 15 images within the same texture family. A modulation index was computed as the difference in firing rate between naturalistic and noise divided by the sum. The index was computed separately for each texture family. For time course plots (Fig. 2c), modulation was computed within 10 ms windows. In all other cases, firing rates were first averaged within an 100 ms window following response onset, and the modulation index was computed on those rates. Response onset was determined by inspection as the time point eliciting a response above baseline; results were nearly identical when using a quantitative criterion based on the standard deviation of the response. Finally, modulation indices were additionally averaged across neurons (Fig. 2e) or across texture families (Fig. 2f).
Basic receptive field properties for each neuron — e.g., receptive field size, surround suppression — were determined offline by using maximum likelihood estimation to fit an appropriate parametric form to each tuning function. These fits were only obtainable for a subset of neurons (81% in V1, 74% in V2) due to incomplete characterization arising from time constraints during the experiment.
fMRI
Subjects
Data were acquired from three healthy subjects with normal or corrected-to-normal vision (all male; age range, 26-30 years). Two subjects were authors. Experiments were conducted with the written consent of each subject and in accordance with the safety guidelines for fMRI research, as approved by the University Committee on Activities Involving Human Subjects at New York University. Each subject participated in at least three scanning sessions: one session to obtain a set of high-resolution anatomical volumes, one session for standard retinotopic mapping (single wedge angular position, and expanding ring eccentricity), and one session to measure differential responses to naturalistic and spectrally-matched noise stimuli. Two subjects participated in an additional scanning session using texture families derived from the crowdsourced psychophysical experiment (described below).
Stimuli
Stimuli were presented using Matlab (MathWorks) and MGL (available at http://justingardner.net/mgl) on a Apple Macintosh computer. Stimuli were displayed via an LCD projector (Eiki LC-XG250) onto a back-projection screen in the bore of the magnet. Subjects laid supine and viewed the stimuli through an angled mirror. All images were presented within a suitably vignetted annular region (inner radius, 2°; outer radius, 8°). We used textures that approximately matched in scale the presentation conditions in the electrophysiological and psychophysical experiments.
Protocol
Blocks of naturalistic and spectrally-matched noise stimuli were presented in alternation. Within each 9 s block, a random sequence of images from one texture family were presented at 5 Hz. Each run consisted of 20 blocks: 10 naturalistic, 10 noise. Different texture families were presented in separate runs, and multiple runs were performed within each session. Subjects performed two runs for each texture family. In each session, a separate localizer run was used to define retinotopic subregions corresponding to the stimulus region. Within each 9 s block of the localizer run, a random sequence of both naturalistic and noise stimuli were presented within the stimulus annulus or the region complementary to the annulus. Each run consisted of 40 blocks: 20 annulus, 20 anti-annulus.
Task
Observers performed a demanding two-back detection task continuously throughout each run to maintain a consistent behavioral state, encourage fixation, and divert attention from the peripheral stimulus. Without attentional control, we have reported large and variable attentional signals in visual cortex33. Digits (0 to 9) were displayed continuously at fixation, changing every 400 ms. The observer used a button press to indicate whether the current digit matched the digit from two steps before.
Preprocessing
All preprocessing and analyses were implemented in Matlab using mrTools (http://www.cns.nyu.edu/heegerlab/?page=software). The anatomical volume acquired in each scanning session was aligned to the high-resolution anatomical volume of the same subject's brain, using a robust image registration algorithm51. Data from the first half cycle (eight frames) of each functional run were discarded to minimize the effect of transient magnetic saturation and allow the hemodynamic response to reach steady state. Head movement within and across scans was compensated for using standard procedures51 The time series from each voxel was high-pass filtered (cutoff, 0.01 Hz) to remove low-frequency noise and drift52.
Analysis
We performed two complementary analyses of fMRI responses to alternating blocks of naturalistic texture and noise stimuli, one to visualize responses, and a second to quantify them for statistical analyses (and for comparisons to psychophysics and physiology). First, for each voxel, response time courses were averaged across texture families, and fit with a sinusoid with period matched to the block alternation (9 s). The coherence between the best-fitting sinusoid and the average time series was used to assess the statistical reliability of differences in cortical activity evoked by naturalistic and noise stimuli, visualized on flattened maps of the occipital lobe (Fig. 4ac).
To quantify responses, we computed an fMRI modulation index, analogous to the index used for single unit measurements. We computed the index as the ratio of two response amplitudes: the amplitude of differential responses to naturalistic versus noise (texture minus noise), and the amplitude of differential responses to naturalistic and noise together versus a blank screen (texture plus noise). To obtain the numerator (texture minus noise), for each texture family, we averaged the time course of each voxel across repeated runs, and then projected it onto a unit-norm sinusoid having period matched to the stimulus alternation, and phase given by the responses to the localizer scan (see above). The reference phase provided an estimate of the hemodynamic delay, and was computed separately for each visual area. The amplitude of projection isolated the component of the response time course that responded positively and differentially to the naturalistic texture stimuli40. To obtain the denominator (texture plus noise), we projected the response time courses from the localizer scan onto a unit-norm sinusoid with the same reference phase. The amplitude of this projection captured the combined response to texture and noise images together, because the localizer scan presented both (randomly interleaved) alternating with a blank screen. Both response amplitudes (texture minus noise, and texture plus noise) were averaged across voxels, and their ratio yielded a modulation index for each visual area. fMRI modulation indices were then either averaged across texture families (Fig. 4b) or analyzed separately (Fig. 4d; Fig. 5e; Fig. 6e). Results were qualitatively similar (and supported the same conclusions) when this fMRI modulation index was replaced by either coherence, or the texture minus noise response amplitudes (without division by texture plus noise response amplitudes).
MRI acquisition
MRI data were acquired on a Siemens 3T Allegra head-only scanner using a head coil (NM-011; Nova Medical) for transmitting and an eight-channel phased array surface coil (NMSC-071; Nova Medical) for receiving. Functional scans were acquired with gradient recalled echo-planar imaging to measure blood oxygen level dependent changes in image intensity53. Functional imaging was conducted with 24 slices oriented perpendicular to the calcarine sulcus and positioned with the most posterior slice at the occipital pole (1500 ms repetition time; 30 ms echo time; 72° flip angle; 2 × 2 × 2 mm voxel size; 104 × 80 voxel grid). A T1-weighted magnetization-prepared rapid gradient echo anatomical volume (MPRAGE) was acquired in each scanning session with the same slice prescriptions as the functional images (1530 ms repetition time; 3.8 ms echo time; 8° flip angle; 1 × 1 × 2.5 mm voxel size; 256 × 160 voxel grid). A high-resolution anatomical volume, acquired in a separate session, was the average of three MPRAGE scans that were aligned and averaged (2500 ms repetition time; 3.93 ms echo time; 8° flip angle; 1 × 1 × 1 mm voxel size; 256 × 256 voxel grid). This high-resolution anatomical scan was used both for registration across scanning sessions and for gray matter segmentation and cortical flattening.
Defining retinotopic regions of interest
Each subject participated in a standard retinotopic mapping experiment, described in detail previously26,54. The data were analyzed, following standard procedures to identify meridian representations corresponding to the borders between retinotopically organized visual areas V1, V2, V3, and V4. There is some controversy over the exact definition of human V4 and the area just anterior to it; we adopted the conventions proposed by Wandell et al., 2007. We used data from an independent localizer scan (see above) to further restrict each visual area to only those voxels responding to the stimulus annulus with coherence of at least 0.25. Qualitatively similar results were obtained using higher or lower thresholds.
Psychophysics (Laboratory)
Observers
Three observers with normal or corrected-to-normal vision participated in the experiments (all male; age range, 26-30 years). Protocols for selection of observers and experimental procedures were approved by the Human Subjects Committee of New York University. Two observers were authors. The other was naive to the purpose of the experiment.
Stimuli
Stimuli were presented on a 41 × 30 cm flat screen CRT monitor at a distance of 46 cm. Texture images were presented within vignetted 4 deg circular patches at three locations equidistant from fixation, each 4 deg eccentricity (one above fixation, one to the lower left, and one to the lower right). A 0.25 degree fixation square was shown throughout the experiment.
Task
Every trial of the 3AFC “oddity” task presented three different image within the three patches: two images were spectrally-matched noise and one was naturalistic, or one was noise and two were naturalistic. The “naturalness” of the naturalistic texture(s) varied across trials, spanning ten points between 0.4 and 0.8, equally spaced on a log scale. If two naturalistic textures were presented on a trial, they had the same level of naturalness. Image patches were presented for 600 ms, after which observers had 1 sec to indicate with a keypress which of the three was the odd one out. There was no feedback during the experiment. Before the experiment, each observer performed a small number of practice trials (~10) with feedback to become familiar with the task. Different texture families were run in separate blocks. Each observer performed 480 trials in each block; the order of conditions and location of the target were appropriately randomized and counterbalanced. Blocks were performed in random order for each subject. Data were collected from 15 texture families.
Analysis
For each texture family, we fit the parameters of a Weibull function that maximized the likelihood of the psychometric data. The function was parameterized with a threshold, slope, and lapse rate55. Estimated lapse rates were typically very small (mean 0.01, maximum 0.06). Threshold was converted to its reciprocal (sensitivity) for all subsequent analyses, and statistics, e.g. correlations, were computed in the log domain (Fig. 5,6,7).
Psychophysics (crowdsourced)
Observers
Several hundred observers (“Turkers”) were recruited for experiments through Amazon.com's Mechanical Turk website. Each was paid $0.40 for approximately 5 minutes of their time. Payment was made so long as Turkers completed the task, regardless of performance. Demographic data were not collected, but demographic studies of the Mechanical Turk28 suggest that our sample reflected gender and age diversity. Participation was restricted to those Turkers achieving 95% approval rating on other Mechanical Turk tasks. Protocols for selection of Turkers and experimental procedures were approved by the human subjects committee of New York University. All Turkers signed an electronic consent form at the beginning of the experiment. We ensured that 10 unique Turkers completed the task for each texture family, but we did not prevent the same Turkers from completing the task for multiple texture families.
Stimuli
We developed a version of our 3AFC task for display in a web browser (see example at http://www.jeremyfreeman.net/public/turk/code/?csv=tex-018-files.csv), using Javascript and HTML. Each trial began with 700 ms blank period, followed by a 600 ms stimulus presentation, and a second 700 ms blank period. As in the laboratory version of the experiment, images were presented in three patches equidistant from fixation. A small red fixation dot was shown throughout the experiment. After the second blank, three arrows were presented near fixation pointing towards the three possible target locations. Turkers were instructed that “One image will look different from the other two — your task is to identify it by clicking the black arrow that points to it.” There was no other explanation of the nature of the stimuli or the conditions. We were unable to verify or control viewing distance, size, eccentricity, or presentation time. However, data obtained from the crowd and from the lab were comparable (Fig. 6b), suggesting that such variations were unimportant, at least with respect to this stimulus and task.
Task
Trial types for the 3AFC task were similar to those in the laboratory experiment, except naturalness was varied across ten points equally spaced on a logarithmic scale between between 0.1 and 1.0, instead of 0.04 to 0.8. This range was chosen because pilot experiments suggested moderately higher thresholds compared to the laboratory data. Each Turker performed 60 trials, and different texture families were run separately. There was no feedback during the experiment, but Turkers performed 6 trials at the beginning with 1.0 naturalness, and were told that these initial trials would be easier than the others. Data were collected from 494 texture families.
Analysis
Each Turker and texture family yielded a psychometric function, based on six trials for each of ten levels of naturalness. Typically, for each texture family, a small number of Turkers performed at or near chance at all naturalness levels, suggesting that they may not have been performing the task appropriately. If data from all Turkers were averaged, the influence of these Turkers would have yielded fitted psychometric functions with unreasonably high lapse rates55. As an alternative, we described the data using a mixture model, with one common psychometric function and an individual lapse rate for each Turker, based on an approach developed in a related problem setting56. The analysis inferred the quality of individual Turkers and appropriately weighted their contribution to estimates of threshold (see Supplementary Analysis for fitting details). Although we consider this approach appropriate for these data, simple averaging of Turker responses yielded qualitatively similar results.
Validation of perceptual-neuronal relationship
We used the crowdsourced sensitivities to validate the relationship between perceptual sensitivity and neuronal response as measured both with fMRI and in single units. From the distribution of 494 sensitivities, we selected 20 texture families that sampled the range of sensitivity, emphasizing the extremes (Fig. 6c), and not including the 15 used previously. In two human subjects, we performed an additional fMRI experiment measuring responses to these 20 texture families. In one monkey, we recorded responses from 16 single units in V2 and 11 single units in V1 to 17 of the texture families (3 of the families were excluded due to experimental time constraints). Experimental procedures and analyses for both fMRI and single-unit experiments were otherwise identical to those described above.
Predicting perceptual sensitivity from texture statistics
All naturalistic textures were generated by matching an image for a particular set of higher-order image statistical parameters derived from an original texture photograph. We used a combination of principal components analysis and multiple linear regression to relate diversity in these parameters to diversity in perceptual sensitivity — and, by extension, neuronal response in V2. We began by computing all parameters for each texture family. The parameters were appropriately transformed so that all varied linearly in image contrast; for example, by taking the signed square root of correlations. Parameters were then Z-scored so that, for each parameter, the mean of its value across the images was 0, and the standard deviation was 1. We then grouped the parameters as follows: (1) marginal statistics (skew and kurtosis) (2) spectral statistics (average energy in each subband), (3) correlations of linear filter responses at neighboring locations, (4) correlations of linear filter responses at neighboring scales, (5) correlations of energy filter responses at neighboring orientations, (6) correlations of energy filter responses at neighboring locations, (7) correlations of energy filter responses at neighboring scales. For each group of parameters g, we constructed the 494 × pg matrix Pg containing the pg parameters in that group for the 494 texture categories. We then reduced the dimensionality of each group of parameters separately using principal components analysis, projecting each parameter matrix into the spaced spanned by the first k components, yielding a 494 × kg matrix P̂g. We used the k components required to capture 70% of the variance in each parameter group (typically between 2 and 6, at most 10), for a total of 35 components across all groups. Overall predictive performance was similar when using only 1 component per parameter group, but that would have made it inappropriate to compare the predictive power of the different parameter groups (see below).
Having reduced the dimensionality of each parameter group, we obtained a combined predictor matrix X, with 494 rows and 35 columns, and used multiple linear regression to predict sensitivity to the parameters. We added a column of ones to the matrix (to account for a constant offset), and solved for the weights that minimized the squared error,
where is a vector of log sensitivities for each of the texture families (as mentioned above, we worked in the log domain because log sensitivities were approximately normally distributed). We removed from analysis any families where thresholds were estimated as greater than 1.0 or less than 0.0 naturalness (only 5% of families), to avoid the influence of outliers arising from unstable threshold estimates.
R2 for the linear model was used to assess prediction accuracy. R2 was computed for the full model fit, as well as using 10-fold cross-validated, where the model was fit to 9/10 of the data and R2 was evaluated on the remaining 1/10, and R2 was averaged over different splits.
Three complementary procedures were used to assess the relative importance of the different parameter groups in predicting sensitivity. When parameter groups are correlated, as ours were, there is no objective decomposition of R2, but for our primary analysis we used a well-established procedure known as LMG or “averaging over orderings”29. For each parameter group, a difference in R2 is computed for two models, only one of which contains the group. This differential R2 depends on the order in which the different parameter groups were added to the model, as well as the size of the model when the group was added, so its value is averaged over all possible order permutations and model sizes. The resulting estimates of R2 for each parameter group exactly partition the full model's R2 (Fig. 7).
As a complementary analysis, we assessed the marginal predictive accuracy of each parameter group by computing R2 when including each parameter group on its own. We also assessed the conditional predictive accuracy of each parameter group by computing the difference in R2 for two models containing all parameter groups, with or without the group of interest. Both additional analyses yielded qualitatively similar results to the LMG procedure, in particular, emphasizing the importance of cross-scale dependencies of energy filter responses.
Statistical testing
Except where noted, all statistical tests for differences of fMRI and single-unit responses between V1 and V2 (Figs. 2,4) or differences in single-unit responses across size conditions (Fig. 3) used two-tailed unpaired t-tests. Relationships among single-unit, fMRI, and psychophysical data (Figs. 5,6), and between single-unit modulation and basic response properties, were tested for significance of correlation using a t-statistic. Sample sizes for statistical tests were greater than 50, except for sample sizes of 15 when analyzing the 15 texture families. There was no evidence of significant deviations from normality for data subjected to statistical tests that assume normality. As noted above, psychophysical sensitivity was expressed on a logarithmic scale because sensitivities were approximately normally distribution in the log domain. Analyses of the significance of modulation for each individual neuron (Fig. 2f) was computed using a randomization test; the neuron's firing rate to each image was randomly assigned to either naturalistic or noise, and the modulation index was computed. This procedure was repeated 10,000 times, and we computed the fraction of the resulting null distribution that exceeded the measured modulation for that neuron.
Supplementary Material
Acknowledgments
This work was supported by NIH grant EY04440, the Howard Hughes Medical Institute, the NYU Center for Brain Imaging, and NSF Graduate Research Fellowships to JF and CMZ. We are grateful to Geoff Boynton for helpful discussions, to Michael Landy for comments on the manuscript, to Michael Brotzmang for help programming the Mechanical Turk experiments, and to members of the Movshon Laboratory for help with physiological experiments.
Footnotes
Author Contributions
JF and CMZ performed the experiments and analysis; all authors designed the experiments, interpreted the results, and wrote the paper.
References
- 1.Schiller PH, Malpeli JG. The effect of striate cortex cooling on area 18 cells in the monkey. Brain Research. 1977;126:366–369. doi: 10.1016/0006-8993(77)90734-x. [DOI] [PubMed] [Google Scholar]
- 2.Sincich LC, Horton JC. The circuitry of V1 and V2: integration of color, form, and motion. Annual Review of Neuroscience. 2005;28:303–326. doi: 10.1146/annurev.neuro.28.061604.135731. [DOI] [PubMed] [Google Scholar]
- 3.Peterhans E, Heydt RVD. Mechanisms of contour perception in monkey visual cortex. II. Contours bridging gaps. Journal of Neuroscience. 1989;9:1749–1763. doi: 10.1523/JNEUROSCI.09-05-01749.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hegdé J, Essen DCV. Selectivity for complex shapes in primate visual area V2. Journal of Neuroscience. 2000;20:1–6. doi: 10.1523/JNEUROSCI.20-05-j0001.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hegdé J, Essen DCV. A comparative study of shape representation in macaque visual areas v2 and v4. Cerebral Cortex. 2007;17:1100–1116. doi: 10.1093/cercor/bhl020. [DOI] [PubMed] [Google Scholar]
- 6.Lee TS, Nguyen M. Dynamics of subjective contour formation in the early visual cortex. Proceedings of the National Academy of Sciences. 2001;98:1907–1911. doi: 10.1073/pnas.031579998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mahon LE, Valois RLD. Cartesian and non-Cartesian responses in LGN, V1, and V2 cells. Visual Neuroscience. 2001;18:973–981. [PubMed] [Google Scholar]
- 8.Ito M, Komatsu H. Representation of angles embedded within contour stimuli in area V2 of macaque monkeys. Journal of Neuroscience. 2004;24:3313–3324. doi: 10.1523/JNEUROSCI.4364-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Anzai A, Peng X, Van Essen DC. Neurons in monkey visual area V2 encode combinations of orientations. Nature Neuroscience. 2007;10:1313–1321. doi: 10.1038/nn1975. [DOI] [PubMed] [Google Scholar]
- 10.Vintch B, Movshon JA, Simoncelli EP. Characterizing receptive field structure of macaque V2 neurons in terms of their V1 afferents. Society for Neuroscience Abstracts. 2010 [Google Scholar]
- 11.El-Shamayleh Y, Movshon JA. Neuronal responses to texture-defined form in macaque visual area v2. Journal of Neuroscience. 2011;31:8543–8555. doi: 10.1523/JNEUROSCI.5974-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhou H, Friedman HS, Heydt RVD. Coding of border ownership in monkey visual cortex. Journal of Neuroscience. 2000;20:6594–6611. doi: 10.1523/JNEUROSCI.20-17-06594.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thomas OM, Cumming BG, Parker AJ. A specialization for relative disparity in V2. Nature Neuroscience. 2002;5:472–478. doi: 10.1038/nn837. [DOI] [PubMed] [Google Scholar]
- 14.Willmore BD, Prenger RJ, Gallant JL. Neural representation of natural images in visual area V2. Journal of Neuroscience. 2010;30:2102–2114. doi: 10.1523/JNEUROSCI.4099-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Simoncelli EP. Statistical models for images: Compression, restoration and synthesis. 31st Asilomar Conference on Signals, Systems & Computers. 1997;1:673–678. [Google Scholar]
- 16.Schwartz O, Simoncelli EP. Natural signal statistics and sensory gain control. Nature Neuroscience. 2001;4:819–825. doi: 10.1038/90526. [DOI] [PubMed] [Google Scholar]
- 17.Karklin Y, Lewicki MS. Emergence of complex cell properties by learning to generalize in natural scenes. Nature. 2009;457:83–86. doi: 10.1038/nature07481. [DOI] [PubMed] [Google Scholar]
- 18.Sigman M, Cecchi GA, Gilbert CD, Magnasco MO. On a common circle: natural scenes and Gestalt rules. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:1935–1940. doi: 10.1073/pnas.031571498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Geisler WS, Perry JS, Super BJ, Gallogly DP. Edge co-occurrence in natural images predicts contour grouping performance. Vision Research. 2001;41:711–724. doi: 10.1016/s0042-6989(00)00277-7. [DOI] [PubMed] [Google Scholar]
- 20.Portilla J, Simoncelli EP. A parametric texture model based on joint statistics of complex wavelet coefficients. International Journal of Computer Vision. 2000;40:49–70. [Google Scholar]
- 21.Freeman J, Simoncelli EP. Metamers of the ventral stream. Nature Neuroscience. 2011;14:1195–1201. doi: 10.1038/nn.2889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Heeger DJ, Bergen JR. Pyramid-based texture analysis/synthesis. Proceedings of SIGGRAPH. 1995:229–238. [Google Scholar]
- 23.Balas B. Attentive texture similarity as a categorization task: comparing texture synthesis models. Pattern recognition. 2008 doi: 10.1016/j.patcog.2007.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Angelucci A, Levitt JB, Walton EJ, Hupe JM, et al. Circuits for local and global signal integration in primary visual cortex. Journal of Neuroscience. 2002;22:8633–8646. doi: 10.1523/JNEUROSCI.22-19-08633.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wandell BA, Dumoulin SO, Brewer AA. Visual field maps in human cortex. Neuron. 2007;56:366–383. doi: 10.1016/j.neuron.2007.10.012. [DOI] [PubMed] [Google Scholar]
- 26.Larsson J, Heeger DJ. Two retinotopic visual areas in human lateral occipital cortex. Journal of Neuroscience. 2006;26:13128–13142. doi: 10.1523/JNEUROSCI.1657-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hillis JM, Ernst MO, Banks MS, Landy MS. Combining sensory information: mandatory fusion within, but not between, senses. Science. 2002;298:1627–1630. doi: 10.1126/science.1075396. [DOI] [PubMed] [Google Scholar]
- 28.Paolacci G, Chandler J, Ipeirotis P. Running experiments on amazon mechanical turk. Judgment and Decision Making. 2010;5 [Google Scholar]
- 29.Grömping U. Estimators of relative importance in linear regression based on variance decomposition. The American Statistician. 2007;61:139–147. [Google Scholar]
- 30.Craft E, Schütze H, Niebur E, von der Heydt R. A neural model of figure-ground organization. Journal of Neurophysiology. 2007;97:4310–4326. doi: 10.1152/jn.00203.2007. [DOI] [PubMed] [Google Scholar]
- 31.Qiu FT, Sugihara T, Heydt RVD. Figure-ground mechanisms provide structure for selective attention. Nature Neuroscience. 2007;10:1492–1499. doi: 10.1038/nn1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fang F, Boyaci H, Kersten D. Border ownership selectivity in human early visual cortex and its modulation by attention. Journal of Neuroscience. 2009;29:460–465. doi: 10.1523/JNEUROSCI.4628-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ress D, Backus BT, Heeger DJ. Activity in primary visual cortex predicts performance in a visual detection task. Nature Neuroscience. 2000;3:940–945. doi: 10.1038/78856. [DOI] [PubMed] [Google Scholar]
- 34.Ferster D, Chung S, Wheat H. Orientation selectivity of thalamic input to simple cells of cat visual cortex. Nature. 1996;380:249–252. doi: 10.1038/380249a0. [DOI] [PubMed] [Google Scholar]
- 35.Malach R, Reppas JB, Benson RR, Kwong KK, et al. Object-related activity revealed by functional magnetic resonance imaging in human occipital cortex. Proceedings of the National Academy of Sciences. 1995;92:8135–8139. doi: 10.1073/pnas.92.18.8135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Thomson MG, Foster DH, Summers RJ. Human sensitivity to phase perturbations in natural images: a statistical framework. Perception. 2000;29:1057–1069. doi: 10.1068/p2867. [DOI] [PubMed] [Google Scholar]
- 37.Felsen G, Touryan J, Han F, Dan Y. Cortical sensitivity to visual features in natural scenes. PLoS biology. 2005;3:1819–1828. doi: 10.1371/journal.pbio.0030342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Felsen G, Dan Y. A natural approach to studying vision. Nature Neuroscience. 2005;8:1643–1646. doi: 10.1038/nn1608. [DOI] [PubMed] [Google Scholar]
- 39.Rust NC, Movshon JA. In praise of artifice. Nature Neuroscience. 2005;8:1647–1650. doi: 10.1038/nn1606. [DOI] [PubMed] [Google Scholar]
- 40.Heeger DJ, Boynton GM, Demb JB, Seidemann E, Newsome WT. Motion opponency in visual cortex. Journal of Neuroscience. 1999;19:7162–7174. doi: 10.1523/JNEUROSCI.19-16-07162.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McDermott JH, Simoncelli EP. Sound Texture Perception via Statistics of the Auditory Periphery: Evidence from Sound Synthesis. Neuron. 2011;71:926–940. doi: 10.1016/j.neuron.2011.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.El-Shamayleh Y, Kumbhani RF, Dhruv NT, Movshon JA. Visual response properties of V1 neurons projecting to V2 in macaque. Society for Neuroscience Abstracts. 2009;404.3 doi: 10.1523/JNEUROSCI.2753-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Glickfeld LL, Andermann ML, Bonin V, Reid RC. Cortico-cortical projections in mouse visual cortex are functionally target specific. Nature Neuroscience. 2013;16:219–226. doi: 10.1038/nn.3300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Adelson EH, Bergen JR. Spatiotemporal energy models for the perception of motion. Journal of the Optical Society of America. 1985;2:284–299. doi: 10.1364/josaa.2.000284. [DOI] [PubMed] [Google Scholar]
- 45.Heeger DJ, Simoncelli EP, Movshon JA. Computational models of cortical visual processing. Proceedings of the National Academy of Sciences. 1996;93:623–627. doi: 10.1073/pnas.93.2.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Carandini M, Heeger DJ. Normalization as a canonical neural computation. Nature Reviews Neuroscience. 2012;13:51–62. doi: 10.1038/nrn3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rust NC, Mante V, Simoncelli EP, Movshon JA. How MT cells analyze the motion of visual patterns. Nature Neuroscience. 2006;9:1421–1431. doi: 10.1038/nn1786. [DOI] [PubMed] [Google Scholar]
- 48.Vintch B, Zaharia AZ, Movshon JA, Simoncelli EP. Efficient and direct estimation of a neural subunit model for sensory coding. Advances in Information Processing Systems. 2012;25:3113–3121. [PMC free article] [PubMed] [Google Scholar]
- 49.Adelson EH. On seeing stuff: the perception of materials by humans and machines. Proceedings of the SPIE. 2001 [Google Scholar]
- 50.Cavanaugh JR, Bair W, Movshon JA. Nature and interaction of signals from the receptive field center and surround in macaque V1 neurons. Journal of Neurophysiology. 2002;88:2530–2546. doi: 10.1152/jn.00692.2001. [DOI] [PubMed] [Google Scholar]
- 51.Nestares O, Heeger DJ. Robust multiresolution alignment of MRI brain volumes. Magnetic Resonance in Medicine. 2000;43:705–715. doi: 10.1002/(sici)1522-2594(200005)43:5<705::aid-mrm13>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 52.Smith AM, Lewis BK, Ruttimann UE, Ye FQ, et al. Investigation of low frequency drift in fMRI signal. Neuroimage. 1999;9:526–533. doi: 10.1006/nimg.1999.0435. [DOI] [PubMed] [Google Scholar]
- 53.Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proceedings of the National Academy of Sciences. 1990;87:9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gardner JL, Merriam EP, Movshon JA, Heeger DJ. Maps of visual space in human occipital cortex are retinotopic, not spatiotopic. Journal of Neuroscience. 2008;28:3988–3999. doi: 10.1523/JNEUROSCI.5476-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling, and goodness of fit. Perception and Psychophysics. 2001;63:1293–1313. doi: 10.3758/bf03194544. [DOI] [PubMed] [Google Scholar]
- 56.Dawid A, Skene A. Maximum Likelihood Estimation of Observer Error-Rates Using the EM Algorithm. Journal of the Royal Statistical Society. Series C (Applied Statistics) 1979;28:20–28. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.