Abstract
Propensity score methods are being increasingly used as a less parametric alternative to traditional regression to balance observed differences across groups in both descriptive and causal comparisons. Data collected in many disciplines often have analytically relevant multilevel or clustered structure. The propensity score, however, was developed and has been used primarily with unstructured data. We present and compare several propensity-score-weighted estimators for clustered data, including marginal, cluster-weighted and doubly-robust estimators. Using both analytical derivations and Monte Carlo simulations, we illustrate bias arising when the usual assumptions of propensity score analysis do not hold for multilevel data. We show that exploiting the multilevel structure, either parametrically or nonparametrically, in at least one stage of the propensity score analysis can greatly reduce these biases. These methods are applied to a study of racial disparities in breast cancer screening among beneficiaries in Medicare health plans.
Keywords: balance, multilevel, propensity score, racial disparity, treatment effect, unmeasured confounders, weighting
1 Introduction
Population-based observational studies often are the best methodology for studies of access to, patterns of, and outcomes from medical care. Observational data are increasingly being used for causal inferences, as in comparative effectiveness studies where the goal is to estimate the causal effect of alternative treatments on patient outcomes. In noncausal descriptive studies, a common goal is to conduct a controlled and unconfounded comparison of two populations, such as comparing outcomes among populations of different races or of patients treated in two different years while making the comparison groups similar with respect to the distributions of some covariates, such as baseline health status and diagnoses.
Whether the purpose of the study is descriptive or causal, comparisons between groups can be biased, however, when the groups are unbalanced with respect to confounders. Standard analytic methods adjust for observed differences between groups by stratifying or matching patients on a few observed covariates or by regression adjustments. But if groups differ greatly in observed characteristics, estimates of differences between groups from regression models rely on model extrapolations that can be sensitive to model misspecification [1]. Propensity score methods [2, 3] have been proposed as a less parametric alternative to regression adjustment to achieve balance in distributions of a large number of covariates in different groups, and have been widely used in a variety of disciplines, such as medical care, health policy studies, epidemiology, social sciences [e.g. 4, 5, and references therein]. These methods weight, stratify or match subjects according to their propensity for group membership (i.e. to receive treatment or to be in a minority racial group) to balance the distributions of observed characteristics across groups.
Propensity score methods were developed and have been applied in settings with unstructured data. However, data collected in many applied disciplines are typically clustered in ways that may be relevant to the analysis, for example by geographical area, treatment center (hospital or physician), or in the example we consider in this paper, health plan. The unknown mechanism that assigns subjects to clusters may be associated with measured subject characteristics that we are interested in (e.g., race, age, clinical characteristics), measured subject characteristics that are not of intrinsic interest and are believed to be unrelated to outcomes except through their effects on assignment to clusters (e.g., location), and unmeasured subject characteristics (e.g., unmeasured severity of disease, aggressiveness in seeking treatment).
Such clustering or multilevel structure raises several issues that have been known in the literature. For example, if clusters are randomly sampled, standard error calculations that ignore clustering are usually inaccurate. A more interesting set of issues arises because measured and unmeasured factors may create cluster-level variation in treatment quality and/or outcomes, which can be a source of confounding if correlated with group assignment at the cluster level [6]. Multilevel regression models that include fixed effects and/or random effects have been developed to give a more comprehensive description than non-hierarchical models provided for such data [e.g. 7]. Despite the increasing popularity of propensity score analyses and the vast literature regarding regional and provider variation in medical care and health policy research [8, 9], the implications of multilevel data structures for propensity score analyses have not been intensively studied, with a few exceptions [10, 11]. Arpino and Mealli [12] addressed this issue explicitly through extensive Monte Carlo simulations that illustrated the benefit of respecting the clustered structure in propensity score matching to protect against bias due to unmeasured cluster-level confounders.
In this article, we focus on propensity score weighting strategies, widely used in medical care, health policy and economics [13, 14, 15, 16]. Through analytical derivations and simulations, we show that ignoring the multilevel structure in propensity score weighting analysis can bias estimates. In particular, we investigate the performance of different modeling and weighting strategies under violation to unconfoundedness at the cluster level. In addition, we clarify the differences and connections between causal and unconfounded descriptive comparisons, and rigorously define a class of estimands for the latter, filling a gap in the literature. We focus on treatments assigned at the individual level. Discussions on treatment assigned at the cluster level (e.g., hospital, health care provider) can be found in [17, 18], among others.
Section 2 introduces our motivating example, a study of racial disparities in receipt of breast cancer screening. Section 3 introduces the propensity score, defines the estimands, and presents propensity-score-weighting analogues to some standard regression models for clustered data, including marginal, cluster-weighted and doubly-robust estimators. Section 4 analytically illustrates the bias caused by ignoring clustering in a simple scenario without observed covariates. Section 5 presents a comprehensive simulation study to examine the performance of the estimators under model misspecification due to observed and unobserved cluster-level covariates. We then apply the methods to the racial disparities study in Section 6. Section 7 concludes with a discussion.
2 Motivating application
Our motivating application is based on the HEDIS® measures of care provided by Medicare health plans. Each of these measures is an estimate of the rate at which a guideline-recommended clinical service is provided to the appropriate population. We obtained individual-level data from the Centers for Medicare and Medicaid Services (CMS) on breast cancer screening of women in these plans [19]. We focused on the difference between whites and blacks, excluding subjects of other races, for whom racial identification is unreliable in this dataset. We also restricted the analysis to plans with at least 25 eligible white enrollees and 25 eligible blacks, leaving 64 plans. To avoid domination of the results by a few very large plans, we drew a random subsample of size 3000 from each of the three large plans with more than 3000 eligible subjects, leaving a total sample size of 56,480.
In a simple comparison, 39.3% of eligible black women did not undergo breast cancer screening compared to 33.5% of white women. Suppose, however, that we are interested in comparing these rates for black and white women with similar distributions of as many covariates as possible. The unadjusted difference in receipt of recommended services ignores observed differences in individual (for example, age and eligibility for Medicaid) and cluster (geographic region, tax status, provider practice model) characteristics between black and white women. Standard propensity score analyses would account for these observed differences, but there may also be unobserved differences among plans related to quality. When such unmeasured confounders differ across groups but are omitted from the propensity score model, the ensuing analysis will fail to control for such differences. For example, analyses that ignore variations across the plans in proportions of minority enrollment might attribute these plan effects to race-based differences in treatment of similarly situated patients. Misspecification can also arise from assuming an incorrect functional form. Sensitivity to misspecification of the propensity score model for unclustered data was examined in [20]. Clustering widens the range of model choices in each step of a propensity-score analysis, as described in the next section.
Our goal is not to establish a causal relationship between race and health service utilization, but simply to assess the difference in the proportion undergoing breast cancer screening between whites and blacks, controlled for individual and plan level effects. In fact, race is not a “treatment” in the conventional sense of causal inference, because it is not manipulable [21]. The propensity score is a tool to balance the covariate distribution between groups for studies with either causal or non-causal purposes, and the methods discussed here are applicable in both settings.
3 Propensity score weighted estimators for multilevel data
3.1 Basics
To simplify, we focus on two-level structures. Consider a sample or population of n units, from cluster h (h = 1, …, H), each including nh units indexed by k = 1, …, nh, and n = Σh nh. Each unit belongs to one of two groups for which covariate-balanced comparisons are of interest, possibly defined by a treatment; in either case we will use the terms “treatment” and “control” to refer to the groups. Let Zhk be the binary variable indicating whether subject k in cluster h is assigned to the treatment (Z = 1) or the control (Z = 0). Also let Uhk be a vector of unit-level covariates, Vh be a vector of cluster-level covariates, and Xhk = (Uhk, Vh). For each unit, an outcome Yhk is observed. The propensity score is defined as e(X) = Pr(Z = 1 | X), the conditional probability of being in (treatment or descriptive) group Z = 1 given covariates X.
We differentiate between controlled descriptive comparisons and causal comparisons. In the descriptive case, “assignment” is to a nonmanipulable state defining membership in one of two groups (subpopulations), and the objective is an unconfounded comparison of the observed outcomes between the groups, e.g., comparing outcomes among populations of different races or of patients treated in two different years, but with balanced distributions of a selected set of covariates. In a causal comparison, assignment is to a potentially manipulable intervention and the objective is estimation of a causal effect, that is, comparison of the potential outcomes under treatment versus control in a common set of units, e.g., evaluating the treatment effect of a drug, therapy or policy which could be applied or withhold for members of a given population.
For a descriptive comparison, we define a general estimand—the population average controlled difference (ACD)—the difference in the means of Y in two groups with balanced covariate distributions:
| (1) |
where the outer expectation is with respect to the marginal distribution of X in the combined population. One could also define similar descriptive estimands over some subpopulations.
For causal comparisons, we adopt the potential outcome framework for causal inference [22]. Under the standard Stable Unit Treatment Value Assumption (SUTVA) [23], which states that the outcomes for each unit are unaffected by the treatment assignments of other units (whether within or across clusters), each unit has two potential outcomes Yhk(z) for z = 0, 1, corresponding to the two treatments. Only one of the two is observed for each unit, and the observed outcome Yhk can be expressed as Yhk = Yhk(1)Zhk + Yhk(0)(1 − Zhk).
A common causal estimand is the population average treatment effect (ATE):
| (2) |
Estimation of a causal effect from observed data is identified by assuming unconfoundedness (no unmeasured confounders), claiming that the treatment is effectively randomized within cells defined by the values of observed covariates, (Y (0), Y (1)) ⊥ Z|X. Under unconfoundedness, Pr(Y (z)|X) = Pr(Y|X,Z = z), so the causal estimand πATE equals the descriptive estimand πACD:
Alternative estimands, such as the population average treatment effect on the treated (ATT), 𝔼[Y (1) − Y (0)|Z = 1], may also be of interest, as in [12]. What is common across these analyses is that means of Y (1) and Y (0) are compared under the same hypothesized distribution of the covariates, as in (1).
Both descriptive and causal comparisons require the overlap assumption, 0 < e(X) < 1, which states that the study population is restricted to values of covariates for which there can be both control and treated units; otherwise the data cannot support an inference about comparisons of outcomes under the two group assignments. Treatment assignment mechanisms satisfying both overlap and nonconfoundedness are called strongly ignorable [2].
The utility of the propensity score resides in the fact that,
| (3) |
if unconfoundedness is assumed for the causal comparison. This estimator weights both groups to a common distribution of covariates, namely the marginal distribution of X in the combined population. Thus, the ACD or the ATE can be estimated by comparing weighted averages of the observed outcomes using the inverse-probability (Horvitz-Thompson or HT) weights whk = 1/e(Xhk) for units with Zhk = 1 and whk = 1/(1 − e(Xhk)) for units with Zhk = 0. It can readily be verified that this weighting balances, in expectation, the weighted distribution of covariates in the two groups. The validity of this method depends, however, on the correctness of the specification of the propensity score, which requires special consideration in clustered data.
3.2 Models for the propensity score
We consider three alternative propensity score models for clustered data, corresponding to different assumptions about the assignment mechanism. A marginal model uses cluster membership only as a link to observed cluster-level covariates. The propensity score thus is a function of the observed covariates, ehk = e(Xhk), as in the logistic model
| (4) |
Such a model yields a valid balancing score as long as the unobserved covariates are conditionally independent of treatment (group) assignment given the observed covariates.
A fixed effects model [24, 25] is augmented with a cluster-level main effect δh, as in the following logistic model:
| (5) |
The δh term absorbs the effects of both observed and unobserved cluster-level covariates Vh, protecting against misspecification due to cluster-level confounders. With maximum likelihood estimation, the observed and predicted numbers of treated cases within each cluster will agree, guaranteeing balance of the HT estimator on both observed and unobserved cluster level covariates. The fixed effects model estimates a balancing score without requiring knowledge of Vh, but might lead to larger variance than the propensity score (the coarsest balancing score) estimated under a correct model with fully observed Vh.
When there are many small clusters, the fixed effects model may lead to unstable propensity score estimates due to the large number of free parameters, an example of the Neyman-Scott incidental parameter problem [26], and the possibility of separation (representation of only one group) in some clusters. In the latter case, the overlap assumption would require exclusion of those clusters from the inferential population. An alternative is to assume a random effects model, augmenting (5) with a prior distribution on the cluster-specific main effects
| (6) |
More generally, the random effects may include random coefficients of some individual-level covariates. To estimate propensity scores from (6), one can plug in a point estimate, such as the posterior mode or the posterior mean of the inverse-probability weight. The distributional assumption on δh in the random effects model greatly reduces the number of parameters compared to the fixed effects model, and allows for “borrowing information” across clusters [24]. However, the random effects model does not guarantee balance within each cluster, due to the shrinkage of random effects toward zero, and therefore is somewhat reliant on inclusion of important cluster-level covariates Vh as regressors. Also, as Mundlak [25] noted, it would produce a biased estimate if the cluster-specific random effects are correlated with any of the covariates. Thus the random effects model represents a compromise between the marginal and fixed effects models, with results converging to those from a corresponding fixed effects model as the sample size per cluster increases.
The goodness of fit of these models can be checked by conventional diagnostics of covariate balance [3], checking the overall and within-cluster balance of the weighted distribution of covariates in the two groups.
3.3 Estimators for the ACD or the ATE
In general there are two types of propensity-score-weighted estimators for the ACD or the ATE, applying the inverse weights to either the observed outcomes (nonparametric estimators) [16], or the fitted outcomes from a parametric model (parametric estimators) as elaborated in Section 3.4. The multilevel data structure offers possibilities for several variations on these inverse-probability-weighted estimators, which are considered here.
A nonparametric marginal estimator is the difference of the weighted overall means of the outcome between the treatment and control groups, ignoring clustering,
| (7) |
where whk is the inverse-probability weight of subject k in cluster h based on the estimated propensity score (e.g., from one of the three models in Section 3.2) with whk = 1/êhk for units with Zhk = 1 and whk = 1/(1 − êhk) for units with Zhk = 0, and for z = 0, 1.
A nonparametric clustered estimator first estimates the ACD or the ATE within each cluster:
where for z = 0, 1, and then takes their mean weighted by the total weights in each cluster, :
| (8) |
The numerator and denominator of one of the terms of (8) will be zero for clusters where all units are assigned to the same group, violating the overlap assumption. To implement the clustered estimator with propensity scores estimated from a fixed effects model, one needs to exclude the clusters with nh0 = 0 or nh1 = 0. This may change the estimand to the ACD/ATE on the subpopulation with overlap in each cluster.
The standard errors of the nonparametric estimators can be obtained straightforwardly via the delta method. But our experience is that the delta method tends to underestimate the uncertainty, and we recommend to use the bootstrap where one obtains the bootstrap samples by resampling the clusters.
An attractive parametric weighted estimator is the doubly-robust (DR) estimator [e.g. 13, 14, 27]:
| (9) |
where
with Ŷz being the fitted (potential) outcome from an outcome model in group z. The name “doubly-robust” refers to the large sample property that π̂dr is a consistent estimator of π if either the propensity score model or the potential outcome model is correctly specified, but not necessary both. In large samples, if e is modeled correctly, π̂dr has smaller variance than the nonparametric inverse weighted estimators. If the potential outcome model is correctly specified, π̂dr may have larger variance than the direct regression estimator, but it provides protection when the model is misspecified. The standard error of the doubly-robust estimator can be estimated using the delta method which appears to work well in practice:
| (10) |
Similarly as for the nonparametric estimators, standard errors can also be estimated via the bootstrap. Note that here the standard error calculation does not take into account the uncertainty in estimating the propensity score. More discussions on this can be found in McCandless et al. [28].
3.4 Models for (potential) outcomes
We now consider several outcome models that can be used in the DR estimators. Note that for a causal analysis, under confoundedness these models translate to models for potential outcomes, which we do not elaborate separately. An additive marginal outcome model has the form
| (11) |
where , and γ is the constant treatment effect. Analogous to the marginal propensity model (4), the marginal outcome model assumes that the cluster effect on the outcomes is only through the covariates. The deeper connection is that the sufficient statistics that are balanced under the marginal propensity score estimator are the same that must be balanced to eliminate confounding differences under model (11), namely the treatment and control group means of X.
A fixed-effects outcome model adjusts for cluster-level main effects and covariates:
| (12) |
where ηh is the cluster-specific main effect. Under this model, all information is obtained by comparisons within clusters, since the ηh term absorbs all between-cluster information. The corresponding random effects outcome model is:
| (13) |
with . A natural extension is to assume a random slope for β and/or a random additive treatment effect, replacing γ by cluster-specific treatment effect γh with (ηh, γh)′ ~ N(0, Σηγ).
One could also consider a random effects model with adaptive centering for the outcome, by centering the treatment indicator (Zhk − Z̄h) as well as the covariates in each cluster. Raudenbush [29] comprehensively discussed the benefits of such a model in directly estimating causal effects.
Interactions between covariates and treatment can be added to models (11), (12) and (13) to allow nonadditive relationships. Analogous generalized linear models (GLM) or generalized linear mixed models (GLMM) can be used for binary or ordinal outcomes.
4 Large-sample properties with unobserved cluster-level confounding
In this section, we investigate the large-sample bias of these estimators under a data generating model representing intra-cluster influence that causes violations of unconfoundedness, in a simple setting with no observed covariates. Let nhz denote the number of subjects with Z = z in cluster h; and . We assume a Bernoulli assignment mechanism with varying rates by cluster:
| (14) |
We assume a continuous outcome model with cluster-specific random intercepts ηh and constant treatment effect π,
| (15) |
where , and τ is the coefficient of the cluster-specific proportion treated dh = nh1 / nh. This model could result from common unmeasured cluster traits that affect both treatment assignment and outcome. In a causal comparison, this could also result from violation to the SUTVA and τ measures the magnitude of the influence (contamination) within cluster. In either case, it is easy to show the ACD or the ATE equals the constant π.
Under the marginal propensity score model, êhk = n1/n is the same for every subject. Let denote the marginal estimator (7), where the subscriptma indicates using the marginal model for the propensity score and superscriptma indicates using the marginal estimator for π. Then
| (16) |
where
that is, the weighted sample variance of the {dh} divided by its maximum possible value. The maximum is attainable if each cluster is assigned to either all treatment or all control, corresponding to a cluster randomized design where the cluster-level ACD or ATE is π + τ. The second and third terms of (16) have expectation zero under the model and approach zero as the number of clusters approaches infinity under mild regularity conditions on nh1 and nh2. Therefore, under the generating model (14) and (15), the large sample bias of the marginal estimator with propensity score estimated from the marginal model is τ𝒱/𝒱0. Heuristically, τ measures the variation in the outcome generating mechanism between clusters and 𝒱/𝒱0 measures the variation in the treatment assignment mechanism between clusters, both of which are ignored in . Similar result was established in the sociology literature [6].
We next consider estimation when clustering information is taken into account in both steps. Using the fixed effects model (5), the estimated propensity score is êhk = nh1/nh. Then the clustered estimator (8) is , where the subscript fe refers to the fixed effects model for the propensity score, and superscript cl refers to using the clustered estimator for π, given by
| (17) |
which converges to π as H and nh increase. Simple calculation shows that the clustered weighted estimator combining the marginal propensity score model with the clustered estimator, , is equivalent to that in (17) and thus also consistent. Furthermore, the marginal estimator with propensity score estimated from the fixed effects model, , is equivalent to (17) only under a balanced design (clusters of equal size). Under an unbalanced design, the estimator remains consistent under the standard regularity condition of being bounded as H goes to infinity, but its small-sample behavior can be quite different.
In summary, in this simple case with violations of standard propensity score assumptions due to unobserved cluster effects, ignoring the clustered structure in both the propensity score and potential outcome models induces bias in estimating the ACD or the ATE; exploiting the structure in at least one of the models gives consistent estimates.
5 Simulation studies
The asymptotics of the previous section assume cluster sample sizes nh going to infinity, and thus do not apply to studies with a large number of small clusters, corresponding to asymptotics in which nh is constant while the number of clusters grows proportionally to the number of total observations. In particular, in the fixed-effects model, the MLEs for δh are inconsistent (due to the fixed number of observations per cluster) and the MLE of α is also inconsistent due to the growing number of cluster-specific intercepts, an example of the Neyman-Scott problem. However, as the primary role of propensity score in the HT estimator is to balance covariates between groups, estimators with propensity scores obtained from a fixed effects model may still give appropriate results in the presence of large number of small clusters, despite the potential issue of consistency. Below we conduct simulations to examine the performance of the proposed methods under various combinations of cluster sample size and number of clusters. Moreover, the simulations are designed to investigate the impact of an unmeasured cluster-level confounder or controlled covariate to the proposed methods.
5.1 Simulation design
The simulation design is similar to but more general than that in Arpino and Mealli [12]. We assume both treatment assignment and outcome generating mechanisms follow two-level random effects models with two individual-level covariates U1, U2 and a cluster level covariate V. Specifically, the treatment assignment follows
| (18) |
where Xhk = (U1,hk, U2,hk, Vh), α = (α1, α2, α3)′ are the coefficients for the fixed effects, and δh ~ N(0, 1) are the cluster-specific random intercepts. We fix α1 = −1, α2 = −.5, and vary α3 = −1 or 1 to give low (around .2) or medium (around .5) overall rates of treatment assignment, respectively. The (potential) outcomes are generated from random effects models as (12), with an extra interaction term between treatment and V :
| (19) |
where ηh ~ N(0, 1) are the cluster-specific random intercepts, β = (β1, β2, β3)′ are the coefficients of the covariates, κ is the coefficient of the interaction, and γh ~ N(0, 1) are the cluster-specific random slopes of treatment. We set κ = 2 and β = (1, .5, β3), while changing β3 to control the magnitude of the effect of V on the outcome.
The individual-level continuous covariate U1 is simulated from N(1, 1) and binary U2 from Bernoulli(.4). The cluster-level covariate V is generated in two ways that are plausible in real applications: (i) uncorrelated with U, with V ~ N(1, 2); (ii) correlated with the cluster-specific intercept in the propensity score model, with Vh = 1 + 2δh + u, where u is an error term. An extreme case of (ii) is that V is a linear function of the cluster-average propensity score, when u ≈ 0. Here we let u ~ N(0, 1). Case (ii) introduces an interaction between treatment and cluster-level random effects. This is expected to cause differences between the fitting of fixed and random effects models when V is omitted, because generally the former cannot readily accommodate the interaction while the later with random slopes for Z can. Another common situation not examined here is that V is correlated with U; omitting V in the analysis in that case is expected to lead to smaller bias than case (i), as including U as a covariate partially compensates for excluding V.
We compare the three propensity score models (4), (5) and (6) in Section 3.2, all fitted with only the individual-level covariates U1, U2, omitting the cluster-level covariate V. We also estimate the propensity score by the true model (18), referred to as the “benchmark model”. With the propensity score estimated from each of these models, we calculate the ATE (or the ACD) by the marginal (7), clustered (8) and DR (9) estimators. For the DR estimators, we fit the three potential outcome models (11), (12) (with cluster-specific intercepts) and (13) (with random intercepts and random slopes for z) in Section 3.4, each fitted with only the individual-level covariates U1, U2, omitting the cluster-level covariate V. As a benchmark, we also estimate the potential outcomes by the true model (19). In total, we compare four models for propensity score and six ATE/ACD estimators (including four DR estimators), giving twenty-four combinations.
Under a two-level balanced design, we simulate from three combinations of number of clusters H and cluster size nh: (1) H = 30, nh = 400, both of which are approximately half of the corresponding numbers in our real application; (2) H = 200, nh = 20; and (3) H = 400, nh = 10, representing a moderate and more extreme cases of large numbers of small clusters. We have also simulated unbalanced designs, results of which are similar to those from the balanced designs and thus are not elaborated here.
Under each simulation scenario, 500 replicates from models (18) and (19) are generated. The random effects models are fitted using the lmer command in the lme4 package in R2.13.2 [30]. For each simulated dataset, we calculate the average absolute bias, the root mean square error (RMSE), and coverage of the 95% confidence interval (CI) of each of the twenty-four estimators for π. The true value of π is calculated by from the simulated units. This is the sample ATE rather than the population ATE which equals κ𝔼(Vh) + 𝔼(γh) = 4, but the difference between the two is usually negligible given the sample sizes considered here.
The 95% confidence intervals for the nonparametric estimators are obtained via the parametric bootstrap approach π̂ ± 1.96σ̂bs, with σ̂bs being the bootstrap standard error, while the standard errors for the DR estimators are obtained via the delta method as in formula (10).
5.2 Results
Table 1 presents the absolute bias, RMSE and coverage of the 95% confidence interval of the estimators in the simulations under the three combinations of H, nh. In each case, α3 = 1 giving an average propensity score of .5 and β3 = 4 giving a large effect of V on the outcomes. In the second and third scenarios, there are on average 20 and 40, respectively, clusters in which all units are assigned to the same treatment. Such non-overlapping clusters are excluded when the cluster-weighted estimates are calculated, yielding a slightly different estimand from the other methods.
Table 1.
Average absolute bias (bias), root mean square error (rmse) and coverage of the 95% confidence interval (%) of different estimators in simulations with V ~ N(1, 2), α3 = 1, β3 = 2, under three combinations of H and nh. Different rows correspond to different models to estimate propensity score, different columns correspond to different outcome models.
| Propensity- | nonparametric1 | doubly-robust | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| score model | marginal | clustered2 | benchmark | marginal | fixed effects | random effects | |||||||||||||
| bias | rmse | % | bias | rmse | % | bias | rmse | % | bias | rmse | % | bias | rmse | % | bias | rmse | % | ||
|
H = 30 nh = 400 |
benchmark | .21 | .31 | 96.4 | .07 | .10 | 99.4 | .029 | .037 | 98.2 | .23 | .33 | 95.8 | .10 | .13 | 95.2 | .029 | .037 | 97.8 |
| marginal | 7.19 | 7.40 | 0 | .27 | .32 | 98.2 | .023 | .029 | 97.4 | 4.46 | 4.51 | 0 | .28 | .34 | 12.6 | .024 | .030 | 97.4 | |
| fixed | .19 | .27 | 99.2 | .07 | .10 | 100 | .030 | .039 | 97.8 | .23 | .35 | 96.4 | .10 | .14 | 96.2 | .030 | .039 | 97.6 | |
| random | .26 | .36 | 96.4 | .07 | .09 | 100 | .029 | .037 | 98.2 | .25 | .34 | 94.6 | .10 | .13 | 94.8 | .029 | .037 | 97.8 | |
|
H = 200 nh = 20 |
benchmark | .84 | .91 | 43.2 | .16 | .19 | 99.0 | .041 | .052 | 97.8 | .82 | .88 | 42.0 | .13 | .19 | 92.6 | .044 | .055 | 96.2 |
| marginal | 7.38 | 7.40 | 0 | .29 | .32 | 72.4 | .036 | .045 | 98.8 | 4.46 | 4.48 | 0 | .16 | .20 | 28.8 | .046 | .057 | 94.4 | |
| fixed | .91 | .99 | 47.4 | .12 | .15 | 100 | .046 | .058 | 98.2 | .67 | .75 | 70.6 | .14 | .18 | 94.2 | .048 | .060 | 96.4 | |
| random | 2.09 | 2.11 | 0 | .13 | .16 | 99.2 | .040 | .050 | 98.2 | 1.59 | 1.61 | 0 | .12 | .15 | 81.4 | .044 | .054 | 96.6 | |
|
H = 400 nh = 10 |
benchmark | .97 | 1.02 | 22.0 | .20 | .23 | 87.8 | .043 | .053 | 97.6 | 1.06 | 1.10 | 10.8 | .13 | .17 | 89.8 | .052 | .065 | 94.6 |
| marginal | 7.48 | 7.50 | 0 | .31 | .33 | 42.0 | .038 | .048 | 98.4 | 4.49 | 4.51 | 0 | .16 | .18 | 30.6 | .067 | .081 | 85.4 | |
| fixed | 1.57 | 1.63 | 6.8 | .12 | .15 | 96.0 | .047 | .059 | 96.8 | 1.25 | 1.29 | 4.2 | .15 | .18 | 82.6 | .055 | .068 | 94.8 | |
| random | 3.07 | 3.09 | 0 | .17 | .20 | 89.2 | .040 | .051 | 97.6 | 2.32 | 2.33 | 0 | .13 | .16 | 62.6 | .056 | .069 | 90.8 | |
Standard errors and confidence intervals for nonparametric estimators are obtained via the bootstrap.
Clusters with all units assigned to one treatment are excluded.
Several consistent patterns emerge from the simulations. First, the estimators that ignore clustering in both propensity score and outcome models (i.e., marginal propensity score with marginal nonparametric or parametric outcome model) have much larger bias (over 100%) and RMSE than all the others. In general, considering clustering in at least one stage greatly improves the estimates in bias and MSE, consistent with the conclusions of Arpino and Mealli [12] in propensity score matching analysis.
Second, the choice of the outcome model appears to have a larger impact on the results than the choice of the propensity-score model. In the presence of unmeasured confounders, ignoring the multilevel structure in the outcome model generally leads to much worse estimates than ignoring it in the propensity score model. For example, in the nh = 400 simulation condition, bias with the nonparametric marginal outcome model ranges from .15 to .17 for the three clustered propensity score models (differences among propensity-score models became more pronounced at smaller cluster sizes). With the marginal propensity score model, bias ranges from .28 for the fixed-effects outcome model to only ≤ .024 for the benchmark and random-effects outcome models, with intermediate levels of bias for the nonparametric cluster-weighted estimator. With the best (benchmark or random effects) outcome models, the choice of propensity-score model had little effect (with nh = 400), while with any propensity-score model the choice of outcome model was important. This result may not generalize to situations in which there are larger differences between groups.
Third, among the DR estimators, those using the benchmark or random effects outcome model perform the best, with virtually identical bias, RMSE and coverage. Thus, inclusion of the random effect protects against the misspecification due to omission of the cluster-level confounder in the benchmark model. The DR estimators with the fixed effects outcome model were more biased, while the ones with the marginal outcome model perform the worst. For example, in the nh = 400 simulation condition, the absolute biases are ≤ .029 for the benchmark and random-effects outcome models, ≥ .10 for the fixed-effects outcome model, and ≥ .23 for the marginal outcome model. The under-performance of the fixed effects outcome model is partly due to the extra uncertainty introduced by estimation of many parameters, as is evident from the steady drop in performance when the number of cluster increases. However, the comparison between the random and fixed effects models here may be unfair, as the outcomes are generated and fitted under a random effects model with the same (normal) error distribution. The fixed effects model might be more robust against random effects distributions that are far from normality. More broadly, all of the parametric outcome models in this simulation were specified with knowledge of the correct individual-level predictors and specification. Hence they do not illustrate one of the important benefits of propensity-score analysis, the ability to explore specification of the propensity-score model without the biasing potential of specification search in the outcome model [2]. Such a benefit is evident in the next point.
Fourth, given the same propensity score model, the nonparametric cluster-weighted estimator generally outperform the DR estimator with a fixed effects outcome model in terms of bias, RMSE and coverage. For example, in Table 1, with nh = 400 and the benchmark propensity score model, bias, RMSE and coverage with the former were .07, .10, and 99.4%, respectively, comparing to .10, .13 and 95.2%, respectively, with the latter. The advantage of the cluster-weighted estimator is even more pronounced when the cluster-level covariate is correlated with the cluster-specific treatment assignment (Table 2). Here the fixed effects outcome model is in fact misspecified. This highlights the main strength of the propensity score methods, protection against misspecification of the outcome model. The propensity score methods (e.g., the DR estimators) may increase the variance comparing to a direct regression estimator when a close-to-truth outcome model specification is known. But a good outcome model is often hard to obtain in practice, especially in complex observational studies. In such situations, the non-parametric propensity score estimators provide a more robust alternative to estimate the ATE or the ACD.
Table 2.
Average absolute bias (bias) and root mean square error (RMSE) of different estimators, with V = 1 + 2δh + u, u ~ N(0, 1), α3 = 1, and β3 = 2. Different rows correspond to different models to estimate propensity score, different columns correspond to different outcome models.
| Propensity- | nonparametric1 | doubly-robust | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| score model | marginal | clustered2 | benchmark | marginal | fixed effects | random effects | |||||||||||||
| bias | rmse | % | bias | rmse | % | bias | rmse | % | bias | rmse | % | bias | rmse | % | bias | rmse | % | ||
|
H = 30 nh = 400 |
benchmark | 1.53 | 2.28 | 88.0 | .34 | .53 | 99.8 | .074 | .110 | 91.6 | 1.35 | 1.86 | 92.0 | .57 | .91 | 90.2 | .075 | .110 | 91.0 |
| marginal | 15.0 | 15.3 | 0 | .58 | .72 | 78.0 | .046 | .059 | 86.0 | 9.40 | 9.54 | 0 | .58 | .73 | 5.2 | .048 | .064 | 85.4 | |
| fixed | 1.25 | 1.63 | 86.0 | .29 | .44 | 99.2 | .069 | .093 | 91.2 | 1.21 | 1.56 | 86.6 | .46 | .63 | 89.0 | .070 | .096 | 90.8 | |
| random | 1.61 | 1.96 | 74.0 | .28 | .42 | 99.6 | .063 | .084 | 92.0 | 1.40 | 1.70 | 73.0 | .41 | .54 | 84.8 | .065 | .087 | 91.2 | |
|
H = 200 nh = 20 |
benchmark | 2.14 | 2.87 | 72.0 | .61 | .85 | 95.8 | .084 | .155 | 95.0 | 2.33 | 4.99 | 95.0 | .77 | 2.77 | 92.0 | .095 | .240 | 95.6 |
| marginal | 15.8 | 15.9 | 0 | .34 | .43 | 66.0 | .048 | .060 | 99.2 | 9.51 | 9.53 | 0 | .29 | .37 | 18.0 | .075 | .091 | 90.6 | |
| fixed | 4.84 | 4.93 | 0 | .26 | .32 | 94.2 | .059 | .075 | 97.4 | 3.82 | 3.81 | 0.8 | .31 | .39 | 76.6 | .071 | .089 | 95.0 | |
| random | 6.10 | 6.15 | 0 | .23 | .29 | 93.8 | .054 | .068 | 98.2 | 4.72 | 2.67 | 0 | .28 | .35 | 66.4 | .069 | .086 | 94.0 | |
|
H = 400 nh = 10 |
benchmark | 2.51 | 3.42 | 48.0 | .49 | .80 | 91.0 | .090 | .150 | 94.4 | 2.46 | 4.30 | 94.0 | .77 | 1.57 | 90.2 | .107 | .158 | 92.8 |
| marginal | 15.7 | 15.8 | 0 | .40 | .48 | 40.4 | .046 | .058 | 98.8 | 9.47 | 9.48 | 0 | .24 | .29 | 21.0 | .106 | .123 | 77.0 | |
| fixed | 6.47 | 6.51 | 0 | .19 | .24 | 92.6 | .052 | .067 | 98.2 | 4.88 | 4.91 | 0 | .24 | .30 | 68.0 | .086 | .105 | 87.4 | |
| random | 7.91 | 7.93 | 0 | .21 | .25 | 83.6 | .048 | .061 | 98.6 | 5.88 | 5.90 | 0 | .22 | .27 | 51.0 | .089 | .107 | 84.6 | |
Standard errors and confidence intervals for nonparametric estimators are obtained via the bootstrap.
Clusters with all units assigned to one treatment are excluded.
Finally, with smaller clusters (holding total sample size constant), performance decreases considerably for all the estimators. The largest drop is observed in the nonparametric marginal estimator (e.g., bias is ≤ .21 when nh = 400, H = 30, but increases to ≥ .97 when nh = 10, H = 400 with the benchmark propensity score) and the DR estimators with the marginal outcome model (e.g., bias is ≤ .23 when nh = 400, H = 30, but increases to ≥ 1.06 when nh = 10, H = 400). Nonetheless, the DR estimators with the benchmark or random effects outcome model maintain their superiority over other estimators as well as their coverage at nominal level regardless of the propensity score model. Considering that H = 400, nh = 10 is a quite extreme example of “large number of small clusters”, these results support the applicability of the DR estimators with a random effects outcome model in such settings. The success of this model may be partially due to its estimation using a penalized likelihood, which mitigates inconsistency in estimation of α.
We also assessed the effect on the performance of the various estimators of doubling the coefficient β3 of cluster-level covariate V in the true outcome model from 2 to 4. Comparing to Table 1, only the nonparametric marginal estimators and the DR estimators with the marginal outcome model were affected, giving nearly doubled biases and RMSEs, while all other estimators performed nearly as before.
The simulations with low average propensity score (Z̄ ≈ .2 with α3 = −1) displayed very similar patterns as the above, but as there were more non-overlapping clusters, performance of the nonparametric cluster-weighted estimator and the DR estimators with fixed effects outcome model deteriorated rapidly with shrinking cluster size.
Simulation results with V correlated with the cluster-specific random intercept in propensity score (setting (ii) in Section 5.1) appear in Table 2. While the patterns across the estimators remain similar to those observed in the previous simulations, much larger biases and MSEs and lower coverages are observed in all the estimators. For example, in the nh = 400 condition, with the benchmark propensity score model, biases of the cluster-weighted estimator, the DR estimator with the benchmark outcome model, and the DR estimator with the fixed effects outcome model are .34, .074, and .57 respectively, comparing to .07, .029, and .10 respectively of the same estimators when V is uncorrelated with δh.
6 Application
We applied our methods to the racial disparity study introduced in Section 2. The individual-level covariates Uhk considered include two indicators of age category (70-80 years, >80 years with reference group 65-69 years; eligibility for Medicaid (1=yes); neighborhood status indicator (1=poor). The plan-level covariates Vh include nine geographical region indicators, tax status (1=for-profit), the practice model of providers (1= staff or group model; 0= network-independent practice association model), and affiliation (1= national; 2= Blue Cross/ Blue Shield; 3= independent). The outcome Y is a binary variable equal to 1 if the enrollee underwent breast cancer screening and 0 otherwise, and the “treatment” z is race (1= black, 0= white).
Since race is not manipulable, the objective of this study is a controlled descriptive comparison. The ACD is the difference between white and black screening rates among patients with characteristics X (implicitly smoothed by models), averaged over the distribution of X in the combined black and white populations. There may be interest in a variety of estimators that control for different sets of covariates. For example, if X only contains individual level covariates, we interpret the ACD as the difference between groups controlled for differences in these individual characteristics such as age or poverty. Including V in the analysis controls for differences in treatment that result from differences in the types of plans in which the two groups enroll. Similarly, balancing on cluster membership accounts for unobserved differences in the quality of health plans that enroll minorities and provides an estimate of differences in treatments between minorities and whites within individual health plans. In the ensuing analyses, we control for all covariates to illustrate their effects and for consistency with the original study [19], although by some definitions these would not all be controlled for in a policy-oriented disparities calculation [31].
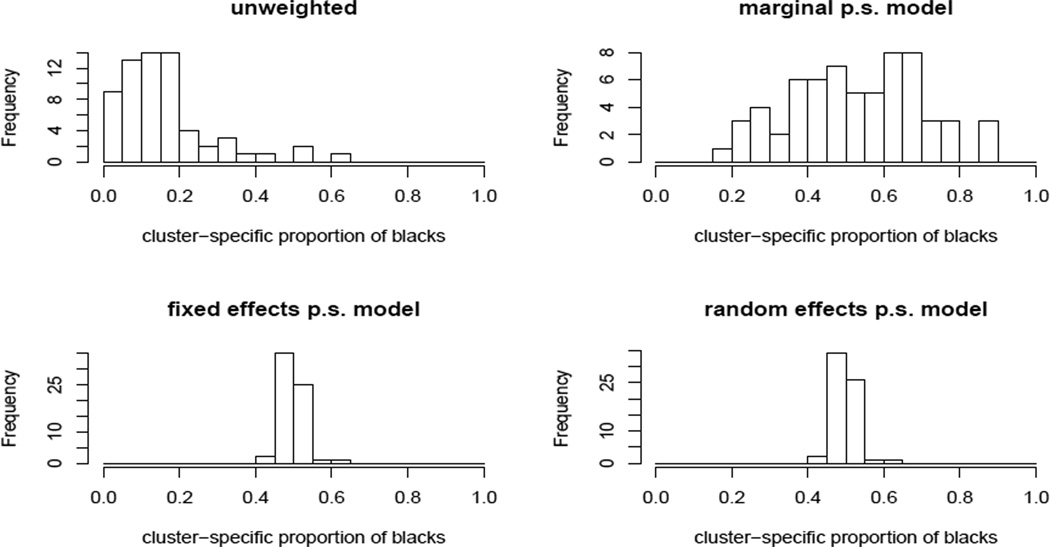
We first estimated the propensity score using the three models introduced in Section 3.2 with all the above covariates included. All models suggest that living in a poor neighborhood, being eligible for Medicaid and enrollment in a for-profit insurance plan are significantly associated with black race. The distributions of the estimated propensity scores for blacks and whites from the marginal model are quite different from those from the random and fixed effects models, which are similar to each other. Inverse probability weighting using a well-estimated propensity score should balance the cluster membership between races. Figure 1 shows histograms of the proportion of black enrollees in each cluster, unweighted and weighted using propensity scores estimated from each model. These proportions vary substantially when unweighted or weighted using the propensity score from the marginal model, but are tightly clustered around 50% when weighted using the fixed or random effects models. Thus, only the latter models provide balance on unmeasured characteristics associated with cluster assignment.
Figure 1.
Histogram of cluster-specific proportions of the weighted numbers of black enrollees using propensity scores estimated from different models. Values close to 0.5 indicate good balance in cluster membership between races.
Using the estimated propensity score, we estimate racial disparity in breast cancer screening among the elder women participating Medicare health plans by the estimators in Section 3.3. Since the outcome is binary, for the DR estimators, we use the logistic regression models corresponding to the three outcome models in Section 3.4 in combination with each of the three propensity score models. Table 3 displays the point estimates with bootstrap standard errors.
Table 3.
Adjusted difference in percentage with standard error (in parenthesis) in the proportion of getting breast cancer screening between blacks and whites. Different rows correspond to different propensity score models and different columns correspond to different outcome models.
| weighted | doubly-robust | ||||
|---|---|---|---|---|---|
| marginal | clustered | marginal | fixed | random | |
| marginal | −4.96 (.79) | −1.73 (.83) | −4.43 (.85) | −2.15 (.41) | −1.65 (.43) |
| fixed | −2.49 (.92) | −1.78 (.81) | −1.93 (.82) | −2.21 (.42) | −1.96 (.41) |
| random | −2.56 (.91) | −1.78 (.82) | −2.00 (.44) | −2.22 (.39) | −1.95 (.39) |
As in the simulations we observed few differences across estimators that account for clustering in at least one stage of the analysis. The DR estimates have smaller standard errors because some variation is explained by covariates in the outcome models. All estimators show the rate of receipt breast cancer screening is significantly lower among blacks than among whites with similar characteristics. Accounting for differences in individual and plan level covariates, but not plan membership, we estimate the rate of screening for breast cancer is 5 percentage points lower in blacks compared to whites. That is, among the elders who participate in Medicare health plans, blacks on average have a significantly lower rate of breast cancer screening than whites, after adjusting for age, geographical region, some socioeconomic status variables and observed health plan characteristics. Accounting for plan membership in either stage of the analysis decreases this difference by about half, suggesting that approximately half the magnitude of the racial difference in breast cancer screening rates in this population is a result of black women enrolling in plans with low screening rates due to factors unobserved in his study and half results from lower probability of black women undergoing screening within each plan.
7 Concluding Remarks
The propensity score is a powerful tool to achieve balance in distributions of covariates in different groups, for both causal and descriptive comparisons. Since they were first proposed in 1983, propensity score methods have gained increased popularity in observational studies in multiple disciplines. In medical care and health policy research, data with hierarchical structure are the norm rather than the exception. However, despite the wide appreciation of propensity score methods among both statisticians and health policy researchers, only a limited literature deals with the methodological issues of propensity score methods in the context of multilevel data. In this paper, we first clarified the differences and connections between non-causal (descriptive) and causal studies, arguing that propensity score methods are applicable to both. We then compared three models for estimating the propensity score and three types of propensity-score-weighting estimators for the ATE or the ACD for multilevel data. Consequences of the violation to the key unconfoundedness assumption in propensity score weighting analysis of multilevel data were explored using both analytical derivations and Monte Carlo simulations.
In summary, for multilevel data, ignoring the multilevel structure in both stages of the propensity-score-weighting analysis leads to severe bias for estimating the ATE or the ACD, in the presence of unmeasured confounders, while exploiting the multilevel structure, either parametrically or nonparametrically, in at least one stage can greatly reduce the bias. In complex multilevel observational data, correctly specifying the outcome model may sometimes be challenging. In such situations, propensity score methods provide a more robust alternative to regression adjustment.
Individuals in the same cluster might influence each other’s treatment assignment or outcome, particularly in applications involving social networks, behavioral outcomes or infectious disease [32, 33]. Such interference may entail violations of SUTVA, introducing cluster-level effects even when there are no unmeasured cluster-level confounders. We have shown that accounting for clustering in propensity score analyses can account for violations that occur at the cluster level. However, more than one level of clustering may be relevant. For example, high-volume surgeons may have improved outcomes that would not be accounted for in an analysis that balances on treating hospital but not surgeon. In addition, in some situations there may be direct interest in spill-over effects, such as in volume-outcome studies. Hong and Raudenbush [34] described the use of a two-stage propensity score model to estimate the propensity for elementary schools to retain low performing kindergarten students and then the propensity for students nested within schools to be retained. These authors relax SUTVA and allow the effectiveness of retention to vary according to how many peers within a child’s school were also retained.
Propensity score weighting without common support can lead to bias. As noted by a reviewer, stratification on the estimated propensity score can reveal regions in the covariate space lacking common support, which should be removed from the causal or descriptive comparison. Stratification also offers some protection against bias arising from the misspecification of the propensity model [35]. A procedure that may combine the virtues of weighting and stratification is to first stratify on the propensity score, then exclude the units (or clusters) without common support, then compute the weighted estimators by stratum, and finally combine the stratum-specific estimates to produce the overall estimate. An interesting topic would be the implication of multilevel structure on such hybrid procedures.
These issues are among a range of open questions remained to be explored. Further systematic research efforts are desired to shed insight to the methodological issues and to provide guidelines for practical applications.
Acknowledgements
This work was partially funded by U.S. NSF grant SES-1155697, grant 138255 of the Academy of Finland, and U.S. National Cancer Institute (NCI) grant to the Cancer Care Outcomes Research and Surveillance (CanCORS) Consortium (U01 CA093344). We thank the associate editor and two reviewers for constructive comments, and Fabrizia Mealli for helpful discussions.
References
- 1.Rubin D. Using multivariate matched sampling and regression adjustment to control bias in observational studies. Journal of the American Statistical Association. 1979;74:318–324. [Google Scholar]
- 2.Rosenbaum P, Rubin D. The central role of the propensity score in observational studies for causal effects. Journal of the Royal Statistical Society: Series B. 1983;70(1):41–55. [Google Scholar]
- 3.Rosenbaum P, Rubin D. Reducing bias in observational studies using subclassification on the propensity score. Journal of the American Statistical Association. 1984;79:516–524. [Google Scholar]
- 4.D’Agostino R. Tutorial in biostatistics: propensity score methods for bias reduction in the comparisons of a treatment to a non-randomized control. Statistics in Medicine. 1998;17:2265–2281. doi: 10.1002/(sici)1097-0258(19981015)17:19<2265::aid-sim918>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 5.Rosenbaum P. Observational Studies. New York: Springer; 2002. [Google Scholar]
- 6.Firebaugh G. Rule for inferring individual-level relationships from aggregate data. American Sociological Review. 1978;43:557–572. [Google Scholar]
- 7.Gatsonis C, Normand S, Liu C, Morris C. Geographic variation of procedure utilization: a hierarchical model approach. Medical Care. 1993;31:YS54–YS59. doi: 10.1097/00005650-199305001-00008. [DOI] [PubMed] [Google Scholar]
- 8.Nattinger A, Gottilieb M, Veum J, Yahnke D, Goodwin J. Geographic variation in the use of breast-conserving treatment for breast cancer. New England Journal of Medicine. 1992;326:1102–1127. doi: 10.1056/NEJM199204233261702. [DOI] [PubMed] [Google Scholar]
- 9.Farrow D, Samet J, Hunt W. Regional variation in survival following the diagnosis of cancer. Journal of Clinical Epidemiology. 1996;49:843–847. doi: 10.1016/0895-4356(96)00176-x. [DOI] [PubMed] [Google Scholar]
- 10.Lingle J. Evaluating the performance of propensity scores to address selection bias in a multilevel context: A monte carlo simulation study and application using a national dataset. Educational Policy Studies Dissertations, Paper 56. 2009 [Google Scholar]
- 11.Su YS, Cortina J. What do we gain? combining propensity score methods and multilevel modeling. APSA 2009 Toronto Meeting Paper. 2009 [Google Scholar]
- 12.Arpino B, Mealli F. The specification of the propensity score in multilevel observational studies. Computational Statistics and Data Analysis. 2011;55:1770–1780. [Google Scholar]
- 13.Robins J, Rotnitzky A, Zhao L. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association. 1995;90(429):106–121. [Google Scholar]
- 14.Robins J, Rotnitzky A. Semiparametric efficiency in multivariate regression models with missing data. Journal of the American Statistical Association. 1995;90(429):122–129. [Google Scholar]
- 15.Hirano K, Imbens G. Estimation of causal effects using propensity score weighting: An application to data on right heart catheterization. Health Services & Outcomes Research Methodology. 2001;2:259–278. [Google Scholar]
- 16.Hirano K, Imbens G, Ridder G. Efficient estimation of average treatment effects using the estimated propensity score. Econometrica. 2003;71:1161–1189. [Google Scholar]
- 17.Oakes J. The (mis)estimation of neighborhood effects: causal inference for a practicable social epidemiology. Social Science and Medicine. 2004;58:1929–1952. doi: 10.1016/j.socscimed.2003.08.004. [DOI] [PubMed] [Google Scholar]
- 18.VanderWeele T. Ignorability and stability assumptions in neighborhood effects research. Statistics in Medicine. 2008;27:1934–1943. doi: 10.1002/sim.3139. [DOI] [PubMed] [Google Scholar]
- 19.Schneider E, Zaslavsky A, Epstein A. Racial disparities in the quality of care for enrollees in medicare managed care. Journal of the American Medical Association. 2002;287(10):1288–1294. doi: 10.1001/jama.287.10.1288. [DOI] [PubMed] [Google Scholar]
- 20.Zhao Z. Sensitivity of propensity score methods to the specifications. Economics Letters. 2008;98(3):309–319. [Google Scholar]
- 21.Holland P. Statistics and causal inference. Journal of the American Statistical Association. 1986;81:945–960. [Google Scholar]
- 22.Rubin D. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66(1):688–701. [Google Scholar]
- 23.Rubin D. Comment on ‘Randomization analysis of experimental data: The Fisher randomization test‘ by D. Basu. Journal of the American Statistical Association. 1980;75:591–593. [Google Scholar]
- 24.Hausman J. Specification tests in econometrics. Econometrica. 1978;46(6):1251–1271. [Google Scholar]
- 25.Mundlak Y. On the pooling of time series and cross section data. Econometrica. 1978;46(1):69–85. [Google Scholar]
- 26.Neyman J, Scott E. Consistent estimation from partially consistent observations. Econometrica. 1948;16:1–32. [Google Scholar]
- 27.Bang H, Robins J. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61:962–972. doi: 10.1111/j.1541-0420.2005.00377.x. [DOI] [PubMed] [Google Scholar]
- 28.McCandless L, Gustafson P, Austin P. Bayesian propensity score analysis for observational data. Statistics in Medicine. 2009;15:94–112. doi: 10.1002/sim.3460. [DOI] [PubMed] [Google Scholar]
- 29.Raudenbush S. Adaptive centering with random effects: An alternative to the fixed effects model for studying time-varying treatments in school settings. Journal of Education Finance and Policy. 2009;4(4):468–491. [Google Scholar]
- 30.Bates D, Maechler M, Bolker B. lme4: Linear mixed-effects models using s4 classes 2011. URL http://cran.r-project.org, R Package Version 0.999375-42. [Google Scholar]
- 31.McGuire T, Alegria M, Cook B, Wells K, Zaslavsky A. Implementing the Institute of Medicine definition of disparities: An application to mental health care. Health Services Research. 2006;41:1979–2005. doi: 10.1111/j.1475-6773.2006.00583.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rosenbaum P. Interference between units in randomized experiments. Journal of the American Statistical Association. 2007;102(477):191–200. [Google Scholar]
- 33.Hudgens M, Halloran M. Towards causal inference with interference. Journal of the American Statistical Association. 2008;103:832–842. doi: 10.1198/016214508000000292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hong G, Raudenbush S. Evaluating kindergarten retention policy: A case study of causal inference for multilevel observational data. Journal of the American Statistical Association. 2006;101:901–910. [Google Scholar]
- 35.Hong G. Marginal mean weighting through stratification: Adjustment for selection bias in multilevel data. Journal of Educational and Behavioral Statistics. 2010;35(5):495–531. [Google Scholar]