Abstract
Motivated by an application to childhood obesity data in a clinical trial, this paper describes a multi-profile hidden Markov model (HMM) that uses several temporal chains of measures respectively related to psychosocial attributes, dietary intake, and energy expenditure behaviors of adolescents in a school setting. Using these psychological and behavioral profiles, the model delineates health states from the longitudinal data set. Furthermore, a two-level regression model that takes into account the clustering effects of students within school is used to assess the effects of school- and community-based interventions and other risk factors on the transition between health states over time. The results from our study suggest that female students tend to decrease their physical activities despite a high level of anxiety about weight. The finding is consistent across intervention and control arms.
Keywords: latent variable, latent Markov model, longitudinal analysis, childhood obesity intervention
1. Introduction
Childhood obesity has now been recognized as a major public health problem that persists from childhood to adolescence and well into adulthood [1]. In 2003–2004, 17.1% of children aged 2 to 19 years were at or above the previously benchmarked 95th percentile of body mass index (BMI), compared with 5–6% in the 1970s [2]. Overweight and obesity in children is associated with numerous adverse health effects including early onset of type 2 diabetes, metabolic syndrome, and cardiovascular diseases [3]. Children who were obese were also more likely to develop into obese adults. These adults would have increased morbidity and chronic diseases compared to those who were not obese during childhood. Thus, preventive and intervention efforts have been focusing on weight gain in children and young adolescents [4, 5].
Partly because of the lack of consideration for contextual factors and an overemphasis on the direct effect of intervention on single outcomes such as BMI, preventive efforts targeting risk behaviors have had only limited effectiveness [6, 7 ]. There is a growing awareness that a multi-dimensional, multi-level, dynamic approach — in terms of study design, intervention strategy, and associated methodologies — should be more extensively deployed. The Working Group Report on future research directions in childhood obesity prevention and treatment (NHLBI, 2007), for example, called for multi-level, multi-component interventions and development of methodologies for comprehensively assessing outcomes in prevention and treatment studies.
This article is motivated by an application that requires a multi-dimensional, dynamic approach in analyzing childhood obesity data. The Louisiana (LA) Health Study [8] is a three-arm intervention cohort study that aims to prevent weight gain in school children in high-poverty rural areas. Besides anthropometric measurements, the LA Health Study also collected extensive data through groups of measurements regarding food intake (at school), physical activity (PA), sedentary behavior, dietary and PA social support, mood and eating attitudes, and family involvement data from parents. Although the primary endpoint of the study was body mass index (BMI) z-score (using NHANES norms) of the students, there exists in the data set a repertoire of rich health outcome measures that could provide a more comprehensive view of changes in students’ weight-related behavior and psychology. Appropriately modeling repeated measurements over time in diet, physical activities, and mental health of the students could shed light on the dynamic relationship between these health characteristics and obesity. Overweight and obese students, for example, face significant mental health and psychosocial barriers that often create concurrent health problems not entirely captured by a single index such as BMI z-score [9].
In this paper, we propose to use a multiple profile approach to form an obesity-relevant characterization of each student. Here a profile refers to a set of empirically derived states within a domain of interest (e.g., physical activity). The multiple profiles we consider in this paper include: (1) a psycho-social profile that indicates the mood and attitude toward eating; (2) a food intake profile that is based on digital photographs of individuals’ meals taken at the school cafeteria before and after lunch; and (3) a physical exercise and sedentary activity profile that is based on self-reported activities. Each of these profiles was defined by a cluster of representative variables, or indicators, which were selected by content experts.
The broadened view of jointly analyzing multiple profiles over time poses several challenges in statistical modeling. First, multiple profiles require the use of multiple groups of observed variables for describing the entire outcome space in a longitudinal setting. Commonly used longitudinal statistical methods including mixed models and generalized estimating equation (GEE) often focus on handling a single outcome variable. Second, for longitudinal data, the serial dependence of observations — on more than one variable in this case — needs to be accounted for. The third statistical challenge is the presence of possible clustering effects for students within the same school. This implies that any modeling approach for delineating risk factors that potentially moderate obesity-related behavioral outcomes also need to account for school-level clustering effects. Finally, the broadening of interest in health outcomes calls for regression models that incorporate covariates as predictors of transition between health statuses over time. While each statistical challenge could be solved individually using existing methods, incorporating all four considerations into a joint model requires novel analytic tools.
One statistical approach that shows promise to solve these challenges is the hidden Markov model (HMM) [10, 11]. The HMM posits that the observed longitudinal data can be described and modeled by two interconnected processes — first, an observed set of data that is a statistical manifestation of a latent set of hidden variables; second, the set of hidden variables that are linked together through a Markov process — that is, the conditional value of the latent variable at time t given its past history is only dependent on its immediate history (i.e., its value at t − 1). This basic HMM setup models a dynamic process of the observed variables — the multiple response indicators, with the serial correlation between responses over time being captured through the Markov assumption on the set of hidden variables. While traditional HMMs typically model a single outcome, it is rather straightforward to extend them to include multiple outcomes by assuming that the multiple outcomes are conditionally independent given the latent (hidden) variable. Scott et al. [12] proposed a Bayesian approach in analyzing multiple continuous responses using non-homogeneous HMM. More recently, Wall and Li [13] used a multiple-indicator HMM for medical utilization data. Ip et al. [14] used discrete multiple indicators to represent the behavioral profile of batterers in an application of HMM to domestic violence. However, all of these approaches only consider a single profile. For example, Wall and Li [13] considered four indicators for medical encounters to represent a meaningful health-state process related to alcoholism treatment. In this paper, we extend the HMM to handle multiple profiles by including an additional process to the HMM — a set of so called hidden superstates that is intended for describing the heterogeneity across the multiple profiles. Details will be provided in the Model section.
There is a substantial literature on handling clustered data in the latent class and latent Markov models that is highly relevant to the current study. A random-effects model, for example, can be used to capture clustered data within the latent class analysis framework [15]. An alternative approach is a marginal approach based on the GEE [16]. In the context of HMM, Altman [17], and more recently Zhang et al. [18], proposed mixed-effects models, which offer a general framework for handling clustered data. Other recent advances in HMM include Desantis and Bandyopadhyay [19] for modeling zero-inflated Poisson counts, and Scharpf et al. [20] and Choi et al. [21] for applications to clustered data in bioinformatics. In this paper, we incorporate into the multi-profile HMM a multi-level model in which a random effect is used to capture the clustering of students within the same school. All features of the multi-profile HMM that have been outlined here are implemented within the maximum likelihood framework for statistical inference, using an extended Matlab toolbox that was based on the work of Murphy [22], Rijmen[23], and Zhang et al. [18].
In Section 2, we describe the LA Health Study data set, and in Section 3, the multi-profile HMM is introduced. Model estimation and evaluation are provided in Section 4, and Section 5 reports the results from applying the multi-profile HMM to the LA Health Study data set. Finally, Section 6 provides some discussion of the results, as well as the strengths and limitations of the approach.
2. Data Description
The LA Health Study was a cluster, randomized, controlled trial that enrolled N = 2, 201 school students across 17 rural school clusters in the state of Louisiana [8]. It is worth noting that Louisiana has one of the highest rates of poor health in the nation. Students were randomly assigned to one of three intervention arms — primary prevention (PP), combined primary and secondary prevention (CP), and no-intervention control (C). PP emphasized the modification of environmental cues, enhancement of social support, and promotion of self-efficacy for health behavior change. CP relies on both the PP approach and an Internet-based educational program reinforced with regular classroom instruction and synchronous online counseling and asynchronous (e-mail) communication for children and their parents. Besides the primary endpoint of body mass index (BMI), other outcome measures were collected in the LA Health Study: (1) energy and nutrient measurements, (2) physical and sedentary activity measurements, and (3) psycho-social measurements. For the first category, digital photos were used for food selection at school, and dietary measures including total calories, macro-nutrient content, and total dietary fat were collected. Physical activities were measured by the Self-Administered Physical Activity Checklist (SAPAC), while sedentary behavior was assessed by questionnaires about number of hours spent on TV, video, computer, homework, and telephone. The Children’s Eating Attitudes Test (ChEAT) and the Child Depression Inventory (CDI) were used to respectively measure eating disorder symptoms and symptoms of childhood depression. Subscales from ChEAT such as social pressure and food preoccupation were used for our analysis. All of the above measurements were taken at baseline, month 18, and month 30.
The purpose of the analysis is to (1) delineate different phenotypes of obesity-related attitude and behavior, (2) model the dynamics of change of attitude and behavior over the course of the study, and (3) assess the impact of intervention, individual-level risk factors, and school-level factors on the dynamics of change of attitude and behavior. As described in the Introduction, three attitudinal and behavioral profiles were used in our subsequent analysis; besides the primary predictor variable intervention status, individual-level covariates including race, BMI, and age, and a school-level covariate of an indicator of free lunch were included in the model.
Because female and male students exhibit rather different developmental trajectories, we conducted separate analyses for each gender. In the interest of saving space, we only show the analysis for female students. Only female students with data on all three time-points were included in this analysis. As a result, the sample contained N=687 female students. Table 1 shows the characteristics of the sample.
Table 1.
Descriptive Statistics of LA Health Female Participants (N = 687)
| Characteristics | Mean/Percentage | SD |
|---|---|---|
| Ethnicity | ||
| White | 23.7 | |
| Black | 74.7 | |
| Others | 1.6 | |
| Baseline Grade | ||
| 4th grade | 39.6 | |
| 5th grade | 32.0 | |
| 6th grad | 28.4 | |
| Randomization Group (%) | ||
| Control | 33.9 | |
| Primary | 38.7 | |
| Primary and Secondary | 27.4 | |
| Age | 13.95 | 1.19 |
| Height (cm) | 157.44 | 7.51 |
| Weight (kg) | 59.33 | 19.31 |
| BMI (kgm−2) | 23.71 | 6.74 |
|
| ||
| Psycho-social profile (factor loading) | ||
| Overconcern | 11.28 | 5.34 |
| Dieting | 8.25 | 3.85 |
| Social Pressure | 6.02 | 3.86 |
| Self-control | 6.31 | 3.01 |
| Depression | 46.33 | 8.33 |
|
| ||
| Food intake profile | ||
| % from Fat | 33.05 | 6.29 |
| % from Protein | 18.34 | 4.65 |
| % from Carbohydrate | 49.68 | 8.72 |
|
| ||
| Physical activity profile (min/day) | ||
| Total TV | 174.28 | 137.71 |
| Before School PA | 7.23 | 18.18 |
| During School PA | 17.80 | 23.98 |
| After School PA | 65.26 | 69.99 |
3. Model
The presentation of the basic HMM in this paper is similar to the ones presented in Scott et al. [12], Ip et al. [14] and Zhang et al. [18]. We present a framework that can be applied to both continuous and discrete outcomes. The term superstate is used to refer to discrete latent (hidden) states that represent phenotypes of individuals with characterization in several domains – e.g., psycho-social, food intake behavior, and physical activity behavior. Within each domain, a latent categorical variable is used to represent different domain-level states. The resulting collection of states is termed a profile. There are numerous possible combinations of the profile states. If there are three profiles and within each profile there are four states, then there are 43 = 64 possible combinations, assuming that an indicator of a profile state can only take 0/1 value. However, some of these combinations would not be empirically supported by the data. The second level of hidden states or superstates is a useful way to capture the heterogeneity across the profiles. Note that this two-level model of hidden states and hidden superstates here should be distinguished from the multi-level, hierarchical linear model for clustered data [24], in the sense that the first level could refer to school, and the second level could refer to students within school. In the current model, school-level clustering effects are accounted for via a mixed effects regression model. In this sense, the proposed model is a two-level HMM as well as a two-level hierarchical linear model.
3.1. The Multiple Profile Discrete and Continuous Hidden Markov Model
Let yiptj denote the discrete response of subject i at occasion t on outcome j in profile p, i = 1, …, N; j = 1, …, Jp; t = 1, …, T, p = 1, …, P. Here, an outcome could be a discrete response (yes/no) to an item such as a survey question, or a continuous measure, such as minutes of physical activity. Hereinafter, the terms “response” and “outcome” are used interchangeably. The variable yiptj can take on a discrete value k = 1, …, Kpj or a continuous value. Specifically, yipt = (yipt1, …, yiptJp)′ denotes the response vector of subject i at occasion t in profile p, represents the response pattern of subject i in profile p, and represents the complete response pattern of subject i. The categorical (unobserved) latent state of subject i at occasion t in profile p is denoted by zipt = 1, …, Sp, named as a profile state thereafter, and zip = (zip1, …, zipt)′ is the latent-state sequence of subject i in profile p. At the second level, the categorical latent state of subject i at occasion t is denoted by , namely as a superstate thereafter. Thus, is the superstate sequence of subject i through the latent space over time. A first-order Markov chain for the latent superstate assumes that the superstate at occasion t + 1 depends only upon the superstate at occasion t — i.e., ∀i, . Accordingly, the multi-profile HMM (MPHMM) contains the following six sets of parameters:
-
τ = (τrs), an S × S matrix of time-homogeneous transition probabilities between latent superstates, where ∀i and ∀t,
(1) In the extended MPHMM, the transition probabilities would depend on subject-specific factors, and we use to denote the transition probability from state at time (t − 1) to state at time t for subject i; i.e.,(2) for given i and t, and 1 ≤ s, r ≤ S.
-
α1 = (α11, …, α1S)′, an S × 1 vector of marginal probabilities of the superstates at occasion 1; i.e., ∀i,
(3) The vector αt = (αt1, …, αtS)′, t = 2, …, T, can be recursively derived by the formula .
- φ = (φprs), a P × S × Sp array of superstate-conditional probabilities in profile p, where ∀i and ∀t,
(4) -
π = (πpsjk), an P × Sp × Jp1 × Kpj array of state-conditional response probabilities in profile p for discrete outcomes, where k is the index of outcome category, k = 1, …, Kpj, and ∀i, ∀t,
(5) where , and Jp1 is the number of discrete outcomes in profile p.
- μ = (μpsj), an P × Sp × Jp2 array of Gaussian mixture means in profile p for continuous outcomes; i.e., ∀i, ∀t,
(6) -
σ = (σpsj), an P × Sp × Jp2 array of Gaussian mixture standard deviations in profile p for continuous outcomes; i.e., ∀i, ∀t,
(7) Jp2 is the number of continuous outcomes in profile p, and Jp = Jp1 + Jp2.
Four conditional independencies are assumed here. First, given a superstate at time t, the profile states at time t are independent from superstates at other time points; i.e.,
| (8) |
Second, given a superstate at time t, the profile states at time t are independent from each other; i.e.,
| (9) |
Third, given profile states, the outcome conditional probabilities are independent from the superstates; i.e.,
| (10) |
Fourth, given a profile state at time t, the outcome conditional probabilities at time t are independent from each other; i.e., ∀t,
| (11) |
From the first two assumptions, we have:
| (12) |
and from the Markov chain assumption,
| (13) |
Hence, the joint probability of a response pattern together with the profile states and the superstates can be written as:
| (14) |
and the marginal probability of a response pattern yi is given by
| (15) |
with the summation over the entire superstate space
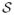 of size ST and each profile state space
of size ST and each profile state space
 of size
.
of size
.
Figure 1 graphically illustrates the MPHMM, where each arrow indicates a conditional probability and for simplicity we have assumed all profiles have the same number of outcomes J.
Figure 1.

An illustration of the multi-profile HMM (MPHMM). Circle indicates observed variable; square indicates latent (hidden) variable. Dependence across time is assumed to be captured by Markov dependence across superstates .
For discrete outcomes, the profile state-conditional probabilities are
| (16) |
where δ(yiptj, k) = 1 if yiptj = k, and 0 otherwise. For continuous outcomes, we have the Gaussian mixture model
| (17) |
3.2. Mixed regression model on superstate transitions
For simplicity, we only consider transition from a specific superstate (for convenience, state S) to all other superstates in the model. The regression model is given by:
| (18) |
where xit is a vector of given fixed-effects covariates, possibly time-varying, and wit is a vector of given random-effects covariates. The coefficients for fixed and random effects are respectively given by γrs and θi, and the intercept term by ζrs. Here, we assume that the random effects is a scalar such that . Extension to a multidimensional model is straightforward, even though the computational burden grows rapidly as the dimension grows. In this specific application, the random effect is used to capture clustering effects within a school [25]. The formulation in (18) can be modified as follows:
| (19) |
where i(g), g = 1, · · ·, G, indicates that individual i is nested within school g, and . The term θi(g) can be interpreted as deviation of the school g from the overall adjusted mean.
4. Model Estimation
The MPHMM is estimated by the maximum likelihood method. The EM algorithm [26] is particularly useful for handling the presence of latent states and random effects within the MPHMM. For historical reasons, a version of the EM algorithm used to estimate the basic HMM is also known as the Baum-Welch algorithm [27]. Here, we extend the Baum-Welch algorithm for inference for the mixed effects model for transition probabilities in (18). Briefly, in the EM terminology, the latent states — including the superstates — and random effects are treated as “missing data.” The objective here is to maximize the conditional expected log-likelihood of the complete data, which includes the observed data y and the latent states z and z★, given y and some provisional estimates for the parameters, where y, z, and z★ respectively denote the vectors of the collections of (yi), (zi), and ( ).
Denote the entire parameter set defined in (1), (3) – (7) and (18) by β and its estimate at the nth iteration of the EM algorithm by β(n). Furthermore, let
where the conditional expected log-likelihood of the complete data Q(β, β(n)) is given by:
| (20) |
where θ = (θi(g)) denotes the individuals’ random effects. For readability, we write θi(g) as θi. Assuming that θ = (θi) and z are independent, we have
where fβ(n)(θi|yi) is the Gaussian posterior density of θi given yi, and from (12) and (13),
| (21) |
The objective function is
| (22) |
in which the joint distribution of the complete data of subject i within (22) is similar to (14):
| (23) |
where is given by model (18).
By taking the logarithm on (23) and substituting (22), we rewrite the objective function as
| (24) |
where h is the inverse link function specified in (18). One appealing feature about (24) is the separability of the six sets of parameters, namely α1s, φ, π, μ, σ, and (ζ, γ, σθ), which can be optimized individually.
Before we study the second and fifth terms of the RHS of (24), we see that the first, third, and fourth terms do not involve the random effects and can be computed separately. The updating equation for maximum likelihood estimates (MLEs)[18] of α1s and φprs are:
| (25) |
| (26) |
For continuous outcomes, we estimate the Gaussian mixture means and variances [28] through the following set of equations:
| (27) |
| (28) |
The above description for the maximization of the first, third, and fourth terms highlights the E- and the M-steps of the EM algorithm: the E-step computes the posterior probabilities and pseudo-counts, whereas the M-step updates the estimates using pseudo-counts via closed-form equations (25) to (28). Here pseudo-counts refer to quantities such as in equation (25). The implementation of EM with mixed effects for discrete outcomes for a single profile is documented in a recent article [18].
For the second and fifth terms of the RHS of (24), which contains both the fixed- and random-effects parameters in the linear poset model, the E-step is similar. However, the M-step does not have a closed-form solution and requires an iterative method. The estimation of fixed effects will be described further below. For the random effects, we use Gauss-Hermite quadrature for integration. Denote the vector of q quadrature points by v = (vl). The corresponding collection of weights , which depend upon the current estimate of the variance structure, , are used to approximate fβ(n)(θi). At a quadrature point vl, denote the transition probability by τitrsl = [τitrs(θi)]θi=vl. The computation of random effects can be conducted using codes for fixed effects HMM by adding a dimension for discretized θ. When θi is a scalar, we reparameterize θi by θi = σθθ̃i, and thus θ̃i ~ N (0, 1). The quadrature points and weights can be evaluated together using the standard normal distribution and these quantities remain constant throughout the iterations, while σθ is treated as one of the covariate coefficients, γ.
The M-step for updating the regression parameters in (18) — the second term in the RHS of (24) — involves an iterative procedure within each EM cycle: denote the parameters of the regression model (ζ, γ, σθ) by ξ. Maximize the following function for the estimate of ξ, given ξ(n) at the nth iteration of the EM algorithm:
| (29) |
where , and . Updating parameter values in (29) follows the Fisher scoring iteration within each EM cycle [29, p. 42]:
| (30) |
where Xit is the design matrix for subject i at time t, and Witrl is given by,
| (31) |
and τitrl = {τitrsl, s = 2, …, S}. Here n* is the inner Fisher scoring iteration index and n is the outer EM loop index. Throughout the inner Fisher scoring iteration, the pseudo-counts remains unchanged.
We also note that in the E-step, the posterior probabilities, or the pseudo-counts, , can be computed by first computing , and then using a junction tree algorithm [30], which is a generalized Baum-Welch algorithm for general Bayesian network in which the HMM is a special case; see [31]. The junction tree is especially efficient for computing the joint distribution when the dimension of the HMM is high [18]. Of note, we used the Viterbi algorithm [32] to the compute the most likely trajectory, and given the most likely trajectory, estimate the profile states. Thus the algorithm considers all previous data and states, and its implementation was adapted from the codes of Murphy [22].
Because the EM algorithm does not directly operate on the marginal likelihood, it does not provide the observed information matrix necessary for computing standard errors. Several methods have been proposed to calculate standard errors for the HMM. Lystig and Hughes [33] provide an overview and also propose an efficient method based upon a forward-backward algorithm. We have extended [33] using the method described in [34], which was based upon the sum of the outer product of the individual contributions to the score function; see also [35].
5. Model determination
Instead of relying solely on a model-selection criterion such as the Bayesian Information Criterion (BIC) for determining the appropriate number of profile- and super-hidden states, we adopted a model evaluation strategy that emphasized the tradeoff between the complexity of models and their clinical interpretations. One important reason for adopting this strategy was that at the second level of the MPHMM, in which the domain-level states were treated as categories of a variable, even with a small number of superstates, interpreting the different combinations of categories of outcome proved to be highly challenging. Since superstates are to be understood in the context of combinations of states from each profile, complex models create high cognitive burden for interpretation and render superstates useless in practice.
Our alternative strategy to solve this problem involved two stages: first, a data-driven hill-climbing procedure for searching the optimal model using a simple fit index [36], the BIC; and second, an expert-driven decision process for refining the model - e.g., combining clinically redundant states - obtained from the first stage. Specifically, the model determination strategy involves the following steps. (1) Start with a small number of profile states and superstates, fit the model and compute a goodness-of-fit index. (2) Increment the number of states by one for one of the profile states, and compare how well the new model fits the data; if the model fit improves very little, then stop, fix the number of states for that specific profile, and go to step (3), else continue to increment the number of profile states until the improvement is insignificant. (3) Increment the number of a second profile state and repeat steps (2). (4) When the number of profile states is determined, increment the number of superstates by one and repeat until there is no significant gain. (5) Inspect models with similar goodness-of-fit indexes for meaningful clinical interpretation and determine the most appropriate model; furthermore combine states if needed. (6) Conduct out-of-sample validation to assess the “sacrifice” for using a simpler model of combined states over the statistically selected model. Steps (1)–(4) search for an empirical solution to the number of profile states and superstates. Like determining the number of factors using a scree plot in factor analysis, Step (1)–(4) inspects the BIC values and selects the model beyond which the gain becomes marginal. In our implementation, to avoid local optima within the EM algorithm, we used 20 random starting values each time when selecting the number of profile states, and 100 random starting values for selecting the number of superstates. While the commonly used BIC has the advantage of ease in computation, we acknowledge that the goodness-of-fit index has limitations for model selection in HMM [37]. As we shall see, using BIC for this application seems to produce a rather robust solution, thus alleviating some concern about its appropriateness. Step (5) uses content experts’ opinions to form a practical solution that could provide useful clinical interpretation. Finally, Step (6) uses 20% of the subjects to form the held-out-sample and trains the model using the remaining 80% of data. The root mean squared root (RMSE) is then computed for the held-out-sample for both the simpler model chosen by the experts and the statistically selected model. Using a five-fold cross-validation design, the RMSEs are then averaged over 5 samples and compared across different measures. This step ascertains the consequences of using a simpler model, measured as prediction errors in the same units as the original measurements.
6. Results
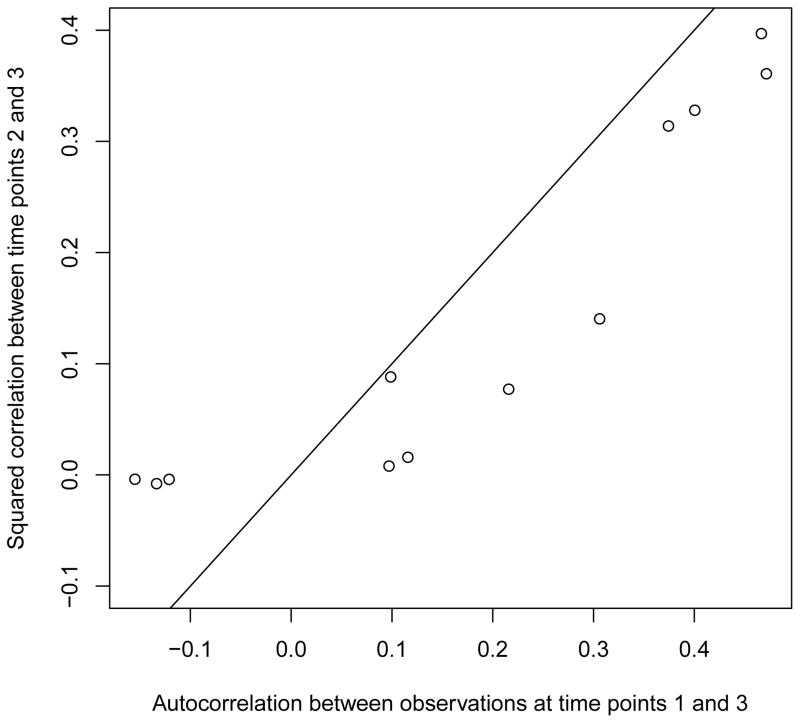
Table 1 provides a brief description of the (continuous) variables used for creating the three separate profiles – psychosocial (PS), food intake (FI), and physical and sedentary activities (PSA). Table 2 reports the results of the hill-climbing algorithm. We started with small values of profile states and superstates S1 = 2, S2 = 2, S3 = 2, and S = 2. Using BIC as the criterion for model fit, the selected model has 4, 3, and 5 states for the PS, FI, and PSA profiles, respectively. For superstate selection, the 3-state model turned out to have a small but insignificant increase (i.e., less than 0.2%) in BIC over the 2-state model. It appeared that the 2-, 3-, and 4-superstate models were all close in terms of their model fit to the data. For comparison, we also computed the BIC value for a simple model that treats the time points and profiles as independent variables. The BIC value of the model is 142,649, which was significantly worse than the joint models of the (4, 3, 5) profile states and the 2, 3, and 4 superstates that were under final consideration. Furthermore, as a check on the Markov assumption, we computed several autocorrelations. Figure 2 shows the scatterplot of autocorrelation between all observed measures at time points 1 and 3, and the squared autocorrelation between observations at time points 2 and 3. Under the Markov assumption, the autocorrelation between observations at time points t and t+2 equals to the square of the autocorrelation between observations at time t and t+1. While the autocorrelations between time points 1 and 3 appear to be slightly higher, there is no strong evidence to invalidate the Markov assumption.
Table 2.
BIC values for hill-climbing model determination. An asterisk represents the starting point of a new search in the succeeding profile.
| PS | FI | PA | Superstate | BIC |
|---|---|---|---|---|
| 2 | 2 | 2 | 2 | 145225 |
| 3 | 2 | 2 | 2 | 142075 |
| 4 | 2 | 2 | 2 | 140574★ |
| 5 | 2 | 2 | 2 | 140426 |
|
| ||||
| 4 | 3 | 2 | 2 | 139657★ |
| 4 | 4 | 2 | 2 | 139382 |
|
| ||||
| 4 | 3 | 3 | 2 | 138668 |
| 4 | 3 | 4 | 2 | 136240 |
| 4 | 3 | 5 | 2 | 134959★ |
| 4 | 3 | 6 | 2 | 134856 |
|
| ||||
| 4 | 3 | 5 | 3 | 135188 |
| 4 | 3 | 5 | 4 | 134853 |
Figure 2.
Scatterplot of lag 1 and squared lag 2 autocorrelations.
To visualize the conditional distributions of the profiles at the domain level of the MPHMM, we depict the results in the form of a dot chart with a bar of length ±2 and with standard deviations centered at the dot. Superstates were visualized by bar charts in which probabilities of belonging to a profile state were stacked on a scale of 0 to 1. With the help of the dot charts and bar-charts for different numbers of super-states, the investigative team was able to determine models that have a manageable number of states and meaningful interpretation.
Figure 3 shows the 4-state conditional distribution of the 4-state psycho-social profile estimated by the MPHMM procedure. Except for the perception of social pressure from peers, the other four variables—over-concern about weight, concern about dieting, concern about self-control, and level of depression — all tend to move in tandem. State 1 is characterized by a high level of concerns and depression, together with a high level of perceived pressure from peers. State 2 is the antithesis of State 1; the level of concerns about weight, diet, self-control, perceived social pressure, and depression for this state is lower than average. State 3 is similar to State 1, except that this group does not have the same high level of perceived social pressure about weight issues. State 4 is almost a mirror-image of State 3.
Figure 3.
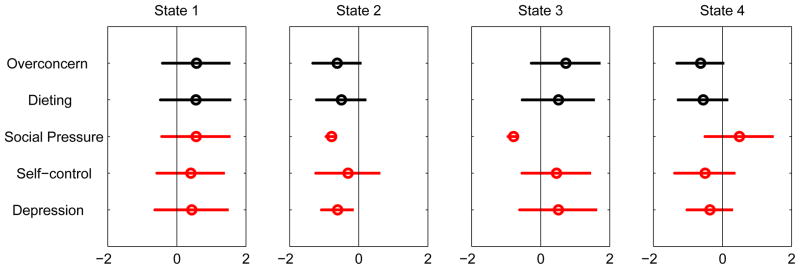
Conditional probability profile of psycho-social factors.
The MPHMM analysis for the 3-state FI profile is shown in Figure 4. State 1 shows that female students who belong to this state tend to have a low-fat, low-protein, high-carb diet. State 2 female students, on the other hand, are a mirror image of State 1 students: they have a higher-fat, high-protein, low-carb diet. State 3 is characterized by slightly high-fat consumption, with average levels of proteins and carbs.
Figure 4.
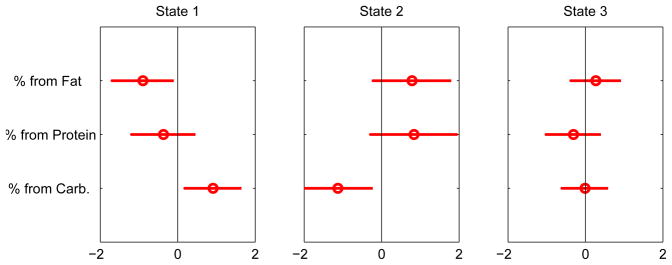
Conditional probability profile of food intake.
Finally, the 5-state PA profile is shown in Figure 5. State 3 distinguishes itself as the state that exhibits a high level of physical activity — before, during, and after school. The other states all show, to various degrees, a low-to-average level of physical activity. The variable “hours of total TV watching” does not seem discriminating. Somewhat to our surprise, the active State 3 female students reported watching even slightly more TV than the other four groups.
Figure 5.
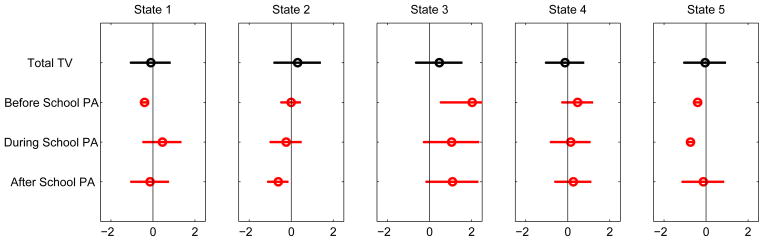
Conditional probability profile of physical activity.
While the states at the first (profile) level appear to make sense to content experts in childhood obesity, the superstates that were derived from the (4, 3, 5)-state models, respectively, for PS, FI, and PA turned out to be still difficult to interpret. After consultation with the content experts, we consolidated the states in the respective profiles to enhance the interpretation of the superstates. For PS, we combined State 1 and State 3 to form a new State 1 that we termed High-Concerns-About-Weight, and State 2 and State 4 to form a Low-Concerns-About-Weight state (Fig. 6). For FI, we did not combine states because the three states were relatively distinct, and we respectively labeled them High-Carb, High-Fat, and Average-Diet (Fig. 4). For PA, we combined the three physically inactive groups – States 1, 2 and 5 - all of which have below-average physical activity. States 3 and 4 were also combined. As a result, the new State 1 (comprise the original States 1, 2, and 5) was labeled Physically-Inactive, and the new State 2 (originally States 3 and 4) was labeled Physically-Active (Fig. 7). The content experts also examined the models with 2, 3, and 4-superstates. It was decided that the 3-superstate model provided the most reasonable interpretation in terms of the clinical meaning of the superstates.
Figure 6.
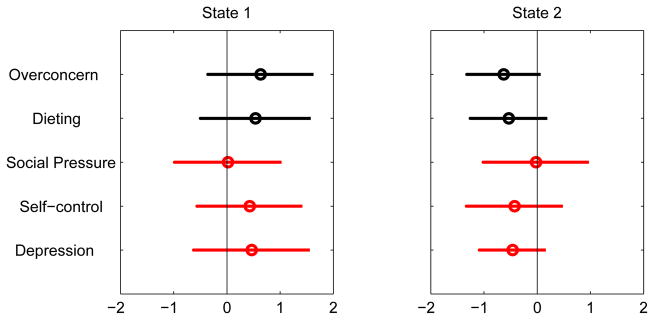
Conditional probability profile of psycho-social after combining states. States 1 and 2 are respectively labeled High-Concerns-About-Weight, and Low-Concerns-About-Weight.
Figure 7.
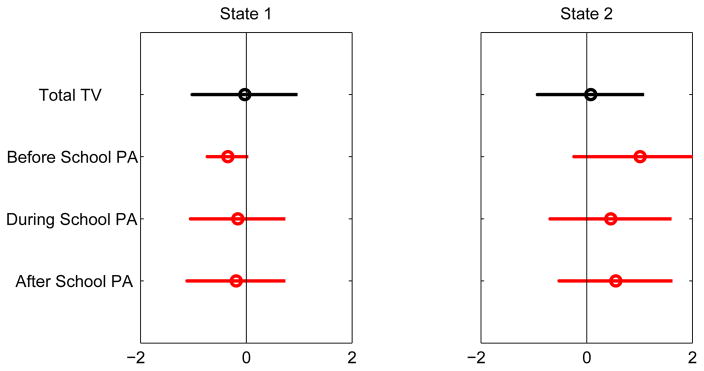
Conditional probability profile of physical activity after combining states. States 1 and 2 are respectively labeled Physically-Inactive and Physically-Active.
The parameters within the consolidated model were determined by applying Eqs. (26) – (28) to the data. In other words, the probabilities of two collapsed states were summed. The M-step was then implemented to obtain the necessary estimates for the collapsed model. Note that this (2,3,2)-state model is different from the (2,3,2)-state model estimated “from scratch” using EM. Consolidating the profile states represented a tradeoff between improving the model interpretability and loss in the goodness of fit. We compared the consolidated model with the model with (2,3,2) profile states and 3 superstates, and the parameter estimates of the two models were almost identical. For the out-of-sample analysis, Table 3 shows the averaged RMSEs of the collapsed (2,3,2)-model and the (4,3,5)-model for all measurements used. Out of the 12 measurements, the (2,3,2) model actually exhibits lower prediction error in 8 of them, which is quite surprising to us. It seems to suggest that the complex model might have overfitted the data.
Table 3.
Averaged RMSEs of the model of combined states and statistically optimal model.
| Measurement | (2,3,2) model | (4,3,5) model |
|---|---|---|
| Overconcern | 1.81 | 2.31 |
| Dieting | 1.44 | 1.57 |
| Social pressure | 1.75 | 1.50 |
| Self-control | 1.27 | 1.38 |
| Depression | 3.49 | 3.75 |
|
| ||
| Percentage from fat | 1.87 | 1.96 |
| Percentage from protein | 1.71 | 1.60 |
| Percentage from carbohydrate | 2.16 | 2.25 |
|
| ||
| Total TV | 10.42 | 10.49 |
| Before school PA | 1.15 | 0.89 |
| During school PA | 1.84 | 1.22 |
| After school PA | 4.74 | 5.10 |
The superstate profiles after consolidation of domain-level states are shown in Fig. 8. The domains PS, FI, and PA are presented in three separate panels, and each column within a panel represents the profile of a superstate for the specific domain. For example, the third column in the PS panel shows that Superstate 3 contains a high proportion of female students with a Low-Concerns-About-Weight profile. This superstate also contains a high proportion of High-Carb (panel 2, column 3) and Physically-Inactive (panel 3, column 3) female students. Therefore, this superstate is dominated by female students who are not concerned about their weight, eat a relatively high-carb diet, and are not physically active. Superstate 2 consists of female students who are rather concerned about weight, consume an average diet, and are physically active. Superstate 1 appears to be a state that is characterized by a high level of concern about weight and diet, a high-carb, high-fat type of diet, and a low-physical-activity lifestyle.
Figure 8.
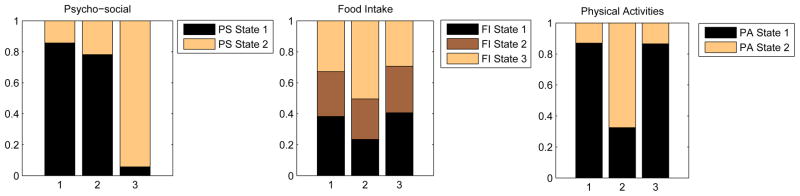
Conditional probability profile of the super states. Profile states are ordered such that the lowest numbered state is at the bottom of the stack.
The transitions over time across the different superstates are revealing. Figure 9 shows the prevalence of the three superstates over time across the three arms. The patterns across all three arms are surprisingly similar: Superstate 2 female students - the High-Concerns-About-Weight, Average-Diet, and Physically-Active individuals - tend to transition to either Superstate 1 or Superstate 3. This trend is confirmed by examining the transition probability table shown in Table 4. Superstate 2, which is characterized by a high level of physical activity, has a high probability of transitioning into State 1 or State 3, respectively, with probabilities 0.36 and 0.35. This implies that the physically active female students tended to engage in less physical activity during the last two time points of the study. From Figure 9, it can be seen that the interventions - both primary and combined primary and secondary - do not substantially moderate the trend, even though there appears to be a small intervention effect in that (1) the interventions tend to increase concern over the PS domain in female students over time, as evidenced by the higher cumulative area of the bars for the High-Concerns-About-Weight group across the three time points in the intervention arms, and (2) the combined intervention group has a slightly higher proportion of Superstate 2 female students than the other two arms at the last time point. From the transition probability table, it can also be seen that Superstates 1 and 3 are essentially absorbing, implying that regardless of their levels of concern about weight, their high-carb-high-fat and inactive lifestyle remain unchanged throughout the period of study.
Figure 9.
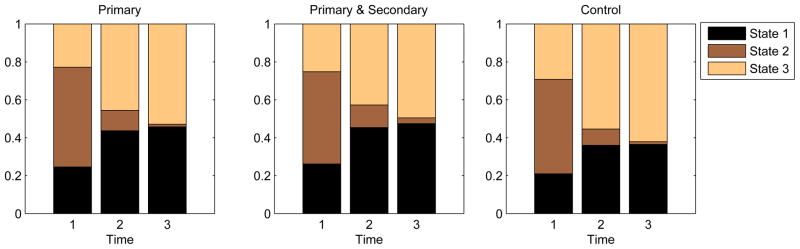
Superstate prevalence comparison over time (1=baseline, 2=18 month, 3=30 month) between the randomization groups. Superstates are ordered such that the lowest numbered superstate is at the bottom of the stack.
Table 4.
Estimated prior probabilities (α) and transition probabilities (τ) between superstates. The entry (i, j) indicates the probability of transition from the i-th superstate to the j-th superstate.
| State 1 | State 2 | State 3 | |
|---|---|---|---|
| α: | 0.22 | 0.50 | 0.28 |
|
| |||
| τ: | 0.94 | 0.00 | 0.06 |
| 0.36 | 0.29 | 0.35 | |
| 0.00 | 0.00 | 1.00 | |
We further examined factors that might moderate the transition from Superstate 2 into Superstate 1 or Superstate 3. A mixed-effects regression model was applied to model the transition probabilities conditional on the current state being Superstate 2 (High-Concern-About-Weight, High-Fat, Physically-Active). The fixed effects we considered included intervention status, race (African American vs. non-African American), and BMI (time-varying). As described in the Model section, a random effect was introduced to account for potential clustering effects of students within the same school. Table 5 shows the estimates in the mixed-effects model. The combined primary and secondary intervention arm shows a significant positive effect in decelerating the transition from Superstate 2 to Superstate 3. The factor BMI is statistically significant and increases the probability of transitioning from the more physically active state to the less physically active and low-concern state (Superstate 3). The random effect does not suggest any statistically significant effect of school clusters. Briefly, the mixed-effect analysis suggests that the combined intervention has a statistically significant positive effect in preventing female students from becoming less active, and higher-BMI female students tend to have a higher chance of becoming less physically active over the period of the study. Because the two other superstates – i.e., Superstates 1 and 3 – are close to absorbing, within rounding error, any analysis that uses them as originating states would not be interesting, and we have not pursued that.
Table 5.
Estimates of mixed-effects model.
| State 2 → State 1 | State 2 → State 3 | |||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Estimates | SE | |t| | Pr > |t| | Estimates | SE | |t| | Pr > |t| | |
| Intercept | 0.248 | 2.660 | 0.093 | 0.926 | 2.719 | 2.753 | 0.988 | 0.323 |
| Primary | 0.166 | 0.617 | 0.269 | 0.788 | −0.599 | 0.604 | 0.992 | 0.321 |
| Combined | −0.319 | 0.492 | 0.648 | 0.517 | −1.067 | 0.537 | 1.987 | 0.047 |
| Black vs. non-Black | −0.624 | 0.523 | 1.194 | 0.232 | 0.919 | 0.605 | 1.519 | 0.129 |
| BMI | 0.022 | 0.031 | 0.703 | 0.482 | −0.202 | 0.048 | 4.190 | <0.001 |
| Free lunch | −0.597 | 0.689 | 0.866 | 0.387 | −0.490 | 0.758 | 0.646 | 0.518 |
| Age | 0.000 | 0.195 | 0.001 | 0.999 | 0.183 | 0.202 | 0.910 | 0.363 |
|
| ||||||||
| σ | 0.245 | 0.260 | 0.944 | 0.345 | ||||
7. Discussion
A recent follow-up paper [38], which also used the LA Health data set, reported a general decrease of physical activities over time, as measured by both self-report and accelerometer, accompanied by a general increase in sedentary activities, for both boys and girls. The general trend was moderated, to different degrees, by participation in the primary and secondary intervention. Because of our focus on methodological development, we have not shown the analysis results for boys, which are in many ways, similar to those for girls. However, our overall results are consistent with the new findings in [38]. The LA Health follow-up paper did not include the psychosocial variables and all analyses were conducted separately for each outcome variable.
This paper demonstrates how multiple profiles, each characterized by a set of several indicators, can be used to jointly describe heterogeneous patterns of behaviors in more than one domain of interest; it also demonstrates how the dynamics of change, manifested across multiple domains, can be captured. The basic model for the task is the HMM. The superstate, as an extension of the hidden states in the basic HMM, can be used to prescribe a parsimonious representation of the potentially large number of combinations of behavioral patterns generated by the individual profiles. The structure of the HMM is also amenable to the use of mixed effects, which render it flexible enough to take into account covariate effects as well as individual-specific effects. In this paper, we exploit the random effects component for modeling school clusters.
Although in this paper we only used continuous variables as profile indicators, the method can be applied to discrete outcome variables as well [14, 18 ]. For cross-sectional data with discrete outcomes, this is equivalent to latent class analysis that contains an additional level of latent “super” class [39], which is related to the hierarchical latent class model [42]. For example, [39] applied a latent (super) class analysis to examine clusters of diabetes patients on their beliefs about several domains including symptom, cause, and medical management of diabetes. Thus, the current paper can be viewed as an extension of the latent (super) class analysis to a longitudinal setting.
The proposed MPHMM methodology has several limitations. First, the model could become difficult to interpret for a large number of profiles, especially when each profile contains a substantial number of hidden states. While computationally more complex MPHMMs are feasible even with a large number of profiles, in practice it is difficult to envision the use of more than three or four profiles for behavioral data. We have followed a hybrid data- and expert-driven approach to determine the appropriate number of states and have consolidated some states to improve interpretation. It is still not clear how the consolidation procedure can be formalized. Currently, the consolidation of states is highly reliant on clinical knowledge of the content experts. Indeed, the LA Health study example demonstrated the challenges for simultaneously handling multiple profiles in a longitudinal setting: first, the number of states could be too large for meaningful interpretation, and second, requirements of interpretation of states at both the local (profile state) level and the global (superstate) level might be different. Our experience suggested that at the global level parsimonious individual profile models were preferred, reflecting the need to reduce the cognitive load in processing and interpreting results across multiple domains. Or, to put it slightly differently, when models were examined individually at the local level, the tolerance for more complex models tended to be higher. Additionally, the out-of-sample validation procedure seems to suggest that the simpler model is empirically rather robust and actually exhibits lower prediction error than the more complex model. Apparently, the strategy for determining the models for respective profile states and for the superstate was not as clean as we wanted it to be. Like other applications in social sciences[40], criteria based on reasonableness, common sense, and clinical interpretation have been used for comparing and selecting models. We present specific details of our experience to illustrate the challenge in arriving at a practical compromise between clinical interpretability of the results and the complexity of statistical models.
We remark here that the profiles estimated from the joint model within each domain using the maximum-likelihood procedure described in the Methods section are not necessarily identical to the profiles estimated using only data from the individual domains. The current approach used the joint model and a hill-climbing strategy to simultaneously determine the number of profile states and superstates. An alternative strategy is to first determine the number of profile states by only using data from each domain and then determine the number of superstates conditioned on the number of profile states. However, as pointed out by a referee, joint model selection in profile states and superstates, while computationally more intensive, would be more consistent with the unified model based on the maximum likelihood procedure.
A second limitation of the method is the potential local optimum issue with the hill-climbing approach for determining the number states. The greedy hill-climbing algorithm described here is not guaranteed to result in a global optimum. Although recent literature shows that the hill-climbing method generally performs well in model selection [41], further refinements, such as a hybrid approach using random permutation of the order of profiles in the hill-climbing sequence, may be necessary for optimizing its performance in multi-profile HMM.
Another limitation of the proposed model is its difficulty in handling the potentially large number of covariates in the transition model. Currently, with only three superstates, the effects of intervention and several other risk factors can be assessed by fitting separate models for transitions of interest (Superstate 2 to 1 and to 3). When the number of (super)states and the number of covariates increase, or when a summary measure is required across all transitions, the current strategy would have limitations. An alternative is to impose an ordinal structure on the states and then apply ordinal statistical methods to the transitions [43, 44]. A Bayesian approach to inference is another potentially fruitful approach for inference when the number of parameters within the HMM is high [12, 45 ]. Finally, another limitation of the proposed model is its strict model assumptions, including the conditional independence assumption, invariance of model structure across time points, and the invariance of the transition matrix. These are, to a certain extent, inherent features of the HMM, which is a special case of the dynamic Bayesian network [46]. Conditional independence assumptions could generally be evaluated by residual analysis, similar to the way the Markov assumption was evaluated in the Results section. The limitation to the structure and the transition parameter may not be an important issue in the current application, which involves a short duration of study. However, in long-range health and medical applications, the assumption of invariance may be questionable. Some recent developments have emerged in the dynamic Bayesian network literature to ease the limitation [47].
Acknowledgments
This study is funded by the following grant: NIH U01HL101066-01.
References
- 1.Koplan J, Liverman C, Kraak V. Preventing childhood obesity: health in the balance. Natl Academy Pr; 2005. [PubMed] [Google Scholar]
- 2.Ogden C, Carroll M, Curtin L, McDowell M, Tabak C, Flegal K. Prevalence of overweight and obesity in the United States, 1999–2004. Jama. 2006;295(13):1549. doi: 10.1001/jama.295.13.1549. [DOI] [PubMed] [Google Scholar]
- 3.Daniels S, Arnett D, Eckel R, Gidding S, Hayman L, Kumanyika S, Robinson T, Scott B, St Jeor S, Williams C. Overweight in children and adolescents: pathophysiology, consequences, prevention, and treatment. Circulation. 2005;111(15):1999. doi: 10.1161/01.CIR.0000161369.71722.10. [DOI] [PubMed] [Google Scholar]
- 4.Dietz W. The obesity epidemic in young children. BMJ. 2001;322(7282):313–314. doi: 10.1136/bmj.322.7282.313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hassink S. Problems in childhood obesity. Primary care. 2003;30(2):357–374. doi: 10.1016/s0095-4543(03)00014-9. [DOI] [PubMed] [Google Scholar]
- 6.Rose G. The strategy of preventive medicine. University Press; 1992. [Google Scholar]
- 7.Macintyre S, Ellaway A. Social epidemiology. New York: Oxford University Press; 2000. Ecological approaches: rediscovering the role of the physical and social environment; pp. 332–348. [Google Scholar]
- 8.Williamson D, Champagne C, Harsha D, Han H, Martin C, Newton R, Jr, Stewart T, Ryan D. Louisiana (LA) Health: Design and methods for a childhood obesity prevention program in rural schools. Contemporary clinical trials. 2008;29(5):783–795. doi: 10.1016/j.cct.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Needham B, Crosnoe R. Overweight and depression during adolescence. Journal of Adolescent Health. 2004;36(1):48–55. doi: 10.1016/j.jadohealth.2003.12.015. [DOI] [PubMed] [Google Scholar]
- 10.Rabiner L. A tutorial on hidden Markov models and selected applications in speech recognition. Readings in speech recognition. 1990;53(3):267–296. [Google Scholar]
- 11.MacDonald I, Zucchini W. Hidden Markov and other models for discrete-valued time series. CRC Press; 1997. [Google Scholar]
- 12.Scott S, James G, Sugar C. Hidden Markov models for longitudinal comparisons. Journal of the American Statistical Association. 2005;100(470):359–370. [Google Scholar]
- 13.Wall M, Li R. Multiple indicator hidden markov model with an application to medical utilization data. Statistics in medicine. 2009;28(2):293–310. doi: 10.1002/sim.3463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ip E, Snow-Jones A, Heckert D, Zhang Q, Gondolf E. Latent markov model for analyzing temporal configuration for violence profiles and trajectories in a sample of batterers. Sociological Methods and Research. 2010;39:222–255. [Google Scholar]
- 15.Qu Y, Tan M, Kutner M. Random effects models in latent class analysis for evaluating accuracy of diagnostic tests. Biometrics. 1996;52:797–810. [PubMed] [Google Scholar]
- 16.Reboussin B, Ip E, Wolfson M. Locally dependent latent class models with covariates: an application to under-age drinking in the usa. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2008;171(4):877–897. doi: 10.1111/j.1467-985X.2008.00544.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Altman R. Mixed hidden Markov models: An extension of the hidden Markov model to the longitudinal data setting. Journal of the American Statistical Association. 2007;102(477):201–210. [Google Scholar]
- 18.Zhang Q, Snow Jones A, Rijmen F, Ip E. Multivariate discrete hidden markov models for domain-based measurements and assessment of risk factors in child development. Journal of Computational and Graphical Statistics. 2010;19(3):746–765. doi: 10.1198/jcgs.2010.09015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Desantis SM, Bandyopadhyay D. Hidden Markov models for zero-inflated Poisson counts with an application to substance use. Statistics in Medicine. 2011;30(14):1678–94. doi: 10.1002/sim.4207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Scharpf RB, Parmigiani G, Pvesner J, Ruczinski I. A hidden Markov model for joint estimation of genotype and copy number in high-throughput SNP chips. Annals of Applied Statistics. 2008;2(2):687–713. doi: 10.1214/07-AOAS155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Choi H, Nesvizhskii AI, Ghosh D, Qin ZS. Hierarchical hidden Markov model with application to joint analysis of ChIP-chip and ChIP-seq data. Bioinformatics. 2009;25(9):1715–1721. doi: 10.1093/bioinformatics/btp312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Murphy K. The Bayes net toolbox for matlab. Computing Science and Statistics. 2001;33(2):1024–1034. [Google Scholar]
- 23.Rijmen F. Technical Report. 2006. BNL: a matlab toolbox for Bayesian networks with logistic regression nodes. [Google Scholar]
- 24.Raudenbush S, Bryk A. Hierarchical linear models: Applications and data analysis methods. Vol. 1. Sage Publications, Inc; 2002. [Google Scholar]
- 25.Singer J. Using SAS proc mixed to fit multilevel models, hierarchical models, and individual growth models. Journal of Educational and Behavioral Statistics. 1998;23(4):323–355. [Google Scholar]
- 26.Dempster A, Laird N, Rubin D, et al. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society Series B (Methodological) 1977;39(1):1–38. [Google Scholar]
- 27.Baum L, Petrie T. Statistical inference for probabilistic functions of finite state markov chains. The Annals of Mathematical Statistics. 1966;37(6):1554–1563. [Google Scholar]
- 28.Bilmes J. Technical Report. 1997. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models. [Google Scholar]
- 29.Fahrmeir L, Tutz G. Multivariate statistical modelling based on generalized linear models. Springer Verlag; New York: 2001. [Google Scholar]
- 30.Lauritzen S, Spiegelhalter D. Local computations with probabilities on graphical structures and their application to expert systems. Journal of the Royal Statistical Society Series B. 1988;50(2):157–224. [Google Scholar]
- 31.Smyth P. Belief networks, hidden Markov models, and Markov random fields: a unifying view. Pattern Recognition Letters. 1997;18(11–13):1261–1268. [Google Scholar]
- 32.Viterbi AJ. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory. 13(2):260269. [Google Scholar]
- 33.Lystig T, Hughes J. Exact computation of the observed information matrix for hidden Markov models. Journal of Computational and Graphical Statistics. 2002;11(3):678–689. [Google Scholar]
- 34.Meilijson I. A fast improvement to the EM algorithm on its own terms. Journal of the Royal Statistical Society Series B (Methodological) 1989;51(1):127–138. [Google Scholar]
- 35.Friedl H, Kauermann G. Standard errors for EM estimates in generalized linear models with random effects. Biometrics. 2000;56(3):761–767. doi: 10.1111/j.0006-341x.2000.00761.x. [DOI] [PubMed] [Google Scholar]
- 36.Russell SJ, Norvig P. Artificial intelligence: A Modern Approach. 2. Prentice Hall; New Jersey: 2003. [Google Scholar]
- 37.Scott S. Bayesian methods for hidden Markov models: Rcursive computing in the 21st century. Journal of the American Statistical Association. 2002;97:337–352. [Google Scholar]
- 38.Williamson D, Champagne C, Harsha D, Han H, Martin C, Newton RJ, Sothern M, Stewart T, Webber L, Ryan D. Effect of an environmental school-based obesity prevention program on changes in body fat and body weight: a randomized trial. Pediatric Obesity. 2012 doi: 10.1038/oby.2012.60. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Grzywacz J, Arcury T, Ip E, Chapman C, Kirk J, Bell R, Quandt S. Older adults’ common sense models of diabetes. American Journal of Health Behavior. 2011;35(3):318–333. doi: 10.5993/ajhb.35.3.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Grusky DB, Hauser RM. Comparative social mobility revisited: Models of convergence and divergence in 16 countries. American Sociological Review. 1984;textbf49:19–38. [Google Scholar]
- 41.Tsamardinos I, Brown LE, Aliferis CF. The max-min hill-climbing Bayesian network structure learning algorithm. Machine Learning. 2006;65(1):31–78. [Google Scholar]
- 42.Vermunt J. Multilevel latent class models. Sociological Methodology. 2003;33(1):213–239. [Google Scholar]
- 43.Rejeski J, Ip E, Bertoni A, Bray G, Evans G, Gregg E, Zhang Q the Look AHEAD Research Group. Slowing the decline of physical disability among aging overweight/obese persons with Type 2 diabetes: The look AHEAD study. The New England Journal of Medicine. 2012;366(13):1209–1217. doi: 10.1056/NEJMoa1110294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ip E, Zhang Q, Rejeski J, Harris TSK. Partially ordered mixed hidden markov model for the disablement process of older adults. Journal of the American Statistical Association. 2013 doi: 10.1080/01621459.2013.770307. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Shirley K, Small D, Lynch K, Maisto S, Oslin D. Hidden Markov models for alcoholism treatment trial data. The Annals of Applied Statistics. 2010;4(1):366–395. [Google Scholar]
- 46.Ghahramani Z. Learning dynamic Bayesian networks. Adaptive Processing of Sequences and Data Structures. 1998:168–197. [Google Scholar]
- 47.Song L, Kolar M, Xing E. Time-varying dynamic Bayesian networks. Advances in Neural Information Processing Systems. 2009;22:1732–1740. [Google Scholar]