The Calculation of Free-Energy Differences by Confinement Simulations. Application to Peptide Conformers

Abstract

Conformational free-energy differences are key quantities for understanding important phenomena in molecular biology that involve large structural changes of macromolecules. In this paper, an improved version of the confinement approach, which is based on earlier developments, determines the free energy of the individual states by progressively restraining the molecular conformations to pure harmonic basins, whose absolute free energy can be computed by normal-mode analysis. The method is used to calculate the free-energy difference between two structurally known molecular states of the alanine dipeptide in vacuo, and the β-hairpin from protein G with an implicit solvation model. In all cases, the confinement results are in excellent agreement with the ones obtained from equilibrium molecular dynamics simulations, which have a much larger computational cost. The systematic and statistical errors of the results are determined and the origin of the errors is identified. The sensitivity of the calculated free-energy differences to structure-based definitions of molecular states is discussed. A variant of the method, which closes the thermodynamic cycle by a quasi-harmonic rather than harmonic analysis, is proposed. The latter is proposed for possible use with explicit solvent simulations.

INTRODUCTION

Many proteins and nucleic acids adopt different conformations as part of their function. This ability, which is encoded in their structure [1], has long been recognized as an important aspect of molecular biology involved in such functions as enzyme catalysis [2, 3], chemo-mechanical transduction [4, 5], ion permeation through lipid membranes [6, 7], and allosteric regulation of protein activity [8, 9], among others. The conformational changes are superposed on the dynamic fluctuations of a given conformer, which are implicated in substrate binding and product release, force transmission, molecular translocation, ion gating in biological channels, as well as chemical reactions, which involve inherently dynamic processes since atomic coordinates change along the reaction coordinate. The conformations accessible to a macromolecule interconvert in solution at varying rates depending on the activation free-energy barrier between them [10, 11]. Their populations at equilibrium, that is the probabilities of the macromolecule having a given three-dimensional structure, is determined by the relative free energies of the associated conformational basins. Thus, the calculation of the difference in the free energy for pairs of states would provide information on the relative thermodynamic stability and allow the determination of their solution concentrations. Moreover, analysis of the calculation is useful for obtaining insights concerning the factors involved in the stability difference.

Because the computation of the free-energy difference between pairs of conformational states of a macromolecule is a difficult task, there exists no general method for doing so, particularly for cases where two conformations differ significantly from each other. Methods, such as thermodynamic integration [12] and the exponential formula [13], which have been increasingly successful in alchemical free-energy simulations [14, 15], are not satisfactory for many conformational problems. If the end-states are significantly different, such methods can require a very large computational effort and can suffer from convergence problems (i.e., the so-called “overlap problem”), which may result in sizeable errors [16]. To improve the configurational overlap, free-energy calculations are usually divided into multiple steps, termed “windows”, which involve intermediate states along a reaction pathway. The choice of the path is critical for an efficient free-energy estimation because some paths lead to considerably faster convergence than others. This results in one of the classic limitations of free-energy methods, since finding a “good” reaction pathway by projecting the conformational transition on one or more order parameters can be a challenging task [17]. In addition to that, any calculated value of the free-energy difference between two states depends on how they are defined. For alchemical free-energy differences (e.g., changing one amino acid to another) this definition is straightforward. However, for conformational free-energy differences, such as those treated here, the definition is somewhat arbitrary and care is required to select meaningful states.

Given these difficulties, considerable effort is being devoted to the development of efficient conformational free-energy methods for biological systems [18]. Two recent promising developments, the “confinement” approach [19] and the “reference system” method [20] avoid the overlap problem by estimating the absolute free energy of the individual states by introducing a reference state whose free energy is easy to calculate. These methods correspond to the “rediscovery” of techniques introduced a long time ago [21–24]. Other new approaches are the “deactivated morphing” [25] based on the use of a nonphysical path in which the internal molecular interactions are completely turned off during the transformation; the “orthogonal space random walk” [26] which makes use of a random walk in both the reaction coordinate space and its generalized force space to speedup convergence; and nonequilibrium approaches such that described in Ref. [27], which are based on measurements of the work performed during nonequilibrium switches between the investigated states.

In the present paper we focus on the confinement method, which was recently proposed by Tyka et al. [19]. The method determines the absolute free energy of the individual states by progressively restraining the molecular conformations to pure harmonic basins, whose absolute free energy can be computed by normal-mode analysis [28–30]. The introduction of the harmonic reference state allows the evaluation of the free-energy change with no need for a direct transformation of one conformational ensemble into the other. We present technical developments that improve the efficiency of the method and show test-case applications on pairs of conformational states of the alanine dipeptide in vacuo, and the β-hairpin from protein G with an implicit solvation model. In all cases, the confinement results are in excellent agreement with the ones obtained from equilibrium molecular dynamics simulations. The analysis provides an understanding of the possible sources of errors in the confinement calculation and suggests ways to correct for them, which is important for future applications to more complex systems. Also, tests were made of the dependence of the calculated free-energy values on the structure-based definition of molecular states used to extract conformations from the corresponding basins. The confinement results are shown to be robust if the investigated basins are structurally homogeneous. Finally, a variant of the method which closes the thermodynamic cycle by quasi-harmonic analysis is proposed. The latter holds promise for extending the use of the confinement approach to systems with an explicit treatment of the solvent. Besides the technical aspects, the paper shows the first application of the method to the determination of the free-energy differences between two states of a polypeptide system, i.e., the β-hairpin of protein G. The β-hairpin is an excellent test-case: (i) it is a rather flexible system with many degrees of freedom; (ii) it preserves the complexity of the free-energy landscape of a real protein in that there is a well defined native state along with a denatured state with a large number of non-native microstates; (iii) it has been characterized in details by computer simulations, so that an exhaustive description of the free-energy basins and barriers among them is available [31]; (iv) its molecular size makes extensive simulations possible and full sampling of the conformational space at equilibrium can be ensured; and (v) its conformational free-energy differences between pairs of states can be computed independently from equilibrium MD and used as a rigorous test of the confinement results. The data presented here indicate that accurate predictions can be obtained at an affordable CPU cost.

The confinement method is reviewed in the next section and the newly introduced methodological improvement are presented. The free-energy difference between states of the alanine dipeptide and the β-hairpin of protein G, as computed by the improved version of the confinement method, is presented in the third section. The section presents an analysis of the possible sources of errors in the confinement calculation. A discussion of the significance of the results is given in the concluding section.

MATERIAL AND METHODS

Approach

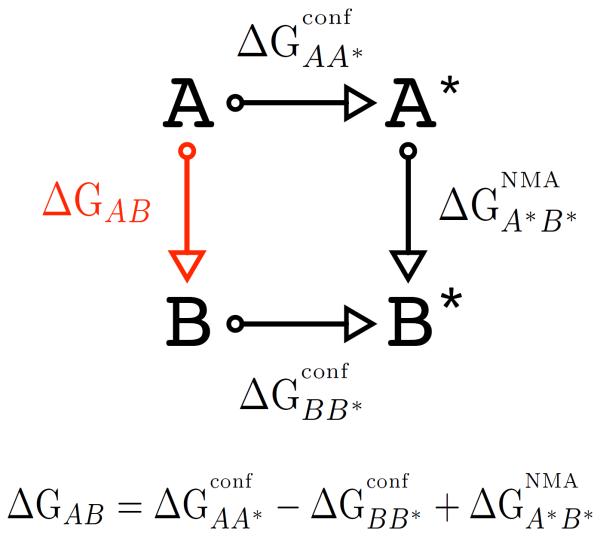
The confinement approach to determine the conformational free-energy difference, ΔG_AB, between two structurally known molecular states (A and B) is illustrated in Fig. 1. The value of ΔG_AB is obtained by transforming each molecular state into a reference state (A* or B*) whose absolute free energy can be computed accurately. Thus, if one can compute the free energy required to transform each actual state to its reference state, ΔG_AB can be determined without evaluating the transformation between the actual states; the latter could require crossing large energy barriers separating nearly non-overlapping regions of conformational space. The key to the efficiency of the method is to choose reference states that are strongly overlapping with the actual states, so that the free-energy difference can be efficiently computed by using standard methods such as thermodynamic integration [12] or the exponential formula [13]. In the confinement method, the reference state is chosen to be a pure harmonic state for which the absolute free energy can be computed analytically by normal-mode or quasi-harmonic analyses, which yield identical results. Starting from each of the two molecular states the system is transformed into the corresponding reference by introducing a harmonic potential with an increasing force constant. During the confinement, the conformational space available to the system is progressively reduced and the work performed by the restraining potential is recorded. The latter corresponds to the free-energy cost of reducing all non-harmonic contributions to the ΔG between the initial (anharmonic) and final (harmonic) states to a negligible value relative to the harmonic term, which can be calculated exactly; it is hereafter referred to as the free energy of confinement. In this analysis, the confinement free energies were computed by thermodynamic integration (see “Methods”). The normal-mode or quasi-harmonic free-energy change between the harmonically restrained states was then applied to close the thermodynamic cycle.

FIG. 1.

Thermodynamic cycle illustrating the confinement method. A and B represent molecular conformations corresponding to two different free-energy basins, and A* and B* represent the associated basins harmonically restrained to appropriate reference states. The free-energies of confinement for the two molecular states (i.e., $\Delta {\mathrm{G}}_{{\mathit{AA}}^{\ast }}^{\text{conf}}$ and $\Delta {\mathrm{G}}_{{\mathit{BB}}^{\ast }}^{\text{conf}}$) are computed by thermodynamic integration. The quantity $\Delta {\mathrm{G}}_{A^{\ast }{B}^{\ast }}^{\text{NMA}}$ is evaluated by normal-mode analysis. The free-energy difference between A and B conformers, ΔG_AB, which is the quantity of interest is obtained by combining the two confinement free energies with $\Delta {\mathrm{G}}_{A^{\ast }{B}^{\ast }}^{\text{NMA}}$ (see Equation).

Theory

Conformational Free-Energy Difference

The free-energy difference between the molecular states A and B is obtained from the thermodynamic cycle depicted in Fig. 1. The calculation is performed as follows. First, a reference state for each free-energy basin is selected. Then, a series of confinement simulations are performed with increasing restraining strengths (k) until the harmonic potential is sufficiently strong that the normal-mode approximation applies well. For each simulation the ensemble-averaged atomic deviations from the reference are computed as a function of k by measuring the average RMSD. These data are numerically integrated to compute the confinement free energy for each molecular state, i.e., $\Delta {\mathrm{G}}_{{\mathrm{AA}}^{\ast }}^{\text{conf}}$ and $\Delta {\mathrm{G}}_{{\mathrm{BB}}^{\ast }}^{\text{conf}}$. At the final restraint strength (k = k_f) a normal mode analysis is performed and the vibrational free-energy difference between the confined states (A* and B*) is computed through the canonical partition function of the classic harmonic oscillator. By combining the two confinements with the normal-mode analysis one obtains the desired free-energy difference

$$\Delta {\mathrm{G}}_{\mathrm{AB}}=\Delta {\mathrm{G}}_{{\mathit{AA}}^{\ast }}^{\text{conf}}-\Delta {\mathrm{G}}_{{\mathit{BB}}^{\ast }}^{\text{conf}}+\Delta {\mathrm{G}}_{A^{\ast }{B}^{\ast }}^{\text{NMA}}$$ (1)

where $\Delta {\mathrm{G}}_{{\mathit{AA}}^{\ast }}^{\text{conf}}={\mathrm{G}}_{A^{\ast }}-{\mathrm{G}}_A$, $\Delta {\mathrm{G}}_{{\mathit{BB}}^{\ast }}^{\text{conf}}={\mathrm{G}}_{B^{\ast }}-{\mathrm{G}}_B$, and $\Delta {\mathrm{G}}_{A^{\ast }{B}^{\ast }}^{\text{NMA}}={\mathrm{G}}_{B^{\ast }}-{\mathrm{G}}_{A^{\ast }}$. Each confinement simulation measures the anharmonic contribution of a given molecular state to the overall free-energy difference ΔG_AB, which is not included in the normal-mode calculation. The confinement free-energy is related to the entropic cost associated with the restriction of the conformational space accessible to the system in a harmonic model. However, it does not coincide with the difference in conformational entropy between the states under study. Perhaps surprisingly and in disagreement with a previous suggestion [25], an analysis of the thermodynamic components of ΔG^conf for the alanine dipeptide indicates that the enthalpic and entropic contributions to the confinement free-energy difference are comparable in magnitude (see “Supplementary Material”). The calculation of each contribution to the conformational free-energy difference (Eq. 1) is described in turn.

Confinement Simulations

Thermodynamic integration [12, 32] expresses the difference in free energy between two states as

$$\Delta \mathrm{G}={\int }_0^1{\langle \partial U(\mathbf{X},\lambda )∕\partial \lambda \rangle }_{\lambda }\mathrm{d}\lambda$$ (2)

where λ is a dimensionless parameter defining the integration path running from 0 to 1, ∂U(X, λ)/∂λ is the derivative of the potential energy with respect to λ, and 〈…〉 indicates an ensemble average at a particular λ. This integration is usually performed numerically by recording individual values of ∂U(X, λ)/∂λ and using the trapezoidal or Simpson's rule.

To calculate the confinement free energy, i.e., ΔG^conf_AA* and ΔG^conf_BB* in Fig. 1, one needs to perturb the free system A at λ = 0 to the restrained system A* at λ = 1. The energy function U(X, λ) is thus

$$U(\mathbf{X},\lambda )=U_{\mathrm{ff}}\left(\mathbf{X}\right)+\frac{1}{2}\lambda k_{\mathrm{f}}{\mid \mathbf{X}-{\mathbf{X}}_0\mid }^2$$ (3)

where U_ff (X) is the energy of the system with coordinate X calculated from the force field, X is the vector of atomic positions, X₀ is the configuration of the reference structure, and k_f is the final restraint force constant at λ = 1. The second term of Eq. 3 is the harmonic potential that is used to confine the system. In principle, any type of restraint is suitable provided that it is sufficiently strong at λ = 1 such that the normal-mode approximation is accurate. Here, we chose a harmonic restraint which is similar in nature to the absolute Cartesian restraint adopted in Ref. [19] except that the atomic coordinates of the reference are implicitly rotated and translated so as to bestfit the atoms of the actual molecular frame. The newly adopted restraining potential, which projects out the contributions to the confinement free energy resulting from the translational and rotational modes, has the advantage that it minimizes the total restraining energy and does not introduce any net force or torque on the system.

If one introduces k = λk_f, Eq. 2 can be restated using k as the variable of integration instead of λ as

$$\Delta {\mathrm{G}}^{\text{conf}}=\frac{1}{2}{\int }_0^{k_{\mathrm{f}}}{\langle {\mid \mathbf{X}-{\mathbf{X}}_0\mid }^2\rangle }_k\mathrm{d}k=\frac{1}{2}{\int }_0^{k_{\mathrm{f}}}{X}_k\mathrm{d}k$$ (4)

where

$$X_k={\langle {\mid \mathbf{X}-{\mathbf{X}}_0\mid }^2\rangle }_k$$ (5)

It follows from Eqs. 4 and 5 that the free energy of confinement can be obtained by simply recording the ensemble averages of the atomic deviations from the reference structure at different restraining strengths, k, and performing numerical integration over these values.

Fluctuations from the reference structure

The most obvious way to compute the ensemble-averaged X_k (Eq. 5) consists in recording the time series of the restraining energy at different values of k. From Eq. 3 it follows that

$$U_{\text{cons}}=\frac{1}{2}\lambda k_{\mathrm{f}}{\mid \mathbf{X}-{\mathbf{X}}_0\mid }^2$$ (6)

Thus, by introducing k

$$\frac{2U_{\text{cons}}}{k}={\mid \mathbf{X}-{\mathbf{X}}_0\mid }^2$$ (7)

and computing the ensemble average

$$X_k=\frac{2{\langle U_{\text{cons}}\rangle }_k}{k}$$ (8)

that is an operational definition of X_k [19]. However, this definition does not allow computation of X_k for the free system (i.e., k equal to zero) and is expected to suffer from numeric instability as vanishing k is approached. Alternatively, X_k can be deduced from the all-atom root-mean-square deviation (RMSD) from the reference structure X₀. In fact, from Eq. 5 and the definition of the ensemble average one can write that

$$X_k=\frac{1}{M}\sum _{j=1}^M{({\mathbf{X}}_j^k-{\mathbf{X}}_0)}^2$$ (9)

where j runs over the M molecular snapshots sampled in the simulation in the presence of the restraining potential with force constant k. Given that the RMSD from the reference of the j-th molecular conformation is

$${\text{RMSD}}_{\mathrm{j}}=\sqrt{\frac{1}{N}{({\mathbf{X}}_j^k-{\mathbf{X}}_0)}^2}$$ (10)

where N the total number of atoms in the molecule, it follows that

$$N\cdot {\text{RMSD}}_j^2={({\mathbf{X}}_j^k-{\mathbf{X}}_0)}^2$$ (11)

Thus, by computing the average over the canonical ensemble and combining the result with Eqs. 5 and 9 one obtains

$$X_k={\langle N\cdot {\text{RMSD}}^2\rangle }_k$$ (12)

which states that the atomic fluctuations X_k can be computed from the ensemble average of the RMSD from the reference structure for each value of the integration variable k. The new definition for X_k is more robust than the one given by Eq. 8. In fact, since the average RMSD has always a finite value even for the free (unrestrained) system, Eq. 12 does not diverge for vanishing k. In this study, Eq. 12 was used to compute the free energy of confinement.

Numerical Integration

The integration scheme proposed by Tyka et al. [19] was applied to compute the free energy of confinement. Numerical integration of the atomic fluctuations from the reference was performed by using the trapezoidal rule in a double log scale and fitting between successive data points with a power law of the form

$$X_k={\mathit{ak}}^b$$ (13)

For two successive data points P_i = (X_ki, k_i) and P_j = (X_kj, k_j) with j = i + 1, the area L_j underneath the fitted curve is given by

$$L_j=\frac{a}{b+1}{\left[k^{b+1}\right]}_i^j=\frac{a}{b+1}{\left[k^{b}k\right]}_i^j$$ (14)

and by substituting Eq. 13 into Eq. 14, one obtains

$$L_j=\frac{1}{b+1}{\left[X_{k}k\right]}_i^j=\frac{1}{b+1}(X_{k_j}{k}_j-X_{k_i}{k}_i)$$ (15)

where b is obtained from Eq. 13 by introducing log X_k

$$\begin{array}{c}\hfill \log X_{k_j}=\log a+b\log k_j\hfill \\ \hfill \log X_{k_i}=\log a+b\log k_i\hfill \end{array}$$ (16)

and subtracting the second equation from the first¹; i.e.

$$b=\frac{\log X_{k_j}-\log X_{k_i}}{\log k_j-\log k_i}$$ (17)

The confinement free-energy change between states A and A* is given by

$$\Delta {\mathrm{G}}^{\text{conf}}{\mathit{AA}}^{\ast }=\sum _j{L}_j$$ (18)

Normal Mode Analysis (NMA)

The absolute free energy of the restrained conformations (A* or B*) is calculated using the classical formula for the canonical partition function of a system of N particles with κ vibrational degrees of freedom [33]

$$Z=\exp (-E_0∕k_{B}T)\prod _i^k\frac{k_{B}T}{h{\nu }_i}$$ (19)

where ν_i is the frequency of the i-th normal mode, E₀ is the potential energy at the minimum, T is the temperature, h is Plank's constant, and k_B is the Boltzmann constant. Knowledge of the partition function enables one to calculate the free energy of the restrained state (G_A*) by

$$G_{A^{\ast }}=-k_{B}T\log Z_A$$ (20)

Thus, the remaining leg of the thermodynamic cycle shown in Fig. 1 is computed directly (without the need to construct a path to transform A into B) as

$$\Delta {\mathrm{G}}_{A^{\ast }{B}^{\ast }}^{\text{NMA}}={\mathrm{G}}_{B^{\ast }}-{\mathrm{G}}_{A^{\ast }}$$ (21)

The normal mode frequencies, which are used to compute $\Delta {\mathrm{G}}_{A^{\ast }{B}^{\ast }}^{\text{NMA}}$ by solving Eqs. 19 and 20, are obtained by finding the eigenvalues of the mass-weighted matrix of second derivatives of the effective energy (Hessian) at the minimum. For this purpose, the reference structure was energy-minimized in the presence of the full restraining potential (i.e., k = k_f) by performing 5000 SD steps followed by 10000 additional ABNR steps; we note that if a well energy-minimized conformation is used as reference, energy minimization in the presence of the restraining potential has a no effect on the structure (see Fig. S9 in the “Supplementary Material”). Normal mode analysis on the resulting structure in the all-atom representation was performed by using the VIBRAN module in CHARMM [34]. Since a best-fit restraint is applied to confine the system, only the 3N − 6 non-zero frequencies corresponding to the internal degrees of freedom are included in calculating G_A* (or G_B*). We note that a quantum mechanical analysis of the vibrational free-energy difference between the harmonically restrained states yields essentially the same result as the classical analysis (see “Supplementary Material” for details).

Quasi-Harmonic Analysis (QHA)

Alternatively, the absolute free energy of the restrained conformations (A* or B*) can be calculated by a quasi-harmonic analysis. In the quasi-harmonic approximation the fluctuations observed during the motions of the system are described by a multivariate Gaussian probability distribution [35]. Under this assumption, a temperature-dependent effective potential of a quadratic form, which results in the Gaussian probability distribution, can be defined [36] and the quasi-harmonic modes computed from the mass-weighted Hessian defined in terms of its elements as F_ij = k_BT (σ⁻¹)_ij. The F_ij are computed from the temperature-dependent variances (diagonal elements) and covariances (off-diagonal elements) of the Cartesian coordinates fluctuations,

$${\sigma }_{\mathit{ij}}=\langle (x_i-{\overline{x}}_i)(x_j-{\overline{x}}_j)\rangle$$ (22)

which are obtained from a molecular dynamics simulation. Thus, by solving the secular equation

$$\text{det}(\mathbf{F}-{\omega }^2\mathbf{M})=\text{det}({\mathbf{M}}^{1∕2}\sigma {\mathbf{M}}^{1∕2}-\frac{\mathit{kT}}{{\omega }^2}1)=0$$ (23)

where M is the mass matrix, one obtains the quasi-harmonic frequencies ω_k, which are used to compute the vibrational entropy in the classical expression

$${\mathrm{S}}^{\text{QHA}}=k_B\sum _{k=1}^{3N-6}\ln \left(\frac{k_{B}T}{h{\omega }_k}\right)$$ (24)

where k_B is the Boltzmann constant, T the temperature, h is the Plank's constant, and ω_k the kth quasi-harmonic frequency. Finally, the quasi-harmonic free energy is determined by

$${\mathrm{G}}^{\text{QHA}}={\mathrm{H}}^{\text{QHA}}-T{\mathrm{S}}^{\text{QHA}}$$ (25)

where H^QHA is the ensemble-averaged effective energy obtained from the MD run.

In the confinement calculation, the quasi-harmonic analysis is applied to the MD run carried out in the presence of the strongest restraining potential (k = k_f) for each molecular state. We note that at large restraining strengths, the harmonic approximation holds and the quasi-harmonic result for the free energy is correct. Although the answers from QHA and NMA must be identical in the limit of the harmonic approximation, the former enables the analysis of a subset of degrees of freedom of the system, thus opening the possibility of using the confinement approach in the context of explicit solvent simulations (see “Discussion”).

Free-energy Profiles

One-dimensional barrier preserving free-energy profiles provide a rigorous yet intuitive description of the system kinetics [37, 38]. Here, cut-based free-energy profiles projected onto the “natural coordinate” [39], which is constructed such that the diffusion coefficient is constant along the profile, were computed for various restrained runs and used to examine the origin of statistical errors in the confinement calculation (see “Results”). For this purpose, the MD simulations were first projected onto the principal component space defined by the distance between all atom pairs [40]. This space is defined by the eigenvectors of the covariance matrix of the interatomic distances. Molecular snapshots sampled by MD were then clustered by binning the first three principal components so as to build an equilibrium kinetic network in which nodes and links correspond, respectively, to molecular configurations and directed transitions between pairs of nodes [41]. Finally, the free-energy profiles were computed by the “pfoldf” method described in Ref. [37]. The resulting profile is invariant with respect to any arbitrary transformation of the reaction coordinate and is plotted as a function of the “natural coordinate”, which is constructed in such a way that the diffusion coefficient is constant along the profile [39].

Systems and Setups

The molecular systems used for this study are the alanine dipeptide and the β-hairpin from protein G. The alanine dipeptide is the N-acetyl-N'-methylamide derivative of alanine, which has become a standard model for theoretical studies [27, 42–46]. The β-hairpin from protein G is a 16-residue peptide that has been shown by NMR to fold even in the absence of the rest of the protein [47]. The β-hairpin peptide, which has the following amino-acid sequence Gly-Glu-Trp-Thr-Tyr-Asp-Asp-Ala-Thr-Lys-Thr-Phe-Thr-Val-Thr-Glu, is an interesting system because in spite of the small size it preserves the complexity of the free-energy landscape of a real protein; i.e., it shows a well defined native state along with a denatured state with a large number of non-native microstates [31].

Alanine dipeptide

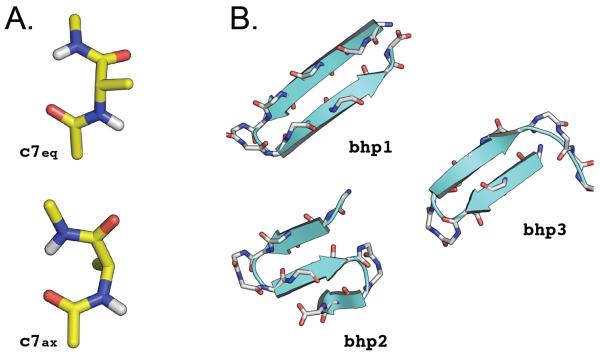
The alanine dipeptide was modeled with the polar-hydrogen potential function (12 atoms) [48] and simulated in vacuo at 300 K with infinite cutoffs for the non-bonded interactions. The system was simulated in vacuo because the corresponding free-energy landscape includes only two significant minima (c7eq and c7ax, see Fig. S1) which are separated by high free-energy barriers (8.5 and 10.5 kcal/mol from c7eq) [49]; i.e., it results in a simplified energy landscape and introduces a challenging task for the determination of the free-energy difference between the states of interest due to the large barriers between them. For all MD simulations, Langevin dynamics with a friction value of 1.0 ps⁻¹ was used; the friction is introduced to enhance the Markovian character of the time evolution of the system so as to improve the sampling efficiency, including energy transfer among the normal modes. The integration time step was set to 1 fs. Such setup ensures that molecular configurations saved every 1000 steps (1 ps) are independent. Two conformational states, called c7eq and c7ax, were considered (see Fig. 2A).

FIG. 2.

Molecular systems and conformational states used for this study. (A) Alanine dipeptide. The c7eq and c7ax molecular structures were considered; they correspond to the deepest free-energy basins at 300 K in vacuo (see Fig. S1). (B) β-Hairpin from protein G. Three molecular states were investigated: the native β-hairpin state (bhp1), the three-stranded β-sheet state (bhp2), and an out-of-register β-hairpin state (bhp3); they were previously identified as representative of the three deepest free-energy basins at 360 K [31]. Molecular representations were drawn with the help of PYMOL [55].

β-Hairpin from protein G

The β-hairpin peptide was modeled with the polar-hydrogen potential function [48] with no blocking groups for the terminal residues (160 atoms). Solvation effects were approximated by the EEF1 effective model [50] which contains screened electrostatic interactions and a Gaussian term to represent the hydrophobic interactions. This model was used to permit comparison with earlier work [31]. Accordingly, MD simulations were carried out at 360 K. Langevin dynamics with a friction value of 1.0 ps⁻¹ was used for all runs to increase sampling efficiency; although such friction is much smaller than the one of water (i.e., 28 ps⁻¹ at 360 K), the thermodynamic properties of the system are, of course, independent of the friction used. The SHAKE algorithm [51] was used to fix the length of the covalent bonds involving hydrogen atoms, which allows for an integration time step of 2 fs. Molecular snapshots were saved every 1000 steps (2 ps). Three conformational states were considered: the native β-hairpin state (bhp1), the three-stranded β-sheet state (bhp2), and an out-of-register β-hairpin state (bhp3); see Fig. 2B. These structures were identified in a previous MD simulation study [31] as representative of the three deepest free-energy basins at 360 K.

Confinement simulation setup

A confinement simulation requires introduction of a number of parameters. The choice for these parameters is not trivial and may be strongly system dependent. They include: (i) the range of restraint strength to be investigated (i.e., k_min and k_max); (ii) the distribution of the restraint strengths in that range; (iii) the number of restrained runs to be performed; (iv) the length of the individual MD runs; (v) the selection of the reference state; and (vi) the structural definition of the free-energy basins corresponding to the molecular states under investigation. The results presented in this paper indicate that it is possible to rationalize the choice of (ii) and (v), while the remaining parameters have to be justified by examining the convergence of the results. Consequently, the parameters for the two systems are given in the corresponding result sections (see below). All restrained MD runs were performed with the program CHARMM [34]. Efficient analysis of the simulations was performed with the program Wordom [52]; the latter was used to identify molecular snapshots belonging to the basins of interest and compute the ensemble-averaged fluctuations from the time series of the all-atom RMSD from the reference structure.

RESULTS

Alanine dipeptide in vacuo

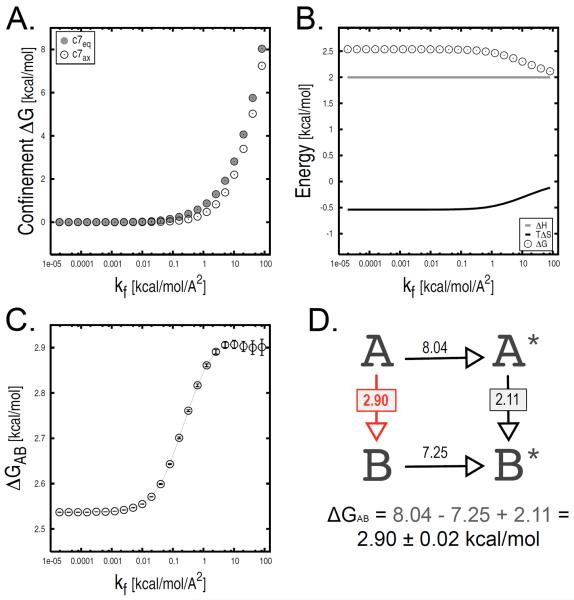
The confinement approach is applied to compute ΔG_AB between the c7eq and c7ax conformational states of the alanine dipeptide in vacuo (Fig. 2A). For the confinement in each minimum, 23 restrained MD simulations with harmonic force constants ranging from 1.95 · 10⁻⁵ to 82 kcal/mol/Ų were performed; intermediate k values are determined from the recursive sequence k_i = 2k_i−1, with k₀ = 1.95 · 10⁻⁵ kcal/mol/Ų. Each MD run was carried out for 20 ns independently of the restraining strength, which corresponds to 20000 molecular frames per run at a saving frequency of 1 configuration/ps. Thus, the total simulation time is 920 ns per confinement calculation (i.e., 23 runs × 20 ns × 2 legs). Deeply energy-minimized conformations were selected as reference structures for each molecular state. The value of the φ dihedral angle was used to assign molecular configurations sampled by MD to the c7eq or c7ax free-energy basins; i.e., given the simple shape of the free-energy surface in vacuo, structures with 0 ≤ φ ≤ 130 were assigned to the c7ax basin and the others to c7eq (see Fig. S1 for details). The time series of the all-atom RMSD from the reference structure were collected for each restrained run and used to compute the ensemble-averaged atomic fluctuations, X_k. Numerical integration of these data points with k_f equal to 82 kcal/mol/Ų yielded confinement free energies of 8.04 and 7.25 kcal/mol for c7eq and c7ax, respectively (see Fig. 3A). NMA on the reference structures minimized in the presence of the largest restraining potential provided a ΔG^NMA of 2.11 kcal/mol (ΔH^NMA and TΔS^NMA are equal to 2.00 and −0.11 kcal/mol, respectively); see Fig. 3B. As described by Eq. 1, the confinement calculation with k_f equal to 82 kcal/mol/Ų yielded a ΔG_AB of 2.90 · 0.02 kcal/mol between c7eq and c7ax in vacuo (Fig. 3D); the free-energy error was approximated by means of the specialized block analysis presented below. This value is in good agreement with the free-energy difference at 300 K obtained from a 6 μs replica-exchange molecular dynamics [53] simulation (3.02 ± 0.13 kcal/mol), and 2.5 (2.96 ± 0.11 kcal/mol) and 4.2 μs (2.92 ± 0.03 kcal/mol) equilibrium MD sampling at 400 and 500 K after Boltzmann reweighting (see “Supplementary Material” for details); ΔG_AB values obtained from these calculations are given in parenthesis. We observe that while the individual contributions on the right-hand side of Eq. 1 keep changing as a function of k_f, the conformational ΔG has converged for k_f larger than 2 kcal/mol/Ų (Fig. 3C).

FIG. 3.

Confinement analysis of the c7eq and c7ax states of the alanine dipeptide in vacuo. All free-energy terms are shown as a function of the final restraint strength k_f. (A) Confinement free energies for both molecular states. (B) Harmonic free-energy difference; both the enthalpic and entropic harmonic contributions are shown. (C) Total free-energy difference (i.e., ΔG_c7ax − ΔG_c7eq) with the associated error. For k_f larger than 2 kcal/mol/Ų, ΔG_AB has converged to a value of 2.90 ± 0.02 kcal/mol. (D) Thermodynamic analysis corresponding to a final restraint strength of 82 kcal/mol/Ų. Molecular states A and B correspond to c7eq and c7ax, respectively.

The analysis was repeated by using a variant of the confinement method that applies a quasi-harmonic analysis (QHA) to compute the free-energy change between the harmonically restrained states. The QHA results are reported in Fig. 4A as a function of k. At the strongest restraining potential (i.e., k_f = 82 kcal/mol/Ų) ΔG_A*B* is equal to 2.10 kcal/mol, which is in excellent agreement with the value obtained from NMA (see above). By solving Eq. 1 the quasi-harmonic variant of the confinement method gives a free-energy change of 2.90 kcal/mol. In analogy to the above, this value has converged for k larger than 2 kcal/mol/Ų (Fig. 4B).

FIG. 4.

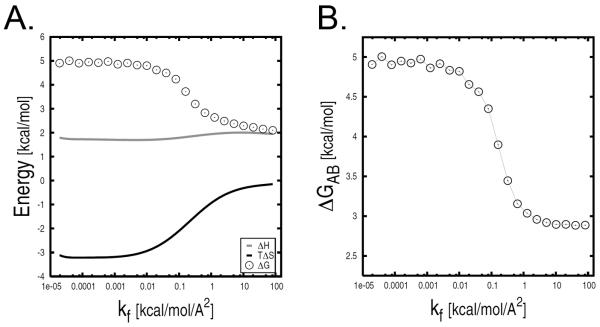
Confinement analysis of the c7eq and c7ax states of the alanine dipeptide in vacuo by the quasi-harmonic variant. (A) Quasi-harmonic free-energy difference as a function of k_f; both the enthalpic and entropic harmonic contributions are shown. (B) Total free-energy difference (i.e., ΔG_c7ax − ΔG_c7eq.) as a function of k;

β-Hairpin from protein G

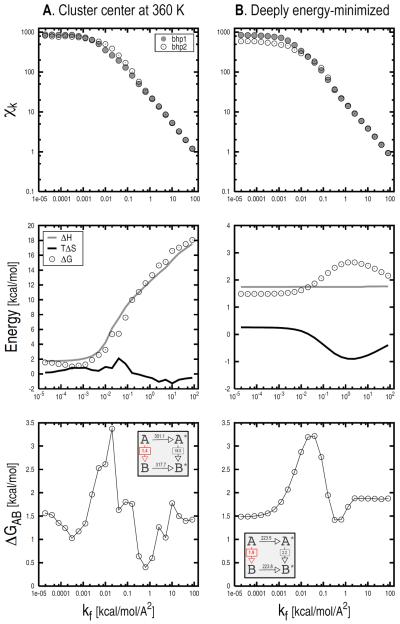
The confinement approach was applied to compute the free-energy difference between basins 1 and 2 of the β-hairpin peptide (see Fig. 2B). For the confinement in each minimum, 23 restrained MD simulations with harmonic force constants ranging from 1.95 · 10⁻⁵ to 82 kcal/mol/Ų were performed; i.e., the setup for the confinement experiment is essentially the same as for the alanine dipeptide. The system was simulated for 100 ns at each restraining strength, which corresponds to 50000 molecular frames per run for a total sampling of 4.6 μs per confinement simulation (i.e., 23 runs × 100 ns × 2 legs). The centers of the most-populated clusters at 360 K were chosen as the reference structures for bhp1 and bhp2; they were found by equilibrium MD simulations at 360 K [31]. Molecular conformations belonging to the respective basins were extracted from the restrained MD runs. Given that an “a priori” definition for a free-energy basin does not exist, a C_α-RMSD of 2.0 Å from the reference structure was arbitrarily chosen as a criterion to define the boundaries of the basin and filter out “non-contributing” conformations, i.e., conformations sampled by MD but considered to be part of other basins (see also below). The time series of the all-atom RMSD from the reference were collected and used to compute the ensemble-averaged atomic fluctuations, X_k. The distribution of the RMSD is relatively broad for low restraining strengths (i.e., k < 1.00 · 10⁻² kcal/mol/Ų), and it becomes much more “peaked” when large force constants are applied (see Fig. S8). Accordingly, X_k values converge rapidly in the high k range, whereas longer simulations are required in the low k range. In the case of β-hairpin, convergence in X_k is rapid in the whole k range; i.e., on the order of a few nanoseconds for k > 1.00 · 10⁻² and dozens of nanoseconds for k < 1.00 · 10⁻² (see Fig. S8). X_k values at different restraint strengths are shown in Fig. 5A (top). Numerical integration of the data points with k_f equal to 82 kcal/mol/Ų yields confinement free energies of 301.11 and 317.73 kcal/mol for bhp1 and bhp2, respectively. NMA on the reference structures minimized by 5000 steps of SD followed by 10000 steps of ABNR in the presence of a restraining potential with a spring constant of 82 kcal/mol/Ų yields a ΔG_A*B* of 18.05 kcal/mol (ΔH^NMA and TΔS^NMA are equal to 17.54 and −0.51 kcal/mol, respectively); see Fig. 5A, middle. The ΔG_AB is determined by solving Eq. 1. Fig. 5A (bottom) shows the value of ΔG_AB as a function of k. When the harmonic approximation applies well (i.e., k > 20 kcal/mol/Ų) similar free-energy difference are obtained. For k_f equal to 82 kcal/mol/Ų the confinement calculation yields a bhp1/bhp2 free-energy difference of 1.42 kcal/mol.

FIG. 5.

Effect of the choice of the reference structure on the confinement results for β-hairpin. The ensemble-averaged fluctuations (X_k), the thermodynamic components of $\Delta {\mathrm{G}}_{A^{\ast }{B}^{\ast }}^{\text{NMA}}$, and the total free-energy change (i.e., ΔG_bhp2 − ΔG_bhp1) are shown at various k_f values from top to bottom, respectively. Results corresponding to different selections for the reference structure are shown: (1) the centers of the most-populated cluster at 360 K; (2) deeply energy-minimized conformations. The insets in the bottom two panels report the numerical values for the various legs of the thermodynamic cycle corresponding to a final restraint strength of 82 kcal/mol/Ų. Molecular states A and B correspond to bhp1 and bhp2, respectively. The analysis indicates that energy-minimized conformations should be used as reference structures (see text).

Selection of the Reference State

We note that the free-energy difference between the confined states strongly depends on the value of k (Fig. 5A, middle). For increasing k, ΔG^NMA increases monotonically until it plateaus at very large restraining strengths (k > 10⁴ kcal/mol/Ų, data not shown). By considering the different contributions to the free-energy change, it is apparent that the enthalpic term (in grey) dominates over the entropic one (in black). The reason for such a behavior lies in the choice of the reference structure for the confinement simulations, which appears not to be appropriate. In fact, a cluster center is a relatively high potential energy conformation which does not correspond to a minimum on the PES. Thus, during the confinement the restraining potential not only reduces the conformational space available to the molecule but performs work against the molecular potential. The latter has important consequences: (i) the enthalpic contribution to ΔG^NMA is largely dominant, thus making NMA essentially useless; (ii) much larger restraining strengths are required to stabilize the enthalpic term in the NMA leg, thus increasing the number of restrained MD runs required; (iii) the free energy required to confine the system is larger than that required to confine it to a minimum of the PES (see below), which results in larger errors in the value of the ΔG_AB.

To verify these hypotheses, the confinement calculation was repeated by selecting deeply energy-minimized conformations as reference structures. The X_k values computed at different strengths are shown in Fig. 5B (top). The confinement free energies for bhp1 and bhp2 obtained for k_f = 82 kcal/mol/Ų are equal to 223.50 and 223.78 kcal/mol, respectively. We note that the selection of energy-minimized structures as references lowers the confinement free energies for bhp1 and bhp2 by 77.28 and 93.9 kcal/mol, respectively. The thermodynamic cycle was finally closed by NMA, which in the presence of a restraining potential with a spring constant of 82 kcal/mol/Ų yielded a ΔG^NMA of 2.16 kcal/mol (ΔH^NMA and TΔS^NMA are equal to 1.76 and −0.40 kcal/mol, respectively). Interestingly and in contrast to what was found above, the enthalpic contribution to the total ΔG^NMA is essentially independent of the strength of the restraining potential (Fig. 5B, middle). As a result, the bhp1/bhp2 free-energy difference shows a much smoother profile as a function of k and has converged to a value of 1.88 kcal/mol at k larger than 2 kcal/mol/Ų (Fig. 5B, bottom). This value is in excellent agreement with the free-energy difference of 1.86 kcal/mol ± 0.12 kcal/mol obtained from 200 μs MD sampling at equilibrium; i.e., the latter was obtained from 50 independent MD simulations at 360 K each of which was 4 μs long (see “Supplementary Material” for details on the calculation). The comparison validates the confinement results.

Treatment of Errors

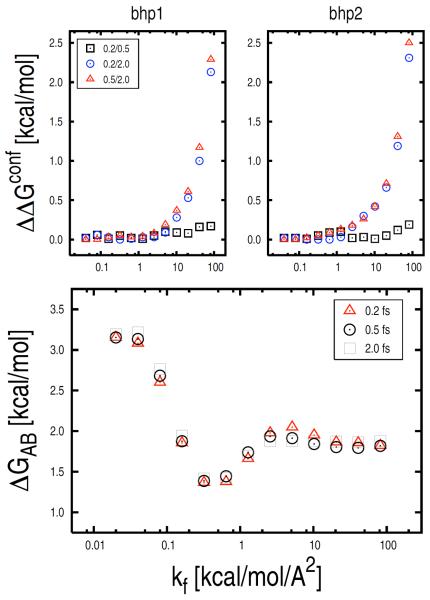
An understanding of the possible sources of errors in a confinement calculation is important for future applications, particularly for more complex systems. Both systematic and statistical errors that can affect the numerical value of the free-energy difference determined by the confinement method were investigated. By “systematic” errors are designated errors that are due to inaccuracies in the estimation of the ensemble-averaged fluctuations arising in the presence of strong restraining forces; the latter may cause a systematic overshooting of the potential energy minimum which leads to an overestimation of the atomic fluctuations. Systematic errors arising from inaccuracies of the potential function, which are difficult to evaluate, are not considered. If the ΔG^NMA between the confined states of β-hairpin is assumed to be exact (Eq. 21), which is reasonable, errors result from the confinement simulations. Systematic errors are likely to occur in the high force-constant range (i.e., k > 10 kcal/mol/Ų) where too large an integration time step may lead to the above mentioned inaccuracies in the ensemble-averaged fluctuations. By contrast, statistical errors are expected to occur in the low force-constant range (i.e., 0 ≤ k ≤ 0.001 kcal/mol/Ų) where sampling of the essentially unconstrained basin can be intrinsically problematic. To address these issues: (i) the confinement simulations were repeated by using smaller integration time steps; and (ii) a specialized block analysis was performed to estimate the error bar on the computed ΔG (see below).

Systematic Errors

To search for systematic errors, the confinement simulations in the high force-constant range (i.e., k > 0.04 kcal/mol/Ų) were repeated by decreasing the integration time step from 2.0 fs to 0.5 and 0.2 fs; i.e., 4 and 10 times smaller than the original value, respectively. X_k values were computed at different restraint strengths and confinement free energies determined as a function of k. As shown in Fig. 6 (top), the reduction of the integration time step results in non-negligible systematic differences in the integrated value of the free energy of confinement; i.e., up to 2.5 kcal/mol. As expected, systematic errors become important (> 0.1 kcal/mol) when k is large (k > 1 kcal/mol/Ų). We note that for very high force constants (k > 2 kcal/mol/Ų) non-negligible systematic differences are found even between the 0.2 and 0.5 fs time-step results, suggesting that very short time steps are required in this range to obtain accurate free-energy values. However, despite the presence of these systematic errors, ΔG_AB obtained from confinement calculations with shorter time intervals are essentially the same (see Fig. 6, on bottom); i.e., ΔG values obtained by solving Eq. 1 with k_f = 82 kcal/mol/Ų for the 0.2, 0.5, 2.0 fs time-step calculations are equal to 1.85, 1.87, and 1.88 kcal/mol, respectively. It is encouraging that the systematic errors in the individual confinement simulations cancel out. Our hypothesis is that for k > 2 kcal/mol/Ų (i.e., the range in which non-negligible systematic errors are found) the β-hairpin states approach the “super-harmonic” region where the restraining potential is so strong that the free energy of the harmonic oscillator becomes independent of the reference structure (see “Supplementary Material”). This behavior, as well as the width of the super-harmonic region in k space, may be system dependent and should be investigated in more detail for larger peptides and proteins.

FIG. 6.

Systematic errors in the confinement calculation. On top, confinement free-energy differences determined by calculations using integration time steps of varying sizes (i.e., 2.0, 0.5, and 0.2 fs) for the β-hairpin states bhp1 and bhp2 are shown as a function of k_f. The reduction of the time-step size results in non-negligible systematic differences. On bottom, ΔG_AB (i.e., ΔG_bhp2 − ΔG_bhp1) is shown as a function of k_f for the same confinement calculations. The free-energy change results are not affected by the systematic errors observed in the confinement simulations (on top).

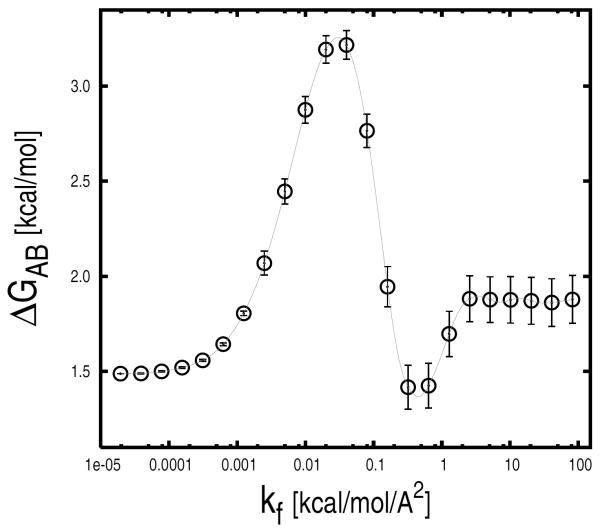
Statistical Errors

Statistical errors in the confinement approach are essentially due to limited sampling in the various restrained runs. Standard analyses, such as block analysis, boot-strapping, etc., could be applied to estimate the statistical uncertainty on the ensemble-averaged fluctuations which are used to compute the free energy of confinement. However, since the individual contributions are strongly non-homogeneous, a correct analysis would require larger weights for errors introduced in runs associated with larger contributions. Because of this complication, statistical errors were estimated by means of a specialized block analysis, which is described in the “Supplementary Material”. Individual and cumulative statistical errors of the free energy of confinement for bhp1 and bhp2 are reported in Fig. 7. In both cases, the largest errors are found in the intermediate k range (i.e., 0.001 < k < 0.3 kcal/mol/Ų); see grey zone in Fig. 7. By contrast, small errors are observed in both the high and low k ranges. The high k result is expected and consistent with the rapid convergence of the ensemble-averaged fluctuations in the presence of strong restraining potentials; the latter is somewhat surprising. As follows from Eq. 15, the contributions of the individual restrained runs to the value of the free energy of confinement depend not only on the size of the ensemble-averaged fluctuations (X_k), which are found to be larger in the low k range, but also on the strength of the restraining potential (k) at which the fluctuations are measured. Thus, for very small values of k the confinement runs make a small, if not negligible, free-energy contribution even in the presence of large fluctuations. Analogously, statistical errors associated with these runs contribute little to the total error of the confinement free energy (see Fig. 7). The analysis indicates that the confinement runs performed in the presence of restraining potentials of intermediate strength are crucial for obtaining accurate free-energy estimates.

FIG. 7.

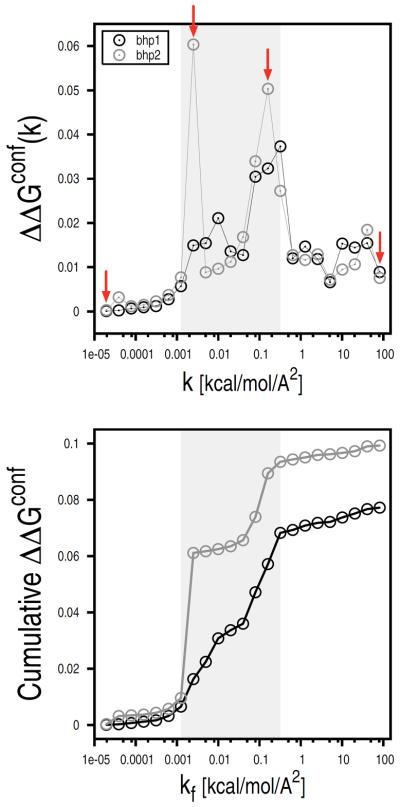
Statistical errors in the confinement calculation. Individual (top) and cumulative (bottom) statistical errors of the free energies of confinement for the β-hairpin states are reported as a function of k_f. Errors of the individual restrained runs were computed by dividing the MD trajectories into eight blocks. Red arrows indicate the restrained runs that were used for the free-energy profile analysis (see Fig. 9). The largest statistical errors were found in the intermediate k range (0.001 < k < 0.3 kcal/mol/Ų) here shown by a light-grey rectangle (see text).

Statistical errors of the confinement simulations were finally combined to obtain an estimate of the total error affecting the free-energy difference determined by the confinement calculation. At 360 K, errors of the free energy of confinement for bhp1 and bhp2 were found to be 0.078 and 0.099 kcal/mol, respectively. Assuming ΔG^NMA in Eq. 1 to be exact, these values were combined by the simple equation

$$\Delta \Delta {\mathrm{G}}_{\mathit{AB}}=\sqrt{{\left[\Delta \Delta {\mathrm{G}}_{{\mathit{AA}}^{\ast }}^{\text{conf}}\right]}^2+{\left[\Delta \Delta {\mathrm{G}}_{{\mathit{BB}}^{\ast }}^{\text{conf}}\right]}^2}$$ (26)

to account for error propagation. For k_f = 82 kcal/mol/Ų, ΔΔG_AB is equal to 0.13 kcal/mol. ΔG values with the associated error are shown in Fig. 8 as a function of the final restraint strength k_f. For k larger than 2 kcal/mol/Ų the ΔG_AB has converged to a value of 1.88 ± 0.13 kcal/mol.

FIG. 8.

Free-energy difference between the β-hairpin states bhp1 and bhp2 (i.e., ΔG_bhp2 – ΔG_bhp1). ΔG_AB values along with the associated error are shown as a function of the final restraint strength, k_f. For k_f larger than 2 kcal/mol/Ų ΔG_AB has converged to a value of 1.88 ± 0.13 kcal/mol.

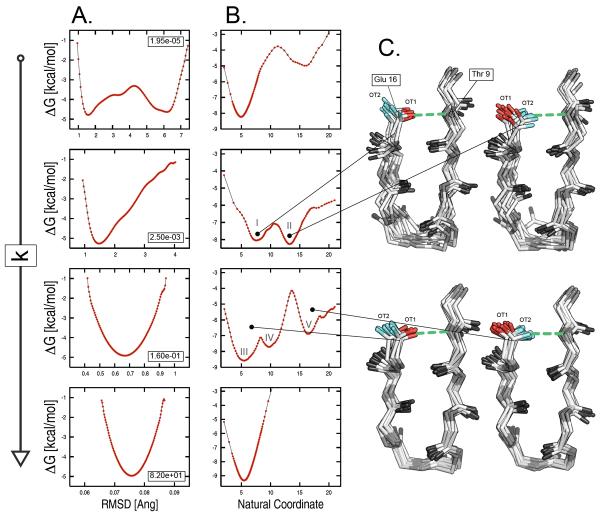
To examine the origin of such statistical errors, the free energy was projected onto the all-atom RMSD from the reference structure for four confinement runs of bhp2 corresponding to restraint strengths of 1.95e-05, 0.0025, 0.16, and 82 kcal/mol/Ų (see red arrows in Fig. 7); these are the lowest and the highest k values, and the two intermediate k values that are associated with the largest errors. At all restraint strengths but the lowest, the free-energy profiles show a single basin surrounded by high barriers (see Fig. 9A). This picture cannot explain the sampling problems detected in the intermediate k range so that the presence of some “hidden complexity” on the underlying free-energy surface must be introduced [31]. To check for that, the free energy was projected onto the “natural coordinate” resulting from a principal component analysis of the interatomic distances (see “Methods”). This time, the profiles corresponding to the low and intermediate restraint strengths show multiple basins separated by relatively high free-energy barriers (see Fig. 9B). The latter are responsible for the large statistical errors found at intermediate k values (see Fig. 7). The structural analysis of the two confinement runs at intermediate k (i.e., for k equal to 0.0025 and 0.16 kcal/mol/Ų) unveiled the origin of the hidden complexity of the free-energy landscape. The comparison of molecular snapshots extracted from basins 4 and 5 for k equal to 0.0025 kcal/mol/Ų, and basins 4 and 7 for k equal to 0.16 kcal/mol/Ų shows a striking difference in the H-bonding interaction between Thr 9 and Glu 16 (see Fig. 9C). The analysis indicates that the largest barrier observed in the free-energy profiles on the “natural coordinate” originates from the occurrence of permutational isomers that interconvert slowly because of H-bonding interactions (see “Supplementary Material” for details); these isomers originate from the lack of symmetry in the calculation of the RMSD from the reference. The introduction of a specialized restraining potential that takes into account the chemical symmetry of the various amino acids is expected to remove such artifacts and increase both the accuracy and efficiency of the confinement approach (Cecchini et al. in progress).

FIG. 9.

Origin of statistical errors in the confinement calculation. The analysis was carried out on a set of four restrained runs for bhp2 with restraint strengths of 1.95e-05, 0.0025, 0.16, and 82 kcal/mol/Ų. The free energy is projected onto (A) the all-atom RMSD from the reference structure and (B) the “natural coordinate” from a principal component analysis of the interatomic distances. The latter shows a complex landscape made of multiple basins separated by high free-energy barriers. Such complexity, which is hidden in the RMSD based free-energy profiles, is responsible for the large statistical errors found in the intermediate k range. (C) Structural analysis of two confinement runs at intermediate k values. Molecular snapshots extracted from basins 4 and 5 for k equal to 0.0025 kcal/mol/Ų, and basins 4 and 7 for k equal to 0.16 kcal/mol/Ų shows a striking difference in the H-bonding interaction between Thr 9 and Glu 16: the H-bond (green dashed line) involves oxygen OT1 of Glu 16 (red stick) in the former basins, and oxygen OT2 (cyan sticks) in the latter.

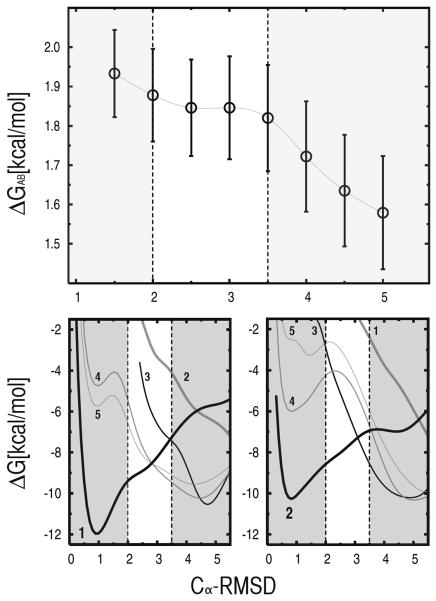
Definition of free-energy basins

The dependence of the confinement results on the definition of the β-hairpin states was investigated. The results presented above were obtained by using a cutoff of 2.0 Å in the C_α-RMSD from the reference structures to define the boundaries of the bhp1 and bhp2 basins. To determine the sensitivity of the calculated free-energy difference to such an “arbitrary” definition, the analysis was repeated by using C_α-RMSD cutoffs ranging from 1.5 to 5.0 Å. Fig. 10 (top) shows that the value of the RMSD cutoff has a sizeable effect on the calculated ΔG_AB, but the confinement results are relatively robust for the limited range of cutoffs between 2.0 and 3.0 Å. Both too conservative or too loose criteria lead to significant changes in the results. To analyze the observed behavior, the free energy of the invidual basins of β-hairpin were projected on the C_α-RMSD from the reference structures for both bhp1 and bhp2; i.e., the free-energy profiles shown in Fig. 10 were generated from the histograms of the C_α-RMSD from the reference of the structural ensembles sampled by equilibrium MD at 360 K and kinetically partitioned as described in Ref. [31]. Fig. 10 shows that an approximate definition of the free-energy basins can still provide correct results if high free-energy conformations are discarded; even though cutoffs of 2.0 and 3.5 Å (dashed lines in Fig. 10) include rather different portions of the free-energy basins 1 and 2, ΔG_AB remains unaltered in this range; i.e., the contribution of high free-energy conformations corresponding to RMSD values larger than 2.0 Å is essentially negligible. Also, “spurious” contributions coming from conformations that are erroneously assigned to the basins of interest are negligible in the range of cutoffs corresponding to stable confinement results (i.e., 2.0 ≤ C_α-RMSD ≤ 3.5 Å); see Fig. 10 (bottom). The same is not true for cutoffs larger than 3.5 Å, where non-negligible contributions coming from other free-energy basins are present. At the same time, cutoffs lower than 2.0 Å correspond to an incomplete description of the actual free-energy basin and lead to incorrect results as well. In particular, a cutoff of 1.5 Å results in the loss of the contribution coming from the shoulder of the free-energy profile of bhp1, which appears to be non-negligible on the calculated ΔG_AB.

FIG. 10.

Dependence of the confinement results on the definition of the free-energy basins corresponding to the investigated molecular states. Here, the data refer to bhp1 and bhp2 states of the β-hairpin peptide. On top, are shown the calculated ΔG_AB values (i.e., ΔG_bhp2 – ΔG_bhp1) as a function of the RMSD cutoff used in the analysis. On bottom, are shown the free-energy projections of the individual basins of the β-hairpin peptide (see Ref. [31]) on the C_α-RMSD from the reference structure of both bhp1 (left) and bhp2 (right) states. The free-energy profiles were generated from the histograms of the C_α-RMSD computed for each basin from the structural ensembles sampled by equilibrium MD at 360 K and kinetically partitioned as described in Ref. [31].

The robustness of the confinement results relative to an approximate definition of the basins is not ensured and may be system dependent. We note that in the case of the β-hairpin state 3, which is structurally more heterogeneous than bhp1 and bhp2 because of its flexible tail, an RMSD-based definition strongly affects the free-energy results in the entire range of cutoffs (see “Supplementary Material” for details).

DISCUSSION

Conformational free-energy differences are key quantities for understanding phenomena in molecular biology that involve large structural changes of macromolecules. Calculation of such free-energy differences are particularly difficult when two conformations of a macromolecule differ significantly from each other and have high barriers between them. The “confinement” approach [19], which is based on early developments [21–24], is a method that avoids this problem because it determines the absolute free energies of the individual states; it uses a thermodynamic cycle in which the states are progressively restrained to pure harmonic basins whose absolute free energy can be computed by normal-mode analysis. In Ref. [19], the confinement approach was tested on a model peptide, Met-enkephalin (${\mathrm{NH}}_3^{+}-\text{Tyr}-\text{Gly}-\text{Gly}-\text{Phe}-\text{Met}-{\text{COO}}^{-}$), and used to estimate side-chain entropies of a 17-residue fragment from ubiquitin [19]. In this paper, an improved version of the method is applied to compute the conformational free-energy difference between two states of the alanine dipeptide in vacuo, and the β-hairpin from protein G with an implicit treatment of the solvent. In all cases, the confinement results are found to be in excellent agreement with the ones obtained from equilibrium molecular dynamics, while requiring a much smaller computational effort. In the case of the β-hairpin, for example, the confinement calculation is more efficient than equilibrium MD by more than one order of magnitude; e.g., 4 μs used in the confinement method and 200 μs equilibrium MD runs yield comparable results. The error bars of the calculated free-energy values, given the potential energy function, are estimated to be on the order of a few tenths of a kcal/mol. Thus, the confinement method, when applied to the two systems studied here, is a technique of high accuracy and precision for computing conformational free-energy differences with relatively little computer time.

The methodological improvements presented in this paper, relative to the earlier work [19], are: (i) a more convenient definition of the ensemble-averaged fluctuations from the reference structure; (ii) the use of a best-fit restraining potential; (iii) the introduction of a rationale for the selection of the reference structure for the confinement runs; (iv) the identification of both systematic and statistical error sources; and (v) the introduction of a quasi-harmonic analysis step as a possible approach to treating a system in explicit solvent. Each of these aspects is discussed in the following.

The ensemble-averaged atomic fluctuations from the reference (X_k) are used to compute the free energy of confinement by numerical integration; see Eqs. 4 and 18. To obtain an accurate estimate of ΔG_AB, it is therefore crucial to minimize the errors in the X_k values. The new definition of X_k based on the all-atom RMSD from the reference is well behaved for all restraining strengths and, unlike the one proposed in Ref. [19], does not diverge for vanishing k.

The newly adopted restraining potential is similar in nature to the absolute restraint described in Ref. [19] except that the atomic coordinates of the reference are implicitly rotated and translated so as to bestfit the atoms of the actual molecular frame. Such a best-fit restraint minimizes the total restraining energy and does not introduce any net force or torque on the system. The former results in lower confinement free energies, thus leading to smaller errors in ΔG_AB; the latter increases the sampling efficiency. Both aspects are shown to be important for a better control of statistical errors.

The selection of the reference structure for the confinement runs has been shown to have important effects on both the efficiency and accuracy of the method (see Fig. 5). Our analysis indicates that energy-minimized molecular conformations represent the optimal choice. Their use reduces the number of restrained simulations required and minimizes the noise in the confinement results.

The occurrence of both systematic and statistical errors in the confinement results has been investigated. By varying the size of the integration time step, sizeable systematic errors have been found that affect the absolute value of the confinement free energy. These errors result from non-negligible “sampling” inaccuracies arising in the presence of large restraining forces; i.e., strong restraint strengths lead to a systematic overshooting of the potential energy minimum thus causing sizeable errors on the value of the ensemble-averaged fluctuations. Nonetheless, confinement calculations applying time steps of different size yield the same ΔG_AB, apparently due to error cancellation. Thus, the confinement approach appears to be robust with respect to such systematic errors and no reduction of the time-step size in the high restraint-strength range seems to be necessary to obtain accurate ΔG values. Statistical errors were evaluated by means of a specialized block analysis designed to account for the variation in magnitude of the contributions of the individual restrained runs to the confinement free energy. The results indicate that the confinement runs carried out in the presence of intermediate restraint strengths are the source of the largest statistical errors. In the low k range (i.e., 0 < k < 0.001 kcal/mol/Ų), where sampling of the essentially unconstrained system is intrinsically problematic, the contributions of the individual runs to the free-energy of confinement are negligible because of the small k values, in spite of the large fluctuations observed. In the high k range (i.e., 0.3 < k < 82 kcal/mol/Ų), the contributions to the free-energy of confinement are large, but the restraining potential is such that the fluctuations rapidly converge to their ensemble average value. The intermediate k values (i.e., 0.001 < k < 0.3 kcal/mol/Ų) make the dominant contributions to the ΔG. In the intermediate k range, despite of the presence of the restraining potential, the system may explore multiple subbasins separated by high free-energy barriers. These are the source of large statistical errors. The barriers are found to originate from the presence of symmetric groups (e.g., two oxygens of carboxyl groups) involved in strongly directional interactions, such as hydrogen bonds. The chemical symmetry of such groups, which has not been considered in the calculation of the restraint energy nor in the definition of the atomic fluctuations, generates “permutational isomers” (i.e., chemically equivalent but distinguishable molecular structures) that in the presence of an active restraining potential result in minima separated by free-energy barriers. Such barriers are artifacts that dramatically reduce the overall sampling efficiency. Moreover, since the multiplicity of such permutational isomers is expected to grow combinatorially with the size of the system, this problem could introduce severe limitations on the application of the method to biologically more relevant systems. Analogous considerations were made to circumvent the permutation problem in confinement calculations of fluid systems [54]. The introduction of a specialized restraining potential that removes the occurrence of permutational isomers is suggested to increase both the accuracy and efficiency of the method, while extending its scope (Cecchini et al. in progress).

An alternative version of the confinement approach has been introduced. It computes the difference in free energy between the confined states by a quasi-harmonic analysis instead of the normal-mode analysis. This variant requires no energy minimization and evaluates the harmonic entropy from the eigenvectors of the covariance matrix, which is directly obtained from the MD runs carried out in the presence of large restraints. The analysis showed that, as expected, the normal-mode and quasi-harmonic variants provide the same (correct) result when sufficiently strong restraining potentials are applied. However, the quasi-harmonic variant enables the analysis of a subset of degrees of freedom in a simple way and holds promise for extending the scope of the confinement method in conjunction with an explicit treatment of the solvent. In this context, one would simulate the molecular states of interest in a bath of explicit waters and apply the confinement protocol only to the protein system. Test applications of this approach are in progress and will be given separately (Cecchini et al., work in progress).

Finally, the convergence rate of the conformational sampling in the confinement approach has to be considered. It has been shown that the contributions of the restrained runs to ΔG_AB in the very low k range are essentially negligible, so that their convergence rate is not a concern. The largest contributions arise in the intermediate range of k (i.e., 0.001 < k < 1 kcal/mol/Ų). Thus, to compute accurate estimates of ΔG_AB, in the absence of permutational isomers (see above), complete sampling is required only in those confinement runs where the system already “feels” the restraining potential and the available conformational space is limited. The latter makes the confinement method very promising for its future applications to more complex systems.

Besides the technical aspects, the present paper shows the first application of the method to the determination of full conformational free-energy differences for a realistic polypeptide system, i.e., the β-hairpin of protein G. The data presented here indicate that accurate predictions can be obtained at an affordable CPU cost; i.e., the analysis of a 4 μs MD trajectory with an identical simulation setup [31] underestimated the conformational ΔG between bhp1 and bhp2 by about 1 kcal/mol, as confirmed by the analysis of a 200 μs MD run (see “Supplementary Material”). It should be noted, however, that the results may depend on the definition of the free-energy basins, which are used to select conformations representative of the investigated molecular states. For the β-hairpin states 1 and 2 it has been shown that an operational definition of the free-energy basin making use of an arbitrary cutoff on the C_α-RMSD from the reference can provide correct results and that the confinement predictions are robust over a wide range of cutoffs. This is not the case for the structurally more heterogeneous state 3 for which an RMSD-based definition of the basin strongly affects the free-energy results in the entire range of cutoffs. This behavior suggests that the analysis of the free-energy trend over a range of cutoffs can be used for judging the quality of the confinement results. In this respect, we note that all methods for calculating free energies will suffer from an inherent arbitrariness in the definition of the molecular states.

The results presented in this paper indicate that the confinement approach is a powerful technique for the accurate determination of conformational free-energy difference at a reasonable CPU cost. Even though its predictive power has to be further tested on systems of greater complexity for which sampling can be inherently problematic, the approach has the potential of becoming a useful tool for the efficient estimation of the free-energy difference between the conformations of a macromolecule particularly for large conformational changes.