Dynamic Dominance Persists During Unsupported Reaching

Abstract

Previous studies examining lateralization of arm movements focused on supported movements in the horizontal plane, removing the effects of gravity. The authors hypothesized that interlimb differences in free reaching would be consistent with the differences shown during supported reaching. Kinematic and kinetic data were collected for the forearm and upper arm segments in a 3-direction reaching task. Results showed lateralization of coordination, reflected by initial movement direction and trajectory curvature. The nondominant arm showed increased initial direction errors, and path curvature associated with a timing deficit between elbow and shoulder peak torques. These coordination deficits did not disrupt final position accuracy. The authors conclude that nondominant arm coordination deficits are similar to those reported previously for horizontal plane movements.

Handedness is a readily observable yet incompletely understood facet of human control of the upper extremity. Given the mechanical similarities between the dominant and nondominant limb, handedness is generally considered to be the result of asymmetries in the neural control of the two limbs. However, the specific mechanisms that give rise to the differences in observed behavior remain controversial.

Early attempts to investigate interlimb differences in control examined kinematic parameters of rapid and brief ballistic movements in an attempt to differentiate planning mechanisms from feedback-mediated error-correction mechanisms. Such movements were presumed to be so brief that little to no feedback-mediated corrections occurred. Measures such as reaction time, movement time, and final accuracy of ballistic movements were presumed to reflect open-loop planning of the movement. The distinction between open- and closed-loop control schemes in handedness was also reflected in studies investigating the role of precision requirements of rapid reaches under controlled visual feedback conditions (Carson, Goodman, Chua, & Elliott, 1993; Elliott, Chua, & Pollock, 1994; Flowers, 1975; Steingruber, 1975; Todor & Cisneros, 1985). However, attempts to differentiate the effects of sensory feedback on control of the dominant and nondominant limbs have provided little coherent insight into the mechanisms that give rise to handedness (Carson, 1992;Carson, Chua, Elliott, & Goodman, 1990; Carson et al., 1993; Elliott et al., 1994; Elliott et al., 1993; Flowers; Roy & Elliott, 1986; Roy, Kalbfleisch, & Elliott, 1994; Todor & Cisneros). Manipulations of target information prior to movement onset yielded longer reaction times in the dominant arm than in the nondominant arm, suggesting some differences in movement planning (Carson, 1992; Carson et al., 1990; Carson, Chua, Goodman, Byblow, & Elliott, 1995; Elliott et al., 1993). Initial hypotheses that these differences reflected a lateralized advantage in the integration of visual feedback (Flowers, 1975) were not supported by studies occluding vision during task execution (Carson et al., 1990; Roy & Elliott, 1986), suggesting that the difference may lie in the differential ability of the two hemispheres to plan movements. These differences are difficult to interpret in a manner that grants insight into the mechanisms of control, and it should be stressed that although longer reaction times could reflect inefficient planning, they might also reflect more sophisticated planning that produces better control, at the expense of planning time. Similarly, dominant arm advantages in movement accuracy might be accounted for by multiple mechanisms. For example, some researchers suggested that the dominant limb has advantages in error-correcting mechanisms, resulting in straighter, more accurate, hand paths (Carson et al., 1993; (Todor & Cisneros, 1985), whereas others suggested that the dominant limb had an advantage in initial movement planning, rendering less corrections necessary (Annett, Annett, & Hudson, 1979; Roy & Elliott, 1986).

Taking the approach that handedness may be characterized by interlimb differences in coordination, we previously investigated how each arm coordinated muscle activity and muscle-related torques with nonmuscle forces, such as limb interaction torques during movements (Bagesteiro & Sainburg, 2002; Sainburg & Kalakanis, 2000). The mechanics of the human arm can yield insights into the control strategies that produce specific patterns of behavior. Forces generated by the musculature must interact with other internally generated forces, such as those arising from deformation of noncontractile tissues such as ligaments and cartilage, and external forces such as those applied by gravity and interactions with tools. Further, the dynamic effects of motion at each segment, quantified as interaction torques, can substantially impact motion of the other limb segments. As these effects are due to the velocity and acceleration of segments, they are particularly prominent in rapid movements such as ball throwing, which are strongly lateralized tasks (Hore, Watts, Tweed, & Miller, 1996).

Our previous studies on horizontal plane reaching movements indicated that dominant arm coordination is characterized by efficient coordination of muscle torques with intersegmental interaction torques, while the nondominant arm shows less efficient coordination strategies. Our dynamic dominance hypothesis describes the advantage of the dominant limb in predicting the dynamic effects of motion to produce efficient movements (Sainburg, 2002), and advantages of the nondominant arm for achieving and maintaining positional stability (Bagestiero & Sainburg, 2003; Duff & Sainburg, 2007; Wang & Sainburg, 2003). This hypothesis stems from studies demonstrating that the coordination of nondominant limb movements varies with the dynamic forces arising from the motion of segments. In contrast, the kinematics of the dominant limb are relatively unaffected by these forces (Bagesteiro & Sainburg, 2002; Sainburg & Kalakanis, 2000). This suggests that the dominant controller employs a more sophisticated mechanism to develop the desired output of the muscular plant, one that accounts for dynamic aspects of movement that are not well accounted for in nondominant arm coordination. Although the kinematics of the limbs vary during task execution, the final performance assessed by radial distance from the target position tends to be similar across limbs (Sainburg; Sainburg & Kalakanis; Shabbott & Sainburg, 2008), suggesting corrective or postural stabilization mechanisms in the nondominant limb that are at least as proficient as those in the dominant limb.

Our previous research on handedness was carried out predominantly with reaching movements constrained to the horizontal plane, and with the limb supported in air sleds. This arrangement allowed for the experimental control over limb mechanical requirements, and had the advantage of preventing subject fatigue. However, it is plausible that our findings for horizontal plane movements may not generalize to unsupported movements made in the vertical plane, due to systematic mechanical differences between movement conditions. For example, it has been suggested that the temporal extent of a movement, or the speed, may be altered by simply scaling precomputed torques that produce the desired path kinematics (Hollerbach & Flash, 1982). In this schema, torques are scaled by a factor that varies as the square of the movement velocity. In an environment without gravity such a scaling produces movements with similar trajectories, at a variety of velocities. However, gravitic torques are unaffected by movement velocity, varying only with limb configuration and orientation. Consequently it may be expected that a system that takes advantage of such simple scaling must treat gravity specially to preserve spatial features of movement paths. Further, in studies of free reaching with the dominant limb, subjects have been shown to take distinctly different paths with and against gravity, despite covering the same space (Gentili, Cahouet, & Papaxanthis, 2007; Papaxanthis, Pozzo, Vinter, & Grinshin, 1998). Although this might be the result of altered kinetic requirements of reversing the direction of movement, removal of gravity disrupts these paths only transiently (Papaxanthis, Pozzo, & McIntyre, 2005; (Papaxanthis, Pozzo, Popov, & McIntyre, 1998). The invariance of path to external loading suggests that subjects are using gravity as an orientation, and planning different kinematics based on this reference rather than incompletely compensating for some kinematic difference. Further, the invariance of paths in gravity and nongravity conditions suggest that gravitic torques are readily separable from internal models of limb kinetics.

In addition to the effect of gravity on the planned kinematics of movement, the motor system must accurately account for gravity to execute a desired kinematic plan. Many studies in the dominant limb have shown strong invariant kinematic features of free reaching movements, which are stable against changes in load, and movement speed implying that the dominant limb plans kinematic trajectories in 3D space (Atkeson & Hollerbach, 1985; Lacquaniti, Soechting, & Terzuolo, 1982; Papaxanthis, Pozzo, & Stapley, 1998; Soechting & Lacquaniti, 1981) The reliable execution of consistent movement plans would require a sophisticated model of the limb to compensate for the varied inertial and gravitic effects encountered under various speed and load conditions.

Given the sophistication with which the dominant limb compensates for gravity and inertial effects, despite the clear mechanical differences in how these effects impact movement, we now ask how the nondominant limb coordination strategy may account for the effects of gravitic torques. If the forward controller utilized by the dominant limb system treats gravity differently than inertial effects, it is plausible that the nondominant limb utilizes the same system to compensate gravity, despite showing deficiencies in anticipation of inertial effects, such as interaction torques.

The purpose of this study is to examine whether the dynamic dominance hypothesis that we developed based on horizontal plane movements can be extended to vertical reaches under more natural movement conditions. To address this, we compared the performance of the dominant and nondominant arms of subjects while performing rapid, unsupported reaches in a parasagittal plane. Two groups of subjects performed with either the right or left hand. We used a group design to prevent the effects of interlimb transfer that we had previously characterized (Bagesteiro & Sainburg, 2005; Sainburg & Wang, 2002; Wang & Sainburg, 2004a, 2004b). To vary the effects of interaction torques at each segment, a three-direction reaching task was utilized, with two directions corresponding roughly to single joint movements of the shoulder and elbow and the third representing a combination of movement at both joints. To investigate the coordination of the limbs we compared torques impulses as well as the timing within the movement at which the occurrence of peak torques at the elbow and shoulder occur. We hypothesized that we would see predictable changes in the muscle torque impulse and the relative timing of the net torque in the dominant limb associated with adapting to the changing dynamic inertial loads. We further expected that the nondominant limb would display errors associated with failure to predict systematic variations in interaction torques. Additionally we expected that the nondominant limb, as a consequence of utilizing a less sophisticated predictive controller, would show trajectory errors consistent with failure to predict the effects of gravity on the arm. As a consequence of these differences we expected to see the nondominant limb display greater path curvature and higher errors in initial path direction than the dominant limb.

Methods

Subjects

All methods utilized in this study were approved by the Pennsylvania State University Institutional Review Board. Twelve neurologically intact right-handed adults, aged from 19 to 25 years old were tested. All subjects were screened for handedness using a modified version of the Edinburgh inventory (Oldfield, 1971). All subjects gave informed consent prior to participation. Subjects were randomly assigned to perform with either their dominant (right), or nondominant (left) hands (n = 6 per group).

Apparatus

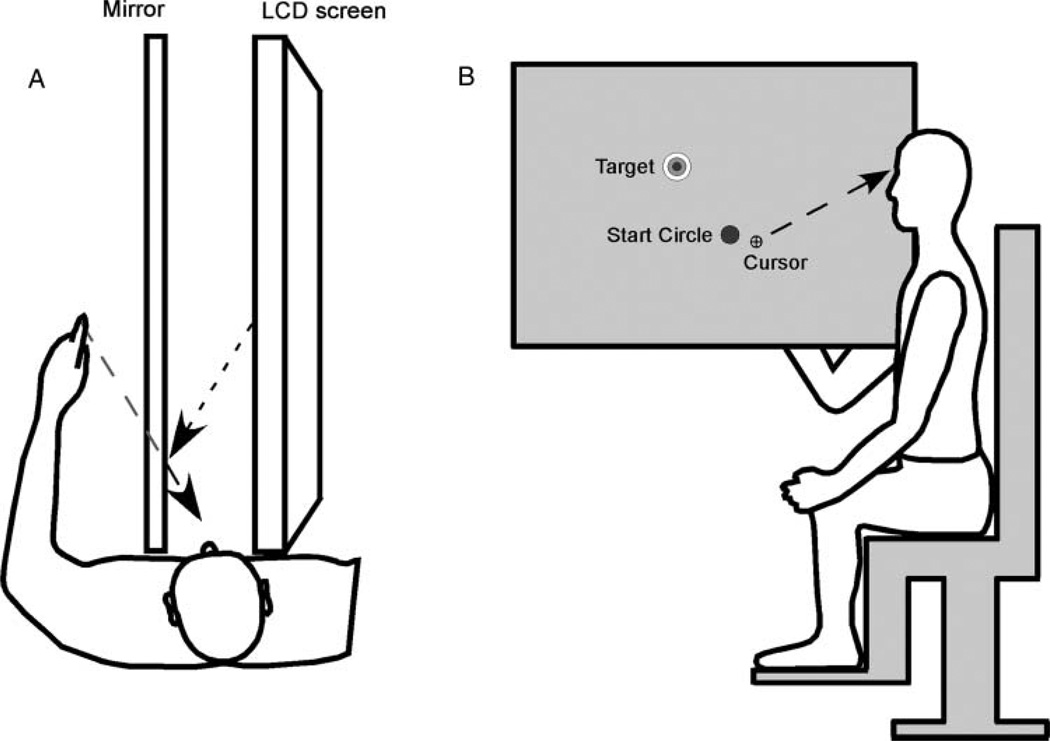
Subjects were seated, with a mirror placed in the parasagittal plane at the performing shoulder and a LCD screen placed in the parasagittal plane at the nonperforming shoulder (Figure 1). A cursor displaying finger position, a start circle and a target were displayed on the screen. Cursor movements on the screen were calibrated such that cursor location was veridical to actual finger location. Subjects were instructed to look at the mirror so that the cursor appeared to be at the finger location, while vision of the hand was occluded by the mirror. The wrist and fingers were splinted to restrict the task to two segment motion. Orientation and position of the upper arm and forearm were collected using a flock of birds six degrees of freedom movement recording system (Ascension Technology, Burlington, VT). Sensors were attached to the back of the hand over the palm, and approximately centered on the upper arm. Digital position and orientation of the sensor were collected at 130 Hz. Fingertip, elbow, and shoulder locations were computed from the raw sensor data using calibrated points collected using a stylus at bony landmarks prior to the first trial.

FIGURE 1.

Experimental setup(A) birds-eye view, (B) lateral view.

Experimental Task

In each trial subjects were shown one of three targets, presented in a psuedorandom sequence. The initial finger position for all three movements was set 15–20 cm in front of the shoulder, with the arm in a configuration that the subject found comfortable. The direction of movement was specified to be −45° (out and down), 0°(horizontally away from the trunk), or 45° (out and up) from the initial position. All targets were displaced from the start position by 50% of the subject’s maximum horizontal reach from the starting location.

To initiate a trial subjects were asked to center the cursor in a starting circle for 300 ms, at which time they would receive an auditory cue to begin movement. Upon receiving the cue, subjects were instructed to reach rapidly to the target and stop with the cursor in the center of the target. To encourage subjects to maintain consistent performance, points were awarded for accuracy. To encourage rapid movements, subjects only received points for performance when the fingertip movement was faster than 1.5 m/s. Subjects performed 90 reaches with targets presented in a randomized order, with all subjects receiving trials in the same order. Cursor feedback was removed at the “go” cue and resumed after the completion of the trial. After completion of the trial, a display of the movement path was presented along with a marker indicating the final finger position. To eliminate learning effects, trials 1–30 were excluded from analysis.

Kinematic Data

Finger, elbow, and shoulder position data were low pass filtered at 8 Hz using a dual pass third-order Butterworth filter. Segment angles were computed from the position data using a moving plane analysis, with the plane defined through the finger, elbow, and shoulder (Schneider & Zernicke, 1990). Movement start and stop were defined to be the first minima below 5% of the peak in the tangential finger velocity to either side of the main peak in the movement tangential velocity. All further analyses were performed on the data between the movement start and movement stop.

Three measures of hand path accuracy were used: initial direction error, path curvature, and final position error. The initial direction error was defined as the angular deviation between a vector defining the instructed movement and a vector passing through the initial finger position and the finger position at peak hand velocity (Figure 2A). In this measure negative angles indicate that the finger path was directed lower than the actual target, while positive angles indicate that the finger path was aimed higher than the target. Path curvature was defined as the major axis of the finger path divided by the minor axis of the finger path. The final position error was the magnitude of the distance between the finger location at movement end and the target.

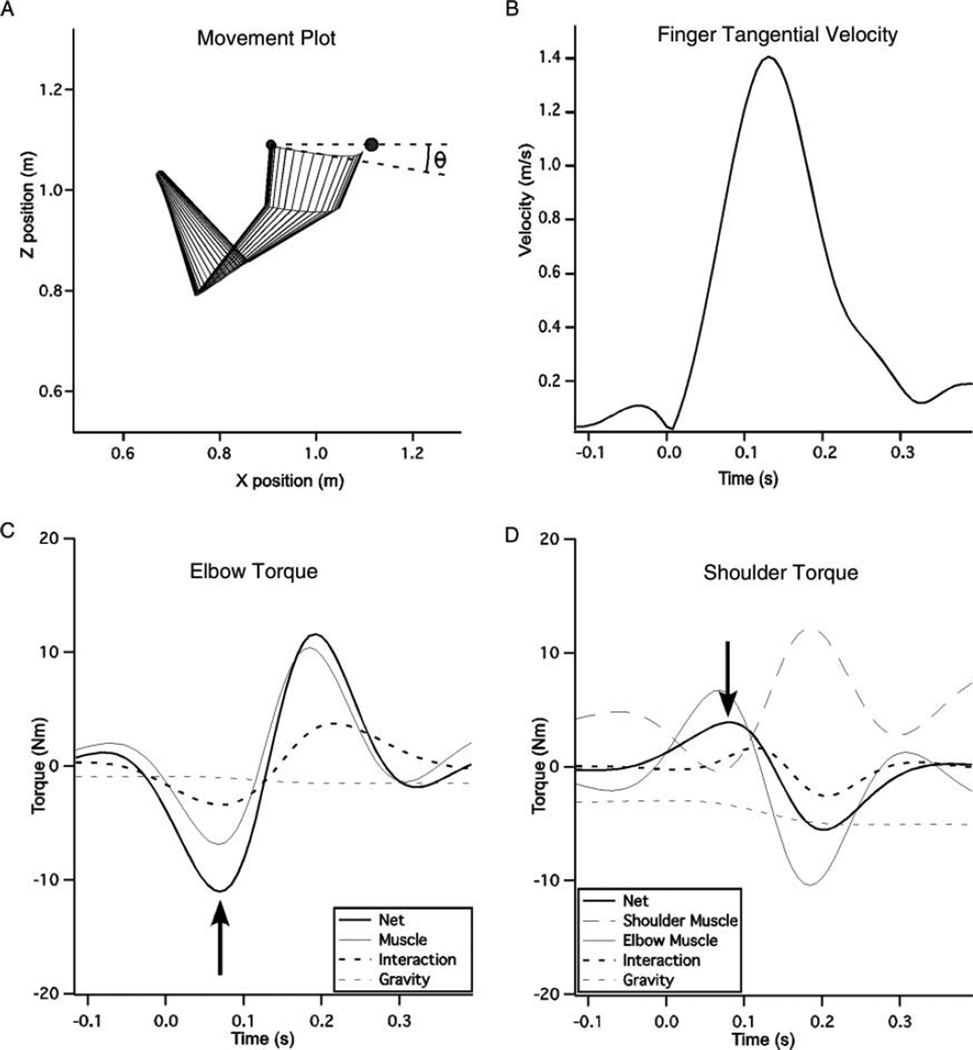
FIGURE 2.

Sample movement with associated data. (A) Example of a single left hand movement to the 0° target. Θ indicates the angle of initial direction error. (B) The tangential finger velocity associated with the movement displayed in (A). (C) Elbow torques computed for the movement in (A). The arrow marks the peak net torque, at which time measures of peak torque are taken. (D) Shoulder torques for the movement in (A). The arrow marks peak net torque. The elbow muscle torque is included here as this torque acts symmetrically across the elbow joint and, consequently, must be accounted for at the shoulder. This results in a sign inverted mirror of the elbow muscle torque acting at the shoulder.

Kinetic Data

Joint torques were computed using an inverse dynamic analysis of the movement based on the kinematic segment angles. We assume here that the upper limb is composed of two rigid links attached by frictionless spherical joints. The moving plane analysis employed to generate the kinematic joint angles allows planar equations of motion to be utilized to compute the joint torques within the moving plane, thus allowing partitioning of the equations into a few terms (Schneider & Zernicke, 1990). Joint torques were partitioned into net torque, interaction torque, and muscle torque and gravitational torque (Figures 2C and 2D), with net torque representing the torque driving rotational acceleration of a segment, the interaction torque arising from the velocity and acceleration of the other segment and the muscle torque comprising the residual of the joint torques once the net and interaction torques are accounted for in the homogeneous form of the equations of motion. The muscle torque is the composite of not only agonist and antagonist activity, but also passive tissue properties such as stiffness and damping of the muscle tissues.

Two measures of arm kinetics were used in this study: torque impulse, and the difference in timing of peak net torque onset between the elbow and shoulder. The torque impulse was taken as the integral of the muscle and interaction torques. For this analysis muscle and interaction torques were considered positive if acting in the same direction as net torque, and negative if acting in the opposite direction. The integrals for torque impulse were computed across two ranges: from the initiation of movement up to the time of peak tangential acceleration of the finger, and from movement start to the end of movement. The range from start to peak acceleration was selected to focus on early differences in control that might reflect differences in prediction of gravitic effects, while the whole movement range reflects previously reported measures of torque impulse that are reflective of the dynamic dominance hypothesis (Bagesteiro & Sainburg, 2002; Sainburg & Kalakanis, 2000). The timing of peak torque onset was taken as the absolute time after movement start at which the peak net torques occurred. The relative timing of elbow and shoulder peak torque was taken as the time at which the peak elbow torque occurred minus the time at which the peak shoulder torque occurred.

Statistics

Right and left hand movements were performed by two different groups (6 subjects each) of right-handed individuals. This was done to eliminate the potential for interlimb transfer effects, which have been well documented for reaching tasks (Sainburg & Wang, 2002; Wang & Sainburg, 2003). All analyses were performed in the statistical processing software JMP (SAS Institute Inc., Cary, NC). Measures analyzed in this study were assessed using individual 2 Hand × 3 Target mixed factor repeated measures analyses of variance (ANOVAs), with subjects as the repeated measure. Post hoc tests were performed only in cases in which an interaction between main effects was observed. In these cases, Tukey’s honest significant difference tests were used to identify specific differences. To assess the relation between relative torque timing and the path kinematics, we performed simple linear regressions on each subject–target case separately for both the 0° and 45° targets. These fits were assessed for significance using an F test in which the F statistic of this analysis constitutes the ratio of mean square errors described by the fit to the mean square of errors not described by the fit. Significance indicates a rejection of the null hypothesis that the model does not predict any of the observed variance in the dependent measure. As a second-stage of analysis we wished to compare the regressions of left-hand subjects to right-hand subjects. For this analysis we converted the slope and intercept of each regression to a z score and performed a repeated measures ANOVA to assess differences in these variables due to hand.

Results

Kinematics

Our targets were designed to require increasing amounts of shoulder motion, as target elevation increased. Figures 3A, 4A, and 5A depict representative limb paths for movements to each target. Stick figure representations of upper arm, forearm, and hand segments are drawn at every data point, while shoulder, elbow, and finger paths connect these segments. The relative angular dispersion of the upper arm segment reflects the shoulder angular motion for each trial. Note that the upper arm stick figures for both arms remain fairly parallel and closely aligned for the −45° target in Figure 3A, but shows large angular displacement for the 45° target in Figure 5A. This increase in required shoulder excursion was related to increased intersegmental coordination requirements across directions, as discussed subsequently.

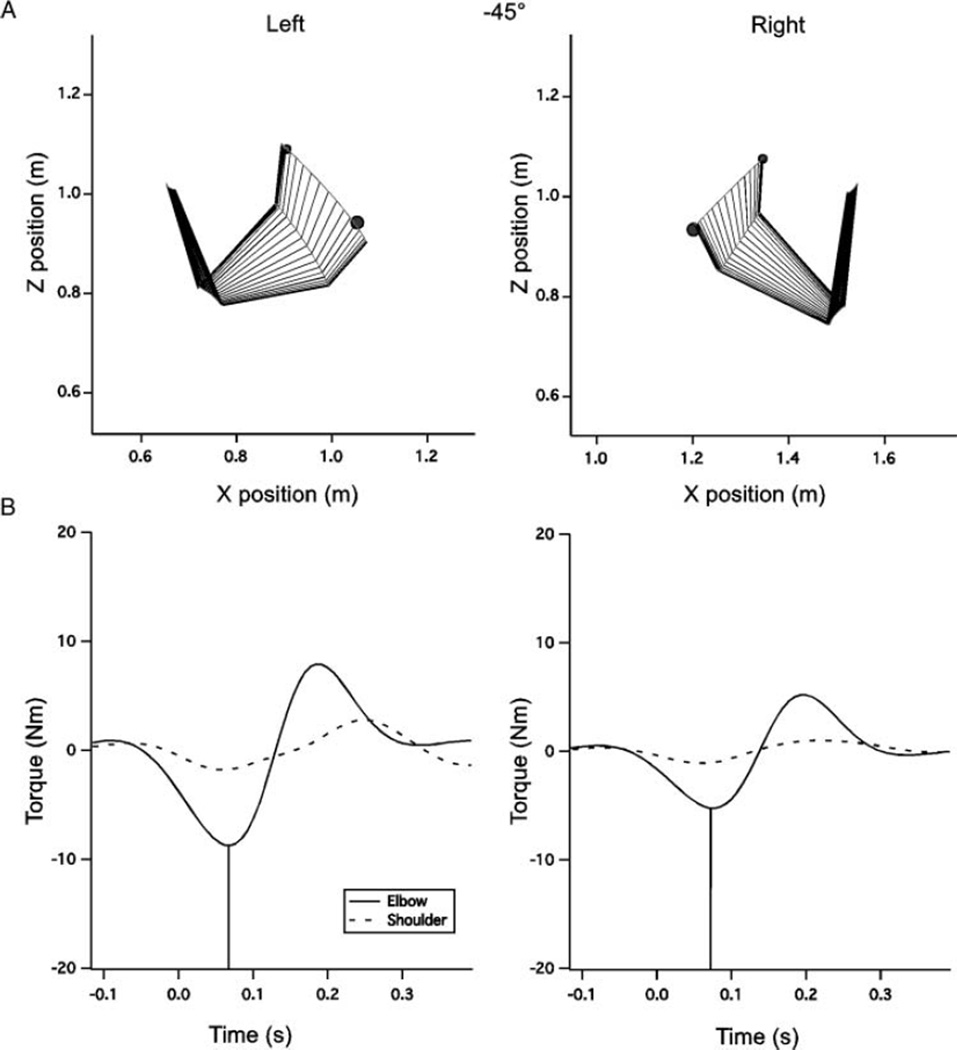
FIGURE 3.

Sample movements to the −45° target. (A) Movement plots for the right and left arms. Both movements are very straight, however, dominant arm movements tend to be slightly straighter. Initial direction error is similar across hands in this direction. (B) Net torques at the elbow and shoulder joints. Vertical lines denote the time of peak elbow torque incidence.

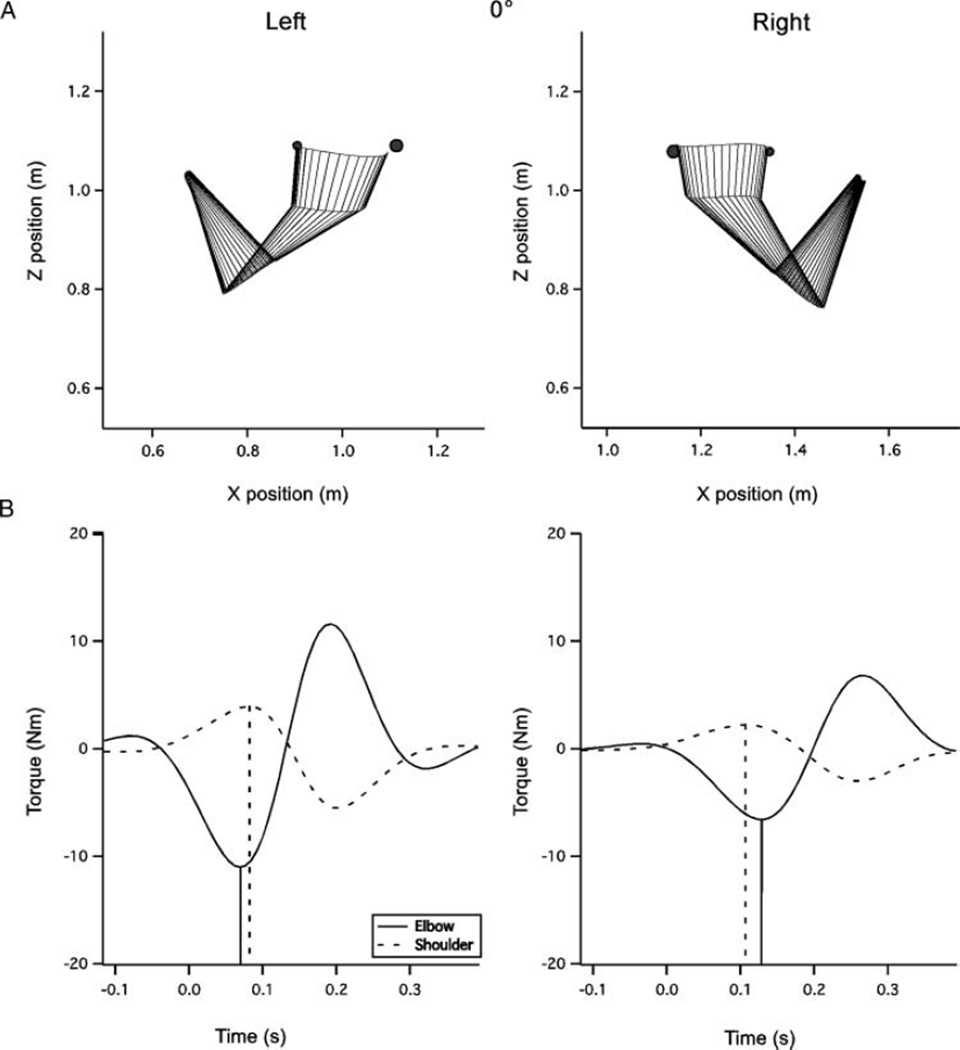
FIGURE 4.

Sample movements to the 0° target. (A) Movement plots for the right and left arms. Both limbs tend to make more curved movements to this target than to the −45° target, however, dominant arm movements still tend to be slightly straighter at this target. The nondominant hand shows a notable undershoot in the initial direction, while dominant paths tend to be directed at the target or slightly above it. (B) Net torques at the elbow and shoulder joints. Vertical lines denote the time of peak torque incidence.

FIGURE 5.

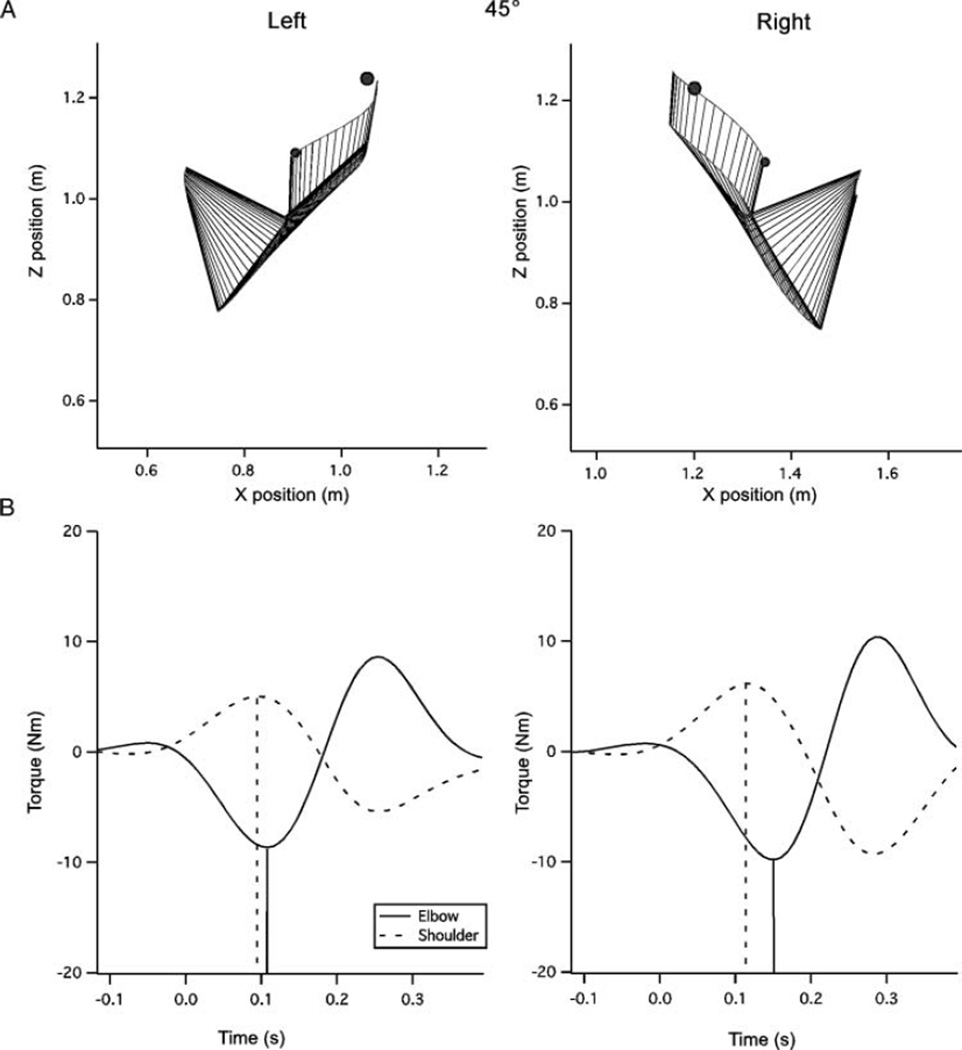
Sample movements to the 45° target. (A) Movement plots for the right and left arms. Movements of both arms display the most curvature to this target, however, dominant arm movements show less differences from the 0° target than the nondominant. The nondominant arm shows a notable undershoot in the initial direction, while the dominant paths tend to be directed at the target or slightly above it. (B) Net torques at the elbow and shoulder joints. Vertical lines denote the time of peak torque incidence.

Final Position Error

Although the mean final position error for both hands increased with the target angle (main effect of target), F(2, 20) = 6.39, p < .01, there was neither a significant difference between the hands (main effect of hand), F(1, 10) = 2.15, p = .17, nor an interaction between hand and target, F(2, 20) = 2.93, p = .08. Despite this, the dominant and nondominant arms showed substantial differences in the kinematic patterns to the three targets.

Initial Direction Error

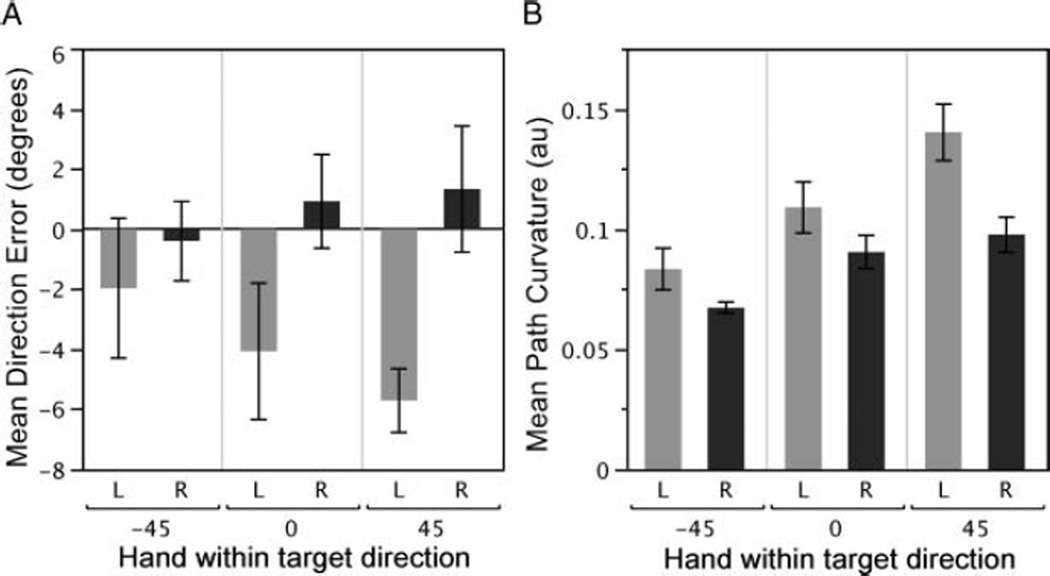
Interlimb differences in initial direction error, summarized in Figure 6A, were driven by a hand by target interaction, F(2, 20) = 3.45, p < .01, wherein the dominant arm produced movements that were, on average, directed on line with the target, while the nondominant arm showed an increasing undershoot as target −45° to 45°. There was also a main effect of hand for direction error, F(1, 10) = 4.80, p = .05, which was related to the larger errors at the 0° and 45° targets. For the example paths in Figure 3A, the right and left paths are very similar. Note that this movement involves mostly elbow motion, with little motion about the upper arm, and no wrist motion due to the splinting. In contrast to the −45° direction, for the 0° and 45° targets shown in Figures 4A and 5A, the left arm direction errors become progressively greater. In contrast to the nondominant arm, dominant arm direction errors were unaffected by target elevation, displaying finger paths directed toward the target for all directions.

FIGURE 6.

Summary of kinematic results. (A) Initial finger path angular deviation from the true target direction. Negative values indicate an undershoot, while positive values indicate aiming higher than the target. (B) Hand path curvature expressed in arbitrary units.

Path Curvature

The combination of substantially greater undershoot with similar final errors in the nondominant hand explains the increasing curvatures of the nondominant finger paths across the target elevations (Figures 4–5A). As summarized in Figure 6B, the curvature of the nondominant limb was greater than that of the dominant limb for all target directions (main effect of hand), F(1, 10) = 6.42, p = .03. Additionally, for both hands the curvature of the finger path increased as the target angle increased (main effect of target), F(2, 20) = 31.07, p < .01, with greatest curvatures for both hands displayed in the 45° direction. There was a significant hand by target interaction for curvature, F(2, 20) = 3.50, p = .05. This reflected a greater dependence of curvature on target elevation for the left hand than the right hand.

Kinetics

Figures 3–5B depict the torques at the shoulder and elbow joints, associated with the exemplar reaches in Figures 3–5A.

Early Torque Impulse

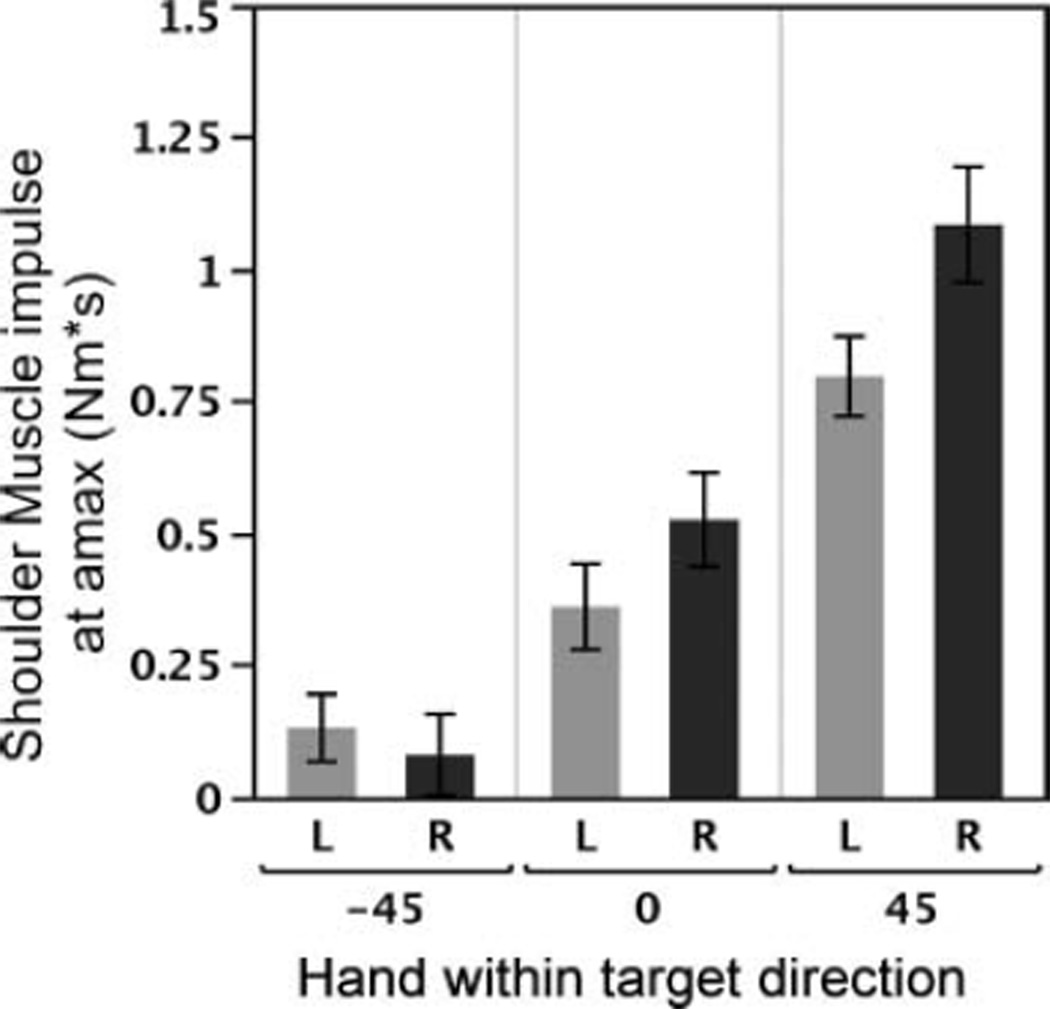
As expected by our target design, the amplitude of elbow muscle and interaction torque impulse varied systematically across directions, reflecting the differences in elbow excursions required with changing target elevation. As a result, for the early impulse we found a main effect of target on elbow muscle, F(1, 20) = 155.23, p < .0001 and interaction torque impulse, F(1, 20) = 239.03, p < .0001. No effect of hand was observed for elbow muscle, F(1, 10) = 0.31, p = .59, or interaction impulse, F(1, 10) = 0.0074, p = .93, and no interaction between hand and target was found for elbow muscle, F(1, 20) = 0.55, p = .59; or interaction torque impulse, F(1, 20) = 0.79, p = .47. At the shoulder a similar main effect of direction was observed, for muscle, F(1, 20) = 85.12, p < .0001; and interaction torque impulse, F(1, 20) = 17.01, p < .0001. Again, no main effect of hand was observed for either shoulder muscle, F(1, 10) = 2.10, p = .18, or interaction torque impulse, F(1, 10) < 0.0001, p > .99, and the interaction torque impulse showed no interaction of hand > and target, F(1, 20) = 1.79, p = .19; however, the muscle torque > impulse did show an interaction between hand and target, F(1, 20) = 3.53, p = .05. Post hoc testing revealed that the only comparison of hand within target which achieved significance was in the 45° direction. Figure 7 shows the shoulder muscle torque impulse across hands and targets, and although no significant difference was found at the 0° target, there is a visible difference between arms consistent with that observed at 45°. This may reflect a difference between hands that scales with the required shoulder joint excursion. Because the 0° direction had lower impulse requirements than the 45° direction, it is possible that in this direction, potential interlimb differences in impulse may be smaller than the intersubject variability of the data. We expect that the elevated muscle torque impulse in the dominant limb may be associated with compensation for gravity, whereas the relatively lower impulse in the nondominant limb could result in an initial deficit in elevating the upper arm against gravity. This interpretation is consistent with the observed errors in initial movement direction.

FIGURE 7.

Shoulder muscle impulse across hand and direction. Hand differences in muscle impulse increase with target elevation, only becoming statistically significant at the 45° target.

Total Torque Impulse

The amplitude of elbow muscle and interaction torque impulse varied systematically across directions, reflecting the differences in elbow excursions required by the different target elevations. Consequently, we observed a main effect of target on elbow muscle, F(1, 20) = 155.23, p< .0001, and interaction torque impulse, F(1, 20) = 239.03, p < .0001, but no effect of hand on elbow muscle torque impulse, F(1, 10) = 0.31, p = .59; or interaction torque impulse, F(1, 10) = 0.0074, p = .93. Nor was there an interaction between hand and target, for elbow muscle, F(1, 20) = 0.55, p = .59; or interaction torque impulse, F(1, 20) = 0.79, p = .47. Similarly, at the shoulder we observed a main effect of target on shoulder muscle, F(1, 20) = 155.23, p <.0001, and interaction torque impulse, F(1, 20) = 239.03, p < .0001, but no effect of hand for shoulder muscle, F(1, 10) = 0.31, p = .59; or interaction torque impulse, F(1, 10) = 0.0074, p = .93. There was no interaction between hand and target for shoulder muscle, F(1, 20) = 0.55, p = .59; or interaction torque impulse, F(1, 20) = 0.79, p = .47.

Torque Timing

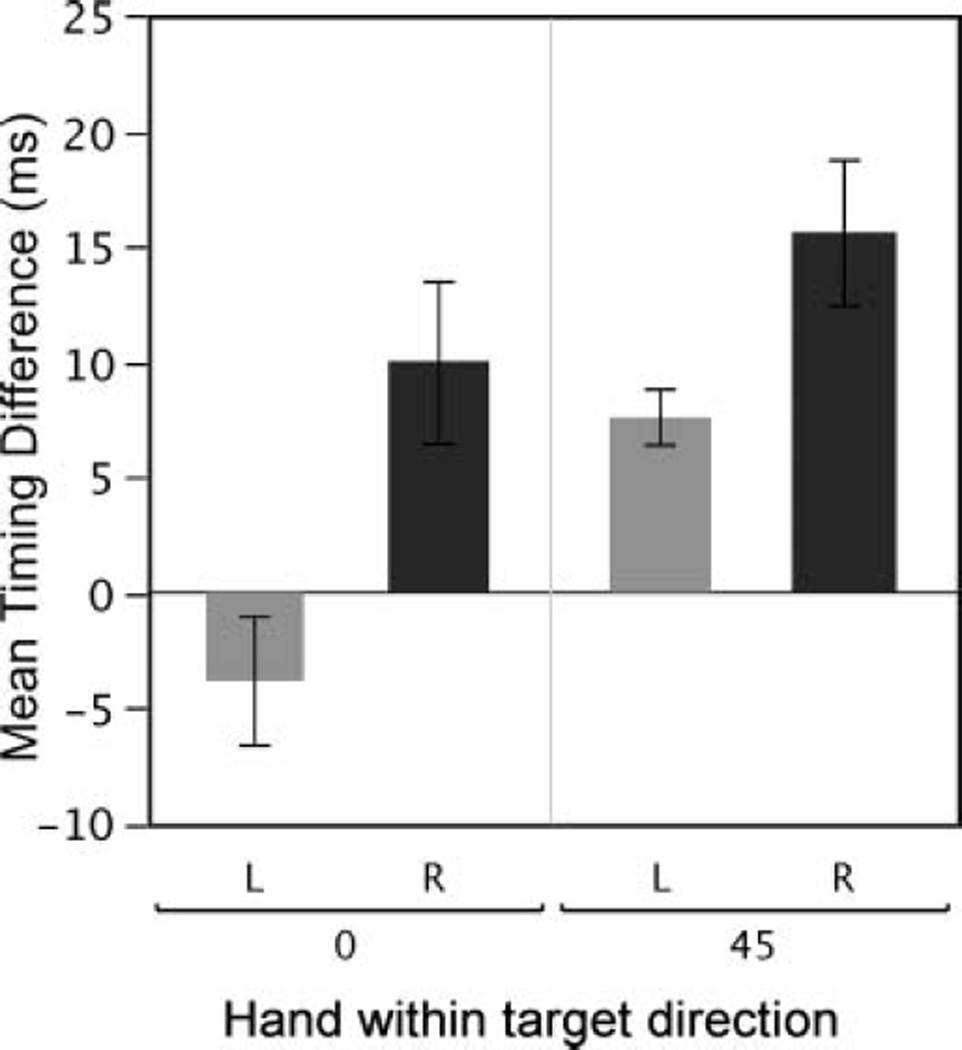
Because of the relatively small peak torques for the –45° target, we restricted our analysis of elbow and shoulder torque relationships to only the 0° and 45° targets. We marked the timing of shoulder and elbow net torques with vertical lines in Figures 4B and 5B. Note that for the right arm, elbow torque lags behind shoulder torque, with greater lag for the 45° than for the 0° target. In contrast, for the nondominant left arm, the elbow tended to act earlier relative to the shoulder at each target, even preceding shoulder peak torque in the 0° direction (Figure 4B). Figure 8 shows the mean shoulderelbow peak torque timing difference across subjects. Note that the left arm difference is smaller, and negative in the 0° direction, indicating that on average the left arm elbow peak torque either preceded that of the shoulder, or showed reduced lag, relative to that of the right arm. As a result, our ANOVA showed a main effect of hand, F(1, 10) = 10.84, p = .01, and target direction, F(1, 10) = 14.88, p < .01, but no interaction between hand and target (2 directions), F(1, 10) = 1.75, p = .22.

FIGURE 8.

Timing difference between elbow and shoulder peak net torque occurrence. Negative values indicate an elbow lead time, while positive values indicate an elbow lag time.

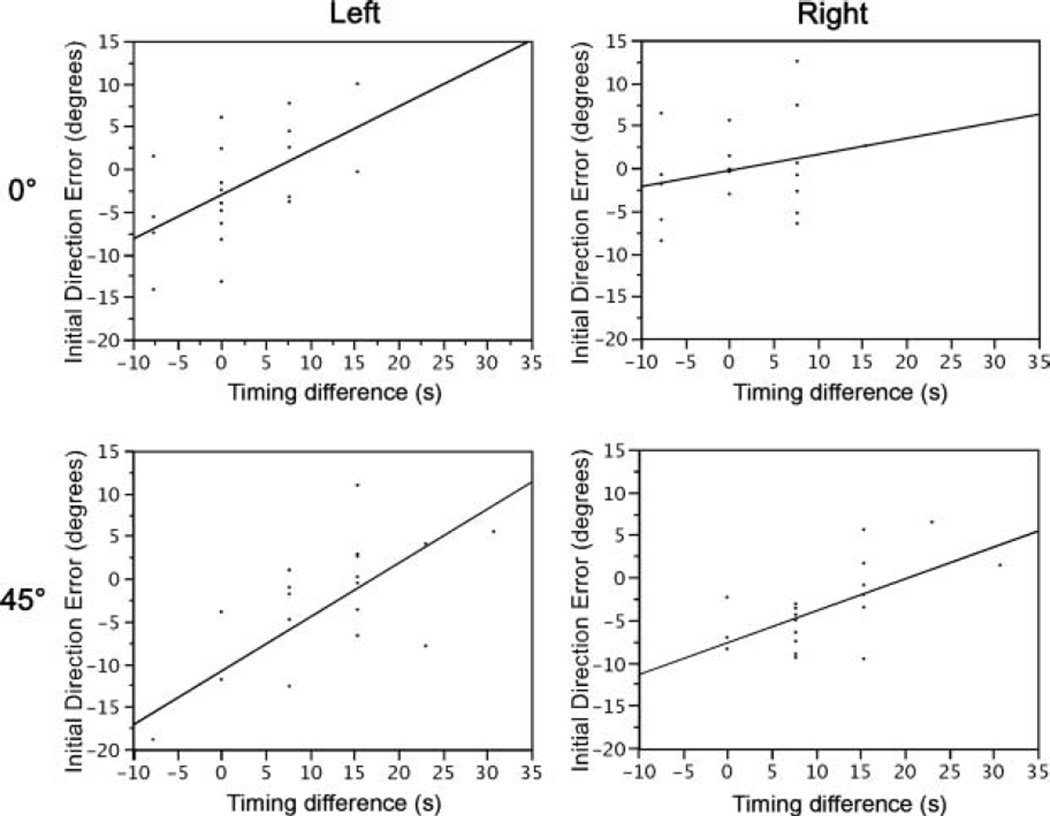
We reasoned that the effect of delaying elbow extensor torque relative to shoulder flexor torque in dominant right arm movements was to elevate the hand toward the targets at movement initiation. In contrast, the more rapid elbow extensor acceleration for the nondominant left arm countered hand elevation, and resulted in the initial direction undershoot, characterized previously. To quantitatively examine the relationship between the elbow-shoulder torque timing and the kinematic differences between the hands we regressed the torque timing against initial direction error, for each subject separately. Our simple linear regression within target (Figure 9), showed a statistically significant correlation between elbow-shoulder torque timing differences and initial direction error, F(1, 30) > 4.17, p < .05, for all subjects. The relative timing of elbow and shoulder are clustered around discrete values (Figure 9). This is due to the 130 Hz frequency of the data digitization, such that the smallest interval that could be resolved was approximately 7.7 ms. To assess the effect of hand, intercept and slope for these regressions were converted to z scores and the left and right fits and subjected to a 2 Direction ×2 Hand ANOVA. No main effect of hand was found in either measure, slope, F(1, 10) = 0.86, p = .37; intercept, F(1, 10) = 0.59, p > .46. Thus, for both hands, initial movement direction was substantially dependent on intersegmental coordination, measured as the timing difference between elbow and shoulder joint net torque profiles. We conclude that the systematic undershoot of left arm movements (exemplified in Figures 3–5A), compared with right arm movements resulted from poor coordination of timing between shoulder and elbow joint torques.

FIGURE 9.

Sample regressions describing correlations between torque timing and initial direction error for a right performing subject and a left performing subject.

Discussion

In this study, we examined dominant and nondominant arm coordination during unsupported, sagittal plane reaches. We hypothesized that interlimb differences in kinematics and kinetics would be consistent with the differences shown in previous studies of horizontal plane reaching. Our results showed substantial interlimb differences in coordination, as reflected by initial movement direction and trajectory curvature, such that dominant arm movements showed lower initial direction errors, and were straighter than nondomi-nant arm movements. The increased initial direction errors of nondominant arm reaches were associated with lower muscle torque impulses in the nondominant arm, and poor timing between peak torques at the shoulder and elbow joints, wherein the left arm displayed early elbow extension in relation to shoulder elevation. We conclude that in vertical plane reaching, nondominant arm intersegmental coordination deficits are similar to the deficits reported previously for horizontal plane movements. In agreement with previous findings, final position accuracy and precision showed no significant differences between the limbs (Sainburg, 2002; Sainburg & Kalakanis, 2000; Shabbott & Sainburg, 2008).

Previous studies in horizontal plane reaching showed substantial interlimb differences in the magnitudes of muscle torques across movement directions. We showed that dominant arm muscle torques were well coordinated with interaction torques, whereas nondominant muscle torques were not (Bagesteiro & Sainburg, 2002; Sainburg & Kalakanis, 2000). In the present study we did not observe differences in muscle and interaction torque impulses consistent with this previous work. This is very likely a consequence of the fact that we did not design the targets in the present study to require specific joint excursions, as was possible in the more constrained studies done in the horizontal plane. In addition, due to the greater freedom to move the scapula, and to change the plane of motion, we expected greater differences in torque profiles between subjects and trials. Nevertheless, our previous studies revealed that incoordination in muscle torque magnitude resulted in discoordination between segment motions, which gave rise to larger direction errors and greater hand path curvatures, but not greater final position errors, in the nondominant arm (Bagesteiro & Sainburg, 2002; Sainburg & Kalakanis, 2000). In this way, the present findings regarding the torque impulse across the entire movement are consistent with our previous horizontal plane studies.

In the present study we introduced an additional measure of impulse calculated between the start of movement and the time at which the finger achieved peak tangential acceleration. In this measure we observed that there was an interaction between target and hand for the muscle impulse. In the case of the 45° target the dominant limb displayed significantly greater muscle torque impulse than the nondominant limb. Because no differences were observed in the elbow impulse this would drive the elbow to accelerate earlier than the shoulder in the nondominant limb. This is consistent with the observed kinematics wherein the nondominant limb showed initial finger paths directed below the target. Because no differences were observed in the early interaction torque impulse, it is reasonable to attribute this effect to the accurate prediction of gravitic torques in the dominant limb, but not in the nondominant limb.

The noted differences in early shoulder muscle impulse but not in the early elbow muscle impulse indicates a shift in the timing of joint acceleration. Indeed in the present study, the coordination of torque events at each joint appear to have contributed the consistent interlimb differences in initial direction and movement curvature. It is apparent that the nondominant limb displays earlier elbow torques relative to shoulder torques when compared with the dominant limb. This means that elbow extension tended to lead shoulder flexion in the nondominant limb but not the dominant limb. This manifested as an error in direction and resulted in nondominant paths that were initially directed below the target, a finding consistent with poor prediction of gravitation loads on the segments. Because the magnitude of total shoulder muscle impulse was similar between the two hands, similar shoulder elevation occurred in the nondominant limb as in the dominant limb. However, this elevation occurred later in the movement. This appeared to be a correction for the initial direction deficit, as reflected by the hooks toward the target, as shown in Figures 3–5A. This initial direction error followed by late corrections resulted in greater curvatures for nondominant movements. The deficiencies in nondominant limb coordination observed here are consistent with the findings of Hore et al. 19960) that dominant limb advantages in throwing accuracy are related to better timing of finger extension relative to whole-limb movement. Although our previous studies showed that nondominant arm deficits in intersegmental coordination arose from poor prediction of interaction torques (Sainburg & Kalakanis, 2000), our present findings suggest that prediction of gravitational torques may also be deficient during vertical reaching movements.

The coordination deficits of the nondominant limb in our present and previous studies suggest that nondominant system is less adept at predicting gravitational and intersegmental dynamics when specifying early movement trajectories, and that this limb relies more on feedback mechanisms to reach the final position with similar accuracy to the dominant arm. This finding is consistent with the dynamic dominance hypothesis, which predicts dominant limb advantages in predicting task dynamics, but not in the corrective or postural phase of movement (Duff & Sainburg, 2007; Shabbott & Sainburg, 2008). In the present study, it is apparent that the dominant limb system produces movements that are directed more accurately toward the target than the nondominant system, reflected in the temporal coordination of the elbow and shoulder torques. In contrast with the early movement errors, the nondominant system did not show significant difference in final position accuracy. Although the difference in initial direction errors precludes a direct comparison of the feedback-mediated control during late movement, we may conclude that the error correction–based control late in the movement is not substantially impaired in the nondominant limb when compared with the dominant limb. This again is consistent with the dynamic dominance hypothesis, which does not predict deficits in feedback-mediated control in the nondominant limb.

Several studies have noted the kinematic consistency of the dominant limb during free reaching, noting that hand paths remain invariant despite changes in loading, movement speed, or gravity (Gentili et al., 2007; Lacquaniti et al., 1982;Papaxanthis, Pozzo, & McIntyre, 1998; Papaxanthis, Pozzo, & Stapley, 1998; Soechting & Lacquaniti, 1981). In keeping with these findings, the present results in the dominant limb show strong suppression of curvature and direction errors in all movement directions. In contrast, we observed that the nondominant limb displays errors in movement direction and curvature consistent with failure to predict the effects of gravity. This is consistent with the dynamic dominance hypothesis, which predicts that the nondominant limb relies on a feedback controller, and consequently will not predictively compensate for gravitational or inertial effects. If this theory does explain the performance deficits of the nondominant limb here then we may expect that nondominant movements will not display the same kinematic invariances that the dominant limb displays.

Consistent with the present results, some researchers have suggested that movement control may be modeled by a two-phase controller specifying first an open-loop plan for movement, followed by a second phase for stabilizing posture in which feedback is utilized to stabilize the limb around the desired configuration (Gottlieb, 1996; Hirayama, Kawato, & Jordan, 1993; Sainburg, Ghez, & Kalakanis, 1999; Scheidt & Ghez, 2007). It is plausible that the nondominant limb relies more on the postural control elements, whereas the dominant arm relies more on the predictive control elements of such a hybrid controller. Because this postural control is derived from configuration errors, joint torques will emerge based on the state of the joint errors without accounting for the activity at other joints, or the effects of gravity (Bizzi, 1987; Bizzi & Abend, 1983; Bizzi, Accornero, Chapple, & Hogan, 1982; Bizzi, Polit, & Morasso, 1976; Feldman, 1986; Flash, 1987; Polit & Bizzi, 1979). A previous transition to the suggested postural phase of movement may result in timing deviations that do not allow the more effective coordination of muscular activity that the dominant limb displays. This would be consistent with the advantages in error correction observed in the nondominant limb responding to unexpected inertial loads (Bagesteiro & Sainburg, 2003). In fact, in the present study, both arms showed similar final position errors, whereas the nondominant arm showed greater initial errors, indicating greater nondominant arm reliance on corrective control mechanisms. Although these findings suggest a greater reliance on feedback-mediated mechanisms, the differences in initial errors preclude drawing conclusions about the relative efficacy of the dominant and nondominant corrective schemes.

Although the present results cannot conclusively distinguish the specific algorithmic differences that give rise to interlimb differences in coordination, the differences observed here are similar to those shown previously in the horizontal plane movements and provide preliminary evidence that our findings generalize across different planes of motion and across different dynamic environments. Further, these findings do indicate at a gross level greater reliance on predictive mechanisms in the dominant limb and greater reliance on feedback in the nondominant limb.