Abstract
To bring cryo electron microscopy (cryoEM) of large biological complexes to atomic resolution, several factors – in both cryoEM image acquisition and 3D reconstruction – that may be neglected at low resolution become significantly limiting. Here we present thorough analyses of four limiting factors: (a) electron-beam tilt, (b) inaccurate determination of defocus values, (c) focus gradient through particles, and (d) particularly for large particles, dynamic (multiple) scattering of electrons. We also propose strategies to cope with these factors: (a) the divergence and direction tilt components of electron-beam tilt could be reduced by maintaining parallel illumination and by using a coma-free alignment procedure, respectively. Moreover, the effect of all beam tilt components, including spiral tilt, could be eliminated by use of a spherical aberration corrector. (b) More accurate measurement of defocus value could be obtained by imaging areas adjacent to the target area at high electron dose and by measuring the image shift induced by tilting the electron beam. (c) Each known Fourier coefficient in the Fourier transform of a cryoEM image is the sum of two Fourier coefficients of the 3D structure, one on each of two curved ‘characteristic surfaces’ in 3D Fourier space. We describe a simple model-based iterative method that could recover these two Fourier coefficients on the two characteristic surfaces. (d) The effect of dynamic scattering could be corrected by deconvolution of a transfer function. These analyses and our proposed strategies offer useful guidance for future experimental designs targeting atomic resolution cryoEM reconstruction.
Keywords: cryoEM, Atomic resolution, Beam tilt, Dynamic scattering, Defocus gradient
1. Introduction
Single particle cryo electron microscopy (cryoEM) can provide the three-dimensional (3D) structure of a biological complex in its native environment. Recent progress has demonstrated that this technique is capable of determining 3D structures to near atomic resolution, allowing the building of backbones or even full atom models of biological complexes that include multi-subunit proteins (Ludtke et al., 2008; Cong et al., 2010; Zhang et al., 2010a), icosahedral viruses (Jiang et al., 2008; Yu et al., 2008, 2011; Zhang et al., 2008, 2010c; Chen et al., 2009; Liu et al., 2010; Wolf et al., 2010; Cheng et al., 2011), helical viruses (and portions of nucleic acid) (Ge and Zhou, 2011). Nevertheless, the current resolution of cryoEM is rarely sufficient to build atomic models of complexes, identify small molecules in the complexes (e.g., tightly bound water molecules or small ligands), resolve carboxyl oxygen atoms of the backbone of amino acids to determine peptide planes, differentiate amino acids with small side-chains, or determine the B-factor of the structures. Such detailed information is critical for studying and understanding the functional mechanisms of biological complexes.
For two-dimensional (2D) crystalline samples, electron crystallography has successfully achieved resolution better than 3 Å for aquaporin (Yonekura et al., 2003; Gonen et al., 2005). In contrast, for non-crystalline samples, for which single particle cryoEM must be used, the resolution of published structures has not reached a comparable level. Some of the limitations of the single-particle cryoEM technique have already been addressed by optimization of sample preparation (Grassucci et al., 2007; Zhou, 2008), use of an electron beam with better coherence (Zhou and Chiu, 1993), minimization of the magnification variation due to defocus during data acquisition (van Duinen et al., 2005), calibration of the magnification by using a standard sample (Olson and Baker, 1989), detection and correction for distortion of electron lens (Capitani et al., 2006), and improvement of particle alignment during image processing (Grigorieff, 2007). Nevertheless, as resolution of single particle cryoEM approaches atomic level, several other limiting factors that are related to the fundamental physics and optics of electron image formation begin to emerge.
Recent advances in high resolution single-particle cryoEM have been reviewed elsewhere (Grigorieff and Harrison, 2011; Zhou, 2011). This paper focuses on theoretical considerations about several of the most significant limiting factors at present for achieving even finer resolution in single particle cryoEM. These factors include the effects of beam tilt, inaccurate determination of defocus, defocus gradient across the depth of a specimen, and dynamic scattering.
2. Results and discussion
2.1. Electron beam tilt
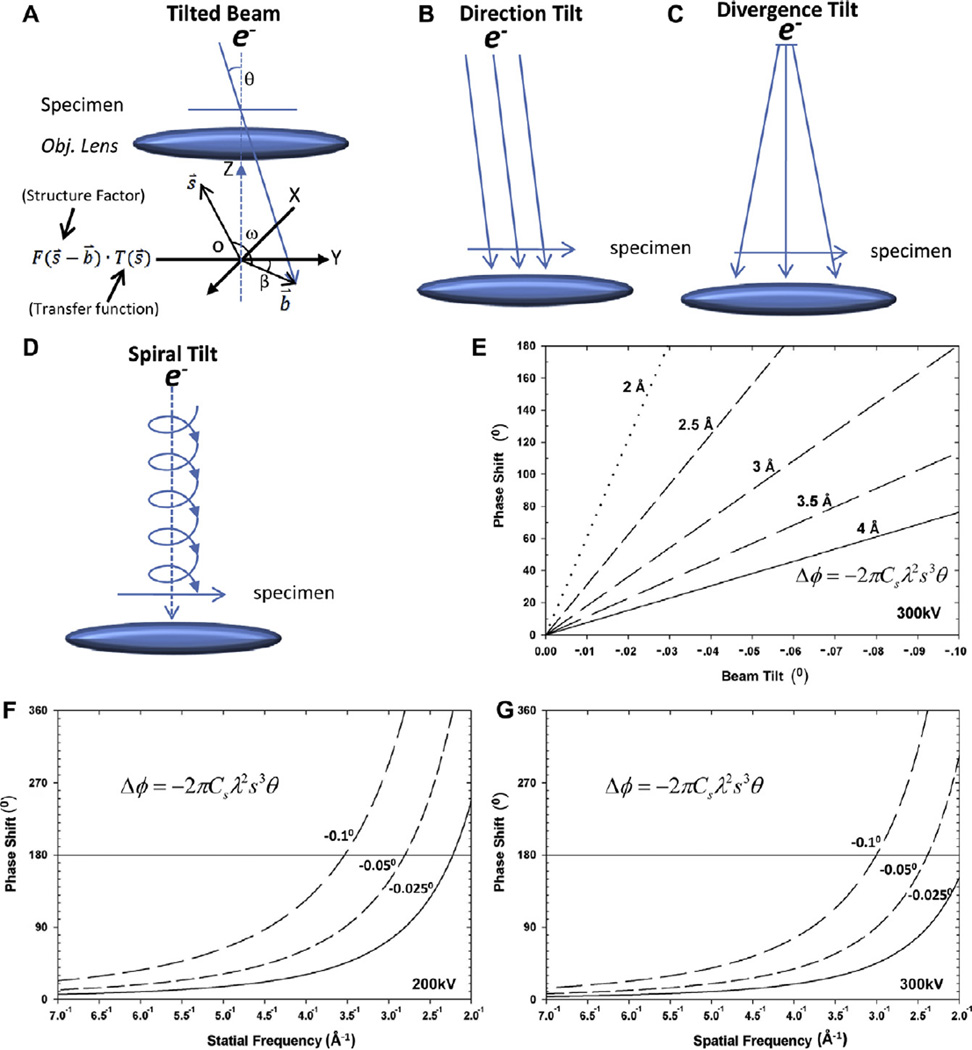
2.1.1. Limitation imposed by beam tilt
To obtain high resolution reconstruction with cryoEM, the incident electron beam should be perfectly parallel to the optical axis, as any beam tilt introduces phase shift to images (Fig. 1A) (Smith et al., 1983). Beam tilt can originate from three sources in electron microscopy: the overall beam tilt relative to the optical axis (‘direction tilt’) (Fig. 1B), beam divergence by over-focus of the C2 condenser lens (‘divergence tilt’) (Fig. 1C), and the spiraling trajectory of electrons in the inhomogeneous magnetic lens (‘spiral tilt’) (Fig. 1D) (Loretto, 1984) [the latter two tilts are also known as local beam tilts since they are position-dependent (Christenson and Eades, 1988; Eyidi et al., 2006)]. Indeed, the ‘total beam tilt’ of images is the vector sum of direction tilt, divergence tilt and spiral tilt. The phase shift (Δφ) induced by beam tilt (b̄) can be expressed as a function of spatial frequency (s) (Smith et al., 1983).
| (1) |
where Δφ is the phase shift in radians. The variables k, D, k⃗ and k⃗0 (see Supplementary material) are defined in (Hawkes, 1980). As discussed in detail by Henderson et al. (1986), the phase shift in equation 1 for images includes two terms (Eqs. (S1)–(S8), see detail in Supplementary material). The first part corresponds directly to the position shift of the whole image in real space, which depends on defocus level (Δf) and the beam tilt (b⃗). In practice, boxing a particle in an image nulls this shift. The magnitude of the observable phase shift is (see Supplementary material):
| (2) |
where ω is the azimuth angle between vectors b⃗ and s⃗ (Fig. 1A). The cubic term determines the effective phase shift – independent of defocus level – due to beam tilt (Fig. 1E–G).
Fig. 1.
Three components of beam tilt and their related phase errors. (A) A diagram illustrating how the deteriorative effects of beam tilt are generated. Above the objective lens, the electron beam and the specimen are in real space; at the back-focal plane of the objective lens, the diagram represents the electron diffraction pattern (in Fourier space) at the X–Y plane. s̄ is a vector that represents a spatial frequency in Fourier space, and T(s̄) represents the aberration transfer function of the objective lens. The effect of beam tilt in the Fourier space is to offset the Fourier origin. The vector (b̄) represents the offset of the Fourier origin and has tilt magnitude θ off the optical axis and tilt direction angle β in the X–Y (Fourier) plane. F(s̄ − b̄) is a Fourier coefficient after consideration of the beam tilt offset and F(s̄ − b̄). T(s̄) is thus the wavefront modulated by the aberration transfer function. (B–D) Diagrams illustrating the three components of beam tilt in an electron microscope. (B) Direction tilt is tilt of the beam relative to the optical axis of the microscope. (C) Divergence tilt is due to a conically shaped electron beam. (D) Spiral tilt is due to the spiral pathway of an electron in a magnetic field. (E) Phase shift as a function of the total beam tilt for different targeted resolutions from 2 to 4 Å (ω = 0°, Cs = 2 mm, accelerating voltage = 300 kV). (F–G) Phase shift as a function of spatial frequency (corresponding to resolutions from 2 to 4 Å) for several tilt angles (−0.025°, −0.05°, −0.1°) (ω = 0°, Cs = 2 mm), accelerating voltage = 200 kV (F) or 300 kV (G).
Since the phase shift induced by beam tilt increases dramatically with spatial frequency (Eq. (2)) (Fig. 1E–G), correcting its effect computationally or experimentally is critical for achieving atomic resolution by single particle cryoEM. Thus, for example, a beam tilt of 0.05° degrees (0.873 mrad) would introduce an unacceptable phase shift of 90.4° for structure factors at 3 Å resolution with Cs equal to 2 mm, λ equal to 0.0197 Å (as would be obtained with a 300 kV accelerating voltage), and ω equal to 0° (Eq. (1)) (Tables 1 and 2). If a phase shift of 45° were acceptable, the allowed beam tilt would be just 0.025° (0.436 mrad) for 3 Å resolution or 0.0074° (0.129 mrad) for 2 Å resolution. Therefore, to reach atomic resolution, the beam tilt must be reduced to such low values.
Table 1.
Phase error by a beam tilt of 0.05° (i.e., 0.87 mrad).*
| Res. (Å) | 100 kV | 200 kV | 300 kV | 400 kV |
|---|---|---|---|---|
| 2.0 | 1075° | 494° | 305° | 211° |
| 3.0 | 319° | 146° | 90.4° | 62.5° |
| 4.0 | 134° | 61.8° | 38.1° | 26.4° |
| 7.0 | 25.1° | 11.5° | 7.1° | 4.9° |
Cs = 2.0 mm and ω = 0 in Eq. (2).
Table 2.
Magnitudes of beam tilt resulting in a phase error of 45°.*
| Res. (Å) | 100 kV | 200 kV | 300 kV | 400 kV |
|---|---|---|---|---|
| 2.0 | 0.002° | 0.005° | 0.007° | 0.011° |
| 3.0 | 0.007° | 0.016° | 0.025° | 0.036° |
| 4.0 | 0.016° | 0.036° | 0.060° | 0.085° |
| 7.0 | 0.090° | 0.195° | 0.316° | 0.457° |
Cs = 2.0 mm and ω = 0 in Eq. (2).
Eq. (2) also shows that the phase shift induced by beam tilt depends on the square of wavelength. Thus, a higher accelerating voltage (e.g., an increase from 200 kV to 300 kV) can reduce the wavelength of the electron from 0.0251 to 0.0197 Å and in turn reduce the phase shift due to beam tilt for each structure factor by 36%. However, in practice, higher accelerating voltage has one disadvantage of reducing image contrast.
2.2. Methods to overcome the effect of total beam tilt
Methods to reduce beam tilt include use of beam-deflecting coils to physically align the beam to the optical axis and use of a collimating lens to produce a parallel beam. In theory, it is also possible to compensate for the effect of beam tilt with image processing software (Henderson et al., 1986), but the efficacy of this approach is limited to some extent by the low signal-to-noise ratio (SNR) of high resolution cryoEM images. Most significantly, the effect of total beam tilt can be completely eliminated by use of a hardware device, a spherical aberration corrector (i.e., Cs = 0 in Eq. (2)). Each of these methods is described below.
2.1.2. Minimizing direction tilt and divergence tilt
Aligning the direction of the electron beam parallel to the optical axis is usually accomplished by adjustment of the rotation center or current center of the objective lens. However, these adjustments are only good enough for medium resolution structural studies, since the remaining direction tilt is typically more than 1 milliradian (1 mrad = 0.0573°) (Henderson et al., 1986; Zemlin, 1989; Koster and de Ruijter, 1992). The ‘coma-free alignment procedure’ provides a more accurate method of reducing direction tilt (Zemlin, 1978; Smith et al., 1983; Koster and de Ruijter, 1992). For experienced users, assisted by visual or computational comparison of power spectra – the aim being equally compromised power spectra for left and right tilts of the beam in the x-direction and up and down tilts of the beam in the y-direction – the error margin of coma-free alignment can be as little as 0.2 mrads (~0.011°), which corresponds to phase shifts of 18.1° at 3 Å and 61° at 2 Å resolution (Table 1) (Zemlin, 1979; Koster and de Ruijter, 1992). For users less experienced in the visual comparison, the residual beam tilt of this procedure could be up to 2 mrads (~0.11°), corresponding to a phase error of 238° at 3 Å resolution for a 300 kV microscope with Cs = 2 mm (Smith et al., 1985; Overwijk et al., 1997). Nevertheless, the coma-free alignment procedure can only minimize direction tilt.
The divergence tilt occurs when the specimen is illuminated with a conical beam instead of a parallel beam (Fig. 1C). The effects of this tilt component could be alleviated by underfocusing the beam with the C2 condenser lens, which however would sacrifice beam coherence (Christenson and Eades, 1988; Zemlin, 1992). Therefore, a better solution is to use a parallel beam in the first place, which can be achieved by addition of a collimating lens like the C3 condenser lens in the FEI Titan Krios microscope (Zhang et al., 2010c). In the absence of such C3 condenser lens, parallel beam can also be achieved. There are two lenses between the C2 condenser lens and specimen: the one just above specimen is the pre-objective lens and the another one above the pre-objective lens is mini-condenser lens. The C2 condenser lens can be carefully coupled to the mini-condenser lens and the pre-objective lens to generate a parallel beam on specimen.
2.1.3. Compensating spiral tilt effect by image processing
Spiral tilt originates from the spiral trajectory of electrons in the magnetic field of the pre-objective lens. The spiral tilt angle of the electron beam with respect to optical axis depends on both the strength of the magnetic field of the pre-objective lens and the distance of individual electrons to the optical axis (Eyidi et al., 2006). For example, the spiral tilt angle is about 0.033°/µm for the Tecnai TF20 TEM (Eyidi et al., 2006), resulting in a phase shift of ~64° at 3 Å resolution or 200° at 2 Å resolution for particles that are 1 µm from the optical axis, about the distance for electrons near the edge of typical micrographs. Although the effect becomes significant only at atomic resolution (e.g., better than 3 Å), spiral tilt cannot be corrected either by instrument alignment or by use of a parallel beam.
Instead, image processing may correct the effect of the total beam tilt vector b̄, specifically its magnitude (θ) and its direction angle (β) (Fig. 1A). However, since particles at different positions have distinctive spiral and divergence tilts (Eq. (S4)) – though the same direction tilt – beam tilt needs to be determined individually for each particle image (Henderson et al., 1986; Wang et al., 1988). In two-dimensional (2D) crystallography, residual beam tilt results in unreliable phase information for structure factors better than 5.5 Å resolution, but correction for the effect of beam tilt recovers the phase information to 3.5 Å resolution (Henderson et al., 1986). However, for single particle cryoEM, accuracy in determining the beam tilt vector is limited by the poor SNR at high resolutions (e.g., 3 Å and better) in cryoEM images, and the effectiveness of the proposed method awaits experimental test.
2.1.4. A spherical aberration corrector can be used to eliminate the effect of total beam tilt
The original purpose of a device to reduce the spherical aberration coefficient (Cs) was to improve the theoretical point resolution of electron microscopes (Zach and Haider, 1995). Designed many years later, a Cs corrector device has been used to achieve subangstrom resolutions (e.g., 0.8 Å) for two-dimensional images of thin metal crystals in the field of material sciences (Zach and Haider, 1995; O’Keefe et al., 2001). For 3D reconstruction of macromolecular complexes, the limitation is mainly due to phase shifts resulting from beam tilt, as described above. Here, we suggest that if the effective spherical aberration coefficient (Cs) of the microscope could be made zero (Cs = 0) through the use of a Cs corrector device, the effect of the total beam tilt would be completely removed (Eq. (2)). Therefore, to avoid inaccuracies of beam tilt alignment and image processing, a spherical aberration corrector is the most desirable way to completely eliminate the degrading effects of total beam tilt (Eq. (2)) and thus facilitate atomic resolution reconstruction of biological complexes. This suggestion represents a new, unintended benefit of Cs corrector technology to be verified experimentally.
3. Accuracy of defocus value determination
3.1. Limitation imposed by variation of defocus values
Under-focusing the objective lens is currently the only successful method to enhance contrast and thus SNR in high-resolution electron-microscope images of weak phase objects (WPO) like biological samples, which are composed of light elements. These images are modulated by the objective lens’ contrast transfer function (CTF) (Eq. (3)). χ is known as the wave aberration function because it includes the effects of spherical aberration Cs and the actual defocus value Δf, the latter is zero for on focus condition, negative for under-focus condition.
| (3) |
| (4) |
Therefore, accurate determination of the under-focus values is essential for deconvolving the effects of the CTF to retrieve precise structural information of the specimen from cryoEM images.
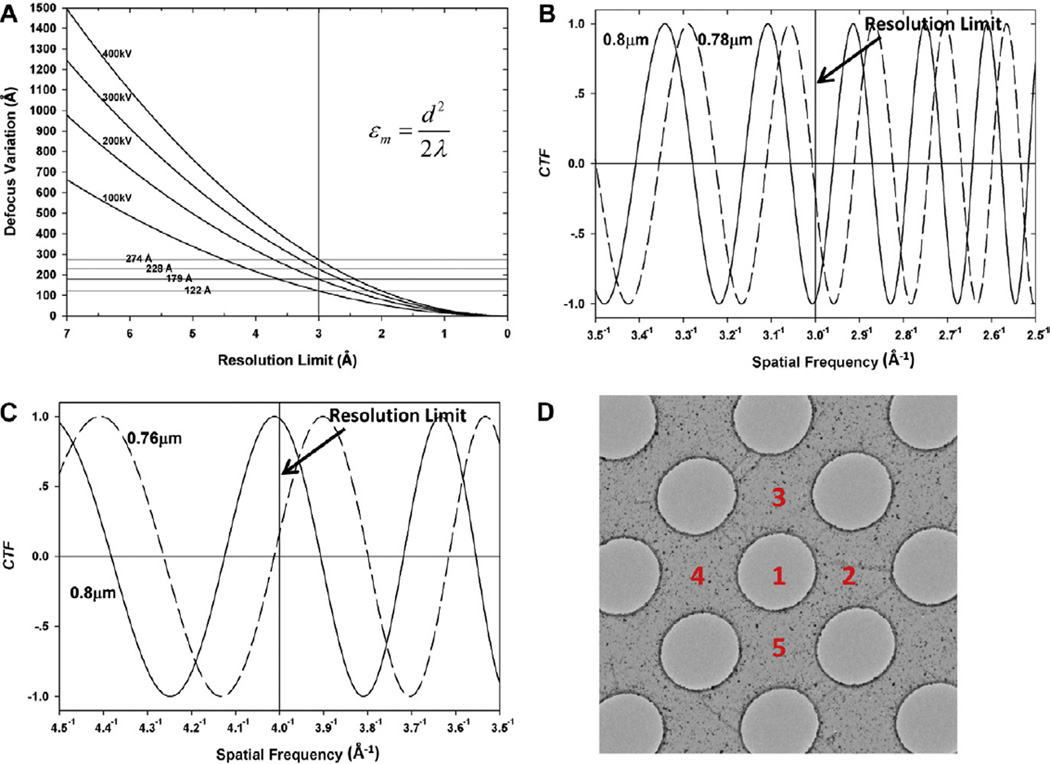
Astigmatism generates variation in defocus values as a function of direction (azimuth angle) within the image. With no astigmatism, defocus values would be the same in all directions, and CTF could be visualized in the Fourier transform of the image as circular rings. With astigmatism, CTF rings takes the form of ellipses, and variation in the defocus values can be described using three parameters: defocus 1 (Δf1), defocus 2 (Δf2) and the angle (β) between the long axis of the ellipse and X axis. Therefore, accurate determination of astigmatism is also essential.
For two reasons, an accurate determination of these values is difficult. First, since the defocus and astigmatism values of images are usually determined by fitting theoretical CTF curves into the power spectrum of cryoEM images, the accuracy of both derived defocus and astigmatism values is inherently compromised by the poor SNR of cryoEM images (Zhou et al., 1996; Mindell and Grigorieff, 2003). Second, since the thickness of embedding ice is usually greater than the diameter of particles, particles in an image may be located at different heights in the ice, leading to defocus variation among different particles. For example, the diameter of a double-layer rotavirus particle is 710 Å, and ice thickness varies between 700 and 1200 Å within a single high resolution image of rotavirus, which could result in ~500 Å focus variation among separate rotavirus particles in the ice (Zhang et al., 2008).
By assume the acceptable shift (Δχ) (Eq. (S10)) of the wave aberration function is π/2, that is, Δχ ≤ π/2, the allowable defocus variation εmax is given by Eq. (5) (Eqs. (S9)–(S12), see detailed deduction in Supplementary material).
| (5) |
Beyond this spatial frequency, more than half of the structure factors would have their phases changed 180° degrees due to the erroneously changed sign of the CTF (Fig. 2B–C, Table 3).
Fig. 2.
Effects of incorrectly determined defocus values and a method to improve the determination of defocus value. (A) Relationship between variation in defocus value and achievable resolution (d) for different accelerating voltages (thus different wavelengths λ of the electron). The four horizontal lines indicate the maximum allowable defocus variation (e.g., εm = 122–274 Å) to obtain a 3-Å resolution structure at different accelerating voltages (100, 200, 300 and 400 kV). (B) CTF curves at underfocus values of 8000 and 7800 Å. With an average defocus of 8000 Å and an individual particle at 7800, the error of just 200 Å in defocus value estimation – the underfocus difference between the two curves – would lead to a transition at 1/3 Å−1. Beyond this spatial frequency, more than half of the structure factors would have their phases changed 180° degrees due to the changed sign of the CTF (i.e., a resolution limit of 3 Å). (C) CTF curves at underfocus values of 8000 Å and 7600 Å, showing a transition at 1/4 Å−1 (i.e., a resolution limit of 4 Å). (D) New method to improve accuracy of defocus determination. Area 1 is the target area to be imaged under low dose condition; areas 2–5 are carbon regions surrounding area 1 to be imaged with higher dose for defocus determination.
Table 3.
Resolution Limit imposed by inaccuracy of defocus determination.
| Res. (Å) | 100 kV | 200 kV | 300 kV | 400 kV |
|---|---|---|---|---|
| 2.0 | 54 Å | 80 Å | 102 Å | 122 Å |
| 3.0 | 122 Å | 179 Å | 228 Å | 274 Å |
| 4.0 | 216 Å | 319 Å | 406 Å | 488 Å |
| 7.0 | 662 Å | 976 Å | 1244 Å | 1494 Å |
Correspondingly, for a certain defocus variation ε, the resolution limit dmax (=1/s) would be determined by Eq. (6).
| (6) |
According to Eqs. (5) and (6), the limiting effect of defocus variation is independent of both specimen size and defocus value (Δf). For example, a defocus variation of 500 Å would produce the same deleterious effect for different specimen sizes (e.g., diameters of 150 vs. 1500 Å) or at different defocus values (e.g., −5000 vs. −30,000 Å). Eq. (6) also shows that improvement in dmax follows the square root of electron wavelength λ (Table 3), so increasing the microscope’s accelerating voltage has limited benefit on the tolerance of defocus variation e. For example, at 3 Å resolution, the acceptable defocus variation is only slightly changed – from 179 to 228 Å – when the accelerating voltage increases from 200 to 300 kV. Compare these values with the 500 Å described at the beginning of this section.
Astigmatism creates variation in defocus values as a function of direction within the image (azimuth angle), and this effect is corrected implicitly by an accurate determination of two defocus 1 (Δf1), defocus 2 (Δf2) values and the angle (β) that describe an elliptical CTF.
3.2. Solutions to improve accuracy of the defocus determination
One way to improve accuracy in defocus and astigmatism determination would be to measure these values at four surrounding areas and to exclude images at tilted areas of the grid. We could do so with a high SNR by use of a high dose of electrons in areas adjacent to the hole. As demonstrated in Fig. 2D, first we would image the intended area 1 in the hole at low dose (e.g., ~20e−/Å2). Then, we would image amorphous carbon in adjacent areas 2–5 with a higher dose (e.g., 200e−/Å2) to measure the defocus values. The method has the side benefit that it could provide the average defocus value of single particles in the hole. However, while this method could determine the average defocus value, it could not resolve defocus variation among particles due to their different heights in ice. The overall effectiveness of the proposed method needs to be determined numerically and experimentally since the centers of ice plane and carbon film may not be the same, and particles may have different height in ice.
To determine the height – and thus the different defocus values – for each particle in ice, we propose to measure the shift of each particle in the image induced by tilting the beam (~10 mrad) (Koster et al., 1987). The shift, given by the first term in Eq. (S7), is linear with height. Since the method would be sensitive to low resolution structural features that possess good SNR, the accuracy of this method would be better than 50 Å (Koster et al., 1987).
Ideally, height variation could be eliminated prior to freezing particles in vitrified ice. Accordingly – though not for atomic resolution – we have floated a thin (~50 Å), flat, carbon, support film evaporated onto mica onto the holey grid, modified to be hydrophilic by glow discharge to encourage all particles to attach to the support film and achieve a uniform defocus level (Zhang et al., 2010b). Of course, the stage of the electron microscope must be adjusted so that the grid is perpendicular to the optical axis. The support film also minimizes ice thickness (which improves image quality), improves accuracy of defocus determination, and reduces the concentration of the sample that is needed. The use of an electrically conductive supporting film like carbon would offer additional advantages: reducing charge on the sample and reducing specimen movement due to charging (Rhinow and Kuhlbrandt, 2008). However, the use of a supporting film might have disadvantages, such as potentially unfavorable interactions with the specimen and the background noise provided by the electrons contained in the underlying 50-Å thickness of carbon – though less than the electrons contained in a 250-Å thickness of ice. Therefore, verifications are indispensible for actual effect of this proposed method.
Astigmatism can be measured by finding the best-fitting elliptical theoretical, 2D CTF pattern to the power spectrum of the image. Given its measurement, astigmatism can be corrected using the stigmator coil associated with the objective lens before data collection. Then, if additional measurements detected residual astigmatism in the recorded image, computational methods could correct the image by deconvolving the Fourier transform of an elliptical CTF defined by defocus values Δf1, Δf2 and the azimuth angle β.
4. Consequences due to a gradient in focus across different heights within the particle
4.1. Resolution limited by focus gradient
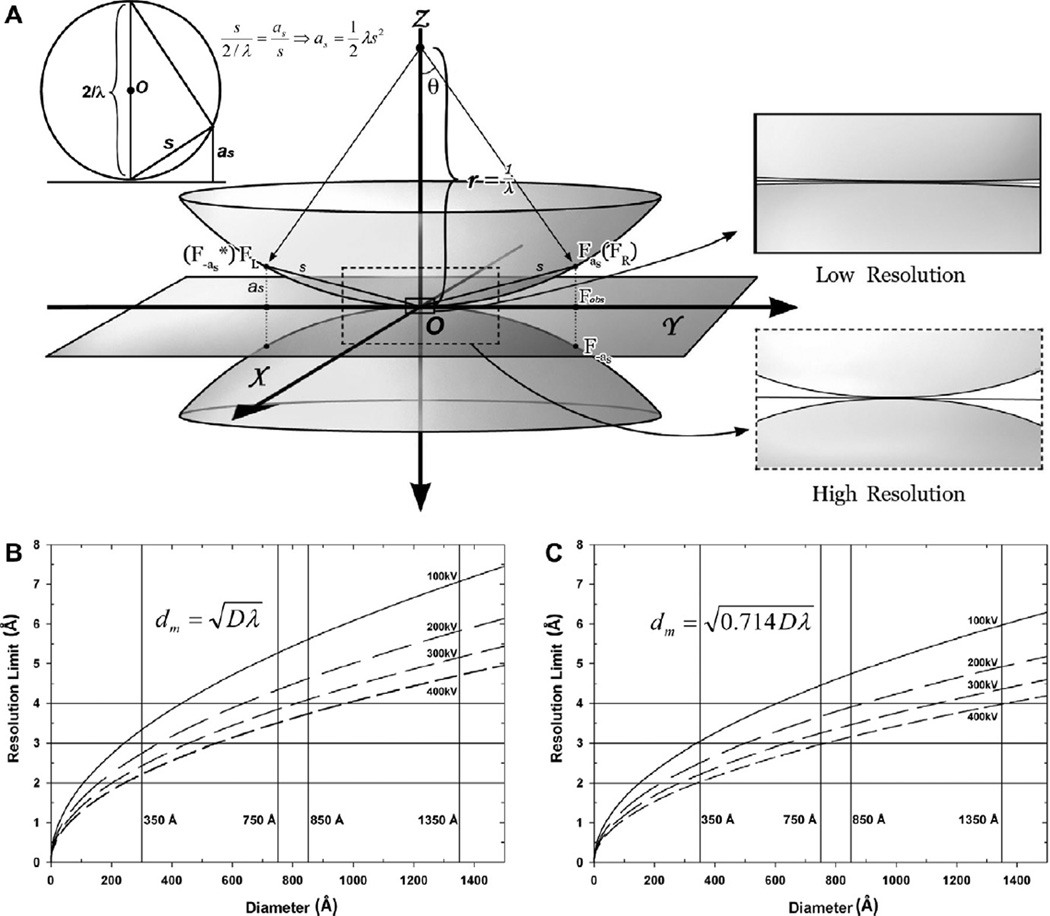
Most 3D reconstruction methods are based on the Central Projection Theorem, which states that the Fourier transform of a 2D projection image is equivalent to the central section of the 3D Fourier transform of the particle being imaged, as illustrated by the plane in Fig. 3A (Crowther, 1971). The Central Projection Theorem is based on the assumption that there is no change in the focus values from the top of a particle to the bottom. The assumption is valid only for small or thin particles. For large particles, the effect of a large gradient in focus values from slice to slice is to add different phase shifts to the electron wavefronts emerging from different slices of the particle. Failure to take this effect into consideration in current software packages based on the Central Projection Theorem thus creates a resolution barrier for the single particle cryoEM (DeRosier, 2000; Wan et al., 2004).
Fig. 3.
Breakdown of the Central Projection Theorem and its limit on the resolution of 3D reconstruction. (A) Illustration of the characteristic surfaces concept in 3D Fourier space. The 2D Fourier transform of a cryoEM image is shown as a flat 2D plane at Z = 0. According to the Central Projection Theorem, this plane is equivalent to the central section of the 3D Fourier transform (i.e., structure factors) of the specimen. When approaching atomic resolution, particularly for large particles, this theorem is no longer valid due to convolution of many contrast transfer functions, each at a different focus value for slices at different heights in the particle. Instead, each Fourier coefficient of the image is the sum of two structure factors, located, respectively, on the top and bottom characteristic surfaces at (X, Y, as) and (X, Y, −as), as described in the text. The upper left inset illustrates that each characteristic surface is a sphere with radius = 1/λ, equivalent to the Ewald sphere (upper left inset). s denotes the spatial frequency at point (X, Y, Z). On the characteristic surfaces, Z is either as (upper surface) or −as (lower surface). The two right insets illustrate that at low resolution, the characteristic surfaces merge into a single, nearly flat section, corresponding to the central section described in the Central Projection Theorem. (B–C) Resolution limit imposed by the Central Projection Theorem at different accelerating voltages based on formulas by Spence (Spence, 1988) (B) and by DeRosier (DeRosier, 2000) (C). The four vertical lines in (B) and (C) indicate typical particle diameters, and the three horizontal lines indicate resolution limits from 2 to 4 Å.
Under the principle of Fresnel propagation of electron wavefront (Eq. (3.16) in Spence, 1988), after propagating for a certain distance “z”, the phase shift of the electron wavefront will be:
| (7) |
Therefore, the phase shift of the electron wavefront from the top to the bottom of a particle with diameter D is:
| (8) |
Assuming that the tolerable phase shift of the electron wavefront due to its Fresnel propagation across the particle is π, the resolution limit without correction of the focus gradient is (Spence, 1988):
| (9) |
If d denotes the resolution,
| (10) |
DeRosier derived a different empirical equation that was equivalent to assuming the tolerable phase shift of the electron wave due to its Fresnel propagation across a particle to be 1.4π instead of π above (DeRosier, 2000). In that case, the resolution limit would become
| (11) |
Based on Eqs. (10) and (11), the particle size allowed by existing implementations is a function of target resolution. If there were no correction for focus gradient, the higher the desired resolution, the smaller the particle we should use. For example, according to Eq. (11), to reach 3 Å or 2 Å resolution using a 300 kV microscope, the acceptable diameter of particles would be 640 Å or 284 Å, respectively (Table 4). For comparison, the diameters D of herpesvirus and aquareovirus particles are 1350 Å and 850 Å, respectively. Conversely, a certain particle size would define the achievable resolution. For these two viruses, the best achievable resolutions would be 4.4 Å and 3.5 Å, respectively. Therefore, in order to break the resolution limit imposed by application of the Central Projection Theorem (Eqs. (10) and (11)) to large particles, we must correct for the focus gradient.
Table 4.
Resolution limit imposed by focus gradient across specimen depth.
| Dia. (Å) | 100 kV | 200 kV | 300 kV | 400 kV |
|---|---|---|---|---|
| 300 | 3.33 Å | 2.74 Å | 2.43 Å | 2.22 Å |
| 600 | 4.71 Å | 3.88 Å | 3.44 Å | 3.14 Å |
| 900 | 5.77 Å | 4.75 Å | 4.21 Å | 3.84 Å |
| 1300 | 6.94 Å | 5.71 Å | 5.06 Å | 4.61 Å |
Limitation based on formula by Spence (1988).
4.2. The Ewald sphere and characteristic surfaces theorem
When considering the focus gradient, the particle φ(x, y, z) can be regarded as a composite of multiple thin slices in real space, each slice at its own focus level. Each slice independently forms its own image, φz(x, y), and the final projection image φobs(x, y) of the particle is the integral of all of these images. That is:
| (12) |
For small particle, all of the slices can be approximated as being at the same height z, and we can use the Central Projection Theorem (Crowther, 1971). However, for a large particle, the focus gradient cannot be neglected, and the Central Projection Theorem becomes invalid. In this case, the projection image φobs(x, y) of the particle is the integral of the images of all the particle slices φz(x, y) (Eq. (12)), but the Fourier transform of the image of each slice at height (lower case) z is modified by a different CTFz, each with its own defocus value (Δf + z) (Wan et al., 2004), where Δf is defocus value the center of the particle. Using Fourier transform and convolution theorem, the Fourier transform of a recorded image can be decomposed as the following (see detailed derivation from Eqs. (S14)–(S27) in the Supplementary material):
| (13) |
where spatial frequency (see Fig. 3A), and .
According to Eq. (13), each observed Fourier coefficient Fobs(X, Y, 0) is composed of a mixture of two unknown structure factors (F), Fas ≡ F(X, Y, as) and F−as ≡ F(X, Y, −as), located in the Fourier space at positions (X, Y, as) and (X, Y, −as), respectively. These two points correspond to mirror points located, on the spheres of the same radius 1/λ, centered, respectively, at (0, 0, 1/λ) and (0, 0, −1/λ), as illustrated by the spherical surfaces in Fig. 3A. These two spheres are termed “characteristic surfaces” (Wan et al., 2004). In analogy to the Central Projection Theorem, we refer to Eq. (13) as Characteristic Surfaces Theorem, which states that a Fourier coefficient of the recorded image is the sum of two Fourier coefficients, one on each characteristic surface. The upper characteristic surface corresponds to the Ewald sphere. Eq. (13) is the same as the formula derived by DeRosier (Eq. (9) in DeRosier, 2000). Therefore, these two computational formulations for overcoming the breakdown of the Central Projection Theorem are equivalent. Eq. (13) indicates that the observed information Fobs is a mixture of two structure factors FR and FL that need to be recovered.
4.3. Recovering structure factors FR and FL from cryoEM images and placing them onto the curved characteristic surfaces
The above concepts of focus gradient and the characteristic surfaces theorem provide the basis for understanding how to implement strategies to recover structural information in real space or Fourier space.
The real-space method, proposed by Jensen and Kornberg (2000), is based on back-projection to correct the effect of focus gradient. To generate multiple z-slices of a particle, the recorded 2D image of each particle is de-convolved by a series of CTFs, each with defocus offset equal to the z distance of the slice from the central plane of the particle. Then, the density at each point in each slice is recovered by averaging the density value at that point from many particles. For this reason, this method has the disadvantage of being very slow.
Alternatively, data retrieval for 3D reconstruction can be implemented in Fourier space. Two slightly different strategies have been implemented, one by Wolf et al. (2006) and another by Leong et al. (2010). The first strategy uses a 3D reference (i.e., a prior reconstruction) to estimate and eliminate errors in recorded images (Wolf et al., 2006). In this strategy, as a constraint, it is assumed that a recorded structure factor Fobs is the simple vector sum of two actual structure factors FR and FL located symmetrically on the Ewald sphere, as shown in the upper surface in Fig. 3A (this assumption may be compared with Eq. (S28)). Then, with this assumption as a constraint, a 3D reference is used to estimate both amplitude and phase of the actual structure factors FR and FL (Wolf et al., 2006). In the second strategy, an iterative procedure is used to recover structure factors (Leong et al., 2010). In this procedure, an intermediate, unrefined 3D model is used to estimate the difference between the Fourier coefficients obtained from an image and that calculated from this model. Then, differences are added back as correcting factors to obtain more accurate Fourier coefficients, which lead to an improved reconstruction (Leong et al., 2010). Both of these approaches are iterative, numerical methods, and neither has demonstrated improvement of resolution of reconstruction when applied to experimental data.
Here, based on the Characteristic Surfaces Theorem, we obtain an analytic solution to correct the effect of focus gradient along the z-axis of the particle. The hidden structure factors F(X, Y, as) and F(X, Y, −as) and the observed structure factor Fobs(X, Y) (Eq. (13)) can be represented as real and imaginary parts. For example:
| (14) |
| (15) |
Expanding the right side of Eq. (13), defining Ras ≡ R(X, Y, as) and R−as ≡ R(X, Y,−as) as the real components, and Ias ≡ I(X, Y, as) and I−as ≡ I(X, Y,−as) as the imaginary components of structure factors F(X, Y, as) and F(X, Y,−as),
| (16) |
| (17) |
where δr = (R−as/Ras − 1) and δi = (I−as/Ias − 1).
The structure factors are continuous functions. For this reason, when two points in reciprocal space are close to one another, as is the case for the upper and lower points (X, Y, as) and (X, Y, −as) at low resolution, the two characteristic surfaces merge into a single horizontal plane (Fig. 3A, the top right inset). Therefore, Ras ≈ R−as and Ias ≈ I−as, making both δr and δi nearly zero. Therefore, at low resolution (i.e., from 20 to 4 Å) the conventional central-section approximation is valid, and the focus gradient may be ignored, for example, for particles with diameter of 1000 Å (at ~4 Å resolution) or thicker (at resolution worse than 4 Å) (Eq. (11)).
The characteristic surfaces curve away from each other when the resolution is high (<4 Å), as shown for large X, Y, Z values in reciprocal space (Fig. 3A and right lower inset of Fig. 3A), where s is large (upper left inset of Fig. 3A). In that case, δr and δi are non-negligible for large particles (Eq. (S21)) like herpesvirus (diameter = 1350 Å).
To recover the hidden structure factors F(X, Y, as) (similarly for F(X, Y,−as)) (Eq. (13)) from a recorded image, we solve for the real and imaginary components Ras and Ias as follows:
| (18) |
| (19) |
where Robs and Iobs can be calculated from the Fourier transform of the image. The two unknown coefficients δr and δi may be approximated using a reference reconstruction [i.e., ], and the recovered structure factor F(X, Y, as) could be used to calculate a new reconstruction. Improvement could be monitored by checking the Fourier-shell cross-correlation coefficient plot and by evaluating density features. This process could be iterated until no further improvement of resolution were obtained. In the special case in which an atomic model of a particle has been built, δr and δi could be calculated more readily and accurately starting from the atomic model. This proposed method could be used to further improve the resolution of 3D reconstructions of aquareovirus, adenovirus and bovine papillomavirus, since their atomic models have already been built from 3D reconstruction without correcting for the effect of focus gradient (Liu et al., 2010; Wolf et al., 2010; Zhang et al., 2010c).
5. Dynamic scattering
5.1. Effects of dynamic scattering
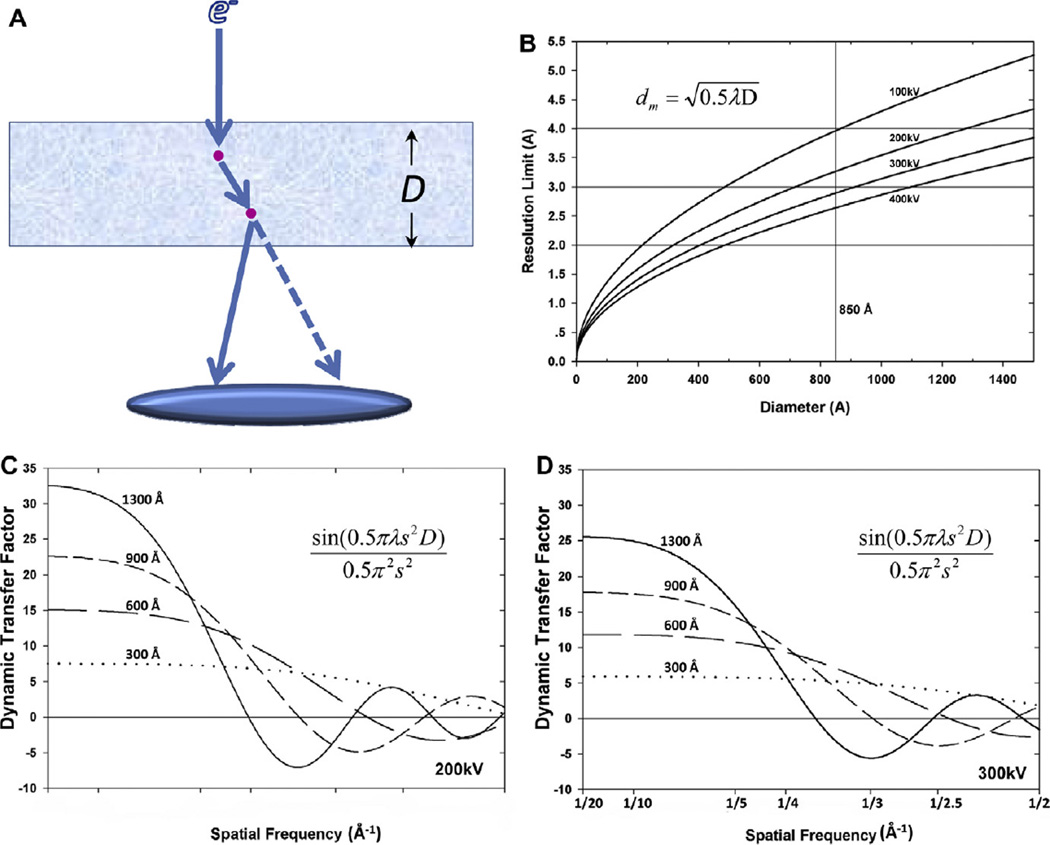
Electrons are scattered much more strongly than X-ray photons by specimens, making it possible to collect structural information for a single biological complex as small as 38 kDa by cryoEM (Henderson, 1995). However, the stronger scattering of electrons also makes the dynamic (multiple) scattering effects of electrons much more severe than that of X-ray photons. Because biological specimens are primarily composed of light elements and are thus weak phase objects, neglect of the effects of dynamic scattering is likely to be valid when the specimen is thin and at low resolution (Glaeser and Downing, 1993). With an increase in specimen thickness and accompanying increase in scattering, and with improvements in targeted resolution, the effect of dynamic scattering becomes significant, making compensation for the effects of dynamic scattering necessary (Glaeser and Ceska, 1989; Grigorieff and Henderson, 1996). By this criterion the particle sizes for most viruses are significantly thick, and the effect of dynamic scattering cannot be ignored at atomic resolution. We therefore analyze and propose a method to correct the effects of dynamic scattering in cryoEM based on a more accurate dynamical analysis method derived by Yang et al., which has been demonstrated to be consistent with the results of the multi-slice method (Yang et al., 2001).
5.2. Phase flip by dynamic scattering
Based on Eq. (6) in Yang et al. (2001) paper, with F(X, Y) as the structure factor of the image without the effects of dynamic scattering, we obtain the effect of dynamic scattering as the following (Eqs. (S29)–(S35) see detail in Supplementary material):
| (20) |
where D is the diameter of the particle and s a spatial frequency. According to Eq. (20), the structure factor of a recorded image is modified not only by CTF, but also by a dynamical transfer function (DTF):
| (21) |
For each s, the DTF thus depends only on the diameter D of the particle. Starting with the recorded image ψ(x, y), the CTF obtained as above (Eqs. (3) and (4)), and the DTF as computed in Eq. (21), we can obtain the corrected F(X, Y) from Eq. (20). Equivalently, one could deconvolve the Fourier transform of the DTF in Eq. (21) in real space.
5.3. Correction for the effects of dynamic scattering by flipping phase
Similar to the CTF, the DTF flips phases of a structure factor when its value is negative; thus, images must be corrected for the DTF in order to correctly retrieve structural information. As apparent in Eq. (21), DTF is a function of specimen diameter (D) and electron wavelength (λ). (For this reason thinner specimens and higher accelerating voltage (i.e., smaller λ) can alleviate the effects of dynamic scattering.) Without correcting for DTF, the resolution limit imposed by dynamic scattering is the lowest spatial frequency (s) at which phase flip occurs, that is, when
| (22) |
where dm denotes the resolution limit in the absence of DTF correction. dm is proportional to the square root of particle diameter (D). For example, the first phase flip due to DTF occurs at resolutions of 2.66 Å for the double-layer rotavirus (diameter D = 710 Å), 2.9 Å for reovirus (D = 850 Å), and 3.65 Å for herpesvirus (D = 1350 Å).
However, as 2D crystal samples are generally thinner than large viruses, one can achieve better resolution for such samples without correcting for the effects of DTF. For example, the thickness of aquaporin-0 crystals is ~160 Å, leading to a resolution limit of 1.26 Å when the DTF effect is not corrected (Eq. (22)). Indeed, the resolution of the aquaporin-0 3D structure has reached 1.9 Å without correction for DTF (Gonen et al., 2005). For thick specimens at atomic resolution, the effects of dynamic scattering would need to be corrected by deconvolving the DTF (Fig. 4C–D). Nevertheless, atomic reconstruction of a large complex such as herpesvirus would be an ideal specimen to validate the concept of DTF (Eq. (21)).
Fig. 4.
Dynamic transfer function (DTF) and its limitation on the resolution in 3D reconstruction. (A) A diagram showing the mechanism of dynamic scattering. “D” denotes the diameter of a particle, and red spots represent atoms in the particle. Solid arrows represent the actual pathway of an electron inside the particle, and the dashed line represents the hypothetical pathway of the electron without considering the dynamic scattering. (B) Resolution limit dm imposed by ignoring dynamic scattering as a function of the particle diameter D at different accelerating voltages. (C and D) Dynamic transfer functions at the accelerating voltage of 200 kV (C) and 300 kV (D) for different particle diameters (300–1300 Å), demonstrating that a higher accelerating voltage can push the resolution limit due to dynamic scattering to a small extent.
It is worth noting that, according to Eq. (20), dynamic scattering also results in an effective focus change of 0.5D, where D denotes the diameter of the particle. This focus change adds to the focus level set by the objective lens (Eq. (20)). If images are used to determine the defocus level, this defocus change would have been included in the defocus value so determined. However, if the defocus level were set based on the image shift induced by beam tilt during image acquisition, this additional 0.5D defocus change would not have been taken into account by the pre-set defocus value, so it should be included in the CTF correction for reconstruction at atomic resolution.
6. Conclusions
Single particle cryo electron microscopy is entering an exciting era of atomic resolution. Here, we have described the cumulative effects of several obstacles to reaching atomic resolution: beam tilt, inaccuracy of defocus value determination, the defocus gradient along the depth of the particle, and dynamic scattering (Tables 1–6). Resolution limits due to beam tilt and inaccuracy of the determination of defocus value are independent of sample thickness (Eqs. (2) and (5)). Resolution limits due to focus gradient through particles and due to dynamic scattering are dependent on specimen thickness, and become more severe for thick specimens (Eqs. (10), (11), and (21)).
Table 6.
Resolution limit imposed by dynamic scattering.
| Dia. (Å) | 100 kV | 200 kV | 300 kV | 400 kV |
|---|---|---|---|---|
| 300 | 2.36 Å | 1.94 Å | 1.72 Å | 1.57 Å |
| 600 | 3.33 Å | 2.74 Å | 2.43 Å | 2.21 Å |
| 900 | 4.08 Å | 3.36 Å | 2.98 Å | 2.71 Å |
| 1300 | 4.90 Å | 4.04 Å | 3.58 Å | 3.26 Å |
Our proposed methods to overcome these limitations include: (1) a better instrument with a Cs corrector or a better instrument alignment to minimize phase errors caused by beam tilt; (2) three methods to improve accuracy in the determination of defocus value; (3) a new iterative method to recover hidden structure factors in the face of the defocus gradient; and (4) undoing flipping to correct for the effect of dynamic scattering.
We note that the effects of dynamic scattering could be determined and corrected independently from the other limiting factors, as this effect depends only on particle size. By contrast, the effects of defocus variation, beam tilt and focus gradient are coupled because these factors alter the phases of structure factors, and the residual error of the one factor affects the determination and correction of the other factors (Krakow et al., 1976; DeRosier, 2000). Nonetheless, it is possible to eliminate one or another of the three coupled factors. For example, the effect of focus gradient by itself can be ignored for small particles, and beam tilt by itself could be eliminated by use of a spherical aberration corrector.
Supplementary Material
Table 5.
Resolution Limit imposed by focus gradient across specimen depth.
| Dia. (Å) | 100 kV | 200 kV | 300 kV | 400 kV |
|---|---|---|---|---|
| 300 | 2.82 Å | 2.32 Å | 2.05 Å | 1.87 Å |
| 600 | 3.98 Å | 3.28 Å | 2.91 Å | 2.65 Å |
| 900 | 4.88 Å | 4.02 Å | 3.56 Å | 3.25 Å |
| 1300 | 5.86 Å | 4.83 Å | 4.28 Å | 3.90 Å |
Limitation based on formula by DeRosier (2000).
Acknowledgments
We thank Prof. Stan Schein for editorial assistance and Prof. Qibin Yang for discussions on dynamic scattering. This research was supported in part by grants from National Institutes of Health (GM071940 and AI069015 to Z.H.Z.). We acknowledge the use of the cryoEM facility at the Electron Imaging Center for NanoMachines supported by NIH (1S10RR23057).
Footnotes
Appendix A. Supplementary data
Supplementary data associated with this article can be found, in the online version, at doi:10.1016/j.jsb.2011.05.004.
References
- Capitani GC, Oleynikov P, Hovmoller S, Mellini M. A practical method to detect and correct for lens distortion in the TEM. Ultramicroscopy. 2006;106:66–74. doi: 10.1016/j.ultramic.2005.06.003. [DOI] [PubMed] [Google Scholar]
- Chen JZ, Settembre EC, Aoki ST, Zhang X, Bellamy AR, Dormitzer PR, Harrison SC, Grigorieff N. Molecular interactions in rotavirus assembly and uncoating seen by high-resolution cryo-EM. Proc. Natl. Acad. Sci. USA. 2009;106:10644–10648. doi: 10.1073/pnas.0904024106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng L, Sun J, Zhang K, Mou Z, Huang X, Ji G, Sun F, Zhang J, Zhu P. Atomic model of a cypovirus built from cryo-EM structure provides insight into the mechanism of mRNA capping. Proc. Natl. Acad. Sci. USA. 2011;108:1373–1378. doi: 10.1073/pnas.1014995108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christenson KK, Eades JA. Skew thoughts on parallelism. Ultramicroscopy. 1988;26:113–132. [Google Scholar]
- Cong Y, Baker ML, Jakana J, Woolford D, Miller EJ, Reissmann S, Kumar RN, Redding-Johanson AM, Batth TS, Mukhopadhyay A, Ludtke SJ, Frydman J, Chiu W. 4.0-A resolution cryo-EM structure of the mammalian chaperonin TRiC/CCT reveals its unique subunit arrangement. Proc. Natl. Acad. Sci. USA. 2010;107:4967–4972. doi: 10.1073/pnas.0913774107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowther RA. Procedures for three-dimensional reconstruction of spherical viruses by Fourier synthesis from electron micrographs. Philos. Trans. R. Soc. Lond B Biol. Sci. 1971;261:221–230. doi: 10.1098/rstb.1971.0054. [DOI] [PubMed] [Google Scholar]
- DeRosier DJ. Correction of high-resolution data for curvature of the Ewald sphere. Ultramicroscopy. 2000;81:83–98. doi: 10.1016/s0304-3991(99)00120-5. [DOI] [PubMed] [Google Scholar]
- Eyidi D, Hébert C, Schattschneider P. Short note on parallel illumination in the TEM. Ultramicroscopy. 2006;106:1144–1149. doi: 10.1016/j.ultramic.2006.04.029. [DOI] [PubMed] [Google Scholar]
- Ge P, Zhou ZH. Hydrogen-bonding networks and RNA bases revealed by cryo electron microscopy suggest a triggering mechanism for calcium switches. Proc. Natl. Acad. Sci. 2011;108 doi: 10.1073/pnas.1018104108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaeser RM, Ceska TA. High-voltage electron diffraction from bacteriorhodopsin (purple membrane) is measurably dynamical. Acta Crystallogr. A. 1989;45(Pt 9):620–628. doi: 10.1107/s0108767389004599. [DOI] [PubMed] [Google Scholar]
- Glaeser RM, Downing KH. High-resolution electron crystallography of protein molecules. Ultramicroscopy. 1993;52:478–486. doi: 10.1016/0304-3991(93)90064-5. [DOI] [PubMed] [Google Scholar]
- Gonen T, Cheng Y, Sliz P, Hiroaki Y, Fujiyoshi Y, Harrison SC, Walz T. Lipid-protein interactions in double-layered two-dimensional AQP0 crystals. Nature. 2005;438:633–638. doi: 10.1038/nature04321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grassucci RA, Taylor DJ, Frank J. Preparation of macromolecular complexes for cryo-electron microscopy. Nat. Protoc. 2007;2:3239–3246. doi: 10.1038/nprot.2007.452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grigorieff N. FREALIGN: high-resolution refinement of single particle structures. J. Struct. Biol. 2007;157:117–125. doi: 10.1016/j.jsb.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Grigorieff N, Harrison SC. Near-atomic resolution reconstructions of icosahedral viruses from electron cryo-microscopy. Curr. Opin. Struct. Biol. 2011;21:265–273. doi: 10.1016/j.sbi.2011.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grigorieff N, Henderson R. Electron-crystallographic refinement of the structure of bacteriorhodopsin. Ultramicroscopy. 1996;65:101–107. doi: 10.1006/jmbi.1996.0328. [DOI] [PubMed] [Google Scholar]
- Hawkes PW. Units and conventions in electron microscopy, for use in ultramicroscopy. Ultramicroscopy. 1980;5:67–70. [Google Scholar]
- Henderson R. The potential and limitations of neutrons, electrons and X-rays for atomic resolution microscopy of unstained biological moleculesQRev. Biophys. 1995;28:171–193. doi: 10.1017/s003358350000305x. [DOI] [PubMed] [Google Scholar]
- Henderson R, Baldwin JM, Downing KH, Lepault J, Zemlin F. Structure of purple membrane from halobacterium halobium: recording, measurement and evaluation of electron micrographs at 3.5 Å resolution. Ultramicroscopy. 1986;19:147–178. [Google Scholar]
- Jensen GJ, Kornberg RD. Defocus-gradient corrected back-projection. Ultramicroscopy. 2000;84:57–64. doi: 10.1016/s0304-3991(00)00005-x. [DOI] [PubMed] [Google Scholar]
- Jiang W, Baker ML, Jakana J, Weigele PR, King J, Chiu W. Backbone structure of the infectious epsilon15 virus capsid revealed by electron cryomicroscopy. Nature. 2008;451:1130–1134. doi: 10.1038/nature06665. [DOI] [PubMed] [Google Scholar]
- Koster AJ, de Ruijter WJ. Practical autoalignment of transmission electron microscopes. Ultramicroscopy. 1992;40:89–107. [Google Scholar]
- Koster AJ, Van Den Bos A, Van Der Mast KD. An Autofocus Method For A TEM. Ultramicroscopy. 1987;21:209–222. [Google Scholar]
- Krakow W, Ast DG, Goldfarb W, Siegel BM. Origin of the fringe structure observed in high resolution bright-field electron micrographs of amorphous materials. Philos. Mag. 1976;33:985–1014. [Google Scholar]
- Leong PA, Yu X, Zhou ZH, Jensen GJ. Correcting for the ewald sphere in high-resolution single-particle reconstructions. Methods Enzymol. 2010;482:369–380. doi: 10.1016/S0076-6879(10)82015-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Jin L, Koh SB, Atanasov I, Schein S, Wu L, Zhou ZH. Atomic structure of human adenovirus by cryo-EM reveals interactions among protein networks. Science. 2010;329:1038–1043. doi: 10.1126/science.1187433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loretto MH. Electron Beam Analysis of Materials. London: Chapman and Hall Ltd; 1984. Electron beam analysis of materials; pp. 7–11. [Google Scholar]
- Ludtke SJ, Baker ML, Chen DH, Song JL, Chuang DT, Chiu W. De novo backbone trace of GroEL from single particle electron cryomicroscopy. Structure. 2008;16:441–448. doi: 10.1016/j.str.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Mindell JA, Grigorieff N. Accurate determination of local defocus and specimen tilt in electron microscopy. J Struct Biol. 2003;142:334–347. doi: 10.1016/s1047-8477(03)00069-8. [DOI] [PubMed] [Google Scholar]
- O’Keefe MA, Nelson EC, Wang YC, Thust A. Sub-Angstrom resolution of atomistic structure below 0.8 A. Philos. Mag. B. 2001;81:1861–1878. [Google Scholar]
- Olson NH, Baker TS. Magnification calibration and the determination of spherical virus diameters using cryo-microscopy. Ultramicroscopy. 1989;30:281–297. doi: 10.1016/0304-3991(89)90057-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overwijk MHF, Bleeker AJ, Thust A. Correction of three-fold astigmatism for ultra-high-resolution TEM. Ultramicroscopy. 1997;67:163–170. [Google Scholar]
- Rhinow D, Kuhlbrandt W. Electron cryo-microscopy of biological specimens on conductive titanium-silicon metal glass films. Ultramicroscopy. 2008;108:698–705. doi: 10.1016/j.ultramic.2007.11.005. [DOI] [PubMed] [Google Scholar]
- Smith DJ, Saxton WO, O’Keefe MA, Wood GJ, Stobbs WM. The importance of beam alignment and crystal tilt in high resolution electron microscopy. Ultramicroscopy. 1983;11:263–281. [Google Scholar]
- Smith DJ, Camps RA, Freeman LA, O’Keefe MA, Saxton WO, Wood GJ. Approaching atomic-resolution electron microscopy. Ultramicroscopy. 1985;18:63–75. [Google Scholar]
- Spence JCH. Experimental High-resolution Electron Microscopy. New York: Oxford University Press; 1988. [Google Scholar]
- van Duinen G, van Heel M, Patwardhan A. Magnification variations due to illumination curvature and object defocus in transmission electron microscopy. Opt. Express. 2005;13:9085–9093. doi: 10.1364/opex.13.009085. [DOI] [PubMed] [Google Scholar]
- Wan Y, Chiu W, Zhou ZH. Full contrast transfer function correction in 3D cryo-EM reconstruction. IEEE Proc. ICCCAS. 2004;2004:960–964. [Google Scholar]
- Wang D, Hovmöller S, Kihlborg L, Sundberg M. Structure determination and correction for distortions in HREM by crystallographic image processing. Ultramicroscopy. 1988;25:303–316. [Google Scholar]
- Wolf M, DeRosier DJ, Grigorieff N. Ewald sphere correction for single-particle electron microscopy. Ultramicroscopy. 2006;106:376–382. doi: 10.1016/j.ultramic.2005.11.001. [DOI] [PubMed] [Google Scholar]
- Wolf M, Garcea RL, Grigorieff N, Harrison SC. Subunit interactions in bovine papillomavirus. Proc. Natl. Acad. Sci. USA. 2010;107:6298–6303. doi: 10.1073/pnas.0914604107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q, Wang Y, Liu Q, Yan X. An accurate analytical approach to electron crystallography. Ultramicroscopy. 2001;87:177–186. doi: 10.1016/s0304-3991(00)00098-x. [DOI] [PubMed] [Google Scholar]
- Yonekura K, Maki-Yonekura S, Namba K. Complete atomic model of the bacterial flagellar filament by electron cryomicroscopy. Nature. 2003;424:643–650. doi: 10.1038/nature01830. [DOI] [PubMed] [Google Scholar]
- Yu X, Jin L, Zhou ZH. 3.88 Å structure of cytoplasmic polyhedrosis virus by cryo-electron microscopy. Nature. 2008;453:415–419. doi: 10.1038/nature06893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu X, Ge P, Jiang J, Atanasov I, Zhou ZH. Atomic model of CPV reveals the mechanism used by this single-shelled virus to economically carry out functions conserved in multishelled reoviruses. Structure. 2011;19:652–661. doi: 10.1016/j.str.2011.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zach J, Haider M. Aberration correction in a low voltage SEM by a multipole corrector. Nucl. Instr. Methods Phys. Res. A. 1995;363:316–325. [Google Scholar]
- Zemlin F. Coma-free alignment of high resolution electron microscopes with the aid of optical diffractograms. Ultramicroscopy. 1978;3:49–60. [Google Scholar]
- Zemlin F. A practical procedure for alignment of a high resolution electron microscope. Ultramicroscopy. 1979;4:241–245. [Google Scholar]
- Zemlin F. Interferometric measurement of axial coma in electron-microscopical images. Ultramicroscopy. 1989;30:311–314. [Google Scholar]
- Zemlin F. Desired features of a cryoelectron microscope for the electron crystallography of biological material. Ultramicroscopy. 1992;46:25–32. doi: 10.1016/0304-3991(92)90005-5. [DOI] [PubMed] [Google Scholar]
- Zhang X, Settembre E, Xu C, Dormitzer PR, Bellamy R, Harrison SC, Grigorieff N. Near-atomic resolution using electron cryomicroscopy and single-particle reconstruction. Proc. Natl. Acad. Sci. USA. 2008;105:1867–1872. doi: 10.1073/pnas.0711623105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Baker ML, Schroder GF, Douglas NR, Reissmann S, Jakana J, Dougherty M, Fu CJ, Levitt M, Ludtke SJ, Frydman J, Chiu W. Mechanism of folding chamber closure in a group II chaperonin. Nature. 2010a;463:379–383. doi: 10.1038/nature08701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Boyce M, Bhattacharya B, Zhang X, Schein S, Roy P, Zhou ZH. Bluetongue virus coat protein VP2 contains sialic acid-binding domains, and VP5 resembles enveloped virus fusion proteins. Proc. Natl. Acad. Sci. USA. 2010b;107:6292–6297. doi: 10.1073/pnas.0913403107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Jin L, Fang Q, Hui WH, Zhou ZH. 3.3 Å cryo-EM structure of a nonenveloped virus reveals a priming mechanism for cell entry. Cell. 2010c;141:472–482. doi: 10.1016/j.cell.2010.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou ZH. Towards atomic resolution structural determination by single-particle cryo-electron microscopy. Curr. Opin. Struct. Biol. 2008;18:218–228. doi: 10.1016/j.sbi.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou ZH. Atomic resolution cryo electron microscopy of macromolecular complexes. Adv. Protein Chem. Struct. Biol. 2011;82:1–35. doi: 10.1016/B978-0-12-386507-6.00001-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou ZH, Chiu W. Prospects for using an IVEM with a FEG for imaging macromolecules towards atomic resolution. Ultramicroscopy. 1993;49:407–416. doi: 10.1016/0304-3991(93)90246-t. [DOI] [PubMed] [Google Scholar]
- Zhou ZH, Hardt S, Wang B, Sherman MB, Jakana J, Chiu W. CTF determination of images of ice-embedded single particles using a graphics interface. J. Struct. Biol. 1996;116:216–222. doi: 10.1006/jsbi.1996.0033. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.