Mechanism and kinetics of a sodium-driven bacterial flagellar motor

Significance

Using new experimental methods, we measure the mechanical output of the bacterial flagellar motor, the rotary molecular machine that propels swimming bacteria, while varying both electrical and chemical components of the ion-motive force that drives it. We find that each independent torque-generating stator in the motor passes 37 ± 2 ions per revolution, at odds with previous indications of 26 or 52 ions. Fitting our data to theoretical models reveals the kinetics of the motor mechanism. Our thorough search of the multidimensional parameter space of generalized motor models, guided by experimental data, is an approach that may be widely applicable.

Abstract

The bacterial flagellar motor is a large rotary molecular machine that propels swimming bacteria, powered by a transmembrane electrochemical potential difference. It consists of an ∼50-nm rotor and up to ∼10 independent stators anchored to the cell wall. We measured torque–speed relationships of single-stator motors under 25 different combinations of electrical and chemical potential. All 25 torque–speed curves had the same concave-down shape as fully energized wild-type motors, and each stator passes at least 37 ± 2 ions per revolution. We used the results to explore the 25-dimensional parameter space of generalized kinetic models for the motor mechanism, finding 830 parameter sets consistent with the data. Analysis of these sets showed that the motor mechanism has a “powerstroke” in either ion binding or transit; ion transit is channel-like rather than carrier-like; and the rate-limiting step in the motor cycle is ion binding at low concentration, ion transit, or release at high concentration.

Ion-motive force (IMF) comprises electrical and chemical transmembrane potentials and is defined as

where V_m is the membrane voltage and Δμ = k_BT ln(C_in/C_out) and q are the transmembrane chemical potential difference and charge of the ions, respectively, with C_in and C_out the internal and external ion concentrations. In most species the primary form of biological free energy is the proton-motive force (PMF), the IMF for H⁺ ions (1). Physiological PMF is typically in the range −150 mV to −200 mV, with the inside electrically negative and slightly alkaline relative to the outside. Some organisms use sodium-motive force (SMF) to drive numerous cellular processes, such as bacterial motility (2), ATP synthesis (3), and active membrane transport (4). Arguably the most important process driven by IMF is ATP synthesis, which generates cellular ATP by forced rotation of the F₁ part of F₁F_O ATP-synthase. F₁ is mechanically coupled to and rotated by F_O, which like the bacterial flagellar motor (BFM) is an ion-driven rotary motor. Understanding the mechanism of these and other ion-driven molecular machines is a fundamental challenge in cellular energetics and biophysics.

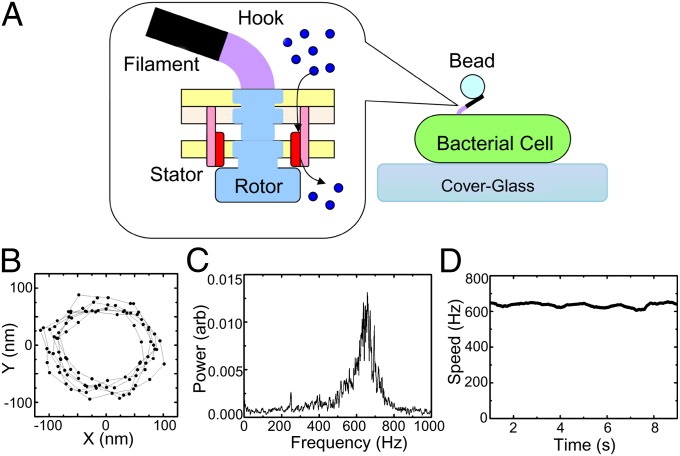
The BFM (Fig. 1A) is a rotary molecular machine that propels many species of swimming bacteria. It couples ion flow, for example protons (H⁺) in Escherichia coli or sodium ions (Na⁺) in Vibrio alginolyticus, to the rotation of extracellular helical flagellar filaments at hundreds of revolutions per second (Hz) (2, 5, 6). Torque is generated by interactions between stator complexes (containing the proteins MotA and MotB in E. coli and PomA and PomB in V. alginolyticus) and the rotor protein FliG (7). In E. coli, each motor can be powered by any number between 1 and at least 11 functionally independent stators (8), which exchange with a membrane-bound pool of “spare” stators on a timescale of minutes (9).

Fig. 1.

Bacterial flagellar motor speed measurement. (A) Schematic of the bacterial flagellar motor and the polystyrene bead rotation assay. Stator proteins couple ion flux to rotation of the rotor. The hook is a universal joint that connects external flagellar filaments to the rotor. Motor rotation is observed via back-focal-plane interferometry of a polystyrene bead attached to the truncated filament. (B) A typical 10-ms X-Y trace of a 200-nm polystyrene bead attached to a fully energized motor, sampled at 10 kHz. (C) The power spectrum of (X + iY) from B shows a clear peak at 660 Hz. (D) The stable rotational speed of the same motor for 10 s.

The most important biophysical method for studying the torque-generating mechanism of the BFM has been to measure its torque–speed curves. This has been done using varying viscous load (10–14) or external torque (15, 16) to control the speed. Fully energized motors with a full complement of stators, driven by H⁺ (10) or Na⁺ (11, 12), show the same characteristic torque–speed curve. There is a plateau of nearly constant torque from stall up to a certain limiting speed, and at higher speeds torque falls more rapidly to zero. The junction between these two domains is relatively sharp and has been called the “knee”. In the wild-type E. coli motor, the knee is at ∼200 Hz and the zero-torque speed is ∼300 Hz (17). Na⁺-driven motors are faster: In V. alginolyticus and the chimeric motor in E. coli the knee speeds are ∼450 Hz and the zero-torque speeds are ∼700 Hz and ∼900 Hz, respectively (11, 12). Torque–speed curves have also been measured for fully energized motors with reduced numbers of stators. The torque generated by H⁺-driven motors with N stators appears to be simply N times the torque generated by a single stator at the same speed (18), a result that has recently been confirmed by measurements close to the zero-torque limit (17, 19). Previously measured torque–speed curves for single-stator Na⁺-driven motors do not extend beyond the knee due to a lack of data points at extremely low load (12). Various models of the mechanism of torque generation in the BFM have been proposed and tested by their ability to predict the torque–speed curve (16, 20–24). The torque plateau is believed to represent a regime where motion of the attached load rather than internal processes in the motor’s mechano-electrochemical cycle is rate limiting, and the system operates with high efficiency close to thermodynamic equilibrium. Thus, the plateau torque is close to the stall torque, and the work done against viscous drag is nearly equal to the free energy of driving ions that is consumed by the motor. As the load is reduced and the motor speeds up, the knee represents the point at which internal processes become rate limiting, and the zero-torque speed is a measure of the limiting rate of the cycle in the absence of load.

The recent development of a Na⁺-driven chimeric flagellar motor in E. coli (25) opened new possibilities for investigation of the mechano-electrochemical cycle of the BFM (26). The PMF that drives the wild-type motor of E. coli is the primary form of free energy in the cell and is consequently tightly regulated and relatively difficult to manipulate. Furthermore, extreme changes in H⁺ concentration equate to extremes of pH, which are expected to affect the stability of motor proteins. On the other hand, the SMF in E. coli is secondary and relatively easy to manipulate, and extremes of [Na⁺] are tolerated by the cell. We have recently demonstrated that the electrical and chemical potential components of the SMF in E. coli can be varied independently via the pH and [Na⁺] of the surrounding medium (27, 28) (Table S1).

In this paper, we measured the torque–speed curves of single-stator Na⁺-driven chimeric motors for each of 25 different combinations of membrane voltage and sodium gradient (27, 28) (Table S1). We chose single-stator motors, to isolate the properties of the fundamental mechanochemical cycle from the complication of interactions between different stators in the same motor. Our set of torque–speed curves is an order of magnitude bigger than any previous torque–speed dataset and allowed a systematic exploration of the parameter space of a minimal four-state kinetic model of the BFM mechanochemical cycle. The four-state kinetic model derives from the simplest possible representation of a carrier-like ion transport mechanism (29, 30) and has been extensively used to model the BFM (31). Rather than choosing a single set of model parameters by educated guesswork, as in all previous attempts to model the flagellar motor, we performed a comprehensive search for sets of values of the 25 model parameters that were consistent with our measured torque–speed curves.

Results

Torque–Speed Curves.

For each unidirectional Na⁺-driven chimeric flagellar motor in E. coli strain YS34 (25, 26), we took 100 or 200 consecutive speed measurements at 0.1-s intervals, using back-focal plane interferometry of polystyrene beads (0.2–1.0 μm diameter), attached to truncated stubs of spontaneously sticky flagellar filaments (Fig. 1) (8, 18). At pH 7 only we replaced polystyrene beads with 100-nm gold beads attached to the flagellar hook via antihook antibody, following the protocol of Yuan and Berg (17) with minor modifications, and obtained the bead position by laser dark-field microscopy (32) rather than back-focal plane interferometry.

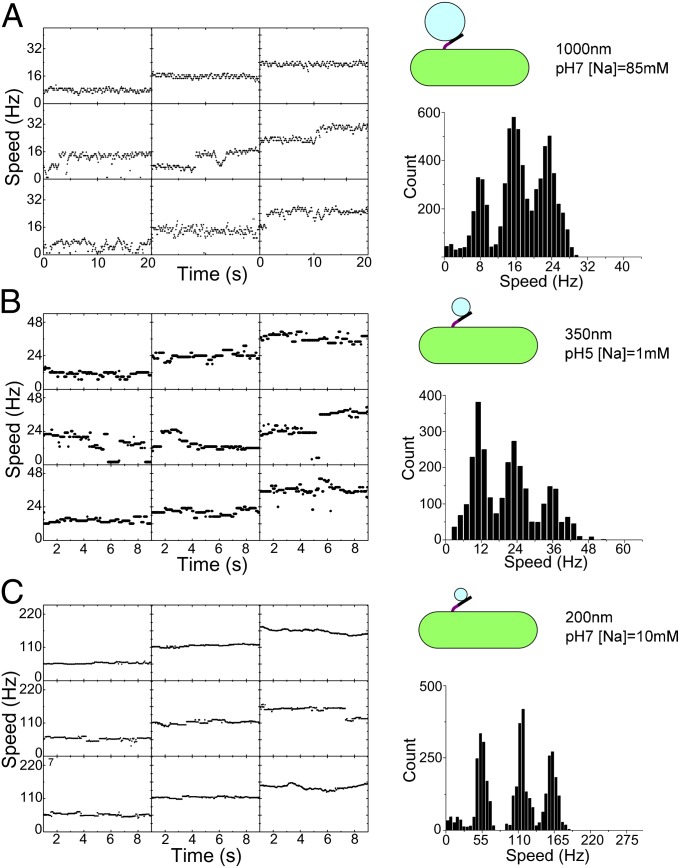
For each of 25 combinations of V_m and Δμ (Table S1), we obtained an average single-stator speed for each of five sizes of polystyrene bead, as illustrated in Fig. 2. Speed-time records for 30–50 cells, with chimeric stator proteins expressed from a plasmid at a range of low levels, were combined into a single speed histogram for each bead size and SMF combination (three typical speed histograms are shown in Fig. 2 A–C, Right, and all 125 are shown in Fig. S1). All histograms showed multiple peaks corresponding to motors containing discrete number of stators. Individual speed records occasionally showed jumps between the same speed levels, when the motor spontaneously gained or lost a stator. The single-stator speed was defined as the mean of a Gaussian fit to the slowest major peak in each histogram, and torque was estimated as speed times the viscous drag coefficient of bead plus filament stub (Materials and Methods). Single-stator speeds were obtained similarly for gold beads at pH 7 (V_m = −140 mV) and the same five values of Δμ. In many cases the speed histograms also allow determination of speeds for motors with two, three, or four stators. Here we concentrate on the SMF dependence of single-stator torque–speed curves. Fig. 3 shows torque–speed curves of single-stator motors under the 25 different SMF conditions listed in Table S1. Each plot collects data at a particular pH, with the corresponding membrane voltage indicated. External [Na⁺] is indicated by symbol color (Fig. 3A, Inset), with all plots using the same color code. Data points fall onto “load lines” defined by torque = drag coefficient × speed, one load line for each type of bead attached to the motor. All 25 torque–speed curves show the same characteristic shape, with a knee separating a plateau near the stall torque from a regime of sharply falling torque at higher speeds. The shapes of the curves change scale but retain their shape as V_m decreases, equivalent to a linear relationship between speed and V_m at each load (33). The plateau torque varies linearly with V_m and Δμ and is proportional to SMF, but the knee- and zero-torque speeds drop more steeply with Δμ than with V_m.

Fig. 2.

Measurement of single-stator speeds. (Left) Speed-time traces from nine different representative cells recorded at the same V_m and Δμ/q with a particular bead size (3 of the total of 125 combinations of SMF and bead size are shown; all 125 are shown in Fig. S1). (Right) Histograms of all speeds recorded under the same conditions. Histograms show distinct peaks corresponding to different numbers of stators in the motor; occasional discrete changes in stator number are visible in the speed-time traces. The single-stator speed was taken from the lowest peak.

Fig. 3.

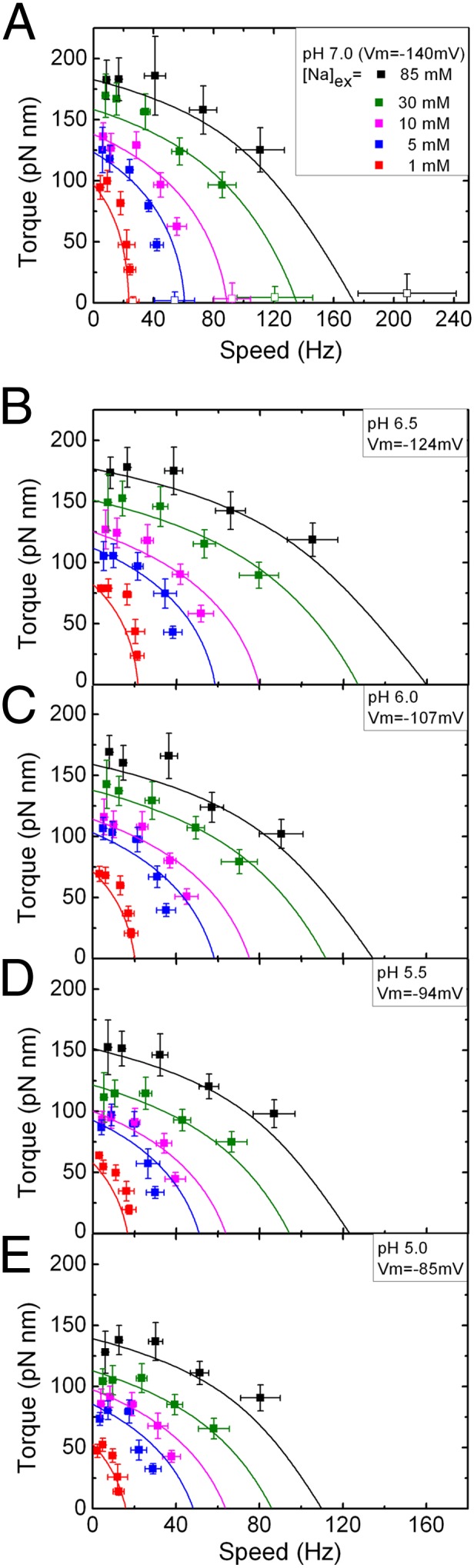
Torque–speed relationships of single-stator BFMs in 25 different SMF conditions. (A) pH 7.0; (B) pH 6.5; (C) pH 6.0; (D) pH 5.5; (E) pH 5.0. Black, [Na]_ex = 85 mM; olive, [Na]_ex = 30 mM; pink, [Na]_ex = 10 mM; blue, [Na]_ex = 5 mM; red, [Na]_ex = 1mM. See Table S1 for the corresponding values of the components of SMF. All data points were measured using polystyrene beads attached to sticky filaments (solid symbols) except for those at the lowest load in A, which were measured by gold particles attached to the hook (open symbols). Lines are calculated torque–speed curves from the best-fitting parameter set of the reduced three-state kinetic model.

Number of Ions per Revolution.

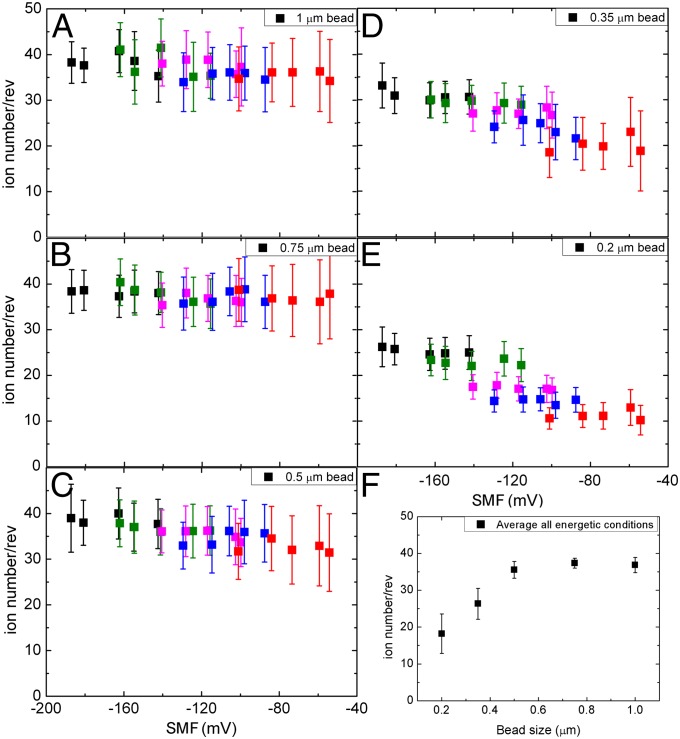
The proportionality between torque and SMF at high load is usually taken to indicate that the motor is tightly coupled (i.e., a fixed number of ions, N, per revolution per stator) and works close to equilibrium in this regime (16). This implies a Stokes efficiency close to 1, where the work done in a revolution (torque × 2π) is equal to the free energy (N × q × SMF) supplied by N ions passing through the motor per revolution. Fig. 4 shows the dependence upon SMF of n = torque × 2π/(q × SMF), which approximates N in the limit of high efficiency and in general is a lower limit to N set by conservation of energy. Symbol colors indicate [Na⁺], using the same color code as in Fig. 3, and SMF is taken from Table S1. For large beads where the motor always operates in the plateau regime (Fig. 4 A and B) n is a constant (37 ± 2), independent of SMF, V_m, and Δμ, consistent with the assumption of tight coupling and high efficiency. For smaller beads n drops, particularly at higher SMF where the motor operates above the knee, with reduced efficiency, where n is no longer expected to be a good approximation to N.

Fig. 4.

(A–E) Lower limits to the number of ions required per revolution, defined as n = torque × 2π/(q x SMF), vs. SMF for different sizes of load. Symbol colors indicate [Na⁺], using the same color code as in Fig. 3. SMF is taken from Table S1. (A) One-micrometer beads; (B) 0.75-μm beads; (C) 0.5-μm beads; (D) 0.35-μm beads; (E) 0.2-μm beads. (F) n vs. bead size for fully energized motors (pH 7, 85 mM [Na⁺]).

Simple Kinetic Model of the Motor.

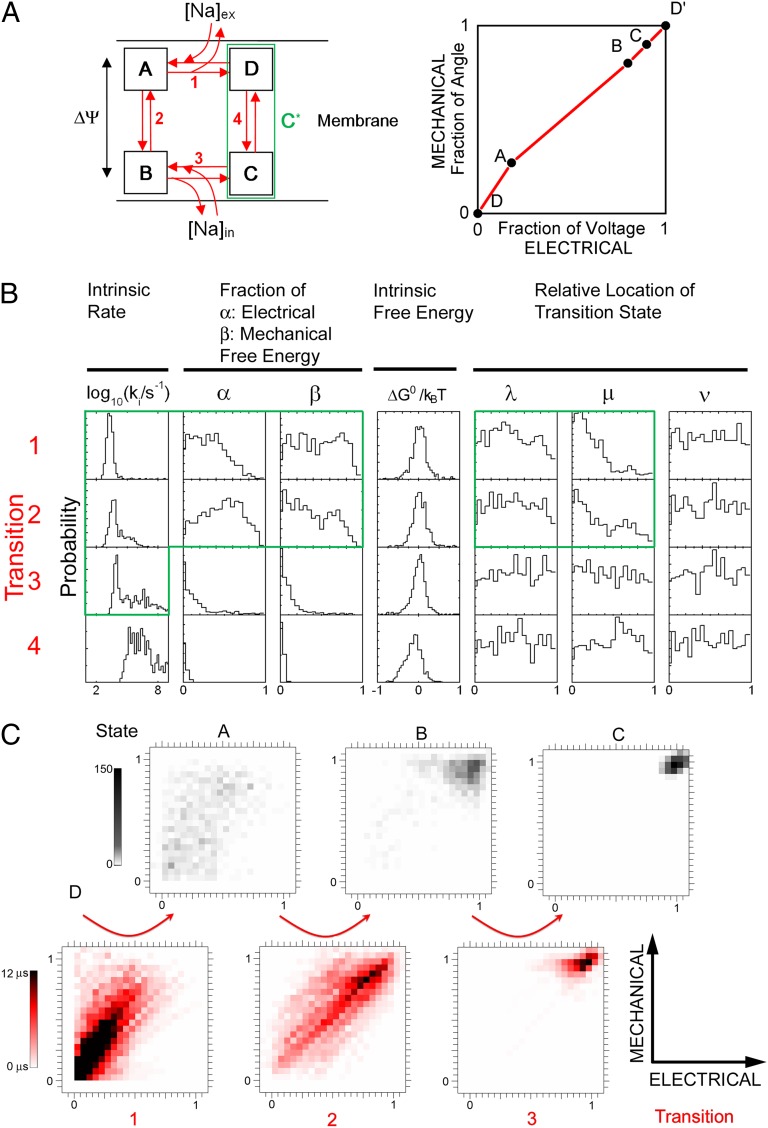
The dataset illustrated in Figs. 3 and 4 is a unique comprehensive measurement of the dependence of BFM torque on speed and the separate components of IMF. Furthermore, by concentrating only on single-stator motors it bypasses any complications due to interactions between stators. This allowed us to make a systematic survey of a minimal kinetic model of the motor’s mechanochemical cycle. The simplest kinetic model that describes the essential features of the motor is shown in Fig. 5A. The model assumes a single kinetic cycle that couples the transit of one ion to rotation through a fixed angle. The motor has four distinct states, labeled A–D, with transitions between them labeled 1–4. A and D can exchange Na⁺ with the external medium via the periplasm and B and C with the cytoplasm. This is equivalent to a carrier-like ion transporter, with the transition AB (=2) carrying ions one at a time across the membrane. The transition CD (=4) represents a reversal of AB with no ion bound. Channel-like ion transport is represented in this model by making CD infinitely fast, which is equivalent to merging C and D into a single state, C*. The four-state model has been used many times to fit torque–speed curves in the flagellar motor (11–14. 31, 34, 35), as has a reduced three-state model that merges states C and D (16).

Fig. 5.

(A) (Left) Kinetic model for the mechano-electrochemical cycle of a stator in the bacterial flagellar motor. Steps 1 and 3 involve exchanges of ions between the stator and periplasm and cytoplasm, respectively. Steps 2 and 4 represent the ion transition process and the stator relaxation process, respectively. Details are in the text. (Right) Schematic representation of the motor mechanism in the two-dimensional space defined by the mechanical and electrical coordinates of the motor. Black circles indicate the states corresponding to one arbitrary set of model parameters and red lines the transitions between them. (B) Normalized probability histograms for each parameter from the 830 parameter sets that were found to be consistent with data. The green boundary encloses the 11 parameters that are retained in the reduced three-state model. (C) Distributions of states (Upper) and average transitions (Lower) in the 830 parameter sets found. Each transition in each parameter set is represented by a line with weight equal to the forward transition time at 1 mM [Na⁺], V_m = 140 mV, torque = 50 pN nm.

The kinetic scheme of Fig. 5A becomes an ion-driven rotary motor if we assume that transitions are tightly coupled to rotation. This does not address the mechanical details of the coupling mechanism, but is a requirement if the motor is to run at high efficiency in the plateau region and usually emerges as a prediction of more detailed mechanical models (21, 22). Following and extending ref. 16, we parameterized the coupling mechanism as follows. Each transition i is assumed to be tightly coupled to a rotation ϕ_i = β_iϕ, where ϕ = 2π /N is the angle that the motor rotates in each mechanochemical cycle and Σ(β_i) = 1. We set N = 37, on the basis of the data illustrated in Fig. 4. Note that this is not equal to the number of directly observable steps per revolution, 26, observed by Sowa et al. (26). We return to the implications of this in Discussion. Each stator performs mechanical work W_i = Γβ_iϕ in step i, where Γ is the torque. Each transition i is further assumed to move charges across the membrane potential, releasing an electrical energy U_i = α_iU, where U = qV_m is the electrical energy released by one ion crossing the membrane and Σ(α_i) = 1 ensures one ion transit per cycle. The motor mechanism can be represented by plotting cumulative values of β_i vs. α_i (Fig. 5A, Right) (16), which locates each state in a two-dimensional space representing the mechanical and electrical coordinates (36). The reference state D is placed at (0,0) in this space, by definition. Finally, each transition has an intrinsic free-energy change 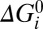, with the constraint Σ(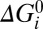) = 0 as required by the second law of thermodynamics. Rate constants for the transitions obey the law of detailed balance, with parameters k_i specifying a “standard” rate constant for each transition, equal to that with Na⁺ concentrations of 1 mM and U_i = W_i = 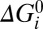= 0. Parameters λ_i, μ_i, and ν_i specify the extent to which V_m, Γ, and 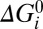respectively influence the forward and backward reaction rates (Materials and Methods). With i = 1–4 the model has 28 parameters (one for each box in Fig. 5B), 25 of which are free after application of the constraints on α_i, β_i, and .

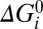Analysis of Parameter Sets That Fit the Data.

Searching a 25-dimensional space is an intrinsically difficult problem. We used a Monte Carlo strategy (Materials and Methods) (37, 38). A cost function quantified the least-squares difference between the data of Fig. 3 and the torque–speed curves predicted by a particular set of model parameters for the corresponding SMF conditions (Materials and Methods). Each parameter set constitutes a point in the 25-dimensional parameter space of the model. A total of 10⁸ randomly selected points were used as the starting points of a search algorithm that found nearby local minima in the cost function. This procedure found 830 local minima corresponding to possible solutions—parameter sets that give a cost function smaller than that expected from our experimental uncertainties (Materials and Methods) (full parameter sets in Dataset S1).

Fig. 5B shows the distribution of each parameter in the set of 830 possible solutions. The standard rate-constants k and intrinsic free-energy differences ΔG⁰ show strongly preferred values. Parameters α and β, which specify which transitions move charges and the rotor, respectively, show trends, as do parameters μ that specify how the work done by torque-generating steps affects forward vs. backward transition rates. Other parameters show flat distributions, indicating that they are not important. A closer examination of the possible solutions yields the following conclusions:

• 1) The intrinsic free-energy differences 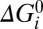are all small compared with the thermal energy, k_BT, where k_B is Boltzmann’s constant and T is absolute temperature. Consequently associated parameters ν are unimportant. The total free energy available per cycle from the transit of one ion, q × SMF, ranges from 2.0 to 7.7 k_BT in our experiments. Any reaction with comparable or larger ΔG⁰ would constitute an energetic barrier that would trap the system. The absence of such barriers indicates that the mechanochemical cycle is smooth, a feature that allows rapid cycling and thus rapid rotation of the BFM.

• 2) Rate constant k₄, for the transition that resets the ion access of the empty motor, is typically fast (note that rate constants were explored and plotted on logarithmic scales and thus that k₄ is typically 10 times to 1 million times faster than k₁ and k₂). α₄ and β₄ are close to zero, showing that torque is not generated nor electrical energy consumed in step 4, and the associated parameters λ₄ and μ₄ are unimportant. Therefore, the motor behaves like an ion channel that does not need to reset when empty or an alternating-access carrier that resets very quickly, and can be described equally well by a reduced three-state model with a single empty state. In more than half of the possible solutions transition 3, ion exchange with the cytoplasm, shows the same pattern as transition 4. Thus, our data raise the possibility that ion exchange with the cytoplasm is fast and plays no role in torque generation, but do not require it.

• 3) Rate constants k₁ and k₂, for extracellular ion exchange and transit, are consistently slow, on the order of 10³ s⁻¹, close to the upper limit of motor speeds. α_1,2 and β_1,2, and the corresponding λ_1,2 and μ_1,2, show preferred values (discussed below), indicating that these are the important transitions that determine the speed of the motor and its torque and SMF dependence. In the majority of solutions (65.5%), k₁ and k₂ are both slow and ion transit is the rate-limiting step except at 1 mM [Na⁺] and high V_m, when ion binding becomes limiting (Fig. S2). We also found less common patterns of rate constants in the set of 830 solutions; in some (30.4%) k₃ replaces k₂ as the limiting transition rate at [Na⁺] > 1 mM, whereas in a few (4.1%) all of k_1,3,4 are fast and k₂ is always rate limiting (Fig. S2).

• 4) The distributions of parameters α_i and β_i in Fig. 5B are best understood in terms of parameter correlations (Fig. S3). Strong positive correlations between α_i and β_i indicate a powerstroke mechanism: Charge movement, driven by V_m, and rotation occur together in a single step. This was previously observed to be necessary to model the characteristic concave-down torque–speed curve of fully energized wild-type H⁺ motors (16). A powerstroke mechanism is further supported by negative correlations between α_i, β_i, and k_i: The powerstroke must be one of the slower, rate-limiting transitions. Correlations between μ_i and α_i (−ve), μ_i and β_i (−ve), and μ_i and k_i (+ve) indicate that the powerstroke, associated with high α and β and low k, is likely to have a low value of μ: External resisting torque speeds up the reverse powerstroke rather than slowing the forward powerstroke. This allows the motor to run at high speeds even at high torque, maximizing mechanical power output. Microscopically, it predicts that the angle of the transition state is close to that of the previous state (39), which is another signature of a powerstroke: The driving electrochemical transition occurs without large-scale movement of the motor as a whole, allowing forced rather than slow diffusive motion of the motor.

• 5) Fig. 5C illustrates the set of 830 solutions in the space defined in Fig. 5A, Right. Fig. 5C, Upper shows the distribution of each state. Fig. 5C, Lower shows the distribution of transitions, weighted by the transition time in the forward direction, at typical values of torque and SMF, to emphasize the important rate-limiting transitions under typical conditions. State A is broadly distributed around the diagonal, and states B and C are clustered near (1, 1). This shows that one or both of transitions 1 or 2, ion binding or ion transit, are powerstrokes. These powerstroke transitions are visible as density along the diagonal in the corresponding transition plots (Fig. 5C, Lower). Examination of the transition distributions at other values of torque and SMF (Fig. S4 A and B) shows that ion-transit powerstrokes are always rate limiting, whereas ion-binding powerstrokes are rate limiting only at low [Na⁺]. Interestingly, in the 30.5% of solutions where transition 3, ion release into the cytoplasm, replaces ion transit as the rate-limiting step at high [Na⁺], the powerstroke remains distributed between transitions 1 and 2 (Fig. S4D). For the 4.1% of solutions where transition 2 is always rate limiting, this transition is always the powerstroke (Fig. S4E).

Reduced Three-State Model.

Analysis of the possible solutions to the four-state model indicates that a reduced three-state model with 11 free parameters, those enclosed by the green lines in Fig. 5B, should be adequate to fit our dataset. The three-state model dispenses with transition 4 by combining states C and D into a single empty state that can bind ions from either side (green box in Fig. 5A) and sets all 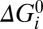= 0, thereby dispensing with parameters ν_i. λ₃ and μ₃ were found to be unimportant and were fixed at 0.5. We used the parameter sets with the lowest 830 cost functions from the original random search of the four-state model as starting points for local minimization within the three-state model, simply discarding the extra 14 parameters. This gave 724 possible solutions with cost function within the experimental uncertainty, nearly as many as the original 830 possible solutions in the four-state model, indicating that little is lost by discarding the extra state and 14 extra parameters. These 724 solutions showed the same patterns as discussed above for the 830 solutions of the four-state model. The lines in Fig. 3 are from the best-fitting parameter set in the three-state model.

Discussion

We measured 25 torque–speed curves with different energetic combinations of SMF in single-stator Na⁺-driven chimeric flagellar motors, vastly extending the range of torque–speed measurements in the BFM. Most previous torque–speed measurements in the BFM have used fully energized motors (11, 14), and previous single-stator torque–speed curves (12, 18) did not clearly observe the knee- or zero-torque speeds. We found that the characteristic shape of the torque–speed curve in fully energized motors with many stators is a property of single stators under all SMF conditions tested, showing that it is a universal feature of the torque-generating mechanism of the BFM, not particular to H⁺ motors or dependent upon full energization or interactions between stators. The plateau torque is directly proportional to SMF, regardless of the relative contributions of V_m and Δμ, consistent with the motor operating close to equilibrium in this regime. The knee- and zero-torque speeds, by contrast, are more sensitive to Δμ than to V_m. We observed this previously (28) and guessed that it might be explained if Na⁺ binding were the rate-limiting step. The extensive new dataset allows a systematic exploration of the space of possible kinetic models of the motor, showing that this guess was an oversimplified interpretation of the results. Ion transit or possibly ion release into the cytoplasm is rate limiting except at the lowest [Na⁺], 1 mM. This agrees with the previously observed Arrhenius-like temperature dependence of motor speed at low load (40), which is a signature of a process with a single type of rate-limiting transition.

Perhaps our most surprising finding is the constant of proportionality between the plateau torque and SMF. If the motor really is close to equilibrium in this regime, this constant can be expressed very simply as the number of ions that flow through the motor per revolution (N). Our measured value of n = 37 ± 2 is strikingly at odds with the recent observation that the same chimeric motor takes 26 steps per revolution at extremely low SMF (26). ATP-driven molecular motors, kinesin (41), myosin (42), and F₁-ATPase (3, 43) take one step per molecule of ATP hydrolyzed, and the step size is set by the periodicity of the track along which motion occurs. We do not believe that the discrepancy is due to a systematic error in our determinations of either torque or SMF. The maximum uncertainty in SMF is 15% at low SMF, with much smaller uncertainties at high membrane voltage and [Na⁺]_ex (27, 28). The dye loading used to measure SMF (27, 28) did not change the measured speed histograms, indicating that it does not damage cells. Most of the uncertainty in torque is due to speed variations in a single motor or between motors and is only 9% for 1-μm beads (12). The speed histograms have been checked with different cultures in several conditions to avoid culture variations. Nonetheless the possibility cannot be absolutely excluded that due to some unknown systematic error the true value of N is actually 26 or 52, with one or two ions per step, as has been suggested (16). Another simple explanation for the discrepancy between our measured n = 37 ± 2 and 26 steps per revolution would be that the motor is not tightly coupled. In this case the true N could be 52, with two ions per step but only 37/52 of the available free energy converted to work. Tight coupling is consistent with all existing experimental data on the flagellar motor, but it has not been definitively proved due to the experimental difficulty of measuring ion flux through the motor (44). However, given the relative ease with which tightly coupled mechanisms can be constructed (20, 22) and the long evolutionary history of the BFM, it is appealing to assume that bacteria would avoid wasting free energy unnecessarily in the motor. We have assumed that the motor is tightly coupled with N = 37. High-resolution cryoelectron-microscopy reconstructions of BFM rotors in Salmonella show an inner ring with 24- to 26-fold symmetry and an outer ring with 32- to 36-fold symmetry (45). A recent structural model based on atomic-resolution crystal structures of the rotor protein that is thought to be the “track” on which stators exert torque, FliG from Aquifex aeolicus, predicts a 34-fold symmetric ring of FliG molecules (46). Thus, our estimate of N is compatible with the latest structural evidence, given the experimental uncertainty and the possibility of slight variations in N between bacterial species. The space between the inner and outer rings in Salmonella has low electron density and might be an elastic link between the rings. Along with elastic linkages between the stators and the cell wall, this could deliver a smoothed torque to the inner ring, hiding the signature of ∼34–37 steps per revolution on the outer ring. The observed 26 steps per revolution in this scenario would be due to static secondary interactions between the cell wall and the rotor, for example between part of the stator and the inner ring, as described in a recent theoretical treatment (23). The discrepancy between our estimate of N = 37 and the observed 26-fold stepping might also be explained in the future by alternative structural models of the rotor and accompanying models of the torque-generating cycle, which propose two types of FliG molecule in the C-ring and stator interactions with both 26- and 34-fold rings (47). Each stator is believed to contain two ion channels, and it is also possible that the motor mechanism does not conform to the simplifying assumptions of our model. For example, the steps caused by ion transit through either channel could be different. A combination of structural, genetic, and biophysical approaches is likely to be required to distinguish between competing models. Elastic linkage between rotary components with different symmetries is also emerging as an important feature in F₁F_O ATP-synthase, in which 3-fold F₁ is driven by F_O that can have any symmetry between 9- and 15-fold (48, 49).

Molecular motors are far too large and slow to be modeled by molecular dynamics. The most detailed models of the BFM to date have used Brownian dynamics, which rely on a separation of timescales between fast transitions among discrete electrochemical states and much slower diffusive movement of whole stators and/or the rotor (21–24). Most published BFM models are purely kinetic, with both electrochemical and rotational dynamics described as transitions between discrete states (10–14, 16, 31, 34, 35). Kinetic models cannot capture all of the details of the motor mechanism, but are very useful in linking the broad characteristics of torque–speed curves to underlying features in the mechano-electrochemical cycle. The parameters of previous kinetic models have been hand selected to fit small datasets, with no attempt to address the question of whether other sets of parameters might fit equally well. Our much larger dataset, with the simplification of single-stator motors and the extra depth of variation in both components of SMF, allows a unique systematic survey of a space of kinetic models. We find that an 11-parameter, three-state model similar to that proposed by ref. 16 fits the data as well as the more general 25-parameter four-state model, thus defining a subset of important parameters. A powerstroke mechanism, also included in ref. 16, is found to be necessary to describe the data. This can be understood in terms of the kinetic model as follows. The torque plateau corresponds to a very wide range of speeds spanned by only small changes in torque. This requires that the rate-limiting step is highly sensitive to load, large β in our model. A substantial input of electrical energy (large α in our model) helps to prevent this step being prohibitively slow at high torque, giving one signature of a powerstroke model. We also see a second signature: The angle of the transition state in the powerstroke is closer to that of the preceding than of the following state (low μ in our model). Our data are consistent with powerstrokes in ion binding from the cytoplasm or ion transit or both. Finally, we find that a smooth underlying free-energy landscape (ΔG⁰ << k_BT in our model), chosen by default for simplicity in earlier models, is necessary to explain the observed data.

Monte Carlo searching of the parameter space of multidimensional biological models is a recent approach, with great advantages over earlier ad hoc methods. The method has been used to explore specific models of circadian clocks (50) and the motor protein myosin V (41), using sparse previously published datasets to define relatively complicated cost functions. Theoretical cost functions, rather than fits to experimental data, have also been used (37). Our large torque–speed dataset allows a thorough exploration of a very general kinetic model, using a simple cost function. Rather than presenting only the current best-fit parameter set, we have examined all of the possible sets that are consistent with our data, providing quantitative estimates of the likelihood of each type of solution.

Conclusion

The BFM offers insights into both molecular motors and transport complexes. Compared with molecular motors driven by ATP hydrolysis, the BFM offers the additional possibility of continuous variability of both the entropic (Δμ) and enthalpic (V_m) parts of the driving free energy. Our kinetic model describes an alternating-access ion transporter, except that ion transport is coupled to torque and rotation rather than being free running or coupled to another electrochemical process. Unlike other transport proteins, the output of a single motor can be directly observed and manipulated relatively easily, via flagellar rotation and variation of the load, respectively. We speculate that some of the lessons we have learned may be applicable to ion transporters in general, particularly those that couple two different kinds of biological free energy.

Materials and Methods

Speed Measurements with Polystyrene Beads.

Cells of E. coli strain YS34 with the flagellar switch-inducing protein CheY, pili protein PilA, and flagellar motor stator proteins MotA and MotB deleted (ΔcheY, ΔpilA, ΔmotAmotB) and with the flagellar filament protein FliC disrupted by transposon insertion (fliC::Tn10) (26, 27) with plasmids pYS11 (fliC sticky filaments) and pYS13 (pomApotB7^E) for inducible expression of chimeric sodium-driven stators in E. coli, containing the proteins PomA and a specific PomB-MotB fusion protein, PotB7^E (25) by isopropyl-β-d-thiogalactopyranoside (IPTG) were grown in T-broth (1% tryptone, 0.5% NaCl) for 5 h at 30 °C from frozen stock containing the appropriate antibiotics and inducers (IPTG, 2–30 μM). Stator proteins were induced at different levels during the growth as described in ref. 28. Cells were sheared to truncate flagella and then suspended in sodium motility buffer (10 mM potassium phosphate, 85 mM NaCl, pH 7.0) at a density of 10⁸ ml⁻¹.

Cells were immobilized using polylysine and polystyrene beads (1.0–0.2 μm diameter) attached to flagella, and speeds were measured using back-focal-plane interferometry as described in ref. 28. Each speed was defined as the largest peak in the power spectrum of the bead position signal from a moving window 1-s long, with windows starting at 0.1-s intervals. All experiments were performed at 23 °C.

The motor torque was calculated as Γ = (f_b + f_f)ω, where f_b and f_f are rotational frictional drag coefficients of the bead and the filament stub, respectively, and ω is the angular velocity. f_b and f_f were estimated as described in ref. 12.

Speed Measurements with Gold Beads.

E. coli strain YS34 carrying pYS13 (26) was grown in T-broth with 25 µg/mL Chloramphenicol and 10–17 µM IPTG at 30 °C for 5 h. Cells were washed three times with motility medium. One-hundred-nanometer gold beads (EM.GC100; BBInternational) were attached to the hook of the flagellar motor via antihook antibody as described in ref. 17 with minor modifications. Cells were attached onto the polylysine-coated coverslip of the tunnel slide and gold beads were imaged onto the face of a quadrant photodiode, using laser dark-field microscopy (32), and sampled at 4 kHz. Motor speed was obtained from bead position as described for polystyrene beads.

Determining Single-Stator Speeds.

Single-stator speeds were determined as described in ref. 28. In each SMF condition, five different bead sizes were used to measure the rotation. Smaller (200 and 350 nm) and larger (500, 750, and 1,000 nm) beads were monitored using laser wavelengths of 632 nm and 1,064 nm, respectively. Beads were selected that showed clean circular orbits in (x, y), indicating minimal surface interaction. Motors were selected for inclusion in speed histograms by the following criteria: (i) orbit radius <200 nm, indicating a short filament stub and thus reliable drag estimates; (ii) low noise in the radial direction of the orbit, at all angles, indicating a well-defined bead attachment; and (iii) narrow peaks in the speed histogram, indicating a stable motor (single-motor speed histograms showing more than one peak were rare, but were selected for Fig. 2). For larger beads and higher SMF, most beads satisfied these criteria. For smaller beads and lower SMF, up to half failed and were not included in further analysis. Thirty to 50 cells were selected for each bead size and SMF condition. The single-stator speeds were taken as the slowest peaks in multiple Gaussian fits to the resulting histograms.

Kinetic Model: Rate Constants.

Detailed balance requires that the ratio of transition rates between any two states n and m, corresponding to step i, satisfies k_nm/k_mn = exp[ΔG_nm/k_BT], where k_B is Boltzmann’s constant, T the absolute temperature, and ΔG_nm the free-energy difference between states. If a forward step i releases electrical energy U_i = α_i U and does work W_i = β_i W, then we may write ΔG_nm = α_i U − β_i W + 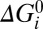, where is intrinsic to the states and is defined as the free-energy difference when U = W = 0 and [Na⁺] = 1 mM. k_i is the standard rate constant of step i, when U = W = Δ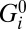 = 0 and [Na⁺] = 1 mM. Parameters λ_i, μ_i and ν_i partition the effects of U_i W_i and ΔG_i respectively between forward and backward transition rates. Rate constants involving Na⁺ binding are proportional to [Na⁺], introducing factors c_in,out = [Na⁺] _in,out/1 mM in the relevant rate-constant equations

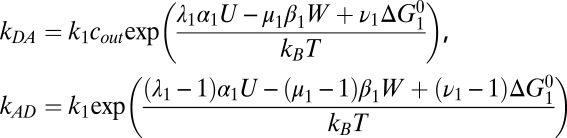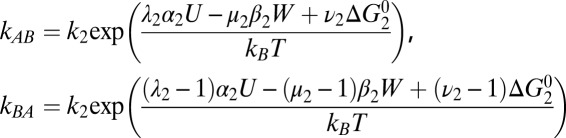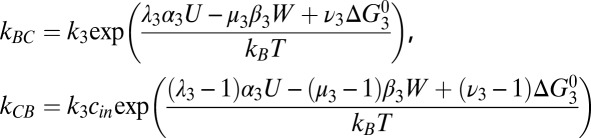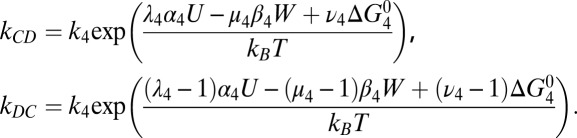Experimental estimates of U = qV_m and c_in follow from external pH and [Na⁺]_out as listed in Table S1 (28). The assumption of tight coupling with torque Γ gives W = Γϕ = 2πΓ/N, with N = 37 ions per step as discussed in the text.

Kinetic Model: Steady-State Solutions.

The steady-state occupancy probabilities satisfy the following equations:

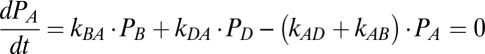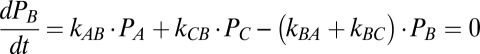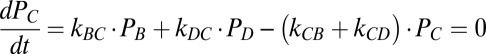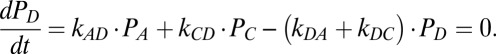From the solution of these four equations we can calculate the rate of the mechano-electrochemical cycle as f = k_AB P_A − k_BA P_B and the rotation rate ω = fϕ.

Fitting Model Parameters to Data.

The four-state model has 25 free parameters, precluding a deterministic search or mapping of the parameter space. We adapted a Monte Carlo search strategy (38), using simplex optimization to find local minima starting from randomly generated points in parameter space. We defined a cost function to determine the quality of fit to experimental data for each parameter set, both during and after the simplex optimization,

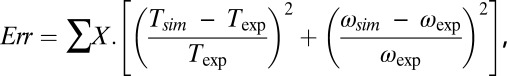where the sum is over experimental data points with speed ω_exp and torque T_exp, and (ω_sim, T_sim) is the intersection of the corresponding load-line and the simulated torque–speed curve. Setting X = 5 for gold bead data and 1 for all other data compensated for the lack of gold bead data for pH < 7. A total of 10⁸ parameter sets were generated, with each parameter selected randomly from a flat distribution in the following ranges: log₁₀(k_i/s⁻¹), [1–9]; λ_i, α_i, μ_i, β_i, ν_i, [0–1]; 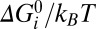[−1 to –1]. About 1 in 10⁴ random parameter sets gave reasonable torque–speed curves. Starting from the 2,000 random parameter sets with the lowest cost function, we used downhill simplex optimization to find nearby minima of the cost function. The simplex method is very fast and simple compared with simulated annealing or evolutionary algorithms, allowing wider sampling of the parameter space. The simplex moved in steps of size either 1/200 or 1/20 of current parameter values, the smaller step size typically giving a solution close to the starting point whereas the larger sometimes converged on a more distant point. The point with the lower cost function was chosen. A total of 830 of these points gave cost functions within the range expected from our experimental errors, defined as

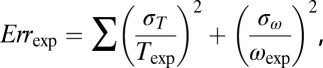where 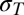and 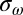are SDs of the torque and speed data points, respectively.