Significance
Hydrogen bond networks play critical structural and functional roles in proteins but have been challenging to study within this complex environment. We incorporated spectroscopic probes into the active site of the bacterial enzyme ketosteroid isomerase to systematically dissect the proton transfer equilibrium within a key hydrogen bond network formed to bound transition state analogs. Our study provides direct insight into the physical and energetic properties of a hydrogen bond network within an enzyme and presents a simple computational model of electrostatic effects within this protein that succeeds due to detailed knowledge of ionization states and a tightly controlled experimental system.
Keywords: computational modeling, enzyme catalysis, protein electrostatics, protein semisynthesis, active site environment
Abstract
Hydrogen bond networks are key elements of protein structure and function but have been challenging to study within the complex protein environment. We have carried out in-depth interrogations of the proton transfer equilibrium within a hydrogen bond network formed to bound phenols in the active site of ketosteroid isomerase. We systematically varied the proton affinity of the phenol using differing electron-withdrawing substituents and incorporated site-specific NMR and IR probes to quantitatively map the proton and charge rearrangements within the network that accompany incremental increases in phenol proton affinity. The observed ionization changes were accurately described by a simple equilibrium proton transfer model that strongly suggests the intrinsic proton affinity of one of the Tyr residues in the network, Tyr16, does not remain constant but rather systematically increases due to weakening of the phenol–Tyr16 anion hydrogen bond with increasing phenol proton affinity. Using vibrational Stark spectroscopy, we quantified the electrostatic field changes within the surrounding active site that accompany these rearrangements within the network. We were able to model these changes accurately using continuum electrostatic calculations, suggesting a high degree of conformational restriction within the protein matrix. Our study affords direct insight into the physical and energetic properties of a hydrogen bond network within a protein interior and provides an example of a highly controlled system with minimal conformational rearrangements in which the observed physical changes can be accurately modeled by theoretical calculations.
Hydrogen bond networks are ubiquitous structural features within proteins, and they play key roles linking secondary and tertiary structural elements and spanning protein–protein interfaces. Such networks are especially common within enzyme active sites, where they position protein and substrate groups for catalysis, stabilize charge rearrangements during chemical transformations, and mediate proton transfers (1). Despite the prevalence and critical structural and functional roles of hydrogen bond networks, incisive dissection of their physical properties within the idiosyncratic interior of folded proteins remains difficult.
Hydrogen-bonded protons are not observed in the vast majority of protein X-ray structures due to the low X-ray scattering power of hydrogen atoms (2). Thus, the presence of hydrogen bond networks is typically inferred from the proximity and orientation of hydrogen bond donor and acceptor groups within refined protein structural models. The inherent inability of most X-ray diffraction studies to monitor proton positions imposes additional challenges for dissecting the physical features that influence the equilibrium protonation states of specific residues along a hydrogen-bonded proton transfer network. Furthermore, it remains extremely challenging to study the electrostatic consequences of charge rearrangements that accompany hydrogen bond-mediated proton transfers. Few experimental methods exist to vary the ionization properties of discrete protein groups incrementally, and structural rearrangements within the protein matrix that typically accompany charge rearrangements complicate computational modeling and the straightforward interpretation of the electrostatic properties of protein active sites and interiors (3–5).
Bacterial ketosteroid isomerase (KSI) from Pseudomonas putida KSI (pKSI) and Comamonas testosteroni KSI has been a powerful system with which to study the physical properties of hydrogen bonds within an enzyme active site (6–13). KSI uses a general base, D40 (pKSI numbering), to deprotonate steroid substrates and form a dienolate reaction intermediate that is stabilized by hydrogen bonds donated by Y16 and protonated D103. Y16 is further linked via hydrogen bonds to Y57 and Y32, forming an extended active site hydrogen bond network in pKSI (Fig. 1A). Phenolic ligands, such as single-ring phenols, two-ring naphthols, and four-ring steroids like equilenin or estradiol, can bind in the KSI active site as negatively charged oxyanions and accept hydrogen bonds from Y16 and D103, mimicking the oxyanion charge localization of the dienolate reaction intermediate and dienolate-like transition states (6–8, 14, 15) (Fig. 1B). A homologous series of bound phenols or naphthols bearing different electron-withdrawing substituents provides a deft experimental tool with which to incrementally vary the proton affinity and negative charge density of the phenolic oxygen (16). These changes tune the structure and strength of hydrogen bonds formed to phenolic ligands (17–19), and thus provide a systematic probe of the physical and energetic properties of the hydrogen bond network within the KSI oxyanion hole (6–9, 11, 13) and the response of the surrounding protein matrix to such changes (20, 21).
Fig. 1.
KSI reaction and reaction intermediate analog. (A) KSI reaction mechanism for isomerization of 5-androstene-3,17-dione. (B) Schematic depiction of an ionized substituted phenol bound at the KSI D40N active site.
Recent studies with the D40N pKSI mutant, which mimics the protonated D40 present in the KSI–dienolate intermediate complex (Fig. 1A), have provided evidence that ligands of increasing pKa are bound as an increasing population of neutral, protonated phenol (11, 13, 22). These results suggest that an unspecified active site residue can ionize with increasing phenol pKa, resulting in a net proton transfer to the bound ligand. We have used site-specific NMR and IR probes and KSI semisynthesis to determine that either of two different Tyrs within the extended hydrogen bond network can ionize, and we have systematically mapped the changes in their equilibrium ionization states as a function of the proton affinity and hydrogen bonding capability of the phenolic ligand. We further measured the electric field changes at discrete active site positions due to charge rearrangements within the hydrogen bond network. We demonstrate that a static continuum electrostatic model with a low dielectric can accurately describe these changes, suggesting a high degree of structural organization and the absence of substantial conformational rearrangement in response to charge rearrangement within the active site.
Results and Discussion
Ionization States of Substituted Phenols Bound to pKSI D40N.
Recent spectroscopic studies suggested that single- and multiple-ring phenolic ligands are bound to pKSI D40N with a neutral, protonated fraction that increases with ligand pKa and reaches a ratio of 50:50 ionized/neutral for a ligand with a solution pKa of 9.7 (13, 22). To dissect and understand the nature and properties of proton transfer within the KSI oxyanion hole, we turned to systematic studies with single-ring phenols, because these compounds are available over a wider pKa range than naphthols or steroids. To probe the ionization state of phenols bound to KSI, we acquired 19F NMR spectra of 4-fluoro–substituted phenols bound to the D40N mutant, because the chemical shift of the 4-fluoro nucleus is a sensitive reporter of changes in phenol ionization state and shifts 7–8 ppm down-field on ionization (8) (Fig. 2A).
Fig. 2.
Spectroscopic and structural analysis of phenols bound to pKSI D40N. (A) 19F NMR spectra and chemical shifts of the 4-F group for F-substituted phenols bound to KSI at pH 7.2 (black peaks) or free in solution (red dashes) at pH 2 (neutral) or pH 12 (ionized). Phenol pKa values are shown in parentheses. (B) Superposition of the 1.30-Å resolution D40N–3-F-4-NO2-phenol (carbon atoms are colored green; PDB ID code 3VGN) and 1.25-Å resolution D40N–phenol (carbon atoms are colored cyan; PDB ID code 2PZV) X-ray crystal structures. Oxygen, nitrogen, and fluorine atoms are colored red, blue, and magenta, respectively.
Prior UV-visible (Vis) and IR absorbance studies have suggested that phenols with pKa values ≤8 are bound to D40N in their ionized, phenolate form (8, 22). In agreement with these prior results, the 4-fluoro nucleus of 3,4,5-F3-phenol (pKa = 8.2) has a 19F chemical shift when bound to pKSI D40N that is 1.5 ppm up-field of that observed for the phenolate anion in solution (Fig. 2A). This modest up-field shift relative to solution is consistent with the ability of aromatic ring currents and other shielding differences between a protein interior and water to result in chemical shift differences of 1–2 ppm for a 19F nucleus (23). In contrast, 3,4-F2-phenol (pKa = 9.1) bound to pKSI D40N displays a chemical shift that is intermediate between the observed values for its neutral (phenol) and ionized (phenolate) forms in solution, suggesting that this phenol binds to pKSI D40N as a mixture of neutral phenol and ionized phenolate and that these forms are rapidly interconverting relative to their 19F NMR frequency difference (additional discussion is provided in SI Text). The 4-F-3-Me-phenol, with a still higher pKa of 9.8, exhibits a chemical shift when bound that is 1.3 ppm up-field of the neutral phenol in solution (Fig. 2A). This series of spectra strongly suggests that single-ring phenols bind to the pKSI D40N mutant with a neutral phenol fraction that becomes significant at a phenol pKa greater than 8 and increases with the phenol pKa until the protonated phenol is the predominantly bound form at or above a pKa of 10. This conclusion is consistent with prior UV and IR studies (13, 22), and it is further supported by 13C NMR and IR results described below.
Structural Similarity of pKSI D40N Bound to Low vs. High pKa Phenols.
To assess whether the change in phenol ionization state for low vs. high pKa phenols is accompanied by conformational rearrangements within or surrounding the hydrogen bond network of the pKSI oxyanion hole, we determined the 1.30-Å resolution X-ray crystal structure of 3-F-4-NO2-phenol (pKa = 6.1) bound to pKSI D40N [data collection and refinement statistics are shown in Table S1, and electron density map is shown in Fig. S1; Protein Data Bank (PDB) ID code 3VGN] and compared this structure with the previously published 1.25-Å resolution structure of the same pKSI mutant bound to unsubstituted phenol (pKa = 10.0) (8). Superposition of the two structures reveals that the overall structures are indistinguishable, that the bound ligands are similarly positioned within the KSI active site, and that the oxyanion hole residues that form the hydrogen bond network to the hydroxylic oxygen of each phenol are nearly identically positioned in both structures (rmsd = 0.130 Å; Fig. 2B). These observations rule out the possibility that gross structural rearrangements within the hydrogen bond network accompany changes in the ionization state of bound phenols. Such rearrangements can complicate the analysis and modeling of electrostatic effects, and their absence in this case is a simplifying feature for the experimental and computational studies that follow.
NMR Identification of Tyr Ionizations in KSI–Phenol Complexes Using Site-Specific 13C-Labeled Tyrs.
We considered either D103 or Y16, both of which directly donate hydrogen bonds to the bound ligand (Figs. 1A and 2B), as the most likely residue to be ionized in the presence of higher pKa phenols. A priori, the carboxylic acid moiety of an aspartic acid (solution pKa of ∼4) would be expected to be much more acidic than that of a Tyr hydroxyl group (solution pKa of ∼10) (24). However, D103 is surrounded by hydrophobic residues that elevate its pKa well above its typical solution value (15, 25, 26), and recent quantum mechanics/molecular mechanics (QM/MM) studies of phenols bound to pKSI D40N have suggested that D103 may be less acidic than Y16 (11). Furthermore, we observed that the D103N/D40N mutant, which preserves hydrogen bonding to residue 103 but ablates its ability to transfer a proton, still binds 4-F-3-Me-phenol (pKa = 9.8) predominantly in its neutral form (Fig. S2), strongly suggesting that D103 is not the residue that ionizes as bound phenols become protonated. Based on this result and on our prior observation of an ionized Tyr in unliganded pKSI D40N (20), we considered Y16 the most likely residue to be ionized when the bound phenol is neutral. The results described below provide evidence for ionization of both Y16 and Y57.
pKSI D40N contains four Tyrs. Y119 is a surface residue located far from the active site, whereas Y32 and Y57 form an active site hydrogen bond network to Y16, which directly donates a hydrogen bond to bound phenols (Figs. 1A and 2B). The chemical shift of the Cζ carbon of Tyr, the carbon atom adjacent to the hydroxyl group, is highly sensitive to the ionization state of Tyr, shifting down-field from 155.5 to 166.3 ppm upon ionization in Tyr-containing peptides in aqueous solution (24). We therefore used 13C NMR of phenol complexes of pKSI D40N containing 13Cζ-labeled Tyr residues to determine whether Y16 or any of the active site Tyr residues ionize upon phenol binding.
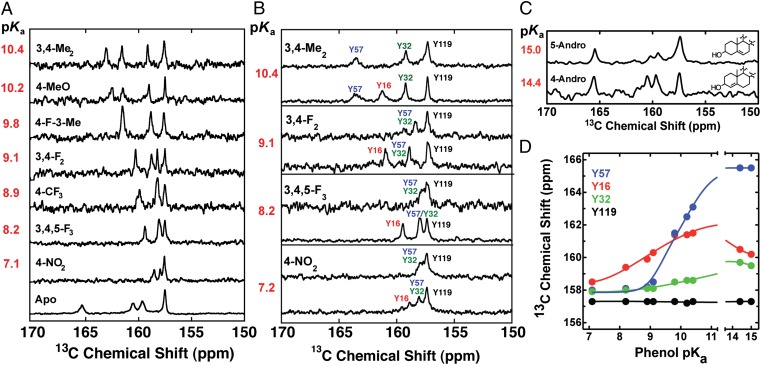
As previously reported by Fafarman et al. (20), the 13C spectrum of unliganded pKSI D40N displays four well-resolved Cζ-Tyr peaks (Fig. 3A, lowest spectrum). The far down-field peak at 165.1 ppm, indicative of an ionized Tyr, was tentatively assigned to Y57 based on comparisons of data and computational models of electrostatic field effects (20). On binding of 4-NO2-phenol (pKa = 7.1), which is fully ionized in complex with pKSI D40N (8), all the observed 13C-Tyr peaks in D40N are shifted up-field to less than 159 ppm (20), as expected for the protonated forms of all four Tyr residues (Fig. 3A). The 1.2-ppm chemical shift dispersion for the discrete Cζ-Tyr peaks is within the range of 1–2 ppm expected for differential shielding contributions arising from the unique local structural environment of each Tyr (27). Binding of phenols with pKa values increasing from 7.1 to 10.4 resulted in no changes in the position of the most up-field peak at 157.3, previously assigned via mutagenesis to the surface Y119 (20), but steadily shifted the position of the remaining active site Tyr peaks further down-field (Fig. 3 A and B). At the highest phenol pKa of 10.4, two peaks have shifted ≥3 ppm down-field (relative to their positions in the D40N–4-NO2-phenolate spectrum) to 163.1 ppm and 161.5 ppm.
Fig. 3.
13C NMR spectra of pKSI D40N containing 13Cζ-Tyr labels. (A) Spectra of recombinant D40N uniformly labeled with 13Cζ-Tyr and bound to a series of phenols with increasing solution pKa (values are colored red, and phenol substituent groups are indicated above each spectrum). Spectra of D40N apoenzyme and 4-nitrophenol-bound D40N were previously published (20). (B) Spectra of recombinant (Lower) or semisynthetic (Upper) D40N/R15K/D21N/D24C (explanations of additional mutations are provided in the main text and SI Materials and Methods) bearing 13Cζ-Tyr labels at all four Tyrs (recombinant) or only at Y32/Y57/Y119 (semisynthetic) and bound to the indicated phenols. Peaks have been assigned as described in the text. (C) Spectra of recombinant D40N uniformly labeled with 13Cζ-Tyr and bound to 5-Andro or 4-Andro. For simplicity, only the A and B steroid rings are shown. (D) Chemical shift for each assigned Tyr peak is plotted as a function of phenol pKa. Trend lines are empirical fits to guide the eye.
Because simple phenols with pKa values >10.4 are not readily available, we acquired spectra of pKSI D40N bound to the cyclohexanolic steroids 5-androsten-3-ol-17-one (5-Andro) and 4-androsten-3-ol-17-one (4-Andro) to mimic binding of phenols with high pKa. These compounds have estimated pKa values of 15.0 (5-Andro) and 14.4 (4-Andro), and 5-Andro was previously shown to bind pKSI D40N in a structurally similar manner to phenols, with the hydroxyl oxygen of its cyclohexanolic A-ring positioned within hydrogen bonding distance of Y16 and D103 (28). Furthermore, prior studies have shown that the multiple distal rings of a steroid do not alter the electrostatic environment within the oxyanion hole, relative to a bound single-ring phenol (29). The 13C NMR spectra of the D40N–5-Andro and D40N–4-Andro complexes showed three up-field peaks at <161 ppm and a single far down-field peak at 165.5 ppm (Fig. 3C), strongly suggesting the presence of a single predominantly ionized Tyr at a ligand pKa of ∼15. In the analyses that follow, we interpret the Andro spectra as reflecting the properties of bound single-ring phenols with equivalent pKa values.
To assign the observed 13C-Tyr peaks in spectra of D40N–phenol complexes (Fig. 3A), we prepared semisynthetic pKSI D40N (a complete description is provided in SI Materials and Methods) by ligating a synthetic peptide containing unlabeled Y16 to a recombinant peptide fragment containing 13Cζ-labeled Y32, Y57, and Y119, and refolding the full-length enzyme out of urea. We acquired 13C spectra for semisynthetic (Y16 unlabeled) and recombinant (uniformly 13C-Tyr–labeled) D40N bound to a series of phenols with pKa values of 7.1–10.4 (Fig. 3B). In the presence of bound phenols with pKa values of 7.1–9.1, the most down-field resonance observed for uniformly 13C-Tyr-labeled D40N is absent in spectra of semisynthetic D40N (Y16 unlabeled), identifying this peak as arising from Y16 in these complexes. In contrast, in a complex between semisynthetic D40N and 3,4-Me2-phenol (pKa = 10.4), the second-most down-field peak at 161.5 pm is missing, identifying this peak as Y16 and indicating a crossover in the identity of the most down-field peak between pKa values of 9.1 and 10.4.
By elimination, the most down-field peak at 163.1 ppm in the 3,4-Me2-phenol spectrum corresponds to either Y57 or Y32. Y32 is the terminal residue in the hydrogen bond network (Figs. 1A and 2B) and, other than Y57, is surrounded by hydrophobic residues that are expected to destabilize ionized Y32. In contrast, Y57 is positioned within hydrogen bonding distance of both Y16 and Y32, and prior results suggest that it has a highly perturbed pKa of 6.3 in the pKSI D40N apoenzyme (20). We therefore assigned the 163.1 ppm peak in the D40N–3,4-Me2-phenol spectrum to Y57. This information and the spectral comparisons with semisynthetic KSI described above allowed us to assign the 13C-Tyr peaks in each spectrum as indicated in Fig. 3B, and the observed chemical shift for each assigned peak is plotted in Fig. 3D as a function of phenol pKa.
Quantitative Modeling of Ionization States Within the KSI Hydrogen Bond Network.
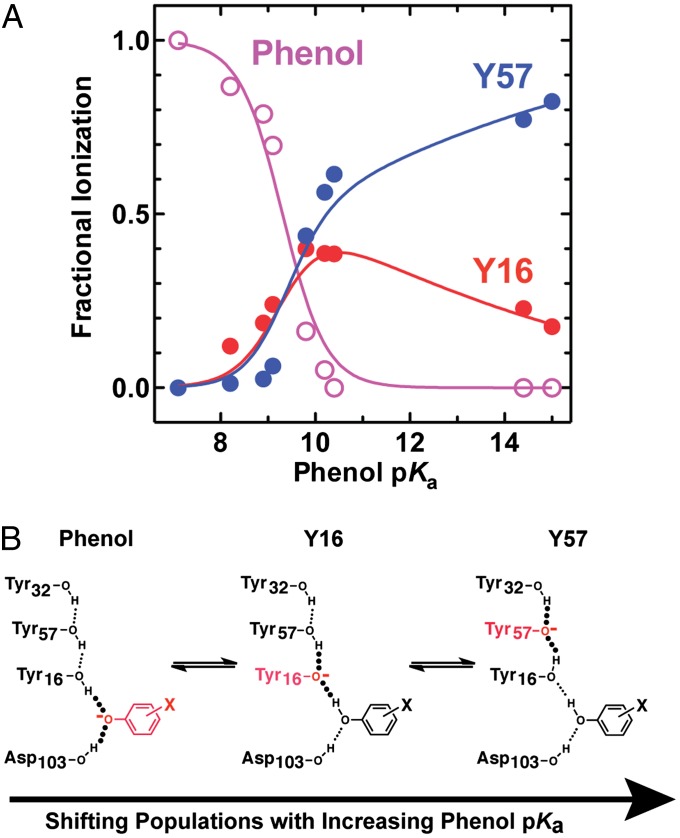
As a basis for modeling and understanding the changes in protonation state of the bound phenol, Y16, and Y57 as a function of phenol pKa and how these charge rearrangements are sensed within the active site, we used the 13C NMR chemical shift changes in Fig. 3 to estimate the fraction of each of these three groups present in its ionized form at equilibrium with differing bound phenols (additional discussion is provided in SI Text). To assign these fractional ionizations (Fig. 4A), we assumed that only a single group is ionized in the KSI active site at any given time, consistent with the observed pH dependence for phenol binding to D40N (8). In this model, proton transfers between the phenol, Y16, and Y57 shift the equilibrium population of each ionized group (Fig. 4B), with the sum of the fractions of each group present in its ionized form at each phenol pKa always equal to 1.
Fig. 4.
Quantitative fractional ionization model of hydrogen bonding groups within the KSI D40N active site with bound phenols of increasing solution pKa. (A) Fractional ionization values (estimated uncertainty ± 0.15) were derived from the 13C NMR data as explained in the main text and SI Materials and Methods. The data were globally fit (R2 values of individual fits = 0.92–0.97) with the equilibrium proton transfer model given in Methods to give best-fit values of 8.6 for parameter a, 0.1 for parameter b (the slope of the linear dependence of Y16 acidity on phenol pKa), and 9.6 for the apparent pKa of Y57. (B) Schematic depiction of the ionization states present within the active site hydrogen bond network whose fractional populations shift as a function of increasing phenol pKa.
The fractional populations of Y16 and Y57 present as ionized tyrosinates (XY16 and XY57) were estimated at each phenol pKa value by first calculating the chemical shift difference between the observed peak position for each Tyr and that observed at a pKa of 7.1 (Fig. 3), where the bound phenol is fully ionized (8, 22) (Fig. 2A) and Y16 and Y57 are thus fully neutral. This value was then divided by the total expected 13C chemical shift dispersion between an ionized and neutral Tyr in the KSI active site (166 ppm minus the observed chemical shift at a phenol pKa of 7.1; additional discussion is provided in SI Materials and Methods) to estimate fractional ionization (Xi) values for each Tyr residue at each phenol pKa. Fractional phenol ionizations (Xphenol) at each pKa value were then estimated indirectly by subtracting the sum of X16 and X57 from 1. The values of Xphenol calculated in this fashion are similar to those previously reported for bound phenols, naphthols, and equilenin based on FTIR and UV-Vis absorbance experiments (13, 22) (Fig. S3) and are qualitatively consistent with the 19F NMR changes described above (Fig. 2A). As discussed in SI Materials and Methods, we estimate the uncertainty in the assigned Xi values as ±0.15.
As quantitatively modeled in Fig. 4A and schematically depicted in Fig. 4B, the proton transfer equilibrium changes systematically as a function of the pKa of the bound phenol. This incremental redistribution indicates that the ionization states of individual residues within the KSI–phenol hydrogen bond network are systematically altered by varying the proton affinity of a single distal group on the bound phenol. The change in the identity of the predominantly ionized Tyr from Y16 to Y57 at low vs. high phenol pKa (e.g., pKa of 7.1–10.4) and the continuing shifts in the ionized populations of these groups above a pKa of 10 (Fig. 4A) directly suggest that the relative proton affinities of these two Tyr groups do not remain constant but change with increasing phenol pKa to favor ionization of Y57 over Y16, a behavior that we are able to accurately model below.
To understand the origin of these ionization changes better and to test whether increases in the phenol proton affinity alone can accurately explain the observed changes, we derived an equilibrium proton transfer model for the hydrogen bond network based on the solution pKa values of the phenols and the apparent pKa values of Y16 and Y57 within the phenol-bound complexes (full derivation and additional discussion are provided in SI Materials and Methods). The apparent pKa values used in this model are a proxy for the relative proton affinities of the hydrogen-bonded groups and do not represent true pKa values in the active site environment. Because our goal is to understand the physical and energetic properties that underpin the observed ionization changes rather than to assign microscopic acid dissociation constants, our analysis does not depend on this simplification. We first attempted to fit the data globally with the simpler model, which assumes constant proton affinities for Y16 and Y57 regardless of the phenol pKa. As expected, this model failed to account for the predominant ionization of Y16 rather than Y57 below a pKa of 10 and could not explain the observed decrease in XY16 above a pKa of 10 (Fig. S4 A and B).
Based on prior linear free energy studies and known physical properties of hydrogen bonds (8, 17, 30–35), we posited that energetic changes in the phenol–Y16 hydrogen bond with increasing phenol pKa would alter the stability of the Y16 anion, and thus modulate its ability to ionize relative to Y57. To account for this effect, we modified our equilibrium proton transfer model to allow the proton affinity of the Y16 anion to vary linearly with that of the phenol (modified expressions are shown in Materials and Methods, with additional discussion provided in SI Materials and Methods). A global fit of this model to the fractional ionization data (Fig. 4A and Fig. S4B) accurately accounted for the observed decrease in XY16 and increase in XY57 at high phenol pKa values. On the basis of this fit, we conclude that these changes in the proton transfer equilibrium occur as the Y16 proton affinity surpasses that of Y57 due to physical and energetic changes in the phenol–Y16 hydrogen bond with increasing phenol pKa. We discuss the physical origins of these hydrogen bond changes in Conclusions.
Incorporation of Nitrile Electric Field Probes and Structural Analysis of KSI Variants.
To evaluate the electrostatic field changes within the protein that accompany proton transfers within the active site hydrogen bond network, we incorporated nitrile (−CN) electric field probes into the pKSI active site. The IR stretching frequency of a nitrile group (in inverse centimeters, cm−1) is linearly sensitive to electrostatic fields (36), and experimental IR frequency shifts can be used to determine the change in local electric field projected along the nitrile bond axis. This conversion is accomplished by using the average linear Stark tuning rate |∆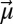 | of 0.65 cm−1/(MV/cm) previously determined for KSI-CN probes (20) and the vibrational Stark effect (VSE) equation
| of 0.65 cm−1/(MV/cm) previously determined for KSI-CN probes (20) and the vibrational Stark effect (VSE) equation 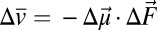 , where
, where 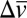 (in cm−1) is the observed IR peak shift between different bound phenols,
(in cm−1) is the observed IR peak shift between different bound phenols, 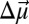 is the difference-dipole moment and is parallel to the −CN bond axis, and
is the difference-dipole moment and is parallel to the −CN bond axis, and 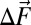 is the field change associated with the changing identity of the bound phenol (further discussion of the VSE can be found in ref. 20 and references therein).
is the field change associated with the changing identity of the bound phenol (further discussion of the VSE can be found in ref. 20 and references therein).
In prior work, we site-specifically incorporated nitrile groups into pKSI by cyanylating a unique Cys introduced by mutation at position M116, M105, or F86 within a Cys-free C69S/C81S/C97S background (20, 29, 37). These positions were selected on the basis of their proximity (3–11 Å) to the key catalytic groups (Fig. 5). Our previous studies of these KSI-CN variants indicated that nitrile incorporation resulted in minimal perturbation to KSI structure, catalytic activity, and ligand binding (20, 29).
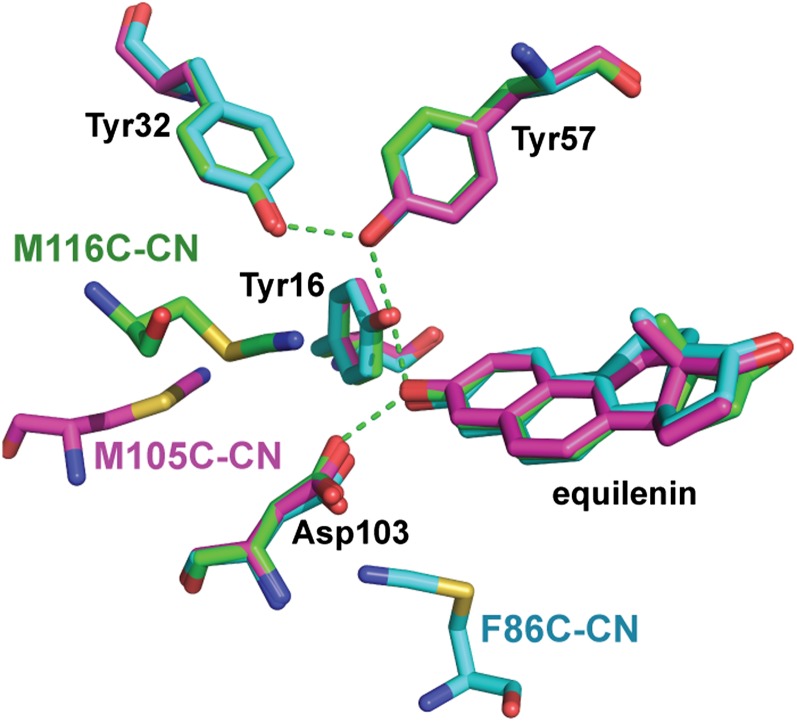
Fig. 5.
Structural comparison of KSI-CN variants bound to equilenin. Superposition of the 1.7-Å resolution D40N/M116C-CN–equilenin (carbon atoms are colored green; PDB ID code 3OWS), the 1.7-Å resolution D40N/F86C-CN–equilenin (carbon atoms are colored cyan; PDB ID code 3OWU), and the 2.3-Å resolution D40N/M105C-CN–equilenin (carbon atoms are colored magenta; PDB ID code 3OWY) X-ray crystal structures. Oxygen, nitrogen, and sulfur atoms are colored red, blue, and gold, respectively. Each KSI-CN variant contained a single nitrile group.
To test for differences in the active site structures of our KSI-CN variants bound to a common ligand, we determined the 1.7-Å resolution X-ray structure of equilenin bound to D40N/M116C-CN (data collection and refinement statistics are shown in Table S1, and an electron density map is shown in Fig. S5; PDB ID code 3OWS) and compared it with the previously published structures of equilenin bound to D40N/F86C-CN (1.7-Å resolution; PDB ID code 3OWU) and D40N/M105C-CN (2.3-Å resolution; PDB ID code 3OWY) (20). As shown in Fig. 5, equilenin binding to the three KSI-CN variants resulted in nearly identical positioning of the bound ligand and of groups within the hydrogen bond network (rmsd = 0.18 Å), and no overall structural changes were observed. Furthermore, the nitrile probe in each structure refined to a single, well-ordered conformation, positioning each nitrile with a unique vantage from which to monitor the electrostatic field effects of ionization changes within the hydrogen bond network.
Measuring the Electrostatic Field Changes from Proton Transfers Within the Hydrogen Bond Network.
The movement of negative charge from the phenolate oxygen to Y16 and Y57 with increasing phenol pKa is expected to alter local electrostatic fields within the KSI active site (20). To directly measure these field changes in discrete regions of the active site, we recorded IR spectra of phenol-bound KSI-CN variants containing nitrile probes at position 86, 105, or 116 (Fig. 6). The spectrum of each KSI-CN variant bound to 3-F-4-NO2-phenol (pKa = 6.1), which is bound as the ionized phenolate, is shown in Fig. 6A. As elucidated previously (20, 37) and discussed in more detail in SI Text, changes in the IR frequency for each nitrile probe across the series of bound phenols report on changes in the local electrostatic field experienced by each probe due to repositioning of charge within the hydrogen bond network.
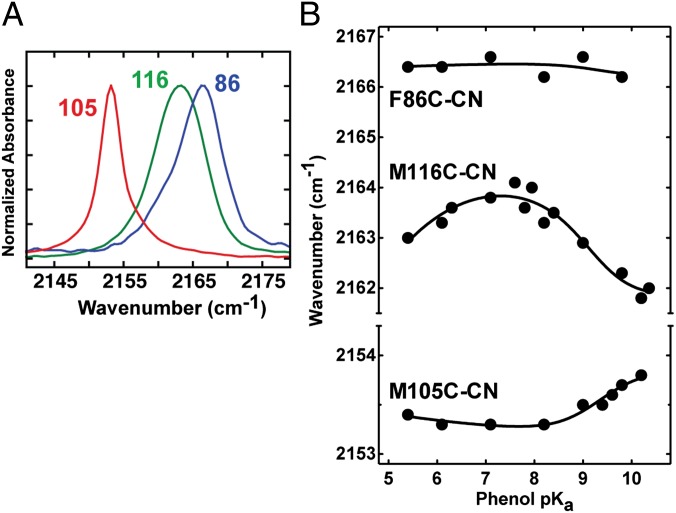
Fig. 6.
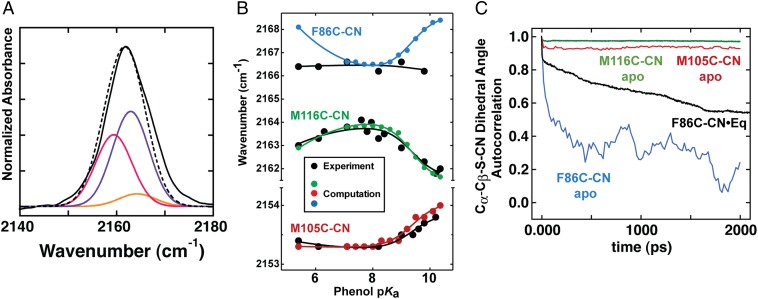
Nitrile IR stretching frequency for KSI-CN variants as a function of phenol pKa. (A) IR spectra in nitrile stretch region of D40N mutants of M105C-CN (red), M116C-CN (green), and F86C-CN (blue) with bound 3-F-4-NO2-phenol (pKa = 6.1). (B) IR peak frequencies for the nitrile stretch of F86C-CN, M116C-CN, and M105C-CN bound to phenols of differing pKa (data are from Table S2). Trend lines are empirical fits to guide the eye. Note that for clarity, the y-axis scale has been expanded for M105C-CN.
For bound phenols with pKa values of 5–8, a range in which negative charge resides predominantly on the phenolate oxygen, the nitrile stretch frequencies of F86C-CN and M105C-CN remain essentially unchanged, whereas that of M116C-CN increases by 1 cm−1 (Fig. 6B). The unique sensitivity of the M116C-CN probe is consistent with its favorable orientation and closer proximity to the oxygen of the bound phenol compared with the more orthogonal orientations and distal positions of the F86C-CN and M105C-CN probes (Fig. 5; distances and angles are given in table S3 of ref. 20). The increase in stretching frequency of the M116C-CN nitrile over this range is qualitatively consistent with an increase in the local electrostatic field projected along the nitrile bond axis due to the increased negative charge localization on the phenolate oxygen that accompanies a three-unit increase in pKa (16, 38).
For bound phenols with pKa values of 8–10, a range in which negative charge is progressively transferred to Y16 and Y57, the IR peak positions of M105C-CN and M116C-CN change by +0.5 cm−1 and −2.0 cm−1, respectively, whereas the nitrile stretch frequency of F86C-CN remains essentially unchanged (Fig. 6B). Conversion of these IR frequency shifts using the VSE equation suggests that the ensemble-averaged field along the nitrile bond axis of M105C-CN and M116C-CN changes by +0.8 MV/cm and −3.1 MV/cm, respectively, whereas the field along F86C-CN changes by less than ±0.1 MV/cm, as the pKa of bound phenol increases from 8 to 10. The unique shifts registered by each probe, which occur despite differences of only a few angstroms in their positions relative to Y16, Y57, and the phenol oxygen (Fig. 5 and Table S3), emphasize the importance of bond directionality and positioning, rather than just proximity, in determining how local electrostatic perturbations are felt by nearby groups.
Discrete Peaks for Hydrogen Bond Tautomers Are Resolved in Nitrile IR Spectra.
To learn more about the proton transfer and negative charge distribution between Y16 and Y57, we carried out additional analyses of the IR spectra for M116C-CN, the nitrile closest to these two groups, bound to phenols with pKa values near 10. In this pKa region, the major fraction of the bound phenol is neutral and the ionized populations of Y16 and Y57 are nearly equal (Fig. 4), suggesting that these Tyr groups have matched or nearly matched proton affinities within the protein interior. This equivalence and the short 2.5-Å O•••O distance observed for the Y16–Y57 hydrogen bond in the 1.25-Å resolution D40N–phenol (pKa = 10) X-ray structure (8) are physical features that can favor formation of a single-well hydrogen bond in which negative charge and the bridging proton would be equally shared and delocalized between the interacting groups (39, 40). Alternatively, interactions with the anisotropic distribution of charges and dipoles within the surrounding heterogeneous protein matrix might result in a double-well potential energy surface for this hydrogen bond despite closely matched proton affinities (41–43), with negative charge discretely localized on either Y16 or Y57.
For a single-well potential, a single, symmetrical IR peak would be expected for the M116C-CN nitrile with bound phenols of pKa of ∼10. In contrast, a double-well potential with interconverting tautomers of ionized Y16 and Y57 (Fig. 4B) would be expected to result in two IR peaks corresponding to negative charge either on Y16 or Y57, provided that interconversion is slow relative to the time scale defined by the inverse of the frequency difference between the two IR peaks. Close examination of the IR spectra of M116C-CN with different bound phenols (Fig. 7A) revealed a high-energy peak shoulder for phenols with pKa values above 9.8 that is more readily detected as an inflection in the numerical first derivative of the absorption spectra for these complexes (Fig. 7B) and suggests the possible presence of two distinct but overlapping peaks. An increasing contribution from a second, spectrally distinct peak would be expected to result in a broader spectral envelope, and this broadening is observed for bound phenols of pKa above 9 (Fig. S6).
Fig. 7.
Analysis of spectral width and asymmetry of the nitrile IR absorption spectra of D40N/M116C-CN bound to phenols of differing pKa. (A) Room temperature IR absorption spectra in the nitrile stretching region of D40N/M116C-CN bound to 4-NO2-phenol (blue), 3-Cl-phenol (red), 4-F-3-Me-phenol (green), and 4-MeO-phenol (black). (B) First derivative of the absorption spectrum calculated from the data in A, highlighting the appearance of a shoulder (inflections, which indicate a shoulder, are marked with arrows) and increasing peak width and asymmetry (i.e., increasing ratio of peak height to trough depth) for higher pKa phenols. (C) Superposition of the nitrile stretch peak observed for 4-F-3-Me-phenol (pKa = 9.8) bound to D40N/M116C-CN at 298 K in buffer (green) or at 80 K in 50% glycerol/buffer (black). (D) Nitrile stretch peak observed for D40N/M116C-CN with bound 2,6-d2-4-F-phenol (pKa = 10.0) at 80 K in 50% glycerol/buffer. A single C-F stretch peak corresponding to the neutral phenol was also observed for this complex at 80 K (Fig. S7B), consistent with our assignment in Fig. 4A that a bound phenol with a pKa of ∼10 is predominantly neutral and supporting assignment of the two peaks in C and D to the KSI tautomers with ionized Y16 or Y57.
To test further for the presence of two distinct IR peaks, we acquired low-temperature spectra at 80 K (SI Materials and Methods). Spectra of M116C-CN bound to 3,4-(NO2)2-phenol (pKa = 5.4) or 5-Andro (pKa = 15) showed only a single nitrile peak (Fig. S7A), as expected, for exclusive or predominant negative charge localization on the phenolate or Y57, respectively (Fig. 4). In contrast, two discrete, narrow peaks separated by 4 cm−1 were observed for the M116C-CN nitrile with bound 4-F-3-Me-phenol (pKa = 9.8) (Fig. 7C) and 2,6-d2-4-F-phenol (pKa = 10.0) (22) (Fig. 7D), providing strong evidence for discrete IR peaks arising from ionized populations of Y16 and Y57. The observation of individual tautomeric peaks indicates that proton transfer across the Y16–Y57 hydrogen bond near a pKa of 10 has a double-well potential energy surface and is significantly slower than the 10-ps time scale set by the frequency difference of 4 cm−1 (0.1 THz) between the two states (additional discussion is provided below and in SI Text). The double-well nature of this hydrogen bond implies that a single unit of negative charge is localized on one of the two interacting groups at any given time, allowing us to model the electrostatic effects of charge rearrangement within the hydrogen bond network on the surrounding protein environment as a sum of these discrete populations.
Computational Modeling of IR Peak Shifts for the Nitrile Probes.
Developing accurate computational models of protein electrostatics is an ongoing challenge, due, in part, to the paucity of experimental benchmarks (20, 44, 45). Although numerous biophysical studies have provided important qualitative insights into the electrostatic properties of proteins, key limitations in each of these approaches have prevented clean, quantitative measurements of electrostatic fields within proteins (ref. 20 and references therein). Our nitrile-based measurements of electric field changes provide a metric by which to test and improve computational models of the electrostatic effects of charge rearrangement within a protein interior. Based on our analysis of the shifting ionization equilibria within the hydrogen bond network (Fig. 4), we carried out continuum electrostatic calculations using the software package DelPhi (described in detail in SI Materials and Methods) to predict the effect of these ionization changes on the stretching frequency of each nitrile probe within the KSI active site. These computations used an internal protein dielectric of 2 to account for the intrinsic polarizability of amino acids but otherwise assumed the absence of structural rearrangements (i.e., the same static structural model was used in all calculations).
We first calculated the expected electric field change and IR peak shift for each probe due to negative charge residing fully on the oxygen of the bound phenol, Y16, or Y57, and then used the fractional charge distribution from Fig. 4A to calculate a population-weighted IR peak shift as a function of ligand pKa. Absolute nitrile stretching frequencies were obtained by adding the calculated peak shift to a chosen reference state, which we selected to be the IR frequency for each KSI-CN variant when bound to 4-nitrophenol (pKa = 7.1) (additional explanation is provided in SI Materials and Methods). This referencing is the only adjustable parameter in calculating peak positions and does not affect the trend or scale of the calculated frequency changes.
To account for differences in charge density on the phenolate oxygen for phenol with different solution pKa values (16, 38), we used QM-calculated atomic charges for three phenolates with differing electron-withdrawing groups as inputs for the DelPhi calculations. We then used the calculated electrostatic field values for the three explicitly modeled phenolates to construct a linear correlation (for each probe position) between phenol pKa and the local electrostatic field due to negative charge on the phenolate oxygen (SI Materials and Methods). For calculating IR peak positions with bound phenols above a pKa of 8, the coexistence of distinct ionization populations (Fig. 4 A and B) that are detectable as discrete species in IR spectra (Fig. 7) required that electric fields be calculated for each separate tautomer, with negative charge on the ligand, Y16, or Y57.
As shown for M116C-CN with bound 4-MeO-phenol (pKa = 10.2) in Fig. 8A and described in more detail in SI Materials and Methods, a population-weighted spectral envelope (dashed black line) was calculated from the sum of three basis spectra (colored lines) whose relative intensities and peak frequencies correspond to the fractional populations and calculated IR frequencies, respectively, for the three tautomers present at this pKa. This modeled composite spectrum closely resembles the observed IR peak for this complex (Fig. 8A, solid black line), supporting assignment of the high-energy features resolved in spectra of M116C-CN bound to high pKa phenols (peak shoulder in Fig. 7A and higher energy peak in Fig. 7 C and D) to the population of ionized Y57. The spectral envelope for the stretching transition of each nitrile probe was calculated in this manner for a series of phenols with discrete pKa values that span the experimental range.
Fig. 8.
Comparison of computational and experimental results for KSI-CN variants. (A) Experimental spectrum of D40N/M116C-CN bound to 4-MeO-phenol (solid black line) modeled with a three-spectra basis set (dashed black line) composed of calculated spectra for negative charge on the hydroxylic oxygen of 4-MeO-phenolate (orange), Y16 (red), or Y57 (violet) and weighted by the fractional populations of these species at a pKa of 10.2 as shown in Fig. 4. (B) Superposition of experimental (black) and calculated (colored) nitrile IR peak shifts for phenols of increasing pKa bound to F86C-CN (cyan), M116C-CN (green), and M105C-CN (red). Computed IR peak shifts were modeled as described in the main text and SI Materials and Methods. Trend lines are empirical fits to guide the eye. Note that the y-axis scale has been expanded for M105C-CN. (C) Plot of the dihedral angle autocorrelation for each probe as a function of time during molecular dynamics simulations of nitrile mobility in the KSI-CN variants. Eq, equilenin.
A plot of the absorbance maximum of each modeled spectrum (colored) vs. the observed IR peak maximum (black) for each probe as a function of phenol pKa is shown in Fig. 8B. The close correspondence between the predicted and observed IR shifts for M116C-CN and M105C-CN with varying phenol pKa suggests that the electrostatic field changes due to charge rearrangement in the active site hydrogen bond network accurately account for the observed trends in IR peak maxima for these two probes.
In contrast to M116C-CN and M105C-CN, our modeling is unable to explain the observed IR frequency trend for F86C-CN. Our calculations predict a significant IR frequency dependence on ligand pKa, but no systematic change is observed experimentally (Fig. 8B). This disagreement can be accounted for by a model in which F86C-CN has greater conformational freedom relative to the other two probe sites due to the steric vacancy generated by mutation of the bulky phenyl ring of the parent F86 residue to a thiocyanate. The additional space may permit this nitrile probe to reorient in response to changes in charge localization between discrete ionized tautomers present across the phenol series, an effect not captured by our calculations, which relied on a static structural model. Indeed, molecular dynamics simulations (described in detail in SI Materials and Methods) suggest that the nitrile of F86C-CN has substantially greater conformational mobility than nitriles at the other two sites and samples a wide distribution of rotamers on the nanosecond time scale (Fig. 8C and Fig. S8; additional discussion is provided in SI Text). These results are consistent with the model above that posits a wide equilibrium distribution of conformers for the F86C-CN nitrile. Nevertheless, recent time-resolved IR studies indicate that this probe does not substantially rearrange on the time scale of tens of picoseconds (21).
Conclusions and Implications
Pauling and Corey recognized over 60 y ago that hydrogen bonds and the extended networks they frequently form are ubiquitous and central components of biological structure and function (46, 47). Hydrogen bonds are typically probed in a coarse fashion by ablating them via site-directed mutagenesis and evaluating the functional consequence of their removal. Although this approach can highlight their general functional importance, it does not reveal the physical properties of the intact hydrogen bonds that underpin their functional roles (8–10, 48), and the energetic effects of mutations can have as much to do with surrounding structural rearrangements in response to hydrogen bond ablation as they do with properties of the hydrogen bonds themselves (49–52). In contrast to these common mutagenic approaches, we have leveraged favorable features of KSI to interrogate the physical and energetic properties of the intact hydrogen bond network formed in the KSI active site and to study the effects of internal charge rearrangement on electrostatic fields within the active site.
Electrostatic Effects of Charge Rearrangement Within the Active Site Hydrogen Bond Network.
A hallmark of protein catalysts and a distinguishing feature from reactions in bulk solution is that enzymes provide a highly structured and chemically heterogeneous solvation environment that has a limited ability for electrostatic rearrangement (1, 49, 53–55). Nevertheless, it has been a formidable challenge to carry out direct experimental tests of the nature and properties of this environment. Our nitrile probes, combined with our ability to reposition charge incrementally within the active site by varying the identity of bound phenols, provided a highly controlled system to test how specific charge rearrangements are sensed in discrete regions of an enzyme active site and how the surrounding protein matrix responds to this charge rearrangement.
Using continuum electrostatic calculations based on a static structural model and an internal dielectric of 2, we found surprisingly close agreement between the calculated and observed field changes for M116C-CN and M105C-CN, the two most ordered sites. This quantitative agreement suggests the absence of substantial electrostatic reorientation within the surrounding protein matrix in response to charge rearrangement within the hydrogen bond network. This finding is consistent with prior time-resolved studies of KSI that suggested a rigid electrostatic environment on the picosecond time scale (21, 56) and extends those observations to the equilibrium time scale. Structural comparison of KSI bound to low vs. high pKa phenols (Fig. 2B) also suggested negligible structural rearrangement at equilibrium, but small rearrangements on the 0.1-Å scale would be difficult to detect reliably by X-ray crystallography even at the 1.3-Å resolution of our structures. Rearrangement of a single charged group by 0.1 Å, however, could be readily detected by IR spectroscopy as a 2-cm−1 shift if movement of this group were parallel to a nitrile probe located ∼4 Å away, given an internal dielectric of 2.
The quantitative agreement between experiment and computation for M116C-CN and M105C-CN contrasts with prior studies of electrostatic changes in proteins due to pH changes, side-chain mutation, and ligand binding, in which qualitative agreement, at best, has been observed between experiment and theory (20, 44, 45, 57, 58). We hypothesize that our simple computational approach succeeded in the present study due to the subtle perturbations of the homologous series of bound phenols (differing only in their meta and para substituent groups) and to the absence of structural and solvent rearrangements that are likely to accompany more gross perturbations, such as pH changes, mutation, or protein–ligand association. This success also suggests that undetermined ionization states and rearrangements that are uncharacterized and difficult to model may be general problems that severely limit computational accuracy. Indeed, many studies have attempted to account for these unknown features by using a higher internal dielectric (e.g., ε = 20) in continuum electrostatic calculations (3–5). Our study provides an example in which a more controlled system with minimal structural rearrangements and incisive knowledge of ionization states may more cleanly isolate electrostatic effects and substantially improve computational accuracy. Nevertheless, we stress that continuum electrostatic models based on a uniform protein dielectric are an incomplete description of the heterogeneous and anisotropic protein environment and are inadequate to describe all the properties and behaviors of these environments. Indeed, the behavior of the F86C-CN probe appears to provide an example of this more complex behavior.
Quantitative Dissection of Hydrogen Bond-Mediated Proton Transfer in the KSI Active Site.
Site-specific NMR probes allowed us to resolve ionization changes in the active site hydrogen bond network that were otherwise invisible in KSI X-ray structures with resolutions as high as 1.1–1.25 Å (8, 15). The ability to fit the ionization data with a simple model based only on the proton affinities of the interacting groups (Fig. 4A) suggests that these incremental ionization changes predominantly arise due to physical and energetic changes in the hydrogen-bonded groups themselves rather than from the propagated effects of conformational rearrangements of distal groups. Internal proton transfer is an expected property of hydrogen bonds formed between groups with similar proton affinities. Our observation of incremental proton transfer from Y16 to the bound phenolate as the proton affinity of the phenol approaches that of Y16 is consistent with extensive studies of hydrogen bond-mediated proton transfer based on small-molecule complexes in solution (19, 34, 42, 59) and is not a unique property of hydrogen bonds formed within the heterogeneous protein environment.
The systematic variation in relative ionized fractions of Y16 and Y57 is readily accounted for by a model in which the energetic stabilization of the Y16 anion provided by the phenol–Y16 hydrogen bond decreases with increasing phenol pKa. Extensive prior hydrogen bond studies in small molecules provide strong evidence that increasing the pKa of a phenol or other hydrogen bond donor (via substituent effects) weakens its ability to donate a hydrogen bond to a common acceptor of lower pKa (17, 18, 32, 34, 60, 61) due, in part, to the decrease in positive charge character of the hydroxylic proton and its weaker interaction with an anionic acceptor (17, 60). Increasing phenol pKa is also expected to lengthen the hydrogen bond to the Y16 anion as the proton affinities of the two groups become increasingly mismatched (8), reducing charge-transfer across the hydrogen bond and increasing negative charge localization on the Y16 anion (30, 31). These changes, which progressively weaken the phenol–Y16 hydrogen bond, destabilize the Y16 anion and thereby favor formation of the Y57 anion instead, which is stabilized by hydrogen bonds from Y16 and Y32 (Fig. 9).
Fig. 9.
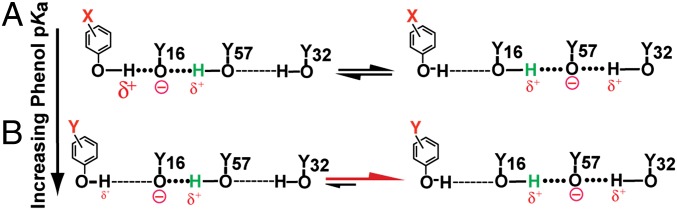
Schematic model for preferential ionization of Y57 vs. Y16 with increasing phenol pKa. Increasing the solution pKa of the bound phenol going from A to B weakens its hydrogen bond to Y16, which destabilizes Y16 ionization and shifts the proton transfer equilibrium toward ionization of Y57, where charge is stabilized by hydrogen bonds from Y16 and Y32. For clarity, the transferred proton is shown in green and the D103–phenol hydrogen bond has been omitted.
This systematic and quantitative dissection of equilibrium proton transfer within the oxyanion hole hydrogen bond network of KSI provides one of the cleanest isolations and interrogations of specific hydrogen bond properties within a complex, heterogeneous, and highly idiosyncratic protein interior. Refinement of these measurements in KSI and determination of related measures in other proteins, along with additional tests in model systems, have the potential to provide basic insights into the energetic properties of hydrogen bonds underlying enzymatic catalysis and the fundamental properties of protein interiors.
Materials and Methods
A full description of all experimental and computational methods and KSI semisynthesis is given in SI Materials and Methods, with additional detail and discussion in SI Text and Figs. S9–S11. KSI mutants were expressed and purified from Escherichia coli using published methods (8). Nitrile labeling and uniform 13C-Tyr incorporation were performed as previously described (20, 29, 37). 19F and 13C NMR spectra were acquired at 20 °C on 500- and 600-MHz (proton frequency) Varian UNITYINOVA NMR spectrometers using previously published methods (8, 9, 37). IR spectra were acquired at room temperature and at 80 K as previously reported (20, 29, 37). Cocrystals of pKSI D40N–3-F-4-NO2-phenolate and D40N/M116C-CN–equilenin were obtained at 20 °C using hanging drop vapor diffusion in accordance with previously published methods (8, 20). X-ray diffraction data were collected at the Stanford Synchrotron Radiation Laboratory and the Advanced Light Source (Lawrence Berkeley National Laboratory), and structure refinement was carried out as previously described (9, 20). Electrostatic calculations were performed with DelPhi (62), as previously published (20).
The Xi of each group in Fig. 4A was globally fit via nonlinear regression using GraphPad Prism to the following equilibrium titration expressions, in which 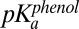 was the independent variable, and apparent pKa values, as defined above, were used to describe the relative proton affinities of the Tyr groups. In the expressions below,
was the independent variable, and apparent pKa values, as defined above, were used to describe the relative proton affinities of the Tyr groups. In the expressions below,  was fit as an adjustable parameter and
was fit as an adjustable parameter and 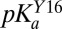 was fit as a linear function of
was fit as a linear function of  according to
according to 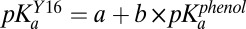 , with a and b as adjustable parameters. A full derivation and description of the fitting is given in SI Materials and Methods.
, with a and b as adjustable parameters. A full derivation and description of the fitting is given in SI Materials and Methods.
 |
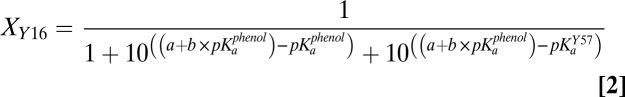 |
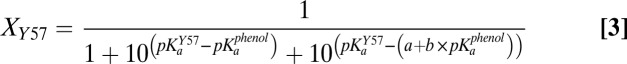 |
Supplementary Material
Acknowledgments
We thank Corey Liu and Steve Lynch for assistance with NMR experiments, Aaron Straight for reagents, Jessica DeMott for contributions to nitrile-labeling experiments, Eliza Reuben for assistance with QM calculations, and John Brauman and Peter Tolstoy for helpful discussions. Portions of this research were conducted at the Advanced Light Source, a national user facility operated by the Lawrence Berkeley National Laboratory; at the Stanford Synchrotron Radiation Laboratory, which is supported by the Department of Energy and the National Institutes of Health (NIH); and at the Stanford Magnetic Resonance Laboratory, which is supported, in part, by the Stanford University Medical School. P.A.S. was supported, in part, by Howard Hughes Medical Institute and G. Lieberman predoctoral fellowships. S.D.F. was supported, in part, by National Science Foundation (NSF) and Stanford Bio-X predoctoral fellowships. Funding was provided by grants to S.G.B. (NIH Grant GM27738) and D.H. (NSF Grant MCB-1121778).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The atomic coordinates and structure factors have been deposited in the Protein Data Bank, www.pdb.org (PDB ID codes 3VGN and 3OWS).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1302191110/-/DCSupplemental.
References
- 1.Fersht AR. Structure and Mechanism in Protein Science. New York: Freeman; 1999. [Google Scholar]
- 2.Ladd MFC, Palmer RA. Structure Determination by X-Ray Crystallography. New York: Kluwer Academic/Plenum; 2003. [Google Scholar]
- 3.Fitch CA, et al. Experimental pK(a) values of buried residues: Analysis with continuum methods and role of water penetration. Biophys J. 2002;82(6):3289–3304. doi: 10.1016/s0006-3495(02)75670-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Antosiewicz J, McCammon JA, Gilson MK. The determinants of pKas in proteins. Biochemistry. 1996;35(24):7819–7833. doi: 10.1021/bi9601565. [DOI] [PubMed] [Google Scholar]
- 5.Karp DA, et al. High apparent dielectric constant inside a protein reflects structural reorganization coupled to the ionization of an internal Asp. Biophys J. 2007;92(6):2041–2053. doi: 10.1529/biophysj.106.090266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Petrounia IP, Pollack RM. Substituent effects on the binding of phenols to the D38N mutant of 3-oxo-delta5-steroid isomerase. A probe for the nature of hydrogen bonding to the intermediate. Biochemistry. 1998;37(2):700–705. doi: 10.1021/bi972262s. [DOI] [PubMed] [Google Scholar]
- 7.Petrounia IP, Blotny G, Pollack RM. Binding of 2-naphthols to D38E mutants of 3-oxo-Delta 5-steroid isomerase: Variation of ligand ionization state with the nature of the electrophilic component. Biochemistry. 2000;39(1):110–116. doi: 10.1021/bi9917838. [DOI] [PubMed] [Google Scholar]
- 8.Kraut DA, et al. Testing electrostatic complementarity in enzyme catalysis: Hydrogen bonding in the ketosteroid isomerase oxyanion hole. PLoS Biol. 2006;4(4):e99. doi: 10.1371/journal.pbio.0040099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sigala PA, et al. Testing geometrical discrimination within an enzyme active site: Constrained hydrogen bonding in the ketosteroid isomerase oxyanion hole. J Am Chem Soc. 2008;130(41):13696–13708. doi: 10.1021/ja803928m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sigala PA, Caaveiro JM, Ringe D, Petsko GA, Herschlag D. Hydrogen bond coupling in the ketosteroid isomerase active site. Biochemistry. 2009;48(29):6932–6939. doi: 10.1021/bi900713j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hanoian P, Sigala PA, Herschlag D, Hammes-Schiffer S. Hydrogen bonding in the active site of ketosteroid isomerase: Electronic inductive effects and hydrogen bond coupling. Biochemistry. 2010;49(48):10339–10348. doi: 10.1021/bi101428e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhao Q, Abeygunawardana C, Gittis AG, Mildvan AS. Hydrogen bonding at the active site of delta 5-3-ketosteroid isomerase. Biochemistry. 1997;36(48):14616–14626. doi: 10.1021/bi971549m. [DOI] [PubMed] [Google Scholar]
- 13.Childs W, Boxer SG. Proton affinity of the oxyanion hole in the active site of ketosteroid isomerase. Biochemistry. 2010;49(12):2725–2731. doi: 10.1021/bi100074s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kuliopulos A, Mildvan AS, Shortle D, Talalay P. Kinetic and ultraviolet spectroscopic studies of active-site mutants of delta 5-3-ketosteroid isomerase. Biochemistry. 1989;28(1):149–159. doi: 10.1021/bi00427a022. [DOI] [PubMed] [Google Scholar]
- 15.Kim SW, et al. High-resolution crystal structures of delta5-3-ketosteroid isomerase with and without a reaction intermediate analogue. Biochemistry. 1997;36(46):14030–14036. doi: 10.1021/bi971546+. [DOI] [PubMed] [Google Scholar]
- 16.Gross KC, Seybold PG. Substituent effects on the physical properties and pKa of phenol. Int J Quantum Chem. 2001;85:569–579. [Google Scholar]
- 17.Shan SO, Herschlag D. Hydrogen bonding in enzymatic catalysis: Analysis of energetic contributions. Methods Enzymol. 1999;308:246–276. doi: 10.1016/s0076-6879(99)08013-1. [DOI] [PubMed] [Google Scholar]
- 18.Shan SO, Loh S, Herschlag D. The energetics of hydrogen bonds in model systems: Implications for enzymatic catalysis. Science. 1996;272(5258):97–101. doi: 10.1126/science.272.5258.97. [DOI] [PubMed] [Google Scholar]
- 19.Brycki B, Brzezinski B, Zundel G, Keil T. 1H and 13C NMR studies of the proton transfer in complexes of substituted phenols with trimethylamine N-oxide. Magn Reson Chem. 1992;30(6):507–510. [Google Scholar]
- 20.Fafarman AT, et al. Quantitative, directional measurement of electric field heterogeneity in the active site of ketosteroid isomerase. Proc Natl Acad Sci USA. 2012;109(6):E299–E308. doi: 10.1073/pnas.1111566109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jha SK, Ji M, Gaffney KJ, Boxer SG. Direct measurement of the protein response to an electrostatic perturbation that mimics the catalytic cycle in ketosteroid isomerase. Proc Natl Acad Sci USA. 2011;108(40):16612–16617. doi: 10.1073/pnas.1113874108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fried SD, Boxer SG. Evaluation of the energetics of the concerted acid-base mechanism in enzymatic catalysis: The case of ketosteroid isomerase. J Phys Chem B. 2012;116(1):690–697. doi: 10.1021/jp210544w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gerig JT. Fluorine nuclear magnetic resonance of fluorinated ligands. Methods Enzymol. 1989;177:3–23. doi: 10.1016/0076-6879(89)77003-8. [DOI] [PubMed] [Google Scholar]
- 24.Richarz R, Wuthrich K. Carbon-13 NMR chemical shifts of the common amino acid residues measured in aqueous solutions of the linear tetrapeptides H-Gly-Gly-X-L-Ala-OH. Biopolymers. 1978;17(9):2133–2141. [Google Scholar]
- 25.Wu ZR, et al. Solution structure of 3-oxo-delta5-steroid isomerase. Science. 1997;276(5311):415–418. doi: 10.1126/science.276.5311.415. [DOI] [PubMed] [Google Scholar]
- 26.Thornburg LD, et al. Electrophilic assistance by Asp-99 of 3-oxo-Delta 5-steroid isomerase. Biochemistry. 1998;37(29):10499–10506. doi: 10.1021/bi980099a. [DOI] [PubMed] [Google Scholar]
- 27.Cavanagh J, Fairbrother WJ, Palmer AG, Skelton NJ. Protein NMR Spectroscopy: Principles and Practice. San Diego: Academic; 1996. [Google Scholar]
- 28.Ha NC, Kim MS, Lee W, Choi KY, Oh BH. Detection of large pKa perturbations of an inhibitor and a catalytic group at an enzyme active site, a mechanistic basis for catalytic power of many enzymes. J Biol Chem. 2000;275(52):41100–41106. doi: 10.1074/jbc.M007561200. [DOI] [PubMed] [Google Scholar]
- 29.Sigala PA, Fafarman AT, Bogard PE, Boxer SG, Herschlag D. Do ligand binding and solvent exclusion alter the electrostatic character within the oxyanion hole of an enzymatic active site? J Am Chem Soc. 2007;129(40):12104–12105. doi: 10.1021/ja075605a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hibbert F, Emsley J. Hydrogen bonding and chemical reactivity. Advances in Physical Organic Chemistry. 1990;26:255–379. [Google Scholar]
- 31.Jeffrey GA. An Introduction to Hydrogen Bonding. New York: Oxford Univ Press; 1997. [Google Scholar]
- 32.Shan SO, Herschlag D. The change in hydrogen bond strength accompanying charge rearrangement: Implications for enzymatic catalysis. Proc Natl Acad Sci USA. 1996;93(25):14474–14479. doi: 10.1073/pnas.93.25.14474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Steiner T, Saenger W. Lengthening of the covalent O-H bond in O-H-O hydrogen bonds re-examined from low-temperature neutron diffraction data of organic compounds. Acta Crystallogr B. 1994;50:348–357. [Google Scholar]
- 34.Stahl N, Jencks WP. Hydrogen bonding between solutes in aqueous solution. J Am Chem Soc. 1986;108(14):4196–4205. [Google Scholar]
- 35.Abraham MH, Grellier PL, Prior DV, Morris JJ, Taylor PJ. Hydrogen bonding. Part 10. A scale of solute hydrogen-bond basicity using log K values for complexation in tetrachloromethane. J Chem Soc Perkin Trans. 1990;2:521–529. [Google Scholar]
- 36.Suydam IT, Boxer SG. Vibrational Stark effects calibrate the sensitivity of vibrational probes for electric fields in proteins. Biochemistry. 2003;42(41):12050–12055. doi: 10.1021/bi0352926. [DOI] [PubMed] [Google Scholar]
- 37.Fafarman AT, Sigala PA, Herschlag D, Boxer SG. Decomposition of vibrational shifts of nitriles into electrostatic and hydrogen-bonding effects. J Am Chem Soc. 2010;132(37):12811–12813. doi: 10.1021/ja104573b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gross KC, Waybold PG, Hadad CM. Comparison of different atomic charge schemes for predicting pKa variations in substituted anilines and phenols. Int J Quantum Chem. 2002;90:445–458. [Google Scholar]
- 39.Cleland WW, Frey PA, Gerlt JA. The low barrier hydrogen bond in enzymatic catalysis. J Biol Chem. 1998;273(40):25529–25532. doi: 10.1074/jbc.273.40.25529. [DOI] [PubMed] [Google Scholar]
- 40.Cleland WW. The low-barrier hydrogen bond in enzymic catalysis. Advances in Physical Organic Chemistry. 2010;44:1–17. [Google Scholar]
- 41.de la Vega JR. Role of symmetry in the tunneling of the proton in double minimum potentials. Acc Chem Res. 1982;15(41):185–191. [Google Scholar]
- 42.Koeppe B, Tolstoy PM, Limbach HH. Reaction pathways of proton transfer in hydrogen-bonded phenol-carboxylate complexes explored by combined UV-vis and NMR spectroscopy. J Am Chem Soc. 2011;133(20):7897–7908. doi: 10.1021/ja201113a. [DOI] [PubMed] [Google Scholar]
- 43.Perrin CL. Are short, low-barrier hydrogen bonds unusually strong? Acc Chem Res. 2010;43(12):1550–1557. doi: 10.1021/ar100097j. [DOI] [PubMed] [Google Scholar]
- 44.Suydam IT, Snow CD, Pande VS, Boxer SG. Electric fields at the active site of an enzyme: Direct comparison of experiment with theory. Science. 2006;313(5784):200–204. doi: 10.1126/science.1127159. [DOI] [PubMed] [Google Scholar]
- 45.Fafarman AT, Boxer SG. Nitrile bonds as infrared probes of electrostatics in ribonuclease S. J Phys Chem B. 2010;114(42):13536–13544. doi: 10.1021/jp106406p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pauling L, Corey RB, Branson HR. The structure of proteins; two hydrogen-bonded helical configurations of the polypeptide chain. Proc Natl Acad Sci USA. 1951;37(4):205–211. doi: 10.1073/pnas.37.4.205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pauling L, Corey RB. Two hydrogen-bonded spiral configurations of the polypeptide chain. J Am Chem Soc. 1950;72(11):5349. [Google Scholar]
- 48.Sigala PA, Tsuchida MA, Herschlag D. Hydrogen bond dynamics in the active site of photoactive yellow protein. Proc Natl Acad Sci USA. 2009;106(23):9232–9237. doi: 10.1073/pnas.0900168106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kraut DA, Carroll KS, Herschlag D. Challenges in enzyme mechanism and energetics. Annu Rev Biochem. 2003;72:517–571. doi: 10.1146/annurev.biochem.72.121801.161617. [DOI] [PubMed] [Google Scholar]
- 50.Kraut DA, Sigala PA, Fenn TD, Herschlag D. Dissecting the paradoxical effects of hydrogen bond mutations in the ketosteroid isomerase oxyanion hole. Proc Natl Acad Sci USA. 2010;107(5):1960–1965. doi: 10.1073/pnas.0911168107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Plapp BV. Site-directed mutagenesis: A tool for studying enzyme catalysis. Methods Enzymol. 1995;249:91–119. doi: 10.1016/0076-6879(95)49032-9. [DOI] [PubMed] [Google Scholar]
- 52.Fersht AR. Relationships between apparent binding energies measured in site-directed mutagenesis experiments and energetics of binding and catalysis. Biochemistry. 1988;27(5):1577–1580. doi: 10.1021/bi00405a027. [DOI] [PubMed] [Google Scholar]
- 53.Jencks WP. Catalysis in Chemistry and Enzymology. Ed 2. New York: Dover; 1987. [Google Scholar]
- 54.Pauling L. Molecular architecture and biological reactions. Chem Eng News. 1946;24(10):1375–1377. [Google Scholar]
- 55.Warshel A, Aqvist J, Creighton S. Enzymes work by solvation substitution rather than by desolvation. Proc Natl Acad Sci USA. 1989;86(15):5820–5824. doi: 10.1073/pnas.86.15.5820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Childs W, Boxer SG. Solvation response along the reaction coordinate in the active site of ketosteroid isomerase. J Am Chem Soc. 2010;132(18):6474–6480. doi: 10.1021/ja1007849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Webb LJ, Boxer SG. Electrostatic fields near the active site of human aldose reductase: 1. New inhibitors and vibrational stark effect measurements. Biochemistry. 2008;47(6):1588–1598. doi: 10.1021/bi701708u. [DOI] [PubMed] [Google Scholar]
- 58.Xu L, Cohen AE, Boxer SG. Electrostatic fields near the active site of human aldose reductase: 2. New inhibitors and complications caused by hydrogen bonds. Biochemistry. 2011;50(39):8311–8322. doi: 10.1021/bi200930f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zundel G. Hydrogen bonds with large proton polarizability and proton transfer processes in electrochemistry and biology. Adv Chem Phys. 2000;111:1–217. [Google Scholar]
- 60.Hine J. Hydrogen-bonded intermediates and stepwise mechanisms for proton-exchange reactions between oxygen atoms in hydroxylic solvents. J Am Chem Soc. 1972;94(16):5766–5771. [Google Scholar]
- 61.Gilli P, Pretto L, Bertolasi V, Gilli G. Predicting hydrogen-bond strengths from acid-base molecular properties. The pK(a) slide rule: Toward the solution of a long-lasting problem. Acc Chem Res. 2009;42(1):33–44. doi: 10.1021/ar800001k. [DOI] [PubMed] [Google Scholar]
- 62.Gilson MK, Sharp K, Honig B. Calculating the electrostatic potential of molecules in solution—Method and error assessment. J Comput Chem. 1988;9(4):327–335. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.