Strain solitons and topological defects in bilayer graphene

Abstract

Bilayer graphene has been a subject of intense study in recent years. The interlayer registry between the layers can have dramatic effects on the electronic properties: for example, in the presence of a perpendicular electric field, a band gap appears in the electronic spectrum of so-called Bernal-stacked graphene [Oostinga JB, et al. (2007) Nature Materials 7:151–157]. This band gap is intimately tied to a structural spontaneous symmetry breaking in bilayer graphene, where one of the graphene layers shifts by an atomic spacing with respect to the other. This shift can happen in multiple directions, resulting in multiple stacking domains with soliton-like structural boundaries between them. Theorists have recently proposed that novel electronic states exist at these boundaries [Vaezi A, et al. (2013) arXiv:1301.1690; Zhang F, et al. (2013) arXiv:1301.4205], but very little is known about their structural properties. Here we use electron microscopy to measure with nanoscale and atomic resolution the widths, motion, and topological structure of soliton boundaries and related topological defects in bilayer graphene. We find that each soliton consists of an atomic-scale registry shift between the two graphene layers occurring over 6–11 nm. We infer the minimal energy barrier to interlayer translation and observe soliton motion during in situ heating above 1,000 °C. The abundance of these structures across a variety of samples, as well as their unusual properties, suggests that they will have substantial effects on the electronic and mechanical properties of bilayer graphene.

Spontaneous symmetry breaking, where the ground state of a system has lower symmetry than the underlying Hamiltonian, occurs in systems ranging from magnetism in solids to the Higgs mechanism in high-energy physics. It leads to multiply degenerate ground states, each with a different “broken” symmetry labeled by an order parameter. In the case of a magnet, the spins locally align, creating a magnetization that plays the role of the order parameter. However, the global orientation of the magnetization can be in one of many directions, determined, for example, by the crystal axes. Locally, the system “spontaneously” chooses one such direction based on external constraints or history. Different local regions can have different orientations, and the boundary between adjacent regions is called a domain wall. Mathematically, this boundary takes the form of a soliton that is finite in width but free to move. Other, more complex topological structures are also possible.

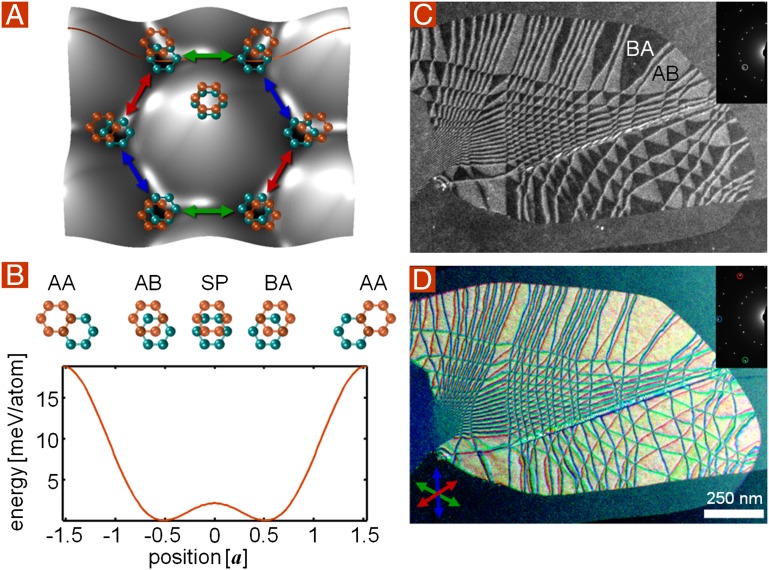
The stacking of two graphene sheets exhibits analogous physics. Fig. 1A shows the energy of bilayer graphene as a function of the relative in-plane displacement u between the two graphene sheets, which we will use as a continuous-order parameter (1). The energy as a function of u is maximal in the high-symmetry state (u = 0) where one layer is directly on top of the other, called AA stacking (Fig. 1 A, center and B, edges). Away from u = 0 are six energy minima, each one with a different direction of the order-parameter vector, and each having magnitude |u| = a, where a is graphene’s bond length. These minima correspond to states that put one of the first layer’s sublattice atoms (A or B) directly on top of its opposite sublattice atom (B or A) in the second layer, called AB or BA stacking, respectively, or collectively called Bernal stacking. Adjacent minima can be most easily traversed by the local change Δu in the order parameter across an AB-to-BA stacking boundary. As shown in Fig. 1A, these translations come in three types depending on the direction of Δu, which we label with colors red, green, or blue. Note that three of the six states shown in Fig. 1A correspond to the same locally distinct broken symmetry (either AB or BA stacking) because a lattice translation vector will transform one member of the trio to another. However, they are globally distinct in that, to go from one to the other, a relative shift in the registry of the two layers is required. The order parameter u captures both of these aspects.

Fig. 1.

The energy landscape for interlayer translation in bilayer graphene leads to certain allowed boundary transitions. (A) van der Waals energy landscape for translating one graphene layer across another (data from ref. 1) with the corresponding orientations of the two layers shown schematically in orange and teal. The central location corresponds to AA stacking, having an order parameter vector u = 0. Around this are six energy minima where |u| = a, corresponding to Bernal-stacked graphene. The two mirror-symmetric phases of Bernal-stacked graphene, AB and BA, are related to each other by three distinct low-energy translation directions |Δu| = a indicated by red, green, and blue arrows. (B) A horizontal line cut through the energy landscape in B, along an armchair direction, reveals that AB is connected to BA through a saddle point (SP) having an energy of 2.1 meV/atom, a factor of 10 lower than the energy of AA-stacked graphene. Across this cut, from left to right, the upper graphene sheet, shown in orange, translates to the right with respect to the lower sheet, shown in teal. (C and D) Dark-field TEM images of bilayer graphene, imaged through an aperture in the diffraction plane, as indicated by circles in the inset. The bilayer graphene is supported by approximately two additional graphene sheets at 16° and 31° relative to the bilayer, which are invisible when imaging although the selected diffraction angles. (C) At nonzero sample tilt, selecting electrons from the [−1010] family of diffraction angles enables us to distinguish AB (gray) from BA (black) domains. (D) Three DF-TEM images taken from the [−2110] diffraction angles indicated in the inset are overlaid in red, blue, and green. Imaged this way, each line is an AB–BA domain boundary, with its color indicating the armchair direction along which the relative translation between graphene layers occurs.

These AB and BA phases can be directly imaged using dark-field transmission electron microscopy (DF-TEM) (2, 3). An aperture in the diffraction plane of the electron microscope selects electrons scattered through a narrow range of diffraction angles, distinguishing between regions of different crystallographic symmetry (4). Imaging through the [−1010] diffraction angles reveals the AB and BA stacking domains, whereas imaging using the [−2110] spots visualizes boundaries between stacking domains. Fig. 1 C and D show a graphene bilayer grown by chemical vapor deposition (CVD) (5) and supported by approximately two additional graphene sheets at 16° and 31° relative to the bilayer, imaged using these techniques. In Fig. 1C, a striking hexagonal array of AB and BA domains is observed. The direction of the order parameter change, Δu, across each domain boundary is shown in the color-composite image in Fig. 1D. Here, images from three of the [−2110] diffraction spots have been colored red, blue, and green, respectively, to match the translations shown in Fig. 1A and summed (Supporting Information, Figs. S1 and S2, gives more details).

Using these images, we can immediately determine whether a boundary is a tensile-strain boundary (Δu perpendicular to the boundary), a shear-strain boundary (Δu parallel to the boundary), or somewhere between. If we assume the translation between an AB and a BA region does not traverse an energetically costly AA-stacked configuration (which we demonstrate to be true with atomic resolution measurements below), then our measurements uniquely determine the strain, Δu, across each boundary. Furthermore, these can be summed to obtain the global interlayer biaxial (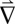u) and rotational (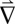× u) strain in the sample. In Fig. 1D, most of the translation vectors are parallel to their boundaries, indicating shear; the observed pattern results from a global relative interlayer rotation between the two graphene sheets. Thus, the observed triangular pattern [which has been previously observed in trilayer graphene (6) and graphite (7)] is similar to a Moiré pattern with the notable difference that, locally, the lattice has relaxed into commensurate Bernal-stacked phases of constant u separated by incommensurate domain walls, each associated with one of the three interlayer translation vectors Δu.

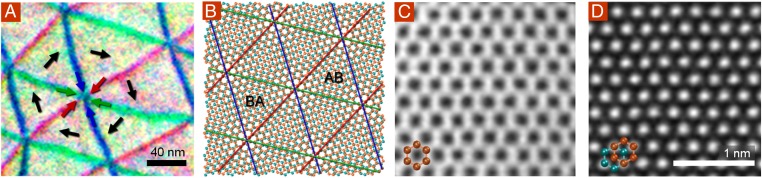
Topological point defects are also evident in Fig. 1C and D. Fig. 2A shows an enlarged region of the color-composite image from Fig. 1D where three domain walls intersect. Superimposed in black are the inferred directions of the order parameter u for each domain, based on the transitions. The order parameter u rotates by 2π on a path that encloses the intersection point. This is thus a topological defect analogous to, for example, a vortex in a superconductor. As with a superconducting vortex, the order parameter must vanish at the center, corresponding here to AA-stacked graphene (u = 0). A topologically equivalent Moiré structure is shown in Fig. 2B; at the center of such structures, AA-stacked graphene (u = 0) is seen.

Fig. 2.

Topological point defect with AA-stacked graphene at its center. (A) An enlarged region of Fig. 1D, showing a topological defect where six domains meet. Each domain (white) is associated with a different order parameter vector, u (black), and each boundary corresponds to an interlayer translation, Δu, as one traverses the boundary in the clockwise direction, shown in red, green and blue. (B) Schematic of two graphene sheets rotated relative to each other, showing a Moiré pattern that is topologically equivalent to the structure in Fig. 2A. Alternating AB- and BA-like regions surround an AA-like core. (C) An atomic-resolution STEM image of the center of a region like that in Fig. 2A where six Bernal-stacked domains meet, showing that such regions exhibit the energetically costly AA stacking. In AA-stacked graphene all atomic sites are visible in a hexagonal array, as indicated by the schematic. (D) A nearby Bernal-stacked region, for reference. In Bernal-stacked graphene, only half of the lattice sites are visible—those corresponding to atoms stacked directly on top of one another, as indicated by the schematic. In C and D, respectively, three and seven frames were cross-correlated and averaged, after applying a 0.2-Å low-pass filter (far below our ∼1.3 Å probe size). Supporting Information gives raw images and details (Fig. S3).

We use fifth-order aberration-corrected annular dark-field (ADF) scanning TEM (STEM) to directly image the stacking with atomic resolution. An electron beam with a ∼1.3-Å probe size is scanned over the sample and the scattered electron intensity is recorded as a function of the beam position. Fig. 2C shows the core of a topological defect where six domains meet, showing (bright) atoms in a hexagonal lattice, as is characteristic of AA-stacked bilayer. In AA-stacked graphene, all atoms in one layer are directly above those in the other, so each atom is visible, and all have similar brightness. The surrounding AB and BA domains appear considerably different. Fig. 2D shows an example of Bernal-stacked bilayer domain, where we observe bright spots with hexagonal symmetry and a spacing of 0.25 nm, close to √3a. These spots correspond to the sites in Bernal-stacked bilayer where two atoms are stacked on top of one another; coherent scattering makes the intensity three to four times brighter than for individual atoms (8). Thus, with AA at its center and AB and BA domains surrounding, the sixfold pattern in Fig. 2A is a direct manifestation of the sixfold-degenerate energy-level landscape shown in Fig. 1A. The AA cores are very high-energy, so they effectively pin the intersections of the three lines together. We rarely observe crossings of domain boundaries that do not respect this threefold rule.

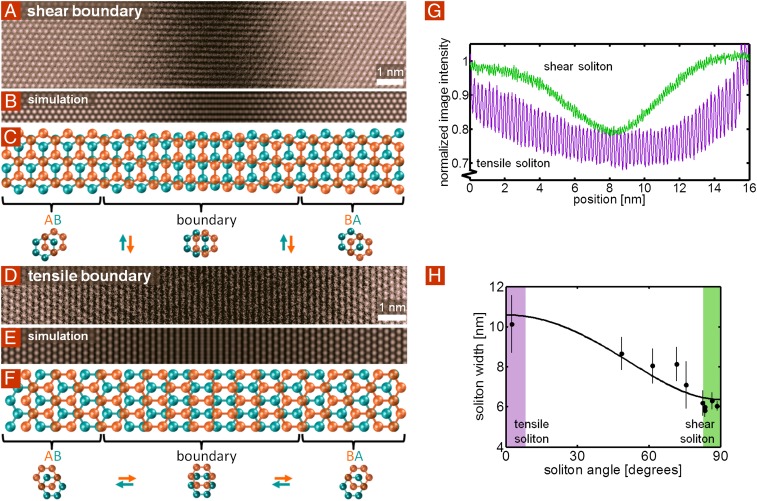
We now examine the soliton boundaries between two stacking phases with atomic resolution. STEM images of boundaries between AB and BA domains exhibiting concentrated shear and tensile strain are shown in Fig. 3 A and D, respectively. Toward the right and left sides of each image, we observe bright spots corresponding to Bernal-stacked bilayer. Toward the center of the boundary the brightness decreases, and this hexagonal pattern evolves into linear features that are horizontal for the shear boundary and vertical for the tensile boundary. This pattern results from the near-overlap of lines of zigzag atoms that occurs as the two layers translate across each other vertically and horizontally, respectively, as indicated schematically in Fig. 3 C and F. Fig. 3 B and E display corresponding simulations of STEM images using multislice quantum mechanical scattering calculations (9, 10), showing excellent agreement with the data (Supporting Information gives details).

Fig. 3.

Imaging solitons with atomic resolution. (A and D) Atomic-resolution STEM images of AB–BA domain boundaries, exhibiting interlayer shear strain and tensile strain, respectively. As one moves across the boundary from left to right, the two sheets translate relative to each other in opposite directions, as indicated by the schematics in C and F. Each image is an average of four adjacent regions along a boundary (details in Supporting Information; raw images in Fig. S4). (B and E) Simulated STEM images of shear and tensile boundaries, respectively, show good agreement with the experimental images in A and D. The atomic coordinates have been specified by the soliton solution to the sine-Gordon equation (1), discussed in Supporting Information. (C and F) Schematics showing shear and tensile boundaries, respectively (not to scale). In C, from left to right, the orange lattice translates downward, whereas the teal lattice translates upward, completing a one-bond-length armchair-direction interlayer translation from AB to BA. Similarly, in F, the orange lattice translates to the right, whereas the teal lattice translates to the left. (G) Vertical line averages of the images in A (green) and D (purple) reveal that the STEM contrast profile across the boundary is approximately Gaussian, and that the shear boundary is significantly thinner than the tensile boundary. A dark reference signal has been subtracted, and the image normalized by the average intensity of Bernal-stacked bilayer graphene. (H) FWHM for the STEM intensity profile for a few different solitons as a function of the absolute value of the angle between the interlayer-translation direction and the soliton boundary-normal. The fit is given by the equation in the text and indicates that the angular dependence of soliton width is explained by the decrease in stiffness associated with a change from tensile strain to shear strain.

The widths of the transition regions are different in the two cases. Fig. 3G shows vertical line averages of images in Fig. 3 A and D, indicating that the shear boundary is significantly narrower than the tensile boundary. For the shear boundary, the average FWHM is 6.2 ± 0.6 nm, whereas for the tensioned boundary the average FWHM is 10.1 ± 1.4 nm (Supporting Information gives details). These widths correspond to maximum strains in each layer of 0.8% and 0.5% for the shear and tensile boundaries, respectively, which occur at the center of each soliton. Fig. 3H displays the soliton width (FWHM) vs. the absolute value of the soliton angle ϕ (the angle between Δu and the boundary normal) obtained via STEM, as described in Supporting Information. The soliton width varies with angle, having a maximum FWHM of ∼11 nm at 0°, corresponding to purely tensile solitons, and decreasing to a minimum of ∼6 nm at 90°, corresponding to purely shear solitons.

The observed widths can be understood as competition between strain energy in the transition region and the misalignment energy cost per unit length of the soliton: 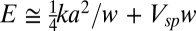, yielding an equilibrium width: 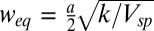. Here, k is the stiffness, V_sp is saddle-point energy per unit area in Fig. 1B, and a = 0.141 nm is the bond length in graphene. The Young’s modulus, Et = 340 N/m (11), is larger than the shear modulus Gt ∼ Et/(2(1 + υ)) = 142 N/m, where υ is the Poisson ratio, predicting that the ratio of the widths of the tensile and shear boundaries is 1.5. This is in reasonable agreement with the experimental results in Fig. 3. A more complete description is given by the two-chain Frenkel–Kontorova model (1), which predicts soliton boundaries between the domains to have width

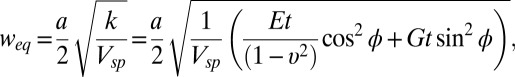where the boundary has an interlayer translation at an angle ϕ relative to the boundary normal. By relating w_eq empirically to the FWHM through STEM image simulations (Supporting Information), we fit the width-vs.-angle model to the data, choosing to treat Et as fixed at its measured value of 340 N/m (11), and taking the Poisson ratio as that measured for graphite (12), υ = 0.16; we then use V_sp and Gt as fitting parameters, and overlay the result in Fig. 3H (solid line). We obtain V_sp = 1.2 meV/atom, Gt = 130 N/m. These values are in excellent agreement with those predicted by theory—V_sp = 1–2 meV/atom (1, 13, 14), Gt = 142 N/m—and imply a line tension for the domain walls in the ∼100 pN range. We also performed width measurements on a greater number of solitons via DF-TEM, observing similar qualitative behavior in the angular dependence of width, but greater variability owing to the influence of out-of-plane corrugations in the graphene on the DF-TEM contrast across solitons, as shown and discussed in Supporting Information. Although the samples presented in the figures have a greater occurrence of shear boundaries than tensile boundaries, in general we see no strong preference for one type of boundary over the other (Supporting Information and Fig. S5 give a few additional examples).

Finally, we examine the mobility of the soliton boundaries. Fig. 4 A–C show a series of DF-TEM images taken with a large beam current (3.6 × 10⁴ e⁻⋅nm⁻²⋅s⁻¹), at 80 keV. The boundaries fluctuate as shown in Movie S1, shifting by tens of nanometers on the scale of minutes, as indicated by the arrows in Fig. 4 A–C. We also see instances where soliton boundaries undergo topological rearrangements. Fig. 4 D and E show one such example, in which two solitons having opposite translation directions, Δu, seem to have contacted each other and annihilated. Because each soliton has an energy cost associated with it, which can be eliminated if this pair combines, these solitons are attracted to each other (15) and can annihilate via an interlayer translation of the intervening domain, here labeled u₀ + Δu.

Fig. 4.

Soliton motion. (A–C) [−2110] DF-TEM images of interlayer solitons taken over the course 43 min while imaging at high beam intensity (Movie S1). Under the influence of the beam, the soliton positions fluctuate by as much as 20 nm, as indicated by the arrows. (D and E) A pair of solitons having opposite translation directions (i.e., boundaries on either side of a region that is one-bond-length-shifted from the surrounding bilayer) may annihilate each other, as seems to have happened in the 3 d between which these images were taken. In the center, where, in D, the solitons are in close proximity, they have joined and disappeared in E. (F and G) First and last frames of DF-TEM taken through a [−1010] diffraction angle at 1,000 °C and later at 1,200 °C, respectively. The boundaries between Bernal-stacking domains get shorter and straighter with time and temperature. For movies, see Movies S2, S3, S4, and S5.

Although motion occurs at high beam currents, in general, at low beam currents (80 keV, ∼3 × 10³ e⁻⋅nm⁻²⋅s⁻¹) and temperatures below 800 °C motion is rare. Above 1,000 °C, motion becomes more prevalent, as shown in Movies S2, S3, S4, and S5. The first and last frames in a temperature series from 1,000 to 1,200 °C are displayed in Fig. 4 F and G, showing that AB and BA domains anneal to form more regular structures, with shorter, straighter boundaries. In the movies, the boundaries typically move in discrete steps, which we attribute to pinning of the solitons by disorder and out-of-plane wrinkles. All of these images and movies show that these solitons are flexible and mobile, and that they can form ordered and complex patterns.

The complex and intriguing patterns of soliton boundaries observed here suggest that they will be an ideal laboratory for studying the physics of topologically protected edge states. For example, the arrays of domain walls seen in Fig. 1 are a unique kind of superlattice structure that has only just begun to be studied theoretically (16) and may be relevant for recent measurements (17, 18) and theory (19) of the electronic structure of twisted bilayer graphene. Furthermore, it may be possible to create devices where the motion of a single domain wall completely changes the conductance of a device in a manner analogous to magnetic domain wall magnetoresistive devices (20–23). These solitons may also provide an explanation for the thermoelectric response at domain walls in multilayer graphene (24), as well as for the mystery of excess subgap transport typically seen in bilayer graphene transport experiments, where a perpendicular electric field is used to open a bandgap in AB- or BA-stacked graphene (25–28). Recent theory predicts that a topologically protected 1D electronic state will form at the soliton boundary (29, 30), and these 1D conducting pathways may be the major source of conduction in these samples. The properties of these 1D states depend on the width and orientation of the domain walls (29), which the measurements above provide explicitly.

Methods

Graphene Growth and Transfer.

Large-grain (30–100 µm) graphene was grown on copper foil (13382; Alfa Aesar) by CVD using the enclosure method of Li et al. (5) using methane and hydrogen flow rates of 1–3 standard cm³/min and 60–120 standard cm³/min, respectively, at 980 °C for 2 h, then cooled. The resulting graphene is predominantly monolayer, with ∼10-µm sixfold symmetric, star-shaped bilayer and multilayer patches at many of its nucleation sites. We then use the methods of Huang et al. (4) to transfer the graphene to 200-nm nitride TEM grids (21535-10; Ted Pella), carbon grids (Q250-AR2; Quantifoil), or heatable ceramic grids (E-AHF21; Protochips).

ADF-STEM.

For STEM imaging, we used a Nion Ultra-STEM100, operated at 60 kV. Imaging conditions were similar to those used in refs. 4 and 31. Using a 25-mrad convergence angle, our probe size was close to 1.3 Å. The images presented in Figs. 2 and 3 were acquired with a low-angle annular dark-field detector with acquisition times between 16 and 40 μs per pixel. Samples were baked for >10 h at 130 °C in ultra-high vacuum before loading into the microscope.

DF-TEM.

TEM imaging and diffraction were conducted using a FEI Technai T12 operated at 80 kV. Acquisition times for dark-field TEM images were 20 s per frame. We used displaced-aperture DF-TEM for the images in the main text. For in situ heating, we used electrically contacted precalibrated Protochips Thermal E-chips with an Aduro sample holder, which allow heating up to 1,200 °C.

Multislice Image Simulations.

We simulated ADF-STEM images using numerical scattering calculations in E. J. Kirkland’s multislice code. In this code, a full quantum mechanical multiple scattering simulation of electrons is propagated through multilayered atomic membranes, producing quantitative simulations of dark-field detector signals (9). Atomic scattering factors are characterized by a 12-parameter fit of Gaussians and Lorentzians to relativistic Hartree–Fock calculations (10).