Abstract
Phanerozoic levels of atmospheric oxygen relate to the burial histories of organic carbon and pyrite sulfur. The sulfur cycle remains poorly constrained, however, leading to concomitant uncertainties in O2 budgets. Here we present experiments linking the magnitude of fractionations of the multiple sulfur isotopes to the rate of microbial sulfate reduction. The data demonstrate that such fractionations are controlled by the availability of electron donor (organic matter), rather than by the concentration of electron acceptor (sulfate), an environmental constraint that varies among sedimentary burial environments. By coupling these results with a sediment biogeochemical model of pyrite burial, we find a strong relationship between observed sulfur isotope fractionations over the last 200 Ma and the areal extent of shallow seafloor environments. We interpret this as a global dependency of the rate of microbial sulfate reduction on the availability of organic-rich sea-floor settings. However, fractionation during the early/mid-Paleozoic fails to correlate with shelf area. We suggest that this decoupling reflects a shallower paleoredox boundary, primarily confined to the water column in the early Phanerozoic. The transition between these two states begins during the Carboniferous and concludes approximately around the Triassic–Jurassic boundary, indicating a prolonged response to a Carboniferous rise in O2. Together, these results lay the foundation for decoupling changes in sulfate reduction rates from the global average record of pyrite burial, highlighting how the local nature of sedimentary processes affects global records. This distinction greatly refines our understanding of the S cycle and its relationship to the history of atmospheric oxygen.
Keywords: Phanerozoic oxygen, sulfate-reducing bacteria
The marine sedimentary sulfur isotope record encodes information on the chemical and biological composition of Earth’s ancient oceans and atmosphere (1, 2). However, our interpretation of the isotopic composition of S-bearing minerals is only as robust as our understanding of the mechanisms that impart a fractionation. Fortunately, decades of research identify microbial sulfate reduction (MSR) as the key catalyst of the marine S cycle, both setting the S cycle in motion and dominating the mass-dependent fractionation preserved within the geological record (1, 3, 4). Despite the large range of S-isotope variability observed in biological studies (4–6), attempts to calibrate the fractionations associated with MSR are less mechanistically definitive (7, 8) than analogous processes influencing the carbon cycle (9, 10). What is required is a means to predict S isotope signatures as a function of the physiological response to environmental conditions (e.g., reduction–oxidation potential).
Microbial sulfate reduction couples the oxidation of organic matter or molecular hydrogen to the production of sulfide, setting in motion a cascade of reactions that come to define the biogeochemical S cycle. In modern marine sediments, sulfide is most commonly shuttled back toward sulfate through oxidation reactions (biotic and abiotic) or scavenged by iron and buried as pyrite (11). It is the balance of oxidation reactions and pyrite burial that influences geological isotope records, which in turn carry historical information on the oxidation state of Earth’s biosphere. Such records generally are thought to indicate that oxidant availability has increased with each passing geologic eon (12). Although playing prominent roles in sedimentary redox cycles (13), oxidation reactions carry only modest S isotopic fractionations (14, 15).* In typical modern marine sediments, the oxidative region of aerobic organic carbon remineralization is separated from the zone of sulfate reduction (where MSR takes place) by an intermediate layer in which both sulfide oxidation and sulfur disproportionation occur (16, 17). Despite sulfur recycling across that boundary layer, the sulfur that is eventually buried as pyrite predominately reflects the isotopic fractionation associated with MSR (18).
Numerous studies show a correlation between microbial sulfate reduction rate (mSRR; SI Text) and the expressed magnitudes of the MSR S isotopic fractionations (19–22). The mSRR depends on a suite of physiological controls (i.e., metabolic enzymes) (23) having variable efficiencies in response to environmental conditions (e.g., nutrient availability, redox potential, etc.; refs. 8 and 24). Such reactions can be presumed to be first-order with respect to a limiting reactant (SI Text and refs. 25 and 26). In the case of MSR, either the electron acceptor (sulfate; ref. 7) or the electron donor (generally, organic carbon (OC); refs. 19, 20, 27, and 28) plays this role. It has been hypothesized that since the Archean–Proterozoic boundary sulfate (oxidant) limitation has not occurred in the water column, but rather has been restricted to significantly below the sediment–water interface. This is consistent with estimates through the Proterozoic and Phanerozoic Eons (29) that suggest seawater sulfate concentrations in excess of the physiologically inferred minimum threshold for MSR (30). It follows that the quantity and quality of OC delivery to the zone of sulfate reduction most often dictates sulfate reduction rates where sulfate is abundant, and consequently play the larger role in determining the sulfur isotope record.
The most direct experimental means of studying the metabolic rate of a bacterial population is to maintain the culture in a chemostat (chemical environment in static). In a chemostat, the input concentration of the limiting substrate (e.g., micronutrient, electron donor, or electron acceptor) dictates the biomass yield (i.e., new biomass per mass substrate used), whereas turnover time of the reactor [dilution rate (D), time−1] dictates growth rate (SI Text and ref. 25). It follows that the mSRR (specifically, the rate of reduction per unit biomass) scales with the availability of the limiting nutrient, and thus with D (19, 25). Limited previous experimental work with open and semiopen experimental systems hints that mSRR inversely correlates with fractionation of the major S isotopes (34S/32S) (19, 31, 32)—a prediction that is reinforced by measurement of the same relationship in modern marine sediments (17, 22). However, the limited range of mSRRs previously explored does not adequately capture the vast range of rates inferred from marine sediments (33–35). In this work we present an empirical calibration of a ∼50-fold change in mSRR, nearly doubling the previous experimental ranges. We also target the minor isotope, 33S, in addition to targeting 34S fractionations; this supplies another dimension for interpreting the geologic record. We then apply this calibration to Phanerozoic isotope records to reveal how secular changes in S isotopic fractionation reflect a temporal history of paleoredox conditions. This enables us to reassess the burial of pyrite and associated changes in environmental conditions across the Phanerozoic Eon.
Results and Discussion
We conducted a suite of continuous-culture experiments with the model sulfate reducing bacterial strain Desulfovibrio vulgaris Hildenborough (DvH). Strain DvH is among the most well-studied sulfate reducers and is genetically tractable (36, 37). Although DvH is nominally a nonmarine strain, the concentration of sulfate in the chemostat was always near modern marine levels (28 mM) and well above known sulfate affinity constants (38). The sole electron donor (lactate) was always the limiting nutrient in these experiments and was provided at a stoichiometric 1:2 or 1:20 ratio with sulfate (Materials and Methods and SI Text).
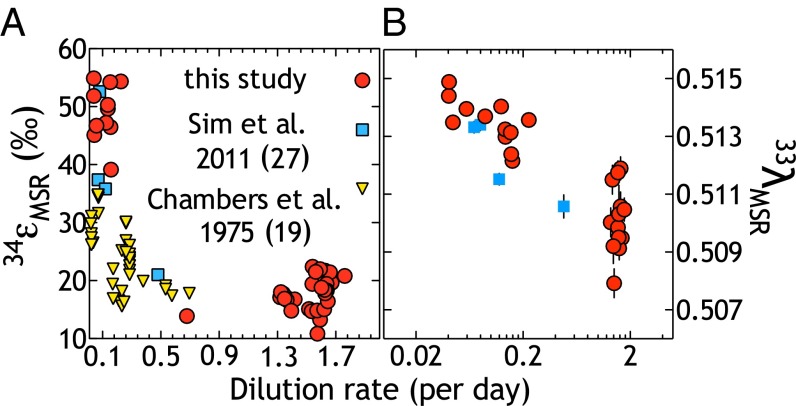
These experiments show that MSR isotope fractionation is strongly inversely dependent on electron donor concentration (Fig. 1). In detail, mSRR follows a first-order nonlinear relationship to D (Fig. 1): as we decrease D, lactate availability and mSRR decline, whereas 34εMSR increases. [The values of 34εMSR and 33λMSR refer to the isotopic differences between the sulfate and sulfide from chemostat experiments (SI Text), whereas 34εGEO and 33λGEO refer to those differences calculated from sulfate and pyrite sedimentary records as time-binned averages (Dataset S1, Table S1, and Eqs. S4–S7). Further definitions are presented in SI Text.] These open-system experiments (Fig. S1 and SI Text) allow for the direct calculation of fractionation factors from the isotopic composition of output sulfate and sulfide (39), without having to apply Rayleigh distillation models addressing closed system (batch) dynamics (40). We demonstrated conservation of elemental and isotopic mass balance throughout the entire experiment (Dataset S1) via the direct measurement of SO42−, H2S/HS−, S2O32−, and S3O62−, the latter two of which were always below detection (2.5 μM) but have been previously detected in semiopen system experiments (31).
Fig. 1.
Multiple sulfur isotope fractionation as a function of dilution rate in chemostat experiments. In these experiments, growth and sulfate reduction rates scale inversely with organic carbon (lactate) delivery rate, expressed here as dilution rate (D, hours−1). This rate dictates the magnitude of major (A) and minor (B) isotope fractionation between sulfate and sulfide. Error bars in A are smaller than the symbols (2σ = 0.3‰), and vertical error bars in B are 2σ SDs. Other studies cited refer to Chambers et al. (19) and Sim et al. (27).
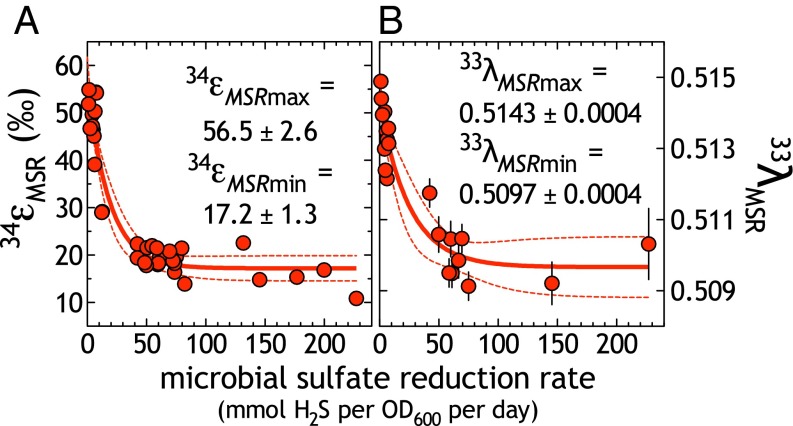
Our data complement and significantly extend previous open-system experiments (8, 19, 27, 41, 42). Over a ∼50-fold change in mSRR (Fig. 1 and Figs. S2 and S3), 34εMSR ranged from 10.9 to 54.9‰ (Fig. 1A), whereas 33λMSR varied from 0.5079 to 0.5144 (Fig. 1B). In addition to aiding in our understanding of environmental/geological records (discussed below), these data allow for an empirically derived fractionation limit for DvH under conditions of electron donor limitation. We apply a nonlinear regression model (43) based on a pseudo-first-order rate expression, appropriate for a reaction in which rate depends on the concentration of a single reactant (Eqs. S8 and S9) (26, 44). The results of the model illustrate the capacity of MSR to exceed the classic 47‰ limit for 34εMSR (Fig. 2 and ref. 45), here suggesting an upper limit of 56.5 ± 2.6‰. The same nonlinear regression model (Eq. S9) predicts a minor isotope limit (in 33λ) at 0.5143 ± 0.0004. Given that our experiments were performed with an axenic population of sulfate reducers, we can definitively rule out contributions from intermediate S-oxidizing or disproportionating organisms (46). However, although the magnitudes of these fractionations exceed the canonical MSR limits (34ε = 47‰), they do not reach the low-temperature equilibrium predictions between sulfate and sulfide in 34ε (at 20 °C, 34ε = 71.3‰; ref. 40).
Fig. 2.
Demonstration of new fractionation limits under electron-donor limitation. A nonlinear regression model (Eqs. S8 and S9) was used to calculate the empirical fractionation limit in (A) 34εMSR (r2 = 0.9151) and (B) 33λMSR (r2 = 0.8905), as a function of mSRR (see also Fig. S2). Bold lines indicate the best-fit estimates with 95% confidence intervals as the thin dashed lines (34εMSR: 51–62‰; 33λMSR: 0.5135–5151). Inset values are the calculated fitting parameters (along with kMSR_ε = 0.054 ± 0.012 and kMSR_λ = 0.0395 ± 0.0158) with SEs used in calculations for 95% confidence interval.
Decoupling the Isotopic Effects of Sulfate Reduction Rates from Pyrite Burial Records.
In modern marine sediments, OC availability is strongly tied to sedimentation rate (47–49). Faster sedimentation (such as in river deltas or on continental shelves) generally leads to more efficient delivery of OC below the depth of oxygen penetration, into the zone of sulfate reduction. (Extreme sedimentation rates deviate from this prediction and can lead to OC dilution.) The absolute flux of OC also scales directly with primary production. The balance of these processes dictates where sulfate reduction occurs with respect to the sediment–water interface, as well as how much sulfate ultimately is reduced (50). Because some fraction of the resulting sulfide will be buried as pyrite—with concomitant release of oxidant to the ocean-atmosphere system—it is critical to determine how the mSRR-dependent isotope fractionation (34εMSR and 33λMSR) influences the S-isotopic records of pyrite relative to coeval sulfate (34εGEO and 33λGEO).
Analogous to the influence of lactate on mSRR in our experimental system, the availability of greater quantities of more highly labile OC to the sulfate reduction zone in modern sediments translates to an increase in sulfate reduction rates, with a corresponding decrease in the magnitude of 34εMSR (24, 35, 51). Conversely, decreases in sulfate reduction rates down a sediment column owing to the modeled loss of OC quality and quantity are consistent with observations that 34εMSR increases (47, 52). Together these ideas describe the concept of net sedimentary sulfate reduction rate (sedSRR; moles of S per square meter per year). The sedSRR, because it integrates the depth-dependent rate through the entire zone of sulfate reduction, must encompass a depth-weighted average of the variable 34εMSR as well as be tightly linked to the initial OC delivery to the sediment–water interface. Data from the modern sea floor (18, 22, 53) confirm the expected inverse relation between bulk in situ sedSRR and the magnitude of the net sedimentary S isotope fractionation (34εGEO).
The concept of sedSRR also contains another important distinction from mSRR. In most environments, measures of microbial population density are lacking, as are measures of the metabolically available OC compounds. Our experimental system quantifies these parameters and enables direct calculation of mSRR. However, in the environment, the useful metrics are the bulk sedSRR and the global sulfate reduction rate (gSRR, moles of S per year). The sedSRR is converted to gSRR through an areal normalization and a reoxidation coefficient (1, 17); further details are presented in Table S2. It is gSRR that is necessary for determining long-term oxidant budgets and global pyrite burial.
We propose that it is possible to decouple the isotopic effects caused by variable sedSRR from the ultimate sedimentary record of S isotopes. For example, under iron-replete conditions, net pyrite burial may increase as a result of more sulfide production and/or an increased sulfide scavenging efficiency by iron (i.e., less oxidation), but at a constant sedSRR. Alternatively, pyrite burial could increase in response to a higher sedSRR, if it were driven by a higher flux of metabolizable OC to the sedimentary zone of sulfate reduction. This comparison can also be extended to include the roles for weathering and changes in the abundance of shallow-water environments (shelf area). We posit that it is possible to differentiate between these scenarios and determine the ultimate control (tectonics vs. OC) on pyrite burial at the global scale: The first case would maintain a constant 34εGEO and 33λGEO, whereas varying sedSRR would be recorded by a change in the fractionation patterns.
Interpreting Phanerozoic Records.
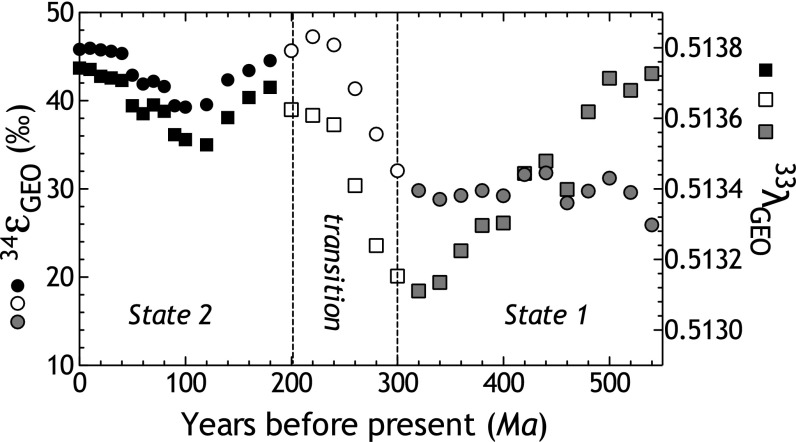
Phanerozoic compilations provide a context for evaluating the potential variability in sedSRR through time. Records of 34εGEO and 33λGEO from Phanerozoic sedimentary basins provide a time-series approximation of the mean isotopic difference between coeval sulfates and sulfides (Fig. 3 and Table S1) (13, 54). In parallel, we use recent estimates for the areal extent of continental shelf and abyssal ocean across Phanerozoic time (Table S1) (55, 56). Assuming that the physical processes dictating OC delivery to sediments today hold throughout the Phanerozoic, shelf environments are generally expected to be OC-rich and support higher sulfate reduction rates than deep-water settings (17, 22). This is reinforced by modern observations, where in shallow water sediments (<1,000 m deep), the area-weighted average sedSRR is 96 μmol SO42–⋅cm–2⋅y−1, whereas in deep-water sediments (>1,000 m deep) it is ∼1 μmol SO42–⋅cm–2⋅y−1.
Fig. 3.
The Phanerozoic S isotope record. SI Text gives compilation, binning strategy, and data handling.
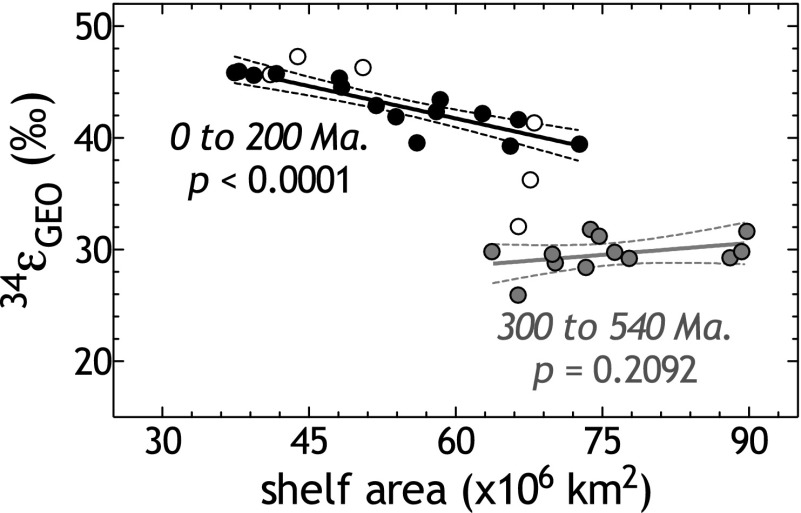
It has long been appreciated that the 34εGEO record through the Phanerozoic carries a definitive structure (13, 57, 58)—the earliest Paleozoic has mean fractionations of ∼30‰ and transitions through the Permian and Triassic to a Meso-Cenozoic average near ∼45‰ (Fig. 3). This temporal distinction also exists for estimates of 33λGEO (Fig. 3) (54). Interestingly, by comparing both isotope metrics (34εGEO and 33λGEO) with estimates of shelf area, we are able to resolve temporal patterns (Fig. 4 and Fig. S4). From our analysis of the compiled datasets (SI Text), we find that as shelf area increases, both 34εGEO and 33λGEO tend to decrease (Fig. 4 and Fig. S4). Closer examination of these data illustrates, however, that the statistical significance of these correlations rests largely on the tightly coupled behavior in the Meso-Cenozoic. In contrast, the Paleozoic has a less coherent relationship (Fig. 4 and Fig. S4). We thus interpret the multiple S isotope record as being divisible into two states offset by a transition. The first state is the early Paleozoic (540–300 Ma), where 34εGEO is lower, shelf areas are larger, and 33λGEO is highly variable; the second state is the Meso-Cenozoic (200–0 Ma), where 34εGEO and 33λGEO are larger and associated with less shelf area. The transition spans at least the Permian and the Triassic (ca. 300–200 Ma).
Fig. 4.
Relating Phanerozoic shelf-area estimates to isotopic records. Data are binned and shaded as in Fig. 3, with the Permian–Triassic in white to highlight this transition. The P values are for the 0–200- and 300–540-Ma intervals. Significant covariance (P < 0.0001) between shelf area isotope metrics only persisted in the last 200 Ma. A similar relationship exists for 33λGEO relative to shelf area (Fig. S4), though a more robust interpretation of 33S records will require a larger geologic database than is currently available.
Although there is relatively less sulfur isotopic variability in the Meso-Cenozoic compared with the Paleozoic, the interval from the Cretaceous to the present (ca. 100–0 Ma) shows increases in 34εGEO and 33λGEO of 7‰ and ∼0.0002, respectively (Fig. 3). [The opposite trends, and by analogy the converse arguments, apply to the Mesozoic interval from 200 to 100 Ma (Fig. 3)]. In our conceptual framework, this may represent a constant sedSRR with a decreasing shelf area (thereby decreasing both gSRR and pyrite burial), or it may represent a decrease in sedSRR with concomitant decline in shelf area. We first consider the case of constant sedSRR: Here, a ∼10% decrease in pyrite burial is required to accommodate the 7‰ increase in 34εGEO (SI Text). Such a fluctuation in pyrite burial is reasonable. However, changes in pyrite burial cannot affect 33λGEO, and as such, the observed variance in 33λGEO means that a change in shelf area alone (as it relates to gSRR) cannot explain the Meso-Cenozoic S isotope record (i.e., sedSRR also must have changed).
As an alternative to a change only in shelf area, our experimental data provide a means to test the second hypothesis: variable sedSRR. The sediment data for 33λGEO vs. 34εGEO through the Meso-Cenozoic are statistically within the relationship extracted from our chemostat data (33λMSR vs. 34εMSR; Fig. S5). This suggests that the dominant control on fractionation is sulfate reduction, and that the geologic data can be interpreted in the context of where they fall on the slope-rate relationship of MSR (Fig. S5). The isotopic record of the Meso-Cenozoic corresponds to an estimated mean 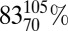 variation in sedSRR if based on our experimentally determined 34εMSR-rate relation, or a mean
variation in sedSRR if based on our experimentally determined 34εMSR-rate relation, or a mean 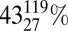 variation in sedSRR if based on the 33λMSR-rate relation [Fig. 5, Fig. S4, and SI Text; 34εMSR- or 33λMSR-derived mSRR is converted to sedSRR by using the Plio-Pleistocene as a reference and assuming that the scaling relationship is constant over time (SI Text)].
variation in sedSRR if based on the 33λMSR-rate relation [Fig. 5, Fig. S4, and SI Text; 34εMSR- or 33λMSR-derived mSRR is converted to sedSRR by using the Plio-Pleistocene as a reference and assuming that the scaling relationship is constant over time (SI Text)].
Fig. 5.
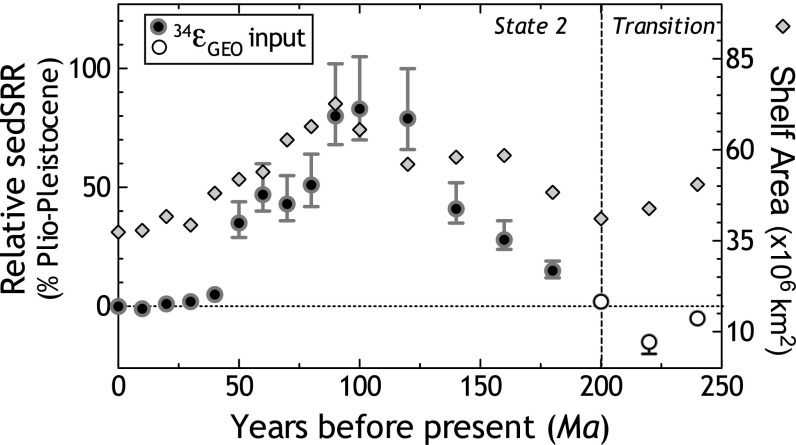
Calculated changes in sedimentary sulfate reduction rates over the Meso-Cenozoic. There is a statistically significant relationship between the calculated relative change in sulfate reduction rate and shelf area over the last 200 Ma, with a Cretaceous maximum nearly 40–80% higher than the Plio-Pleistocene average. Before 200 Ma, rate predictions from 34εGEO and 33λGEO are not always convergent or statistically robust (Fig. S4). The sedSRR calculated using the 33λGEO as input is presented in Fig. S4 but should be interpreted with care given the modestly sized dataset underpinning Phanerozoic predictions (54).
We postulate that synergistic changes in sedSRR and shelf area work together to explain the Meso-Cenozoic S isotope record. The pattern of change in sedSRR between 200 Ma and 0 Ma is also significantly correlated to the variability in shelf area over that same interval (Fig. 5 and Fig. S4). This implies that sedSRR and shelf area are at least partially inseparable variables, although the underlying coupling between them is not immediately clear. Importantly, an increase in sedSRR is not simply an increase in the molar flux of sulfate reduction, proportional to increased shelf area. An increase in sedSRR requires a change in the local mSRR integrated in a local sediment column. This must signal a response to availability of the limiting reactant—in this case, OC—either via its quantity or quality delivered to the sedimentary zone of sulfate reduction. We hypothesize that changes in the absolute flux of nutrients (59) to shelf environments is influencing the location and intensity of primary productivity, changing the delivery of OC to the sediments, and influencing the sedSRR. In this way, sedSRR joins the many other sedimentary biogeochemical processes known to respond to varying nutrient regimes (60). Further refining the structure of the Meso-Cenozoic record may provide critical insight into what processes are playing a prominent role in setting sedSRR, and we consider the consequences of this prediction below. However, we first consider the different patterns apparent in the Paleozoic records.
Our mechanistic understanding of the S isotope record of the last 200 Ma does not explain the 33λGEO–34εGEO relationship of the Paleozoic. Compared with the mid-Cenozoic, the early-mid Paleozoic (540–300 Ma) records a similar variance in 34εGEO values (∼6‰ around an era mean of ∼30‰), but three times the variability in 33λGEO (a continuous decrease of ∼0.0008; Fig. 3). This results in a significant departure of the Paleozoic from the 33S to 34S slope-rate relationship that defines the last 200 Ma (Fig. 4 and Fig. S5). The lower overall 34εGEO during the Paleozoic (∼30‰), if paired with the lowest Paleozoic 33λGEO from that same interval (Pennsylvanian; Fig. S4), may indeed relate to an elevated sedSRR and greater areal extent of shallower sea floor (Fig. 4). However, the failure of the Paleozoic data to plot on the 33λMSR vs. 34εMSR line (Fig. S5) not only undermines any confidence in applying our experimental calibration to this earlier interval (SI Text), it also is consistent with the observed weak relationship between the 34εGEO and 33λGEO data to shelf area (Fig. 4). This suggests that the general decoupling of 34εGEO from 33λGEO within the Paleozoic is not readily attributable only to changes in sedSRR. The breakdown of the observed relationships that applied in the Meso-Cenozoic suggests that, for the Paleozoic, a conceptual model that ascribes changes in 34εGEO and 33λGEO to a codependent relationship between sedSRR and shelf area is insufficient. Because fluctuations in 33λGEO for the Paleozoic are largely independent of changes in 34εGEO, there must be additional forcings.
Modeling studies illustrate how such an isotopic decoupling can be produced, either through an increase in reoxidative fluxes and associated processes (61) or through non-steady-state behavior (62). The former may seem unlikely given lower estimated oxygen partial pressure (pO2) during the first two-thirds of the Paleozoic (63). However, lower pO2 also implies a sulfate reduction zone closer to the sediment–water interface, or perhaps within the water column. Under these conditions, the delivery of oxidant to the sulfate reduction zone is no longer diffusion-limited, and as a result reoxidation reactions may be fractionally more important despite lower overall pO2. This includes both classic sulfide oxidation [at the expense of oxygen, nitrate, manganese (IV) oxides, and iron (III) oxide-hydroxides] as well as disproportionation reactions. Both have been tentatively shown to produce a negative slope of the 33λA–B vs. 34εA–B isotope relationship (15, 61). The shallow slope of the Paleozoic 33λGEO vs. 34εGEO data suggests that this opposite isotopic directionality partially is expressed and preserved (64). A change in the location and flux through reoxidation reactions is also dependent on the proximity to iron (water column vs. sediment), given that pyrite formation is a terminal sink (i.e., reoxidation inhibitor) for aqueous sulfide (65). Non-steady-state behavior of the Paleozoic S cycle is also possible and necessarily relates to seawater sulfate concentrations; however, current estimates suggest Paleozoic sulfate was abundant enough to circumvent such direct, first-order microbial control on fractionation (29). We therefore favor the explanation that a fundamentally different zonation of the paleoredox boundary in the Paleozoic decoupled the controls on S isotopes from sedimentary processes (sedSRR) and shelf area effects. Although speculative, this idea is testable using modern environments with strong redox gradients.
Equally as intriguing as the difference between the early Paleozoic and the last 200 Ma is the isotopic transition captured during the Permian and Triassic (Fig. 3 and Fig. S4). The generally weak correlations between 34εGEO and 33λGEO within the Paleozoic are followed by a 15‰ increase in average 34εGEO and a 0.0005 increase in 33λGEO. This implies a major state change to the global biogeochemical S cycle across 100 Ma spanning the Permo-Triassic boundary. Complementary geochemical metrics (δ13C, δ18O, and 87Sr/86Sr) also record major changes as Earth transitioned from the later Paleozoic to late Triassic (66). A recent statistical treatment elegantly points to the assembly and breakup of Pangaea as the explanation for this state change (56). Pangaea formed during the end of the Paleozoic and began to rift during the Triassic (67). This clearly relates to shelf area (55), but also affects primary production (OC) through the effect of continental weathering on nutrient budgets (68). Although this transition in the S cycle encapsulates the Permo-Triassic boundary, it began tens of millions of years before the Permian–Triassic extinction. Such a protracted time scale for the isotopic transition (from 300 to 200 Ma) may implicate the possible cause as a change in the ratio of S to Fe from rivers (65) associated with a Carboniferous increase in pO2 (63).
Conclusions
We propose that changes in sulfate reduction rates in marine sediments, rather than global pyrite burial, dictated S isotope records over the last 200 Ma. The post-Triassic geological record suggests that sedSRR increased to a mid-Cretaceous apex and then slowed again over the last 100 Ma (Fig. 5). What, then, controlled sedSRR? During this interval our estimates of sedSRR correlate strongly with estimates for shelf area (Fig. S4B). To the degree that global shelves capture weathering fluxes and modulate nutrient delivery to primary producers, they may not only dictate the quantity and quality of organic matter reaching the zone of sulfate reduction, but they also help dictate the position of this zone with respect to the sediment–water interface. Thus, if the combination of OC delivery and sedimentation rate controls sedSRR, marine sedimentary S isotope compositions may reflect a combination of Meso-Cenozoic productivity and shelf area. For this relationship to hold (i.e., to maintain the direct connection to shelf area), it requires that pO2 be elevated in the Meso-Cenozoic relative to the early/mid-Paleozoic (63), because it must relegate the locus of sulfate reduction to be (on average) below the sediment–water interface. Encouragingly, this provides a facies-testable hypothesis, applicable to high-resolution datasets from Phanerozoic sections where multiple biogeochemical isotope proxies are measurable and interpretable (69).
The Paleozoic 33λGEO vs. 34εGEO relationship requires significant contribution from processes other than changing OC delivery rates or total shelf area. As such, building a quantitative understanding of the Paleozoic sulfur cycle remains difficult. The disagreement between Paleozoic sedimentary data and our experimental calibration leaves room for other S metabolisms to contribute significantly to the observed S fractionations (biotic and abiotic sulfide oxidation, as well as disproportionation). Indeed, if a major difference between the Paleozoic and Meso-Cenozoic is the locality and magnitude of sulfide reoxidation—the water column in the Paleozoic vs. the sediments in the Meso-Cenozoic—then the delivery of reactive iron to the zone of sulfate reduction (55, 70) will determine whether most iron sulfides are syngenetic or diagenetic. This in turn influences the net pyrite burial flux and the balance of global oxidants. Further measurements and modeling are required to define these fluxes over both eras. Still, we can state with some confidence that recent multiple S isotope records do not require changes in pyrite burial over the last 200 Ma. Recent sediments carry a detailed and rich repository of small-scale microbial activities, and the magnitude of overall S fractionations likely reflects global oxidant budgets working in tandem with major tectonic changes.
Ultimately it is the reduction potential trapped in pyrite and organic matter—rather than the rate of sedimentary sulfate reduction—that influences Earth’s surface oxidant budget on billion-year time scales. Our hypotheses suggest that pyrite burial flux (and by extension its contribution to pO2) has not changed dramatically in recent times. Conversely, changes in pyrite burial flux remain a potentially critical control on the oxidant budget during the first half of the Phanerozoic. Continued measurements of geological materials (marine pyrites, sulfates, and terrestrial deposits), coupled with additional microbial experimentation and biogeochemical modeling, promise to yield further insight into the behavior of the S cycle over Earth’s history.
Materials and Methods
An experiment with DvH in a custom-built chemostat was run with lactate as the sole electron donor and rate-limiting nutrient for sulfate reduction. The dilution rate was varied over 43-fold (D ∝ mSRR), with measurements of the following biological, geochemical, and isotopic parameters on all samples (Dataset S1): temperature, pH, dilution rate, cell density, sulfide production rate (the sole detectable sulfate reduction product), acetate production rate, 33α and 34α of sulfate and sulfide, and cell density. By measuring the difference between the S-isotope compositions of sulfate and sulfide, and because S-mass balance is closed with these two pools alone (i.e., no thionates detected), we may directly calculate the 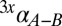 and
and 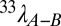 . Specific growth rate is calculated by measuring the dilution rate and the rate of change in optical density between time points (Dataset S1). The nonlinear regression models (based on pseudo-first-order kinetics) are applied to the experimental data,34εMSR or 33λMSR vs. mSRR, allowing us to calculate theoretical 34εMSRmax and 33λMSRmax, along with corresponding fitting parameters, SEs, and 95% confidence interval (Fig. 2). We compare between models by examining the goodness of fit from each model (Fig. S3). The resultant expressions relate a measured isotopic fractionation (Eqs. S8 and S9) to mSRR and the fitted kinetic constant (k) to extract fractionation limits (e.g., 34εMSRmax and 34εMSRmin). Relative sedSRRs are calculated with Eqs. S12–S14. Phanerozoic data compilations and isotope mass-balance models are detailed in SI Text.
. Specific growth rate is calculated by measuring the dilution rate and the rate of change in optical density between time points (Dataset S1). The nonlinear regression models (based on pseudo-first-order kinetics) are applied to the experimental data,34εMSR or 33λMSR vs. mSRR, allowing us to calculate theoretical 34εMSRmax and 33λMSRmax, along with corresponding fitting parameters, SEs, and 95% confidence interval (Fig. 2). We compare between models by examining the goodness of fit from each model (Fig. S3). The resultant expressions relate a measured isotopic fractionation (Eqs. S8 and S9) to mSRR and the fitted kinetic constant (k) to extract fractionation limits (e.g., 34εMSRmax and 34εMSRmin). Relative sedSRRs are calculated with Eqs. S12–S14. Phanerozoic data compilations and isotope mass-balance models are detailed in SI Text.
Supplementary Material
Acknowledgments
We thank A. Pearson for detailed comments that greatly improved this manuscript, C. Cavanaugh, C. Hansel, T. Laakso, and J. C. Creveling for comments that helped along earlier versions of this manuscript, and Tim Lyons and an anonymous reviewer for thoughtful commentary. A. Masterson, E. Beirne, and M. Schmidt provided expert analytical assistance. The National Science Foundation (NSF) Graduate Research Fellowship Program (W.D.L.), Microbial Sciences Initiative at Harvard (W.D.L. and D.T.J.), National Aeronautics and Space Administration (NASA)–NASA Astrobiology Institute, NSF Earth Sciences/Instrumentation and Facilities, NSF Faculty Early Career Development Program, and Harvard University (D.T.J.) all supported this work.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 11217.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1218874110/-/DCSupplemental.
*Variability in 3xS of a measured pool, y, is tracked through δ3xSy: 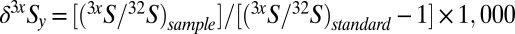 , where x = 3, 4, or 6 and y is a distinct S-bearing species or operationally defined pool. The difference between two pools (y = A or B, e.g., sulfate and sulfide or sedimentary sulfate and pyrite) is calculated rigorously (i.e., not a simple arithmetic difference), as must be done in studies tracking both major and minor isotope variability:
, where x = 3, 4, or 6 and y is a distinct S-bearing species or operationally defined pool. The difference between two pools (y = A or B, e.g., sulfate and sulfide or sedimentary sulfate and pyrite) is calculated rigorously (i.e., not a simple arithmetic difference), as must be done in studies tracking both major and minor isotope variability: 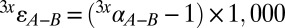 , where
, where 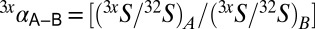 . Variability in 33S is tracked through 33λ:
. Variability in 33S is tracked through 33λ: 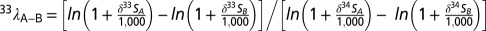 . Qualitatively, 33λ describes the slope of a line connecting two points on a δ33S vs. δ34S plot.
. Qualitatively, 33λ describes the slope of a line connecting two points on a δ33S vs. δ34S plot.
References
- 1.Canfield DE. The evolution of the Earth surface sulfur reservoir. Am J Sci. 2004;304(10):839–861. [Google Scholar]
- 2.Farquhar J, Bao HM, Thiemens M. Atmospheric influence of Earth’s earliest sulfur cycle. Science. 2000;289(5480):756–759. doi: 10.1126/science.289.5480.756. [DOI] [PubMed] [Google Scholar]
- 3.Strauss H. The isotopic composition of sedimentary sulfur through time. Palaeogeogr Palaeoclimatol Palaeoecol. 1997;132(1):97–118. [Google Scholar]
- 4.Johnston DT. Multiple sulfur isotopes and the evolution of Earth’s surface sulfur cycle. Earth Sci Rev. 2011;106(1–2):161–183. [Google Scholar]
- 5.Detmers J, Brüchert V, Habicht KS, Kuever J. Diversity of sulfur isotope fractionations by sulfate-reducing prokaryotes. Appl Environ Microbiol. 2001;67(2):888–894. doi: 10.1128/AEM.67.2.888-894.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Johnston DT. Touring the biogeochemical landscape of a sulfur-fueled world. Elements. 2010;6(2):101–106. [Google Scholar]
- 7.Habicht KS, Gade M, Thamdrup B, Berg P, Canfield DE. Calibration of sulfate levels in the archean ocean. Science. 2002;298(5602):2372–2374. doi: 10.1126/science.1078265. [DOI] [PubMed] [Google Scholar]
- 8.Canfield DE. Isotope fractionation by natural populations of sulfate-reducing bacteria. Geochim Cosmochim Acta. 2001;65(7):1117–1124. [Google Scholar]
- 9.Park R, Epstein S. Carbon isotope fractionation during photosynthesis. Geochim Cosmochim Acta. 1960;21(1–2):110–126. [Google Scholar]
- 10.Laws EA, Popp BN, Bidigare RR, Kennicutt MC, Macko SA. Dependence of phytoplankton carbon isotopic composition on growth-rate and CO2 (AQ) - Theoretical considerations and experimental results. Geochim Cosmochim Acta. 1995;59(6):1131–1138. [Google Scholar]
- 11.Canfield DE. 2001. Biogeochemistry of sulfur isotopes. Stable Isotope Geochemistry, eds Valley JW, Cole DR, Reviews in Mineralogy and Geochemistry, Vol 43, pp 607–636.
- 12.Holland HD. The oxygenation of the atmosphere and oceans. Philos Trans R Soc Lond B Biol Sci. 2006;361(1470):903–915. doi: 10.1098/rstb.2006.1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Canfield DE, Farquhar J. Animal evolution, bioturbation, and the sulfate concentration of the oceans. Proc Natl Acad Sci USA. 2009;106(20):8123–8127. doi: 10.1073/pnas.0902037106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fry B, Gest H, Hayes JM. Isotope effects associated with the anaerobic oxidation of sulfide by the purple photosynthetic bacterium, Chromotium vinosum. FEMS Microbiol Lett. 1984;22(3):283–287. doi: 10.1016/0378-1097(85)90318-0. [DOI] [PubMed] [Google Scholar]
- 15.Zerkle AL, Farquhar J, Johnston DT, Cox RP, Canfield DE. Fractionation of multiple sulfur isotopes during phototrophic oxidation of sulfide and elemental sulfur by a green sulfur bacterium. Geochim Cosmochim Acta. 2009;73(2):291–306. [Google Scholar]
- 16.Canfield DE. Models of oxic respiration, denitrification and sulfate reduction in zones of coastal upwelling. Geochim Cosmochim Acta. 2006;70(23):5753–5765. [Google Scholar]
- 17.Canfield DE, Thamdrup B, Kristensen E. Aquatic Geomicrobiology. Advances in Marine Biology. Vol 48. New York: Academic; 2005. [DOI] [PubMed] [Google Scholar]
- 18.Jorgensen BB. Theoretical model of the stable isotope distribution in marine sediments. Geochim Cosmochim Acta. 1979;43(3):363–374. [Google Scholar]
- 19.Chambers LA, Trudinger PA, Smith JW, Burns MS. Fractionation of sulfur isotopes by continuous cultures of Desulfovibrio desulfuricans. Can J Microbiol. 1975;21(10):1602–1607. doi: 10.1139/m75-234. [DOI] [PubMed] [Google Scholar]
- 20.Kaplan IR, Rittenberg SC. Microbiological fractionation of sulphur isotopes. J Gen Microbiol. 1964;34(2):195–212. doi: 10.1099/00221287-34-2-195. [DOI] [PubMed] [Google Scholar]
- 21.Harrison AG, Thode HG. Mechanism of the bacterial reduction of sulphate from isotope fractionation studies. Trans Faraday Soc. 1958;54:84–92. [Google Scholar]
- 22.Goldhaber MB, Kaplan IR. Controls and consequences of sulfate reduction rates in recent marine sediments. Soil Sci. 1975;119(1):42–55. [Google Scholar]
- 23.Peck HD, Jr, LeGall J, Vanbeeumen J. Biochemistry of dissimilatory sulphate reduction. Philos Trans R Soc Lond B Biol Sci. 1982;298(1093):443–466. doi: 10.1098/rstb.1982.0091. [DOI] [PubMed] [Google Scholar]
- 24.Jorgensen BB. Mineralization of organic matter in the sea bed: The role of sulfate reduction. Nature. 1982;296(5858):643–645. [Google Scholar]
- 25.Herbert D, Elsworth R, Telling RC. The continuous culture of bacteria; a theoretical and experimental study. J Gen Microbiol. 1956;14(3):601–622. doi: 10.1099/00221287-14-3-601. [DOI] [PubMed] [Google Scholar]
- 26.Monod J. La technique de culture continue theorie et applications. Ann Inst Pasteur (Paris) 1950;79:390–410. [Google Scholar]
- 27.Sim MS, Ono S, Donovan D, Templer SP, Bosak T. Effect of electron donors on the fractionation of sulfur isotopes by a marine Desulfovibrio sp. Geochim Cosmochim Acta. 2011;75(15):4244–4259. [Google Scholar]
- 28.Habicht KS, Canfield DE. Sulfur isotope fractionation during bacterial sulfate reduction in organic-rich sediments. Geochim Cosmochim Acta. 1997;61(24):5351–5361. doi: 10.1016/s0016-7037(97)00311-6. [DOI] [PubMed] [Google Scholar]
- 29.Horita J, Zimmermann H, Holland HD. Chemical evolution of seawater during the Phanerozoic: Implications from the record of marine evaporites. Geochim Cosmochim Acta. 2002;66(21):3733–3756. [Google Scholar]
- 30.Ingvorsen K, Jorgensen BB. Kinetics of sulfate uptake by fresh-water and marine species of desulfovibrio. Arch Microbiol. 1984;139(1):61–66. [Google Scholar]
- 31.Davidson MM, et al. Sulfur isotope enrichment during maintenance metabolism in the thermophilic sulfate-reducing bacterium Desulfotomaculum putei. Appl Environ Microbiol. 2009;75(17):5621–5630. doi: 10.1128/AEM.02948-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stam MC, Mason PRD, Pallud C, Van Cappellen P. Sulfate reducing activity and sulfur isotope fractionation by natural microbial communities in sediments of a hypersaline soda lake (Mono Lake, California) Chem Geol. 2010;278(1–2):23–30. [Google Scholar]
- 33.Boudreau BP, Westrich JT. The dependence of bacterial sulfate reduction on sulfate concentration in marine-sediments. Geochim Cosmochim Acta. 1984;48(12):2503–2516. [Google Scholar]
- 34.Canfield DE. Sulfate reduction in deep-sea sediments. Am J Sci. 1991;291(2):177–188. doi: 10.2475/ajs.291.2.177. [DOI] [PubMed] [Google Scholar]
- 35.Canfield DE, et al. Pathways of organic carbon oxidation in three continental margin sediments. Mar Geol. 1993;113(1–2):27–40. doi: 10.1016/0025-3227(93)90147-n. [DOI] [PubMed] [Google Scholar]
- 36.Heidelberg JF, et al. The genome sequence of the anaerobic, sulfate-reducing bacterium Desulfovibrio vulgaris Hildenborough. Nat Biotechnol. 2004;22(5):554–559. doi: 10.1038/nbt959. [DOI] [PubMed] [Google Scholar]
- 37.Keller KL, Wall JD. Genetics and molecular biology of the electron flow for sulfate respiration in desulfovibrio. Front Microbiol. 2011;2(135):1–17. doi: 10.3389/fmicb.2011.00135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tarpgaard IH, Roy H, Jorgensen BB. Concurrent low- and high-affinity sulfate reduction kinetics in marine sediment. Geochim Cosmochim Acta. 2011;75(11):2997–3010. [Google Scholar]
- 39.Hayes JM. 2001. Fractionation of carbon and hydrogen isotopes in biosynthetic processes. Stable Isotope Geochemistry, eds Valley JW, Cole DR, Reviews in Mineralogy and Geochemistry, Vol 43, pp 225–277. [Google Scholar]
- 40.Johnston DT, Farquhar J, Canfield DE. Sulfur isotope insights into microbial sulfate reduction: When microbes meet models. Geochim Cosmochim Acta. 2007;71(16):3929–3947. [Google Scholar]
- 41.Farquhar J, Canfield DE, Masterson A, Bao H, Johnston D. Sulfur and oxygen isotope study of sulfate reduction in experiments with natural populations from Faellestrand, Denmark. Geochim Cosmochim Acta. 2008;72(12):2805–2821. [Google Scholar]
- 42.Stam MC, Mason PRD, Laverman AM, Pallud C, Van Cappellen P. S-34/S-32 fractionation by sulfate-reducing microbial communities in estuarine sediments. Geochim Cosmochim Acta. 2011;75(14):3903–3914. [Google Scholar]
- 43.Motulsky HJ, Ransnas LA. Fitting curves to data using nonlinear regression: A practical and nonmathematical review. FASEB J. 1987;1(5):365–374. [PubMed] [Google Scholar]
- 44.Habicht KS, Salling LL, Thamdrup B, Canfield DE. Effect of low sulfate concentrations on lactate oxidation and isotope fractionation during sulfate reduction by Archaeoglobus fulgidus strain Z. Appl Environ Microbiol. 2005;71(7):3770–3777. doi: 10.1128/AEM.71.7.3770-3777.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rees CE. Steady-state model for sulfur isotope fractionationin bacterial reduction processes. Geochim Cosmochim Acta. 1973;37(5):1141–1162. [Google Scholar]
- 46.Sim MS, Bosak T, Ono S. Large sulfur isotope fractionation does not require disproportionation. Science. 2011;333(6038):74–77. doi: 10.1126/science.1205103. [DOI] [PubMed] [Google Scholar]
- 47.Westrich JT, Berner RA. The role of sedimentary organic-matter in bacterial sulfate reduction: The G model tested. Limnol Oceanogr. 1984;29(2):236–249. [Google Scholar]
- 48.LaRowe DE, Van Cappellen P. Degradation of natural organic matter: A thermodynamic analysis. Geochim Cosmochim Acta. 2011;75(8):2030–2042. [Google Scholar]
- 49. J. Middleburg (1989) A simple rate model for organic matter decomposition in marine sediments. Geochim Cosmochim Acta 53(7):1577–1581.
- 50.Hartnett HE, Keil RG, Hedges JI, Devol AH. Influence of oxygen exposure time on organic carbon preservation in continental margin sediments. Nature. 1998;391(6667):572–575. [Google Scholar]
- 51.Canfield DE. Factors influencing organic carbon preservation in marine sediments. Chem Geol. 1994;114(3–4):315–329. doi: 10.1016/0009-2541(94)90061-2. [DOI] [PubMed] [Google Scholar]
- 52.Berner RA. 1980. A rate model for organic matter decomposition during bacterial sulfate reduction in marine sediments. Biogeochemistry of Organic Matter at the Sediment-Water Interface, International Colloquium of the CNRS, Vol 293, pp 35–44. [Google Scholar]
- 53.Aharon P, Fu BS. Microbial sulfate reduction rates and sulfur and oxygen isotope fractionations at oil and gas seeps in deepwater Gulf of Mexico. Geochim Cosmochim Acta. 2000;64(2):233–246. [Google Scholar]
- 54.Wu NP, Farquhar J, Strauss H, Kim ST, Canfield DE. Evaluating the S-isotope fractionation associated with Phanerozoic pyrite burial. Geochim Cosmochim Acta. 2010;74(7):2053–2071. [Google Scholar]
- 55.Halevy I, Peters SE, Fischer WW. Sulfate burial constraints on the Phanerozoic sulfur cycle. Science. 2012;337(6092):331–334. doi: 10.1126/science.1220224. [DOI] [PubMed] [Google Scholar]
- 56.Hannisdal B, Peters SE. Phanerozoic Earth system evolution and marine biodiversity. Science. 2011;334(6059):1121–1124. doi: 10.1126/science.1210695. [DOI] [PubMed] [Google Scholar]
- 57.Garrels RM, Lerman A. Phanerozoic cycles of sedimentary carbon and sulfur. Proc Natl Acad Sci USA. 1981;78(8):4652–4656. doi: 10.1073/pnas.78.8.4652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Berner RA. A model for calcium, magnesium and sulfate in seawater over Phanerozoic time. Am J Sci. 2004;304(5):438–453. [Google Scholar]
- 59.Canfield DE. Reactive iron in marine sediments. Geochim Cosmochim Acta. 1989;53(6):619–632. doi: 10.1016/0016-7037(89)90005-7. [DOI] [PubMed] [Google Scholar]
- 60.Tsandev I, Slomp CP, Van Cappellen P. Glacial-interglacial variations in marine phosphorus cycling: Implications for ocean productivity. Global Biogeochem Cycles. 2008;22(4):1–14. [Google Scholar]
- 61.Johnston DT, et al. Active microbial sulfur disproportionation in the Mesoproterozoic. Science. 2005;310(5753):1477–1479. doi: 10.1126/science.1117824. [DOI] [PubMed] [Google Scholar]
- 62.Johnston DT, et al. Evolution of the oceanic sulfur cycle at the end of the Paleoproterozoic. Geochim Cosmochim Acta. 2006;70(23):5723–5739. [Google Scholar]
- 63.Bergman NM, Lenton TM, Watson AJ. COPSE: A new model of biogeochemical cycling over Phanerozoic time. Am J Sci. 2004;304(5):397–437. [Google Scholar]
- 64.Johnston DT, et al. Multiple sulfur isotope fractionations in biological systems: A case study with sulfate reducers and sulfur disproportionators. Am J Sci. 2005;305(6–8):645–660. [Google Scholar]
- 65.Poulton SW, Canfield DE. Ferruginous conditions: A dominant feature of the ocean through Earth’s history. Elements. 2011;7(2):107–112. [Google Scholar]
- 66.Prokoph A, Shields GA, Veizer J. Compilation and time-series analysis of a marine carbonate delta O-18, delta C-13, Sr-87/Sr-86 and delta S-34 database through Earth history. Earth Sci Rev. 2008;87(3–4):113–133. [Google Scholar]
- 67.Torsvik TH, Van der Voo R. Refining Gondwana and Pangea palaeogeography: estimates of Phanerozoic non-dipole (octupole) fields. Geophys J Int. 2002;151(3):771–794. [Google Scholar]
- 68.Cardenas AL, Harries PJ. Effect of nutrient availability on marine origination rates throughout the Phanerozoic eon. Nat Geosci. 2010;3(6):430–434. [Google Scholar]
- 69.Jones DJ, Fike DA. Dynamic sulfur and carbon cycling through the end-Ordovician extinction revealed by paired sulfate–pyrite δ34S. Earth and Planetary Science Letters. 2013;363:144–155. [Google Scholar]
- 70.Raiswell R. Iron transport from the continents to the open ocean: The aging-rejuvenation cycle. Elements. 2011;7(2):101–106. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.