Rational modification of protein stability by targeting surface sites leads to complicated results

Abstract

The rational modification of protein stability is an important goal of protein design. Protein surface electrostatic interactions are not evolutionarily optimized for stability and are an attractive target for the rational redesign of proteins. We show that surface charge mutants can exert stabilizing effects in distinct and unanticipated ways, including ones that are not predicted by existing methods, even when only solvent-exposed sites are targeted. Individual mutation of three solvent-exposed lysines in the villin headpiece subdomain significantly stabilizes the protein, but the mechanism of stabilization is very different in each case. One mutation destabilizes native-state electrostatic interactions but has a larger destabilizing effect on the denatured state, a second removes the desolvation penalty paid by the charged residue, whereas the third introduces unanticipated native-state interactions but does not alter electrostatics. Our results show that even seemingly intuitive mutations can exert their effects through unforeseen and complex interactions.

The mutation of charged surface residues to enhance electrostatics is a popular approach in protein engineering (1). Target residues are often selected using estimates of the protein electrostatic potential (2). This approach relies on identifying residues that are involved in unfavorable electrostatic interactions, typically with residues of the same charge, or on identifying sites where new favorable electrostatic interactions can be introduced (3). Solvent-exposed charged residues are thought to not be involved in critical packing interactions in the native state, to not suffer large desolvation penalties upon protein folding, nor to make significant interactions in the denatured-state ensemble (DSE). Thus, residues to be targeted are typically chosen on the basis of calculations of protein native-state ensemble (NSE) electrostatics. Methods ranging from simple inspection of the protein surface, modified Tanford–Kirkwood approaches (3, 4) and Poisson–Boltzmann (PB) calculations have been used (5–7). Irrespective of the details, the general strategy is based on the assumption that surface electrostatic interactions can be modified without altering other native-state interactions and without altering DSE energetics. An attractive feature of these approaches is that they are computationally inexpensive and, unlike selection-based methods or directed evolution, involve the generation of a limited number of mutants. Any increase in stability is generally assumed to result from modification of NSE electrostatics. We show that this approach leads to complicated and unanticipated results, even for very simple proteins.

We use the villin headpiece subdomain HP36 as our model system. HP36 is a small three-helix protein that has become an extremely popular model system for experimental and computational studies of protein folding, owing to its small size, simple topology, and microsecond folding kinetics (Fig. 1A) (8–17). Despite its small size, HP36 folds cooperatively and is stabilized by a typical balance of interactions (18).

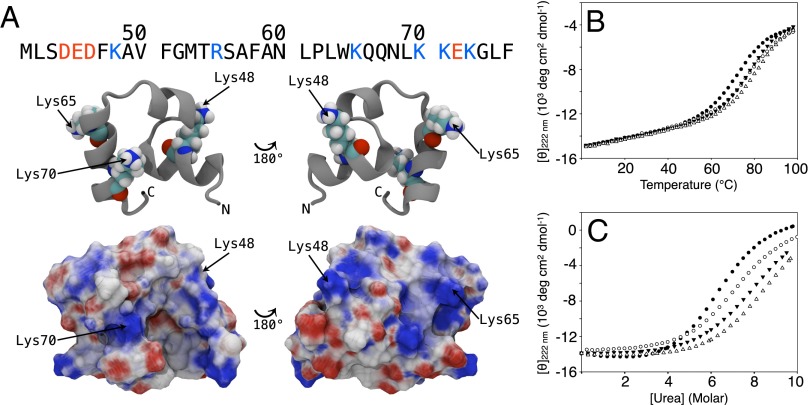
Fig. 1.

Mutation of solvent-exposed surface lysines stabilizes HP36. (A) The structure and sequence of HP36 showing the location of the lysine side chains. (B) Mutation of the surface lysines K48, K65, or K70 increases the melting temperature. Thermal unfolding curves are shown for WT HP36 (●), K48M (▼), K65M (□), and K70M (△). (C) Mutation of the surface lysines K48, K65, or K70 increases ΔG°_unfolding. Urea-induced unfolding curves are shown for WT HP36 (●), K48M (▼), K65M (□), and K70M (△). Experiments were conducted at pH 5.0 in 10 mM sodium acetate and 150 mM sodium chloride.

Results

Mutation of Surface Lysines Significantly Increases HP36 Stability and Does Not Perturb Its Structure.

HP36 contains 10 charged residues: four Asp/Glu, one Arg, and five Lys residues, all located on the surface, with the exception of D44 and R55, which form a salt bridge and are partially buried. The N and C termini are also on the surface (Fig. 1A and SI Appendix, Fig. S1). Herein, we use a numbering system corresponding to the full-length villin headpiece: the first subdomain residue is L42; our construct contains an additional Met at the N terminus (M41) that does not affect the structure or folding of the protein (19). The calculated pI of the domain is 9.4 and the net charge at pH 7 is +2, depending on the exact pK_a of the N terminus.

We individually mutated each lysine to a methionine, chosen because methionine is approximately isosteric for lysine. Lysine-to-methionine mutations at positions 71 or 73 had no significant effect on stability (SI Appendix, Table S1, and SI Appendix, Fig. S2), but were stabilizing at positions 48, 65, and 70 (Fig. 1 B and C), increasing ΔG° of unfolding by 0.7–1.2 kcal⋅mol⁻¹ and the melting temperature (T_m) by 4–9 °C depending upon the site (Table 1). Lysine-to-norleucine substitutions at positions 65 and 70 have previously been shown to be stabilizing (9, 20). Circular dichroism and NMR experiments showed that the methionine substitutions do not alter the structure of the domain (SI Appendix, Figs. S3 and S4) and the values of ΔH° of unfolding are very similar to that of WT HP36, arguing that core packing is not disturbed (Table 1).

Table 1.

Thermodynamic parameters for the unfolding of WT HP36 and the mutants

Protein	Tm, °C	ΔH°(Tm), kcal⋅mol−1	ΔG°, kcal⋅mol−1	m-value	CM*, M
WT HP36	73.0 ± 0.2	31.82 ± 0.33	3.17 ± 0.06	0.52 ± 0.01	6.2
K48M	78.0 ± 0.4	34.07 ± 0.38	4.11 ± 0.08†	0.52 ± 0.01‡	7.9
K65M	77.2 ± 0.6	33.20 ± 0.65	3.87 ± 0.08†	0.52 ± 0.01‡	7.2
K70M	82.2 ± 0.7	33.44 ± 0.44	4.37 ± 0.08†	0.52 ± 0.01‡	8.4

Experiments were conducted in 10 mM sodium acetate, 150 mM sodium chloride at pH 5.0. SEs of the fit are provided as measures of parameter uncertainty.

^*The C_M value was determined by calculating the derivative of the plot of CD signal vs. [urea].

^†The ΔG° values are calculated using the following: ΔG° = C_M × m value.

^‡The high thermal stability of the variants prevents an accurate determination of the m-value (given in kilocalories per mole-molarity), so the value of WT HP36 is used.

Native-State Electrostatic Interactions Cannot Account for the Increase in HP36 Stability.

K48, K65, and K70 are solvent exposed and the observed increase in stability upon their replacement with methionine would traditionally be ascribed to the alteration of native-state electrostatics. To determine the molecular basis for the stabilization, we first measured the native-state pK_a values for all acidic residues of WT HP36 and each mutant using NMR (SI Appendix, Figs. S5–S8). pK_a shifts upon mutation are sensitive reporters of changes in the electrostatic environment (21–26). In WT HP36, the pK_a values of D44, E45, and D46 are lower than model compound values by 0.4–1 pK_a units, indicating that these residues make favorable NSE electrostatic interactions; E72 and the C terminus have pK_a values near model compound values (Table 2).

Table 2.

Native-state pK_a values for the acidic residues in HP36 WT and the mutants

Residue	WT HP36 native-state pKa value	K70M native-state pKa value	K65M native-state pKa value	K48M native-state pKa value
D44	3.04 ± 0.12	3.03 ± 0.07	3.03 ± 0.06	3.23 ± 0.07
E45	3.95 ± 0.02	4.13 ± 0.10	4.15 ± 0.09	4.68 ± 0.09
D46	3.44 ± 0.11	3.34 ± 0.05	3.33 ± 0.05	3.38 ± 0.05
E72	4.37 ± 0.03	4.43 ± 0.02	4.36 ± 0.14	4.41 ± 0.03
C terminus	3.17 ± 0.14	3.13 ± 0.08	2.91 ± 0.10	2.90 ± 0.06

The uncertainties are the SE to the fits. Experiments were performed at 25 °C in 90% (vol/vol) H₂O, 10% (vol/vol) D₂O, 10 mM sodium acetate, and 150 mM sodium chloride.

The effect of the K48M mutation is striking: it significantly perturbs the pK_a of E45, increasing it by more than 0.7 pK_a units, but affects the other pK_a values by only 0.04–0.19 pK_a units. The mutation thus results in loss of favorable native-state electrostatic interactions, yet it still stabilizes the protein, a result that would not be predicted by methods that consider only native-state electrostatics. The acidic group pK_a values in the K65M and K70M mutants are similar to those of WT: The largest pK_a shift is only 0.2 units and three residues experience shifts of less than 0.1 units. We conclude that the K65M and K70M mutations do not significantly alter the NSE electrostatic environment sensed by the acidic residues, even though they stabilize the domain. Thus, the mutants must exert their stabilizing effects by other means; possibilities include attenuating repulsive interactions, the introduction of nonelectrostatic interactions, or the alteration of DSE energetics. These potential mechanisms are systematically examined below.

We conducted a computational analysis of the domain to gain atomistic insight into NSE electrostatics. Our approach to calculating the electrostatic contribution of a side chain to protein stability is based on solving the linearized PB equation, and compares a charged group to an uncharged hydrophobic isostere. For each side chain, the calculations yield a solvation free energy ΔΔG°_solv and an electrostatic interaction energy ΔΔG°_inter. The sum of the two energetic terms, ΔΔG°_elec, reports whether the charged or uncharged analog is more favorable in a particular conformation; the balance rests on whether a group participates in enough favorable interactions to overcome the desolvation penalty it incurs. In our model, ΔΔG°_elec corresponds to “turning on” the charges, and thus a negative value indicates that the polar analog is preferred over the isostere. For WT HP36, we generated a 1.0-μs molecular dynamics (MD) trajectory in explicit solvent, extracted 1,000 snapshots at 1-ns intervals, and performed PB calculations on each. Use of an ensemble of structures allows us to take into account the effects of protein dynamics, both at the backbone and the side-chain levels. Despite the popularity of HP36 in the protein folding field, computational studies have typically focused on its folding and the analysis of backbone conformations, rather than on specific side chain–side chain interactions.

At the simulation temperature of 300 K, the protein molecule remained folded and occupied native-like conformations exclusively. Analysis of the MD-derived NSE revealed a number of transient electrostatic contacts, including a set of dynamic salt bridges: D44–R55, E45–K48, E72–K73, K70–C terminus, as well as the interaction between the two termini. To visualize the electrostatic contribution of a particular residue as a function of simulation time, we use a heat map representation, in which the interaction strength in a particular snapshot is represented as a color-coded bar (Fig. 2 A–C); the darker the bar, the stronger the interaction.

Fig. 2.

Heat map representation of time-dependent electrostatic interactions made by K48, K65, and K70 in the 1,000-member structural ensemble derived from a 1-μs MD simulation of WT HP36. Each heat map row represents a molecular interaction partner; average electrostatic interaction energy is indicated on the Right of each row. The color scheme is white for no interaction, light blue for a repulsive interaction, and shades of grayscale for attractive interactions; darker shades represent stronger interactions. (A) K48 interacts favorably with E45; this salt bridge is made and broken dynamically. (B) K65 makes no significant electrostatic interactions. (C) K70 interacts dynamically with the C terminus (76 carbonyl). (D) Summary of electrostatic contributions of K48, K65, and K70 to stability. Only K48 makes compensatory interactions to overcome its desolvation penalty. Free energies are given in kilocalories per mole.

The calculated interaction free energy between E45 and K48 is the second strongest in the protein (ΔΔG°_inter of −4.67 kcal⋅mol⁻¹), after the critical D44–R55 salt bridge. We found that, as a unit, the E45–K48 salt bridge is able to overcome its desolvation penalty and contributes favorably to protein stability (ΔΔG°_elec of −0.51 kcal⋅mol⁻¹) relative to a peptide model of the unfolded state (Methods). The electrostatic contribution of K70 is neutral, to protein stability (ΔΔG°_elec of +0.11 kcal⋅mol⁻¹) due to its transient interactions with the C terminus. Due to lack of nearby interaction partners, K65 is unable to overcome its desolvation penalty of 1 kcal⋅mol⁻¹ and contributes unfavorably to protein stability (ΔΔG°_elec of +1.07 kcal⋅mol⁻¹).

Relief of Charge Repulsion Between Positively Charged Side Chains Cannot Account for the Stabilizing Effects of the HP36 Mutants.

The positively charged groups of HP36 are distributed throughout its structure. In principle, reduction of charge repulsion might contribute to the stabilization induced by the mutants, because a Lys-to-Met substitution reduces the net positive charge of the protein. However, our calculations demonstrate that charge repulsion is not a significant energetic contributor to the native-state stability of WT HP36. Analysis of the MD structural ensemble revealed that the basic groups are well separated from each other and come into proximity infrequently. The closest average pairwise distance between any two basic groups in WT HP36 is 9.1 Å for R55 and the N terminus (corresponding to a calculated ΔΔG°_inter of +0.63 kcal⋅mol⁻¹); other average pairwise distances are greater than 11 Å (SI Appendix, Fig. S9).

We measured the stability of each HP36 variant as a function of pH, and analyzed the experimental values of ΔΔG°_mutation (pH) = ΔG°_mutant (pH) – ΔG°_wt (pH) to further test if the mutants exert their effects by relieving charge repulsion (SI Appendix, Fig. S10) (27). If the increased stability were due only to changes in native-state charge repulsion, then the stability difference between the mutant and WT should be maintained at low pH because the lysines remain fully protonated, provided other interactions do not change. The stability difference between K65M and WT is decreased when the pH is lowered, from 0.6 kcal⋅mol⁻¹ at pH 6 to 0.1 kcal⋅mol⁻¹ at pH 2. The difference between K48M and WT also decreases as the pH is lowered, from 0.8 kcal⋅mol⁻¹ at pH 6 to 0.3 kcal⋅mol⁻¹ at pH 2. These observations, in agreement with the MD simulations, argue that changes in charge repulsion between Lys residues in the native state are not the major reason for the increased stability of these mutants. The difference in stability between K70M and WT HP36 is less sensitive to pH, ranging from 1.0 kcal⋅mol⁻¹ at pH 6 to 0.7 kcal⋅mol⁻¹ at pH 2.

Changes in Desolvation Penalties Contribute to the Increase in Stability for K65M, but Not K48M or K70M.

We also conducted a computational analysis of the mutants. MD trajectories were run for 200 ns for each mutant, and PB analysis was performed as discussed previously. All mutants remained folded during the time course of the simulation. The analysis shows that the increased stability of K65M results from reduction of the folding desolvation penalty at this site, but desolvation cannot account for the effects of K48M or K70M mutations. In all simulations, K65 pays a desolvation penalty of about 1 kcal⋅mol⁻¹ yet makes inadequate compensatory interactions to overcome this penalty (SI Appendix, Table S3); thus, mutation to a neutral residue will stabilize the domain.

Unfolded State Effects Account for the Increase in Stability of the HP36 K48M Variant.

The overwhelming majority of protein stability and folding studies implicitly assume that mutations do not perturb the energetics of the DSE or that, if they do, their effects are small. It is harder to study the DSE, and this assumption is difficult to test and often goes unchallenged. Fortunately, electrostatic interactions in the DSE can be probed by combining pH-dependent stability analysis with pK_a measurements (28–32). The Tanford–Wyman linkage relationship defines the pH dependence of protein stability as follows:

where ΔQ is the difference in the number of protons bound in the native and denatured ensembles, and pH_ref is an arbitrarily chosen reference pH. The linkage relationship is exact and can be rewritten in terms of NSE and DSE pK_a values, provided that titration behavior can be described as a sum of individually titrating sites as follows:

where pK_i,N and pK_i,D are the NSE and DSE pK_a values for residue i (29). The left-hand side of Eq. 2 can be measured experimentally, as can the native-state pK_a values. The DSE pK_a values are unknown; measuring pK_a values in the urea-unfolded state is not relevant because its conformational ensemble differs from the DSE found under native conditions. The linkage relationship can be used to compare the actual DSE to models of a “fully” unfolded protein, by using model compound pK_a values. Disagreement between the measured and calculated stability differences unambiguously indicates the presence of DSE effects that perturb the protein pK_a values away from model compound values (32). However, agreement between the calculated and experimental results does not mean that the environment of each acidic residue is unperturbed in the DSE: some sites may make favorable interactions, whereas others make unfavorable ones, with the effects offsetting each other. We chose a set of peptide fragments derived from HP36 as unfolded-state model compounds. It is important to stress that we are not proposing that actual DSE behavior can be captured by a set of peptides; rather, we use the peptides to account for local sequence effects (33). Comparison of the measured and predicted pH-dependent ΔΔG° allows the detection of DSE electrostatic effects beyond those captured by the set of model peptides.

Because D44, E45, and D46 are adjacent in sequence, we first tested whether they titrate independently in the native state and the model peptide. In the WT MD ensemble, the carboxylates are all well separated from each other: the shortest average pairwise distance is 7.5 Å, whereas the others are 8.8 Å or greater (SI Appendix, Fig. S11). Two of the three groups are involved in favorable charged interactions with other residues: D44 forms a salt bridge with R55, whereas E45 interacts with K48. NSE PB calculations revealed that, despite their adjacency in sequence, the three acidic residues interact weakly (roughly +0.4 kcal⋅mol⁻¹). The fact that the K48M mutation selectively perturbs the native-state pK_a of E45 provides additional indirect evidence that the acidic residues are titrating independently; if they were not, then the mutation is likely to perturb all of them. In the K48M MD ensemble, E45 experiences fewer favorable electrostatic interactions (ΔΔG°_elec of +0.22 kcal⋅mol⁻¹, compared with −2.33 kcal⋅mol⁻¹ in the WT ensemble), consistent with the observed significant increase in the E45 pK_a upon the K48M mutation.

We next determined the pK_a values in a small peptide containing these residues using NMR (SI Appendix, Table S2, and SI Appendix, Figs. S12–S16). The pK_a values of D44, E45, and D46 in the peptide fragment corresponding to residues 41–53 are all close to random coil values, providing additional evidence that the groups titrate independently. We further tested the hypothesis of independently titrating sites by synthesizing a peptide in which E45 was replaced by glutamine. The pK_a values of both D44 and D46 are essentially identical in the two peptides, arguing that E45 does not significantly perturb their pK_a values (SI Appendix, Fig. S16, and SI Appendix, Table S2).

Fig. 3 shows the pH dependence of ΔΔG° for all HP36 variants. The measured and predicted curves agree for WT, K70M, and K65M, indicating that these mutations have negligible net effect on DSE electrostatics. However, the curves diverge for K48M, demonstrating that the mutation alters DSE interactions. The K48M mutant experiences unfavorable DSE interactions that perturb electrostatics relative to the model peptides; the mutation thus unmasks unfavorable electrostatic interactions in the DSE. The mutation destabilizes the DSE, and this effect compensates for its unfavorable impact on the native-state electrostatics. Thus, the K48M mutant stabilizes the protein by removing favorable interactions in both the NSE and DSE, a mechanism that would be impossible to predict using traditional structure-based design algorithms. Note that analysis of just the WT protein would lead to the erroneous conclusion that the acidic residues experience unperturbed electrostatic environments in the DSE. The K48M mutant data indicate that some sites experience favorable interactions in the DSE and other unfavorable ones.

Fig. 3.

pH-dependent stability analysis reveals that K48M mutation alters DSE interactions. A–D represent schematic illustrations of the approach. (A) The calculated and experimental curves agree when the DSE pK_a values are equal to model compound values. (B) Agreement could also result from cancellation of favorable and unfavorable DSE interactions. (C) Significant DSE electrostatic interactions will lead to a deviation between the calculated and experimental curves. In this case, favorable DSE interactions are considered. Unfavorable DSE interactions lead to a deviation of the opposite sense. (D) The case in which there are both favorable and unfavorable DSE interactions and in which one of these is perturbed by mutation. The open circle represents the mutation of a positively charged residue to a neutral. In this case, the calculated and experimental curves of the mutant diverge. The example corresponds to the mutation eliminating a favorable DSE interaction. Experimental pH-dependent stability analysis for (E) HP36 WT, (F) K48M, (G) K65M, and (H) K70M. The continuous lines represent the calculated stability change calculated with Eq. 2 using native-state pK_a values and model compound values. The filled circles represent the measured stability change from urea-induced unfolding experiments. The filled triangles represent the calculated stability change using the Gibbs–Helmholtz equation from thermal unfolding. The open triangles represent the calculated stability change using Gibbs–Helmholtz equation from thermal unfolding experiments with a ΔC_p° value 0.43 kcal⋅mol⁻¹⋅K⁻¹. Free energies are provided in kilocalories per mole. Error bars represent the SD of three repeat experiments.

K70M Mutation Introduces New Native-State Interactions but Does Not Perturb NSE or DSE Electrostatics.

The K70M mutation has the largest effect upon stability but appears to have no significant effect upon either denatured- or native-state electrostatics, as judged by native-state pK_a measurements and pH-dependent stability analysis. Analysis of the high-resolution crystal structure of the mutant reveals an unexpected result; the mutation leads to the introduction of new packing interactions with the phenylalanine core (Fig. 4) (19). The hydrophobic Met side chain folds back so that it makes extensive contacts with the phenylalanine core. We conducted a 200-ns simulation of K70M and analyzed potential NSE interactions made by each residue. The results support the experimental data and confirm that the K70M mutation does not alter native-state electrostatic interactions but rather derives most of its stabilizing effect from van der Waals packing interactions between M70 and the core phenylalanines. Our analysis predicts that mutation to a smaller nonpolar side chain will have less effect at this position. Consequently, we examined a K70A mutation; this mutant folds cooperatively and, in agreement with our prediction, has a lower free energy of folding and T_m relative to K70M (SI Appendix, Table S2, and SI Appendix, Fig. S17).

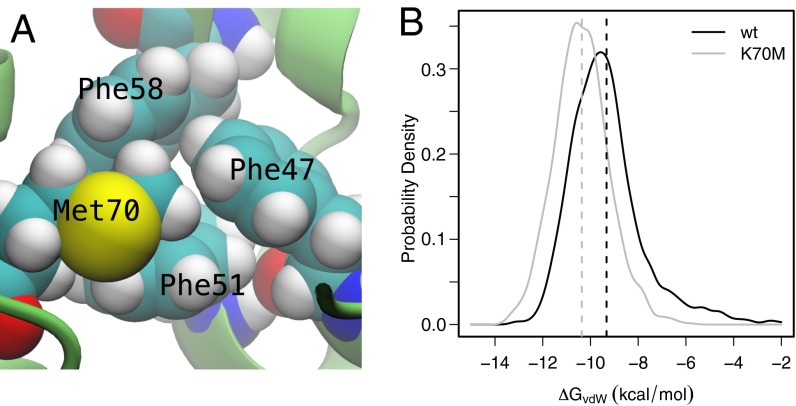
Fig. 4.

(A) A high-resolution crystal structure of the K70M variant of HP36 reveals that the mutation introduces new native-state packing interactions. The side chain of M70 packs against the triphenylalanine core of HP36. (B) Analysis of the van der Waals packing interactions at position 70 in the WT and K70M MD ensembles revealed that, on average, M70 interacts more favorably than K70 by 1.0 kcal⋅mol⁻¹.

Discussion and Conclusions

We have presented three different mechanisms for increasing protein stability upon replacement of a surface charged residue with a neutral as follows: (i) reduction of the desolvation penalty at the mutation site upon folding; (ii) introduction of new favorable packing interactions in the native ensemble; (iii) removal of favorable electrostatic interactions in both native and denatured ensembles, with the magnitude of the DSE effect being larger. Only one of the stabilizing mutations would have been predicted by standard electrostatics-based protein design approaches. The native-state–centric PB-based approach fails to predict that K48M or K70M mutations would be significantly stabilizing, and suggests that the K73M mutation should be stabilizing, even though it is not.

The DSE interactions involving K48 are unlikely to be due to local sequence effects; there is residual helical structure in the DSE of HP36, but peptide fragment studies show that it requires more than local interactions to form (33). Earlier work has shown that a peptide corresponding to residues 41–53 (the first helix) is largely unstructured in isolation (34, 35), and the pK_a values of D44, E45, and D46 in the peptides are all close to random coil values.

It is natural to inquire about the generality of our findings. DSE electrostatic interactions have been detected in a range of proteins of diverse structure (30, 36–42), and there are examples of mutations that alter DSE energetics (43). There are also numerous examples in which mutation of charged surface residues leads to effects that differ in magnitude or even directionality from the expected results. DSE effects and the introduction of unanticipated NSE interactions likely contribute to this discrepancy. Although there is still no robust computational approach to reliably determine DSE electrostatic interactions, they can be detected experimentally by considering the Tanford–Wyman linkage relationship. However, the results presented here show that investigation of only the WT protein can lead to misleading conclusions about the presence or absence of DSE electrostatic interactions.

The analysis reported herein also underscores the importance of considering protein dynamics and relaxation; significantly different computational results are obtained if only the static X-ray structure is used. This is very likely a general effect, because surface residues are involved in crystal contacts and interact with component of the crystallization buffer, including salts and stabilizing agents. In addition, many X-ray structures are solved at low temperatures, which dampens molecular fluctuations.

Methods

Sample Preparation.

Full-length HP36 variants were expressed as a C-terminal fusion linked to the N-terminal domain of L9 by a factor Xa cleavage site and purified by cation exchange chromatography and reverse-phase HPLC, as described previously (19). Uniformly labeled ¹³C¹⁵N HP36 was produced in M9 minimal medium supplemented with ¹⁵NH₄Cl and ¹³C glucose. Peptides were synthesized by standard solid-phase Fmoc chemistry and purified by reverse-phase HPLC. The identities of the proteins and peptides were confirmed by matrix-assisted laser desorption and ionization time-of-flight mass spectrometry.

Protein Stability Measurements.

Protein stability was measured by CD-monitored urea and thermal unfolding experiments in buffer containing 10 mM sodium acetate and 150 mM sodium chloride. Urea-induced unfolding was performed at 25 °C by monitoring ellipticity at 222 nm. Thermal unfolding experiments were performed over the range of 2 °C to 94 °C in 2 °C intervals. The unfolding curves were analyzed using standard methods: the free energies of unfolding were measured using urea denaturation with linear extrapolation to 0 M urea. This approach is valid for HP36 and gives the free energy difference between the NSE and DSE in buffer (18, 19). Thermal unfolding was used to measure stability at low pH because achieving low pH values in urea solutions requires the addition of significant amounts of acid. Thermal reversibility was confirmed by comparing the initial CD signal at the start of a run to the signal measured after the run was completed and the sample was cooled to the starting temperature.

Protein pK_a Measurements.

The pK_a values of Asp/Glu side chains in WT HP36 were measured using NMR, by following the chemical shifts of the side-chain carboxyl carbons over the pH range of 2–7. The pK_a values in the mutants were measured by observing the chemical shifts of the Hβ and Hγ protons over the same pH range. The pK_a of the C terminus was determined by following the Hα chemical shifts of F76. Peptide pK_a measurements were carried out in similar fashion. Chemical shift data were fit to the Henderson–Hasselbalch equation to yield the pK_a.

Computational Methods.

The proteins were solvated in an orthorhombic box of ∼2,500 TIP3P water molecules, and the solvated system was charge-neutralized by adding K⁺ and Cl⁻ ions to a final concentration of 150 mM. To avoid self-interactions in the periodic cell, the dimensions of the water box were such that the protein was 10 Å away from any side. System setup was carried out in CHARMM (44) using a locally modified solvation input script, using the CHARMM22-CMAP molecular mechanics force field (45). Isothermal–isobaric (NPT) ensemble molecular-dynamics simulations were carried out with the NAMD 2.6 engine (46) compiled for the BlueGene/L architecture. All bonds involving hydrogen atoms were constrained to their equilibrium lengths using SHAKE. We used a cutoff of 12 Å for all Lennard–Jones and short-range electrostatic interactions. Long-range electrostatic interactions were treated with a particle mesh Ewald method using a 48 × 45 × 40 grid and a fourth-order interpolation scheme. The simulation time step was set to 2 fs, and nonbonded interactions were evaluated every step. The constant pressure of 1 atm was maintained with the Nosé–Hoover Langevin piston pressure control.

Electrostatic contributions of HP36 side chains to protein stability were obtained using standard methods by solving the linearized Poisson−Boltzmann equation using a multigrid finite-difference solver distributed with the Integrated Continuum Electrostatics (ICE) software package (available for licensing through the Massachusetts Institute of Technology Technology Licensing Office). Dielectric constants of 2 and 80 were used for the solute and solvent, respectively. The dielectric boundary was defined by the molecular surface using a 1.4-Å radius probe, with radii optimized for this purpose (47). The ionic strength was set to 145 mM, with a 2-Å ion exclusion layer. A 129-unit grid was used with overfocusing boundary conditions (the longest dimension of the molecule occupying 23%, then 92%, and finally 184% of one edge of the grid). The electrostatic contribution of a side chain at position i to the unfolded state was modeled by its interactions with the (i − 1)_carbonyl − i − (i + 1)_amino “tripeptide” in the absence of any other protein groups; the peptide conformation was unchanged from that in the folded protein. Figures were rendered with VMD (48).