Simulation techniques in hyperthermia treatment planning

Abstract

Clinical trials have shown that hyperthermia (HT), i.e. an increase of tissue temperature to 39-44°C, significantly enhance radiotherapy and chemotherapy effectiveness (1). Driven by the developments in computational techniques and computing power, personalized hyperthermia treatment planning (HTP) has matured and has become a powerful tool for optimizing treatment quality. Electromagnetic, ultrasound, and thermal simulations using realistic clinical setups are now being performed to achieve patient-specific treatment optimization. In addition, extensive studies aimed to properly implement novel HT tools and techniques, and to assess the quality of HT, are becoming more common. In this paper, we review the simulation tools and techniques developed for clinical hyperthermia, and evaluate their current status on the path from “model” to “clinic”. In addition, we illustrate the major techniques employed for validation and optimization. HTP has become an essential tool for improvement, control, and assessment of HT treatment quality. As such, it plays a pivotal role in the quest to establish HT as an efficacious addition to multi-modality treatment of cancer.

Introduction

Hyperthermia treatment planning (HTP) is defined as the process that begins with obtaining patient data and establishing, by electromagnetic (EM), ultrasound (US), and/or thermal modeling, a set of treatment parameters that maximize treatment quality. The taskforce report of European society for hyperthermic oncology (ESHO) and committee for concerted action in bio-medical engineering (COMAC BME) of 1992 (2) was the first comprehensive document to summarize all available techniques and measurement data required for HTP and validation. The topical review by Lagendijk (3) extended that work to include thermal techniques, and described the state of the art in HTP in 2000. In the last decade, significant progress has been made on the availability and accuracy of EM and US simulation tools and techniques. In addition, thermal simulations based on the Pennes bioheat equation (PBHE) (4) have been implemented in commercial software packages for clinical planning. The importance of HTP in the current clinical setting is illustrated by the recent decision of ESHO to include HTP in their quality assurance guidelines for deep hyperthermia (5, 6).

In this paper, we describe a selection of tools and techniques that are being used for planning and guiding hyperthermia (HT) treatments. Specifically, we analyze EM, US, and thermal simulation tools and techniques, with a strong focus on the potential to improve clinical results. In addition, we address methods to perform validation of numerical algorithms. Also, we describe methods to quantify the influences of those uncertainties that cannot be controlled. Finally, we describe how HTP can be used, not only for pre-planning, but also in feedback control strategies and to assess the overall quality of treatment.

Hyperthermia treatment planning

Simulations for HTP can be divided into three distinct tasks:

1. generation of the patient model.

2. calculation of the distribution of power deposited in the tissue.

3. calculation of the resulting temperature distribution in the tissue.

First, the geometry and tissue properties of the involved body region must be carefully identified. Several companies have preprocessed and made available human body models of typical adult male, adult female, and small child anatomies that have geometric, electromagnetic, and thermal properties included. For improved accuracy, patient specific modeling is performed by segmenting tissues using computed tomography (CT) or magnetic resonance (MR) images of the actual subject. Next, the specific absorption rate (SAR), or more generally the power density (PD), distribution, is determined by EM or US modeling approaches. Once the PD pattern is established, the temperature (T) distribution can be predicted based on thermal redistribution of energy within the heated region with consideration of the impact of physiological aspects such as perfusion and core temperature. While SAR modeling has matured, and good accuracy is now possible in some EM applications (7), there are limitations due to imprecise modeling of patient anatomy, tissue interfaces, and tissue properties. In addition, for EM-HTP, there are still difficulties in modeling the behavior of some applicators, e.g. due to the impact of loading conditions and cross-coupling. For US-HTP, full wave modeling of acoustic propagation and the computational requirements remain an issue. Accurate prediction of T distributions with thermal modeling is an even greater challenge. Large deviations in thermal tissue properties and their variation during the course of heating make in vivo temperatures difficult to predict. Hence, although the temperature level achieved throughout the tumor is believed to determine treatment quality, optimization of heating in current clinical applications is often performed by optimizing the SAR distribution (8). Figure 1 provides a scheme of the steps required for HTP. In step one, CT or MR imaging data is converted into a 3D representation of the patient by delineating different normal and tumor or target tissue regions. 3D models are obtained by assigning corresponding electrical, ultrasonic, and thermal properties to each 3D tissue structure. Next, a model of the applicator with the required degree of complexity and the patient model are combined and used to compute the PD and thermal distributions. Optimization of these distributions can be performed at the PD or temperature “level”. It is also possible to combine the optimization and thermal simulation steps (9, 10).

Figure 1.

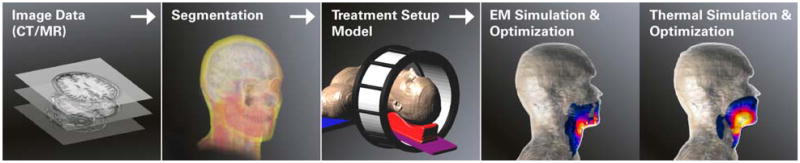
Schematic workflow for EM-HTP, using head and neck hyperthermia as example. In US-HTP the EM simulation & optimization step is replaced by US simulation & optimization.

3D patient modeling

Patient modeling is an important but challenging part of HTP. Time-efficient and easy-to-use segmentation algorithms for delineation of tissues on CT or MR data are a precondition for the 3D models that are required for clinical application of patient-specific HTP (11). The required detail of the models depends on the desired accuracy, which should be assessed carefully for each application. Typically requirements are far higher than for example in radiotherapy, as more tissues need to be distinguished to correctly capture the important impact of strong dielectric property and perfusion variations between tissues, e.g. for hot-spot prediction. Investigators have identified substantial dependences of PD and temperature distributions on both the patient models and the temperature algorithm used (3, 12, 13). Wust et al. showed that surface models, i.e. delineated tissue boundaries for each distinct organ or tissue region, each with assigned homogenous dielectric properties, match clinical results better than models that attempt to derive heterogeneous dielectric properties directly from CT data (14, 15). Similar results were obtained from attempts to use to MR-derived heterogeneous tissue models (16, 17). Ever since, surface models have become the standard, especially for EM-HTP. Tissue properties, however, are non-homogeneous and vary between patients. For dielectric properties, variations of 30% or more have been measured in postmortem humans (18, 19), and even greater variations were shown in breast (20, 21) and brain, by means of MR measurements (22). Fortunately, the influence of those uncertainties on the SAR of deep-regional phased-array applicators has been found to be typically less than 10% (23, 24).

Creating surface models of numerous organs from CT and/or MRI data of each patient requires many man-hours and, which hinders clinical acceptance. Therefore, researchers have begun investigating the increase in segmentation speed and reduction in operator time demands offered by atlas-based segmentation techniques (25, 26). This semi-automatic method requires a library of accurately segmented patient models that incorporate all the relevant tissue-shape variations.

Power absorption simulation techniques

Electromagnetic

In the past three decades, many numerical techniques have been applied in the simulation of EM thermal therapy for cancer. Excellent reviews on numerical codes can be found in Hand et al. (27) and Deuflhard et al. (28) summarized the mathematics required in deep-regional hyperthermia.

In addition to a good patient model, the applicator model is very important for the treatment plan quality. Progress in computation tools now allow generation of more-precise 3D representations of the applicator, e.g., in CAD format, for realistic EM simulations. In addition to physical geometry, the model must numerically reproduce the applicator behavior and its interaction with the tissue, which requires careful discretization and source implementation in the EM model (29). The resolution required for the model depends on the numerical technique and applicator type. Modeling the antenna excitation is also critically important, especially for quantitative SAR prediction (29). In general, an experienced EM designer must make suitable simplifications, and the EM model must be validated first in flat or cylindrical phantoms before proceeding to complex heterogeneous tissue geometries. In addition, applicators should be designed such that they facilitate accurate modeling, e.g., low dependence on load impedance and good control of cross-coupling between antennas.

Achieving maximum benefit from HTP requires a sound translation of the model setup and parameters into the clinic. Translation errors in transferring the applicator settings from the HTP system to the treatment room can seriously reduce the benefit of HTP parameter optimizations. Numerous studies have shown the importance of establishing uncertainties and validating calculated output parameters. Parameters studied for phased arrays are intensity, i.e. amplitude or power, and phase-differences between the antenna drive signals (30-33). Further, variation in the position of the patient relative to the antenna array has been shown to be critically important (34). Also, the posture of the patient during CT or MR image acquisition should match that used for the HT treatment to avoid planning errors. Finally, the shape of the water bolus must be accurately modeled. Uncertainties in water bolus shape have been shown to be important both in superficial (35, 36) as well as deep-regional hyperthermia (34).

HT treatments are normally limited by hotspots in healthy tissue. For EM HT, these are typically caused by electric (E) field maxima at locations with high dielectric contrast (e.g. bone-muscle interfaces). To minimize these hotspots, several objective functions are utilized to optimize antenna phase and amplitude excitation parameters (37). Other parameters, such as patient positioning, are typically not optimized due to the associated prohibitive effort. Optimization is highly application-specific, and numerous papers have been published on phase/amplitude optimization of array applicators (37-45). For some optimization functions, specialized and rapid optimization methods can be used, such as the generalized eigenvalue (GenEV) technique (46) or the virtual source method (40). When more flexibility in the formulation of the optimization function is required, genetic algorithms, or variants such as particle swarm optimization, may be used. While genetic algorithms are usually slower and have the disadvantage of potentially not finding a globally optimal configuration, they do tend to find settings less sensitive to antenna steering uncertainties. Exploiting graphical processing units (GPU's), near real-time (10s) optimization using the particle swarm optimization method followed by line-search, was shown to be clinically feasible for effective adaptation to patient complaints (47). Current research is focused towards optimization functions that rely largely on pre-computed information to enable real-time re-optimization (48) or on the use of multi-goal optimization to determine a large number of pareto-optimal settings (49). Both of these approaches can be used to adapt the treatment plan by reweighting different objectives such as tumor temperature, avoidance of regional hotspots, etc.

Errors in the PD predictions must be minimized to avoid sub-optimal clinical outcome and safety issues. Hence, quantitative validation of HTP systems is essential, followed by regular quality assurance (QA) of treatment equipment, e.g. by means of hardware calibrations and regular verification of the heating patterns (5, 6, 32).

Unfortunately, such measurements are time-consuming and costly, so it is common practice to test the validity of the numerical code by comparison to analytical solutions of simple problems. Hence, when choosing appropriate HTP software or solvers, it is of great importance to again validate numerical results against 2D or 3D measurements. These validation measurements should be performed using dedicated phantoms containing well-characterized tissue-simulating materials and accurate, calibrated equipment, such as fiber-optic temperature sensors, infra-red thermography, and electric field sensors (50-52). In addition to phantom measurements, extensive sensitivity studies and (Monte Carlo) uncertainty analyses can be used to assess the impact on HTP predictions of uncertainties in modeling parameters like tissue properties and their age dependence, discretization, and boundary conditions (53).

Recently, EM-HTP is beginning to be used in applications like preplanning-assisted real-time treatment guidance. Since preplanning-optimized treatment settings often cannot avoid treatment-limiting hotspots completely, strategies are under development to convert information such as temperature readings from invasive, intraluminal (54), or non-invasive temperature measurements (55-59) into adjusted settings based on HTP optimization. In addition, objective and reproducible techniques were developed to also exploit subjective information, such as complaints from the patient, into feedback for real-time adjustment of pre-planned settings (60). Effective use of complaint-adaptive steering has been documented in a randomized trial in which clinically evaluated objective measures were applied (61, 62). Recently, the visualizer for electromagnetic dosimetry and optimization (VEDO), a software tool specifically designed to reduce the complexity of SAR-steering, was developed (47, 63). This tool shows how interference patterns between the fields from different antennas, combined with the dielectric inhomogeneity of the human body, result in hotspots, causing patient pain complaints. By displaying the calculated SAR superimposed on CT (or MRI) anatomy information during treatment, VEDO makes it easier to correlate patient complaints to the energy deposition characteristics predicted by the treatment plan. Simulation-based steering with VEDO is currently under clinical investigation for systems with a higher number of antennas and early results, quantified using the mean predicted target SAR and temperature, are promising.

The use of HTP has been very influential in the evaluation and development of new EM applicators (29, 51, 53, 64-67). Furthermore, HTP has been used to study the efficacy of clinical steering guidelines (68) and for the selection of appropriate applicators for specific disease conditions (7).

Ultrasound

HTP based on full-wave 3D simulations is a challenge for HT applications involving US. The small wavelength and the consequent need for high resolution, results in extremely large computational domains, especially for applicators that focus the energy deeply in the body, i.e. which require modeling of a large anatomical region. This makes the application of full-wave 3D simulations cumbersome for US-HTP, especially for array applicators that may have several hundreds of transducers. Therefore careful application-specific approximations are required for reasonable calculation time and accuracy. Alternatively, high performance computing (HPC) techniques for the acceleration of computations, e.g. the use of computer clusters and graphical processing units (GPU), may gradually make full-wave 3D US-HTP more applicable (69). However, to date, US-HTP has been used most frequently to optimize or adapt the aperture of US phased-arrays to the tumor location and/or shape (70-72). Nonetheless, the need for US-HTP is becoming more and more apparent in applications where the small focal volume of the US field produced is inadequate for the larger target volumes. In addition, US-HTP would be valuable in cases where motion-compensation is necessary to handle respiratory motion, or to prevent bone or air interfaces from interfering with the treatment.

Another issue faced by researchers is the lack of reliable tissue acoustic properties, which are necessary to perform realistic and accurate simulations. Although multiple studies were reported over the years (73, 74), the properties have still not been determined for all relevant tissues, frequencies and temperatures and the employed measurement techniques suffer from technical limitations. Also, much of the available measurement data was acquired with what is known as “phase-dependent” experimental techniques, which were later proven to be unreliable (74). Recent studies (75) reported on novel measurement approaches, and measurements on porcine and human samples are currently underway.

US exposure is often characterized in terms of the acoustic field determined under free-field conditions in water, where “free-field” describes circumstances in which the US beam is not affected by boundaries or other obstacles (76). While most human soft tissues have acoustic properties similar to those of water, there are scattering effects at air, fat, and bone interfaces as well as strong absorption in the periosteum of bone. Thus, precise modeling of those tissues is essential for accurate planning. Furthermore, it should be noted that most equations used for numerical modeling of ultrasonic wave propagation (most notably the Westerveld Equation) are derived based on the assumption that thermo-viscous fluids can approximate the modeled media. Consequently, a common simplification in US simulations is to consider only the propagation of longitudinal acoustic waves, while neglecting shear waves, which are non-negligible in hard tissues like bone. A number of studies, however, did show the possibility to accounting for shear waves using the mode conversion technique (77, 78). Finally, elastic waves in bones are generally not modeled in routine studies of US power deposition in soft tissue, but can be approximated for improved accuracy when the tissue target is near bone (79).

The methods below describe the basic approaches used to compute acoustic waves in soft tissues in order of increasing complexity:

• Incident field method: US-HTP tools are most often based on methods that calculate the radiation patterns and transient pressure fields of single transducers and phased arrays in homogeneous media. These methods use point-source superposition (the Rayleigh-Sommerfeld integral), impulse responses for simple geometries, or the fast near-field method (80, 81) to calculate and project the fields produced by simple transducer geometries on planes along the propagation direction.

• Angular spectrum method (ASM): This method is a very fast spatial-frequency domain technique derived from Fourier optics (82). A modified version of this method, i.e. “hybrid-SM” (83), can account for effects like attenuation, non-linearity, and even inhomogeneity. These features make ASM ideal for US-HTP, although the method is limited in terms of the transducer geometries it can model and complex wave phenomena like back-scattering and nonlinearity are merely approximated.

• Full-wave method: Full-wave propagation generally uses integral equations to predict full-wave propagation, absorption, and temperature distributions in tissue. Generally it fully accounts for all effects of acoustic and thermal heterogeneities (84). However, full-wave treatment planning is still limited to specific applications and frequency ranges, since enormous computational resources are required for sufficiently fine discretization with respect to the wavelength. Although computationally expensive, full-wave methods provide the most accurate predictions for HTP (Figure 2).

Figure 2.

US pressure field prediction for a model of the InSightec ExAblate4000 system, illustrating the feasibility of 3D full-wave simulation for this system with 1024 independently driven transducers. The obtained pressure distribution is displayed with a logarithmic color scale on three orthogonal planes through the target. The distorting impact of tissue parameter inhomogeneity on the focus shape is clearly visible. Modeling allows to plan dynamic focus scanning, for contiguous heating of large tissue volumes.

Freely available software include Field II (Impulse response) (85), the faster Focus (Fast Near-field Method and ASM) (86, 87) and k-wave (ASM) (88, 89).

Despite the innate need for optimization of pressure fields, little progress has been made in the area of optimization of US PD in tissue. Although theoretically possible (90), the large number of elements typically in therapeutic US transducer arrays, i.e. up to 1024, combined with the need for enormous computational resources for full-wave simulations, render most patient-specific optimization techniques impractical. However, the use of incident-field methods, dramatically reduces the computational cost, and applications of US-HTP with numerically computed phase-corrections have been reported (91-93). Such a case is liver ablation where optimization is necessary in order to minimize the ribcage scattering (intercostal space targeting). Modeling was used to generate a focus in a target partly obscured by ribs (94).

Validation in US-HTP is typically limited to that of the different numerical software approaches used to calculate the predicted acoustic and thermal energy depositions. In terms of validating US solvers, a number of approaches, ranging from analytical validation against pre-computed fields to comparison against measured US fields in water-tank setups, have been used. Usually the pressure and temperature generated by actual transducers in the presence of acoustically characterized tissue (skull (95, 96) and bovine femur(97-99)), man-made samples (100, 101), or phantoms (102), was measured using movable hydrophone and/or thermocouples and compared to numerical results. However, to date, no comprehensive validation of the entire US-HTP procedure has been presented, and the efficacy of the treatment is usually evaluated by online monitoring of the induced temperature increase and/or radiation force (103-105).

In clinical hyperthermia applications, US-HTP is typically used with incident-field US solvers to optimize the steering parameters of the transducer elements to maximize thermal dose in the target volume. US and MR imaging are often combined to image and control the position of the US beam focus during heating. In this setting, US-HTP is applied to adjust settings such that underexposed regions also get heated, e.g. by scanning the focus and dynamically covering the entire target volume. Input parameters for planning specify the US transducer (array) geometries, dimensions and positions, the focal length and diameter of each transducer, and tissue geometry (anatomy), boundary conditions, interfaces, and properties. With this input, the radiation pattern of the transducer array is then optimized, usually with incident-field-based simulations to obtain the desired depth, shape, and/or trajectory of heating (76).

Moros et al. used US-HTP to develop the SURLAS applicator (106) and to assess the impact of having bone (ribs) in the ultrasound beam path (79, 107). Regarding US-HTP, they concluded that improvements in accuracy and especially calculation speed are required to facilitate more-routine clinical application (108).

For interstitial and catheter-based heating approaches, with even higher US frequencies used, the resolution required for accurate thermal and SAR modeling close to the device is even more stringent than for physically larger external transducers, due to smaller wavelengths, more localized heating and high thermal gradients. Nevertheless, the feasibility and accuracy of HTP for these applications have been demonstrated in both interstitial (109) and intraluminal (110) applications. The UCSF research team also used HTP to establish guidelines that restrict pelvic bone heating during prostate thermal therapy (111).

Temperature Distribution Simulation Techniques

While SAR modeling is maturing rapidly, the accuracy of temperature predictions is lagging behind. This is due to large uncertainties in the thermal properties of tissue, which vary between patients, within the patient, within each tissue, over time, and as a non-linear function of tissue temperature. The variation with time is even more pronounced with varying temperature (spatially and temporally) due to the nonlinear and patient-specific physiological response of thermoregulation. The spacing of thermally significant blood vessels is heterogeneous, affected by tumor growth and changes with both temperature and thermal dose. Thus, an accurate 3D prediction of the thermal tissue properties is an extreme challenge. The discrete vasculature (DIVA) model (112) considers the impact of individual vessels. Currently, however, devising even a moderately detailed vascular tree can take up to a month of man hours. Thus, the method most commonly used to model heat transfer in living tissue is the PBHE (113), a continuum model that models the impact of perfusion as an isotropic heat sink. Mathematically, it is expressed as:

$$\rho c\frac{\partial T}{\partial t}=\nabla \cdot (k\nabla T)+\rho Q+\rho S-{\rho }_b{c}_b\rho \omega (T-T_b),$$

where T is the temperature, t is the time, ρ is the volume density of mass, c is the specific heat capacity, k is the thermal conductivity, ω is the volumetric blood perfusion rate, Q is the metabolic heat generation rate, S is the specific absorption rate (SAR), and the subscript b denotes a blood property. For clarity, we omitted the parameter dependencies on T, t and spatial position r. This model includes heat conduction in tissue and accounts for energy inputs from metabolism (Q) and external power sources (S). Note that computations of the SAR and temperature modeling are usually decoupled, to reduce the complexity and computational requirements. The last part of the equation accounts for convective cooling by blood perfusion, which is assumed to be non-directional, thus, heat disappears from the tissue via a non-directional heat-sink term. For modeling a regional temperature distribution in tissue with healthy microvasculature and blood flowing through vessels with isotropically distributed orientations, the validity of this equation has been demonstrated. However, for accurate modeling of the impact of blood vessels with dimensions exceeding 0.2mm diameter on the local tissue temperature, the directional effects of blood flow cannot be ignored (114). Many numerical implementations of the PBHE exist, but the most common method is based on the finite difference time domain (FDTD) method (115). Boundary conditions are used to account for convective or sweating heat loss at the patient surface. In some implementations, the temperature dependence of tissue parameters (especially perfusion) is considered, and models that permit body core heating via an increasing blood temperature exist (116)

To capture directional heat flow through tissue, various models have been developed, including the addition of convective terms (117, 118), tensorial effective conductivity (117, 118) and discrete vasculature (DIVA) models (112). The latter have been developed to take into account the non-continuum nature of perfusion and non-equilibrium effects. Thermally significant vasculature is modeled, taking into account vessel size as well as velocity and direction of blood flow (3, 119-122). In DIVA models, a realistic vessel tree is obtained from imaging, e.g. using MRI, and included in the thermal model. One problem is this produces at best a snapshot of the vasculature at the time of imaging, whereas vessel size varies in time and temperature. Another problem of DIVA models is that generation of a vessel tree is a tedious procedure that involves many manual interactions and approximations (3). In addition, only vessels 0.6mm diameter and larger can currently be identified with MRI (123), whereas heat exchange is thermally significant in vessels down to 0.2mm diameter. Therefore, attempts have been made to generate artificial vessels (112, 124-126)}, and Craciunescu et al (127) investigated ways to combine vessel tree data with perfusion maps to include heterogeneous perfusion on a micro scale.

Regardless of how accurately the blood vessel tree is modeled prior to heating, static PBHE and DIVA models are only approximate, since blood vessel size and perfusion rates change dramatically as a function of temperature and duration of heating. Several groups have demonstrated changes in tissue blood perfusion of over 10 times during heating in the 40–45°C range (128-131). Therefore, amendments to the PBHE that incorporate the significantly temperature-dependent nonlinear effects on thermal tissue characteristics have been proposed. The simplest example is to incorporate temperature dependent parameters (13). Another example of an amended PBHE model is the use of mixed models that incorporate effective conductivity (2, 132). In these models, the tissue dependent conductivity k from the PBHE is replaced by k_eff = k(1 + Cω), where ω denotes perfusion and C is an empirical factor that must be experimentally assessed for each application and per tissue. Other thermal models treat arterial and venous blood temperature as spatially and temporally variable. An overview of these models is provided by Arkin et al (117).

At this time, variations of the PBHE method are generally used for thermal modeling of clinical applications because they: 1) lead to reasonable estimates within the known uncertainty of tissue properties; and 2) can be applied without inclusion of accurate vascular trees, which are computationally unmanageable for large tissue regions. However, thermal predictions are very sensitive to thermal parameters, and little data is available on these properties or their variation between patients and under heat stress. Therefore, an extensive uncertainty evaluation per application and treatment site is essential to quantify the accuracy of patient-specific predictions. A Monte-Carlo uncertainty analysis is a valuable tool for addressing this uncertainty due to the strong correlation between thermal parameters. The IT'IS database (133) provides the thermal parameters for the PBHE of many tissues, as well as the variation of the values reported in literature. This information can be used as input for rigorous uncertainty assessments aimed at understanding the resulting variation in PD and temperature distributions, as is the current standard in EM dosimetry (134).

Several investigators have studied the use of thermal modeling to optimize phase and amplitude, i.e. the electronic steering parameters of phased-array applicators (40, 41, 44). Most often, the approach is based on optimization of EM power deposition performed prior to calculation of the resulting temperature distribution. When nonlinear thermal models are used, e.g. to consider thermoregulation, often the optimization includes numerically expensive repeated simulations. Alternatively, more advanced approaches permit the optimization and thermal modeling problem to be solved in a combined approach, e.g. using the partial differential equation (PDE) constraint interior point optimization (9, 10).

Although validation in phantoms has been performed successfully, continued progress in clinical validation of temperature treatment planning is required. In patients, validation of thermal models has traditionally been performed by means of invasive and intraluminal temperature measurements. Unfortunately, these methods are cumbersome, can lead to complications, and provide information only for a small number of locations. The development of MR hybrid hyperthermia systems with thermal imaging capability has opened the door to acquisition of thermal tissue properties during heating (135) and validation of preplanned SAR (67) and temperature profiles (58). However, since only a limited number of such hybrid systems are currently available, it will take time before real-time treatment planning re-optimization based on thermal simulations has matured sufficiently to be accepted for clinical hyperthermia treatments.

Although thermal models have limitations for accurate prediction of temperature distributions in heterogeneous perfused tissue, there are numerous applications that can benefit from thermal modeling. Certainly, thermal models are an excellent tool for best- and worst-case scenario analyses (136). In addition, they can be used to intelligently interpolate temperatures between sparsely measured points. Thermal modeling has also been used successfully to study the influence of water bolus cooling on expected temperature distributions of superficial heat applicators (137-140) and to investigate the influence of uncertainties in thermal parameters on applicator choice for deep-regional hyperthermia (24, 53, 141). With continued development, temperature modeling is expected to become useful for prediction of thermal dose and treatment outcome.

Dose concepts and HT optimization

Defining an optimization function with clinical relevance for the combined treatment of HT with other treatment modalities like radiotherapy and chemotherapy, is not straightforward, due to the multiple interaction mechanisms involved. Thermal optimization can aim at one or more of the following goals: to achieve a target temperature distribution, to optimize heating of tumor compared to healthy tissue, avoidance of hotspots, and maximized tumor coverage. In some cases, rather than temperature, thermal dose quantities are optimized, e.g., CEM43°C (thermal iso-effect dose) (142), which is similar to an “Arrhenius relationship”. This formulation has been shown to correlate with outcome in clinical trials, although it was derived from rodent studies for thermal damage only (143-145).

To reduce the influence of outliers, clinical temperatures are often expressed in terms of percentile ranking. The T50, for example, indicates that 50% of measured points exceed a given temperature value, i.e. the median temperature. When the time of heating is taken into account, parameters such as the CEM43°C T90, which converts the temperature-time profile of any given heating session into the equivalent number of minutes for which 90% of the tumor exceeds 43°C, may be calculated.

An alternative concept is the TRISE parameter introduced by Franckena et al. (146). This parameter specifies the increment of T50 that was measured, averaged over all treatments and intended minutes of total treatment time actually delivered. In a clinical trial with 420 patients treated for locally advanced cervical cancer (LACC), TRISE correlated with both tumor control and survival, whereas CEM43T90 correlated only with survival (146).

Although research that considers the transient nature of heating has been performed, typically only the steady-state temperature distribution, e.g. the mean target temperature, is optimized in current HTP. It should be noted that uncertainties in thermal tissue properties can severely restrict the improvement possible from thermal optimizations, as compared to possible benefits from PD optimization, using e.g. the hotspot target coefficient (HTQ) (8, 53). Furthermore, PD-related indicators such as, i.e., the 25% or 50% of the maximum iso-SAR coverage over the target region, also have been shown to correlate with clinical outcome (147). Hence, although temperature-based dose concepts provide the most promising approaches for optimization goals, using temperature-based optimization is still the topic of debate (148).

Commercial treatment planning packages

The last two decades have witnessed a shift in emphasis from development of modeling algorithms and simulation software approaches to the use of high-level integrated multi-physics HTP programs and systems for applicator design and clinical treatment planning. Non-commercial programs have been developed by groups such as the University Medical Center Utrecht (3), the University of California San Francisco (109, 149), and Duke University (150) in planning for specific applicators and treatment sites.

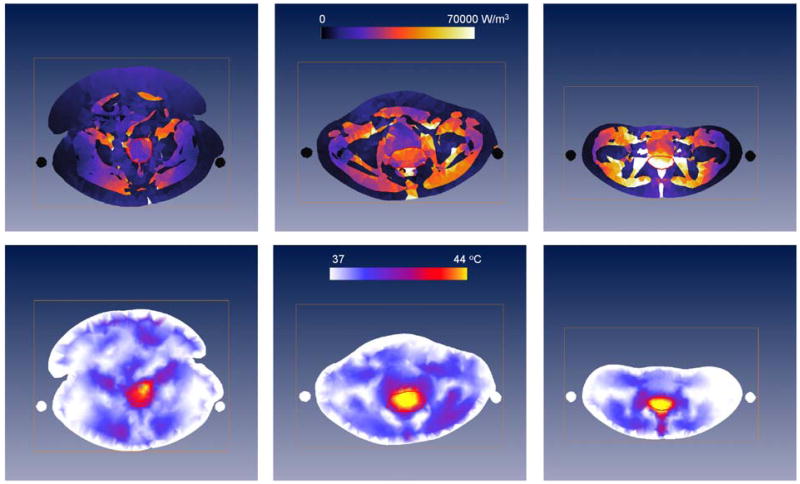
The most widely used commercial HTP system is Sigma-HyperPlan, which was specifically designed for deep hyperthermia with the BSD2000 system (151) (Dr. Sennewald Medizintechnik GmbH, Munich Germany). Sigma-HyperPlan was developed at the Konrad Zuse Institute (28) and has been evaluated for clinical use at the Charite Klinikum (15, 55, 148, 152), Erasmus MC (34, 60, 62, 68, 153), and Duke University (154). Figure 3 shows the PD (top row) and temperature (bottom row) distributions predicted by Sigma-HyperPlan for patients of different dimensions using the same applied power and phase parameters, and with the same maximum temperature in normal tissue (bottom row). Clearly, patient-anatomy largely influences the distributions obtained during deep HT, and hence patient-specific modeling is required. In addition, large differences between PD and temperature distributions are found in this theoretical study, which advocates the use of temperature-based optimization.

Figure 3.

Cross-sections of the PD for 400W (upper row) and temperature distributions (lower row) predicted by Sigma-HyperPlan for a large (left), average (middle) and slim (right) patient with a cervical tumor (red contour). Visible are also the slings on which the patient is positioned during deep HT (black or white circles on each side of the patient). The temperature distributions are obtained by increasing power until 44°C in healthy tissue is reached.

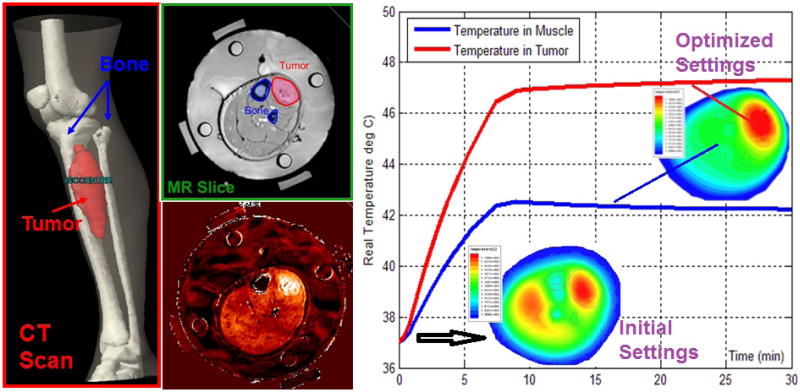
In the last decade, a second commercial HTP package was developed, based on SEMCAD X (SPEAG, Zurich, Switzerland) and introduced by the Erasmus MC group for clinical planning of superficial HT (7) and deep HT (51). SEMCAD X, originally developed as a software tool for high-resolution EM simulations involving complex anatomical models, allows creation and analysis of various applicator models. Addition of the segmentation tool iSEG (www.zurichmedtech.com), multiple thermal solvers (PBHE, keff, DIVA), and several SAR and temperature optimization approaches as well as post-processing routines for dose and effect quantification has elevated SEMCAD X to a flexible HTP framework. Recently, a third integrated HTP package, i.e. ALBA HTPS (www.albahyperthermia.com), has become available. This package is based on the EM and thermal kernels of the CST multi-physics simulator (www.cst.com) and was developed in cooperation with the University of Rome Tor Vergata. Finally, although not integrated HTP platforms, COMSOL (www.comsol.com) and HFSS (www.ansys.com) provide most of the simulation functionality required for HTP when combined with separate programs for tissue segmentation. For HFSS, Duke University showed that integration of commercial segmentation and EM and a thermal solver with MR based thermometry enables optimization of HT quality (Figure 4) (155). In this study, they demonstrated that a pre-treatment plan could be significantly optimized, within minutes, using on the basis of real-time temperature monitoring feedback.

Figure 4.

Combined use of segmentation, EM, and thermal solvers to generate initial temperature distributions in the pretreatment phase. During treatment, the MR temperature imaging (MRTI) provides feedback to empirically determine patient specific parameters, e.g., perfusion. This information was used to steer the beam effectively to the target tumor on right side of leg and away from muscle at the left of bone (67, 155).

Outlook/Discussion

In recent years, HTP has begun to emerge into practical clinical use. The main strength of simulations is that the effectiveness of different scenarios can be judged before the HT session to aid in selection of patient, applicator or treatment approach, specific power excitation planning, and clinical outcome prediction. In addition, simulations are helpful for assessing treatment risks to the patient, e.g. effect of metallic implants, or operator. HTP simulation tools can be used to develop enhanced treatment approaches or, retrospectively, to analyze treatment quality. Other areas where HTP tools play an important role are the education and training of hyperthermia technicians and physicians, treatment visualization, development of QA guidelines and protocols, and basic research to increase understanding of hyperthermia treatments or assess related uncertainties and the impact of individual parameters. In our experience, treatment plans provide an objective basis for stimulating interdisciplinary discussions and as well as an excellent venue for continuous training and improvement in therapy.

For the future, we expect that thermal modeling will continue to mature and will be used to prospectively compare treatment options, optimize treatments as well as to enrich temperature measurement data. In treatments where non-invasive measurement of 2D and 3D thermal distributions is possible, HTP models will be complemented with fast optimization feedback control algorithms that can correct for model errors and uncertainties (39-41, 156). For treatments where MR thermal imaging is not a realistic option, thermal models are even more critical for improving treatment quality. Due to the overlapping and complementary information obtained, further innovation of prospective PD and thermal modeling should go hand-in-hand with development of non-invasive thermometry approaches. In vivo validation of the developed HTP tools and assessment of the offered benefit will be of critical importance going forward, as will be the development of tools that are suitably embedded in the clinical work-flow for routine clinical use.

Conclusions

HTP has demonstrated major progress over the past decade and is rapidly gaining ground in practical clinical application. Even when its limitations and ongoing development are considered, HTP in its current form is already improving treatment quality. HTP has demonstrated its usefulness in the design of new heating equipment, in providing critical understanding of the relative role of multiple conflicting treatment parameters, in guiding the development of updated treatment protocols, and in the education and training of technologists and physicians. Finally, the advent of non-invasive measurement strategies is expected to be a strong stimulant for improved accuracy of patient-specific simulations and real-time treatment optimization strategies.