Using Models to Predict the Future: What To Do When The Data Run Out?

Introduction

Although clinical trials often provide “best evidence” comparing the effectiveness of alternative management strategies, such evidence can be limited in duration or the results reported, causing clinicians and policy analysts to wonder “What if?”. Models of the clinical prognosis, often over patients’ lifetimes (the long haul), are perhaps weaker evidence but can help answer questions about the management of individual patients and can place that best evidence into the context of clinical reality.

Clinicians treating patients after percutaneous coronary intervention face complex choices among antithrombotic agents. Although thienopyridines plus aspirin have emerged as the standard of care, uncertainty exists when balancing risks with benefits of newer agents such as prasugrel. Certain variants of the pro-drug activating enzyme CYP2C19 produce less active drug and have decreased efficacy in preventing ischemic events (1). Guzauskas presents deterministic and probabilistic models (2) comparing the outcomes of the 15-month TRITON trial (3) of two thienopyridines and a 2C19 genotype-guided strategy. This careful analysis provides important insights but leaves unanswered questions. Investigators, clinicians and policy makers often muse on how to translate a trial of limited duration into clinical policy and action. Clearly, the post-trial time horizon can have important impacts on the benefits and risks (and indeed the costs) of a therapy. Longer windows (e.g., waiting for half the patients to die to observe median survival or for all the trial patients to die to observe average survival or life expectancy) may be impractical and expensive.

We often think of different horizons when considering a trial. First, we have the trial or data collection horizon, sometimes referred to as the hard data or evidence period. Some policy analysts only consider this hard evidence horizon. Second, we have the modeling or analytic horizon, which often extends beyond the trial horizon and may often be based on observational or registry data. Finally, we have the lifetime horizon that can extend even beyond the observational data and reflect assumptions about the future. We typically have less confidence about the longer horizons. With an analysis of the 1995 GUSTO trial of thrombolytic therapy in patients with acute myocardial infarction, Mark (4) modeled with all three horizons---the trial, observational data from the Duke Cardiovascular Database and population-wide vital statistics. The concept of multiple modeling horizons with differing data sources can be seen in Figure 1, which illustrates hypothetical survival from three data sources: TRITON, Nottingham, and population wide vital statistics. Beyond using registry data, the emergence of electronic medical records and claims databases makes it possible to examine long-term outcome data, although selection biases and the lack of formal criteria for certain events remains problematic.

Figure 1. Hypothetical Survival Curves in Three Horizons.

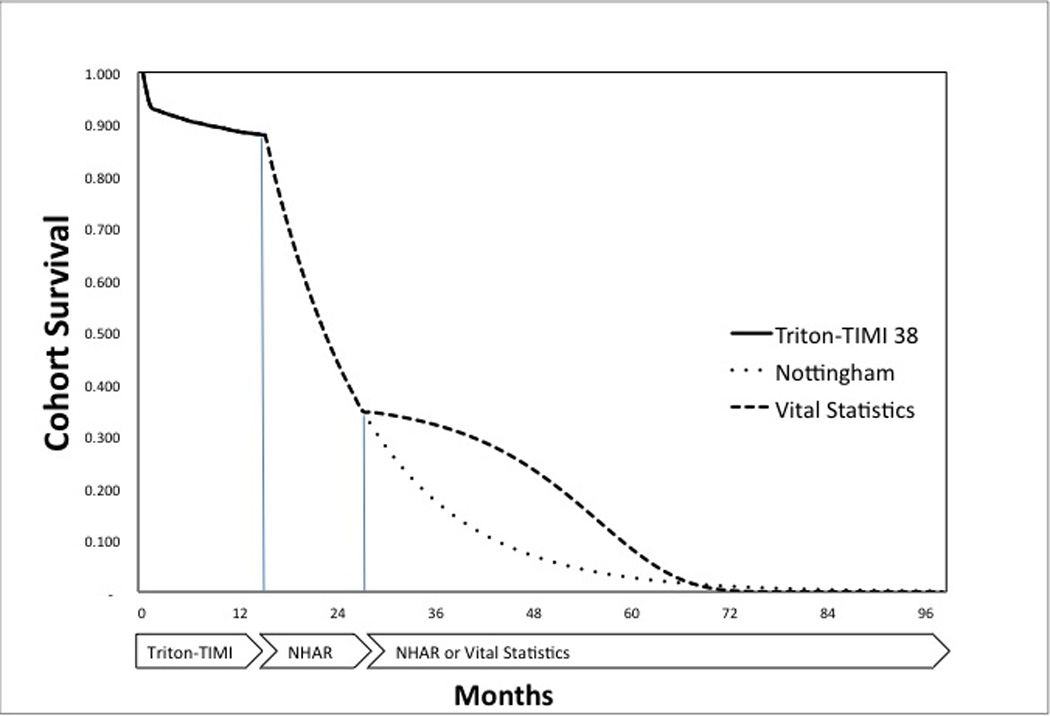
The solid line represents the data from the TRITON trial. The dotted lower curve represents older data from the Nottingham Heart Attack Register (NHAR) with assumed constant mortality rates, Guzauskas’s assumption. The dashed line represents an alternative assumption based vital statistics data from life tables and if true would suggest even better survival with antithrombotic treatment. The sharp inflection at 15 months reflects Grazaukas’s arbitrary assumption that thienopyridine’s therapeutic efficacy disappears suddenly after the TRITON trial horizon.

Guzauskas considers only two horizons and data sources--- the 15-month data from the TRITON trial and long-term data ultimately drawn from the Nottingham Heart Attack Register (5). Guzauskas assumes that the mortality rates in a long-term Markov or state transition simulation (as borrowed from Main and Palmer (6) and ultimately from Palmer and Sepulcher (7) in their study of glycoprotein IIb/IIIa antagonists in myocardial infarction) are constant and relevant, now two decades later. Guzauskas concludes that the risks of increased bleeding and benefits of decreased cardiovascular events offset one another, producing what is essentially a close call (8), as Wivott concluded in the original trial report (3). Although Guzauskas has been explicit about his model, the implications of his assumptions (e.g., a higher mortality rate based on older registry data) may not be obvious to the reader. Further, he assumed that patients who have lower levels of active thienopyridine because of certain variant 2C19 alleles have an increase rate of ischemic events but do not have a correspondingly decreased incidence of bleeding events. In this commentary, we explore some of the implications of such assumptions.

In Main and colleagues’ original model (6), long-term prognosis explicitly reflected subsequent myocardial infarctions and death, but neither strokes nor bleeding events. Further, the underlying registry data from that model was drawn from 1992 and 1998 cohorts. The prognosis of patients with ischemic heart disease (IHD) has improved substantially in the past 15 years, hypothetically allowing the underlying natural increase of mortality rates with increasing age to become more evident, revealing the typical sigmoid shape survival curve (Figure 1, dashed line). To explore this further, we replaced the constant rate of death for IHD with an age-adjusted rate based on CDC life tables and added an excess mortality rate to reflect increased mortality due to IHD. After five years without a subsequent myocardial infarction, we allowed that IHD rate to decline over time. Our analysis showed an even closer call, although pharmacogenomic testing became ever so slightly the preferred strategy. Further, because the older Nottingham data have a far lower survival than either the TRITON data or vital statistics data, we question their relevance in 2012.

Guzauskas appropriately reports both 15-month (the trial horizon) and lifetime projected results, considering both survival and quality of life. The quality of life adjustments are drawn from a 5-year-old study by Sullivan and Ghushchyan (9), using a well-validated preference assessment instrument (the EQ-5D). Similar data were reported earlier by Fryback in the Beaver Dam Study (10). The assumptions in Guzauskas’s Table 1 (2) raise some questions. The long-term burden of a stroke appears only slightly lower than having uncomplicated IHD. These data challenge our clinical experience, especially because the strokes in the TRITON study were most likely hemorrhagic. Nonetheless the inclusion of quality of life in this study is useful.

Models serve to make one’s assumptions explicit; as such, they can always be criticized. Guzauskas must be applauded for the clarity of his paper, allowing us to reproduce its main results. Beyond interpreting the data from a trial, models also allow one to ask “What if?” other assumptions were the case. What if the thienopyridine were continued beyond 15 months? What if patients with the variant genotypes also had a lower risk of bleeding? What if the long-term survival were higher? The choice of model can make a difference, especially because Guzauskas’ results are a toss up (8). With little difference, on balance, between long and short-term health outcomes, the choice may be driven by drug availability and cost.

Guzauskas did not consider cost, but in a world of limited resources cost cannot be ignored. We cannot just select the more effective therapy irrespective of the comparative cost. Health outcomes are often imprecise and include substantial variability from patient to patient. When the mean or median differences are small or when random or patient-specific variability leads us to conclude there is no statistically significant difference between therapies, but if one treatment costs $500 while another costs $50,000, it would be wasteful to select the $50,000 option. We could afford to treat 100 patients with the $500 option for every patient for whom we chose the more expensive option. There is no single right answer here. It depends on what question is being asked, by whom, and what resources are available.

Guzauskas concludes that genotyping offers promise, a conclusion that seems at variance with his analysis that suggests that the choice is a close call. However, broadening the analysis to flesh out a more current long-term model and including the possibility that patients with the variant genotypes may have a lower incidence of bleeding might enhance the utility of genotyping.

Another set of more technical issues, important for both modelers and model users, is the distinction between rates (events per unit time) and probabilities (events in a population at risk). Event rates may be adjusted if one knows the hazard ratios, as shown in Guzauskas’s Table 1 (2). Probabilities can be adjusted with likelihood ratios, relative risks or treatment efficacies. When adjusting probabilities upward (relative risks > 1), we must be cautious that the adjusted probabilities do not exceed 1.0. It is often better to convert the probability to a rate, adjust the rate with a hazard ratio, and convert the adjusted rates back to probabilities for use within the model, which requires transition probabilities. Alternatively probabilities can be converted to odds, modified by likelihood ratios, and reconverted back to probabilities. In this model the occurrence of events is presented as probabilities (e.g., non-fatal MI) and adjustments as hazard ratios. We assume the proper conversions took place..

Guzauskas assumed that the hazard of IHD events for patients with the 2C19 variants receiving clopidogrel is increased (hazard ratios of 1.45–1.84), but logic would suggest that such variant patients might also have a lower risk of bleeding because they presumably have less active drug. Mega’s meta-analysis (1) reports the effect of 2C19 genotypes on ischemic events but not on bleeding rates. Because Guzauskas stuck to the reported evidence, he chose to model the variants’ effect on IHD events but not the potentially diminished bleeding risk. We extended his model assuming that both IHD events and bleeding events are affected by variant status, arbitrarily assigning a bleeding hazard ratio of 0.70 for patients with the 2C19 variants. In that case, the close call became even closer. But if that hazard ratio for bleeding were below 0.47, clopidogrel becomes the slightly preferred strategy.

Because clinical trials rarely collect data over a lifetime horizon even though long-term prognosis can be relevant to clinical (and policy) choices, it is important to make and explore explicit assumptions by building models of the future. An accurate, well-constructed model will better inform the choice. Guzauskas here offers an explicit, open, competent model that should form the basis for current choices and perhaps inform future ones, when better, more contemporary and more complete data about long-term survival and about the effect of variant genotypes on short-term risks of thienopyridine complications become available.