Quantitative Imaging Methods for the Development and Validation of Brain Biomechanics Models

Abstract

Rapid deformation of brain tissue in response to head impact or acceleration can lead to numerous pathological changes, both immediate and delayed. Modeling and simulation hold promise for illuminating the mechanisms of traumatic brain injury (TBI) and for developing preventive devices and strategies. However, mathematical models have predictive value only if they satisfy two conditions. First, they must capture the biomechanics of the brain as both a material and a structure, including the mechanics of brain tissue and its interactions with the skull. Second, they must be validated by direct comparison with experimental data. Emerging imaging technologies and recent imaging studies provide important data for these purposes. This review describes these techniques and data, with an emphasis on magnetic resonance imaging approaches. In combination, these imaging tools promise to extend our understanding of brain biomechanics and improve our ability to study TBI in silico.

1. Introduction

1.1. Mechanical Strain and Strain Rate are Crucial Factors in Traumatic Brain Injury

Traumatic brain injury (TBI) is a major health problem in both children and adults; approximately 1.7 million new cases arise each year in the United States (1). In 1999, more than 5 million Americans had disabilities resulting from TBI, incurring costs estimated at $56.3 billion annually (2). TBI is a global health issue, with the incidence of brain injury due to traffic accidents even higher in Latin America and sub-Saharan Africa (150–170 per 100,000) than in the United States and Europe (3). Mild TBI is the most prevalent form of head injury, with more than 300,000 sports-related concussions per year in the United States (4). Concussions have been observed in American football at skull accelerations estimated to be in the range of 800–1,000 m s⁻² (5). Furthermore, blast-induced TBI has emerged as one of the most important medical problems related to military deployment (6). The effects of brain trauma can be lasting—TBI is an established risk factor for Alzheimer's disease, especially in combination with the ε4 allele of apolipoprotein E (7, 8). The mechanism of this increased risk is not clear, but it is plausible that TBI affects the brain via mechanically induced changes in handling and metabolism of amyloid β peptide, as supported by studies reporting accelerated amyloid β deposition following TBI in mice expressing mutant human amyloid precursor protein (9, 10).

The physical process underlying most TBI is rapid deformation of brain tissue caused by acceleration of the skull (11). In concussions, mild tissue strain is thought to cause diffuse, mechanically induced depolarization of cortical neurons (12). In severe trauma, diffuse axonal injury occurs throughout the white matter of the brain, as axons are stretched beyond a physiological injury threshold (11). The clearest studies of the relationship between rapid neural tissue deformation and injury have been performed outside the brain—for example, on the guinea pig optic nerve (13) and in in vitro cell cultures or tissue slice preparations (3, 14, 15). These studies show clearly the effects of large strain on functional and morphological properties of axons (e.g., 13). Although in vitro experiments are essential to understand the pathology of brain injury, to be relevant they should replicate the key physical conditions experienced by neurons and axons in the intact brain.

For decades, the details of brain deformation in human TBI have remained the subject of much speculation and indirect study. An example is injury in the frontal lobe of the brain that presents from occipital impacts far from the impact site—known as contrecoup injury (11, 16). Many explanations of contrecoup injury have been proposed (12, 16), but definitive measurements of brain deformation needed to evaluate competing hypotheses have only recently become available. This review summarizes the state of the art in acquiring these data.

1.2. Computer Models are Highly Promising but Require Data for Parameterization and Validation

Computer simulations of TBI offer enormous potential, especially to replace experiments that cannot be performed for ethical reasons (e.g., injury-level accelerations in humans) or that are extremely difficult or expensive. However, simulations require accurate models of tissue and tissue connectivity and, most importantly, experimental data to confirm the accuracy and predictive ability of these models. Lacking such data, numerical predictions of brain deformation remain uncertain. One of the most important reasons to measure deformation in the human brain is to improve the quality and credibility of numerical models.

Computer models of slow (quasi-static) brain deformation have been developed by Miga and coworkers (17, 18), Miller and coworkers (19–21), and Ji et al. (22) for neurosurgical applications. The goals of such models are to update presurgical magnetic resonance (MR) or computed tomography (CT) scans of the brain during surgery and to assist in surgical planning. Although these quasi-static deformations are not a focus of this review, several commonalities exist in the associated imaging needs and technologies, including the need for validation, the need for accurate material data, and the need for careful consideration of boundary conditions.

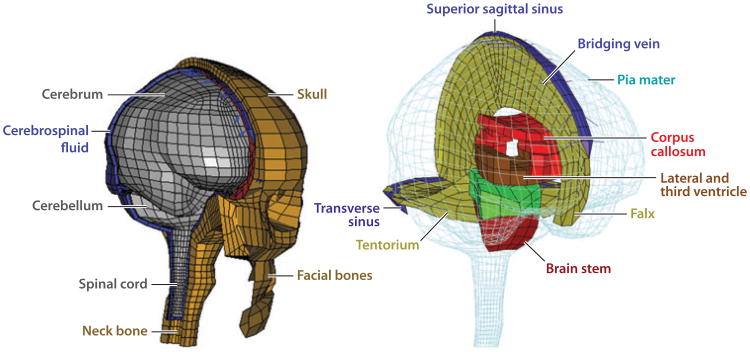
A great many finite-element (FE) models describe human head and brain motion during rapid acceleration (23–28). We highlight one example to describe both the successes and challenges associated with this type of modeling and to set the stage for the role of imaging studies. The Wayne State University Brain Injury Model (29) is a FE model of an adult human male head, with accurate geometry and anatomical features [e.g., scalp, skull, dura, falx cerebri, tentorium, blood vessels, white and gray matter, cerebrospinal fluid (CSF)] represented by different material properties in different interacting regions, each connecting to its neighbors through prescribed boundary and interaction conditions. Although the technology available to input detail into this model is remarkable, that available to validate the model has lagged behind. The state of the art has been comparison with intracranial pressure data from cadaver impact tests (30, 31). Measurements of pressure are coarse, and a broad range of tissue models can replicate a single pressure trace. Needs for spatial resolution and for validation at the level of the parameters implicated in TBI, such as tissue strain and strain rate fields, motivate the emerging class of noninvasive technologies described in this review.

Similarly, efforts to understand and prevent blast-induced TBI have motivated development of mathematical models of blast-induced pressure fields affecting the human head. The mechanical loading applied in such models takes advantage of decades of theoretical development and experimental validation of blast physics. These models also include detailed anatomy of the head and brain, determined by magnetic resonance imaging (MRI) (Figure 1). However, constitutive models of tissue used in these simulations are simplified and not calibrated to direct mechanical tests of tissue response in vivo. Taylor & Ford (32) use linear viscoelastic tissue, and Nyein et al. (33) use isotropic, hyperelastic brain tissue augmented with model viscoelastic behavior. These simplified models may be appropriate to predict the brain's responses to blast-induced mechanical loadings, but the accuracy of such predictions is yet to be established, which underscores the importance of direct comparison with experimental measurements.

Figure 1.

The technology underlying the physical discretization of computational models of the human head can now produce remarkable anatomic accuracy and predictions of mechanical fields at very fine spatial resolution. However, mathematical models and material data for the tissues, structures, and interactions within the brain have lagged behind, as have data for validation of model predictions. This review summarizes the state of the art in the collection of such data on brain biomechanics in vivo. Adapted from Reference 28, with permission.

In summary, the development of imaging-based technologies for brain biomechanics is driven by three needs. The first is the need to estimate and validate material properties that serve as inputs to mechanical models. The brain is a heterogeneous structure whose different constituents (e.g., cortical gray matter, white matter, subcortical gray matter, and cerebellum) likely have different nonlinear, viscoelastic, and anisotropic mechanical properties. The second is the need to estimate and validate boundary conditions and interaction models. The brain is surrounded by CSF and attached by a variety of materials (vessels, membranes, sheathed nerves) to the skull. The skull has several bony prominences, particularly at the base, that restrict motion of the brain relative to the skull. The membranes surrounding the brain (pia mater, arachnoid mater, and dura mater) are all stiffer than the brain. The dura mater includes structures (the falx cerebri and tentorium) that clearly interact with and constrain the motion of the brain parenchyma. The third need is to test hypotheses and validate models and their predictions. For example, interfacial structures might be critically important to the mechanisms of impact- and blast-induced TBI, but data to test this hypothesis are only beginning to become available.

1.3. Challenges in Making Meaningful Measurements of Brain Motion

The human brain is well-hidden, well-protected, delicate, metabolically active, and anatomically complex. These properties make the study of brain deformation daunting. Brain tissues of other large mammals have material and neurophysiological properties similar to those of the human brain, but geometry and boundary conditions unique to the human brain are likely important in determining its response to impact or blast. Cadaver studies are complicated by numerous factors, especially changes in the mechanical state of the brain and its environment post mortem (34). Accordingly, imaging studies to illuminate TBI have been pursued along two general lines: (a) animal and cadaver studies that address general mechanisms of injury, particularly the material response of brain tissue, and (b) human studies that are noninvasive and that target TBI indirectly by determining the response of the intact brain to subinjurious mechanical stimuli.

In this review, we summarize the contributions of imaging to the understanding of TBI and to the development of accurate numerical simulations of brain biomechanics. We emphasize recent MRI-based studies, because they provide full-field measurements of time-varying deformation in the living brain. Finally, we discuss some of the many remaining challenges and possibilities for future work in this area.

2. Technical Requirements for Imaging Rapid Brain Deformation

TBI involves spatial and temporal variations in brain motion. Quantification of intracranial deformation has been approached in two ways. The first, exemplified by the studies of Hardy et al. (35) and Zou et al. (36), involves tracking a small number of physical markers. These authors imaged neutrally buoyant markers embedded within a cadaveric brain, using high-speed X-ray images taken in two orthogonal planes. Triangulation of marker positions over time yielded a time course of their displacements. The second approach uses the image contrast itself, typically resulting in much higher spatial resolution. This method leads to a sequence of two-dimensional (2D) images (or 3D image volumes) acquired over time and stored as 3D arrays (M × N pixels ×P sample times) or 4D arrays (M × N × K voxels ×P times). We summarize in this section the analysis of strain and deformation needed to interpret these data.

2.1. Displacement and Strain Fields

Deformation estimation typically begins with image processing to extract displacement fields. Deformation is quantified by comparing a deformed configuration of the imaged brain with an undeformed reference configuration of the imaged brain, in terms of a displacement field and its spatiotemporal derivatives. The location of each material point of the body is defined by its position X in the reference configuration and its position x(X,t) = X + u(X,t) in the deformed configuration, where the displacement field u(X,t) is a vector field representing the displacement at time t of the material point that was initially at position X at time t = 0.

Displacement fields are commonly estimated by tracking markers in each image that identify material points. Because multiple markers are used to define a spatial field, establishing the correspondence between markers in deformed and reference configurations is a critical step. Some imaging techniques, such as phase-contrast MRI, provide direct measurements of displacement or velocity for each voxel, eliminating the problem of correspondence. Digital image correlation techniques may also be used to estimate displacement fields (37).

Displacement fields take into account deformation, rigid-body translation, and rigid-body rotation. Strain measures of interest isolate deformation and are based on the deformation gradient tensor field, F(X, t), which maps an infinitesimal vector dX in the reference configuration to a corresponding vector dx(X, t) in the deformed configuration:

$$\mathbf{\text{dx}}(\mathbf{\text{X}},t)=\mathbf{\text{F}}(\mathbf{\text{X}},t)\mathbf{\text{dx}}.$$ (1)

An example of an appropriate strain tensor is the Green–St. Venant strain tensor:

$$\mathbf{\text{E}}(\mathbf{\text{X}},t)=\frac{1}{2}({\mathbf{\text{F}}}^T(\mathbf{\text{X}},t)\mathbf{\text{F}}(\mathbf{\text{X}},t)-\mathbf{\text{I}}),$$ (2)

where I is the identity tensor. Whereas F(X, t) includes the effects of rotation, E(X, t) does not, so that E(X, t) vanishes in a body that rotates but does not deform. Strain is a nondimensional measure of deformation. Normal strains can describe the change in the length of a line relative to its length in the reference configuration; for example, 0.05 strain corresponds roughly to a 5% change in length. In the limit of infinitesimal deformations, shear strains describe the change in angle between lines that are perpendicular in the reference configuration.

2.2. Spatial and Temporal Resolution, Discretization, and Noise

Converting from a series of pixelated images to a strain field involves tracking specific image features (markers) through the series and presents challenges associated with both spatial resolution and temporal resolution. Spatial resolution of displacement fields is determined by the spacing between tracked markers, which is typically larger than the pixel resolution. Because finite difference approximations are used to estimate the spatial derivatives in Equation (1), strain can be estimated accurately only if the distance between tracked points is much less than the characteristic wavelength or spatial feature of interest. Temporal sampling must be sufficiently fast to resolve displacements, and image acquisition must be sufficiently fast to avoid blurring. The timescales for impacts and pressure pulses associated with TBI pose challenges. As an alternative to studying short transient events directly, harmonic excitation can be used to characterize the behavior of the skull and brain, and the duality between frequency and time domain responses can be exploited (38). For harmonic behavior, the sampling rate must exceed twice the frequency of the behavior itself (39), and to accurately capture transient response, the temporal sampling rate must be at least twice the highest frequency of interest. In practice, higher temporal sampling rates are always helpful to characterize continuous behavior.

3. Imaging Studies in Physical Brain Surrogates, Animals, and Cadavers

3.1. Imaging Studies of Deformation in Physical Models

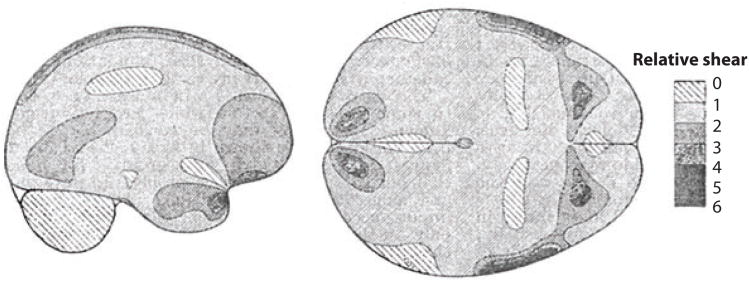
Much of our current insight into the mechanics of TBI comes from imaging of physical models: soft materials encased in rigid containers exposed to accelerations. In a classic study, Holbourn (40) filled models of a cross section of human skull with a gelatin mixture, sheared it by imposing large linear and angular accelerations of the skull, visualized strains with a polariscope, and depicted the strains using hand drawings (Figure 2). More recently, Margulies et al. (41) and Meaney et al. (42) filmed the motion of grid patterns in gel inside animal and human skulls during imposed angular acceleration (Figure 3). The amplitudes (∼10⁵ rad s⁻²) and durations (15–20 ms) of angular acceleration used in these studies reached levels associated with diffuse axonal injury in pigs (42). Large shear strains (0.10–0.30) were observed in these studies. Gel models, however, lack anatomic details such as vasculature, heterogeneous tissue structure, and CSF. This lack likely oversimplifies the response characteristics of the human brain, whose anatomic detail may, in fact, dramatically affect its response to impact or blast loading.

Figure 2.

The earliest estimates of acceleration-induced shear strain fields within the human brain are those of Holbourn (40), who observed shear deformation patterns within gelatin-filled skulls due to occipital impact and angular acceleration/lateral impact. The scale bar represents the relative magnitude of shear in arbitrary units. Recent magnetic resonance imaging data have shown that shear strain patterns within a gelatin-filled skull differ fundamentally from those within a living human owing to several factors including brain architecture, vasculature, and attachment to the skull. Adapted from Reference 40.

Figure 3.

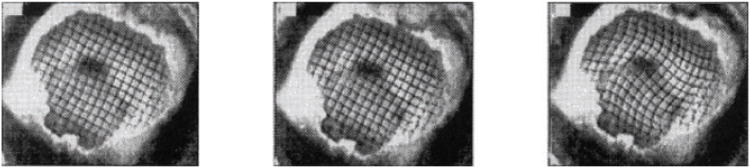
High-speed and high-resolution videography techniques have enabled studies of physical models of the brain that undergo large deformations at high strain rates. The skull of a miniature pig was filled with two layers of silicone gel; a grid pattern was painted between the layers. The assembly was subjected to angular accelerations of 50,000–200,000 rad s⁻² while grid deformation was recorded at 1,000 frames per second. Adapted from Reference 42.

3.2. Visualization of Brain Deformation in Animal Studies

Imaging studies have long been performed in the brains of live animals, as well as post mortem in fresh animal brain specimens. Pudenz & Shelden (16) replaced the top half of the skull of a macaque monkey with transparent plastic and filmed the top of the brain during blunt impact at 2,000–3,000 frames per second. Results, presented as hand-drawn sketches in their 1946 paper, confirmed that impact leads to relative motion of the brain within the skull and that the brain rotates and deforms after impact. Nonetheless, internal brain deformations could not be visualized, and deformations were not quantified.

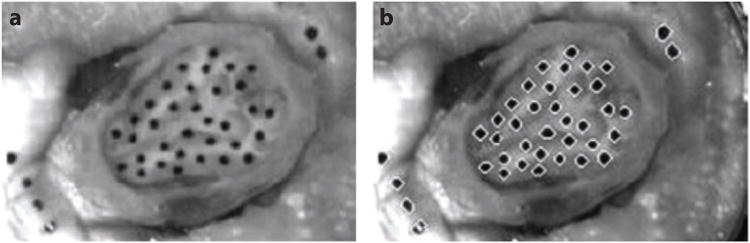
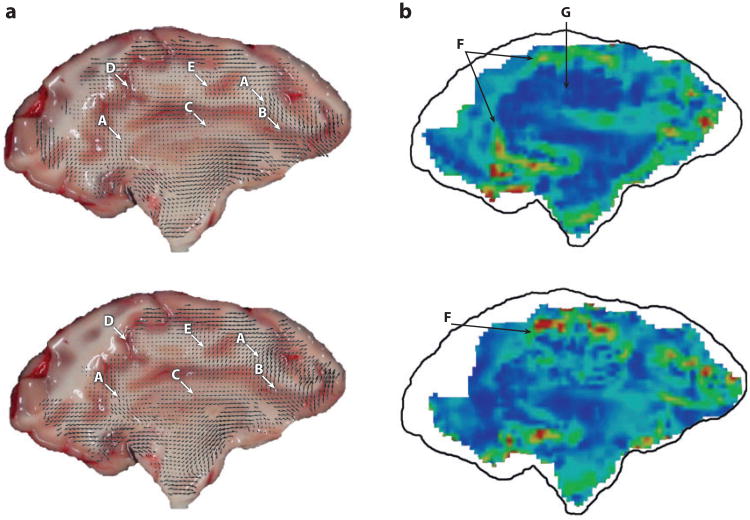
Two recent high-speed optical imaging studies of deformation of the pig brain, post mortem, illustrate the potential and challenges associated with these methods. Ibrahim et al. (43) studied the response of the piglet brain in situ (post mortem, but within the skull) to high angular acceleration (Figure 4). The head of the piglet was transected so that an interior plane of the brain was exposed. This surface was marked, and the entire transected head was held securely in a container with a transparent cover. The assembly was subjected to angular accelerations believed to be adequate to cause injury, and high-speed (2,500 frames per second) images were acquired. Peak shear strains estimated from the displacements of surface marks (strain estimation methods are discussed below) typically exceeded 0.2. Lauret et al. (44) accelerated to ∼2,000 m s⁻² sagittal slices of pig brain, 4 mm thick, contained within a flat, stiff container with a skull-shaped cross section and a transparent cover. Images acquired at 1,600 frames per second were analyzed using digital image correlation to compute the displacement field of a random speckle pattern painted on the exposed brain surface (Figure 5). For each small region of the reference image, the local displacement that produced the highest correlation with the deformed image was taken as the true displacement. Peak strains of 0.10 to 0.20 were observed. The strength of these two studies is the ability to image at strains and strain rates similar to those observed in TBI. The shared drawback is the restriction to image strains on the surface of a portion of the brain ex vivo, with dramatically altered boundary conditions.

Figure 4.

Progress on understanding acceleration-induced strain in the animal brain in situ has been made through high-speed video studies. The exposed flat surface of the hemisected brain of a juvenile pig was marked with India ink (a), and the skull and brain were covered by a layer of lubricant and by a transparent Plexiglas cover plate. Strain fields were estimated from marker positions (b) during an angular acceleration pulse with a peak magnitude of ∼10,000 m s⁻². Reproduced from Reference 43.

Figure 5.

High-speed video techniques have been applied to image thin slices of brain tissue subjected to high accelerations in vitro, to gain information about their mechanical response at high strains and strain rates. The trade-off is the absence of the natural structural attachments and mechanical environment of the brain. Here, displacement (a) and strain fields (b) are shown at 12 ms (top) and 23 ms (bottom) postimpact, measured in sagittal slices (4 mm thick) of a pig brain encapsulated with artificial cerebrospinal fluid in a rigid cavity and subjected to linear accelerations of approximately 2,000 m s⁻². In panel a, the uppercase letters A–E indicate areas where tissue heterogeneity is observed to affect the displacement field; in panel b, the letters F and G indicate vertical (F) and horizontal (G) sulci. Adapted from Reference 44.

Studies in the intact living animal brain have been performed on small animals using MRI methods. Using MR tagging (described in Section 4), Bayly et al. (45) measured strain fields in response to closed-skull indentation in a juvenile rat. The combined response of the deformable skull and of the heterogeneous, compliant, partitioned brain determined the strain field; this theme is consistent with the idea of the brain as a structure as well as a material and consistent with observations taken on humans as described below. Using MR elastography (described in Section 5), Clayton et al. (46) measured intracranial strains induced by harmonic loading in brains of living mice.

The great advantage of imaging studies in animals is the ability to characterize large deformation behavior in the intact brain. The most important shortcoming is that the anatomy of the human brain and skull differs greatly from those of other animals. The studies detailed below suggest that brain geometry and the details of the interface between the brain and skull are among the most important factors in the brain's mechanical response to mild impact, and this could well be the case for severe impact and blast loading as well. Although qualitative observations on the general features of brain injury can be derived from brain indentation studies in rodents, relating these to acceleration-induced injury in humans is challenging. A key limitation is the scaling effect (47, 48): The acceleration required to attain a specific level of strain in an animal model scales nonlinearly with brain mass and size. As a result, the acceleration levels needed to produce closed-head acceleration-induced TBI in the mouse are not feasible for MR studies.

3.3. Visualization of Brain Deformation in Cadavers

Hardy et al. (35) used high-speed (250–1,000 frames per second) biplanar X-ray imaging to track the displacement of 11 neutral-density radio-opaque markers in the brains of cadavers during impacts. Although these displacement fields are informative, the limited spatial resolution of the markers made it impossible to determine local tissue strain (35). In addition, the mechanical properties of the cadaver brain differ significantly from those of a live subject (49), not with standing the considerable efforts taken to maintain perfusion of the tissue (34). Despite these challenges, Zou et al. (36) reanalyzed these data and obtained informative estimates of brain motion relative to the skull that likely provide a lower bound on actual displacements, and they described qualitative features of the displacement field consistent with those of earlier MR studies, including an important role for brain rigid-body rotation at lower accelerations.

4. Measurement of Human Brain Motion by Tagged Magnetic Resonance Imaging

Inherently noninvasive and benign, MRI is particularly well suited to study brain tissue. Its signal derives from the spin precession of hydrogen nuclei in a strong magnetic field. Spins, which align predominantly with the magnetic field, are “tipped” by radiofrequency (RF) pulses; the frequency and phase of the ensuing precession are associated with spatial location (“encoded”) by gradients in the magnetic field. In classic anatomical MRI, image contrast arises from tissue-specific differences in water content or rates of signal decay. Different tissues, such as white or gray matter, exhibit differences in the decay of longitudinal (T1) or transverse (T2) components of spin magnetization, enabling acquisition of detailed static T1-weighted or T2-weighted anatomical images. Whereas such images are the most common application of MRI, manipulation of spin amplitude and phase by magnetic gradients and RF pulses can be used to measure motion. These techniques have been applied and adapted to the study of brain biomechanics increasingly over the past decade. In Sections 4 and 5, we review some of the techniques that have recently produced valuable data and summarize the insight into brain deformation mechanisms provided by these data.

4.1. Acquisition of Tagged Magnetic Resonance Images

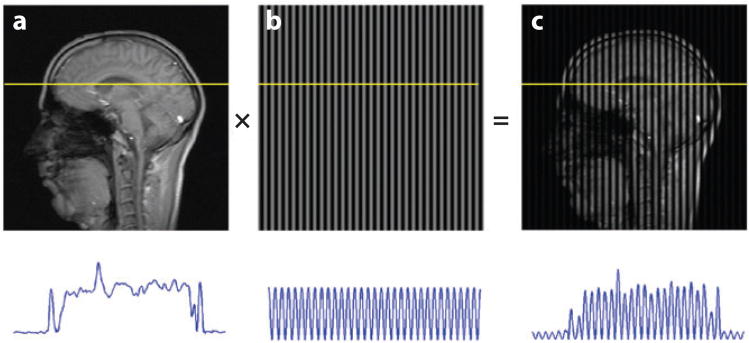
Zerhouni et al. (50) and Axel & Dougherty (51, 52) pioneered “tagging” of MR images with grid lines (also known as tag lines) and tracking these grids to quantify cardiac deformation and mechanics. MR taglines are variations in brightness superimposed noninvasively onto MR images to act as markers for tracking motion. RF pulses applied in combination with magnetic gradients produce temporary sinusoidal variations in longitudinal magnetization, leading to differences in intensity (51, 52) that appear as dark and bright taglines superimposed on the images (Figure 6). These taglines move with the tissue (Figure 7) and can be tracked to characterize its kinematics.

Figure 6.

Tagged magnetic resonance (MR) images provide the ability to track displacement of tissue in human volunteers. These images are obtained by modulating the longitudinal magnetization of spin packets. Transient sinusoidal patterns of longitudinal magnetization are produced noninvasively in tissue by the combination of radiofrequency pulses and magnetic field gradients; the remainder of the MR pulse sequence is a standard fast gradient-echo scheme. The resulting tagged image (c) is a product of the spin-density image (a) and the sinusoidal pattern (b).

Figure 7.

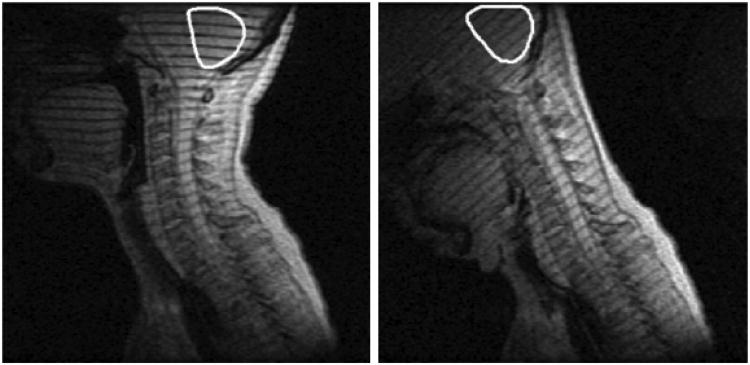
Magnetic resonance (MR) tagging approaches provide data on the relative motion and interactions of structures within the brain. Shown here is the first-ever evidence of relative rotations of brain structures during a normal physiological motion. Cerebellar displacement was measured from tagged MR images of the brain acquired in vivo during voluntary quasi-static flexion of the neck, and the cerebellum was found to rotate relative to both the skull and surrounding tissue. Reproduced from Reference 57.

After tagging, a standard MRI pulse sequence, usually a fast gradient-echo sequence, is used to acquire image data in spatial frequency space (k-space). To achieve the high temporal resolution required to characterize rapid deformation, only a single line of k-space is acquired during one event. To obtain adequately resolved images, motion is repeated, and a new line of k-space is acquired. This repeats until a sufficiently large portion of k-space is acquired. Spatial images are then obtained by inverse Fourier transform of the k-space data.

4.2. Analysis of Tagged Images

Young et al. (53) demonstrated the basic principles of strain estimation from tagged MRI data using data obtained from phantoms. Osman et al. (54, 55) proposed the harmonic phase (HARP) method for estimation of strain in cardiac MRI. In the HARP approach, deformation is estimated from the phase angle of the complex image derived by selectively filtering and then inverting the Fourier transform of the tagged image. The Fourier transform of a tagged MR image has peaks corresponding to the spatial frequencies of the periodic tagging pattern. If the Fourier transform is filtered, retaining only data from spatial frequencies near such a peak, and then inverted, the resulting image is complex. The harmonic phase of this complex image is a material property of the tagged tissue, which can thus be tracked to measure 2D displacement and strain.

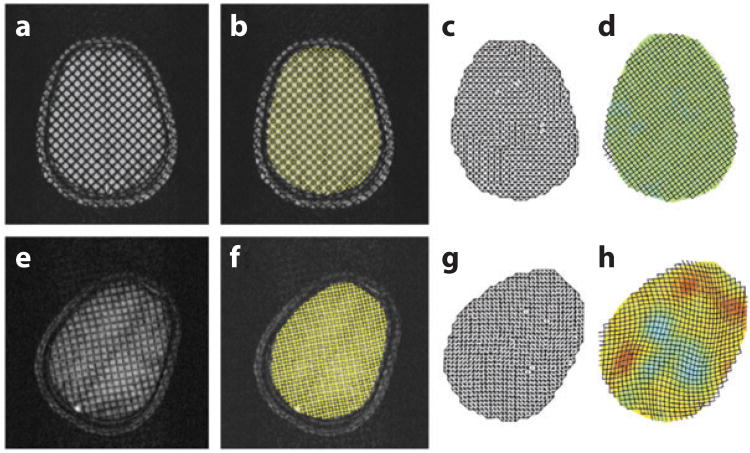
Contours of constant phase provide precise locations of synthetic taglines in the reference and deformed images (Figure 8). Phase contours at 0 and π/2 radians correspond to maxima and minima of the taglines (Figure 3). The 10-mm tagline spacing in Figure 8 effectively provides 5-mm spatial resolution for displacement and strain measurements. To compute displacement and strain fields, the intersections of the isophase contours are found automatically and used as vertices of a triangular mesh in the reference image (Figure 8c). The same triangular mesh-ordering scheme is applied to the corresponding intersection points in the deformed image (Figure 8d). The result is a set of undeformed and deformed triangles. A strain tensor is estimated for each triangle, under the assumption that the strain field is locally homogeneous, using Equations (1) and (2). One detailed validation of the application of tagged MRI and HARP strain analysis involved imposing a known angular acceleration to a rigid cylinder containing a well-characterized gel (56). Agreement to within a few percent was found between experimental measurements and both analytical and numerical predictions; this agreement provides confidence in the measurement technique.

Figure 8.

Mechanical strains can be extracted semiautomatically from tagged magnetic resonance images. Here, the procedure is applied to estimate intracranial strains resulting from angular deceleration of the skull. The reference images acquired prior to initiation of head motion (a–d) are compared with the deformed images (e–h). The centers of taglines in the images shown in panels a and e are detected by the harmonic phase algorithm and superimposed in yellow in panels b and f. Triangular meshes (c,g) are compared to estimate deformation gradients, and (dimensionless) strain fields (d,h) are estimated from the deformation gradients. In panels d and h, the displacements are amplified by a factor of 5 for illustration. Adapted from Reference 60. See also Supplemental Movie 1 (follow the Supplemental Materials link from the Annual Reviews home page at http://www.annualreviews.org).

4.3. Magnetic Resonance Tagging Studies of Brain Deformation

Motion of the brain with respect to the skull may be caused by inertial effects, as well as by forces from connecting anatomical structures. Recent imaging studies have provided data on relative brain-skull displacement due to slow (quasi-static) motion of the head, as well as data on displacements and deformations due to imposed linear or angular accelerations.

4.3.1. Quasi-static motion

The first MR studies to describe relative brain-skull displacement resulting from motion of the head involve quasi-static neck flexion (∼50°) (57, 58). Tagged MR images of the midsagittal plane of the head showed relative displacements of 1–3 mm between the brainstem and skull near the foramen magnum, and 2°–6° rotation of the cerebellum relative to the skull (Figure 7). In these quasi-static studies, brain deformation and relative motion between the brain and skull were produced by gravity and by tension in the spinal cord, rather than by dynamic or inertial loading. However, even in these quasi-static loading conditions, relative motion plays an important role in the mechanical response of the brain.

4.3.2. Occipital deceleration

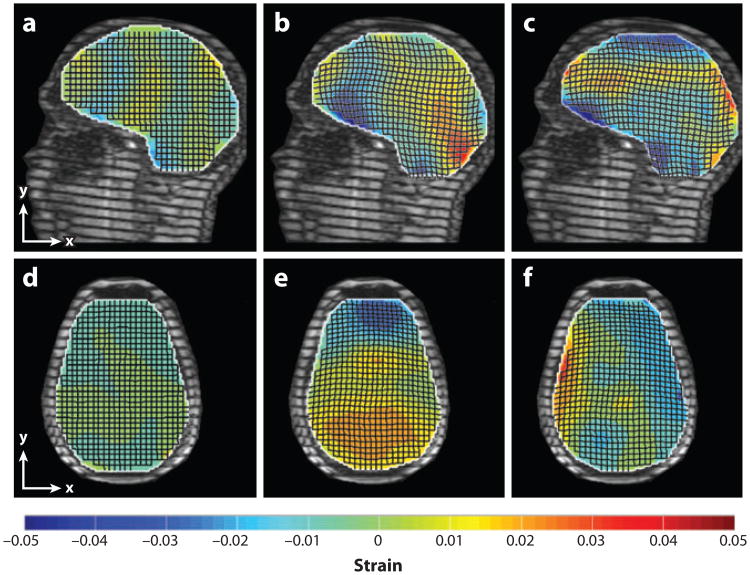
Bayly et al. (59) obtained tagged images of the brains of human subjects experiencing mild linear acceleration, roughly analogous to a mild occipital impact, inside a clinical MR scanner. The head of the supine subject was supported by an elastic pocket in a fiberglass frame. When the subject released a latch, the frame dropped approximately 2 cm and hit a rubber stop, decelerating the head in its elastic harness. An optical sensor synchronized the MRI sequence with the motion. Peak decelerations measured with a head-mounted accelerometer were 20–30 m s⁻² (∼2–3g, where g is the acceleration of gravity), a magnitude associated with landing after a short vertical jump. The brain deforms slightly but visibly under these accelerations (Figure 9), with strains of 0.02–0.05 typical.

Figure 9.

Deformations associated with mild, physiological impact result in peak strains of up to 5%. The (dimensionless) strain fields shown (color bar) were superimposed over displacement fields in tagged images of the brain acquired during mild occipital impact. (a–c) Sagittal images. (a) Baseline shear strain, E_xy (undeformed). (b) Normal strain, E_xx. (c) Shear strain, E_xy . (d–f) Transverse images. (d) Baseline shear strain, E_xy (undeformed). (e, f) Deformed brain normal strain E_yy and shear strain E_xy. Adapted from Reference 59.

Notably, compression in frontal regions and stretching in posterior regions were observed, despite the occipital impact being a loading that would produce compression in the posterior regions of a continuous solid head. The motion of the brain appears constrained by structures at the frontal base of the skull; the brain must pull away from such constraints before it can compress against the occipital bone. This mechanism is consistent with observations of contrecoup injury in occipital impact and emphasizes the critical role of the brain-skull interface (boundary conditions) in determining brain deformation.

4.3.3. Angular acceleration

Sabet et al. (60) measured the response of the human brain to mild angular skull acceleration imparted on a human volunteer inside an MR scanner, using a custom MR-compatible device to constrain repeated angular accelerations to ∼250–300 rad s⁻² (∼15% of that associated with heading of a soccer ball; see Reference 61). Tagged MR images of the moving brain, obtained by synchronizing MR imaging with head motion, were acquired in 3–4 axial planes in each subject. The brain showed consistent patterns of radial-circumferential shear strain (Figure 8) that were quite distinct from those observed in a viscoelastic gel cylinder subjected to angular acceleration. Results show that strain fields in the brain are clearly mediated by tissue heterogeneity, divisions between regions of the brain (such as the central fissure and central sulcus), and the brain's tethering and suspension system, including the dura mater, falx cerebri, and tentorium membranes. These findings again highlight an important mechanical role for peripheral structures in the brain.

4.3.4. Frontal deceleration

Feng et al. (62) measured displacement of the human brain during mild frontal skull impact constrained to the sagittal plane (Figures 9 and 10). Although head motion was dominated by translation, the dominant response of the brain was to slide relative to the skull (63). Linear decelerations of the skull were near 1.5g, and angular accelerations of the skull were approximately 120–140 rad s⁻². Relative displacements of 2–3 mm between the brain and skull were typical; regions of smaller displacements reflected the tethering effects of brain-skull connections. Strain fields exhibited maximal principal strains of 0.05 or greater. These experiments highlight an important role for brain-skull tethering in controlling peak strains. Table 1 summarizes observations of brain displacements and strains due to motion of the head.

Figure 10.

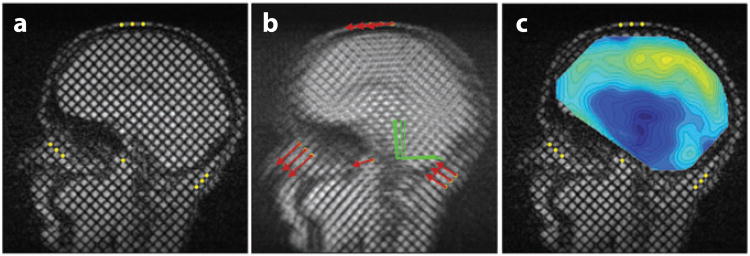
Magnetic resonance (MR) studies have shown that sliding of the brain relative to the skull is attenuated at regions of attachment between the brain and meninges, and that rotation is a dominant mode of the response of the brain to physiological linear acceleration of the head. Relative displacements of the brain with respect to the skull are shown, estimated from tagged MR images acquired during mild frontal impact. (a) Tagged reference image with markers (yellow dots) on reference points that move with the skull. (b) Summed tagged images acquired at 6-ms intervals during the head drop and deceleration. The trajectories of the marker points are shown as red arrows; the position and orientation of a skull-fixed coordinate system are shown as green lines. (c) Contour maps of the relative displacement of the brain with respect to the skull-fixed coordinate system. See Supplemental Movie 2. Adapted from Reference 62.

Table 1. Magnetic resonance imaging (MRI)-based estimates of brain displacement and strain (healthy living human subjects).

Reference	Acceleration	Displacement	Strain	Description
Poncelet et al. (67)	–	≤0.5 mm	–	Intrinsic pulsatile brain motion
Reese et al. (68)	–	–	0.002	Intrinsic pulsatile brain motion
Ji et al. (57)	Quasi-static	0.8–1.6 mm	–	Quasi-static cervical spine flexion
Bayly et al. (59)	20–30 m s−2 (2–3g)	–	0.02–0.05	Low-amplitude occipital impact
Ji & Margulies (58)	Quasi-static	1–3 mm	–	Quasi-static cervical spine flexion
Sabet et al. (60)	250–300 rad s−2	–	0.02–0.06	Low-amplitude angular acceleration
Feng et al. (62)	1.5g, 120–140 rad s−2	2–3 mm	≤0.05	Low-amplitude frontal impact

5. Measurement of Human Brain Motion by Phase-Contrast Imaging and Magnetic Resonance Elastography

Phase-contrast MRI methods measure the relative angular position (i.e., phase) of the net transverse magnetization vector for each isochromat (spin packet). Because for each isochromat the magnetization vector precession rate (frequency) depends on the local magnetic field strength, isochromats moving in the presence of a spatially varying magnetic field (gradient) have a different phase than those that remain motionless in the same magnetic field. Muthupillai et al. (64) harnessed this concept to develop magnetic resonance elastography (MRE). They imaged steady-state, harmonic shear wave propagation in biological materials by synchronizing an applied mechanical vibration with an oscillatory magnetic field gradient, and they estimated the material's shear modulus from the shear wave velocity. MRE was developed originally to calculate elastic properties of tissue and to detect diseased or degenerating tissue through differences in propagation speed associated with differences in stiffness (65, 66). Poncelet et al. (67) demonstrated the use of phase-contrast MRI to measure motion in the brain parenchyma of human subjects during physiological pulsatile motion and voluntary head shaking. Reese et al. (68) used phase-contrast MRI to estimate 3D strain fields in the human brain due to pulsatile motion (Figure 11).

Figure 11.

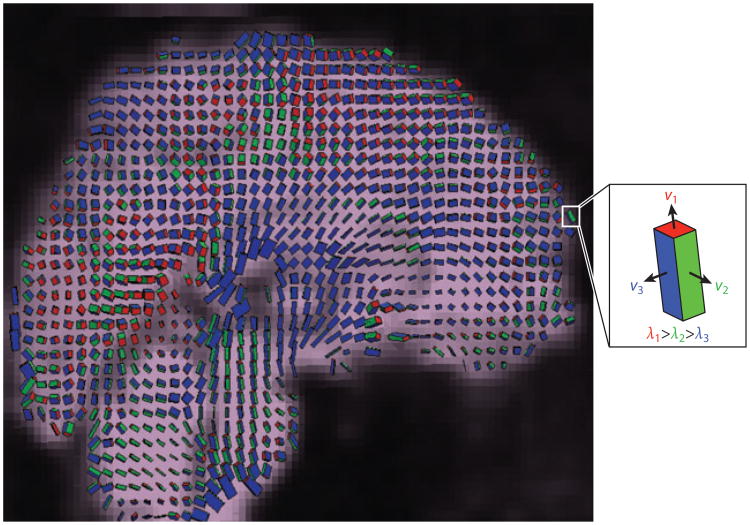
Phase-contrast MRI allows high spatial resolution imaging of the three-dimensional displacement and strain fields in the moving brains of live human subjects. Shown here is the strain tensor field in the human brain due to normal pulsatile motion of the brain parenchyma. Box icons are color coded and scaled to represent the eigenvalues λ_i and scaled eigenvectors υ_i(λ_i) of the strain rate tensor at each voxel. Adapted from Reference 68.

We describe here the initial implementations of MRE that targeted linear-elastic, homogeneous, isotropic materials, along with recent advances that enabled its application to brain tissue, which is viscoelastic, heterogeneous, anisotropic, and nonlinear. Our focus is data and methods for incrementally linear, homogeneous tissue that exhibits viscoelasticity, the latter property is especially important in brain tissue, which, like most biological materials, appears stiffer at higher rates of deformation.

5.1. Principles of Magnetic Resonance Elastography

MRE measures oscillating shear displacements caused by harmonic vibration. Measurements of harmonic displacement are obtained by modulating the gradient field of the MR scanner at the vibration frequency (64). Application of this sequence leads to images in which phase contrast is developed between vibrating spins.

If oscillating gradients of constant amplitude, frequency, and duration are applied in three orthogonal directions, a vector of motion-induced phase, φ, is obtained at each voxel in the image space. The oscillatory displacement, u, of the voxel is proportional to the phase, φ, of the tissue spins obtained from elastography images. We define the position of a spin packet in a 3D sample as x(X, t) = X+u(X,t), where u(X,t) = u₀ cos(ωt−k · X+θ), in which u₀ describes the vibration amplitude and direction, and X, ω, k, and θ are the initial position of the spin packet, vibration frequency, spatial frequency vector, and vibration phase, respectively. Then the component of the MR phase in the direction of the gradient is (66)

$${\varphi }_{\mathbf{\text{G}}}(\mathbf{\text{X}},\theta )=\gamma \underset{0}{\overset{2\pi N/\omega }{\int }}\mathbf{\text{G}}(\mathbf{\text{t}})\cdot \mathbf{\text{x}}(\mathbf{\text{X}},t)\mathit{\text{dt}}=\frac{\gamma \pi N({\mathbf{\text{G}}}_0\cdot {\mathbf{\text{u}}}_0)}{\omega }\text{cos}(\theta -\mathbf{\text{k}}\cdot \mathbf{\text{X}}),$$ (3)

where φ_G(X, θ) is the component of the MR phase vector in the direction of G(t), γ is the gyro-magnetic ratio, N is the number of cycles, and G(t) = G₀ cos(ωt) is the magnetic field gradient. Thus, tracking phase in three orthogonal directions allows the three components of the displacement field to be obtained.

5.2. Estimation of Elastic Properties from Magnetic Resonance Elastography Data

Data from MRE studies consist of displacement fields. If estimates of material parameters are to be obtained, these displacement fields must be interpreted in the context of elastodynamics. One approach is to fit the data directly to the differential equations governing elastic wave propagation. Alternative approaches include the application of the principle of virtual work, or the use of general signal processing techniques to estimate the local wavelength of the image data.

5.2.1. Fitting of elastic wave equations

The equation governing 3D wave propagation in a linear, homogenous, isotropic, unbounded medium is described by

$$\rho \frac{{\partial }^2\mathbf{\text{u}}(\mathbf{\text{X}},t)}{\partial t^2}=\mu {\nabla }^2\mathbf{\text{u}}(\mathbf{\text{X}},t)+(\lambda +\mu )\nabla (\nabla \cdot \mathbf{\text{u}}(\mathbf{\text{X}},t)),$$ (4)

where ρ is the material density, λ and μ are the Lamé constants, and derivatives are relative to the reference configuration (69). The dilatation (u_d(X, t)) and shear (u_s(X, t)) components of u(X, t), where (X, t) = u_d(X, t) + u_s(X, t), satisfy Equation (4) independently and may be calculated from Equation (4) using the divergence and curl of u(X, t), noting that ∇ · u_s(X, t) = 0 and ∇ × u_d(X,t) = 0. Dilatational waves (also known as pressure, compression, longitudinal, or irrotational waves) travel at a speed of $c_L=\sqrt{\frac{\lambda +2\mu }{\rho }}$, and shear waves (also known as distortional, transverse, or equivoluminal waves) travel at a speed of $c_s=\sqrt{\frac{\mu }{\rho }}$. In general, the two modes are coupled through boundary conditions on u(X, t) and on the stress field, which is related to u(X, t) through strain-displacement and constitutive relations (70). For a displacement field due solely to shear deformation, Equation (4) reduces to

$$\rho \frac{{\partial }^2{\mathbf{\text{u}}}_{\mathbf{\text{s}}}(\mathbf{\text{X}},t)}{\partial t^2}=\mu {\nabla }^2{\mathbf{\text{u}}}_{\mathbf{\text{s}}}(\mathbf{\text{X}},t),$$ (5)

which can be solved to identify the elastic shear modulus, μ.

In general, within geometrically complex inhomogeneous media, dilatational and shear components of a wave field are coupled. The dilatational component of the displacement field (second term in Equation 4) may distort material parameter estimates if pure shear deformation is assumed and Equation (5) is used (71). Taking the curl of the measured displacement field eliminates the dilatational component (71, 72); the resulting data can be fitted to the equations above, after the curl operator has been applied. However, spatial derivatives involved in the curl operation amplify the effects of noise. Spatial filtering can remove long-wavelength components, but at the risk of mischaracterizing regions of unexpectedly high stiffness (71, 73); the appropriate band limits of the spatial filter are seldom clear a priori. Clayton et al. (46) showed that estimates of mouse brain material properties differed slightly in measurements made between 600 and 1,800 Hz, depending on whether curl or spatial filtering was used to remove dilatational components.

When an imperfect theoretical model is used to interpret data from a physical system, evaluation of the goodness of fit, or applicability of the model to the data, is essential. Atay et al. (74) introduced the normalized residual error (the variance in the data that is not explained by the model) as a measure to evaluate confidence in local estimates of stiffness.

5.2.2. Local wavelength estimation

Elastic moduli may be estimated without explicitly fitting the equations of motion. A technique named local frequency estimation (LFE) (75) has been used to find the local wavelength, Λ_s, of propagating shear waves from spatiotemporal images of the wave field. The propagation speed is found simply from c_s = Λ_sf, where f = ω/2π is the actuation frequency (Hz). The shear wave velocity relationship ( $c_s=\sqrt{\mu /\rho }$) can then be used to infer material stiffness:

$$\mu =\rho c_s^2=\rho {\Lambda }_s^2{f}^2.$$ (6)

Several investigators (e.g., 73, 101) have used this approach to estimate the elastic shear modulus of tissues. The advantage of this approach is that the need for two or three numerical derivatives is circumvented, but, without a way to formally decouple shear and dilatational displacement components, estimates suffer from corruption by dilatational waves. Our group has applied LFE to local rotation fields estimated from the curl of displacement fields measured during wave propagation in the human brain in vivo (105). The use of local rotation in LFE is motivated by physics (it allows the decoupling of distortional and dilatational components of the wave field) and relative insensitivity to noise, as it requires only one spatial derivative.

5.2.3. Other methods

Other approaches to inverting MRE data involve energy principles. Romano et al. (76) employed a variational technique to invert a weak form of the equations of motion. Closely related is the work of Pierron and coworkers (77, 78), who used the virtual fields method to estimate material parameters from full-field displacement or strain data. Van Houten et al. (79) developed an inverse FE method to estimate material parameters in subzones of the image volume. Manduca et al. (73) describe LFE, algebraic direct inversion, and phase gradient approaches.

5.3. Estimation of Viscoelastic Properties from Magnetic Resonance Elastography Data

The viscoelastic correspondence principle allows the purely linear-elastic equations of motion to be generalized to analogous viscoelastic equations via Laplace or Fourier transform (80–82), allowing elastic moduli to be replaced with corresponding complex viscoelastic moduli without requiring a specific rheological model. The linear modulus μ in Equation (5) is replaced in Laplace or Fourier space by the transformed linear-viscoelastic complex shear modulus, G(iω) = G′(ω) + iG″ (ω), where G′ (ω) and G″ (ω) are the frequency-dependent storage and loss modulus, respectively, and viscoelastic estimates can be made.

Alternatively, in cases in which the wave field is well characterized by 1D propagation of plane waves or those in which it can be directionally decomposed into the superposition of several plane wave fields, logarithmic decrement methods can be used to extract the attenuation parameter α (69, 84). The solution of plane distortional wave propagation in an isotropic viscoelastic medium relates storage (G′) and loss (G″) components of the complex shear modulus to the spatial attenuation constant α and wavenumber k, equivalent to k = 2π/Λ, as follows (69, 84):

$$\left[\begin{array}{cc}{k}^2-{\alpha }^2& 2\alpha k\\ -2\alpha k& k^2-{\alpha }^2\end{array}\right]\left\{\begin{array}{c}G\prime \\ G″\end{array}\right\}=\left\{\begin{array}{c}\rho {\omega }^2\\ 0\end{array}\right\}.$$ (7)

5.4. Anisotropic Material Models

White matter, composed largely of aligned axonal fibers and associated myelin sheaths, is expected to be mechanically anisotropic (83). In an anisotropic material, the speed of propagation varies with direction (69, 84), motivating approaches to quantify some aspects of material anisotropy using MRE (71). However, to our knowledge, this has not been applied to brain tissue.

5.5. Magnetic Resonance Elastography Imaging Studies

MRE principles and techniques have now been used to estimate mechanical properties in a range of tissues and organs. MRE has also been applied to surrogate biomaterials, both for validating the technique and for characterizing the mechanical response of these materials.

5.5.1. Magnetic resonance elastography validation studies

MRE is attractive because it is noninvasive, but is challenging to apply because it is inherently indirect: Mechanical properties are inferred from displacement fields arising from vibratory motion. Broad variation in reported MRE estimates of tissue mechanical properties has led to several efforts to evaluate the accuracy of MRE estimates through comparison with mechanical properties measured by direct mechanical tests (64, 74, 85–91). The following conclusions were reached:

1. Direct mechanical tests of biological tissue are difficult to perform, and results can vary significantly with variations in test procedure and experimental conditions (92). Brain tissue is particularly compliant, fragile, and slippery, and its properties vary with temperature, hydration, blood pressure, and time post mortem.

2. Brain tissue is viscoelastic. To be relevant, tissue phantoms used in studies to evaluate MRE should mimic the viscoelastic response of living tissue.

3. Because viscoelastic material parameters are usually frequency dependent, direct mechanical tests performed for comparison with MRE should be performed at the same driving frequency.

Validation studies have been performed in animal brain tissue by comparing estimates from MRE in vivo with direct mechanical measurements ex vivo. Investigators have used MRE to quantify the components of the viscoelastic shear modulus of porcine brain tissue (93) and bovine liver tissue (94) and directly compared results with those yielded by oscillatory rheometry. Both studies showed qualitative agreement of trends in the values of G′ (ω) and G″ (ω) with frequency, but rheological tests of porcine brain tissue were performed at a much lower frequency (0.1 to 10 Hz) than that offered by MRE (80–140 Hz), making interpretation of results inconclusive.

However, more conclusive validation is available for gels. Okamoto et al. (91) developed a dynamic shear test to measure the complex shear modulus of a tissue-mimicking gel material at frequencies ranging from 20 Hz to 200 Hz. This allowed for direct comparison with MRE at the same frequencies. A close agreement between MRE results and dynamic shear test results at overlapping frequencies supports MRE applicability over a wide frequency range.

5.5.2. Magnetic resonance elastography studies of brain material properties

Numerous recent MRE studies of the brain in human subjects have been performed (72, 95–100), with high-resolution displacement fields resulting (Figure 12 and Supplemental Movie 3). Methods of Sinkus, Bilston, and collaborators (72, 100) are typical, involving harmonic motion to the skull through a vibrating bite bar. MRE data lie well within the range of data obtained by shear and indentation tests ex vivo (Figure 13) but are nevertheless somewhat variable. For example, McCracken and coworkers (95), who used 80-Hz excitation and fit a pure elastic model to their data, found shear moduli of 5.3 ± 1.3 kPa for cortical gray matter and 10.7 ± 1.4 kPa for white matter. Kruse et al. (101), who applied LFE to displacement wave fields to estimate elastic parameters, found 5.2 ± 0.4 kPa for gray matter and 13.6 ± 1.3 kPa for white matter at 100-Hz driving frequency. Clayton and coworkers recently used LFE on the isolated distortional component of the displacement field to calculate viscoelastic material parameters of gray and white matter at 45, 60, and 80 Hz and found that both gray and white matter storage moduli varied over this frequency range: 2.8–4.4 kPa (gray) and 3.7–4.7 kPa (white) (105). Green et al. (72) used 90-Hz excitation and found cortical gray matter (3.1 ± 0.1 kPa) stiffer than white matter (2.7 ± 0.1kPa). For reference, we note that Thibault & Margulies (102), using direct mechanical measurements (dynamic shear tests) of pig brain gray matter ex vivo, found G(iω) = 1.2 ± i 0.8 kPa at 50 Hz and G(iω) =1.5 ± i1.3 kPa at 100 Hz. Experimental approaches and parameter estimates from different MRE studies are summarized in Table 2.

Figure 12.

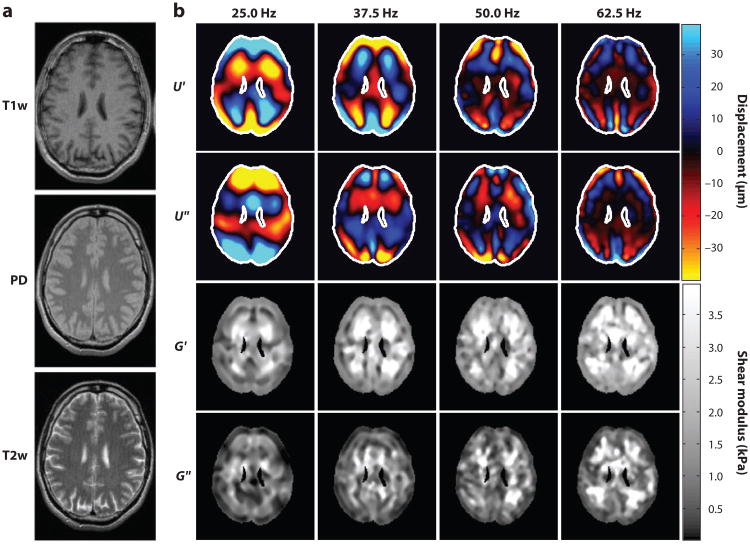
Magnetic resonance elastography (MRE) produces estimates of intracranial displacement fields observed in response to dynamic pressure loading of the skull. These can be inverted to estimate spatially varying mechanical properties of brain tissue. Example displacement fields shown here are obtained from a single-slice multifrequency MRE experiment. (a) Standard MR anatomical images: T1-weighted (T1w), proton density (PD), and T2-weighted (T2w) contrast. (b) Wave images and parameter fields. U′ and U″ denote the real and imaginary parts of the first harmonic component U(x, y, ω) of the displacement field. The complex modulus images (G′ and G″) denote the real and imaginary parts of the complex shear modulus G(x, y, ω). The driving frequencies are given above the columns. Reproduced from Reference 99.

Figure 13.

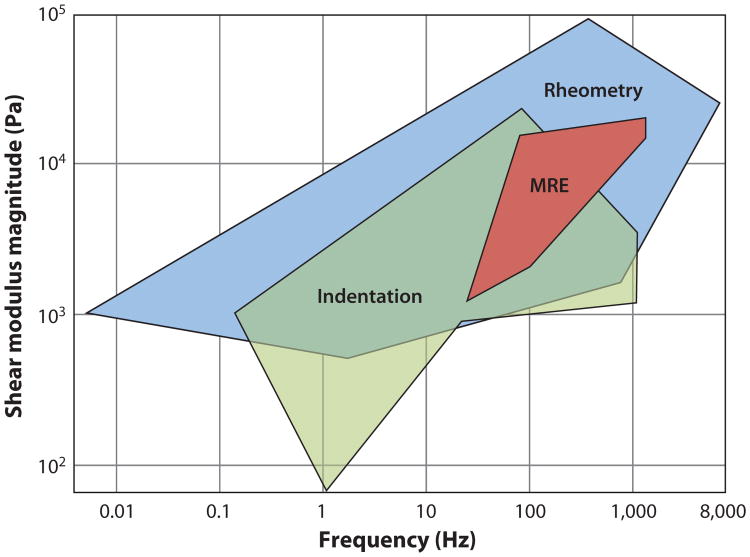
Magnetic resonance elastography (MRE) provides noninvasive estimates of living brain tissue in human volunteers. MRE-based estimates of brain tissue shear modulus vary among different studies but lie within the range of estimates obtained in vitro by direct mechanical tests. Adapted from Reference 104.

Table 2. Magnetic resonance elastography (MRE)-based estimates of brain elastic or viscoelastic mechanical properties (healthy living human subjects).

Reference	Frequency (Hz)	G′ (kPa)			G″ (kPa)			Actuator
		Gray	White	Average	Gray	White	Average
Sack et al. (99)	25	–	–	1.1 ± 0.2	–	–	0.5 ± 0.1	Head rocker
Sack et al. (99)	37.5	–	–	1.3 ± 0.3	–	–	0.6 ± 0.1	Head rocker
Clayton et al. (105)	45	2.8 ± 0.5	3.7 ± 0.8	–	0.80 ± 0.2	1.3 ± 0.4	–	Acoustic pressure
Sack et al. (99)	50	–	–	1.5 ± 0.2	–	–	0.6 ± 0.1	Head rocker
Clayton et al. (105)	60	3.1 ± 0.3	3.3 ± 0.1	–	1.7 ± 0.3	2.0 ± 0.1	–	Acoustic pressure
Sack et al. (99)	62.5	–	–	2.0 ± 0.2	–	–	0.8 ± 0.1	Head rocker
McCracken et al. (95)	80	5.3 ± 1.3	10.7	–	–	–	–	Bite bar
Clayton et al. (105)	80	4.4 ± 0.3	4.7 ± 0.6	–	2.3 ± 0.2	2.4 ± 0.5	–	Acoustic pressure
Zhang et al. (100)	80	2.3 ± 0.2	2.4 ± 0.2	–	1.1 ± 0.0	1.2 ± 0.2	–	Bite bar
Green et al. (72)	90	3.1 ± 0.1	2.7 ± 0.1	–	2.5 ± 0.2	2.5 ± 0.2	–	Bite bar
Kruse et al. (101)	100	5.2	13.6	–	–	–	–	Bite bar

6. Discussion and Conclusions

Imaging is an important component of the study of TBI mechanics, complementary and essential to efforts in modeling and simulation. It is likely that both simulation and imaging of biomechanics will play a major role in the effort to prevent TBI. Accurate computer models would also be valuable to those researching the neuropathology of TBI who wish to understand the direct effects of mechanical insult and separate these primary effects from delayed, or secondary, effects. However, without accurate mechanical parameters and careful validation by experimental studies such as those reviewed here, simulations will be neither reliable nor useful.

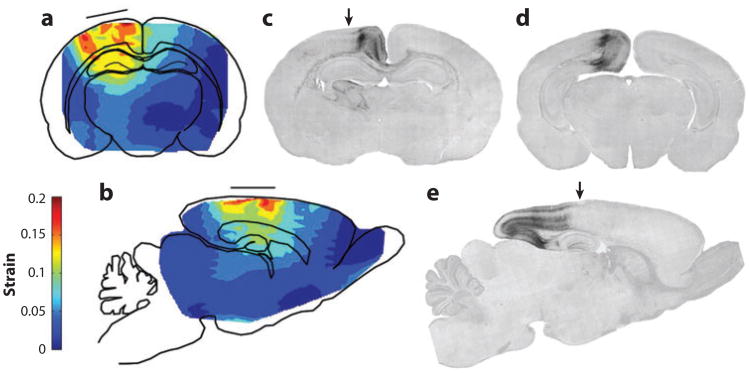
Important open questions remain, however. Perhaps the most important decision is which quantities to measure or calculate. Although strain and strain rate are known to be important metrics of tissue disruption, they may not be the only factors in injury severity. Imaging studies may help answer these questions. An example is the recent study of closed-head injury in the juvenile rat (45, 103), in which images of mechanical strain, obtained by MR tagging, are compared directly with histological images (Figure 14) to gain insight into neuropathological mechanisms (45). This study shows not only that local measures of strain are important to the outcome in an injury-level event but also that other (biological) factors play an important role. Strain fields correlate with, but do not replicate, patterns of neuronal apoptosis. The pattern of neuronal apoptosis was well explained, however, by the intersection of the strain field with the axonal tracts connecting these neurons to their synaptic partners.

Figure 14.

Intracranial strain and strain rate fields are important in understanding the response of brain tissue to mechanical trauma, but injury mechanisms are complicated. Although strain fields are clearly related to apoptotic cell death in a closed-head model of traumatic brain injury in the juvenile rat, cell death is not directly colocalized with strain, and much injury occurs downstream of regions of high strain. (a, b) Schematic depictions of coronal (a) and sagittal (b) sections of the juvenile (P7) rat brain, illustrating the pattern of (dimensionless) strain magnitude during parasagittal indentation of the flexible skull. The location of the impactor tip is shown by the solid horizontal line. (c,d,e) Activated caspase-3-stained sections from a P8 rat brain 24 h postimpact; caspase-3 is a sensitive indicator of apoptosis. Arrows in panels c and e indicate the direction of impact and the center of the impact site. Panels c and d are coronal sections cut in a rostrocaudal plane slightly caudal to the impact site (c), or at a much more caudal level (d). These sections show that the delayed pathological reaction at the cerebrocortical level is primarily concentrated medial to the point of impact. Panel e is a sagittal section revealing that this cerebrocortical delayed pathological reaction extends in a caudal (but not rostral) direction. Reproduced from Reference 45.

The pervasive technical challenge that underlies all work on the biomechanics of TBI is predicting the response of the human brain to high loading without performing direct tests. Because it is impossible to study directly the mechanics of TBI in humans, different models (gel surrogates, animal, cadaver, and human) and imaging techniques are required to span the range of necessary data. For example, to understand the effects of the human anatomy, data must be acquired in humans at safe, physiologically relevant levels of strain and strain rate; yet data from animal models or in vitro studies are needed to understand the nonlinear properties of the brain during large deformation. Results from studies in gel surrogate phantoms can be compared with carefully controlled laboratory tests and closed-form solutions. The complete picture of brain biomechanics will be a mosaic of the results of such complementary studies.

Imaging studies have been pursued for decades to understand the motion of the brain that occurs in response to impact or acceleration of the skull. Recent advances have exploited high-speed video, digital image correlation, and MRI techniques developed specifically to visualize and characterize fast events. We believe that MRI-based techniques in particular provide a window into the complex structural interactions that modulate mechanical injury in the human brain.

Imaging studies will continue to help develop a comprehensive picture of the brain's behavior when the skull accelerates and to illuminate how the transduction of mechanical stresses to the brain relates to brain injury. Continued effort in these directions promises to have great impact on our scientific understanding of TBI and our ability to prevent and treat brain injury.

Summary Points.

1. Imaging of brain biomechanics is important for validation and calibration of biomechanical models and for testing of hypotheses about the mechanical response of the brain.

2. At physiologically relevant acceleration magnitudes, the meninges, vessels, and sheathed cranial nerves arrest brain motion; wave motion is not observed; and higher strains associated with brain-skull attachment appear at sites associated with contrecoup injury.

3. Strains on the order of 5% are common in the brain in response to daily activity.

4. At high acceleration levels in cadavers, high-speed biplanar X-ray images suggest that the meninges are unable to resist inertial forces, and broad brain-skull contact may occur.

5. High-speed video imaging allows measurement of large deformations at high strain rates in brain slices or brain sections in situ or in vitro.

6. MR tagging studies show that the dominant response of the human brain to skull acceleration is one of rotation and sliding, arrested by connections between the brain and skull.

7. MRE provides both visualization of wave propagation patterns and noninvasive estimates of frequency-dependent brain biomechanical properties.

Future Issues.

1. Future imaging studies of brain biomechanics should address increased temporal resolution. Impact and blast are fast events. Submillisecond temporal resolution would be ideal to sample high-frequency transients.

2. Efficient schemes to acquire 3D displacement measurements throughout 3D image volumes with finer spatial resolution should be developed. In MR techniques that require repeated motion, limiting the number of repetitions required to acquire an image is important.

3. The roles of the meninges, CSF, and vasculature in the transmission of loads to the brain must be clarified.

4. The effects of spatial inhomogeneity and anisotropy on the mechanics of the brain need to be determined.