Alert Response to Motion Onset in the Retina

Abstract

Previous studies have shown that motion onset is very effective at capturing attention and is more salient than smooth motion. Here, we find that this salience ranking is present already in the firing rate of retinal ganglion cells. By stimulating the retina with a bar that appears, stays still, and then starts moving, we demonstrate that a subset of salamander retinal ganglion cells, fast OFF cells, responds significantly more strongly to motion onset than to smooth motion. We refer to this phenomenon as an alert response to motion onset. We develop a computational model that predicts the time-varying firing rate of ganglion cells responding to the appearance, onset, and smooth motion of a bar. This model, termed the adaptive cascade model, consists of a ganglion cell that receives input from a layer of bipolar cells, represented by individual rectified subunits. Additionally, both the bipolar and ganglion cells have separate contrast gain control mechanisms. This model captured the responses to our different motion stimuli over a wide range of contrasts, speeds, and locations. The alert response to motion onset, together with its computational model, introduces a new mechanism of sophisticated motion processing that occurs early in the visual system.

Introduction

The visual world contains a flood of information and represents a significant burden for the visual system to process rapidly and reliably. Therefore, instead of processing every bit of information as it arrives, the brain uses attention to select elements in the visual scene for immediate consideration. Generally, attention has been thought of as having two components: “top-down” processing, which focuses on task-based cues and “bottom-up” processing, which relies on the salience of image-based cues. (James, 1890; Treisman and Gelade, 1980; Bergen and Julesz, 1983; Koch and Ullman, 1985; Nakayama and Mackeben, 1989; Braun and Sagi, 1990; Nothdurft, 1991, 1993; Hikosaka et al., 1996; Braun and Julesz, 1998; Braun et al., 2001).

The detection of the onset of motion is an example of bottom-up processing (Abrams and Christ, 2003). Motion onset can signal the presence of nearby predators or prey or impending dangers; the ability to recognize these types of visual cues quickly and reliably likely offers a significant benefit to one's survival and well being (Allman, 1999). Behaviorally, motion onset captures attention more strongly than smooth motion (Abrams and Christ, 2003; Christ and Abrams, 2008). Motion onset is also known to elicit a characteristic evoked cortical potential (MacKay and Rietveld, 1968; Clarke, 1973; Kubová et al., 1990; Kuba and Kubová, 1992), and cells in the lateral interparietal area are strongly stimulated by motion onset (Kusunoki et al., 2000).

Highlighting the relevance of motion processing to vision, the retina carries out many forms of complex motion processing. Different subsets of ganglion cells respond to specific kinds of motion, such as motion in a preferred direction (Barlow and Levick, 1965), local motion relative to the wide-field background (Lettvin et al., 1959; Olveczky et al., 2003), looming or approaching motion (Ishikane et al., 2005; Münch et al., 2009), acceleration (Thiel et al., 2007), and motion reversal (Schwartz et al., 2007); retinal ganglion cells also display anticipatory firing in the case of objects in smooth motion (Berry et al., 1999). Therefore, we asked: Does the retina play a role in the detection of motion onset as well?

Here, we show that a subset of ganglion cells in the salamander retina, the fast OFF type, responds differently to motion onset than to smooth motion. Following motion onset, fast OFF cells exhibit a sharp, transient burst of firing, with a peak firing rate two to four times larger than that evoked by smooth motion. Although this alert response to motion onset is present for both bright and dark bars, we show that it is determined entirely by the action of the OFF pathway. We further present a phenomenological model of the ganglion cell light response that combines simple gain control feedback mechanisms (Shapley and Victor, 1981; Berry et al., 1999; van Hateren et al., 2002) and a subunit cascade structure (Victor and Shapley, 1979; Victor, 1988; Baccus et al., 2008). This adaptive cascade model (ACM) reproduces the experimental recordings for motion onset, smooth motion, and bar appearance over a wide range of contrasts, speeds, and locations.

Materials and Methods

Recording.

Retinal tissue was obtained from larval tiger salamanders (Ambystoma tigrinum) of either sex and continuously perfused with oxygenated Ringer's medium at room temperature. Ganglion cell action potentials were recorded extracellularly from a multi-electrode array with 252 electrodes spaced 30 μm apart (MultiChannel Systems). Details of the recording and spike-sorting methods are described elsewhere (Marre et al., 2012).

Visual stimulation.

Visual stimuli were presented on a computer monitor running at 60 Hz (Puchalla et al., 2005). Bars of light were presented on a gray background and were 162 μm wide, traveling at several contrasts and speeds. Contrast was defined as the percentage change in light intensity from the background intensity. Speeds varied from 0.27 to 3.24 mm/s on the retina. Smooth motion stimuli consisted of a bar moving from one side of the monitor to the other at a constant speed. Motion onset stimuli consisted of a bar appearing and holding in place for 1 s and then moving at a constant speed. “Growing” stimuli consisted of a bar appearing and holding for 1 s, then having the leading edge move until the bar had doubled in size, holding for 0.5 s, and then disappearing. “Shrinking” stimuli were the same as the growing stimuli except the trailing edge moved until it reached the leading edge causing the bar to effectively vanish. Bars appeared at five different locations spaced 162 μm apart, except for the recording shown in Figures 1D and 4, which featured nine different starting locations spaced 81 μm. In each recording, the different stimuli were all randomly interleaved to minimize the effect of long-term drift or adaptation on our results.

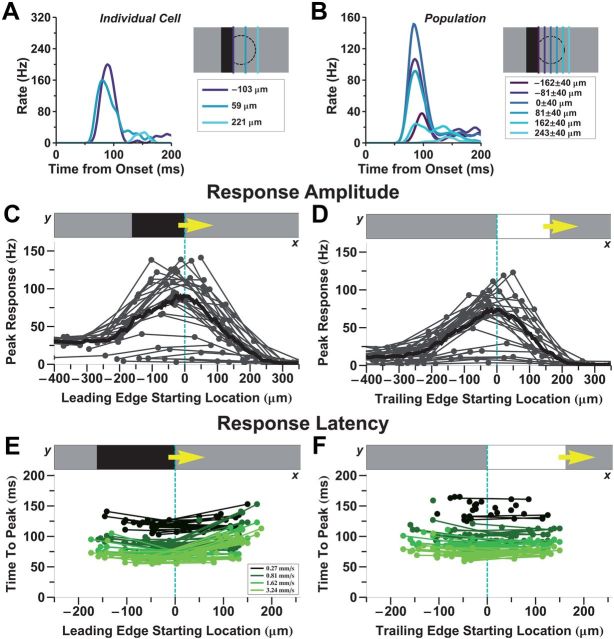
Figure 1.

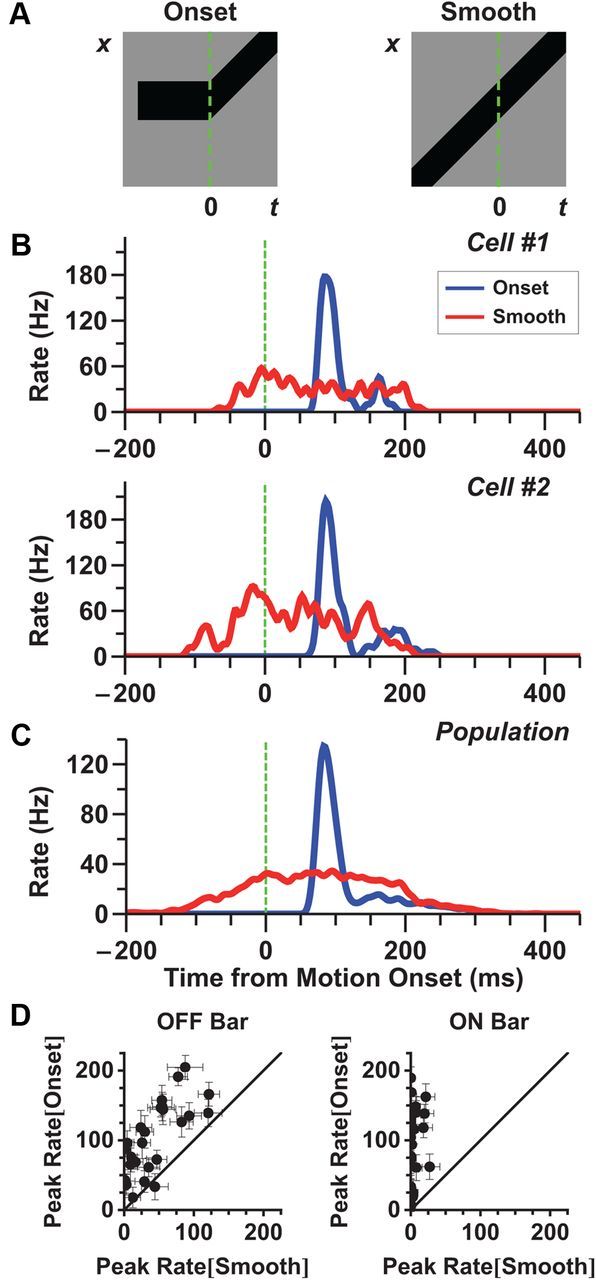
The “alert response ” to motion onset is larger than the response to smooth motion. A, Stimulus diagrams for motion onset (left) and smooth motion (right); the green line shows the time of motion onset. Note that after motion onset, the two stimuli are identical. B, Firing rate of two individual fast OFF ganglion cells to motion onset (blue) and smooth motion (red). Starting locations of the bar were chosen so that the leading edge of the bar was as close to the receptive field center as possible. Note that the response to the initial appearance of the bar is not shown. It is shown in Figure 7B. C, Average firing rate of a population of 31 fast OFF cells. Motion onset responses for each cell were chosen from a starting location closest to its receptive field center coordinate and within 81 μm. D, Peak firing rate following motion onset versus firing rate during smooth motion at the same time (dots are individual fast OFF cells). Left, dark bars; right, bright bars. Error bars indicate 95% confidence intervals.

Figure 4.

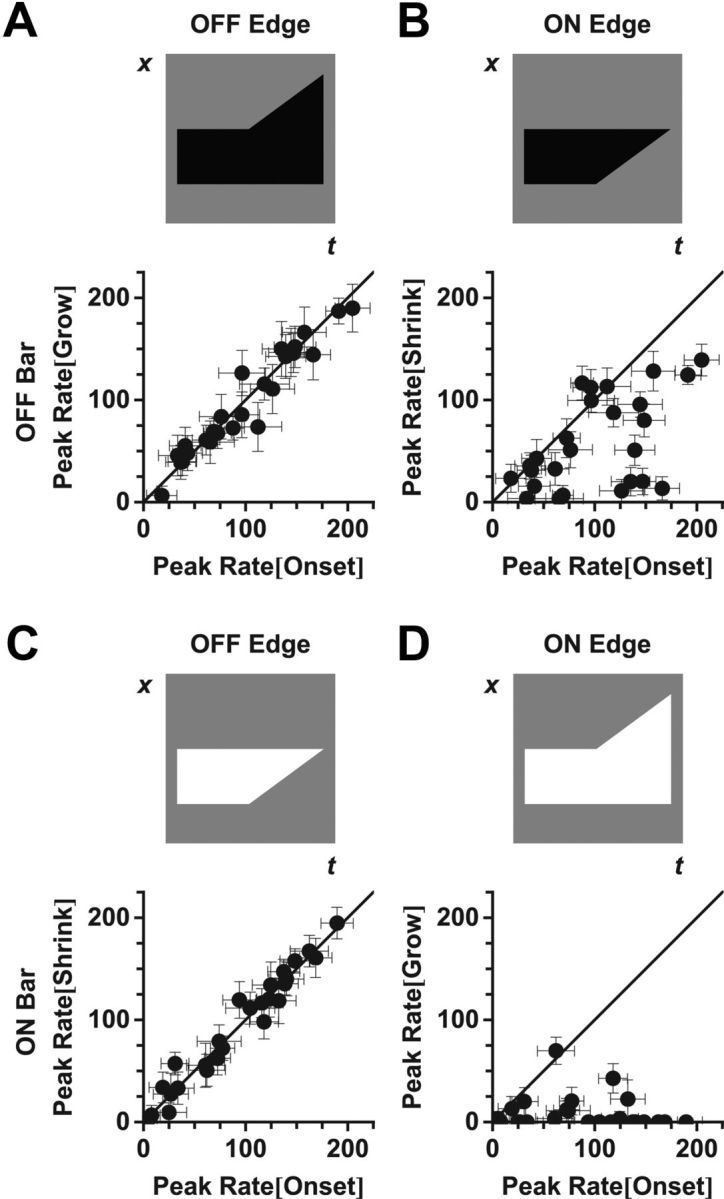
The response to motion onset is strongly correlated with the motion of the OFF-polarity edge. Peak firing rate of 26 fast OFF cells for motion of the individual leading (grow) or trailing (shrink) edges versus the peak firing rate for full motion onset. Top, Stimulus schematics. Grow and shrink amplitudes were calculated at the same bar position as for motion onset. A, B, Dark bars. C, D, Bright bars. A, C, OFF-polarity edges. B, D, ON-polarity edges.

Receptive fields.

Spatiotemporal receptive fields were measured by reverse correlation to random flicker presented at 30 Hz. Random flicker consisted of 60 strips each 54 μm wide oriented parallel to the moving bar stimuli. The receptive field for each ganglion cell was measured from the (time-reversed) spike-triggered average during random flicker stimulation and is denoted as follows: K(x,t). To determine the spatial kernel of the ganglion cell's receptive field, the location in space of the extremal response, x*, was first identified. Next, the time course of the receptive field at x* was estimated as K(x*,t). The temporal response at every point in space was projected onto the extremal time course, B_G^(emp)(x)=∫dt K(x*,t)K(x,t), to estimate the spatial sensitivity profile. We fit this function with a difference of Gaussians form:

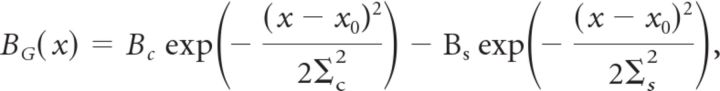with a center coordinate x₀, parameters B_c and B_s describing the relative strength of the center and surround, and parameters ∑_c and ∑_s describing their radii. Note that the center coordinate x₀ is not necessarily the same as x*. The temporal kernel of the ganglion cell, C_G(t), was calculated by averaging the temporal response of every location within the receptive field center:

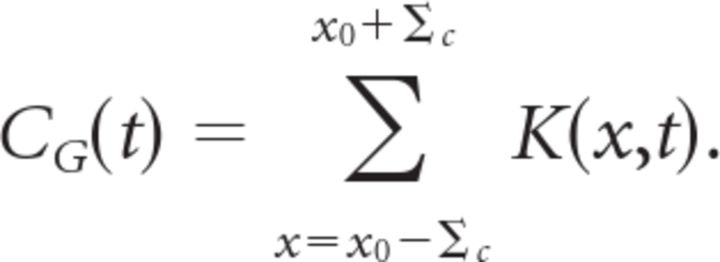Spatial kernels were then normalized so that their peak values were equal to one. Temporal kernels were normalized so that they integrated to unity. For the 91 fast OFF cells measured in this study, the average radius of the receptive field center was Σ_c = 94 ± 29 μm and the average radius of surround was Σ_s = 378 ± 157 μm. Specifically, we derived receptive field parameters for our model from the fast OFF cells recorded in a given retina. Our model fits came from data from two retinas having Σ_c = 85 and 90 μm and N = 32 and 21 fast OFF cells, respectively. For the two models we formed, the surround radii were Σ_s = 485 and 440 μm.

ACM.

The ACM consisted of 600 bipolar cells arranged on a one-dimensional lattice with cells equally spaced at 5 μm intervals and having center coordinates {x_i}. We used such a large array of bipolar cells to cover the entire receptive field surround (1–σ width ∼0.8 mm) sufficiently that there were no significant edge effects as the smoothly moving bar entered the surround. Each bipolar cell had a center-surround receptive field given by the following spatiotemporal response kernel that transforms the light intensity in space and time s(x,t) into a soma voltage as follows:

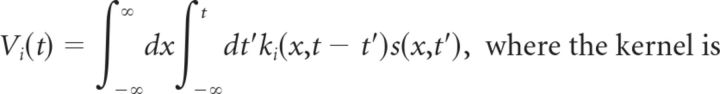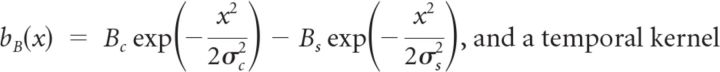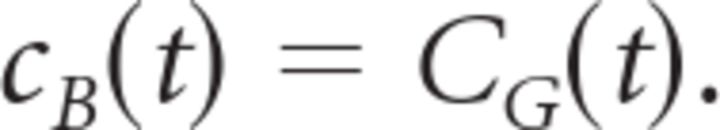The spatial profile of every bipolar cell had a center radius of σ_c = 50 μm, a surround radius larger in the same proportion as for the ganglion cell, σ_s = (∑_s/∑_c)σ_c ≈ 200 μm, and the same relative strengths as the ganglion cell. Given this center radius and the spacing between bipolar cells, each point in space was covered by the overlapping receptive fields of 10 bipolar cells. This amount of overlap is biologically reasonable as bipolar cells are normally arranged in a 2D lattice in the actual retina and an extended bar of light encounters multiple bipolar cells at each of its positions. As we sought to fit the average responses of a population of fast OFF cells, we chose the spatial and temporal kernels used in the ACM to be the average kernel computed over all of the fast OFF ganglion cells obtained from a single experimental recording. These choices closely match published data for salamander bipolar cells (Baccus and Meister, 2002).

The transformation from voltage at the bipolar soma to glutamate release involved a nonlinear function and a gain control mechanism. The total response of the bipolar cell i was as follows:

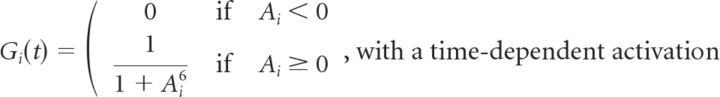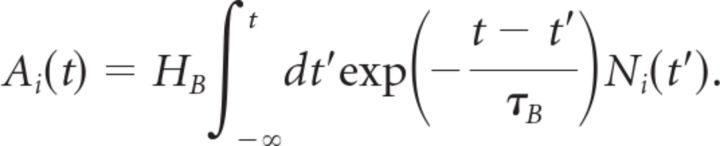Notice that the nonlinear function is thresholded at θ_B. The gain control mechanism has a time constant τ_B and a gain variable H_B that sets the contrast scale at which the gain control mechanism begins to act. These are free parameters of the model that were adjusted for the best fit to our experimental data. The functional form of the gain control mechanism used in the ACM was based on a form previously used to describe motion anticipation in salamander fast OFF cells (Berry et al., 1999), with the exception that the exponents, 6 for the bipolar gain control and 1 for the ganglion gain control mechanism, were selected to produce the best experimental fits. We also tried a standard sigmoidal function to model gain control, having a free parameter for the width and another for the slope. This functional form did not result in any significant improvement to the model's performance (data not shown).

The bipolar cells make synaptic contacts onto the ganglion cell with weights given by their spatial position relative to the ganglion cell: w_i = B_G (x_i). Notice that this function has the same spatial dependence as the ganglion cell's spatial profile, with the ganglion cell at center coordinate x₀ = 0. Following this spatial convergence, the ganglion cell has a soma voltage given by the following:

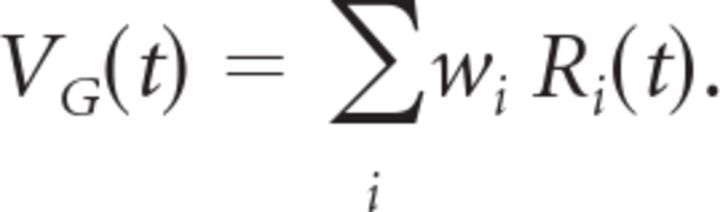Finally, the ganglion cell has its own nonlinear function and gain control mechanism with a functional form analogous to that of each bipolar cell. The ganglion cell has different parameters: time constant τ_G, gain variable H_G, and threshold Θ_G. The ganglion cell also has a refractory period that limits it maximum response to N_G^max as follows:

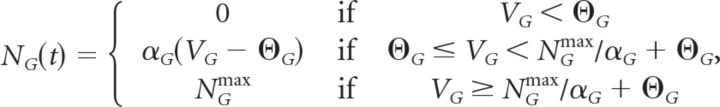as well as a less severe gain control function with an exponent of 1 instead of 6 as follows:

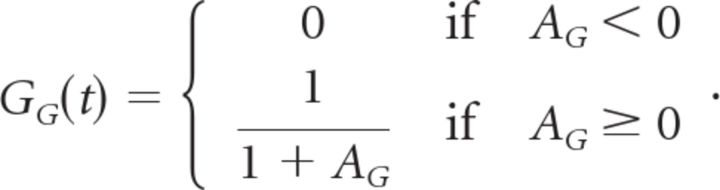Finally, the output of the ganglion cell, R_G(t) = G_G(t)N_G(t), represents the predicted firing rate of the model.

Model parameters.

The ACM features eight free parameters. Parameters were chosen using an automated minimization function (“fmincon”; MATLAB 2010) fit simultaneously to the motion onset and smooth motion responses. Given the complex form of the ACM, there is no guarantee that any set of parameters is the globally optimal set. However, we initialized the parameters with a variety of values and found that they always converged to the same final values, with the exception of H_G and α_G, whose values can approximately trade off for each other. The simulations fit to the datasets shown in Figures 8 and 9 came from two different retinas (note the slightly different responses to same stimulus condition: 100% contrast, 0.27 mm/s bar speed conditions, upper two plots of both figures). Therefore we allowed for slightly different parameters between the two datasets. The parameters used in Figure 8 are shown in the table below, while the parameters used in Figure 9 were all within 20% of those used in Figure 8.

Figure 8.

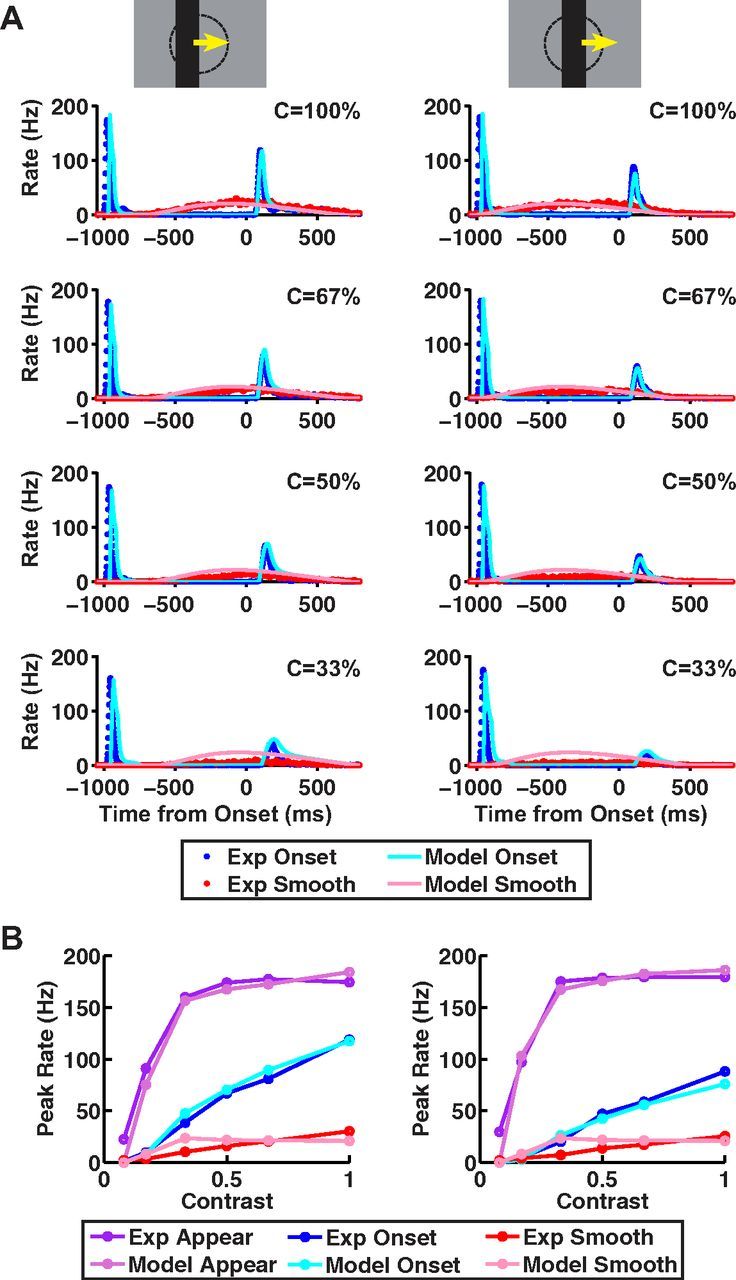
Data and ACM predictions for different stimulus contrasts. ACM responses for different contrast bars moving at a speed of 0.27 mm/s, where either the bar's leading edge starts on center coordinate (left) or the bar's center starts on center coordinate (right). All motion conditions are illustrated in Figure 1. A, Model firing rates versus time from motion onset for smooth motion (pink) and motion onset (light blue), plotted together with the average firing rate for fast OFF ganglion cells for smooth motion (red) and motion onset (blue). B, Peak firing rate versus contrast for responses to bar appearance (purple), motion onset (blue), and smooth motion (red); purple, blue, and red lines: experimental data; light purple, light blue, and pink lines, ACM.

Figure 9.

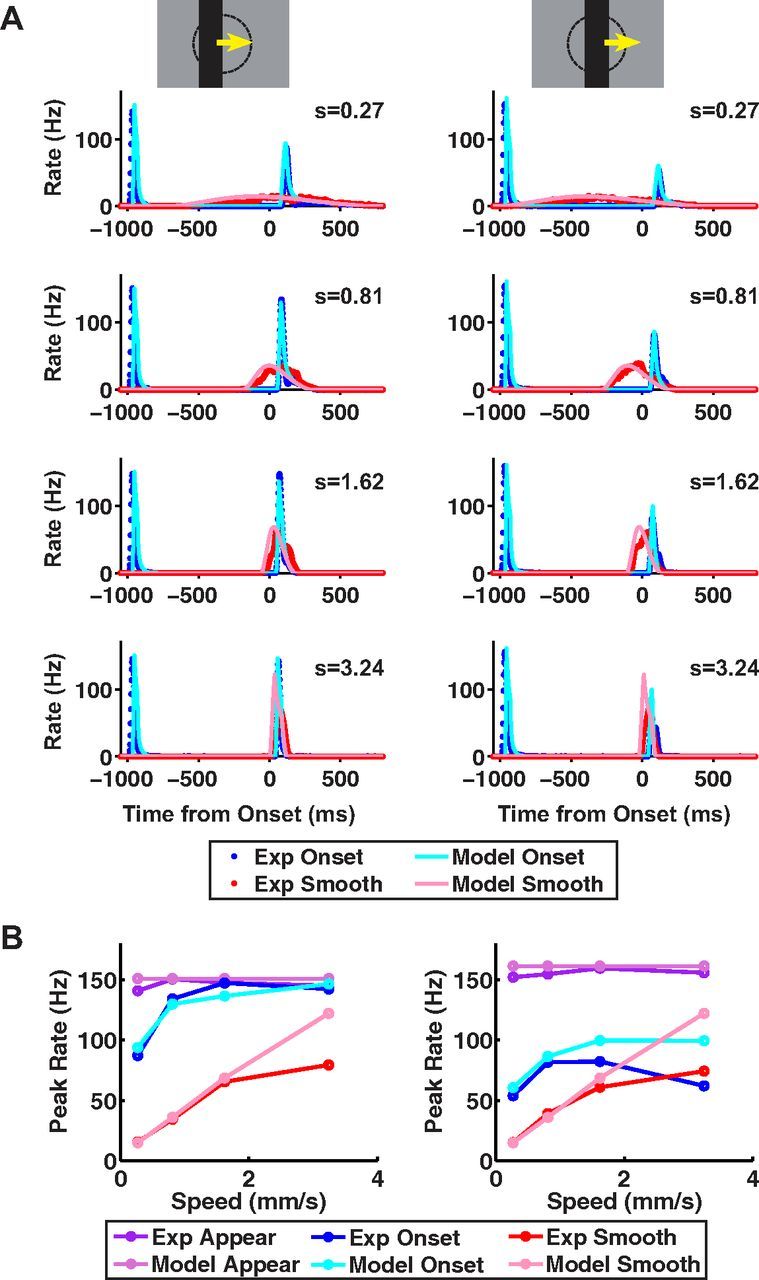
Data and ACM predictions for different stimulus speeds. ACM responses to 100% contrast bars moving at different speeds, where either the bar's leading edge starts on center coordinate (left) or the bar's center starts on center coordinate (right). All motion conditions are illustrated in Figure 1. A, Model firing rates versus time from motion onset for smooth motion (pink) and motion onset (light blue), plotted together with the average firing rate for fast OFF ganglion cells for smooth motion (red) and motion onset (blue). B, Peak firing rate versus contrast for responses to bar appearance, motion onset, and smooth motion; purple, blue, and red lines: experimental data; light purple, light blue, and pink lines, ACM.

Firing rates.

The firing rates of each cell were calculated by binning the responses in 2 ms time bins and then smoothing them with a Gaussian filter whose radius was 10 ms.

Cell classification.

Cells were classified based on the methods described by (Segev et al., 2006). In brief, the functional classification method we used consisted of classifying each cell based on the temporal profile of its receptive field, C_G (t), as measured by reverse correlation to spatiotemporal white noise (randomly flickering strips, width 9 μm). Cells were classified as OFF or ON type cells based on whether the peak of the temporal profile was above (ON) or below (OFF) zero. This classification scheme is different from the classical definition of ON or OFF cells based on the responses to flashing spots in their receptive field center (Hartline, 1938) and does not classify any cells as ON-OFF type. However, the majority of fast OFF ganglion cells responded to both increases and decreases in light, which would classify them as ON-OFF cells according to the criteria of Hartline (1938). Because these cells responded more strongly to decreases in light, their spike-triggered average was OFF-type (Fairhall et al., 2006; Gollisch and Meister, 2008). Our classification had a few simplifications compared with Segev et al. (2006). Biphasic and monophasic OFF cells were grouped together into a class called fast OFF cells, and this class thus comprised ∼37% of all the ganglion cells in the salamander retina. Both fast ON and slow ON cell types were grouped together into a class called ON cells, and this class comprised ∼12% of all the ganglion cells.

Results

Characterizing the alert response to motion onset

Previous studies have shown that retinal ganglion cells respond to smooth motion of a bar with a sustained increase in firing rate that tracks the location of the bar's leading edge (Lettvin et al., 1959; Rodieck, 1965; Rodieck and Stone, 1965; Grüsser-Cornehls and Himstedt, 1973; Hamasaki et al., 1973; Lee and Willshaw, 1978; Cohen et al., 1980; Berry et al., 1999). To compare retinal processing of continuous motion against that of the onset of motion, we designed a stimulus in which a bar appeared and remained in place for 1 s, and then abruptly began moving at a constant speed (see Materials and Methods). We aligned the motion onset stimulus with the smooth motion stimulus such that the two stimuli were exactly identical after motion onset (Fig. 1A). Note that the response to the initial appearance of the bar is quite similar to the motion onset response (see Fig. 6). If ganglion cells were merely providing a real-time, instantaneous encoding of the visual scene, identical stimuli would produce identical responses. In contrast, history dependence such as that resulting from gain control or adaptation (Shapley and Victor, 1979b, 1981; Shapley and Enroth-Cugell, 1984; Victor, 1987, 1988; Smirnakis et al., 1997) can lead to differences in the responses.

Figure 6.

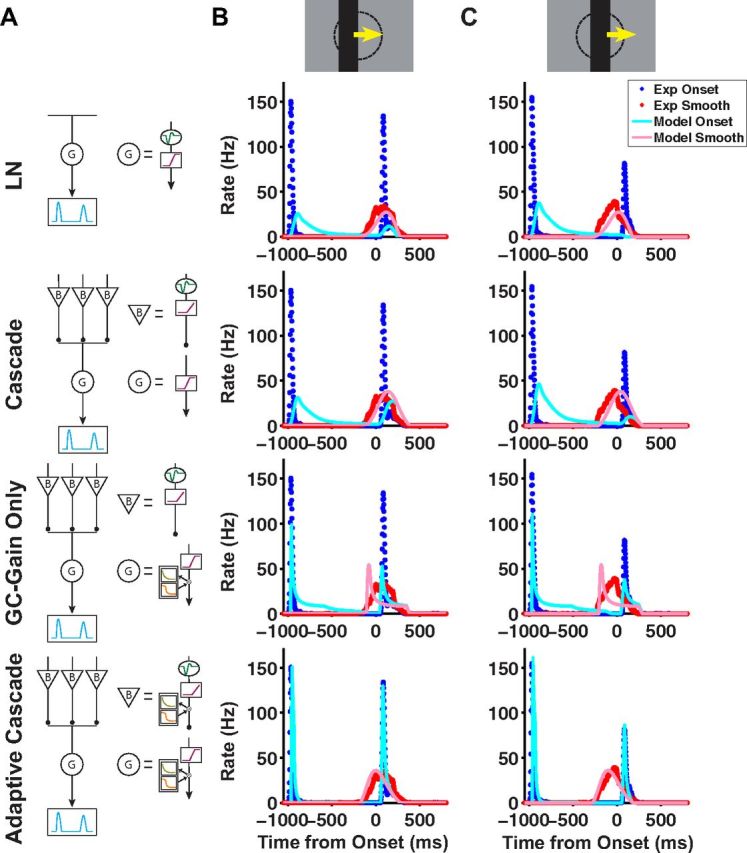
Different models fit to the motion onset response. A, Schematic diagrams of four different models: LN (first row), cascade (second row), cascade with gain control only at the ganglion cell level (third row), and adaptive cascade (fourth row). B, C, Model simulations of dark bars moving at a speed of 0.81 mm/s, where the bar's leading edge starts on center coordinate (B) and where the bar's center starts on center coordinate (C). Model firing rates versus time for motion onset (light blue) and smooth motion (pink) plotted together with the average firing rate for fast OFF ganglion cells for motion onset (blue) and smooth motion (red). In each row, the model used corresponds to the schematic in A.

Using a multi-electrode array to record spikes from salamander retinal ganglion cells, we measured the responses to both motion onset and smooth motion. When the bar started moving close to the receptive field center of a fast OFF cell, the cell responded with a sharp burst of firing that occurred ∼80 ms after motion onset (Fig. 1B,C). This response was very different from the response to smooth motion, both in amplitude and in duration. For the given conditions, the peak amplitude of the response to motion onset was 4.4 ± 0.6 times greater than the corresponding smooth motion response at the same time (n = 31 cells, Fig. 1C). This ratio varied depending on the contrast and speed of the bar, but the response to motion onset was consistently larger than that to smooth motion (Figs. 8B, 9B). The response to motion onset was also much briefer, lasting only ∼75 ms, while the response to smooth motion generally lasted at least 250 ms at the speeds tested. Clearly, the responses to smooth motion and motion onset are qualitatively different, and we refer to the latter as the “alert response” because of its elevated, transient firing rate.

Individual fast OFF cells exhibited a stronger response to motion onset than smooth motion for both bright and dark bars (Fig. 1D). We also analyzed responses of other classes of ganglion cells—medium OFF, slow OFF, and ON cells—but none of these cell types exhibited a strong alert response (Fig. 2). Fast OFF cells are a numerous cell type, comprising ∼37% of all of the ganglion cells in the salamander (Segev et al., 2006).

Figure 2.

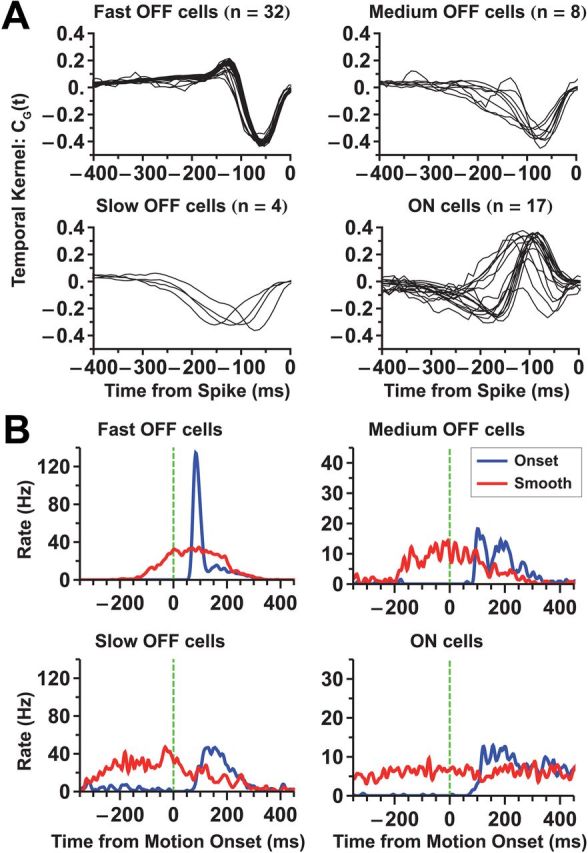
Classification of ganglion cell types. A, Temporal kernels of ganglion cells obtained from reverse correlation to random flicker stimulation. The ganglion cell population was divided into four functional types (fast OFF, medium OFF, slow OFF, ON). Kernels of cells of the same functional type are plotted together. B, Population average responses of all four cell types to motion onset (blue) and smooth motion (red) of a dark bar. Note that the fast OFF cells have a significantly stronger response to motion onset than to smooth motion; slow OFF cells also show some analogous enhancement.

The alert response is dominated by the OFF-polarity edge of a moving bar

Ganglion cell responses to motion onset depended on the location of the object within the cell's receptive field. At different locations within the receptive field center, the firing rate had a similar, transient shape (Fig. 3A,B) as well as a approximately constant latency (Fig. 3E,F). However, the response amplitude depended strongly on the location (Fig. 3C,D). For a dark bar, the maximum response was observed when the leading edge was centered on the receptive field of the ganglion cell (Fig. 3C). When the bar started moving before entering the cell's receptive field center, responses to motion onset and smooth motion were essentially identical. This property appears as a constant response amplitude for the most negative starting positions. At the other extreme, when the bar started moving at a location beyond the cell's receptive field center, there was no response. These results are consistent with the interpretation that the response to motion onset is driven by mechanisms associated with the receptive field center.

Figure 3.

The OFF-polarity edge elicits the strongest response to motion onset. A, B, Firing rate versus time for either an individual ganglion cell or a population, respectively, following motion onset at different receptive field locations (colors), as shown by the schematics. C, D, Peak firing rate of the motion onset response as a function of distance of the OFF-polarity edge to the receptive field center. For dark bars, this is the leading edge (C); for bright bars, this is the trailing edge (D). Each thin line represents a single fast OFF cell (n = 21 cells), and each dot represents a start location of the bar for that cell. All data are filtered with a Gaussian spatial kernel (radius = 20 μm) and summed to give an average spatial profile (thick line). Bar speed is 0.81 mm/s. E, F, Response latency for many ganglion cells as a function of the bar's start location (dots and thin lines); different colors are for different motion speeds.

While the strongest alert response, in the case of a dark bar, occurred when the leading edge began on the cell's receptive field center (Fig. 3C), the maximum response for a bright bar occurred when the trailing edge started on the receptive field center (Fig. 3D). The trailing edge of a bright bar represents a sudden decrease in light intensity (transition from white to gray), as is also true for the leading edge of a dark bar (transition from gray to black). Thus, these results suggest that it is the OFF-polarity edge of the moving bar that is responsible for the alert response.

To distinguish responses to the leading edge and to the trailing edge of the moving bar, we developed stimuli in which only a single edge of the bar moved at a time. Movement of only the bar's leading edge caused the bar to become larger (grow), while movement of only the trailing edge caused the bar to become smaller (shrink). The dynamics of responses to these single moving-edge stimuli were very similar to the dynamics of responses to full motion onset, with a sharp peak of firing shortly after edge motion onset (data not shown). Hence, we decided to characterize responses by their peak-firing rate.

We found that, for dark bars, the grow condition elicited almost identical responses to the full motion onset condition (Fig. 4A; Pearson r = 0.965). Similarly, for bright bars, the shrink condition elicited almost identical responses to the full motion onset condition (Fig. 4C; Pearson r = 0.975). These results are again consistent with hypothesis that the OFF-polarity edge drives the alert response to motion onset. What was surprising was that the other two conditions, involving motion onset of ON-polarity edges only, could sometimes drive appreciable responses, especially for a shrinking dark bar (Fig. 4B). If activation of the ON and OFF pathways was simply summed linearly at the level of the ganglion cell, one might expect that the firing rate evoked by the full motion onset stimulus, having both leading and trailing edges, would be larger than the rate evoked by motion of the OFF-polarity edge alone. However, this was not the case (Fig. 4A,C). A plausible mechanism to explain this phenomenon is crossover inhibition between ON and OFF pathways (Manookin et al., 2008; Molnar et al., 2009; Werblin, 2011; Bölinger and Gollisch, 2012; Buldyrev et al., 2012). In our case, strong activation of the OFF pathway is hypothesized to suppress the activation of the ON pathway.

To further investigate the role of the ON and OFF pathways, we used the mGluR6 receptor blocker, L-AP4, which abolishes light responses in ON bipolar cells (Slaughter and Miller, 1981; Yang, 2004). As expected, this drug abolished the response to the appearance of a bright bar, but did not affect the peak firing rate in response to the appearance of a dark bar (Fig. 5A). Responses to motion onset of ON-polarity edges (bright bar growing or dark bar shrinking) were abolished by L-AP4, while response to OFF-polarity edges (dark bar growing or bright bar shrinking) were unaffected (Fig. 5B,C). Finally, the peak firing rate evoked by full motion onset was also unaffected (Fig. 5D). These results once again demonstrate that the alert response to motion onset arises entirely from the OFF pathway, which is activated by the OFF-polarity edge of the moving bar.

Figure 5.

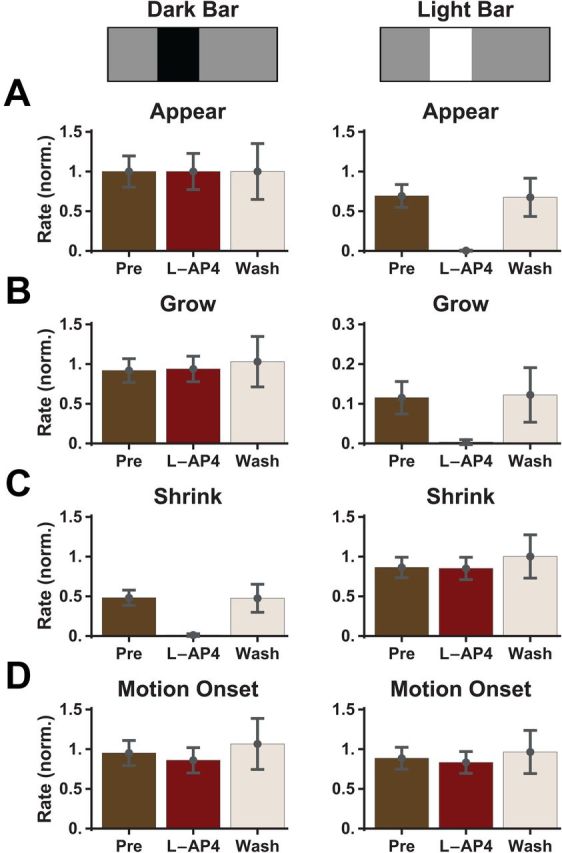
The alert response to motion onset is unaffected by L-AP4. A–D, Peak firing rate for ganglion cells responding to bar appearance (A), motion onset of the leading edge (grow, B), motion onset of the trailing edge (shrink, C), and full motion onset (D). Colors show response in control conditions (brown), after application of L-AP4 (burgundy; 50 μm), and after drug washout (beige). Responses in each condition were averaged over n = 11 cells and separately normalized by the peak firing rate following the appearance of the dark bar. Error bars indicate SEM confidence intervals.

Constructing a computational model of the responses to motion onset and smooth motion: the ACM

Having characterized the motion onset response, we next sought to design a phenomenological model that could capture the ganglion cell responses that we observed experimentally. This type of model has been used to describe the mechanisms underlying many retinal computations (for review, see Gollisch and Meister (2010)). We attempted to reproduce the responses to three different classes of stimuli: bar appearance, motion onset, and smooth motion over a range of contrasts and speeds. The classical receptive field model, or linear–nonlinear (LN) model (Rodieck and Stone, 1965), has been shown to be unable to reproduce the smooth motion response accurately (Berry et al., 1999); here also, it was also unable to capture the response to motion onset (Fig. 6, top). Instead, we found that a model including two well known aspects of cellular physiology in the retina—rectified receptive field subunits and contrast gain control (Shapley and Victor, 1979a; Victor, 1988; van Hateren et al., 2002; Bölinger and Gollisch, 2012)—was able to capture ganglion cell responses. While rectified subunits and gain controls are well known computational elements, they have not been combined before to describe ganglion cell responses to spatiotemporal stimuli.

These additional features of the model were suggested to us by robust qualitative properties of the experimental responses. First, motion onset induced a peak in the firing rate regardless of the specific position at which the bar started to move within the cell's receptive field center (Fig. 3). A model that relies upon linear spatial summation, as does the LN model, fails to reproduce this property: as the initial position of the ON-polarity edge starts closer to the receptive field center (and, hence, as the OFF-polarity edge starts farther away), the response gets weaker and can even be abolished in cases when the ON-polarity edge elicits a negative linear response (Fig. 6C, first row). To address this issue, we invoked nonlinear spatial subunits in the receptive field, as used in models of “Y-type” ganglion cells in the cat (Shapley and Victor, 1979a) and of fast OFF ganglion cells in the salamander (Olveczky et al., 2003; Baccus et al., 2008; Bölinger and Gollisch, 2012) and mouse (Münch et al., 2009). In this revised picture, the ganglion cell sums over spatially local subunits that are individually rectified, so that inhibition in a given subunit cannot cancel excitation in another subunit (see Materials and Methods). In the case of the motion of a dark bar, this rectification prevents the effect of the trailing, ON-polarity edge to cancel that of the leading, OFF-polarity edge, regardless of their positions within the receptive field center. In α-type ganglion cells, these nonlinear local subunits appear to be individual bipolar cells (Demb et al., 2001; Schwartz and Rieke, 2011). Analogous models of salamander fast OFF cell responses also assume that nonlinear receptive field subunits are individual bipolar cells (Olveczky et al., 2003; Baccus et al., 2008).

Gain control offered a natural way to capture the difference between the response to motion onset versus smooth motion. As mentioned, if the response mechanisms were instantaneous, the responses would not differ since the two stimuli are identical after motion onset. Hence, ganglion cells must use a form of history dependence in producing their responses. In the presence of gain control, the response to smooth motion is suppressed as, at any given time, subunits that have been activated by an earlier segment of the stimulus now have reduced gain; conversely, gain control does not affect the response to motion onset, at least in the initial phase of the response. Several qualitatively similar models of gain control have been presented in the literature (Victor, 1987; Berry et al., 1999; van Hateren et al., 2002).

We chose to implement a form of gain control that was previously used to describe motion anticipation in salamander fast OFF cells (Berry et al., 1999), in which excitatory input reduces the gain of the response to subsequent stimuli (see Materials and Methods). Because this gain control takes a certain amount of time to develop, we reasoned that the early response to motion onset would be insensitive to it, while the response to matched smooth motion would be suppressed. A novel aspect of our model is the inclusion of gain control mechanisms at both the bipolar and ganglion cell levels. For predicting the response to smooth motion alone, only a ganglion cell gain control mechanism was necessary (Berry et al., 1999), but gain control is required at multiple levels to account for responses to a wider class of stimuli. Specifically, when we optimize the parameters of a model with gain control only at the ganglion cell level, the gain control must be more severe to capture the motion onset response and this causes a rapid truncation of the response to smooth motion (Fig. 6, third row). A model with gain control only at the bipolar cell level does not reproduce the anticipatory effects measured during smooth motion (Berry et al., 1999), because this gain control can only produce a spatial shift on the scale of the bipolar cell receptive field.

Finally, because we found experimentally that the ON pathway did not contribute in any way to the alert response (Fig. 5), we simplified our model by implementing the OFF pathway alone. Because the ON pathway is required to capture the response to the appearance of a bright bar (Fig. 5) as well as to the smooth motion of a bright bar (data not shown), we chose to focus only on modeling the responses to dark bars.

The ACM reproduces the responses to stimulus appearance, motion onset, and smooth motion

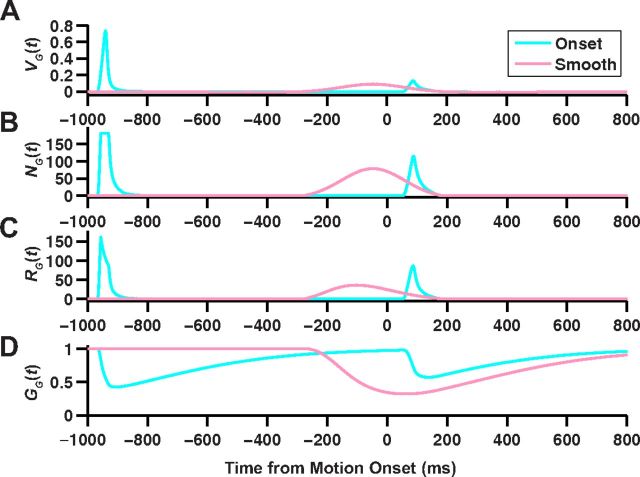
The ACM is schematized in Figure 7A. Using this model, we reproduced quantitatively the time-varying firing rate of ganglion cells responding to bar appearance, motion onset, and smooth motion (Fig. 7B). Clearly, the model differentiates motion onset from smooth motion. At the time of motion onset (t = 0), the ganglion cell gain control has already been activated for the smooth motion stimulus (gain ≈ 0.5), while it is still at its baseline value (gain ≈ 1) for motion onset. Because of the delay of the gain control mechanism, embodied by a temporal filter with a time constant of 190 ms (Table 1), even at the time of the peak response to motion onset, the gain is still not fully reduced as compared with the smooth motion case (Fig. 7B, dashed line).

Figure 7.

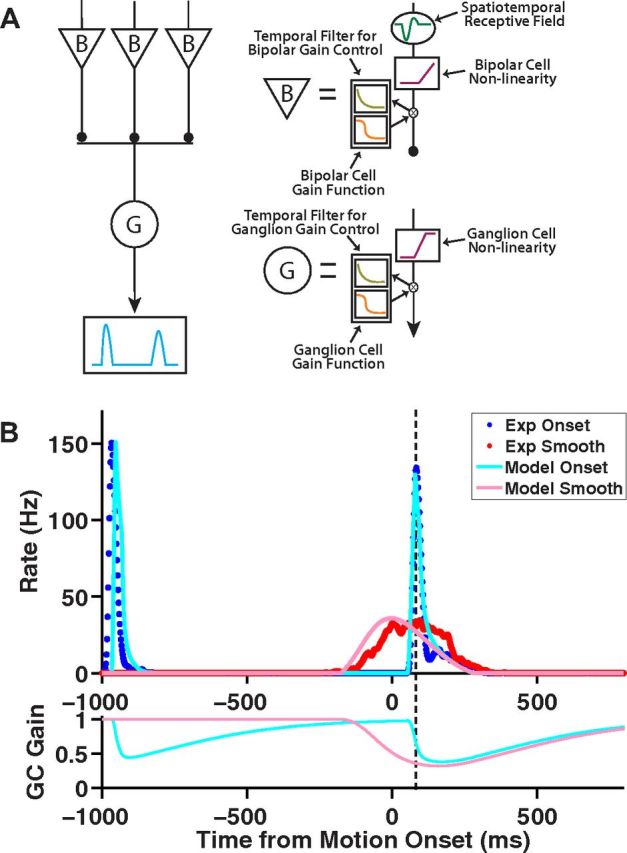
The ACM captures the alert response to motion onset. A, Schematic illustration of the ACM (see text for details). B, Top, Model responses to a dark bar that appears at t = −1 s, holds, and begins moving at t = 0 s for motion onset (light blue) as well as for a bar in smooth motion (pink). Population average firing rate for fast OFF ganglion cells responding to motion onset (blue) and smooth motion (red). Bottom, Time-varying gain of the model ganglion cell responding to motion onset (light blue) and smooth motion (pink). Dashed line marks the time of the maximum motion onset response. Bar moved at a speed of 0.81 mm/s; motion onset began with the bar's leading edge on the receptive field center coordinate.

Table 1.

Parameter values for the ACM

Parameter	Description	Value
θB	Bipolar cell threshold	5.32 Hz
HB	Amplitude of bipolar cell gain control	6.11 e-3s−1
τB	Time constant of bipolar cell gain control	100 ms
ΘG	Ganglion cell lower threshold	0 Hz
NGmax	Ganglion cell upper threshold	212 Hz
αG	Slope of ganglion cell nonlinearity	1110 Hz
HG	Amplitude of ganglion cell gain control	3.59 e-4s−1
τG	Time constant of ganglion cell gain control	189.5 ms.

Broad applicability of the ACM to different contrasts, speeds, and locations

To probe the robustness of the ACM, we examined the model's performance for different stimulus contrasts (Fig. 8) and speeds (Fig. 9). In the contrast series, we chose to move the bar at a slow speed (0.27 mm/s) to allow for the gain control mechanism to be most effective. Experimentally, as contrast decreased, the response to motion onset became slower and its amplitude decreased (although it still remained larger than the response to smooth motion). The model closely reproduced the responses for different contrasts over all three stimulus classes (appearance, motion onset, and smooth motion). We also examined the response to onset motion starting at two different locations on the ganglion cell's receptive field: with the bar's leading edge on the center coordinate (Fig. 8, left) and with the bar's center on the center coordinate (Fig. 8, right). The model captured the detailed temporal dynamics of the ganglion cell's firing rate (Fig. 8A) as well as the peak firing rate (Fig. 8B) across stimulus contrasts, except for the smooth motion response at low contrast (Fig. 8A, fourth row).

The model similarly captured ganglion cell behavior for different stimulus speeds (Fig. 9). For fast OFF cells, as the bar speed increased, the alert response to motion onset occurred more quickly and increased in amplitude. When we compared the model's prediction to our experimental results, we found that, once again, the model performed well, although we noted some deviations at the highest speed tested. Higher speeds give the contrast gain control mechanism less time to fully develop, which, in principle, should cause the motion onset and smooth motion responses to become more similar in amplitude. This behavior held when the bar's center began moving on the receptive field center (Fig. 9, right). However, when the bar's leading edge began moving on the cell's receptive field center, the response was stronger than for smooth motion at all speeds tested (Fig. 9, left).

Bipolar cell and ganglion cell gain controls in the model

Our goal in formulating a computational model was to predict the time-varying firing rate of ganglion cells, as compactly as possible, and we found that gain control at both the bipolar cell and the ganglion cell levels contributed to the alert response (Figs. 10, 11). Experimental evidence indicates that bipolar cells and ganglion cells each come with their own individual gain control mechanisms (Awatramani and Slaughter, 2000; DeVries, 2000; Brown and Masland, 2001; Kim and Rieke, 2001; Rieke, 2001; Baccus and Meister, 2002; Beaudoin et al., 2007; Jarsky et al., 2011; Oesch and Diamond, 2011; Bölinger and Gollisch, 2012). Although we modeled the two gain control mechanisms with the same general form, they used different parameters causing them to have quantitatively different behavior (Fig. 12).

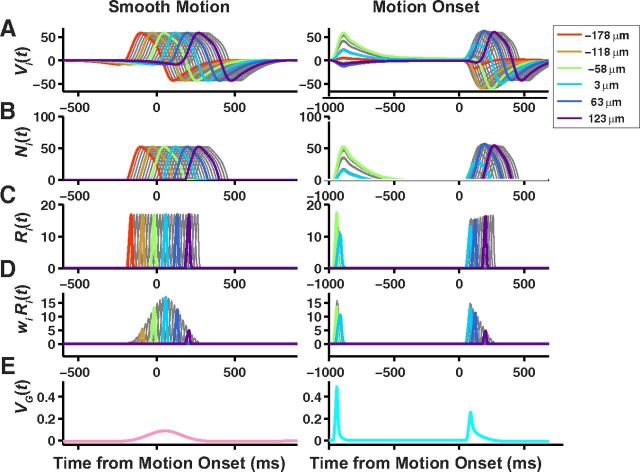
Figure 10.

Bipolar cell processing in the ACM. Stages of bipolar cell processing during the ACM for smooth motion (left) and motion onset (right). Each trace in the top four rows is the response of a single bipolar cell. Colors denote responses of every twelfth bipolar cell. A, Linear response of each bipolar cell soma as a function of time, V_i(t). B, Response of each bipolar cell after passing the soma voltage through the nonlinearity function, N_i(t). C, Response of each bipolar cell after applying the gain control mechanism, R_i(t). D, Response of each bipolar cell scaled by its synaptic weight onto the ganglion cells, w_i R_i(t). E, Soma voltage of the ganglion cell, V_G(t).

Figure 11.

Ganglion cell processing in the ACM. Stages of ganglion cell processing in the ACM for smooth motion (pink) and motion onset (light blue). A, Soma voltage of the ganglion cell, V_G(t). B, Response of the ganglion cell after passing the soma voltage through the nonlinear function, N_G(t). C, Final firing rate of the ganglion cell, R_G(t). D, Time-varying gain of the ganglion cell, G_G(t).

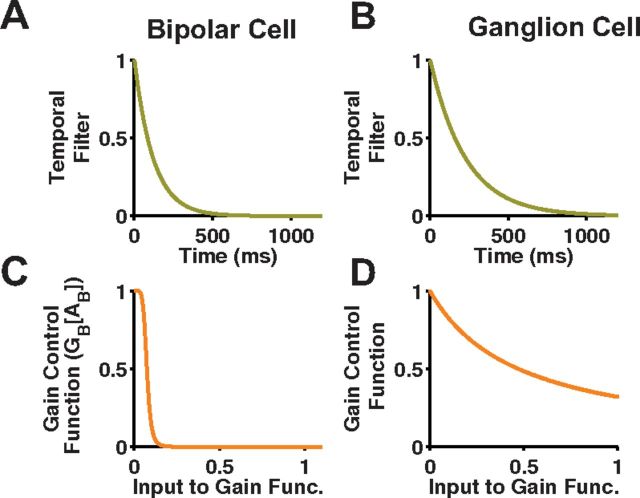
Figure 12.

Bipolar and ganglion cell gain control mechanisms. A, Bipolar cell temporal filter with time constant, τ_B. B, Ganglion cell temporal filter with time constant, τ_G. C, Bipolar cell gain control function, G_B[A_B]. D, Ganglion cell gain control function, G_G[A_G].

Compared with the ganglion cell gain control, the bipolar cell gain control had a shorter time constant and transitioned between no gain and full gain over a much shorter range of input values (Fig. 12, bottom). Stronger bipolar cell gain control was necessary to truncate the model's response to bar appearance and motion onset, as the temporal kernel of the bipolar cell, which was set without any free parameters, allowed a sustained response that was not seen experimentally. If gain control at the bipolar cell level is discarded, the best fit parameters select a ganglion cell gain control so strong that it suppressed the smooth motion response too much (Fig. 6, third row). In a previous study of the cat Y-cell that included gain control both before and after the subunit nonlinearity, the earlier gain control mechanism dominated, in agreement with the stronger bipolar cell gain control found here in the ACM (Shapley and Victor, 1980). Similarly, gain control in α-type ganglion cells was dominated by changes in its presynaptic input and was largely insensitive to inhibitory blockers, suggesting a bipolar cell origin (Beaudoin et al., 2007).

Despite the nonlinear effects of the gain control mechanism in the ACM, they did not significantly distort the model's spatiotemporal receptive field, as calculated by simulating the model's response to flickering white noise (Fig. 13). The model's simulated spatial kernel had a narrower surround component than the original experimental kernel (Fig. 13C); however, this is most likely caused by the lack of medium- or wide-field amacrine inhibition of the ganglion cell surround, which was not accounted for by the ACM.

Figure 13.

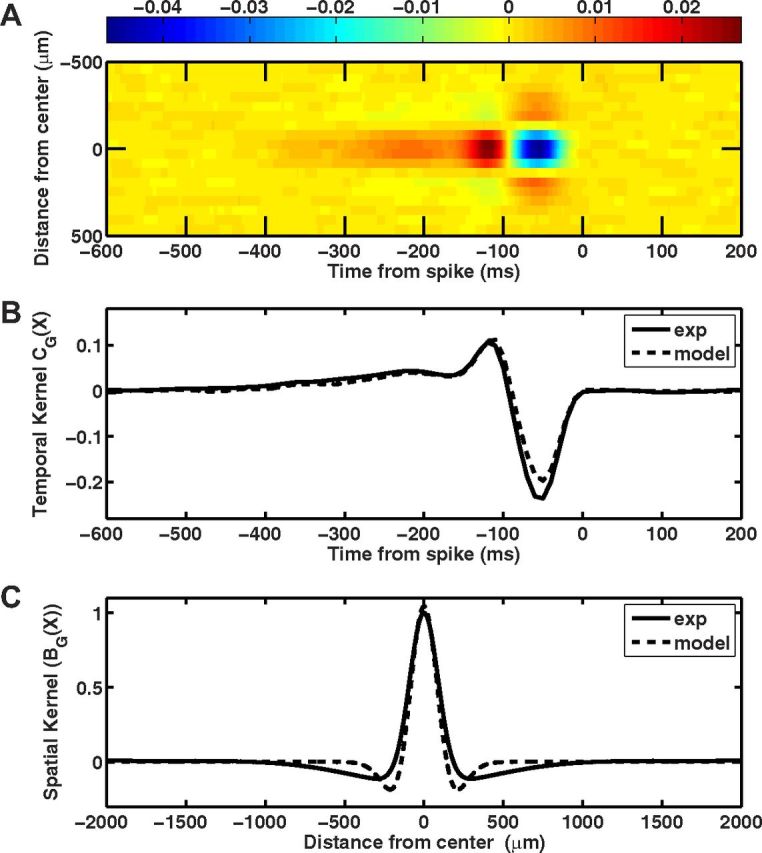
The subunit and gain control parameters do not alter the temporal and spatial kernels of the ACM. A, Space-time plot of the ACM's receptive field, measured by reverse correlation during random flicker stimulation. Parameters for the random flicker stimulus were the same used during the experimental recordings. B, Temporal kernel of the model (dashed line) compared against fast OFF ganglion cells (solid line). C, Spatial profile of the model (dashed line) compared against fast OFF ganglion cells (solid line).

Discussion

We found that a significant fraction of retinal ganglion cells exhibited a novel, “alert” response to the sudden onset of motion, firing a transient burst that qualitatively resembled the response to the sudden appearance of an object rather than the response to smooth motion. Even though the ganglion cells were fast OFF-type, they generated a transient burst of firing for the onset of motion for both bright and dark bars. We demonstrated that both of these responses were generated by the OFF-polarity edge of the moving bar. Finally, we developed a phenomenological model, the ACM that accurately predicted the time-varying firing rate in response to the appearance, motion onset, and smooth motion of a bar over a wide range of contrasts, speeds, and locations. This model involved rectified subunits within the receptive field along with mechanisms of gain control at both the subunit and ganglion cell level. Following many previous studies, we identify the subunits in our model with individual bipolar cells (Victor and Shapley, 1979; Demb et al., 2001; Bölinger and Gollisch, 2012).

Salience ranking of appearance, motion onset, and smooth motion

As mentioned, the onset of motion is a very salient stimulus, much more so than smooth motion (Abrams and Christ, 2003). These authors report, further, that the appearance of a new object is more salient than motion onset, thereby suggesting an informal “salience ranking” of appearance (new object), motion onset (new motion), and smooth motion (old motion) (Christ and Abrams, 2008). From our experimental recordings, we found that this ranking is also present in the peak firing rates of retinal ganglion cells. The appearance of a bar elicited the strongest response, while motion onset elicited a stronger response than smooth motion (Figs. 8B, 9B). This ranking held for every contrast and speed we tested.

The structure of the ACM offers some clues to the mechanisms through which these differentiated responses may arise. The appearance of a bar simultaneously stimulates every bipolar cell whose receptive field center is within range of the bar, providing a maximal input to the ganglion cell through spatial summation (Fig. 10). Motion onset stimulates bipolar cells sequentially, rather than simultaneously. This sequential stimulation causes the response to motion onset to be smaller than the response to appearance, although in the limit of sufficiently high speed the two responses become identical (Fig. 9B). Finally, smooth motion produces the smallest response because not only does it stimulate bipolar cells sequentially, but it also triggers strong suppression via gain control (Fig. 11). Our findings suggest that the retina may contribute to bottom-up attentional processing by generating qualitatively different firing dynamics for different categories of object motion as well as by generating different peak firing rates.

Biophysical mechanisms of gain control in bipolar cells

Multiple biophysical mechanisms could underlie the bipolar gain control in our model. A mechanism with considerable experimental support is synaptic depression at the bipolar cell axon terminal. Direct measurement of glutamate release from rod bipolar cells shows a severe gain control: sustained depolarization of the presynaptic rod bipolar cell (RBC) produces an excitatory current in the postsynaptic AII amacrine cell that features an initial transient response that decays by a factor of 10–20 over a timescale of 20–40 ms (Singer and Diamond, 2003, 2006; Wan and Heidelberger, 2011). Furthermore, paired flashes of light induced synaptic depression in RBCs that lasted for 100–200 ms, similar to the timescale of the gain control in our model (Dunn and Rieke, 2008). This transient response is due to the depletion of the readily releasable pool (RRP) of vesicles in the bipolar cell ribbon synapse (Singer and Diamond, 2006). Similar depression in vesicle release has been directly observed in the Mb1 bipolar cell (Mennerick and Matthews, 1996; von Gersdorff and Matthews, 1996; von Gersdorff et al., 1996; Burrone and Lagnado, 2000; Palmer, 2010).

Synaptic depression via depletion of the RRP is only one of several different adaptive mechanisms in bipolar cells. Other possibilities include Ca²⁺ channel inactivation (von Gersdorff and Matthews, 1996; Palmer et al., 2003) as well as glutamate transporter activation at bipolar cell terminals (Veruki et al., 2006). Ca²⁺ channel inactivation was found to contribute more to luminance adaptation than to contrast adaptation (Jarsky et al., 2011). However, the motion of the bar changed light intensity at a given point on the retina for 50–600 ms, depending on speed, and this is long enough, especially at the slowest speeds, to trigger adaptation to luminance.

Another mechanism of gain control in bipolar cells is inhibitory feedback from amacrine cells onto bipolar cell terminals (Dowling and Werblin, 1969; Burkhardt, 1972; Toyoda and Fujimoto, 1984; Tachibana and Kaneko, 1987; Werblin et al., 1988; Dong and Werblin, 1998; Roska et al., 1998). This inhibitory feedback has been shown to play a role in motion detection (Werblin et al., 1988) as well as in making bipolar cell outputs more transient (Thibos and Werblin, 1978a,b; Roska et al., 1998). Amacrine cell synapses onto bipolar cell terminals have also been shown to contribute more to contrast adaptation than the amacrine cell synapses onto ganglion cell dendrites (Zaghloul et al., 2007). If the amacrine cell feedback operates in a linear regime, then this feedback would be captured by our empirically determined bipolar cell temporal kernel, k(x,t). If, however, amacrine feedback is nonlinear, then it would play a role similar to our gain control mechanism, where for small activation of the bipolar terminal feedback would have little effect, but for large activation the terminal's output would be strongly suppressed.

In sum, the bipolar cell gain control in our phenomenological model potentially includes effects arising from multiple biophysical mechanisms. This illustrates both a strength and weakness of this form of model. On the one hand, our model can capture multiple circuit mechanisms with a small set of free parameters; on the other hand, it does not provide tight constraints on the biophysical mechanism.

Biophysical mechanisms of gain control in ganglion cells

Ganglion cell gain control can arise from intrinsic mechanisms that modulate the transformation of input currents to firing rate (Kim and Rieke, 2001; Zaghloul et al., 2005; Beaudoin et al., 2007). The primary mechanism of intrinsic gain control appears to be slow inactivation of Na⁺ channels (Kim and Rieke, 2003), as it is not dependent on voltage or calcium-dependent processes (Beaudoin et al., 2007). Slow Na⁺ channel inactivation has both spike-dependent and spike-independent forms, with time constants ranging from ∼100 ms up to ∼1 s (Kim and Rieke, 2003). The faster timescale, arising in the spike-dependent mechanism, matches reasonably well with the time constant in our model; the slower timescales might not come into play here because bar motion did not last long enough to probe them. The overall strength of the effect, suppressing the Na⁺ current approximately by a factor of two (Kim and Rieke, 2003), also matched the magnitude of the gain control mechanism in our model. Finally, the form of our model, namely, gain control acting after the static nonlinear function, N_G(see Materials and Methods), agrees with the spike-dependent mechanism of slow Na⁺ channel inactivation, as the spiking rate is determined by the input current-to-spiking transfer function.

Additional evidence from the guinea pig has shown that K⁺ channel inactivation can also contribute to gain control in ganglion cells (Weick and Demb, 2011). If such a mechanism were present in the salamander retina, its function in differentiating motion onset from smooth motion would be very similar to that described here. Smooth motion of an object would stimulate a ganglion cell's surround, resulting in K⁺ inactivation, and thus suppression of the smooth motion response. Motion onset, on the other hand, would not stimulate the surround and thus not activate the gain control mechanism, thereby avoiding suppression.

Ganglion cell gain control could also arise from feedforward inhibition from amacrine cells. In fact, there is evidence that amacrine cells contribute to wide-field gain control mediated by the receptive field surround (Werblin, 1972; Enrothcugell and Jakiela, 1980; Zaghloul et al., 2007). However, wide-field stimulation was limited during our experimental recordings, since our stimulus consisted of a single bar on a gray background. If smaller receptive field amacrine cells had nonlinear feedforward inhibition onto the ganglion cell, their action would again be qualitatively similar to our ganglion cell gain control and thus could contribute to it. What distinguishes amacrine cell inhibition that contributes to the bipolar gain control from the ganglion cell gain control? The essential difference in our model is that bipolar gain control operates after integration by a small spatial receptive field, while ganglion cell gain control has a large receptive field. Thus, the effect of narrow-field (<100 μm dendrites) amacrine cell inhibition would likely be captured by the bipolar cell gain control, while medium-field (∼100–300 μm dendrites) amacrine cell inhibition would likely be captured by the ganglion cell gain control. A recent study of salamander ganglion cells observed a mechanism of local gain control on the receptive field center mediated by amacrine cells (Bölinger and Gollisch, 2012).

Disregarding of ON pathway inputs during motion onset

One curious finding is that the motion onset response is completely explained by the properties of its input from the OFF pathway, despite the fact that stimuli that only trigger the ON pathway (ON grow and OFF shrink stimuli; Fig. 4) can drive ganglion cell firing. In our model, we account for this by only including OFF bipolar cells. Clearly, this is a simplification of the actual neural circuitry underlying actual fast OFF cells, as many of these cells are also of the ON-OFF type, suggesting that they receive inputs from both ON and OFF bipolar cells. This simplification is successful for predicting the responses to dark bars but breaks down for other visual stimuli, such as a smoothly moving ON bar. While we cannot fully explain how fast OFF cells can disregard inputs from the ON pathway, we hypothesize that crossover inhibition from glycinergic amacrine cells may play a role (Pang et al., 2007; Molnar et al., 2009). For example, when a visual stimulus strongly activates OFF bipolar cells, as in motion onset, they may suppress or inhibit the response of the ON bipolars, such that the ON pathway does not add any appreciable excitation to the ganglion cells.