SUMMARY
While it is commonly assumed that decisions taken slowly result in superior outcomes, is it possible that optimal decision making does not always require sacrificing speed? For odor categorization decisions, it was previously shown that rats use <300 ms regardless of difficulty, but these findings could be interpreted as a tradeoff of accuracy for speed. Here, by systematically manipulating the task contingencies, we demonstrate that this is the maximum time over which sampling time can improve accuracy. Furthermore, we show that decision accuracy increases at no temporal cost when rats can better anticipate either the identity of stimuli or the required timing of responses. These experiments suggest that uncertainty in odor category decisions arises from noise sources that fluctuate slowly from trial-to-trial rather than rapidly within trials and that category decisions in other species and modalities might likewise be optimally served by rapid choices.
INTRODUCTION
Studies of reaction times have helped to constrain theories of decision making, leading to a prominent class of models in which performance is limited by a random noise process that is integrated during the presentation of a stimulus to improve the signal-to-noise ratio (Luce, 1986; Ratcliff and Smith, 2004). Such integration models can account for several commonly observed relationships between the time and accuracy of decisions: (1) when problem difficulty is increased, reaction times increase; (2) when stimulus sampling time is controlled, performance increases with increased sampling duration; and (3) for a given problem subjects can change their “speed-accuracy tradeoff” (SAT), responding more accurately at a cost of slower responses or more quickly at a cost of reduced accuracy. Integration models thus capture and help to explain the intuition that optimal performance under uncertainty benefits from prolonged processing time. In addition to accounting for a range of human behavioral data, simultaneous recordings of neural activity in primates have shown neural correlates resembling the integrator variables posited in the models (Roitman and Shadlen, 2002; Ratcliff and Smith, 2004).
Studies of odor discrimination in rats have suggested, somewhat counterintuitively, that under some circumstances decision making shows little benefit from increased sampling beyond a single sniff (Uchida and Mainen, 2003; Uchida et al., 2006). These experiments used a two-alternative forced-choice task in which eight different binary odor mixture stimuli were randomly interleaved and rewarded according to a categorical boundary. As mixture ratios approached the category boundary, choice accuracy dropped to near chance, yet odor sampling time increased only 30 ms (Uchida and Mainen, 2003).
One possible explanation for the failure of subjects in this study to slow down their responses in the face of more uncertain decisions is that they may have always set a relatively low evidence threshold, leading to consistently rapid responses at a cost of accuracy (Khan and Sobel, 2004). A key prediction of this untested “SAT hypothesis” is that, given the right incentives and training, rats should be able to change their speed-accuracy tradeoff and respond more slowly and accurately. An alternative explanation is that the subjects were making optimal decisions but that integration would not be helpful for improving accuracy in this task.
Can’t additional information always improve a decision? How could integration fail to improve accuracy of uncertain decisions? One plausible explanation is that integrator models assume decision accuracy is limited by stimulus noise that is temporally white (uncorrelated in time). Temporal correlations in decision noise can defeat an integrator by limiting the ability of averaging to improve signal-to-noise ratio, thereby diminishing the benefits of repeated sampling (Uchida et al., 2006). In the limit, if noise fluctuations are completely correlated within a trial (i.e., only varying across trials), then the benefits of temporal integration within a single trial disappear entirely. Thus, if olfactory categorization decisions cannot be improved by extended sampling time, this result would suggest that there may be an important source of uncertainty that is missing from standard integration-based decision models but may dictate the speed-accuracy relationships of some classes of decision problems.
Here, we sought to distinguish these two general possibilities using a series of experiments on the odor categorization task in which we systematically tested the impact of manipulations of training and task structure on decision speed and accuracy. Through manipulations of reward contingencies, we were able to slow down the subjects’ odor sampling times, but this failed to increase performance. Conversely, by increasing the predictability of stimuli and the timing of a response deadline, we were also able to increase accuracy, but this increase did not come at a cost of speed. Thus, the results support the idea that the limiting uncertainty in this class of decisions is different than the uncorrelated stimulus noise assumed in standard decision models. These results can also help to reconcile apparently disparate findings from previous studies of olfactory decision making (Abraham et al., 2004; Rinberg et al., 2006).
RESULTS
The Odor Mixture Category Decision Task
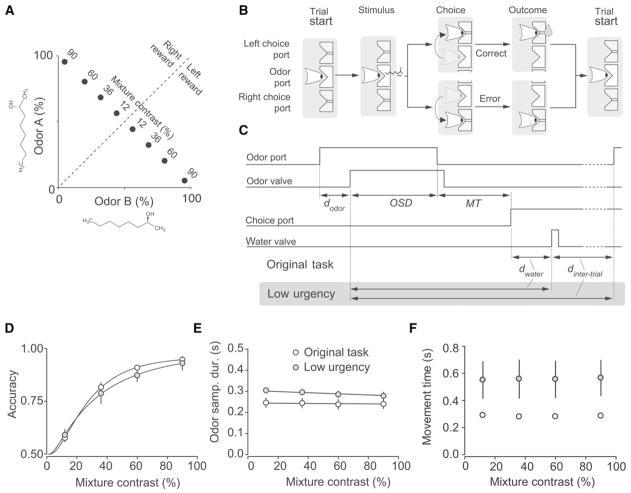
We trained and tested male Long-Evans rats on the same two-alternative choice olfactory categorization task employed previously (Uchida and Mainen, 2003). Each odor stimulus was a binary mixture of two odorants and choices were rewarded according to the dominant component (Figure 1A). The difficulty of the problem was controlled by the difference of the stimulus from the boundary (50/50), denoted the “mixture contrast,” which was randomly varied from trial-to-trial. A subject initiated a trial by a nose poke into the center port where an odor was delivered (Figure 1B). It then responded by moving to either the left or right choice port where it received water reward for correct responses and no reward for incorrect responses. In this task the reaction time (RT) consists of two components, the odor sampling duration (OSD) and the movement time (MT) (Figure 1C and see Figure S1 available online). As reported previously (Uchida and Mainen, 2003), we observed a strong dependence of performance accuracy on mixture contrast (Figure 1D; p < 0.005, ANOVA post hoc multiple comparison test at p < 0.01). In contrast, there was no significant dependence of OSD (Figure 1E; p = 0.88, ANOVA) or MT on mixture contrast (Figure 1F; p = 0.9, ANOVA).
Figure 1. Two Alternative Odor Mixture Categorization Task.
(A) Stimulus design. Two odorants (the stereoisomers S-(+)-2-octanol and R-(−)-2-octanol) were mixed in different ratios and rewarded according to the majority component. Odor mixture contrasts determine the difficulty of the stimulus, with lower contrasts being harder.
(B) Sequence of events in a behavioral trial, illustrated using a schematic of the ports and the position of the snout of the rat.
(C) Illustration of the timing of events in a typical trial in both the original task and low urgency conditions task. Nose port photodiode and valve command signals are shown (thick lines). Measurements of odor sampling duration (OSD) and movement time (MT), as well as imposed delays (dodor, dwater, and dintertrial) are indicated by arrows for two conditions. In the original conditions, dodor and dwater were drawn from uniform distributions with ranges of [0.3, 0.6] and [0.1, 0.3], respectively, and dintertrial had a minimum of 4 s. In the low urgency conditions, dodor was drawn from an exponential distribution with mean of 0.5 s clipped between 0.1 and 2.0 s, dwater had a minimum of 2 s, and dintertrial had a minimum of 10 s. See Experimental Procedures for details. Note that the intervals between events varied from trial to trial because of the variability in the timing of port entries and exits, and the random delays between port entries and odor or water valve openings. Dashed lines indicated omitted time.
(D–F) Comparison of performance in low urgency conditions designed to minimize incentives for rapid responding compared to the “original” task conditions of Uchida and Mainen (2003). Population data for the comparison of task performance under low-urgency conditions (filled symbols) and original task (open symbols). Mean accuracy (D), mean of the median OSD (E), and mean of the median MT (F) are plotted as a function of stimulus difficulty (mixture contrast). Error bars are mean ± SEM (n = 4 rats). Accuracy data was fitted to a Weibull function.
See also Figure S1.
To remove any incentives for rapid responding, we trained a different set of naive rats under “low urgency” conditions with a fixed minimum interval between the beginning of odor sampling and the delivery of reward between the start of consecutive trials (Figure 1C). These rats indeed showed significantly longer OSD and MT (Table 1; Figures 1E, 1F, S1B, and S1C) but, interestingly, showed neither an improvement in accuracy (Figure 1D; Table 1) nor any dependence of OSD or MT on task difficulty (Figures 1E and 1F; Table 1).
Table 1.
Summary of Statistical Tests
| A | Contrast | Original Task | Low Urgency |
|---|---|---|---|
| Mean ± SEM | Mean ± SEM | ||
| Accuracy (%) | 90 | 95 ± 0.8 | 93 ± 0.8 |
| 60 | 91 ± 0.8 | 87 ± 0.8 | |
| 36 | 82 ± 2.3 | 79 ± 2.3 | |
| 12 | 58 ± 1.9 | 59 ± 1.9 | |
| OSD (ms) | 90 | 240 ± 22 | 279 ± 22 |
| 60 | 238 ± 24 | 286 ± 24 | |
| 36 | 244 ± 23 | 296 ± 23 | |
| 12 | 246 ± 23 | 305 ± 23 | |
| Avg | 242 ± 23 | 291 ± 23 | |
| MT (ms) | 90 | 287 ± 10 | 565 ± 10 |
| 60 | 280 ± 10 | 556 ± 10 | |
| 36 | 279 ± 10 | 558 ± 10 | |
| 12 | 290 ± 13 | 551 ± 13 | |
| Avg | 284 ± 3 | 557 ± 3 |
| B | Test Task | Original Task
|
Low Urgency
|
||||
|---|---|---|---|---|---|---|---|
| Low Urgency | Punished Errors | Task Water Only | Task Water Plus | Fixed Go Signal | Blocked Stimuli | ||
| Baseline task | Original task | Original task | Control group | Control group | Original task | Interleaved stimuli | |
|
| |||||||
| Figure | 1D and 1E | 2Aii and 2Aiii | 2B | 2B | 3C and 3D | 5A–5C | |
|
| |||||||
| Accuracy | Difficulty | +++ | +++ | +++ | +++ | +++ | +++ |
|
| |||||||
| Task | 0.4 | 0.0153 | 0.16 | 0.017 | 0.0688 | +++** | |
|
| |||||||
| Both | 0.8 | 0.28 | 0.81 | 0.98 | 0.0095 | 00115 | |
|
| |||||||
| OSD | Difficulty | 0.83/+++* | 1 | 0.71 | 0.53 | 0.0145 | 0.57 |
|
| |||||||
| Task | +++ | +++ | 0.35 | 0.27 | +++ | 0.58 | |
|
| |||||||
| Both | 0.98 | 0.95 | 1 | 0.99 | 0.9 | 0.51 | |
|
| |||||||
| MT | Difficulty | 0.9998 | 0.93 | 0.9 | 0.87 | 0.99 | 0.42 |
|
| |||||||
| Task | +++ | +++ | 0.2276 | 0.0584 | 0.79 | 0.65 | |
|
| |||||||
| Both | 0.9996 | 0.96 | 0.9962 | 0.98 | 1 | 0.6 | |
(A) Mean accuracy, mean of median OSD and MT values of individual rats (±SEM) across sessions in original and low-urgency tasks. Averages across rats shown here are plotted in Figure 1.
(B) For six different task manipulations (rows), we analyzed three dependent variables—(1) performance accuracy (Accuracy), (2) median odor sampling duration (OSD), and (3) median movement time (MT)—in two different conditions (Test Task and Baseline Task). The figure associated with each comparison is indicated (row “Figure”). For each case, we performed a two-way ANOVA with mixture contrast (Difficulty) as one independent variable and the task condition (Task) as the other. Significance values are reported for the dependence of each dependent variable on each independent variable with values of p < 0.001 indicated as “+++.” For each comparison a different set of rats (n = 4) was tested in each the two conditions, except for the Blocked Stimuli comparison, in which the same rats (n = 6 rats) were tested with blocked and interleaved stimuli. Significant difference is indicated by (*) for p < 0.001 Friedman test for paired samples and (**) for p = 0.0086 Wilcoxon rank test (12% and 36% mixture contrast).
Manipulations of Motivation
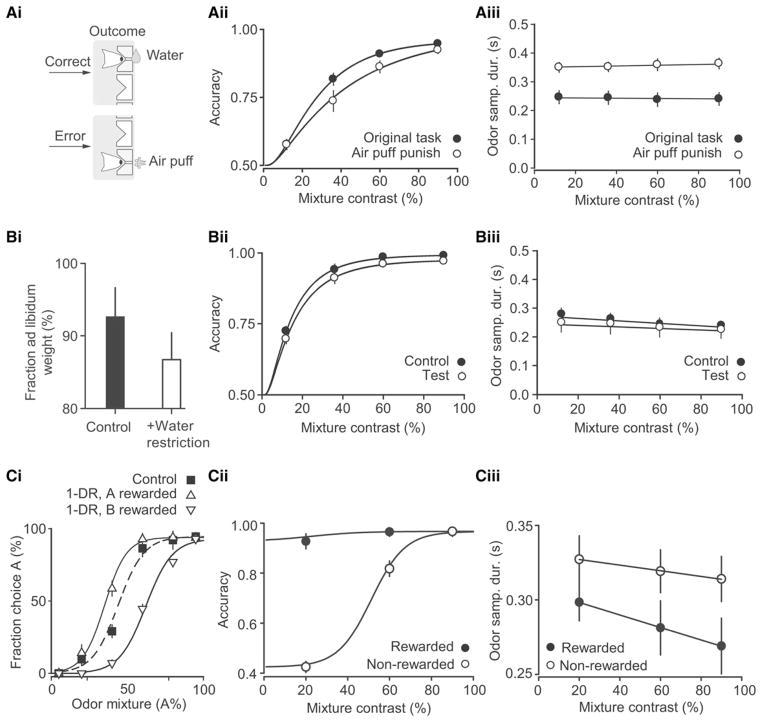
Since removing incentives for rapid responding was effective in slowing rats but did not yield an increase in accuracy, we next tried increasing the cost of errors by introducing a punishment for incorrect trials in the form of an air puff delivered to the snout (Paton et al., 2006). This manipulation increased the OSD and MT (Figure 2Aiii; Table 1) but again failed to induce an increase in accuracy (Figure 2Aii; Table 1). Therefore, we next tested the effects of increasing the incentive to obtain correct responses by eliminating water outside the task, increasing task difficulty and decreasing the number of available trials (see Experimental Procedures for details). Although this manipulation produced a drop in body weight of test subjects compared to controls (Figure 2Bi) demonstrating its effectiveness, there was no difference in accuracy, OSD or MT between test and control groups (Figures 2Bii and 2Biii; Table 1).
Figure 2. Impact of Manipulations of Motivation (Reward, Punishment) on Speed and Accuracy of Discrimination.
(A) Effect of air puff punishment. Comparison of the original task conditions (filled circles) to the low-urgency task with air puff punishment for error choices (open circles). (Ai) Schematic showing delivery of air puff to the snout of an animal from the water delivery port. (Aii) Accuracy as a function of stimulus difficulty (mixture contrast). (Aiii) Median OSD as a function of stimulus difficulty (mixture contrast). Error bars are mean ± SEM (n = 4 rats).
(B) Water restriction experiments. Control group (open symbols): 50 min session duration, no time out for errors, and a fixed amount of water (Wfree) was given outside the task (see Experimental Procedures). Test group (open symbols): 30 min session duration, 10 s time out for errors, and no water given outside task. (Bi) Mean body weight as fraction of ad libitum weight. See also Figure S2. (Bii) and (Biii) are as for (Aii) and (Aiii).
(C) One-direction reward (1DR) experiment. (Ci) Choice performance was biased in blocks where correct choices were rewarded only on one side (open triangles and solid lines) compared to when correct choices were rewarded on both side (filled square dashed line). The direction of bias was always toward the rewarded port. Error bars are mean ± SEM (n = 3 rats). (Cii) and (Ciii) are as for (Aii) and (Aiii).
To directly assess the impact of differential reward expectation on measures of response time, we trained another set of rats on a one-direction-rewarded (1DR) version of the two-alternative choice task. In this task version, only responses to one choice direction were rewarded (when correct) and this rewarded direction changed across blocks within a session. As expected, animals were biased to choose the rewarded side (Figure 2Ci) and performance increased for the rewarded side for the difficult odor mixtures (Figure 2Cii). We found that OSD for nonrewarded choices was slower than for the rewarded ones (Figure 2Ciii). Moreover the effect of stimulus difficulty on OSD was diminished for the nonrewarded choices (Figure 2Ciii), those choices whose difficulty no longer predicted the likelihood of reward availability. These results suggest that the effect of difficulty on OSD arises not only from varying perceptual uncertainty but also reflects the effect of difficulty on reward expectation and hence response speed.
Manipulation of Sampling Time using a Response Deadline (Go Signal)
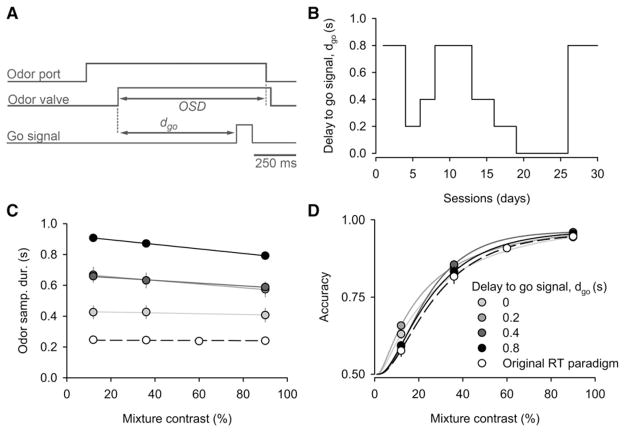
Having seen that response times are sensitive to reward and punishment but that changes in OSD did not produce significant changes in accuracy, we next sought to test the possible effect of larger changes in stimulus sampling time by manipulating the OSD more directly. To do so, following a previous study (Rinberg et al., 2006), we introduced an auditory go signal to cue the timing of the response while the odor stimulus continued to cue the correct choice direction (Figure 3A). Responses initiated prior to the go signal were not rewarded regardless of choice. We first trained subjects to wait for the go signal (see Experimental Procedures). After training, we used fixed go-signal delays of 0, 0.2, 0.4, and 0.8 s, each repeated for 3–6 sessions before switching (Figure 3B). Within each session odor mixtures of the same difficulties as the RT task were randomly interleaved from trial-to-trial. Subjects obeyed the go signal, resulting in much longer OSDs than those seen in the original RT task (Figure 3C; Table 1). However, despite the substantial increase in odor sampling durations, we observed no change in accuracy (Figure 3D; Table 1; Figure S3). Indeed, accuracy of the rats trained in the original RT task (Figure 1) was nearly identical to the performance of the rats in the go-signal task. (Figure 3D, open circles versus filled circles, and Figure S4).
Figure 3. Prolonged OSDs Instructed using a Go Signal Fail to Improve Performance Accuracy.
(A) Schematic of the go-signal task. An auditory go signal was played after a delay dgo from odor onset and subjects were required to remain in the odor port until after dgo (see Experimental Procedures).
(B) Time line of go-signal delays across sessions.
(C) Mean of the median OSD as a function of mixture contrast and the length of go-signal delay (n = 4 rats). Shades of gray represent different go-signal delays. Open circles and dashed line indicate the results from a different set of subjects in the original RT task (Figure 2).
(D) Mean performance accuracy with different go-signal delays.
See also Figure S3.
The failure to observe an increase in performance accuracy with longer go signals was surprising, given that Rinberg et al. (2006) did find such an increase using apparently similar conditions. Therefore, we next turned to examine whether overlooked differences in task structure might account for this discrepancy. We first noted that while we had tested subjects on a given go-signal delay for hundreds of trials in a row, Rinberg et al. randomly interleaved go signals of different delays in a single session. Previous studies have shown that the ability to anticipate the time at which a brief stimulus will be presented can affect reaction time and accuracy of performance (Griffin et al., 2001; Nobre, 2001; Correa et al., 2006; Katzner et al., 2012). We therefore hypothesized that expectation of (or readiness to respond to) the timing of the go signal would also affect performance in this task. Specifically, we reasoned that when go-signal delays vary randomly from trial-to-trial, the subject may not respond as accurately as when responses are self-paced or instructed by a go signal delivered at a constant delay.
Manipulation of the Predictability of the Response Deadline (Go Signal)
The predictability of random go-signal times has been formalized by the notion of “hazard rate,” defined as the probability that a signal will occur given that it has not already occurred (Luce, 1986). The “subjective hazard rate” (Janssen and Shadlen, 2005) is an extension of this concept that takes into account the finding that the variance of subjective time estimation increases proportionally to the interval duration (Gibbon, 1977; Gallistel and Gibbon, 2000). By calculating the subjective hazard rate for the experimental distribution of go-signal times, a quantitative prediction of performance as a function of go-signal delay can be obtained. To test the idea that hazard rate impacts go signal performance, we compared performance of subjects on two different distributions of go signals, formed using uniform and exponential probability densities, which have very different hazard rates. These distributions, their hazard rates and subjective hazard rates are depicted in Figure S4. The subjective hazard rate for go signals in the uniform condition rises with time toward the end of the distribution interval; therefore performance in this condition is expected to increase relatively slowly over the distribution interval. In contrast, the exponential distribution has a much flatter subjective hazard rate; therefore, performance in this condition is expected to rise relatively more quickly resulting in relatively better performance at short delays.
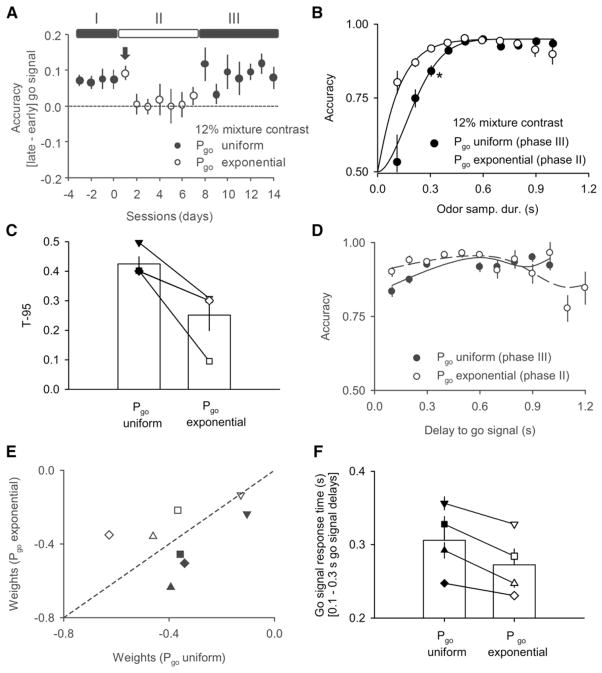
Rats were tested first on the uniform distribution for several consecutive sessions (phase I), then on the exponential distribution (phase II) and then again on the uniform distribution (phase III) (Figure 4A). A single difficult odor mixture pair (12% mixture contrast) was used throughout. As predicted, the performance advantage for long go-signal delays was smaller when the exponential distribution was used (phase II; Figure 4A). Plotting performance as a function of odor sampling duration also revealed, as predicted, a longer rise time in the uniform distribution (rising-hazard rate) condition compared to the exponential distribution (flat-hazard rate) (Figures 4B and 4C). Fitting the theoretical subjective anticipation functions to the observed performance accuracy functions (Janssen and Shadlen, 2005) showed the predicted dependence on the experimental hazard rate (Figures 4D and 4E). Finally, we also observed corresponding changes in latency to respond to the go signal (Figure 4F); again as predicted by the hypothesis that temporal anticipation affects the readiness to respond to the go signal. Latency differences were particularly apparent when comparing the response time to early go signals under the two distributions. Changes in performance induced by switching go-signal distributions were reversible but took 1–2 sessions (>500 trials) to develop (Figure 4A; note first session after switch from phase I to phase II).
Figure 4. Performance Accuracy Depends on the Distribution of Go-Signal Delays.
Go-signal delays are chosen from a uniform distribution (filled symbols) or exponential distribution (open symbols). Note that an exponential distribution results in a flat hazard rate function while a uniform distribution result in a rising hazard rate function. A difficult single mixture pair (12% mixture contrast) was used throughout.
(A) Mean difference in performance accuracy between trials with late (0.7–1.0 s) and early (0.1–0.3 s) go-signal delays (n = 4 rats). Time 0 denotes the last point before changing from uniform distribution (rising hazard rate) to exponential distribution (flat hazard rate). Filled symbols: uniform distribution (phases I and III); open symbols: exponential distribution (phase II). Note that the switch in performance accuracy from exponential to uniform distribution is expressed only on the second day after the switch (arrow) but that there is no such delay switching back to the uniform distribution.
(B) Mean performance accuracy as a function of OSD for two different go-signal distributions pooled across all rats (n = 4 rats). Filled circles: uniform distribution (phase III); open circles: exponential distribution (phase II). Star: accuracy significantly different (for the largest OSD) between the two conditions (p < 0.01; one tailed z test for proportion).
(C) Mean T95 (shortest OSD that gave 95% of maximum accuracy) for two different go-signal distributions (n = 4 rats; p < 0.05, Friedman paired test). Individual rats are shown with different symbols. Filled symbols: uniform distribution (phase III); open symbols: exponential distribution (phase II).
(D) Mean performance accuracy as a function of go-signal delays for the population data. The solid line is the fitted subjective anticipation function in the two conditions (black solid line: go signal with a uniform distribution, phase III; dashed line: go signal with an exponential distribution; phase II).
(E) Weights associated with rising and flat theoretical subjective anticipation functions after fitting to the discrimination performance curve of individual rats (different symbol shapes) in two different conditions (open symbols: go signals with a uniform distribution; closed symbols: go signals with an exponential distribution). Note that in the uniform condition weights are higher for the rising anticipation and in the exponential condition weights are higher for the flat anticipation. See also Figure S4.
(F) Comparison of reaction times to short (0.1–0.3 s) go signals in the two conditions. Individual rats shown in different symbols as shown in (C) (n = 5 sessions).
Could temporal anticipation and integration coexist in this task? Rinberg et al. (2006) observed that the time to reach maximal accuracy increased with difficulty using uniform distribution of go signals. We analyzed accuracy conditional on odor sampling duration for the uniform go-signal distribution as well as for the exponential distribution and the reaction time task. In each case, we observed no relationship between time to peak (“T95”) and difficulty (Figure S5).
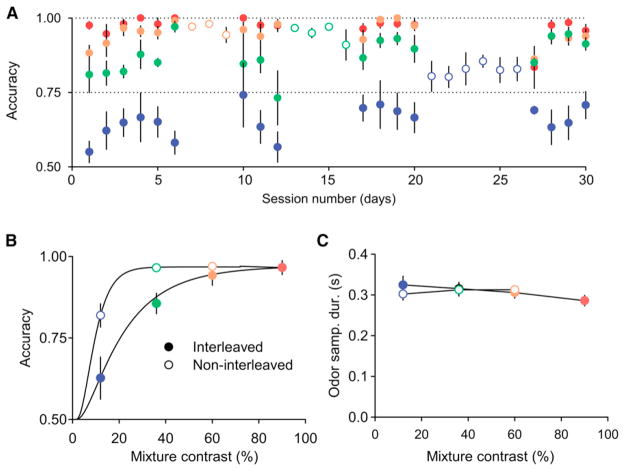
Manipulation of Stimulus Predictability: Blocked versus Interleaved Context
Interestingly, we noted that performance accuracy in this task version was not only better than the RT performance but also substantially better than in the preceding go-signal task (compare Figure 4B and Figure 3D). The major factor that might account for this difference was that in the first go-signal task (as well as the RT tasks), odor stimuli of various difficulties were pseudo-randomly interleaved within a session (“interleaved”), whereas in the latter task, a single difficult pair of stimuli (12% mixture contrast) was presented in a block during an entire session (“noninterleaved” or “blocked”). We therefore inquired whether blocking stimuli increased discrimination accuracy, perhaps by increasing stimulus predictability.
To test this idea, we made a direct comparison of accuracy on interleaved versus blocked stimuli in the RT paradigm. First, a new set of rats was trained to asymptotic performance on interleaved stimuli in low-urgency conditions. Subsequently, they were then tested sequentially on blocks of the three most difficult odor mixture pairs (Figure 5A). Switching to the blocked, noninterleaved condition produced a significant increase in accuracy for a given stimulus pair, especially for the two most difficult stimulus conditions (Figure 5B; Table 1). Performance levels on the 12% mixture contrast pair was similar to that observed in the blocked stimulus version of the go-signal task. However, despite the increase in accuracy compared to the interleaved condition, odor sampling durations remained identical between the two conditions (Figure 5C; Table 1). The improvement in accuracy on blocked stimuli developed rapidly (within 20 trials; data not shown) and consisted of both a transient component that disappeared when returning to interleaved conditions (about 2/3 of the total) and a long-lasting component that persisted (about 1/3) (Figure 5A; compare first and last sets of interleaved sessions).
Figure 5. Reducing the Range of Mixture Contrasts Results in Increase in Performance Accuracy at No Cost of Speed.
(A) Mean performance accuracy of 6 rats over the course of 30 days of training. Filled circles: sessions with interleaved mixture contrasts; open circles: sessions with the blocked (noninterleaved) condition. Color indicates mixture contrast. The mean accuracy during the last 100 trials in a session is shown.
(B) Mean performance accuracy (n = 6 rats). Psychometric curve was fit using a Weibull function. Filled and open symbols represent interleaved and blocked conditions.
(C) Mean of the median OSD (n = 6 rats).
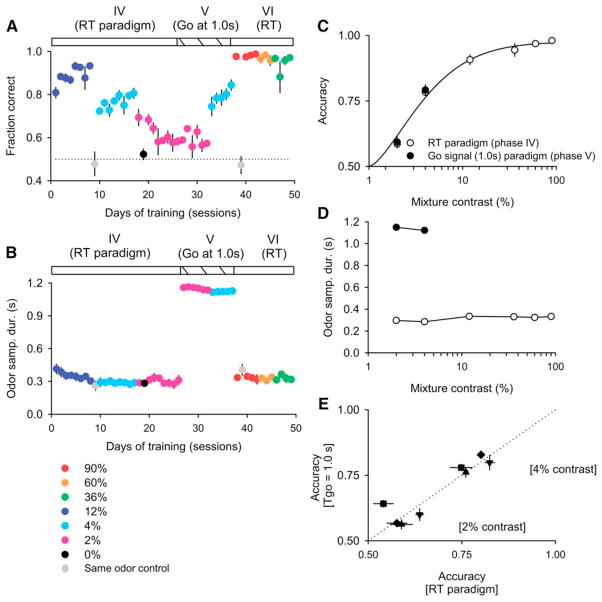
Asymptotic Performance in Odor Mixture Discrimination within 300 ms
This experiment implies that the performance accuracy benefits observed in previous go-signal tasks compared to RT tasks are simply due to testing with blocked stimuli. To test this directly, the same four subjects that were tested on the go-signal task with blocked odor pairs (Figure 4) were subsequently trained to asymptotic performance in the RT paradigm also using blocked odor pairs (Figures 6A and 6B, phase IV). The stimulus difficulty was increased over consecutive days. Accuracy on the most difficult stimulus pair (12% mixture contrast) improved remarkably, from <70% on the interleaved condition to 91% ± 1% in the blocked condition (Figures 6A and 6C). We therefore introduced two successively more difficult problems: 4% and 2% mixture contrast, both obtained by using liquid dilutions of the 12% mixture stimuli (see Experimental Procedures for details). Accuracy on these stimuli, more difficult than any used previously by our group or others, was significantly above chance (Figures 6A and 6C) but was not associated with an increase in OSD (Figures 6B and 6D). Finally, we reintroduced a go signal at a fixed delay of 1 s (Figures 6A and 6B, phase V). The duration was fixed in order to allow optimal anticipation and subjects were trained for 5–6 sessions. Despite much longer OSD compared to the RT condition (Figures 6B and 6D) there was no significant difference in accuracy (p = 0.91, two-way ANOVA for difficulty and OSD instruction) (Figure 6E). Thus, maximal odor categorization accuracy was achieved by rats in self-paced conditions with <300 ms odor sampling time and could not be further improved by providing additional time for stimulus integration. The only impact of the go signal was to decrease performance when it was not fully anticipated, as can be seen by comparing accuracy in Figure 4B and Figure 6C (12% contrast).
Figure 6. Accuracy in RT Paradigm Is as High as that Obtained with Prolonged Odor Sampling.
(A) Accuracy of rats in a RT paradigm and in fixed 1.0 s go-signal paradigm (n = 4 rats).
(B) Mean median OSD. Day 9 and 39 are control sessions using the same odor in all odor channels keeping all other task and reward parameters constant. Day 19 is a control session with a 50/50 air mixing of two odorized air streams each of a 55/45 and a 45/55 premixed odors.
(C) Comparison of performance accuracy for rats trained on 1.0 s go signal (closed circles) and on RT paradigm (open circles) (n = 4 rats).
(D) Mean median OSDs in the two paradigms (n = 4 rats). Note that error bars are smaller than the symbols.
(E) Comparison of the mean accuracies between the go-signal and RT paradigms for two mixture contrasts (2% and 4%) for four individual rats (different symbols) (n = 5 sessions).
See Figure S5.
DISCUSSION
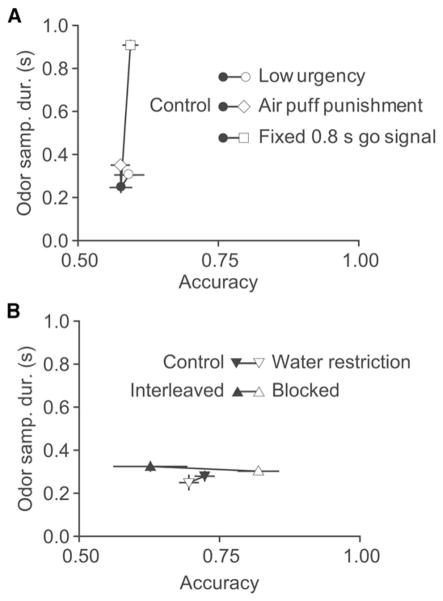
Studying rats performing an odor categorization task, we found that accuracy improves with stimulus sampling time only up to about 300 ms, consistent with previous studies showing rapid olfactory decisions (Karpov, 1980; Laing, 1985, 1986; Uchida and Mainen, 2003; Wesson et al., 2008). Using reward (and punishment) manipulations (Figures 1 and 2) and a response go signal (Figure 3), we were able to increase rats’ sampling time, but this failed to improve accuracy. We also documented that reducing the stimulus set size (Figure 4) or the expectancy of the go signal (Figure 5) increased rats’ accuracy, but with no temporal cost. Thus we found that speed and accuracy varied independently in this task (summarized in Figure 7). Taken together, as we will discuss below, we favor the interpretation that rapid performance on odor categorization is an adaptive decision strategy in the face of uncertainty that is not reduced by prolonged within-trial stimulus sampling and not simply a tradeoff of accuracy for speed.
Figure 7. Dissociation of Accuracy and Speed.
(A) Summary of experiments in which OSD was affected.
(B) Summary of experiments in which accuracy was affected. Each pair of connected dots compares population performance accuracy and OSD for the difficult mixture contrast (12%) for a given manipulation (different manipulations shown with different symbols and control groups are shown with filled symbols and experimental groups with open symbols; see legend).
Error bars indicate SEM. For all experiments n = 4 rats except blocked versus interleaved (n = 6 rats).
Our data also suggest an explanation of the apparent discrepancies between the studies of Uchida and Mainen (2003) and Abraham et al. (2004) and Rinberg et al. (2006) that is not based on differences in SAT. The higher accuracy reported in Abraham et al. (2004) and Rinberg et al. (2006) could be attributed to the use of blocked rather than interleaved stimulus difficulties (Figure 5). The greater change in response times with difficulty (additional 40 ms) reported by Abraham et al. (2004) could be explained by effects of reward expectation on response speed (Figure 2C). Finally, the increase in performance with go-signal delay over 500 ms reported in Rinberg et al. (2006) could be explained by increasing go-signal anticipation over time (i.e., increasing hazard rate) (Figures 3 and 4). Comparing across studies and across conditions, the best performance overall was achieved within <300 ms odor sampling, by well-trained rats performing the reaction time task in the present study (Figure 6). Thus, differences in results across these studies appear to reflect performance effects arising from differences in predictability of stimuli and responses, together with difference in reward structure across tasks, rather than differences in SAT.
The Role of Reward and Motivation in Decision Tasks
The reinforcement structure of a task based on conditioned responses is likely to affect the strategy of the animal with respect to speed and accuracy tradeoffs in perceptual decisions. Indeed, the dependence of RT on reward value in a decision task has been used previously as an index of motivation (Lauwereyns et al., 2002; Roesch and Olson, 2004). When mistakes are more costly in lost opportunity, in time or in effort, then SAT should be biased toward slower and more accurate responses. To induce such a change, we set the timing of task events (stimulus onset, minimum reward delay, intertrial interval) using minimal intervals so that increases in odor sampling period would not produce reward delays or drops in average reward rates. We applied these “low-urgency” conditions from the beginning of training to avoid initial learning of rapid responses. We also performed experiments in which we increased the cost of mistakes using aversive reinforcement and in which we increased the value of water reward by requiring animals to perform more trials to obtain the same amount of water. The low urgency and aversive reinforcement experiments had demonstrable effects on behavior, together slowing odor sampling time by around 100 ms. However, they did not result in increases in choice accuracy compared to the baseline condition, failing to support the SAT hypothesis.
It is worth noting that in a perceptual decision task the expected reward probability covaries with difficulty, which in turn might produce co-variations in RT that could be confounded with stimulus integration. Based on our observations, we infer that a substantial portion of the 30 ms difficulty dependence we observed might be due to motivational effects on RT, with more uncertain stimuli prompting slower responses because of lower predicted reward value (Figure 2C). One can also infer that the leaving times for correct “no-stay” responses to unrewarded odors previously used to index RT (Abraham et al., 2004) may reflect such motivational effects.
Stimulus Context: Interleaving versus Blocking Stimuli
We observed a strong effect of the number of interleaved stimuli on odor categorization accuracy. Reducing the stimulus set from 8 to 2 odors produced a substantial increase in accuracy (from around 60% to 80% correct on the hardest pair). This increase developed rapidly (over tens of trials) and was largely, but not entirely, reversed upon return to the blocked condition. Similar “stimulus context” effects have been described previously (Green, 1961). We can consider several possible interpretations of this effect. First, the presence of easier trials in the interleaved condition might decrease the incentive to try for difficult ones. However, manipulation of motivational conditions failed to boost performance (Figures 2A and 2B) making this interpretation unlikely. Second, the increase in performance in the noninterleaved condition might reflect the ability to better predict the stimulus when the size of the stimulus ensemble is limited. Third, the changes across conditions might reflect a form of adaptation to the change in the range of mixture contrast, similar to the phenomenon of contrast adaptation in the visual system (Ohzawa et al., 1982). Forth, decreasing the range of stimuli may decrease the ambiguity of the category boundary (Kepecs et al., 2008) and hence improve performance (Grinband et al., 2006). Further work will be needed to distinguish these or other possibilities.
Temporal Anticipation of a Response Deadline Modulates Accuracy
In order to control stimulus duration, we manipulated odor sampling time by requiring the animal to withhold responding until the occurrence of an auditory go signal that varied randomly in time. When the probability density function of the go signal in this paradigm was uniform, accuracy increased over 500 ms. One possible explanation offered for such an effect is the accumulation of sensory evidence with time (Rinberg et al., 2006). However, we also observed that changing the probability density function to an exponential distribution reduced the interval over which performance increased to around 300 ms. This change clearly cannot be explained by temporal integration of evidence, but indicates that temporal anticipation of the occurrence of the go signal modulates decision accuracy (Hanks et al., 2011). Consistent with this interpretation, increasing accuracy was accompanied by decreasing response time to the go signal. In addition, it is critical to note that maximal performance in go-signal tasks never exceeded performance in the equivalent RT paradigm. Thus, go signals can reduce accuracy when it is not fully anticipated, but cannot increase accuracy. Finally, when plotting accuracy conditioned on odor sampling duration, we observed no relationship between time to peak and difficulty for individual animals (Figure S5), as might be expected from integration. In sum, the effects of go-signal delay on performance accuracy and RT are parsimoniously explained as effects of go-signal anticipation but are not easily explained as effects of integration time.
Temporal expectation can be considered an orientation or allocation of “attention in time” (Griffin et al., 2001; Nobre, 2001; Correa et al., 2006). Most studies of attention in time involve anticipation of a brief stimulus cue at a random time interval. Such temporal attention has been shown to modulate activity in neocortical neurons (Ghose and Maunsell, 2002; Janssen and Shadlen, 2005; Jaramillo and Zador, 2011). Our protocol differed from such studies in using a constant stimulus presentation in conjunction with a temporally randomized response signal. Therefore go-signal anticipation effects might act at the stage of motor preparation and execution as opposed to sensory processing (McDonald et al., 2000; Correa et al., 2006).
Speed-Accuracy Tradeoff and the Origin of Decision Noise
These data have some potential implications with respect to possible sensory integration processes operating during olfactory categorization decisions. First, it is important to note that an odor sampling duration of 300 ms does not imply 300 ms of integration. RTs also include “nondecision time” representing delays from sensory and motor processes that do not contribute to integration. It is typical in RT models to include delays of 200–300 ms or more (Luce, 1986; Mazurek et al., 2003). Although the length of nondecision times are not easy to estimate independently, molecular manipulations of olfactory bulb circuitry can lead to increases or decreases in sensory neural responses on the order of 100 ms (Abraham et al., 2010). Assuming 100–150 ms motor delays, only 50–100 ms would remain for integration processes within the 300 ms OSD.
A measurement more directly related to integration time is the change in RT from the easiest to most difficult stimulus. The small difference we observed, 30 ms, is consistent with the conclusion that nondecision delays make up the bulk of a 300 ms RT and that the incoming signal strength is high relative to the “bound” or threshold of evidence so that a decision is reached relatively quickly. As discussed above, part of this 30 ms difference might also result from motivational differences between easy and difficult stimuli. These in turn are consistent with lack of improvement with longer enforced sampling durations. At the same time, these observations do not strongly imply integration. Models with little or no integration, e.g., “sequential sampling” models (Watson, 1979), can also produce dependence of RT on stimulus duration, increase in RT with difficulty (Ditterich, 2006) and the speed-accuracy tradeoffs with changing evidence threshold.
Two of our observations are not readily reconciled with standard integration models. First is the fact that manipulations of urgency slowed subjects’ odor sampling times substantially, around 100 ms or around 30%, but did not increase accuracy. A “collapsing bound” (i.e., evidence threshold decreasing with time) is considered a mechanism for urgency in the integration model (Bowman et al., 2012; Drugowitsch et al., 2012). A reduction in the collapse rate could explain the increases in reaction time we observed in low urgency conditions, but would entail an increase in accuracy, which was not found. The second observation not readily explained is the increase in performance with reduction in the number of interleaved stimuli (Figure 5). This effect could be explained by an increase in the subject’s decision bound, but this would imply a concomitant increase in RTs, which did not occur.
What can account for the failure of rats to show expected speed-accuracy tradeoffs? First, it remains possible that our training regime was somehow faulty or that rats are incapable of optimal task performance. However, due to the arguments we have laid out above, we believe that the answer is more likely that rats are indeed performing their best, but that some of the inherent assumptions of integration models are not met by the odor categorization task. A second possibility is that the information on which the decision is based decreases with time, as for example might occur with sensory adaptation. However, Uchida and Mainen (2003) found no increase in RT with 100-fold stimulus dilutions that would be expected to reduce the effects of adaptation, making this explanation unlikely. A final possible class of explanation, that we believe is worthy of careful consideration, is that the noise that limits performance in the categorization of odor mixtures is not of the type postulated by integration models. Any scenario in which noise is highly correlated from sample to sample within a trial would violate the key assumption that noise is temporally uncorrelated and would curtail the benefits of integration.
As a specific hypothesis for a source of trial-by-trial noise could arise in odor mixture categorization decisions, consider that in this task the category boundary between left and right odor classes is set by the experimenter and must be learned by the subject through trial-by-trial reinforcement. Any trial-to-trial variability in the category boundary due to reinforcement learning would produce a source of noise that is completely correlated within individual trials. Therefore, if uncertainty about the precise category boundary dominates over stimulus uncertainty, the benefits of integration within a single trial would be curtailed, tilting the optimal speed-accuracy tradeoff toward shorter sampling times for even an optimal subject. Further experiments will be needed to test this hypothesis.
Under this interpretation, the present results are likely to reflect features of the task rather than the modality or species. This has several implications. First, rodents performing tasks that are dominated by uncorrelated sensory noise may indeed show the expected benefits of extended temporal integration (B.W. Brunton and C. Brody, 2009, Soc. Neurosci., abstract; P. Reinagel et al., 2012; Sanders and Kepecs, 2012). Second, decisions that favor short sampling time are likely not to be limited to rodents or olfaction (Uchida et al., 2006; Kahneman, 2011; Stanford et al., 2010). Indeed, it has long been appreciated that performance on psychophysical tasks may saturate with as little as 100–200 ms of stimulus exposure (Barlow, 1958; Watson, 1979). For example, in random dot motion discrimination by humans, if difficulty is manipulated by lowering coherence, accuracy increases up to 3 s of stimulus exposure, but if it is manipulated by lowering contrast, only up to 0.3 s (Burr and Santoro, 2001). Finally, the present results are likely not applicable to all olfactory decisions but specific to olfactory categorization decisions. Different tasks such as odor detection, odor mixture segmentation or odor source tracking will each make different demands, tapping into different underlying neural mechanisms to overcome different sources of uncertainty.
EXPERIMENTAL PROCEDURES
Animal Subjects
Thirty-seven male Long-Evans rats (250 g at the start of training) were trained and tested using procedures approved by the Cold Spring Harbor Laboratory, Institutional Animal Care and Use Committee. Rats were trained and tested on a two-alternative choice odor mixture categorization task where water was used as a reward as described previously (Uchida and Mainen, 2003). The animals were pair-housed (except where noted) and maintained on a reverse 12 hr light/dark cycle and tested during their dark period. Each rat performed one session of 45–60 min per day (250–400 trials), 5 days per week for a period of 8–20 weeks. Rats were allowed free access to food but were restricted to water available during the behavioral session and for 30 min after the session and during non training days; water amounts were adjusted to ensure animals maintained no less than 85% of ad libitum weight at any time. A different set of naive rats were used for each experimental condition unless otherwise noted.
Testing Apparatus and Odor Stimuli
The behavioral setup consisted of a box of 20 × 20 cm with a panel containing three conical ports (2.5 cm diameter, 1 cm depth) (Uchida and Mainen, 2003). Each port was equipped with infrared photodiode/phototransistor pair that registered a digital signal when a rat’s snout was introduced into the port (“nose poke”), allowing us to determine the position of the animal during the task with high temporal precision. Odors were delivered from the center port and water from the left and right ports. Port signals were recorded and valves controlled by a computer running custom software written in Matlab (Mathworks, Natick, MA) equipped with multipurpose data acquisition cards (E-series, National Instruments, Austin, TX).
Odor delivery was controlled by a custom made olfactometer (Uchida and Mainen, 2003). The test odors were S-(+) and R-(−) stereoisomers of 2-octanol (Figure 1A), chosen because they have identical vapor pressures and similar intensities. We used relatively low concentration of odorants by diluting 50 ml/min odorized air in a total of 1,000 ml/min clean air stream and 1:10 in mineral oil (total dilution factor: 0.005). Mixture ratios of 5/95, 20/80, 32/68, and 44/56 and their complements (95/5, etc.) were generated using pure odorants and adjusting the flow rates of two independent mass flow controllers (Aalborg, Orangeburg, NY) in appropriate ratios to sum to 50 ml/min (e.g., at 20/80 one flow controller delivers 10 ml/min and the other 40 ml/min). Ratios of 48/52 and 49/51 were generated by substituting liquid mixtures in 45/55 and 55/45 ratios for the pure odorants and further diluting with air. In control sessions, the same odorant was used in both air streams or two odors were delivered at 50/50 ratio. Performance in these sessions was no different than chance (50%) over ≥100 trials (see Figure 6A).
Reaction Time Paradigm
Rats initiated a trial by entering the central odor-sampling port, which triggered the delivery of an odor. To prevent rats from developing a ballistic “odor poke” movement into and out of the odor sampling port (Friedrich, 2006), the odor onset was subject to delay (dodor) drawn from a random distribution (original paradigm: uniform random distribution with a range of [0.3, 0.6 s]; low urgency paradigm: exponential, mean 0.5 s, offset at 0.1 and clipped at 2.0 s) (Figures 1C and S1). The odor was available for up to 1 s. In the reaction time task (Uchida and Mainen, 2003), rats could exit from the odor port at any time after odor valve opening and make a movement to either of the two reward ports. Trials in which the subject left the odor sampling port before odor valve opening were considered invalid (see Figure S1). Odor delivery was terminated as soon as the rat exited the odor port. Stimuli were presented in pseudorandom order resulting in 50% chance performance. Reward was available for correct choices for up to 4 s after the rat left the odor sampling port in the original task; in the low urgency condition it was available for 8 s (5 s in water manipulation task phase III; Figure 2B) after odor valve onset. Trials in which the subject failed to respond to one of the two choice ports within the reward availability period were also considered invalid. Invalid trials comprised 19.9 ± 6.6% (mean ± SEM, n = 4 rats). Invalid trials were not included in the calculation of performance accuracy or reaction times (OSD, MT).
For correct trials, water was delivered from gravity-fed reservoirs regulated by solenoid valves after the subject entered the choice port (original paradigm: dwater [0.1–0.3 s] from water port entry; low-urgency paradigm: minimum delay, dwater = 2 s from odor valve onset; Figure 1C). Reward amount (wrew), determined by valve opening duration, was set to 0.03 ml and calibrated regularly. Error choices resulted in water omission but were otherwise unsignaled, except in the “air puff” paradigm (Figure 2) in which an air puff was delivered to the snout of the rat through a tube inserted adjacent to the water delivery tube in the two choice ports. In the reaction time tasks, invalid trials were not signaled. A new trial was initiated when the rat entered odor port, as long as a minimum interval (dintertrial) had elapsed (original paradigm: 4 s from water delivery; low urgency paradigm: 10 s from odor valve onset; see Figure 1C). A “time out” penalty of 10 s was added to dintertrial for incorrect choices in the water manipulation task phase III (Figure 2B). The experienced interval between consecutive trial onsets was 7.3 ± 0.3 in the original paradigm and 11.5 ± 0.1 s in the low urgency conditions (n = 4 rats).
Water Manipulation
For the water manipulation task (Figures 2B and S2), eight naive rats, individually housed, were first trained on the low-urgency RT task (with 6 s dintertrial) to asymptotic performance under normal water restriction. Approved animal care and use procedures were strictly observed during the water restriction regime. Training was ceased and rats were given ad libitum food and water until stabilization of weight and water consumption (Wadlibitum, range of 50 ± 20 ml/day). Water restriction was then resumed with the available water, Wfree, set at 0.5·Wadlibitum, delivered using a syringe fitted with a Lixit valve (Lixit Animal Care Products, Napa, CA). Weights were monitored for 3 days and then training was resumed with session length fixed at 256 trials. At the beginning of the experiment, a baseline was established for all rats. The amount of free water available outside the task, Wfree, was set at 0.17·Wadlibitum and the volume of water reward (Wreward) was set individually for each rat such that the total water available in the task Wtask was approximately 2·Wfree (Figure S2). The testing consisted of three phases (I–III). (Phase I) For the test group, only Wfree was reduced to 0 while maintaining Wreward constant. (Phase II) We doubled the relative frequency of occurrence of the most difficult mixture ratios (56/44 and 44/56) for the test group. (Phase III) An additional 10 s time out punishment for error trials was introduced and the maximum time allowed for session completion was reduced from 50 to 30 min. This manipulation decreased the amount of water consumed by the test group and produced a drop in body weight (86.69% ± 3.8% of original weight test group versus 92.63% ± 3.7% control group). No rat dropped below 85% of initial ad libitum body weight at any time.
One-Direction Rewarded Task
Three naive rats were trained on the 1DR task (Figure 2C). Each session began with 400 trials where both sides were rewarded and then reward were provided only for one choice direction (when correct) and this rewarded direction changed across blocks of 100 correctly performed trials (~120–140 trials total). Reward were delayed for 1 s after entry into the water-port. We provided auditory feedback for both correct and error choices for both the rewarded and unrewarded sides. To ensure that rats responded to the nonrewarded direction following incorrect choices we repeated the same stimulus in the next trial. Repeated trials were removed from the analysis.
Go-Signal Paradigm
Go-signal paradigms were similar to reaction time paradigm except rats were required to stay in the odor sampling port until a 2 kHz, 100 ms pure tone was delivered after delay dtone after odor valve onset (Figure 3A). Otherwise, the task timing was identical to the low urgency version of the RT task (Figure 1C). The following three conditions were considered invalid trials and were not rewarded and not counted in accuracy or OSD measurements: (1) short odor poke trials (withdrawal from the odor port before the go-signal) resulted a short white noise burst (120 ms) and 4 s increase in dintertrial. (2) Long odor poke trials (withdrawal >1.0 s after the go-signal) triggered a long white noise burst (3 s) and 4 s increase in dintertrial. (3) Delayed choice trials (failure to enter a choice port within 4 s after a valid odor sampling period) were invalid but not signaled in any way and did not result in any increase in dintertrial.
In a first set of go-signal experiments (Figure 3), a single go-signal delay was used in each session and a range of odor mixtures (12% to 90% mixture contrast) were randomly interleaved within the session, as in the RT paradigms. Go-signal delays were changed from session to session while the odor stimuli remained constant (Figure 3B). The set of rats tested in this paradigm were naive at the beginning of training.
In a second set of go-signal experiments (Figure 4), a single odor mixture pair was delivered in each session and go-signal times were randomly varied within a session. In these experiments, a single set of four rats was used in five sequential phases (I–V). (I) A pseudorandom go-signal delay (dgo) for each trial was drawn from a uniform distribution (0.1–1.0 s in 0.1 s increments). Mixture ratio difficulty was increased after stable performance was achieved (8–10 sessions per ratio) (Figure 4A, phase I). (II) dgo was drawn from an exponential distribution (mean 0.3 s) using the 12% mixture contrast stimuli (Figure 4A, phase II). (III) Subjects were retested using uniformly distributed go-signal delays while keeping the same stimuli (Figure 4A, phase III). (IV) Subjects were tested on the RT paradigm by eliminating the go-signal while keeping other task parameters constant. After reaching stable performance, two more difficult mixture contrasts (4% and 2% mixture contrast) were sequentially introduced (Figure 6A, phase IV). (V) Rats were returned to a go-signal paradigm with dgo = 1.0 s at 2% mixture contrast and then trained to stable performance on 4% mixture contrast (Figure 6A, phase V). (VI) RT performance was measured on three easier ratio pairs (Figure 6A, phase VI).
Training
The training sequence consisted of (1) handling and habituation to the behavior box (3 sessions); (2) water-port training (1 day); (3) odor-port training, in which a single odor (usually ethyl butyrate) was rewarded at either port and the required center poke duration was increased from 0 to 300 ms (2–4 sessions); (4) introduction of test odors in 5:95 and 95:5, rewarded at left and right choice ports with assignments counterbalanced across rats (1–3 sessions); (5) introduction of increasingly difficult mixture ratio pairs rewarded at the side corresponding to the dominant component (4–7 sessions). Go-signal task training occurred between phase III and IV. For the purpose of experiments involving training on a new stimulus or condition, stable or asymptotic performance was defined as <5% change in performance over ≥5 sessions.
Performance Accuracy and OSD Analysis
All the analysis was performed in Matlab 6.5 Release 13. Behavioral accuracy was defined as the percentage of correct choices over the total number of correct and incorrect choices. Odor sampling duration (OSD) was calculated as the difference between odor valve actuation until odor port exit, with 100 ms subtracted to account for the delay from valve opening to odor reaching the nose (Feierstein et al., 2006; Figure 1C). Movement time (MT) was defined as the time between odor port exit and choice port entry. We excluded from calculation of performance accuracy and OSD trials in which odor port withdrawal occurred less than 100 ms after odor onset (<10% of trials) or before the go signal in go-signal paradigms (<25% of trials) and trials in which no choice was made or choice port entry occurred after the response deadline (<1% of trials) (Figure S1E). Performance accuracy as a function of mixture difficulty was fitted with a Weibull function using a maximum likelihood method and OSDs using a linear regression, except in Figure 2Cii where a logistic regression using binomial distribution was used. Logistic regression was also used to fit the psychometric function in Figure 2Ci. Error bars are mean ± SEM (n across rats) or mean ± SD (n across sessions). The effect of difficulty on accuracy or OSD was tested using one-way ANOVA with pairwise comparisons between different mixture contrast ratios (MULTCOMPARE function in Matlab) at a significance level of p < 0.0125 (i.e., adjusted for multiple comparisons).
Subjective Hazard Rate Analysis
In order to estimate the ability of the subject to anticipate the occurrence of a go signal, we calculated the subjective anticipation function, as described in Janssen and Shadlen (2005). First, we assume that the uncertainty in time estimation scales with elapsed time (“scalar timing” [Gibbon, 1977; Gibbon et al., 1997; Janssen and Shadlen, 2005]) such that a go signal which occurred at time t is perceived at time t ± σ(t), where
| (Equation 1) |
where the coefficient of variation or Weber fraction (ϕ) = 0.15 (Gibbon et al., 1997). Therefore, a subjective estimate of the go-signal distribution was computed by smoothing the probability distribution with a normal distribution whose standard deviation was proportional to the elapsed time (Equation 1; Figures S4E and S4F)
| (Equation 2) |
The expectation of the go signal was then calculated according to its hazard rate (Janssen and Shadlen, 2005):
where h(t) is the hazard rate, s(t) the subjective probability density function of go-signal delays dgo and S(t) the cumulative probability density function of subjective go-signal delays.
Performance accuracy was plotted as a function of delay to the go signal because the subjective anticipation is a function of go-signal times and not OSDs. The subjective anticipation functions (Figures S4G and S4H) (for uniform and exponential distributions) were fitted to the performance accuracy functions (Figure 4D) using the following equation:
where r(t) is the instantaneous performance accuracy, c0 is a constant term, sunif and sexp are the subjective anticipation function for uniform and exponential distributions (Equation 1), and c1 and c2 are the weighting coefficients for the two anticipation functions. Optimal parameters were found using a downhill simplex method, FMINSEARCH function in Matlab.
Supplementary Material
Acknowledgments
We would like to thank past and present members of the Mainen Laboratory for many helpful discussions and Drs. Joseph J. Paton, Dmitry Rinberg, and Anne Churchland for their comments on an earlier version of this paper. This work was supported by the National Institutes on Deafness and Other Communication Disorders (DC006104) and Cold Spring Harbor Laboratory.
Footnotes
Supplemental Information includes five figures and can be found with this article online at http://dx.doi.org/10.1016/j.neuron.2013.02.010.
References
- Abraham NM, Spors H, Carleton A, Margrie TW, Kuner T, Schaefer AT. Maintaining accuracy at the expense of speed: stimulus similarity defines odor discrimination time in mice. Neuron. 2004;44:865–876. doi: 10.1016/j.neuron.2004.11.017. [DOI] [PubMed] [Google Scholar]
- Abraham NM, Egger V, Shimshek DR, Renden R, Fukunaga I, Sprengel R, Seeburg PH, Klugmann M, Margrie TW, Schaefer AT, Kuner T. Synaptic inhibition in the olfactory bulb accelerates odor discrimination in mice. Neuron. 2010;65:399–411. doi: 10.1016/j.neuron.2010.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barlow HB. Temporal and spatial summation in human vision at different background intensities. J Physiol. 1958;141:337–350. doi: 10.1113/jphysiol.1958.sp005978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman NE, Kording KP, Gottfried JA. Temporal integration of olfactory perceptual evidence in human orbitofrontal cortex. Neuron. 2012;75:916–927. doi: 10.1016/j.neuron.2012.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burr DC, Santoro L. Temporal integration of optic flow, measured by contrast and coherence thresholds. Vision Res. 2001;41:1891–1899. doi: 10.1016/s0042-6989(01)00072-4. [DOI] [PubMed] [Google Scholar]
- Correa A, Lupianez J, Madrid E, Tudela P. Temporal attention enhances early visual processing: a review and new evidence from event-related potentials. Brain Res. 2006;1076:116–128. doi: 10.1016/j.brainres.2005.11.074. [DOI] [PubMed] [Google Scholar]
- Ditterich J. Stochastic models of decisions about motion direction: behavior and physiology. Neural Netw. 2006;19:981–1012. doi: 10.1016/j.neunet.2006.05.042. [DOI] [PubMed] [Google Scholar]
- Drugowitsch J, Moreno-Bote R, Churchland AK, Shadlen MN, Pouget A. The cost of accumulating evidence in perceptual decision making. J Neurosci. 2012;32:3612–3628. doi: 10.1523/JNEUROSCI.4010-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feierstein CE, Quirk MC, Uchida N, Sosulski DL, Mainen ZF. Representation of spatial goals in rat orbitofrontal cortex. Neuron. 2006;51:495–507. doi: 10.1016/j.neuron.2006.06.032. [DOI] [PubMed] [Google Scholar]
- Friedrich RW. Mechanisms of odor discrimination: neurophysiological and behavioral approaches. Trends Neurosci. 2006;29:40–47. doi: 10.1016/j.tins.2005.10.004. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gibbon J. Time, rate, and conditioning. Psychol Rev. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Ghose GM, Maunsell JH. Attentional modulation in visual cortex depends on task timing. Nature. 2002;419:616–620. doi: 10.1038/nature01057. [DOI] [PubMed] [Google Scholar]
- Gibbon J. Scalar expectancy theory and Weber’s law in animal timing. Psychol Rev. 1977;84:279–325. [Google Scholar]
- Gibbon J, Malapani C, Dale CL, Gallistel C. Toward a neurobiology of temporal cognition: advances and challenges. Curr Opin Neurobiol. 1997;7:170–184. doi: 10.1016/s0959-4388(97)80005-0. [DOI] [PubMed] [Google Scholar]
- Green DM. Detection of auditory sinusoids of uncertain frequency. J Acoust Soc Am. 1961;33:897. [Google Scholar]
- Griffin IC, Miniussi C, Nobre AC. Orienting attention in time. Front Biosci. 2001;6:D660–D671. doi: 10.2741/griffin. [DOI] [PubMed] [Google Scholar]
- Grinband J, Hirsch J, Ferrera VP. A neural representation of categorization uncertainty in the human brain. Neuron. 2006;49:757–763. doi: 10.1016/j.neuron.2006.01.032. [DOI] [PubMed] [Google Scholar]
- Hanks TD, Mazurek ME, Kiani R, Hopp E, Shadlen MN. Elapsed decision time affects the weighting of prior probability in a perceptual decision task. J Neurosci. 2011;31:6339–6352. doi: 10.1523/JNEUROSCI.5613-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssen P, Shadlen MN. A representation of the hazard rate of elapsed time in macaque area LIP. Nat Neurosci. 2005;8:234–241. doi: 10.1038/nn1386. [DOI] [PubMed] [Google Scholar]
- Jaramillo S, Zador AM. The auditory cortex mediates the perceptual effects of acoustic temporal expectation. Nat Neurosci. 2011;14:246–251. doi: 10.1038/nn.2688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahneman D. Thinking Fast and Slow. New York: Farrar, Straus and Giroux; 2011. [Google Scholar]
- Karpov AP. Analysis of neuron activity in the rabbit’s olfactory bulb during food-acquisition behavior. In: Thompson RF, Hicks LH, Shvyrkov VB, editors. Neural Mechanisms of Goal-Directed Behavior. New York: Academic Press; 1980. pp. 273–282. [Google Scholar]
- Katzner S, Treue S, Busse L. Improving behavioral performance under full attention by adjusting response criteria to changes in stimulus predictability. J Vis. 2012;12 doi: 10.1167/12.10.1. http://dx.doi.org/10.1167/12.10.1. [DOI] [PubMed] [Google Scholar]
- Kepecs A, Uchida N, Zariwala HA, Mainen ZF. Neural correlates, computation and behavioural impact of decision confidence. Nature. 2008;455:227–231. doi: 10.1038/nature07200. [DOI] [PubMed] [Google Scholar]
- Khan RM, Sobel N. Neural processing at the speed of smell. Neuron. 2004;44:744–747. doi: 10.1016/j.neuron.2004.11.024. [DOI] [PubMed] [Google Scholar]
- Laing DG. Optimum perception of odor intensity by humans. Physiol Behav. 1985;34:569–574. doi: 10.1016/0031-9384(85)90050-2. [DOI] [PubMed] [Google Scholar]
- Laing DG. Identification of single dissimilar odors is achieved by humans with a single sniff. Physiol Behav. 1986;37:163–170. doi: 10.1016/0031-9384(86)90400-2. [DOI] [PubMed] [Google Scholar]
- Lauwereyns J, Watanabe K, Coe B, Hikosaka O. A neural correlate of response bias in monkey caudate nucleus. Nature. 2002;418:413–417. doi: 10.1038/nature00892. [DOI] [PubMed] [Google Scholar]
- Luce RD. Response Times: Their Role in Inferring Elementary Mental Organization. New York: Oxford University Press; 1986. [Google Scholar]
- McDonald JJ, Teder-Salejarvi WA, Hillyard SA. Involuntary orienting to sound improves visual perception. Nature. 2000;407:906–908. doi: 10.1038/35038085. [DOI] [PubMed] [Google Scholar]
- Mazurek ME, Roitman JD, Ditterich J, Shadlen MN. A role for neural integrators in perceptual decision making. Cereb Cortex. 2003;13:1257–1269. doi: 10.1093/cercor/bhg097. [DOI] [PubMed] [Google Scholar]
- Nobre AC. Orienting attention to instants in time. Neuropsychologia. 2001;39:1317–1328. doi: 10.1016/s0028-3932(01)00120-8. [DOI] [PubMed] [Google Scholar]
- Ohzawa I, Sclar G, Freeman RD. Contrast gain control in the cat visual cortex. Nature. 1982;298:266–268. doi: 10.1038/298266a0. [DOI] [PubMed] [Google Scholar]
- Paton JJ, Belova MA, Morrison SE, Salzman CD. The primate amygdala represents the positive and negative value of visual stimuli during learning. Nature. 2006;439:865–870. doi: 10.1038/nature04490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychol Rev. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinagel P, Mankin E, Calhoun A. Speed and accuracy in a visual motion discrimination task as performed by rats. 2012 arXiv, arXiv:1206.0311, http://arXiv.org/abs/1206.0311.
- Rinberg D, Koulakov A, Gelperin A. Speed-accuracy tradeoff in olfaction. Neuron. 2006;51:351–358. doi: 10.1016/j.neuron.2006.07.013. [DOI] [PubMed] [Google Scholar]
- Roesch MR, Olson CR. Neuronal activity related to reward value and motivation in primate frontal cortex. Science. 2004;304:307–310. doi: 10.1126/science.1093223. [DOI] [PubMed] [Google Scholar]
- Roitman JD, Shadlen MN. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J Neurosci. 2002;22:9475–9489. doi: 10.1523/JNEUROSCI.22-21-09475.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders JI, Kepecs A. Choice ball: a response interface for two-choice psychometric discrimination in head-fixed mice. J Neurophysiol. 2012;108:3416–3423. doi: 10.1152/jn.00669.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanford TR, Shankar S, Massoglia DP, Costello MG, Salinas E. Perceptual decision making in less than 30 milliseconds. Nat Neurosci. 2010;13:379–385. doi: 10.1038/nn.2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uchida N, Mainen ZF. Speed and accuracy of olfactory discrimination in the rat. Nat Neurosci. 2003;6:1224–1229. doi: 10.1038/nn1142. [DOI] [PubMed] [Google Scholar]
- Uchida N, Kepecs A, Mainen ZF. Seeing at a glance, smelling in a whiff: rapid forms of perceptual decision making. Nat Rev Neurosci. 2006;7:485–491. doi: 10.1038/nrn1933. [DOI] [PubMed] [Google Scholar]
- Watson AB. Probability summation over time. Vision Res. 1979;19:515–522. doi: 10.1016/0042-6989(79)90136-6. [DOI] [PubMed] [Google Scholar]
- Wesson DW, Carey RM, Verhagen JV, Wachowiak M. Rapid encoding and perception of novel odors in the rat. PLoS Biol. 2008;6:e82. doi: 10.1371/journal.pbio.0060082. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.