Sparse multi-shell diffusion imaging

Abstract

Diffusion magnetic resonance imaging (dMRI) is an important tool that allows non-invasive investigation of neural architecture of the brain. The data obtained from these in-vivo scans provides important information about the integrity and connectivity of neural fiber bundles in the brain. A multi-shell imaging (MSI) scan can be of great value in the study of several psychiatric and neurological disorders, yet its usability has been limited due to the long acquisition times required. A typical MSI scan involves acquiring a large number of gradient directions for the 2 (or more) spherical shells (several b-values), making the acquisition time significantly long for clinical application. In this work, we propose to use results from the theory of compressive sampling and determine the minimum number of gradient directions required to attain signal reconstruction similar to a traditional MSI scan. In particular, we propose a generalization of the single shell spherical ridgelets basis for sparse representation of multi shell signals. We demonstrate its efficacy on several synthetic and in-vivo data sets and perform quantitative comparisons with solid spherical harmonics based representation. Our preliminary results show that around 20–24 directions per shell are enough for robustly recovering the diffusion propagator.

1 Introduction

A popular dMRI acquisition technique is High Angular Resolution Diffusion Imaging (HARDI), which involves acquiring diffusion information for a single b-value (single shell) in several gradient directions uniformly spread on a sphere [1]. While this protocol allows for resolving the angular structure of the neural fibers, it does not provide information about the radial signal decay, which is sensitive to white matter anomalies.

To obtain accurate information about the neural architecture, diffusion spectrum imaging (DSI) was proposed by [2]. This high resolution technique requires upwards of 512 gradient directions and more than an hour to scan each subject (spatial resolution of 2 mm³), which makes it impractical to use in clinical settings. A few works have attempted to reduce the scan time using compressed sensing for DSI [3, 4], however, the acquisition time is still too long for clinical applications. Consequently, other imaging schemes have been proposed, namely, Hybrid Diffusion Imaging (HYDI) [5], Diffusion Propagator Imaging (DPI) [6], Diffusion Kurtosis Imaging (DKI) [7], spherical polar Fourier basis [8] and high-order tensor models [9, 10], all of which fall under the category of multi-shell imaging (MSI). Each of these techniques captures different aspect of the underlying tissue geometry. They acquire important information about the neural tissues, which are missed by HARDI methods, yet, they are seldom used in clinical studies due to their long scan times. In general, it takes around 30–50 minutes to scan each subject with: 2 mm³ spatial resolution, 60 gradient directions per shell, 2–4 shells with b-values of 1000 to 6000. The acquisition time is directly proportional to the number of gradient direction acquisitions. Thus, if we can reduce the number of gradient acquisitions by half (without sacrificing the quality), the scan time reduces by 50%. This fact is the main motivation behind the proposed work.

In order to recover the MSI signal from very few measurements N, we propose to use the theory of compressive sampling (CS). Formalizing such a reconstruction approach in the context of MSI constitutes the main contribution of this work. In particular, we propose to generalize the spherical ridgelets (SR) basis of [11] for the case of multi-shell signals. We demonstrate that the MSI signal representation in the proposed basis is indeed sparse and compute error statistics on synthetic data sets. Further, the representation allows for a direct quantification of the signal decay as a function of b-values, which can be a useful measure in neuroimaging studies.

2 Compressive Sampling

The diffusion signal S(q) is a real-valued function, which determines the value of S at location q in q-space. The scalar q is given by q = ||q||, with q = qu, where u ∈ 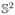. In the context of MSI, the signal S(q) is measured along N discrete orientations ${\{{\mathbf{u}}_k\}}_{k=1}^N$ for several different q values (Q shells). Thus, for each q value, measurements are made along N directions uniformly spread on a sphere, giving the measurements a multi-shell (also referred to as multi-b or multi-q) structure. In such a case, all experimental information on S(q) is represented by its NQ values ${\{S_k\}}_{k-1}^{NQ}$ corresponding to each of the q values. The most fundamental question in this regard is: what is the minimum number of diffusion directions N (on each shell) required to unambiguously represent the signal S(q) in terms of its discrete values S_k?

A particularly important answer to the above question is offered by the theory of CS [12, 13]. In particular, the theory specifies conditions under which the original signal S(q) can be perfectly recovered from a much smaller number of its samples than what would be required by the classical sampling theory. Since diffusion measurements are linear, the discrete values S_k can be expressed in the form of inner products S_k = 〈S(q), ϕ_jk (q)〉, with ${\{{\varphi }_{jk}\}}_{k=1}^N$ being a subset of a Dirac sampling basis {ϕ_i}_i∈. Moreover, let {ψ_j}_j∈ be another basis in the signal space, which we will use for representation of S(q). In particular, we are interested in representing the diffusion (MSI) signal S(q) in the form of a linear combination S(q) = Σ_j∈ c_jψ_j(q), where denotes the set of indices over which the basis functions ψ_j are counted. Note that, in a more general setup, the set {ψ_j}_j∈ may be overcomplete, but finite, with its total number of elements being equal to M. Then, the theory of CS proves that an accurate approximation of S is possible from only (μ² log(M)L) of its measurements, if the following conditions are satisfied:

1. S is assumed to be sparsely representable by {ψ_j}_j∈, which implies that the number L of non-zero coefficients c_j is significantly less than M.

2. The bases {ϕ_i}_i∈ and {ψ_j}_j∈ are incoherent, implying that the value of μ = sup_i,j |〈ϕ_i(q), ψ_j(q)〉| is relatively small.

The above considerations suggest that the applicability of CS to MSI depends on the availability of a basis {ψ_j}_j∈ for which the assumptions (a) and (b) above would be valid. Such a basis was introduced for HARDI data in [11], where it is called a basis of spherical ridgelets. In the next section, we demonstrate how to generalize this basis for sparse representation of MSI signals. Just as in the case of HARDI, the energy of the proposed basis of spherical ridgelets is distributed alongside the great circles of 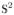(for every shell), which is very incoherent with respect to the Dirac sampling basis {ϕ_i}_i∈. Thus, the amount of incoherence μ for this basis is 0.56. Note that, this value is computed by normalizing each of the basis elements {ψ_j}_j∈ to unit norm.

3 Methods

Spherical ridgelets (SR) were proposed in [14, 11] following the theory of multiresolution analysis on the sphere. For the case of HARDI data, the SR basis is given by: IF:= {Ψ_j,v | v ∈ 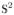, j ∈ IN ∪ {−1}}, where

$$\begin{array}{l}{\mathrm{\Psi }}_{j,\mathbf{v}}=\frac{1}{2\pi }\{\begin{array}{ll}{\mathcal{K}}_{0,\mathbf{v}},\hfill & \text{if}j=-1,\hfill \\ {\mathcal{K}}_{j+1,\mathbf{v}}-{\mathcal{K}}_{j,\mathbf{v}},\hfill & \text{if}j\in \text{IN},\hfill \end{array}\text{with},\\ {\mathcal{K}}_{j,\mathbf{v}}(\mathbf{u})=\sum _{n=0}^{\infty }\frac{2n+1}{4\pi }{\lambda }_n{\kappa }_j(n)P_n(\mathbf{u}·\mathbf{v}),\text{where},{\kappa }_j(n)=\kappa (\rho ,2^{-j}n)\\ \kappa (\rho ,x)=exp\{-\rho x(x+1)\},{\lambda }_n=\{\begin{array}{ll}2\pi {(-1)}^{n/2}\frac{1·3\cdots (n-1)}{2·4\cdots n},\hfill & \text{if}n\text{is}\text{even}\hfill \\ 0,\hfill & \text{if}n\text{is}\text{odd}.\hfill \end{array}\end{array}$$ (1)

where P_n is the legendre polynomial of order n, u ∈ 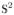and ρ is a user-defined parameter. Notice that, the basis functions Ψ_j,v can only represent signals defined on a single spherical shell.

3.1 From single to multiple shells

The structure and magnitude of the signal varies significantly as the b-value (or q-value) increases. This is evident from Figure 1, where in the top row we show the frequency spectrum (in spherical harmonic basis) required to represent signals with increasing b-values. Notice that, a). higher frequencies are required to represent sharper diffusion signals, and b). the signal decays in magnitude with b-values. We propose to use these two important facts in designing the MSI SR basis:

$${\mathcal{K}}_{j,\mathbf{v}}(\mathbf{q})=\underset{I_1}{\underbrace{exp(-\alpha q^2)\{1-\sum _{m=0}^h{a}_m{H}_m(q)\}}}\underset{I_2}{\underbrace{\sum _{n=0}^{\infty }\frac{2n+1}{4\pi }{\lambda }_n{\kappa }_j(q,n)P_n(\mathbf{u}·\mathbf{v}),}}$$ (2)

where H_m are hermite polynomials of order m, and κ_j(q, n) is now a function of q given by: κ(q, n) = exp (−βW(q)n(n + 1)), with W(q) given by the Weibull distribution function: $W(q)=\frac{k}{l}{\left(\frac{q}{l}\right)}^{k-1}exp(-{(q/l)}^k)$ where we set k = 0.8, l = 2 in this work and β is a constant. We now describe the rationale behind choosing such a function by individually examining the terms I₁ and I₂.

Fig. 1.

Top row (bar graph) shows the spherical harmonic frequency spectrum (upto order 8) required to represent each of the signals at the bottom. Also notice the decay in amplitude of the signal as the b-values increase.

The term I₁ essentially models the decay rate of the signal magnitude. Some studies have shown a biexponential decay of the signal [15], while others have seen diffraction patterns with high q-values [16]. The expression $I_1=exp(-\alpha q^2)\{1-{\sum }_{m=0}^h{a}_m{H}_m(q)\}$ can model both these phenomena, with the term $1-{\sum }_{m=0}^h{a}_m{H}_m(q)$ modeling the departure from an exponential decay. Note that, the Hermite polynomials are capable of modeling diffraction patterns as shown in [16] and hence we use it in our model.

The term I₂ models the frequency component (sharpness) of the signal. As n increases in the summation in I₂, the legendre polynomial P_n incorporates higher frequencies. The desired behavior of the combined term κ(q, n)P_n is to use only low frequencies for lower q-values and incrementally allow higher frequencies with increasing q. Thus, the term κ(q, n) should act as a bandpass filter by selectively adding high frequency components of P_n for the appropriate q-values. This behavior can be modeled by choosing W(q) to be a Weibull distribution function with parameters l = 2, k = 0.8. This function has a heavy tail, preventing the value of W(q) from converging to zero too quickly as in an exponential function.

Combining the effects of increasing frequency and decreasing signal magnitude results in the desired behavior for sparse representation of multi-shell signals. The free parameters of this model are α and ${\{a_m\}}_{m=1}^h$ along with the sparse set of weights c for the overcomplete basis. Note that, if we set α = 0 and ${\{a_m\}}_{m=1}^h=\{0\}$, then the expression for (q) in (2) reduces to that for a single shell HARDI (1), with the parameter ρ in (1) determined by evaluating W(q) for a specific q-value. Thus, the proposed basis is a generalization of the spherical ridgelets of [14]. We should note that the basis is still given by IF:= {Ψ_j,v | v ∈ 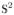, j ∈ IN ∪ {−1}}, as defined before, albeit with the modified form of the function (q).

3.2 Sparse Estimation

Given the measurements ${\{S({\mathbf{q}}_i)\}}_{i=1}^{NQ}$, one can use (2) to compute the values of the spherical ridgelet basis for all q_i (Q is the total number of shells and N is the number of gradient directions per shell). The resulting values can be then stored into an NQ × M matrix , where M is the number of elements in the overcomplete basis as defined in [11]. We use 3 discrete resolution levels {−1, 0, 1} for each shell and set h = 3 in equation (2). Subsequently, if c ∈ IR^M is defined to be a (column) vector of ridgelet coefficients and y:= [S(q₁), S(q₂), …, S(q_NQ)]^T, then the measurement model can be formally expressed as c = y + e, where e is an error vector that accounts for both measurement and model noises. From the theory of CS, a sparse estimate of coefficients c can be found by solving

$$\mathbf{c}=arg\underset{\mathbf{c}}{min}{\left|\right|\mathbf{c}\left|\right|}_1\text{subject}\text{to}{\left|\right|\mathcal{A}\mathbf{c}-y\left|\right|}_2\le \eta .,$$ (3)

where η depends on the level of noise expected in the signal. Note that (3) is a convex optimization problem, and can be solved using the L₁ homotopy algorithm of [17]⁴.

In the present scenario, we not only have to estimate the sparse vector c, but also the parameters for the radial decay. We do this by the method of coordinate descent, wherein the coefficients c and {α, a_m} are estimated alternately. The estimation framework is as follows:

The gradient with respect to a_m is given by < [..∇_am Ψ_j,v..]c, c − y >, where < ., . > is the euclidean inner product. The gradient only affects the radial part of Ψ_j,v, resulting in ∇_amΨ_j,v = −2e^−αq2 H_m(q)I₂, where I₂ is as defined in (2). A similar expression for gradient of α can be easily deduced from (2).

4 Experiments

Synthetic Data

We tested the proposed algorithm on synthetic data and quantitatively compared it with the solid spherical harmonics (SH) based method of [6]. Synthetic data sets were generated using a mixture of biexponential models: S(q) = Σ_i f_iG_i(q), where f_i are weight fractions set to 1/F, where F is the number of fibers and G_i(q) = 0.7 exp(−q²uDu^T) + 0.3 exp(−θq²uDu^T), where D = diag{0.0017, 0.0003, 0.0003} and θ = 1/3. Four different b-values were used b = {1000, 2000, 4000, 6000} to obtain 4 shells. Rician noise was added to each shell so that the SNR for each of the shells was: {5, 4, 3, 2} respectively, where SNR is defined by σ_s/σ_n, with σ_s being the standard deviation of signal and σ_n the standard deviation of noise. 1000 random samples were generated by randomly choosing the number of fiber crossings (maximum of 3) and random orientation between the fibers. Two different error metrics were used to determine the quality of fit using the proposed SR basis and the SH basis of [6]: (i) Normalized Mean Squared Error (NMSE) given by $\frac{{\left|\right|S(\mathbf{q})-\widehat{S}(\mathbf{q})\left|\right|}^2}{{\left|\right|S(\mathbf{q})\left|\right|}^2}$, where Ŝ(q) is the estimated signal. (ii) Average Angular Error (AAE) was computed between principal diffusion directions of the known ground truth and the ones estimated from the diffusion propagator. For the SR basis, the propagator was computed numerically as in [5]. Error statistics were computed by estimating the signal using different number of measurements K = [16, 32] per shell. Thus, with K = 16, only a total of 64 measurements (for 4 shells) were used in estimating the signal.

Figure 3(a) shows NMSE as computed for each of the 4 shells for various K. Also shown is the AAE for various K and different number of crossing fibers. As seen in the figures, the proposed SR basis better fits the signal with lower errors for higher b-values. K = [20, 24] per shell seems to be sufficient to model the MSI signal without significant errors. The SH basis on the other hand tends to oversmooth the signal (as seen by higher NMSE and AAE). We should note that, having 4 shells is not a necessity for our method, but we used it to demonstrate the accuracy with which the proposed SR basis fits the signal for all b-values.

Fig. 3.

Top left (a) shows the propagator for radius R₀ = 20 μm with K = 60. The remaining figures show a zoomed-in version (the black box) of the propagator as computed by estimating the signal with K = 16, 28 per shell. Note that the values of the propagator were scaled to uniform size for better visualization.

In-vivo Data

Our in-vivo data consisted of a human brain scanned on a 3T Siemens scanner with the following parameters: 2.5 mm³ spatial resolution, b = {900, 2000, 5600} and 60 gradient directions per shell. For each shell, the signal was subsampled to obtain the desired measurements for different K = [16, 32] and the proposed SR basis was used to fit the data. Figure 4 shows the diffusion propagator for various K and radius R₀ = 20 μm.

5 Conclusion

In this paper, we introduced a generalization of the spherical ridgelet basis for modeling multi-shell diffusion signal. The representation in this basis is sparse and as such allows one to faithfully recover the signal with few gradient directions (around 20–24 per shell). The proposed representation models the radial decay and the frequency components separately. Thus, one can compute a measure of the “overall” signal decay at each voxel. Future work involves examining its correlation with the underlying tissue properties. This work also showed results on in-vivo data with 3 shells and the same number of directions for each shell. Figuring out the optimum number of shells, the corresponding b-value and the distribution of gradient directions is still a topic of active research. We hope that by recovering the signal from sparse measurements on each shell and with a few (2–3) shells, we will be able to reduce the scan time of MSI significantly and thus make it clinically feasible⁵.

Fig. 2.

The left two figures (a) show the NMSE for different values of K = [16, 32] (x-axis) and for b={1000, 2000, 4000, 6000}. First figure is with SR basis and second with SH basis. (b) shows AAE in degrees (x-axis is K) for different number of crossing fibers (1,2,3). 3^rd figure is with the proposed SR basis and 4^th with the SH basis of [6].

Algorithm 1.

Algorithm for sparse estimation of MSI data

1:	Initialize α = α0 and am = {0}.
2:	while ||c||1 is decreasing do
3:	Estimate c using equation (3).
4:	Update α and ${\{a_m\}}_{m=1}^h$ using gradient descent of || c − y||2.
5:	end while