Functional Impact of Dendritic Branch-Point Morphology

Abstract

Cortical pyramidal cells store multiple features of complex synaptic input in individual dendritic branches and independently regulate the coupling between dendritic and somatic spikes. Branch points in apical trees exhibit wide ranges of sizes and shapes, and the large diameter ratio between trunk and oblique dendrites exacerbates impedance mismatch. The morphological diversity of dendritic bifurcations could thus locally tune neuronal excitability and signal integration. However, these aspects have never been investigated. Here, we first quantified the morphological variability of branch points from two-photon images of rat CA1 pyramidal neurons. We then investigated the geometrical features affecting spike initiation, propagation, and timing with a computational model validated by glutamate uncaging experiments. The results suggest that even subtle membrane readjustments at branch points could drastically alter the ability of synaptic input to generate, propagate, and time action potentials.

Introduction

Dendritic integration and compartmentalization in hippocampal pyramidal neurons are believed to play a direct role in spatial information processing (Nolan et al., 2004; Morita 2008). Local distribution of active properties (Losonczy et al., 2008), dendrite/trunk diameter ratio (Migliore et al., 2005), and synaptic location (Li and Ascoli, 2006) are all key determinants of dendritic Na⁺ spike (d-spike) initiation and propagation (Golding and Spruston, 1998; Gasparini et al., 2004). At the same time, a rich repertoire of biological mechanisms can dynamically change dendritic computation in response to cell activity (Johnston and Narayanan, 2008). Synaptic (Caporale and Dan, 2008), intrinsic (Turrigiano et al., 1994), and structural (Bourne and Harris, 2008) plasticity, respectively, regulate the strength of input signals, ionic channel expression (and/or biophysical properties), and local morphology. Moreover, activity-dependent structural and functional changes may co-occur, as in synapses changing their shape and size when potentiating or depressing.

CA1 pyramidal neurons are characterized by a thick apical trunk from which arise spiny oblique dendrites. Although these dendrites are thin (∼0.5 μm in diameter) and represent only ∼35% of the dendritic wiring, they receive approximately half of the total excitatory inputs (Megías et al., 2001) and may act as independent computational units within the dendritic tree (Poirazi and Mel, 2001; Losonczy et al., 2008). With high local input impedance, high-impedance mismatch with the main trunk, and high active excitability, obliques are ideally suited to perform local computation, while still contributing to the overall neuronal output (Rabinowitch and Segev, 2006; Katz et al., 2009). The influence of dendritic morphology on the input/output relationship has been investigated extensively in cortical and hippocampal neurons (Mainen and Sejnowski, 1996; Krichmar et al., 2002; Schaefer et al., 2003; Komendantov and Ascoli, 2009). In contrast, the morphological diversity and functional role of the bifurcation between oblique dendrites and the apical trunk has been essentially ignored and experimentally unexplored.

This work investigates the role of branch-point morphology in determining the minimum synaptic stimulation required to generate either a d-spike in an oblique branch or a somatic action potential (AP). In CA1 pyramidal neurons, dendritic compartmentalization can be regulated by active properties, such as potassium channels (Cai et al., 2004). Although the effects of synaptic and intrinsic plasticity on spike initiation and propagation have been investigated extensively (Canepari et al., 2007; Remy et al., 2009), the functional consequences of morphological changes at dendritic bifurcations are unknown and difficult to explore experimentally. We observed that branch points in the apical dendrites of CA1 pyramidal neurons exhibit considerable structural variability, which might result from activity-dependent regulation. Our results suggest that minor (possibly dynamic) alterations of a small patch of membrane at dendritic bifurcations might have major and opposite effects on the probabilities to initiate and propagate a spike, as well as on its onset and temporal reliability. Much as structural plasticity of dendritic spines can control electric compartmentalization and synaptic communication (Grunditz et al., 2008; Fu and Zuo, 2011), bifurcation morphology might be a powerful regulator of branch excitability and coupling.

Materials and Methods

Hippocampal slice preparation and patch-clamp recordings.

Image acquisition and glutamate uncaging slice experiments were performed by Drs. Judit K. Makara and Jeffrey C. Magee at the Janelia Farm Research Campus of the Howard Hughes Medical Institute (Ashburn, VA); these data have then been kindly ceded to the authors. Adult (8- to 12-week-old) male Sprague Dawley rats were used to prepare transverse slices (400 μm) from the middle to dorsal part of the hippocampus similarly to previous descriptions (Magee, 1998), according to methods approved by the Janelia Farm Institutional Animal Care and Use Committee. Experiments were performed at 33–35°C in ACSF containing the following (in mm): 125 NaCl, 3 KCl, 25 NaHCO₃, 1.25 NaH₂PO₄, 1.3 CaCl₂, 1 MgCl₂, 25 glucose, 3 Na-pyruvate, and 1 ascorbic acid (saturated with 95% O₂ and 5% CO₂). Cells were visualized using an Olympus BX-61 epifluorescent microscope equipped with differential interference contrast optics under infrared illumination and a water-immersion lens (60×, 0.9 numerical aperture; Olympus). Current-clamp whole-cell recordings from the somata of hippocampal CA1 pyramidal neurons were performed using a Dagan BVC-700 amplifier in the active “bridge” mode, filtered at 3 kHz and digitized at 50 kHz. Patch pipettes (2–6 MΩ) were filled with a solution containing 100 μm Alexa Fluor 488 and the following (in mm): 120 K-gluconate, 20 KCl, 10 HEPES, 4 NaCl, 4 Mg₂ATP, 0.3 Tris₂GTP, and 14 phosphocreatine, pH 7.25. Series resistance was <20 MΩ. All neurons had resting membrane potentials between −58 and −65 mV. The membrane potential was kept slightly hyperpolarized (approximately −65 to −70 mV), to better isolate local Na⁺ spikes from axosomatic APs.

Two-photon imaging and uncaging.

A dual galvanometer-based two-photon scanning system (Prairie Technologies) was used to obtain fluorescent images of Alexa Fluor 488-loaded neurons and to uncage glutamate at individual dendritic spines (Losonczy and Magee, 2006; Losonczy et al., 2008; Makara et al., 2009). Two ultrafast pulsed laser beams (Chameleon Ultra II; Coherent) were used, one at 920 nm for imaging Alexa Fluor 488 (Invitrogen) and one at 720 nm to photolyze 4-methoxy-7-nitroindolinyl-caged l-glutamate (MNI–glutamate) (Tocris Cookson; 10 mm applied through a pipette above the slice). Laser beam intensity was independently controlled with electro-optical modulators (model 350-50; Conoptics).

All uncaging experiments were performed in proximal apical first-order oblique dendrites, branching off from the soma or from the apical trunk within 60 μm from the soma. Local dendritic Na⁺ spikes were evoked by synchronous uncaging of MNI–glutamate at a spatially close cluster of 4–12 visually identified spines (0.2 ms uncaging duration with 0.1 ms intervals between exposures for scanning mirror repositioning). Generation of a local spike could be unequivocally identified by the appearance of a fast spikelet on the rising phase of the compound glutamate-uncaging-induced EPSP (gluEPSP) and a corresponding peak on the dV/dt (instantaneous rate of voltage change over time) of the voltage signal (Losonczy and Magee, 2006; Losonczy et al., 2008; Makara et al., 2009). To determine spike threshold (as measured at the soma) at a given dendritic location, the uncaging laser power was adjusted to the lowest level that was sufficient to evoke the spike with synchronous uncaging, and the same power was used to record the individual spine responses (with 210 ms interval) in the same experimental session (see Fig. 2C–E). Spike threshold was calculated as the arithmetic sum of the individual gluEPSPs.

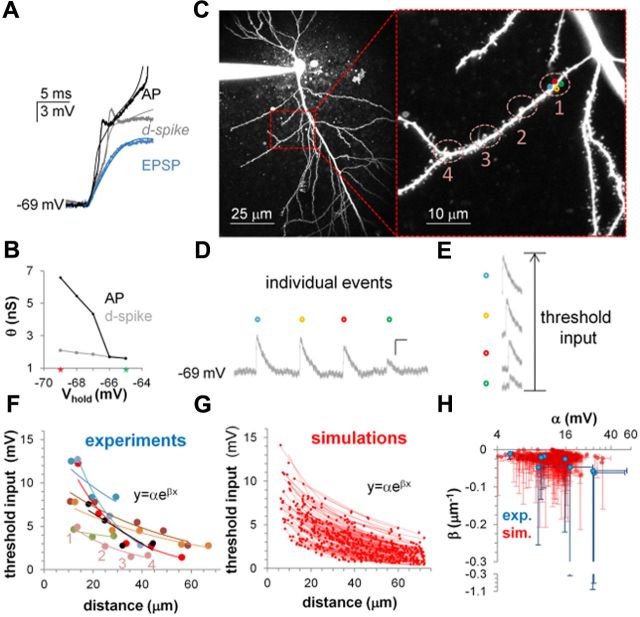
Figure 2.

Experimental validation of the computational model. A, Experimental (noisy lines) and simulated (smooth lines) voltage traces recorded in the soma at different stimulation intensities: subthreshold EPSP (blue), θ_d-spike (gray), and θ_AP (black). B, Simulations showing the effect of hyperpolarization on a branch with coupled d-spike and AP thresholds; the morphological parameters of the model were measured from the branch used for the voltage trace experiment in A. Green and red marks on the x-axis represent membrane resting potential and experimental holding potential, respectively. C, Low-magnification (left) and high-magnification (right) of a representative oblique dendrite, with numbered labels identifying two-photon glutamate uncaging locations. Colored circles within location 1 show the four spines used for two-photon glutamate uncaging at that location. D, Individual gluEPSPs for the four spines (colored circles in C), activated 210 ms apart from each other, at d-spike threshold. Calibration: 50 ms, 0.5 mV. E, Arithmetic sum of the individual responses at d-spike threshold (same calibration in D); this sum equals the “threshold input” in F. F, Computed threshold input, defined as the equivalent peak somatic depolarization evoked at θ_d-spike. This parameter was calculated by summing the voltage peaks recorded from a number of individually stimulated synapses that, when activated together, would trigger a d-spike (D, E). These values were collected for different branches (colors) as a function of the stimulation distance from the branch point and fitted with exponential functions. G, Simulation of the experimental design from C, using the branch-point morphological parameters measured from 171 oblique dendrites. Lines represent exponential fittings of peak somatic depolarization during a d-spike, for branches stemming from the main trunk at a random distance between 0 and 100 μm from the soma. H, Exponential fitting parameters of experimental (blue) and modeling (red) data; error bars represent 95% confidence intervals of best-fitting values. Note that the bottom part of the ordinate axis (from −0.3 to −1.1) has a separate compressed scale to accommodate three confidence interval outliers.

Morphological analyses.

Morphological measurements were extracted with NIH ImageJ from high-resolution (>5 pixel/μm on x/y) image stacks of CA1 pyramidal neurons. Branch-point tapering measures were collected from 2D maximum intensity for individual image stacks, selecting the branches that were quasi-parallel to the x/y plane for highest resolution. Four morphological parameters were recorded for each of the 171 branches of the 69 CA1 pyramidal neurons: (1) d_trunk (diameter of main trunk); (2) d_dend (diameter of the dendrite); (3) lc (length of the tapering cylinder); and (4) d_taper (diameter of the tapering region at the trunk). From these parameters, we computed the branch-point surface (surf) as the lateral surface area of the circular conical frustum using the following formula:

Neurons were imaged either before (n = 52 neurons) or after (n = 17) uncaging. None of the measured distributions (d_dend, d_trunk, d_taper, and lc) revealed any statistical difference between the two conditions (p > 0.2 in all cases), indicating that glutamate uncaging did not significantly affect local branch morphology. To minimize the possible bias introduced by subjective measurements, a different coauthor blindly re-extracted and independently analyzed the morphological features from a subsample of the branches (n = 30). The two sets of measurements for each morphological feature were highly correlated (R² > 0.87) and not significantly different (p > 0.1). The average difference was <6% for every parameter, and the discrepancy between any two individual measurements never exceeded 18%.

Computational model.

All simulations were implemented and run in NEURON (Hines and Carnevale, 1997) version 7.2 with variable time step, on a 64-bit Pentium quad-core Dell XPS laptop under Windows 7. Model and simulation files are available for public download under the ModelDB section (accession number 146509) of the Senselab database (senselab.yale.med.edu/ModelDB). Because of the variable resolution of available digital reconstructions of dendritic morphology (Scorcioni et al., 2004) and for the sake of parsimony and standardization, we implemented a simplified T-shaped multicompartmental model. Unless otherwise noted, the model used for all simulations consisted of three segments: (1) a 240-μm-long trunk; (2) a 120-μm-long oblique dendrite; and (3) a bifurcation tapering segment stemming off the middle of the trunk and connecting one end of the oblique dendrite. All simulations used the morphological parameters measured from the image stacks.

The same active and passive properties previously described and validated (Migliore et al., 2005) were used in all cases. Briefly, τ_m = 28 ms, R_m = 28 kΩ-cm², R_a = 150 Ω-cm, I_Na and I_Kdr uniformly distributed throughout the membrane surface (with peak conductances g_Na = 0.25 nS/μm² and g_Kdr = 0.1 nS/μm²); I_h and I_KA linearly increased with distance, dist, as g_KA = 0.3 × (1 + dist/100) and g_h = 0.0005 × (1 + 3dist/100) (Hoffman et al., 1997; Magee, 1998). AMPA-type excitatory synapses (0 mV reversal potential) were implemented using the NEURON double-exponential function Exp2Syn(), with rise (0.5 ms) and decay (3 ms) times consistent with experimental measurements (Andrasfalvy and Magee 2001).

To validate the model against two-photon uncaging experiments, in a subset of simulations, we stochastically chose three synaptic locations on the dendrite between 10 and 75 μm from the branch point for each set of morphometric parameters, positioning the recording electrode on the trunk at a random distance between 0 and 100 μm from the branch point. For each synaptic location, we increased the synaptic strength to elicit a d-spike while recording the trunk depolarization. For all other simulations, the model included two recording electrodes: one at the location of the synaptic input (at 38 μm from the branch point unless otherwise stated) and one in the trunk at 84 μm from the branch point. The stimulation protocol consisted of progressively increasing for each branch-point configuration the strength of the synapse to record an EPSP, a d-spike, or an AP (and its onset). θ_d-spike and θ_AP were defined as the synaptic input strength necessary to evoke either a d-spike or an AP, respectively.

Results

Branch-point morphology is remarkably diverse and heavily affects dendritic spike initiation and propagation

To characterize branch-point morphology in CA1 pyramidal neurons, we identified 171 bifurcations between oblique branches and the main apical trunk from two-photon confocal microscopy image stacks of 69 neurons, 18 of which were used in a previous study (Makara et al., 2009). For each of these, we measured and analyzed four parameters (Fig. 1A): (1) d_trunk; (2) d_dend; (3) d_taper; and (4) lc (all defined in Materials and Methods). All parameters, as well as surf and the d_dend/d_trunk ratio, showed a considerably broad range of values (Fig. 1B) and several significant correlations (d_dend vs lc, r = 0.57, p < 0.001; d_trunk vs surf, r = 0.52, p < 0.001; d_trunk vs lc, r = 0.48, p < 0.01; d_dend vs d_trunk, r = 0.41, p < 0.05; r values are Pearson's product moment correlation coefficients).

Figure 1.

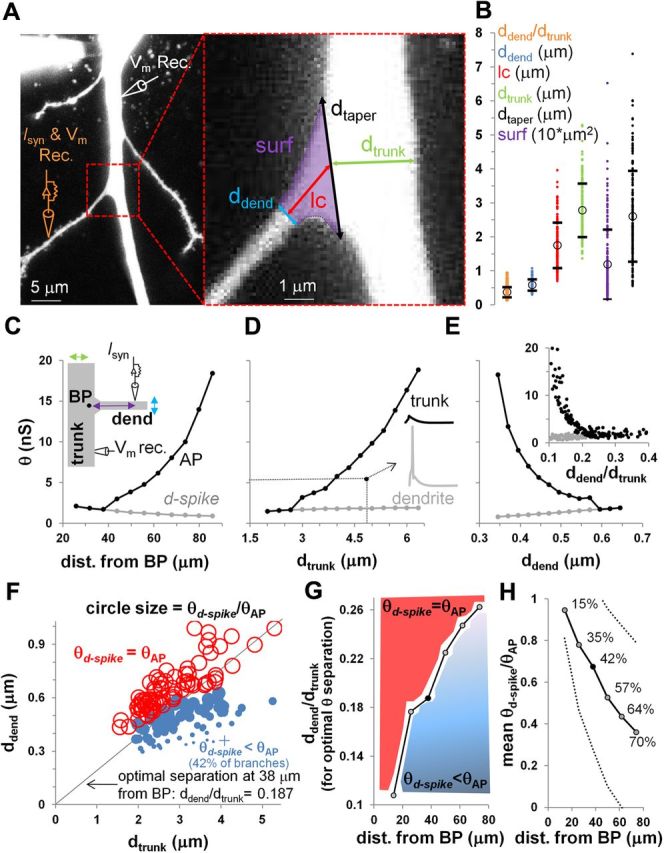
Branch-point (BP) morphology affects the thresholds for dendritic and somatic spike generation. A, Left, Representative confocal image illustrating the simulation setup (orange, stimulating and recording electrode; white, recording electrode). Right, Expanded view of the bifurcation between the main trunk and the oblique branch, with the measured morphometric parameters: d_dend, d_trunk, surf, and lc. B, Parameter distributions for the 171 branches measured from image stacks; circles and horizontal lines mark averages and SDs, respectively. C–E, Stimulation threshold (θ) to generate a local d-spike (gray line) or an AP in the trunk (black line) in the computational model, as a function of the distance of the input from the branch point (C), the trunk diameter (D), the diameter of the oblique dendrite (E), and the oblique/trunk diameter ratio (inset in E). The inset in C depicts a schematic of the computational model in which purple, green, and blue arrows show the manipulated parameters in C, D, and E, respectively. The inset in D shows dendritic and trunk voltage traces during a 5 nS synaptic stimulation at 38 μm from the branch point. Except for the independent variables in each of the main panels, average branch morphometric values (B) and a 38 μm synaptic distance from the branch point were used for all parameters. In contrast, the inset in E used the original values extracted from the 171 bifurcations. F, Linear discriminant analysis identifies, for a specific synaptic distance from the branch point (38 μm), the optimal d_dend/d_trunk diameter ratio allowing thresholds separation. Red and blue circles show synapses with coupled (θ_d-spike = θ_AP) and compartmentalized (θ_d-spike < θ_AP) thresholds, respectively. Symbol size represents θ_d-spike/θ_AP threshold ratio, and the + symbol indicates the single case in which the d-spike never propagated into the trunk, even with a stimulation of 40 nS. G, Optimal d_dend/d_trunk values for threshold separation as a function of stimulation distance from the branch point. Red area depicts coupled synapses, blue gradient shows different degrees of thresholds separation, with darker shade indicating greater compartmentalization. The black dot corresponds to data shown in F. H, Black line, Average level of branch compartmentalization for the compartmentalized branches as a function of the synaptic distance from the branch point. Percentages, Amount of compartmentalized branches; dotted lines, average ± SD level of branch compartmentalization.

We quantified the morphometric variability of each feature by the coefficients of variation (CVs) across all branch points pooled together (overall CV) as well as between and within neurons. The between-neuron CV was computed on the averages of the appropriate feature over all branches of each neuron. The within-neuron CV was the average of the corresponding CVs for each feature computed for the set of branch points within every neuron. This latter metric was only computed over the 33 neurons with at least three characterized branches. The least variable features were d_dend and d_trunk (overall CV, 28.2 and 28.3%, respectively). Interestingly, d_dend displayed greater variability within than between neurons (23.7 vs 19.2%), whereas the opposite held for d_trunk (within CV, 17.4%; between CV, 24.3%). In contrast, surf was the most variable feature (CV values of 86.1, 62.5, and 58.4%, respectively, for overall, between, and within neurons).

Propagation of d-spikes from the oblique onto the trunk is mainly modulated by d_dend/d_trunk via impedance mismatch (Migliore et al., 2005), and the observed morphological diversity might imply a corresponding functional diversity in local computation. To investigate the effect of different, experimentally measured, branch-point morphologies on the coupling between d-spikes and somatic APs, we used a computational model to determine the stimulation thresholds necessary for local spike initiation and propagation. First, to demonstrate the main effect, using the average values of d_dend, d_trunk, lc, and d_taper, we found the minimum peak synaptic conductances eliciting a local d-spike and a propagated AP in the trunk (θ_d-spike and θ_AP, respectively) as a function of the input location. A synapse on the oblique branch is considered fully coupled to the trunk if the stimulus thresholds to generate a d-spike and an AP are the same, i.e., any d-spike would trigger an AP. Conversely, a synapse is highly uncoupled if the two thresholds are very different, i.e., a broad range of input strengths would generate a d-spike but not an AP. The results suggested that synapses are fully coupled relatively near (<40 μm) the bifurcation point, but the d-spike and AP thresholds dramatically diverge farther on the oblique dendrite (Fig. 1C). More specifically, the distance of the input from the branch point had opposite effects, respectively, decreasing θ_d-spike and increasing θ_AP.

Next, we fixed the synaptic location on the oblique branch (at 38 μm from the bifurcation) and examined the influence of using values for d_trunk and d_dend within the measured experimental range. Increase in trunk diameter resulted in a large rise in θ_AP but had negligible consequences for θ_d-spike, with uncoupling at d_trunk > 2.7 μm (Fig. 1D). In contrast, θ_d-spike increased with the oblique diameter, with full coupling at d_dend > 0.6 μm (Fig. 1E); in thinner branches, θ_AP steeply increased as d_dend decreased and was 20 times larger than θ_d-spike at d_dend = 0.35 μm.

We also computed the initiation and propagation thresholds at a fixed distance from the bifurcation using the experimentally measured values of oblique and trunk diameters (Fig. 1E, inset). From these data, we determined the oblique/trunk diameter ratio that best discriminates between coupled and uncoupled branches (Fig. 1F). The optimally discriminating diameter ratio increased with the distance of the input from the bifurcation (Fig. 1G). Moreover, coupling diminished with distance from the bifurcation as indicated by both the decreasing mean ratio between d-spike and AP thresholds and the increasing percentage of uncoupled branches (Fig. 1H).

These results show that relatively small differences in d_dend/d_trunk, well within the observed range of morphological diversity in the apical trees of CA1 pyramidal neurons, could have dramatic and opposing effects on the thresholds for dendritic spike initiation and propagation.

Experimental validation of the computational model

To test the physiological plausibility of the simulation results, we designed two experiments that are both relevant to the phenomena under consideration and practically achievable with available technology. First, we investigated the conditions to observe dendritic uncoupling in the slice preparation, i.e., a d-spike in the absence of somatic AP. Next, we experimentally characterized the threshold input for somatic spikes at various synaptic distances along the oblique dendrite from the bifurcation with the main trunk. In both cases, we showed that the computational model used in this study qualitatively and quantitatively reproduces the empirical findings.

A separation of θ_d-spike and θ_AP is generally not observed in primary branches of CA1 pyramidal neurons: if a dendritic stimulation is sufficient to initiate a local Na⁺ spike, it typically evokes a somatic AP. However, these experiments seldom target the thinner obliques at farther distances from the branch point, i.e., the conditions in which threshold separation is predicted by the computational model. We hypothesized that a moderate somatic hyperpolarization could separate θ_d-spike and θ_AP even for average or thicker branches stimulated closer to the bifurcation with main trunk. Using two-photon glutamate uncaging, a small cluster of synapses was stimulated with progressively higher laser powers in a fixed location on the oblique dendrite. At a holding potential ∼4 mV below resting, d-spikes were clearly visible (Fig. 2A). When the geometric parameters recorded from this experiment were used in the computational model (d_dend = 0.65 μm, d_trunk = 2.7 μm, distance from branch point of 30 μm), simulations confirmed that the oblique dendrite would be fully coupled at or above −66 mV but that threshold separation would be observable at or below −67 mV (Fig. 2B). Moreover, the simulated EPSPs, d-spikes, and APs were consistent with the experimental traces (Fig. 2A).

Dendritic filtering is affected by a combination of passive, active, and morphological characteristics, which together determine the synaptic input strength required to generate d-spikes and APs under normal conditions. A second series of experiments investigated how the somatically recorded threshold input varied with stimulus locations (Fig. 2B–H). The experimental approach was to synchronously uncage glutamate in a group of spines (Fig. 2B) and increase the intensity of each laser beam to evoke a d-spike or an AP (Fig. 2C). To circumvent the nonlinearity involved in synaptic spatial/temporal summation, the input threshold was calculated as the arithmetic sum of the unitary events, obtained by stimulating the spines asynchronously, with a 210 interval from each other (Fig. 2D,E) (Losonczy and Magee, 2006). With this protocol, small clusters of synapses (three to five) were stimulated in different obliques (Fig. 2F, different colors) at varying distances from the branch point (Fig. 2F, same-colored circles). The decrease of threshold input with distance could be well described in all cases with exponential functions. With the model, we then simulated this experimental design, stochastically sampling three synaptic locations in the oblique dendrite in a representatively large number of trials. The resulting simulations also demonstrated an exponential decrease of threshold input with distance (Fig. 2G). The distributions of both decay and multiplicative fitting parameters were fully consistent between model and experiments (Fig. 2H) and showed no significant difference in either the Mann–Whitney or Student's t tests (p > 0.1).

These results support the physiological plausibility of the computational model, encouraging a deeper investigation on the potential functional consequences of the observed morphological diversity at apical branch points.

Functional effects of structural plasticity at branch points

Experience can modulate a branch ability to convey signals to the rest of the neuron (Makara et al., 2009) via alterations in synaptic conductances (Tyler et al., 2007), ion channel properties (Sun, 2009), and spine morphology (Tropea et al., 2010). Our results suggest that local adjustments in branch-point morphology might also play a role in this computation. However, nothing is known about the extent and dynamics of morphological plasticity at the bifurcation between the apical trunk and oblique branches in CA1 pyramidal neurons. We re-examined the available experimental evidence originally acquired to investigate spine growth (Park et al., 2006) and filopodial sprouting (Smith and Jahr, 1992). Video captures (http://www.sciencedirect.com/science/article/pii/S0896627306008294#mmc6 and http://smithlab.stanford.edu/Smithlab/Dendro_Filopod_Movies.html) demonstrate changes in both shape and size of branch points during spontaneous activation, glutamate stimulation, or induction of long-term potentiation (Fig. 3B). This evidence raises the possibility that the observed morphological diversity of branch points could result from activity-mediated modifications.

Figure 3.

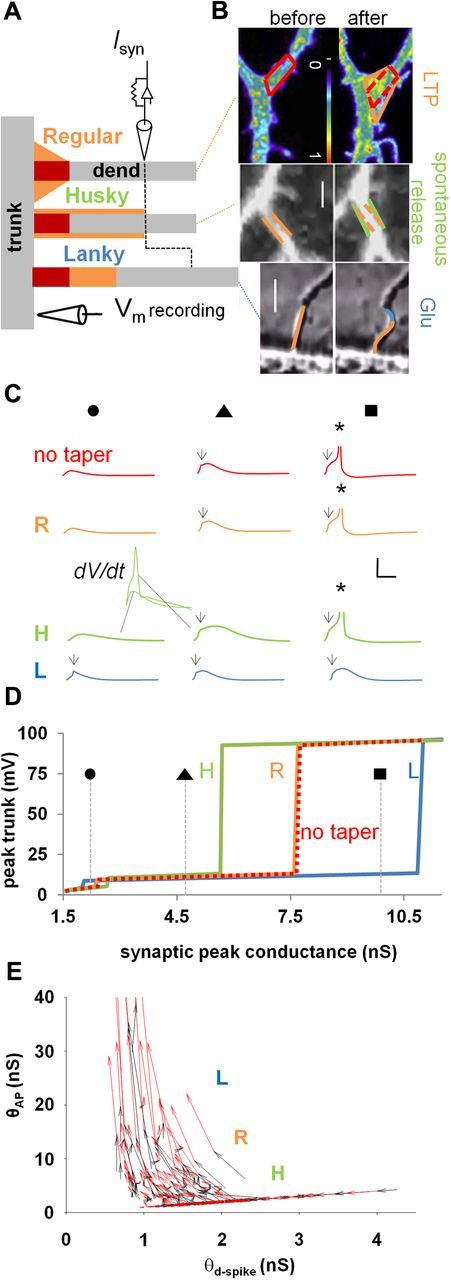
Potential functional effects of bifurcation morphological dynamics. A, Top, Regular, typical morphology. Middle, In the husky morphology, the tapering surface is redistributed to increase the dendritic diameter from the branch point up to the synaptic location. Bottom, In the lanky morphology, the tapering surface is used to increase the distance of the synaptic input from the branch point. In all cases, red indicates the membrane portion without a tapering surface; gray and black symbols schematically show the location of the synaptic input on the dendrite and of the recording electrode in the trunk, respectively. B, Top, Branch-point exocytosis of transferrin receptor (TfR)-pHluorin after glycine-induced LTP in rat CA1 pyramidal neuron. TfR-pHluorin fluorescence was imaged before or 20 min after glycine stimulation. The bar (10 μm) is a pseudocolor intensity scale. Image reproduced with permission from Park et al. (2006). Orange and red lines highlight the contour of the branch-point tapering region before (left, no taper) and after (right, regular) LTP induction. Middle, Imaging of CA1 pyramidal neuron dendrites during spontaneous activation at time 0 (left) and 60 (right) min. Green and orange lines show a regular-to-husky transformation. Scale bar, 1 μm. Bottom, Response of a rat CA1 pyramidal neuron in a cell culture to a pulse of glutamate applied from a micropipette. Orange and blue lines depict the transformation from regular to lanky. Scale bar, 5 μm. Middle and bottom images are snapshots from the videos described by Smith and Jahr (1992), courtesy of Dr. S. Smith (Stanford University, Palo Alto, CA). C, Trunk voltage traces for four tapering shapes (without tapering membrane in red, regular in orange, husky in green, lanky in blue). Insets in middle plots represent trunk dV/dt in the absence or presence of a local spike. Symbols on top represent specific synaptic strengths, indicated in D. Arrows and asterisks indicate d-spike and AP, respectively. D, Trunk peak voltage as a function of synaptic peak conductance shows the compartmentalization associated with husky (H), regular (R), and lanky (L) branch points. E, Effect of changing branch-point morphology on θ_d-spike and θ_AP. Black arrows show husky-to-regular changes; red arrows depict regular-to-lanky effects. For the simulations of the branch point illustrated in this figure, the synaptic input was at 38 μm from the branch point for the regular and husky configurations and at 42.51 ± 5.25 μm (mean ± SD) for the lanky case.

To what degree might the structural plasticity in a limited neighborhood of the branch point affect dendritic and somatic spikes? We tested computationally the potential functional effect of a modest local reorganization of the bifurcation membrane. In particular, we started from an initial “regular” shape of the branch point between the main apical trunk and oblique branch (Fig. 3A, top, orange plus red; compare with the post-LTP case in B), with geometric parameters corresponding to the average measured values (Fig. 1B). Then we systematically manipulated a fraction of the measured tapering surface area (the orange portion, henceforth referred to as the “fringe” membrane) in different ways: (1) no taper, eliminating the fringe membrane [Fig. 3A, top branch red only (no orange); compare with the pre-LTP case in B]; (2) husky shape, obtained by redistributing the fringe membrane to thicken (on average ∼0.1 μm for synaptic stimuli located at 50 μm from the branch point) the oblique branch up to the stimulus location (Fig. 3A, middle branch, orange plus red; compare with the t = 60 min spontaneous activation case in B); and (3) lanky shape, obtained by redistributing the fringe membrane to elongate the oblique, increasing the path distance (on average ∼4.7 μm) between the synapse and the bifurcation (Fig. 3A, bottom branch, compare with the after glutamate case in B).

For each of the four conditions (regular, no taper, husky, and lanky), we determined the θ_d-spike and θ_AP thresholds, as in Figure 1C–E. Rearrangement on the fringe membrane (from regular to husky or lanky) strongly influenced both local and propagated responses in complementary and opposite directions. Specifically, stimulation intensities below θ_d-spike threshold for regular dendrites could often elicit a d-spike in lanky, but never in husky, dendrites (Fig. 3C, left), as also confirmed by trunk voltage derivatives (Fig. 3C, green inset). Conversely, stimuli above θ_AP threshold in regular dendrites would always initiate somatic APs in husky dendrites but, in many cases, failed to do so in lanky branches (Fig. 3C, right). More generally, husky dendrites had a considerably higher threshold for dendritic spikes than regular branches but a considerably lower threshold for somatic spikes, whereas the exact opposite occurred in lanky dendrites (Fig. 3D). As a result, the range of stimulus intensities that would elicit a d-spike but not a somatic AP was twice as broad in lanky and twice as narrow in husky dendrites compared with regular branches.

Surprisingly, the presence itself of the fringe membrane never made any difference in trunk voltage and/or spike initiation and propagation thresholds, between the regular (tapering) and no taper configurations (Fig. 3C,D, orange and red traces). In other words, the amounts of input necessary to trigger dendritic or somatic spikes was not affected by the size of the tapering membrane (regular vs no taper) but by its local redistribution (husky vs lanky).

Thus, limited alterations in branch-point morphology allow for substantial bidirectional changes in the synaptic thresholds necessary to generate a local d-spike and to propagate it to the soma (Fig. 3E). Such a modest structural rearrangement could result from the local shift of an amount of membrane corresponding to the average measured fringe tapering surface, which is well within the observed variability in bifurcation morphology. This mechanism might allow neurons to greatly increase the coupling of synapses to the trunk or else to isolate a branch from the rest of the neuron.

Regulation of dendritic and somatic spiking by branch-point morphology in relation to I_KA

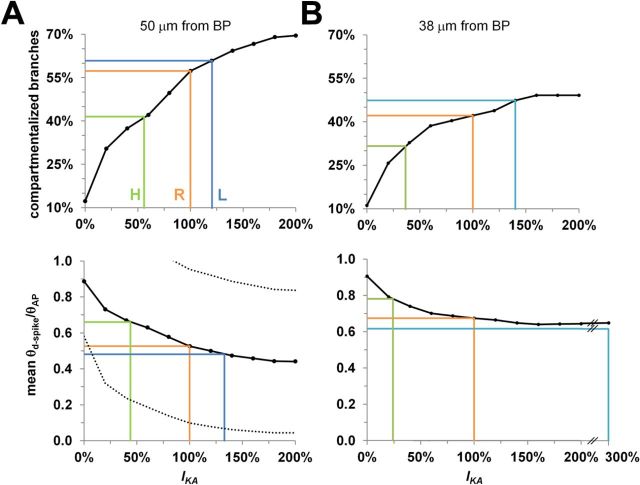
The A-type K⁺ conductance (I_KA) is strongly regulated in the oblique dendrites of CA1 pyramidal neurons (Shah et al., 2010; Sun et al., 2011), providing a powerful mechanism to compartmentalize the oblique branches (Frick et al., 2003; Migliore et al., 2005). We compared the influence of structural plasticity at branch points on dendritic and somatic spike thresholds with the effect of I_KA blockage or overexpression. I_KA was regulated (0–200%) in all the branches, and synaptic stimulation was placed at 50 μm from the branch point. Additionally, we looked at the number of compartmentalized branches and at the average amount of compartmentalization for the regular, the husky, and the lanky cases, to see how they compared with I_KA modulation. In control conditions (100% I_KA, regular branches), the proportion of branches displaying lower thresholds for initiation than for propagation of a local spike (θ_d-spike < θ_AP) depends on the distance from the bifurcation (Fig. 1H). With a stimulus 50 μm from the branch point, ∼55% of the oblique dendrites were compartmentalized, and 45% were fully coupled with the trunk. In this condition, the average threshold ratio for d-spikes and somatic APs in the compartmentalized branches was ∼0.5. Completely blocking I_KA reduced the fraction of compartmentalized branches to 12%, and these had a threshold ratio close to 0.9. In contrast, doubling I_KA increased the fraction of compartmentalized branches to ∼70%, and these had a threshold ratio close to 0.44 (Fig. 4A). A regular-to-husky morphological transformation corresponded functionally to almost halving the distribution of dendritic I_KA, whereas going from regular to lanky was equivalent to a ∼20% I_KA increase (Fig. 4A). Additionally, the effect of branch-point transformation was even more substantial for closer input. At 38 μm from the branch point, even a 300% increase in I_KA was insufficient to match a regular-to-lanky change in average dendritic compartmentalization (Fig. 4B).

Figure 4.

Functional effects of I_KA relative to variation in branch-point morphology. A, Top, Fraction of compartmentalized branches as a function of I_KA activation in the regular case, with synapses distributed at 50 μm from the branch point (BP). The orange line indicates the compartmentalized fraction with baseline I_KA activation. The horizontal green and blue lines mark the compartmentalized fraction in the same conditions for husky (H) and lanky (L) configurations, respectively. The vertical green and blue lines denote the levels of I_KA activation that yield the same compartmentalization in the regular (R) case. Bottom, Average amount of compartmentalization for uncoupled branches (θ_d-spike/θ_AP < 1) as a function of I_KA. The green and blue lines indicate the level of I_KA activation in the regular case that yields the same compartmentalization amount as baseline I_KA in the husky and lanky configurations, respectively, as in A. Dotted lines denote SD of compartmentalization amounts. B, Same as A, but synaptic distance from the branch point in the regular case was 38 μm instead of 50 μm.

Therefore, the effect of branch-point morphological plasticity is of the same order of magnitude as that caused by alterations of active conductances. These results raise intriguing alternative hypotheses on the possible functional contribution of these two distinct mechanisms (I_KA and branch-point morphology) in controlling branch compartmentalization. Specifically, I_KA regulation and structural plasticity might compensate each other homeostatically, they might operate independently, or their actions might be coordinated synergistically.

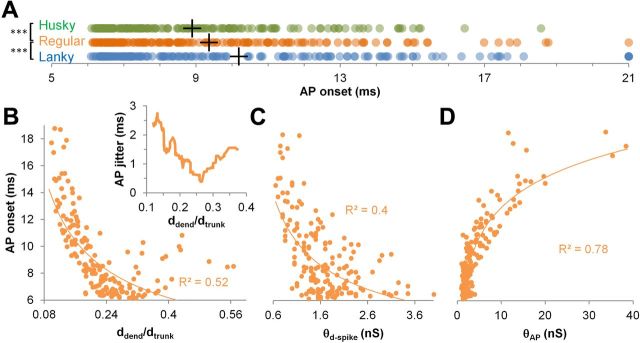
Branch-point morphology affects delay and jitter of AP onset

The delay between dendritic stimuli and AP onset may affect the phase of signal relative to hippocampal rhythms. Thus, we investigated whether the observed morphological diversity of oblique branches could influence AP onset in response to threshold stimulation. For regular branches, AP onset ranged over 3.5-fold, with a jitter (SD) approximately equivalent to one-third of the average value (9.4 ± 3.1 ms; Fig. 5A). Transforming branch points into husky and lanky morphologies reduced and increased AP onset, respectively. On average, APs in lanky dendrites were 15% slower than in husky (10.2 vs 8.9 ms). The differences in AP onset between regular, husky, and lanky dendrites were all highly significant (p < 10⁻⁵, one-tailed paired t test). Additionally, APs generated by lanky dendrites were on average 60% more jittery (4 ms) than by husky branches (2.6 ms).

Figure 5.

Temporal consequences of branch-point morphology variation. A, AP delay onset for husky (H, green), regular (R, orange), and lanky (L, blue) dendrites (+ symbols are averages; ***p < 10⁻⁵, 1-tailed paired t test). B, Effects of d_dend/d_trunk diameter ratio on onset and jitter (inset) in regular branches. AP onset jitter was calculated as the AP onset SD over a sliding window of 20 branches. Line in the main figure is a power fit. C, Power relationships between d-spike threshold and AP onset in regular branches. D, Logarithmic relationship between AP threshold and onset in regular branches. BP, Branch point.

The d_dend/d_trunk diameter ratio was the most relevant morphological feature affecting AP onset (Fig. 5B). Larger diameter ratios, corresponding to smaller mismatch between oblique and trunk, resulted in earlier onset. Interestingly, diameter ratios close to average (0.265) minimized AP onset jitter, whereas larger and smaller values increased jitter by several fold, from 0.38 up to 2.75 ms (Fig. 5B, inset). AP onset had a negative correlation with the d-spike threshold (Fig. 5C) and a strongly significant positive correlation with the AP threshold (Fig. 5D).

Functional effects of branch-point morphology on an anatomically and biophysically realistic model

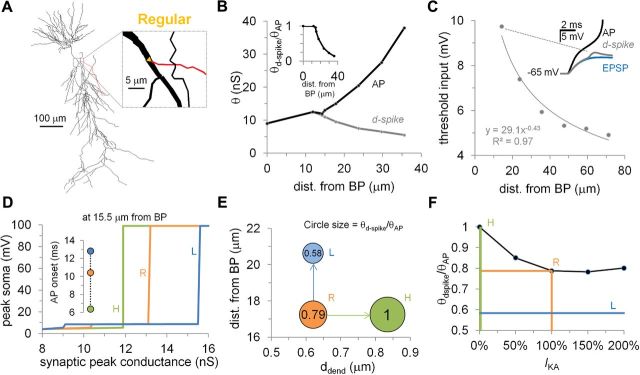
The reduced model does not faithfully reproduce capacitive load of the soma and axon initial segment, as well as of the complex dendritic arbors of hippocampal neurons. To test whether these factors might affect the conclusions of this study, we replicated our most significant simulations using an existing anatomically and biophysically realistic model of a hippocampal CA1 pyramidal neuron (Ferrante et al., 2008; ModelDB accession number 119283). Specifically, we followed the same simulation protocol as in the reduced model, performing somatic recording while stimulating a specific proximal oblique dendrite (Fig. 6A). Compared with the reduced model, the selected branch demonstrated an even greater level of compartmentalization, which started at 15 μm from the branch point and at 35 μm reached a θ_d-spike/θ_AP threshold ratio of 0.15 (Fig. 6B). Similar to the experiments and the trunk recordings in the reduced model, the amplitude of the somatic signal decayed exponentially with the synaptic distance from the branch point (Fig. 6C). Increasing the power of the stimulation (synaptic strength) evoked, in order, EPSPs, d-spikes, and APs (Fig. 6C, inset).

Figure 6.

Effects of branch-point morphology on a realistic neuronal model. A, Reconstructed soma and dendritic arborizations of a hippocampal CA1 pyramidal neuron (Ferrante et al., 2008; ModelDB accession number 119283). Inset shows magnification of the branch-point area and the oblique dendrite selected for all simulations. The branch-point morphological parameters were set to the averages of the experimentally recorded values (Fig. 1B). B, Stimulation threshold (θ) to generate a local dendritic spike (d-spike, gray line) or a somatic AP (black line) as a function of the distance of the input from the branch point (BP; compare with Fig. 1C). Inset depicts θ_d-spike/θ_AP threshold ratio as a function of the distance of the input from the branch point (compare with Fig. 1H). C, Exponential decay of the computed threshold input as a function of the distance of the synaptic input from the branch point (compare with Fig. 2C,D). Inset, Gray voltage trace shows the d-spike for the specific computed threshold input; AP (black line) and voltage signatures for the same synaptic cluster are also shown (compare with Fig. 2A). D, Somatic peak voltage as a function of synaptic peak conductance shows the compartmentalization associated with husky (H, green), regular (R, orange), and lanky (L, green) branch points (compare with Fig. 3D). Inset, AP onset time for the three morphological configurations: husky, regular, and lanky. E, Symbol size represents θ_d-spike/θ_AP threshold ratio as a function of d_dend and synaptic distance from the branch point for the husky, regular, and lanky branch shapes (compare with Figs. 1F, 7A). F, Amount of compartmentalization (θ_d-spike/θ_AP < 1) as a function of I_KA activation. The orange line indicates the regular branch compartmentalization with baseline I_KA activation. The green and blue lines mark the branch compartmentalization corresponding to the husky and lanky configurations, respectively (compare with Fig. 4C,D).

Next we tested the functional effects of branch-point transformations to husky or lanky morphologies for a synapse located in a region of the selected dendrite (15.5 μm) that was moderately compartmentalized (θ_d-spike/θ_AP = 0.79) in the regular (original) morphology. The husky transformation made these synapses fully coupled with the soma (θ_d-spike/θ_AP = 1), whereas the lanky configuration increased compartmentalization by 36% (θ_d-spike/θ_AP = 0.58) compared with the regular branch (Fig. 6D,E). As in the reduced model, lanky dendrites had strongly delayed AP onsets with respect to husky dendrites (∼13 vs ∼6.5 ms, respectively; Fig. 6D, inset).

Last, as in the reduced model, we modulated the I_KA distribution from 0 to 200% to compare the resulting effect on dendritic compartmentalization with that obtained by morphological change at the branch point. Completely blocking I_KA (0%) made the synapses fully coupled with the rest of the neuron, having the same functional effect of a husky branch. Conversely, for this specific synaptic location, there was no increase in I_KA that could reproduce the functional effect of a lanky dendrite (θ_d-spike/θ_AP = 0.58). The maximum compartmentalization (θ_d-spike/θ_AP = 0.78) was obtained by increasing I_KA to 150%, which remained very close to the regular case (θ_d-spike/θ_AP = 0.79).

Together, these results suggest that the somatic capacitance and dendritic arborization of real neurons may amplify the effects predicted by the reduced model.

Discussion

To the best of our knowledge, this report provides the first quantification of the considerable morphological diversity of dendritic bifurcations between the apical trunk and the oblique branches in CA1 pyramidal neurons. The key result of this study is that such diversity may significantly affect the coupling of synaptic inputs to somatic output. Specifically, computational simulations prove that the observed variability of branch morphology yields a broad range of functional compartmentalization. This phenomenology can be summarized in a surface plot (Fig. 7A) in which the oblique diameter and the distance of the stimulus from the bifurcation are the independent variables and the local and propagated spike threshold(s) are the dependent variable(s). Relevant experiments (Fig. 2) indicate that the biophysical parameters of the model are adequate to reproduce empirical electrophysiological recordings.

Figure 7.

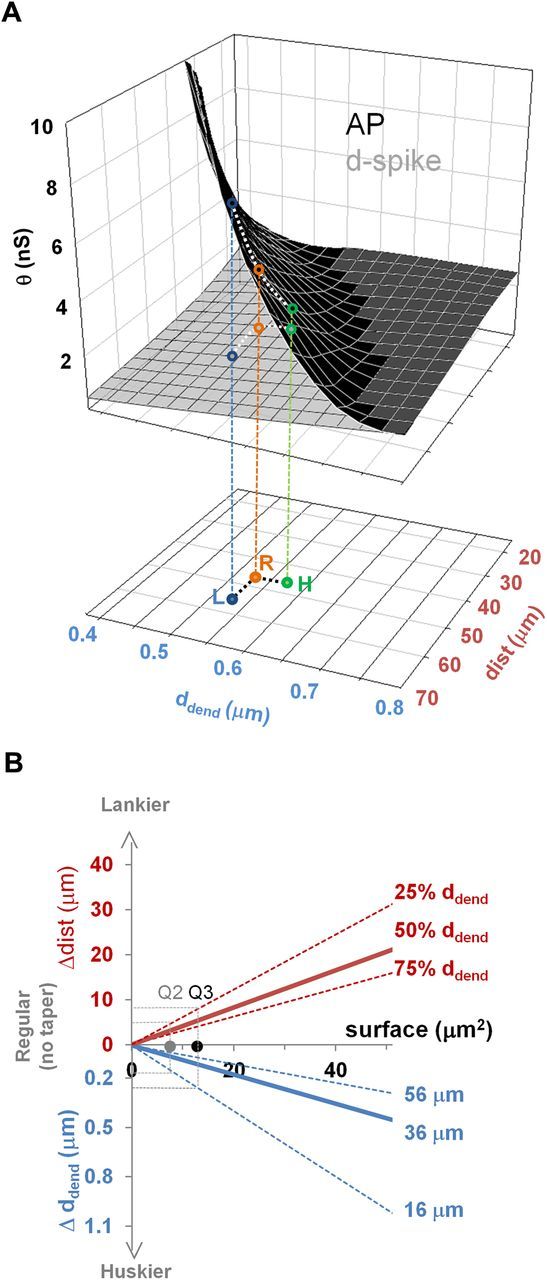
Functional consequences of changing branch-point morphology. A, Top, Threshold separation (θ_d-spike, gray; θ_AP, black), as a function of the oblique branch diameter and of the distance of the synaptic input from the branch point; the white dotted lines indicate the threshold change with branch-point morphology. Bottom, Representative parameters for a regular branch (R, orange dot) and the corresponding husky (H, green dot) and lanky (L, blue dot) branches obtained by reconfiguring the fringe taper membrane. The vertical projections (orange, blue, and green lines) indicate the corresponding threshold separation effects. B, Top (red), Amount of elongation obtained by reconfiguring the fringe membrane from regular to lanky as a function of the taper surface area at the first, median, and third quartiles of oblique branch diameter. Bottom (blue), Amount of thickening obtained by reconfiguring the fringe membrane from regular to husky as a function of the branch-point surface for a three stimulation distances from the bifurcation. Gray and black dots and dotted lines denote the effects for the median (Q2) and third (Q3) quartiles of the measured surface distribution, respectively.

Fringe tapering membrane as a currency for compartmentalization

Available evidence from time-lapse imaging indicates that oblique branches of CA1 pyramidal neurons can change their shape and size in a matter of minutes under normal conditions. Thus, we hypothesized that branch-point morphology could dynamically adapt over a husky–lanky continuum (Smith and Jahr, 1992; Park et al., 2006). Such transitions effectively constitute movements along the independent axes of the above-described surface plot, reflected by functional consequences along the dependent axis. Within realistic parameter ranges (measured oblique diameter of 0.33–0.75 μm, reasonable path distance of the stimulus from the bifurcation of 0–70 μm), the local spiking threshold ranges from ∼0.1 to ∼10 nS. The low and high ends of this span approximately correspond to activating a single excitatory synapse or (quasi-synchronously) all the excitatory synapses on the oblique branch.

This mechanism has been neglected in experiments so far, but, surprisingly, our model predicts that a local rearrangement of the fringe tapering membrane can switch virtually any oblique branch between fully coupled (θ_d-spike = θ_AP) and strongly compartmentalized (θ_d-spike ≪ θ_AP). The “typical” branch, corresponding to the average experimental measurements (Fig. 7A, red dot), is moderately compartmentalized in the regular tapering shape (θ_AP ≈ 2 × θ_d-spike for stimuli at 45 μm from the branch point). Morphing the fringe membrane to a lanky shape (blue dot) halves the d-spike threshold and doubles the AP threshold (higher compartmentalization). Conversely, changing to a husky shape (green dot) causes the two thresholds to converge to closer values (higher coupling). This suggests that the bifurcation tapering membrane can be a quintessential determinant of local and global excitability.

To generalize and quantify this conclusion, it is useful to compute the extent of the functionally relevant alterations (path distance and dendritic diameter) per unit of rearranged fringe membrane (Fig. 7B). Clearly, it takes more membrane area to elongate thicker than thinner branches. Similarly, more membrane area is required to thicken the dendritic path to distal compared with proximal stimulus locations. Notably, the median measured fringe membrane area is sufficient to yield dramatic changes across the bottom, median, and top quartiles of oblique dendritic diameters and through a wide span of distances along the branch path. Thus, the fringe tapering membrane at branch point could act as currency to bidirectionally exchange for synaptic compartmentalization or coupling.

The lower threshold for dendritic spikes would enable compartmentalized branches to express higher local activity without affecting overall synaptic integration and signal processing in the rest of the neuron. Periods of increased local firing may facilitate the rapid adjustment of synaptic conductances and other activity-dependent plastic processes.

Branch-point morphology and other determinants of the input/output relationship

Our computational simulations predict that minor structural differences at the branch point can produce major alterations in the integrative properties of oblique dendrites. Independent of whether such structural differences might dynamically result from experience-dependent plasticity, they are well within the observed range of natural variability. The ensuing functional changes in local and propagated spiking thresholds are comparable in magnitude with those produced by modulation of active properties, such as I_KA. Thus, morphological differences between branches might reverse or accentuate the local regulation of voltage-gated conductances. The recently demonstrated selective exocytosis of post-Golgi cargo at branch points (Cui-Wang et al., 2012) may provide the mechanism for continuous control over membrane addition. In CA1 pyramidal neurons, I_KA has recently been involved in synaptic scaling (Ito and Schuman, 2009), and Kv1.1 and Kv1.4 knockdown ablate LTP (Meiri et al., 1998). Branch-point morphology thus adds a third factor in this interaction. Because branch-point morphological plasticity can affect both local and global spike thresholds (Fig. 1) and AP timing (Fig. 5), we suggest that this mechanism might also play a strong role in modulating spike-timing-dependent plasticity. Additionally, although I_KA is specifically involved in compartmentalization, several other channels affect signal propagation, including I_Ca and I_h (Magee, 1998; Cai et al., 2004; Migliore et al., 2004; Johnston and Narayanan, 2008).

In neocortical neurons, the interrelation among dendritic cross-sections at branch points may facilitate spreading depolarization (Kubota et al., 2011), and the ratio of proximal over distal oblique branches affects the coupling between somatic and dendritic spikes (Schaefer et al., 2003). It is unknown whether similar considerations apply to CA1 pyramidal neurons and whether the findings of the present study are applicable to other neuron types. How branch-point morphology affects the spatiotemporal integration of multiple synaptic signals at different input frequencies also remains to be determined. We have shown that, at threshold, husky dendrites were on average faster and more precise (60% less jittery) than lanky branches. These results suggest that small branch-point morphological transformations might also affect the synchrony of synaptic input from different branches. It is becoming clear that the branch propagation of EPSPs and d-spikes depends on the interplay between dendritic morphology, synaptic dynamics, and membrane biophysics.