Protracted Postnatal Development of Sparse, Specific Dentate Granule Cell Activation in the Mouse Hippocampus

Abstract

The dentate gyrus (DG) is a critical entry point regulating function of the hippocampus. Integral to this role are the sparse, selective activation characteristics of the principal cells of the DG, dentate granule cells (DGCs). This sparse activation is important both in cognitive processing and in regulation of pathological activity in disease states. Using a novel, combined dynamic imaging approach capable of resolving sequentially both synaptic potentials and action potential firing in large populations of DGCs, we characterized the postnatal development of firing properties of DG neurons in response to afferent activation in mouse hippocampal-entorhinal cortical slices. During postnatal development, there was a protracted, progressive sparsification of responses, accompanied by increased temporal precision of activation. Both of these phenomena were primarily mediated by changes in local circuit inhibition, and not by alterations in afferent innervation of DGCs because GABA_A antagonists normalized developmental differences. There was significant θ and γ frequency-dependent synaptic recruitment of DGC activation in adult, but not developing, animals. Finally, we found that the decision to fire or not fire by individual DGCs was robust and repeatable at all stages of development. The protracted postnatal development of sparse, selective firing properties, increased temporal precision and frequency dependence of activation, and the fidelity with which the decision to fire is made are all fundamental circuit determinants of DGC excitation, critical in both normal and pathological function of the DG.

Introduction

The dentate gyrus (DG) constitutes the first component of the canonical trisynaptic circuit in the hippocampus and functions as a key regulator of cortical input to the hippocampus. Its primary input, the perforant pathway (PP), arises from neurons in layer II of the entorhinal cortex (EC) (Steward and Scoville, 1976; Amaral and Cowan, 1980). EC innervation of the principal cells of the DG (DGCs) is promiscuous, exhibiting massive convergence and divergence. Individual EC neurons innervate large areas of the DG (Tamamaki and Nojyo, 1993), and small regions of the DG receive input from widespread regions of the EC (van Groen et al., 2003). In recording studies in vivo, DGCs exhibit spatially selective firing in extremely small subpopulations of neurons (Jung and McNaughton, 1993; Leutgeb et al., 2007; Neunuebel and Knierim, 2012). Therefore, based on the contrast with their broad afferent innervation pattern, it is likely that the sparse, specific firing characteristics of DGCs emerge from local factors within the DG.

These include intrinsic biophysical properties making these neurons extremely reluctant to fire, particularly in bursts, and the powerful feedforward, feedback, and tonic inhibition evident within the DG circuit originating from multiple interneuron populations (Coulter and Carlson, 2007; for review, see Acsady and Kali, 2007). This circuitry confers sparse firing characteristics onto DGCs and also endows the DG with the capability of preventing relay of pathological, synchronous cortical activity into the hippocampus, regulating seizure activity in states, such as epilepsy. This latter phenomenon has been termed dentate gating (Heinemann et al., 1992; Lothman et al., 1992). The majority of studies examining DG activation patterns have been conducted using unit recordings in vivo, which cannot resolve circuit determinants of firing behavior. Little attention has been focused on either the development of the ensemble neuronal firing characteristics or circuit gating behavior within the DG during early postnatal maturation.

In the present study, we investigated how properties of DG circuit gating function and DGC activation behavior varied during postnatal development by using a novel strategy involving combined sequential functional imaging of synaptic potentials and cellular activation patterns using voltage-sensitive dye (VSDI) and multicellular calcium imaging (MCI), respectively. We found that DGC action potential (AP) firing selectivity increased as postnatal development progressed, achieving adult levels of sparse activation by 30 d postnatal (P30). This was accompanied by both an increase in the temporal precision of activation and emergence of DG gating behavior. The developmental delays in achieving adult levels of sparse AP firing and temporal precision of responses were normalized between various age groups by perfusion with the GABA_A antagonist, picrotoxin, suggesting that emergence of these developmentally dependent phenomena were primarily the result of changes in local circuit inhibition. We also found that sparse activation of DGC firing was precise, with the same small set of cells responding similarly to multiple stimuli. The delayed postnatal development of DG gating, sparse activation behavior of DGCs, and temporal precision of activation have significant implications for both normal and pathological function of the hippocampus.

Materials and Methods

Animals and tissue preparation.

Brains of male C57BL/6 mice (P12-P60) were removed and blocked in ice cold artificial cerebrospinal fluid (ACSF) with NaCl replaced with an equal osmolarity concentration of sucrose ACSF composed of the following (in mm): 87 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 75 sucrose, 10 glucose, 26 NaHCO₃, 1 CaCl₂-2H₂O, and 2 MgSO₄. Horizontal hippocampal entorhinal cortical slices (350 μm) were cut with a vibrating tissue slicer (zero z Vibratome 3000) and submerged in ice-cold sucrose ACSF. Slices were then incubated in a calcium indicator loading chamber and bubbled with 95% O₂/5% CO₂ at 37°C. The calcium indicator loading solution was composed of either 4 μl of 0.5% Fura-2-AM (for multiphoton imaging, Invitrogen) or 4 μl of 0.5% Oregon Green BAPTA-1 AM (for confocal imaging, Invitrogen), 4 μl of 20% pluronic acid (Invitrogen) in DMSO and 4 μl of 15% Cremophor (EL) (Invitrogen) in DMSO and 4 ml of oxygenated ACSF (composition in mm: 125 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 10 glucose, 26 NaHCO₃, 2 CaCl₂-2H₂O, 1 MgSO₄). During loading, slices were maintained at 37°C and continuously exposed to humidified 95% O₂/5% CO₂ to maintain osmolarity, oxygen, and pH levels. Slices were loaded for 35 min and then washed and incubated in fresh oxygenated ACSF at room temperature for at least 45 min to allow AM-ester dyes to cleave. (Takano et al., 2012). Slices were then stored in oxygenated ACSF for up to 6 h without deterioration of response.

Immediately before transferring slices to the microscope stage for imaging, Fura-2-AM-loaded slices were further stained in an oxygenated submersion chamber containing 0.0125 mg/ml of the VSD di-3-ANEPPDHQ (Invitrogen) in ACSF for 20 min (Carlson and Coulter, 2008). After staining, slices were placed in a 36°C heated submersion recording chamber.

Microelectrode stimulation and recording.

For stimulation of the granule cell layer, a bipolar tungsten-stimulating electrode was placed adjacent to the hippocampal fissure between the suprapyramidal blade and apex of the granule cell layer (defined as the midpoint between the suprapyramidal and infrapyramidal blades; see Fig. 2A). For extracellular recording, a tungsten recording electrode was positioned in the dentate molecular layer of the suprapyramidal or infrapyramidal blades. Recording electrodes were always >500 μm away from the stimulating electrode and outside the imaging field to avoid electrical artifacts and electromagnetic noise from the excitation laser.

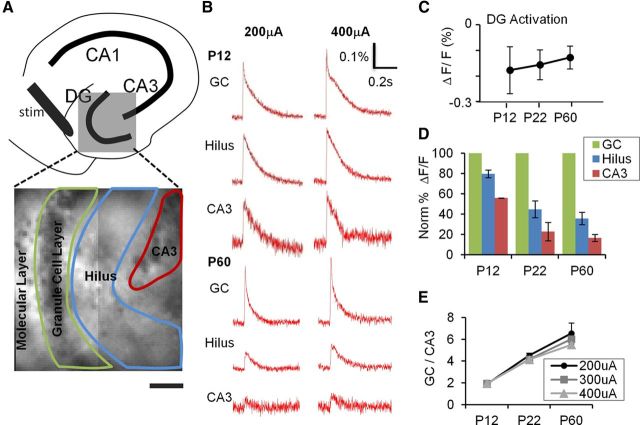
Figure 2.

Postnatal development of DG gating behavior. A, Top, A schematic illustration depicting subregions of the hippocampus. Bottom, The DG (gray box) is expanded in a VSD image with an overlay of the ROI delineating subregions used to measure DG responses elicited by PP stimulation. B, VSDI time-resolved fluorescence plots for the subregions depicted in A for P12 (top) and P60 (bottom) animals. PP stimulation elicits comparable depolarizations in the GC, hilus, and CA3 at P12, but little depolarization of hilus and CA3 at P60, despite robust responses in GC. C, DG response amplitude (ΔF/F₀) is comparable at all developmental ages (elicited by a 400 μA PP stimulus). D, P12, P22, and P60 mice (n = 8 slices in 3 animals, n = 7 of 2 animals, and n = 6 of 2 animals, respectively), show progressively less propagation of synaptic responses through GC (green) to hilus (blue) and CA3 (red). All data points are normalized to GC layer response at 400 μA, which is equivalent across groups (see C). E, Plots of DG gating function, the ratio of GC to CA3 activation intensity, depict the significant increase in the DG gating property as postnatal development progresses, at several stimulus intensities (200 μA (●), 300 μA (■), and 400 μA (▴). p < 0.001 for the animal age factor affecting gating (two-way ANOVA). p = 0.16 for stimulus intensity affecting gating (two-way ANOVA).

Stimulus intensity standardization.

Stimulus intensity was standardized across developmental stages using field EPSP slope measurements. This was done because fEPSP and VSDI EPSP experiments record different information. fEPSP recordings sample current flux through the extracellular space, and, in addition to changing amplitude with increasing intensity stimulation, will vary in slope, amplitude, and sign depending on the location of the recording site relative to the current sinks and sources created by the synaptic response. VSDI EPSP experiments record transmembrane voltage, which may vary slightly depending on the ROI sampled relative to the synaptic input site resulting from intrinsic cell properties, but otherwise are insensitive to sources and sinks generating current flux in the extracellular space. However, peak voltage measures of EPSPs will begin to flatten at higher stimulus intensities because of driving force changes during larger responses. This will not occur in fEPSP measurements. In addition, evoked synaptic responses are compound events, comprised of both EPSPs and IPSPs. IPSPs tend to activate at longer latencies and to be recruited more at higher stimulus amplitudes because (1) they are polysynaptic and (2) they are mediated by channels with slower kinetics compared with EPSPs. Measuring fEPSP slope is likely to enhance contributions of EPSPs by sampling earlier during the synaptic event compared with recording peak depolarizing PSP responses in VSDI recordings. This facilitates stimulus standardization.

Slice viability was verified using local field potential recordings. Stimulating electrode placement was determined by ensuring that the stimulation site elicited similar responses in both suprapyramidal and infrapyramidal blades. Local field potential recordings were monitored online during the optical recordings to verify the ongoing viability of slices. Local field potentials were recorded using a Microelectrode AC Amplifier (Model 1800, AM Systems). Electrical data were collected using Clampex 9.0 (Molecular Devices) software.

Juxtacellular loose-patch recordings.

Juxtacellular loose-patch current-clamp recordings were conducted in Fura-loaded slices to explore the relationship between AP firing and calcium transients in DGCs. Patch electrodes (5–7 MΩ resistance, filled with ACSF) were positioned juxtacellularly to DGCs of interest, and negative pressure was applied to acquire low resistance seals of >50 MΩ. Seal quality was monitored during recordings. Current-clamp recordings were made using a Multiclamp 700B amplifier (Molecular Devices) and sampled at 10 kHz with a Digidata 1332A analog-digital converter (Molecular Devices). Electrical data were collected using Clampex 9.0 (Molecular Devices). Data were analyzed and stimulation artifacts were removed in Clampfit 10 (Molecular Devices).

VSDI and MCI.

An integrated multiphoton/epifluorescence microscopy system enabled the use of two sequential, distinct imaging techniques combined with simultaneous electrical recording in the same slice. An Olympus BX-61 fixed stage microscope with a 20× (XLUMPlanFl, NA = 0.95) water immersion objective (Olympus) was used in this study. This magnification allowed individual cells to be readily resolved during MCI while still preserving the ability to visualize network activation and signal propagation with VSDI techniques.

VSD fluorescence signals were captured with a high-speed 80 × 80 pixel CCD camera (NeuroCCD-SM, Redshirt Imaging) at a 1000 Hz frame rate. We used a collimated light-emitting-diode emitting with a peak intensity at 505 nm (LEDC9, ThorLabs) to excite the VSD (di-3-ANEPPDHQ). VSDI was achieved by using a Chroma U-N41002 (Chroma Technology) filter cube, comprised of an excitation filter (535 nm/50 nm), an emission filter (610 nm/70 nm), and a dichroic mirror (565 nm-LP). All filter widths are given as the full width at half-maximum (Fig. 1). Electrical stimulation and onset of imaging trials were controlled by an electrical trigger with a delay of 1 s before stimuli to obtain a baseline for imaging analysis. Repeated measurements of 4 trials were taken, and trials were averaged to increase the signal-to-noise ratio.

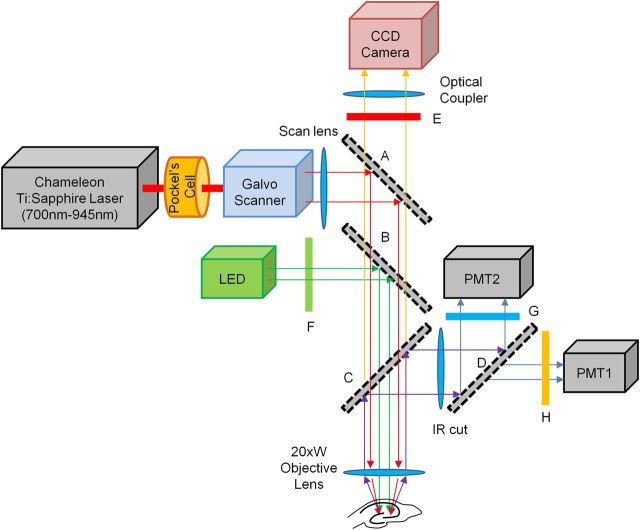
Figure 1.

System diagram for the sequential VSD and calcium imaging microscope. A Prairie Technologies Ultima Multi-Photon Microscopy system mounted on an Olympus BX-61 microscope equipped with a sliding mirror (A) and a filter wheel, by which either a 565 nm LP (long-pass) filter (B) or a 660 nm LP filter (C) can be selected. For VSD imaging, the mirror (A) is removed and the LP filter (B) was inserted. Excitation light (505 nm center wavelength with 30 nm full width at half-maximum) from a collimated LED (LEDC9, Thorlab) was guided through a 535 nm/50 nm (center wavelength/width) BP (band-pass) filter (F), reflected by a LP filter (B) and focused on the specimen by an objective lens (Olympus XLUMPlanFl, 20×, NA = 0.95). Fluorescence emission was collected by the same objective lens and guided to the CCD camera (NeuroCCD-SM, Redshirt Imaging) through the LP filter (B), a 610 nm/70 nm BP filter (E), and an optical coupler. For calcium imaging, the mirror (A) and the LP filter (C) were selected and 780 nm excitation light from the Ti:Sapphire laser (Chameleon, Coherent) was guided by the mirror (A), through the LP filter (C) and focused on the specimen. Fluorescence emission was reflected by the LP filter (C) and separated into two channels by a 495 nm LP filter (D). A 460 nm/50 nm BP filter (G) and 607/45 nm BP filter (H) were placed in front of each PMT detector. PMT 2 detected the emission signals from the calcium indicator.

For MCI, Fura-2-AM was excited using a Prairie Technology Ultima Multiphoton Imaging System attached to the Olympus BX-61 fixed-stage microscope. The setup included external nondescanned dual-channel reflection/fluorescence detectors and a diode-pumped, wideband mode-locked Ti:Sapphire femtosecond laser (720–950 nm, <140 fs; 90 MHz, Chameleon, Coherent; Fig. 1). Fura-2 (MCI) and di-3-ANEPPDHQ (VSDI) were selected based on the minimal overlap of emission and excitation spectra to allow adequate separation of signals in each imaging modality (Table 1). For the excitation/emission for the calcium imaging light path, emitted fluorescence was collected with the same objective lens, reflected by a dichroic mirror (660 nm LP) and passed through an IR cutoff filter (650 nm SP) (Chroma Technology). An additional dichroic filter (495 nm LP) and bandpass filter (460 nm/50 nm) were used to further separate VSD and calcium indicator fluorescence (Fig. 1). The optical data were then passed through a preamplifier and a 12-bit analog to digital converter. Images were acquired at a frame rate of ∼10 Hz. Stimuli were repeated four times.

Table 1.

Specifications for VSD and calcium imaging probes

Modality	Dye	Ex535 1P	Ex780 2P	Em460 (% max)	Em610 (% max)
Ca2+ imaging	Fura-2	0% max at 340 nm	Ca2+-free 8.1 GM	98	0
			Ca2+-bound 0.3 GM
VSD imaging	di-3-ANEPPDHQ	50% max at 510 nm	NA/4 GM	2	95

In VSD imaging, 535 nm light, the center wavelength of the excitation band-pass (BP) filter (F in Fig. 1), effectively excites di-3-ANEPPDHQ in the single photon (1P) excitation process, but not Fura-2. In calcium imaging, two-photon (2P) absorption cross-section at 780 nm for Fura-2 Ca²⁺-free form (8.1 GM) is much larger than the Ca²⁺-bound form (0.3 GM) (Wokosin et al., 2004), causing fluorescence signal to extinguish during neuronal activity (e.g., calcium influx through voltage-gated calcium ion channels). The fluorescence traces for calcium imaging in the subsequent figures were all inverted for visual intuition. For detecting Fura-2 signal, a 460 nm band-pass filter (G in Fig. 1) was chosen based on the peak Fura-2 emission spectra. The 2-photon absorption cross-section for di-3-ANEPPDHQ could not be found, but it was reported to be ∼4 GM for a similar molecule, di-8-ANESPPDHQ (Fisher et al., 2008). This indicates that the 780 nm light could excite di-3-ANEPPDHQ by the 2-photon excitation process, but emission ∼460 nm is very weak, and the majority of emission from VSD dye channel can be blocked by the filters (D and G in Fig. 1).

NA, Not applicable.

Confocal MCI.

For confocal MCI, Oregon Green BAPTA-AM-loaded slices were imaged using a Live Scan Swept Field Confocal Microscope (Nikon Instruments) equipped with an Ar/Kr ion laser (Inova 70C, Coherent, excitation 488 nm) operated with NIS-elements software (Nikon). Images were acquired with a water immersion 40× lens (NA = 0.8) and a Cascade 128+ CCD camera (Photometrics). This system allowed capture of images at 320 Hz with full frame resolution (128 × 128 pixels).

Data analysis.

VSDI data were analyzed using custom written algorithms in IGOR 6.0 (Wavemetrics). Reference frames were calculated as the average of 60 ms before stimulation. All data points were normalized using in-house algorithms to reflect the change in fluorescence compared with baseline (ΔF/F₀) (Ang et al., 2006). Local VSD signals were calculated by integrating ROI encompassing the granule cell layer (GC), the hilus, and the molecular layer (Fig. 2A).

For MCI, the field of view at 20× magnification allowed us to capture 60–100 Fura-loaded cells per image, with multiple regions studied per slice (see Fig. 4A). Manual construction of small oval or round ROI encompassing the soma was used to analyze activity of these cells. The average intensities of ROI were calculated as a function of time and exported as a text file (Takano et al., 2012). Stimulus-locked peaks were extracted in ROI response traces using a ΔF/F₀ area as threshold to detect events in a given cell ROI, and responses were verified visually. This supervised detection algorithm was used to determine activation of each cell in response to the stimulus. Each cell's activity was observed over time and across conditions using an ID number attached to the ROI delineating each cell. Picrotoxin (PTX), a GABA receptor antagonist, was applied (50 μm) at the end of all experiments to confirm that individual neurons were able to be activated by the afferent stimulus. Cells that were inactive in both control and PTX conditions were excluded from further analysis. The proportion of these inactive cells did not differ between developmental stages (36.7 ± 9.6% and 28.2 ± 5.8% for P12 and P60, respectively, not significantly different, t test). These inactive cells are likely to be a combination of glial cells, and damaged and/or deafferented neurons.

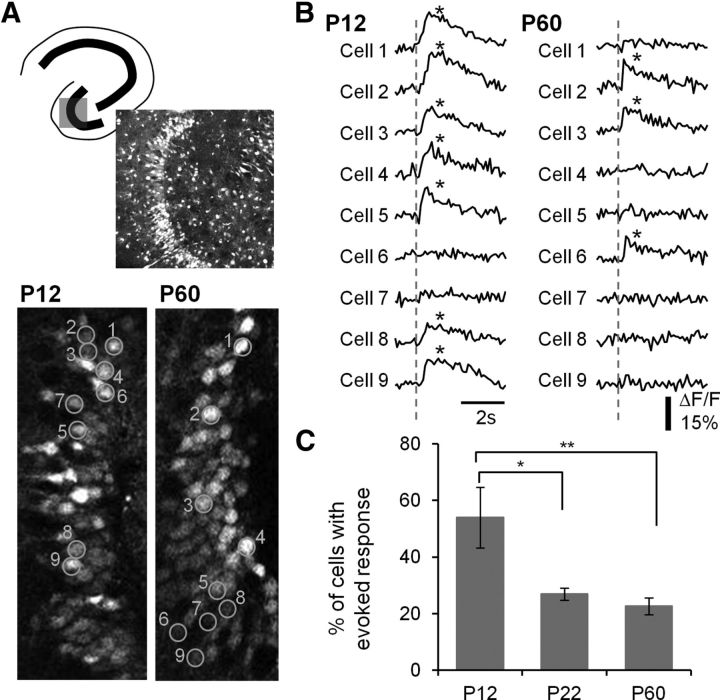
Figure 4.

Decreased DGC activation during postnatal development. A, Top, Schematic of a hippocampal slice depicting the imaged area in the DG and a Fura2-loaded DG of a P12 mouse (370 μm × 370 μm). Bottom, Image of P12 and P60 DGCs, with ROI created on a random sample of cells (orange) (90 μm × 200 μm). Numbers denote cell identification with time-resolved fluorescence responses depicted in B. B, Representative traces of time-resolved calcium imaging responses for the ROI in the P12 and P60 images in A. The dotted line indicates the time when PP stimulation (400 μA) occurred. An asterisk indicates detection of a calcium transient. C, Plot of the percentage DGC activation by PP stimulation for P12, P22, and P60 animals. Note the decrease in cell activation with postnatal development. p < 0.0001 for the animal age factor (ANOVA). *p < 0.05, significant differences between P12 and P22 (Tukey's multiple-comparison post hoc testing). **p < 0.01, significant differences between P12 and P60 groups (Tukey's multiple-comparison post hoc testing). P12: n = 322 PTX-active cells in 10 imaged regions; P22: n = 198 in 10 imaged regions; P60: n = 239 of 12 imaged regions.

Calcium transient onset time estimation.

For confocal recordings of calcium transient onset latencies at higher temporal resolution, we determined that the rising phase of ΔF/F₀ responses was exponential in shape. To estimate onset time, windowed traces were fitted to a 4 parameter exponential equation, where A is amplitude, B is the time constant, C is the onset time, and D is an offset:

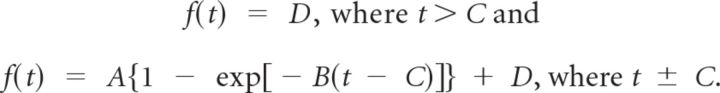We estimated “onset time” from parameter C in the above equation. Transients in which the coefficient of determination, R², was <0.5 were omitted from further analysis.

Statistical analysis.

All values are expressed as mean ± SEM. For comparisons between groups, statistical significance was tested using either a one- or two-way ANOVA, a t test, or for non-normally distributed data, a Mann–Whitney U test. Differences in population distributions were assessed using a Kolmorgorov–Smirnov test. p values <0.05 were considered evidence of statistical significance.

Statistical assessment of DGC activation behavior using a logistic regression model.

We fit two logistic regression models to test the null hypothesis that individual cells within a particular slice respond in a stochastic fashion to repeated stimuli, against the alternative that the probability of response in later stimuli is a function of the cell's earlier propensity to respond to stimulation. A response for each cell was collected for each of four sequential stimuli. We used the data from the final stimulus as the outcome in the model. Under the null hypothesis, the data can be adequately fit using a model that includes terms for each of the slices to adjust for differences in the overall rate of response to stimuli. Under the alternative, the response patterns from the earlier stimuli predict response to the subsequent stimuli. We considered two alternative models, the first where we included a predictor (respond yes or no) for each of Stimuli 1, 2, and 3 and the second where we included only the response to Stimuli 2 and 3. The null and alternative models were identical except for the inclusion of the predictors using the earlier stimuli. We chose the model based on response to Stimuli 2 and 3 using the Akaike Information criteria. The significance of the pattern of response to each of the earlier two stimuli was assessed using a likelihood ratio test and the significance of individual terms in the model assessed using Wald tests. Estimates and SEs of the estimates of the probability of response conditional on the previous response pattern were computed from the model. The logistic regression models were implemented in R2.13.

Results

Development of DG gating function–VSDI recordings

Anatomical studies have demonstrated that the rodent DG and its principal neurons, DGCs, exhibit a protracted, predominantly postnatal development. Within the DG, inhibitory interneurons are already present at birth and, although not mature, possess extensive dendritic and axonal arborizations (Schlessinger et al., 1978; Amaral and Kurz, 1985; Lubbers et al., 1985; Seay-Lowe and Claiborne, 1992). The principal cells of the DG, DGCs, however, are mostly generated in 2–3 weeks after birth and migrate to their appropriate locations (Schlessinger et al., 1978; Rickmann et al., 1987). In a relatively unique phenomenon, DGCs continue to be generated throughout life (Altman and Das, 1965; Eriksson et al., 1998; van Praag et al., 2002). During the perinatal period, afferent innervation by the EC arrives early, before the birth of most DGCs, and, as DGCs are born and mature, EC synapses in the molecular layer of the DG increase up to eightfold by P21 (Fricke and Cowan, 1977; Cowan et al., 1980). During this period of explosive synaptogenesis in the DG, rodent pups are navigating their environment, weaning, and accomplishing rudimentary, hippocampal-dependent cognitive tasks (Schenk, 1985; Ainge and Langston, 2012). Clearly, a critical question is as follows: how does this protracted postnatal development of the anatomic circuit impact the function of the DG, and by extension, the cognitive capabilities of the animal?

To begin investigation of postnatal development of function of the DG, VSDI was used to assess one major role of this circuit: regulation of propagation of EC inputs to downstream structures in the hippocampus, in slices prepared from animals of varying ages. Network activation was measured separately in the granule cell layer (GC), hilus, and area CA3 in each slice using measurement of EC stimulation-evoked synaptic voltage signals in distinct ROI, as shown in Figure 2A. To standardize stimulus intensities, we first measured input/output curves using field EPSP slope measurement in slices prepared from each age group (P12, P22-P30, and P60-P61). Input/output plots overlapped extensively and did not differ statistically, and there was no substantive difference in maximal fEPSP slope for all postnatal ages (two-way ANOVA and one-way ANOVA, respectively, not significant), justifying the use of identical stimulus intensities in all groups in subsequent imaging studies. We next used VSDI to examine how afferent input to the DG (PP stimulation) activated downstream structures in hilus and area CA3 (Fig. 2B–E). In agreement with our field potential recordings, there was no difference in the amplitude of depolarization evident in the GC region between developmental stages, with similar response levels evident at all stimulus intensities in slices prepared from P12, P22-P30, and P60 animals (Fig. 2B,C). However, there were differences in the kinetics of the VSDI responses evident in GC ROI between P12 and P60 stages. P12 responses had a pronounced slowing on the falling phase of the PP-evoked postsynaptic potential relative to P60 responses (Fig. 2B, top). We attribute this extended synaptic response to a combination of the longer membrane time constants in immature granule cells and the depolarizing effects of GABAergic inhibition evident in DGCs at these early developmental stages (Liu et al., 1996; Hollrigel et al., 1998). In support of this hypothesis, application of bumetanide (20 μm), a blocker of the chloride accumulator NKCC1, significantly accelerated the decay kinetics of the VSD-recorded postsynaptic potential in slices prepared from P12 animals (PSP τ_decay = 229 ± 56 and 106 ± 20 ms for control and bumetanide exposed conditions, p = 0.015, paired t test). We have also seen a similar slowing in the decay phase of EC stimulus-induced synaptic depolarizations recorded using VSDI in adult animals during the development of epilepsy, when DGC transmembrane chloride gradients are disrupted (Pathak et al., 2007).

Despite the similarity in GC responses, the magnitude of postsynaptic potentials elicited in both the hilus and area CA3 varied significantly during postnatal development (Fig. 2B,D,E). At the earliest stage of development examined (P12), there were large postsynaptic potentials elicited in both the hilus and area CA3 after PP stimulation, which gradually decreased as development progressed, with smaller postsynaptic potentials elicited in P22-P30 animals and very low levels of responses in these downstream structures in slices prepared from adult animals (P60, Fig. 2B,D). We quantified this network propagation by calculating a ratio of responses in the GC area relative to area CA3 (GC/CA3). For this measure, ratios close to 1 signify little filtering of input, and ratios <1 indicate restriction in propagation of postsynaptic potentials to downstream structures. When this ratio was plotted against developmental stage, a clear trend was evident (p < 0.001), with decreasing responses in downstream structures by PP stimulation as development progressed (Fig. 2E).

MCI of DGC activation to afferent stimulation

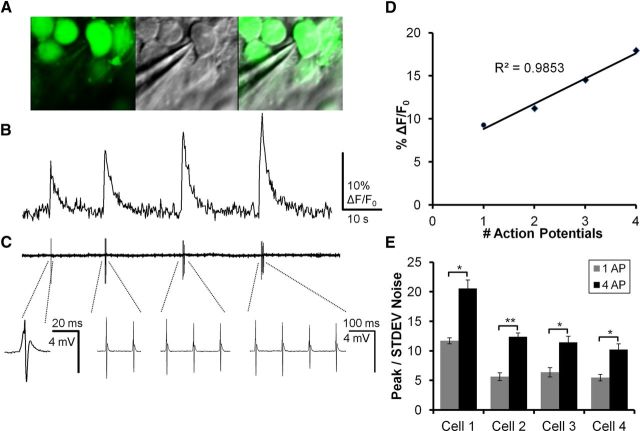
The developmental reduction in downstream responses of hippocampal structures after PP stimulation could be the result of decreases in DGC excitability or an alteration in properties of mossy fiber-induced synaptic responses or targets, with neither of these possibilities being mutually exclusive. VSDI is a useful tool to study the spatiotemporal properties of synaptic potentials in circuits, but, because of requirements for signal averaging necessary to increase signal to noise, it has little utility in resolving cellular action potential activation (for review, see Carlson and Coulter, 2008). To compensate for this limitation in VSDI and allow examination of stimulus-induced AP activation in large numbers of individual DGCs simultaneously, each slice was loaded with both VSD and calcium indicator. This allowed us to combine imaging strategies sequentially in the same slice. Each slice was first imaged using VSDI and epifluorescence microscopy, followed by MCI using 2-photon microscopy. Because of activation of high threshold calcium channels, there is a selective influx of calcium in the neuronal soma linked to AP activation. Accompanying this influx is an alteration in fluorescence signal in calcium indicator-loaded neuronal cell bodies, which can be resolved in MCI studies (Fig. 3). This allows dynamic imaging-based assessment of AP responses in large populations of individual neurons with cellular resolution (Stosiek et al., 2003; Ikegaya et al., 2004; Cossart et al., 2005; Sasaki et al., 2008; Vogelstein et al., 2009; Takano et al., 2012). Juxtacellular loose-patch current-clamp recordings were conducted in Fura-loaded slices to explore the relationship between AP firing and calcium transients in DGCs in response to PP activation. Figure 3A illustrates the juxtacellular placement of a patch electrode next to a Fura 2-AM-labeled DGC for loose-patch recording (specimen records for imaging and patch recording from this cell are illustrated in Fig. 3A,B). Fura fluorescence changes measured from this DGC in response to PP stimulation eliciting 1–4 APS are depicted in Figure 3B. Figure 3C illustrates the simultaneously recorded APs measured from the same cell using loose-patch recording. The relationship between calcium transient amplitude and AP number is analyzed in the graph in Figure 3D, where peak fluorescence response is plotted against the AP number observed in loose-patch recording. These two measures were linearly correlated (Pearson r = 0.9835), supporting the significant link between AP number and calcium transient amplitude. Figure 3E shows the peak calcium fluorescence (ΔF/F₀) responses recorded from 4 different DGCs, in response to activation of 1 and 4 APs, normalized to the SD of baseline signal noise (3 or 4 trials per cell). For single APs, each DGC had a calcium transient peak ≥4-fold higher than the SD of baseline noise (7.9 ± 1.48 SD). This demonstrates that calcium transients elicited by single APs can readily be resolved from baseline noise in all cells. Calcium transients for responses elicited by 4 APs were larger, averaging 13.64 ± 2.35 times noise. For all cells recorded, calcium transient peaks for 4 action potentials were significantly larger than for 1 action potential (Cell 1, p = 0.016; Cell 2, p = 0.0003; Cell 3, p = 0.021; Cell 4, p = 0.010, paired t test). On average, 1 AP generated a calcium transient that was 53% the magnitude of a 4 AP transient. We have previously reported a similar relationship between calcium transient peaks and action potential firing for Oregon Green BAPTA-AM-loaded hippocampal neurons in MCI studies using our fast confocal microscopy system (Takano et al., 2012, their Fig. 1).

Figure 3.

Relationship of AP activation to calcium transient amplitude in DGCs. A, Left, A 2-photon image of DGCs loaded with Fura2-AM in a P60 mouse. Middle, Dodt contrast image showing the electrode used for loose-patch recording of APs. Right, Merge of Fura2-AM and Dodt contrast depicting robust Fura labeling in the recorded DGC. B, Calcium imaging transients elicited by stimulation of the PP with 10 Hz trains containing 1, 2, 3, and 4 pulses. C, Top, Loose-patch recording time-locked with calcium imaging trace in B. AP activation coincides with onset of calcium transients. Stimulus artifacts have been removed digitally. Bottom, Higher temporal resolution traces of loose-patch recordings in which individual APs can be resolved. The single AP to the left is depicted at an expanded time scale, whereas the remainder (2, 3, and 4 APs) are depicted at a compressed time scale. D, Plot of AP activation versus calcium transient magnitude for the responses depicted in B. Calcium transient amplitude correlated with AP firing (Pearson's coefficient r² = 0.9853). E, Ratio of calcium transient amplitude to the SD of baseline noise for 4 patch-recorded DGCs. Every cell had a calcium transient peak ≥4 times the SD of baseline noise (mean ± SE, 7.9 ± 1.48). Calcium transients for responses elicited by 4 APs averaged 13.64 ± 2.35 times the SD of the noise (mean ± SE). Calcium transient peaks for 4 APs were significantly larger than for 1 AP (Cell 1, p = 0.016; Cell 2, p = 0.0003; Cell 3, p = 0.021; Cell 4, p = 0.010). On average, 1 AP generated a calcium transient that was 53% the magnitude of a 4 AP transient.

To accomplish our goal of determining cellular activation in populations of DGCs, calcium indicator fluorescence fluctuations were imaged in the same slice and regions in response to the same stimulus as VSDI recordings (Fig. 4A). Select Fura 2-AM-loaded DG regions together with cellular ROI used for analysis are shown in representative P12 and P60 slices in Figure 4A. Figure 4B depicts representative traces for individual cellular ROI (numbers correspond to image in Fig. 4A) from P12 and P60 slices derived from calcium imaging of GCs. Asterisks denote calcium transients resolved with an automated detector (see Materials and Methods). There was a clear increased proportional activation of DGCs by PP stimulation in slices prepared from P12 compared with P60 animals, with 7 of 9 P12 DGCs exhibiting activation compared with 3 of 9 for P60 DGCs. To quantify this effect across development, we wanted to ensure that all DGCs included in the analysis had the capability of activating. To accomplish this, we applied PTX (50 μm), a GABA_A antagonist, at the end of each experiment, and limited our subsequent analysis to neurons that exhibited stimulus-evoked calcium transients in the presence of PTX. Examining the proportion of PTX-active cells that also activated in normal ACSF across developmental ages (Fig. 4C), we found that more than half of P12 DGCs activated in response to afferent stimulation, which decreased to 20% of neurons at P22-P30 and P60. This decrease in proportional activation was statistically significant (ANOVA, p < 0.0001, with Tukey's multiple-comparison post hoc testing demonstrating significant differences between P12 and P22 [p < 0.05] and P12 and P60 groups [p < 0.01]). In addition to serving as a method to ensure that we expressed responsive cell proportion relative to the overall population of viable neurons, PTX perfusion also demonstrated that the escalating sparsification in activation of DGCs during postnatal development was largely mediated by changes in local circuit inhibition rather than enhanced selectivity of afferent input targeting because we observed that blockade of inhibition normalized response proportion between postnatal developmental ages (63.3 ± 9.6%, and 71.8 ± 5.8% for P12 and P60 animals in PTX, not significantly different, t test).

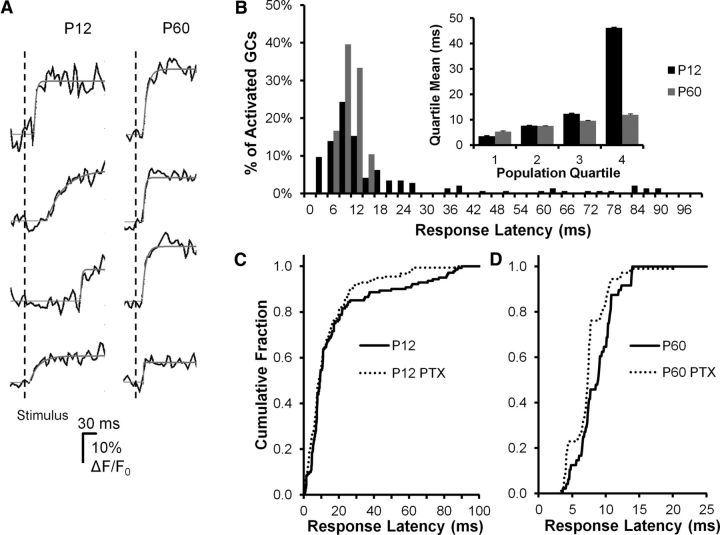
Information processing is mediated not only by the identity of cells that activate, but also by the temporal patterns of activation. Precise activation latencies time-locked to the occurrence of the afferent input retain specific information about the temporal properties of the stimulus. In the adult DG, the fast kinetics of excitatory synaptic potentials endows DGCs with the property of coincidence detectors resulting from the narrow activation and integration window generated by this characteristic (Schmidt-Hieber et al., 2007). To assess how the timing of cell activation relative to afferent input varied with postnatal development, we conducted a second set of MCI experiments on a specialized microscope capable of frame rates up to ∼1 kHz (Nikon Live Scan Swept Field Confocal Microscope). Using this system, we were able to acquire MCI onset activation information from DGCs after PP stimulation at a 128 × 128 pixel frame rate of 320 Hz (Fig. 5). We determined this to be the highest temporal resolution possible using this microscope given the photon density emitted by the Oregon Green bulk-loaded cells during activation. Using this system increased our temporal resolution >30-fold compared with the 10 Hz frame rates used on the multiphoton microscope during MCI (Fig. 4). Examining the time course of onset of MCI responses after PP stimulation and computing onset times using a curve-fitting algorithm (Fig. 5A), we were able to resolve a large, statistically significant difference in the distribution of ensemble activation times between early postnatal (P12) and adult (P60) animals. This was evident in the histogram in Figure 5B as a multimodal distribution of response latencies for P12 animals, with early (5–15 ms) and late (15–100 ms) components (black bars), compared with a unimodal distribution of response latencies confined to early (5–15 ms) time points for P60 animals (gray bars; P12 distribution different from P60, p = 0.00068, Kolmogorov–Smirnov test; Fig. 5B). The multimodal distribution of onset latencies in P12 animals may be the result of the wide variance in cell developmental stage at this animal age (Liu et al., 1996), where birth, migration, and differentiation of neurons are still ongoing. Fast activating responses may reflect more mature DGCs, whereas slow, long latency responses may derive from less mature, more recently born DGCs (Schlessinger et al.,. 1978; Rickmann et al., 1987; Hollrigel et al., 1998). However, the late responses were not the result of spontaneous activity, which was evident in some P12 cells. Examining this activity in detail, we found that 2.4% of P12 granule cells exhibited spontaneous activity, with an event frequency of 0.013 Hz. Given that the activation window examined after stimulus in Figure 5 was 100 ms, and activity in 160 P12 DGCs was plotted, <1 (0.05) spontaneous event would be expected to contribute to the ensemble activation for the entire population in Figure 5.

Figure 5.

DGC activation timing precision increases during postnatal development. A, Sample DGC calcium imaging traces from a P12 (left) and a P60 animal, demonstrating variability in response onset time after PP stimulation between groups. Onset time is estimated from exponential fits (solid lines, see Materials and Methods). The P12 response onsets are more variable, with frequent later events. PP stimulus time is indicated by the vertical line. B, Histogram plotting population percentage against response latency for P12 (black bars) and P60 (gray bars) animals. The late events are restricted to the P12 population, whereas P60 responses are limited to the first 15 ms after stimulation. These population distributions of response latency were significantly different (Kolmogorov–Smirnov test, p = 0.00068). Inset, Further illustration of the differences between groups by plotting the mean response latencies broken down by population quartiles. For the first three quartiles, there is very little difference between groups, whereas in the fourth population quartile, there is a fivefold longer average response latency in P12 DGCs. C, D, Sensitivity of response onset time to GABA antagonist (PTX, 50 μm) perfusion in P12 (C) and P60 (D) DGCs. Both populations exhibited PTX sensitivity in response latencies, but the nature of these effects differed. For P12 DGCs (C), PTX specifically blocked late activating responses (>20 ms latency), with little or no effect on early responses (0–15 ms), which constituted the majority of the population. A Kolmogorov–Smirnov test for overall differences between populations was not significant (p = 0.123); however, untreated cells had a slightly longer mean latency (p = 0.043, 10.1 vs 7.7 s, t test after log-transforming the data). For P60 DGCs (D), PTX shifted the entire curve to the left (Kolmogorov–Smirnov test p < 0.0001), consistent with a significant decrease in response latency. P12: N = 3 animals, 28 fields, 141 cells. P60: N = 3 animals, 22 fields, and 48 cells.

We also examined the role played by local circuit GABAergic inhibition in determining onset latencies of DGCs after PP stimulation. Application of the GABA_A antagonist, PTX (50 μm), had distinct effects on activation times in the P12 and P60 age groups (Fig. 5C,D). In the P12 group, PTX specifically blocked late activating responses, with little or no effect on early responses, which constituted the majority of the population. This suggested that GABAergic inhibition might exert a delayed, excitatory effect on a subpopulation of DGCs in this age group, presumably immature cells with depolarizing GABA responses (Hollrigel et al., 1998). The Kolmogorov–Smirnov test did not indicate differences in the overall distribution of latencies between PTX-treated and untreated cells (p = 0.123). We hypothesized that, although the overall distribution may have been similar between the two groups, components of the distribution differed. Examination of Figure 5C suggests that the distributions were largely similar, particularly at shorter response latencies. However, we noted that the P12 group appeared to be skewed to the right, with control cells tending to show longer response latencies. Thus, as a secondary analysis, we tested whether the means of the two conditions were similar using a t test after log-transforming the data to achieve approximate normality. We found that control cells had a slightly longer mean latency than PTX-treated cells (p = 0.043, 10.1 vs 7.7 ms), which may reflect the shift in the distribution toward longer latency. Given the differing results for the two statistical tests and significance level near 0.05, these results should be interpreted with some caution and subject to confirmation in future studies. PTX had a different effect on P60 onset latencies, where it shifted the entire distribution to shorter AP activation times (Kolmogorov–Smirnov test, p < 0.0001, Fig. 5D), suggesting that feedforward interneurons may activate so rapidly in adult animals that they affect the onset kinetics of monosynaptic, PP-originating EPSPs.

Repeatibility of the active versus silent DGC response

PP innervation of the DG shows remarkable divergence and convergence (Tamamaki and Nojyo, 1993; van Groen et al., 2003). Given this apparent lack of input specificity, we were interested in determining how robust and repeatable is the decision made by individual DGCs to activate or fail to activate in response to PP stimulation. A deterministic, specific response would be reflected in a repeatable decision being made, in which cells that activate to a given stimulus continue to fire repeatedly and cells that fail to activate initially repeatedly fail to respond to subsequent stimuli. A stochastic process would be reflected in random activation, without evidence of repeatability. We were also interested in whether these response characteristics changed during postnatal development, as the DG circuit matures.

To examine these issues, we repeatedly stimulated the PP at 5 s intervals and assessed the overlap in populations of DGCs, which activate or do not activate at differing stages of postnatal development. At the end of the experiment, we applied PTX (50 μm) and repeated the stimulus. Only neurons that responded to stimulation in the presence of PTX were included in our analysis. We divided DGCs into responsive and nonresponsive populations, defined as PTX-responsive neurons that either activated or did not activate in response to the first stimulus in normal medium. We then examined how these two populations of cells responded to subsequent stimuli (Fig. 6). In Figure 6A, B, specimen records are depicted for 5 responsive (top) and 5 nonresponsive DGCs (bottom), in a slice prepared from a P12 (Fig. 6A) and a P60 (Fig. 6B) animal. Examining the responses to subsequent, identical stimuli at 5 s intervals, it is evident that DGCs responded similarly to subsequent stimuli. Cells that activated to the first stimulus continued to activate frequently to subsequent stimuli, and cells that did not activate rarely activated to subsequent stimuli.

Figure 6.

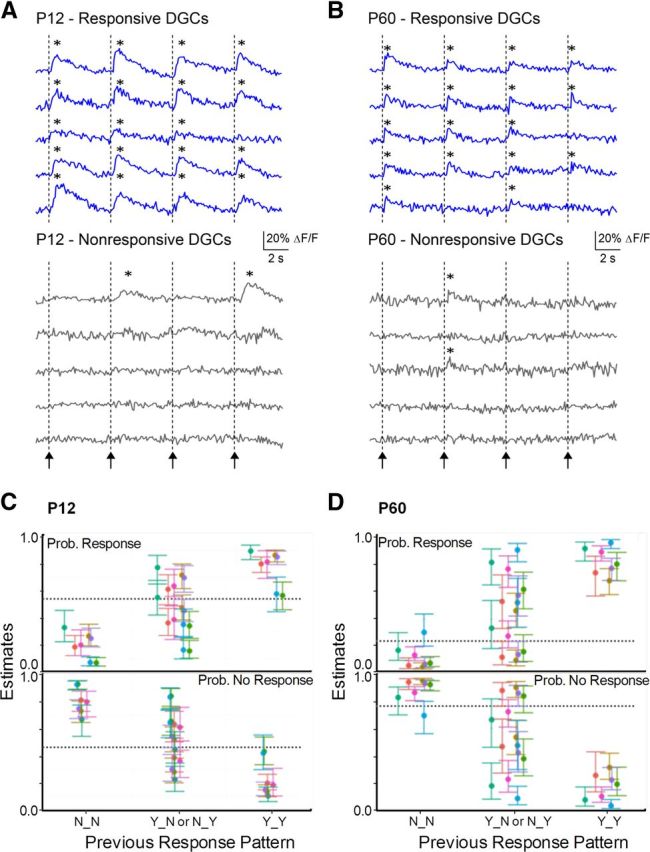
Repeatability of activate/remain silent DGC response. A, B, Calcium transient traces in representative DGCs in P12 and P60 animals, respectively, in response to 4 PP stimuli. Arrows/dotted lines indicate onset of PP stimulation (400 μA). Responsive cells (A, B, top) were defined as DGCs that activated to the first stimuli, and nonresponsive cells as DGCs that failed to activate to the first stimulus (A, B, bottom). Responsive cells at both ages responded frequently to subsequent stimuli, whereas nonresponsive cells did not. *Calcium transient was detected. C, D, Estimate of probability of response or nonresponse in Stimulus 4 given the previous pattern of response in Stimuli 2 and 3 for P12 (C) and P60 (D) groups (see Materials and Methods for model details). N_N, no response in both; Y_N, response in Stimulus 2 and not Stimulus 3; N_Y, no response in Stimulus 2 but response in Stimulus 3; Y_Y, response to both. Error bars indicate SEM; each color indicates a different slice. The hyphenated line indicates the probability of a response at Stimulus 4 across all cells and slices. The activation behavior of both P12 and P60 DGCs was strongly influenced by their previous behavior: cells that exhibited responses to Stimuli 2 and 3 had a high probability of activating to Stimulus 4, whereas cells that did not activate to Stimuli 2 and 3 had a low probability of responding to Stimulus 4, in all slices (n = 7 for both P12 and P60) and at both developmental stages. Cells with mixed responses to Stimuli 2 and 3 (Y_N or N_Y) had variable probabilities of activating to Stimulus 4. Random behavior would be predicted by responses probabilities at the overall population mean (dotted line in plot).

To analyze this trend evident in the specimen records in Figure 6A, B, we fit a logistic regression model using the data from Stimulus 4 as the outcome and the data from the previous two stimuli as predictors, to assess whether the previous behavior of a neuron to stimulation influenced its subsequent behavior. The P12 dataset contained 240 cells across seven slices. Across all slices, 48.9% of cells responded to Stimulus 4. The propensity of a cell to respond in Stimulus 4 was highly dependent on its responses to Stimulus 3 (p < 0.0001) and Stimulus 2 (p = 0.013). Figure 6C shows the propensity to respond (top) or not respond (bottom) for cells from each slice as a function of their previous response pattern. For cells with no response at either Stimulus 2 or Stimulus 3 (N_N), the probability of response at Stimulus 4 ranged from 7.0% to 33% depending on slice; in contrast, for cells that responded to both Stimulus 2 and Stimulus 3 (Y_Y), the stimulation 4 response probability varied from 56.6% to 89.6%.

The propensity of a P60 cell to respond to stimulus 4 was highly dependent on its propensity to respond to Stimulus 2 (p < 0.0001), and also positively associated with its propensity to respond to Stimulus 3, although this association did not achieve strict statistical significance (p = 0.075). Figure 6D shows the propensity to respond (top) or not respond (bottom) for cells from each slice as a function of their previous response pattern. For cells with no response to Stimulus 2 and 3 (N_N), the probability of response at Stimulus 4 ranged from 3.4% to 29.3%; in contrast, for cells that responded to both Stimulus 2 and 3 (Y_Y_), the probability of response at stimulus 4 varied from 67.6% to 96.1%.

For both the P12 and P60 data, similar results were found using stimulus 3 as the outcome and the response from Stimulus 1 and 2 as predictors (results not shown). The results for the P60 and P12 data differed in that, the propensity to respond at Stimulus 4 showed the strongest association with the propensity to respond at Stimulus 3 for the P12 group, and to the propensity to respond at Stimulation 2 for the P60 group. Nevertheless, the P12 and P60 data provide strong evidence against the hypothesis of stochastic response patterns.

The results of our analysis refute the null hypothesis of no relationship between previous and subsequent responses and strongly support the hypothesis of deterministic response patterns (p < 0.0001 for an association for both P12 and P60). This is concordant with the finding that ensemble activation of populations of DGCs to afferent stimulation was repeatable and precise, and therefore more consistent with a deterministic than a stochastic process.

Selective recruitment of DGC responses by θ and γ frequency stimulation

The data described above reflect DGC activation to single PP stimuli (Fig. 4) or to repeated stimuli at low frequencies (0.2 Hz, Fig. 6). During spatial navigation, the DG receives γ and θ frequency input from grid cells within the medial EC. How do these more natural stimulus patterns (θ and γ frequency inputs) modify DGC activation, and does this vary with postnatal development? To address this question, we used Oregon Green BAPTA-AM-loaded DGCs in slices prepared from P12 and P60 animals and examined activation in response to varying frequency inputs (δ, 1 Hz; θ, 5 and 10 Hz; and γ frequency, 60 Hz ranges) using the fast confocal microscope. The kinetics of Oregon Green are faster than Fura 2 during AP-elicited calcium transients, and the frequency response of the confocal microscope is much faster than the multiphoton microscope used in most experiments, allowing us to better resolve individual responses to varying frequency inputs in DGCs.

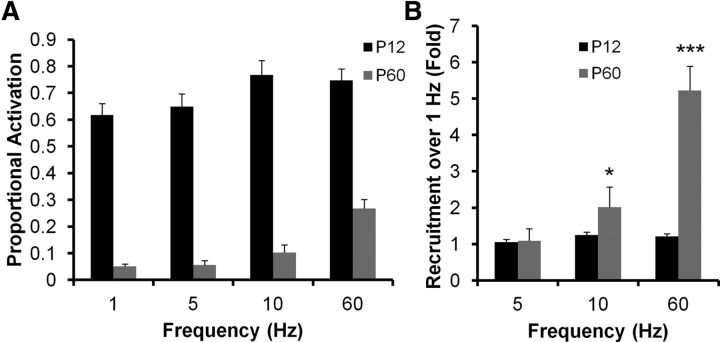
Figure 7A plots the proportional activation of DGCs from P12 (black bars) and P60 (gray bars) animals to 1, 5, 10, and 60 Hz PP stimulation. There is very little additional recruitment of P12 DGCs by higher frequency stimulation, whereas there is significant further DGC recruitment in P60 animals in response to 10 and 60 Hz stimulation (Fig. 7A). This is better visualized by normalizing response recruitment to the proportional activation evident in response to 1 Hz stimulation (Fig. 7B). There is little or no additional activation at 5, 10, and 60 Hz for cells from P12 animals, whereas there is a twofold and fivefold greater recruitment for 10 and 60 Hz stimulation, respectively, for P60 animals (P12 and P60 distributions differ significantly, p < 0.0001, two-way ANOVA). Although P60 DGCs exhibit lower basal activation (Fig. 4), they are readily recruited at input frequencies overlapping those encountered during normal cognitive processing in awake, behaving animals. This differs from P12 animals, which show significant basal activation (Fig. 4), but no additional recruitment with higher frequency inputs.

Figure 7.

Increased θ and γ frequency recruitment of DGCs during postnatal development. A, B, Responses of DGCs from P12 (black bars) and P60 (gray bars) animals to varying frequency stimulation of the PP (1, 5, 10, and 60 Hz). A, Raw mean percentage activation. B, Percent recruitment normalized to the activation evident during 1 Hz stimulation. Note that P12 DGCs, although more active overall, exhibited very little frequency recruitment, whereas P60 DGCs were significantly recruited by θ (5–10 Hz) and γ (60 Hz) frequency stimulation of the PP (two-way ANOVA). Both frequency and age effect are significant (p < 0.0001). *p < 0.05, 1 vs 10 Hz for P60 (Bonferroni post hoc test). ***p < 0.001, 1 vs 60 Hz for P60 (Bonferroni post hoc test). n = 3 animals, 6 slices, 11 fields, 629 cells for P12; n = 3 animals, 4 slices, 5 fields, 366 cells for P60.

Regional distinction in proportional DGC activation

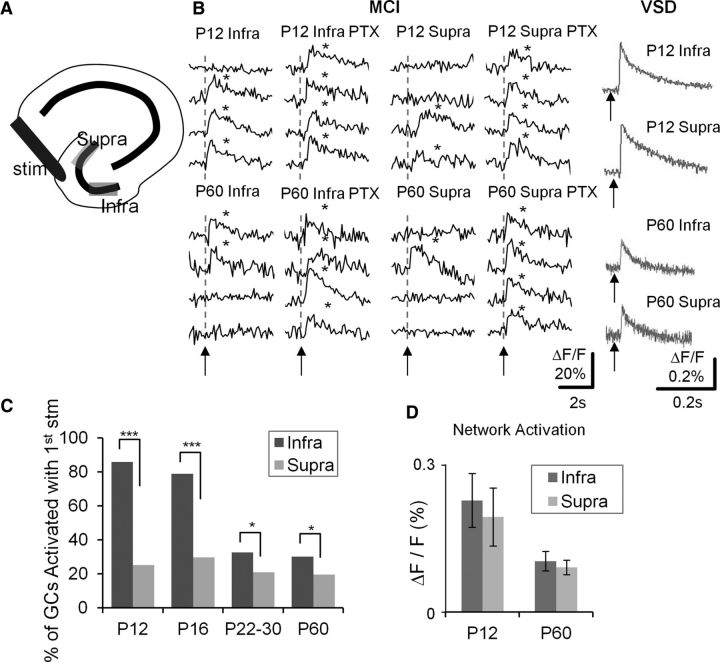
Anatomic studies have described regional distinctions between the infrapyramidal and suprapyramidal blades of the DG. The suprapyramidal blade of the DG has more GABAergic inhibitory interneurons than the infrapyramidal blade (Seress and Pokorny, 1981; Woodson et al., 1989), and interneurons in the suprapyramidal blade are more densely innervated by mossy fibers (Ribak and Peterson, 1991). Both of these distinctions have the potential to increase the strength of feedforward and feedback inhibition in the suprapyramidal blade relative to the infrapyramidal blade, critical processes regulating DGC activation. To assess possible functional differences in the suprapyramidal and infrapyramidal blades associated with these anatomic differences in inhibitory innervation, we examined DGC activation in response to PP stimulation in the two blades at varying stages of postnatal development using MCI. Figure 8A depicts the regions defined in our studies as suprapyramidal and infrapyramidal blades of the DG. In Figure 8B, MCI specimen records of cell activation in response to PP stimulation are depicted for DGCs in the infrapyramidal and suprapyramidal blades in slices prepared from P12 (top traces) and P60 (bottom traces) animals. Note that all cells (P12 and P60) were responsive in PTX and that an increased proportion of DGCs exhibited activation in the infrapyramidal blade relative to the suprapyramidal blade. This trend, evident in these specimen records, was present in all recordings. Figure 8C plots the proportional activation of DGCs in the infrapyramidal and suprapyramidal blades at all postnatal developmental stages sampled. The distinction in proportional activation between the two blades was statistically significant and retained throughout development (p < 0.01 to p < 0.05, depending on developmental stage). Also, the gradual reduction in proportional DGC activation evident across ages (Fig. 4C) was primarily the result of a pruning of activation in the infrapyramidal blade with development, which gradually decreases from 85% to 20% in P12 and P60 animals (Fig. 8C). The suprapyramidal does not show a similar decrease, maintaining activation levels of 15–20% throughout postnatal development (Fig. 8C). To the right of these MCI specimen records in Figure 8B are sequential VSDI traces (gray) recorded in the same slices from the same regions examining the EPSP amplitudes in the suprapyramidal and infrapyramidal blades at both postnatal ages. These responses were similar, so differences in proportional activation of DGCs between blades are not the result of gross differences in PP innervation strength in these two DG subregions. This was true for all recordings (Fig. 8D).

Figure 8.

Enhanced proportional activation of DGCs in the infrapyramidal blade of the DG. A, Schematic depicting the hippocampus with the suprapyramidal and infrapyramidal blades. B, Traces are calcium imaging responses from representative DGCs in the infrapyramidal (Infra) and suprapyramidal (Supra) blade of the DG, in P12 (top) and P60 (bottom) animals. Responses were recorded in control medium, and in the presence of the GABA antagonist, PTX (50 μm). Gray traces (right) represent VSDI responses of PP-evoked EPSPs in the infrapyramidal and suprapyramidal blades of P12 (top) and P60 (bottom) animals. Asterisks denote detection of a calcium transient. Note that there is enhanced proportional activation of DGCs in the infrapyramidal compared with the suprapyramidal blades at both ages, despite the fact that VSDI-recorded EPSPs were comparable. C, Aggregate population plots of percentage DGC activation in infrapyramidal and suprapyramidal blades in 4 developmental ages (P12, P16, P22–P30, and P60). Note that enhanced DGC activation is evident at all ages. *p < 0.05 (Fisher's exact test). ***p < 0.001 (Fisher's exact test). P12: n = 10 samples of 2 animals; P16: n = 10 of 2; P22–P30: n = 20 of 3; P60: n = 24 of 4. D, Averaged VSDI-recorded PP-evoked EPSPs in P12 and p60 animals. Note that there was no difference between the infrapyramidal and suprapyramidal blades (P12, n = 7 slices of 2 animals; P60, n = 6 of 1).

Discussion

In adult mice, DGCs exhibited sparse, selective, and tightly tuned activation in response to PP stimulation. In these adult animals, ∼20% of the viable neuronal population responded to strong afferent stimulation. These properties of activation depended on inhibitory modulation within the circuit because the majority of cells responded in the presence of a GABA antagonist, PTX. The adult pattern of DGC activation emerged in a protracted manner during postnatal development. In animals during the first 2 postnatal weeks, there was much less selectivity, with 60% of DGCs activating in response to afferent stimulation, with significantly less precise temporal tuning. Both the developmental regulation of sparse activation behavior and increased temporal fidelity of responses were dependent on changes in local circuit GABAergic inhibition because blockade of GABA receptors normalized responses across developmental stages. Even on a background of this large difference in AP firing selectivity, several aspects of DGC responses appeared early in development and were retained. These included the robust, repeatable nature of an individual cell's propensity to activate or remain silent in response to afferent activation and a preferential residence of active cells in the infrapyramidal compared with the suprapyramidal blade.

The proportion of neurons within a circuit that respond to stimulation of an afferent input, and the mechanisms that regulate this decision to activate in individual neurons are among the most fundamental aspects of circuit function. The activation process is most frequently examined in vivo, often during execution of behavioral tasks. However, in vitro approaches, such as those used in the present study, may also be important in characterizing these fundamental aspects of circuit behavior because more variables can be controlled, and neurons are more accessible for detailed biophysical analysis. The applicability of in vitro studies can be controversial, however. Issues center around two main caveats, which could complicate interpretation: (1) Has the circuit been disrupted during the experimental preparation? (2) Are the mechanisms regulating activation elucidated in vitro also relevant to in vivo processing?

Our combined imaging approach has allowed us to examine the spatiotemporal properties of afferent activation in the DG using VSDI approaches, as well as patterns of cellular activation in large numbers of neurons with single-cell resolution using MCI and 2-photon microscopy. This allows determination of afferent pathway function while still permitting proportional cell activation to be assessed. We also verify that the majority of cells we image and all the neurons that we analyze are viable and able to activate appropriately. These constitute unique strengths of our combined approach. The question concerning the relevance of the present findings to developmental regulation of cell activation propensity in vivo remains to be determined. However, there is one remarkable similarity to in vivo studies: the sparse but specific firing in DGCs described during spatial navigation (Jung and McNaughton, 1993; Leutgeb et al., 2007; Neunuebel and Knierim, 2012) is very similar to our findings in vitro in more mature animals.

New data are emerging, which suggest that the same sparse population of DGCs may activate in multiple environments (Leutgeb et al., 2007; Alme et al., 2010), rather than sparse firing of multiple distinct populations of DGCs in diverse environments (Jung and McNaughton, 1993; Chawla et al., 2005). This may be mediated by combined activation of both newly born and perinatally born DGCs in the adult brain (Marin-Burgin et al., 2012). The concept that sparse populations of DGCs activate in multiple environments may require significant modification in the conceptual framework describing cognitive processing within this circuit (Clelland et al., 2009; Nakashiba et al., 2012). Regardless of the identity of active DGCs, they play a critical role in hippocampal function. A recent study used optogenetic techniques to reactivate neurons within the DG, which had activated during acquisition of a fear memory task. This reactivation of this small population of DGCs recapitulated the learned behavior, supporting the importance of DGC coding in cognitive processing (Liu et al., 2012).

Some characteristic components of DGC activation were present early in postnatal development and maintained into adulthood. One of these was the robustness of the decision to activate or not activate in response to a given stimulus. This is a characteristic seen in DGC recordings during spatial navigation (Jung and McNaughton, 1993; Leutgeb et al., 2007; Neunuebel and Knierim, 2012), and in activity reporter studies examining Arc RNA expression patterns after repeated similar environmental exposures (Chawla et al., 2005). In a slice study of DG inhibitory circuitry responding to PP activation, Ewell and Jones (2010) described frequency-tuned basket cell-mediated inhibition, which contributed to sparsification of DGC output that was present in P12-P21 animals. Thus, significant components of the DG inhibitory circuit are online early during postnatal development and may be the substrate defining the robust nature of the decision to activate or remain silent evident at this age.

A recent study used MCI to examine PP stimulation-induced DGC activation, focusing on differential properties of newborn and perinatally born neurons in adult animals (Marin-Burgin et al., 2012). Notably, there were significant increases in the proportional activation of DGCs in adult animals reported in this study (60%) relative to the present findings (20%, Fig. 4). This 60% level of activation could not be considered sparse, an important conclusion of the present study. This conflict in proportional activation measures could be the result of methodological differences between the two studies. Both studies normalized responses to the proportion of cells activated in the presence of GABA antagonists. However, Marin-Burgin et al. (2012) used epifluorescence microscopy and averaged multiple trials to derive their 60% activation estimate, whereas the present study used 2-photon microscopy and reported activation in individual trials. Both of these methodological differences could contribute to differences in proportional activation estimates. Epifluorescence microscopy collects fluorescence from the focal plane, and out of focus regions, whereas 2-photon microscopy only excites fluorescence within a narrow focal plane with a 1–2 μm depth. This could account for the difference in proportional activation reported in the two studies because neurons out of the focal plane can factor into the overall estimate of activation proportion. A second contributor might be the 5 trial signal averaging used by Marin-Burgin et al. (2012) to calculate activation. Our imaging approach could resolve activation of individual APs in single trials with signals >5 SD larger than noise levels. Averaging over multiple trials would increase activation estimates by 30–50% because initially nonactive cells can be recruited ∼40% of the time by additional stimuli.

The preferential recruitment of DGCs in the infrapyramidal compared with the suprapyramidal blade was particularly strong in early postnatal animals and may be mediated by differences in anatomic measures of inhibition between the two regions. The suprapyramidal blade has more GABA-inhibitory interneurons than the infrapyramidal blade (Seress and Pokorny, 1981; Woodson et al., 1989), and the inhibitory neurons in the suprapyramidal blade are more densely innervated by mossy fibers (Ribak and Peterson, 1991). Our findings of enhanced DGC activation in the infrapyramidal blade are not in agreement with Arc RNA expression studies of cellular activity during spatial navigation (Chawla et al., 2005) or with a combined physiology/imaging study (Scharfman et al., 2002). These groups found that the suprapyramidal blade exhibited greater proportional activation. However, these studies were conducted in more septal regions of the hippocampus than the temporal pole studied in the present study, which may explain these divergent findings. The suprapyramidal blade activation preference disappears in more temporal locations (Scharfman et al., 2002).

Given that local circuit inhibition is a prime mediator of sparse, specific activation properties of DGCs (Nitz and McNaughton, 2004; Schmidt-Hieber et al., 2007; Ewell and Jones, 2010; Sambandan et al., 2010), and that there is significant variation in inhibitory properties in the DG during postnatal development (Hollrigel et al., 1998), the sensitivity of developmental changes in DGC activation propensity and AP firing precision to GABA blockers is not unexpected. However, what is surprising is that both of these developmental changes in DGC activation completely normalize in the presence of PTX. This raises the intriguing possibility that the identity and characteristics of DGC activation may not be defined exclusively by specificity in PP inputs onto DGCs. Rather, they may also be defined to a significant extent by feedforward inhibition, which in turn must be mediated by precise PP inputs onto interneurons. This provides a permissive environment allowing small populations of DGCs to activate, potentially to multiple sets of inputs (Leutgeb et al., 2007; Alme et al., 2010). This suggests that, because information is not coded exclusively in the identity of granule cells that activate, these cells may use a combination of a rate code and cellular identity output to discriminate input properties, a hypothesis requiring further testing.

The neuronal representation of space within the hippocampus and EC of rodents exhibits a protracted postnatal development, stabilizing at adult levels by 3.5–4 weeks postnatal (Langston et al., 2010). Capabilities in conduct of spatial memory tasks also exhibit a similar protracted postnatal development (Schenk, 1985; Rudy et al., 1987; Ainge and Langston, 2012). Given that appropriate activity within the DG is an important component of these tasks, the delays in development of adult levels of sparse and selective DGC activation, temporal tuning, and frequency-dependent recruitment in response to EC activation described in the present study may contribute to delays in development of both neuronal representations of space and of adult levels of competence in spatial memory tasks.