Critical Casimir Forces in Cellular Membranes

Abstract

Recent experiments suggest that membranes of living cells are tuned close to a miscibility critical point in the two-dimensional Ising universality class. We propose that one role for this proximity to criticality in live cells is to provide a conduit for relatively long-range critical Casimir forces. Using techniques from conformal field theory we calculate potentials of mean force between membrane bound inclusions mediated by their local interactions with the composition order parameter. We verify these calculations using Monte Carlo simulations where we also compare critical and off-critical results. Our findings suggest that membrane bound proteins experience weak yet long-range forces mediated by critical composition fluctuations in the plasma membranes of living cells.

Cellular membranes are two-dimensional (2D) liquids composed of thousands of different lipids and membrane bound proteins. Though once thought of as uniform solvents for embedded proteins, a wide array of biochemical and biophysical evidence suggests that cellular membranes are quite heterogeneous (reviewed in Refs. [1,2]). Putative membrane structures, often termed ‘rafts,’ are thought to range in size from 10–100 nm, much larger than the α ~ 1 nm size of the individual lipids and proteins of which they are composed. This discrepancy in scale presents a thermodynamic puzzle: naive estimates predict enormous energetic costs associated with maintaining heterogeneity in a fluid membrane [3].

Parallel work in giant plasma membrane vesicles (GPMVs) isolated from living mammalian cells presents a compelling explanation for the physical basis of these proposed structures. When cooled below a transition temperature around 25 °C, GPMVs phase separate into two 2D liquid phases [4] which can be observed by conventional fluorescence microscopy. Quite surprisingly, they pass very near to a critical point in the Ising universality class at the transition temperature [5]. Near a miscibility critical point, the small free energy differences between clustered and unclustered states could allow the cell to more easily control the spatial organization of the membrane, lending energetic plausibility to the proposed structures. Although analogous critical points can be found in synthetic membranes [6–8] these systems require the careful experimental tuning of two thermodynamic parameters, as in the Ising liquid-gas transition where pressure (equivalent to the Ising magnetization) and temperature must both be tuned. Although it has been suggested that biological systems frequently tune themselves towards dynamical and other statistical critical points [9], so far as we know membranes are the clearest example of a biological system which appears to be tuned to the proximity of a thermal critical point.

Other plausible theoretical models have focused on 2D microemulsions (stabilized by surfactants [10], coupling to membrane curvature [11], or topological defects in orientational order [12]), but none has emerged from direct, quantitative experiments on membranes from living cells. It has been argued that Ising fluctuations should have vanishing contrast between the two phases [11]. While this is true of macroscopic regions, a region of radius R of lipids of size α ~ 1 nm should have contrast ~(R/α)^−β/ν = (R/α)^−1/8, leading to predicted composition differences of 0.7 at the physiologically relevant 20 nm scale, and differences of 0.5 at the R = 400 nm scale of fluorescence imaging [5]; on the length scales of interest there is plenty of contrast. Indeed, our calculations of Ising-induced forces take place at and above the critical point, where the macroscopic contrast is of course zero.

How might a cell benefit by tuning its membrane near to criticality? Presuming that functional outcomes are carried out by proteins embedded in the membrane, we focus on the effects that criticality might have on them. For embedded proteins, proximity to a critical point is distinguished by the presence of large, fluctuating entropic forces known as critical Casimir forces. Three-dimensional critical Casimir forces have a rich history of theoretical study [13]. In more recent experimental work [14] colloidal particles clustered and precipitated out of suspension when the surrounding medium was brought to the vicinity of the liquid-liquid miscibility critical point in their surrounding medium. Two-dimensional Casimir forces like the ones studied here have been investigated for the Ising model using numerical transfer matrix techniques [15] for a demixing transition using Monte Carlo simulations [16] and for shape fluctuations using perturbative analytical methods [17,18]. Here we estimate the magnitude of composition mediated Casimir forces arising from proximity to a critical point, both in Monte Carlo simulations on a lattice Ising model, and analytically, making use of recent developments in boundary conformal field theory (CFT) [19–21]. Our motivation is biological: in a cellular membrane, these long-range critical Casimir forces could have profound implications. More familiar electrostatic interactions are screened over around 1 nm in the cellular environment, whereas we find the composition mediated potential can be large over tens of nanometers.

Critical Casimir forces are likely utilized by cells in the early steps of signal transduction where lipid mediated lateral heterogeneity has been shown to play vital roles. Many membrane bound proteins segregate into one of two membrane phases when biochemically extracted with detergents at low temperatures [22], or when proteins are localized in phase separated GPMVs [5]. Furthermore, there is evidence that some receptors change their partitioning behavior in response to ligand binding or downstream signaling events [23]. Modeling this as a change in the coupling between the receptor protein and the Ising order parameter predicts that these bound receptors will see a change in their interaction partners. Supporting this view, ligand binding to receptors is often accompanied by spatial reorganization in which receptors and downstream molecules move into close proximity of one another [1,24], perhaps because they now share a preference for the same Ising phase. Perturbations to the lipid composition of the membrane, like cholesterol depletion [25], typically disrupt this spatial reorganization [24] and have dramatic effects on the final outcomes of signaling [26–28], in our view by taking the membrane away from its critical point and interfering with the resulting long-range forces.

We take three approaches to estimating the form of these potentials. We first consider two point-like proteins which interact with the local order parameter like local insertions of magnetic fields h₁ and h₂ at x = 0 and x = d. To calculate the resulting potential we write a Hamiltonian for the combined system of the Ising model with order parameter φ(x) plus proteins as H([φ(x)], d) = H_Ising ([φ(x)]) + h₁ φ(0) + h₂φ(d). We then write a partition function for the combined system Z(d) = ∫ D[φ(x)]e^−βH [(φ(x),d)] and solve to lowest order in h giving the potential U_eff (d) = − log[Z(d)] + log[Z(∞)] = − h₁ h₂ C(d), with C(d) = 〈φ(0)φ(d)〉 the correlation function. C(d) ~ d^−η when d ≪ ξ with η = ¼ in the Ising model and C(d) ~ d^−1/2 exp(−d/ξ) for d ≫ ξ. The potential is attractive for like, and repulsive for unlike, field insertions, in agreement with the scaling of the CFT result as we will show below. A protein which does not couple to the order parameter can still feel a long-range force if it couples to the local energy density. The energy density is also correlated with a d⁻² dependance. However, the magnitude of both of these potentials, as well as their shape at distances d ~ r require the Monte Carlo and CFT approaches described below.

Secondly, we numerically calculated potentials using Monte Carlo simulations on the lattice Ising model for like and unlike disk-shaped inclusions. Although absolute free energies are difficult to obtain from Monte Carlo techniques, differences between the free energies of two ensembles, δ F, conditioned on a subset of the degrees of freedom, are readily available provided the degrees of freedom in the two ‘macrostates’ can be mapped onto each other and have substantial overlap. This information is implicitly used in a Monte Carlo scheme where both ‘macrostates’ are treated as members of a larger ensemble and are switched between so as to satisfy a detailed balance. The Bennett method [29,30] uses this information more explicitly, noting that exp(−βδF) = 〈e−βδE〉 can be estimated without bias from either distribution.

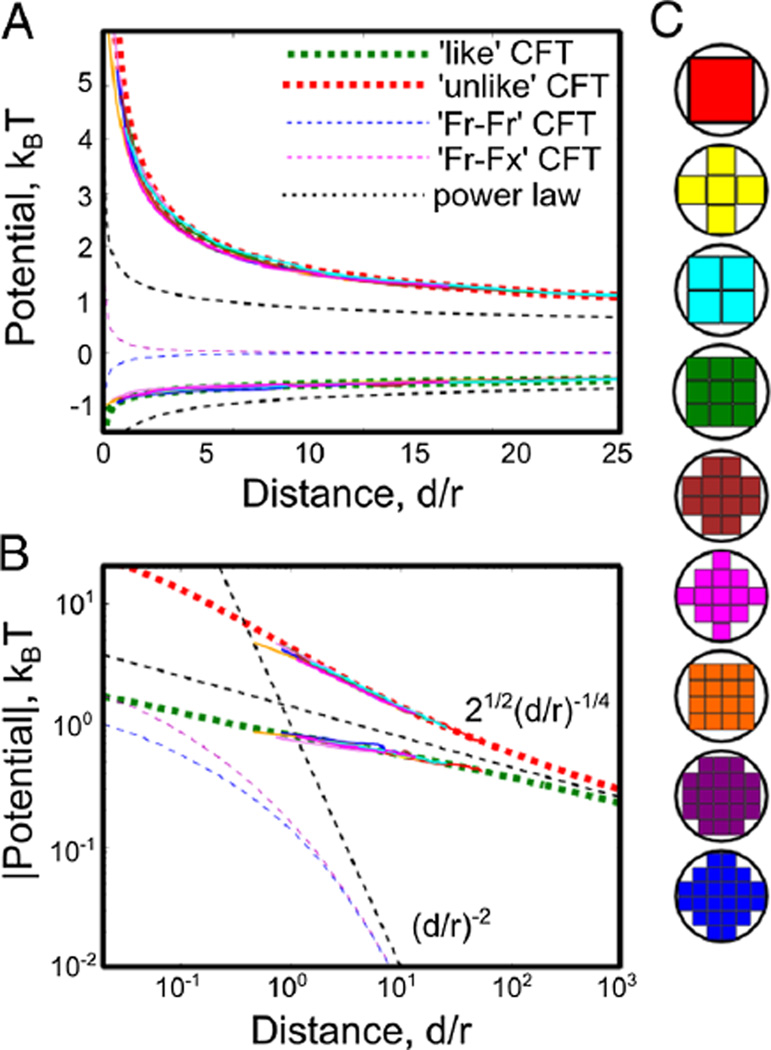
Our ‘macrostates’ are the location of two blocky ‘disks’ as shown in Fig. 1(c). All spins either contained in or sharing a bond with these disks are constrained to be either all up or all down. We map the degrees of freedom in one macrostate to a neighboring one by moving all of the spin values one lattice spacing to the right or left of the fixed spin region onto fixed spins on the other side. By integrating our measured βδF = − log〈exp(−βδE)〉 over many sites outwards to infinity, we can in principle measure this potential to arbitrary distance. However, because the potential is long-range at T_c, we integrate it out to 50 lattice spacings and add the CFT prediction for the potential at that distance as described below. We perform simulations using the Wolff algorithm on 500 × 500 lattices under the constraint that any cluster which intersects a disk is rejected, enforcing our fixed boundary conditions. We supplement these with individual spin flips near the inclusions where almost all Wolff moves are rejected. The resulting potentials are plotted in Fig. 1(a). We collapse the Monte Carlo curves by using the effective radius given by the farthest point from the origin contained in the blocky lattice inclusion as the effective radius.

FIG. 1.

(color online). (A–B) Effective potentials between bound inclusions are plotted on linear (A) and log-log (B) graphs, for inclusions where r₁ = r₂ = r. We measure these potentials using Bennet method simulations for like and unlike BCs at T_c as described in the text for each of the blocky disks shown in (C) [thin lines, colors as in (C)]. Each curve is plotted collapsed by using r as the distance to the farthest point from its center, with no free parameters, although the value of the potential is fit at the farthest accessible simulation point, where we add the CFT prediction. The full CFT predictions (thick dashed lines) are in excellent agreement with simulation data even for very small inclusions. The power law predictions (thin dashed line) agree with the CFT predictions for large d/r.

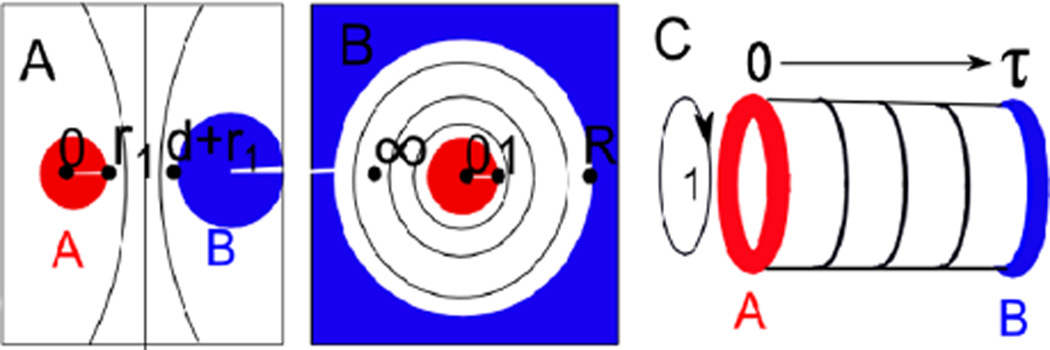
Finally, we use conformal field theory to make an analytical prediction for the form of these potentials. Our calculation makes extensive use of the conformal invariance of the free energy which emerges at the critical point. An element from the global conformal group can take us from the configuration in Fig. 2(a) to that shown in Fig. 2(b) where the two disks are concentric with spatial infinity in Fig. 2(a) now lying between the two cylinders on the real axis. The radius of the outer circle R(d, r₁, r₂) is now given by

$$R(d,r_1,r_2)=\frac{x-2+\sqrt{{(x-2)}^2-4}}{2},x=\frac{(d+2r_1)(d+2r_2)}{r_1{r}_2}.$$ (1)

FIG. 2.

(color online). We consider potentials of mean force in configuration (A), with disks of radius r₁ and r₂ separated by a distance d with boundary conditions A and B. We conformally map this to configuration (B), where both disks are centered on the origin, with the first at radius 1 and the second at radius R(d, r₁, r₂). We then map this to a cylinder shown in (C) of circumference 1 and length −iτ = log(R)/2π where we associate restricted partition functions in an imaginary time 1 + 1 dimensional quantum model with potentials of mean force in the original configuration.

The much larger local conformal group, particular to two dimensions, is the set of all analytic functions. We use the transformation $z\prime =\frac{\text{log}(z)}{2\pi }$ gluing together the boundaries at x = 1 and x = 0 to give the cylinder shown in Fig. 2(c) with a circumference of 1 and length

$$\tau (d,r_1,r_2)=i\text{log}[R(d,r_1,r_2)]/2\pi .$$ (2)

This transformation breaks global conformal invariance and so increases the free energy by c log(R) / 12 [20], where c = 1/2 in the Ising model. Defining a 1 + 1 dimensional quantum theory on the cylinder (see Ref. [20]) with ‘time’ t running down its length, our Hamiltonian for t translation is $H=2\pi (L_0+{\mathrm{L̄}}_0-\frac{c}{12})$, where L₀ + L̄₀ is the generator of dilation in the plane.

Partition functions in this geometry are linear sums of characters of the conformal group. The representations of the conformal group particular to the Ising universality class have characters given by [20,31]

$${\chi }_0(\tau )=\frac{1+q^2+q^3+\cdots }{q^{1/48}}=\frac{1}{2\sqrt{\eta (\tau )}}[\sqrt{{\theta }_3(q)}+\sqrt{{\theta }_4(q)}]{\chi }_{1/16}(\tau )=\frac{1+q+q^2+2q^3+\cdots }{q^{1/48-1/16}}=\frac{1}{\sqrt{2\eta (\tau )}}[\sqrt{{\theta }_2(q)}]{\chi }_{1/2}(\tau )=\frac{1+q+q^2+\cdots }{q^{1/48-1/2}}=\frac{1}{2\sqrt{\eta (\tau )}}[\sqrt{{\theta }_3(q)}-\sqrt{{\theta }_4(q)}],$$ (3)

where q = exp(i πτ), with η(τ) the Dedekind η function and with θ(τ) the Jacobi, or elliptic. theta functions.

Conformally invariant boundary conditions (BCs) can be deduced by demanding consistency between two parametrizations of the cylinder [31]. In one, time moves from one BC to the other across the cylinder with the usual Ising Hamiltonian. Alternatively, time can move around the cylinder with the BCs now entering into the Hamiltonian. There are three allowed BCs [31], which by considering symmetry can be associated with ‘up’, ‘down,’ and ‘free.’ These three BCs have four nontrivial potentials between them: a repulsive ‘unlike’ interaction between ‘up’ and ‘down’ BCs, an attractive ‘like’ interaction between ‘ups’ and ‘ups’ or ‘downs’ and ‘downs’, an attractive ‘free-free’ interaction between two ‘free’ BCs, and a repulsive ‘free-fixed’ interaction between a ‘free’ BC and either an ‘up’ or a ‘down.’

The free energy in the configuration shown in Fig. 2(a) can be interpreted as a potential of mean force between the bound inclusions. Choosing the convention that the potentials go to 0 as d → ∞, the potential is given by U(d) = F_AB (τ) = F_AB (∞). After undoing the mapping which changes the free energy by a central charge dependent factor so that F_AB (τ) = − logZ_AB (τ) + cπτ/6 (with k_BT = 1) the potentials are given by

$$U_{\text{like}}(d,r_1,r_2)=-\text{log}[{\chi }_0(2\tau )+{\chi }_{1/2}(2\tau )+\sqrt{2}{\chi }_{1/16}(2\tau )]-\frac{i\pi \tau }{12}{U}_{\text{unlike}}(d,r_1,r_2)=-\text{log}[{\chi }_0(2\tau )+{\chi }_{1/2}(2\tau )-\sqrt{2}{\chi }_{1/16}(2\tau )]-\frac{i\pi \tau }{12}{U}_{\mathrm{F}\mathrm{r}-\mathrm{F}\mathrm{r}}(d,r_1,r_2)=-\text{log}[{\chi }_0(2\tau )+{\chi }_{1/2}(2\tau )]-\frac{i\pi \tau }{12}{U}_{\mathrm{F}\mathrm{r}-\mathrm{F}\mathrm{x}}(d,r_1,r_2)=-\text{log}[{\chi }_0(2\tau )-{\chi }_{1/2}(2\tau )]-\frac{i\pi \tau }{12}$$ (4)

with χh as defined in Eq. (3), and τ as defined in Eqs. (1) and (2). These potentials are plotted on regular and log-log graphs in Fig. 1. Their form is in agreement with the numerical results obtained using the transfer matrix methods in Ref. [15].

At large d, we can examine the asymptotics of the potentials using the form of each potential in Eq. (4) and the series expansion of the characters as shown in Eq. (3). For fixed BCs, the leading contribution to the potential of mean force is equal to $\pm \sqrt{2{(r_1{r}_2)}^{1/4}}{d}^{-(1/4)}$, with a sign which differs depending on whether the two BCs are like or unlike, in agreement with the point like approximation. For potentials that involve at least one ‘free’ BC, similar analysis shows that the leading contribution is proportional to d⁻². All four potentials diverge at short distances like ± d^−1/2 where in all cases the sign is positive unless both BCs are identical. We note that the origins of the two techniques leading to the curves shown in Fig. 1 are very different, arguably as different from each other as each are from a lipid bilayer. The very close agreement, even at lengths comparable to the lattice spacing, speaks to the power of universality.

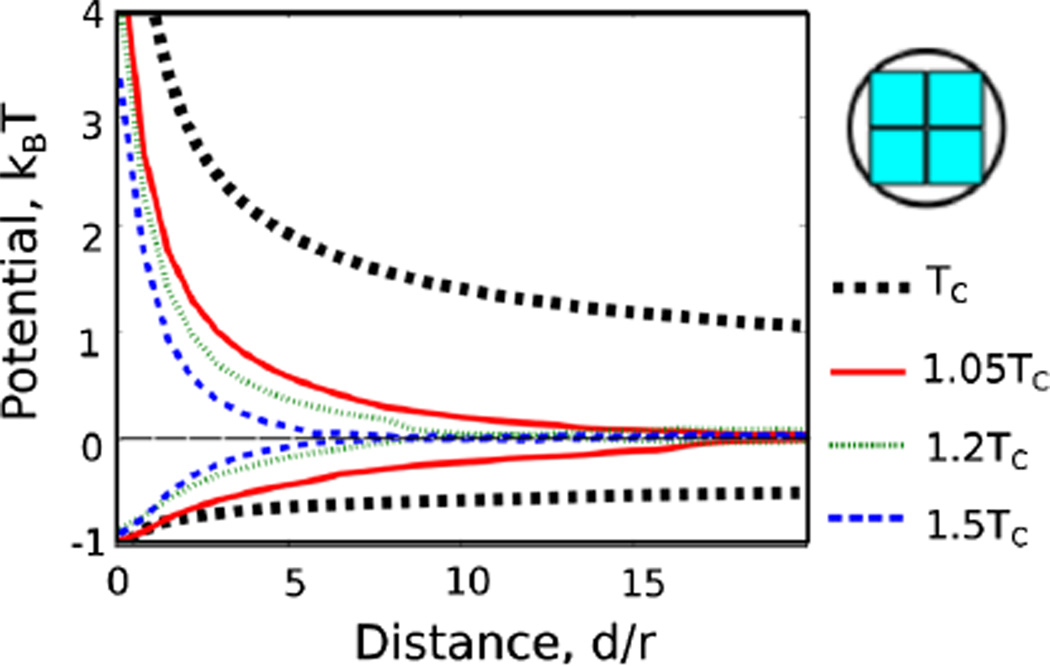
We also compare the form of the potential with Monte Carlo results obtained at temperatures away from the critical point where the potential has a range given roughly by ξ. In each case the resulting potential is a one-dimensional cut through a four-dimensional scaling function which could depend nontrivially on d/r₁, d/r₂,d/ξ and the ‘polar’ coordinate h/t^βδ [32] describing the proximity to criticality. The dashed lines show the CFT prediction for T = T_c, with numerical results at 1.05, 1.1 and 1.2T_c, all for the 2 × 2 block sphere shown at the right in Fig. 3. The repulsive potential is both deepest and sharpest at T_c, while the attractive force is sharpest slightly above T_c, with the final potential of very similar magnitude.

FIG. 3.

(color online). We compare our critical results with potentials obtained from Monte Carlo simulations away from the critical point along the temperature axis. As can be seen, the potentials have the longest range at the critical point. The repulsive interaction is also steepest at the critical point, though the attractive one has a larger force at short distances slightly away from the critical point.

We expect our results to apply, with a few caveats, to proteins embedded in real cell membranes. Proteins couple to their surrounding composition through the height of their hydrophobic regions, through the interactions of their membrane-proximal amino acids with their closest lipid shell, and by the covalent attachment to certain lipids which themselves strongly segregate into one of the two low temperature phases. In simulation our proteins couple strongly to their nearest neighbor lipids leading to potentials in excellent agreement with CFT predictions that are very different in origin. These are expected to describe any uniform boundary condition in an Ising liquid, in the limit where all lengths are large compared to the lattice spacing. When separated by lengths on the order of a lipid spacing (1 nm) we might expect additional corrections to this form, and in particular, a weakly coupled protein may have a behavior intermediate between a ‘free’ and a ‘fixed’ BC. In addition, a protein that couples nonuniformly around its boundary might have interesting behavior not addressed here. We note that our boundary conditions couple to two long-range scaling fields—the magnetization field which falls off with the a power of −1/4 and the energy density which falls off with a power of −2, both of which must be present in membranes or any other system near an Ising critical point.

It is interesting to compare this composition mediated force to other forces that could act between membrane bound proteins. Electrostatic interactions are screened over around 1 nm in the cellular environment, making them essentially a contact interaction from the perspective of the cell. There is an analogous shape fluctuation mediated Casimir force that falls off like d⁻⁶ [17,18], and that is therefore also very short range. Membrane curvature can also mediate forces with a leading attractive term that falls off like d⁻² and a leading repulsive term that falls off like d⁻⁴. Although they decay with a much larger power than the critical Casimir forces described above, curvature mediated potentials depend on elastic constants and are not bound to be of order k_BT, allowing them to become quite large at shorter distances. Using typical values [33] the potentials are comparable at lengths −5–10 nm to the composition mediated potential we find here [34]. There are numerous examples of biology using these relatively short range but many k_BT potentials for coordinating energetically expensive and highly irreversible events like vesiculation [33]. We propose that critical Casimir forces could mediate long-range and reversible interactions useful for regulating a protein’s binding partners. More generally, this work demonstrates that the hypothesis of criticality enables a quantitative understanding of the broad range of phenomena frequently associated with ‘raft’ heterogeneity in cell membranes.