Abstract
Mechanisms related to the adverse effects of corticosteroids on glucose homeostasis were studied. Five groups of adrenalectomized (ADX) rats were given methylprednisolone (MPL) intravenously at 10 and 50 mg/kg, or a continuous 7 day infusion at rates of 0, 0.1, 0.3 mg/kg/h via subcutaneously implanted Alzet mini-pumps. Plasma concentrations of MPL, glucose and insulin were determined at various time points up to 72 h after injection or 336 h after infusion. The pharmacokinetics of MPL was captured with a two-compartment model. The Adapt II software was used in modeling. Injection of MPL caused a temporary glucose increase over 6 h by stimulating gluconeogenesis. The glucose changes stimulated pancreatic β-cell secretion yielding a later insulin peak at around 10 h. In turn, insulin can stimulate glucose disposition. However, long-term MPL treatment caused continuous hyperglycemia during and after infusion. Insulin was increased during infusion, and immediately returned to baseline after the infusion was terminated, despite the almost doubled glucose concentration. A disease progression model incorporating the reduced endogenous glucose disposition was included to capture glucose homeostasis under different treatments. The results exemplify the importance of the steroid dosing regimen in mediating pharmacological and adverse metabolic effects. This mechanistic pharmacokinetic/pharmacodynamic (PK/PD) model quantitatively describes the induction of hyperglycemia and provides additional insights into metabolic disorders such as diabetes.
Keywords: corticosteroids, methylprednisolone, pharmacodynamics, pharmacokinetics, glucose, insulin
Introduction
Synthetic corticosteroids (CS) are used widely for their antiinflammatory and immunosuppressive effects. Intensive short-term therapy of high-dose CS is of considerable value in the treatment of respiratory failure, acute asthma and anaphylactic shock. The CS are among the most important drugs for diseases such as lupus erythematosus, rheumatoid arthritis and organ transplantation [1]. For continuous relief of clinical symptoms, some patients require chronic therapy for months or even years. The appearance of adverse drug effects in metabolic systems is considerably dependent on the duration of CS treatment. Alteration of glucose tolerance represents one of the most serious side effects associated with CS treatment.
Glucocorticoids were named for their glucose-regulating properties and have diverse effects on carbohydrate, lipid, protein and nucleic acid metabolism [2]. Although endogenous steroids are secondary to insulin in regulating glucose metabolism, they influence gluconeogenesis and play a protective role against glucose deprivation, especially under stress and starvation.
Excess CS increase hepatic glucose production and decrease glucose uptake/utilization in peripheral tissues [2]. Thus hyperglycemia and decreased carbohydrate tolerance may be observed with CS treatment. The extent of these effects depends on insulin, which opposes many CS actions. Insulin secretion from pancreatic β-cells increases in response to the steroid-induced blood glucose. Therefore, in a nondiabetic individual receiving short-term CS, elevated insulin concentrations counterbalance the CS effect so that the fasting blood glucose concentration is maintained within the normal range. In a patient with impaired glucose tolerance or insulin insufficiency, CS in excess exacerbate the system abnormalities, resulting in possible steroid-diabetes [3].
In spite of the rich literature concerning CS effects on glucose regulation, limited information is available regarding the complete time profile and reversibility of dynamic changes. This is of special importance because of the nature of diabetes as a progressive disease.
The development of mechanistic PK/PD models for CS effects is essential for quantitative understanding of its action. The principal controlling factors for glucose homeostasis are glucose stimulatory effects on β-cell secretion, insulin stimulatory effects on glucose utilization and insulin inhibitory effects on glucose production. Estimating system parameters that describe glucose and insulin signaling as well as drug-specific parameters that describe CS potency is crucial for understanding the control mechanisms of the metabolic system.
In this study, the time courses and reversibility of the metabolic alterations in glucose and insulin following acute and chronic administrations of MPL were investigated in rats. Rat body weights were also monitored due to the catabolic effect of MPL observed previously [7]. Rats were adrenalectomized to eliminate the complexity of endogenous corticosterone effects on glucose regulation. The major goal was to develop a mechanism-based PK/PD model that can quantitatively describe CS effects on glucose/insulin metabolism, provide insights on their mechanisms of action, and understand the internal controls of this biological system. The results illustrate the development of steroid-diabetes and could assist in understanding the mechanisms underlying CS-induced adverse effects.
Materials and Methods
Animals
Six male ADX Wistar rats weighing 225–275 g and 12 rats weighing 325–375 g were purchased from Harlan-Sprague Dawley Inc. (Indianapolis, IN). All animals were housed in a 12 h light/dark cycle and acclimatized in a constant temperature environment of 22°C for at least 1 week. Rats had free access to rat chow and 0.9% NaCl drinking water. One day prior to the study, all rats underwent right external jugular vein cannulation under ketamine/xylazine anesthesia. Cannula patency was maintained with sterile 0.9% saline. This research adhered to the ‘Principles of Laboratory Animal Care’ (NIH publication 85–23, revised 1985) and was approved by the University at Buffalo Institutional Animal Care and Use Committee.
Experimental
Methylprednisolone sodium succinate (Solu-Medrol®, Pharmacia & Upjohn Company, Kalamazoo, MI) was reconstituted with the supplied diluents. Rats weighing 225–275 g were divided into two groups to receive a single injection of 10 or 50 mg/kg MPL via the cannula over 30 s. Rats weighing 325–375 g were divided into three groups to receive a continuous infusion of MPL (0.1 or 0.3 mg/kg/h) or saline via Alzet osmotic mini-pumps (Model 2001, flow-rate 1 μl/h, Alza Corp., Palo Alto, CA). For each rat, the MPL concentration of the pump solution was prepared based on its predose body weight. After overnight equilibration in saline at 37°C, the pumps were implanted subcutaneously between the rat shoulder blades at time 0 and removed at 168 h under halothane anesthesia (<5 min) to ensure a 7 day infusion. The body weights of each rat were recorded before pump implantation and on a daily basis up to 336 h.
Blood samples were taken from the cannula into heparinized syringes at pretreatment and at 0.5, 1, 2, 4, 5, 6, 8, 10, 12, 24, 36, 48, 72 h for injected animals, or at 3, 6, 12, 24, 48, 72, 96, 144, 168 (before pump removal), 172, 180, 192, 216, 264, 336 h for infused animals. Sampling times were selected based on previous studies of MPL PK and dynamic effects. The MPL PK were only measured at selected time points to minimize blood sample volumes and for confirmation purposes in relation to published results from our laboratory in which the same drug, dose and type of animal were used [5–7]. Plasma was harvested from blood and stored at –20°C until analysed. The blood volume taken was less than 0.9% of body weight.
Assays
Plasma MPL concentrations were measured by a normal-phase high-performance liquid chromatography method with a quantitation limit of 10 ng/ml [4].
A modified enzymatic assay kit (Sigma Diagnostics, St Louis, MO) was used to determine plasma glucose. In brief, 10 μl double distilled water (as blank), glucose standards, quality control and plasma samples were added in duplicate to a 96-well microplate containing 90 μl double distilled water in each well. Then, 50 μl 0.3n barium hydroxide and 50 μl 0.3n zinc sulfate were added to each well for deproteinization. The plate was centrifuged at 3400 rpm for 15 min, and 20 μl supernatant was then transferred to another 96-well plate. Subsequently, 200 μl reaction solution containing 4.92 unit/ml glucose oxidase, 0.98 purpurogalin unit/ml peroxidase and 0.039 mg/ml o-dianisidine dihydrochloride was added and the plate was incubated for 30 min at 37°C. Glucose oxidase mediates the production of gluconic acid and H2O2 from glucose oxidation. The o-dianisidine is then oxidized by H2O2 and peroxidase yielding a brown color. The optical density was read at 450 nm using a microplate reader and the sample concentration was calculated based on the standard curve. The assay has a sensitivity of 25 mg/dl.
Plasma insulin concentrations were measured using a rat-specific enzyme-linked immunosorbent assay kit (1-2-3 Rat Insulin ELISA, ALPCO Diagnostics, Windham, NH). In this assay, rat insulin in the sample reacted with peroxidase-conjugated mouse monoclonal anti-insulin antibody solution and the mouse monoclonal anti-insulin antibodies coated on the microplate. Plates were then washed to remove the unbound enzyme labeled anti-insulin antibody. The bound conjugate was detected by reaction with 3,3′,5,5′-tetramethylbenzidine. The generated yellow color was read spectrophotometrically at 450 nm and the sample concentration was calculated according to the standard curve. The analysis was performed in duplicate and controlled by Mammalian/Rat Insulin Two-Level Control (ALPCO Diagnostics, Windham, NH). The limit of quantitation for this assay is 0.07 ng/ml.
Pharmacokinetic/pharmacodynamic model
Pharmacokinetics
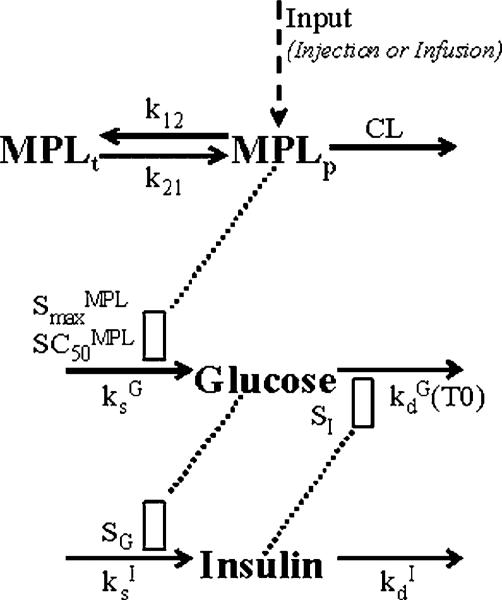
The MPL pharmacokinetics was described by a two-compartment model with bolus input (injection study) or zero-order input (infusion study) into the central compartment (Figure 1):
| (1) |
| (2) |
| (3) |
where Ap and At represent the amount of drug in the plasma and tissue compartments. MPLp is the plasma methylprednisolone concentration, CL is the drug clearance, Vp is the central volume of distribution, and k12 and k21 are the distribution rate constants. For the infusion study, k0 is the zero-order rate constant of drug input into the plasma.
Figure 1.
PK/PD model of MPL effects on glucose regulation. Parameters and differential equations for the model are defined in Equations (1–3), (6–12). The dotted line and open rectangles represent stimulation of the various processes via indirect mechanisms. Symbols are defined in the tables.
Since limited PK data at only two time points were collected for confirmation purposes in the injection study, all PK parameters were fixed based on published results from our laboratory in which the same drug, dose and type of animal were used [5,6]. Due to experimental limitations, PK samples could not be collected immediately after implantation and removal of the infusion pump. Therefore, the ascending part of the PK curve after infusion started which contains information regarding drug absorption, and the descending part of the PK curve after infusion finished, which contains information regarding the drug distribution and elimination, were unavailable. Only the apparent CL for the infusion study was estimated by fitting the data and other PK parameters were fixed according to a previous infusion study [7]. Once the pharmacokinetic parameters were obtained, they were fixed in the following dynamic analysis.
Body weight
The catabolic effects of MPL on whole body weights upon long-term dosing were described by indirect response model IV [7,8] with the stimulation function applied to the degradation rate (Figure 3):
| (4) |
where Bwt0 represents the predose body weight at time zero and %Bwt represents the rat body weight expressed as the percentage of its predose body weight Bwt0 (i.e. %Bwt = Bwt/Bwt0*100%). Without drug treatment, body weight is controlled by the zero-order production rate constant and the first-order degradation rate constant . The and are drug-specific parameters representing the maximum possible stimulation of and the plasma MPL concentration required for half-maximal stimulation. Rats kept growing without drug treatment, hence the system was not at steady-state at time zero. Once the steady-state body weight (%Bwtss = Bwtss/Bwt0) was achieved, the system would produce the following relationship:
| (5) |
Body weights of the three rat groups receiving 7 day infusions were fitted simultaneously using the proposed model. The initial condition for Equation (4) was fixed as 100%. The predose body weight Bwt0 was fixed as the mean body weight of 3–4 animals at time zero for each dose group.
Figure 3.
Indirect response model for effects of MPL on body weight (top) and the time course of changes in body weight for the saline (▲), 0.1 (●) and 0.3 (○) mg/kg/h infusion groups. The open rectangle in the diagram represents stimulation of body weight loss by MPL plasma concentration via indirect mechanisms. Lines in the bottom graph are results of the simultaneous fittings with Equations (4) and (5). The symbols and PD parameters are listed in Table 2.
Glucose-insulin dynamics
Blood glucose has both exogenous sources such as food intake and endogenous sources such as gluconeogenesis and glycogen breakdown. It can be consumed for energy or stored as glycogen or fat in peripheral tissues. The major hormonal regulators for glucose are insulin and glucagon. Once glucose concentrations rise, it will be transported into pancreatic β-cells, activate a series of signal transductions, and stimulate insulin synthesis and release. Insulin has broad glucose-lowering effects by inhibiting its input such as gluconeogenesis and glycogenolysis, as well as by stimulating its output such as glucose uptake into peripheral tissues, glycogen synthesis, triglyceride synthesis and storage [9]. This metabolic system is maintained in balance in normal physiological states. If glucose is induced continuously by exogenous compounds, saturation and/or desensitization of transporters/enzymes/receptors may occur [28]. The balance will be disturbed and the system may progress into a pathological state without proper internal control. Hyperglycemia, insulin resistance and/or diabetes may evolve [30].
The CS can affect glucose metabolism by increasing hepatic gluconeogenesis and decreasing glucose uptake and utilization in peripheral tissues [1]. These influences may result in hyperglycemia and eventually lead to steroid-diabetes. Treatment with CS can also cause increased insulin concentrations and even pancreatic β-cell hyperplasia upon long-term dosing. However, these elevations are secondary to the CS-induced hyperglycemia, because CS do not have direct effects on insulin secretion [2].
Based on the above mechanisms, a PD model incorporating glucose/insulin inter-regulations, MPL effect on glucose, and disease progression was developed as depicted in Figure 1. The following equations were fitted to glucose and insulin data from all treatments simultaneously:
| (6) |
| (7) |
where G and I represent glucose and insulin plasma concentrations. Glucose is constantly produced with a zero-order rate constant and utilized with a first-order rate constant . The CS effect on glucose was described by MPLp-dependent sigmoidal stimulation of presumably via simulating gluconeogenesis. The and are drug-specific parameters representing the maximum possible stimulation of and the plasma MPL concentration required for half-maximal stimulation. Insulin controls glucose concentrations by stimulating its disposition with a linear efficiency constant (SI). The change of insulin from its baseline value at time zero (I0) was used to drive this stimulatory effect.
In hyperglycemic disease states, the glucose disposition rate decreases with time and is defined as:
| (8) |
| (9) |
where T0 is a time-dependent variable describing the duration of glucose concentration above its baseline value at time zero (G0), i.e. T0 = 0 when G≤G0 at baseline; once G>G0, T0 = T. Before treatment, the first-order rate is at its baseline value , which represents the combination of endogenous glucose utilization and storage. At high glucose concentrations, the inhibition of is dependent on the length of hyperglycemic duration T0 and is characterized by the maximum achievable inhibition , the hyperglycemic duration required for 50% maximal inhibition , and the Hill factor γG. This time-dependent decrease of could be explained by the possible saturation, desensitization or down-regulation of transporters/enzymes/receptors in glucose uptake, utilization and storage pathways.
As shown in Equation (7), insulin is also produced at a zero-order rate and degraded at a first-order rate . Change of glucose from its steady-state value (Gss) can stimulate insulin production with a linear efficiency constant SG. The Gss represents the steady-state glucose concentration without MPL and insulin action, and is defined as:
| (10) |
At time zero, the system was assumed to be at its physiological steady-state and Equations (6) and (7) yielded the following baseline equations:
| (11) |
| (12) |
where initial values G0 and I0 were fixed as the mean glucose and insulin concentrations of 3–4 animals at time zero for each dose group.
Other PD models containing MPL-induced temporary glucose production (sigmoidal stimulation of by MPL within limited time duration), MPL inhibition of glucose utilization (sigmoidal inhibition of by MPL), or insulin inhibition of glucose production (sigmoidal inhibition of by I) were also tested.
Data analysis
Differences in the plasma glucose and insulin time profiles between different treatment groups for both injection and infusion studies were tested for statistical significance using a two-way, repeated measures ANOVA. Statistical analyses were performed using SAS 8.0 (SAS Institute Inc., Cary, NC), and the level of significance for each test was α = 0.05.
Naive-pooled data from the 3–4 animals in each dose group were used to fit the PK/PD models using ADAPT II software [10]. The maximum likelihood method was used with variance model specified as V(σ,θ,-ti) = σ2●Y(θ,ti)σ2, where V(σ,θ,ti) is the variance for the ith point, Y(θ,ti) is the ith predicted value from the PK/PD model, θ represents the estimated structural parameters, and σ1, σ2 are the variance parameters which were estimated. Various proposed PD models for glucose-insulin dynamics were fitted and compared. The final model was selected based on visual inspection of curve fitting, estimator criterion value, sum of squared residuals, Akaike information criterion, Schwartz criterion and confidence of parameter estimations. Only results of the final model fitting is presented in this paper due to the extensive model comparisons conducted.
Results
Pharmacokinetics
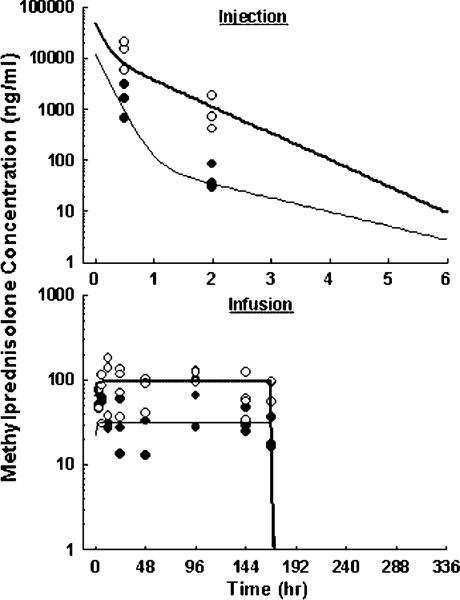
The plasma MPL concentration-time profiles are shown in Figure 2 and Table 1 lists the PK parameters. Because of the major purpose of investigating dynamic regulations in this study and the rich PK information from our previous studies [5,6], MPL concentrations were measured at only two time points after injection to reduce total blood loss. Simulations using established parameters well captured the current single-dose results. Subcutaneous infusion using osmotic pumps produced constant MPL exposure for 7 days. Because of its short elimination half-life (~30 min), MPL concentrations had reached steady-state by the first sampling point after pump implantation (3 h) and diminished below the detection limit by the first sampling point after pump removal (172 h). The ascending part of the MPL concentration profile which reflects the absorption rate of the drug was unavailable. With high lipophilicity, MPL should easily diffuse in the subcutaneous space. Therefore, it was assumed that the bioavailability was complete and the absorption rate was much faster than the rate of drug release from the pump. Model fitting yielded the drug clearance of 3.15 l/h/kg, and predicted steady-state concentrations of 31.7 and 95.2 ng/ml during low- and high-dose infusions.
Figure 2.
Pharmacokinetics of MPL upon administration of 10 (●) and 50 (○) mg/kg intravenous injection (top), or 0.1 (●) and 0.3 (○) mg/kg/h subcutaneous infusion for 7 days (bottom). Symbols are observed drug concentrations. Lines in top graph are results of simulation using established parameters. Lines in bottom graph are results of the simultaneous fitting with Equations (1–3). The PK parameters are listed in Table 1.
Table 1.
Pharmacokinetic parameters for methylprednisolone
| Parameter | Definition | Estimate Dose, mg/kg |
CV% | ||
|---|---|---|---|---|---|
| 10 | 50 | Infusions | |||
| CL (l/h/kg) | Clearance | 4.04 | 3.17 | 3.15 | 7 |
| Vp (l/kg) | Central volume | 0.82 | 0.97 | – | Fixed |
| k12 (h–1) | Rate constant | 0.32 | 2.70 | – | Fixed |
| k21 (h–1) | Rate constant | 0.68 | 2.75 | – | Fixed |
Body weights
Animals receiving the saline infusion showed continuously increasing body weights over the 2 week time period (Figure 3). This differed from the constant weights found previously [7,8], which may be attributed to the longer experimental time frame in the current study (2 vs 1 week). The 7 day infusion of MPL caused pronounced losses in rat body weights, and this alteration was reversible with weights increasing faster than natural growth once MPL infusion was terminated at 168 h. Weights in the low- and high-dose groups fell to 87.8±6.1% and 83.8±1.6% of predose values by 168 h. The lower weight at 192 h, which appeared also in the control group, was possibly due to the effect of surgery (pump removal under halothane) at the end of infusion.
The model captured the body weight changes in all groups simultaneously. The PD parameters are listed in Table 2. The estimated %Bwtss of 106% implies that the rats will have a maximum achievable body weight of 340–359 g with the body weight Bwt0 of 320–338 g before treatment. The capacity parameter of 0.60 suggests that rats may lose weight to as low as 66.4% of predose weights with maximum drug toxicity, assuming it is not lethal. The drug sensitivity of 14.5 ng/ml indicates that the MPL concentration was maintained above its SC50 value during both low- and high-dose infusions. The model predicted that rats could lose weights to as low as 75.3% and 69.9% with continuous low and high infusions, but this was not achieved at the end of 7 days.
Table 2.
Pharmacodynamic parameters for body weight changes
| Parameter | Definition (doses) | Estimate | CV% |
|---|---|---|---|
| Weight loss rate constant | 0.0030 | 23 | |
| Maximal stimulation | 0.60 | 20 | |
| Stimulation constant | 14.5 | 37 | |
| %Bwtss (%) | Maximal percent weight | 106.3 | 2 |
| Bwt0 (g) | Predose weight (0, 0.1, 0.3) | 338, 333, 320 | Fixed |
| a | Weight gain rate (0, 0.1, 0.3) | 108, 106, 102 | 26 |
Secondary parameter.
Glucose-insulin dynamics
The preliminary studies showed that ketamine/xylazine anesthesia causes an immediate increase in plasma glucose and a decline in plasma insulin, and this alteration was reversible within 12 h (data not shown). This finding is consistent with published results in animals [11,12]. Prolonged exposure to halothane (1.5% for 1 h) is associated with changes in carbohydrate metabolism in rat muscle [13]. Hence, pump implantation and removal were performed under short halothane anesthesia (<5 min), which produced no changes in plasma glucose and insulin (data not shown).
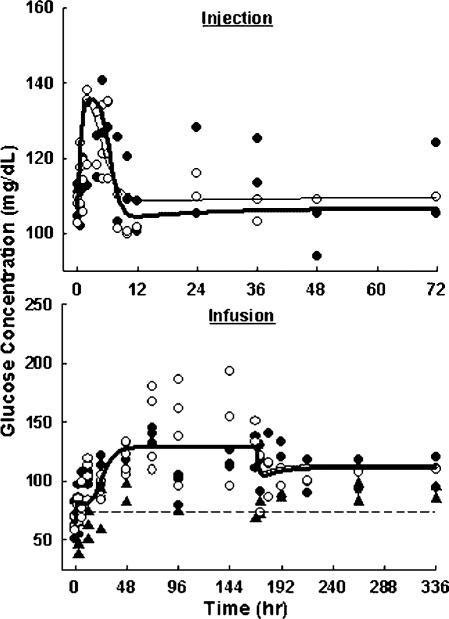
As shown in Figure 4, plasma glucose temporarily increased from 110±5 to 131±5 mg/dl after 10 mg/kg MPL injection, and from 107±4 to 124±10 mg/dl after 50 mg/kg injection. Glucose concentrations peaked at around 6 h and quickly returned to baseline after 12 h. Significant differences between the glucose profiles of the two injection groups were found (p = 0.02). As shown in Figure 5, plasma insulin markedly increased from 0.15±0.10 to 1.21±0.09 ng/ml after the 10 mg/kg MPL injection, and from 0.24±0.14 to 2.21±0.07 ng/ml after the 50 mg/kg injection. Insulin profiles showed a delayed increase to a maximum at around 10 h followed by a slow return to baseline by 72 h. This insulin induction was highly dose-dependent in regard to the time courses with p = 0.0008. Both glucose and insulin showed reversible changes after single dose MPL, suggesting that homeostasis of the system was maintained.
Figure 4.
Plasma glucose versus time profiles upon administration of 10 (●) and 50 (○) mg/kg MPL injection (top), or saline (▲), 0.1 (●) and 0.3 (○) mg/kg/h MPL infusion for 7 days (bottom). Lines are results of the simultaneous fittings of glucose and insulin with Equations (6–12). The PD parameters are listed in Table 3.
Figure 5.
Plasma insulin versus time profiles upon administration of 10 (●) and 50 (○) mg/kg MPL injection (top), or saline (▲), 0.1 (●) and 0.3 (○) mg/kg/h MPL infusion for 7 days (bottom). Lines are defined as in Figure 4.
In control animals, glucose and insulin time courses showed no significant changes during and after saline infusion. This suggests that performance of surgery (pump implantation and removal) under halothane had no effect on the PD markers. During drug infusions, plasma glucose continuously increased from 66±14 to 120±16 mg/dl with 0.1 mg/kg/h MPL infusion, and from 65±5 to 142±12 mg/dl with 0.3 mg/kg/h infusion. Glucose concentrations rose fast in the first 48 h and approached a pseudo plateau in the following 5 days. Once the pump was removed, glucose exhibited a small decrease and then stayed elevated at levels of 107±18 (low-dose) and 111±1 mg/dl (high-dose) until the end of the study (336 h). Both drug-treated groups showed significantly different time profiles from the control group (p<0.001). There were no significant differences between the two dose groups (p = 0.88). Insulin concentrations showed continuous increases from 0.62±0.28 to 4.16±0.73 ng/ml with low-dose MPL 7-day infusion, and from 0.26±0.11 to 7.37±0.72 ng/ml with high-dose infusion. However, once drug input was stopped at 168 h, plasma insulin immediately returned to baseline in both dose groups. Both treated groups showed significantly different time profiles from the control group (p<0.001). Insulin induction during MPL infusion was dose-dependent with p = 0.0001. The continuous hyperglycemia during and after long-term MPL treatment suggests that irreversible changes had occurred in the system. The fast insulin return to baseline after infusion despite the almost doubled glucose concentration implies possible dysfunctions in glucose-induced insulin secretion.
Figures 4 and 5 show the fittings of the naive-pooled data using the PD model for glucose-insulin dynamics (Equations (6–12)), and Table 3 lists the parameter estimates. This model represented the final selection after comparing several other mechanistic models. Our model nicely captured the temporary glucose and insulin increases after short-term MPL treatment, and adequately predicted the continuous hyperglycemia and reversible insulin induction with long-term dosing.
Table 3.
Pharmacodynamic parameters for glycemic effects
| Parameter | Definition (doses) | Estimate | CV% |
|---|---|---|---|
| Glucose dynamics | |||
| Glucose utilization rate constant | 1.48 | 47 | |
| SG (mg/dl)–1 | Glucose sensitivity | 1.41 | 31 |
| Maximal stimulation | 0.29 | 16 | |
| Stimulation constant | 9.31 | 52 | |
| Maximal inhibition | 0.42 | 5 | |
| Inhibition constant | 22.5 | 11 | |
| γ G | Hill factor | 4.32 | 51 |
| G0,injection (mg/dl) | Baseline glucose (10, 50) | 110, 107 | Fixed |
| G0,infusion (mg/dl) | Baseline glucose (0, 0.1, 0.3) | 74, 66, 65 | Fixed |
| a | Glucose production rate (10, 50) | 162, 158 | 47 |
| a | Glucose production rate (0, 0.1, 0.3) | 109, 98, 96 | 47 |
| Insulin dynamics | |||
| Insulin degradation rate constant | 0.038 | 37 | |
| SI (ng/ml)–1 | Insulin sensitivity | 0.014 | 71 |
| I0,injection (ng/ml) | Baseline insulin (10, 50) | 0.15, 0.24 | Fixed |
| I0,infusion (ng/ml) | Baseline insulin (0, 0.1, 0.3) | 0.78, 0.26, 0.26 | Fixed |
| a | Insulin secretion rate (10, 50) | 0.0057, 0.0091 | 37 |
| a | Insulin secretion rate (0, 0.1, 0.3) | 0.03, 0.01, 0.01 | 37 |
Secondary parameter.
Baseline parameters G0 and I0 were fixed for each study and each dose group separately to account for the high variability of glucose and insulin concentrations. Animals in the infusion study appeared to have lower baseline glucose and higher baseline insulin than animals in the infusion study. This was due to the different characteristics of rats used in each study. Heavier and older rats were used in the infusion study for better toleration of the adverse events caused by long term MPL administration. This resulted in differing glucose and insulin production rate constants, but otherwise the profiles were fitted with a universal set of parameters.
Physiological parameters , SG, and SI describe the glucose-insulin regulation system in the normal status. The efficiency of glucose in stimulating insulin secretion, reflected by the SG value of 1.41 (mg/dl)–1 implies that insulin production rate would increase 1-fold when glucose concentrations increase 0.7 mg/dl. Similarly, SI reflects the ability of insulin to stimulate glucose utilization. The fast return phase of plasma glucose after short-term induction was governed partly by its endogenous degradation rate constant , and partly by the effect of insulin. The slow return phase of plasma insulin was controlled by its natural degradation rate constant . The calculated glucose production rate agrees with the hepatic glucose production rate of 1 mg/kg/min in the literature [14] assuming the volume of distribution of glucose is 2.9 dl/kg in rats [15].
The and are drug-specific parameters characterizing MPL effects on glucose regulation. The low estimate of 9.31 ng/ml indicates the relatively high sensitivity of MPL for regulating glucose. Plasma MPL concentrations were maintained above its SC50 for 5–6 h after injection, and during the entire 7 day infusion.
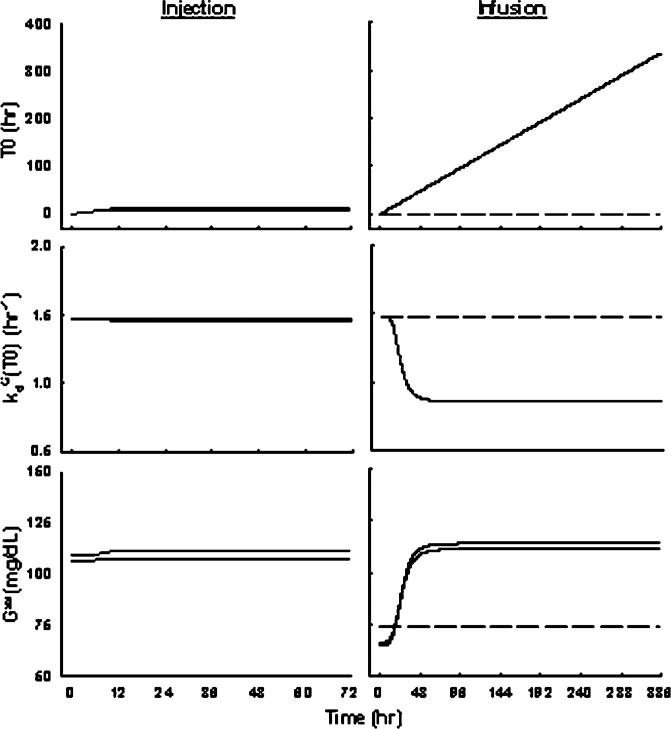
Parameters , and γG describe the system abnormalities underlying progression of hyperglycemia with long-term treatment. The dependent variable T0 describes the duration of glucose concentration above its baseline value at time zero (G0). Due to the hypothesis of glucose toxicity, glucose degradation rate decrease with time during hyperglycemia, i.e. inhibited by duration T0. The of 0.42 suggests that glucose degradation rate could be inhibited to as low as 0.86 h–1. The high γG estimate of 4.32 indicates a fast system adaptation once was achieved by 1 day of continuous MPL exposure. Without these pathological parameters, glucose concentrations would be greatly under-predicted during infusion and return to baseline after infusion (data not shown). Figure 6 shows the simulated profiles for T0, kd(T0) and Gss after MPL treatment. After single-doses, glucose was only temporarily induced (T0 small, limited duration) therefore causing very little change of the system (kd(T0) and Gss almost remained constant). With long-term treatment, glucose was continually induced during infusion and caused a reduced glucose disposition rate to a minimum after 2 days, which could be explained by saturation/desensitization of transporters or enzymes. This dysfunction in glucose utilization was irreversible, therefore causing the extended hyperglycemia. Since maximum impairment was achieved, glucose would stay at a new steady-state governed by the balance of its production and altered disposition rates. This newly established steady-state controlled insulin secretion, therefore no further insulin was induced after MPL administration was terminated.
Figure 6.
Simulations of T0, and Gss versus time profiles upon administration of 10 and 50 mg/kg MPL injection (left), or saline, 0.1 and 0.3 mg/kg/h MPL infusion for 7 days (right) using Equations (6–12) with parameters fixed as in Table 3.
Discussion
The clinical usage of CS can exacerbate existing diabetes and can precipitate ‘steroid-diabetes’. In patients without diabetes, the risk for this complication is increased with a family history of diabetes, aging, obesity and increasing dose [3]. Studies in renal transplant recipients receiving chronic CS showed that steroid-induced diabetes develops in 6% to 48% of patients [16,17]. In this study, ADX animals developed irreversible hyperglycemia with continuous MPL infusion for 7 days. This mimicked the early phase of disease progression in drug-induced diabetes. Pronounced body weight loss was observed in rats during the 7 day infusion, which was consistent with previous observations [7]. This dose and duration-dependent catabolic effect of MPL was well captured by our modeling of body weight. This PK/PD model successfully characterized the glucose metabolic system at the normal state, in the disease state, its response to drug treatment, and how the system homeostasis was disturbed.
Increased glucose and insulin concentrations after various CS treatments have been described in humans and animals [18,19]. Pellacani and coworkers reported that after acute administration of 80 mg MPL to healthy volunteers, an alteration of glucose tolerance, as expressed by the increased glycemic AUC and insulinemic AUC after oral glucose tolerance test with 75 g glucose, occurred after 2 h. This glucose intolerance was completely normalized at 24 h [20]. This prompt reversibility of the negative effect on glucose tolerance is consistent with our results. Thomas et al. reported that hyperglycemia (1.5-fold) and hyperinsulinemia (4-fold) evolved in mice treated with dexamethasone 2.5 mg/kg/day for 10 days [21], which was qualitatively comparable with our findings. However, little information was available in the literature about system characteristics after chronic treatment. It is of special importance to assess whether irreversible damage of the metabolic system is produced by long-term therapy. Therefore, rats were monitored for a 1 week wash-out period after the 7 day infusion in our study.
The exact mechanism responsible for the alteration of glucose metabolism and insulin action following exogenous CS administration is still unclear. The CS can both increase glucose production and decrease glucose disposition. Essentially every step in the gluconeogenic pathway is enhanced by CS. These steroids up-regulate gluconeogenic enzymes such as phosphoenolpyruvate carboxykinase and glucose-6-phosphatase [22,23]. They also induce several transaminases, which produce gluconeogenic precursors. The CS decrease protein synthesis and increase protein breakdown in several tissues, resulting in an increased release of amino acids, which serve as gluconeogenic precursors. The CS also increase gluconeogenic substrates by increasing glycerol release from fat cells [24]. A second major effect of CS on carbohydrate metabolism results from their inhibition of glucose uptake and metabolism in peripheral tissues. In adipose tissue, they can decrease the number of glucose transporters by suppressing RNA and protein synthesis [24]. The CS also affect actions of other hormones and second messengers. The CS inhibit cyclic AMP (cAMP) phosphodiesterase which degrades cAMP [25,26]. Thus, tissue cAMP could rise and the many actions of cAMP would be observed. The CS may also influence insulin action by altering both insulin receptor and postreceptor functions [27]. There is no direct effect of CS on insulin secretion.
All of the above mechanisms may contribute, at least in part, to the hyperglycemic/hyperinsulinemic effect of MPL. Other PD models based on mechanisms of CS action on either stimulating glucose production or inhibiting glucose disposition have been tested. Although both mechanisms may be relevant, a model with CS actions on both processes would result in overparameterization. A model with stimulation of production better captures the data, and was consistent with the predominant role of CS in controlling gluconeogenesis.
The body can sense and respond to elevated blood glucose by secreting insulin. The change of glucose instead of the absolute glucose concentration was used as a stimulator for insulin secretion in the PD models. This worked better to prompt alterations in the homeostasis of the system.
Insulin can both decrease hepatic glucose production and increase glucose disposition in peripheral tissues. This hormone inhibits gluconeogenesis and glycogenolysis in the liver. It has recently been suggested that insulin's hepatic action is secondary to its effects on peripheral tissues [9]. Insulin has long been known to increase glucose uptake in muscle and fat via relocation of the GLUT-4 transporter. Insulin also promotes the disposition of glucose within cells through effects on glycogen synthesis and glucose oxidation.
Glycemic control by insulin with inhibiting input or stimulating output were both tested in model development. Stimulation of glucose utilization better captured the data and was in agreement with insulin's major actions in peripheral tissues. Change of plasma insulin instead of the absolute insulin concentration was used as a stimulator for glucose disposition.
Chronic hyperglycemia is well known to cause insulin resistance [28]. Impairment of insulin-mediated glucose uptake is one of the first manifestations of insulin resistance. Glucose can induce desensitization of glucose transporters in adipose tissue, the so-called ‘glucose toxicity’ [29]. The synthesis of muscle glycogen accounts for most of the total body glucose disposal. Under hyperglycemic-hyperinsulinemic conditions, defective muscle glycogen synthesis via decreased hexokinase activity plays a major role in causing insulin resistance [30]. Recent publications identified the role of the hexosamine pathway in mediating hyperglycemia-induced insulin resistance [31]. Excessive glucose was transported into muscle cells via the non-insulin-sensitive GLUT-1 transporter and phosphorylated via the non-insulin-sensitive hexokinase isoform. Following a series of reactions, the end-product UDP-N-acetylglucosamine may undergo O-linked glycosylation which may cause alteration of insulin signaling in target cells and inhibit its function such as the translocation of GLUT-4.
Since it was not clear whether the changes in glucose uptake and utilization were primary drug effects or secondary system alterations during CS-induced long-term hyperglycemia, a semi-mechanistic disease progression model incorporating reduced endogenous glucose disposition with duration of hyperglycemia was used to capture the irreversible changes observed in glucose homeostasis after chronic dosing. This modification provides the model flexibility to predict disease progression with any hyperglycemic factor, such as high-fat diet, poor living habits, aging and other drugs.
Many researchers have explored the modeling of the carbohydrate system. Several mechanistic models had been developed for simulating glucose profiles and optimizing insulin therapy in insulin-dependent diabetes [32]. Comprehensive models incorporating all the major processes of glucose, insulin, glucagon dynamics and their interrelationships were used to simulate carbohydrate regulation under various pathophysio-logical situations [33,34]. These models, although mimicking the underlying mechanisms, were too complex for fitting experimental data, and could only be used for simulation purposes.
The so-called ‘minimal models’ are widely used to analyse results from intravenous or oral glucose tolerance tests, and then estimate metabolic indices of ‘glucose effectiveness’, ‘insulin sensitivity’ and ‘β-cell sensitivity’ [35–37]. These models are partly mechanism-based and can be used to quantitate the glucose regulation system from routine clinical tests. However, glucose and insulin profiles are not fitted simultaneously. Glucose kinetics are described only when insulin concentrations are specified, and insulin kinetics are described only when glucose concentrations are given as input [38]. Furthermore, drug effects on the system are determined by comparing estimated metabolic indexes before and after treatment. Although this would provide some indications about what process was affected by the treatment, the nonlinear, time-dependent drug effect is not quantitatively described.
Although our model successfully described all glucose and insulin dynamics simultaneously, it was limited by several factors. Some known mechanisms (such as the presence of insulin-dependent and insulin-independent glucose utilization pathways, and insulin in tissue, not in plasma as the stimulator for glucose utilization) were overlooked to avoid overparameterization. Plasma MPL concentration was used as the driving force for drug action. However, it is well-appreciated that CS act by binding to their receptors, and then affect message and proteins of the enzyme/receptor/transporter(s) involved in glucose metabolism [39]. Studies involving intermediate receptor/gene/protein-mediated processes would provide more insights into understanding CS effect on glucose. Model complexities obliged the use of the linear stimulation coefficients SG and SI that limit prediction capability. The rats were adrenalectomized to eliminate endogenous corticosterone effects, which might have distorted the natural glucose homeostasis owing to the disturbed endocrine system.
In summary, hyperglycemia and hyperinsulinemia evolved after CS treatment of rats. This systemic change was temporary after acute dosing. Chronic dosing was associated with additional complexities which caused irreversible disturbance of system homeostasis. Mechanistic PK/PD modeling not only allows quantitation of drug effects but also provides additional insights on glucose-insulin relationships. In addition, the proposed model could be applied to other drugs and diseases related to this metabolic system.
Acknowledgements
Financial support for this research was provided by Grant GM24211 from the National Institutes of Health. The authors would like to thank Ms Suzette Mis for performing the HPLC assay, and Ms Xiao Tan for technical assistance for glucose and insulin assays in the infusion study.
References
- 1.Wilcke JR, Davis LE. Review of glucocorticoid pharmacology. Vet Clin North Am Small Anim Pract. 1982;12:3–17. doi: 10.1016/s0195-5616(82)50001-0. [DOI] [PubMed] [Google Scholar]
- 2.Baxter JD, Forsham PH. Tissue effects of glucocorticoids. Am J Med. 1972;53:573–589. doi: 10.1016/0002-9343(72)90154-4. [DOI] [PubMed] [Google Scholar]
- 3.Hirsch IB, Paauw DS. Diabetes management in special situations. Endocrinol Metab Clin North Am. 1997;26:631–645. doi: 10.1016/s0889-8529(05)70271-1. [DOI] [PubMed] [Google Scholar]
- 4.Haughey DB, Jusko WJ. Analysis of methylprednisolone, methylprednisone and corticosterone for assessment of methylprednisolone disposition in the rat. J Chromatogr. 1988;430:241–248. doi: 10.1016/s0378-4347(00)83159-x. [DOI] [PubMed] [Google Scholar]
- 5.Sun YN, DuBois DC, Almon RR, Jusko WJ. Fourth-generation model for corticosteroid pharmacodynamics: a model for methylprednisolone effects on receptor/gene-mediated glucocorticoid receptor down-regulation and tyrosine amino-transferase induction in rat liver. J Pharmacokinet Biopharm. 1998;26:289–317. doi: 10.1023/a:1023233409550. [DOI] [PubMed] [Google Scholar]
- 6.Sun YN, DuBois DC, Almon RR, Pyszczynski NA, Jusko WJ. Dose-dependence and repeated-dose studies for receptor/gene-mediated pharmacodynamics of methylprednisolone on glucocorticoid receptor down- regulation and tyrosine aminotransferase induction in rat liver. J Pharmacokinet Biopharm. 1998;26:619–648. doi: 10.1023/a:1020746822634. [DOI] [PubMed] [Google Scholar]
- 7.Ramakrishnan R, DuBois DC, Almon RR, Pyszczynski NA, Jusko WJ. Pharmacodynamics and pharmacogenomics of methylprednisolone during 7-day infusions in rats. J Pharmacol Exp Ther. 2002;300:245–256. doi: 10.1124/jpet.300.1.245. [DOI] [PubMed] [Google Scholar]
- 8.Dayneka NL, Garg V, Jusko WJ. Comparison of four basic models of indirect pharmacodynamic responses. J Pharmacokinet Biopharm. 1993;21:457–478. doi: 10.1007/BF01061691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Flakoll PJ, Carlson MG, Cherrington AD. Chapter 14. Physiologic action of insulin. In: LeRoith D, Taylor SI, Olefsky JM, editors. Diabetes Mellitus A Fundamental and Clinical Text. 2nd edn. Lippincott Williams & Wilkins; Philadelphia: 2000. pp. 148–161. [Google Scholar]
- 10.D'Argenio DZ, Schumitzky A. BioMedical Simulations Resource; Los Angeles: 1997. ADAPT II User's Guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software. [Google Scholar]
- 11.Tranquilli WJ, Thurmon JC, Neff-Davis CA, et al. Hyperglycemia and hypoinsulinemia during xylazine-ketamine anesthesia in thoroughbred horses. Am J Vet Res. 1984;45:11–14. [PubMed] [Google Scholar]
- 12.Hindlycke M, Jansson L. Glucose tolerance and pancreatic islet blood flow in rats after intraperitoneal administration of different anesthetic drugs. Ups J Med Sci. 1992;97:27–35. doi: 10.3109/03009739209179279. [DOI] [PubMed] [Google Scholar]
- 13.Ferreira LD, Palmer TN, Fournier PA. Prolonged exposure to halothane and associated changes in carbohydrate metabolism in rat muscles in vivo. J Appl Physiol. 1998;84:1470–1474. doi: 10.1152/jappl.1998.84.4.1470. [DOI] [PubMed] [Google Scholar]
- 14.Nawano M, Oku A, Ueta K, et al. Hyperglycemia contributes insulin resistance in hepatic and adipose tissue but not skeletal muscle of ZDF rats. Am J Physiol Endocrinol Metab. 2000;278:E535–E543. doi: 10.1152/ajpendo.2000.278.3.E535. [DOI] [PubMed] [Google Scholar]
- 15.Sato S, Katayama K, Kakemi M, Koizumi T. A kinetic study of chlorpromazine on the hyperglycemic response in rats. II. Effect of chlorpromazine on plasma glucose. J Pharmacobiodyn. 1988;11:492–503. doi: 10.1248/bpb1978.11.492. [DOI] [PubMed] [Google Scholar]
- 16.Ruiz JO, Simmons RL, Callender CO, Kjellstrand CM, Buselmeier TJ, Najarian JS. Steroid diabetes in renal transplant recipients: pathogenetic factors and prognosis. Surgery. 1973;73:759–765. [PubMed] [Google Scholar]
- 17.Arner P, Gunnarsson R, Blomdahl S, Groth CG. Some characteristics of steroid diabetes: a study in renal-transplant recipients receiving high-dose corticosteroid therapy. Diabetes Care. 1983;6:23–25. doi: 10.2337/diacare.6.1.23. [DOI] [PubMed] [Google Scholar]
- 18.Schulz TB, Jorde R, Burhol PG. Fasting portal vein plasma levels of gastric inhibitory polypeptide (GIP) and extractable fasting GIP in the duodenal wall in rats treated with methylprednisolone or alloxan compared with normal controls. Scand J Gastroenterol. 1982;17:487–490. doi: 10.3109/00365528209182236. [DOI] [PubMed] [Google Scholar]
- 19.Thompson MD, Gallagher WJ, Iaizzo PA, Lanier WL. The effect of chronic dexamethasone-induced hyperglycemia and its acute treatment with insulin on brain glucose and glycogen concentrations in rats. Anesthesiology. 2000;93:1279–1284. doi: 10.1097/00000542-200011000-00022. [DOI] [PubMed] [Google Scholar]
- 20.Pellacani A, Fornengo P, Bruno A, et al. Acute methylprednisolone administration induces a transient alteration of glucose tolerance and pyruvate dehydrogenase in humans. Eur J Clin Invest. 1999;29:861–867. doi: 10.1046/j.1365-2362.1999.00553.x. [DOI] [PubMed] [Google Scholar]
- 21.Thomas CR, Turner SL, Jefferson WH, Bailey CJ. Prevention of dexamethasone-induced insulin resistance by metformin. Biochem Pharmacol. 1998;56:1145–1150. doi: 10.1016/s0006-2952(98)00151-8. [DOI] [PubMed] [Google Scholar]
- 22.Chan L, Means AR, O'Malley BW. Steroid hormone regulation of specific gene expression. Vitam Horm. 1978;36:259–295. doi: 10.1016/s0083-6729(08)60986-3. [DOI] [PubMed] [Google Scholar]
- 23.Jin JY, DuBois DC, Almon RR, Jusko WJ. Receptor/gene-mediated pharmacodynamic effects of methylprednisolone on phosphoenolpyruvate carboxykinase regulation in rat liver. J Pharmacol Exp Ther. 2004;309:328–339. doi: 10.1124/jpet.103.061515. [DOI] [PubMed] [Google Scholar]
- 24.Baxter JD. Glucocorticoid hormone action. Pharmacol Ther [B] 1976;2:605–669. doi: 10.1016/0306-039x(76)90010-6. [DOI] [PubMed] [Google Scholar]
- 25.Manganiello V, Vaughan M. An effect of dexamethasone on adenosine 3′,5′-monophosphate content and adenosine 3′,5′-monophosphate phosphodiesterase activity of cultured hepatoma cells. J Clin Invest. 1972;51:2763–2767. doi: 10.1172/JCI107096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jin JY, Almon RR, DuBois DC, Jusko WJ. Modeling of corticosteroid pharmacogenomics in rat liver using gene microarrays. J Pharmacol Exp Ther. 2003;307:93–109. doi: 10.1124/jpet.103.053256. [DOI] [PubMed] [Google Scholar]
- 27.Pagano G, Cavallo-Perin P, Cassader M, et al. An in vivo and in vitro study of the mechanism of prednisone-induced insulin resistance in healthy subjects. J Clin Invest. 1983;72:1814–1820. doi: 10.1172/JCI111141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rossetti L, Giaccari A, DeFronzo RA. Glucose toxicity. Diabetes Care. 1990;13:610–630. doi: 10.2337/diacare.13.6.610. [DOI] [PubMed] [Google Scholar]
- 29.Marshall S, Bacote V, Traxinger RR. Discovery of a metabolic pathway mediating glucose-induced desensitization of the glucose transport system. Role of hexosamine biosynthesis in the induction of insulin resistance. J Biol Chem. 1991;266:4706–4712. [PubMed] [Google Scholar]
- 30.Shulman GI. Cellular mechanisms of insulin resistance in humans. Am J Cardiol. 1999;84:3J–10J. doi: 10.1016/s0002-9149(99)00350-1. [DOI] [PubMed] [Google Scholar]
- 31.Yki-Jarvinen H, Makimattila S. Insulin resistance due to hyperglycaemia: an adaptation protecting insulin-sensitive tissues. Diabetologia. 1997;40(Suppl 2):S141–S144. doi: 10.1007/s001250051431. [DOI] [PubMed] [Google Scholar]
- 32.Berger MP, Rodbard D. A pharmacodynamic approach to optimizing insulin therapy. Comput Methods Programs Biomed. 1991;34:241–253. doi: 10.1016/0169-2607(91)90107-5. [DOI] [PubMed] [Google Scholar]
- 33.Cobelli C, Federspil G, Pacini G, Salvan A, Scandellari C. An integrated mathematical model of the dynamics of blood glucose and its hormonal control. Math Biosci. 1982;58:27–60. [Google Scholar]
- 34.Sturis J, Polonsky KS, Mosekilde E, Van Cauter E. Computer model for mechanisms underlying ultradian oscillations of insulin and glucose. Am J Physiol. 1991;260:E801–E809. doi: 10.1152/ajpendo.1991.260.5.E801. [DOI] [PubMed] [Google Scholar]
- 35.Cobelli C, Bier DM, Ferrannini E. Modeling glucose metabolism in man: theory and practice. Horm Metab Res Suppl. 1990;24:1–10. [PubMed] [Google Scholar]
- 36.Dalla Man C, Caumo A, Cobelli C. The oral glucose minimal model: estimation of insulin sensitivity from a meal test. IEEE Trans Biomed Eng. 2002;49:419–429. doi: 10.1109/10.995680. [DOI] [PubMed] [Google Scholar]
- 37.Toffolo G, Cobelli C. The hot IVGTT two-compartment minimal model: an improved version. Am J Physiol Endocrinol Metab. 2003;284:E317–E321. doi: 10.1152/ajpendo.00499.2001. [DOI] [PubMed] [Google Scholar]
- 38.Zhang B, Saku K, Arakawa K. Quantification of the effects of troglitazone on insulin sensitivity and beta-cell function in Watanabe heritable hyperlipidemic rabbits: a minimal model analysis. Metabolism. 1997;46:273–281. doi: 10.1016/s0026-0495(97)90253-5. [DOI] [PubMed] [Google Scholar]
- 39.Jusko WJ. Receptor-mediated pharmacodynamics of corticosteroids. Prog Clin Biol Res. 1994;387:261–270. [PubMed] [Google Scholar]